正等轴测图画法练习
轴测图--正等轴测图的画法【共14张】

斜铁块三视图
二.例题演示:斜铁块的正等测画法
1.分析形体定原点
由视图可知该形体为长方体被垂直V面 的截面所截而成。
将形体的右后下方的点作为坐标原点 主视图的原点O和坐标轴OX、OZ如图示 俯视图的原点和坐标轴OX、OY如图示
回顾:主视图反应左右和上下的方位 俯视图反应左右和前后的方位
三.练习正:等画测正六棱柱的正等测 练习:画正六棱柱的正等轴测图
重点:正等轴测图的作图步骤和思路 难点:合理选取坐标原点
1、习题册P22 第一题。 2、预习斜二测。
轴测图--正等轴测图的画法
1、轴测图与三视图的异同
三视图 三面投影
每个视图 反应两个尺寸
度量性好 立体感差
轴测图 单面投影 反应三个尺寸
度量性差 立体感强
2、轴测投影的基本性质
平行性和度量性
3、正等轴测轴的画法
轴间角120°,轴向伸缩系数0.82,简化为 1
根据正投影画正等轴测图
一.讲解正等测的画图步骤、思路
任
务
二.例题演示:斜铁块的正等测画法
分
解
三.练习:画正六棱柱的正等测图
一.讲解正等测的画图步骤、思路
{ 1.分析形体定原点 在正投影图上确定
坐标原点O 坐标轴OX、OY、OZ
2.画正等轴测轴
3.画各顶点或端点的轴测投影
4.连接相关点,完成轴测图。
依据:平行性和度量性
1 二.例题演示:斜铁块的正等测画法
二.例题演示:斜铁块的正等测画法
2.画正等轴测轴
O1Z1竖直方向, O1X1、O1Y1与O1Z1两为0.82, 简化为1.
回顾
二.例题演示:斜铁块的正等测画法 3.画各顶点或端点的轴测投影
任务2 绘制圆柱的正等轴测图

步骤与画法
图例
步骤与画法
图例
1.选取圆心为坐标 原点作坐标轴,在俯视图 中作圆的外切正方形
3. 连接 1D1、1C1、2A1、 2B1,交菱形对角线与 3、 4,则 1、2、3、4 即为四 段圆弧的圆心
2.作轴测轴,再按圆 的外切正方形画出菱形
4,如图(b)所示。
(2)过切点1、2分别作相应棱线的垂线,
得交点O1,过切点3、4分别作相应棱线的垂线,
得交点O2,如图(c)所示。 (3)以O1为圆心,O11为半径作圆弧,以O2
(c)
(d)
为圆心,O23为半径作圆弧,得平板上底面两圆
角的轴测图。将圆心O1、O2下移平板厚度,再
用与上底面圆弧相同的半径分别作两圆弧,得
平板下底面圆角的轴测图,如图(d)所示。
(4)在平板右端作上、下小圆弧的公切线,
描深可见部分轮廓线,完成圆角平板的正等轴
(e)
测图,如图(e)所示。
3.作支座的正等轴测图 如图(a)所示的支座,由两部分组成,底板为带有圆孔的圆角平板,立板
为带有圆孔的半圆头板。
作图步骤: (1)画出圆角平板的轴测图,如图(b)所示。 (2)画出底板两侧的圆孔及立板顶部的圆弧,定下角点A、B、C、D并作圆
(a)
(b)
知识链接
一、圆的正等测投影
在平面立体的正等轴测图中,平行于坐标面的正方形变成了菱形,如果在 正方形内有一个圆与其相切,显然圆随正方形的四条边变成了内切于菱形的 椭圆。
二、圆的正等测画法
由上面分析知,平行于坐标面的圆的正等轴测图都是椭圆,虽然椭圆的方 向不同,但画法相同。各椭圆的长轴都在外切菱形的长对角线上,短轴在短 对角线上。
绘图正等轴测图的画法

正等轴测图的分类
正等轴测图可以分为正等侧轴测 图和正等俯轴测图两种类型。
正等侧轴测图是从物体的左侧投 影,而正等俯轴测图是从物体的
顶部投影。
在实际应用中,根据需要选择不 同类型的正等轴测图来表示物体。
02
正等轴测图的绘制方法
坐标系的建立
确定原点
选择一个基准点作为原点,通常 将原点设置在图形中心或任意方
THANKS
感谢观看
添加尺寸标注
标注长度
根据需要标注图形各部分的长度,利用坐标值和单位 长度计算标注值。
标注角度
标注图形各部分之间的角度,利用坐标值和单位长度 计算标注值。
标注高度
标注立体图形的高度,利用坐标值和单位长度计算标 注值。
03
正等轴测图的绘制技巧
选择合适的视图角度
确定合适的角度
选择一个能够清晰展示物体特征的视角,使物体在正等轴测图中 呈现最佳的立体效果。
04
常见错误及纠正方法
尺寸标注不准确
总结词
在绘制正等轴测图时,尺寸标注的准确性至关重要,因为错误的尺寸会导致图 纸的误导。
详细描述
在进行尺寸标注时,要确保使用正确的测量工具,并仔细检查每个尺寸,确保 它们与实际物体或设计相符。如果发现尺寸标注错误,应及时更正,并重新测 量和标注。
投影关系不正确
绘制复杂立体图形
总结词:运用技巧
详细描述:复杂立体图形在正等轴测图中需要更高的技巧。在绘制过程中,需要 灵活运用各种绘图技巧,如旋转、缩放、镜像等,以准确表达立体图形的形状和 结构。同时,需要注意轴测投影的特性,确保图形符合视觉习惯。
绘制组合体正等轴测图
总结词:综合运用
详细描述:组合体是由多个简单立体图形组合而成的复杂物体。在绘制组合体的正等轴测图时,需要综合运用前面学到的各 种技巧和方法,根据组合体的结构特点选择合适的表达方式。同时,需要注意各部分之间的相对位置和连接关系,确保整体 效果协调一致。
正等轴测图
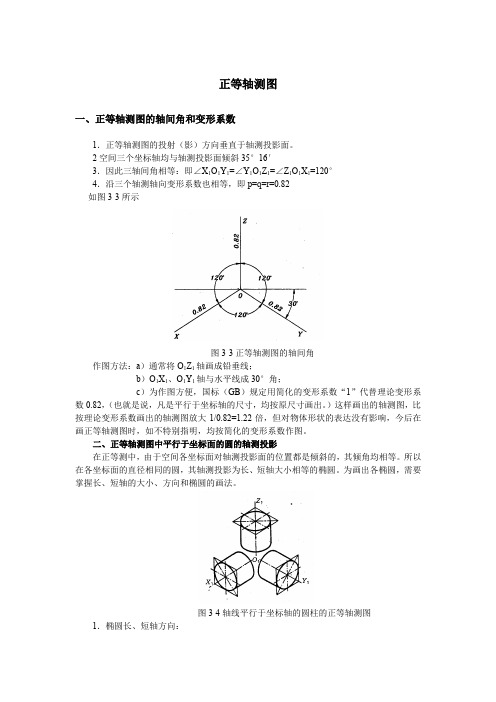
正等轴测图一、正等轴测图的轴间角和变形系数1.正等轴测图的投射(影)方向垂直于轴测投影面。
2空间三个坐标轴均与轴测投影面倾斜35°16′3.因此三轴间角相等:即∠X1O1Y1=∠Y1O1Z1=∠Z1O1X1=120°4.沿三个轴测轴向变形系数也相等,即p=q=r=0.82如图3-3所示图3-3正等轴测图的轴间角作图方法:a)通常将O1Z1轴画成铅垂线;b)O1X1、O1Y1轴与水平线成30°角;c)为作图方便,国标(GB)规定用简化的变形系数“1”代替理论变形系数0.82,(也就是说,凡是平行于坐标轴的尺寸,均按原尺寸画出。
)这样画出的轴测图,比按理论变形系数画出的轴测图放大1/0.82=1.22倍,但对物体形状的表达没有影响,今后在画正等轴测图时,如不特别指明,均按简化的变形系数作图。
二、正等轴测图中平行于坐标面的圆的轴测投影在正等测中,由于空间各坐标面对轴测投影面的位置都是倾斜的,其倾角均相等。
所以在各坐标面的直径相同的圆,其轴测投影为长、短轴大小相等的椭圆。
为画出各椭圆,需要掌握长、短轴的大小、方向和椭圆的画法。
图3-4轴线平行于坐标轴的圆柱的正等轴测图1.椭圆长、短轴方向:平行于X1O1Y1坐标面的圆(水平圆)等测为水平椭圆长轴⊥O1Z1轴短轴∥O1Z1轴平行于X1O1Z1坐标面的圆(水平圆)等测为水平椭圆长轴⊥O1Y1轴短轴∥O1Y1轴平行于Y1O1Z1坐标面的圆(水平圆)等测为水平椭圆长轴⊥O1X1轴短轴O1X1轴综上所述:椭圆的长轴⊥与圆所平行的坐标面垂直的那个轴,短轴则平行与该轴测轴。
例如:水平圆的正等测水平椭圆,长轴垂直于圆所平行的水平面垂直的轴测轴Z1轴,短轴则∥Z1轴。
图3-5平行于坐标面的圆的正等轴测图图3-6 2.椭圆长、短轴的大小长轴:是圆内平行于轴测投影面的直径的轴测投影。
因此:(1)在采用变形系数0.82作图时,椭圆长轴大小为d,短轴大小为0.58d。
任务五 绘制正等轴测图[13页]
![任务五 绘制正等轴测图[13页]](https://img.taocdn.com/s3/m/af65521071fe910ef12df8a5.png)
测图称为斜用轴正测投图影。法得到的轴测图称为正等 轴测图,简称
正等测。
当三个坐标轴与轴测投影面倾斜的角度相同时,用正投影法得
到的轴测图称为正等轴测图,简称正等测。
任务五 绘制正等轴测图
实例分析
2.正等轴测图的行程及参数
(1)轴测轴:直角坐标轴 OX、OY、 OZ在轴测投影面上的投影O1X1、 O1Y1、O1Z1称为轴测投影轴,简称 轴测轴。
任务五 绘制正等轴测图
实例分析
2.回转体的正等轴测图画法
平行于坐标面 的正等轴测图为椭 圆。做圆的正等轴 测图时,应弄清椭 圆的长、短轴方向。
四心圆法的作 图步骤如下图所示。
任务五 绘制正等轴测图
实例分析 2.回转体的正等轴测图画法 三种位置平面圆及圆柱的正等轴测图。
任务五 绘制正等轴测图
实例分析
2.回转体的正等轴测图画法 用四心回圆转法体绘的制正圆等柱轴的测图正画等法轴测图。
任务五 绘制正等轴测图
任务实施
已知形体 的两面视图如 右图(a)所示, 绘制该形体的 正等轴测图(尺 寸从三视图中 量取)。具体步 骤如右图所示。
任务五 绘制正等轴测图
知识拓展
一、 斜二轴测图
1.斜二轴测图的形成 当物体上的两个坐标轴 OX、OZ与轴测投影面平行, 而投射方向与轴测投影面倾斜 时,所得的轴测图称为斜二轴 测图,如右图所示。
(2)轴间角:轴测轴之间的夹角称 为轴间角。
(3)轴向伸缩系数:在空间三坐标 轴上,分别取长度 OA、 OB、 OC, 它们的轴测投影长度为O1A1、O1B1、 O1C 1 ,令p1=O1A1/OA,q1=O1B1/OB, r1=O1C1/OC,则p1、q1、r1分别称为 OX、OY、 OZ轴的轴向伸缩系数。
正等轴测图的画法
一、学习目标:
1、会画正六棱柱的正等轴测图 2、会画圆柱的正等轴测图 3、会画螺钉毛坯的正等轴测图
二、重、难点:
1、重点:基本体的正等轴测图 2、难点:圆柱的正等轴测图
目标1 目标2 目标3
正等轴测图的画法的基本知识
1、轴间角:三个均为120° 2、轴向变形系数:p= q = r ≈0.82 3、简化轴向变形系数:p= q = r ≈1
思考? 结论:放大1/0.82
Z1 ——
简化以后是放大了还是缩 ——1.22倍 小了?
120°
X1
120°
Y1
120°
平面体的正等轴测图画法
例1: 正六棱柱的正等轴测图的画法
z
Z1
x
O1
X1
y
Y1
平面体的正等轴测图画法
例1: 正六棱柱的正等轴测图的画法
z
Z
x
O1
X
y
Y
平面体的正等轴测图画法
例1: 正六棱柱的正等轴测图的画法
z
x
y
返回目标
曲面体的正等轴测图画法
z1
x
x1 y1
y
ห้องสมุดไป่ตู้
四心法近似画法 (辅助圆求八点)
曲面体的正等轴测图画法
例题2:圆柱的正等轴测图的画法
Z Z1
X
X
X1 Y
Y1
曲面体的正等轴测图画法
例题2:圆柱的正等轴测图的画法
Z
X
X
Y
返回目标
练习
返回目标
小结:
1、正等轴测图的轴间角
2、正等轴测图的轴向变形系数
3、正等轴测图的的画法
作业:
习题集59页
正等轴测图
(1)画圆
基本图形的画法
“正等测圆”的画法 类似,只是把画“正 方形”改为画“菱形” 而已
(2)画圆柱体
①画两个正等测圆
②用两条平行线连接两个正 等测圆
(3)画立方体
①画正等测正方形(两条虚线)
②确定立方体的高,画四角 垂线(内侧垂线为虚线)
③画一个平行于底面的正等 测正方形
(4)画锥体
①画两条与水平面成30°角的射 线
正等轴测图
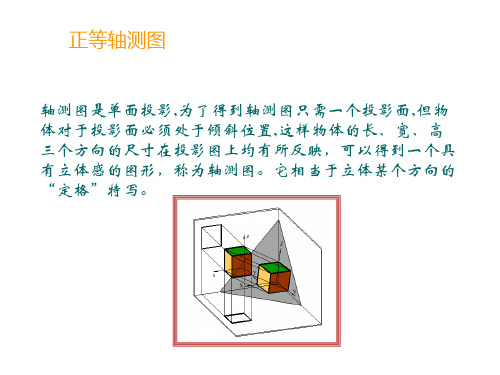
轴测图是单面投影,为了得到轴测图只需一个投影面,但物 体对于投影面必须处于倾斜位置,这样物体的长、宽、高 三个方向的尺寸在投影图上均有所反映,可以得到一个具 有立体感的图形,称为轴测图。它相当于立体某个方向的 “定格”特写。
轴测图示例
投影图无立体感,度量性好; 轴测图立体感强,度量性差。
正等轴测图
• 正等轴测图是一种表现物体三维结构的 图,、Y、Z三维,与数学的坐标系一致!
Z
13200度度
120度 30度
X
Y
Z
X
Y
Z
X
Y
画法小结
1、画出三维; 2、继续画出长80mm,宽50mm,高40mm 的长方体的正等轴测图; 3、画出长方体削去两刀的绘制,最后剩余的 部分用铅笔把轮廓线加深、加粗凸显出来;
②画一条垂线
③连接线(内侧为虚线)
轴测图练习题

练习1:画出三面投影,然后画出纵向和横向两个方向的剖 视图。
练习1:画出三面投影,然后画出横向的剖视图。
有3个住店,要30块钱。但是老板说优惠5 块钱让服务员给那3个人,但是服务员自己 咪了2块钱,给那3个人一人一块钱。问题3 个人一个人是9块钱,3个是27块加上服务 员的2块是29块,那一块钱去哪了!
圆 • 心,3A为半径作圆弧;以4点为圆心, 4C为半径作圆弧,四段圆弧相切连接, • 擦掉多余的弧线,加粗图线,作图完成,如图4-9d所示。
(a)
(b)
(c)
图4-9 作水平圆的正等测图
(d)
一、曲面体正等测图画法
【例4-7】如图4-10(a)所示,已知组合柱的两面 投影,作正等测图。
二 曲面体正等测图的画法
【练习题2】已知组合柱的两面投影,利用切割法作 正等测图。
第二节 斜二测图的画法
一 平面体斜二测图的画法
【练习题3】已知组合柱的两面投影,利用特征面法 做斜二测图(以V面投影为特征面)。
2.如果你有无穷多的水,一个3公升的提桶,一个 5公升的提桶,两只提捅形状上下都不均匀,问 你如何才能准确称出4公升的水?
第一步:5公升的桶装5公升的水倒3公升水放 到3公升的桶里面,剩下2公升的水 第二步:把剩下的2公升水倒到3公升的空桶里 面,此时就剩下1公升的容量 第三步: 把5公升的桶装满,倒1公升水往3公 升的桶里面 第四步:此时5-1=4.
练习题5:斜二测图的应用
根据下图的房间的布局,画出采暖系统施工图( 斜二测图)。要求:每个房间布置1个采暖设备,楼道 视长度布置1-3个采暖设备,所有采暖设备均布置在屋 内窗台下。管道用实线表示,矩形方块表示散热器。 回水管用虚线表示。管道全部靠墙布置。注意图上的 标高、楼板位置、水流方向、管径变化。
正等轴测图

2、分别过X、Y轴20 处点分别作Y、X轴平 行线,作出立方体底 面。
3、分别过立方体底 面各顶点作Z轴平行 线高度都为30。连接 各顶点作出立方体。 4、擦除轴线及不看 见轮廓线,加深立方 体可见轮廓线。
宽
ห้องสมุดไป่ตู้
注意:在X、Y、Z轴上各产生 0.82的变形量,但在实际绘图 中,其变形量通常规定为1, 即不产生变形。
一 设计表现图
4、正等轴测图
平面结构形体的 正等轴测图的绘制
Z
正等轴测图轴线画法
X
120° O 120°
Z Z
120° 120°
绘制步骤:
120°
Y
1、利用角尺A作水平辅助线 段。 2、角尺A不动,利用角尺B作 水平线段垂线Z轴交于O。
( 30° X X
O O 120°
120°
3、角尺A、B水平上移,利用 角尺A(30°)斜边从O点引 出X轴。
120
120
X
X
正等轴测图绘制方法 叠加法
Z
O X Y
园的正等轴测图
园的正等轴测图
Y Y
4、使用方法3作出Y轴。 5、擦除辅助线段;绘制箭头; 进行轴线标注。
正等轴测图绘制方法一
坐标法(例:作20×20×30立方体) 绘制步骤: Z 1、作正等轴测轴,
高 30 长 20 X 20 30 20 O 20 Y
根据形体尺寸在X轴 上画其长;在Y轴上 注意三角尺 画其宽;在Z轴上画 其高。 的配合运用
第三视图 正等轴测图的画法

第三视图和正等轴测图的画法第三视角投影在欧美、日本及港台等地区的教学、设计、生产和商贸中被广泛使用。
近年来,随着与国际社会交流合作的不断深入,第三视角投影在我国的应用日渐广泛。
例如我们毕业生前往就业的外资企业(鸿准、富士康、台积电等)以及对外做出口订单的国内企业大多采用第三视角。
而我们对该方法的学习了解相对匮乏。
本文将结合范例对第三视角的投影和作图规则进行介绍及归纳总结,作为对机械制图知识的补充,以便大家查阅和更为深入的研究。
⑴认识第三视角的空间由来水平投影面H和正立投影面V将三维空间分割为如下第一组图的四部分,可以构成四组投影体系。
如图可以分辨出第三视角投影面位置。
⑵投影面及展开如果将第三视角的两个H和V平面取出,再辅助一个侧立投影平面P,那么就构成了第三角投影体系。
在这个体系中,物体位于三个平面包裹着的内部。
所以,投影平面总是在人和物体之间。
三个投影面得到投影后可以旋转到与V共面的位置。
下面是一个实例的投影三视图,观察方向分别是:下面是它的展开视图:在主视图中反应的是长和高,右视图中反应的是高和宽,俯视图中反应的是长和宽。
⑶投影规律分析第三视角三视图的仍然符合主和俯视图长对正,主和右视图高平齐,俯和右视图宽相等的“三等”投影规律。
⑷正等轴测图的画法第三视角正等轴测图的轴间角为120度,轴向变形系数都是按照1来近似绘制。
其正等轴测图符合轴测投影规律即:一、实物中与投影轴平行的轮廓线,在轴测图中仍与轴测轴平行;二、实物中相互平行的轮廓线,在轴测图中仍相互平行。
绘制过程中要按轴向1:1进行测量进行。
椭圆和圆角的画法与第一视角的画法并无区别。
总结:第三视角三视图和正等轴测图和第一视角的三视图和正等轴测图在画法操作上并没有多少本质的区别。
但是在看图方向和投影方向是不一样的。
第一视角是人(观察者)->物体->投影平面;而第三视角是人(观察者)->投影平面-> 物体。
在绘制正等轴测图中强调显示的是前视、顶视和右视三个表面。
正等测轴测图的画法2
(2) 画出正等测轴测轴
(3) 从三视图上直接量取与坐标轴平行的 线段画到相应的轴测轴的对应位置,从而 画出物体的轴测图
(一) 平面立体正等测轴测图的画法
(二) 曲面立体正等测轴测图的画法
1、平行H面的圆的画法:四心圆法 Z
o4
o2
o5
o3
2. 圆柱体的正等测图的画法
S
Y
二、 轴间角和轴向伸缩系数
投影线方向 轴向伸缩系数 投影线与轴测投影面垂直 p1=q1=r1=0.82
特
简化轴向伸缩系数
p=q=r=1
Z1 性
轴间角
120°O
1
120°
X1
120°
Y1
边长为L的正 方形的轴测图
按简化轴向伸缩系数绘制
按实际轴向伸缩系数绘制
0.82L
L
三、正等测轴测图的基本作图方法
3、 轴测投影的基本性质
(1)物体上相互平行的线段的轴测投影仍相互平行;
(2)物体上平行于坐标轴的直线段的轴测投影仍与相应 的轴测轴平行;
(3)物体上原来平行于坐标轴的线段,在轴测图中可以 按其原来的尺寸乘以轴向伸缩系数后,再沿着相应的轴测 轴定出其投影的长短。
凡是与坐标轴平行的直线,就可以在轴测图 上沿轴向进行度量和作图。
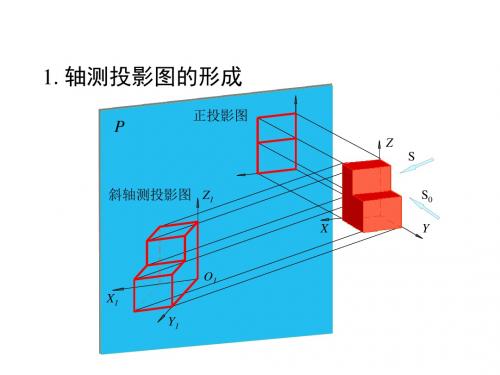
1. 轴测投影图的形成
P
正投影图
Z S
斜轴测投影图 Z1
X
O
S0 Y
O1 X1 Y1
2、三视图与轴测图的比较
三视图可以较完整地确切地表达出零件各部分的形状,且作图方便,但 这种图样直观性差; 轴测图能同时反映形体长、宽、高三个方向的形状,具有立体感强,形 象直观的优点,但不能确切地表达零件原来的形状与大小.且作图较复杂, 因而轴测图在工程上一般仅用作辅助图样。
