二次函数压轴题最短路径问题
二次函数压轴(最短路径).docx

26. (12分)(2015*天水)在平面直角坐标系屮,已知y= - 2x?+bx+c (b、c为常数)的顶2点为P,等腰直角三角形ABC的顶点A的坐标为((),・1),点C的坐标为(4, 3),直角顶点B在第四象限.(1)如图,若抛物线经过A、B两点,求抛物线的解析式.(2)平移(1)中的抛物线,使顶点P在直线AC±并沿AC方向滑动距离为返时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.(3)在(2)的情况卜,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q, 取BC的屮点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.考点:二次函数综合题.分析:(1)先求出点B的处标,然后利用待定系数法求出抛物线的函数表达式;(2)如答题图2,设顶点P在直线AC±并沿AC方向滑动距离迈吋,到达P',作P,M lly轴,PMIIx轴,交于M点,根据白线AC的斜率求得AP' PM是等腰直角三角形,进而求得抛物线向上平移1个单位,向右平移1个单位,从而求得平移后的解析式,进而求得为x轴的交点,与直线AC的交点,即可证得结论;(3)如答图3所示,作点B关于直线AC的对称点B',由分析可知,当B,、Q、F (AB 屮点)三点共线时,NP+BQ最小,最小值为线段B‘ F的长度.解答:解:(1)丁等腰直角三角形ABC的顶点A的处标为(0, - 1), C的坐标为(4, 3)二点B的坐标为(4, - 1).•••抛物线过A (0,・1), B (4,・1)两点,「c二 _]-2><16+4b+c二-1 'I 2解得:b=2, c= - 1,•••抛物线的函数表达式为:y=・-X2+2X - 1.2(2)如答题图2,设顶点P在直线AC ±并沿AC方向滑动距离返时,到达P',作P,Mlly轴,PMIIx轴,交于M点,•.•点A的坐标为(0, - 1),点C的坐标为(4, 3),・•・直线AC的解析式为y=x- 1,丁直线的斜率为1,PM是等腰直角三角形,•••PP' =V2,.-.P/ M=PM=1,.•.抛物线向上平移1个单位,向右平移1个单位,T+2X-1=4(X-2)2+B•••平移后的抛物线的解析式为y=-^ (x-3) ?+2,令y=0, 则F("2+2,解得X[ = l, X=52,•••平移后的抛物线与x轴的交点为(1, 0), (5, 0), 丨尸一1&-3)2+2 (x=i ( x=3解{ 2 ,得』或][尸x-l 1尸°1应二平移后的抛物线与AC的交点为(1, 0),•••平移后的抛物线与直线AC交于x轴上的同一点(1, 0).(3)如答图3,取点B关于AC的对称点B',易得点B'的坐标为(0, 3), BQ=B, Q, 取AB中点F, 连接QF, FN, QB',易得FNIIPQ,且FN二PQ,•••四边形PQFN为平行四边形./.NP=FQ.••.NP+BQ二FQ+B,Q>FB^ =^22+42=2Vl-.•.当B'、Q、F三点共线时,NP+BQ最小,最小值为2馅.点评:本题为二次函数中考压轴题,考查了二次函数的图彖与性质、待定系数法、一次函数、儿何变换(平移,对称)、等腰直角三角形、平行四边形、轴対称-最短路线问题等知识点,考查了存在型问题和分类讨论的数学思想,试题难度较大.28. (12分)(2015*西宁)如图,在平面直角坐标系xOy屮,以M为顶点的抛物线与x轴分别相交于B, C两点,抛物线上一点A的横处标为2,连接AB, AC,正方形DEFG的一边GF在线段BC上,点D, E在线段AB, AC ±, AK丄x轴于点K,交DE于点H,下表给出了这条抛物线X• • •-204810• • •y r0595P• • •(1)求出这条抛物线的解析式;(2)求正方形DEFG的边长;(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP 的周长最小?若存在,请求出P, Q两点的处标;若不存在,请说明理由.考点:二次函数综合题.分析:(1)利用已知表格中数据结合顶点式直接求出抛物线解析式即可;(2)百先得出四边形HEFK为矩形,再利用△ADE S/X ABC,得出正方形DEFG的边长;(3)首先求岀AB所在直线解析式,进而得出D点坐标,再求出直线A' D'的解析式得出Q'的坐标即可.解答:解:(1)由图表可得:抛物线的顶点坐标为:(4, 9),设函数解析式为:y=a (x - 4) 2+9 (a*0),把点(0, 5)代入尸a (x-4) 2+9,解得:a=-X4・••函数解析式为:y=--i (x-4) 2+9;(2)设正方形DEFG的边长为m,VAK±x$fll,・•・ ZAKC=90°,J ZDEF=ZEFG=90°,・・・四边形HEFK为矩形,.e.HK=EF=m,•・•点A在抛物线尸・* (x・4) ?+9上,横坐标为2,y= - — (x - 4) 2+9=8,4・••点A的坐标为:(2, 8),・•・AK=8,・•・AH=AK・HK=8・m,由题意可得:B ( - 2, 0), C (10, 0),・・・BC=12,•・・DE〃BC,A AADE^AABC,・AH_ DE••---- — -- 9AK BC•in•• ----- —-- 98 12…m=-——・・・正方形的边长为:単5(3)存在,理由:过顶点M作抛物线的对称轴直线1: x=4,设点A关于直线1: x=4对称点为A' , A'点的坐标为:(6, 8), ・•・设AB所在直线解析式为:y=kx+b,.(8=2k+b••(0=_2k+b,解得•・产◎[b二4・・・AB所在肓线解析式为:y=2x+4,•・・D在直线AB上,DG=—,5・・・点D的纵坐标为:単,5由2x+4=—,5解得:x=2,5・••点D的坐标为:G,竽),5 5设点D关于x轴对称点为D',则D'(辛,-单),5 5连接A' D z交对称轴于点P,交x轴于点Q,连接AP, DQ, 则四边形ADQP的周长最小,设总线A' D'的解析式为:尸k' x+b',[6k, +b,二8•••舍出二-学15 5K 7 解得:心・・・直线A' D f的解析式为:尸学X-卑,7 7当x=4 时,y=—x4 -—,・・・P (4, —),7 7 7 7当y=0 时,x=-,2・・・Q点坐标为:(号,0).。
二次函数典型例题——最短路径

二次函数典型例题——最短路径1、已知抛物线2:(1)1C y x m x =-++的顶点在坐标轴...上. (1)求m 的值;(2)0>m 时,抛物线C 向下平移n (n > 0)个单位后与抛物线C 1:c bx ax y ++=2关于y 轴对称,且1C 过点(n ,3),求C 1的函数关系式; (3)03<<-m 时,抛物线C 的顶点为M ,且过点P (1,y 0)问在直线1-=x 上是否存在一点Q 使得△QPM 的周长最小,如果存在,求出点Q 的坐标, 如果不存在,请说明理由.(1)m 的值=1,-1,-3;(2)C 1的函数关系式:22y x x =+;(3)Q 的坐标4(1,)3-.2、在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B .⑴直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3)已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值. 解:(1)21(2)4A n n +,,()B n n ,. (2) d =AB =A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+∴ 当14n =时,d 取得最小值18.当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB =PM . (如图10)(3) ∵ 对一切实数x 恒有 x ≤y ≤2124x +, ∴ 对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ① 图10xy111APBMO3、已知关于x 的一元二次方程()0312=-+--m x m x .(1)求证:不论m 取何值时,方程总有两个不相等的实数根.(2)若直线()31+-=x m y 与函数m x y +=2的图象1C 的一个交点的横坐标为2,求关于x 的一元二次方程()0312=-+--m x m x 的解.(3)在(2)的条件下,将抛物线()312-+--=m x m x y 绕原点旋转︒180,得到图象2C ,点P 为x 轴上的一个动点,过点P 作x 轴的垂线,分别与图象1C 、2C 交于N M 、两点,当线段MN 的长度最小时,求点P 的坐标.解:(1)证明:()[]()3412----=∆m m124122+-+-=m m m 1362+-=m m()432+-=m∵不论m 取何值时,()032≥-m ∴()0432>+-m ,即0>∆∴不论m 取何值时,方程总有两个不相等的实数根. (2)将2=x 代入方程()0312=-+--m x m x ,得3=m再将3=m 代入,原方程化为022=-x x , 解得2,021==x x . (3)将3=m 代入得抛物线:x x y 22-=,将抛物线x x y 22-=绕原点旋转︒180得到的图象2C 的解析式为:x x y 22--=.设()0,x P则()3,2+x x M ,()x x x N 2,2--()()25212322232222+⎪⎭⎫ ⎝⎛+=++=---+=x x x x x x MN∴当21-=x 时,MN 的长度最小,此时点P 的坐标为⎪⎭⎫⎝⎛-0,21(昌平)27.已知抛物线2y ax bx c =++经过原点O 及点A (-4,0)和点B (-6,3). (1)求抛物线的解析式以及顶点坐标;(2)如图1,将直线2y x =沿y 轴向下平移后与(1)中所求抛物线只有一个交点C ,平移后的直线与y 轴交于点D ,求直线CD 的解析式;(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD 距离最短的点的坐标及该最短距离.yx图1BACD O yx图2CD O解:(1)∵ 抛物线经过()0,0,()4,0- ,()6,3-三点,∴ 01640,366 3.c a b a b =⎧⎪-=⎨⎪-=⎩ ………………………………………… 1分解得 1410a b c ⎧=⎪⎪=⎨⎪=⎪⎩,,. …………………………… 2分∴ 抛物线的解析式为214y x x =+.∵()()22211144421444y x x x x x =+=++-=+-∴抛物线的顶点坐标为()2,1-- ……………3分 (2)设直线CD 的解析式为2y x m =+,根据题意,得2124x x x m +=+, …………… 4分 化简整理,得2440x x m --=,由16160m ∆=+=,解得1m =-, ……………… 5分∴直线CD 的解析式为21y x =- .(3)点的坐标为()2,7, …………………………… 6分. ……………………… 7分。
次函数之距离最小

二次函数之最短路径问题例1.(广东)已知二次函数y=x 2-2mx+m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC+PD 最短若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.例2.(甘肃兰州)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线y =23x 2+bx +c 经过点B ,且顶点在直线x =52上.(1)求抛物线对应的函数关系式;(2)若把△ABO 沿x 轴向右平移得到△DCE ,点A 、B 、O 的对应点分别是D 、C 、E ,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD ,已知对称轴上存在一点P 使得△PBD 的周长最小,求出P 点的坐标;例3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例4.(湖南郴州)已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小若存在,请求出点G的坐标;若不存在,请说明理由.例5.(辽宁)如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点.(1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标;(2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由; (3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.例6.(山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x 2+2x+3与x 轴交于A 、B 两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求直线AC 的解析式及B 、D 两点的坐标;(2)点P 是x 轴上一个动点,过P 作直线l ∥AC 交抛物线于点Q ,试探究:随着P 点的运动,在抛物线上是否存在点Q ,使以点A 、P 、Q 、C 为顶点的四边形是平行四边形若存在,请直接写出符合条件的点Q 的坐标;若不存在,请说明理由.(3)请在直线AC 上找一点M ,使△BDM 的周长最小,求出M 点的坐标.A O xyBFCA O xyBFC例7.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P 是∠AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使∠CPN=90°若存在,请直接写出点P的坐标.例8.(德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.练习:(烟台)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.例10.已知抛物线y=ax2+bx+1经过点A(1,3)和点B(2,1)。
常考二次函数综合题整理(全)

常考二次函数综合题整理 题型一最短路径问题1、如图,抛物线y=﹣12x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,并证明你的结论;(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.【变式】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;题型二最大面积(线段最长)问题2、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?并求出这个最大值.3、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH△x轴于点H,与BC交于点M,连接PC,求线段PM的最大值.【变式】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,过点P作PE△y轴于点E,连接AE.求△PAE面积S的最大值;题型三 存在点构成等腰三角形问题4、如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.5、如图,已知二次函数y=ax 2+bx+3的图象交x 轴于点A (1,0),B (3,0),交y 轴于点C .(1)求这个二次函数的表达式;(2)直线x=m 分别交直线BC 和抛物线于点M ,N ,当△BMN 是等腰三角形时,直接写出m 的值.【变式】已知二次函数y=ax 2+bx ﹣3a 经过点A (﹣1,0)、C (0,3),与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 、DB ,求证:△BCD 是直角三角形;(3)在对称轴右侧的抛物线上是否存在点P ,使得△PDC 为等腰三角形?若存在,求出符合条件的点P 的坐标;若不存在,请说明理由.【变式】如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点()0,2C -,点A 的坐标是()2,0,P 为抛物线上的一个动点,过点P 作PD x ⊥轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线1x =-.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且14PE OD =,求PBE ∆的面积. (3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的下方,是否存在点M ,使BDM ∆是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.题型四 存在点构成直角三角形问题6、如图,抛物线2y ax bx 4=+-经过()A 3,0-,()B 5,4-两点,与y 轴交于点C ,连接AB ,AC ,BC .()1求抛物线的表达式;()2求证:AB 平分CAO ∠;()3抛物线的对称轴上是否存在点M ,使得ABM V 是以AB 为直角边的直角三角形,若存在,求出点M 的坐标;若不存在,请说明理由.【变式】如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点.(1)求抛物线的解析式和直线AC 的解析式;(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.●题型四存在点构成等腰直角三角形问题7、已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)过点P作x轴的垂线,交线段AB于点D,再过点P做PE△x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.●题型四存在点构成平行四边形问题8、如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.()B-,对称轴为直线l,点M是线段AB的中点.0,5(1)求抛物线的表达式;(2)写出点M的坐标并求直线AB的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.【变式】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).(1)求抛物线的函数解析式,并写出顶点D的坐标;(2)如图,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.9、如图,已知抛物线y=12x2+bx+c与直线AB:y=12x+12相交于点A(1,0)和B(t,52),直线AB交y轴于点C.(1)求抛物线的解析式及其对称轴;(2)设点M是抛物线对称轴上一点,点N在抛物线上,以点A、B、M、N为顶点的四边形是否可能为矩形?若能,请求出点M的坐标,若不能,请说明理由.10、如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B.(1)求抛物线的解析式.(2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标.(3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E.是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由.11、如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.(1)求抛物线解析式;(2)在x轴下方且在抛物线对称轴上,是否存在一点Q,使△BQC=△BAC?若存在,求出Q点坐标;若不存在,说明理由.12、如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.(1)求抛物线的解析式;(2)过点A的直线交直线BC于点M.连接AC,当直线AM与直线BC的夹角等于△ACB 的2倍时,请直接写出点M的坐标【变式】如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C 两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.【变式】如图,抛物线y=ax 2+bx+c 经过A (﹣1,0),B (4,0),C (0,3)三点,D 为直线BC 上方抛物线上一动点,DE△BC 于E .(1)求抛物线的函数表达式;(2)如图1,求线段DE 长度的最大值;(3)如图2,设AB 的中点为F ,连接CD ,CF ,是否存在点D ,使得△CDE 中有一个角与△CFO 相等?若存在,求点D 的横坐标;若不存在,请说明理由.【变式】如图,已知顶点为(0,3)C -的抛物线2(0)y ax b a =+≠与x 轴交于A ,B 两点,直线y x m =+过顶点C 和点B .(1)求m 的值;(2)求函数2(0)y ax b a =+≠的解析式;(3)抛物线上是否存在点M ,使得15MCB ∠=︒?若存在,求出点M 的坐标;若不存在,请说明理由.题型七 存在点使三角形相似问题13、如图,以D 为顶点的抛物线y=﹣x 2+bx+c 交x 轴于A 、B 两点,交y 轴于点C ,直线BC 的表达式为y=﹣x+3.(1)求抛物线的表达式;(2)在x 轴上是否存在一点Q ,使得以A 、C 、Q 为顶点的三角形与△BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.14、如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣12x﹣1交于点C.(1)求抛物线解析式及对称轴;(2)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.【变式】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(32,0),且与y轴相交于点C.(1)求这条抛物线的表达式;(2)求△ACB的度数;(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE△AC,当△DCE 与△AOC相似时,求点D的坐标.【变式】如图,抛物线y=12x2+bx+c与直线y=12x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).(1)求抛物线的解析式;(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ△PA交y轴于点Q,问:是否存在点P 使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.题型七二次函数与圆结合问题15、如图,△E的圆心E(3,0),半径为5,△E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.(1)求抛物线的解析式;(2)判断直线l与△E的位置关系,并说明理由;(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.16、如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣x+与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).(1)求抛物线m的解析式;(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.【变式】在平面直角坐标系中,二次函数y=ax2+53x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣13x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.【变式】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B (点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP△x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.。
备战2024年中考数学压轴题之二次函数篇(全国通用)二次函数-主从联动(瓜豆原理)求最小值(学生版)

第十四讲二次函数--主从联动(瓜豆原理)求最值必备知识点一、轨迹为线段引例:如图,P 是直线BC 上一动点,连接AP ,取AP 中点Q ,当点P 在BC 上运动时,Q点轨迹是?【分析】当P 点轨迹是直线时,Q 点轨迹也是一条直线.可以这样理解:分别过A 、Q 向BC 作垂线,垂足分别为M 、N ,在运动过程中,因为AP=2AQ ,所以QN 始终为AM 的一半,即Q 点到BC 的距离是定值,故Q点轨迹是一条直线.【引例】如图,△APQ 是等腰直角三角形,∠PAQ=90°且AP=AQ ,当点P 在直线BC 上运动时,求Q点轨迹?知识导航【分析】当AP与AQ夹角固定且AP:AQ为定值的话,P、Q轨迹是同一种图形.当确定轨迹是线段的时候,可以任取两个时刻的Q点的位置,连线即可,比如Q点的起始位置和终点位置,连接即得Q点轨迹线段.【模型总结】必要条件:主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);主动点、从动点到定点的距离之比是定量(AP:AQ是定值).结论:P、Q两点轨迹所在直线的夹角等于∠PAQ(当∠PAQ≤90°时,∠PAQ等于MN与BC夹角)P、Q两点轨迹长度之比等于AP:AQ(由△ABC∽△AMN,可得AP:AQ=BC:MN)二、轨迹为圆引例1:如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.考虑:当点P在圆O上运动时,Q点轨迹是?【分析】观察动图可知点Q轨迹是个圆,而我们还需确定的是此圆与圆O有什么关系?考虑到Q点始终为AP中点,连接AO,取AO中点M,则M点即为Q点轨迹圆圆心,半径MQ是OP一半,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.【小结】确定Q点轨迹圆即确定其圆心与半径,由A、Q、P始终共线可得:A、M、O三点共线,由Q为AP中点可得:AM=1/2AO.Q点轨迹相当于是P点轨迹成比例缩放.根据动点之间的相对位置关系分析圆心的相对位置关系;根据动点之间的数量关系分析轨迹圆半径数量关系.引例2:如图,P是圆O上一个动点,A为定点,连接AP,作AQ⊥AP且AQ=AP.考虑:当点P在圆O上运动时,Q点轨迹是?【分析】Q点轨迹是个圆,可理解为将AP绕点A逆时针旋转90°得AQ,故Q点轨迹与P点轨迹都是圆.接下来确定圆心与半径.考虑AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO;考虑AP=AQ,可得Q点轨迹圆圆心M满足AM=AO,且可得半径MQ=PO.即可确定圆M位置,任意时刻均有△APO≌△AQM.引例3:如图,△APQ是直角三角形,∠PAQ=90°且AP=2AQ,当P在圆O运动时,Q点轨迹是?【分析】考虑AP⊥AQ,可得Q点轨迹圆圆心M满足AM⊥AO;考虑AP:AQ=2:1,可得Q点轨迹圆圆心M满足AO:AM=2:1.即可确定圆M位置,任意时刻均有△APO∽△AQM,且相似比为2.【模型总结】为了便于区分动点P、Q,可称点P为“主动点”,点Q为“从动点”.此类问题的必要条件:两个定量主动点、从动点与定点连线的夹角是定量(∠PAQ是定值);主动点、从动点到定点的距离之比是定量(AP:AQ是定值).【结论】(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠PAQ=∠OAM;(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP:AQ=AO:AM,也等于两圆半径之比.按以上两点即可确定从动点轨迹圆,Q与P的关系相当于旋转+伸缩.古人云:种瓜得瓜,种豆得豆.“种”圆得圆,“种”线得线,谓之“瓜豆原理”.例题演练1.如图①,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C,连接BC,点P是抛物线上一动点.(1)求二次函数的表达式.(2)当点P不与点A、B重合时,作直线AP,交直线BC于点Q,若△ABQ的面积是△BPQ面积的4倍,求点P的横坐标.(3)如图②,当点P在第一象限时,连接AP,交线段BC于点M,以AM为斜边向△ABM外作等腰直角三角形AMN,连接BN,△ABN的面积是否变化?如果不变,请求出△ABN的面积;如果变化,请说明理由.2.如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A、C两点,抛物线y=x2+bx+c 经过A、C两点,与x轴的另一交点为B.(1)求抛物线解析式;(2)若点M为x轴下方抛物线上一动点,当点M运动到某一位置时,△ABM的面积等于△ABC面积的,求此时点M的坐标;(3)如图2,以B为圆心,2为半径的⊙B与x轴交于E、F两点(F在E右侧),若P点是⊙B 上一动点,连接PA,以PA为腰作等腰Rt△PAD,使∠PAD=90°(P、A、D三点为逆时针顺序),连接FD.求FD长度的取值范围.3.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2x+c与x轴交于点A(1,0),点B(﹣3,0),与y轴交于点C,连接BC,点P在第二象限的抛物线上,连接PC、PO,线段PO交线段BC于点E.(1)求抛物线的表达式;(2)若△PCE的面积为S1,△OCE的面积为S2,当时,求点P的坐标;(3)已知点C关于抛物线对称轴的对称点为点N,连接BN,点H在x轴上,当∠HCB=∠NBC 时,①求满足条件的所有点H的坐标②当点H在线段AB上时,点Q是平面直角坐标系内一点,保持QH=,连接BQ,将线段BQ绕着点Q顺时针旋转90°,得到线段QM,连接MH,请直接写出线段MH的取值范围.4.如图,抛物线y=﹣x2﹣3x+4与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)若以点C为圆心,1为半径的圆上有一动点P,连接BP,点Q为线段BP上一点,且BQ=BP,求线段OQ的最大值;为线段BP上一点,且BQ=BP,求线段OQ的最大值;(2)若点D为抛物线上一点且横坐标为﹣3,点E为y轴上一点,点F在以点A为圆心,2为半径的圆上,求DE+EF的最小值;(3)若以点B为圆心,3为半径作圆,与x轴的正半轴交于点H,点M是⊙B上的一动点,连接AM,以AM为直角边向下作等腰Rt△MAN,且∠MAN=90°,连接NH,求线段NH长度的取值范围.。
二次函数压轴题专题一 最短路径问题

二次函数压轴题专题一最短路径问题——和最小知识梳理最短路径就是无论在立体图形还是平面图形中,两点间的最短距离,常涉及以下 两个方面:1、两点之间,线段最短;2、垂线段最短。
常用思考的方式:1、把立体转化为平面;2、通过轴对称寻找对称点。
解题总思路:找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
例题导航例1:如图A 是锐角∠MON 内部任意一点,在∠MON 的两边OM ,ON 上各取一点B ,C ,组成三角形,使三角形周长最小.例:如图,A.B 两地在一条河的两岸,现要在河上建一座桥MN ,桥造在何处才能使从A 到B 的路径AMNB 最短?(假设河的两岸是平行的直线,桥要与河垂直) 解:1.将点B 沿垂直与河岸的方向平移一个河宽到E , 2.连接AE 交河对岸与点M,则点M 为建桥的位置,MN 为所建的桥。
证明:由平移的性质,得 BN ∥EM 且BN=EM, MN=CD, BD ∥CE, BD=CE, 所以A.B 两地的距:AM+MN+BN=AM+MN+EM=AE+MN, 若桥的位置建在CD 处,连接AC.CD.DB.CE, 则AB 两地的距离为:AC+CD+DB=AC+CD+CE=AC+CE+MN,在△ACE 中,∵AC+CE >AE, ∴AC+CE+MN >AE+MN,即AC+CD+DB >AM+MN+BN 所以桥的位置建在CD 处,AB 两地的路程最短。
例:如图,A 、B 是两个蓄水池,都在河流a 的同侧,为了方便灌溉作物,•要在河边建一个抽水站,将河水送到A 、B 两地,问该站建在河边什么地方,•可使所修的渠道最短,试在图中确定该点。
作法:作点B 关于直线 a 的对称点点C,连接AC 交直线a 于点D ,则点D 为建抽水站的位置。
证明:在直线 a 上另外任取一点E ,连接AE.CE.BE.BD,··CDA BEa∵点B.C 关于直线 a 对称,点D.E 在直线 a 上,∴DB=DC,EB=EC, ∴AD+DB=AD+DC=AC, AE+EB=AE+EC在△ACE 中,AE+EC >AC, 即 AE+EC >AD+DB所以抽水站应建在河边的点D 处,常见问题归纳“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DElBAllllBAOBOB+EF +CF 最小,则点E ,F 即为所求.⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y轴正半轴.点P 在什么位置时PA +PB 最小?过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.二次函数中最短路径例题例1.(13广东)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标; (3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BOB Oll练习1.(11菏泽)如图,抛物线y =12x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.练习2.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.例2.(14海南)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由.【思路点拨】 (1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出; (3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5,∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN•MN -12OM •OE =12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1=-x 2+92x +92 =-(x -94)2+15316 ∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316). (3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值. 如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1);作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图2练习3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1;(3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.例4.(14福州)如图,抛物线y =12(x -3)2-1与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了. (1)求点A ,B ,D 的坐标; (2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x -3)2-1=0解出方程,即可得出点A ,B 的坐标;(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可.【解题过程】解:(1)顶点D 的坐标为(3,-1).令y =0,得12 (x -3)2-1=0,解得x 1=3+2,x 2=3-2.∵点A 在点B 的左侧,∴A 点坐标(3-2,0),B 点坐标(3+2,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,-1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72-(-1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90︒.∵∠MOE +∠COH =90︒,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90︒,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90︒.设AE 交CD 于点F .∴∠ADC +∠AFD =90︒.又∵∠AEO +∠HFE =90︒, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.∵y =12 (x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1).此时Q 点坐标为(3,1)或(195,135).例5.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ .(3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM . (ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值?若存在,求出点F 的坐标;若不存在,请说明理由.【解题过程】解:(1)由题意,得⎩⎨⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎨⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1; (2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt △POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ; (3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°.∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′,∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点.∵D (1,1),∴F 的横坐标为1,∴F (1,54).l。
九年级数学上册复习专题15二次函数中最短路径问题

专题15二次函数中最短路径问题【做题思路】:一般在二次函数中,会求PA+PC的最小值,且点P为动点;对于这类问题,首先将动点所在直线作为“河”,根据“将军饮马问题”的作图步骤,作出图形。
【做题步骤】:①首先找出“河”:动点所在直线就是“河”;②选出其中一个特殊定点,做关于“河”的对称点;③连接对称点与另一个定点;④连线与河的交点即为动点所在位置,连线长度即为最短路径长(可以用两点之间距离公式);【变换类型】求一个三角形的周长最短:周长就是三条线段相加,其中有一条线段是确定的,两条线段长随着动点运动而变化,那么只需要求出与动点相连两定点的线段最小值即可,也就是求两个线段的最小值。
【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题-即已知起始结点,求最短路径的问题.②确定终点的最短路径问题-与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题-即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题-求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.【十二个基本问题】1.直线y =23x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( )A .(-3,0)B .(-6,0)C .(-52,0) D .(-32,0) 2.如图,点P 是边长为1的菱形ABCD 对角线AC 上的一个动点,点M,N 分别是AB,BC 边上的中点,则MP+PN 的最小值是( )A .12B .1C D .23.如图,在平面直角坐标系中,已知点A (2,3),点B (﹣2,1),在x 轴上存在点P 到A ,B 两点的距离之和最小,则P 点的坐标是 .4.如图,A (3,4),B (0,1),C 为x 轴上一动点,当△ABC 的周长最小时,则点C 的坐标为_________.1.如图,已知直线y=12x+1与y 轴交于点A ,与x 轴交于点D ,抛物线y= 12x 2+bx+c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使|AM ﹣MC|的值最大,求出点M 的坐标__________.2.如图,抛物线y=﹣x 2﹣2x+3与x 轴交于A 、B 两点,与y 轴交于C 点,M 点在抛物线的对称轴上,当点M 到点B 的距离与到点C 的距离之和最小时,点M 的坐标为_____.3.如图,已知直线1y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为(1,0).在抛物线的对称轴上找一点M ,使AM MC -的值最大,求出点M 的坐标___阅读材料:例:说明代数式的几何意义,并求它的最小值.P (x ,0)是x 轴上P 与点A (0,1P 与点B (3,2)的距离,所以原代数式的值可以看成线段PA 与PB 长度之和,它的最小值就是PA +PB 的最小值.设点A 关于x 轴的对称点为A′,则PA =PA′,因此,求PA +PB 的最小值,只需求PA′+PB 的最小值,而点A′、B 间的直线段距离最短,所以PA′+PB 的最小值为线段A′B 的长度.为此,构造直角三角形A′CB,因为A′C=3,CB =3,所以A′B=.根据以上阅读材料,解答下列问题:(1)P (x ,0)与点A (1,1)、点B 的距离之和.(填写点B 的坐标)(2)代数式已知()()1,2,7,4A B ,M ,N 是x 轴上两动点(M 在N 左边),3MN =,请在x 轴上画出当AM MN NB ++的值最小时,M ,N 两点的位置.1.如图1,抛物线2y ax bx =+与x 轴交于点A ,对称轴与抛物线交于点()2,2B -,与x 轴交于点C .(1)求抛物线的解析式.(2)点D 是y 轴上的动点,求DAB ∆的最小周长.(3)如图2,点P 是抛物线上一个动点,,PA PO 分别与BC 交于点,M N .①若动点P 在第一象限,问MC NC -的值是否发生变化.若不变,求出其值;若发生变化,请说明理由. ②若动点P 在第二象限,请给出①中类似的关于MC 与NC 长的结论(不必证明).2.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A 、B 两点,与y 轴交于点C ,其中()30A -,、()0,2C -.(1)求这条抛物线的函数表达式.(2)在对称轴上是否存在一点P ,使得PBC ∆的周长最小.若存在请求出点P 的坐标.若不存在请说明理由.3.如图,已知直线33y x =-分别交x 轴、y 轴于A 、B 两点,抛物线2y x bx c =++经过A 、B 两点,点C 是抛物线与x 轴的另一个交点(与A 点不重合).(1)求抛物线的解析式;(2)在抛物线的对称轴上求一点P ,使ABP ∆的周长最小,并求出最小周长和P 点的坐标;(3)在抛物线的对称轴上,是否存在点M ,使ABM ∆为等腰三角形?若不存在,请说明理由;若存在,求出点M 的坐标.4.如图,一元二次方程x 2+2x,3=0的两根x 1,x 2,x 1,x 2)是抛物线y=ax 2+bx+c 与x 轴的两个交点C,B 的横坐标,且此抛物线过点A,3,6,, ,1)求此二次函数的解析式;,2)设此抛物线的顶点为P ,对称轴与线段AC 相交于点G ,则P 点坐标为 ,G 点坐标为 , ,3)在x 轴上有一动点M ,当MG+MA 取得最小值时,求点M 的坐标.5.如图,以D 为顶点的抛物线2y ax 2x c =++交x 轴于点A ,(6,0)B ,交y 轴于点(0,6)C .(1)求抛物线的解析式;(2)在直线BC 上有一点P ,使PO PA +的值最小,求点P 的坐标;(3)在x 轴上是否存在一点Q ,使得以A ,C ,Q 为顶点的三角形与BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由. 6.如图,抛物线y=12x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A(一1,0). (1)求抛物线的解析式及顶点D 的坐标; (2)判断△ABC 的形状,证明你的结论;(3)点M 是x 轴上的一个动点,当△DCM 的周长最小时,求点M 的坐标.7.如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A,,1,0,B,3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点.,1)求抛物线的解析式和直线AC 的解析式;,2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;,3)试探究:在拋物线上是否存在点P ,使以点A,P,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.8.在平面直角坐标系中,O 为原点,抛物线2(0)y ax x a =≠经过点3)A -,对称轴为直线l ,点O 关于直线l 的对称点为点B .过点A 作直线//AC x 轴,交y 轴于点C . (Ⅰ)求该抛物线的解析式及对称轴;(Ⅱ)点P 在y 轴上,当PA PB +的值最小时,求点P 的坐标; (Ⅲ)抛物线上是否存在点Q ,使得13AOC AOQ S S ∆∆=,若存在,求出点Q 的坐标;若不存在,请说明理由. 9.如图,直线43y x =与抛物线268y x x =-+交于A ,B 两点(其中点A 在点B 的左侧),与抛物线的对称轴交于点C ,抛物线的顶点为D ,点B 的坐标为()6,8,在抛物线的对称轴上找一点F ,使35BF CF +的值最小,求满足条件的点F 的坐标.试卷第11页,总11页。
二次函数常见压轴题目类型

二次函数常见压轴题题目类型 一:定值问题1.如图,直线1y x =+与抛物线222y x mx m m =-++交于A,B 两点(点A 在点B 的左边)。
求证:无论m 为何值,AB 的长总为定值。
2.如图,抛物线243y x x =-+与x 轴交于A,B 两点,与y 轴交于点C,将直线BC 沿y 轴向上平移交抛物线于点M,N ,交y 轴于点P ,求PM PN -的值。
3.如图,已知直线()90y kx k k =-<与抛物线223y x x =--交于A,B 两点,与x 轴交于点P ,过点A 作AC ⊥x 轴于点C,过点B 作BD ⊥x 于点D ,求证:PD PC ⋅为定值。
4.如图,抛物线的顶点坐标为C (0,8),并且经过A (8,0),点P 是抛物线上点A,C 间的一个动点(含端点),过点P 作直线8y =的垂线,垂足为点F,点D ,E 的坐标分别为(0,6),(4,0),连接PD,PE,DE 。
(1)求抛物线的解析式(2)猜想并探究:对于任意一点P ,PD 与PF 的差是否为固定值,如果是,请求出此定值,如果不是,请说明理由。
二.二次函数与角度问题1.如图,抛物线232y x x =-+-与x 交于A,B 两点,与y 轴交于点C ,点P 在抛物线上,∠ACB=∠BCP ,求点P 的坐标物线,且DM 平分∠OME,求点E 的坐标。
3.抛物线2y ax c =+与x 轴交于A 、B 两点,顶点为C,点P 在抛物线上,且位于x 轴的下方。
(1)如图1,若点P (1,3-),B (4,0),①求该抛物线的解析式;②若D 是抛物线上的一点,满足∠DPO=∠POB ,求点D 的坐标(2)如图2,在(1)中的抛物线解析式不变的条件下,已知直线PA 、PB 与y 轴分别交于E 、F 两点,点P 运动时,OE+OF 是否为定值?若是,试求出改定值;若不是,请说明理由。
物线第四象限上一点,∠PCB=∠ACO ,求点P 的坐标5.如图,过点(1,4-)的抛物线与x 轴交于点()10,(30)A B -,,,与y 轴交于点C 。
中考压轴题二次函数求最短距离

20XX 年中考数学二次函数求最短距离备考专题训练知识点:1.点到直线的距离直线外一点到直线的距离垂线段最短。
2.直线与直线的距离 两直线间垂线段最短。
3.在直线上找一点与直线同侧两点(不在直线上)的连线距离和最短的求法 首先找同侧两点中任一点关于该直线对称的点,再将同侧另一点与对称点连线,该连线与直线的交点即为所求。
中考真题训练1.如图,在锐角ABC △中,4245AB BAC =∠=,°,BAC ∠的平分线交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是___________ .ABCDN M(第1题图)2.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q 的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.3.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式;⑵动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标。
(第2题)4 x2 2A8 -2 O-2 -4 y 6B C D -444.如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t >,tan 3BAC ∠=,抛物线经过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点. (1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值;(3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.二次函数求最短距离参考答案1.如图,已知点A (-4,8)和点B (2,n )在抛物线2y ax =上.(1) 求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得AQ +QB 最短,求出点Q的坐标;(2) 平移抛物线2y ax =,记平移后点A 的对应点为A ′,点B 的对应点为B ′,点C (-2,0)和点D (-4,0)是x 轴上的两个定点.① 当抛物线向左平移到某个位置时,A ′C +CB ′ 最短,求此时抛物线的函数解析式;② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A ′B ′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,OACBxy请说明理由.解:(1) 将点A (-4,8)的坐标代入2y ax =,解得12a =.……1分将点B (2,n )的坐标代入212y x =,求得点B 的坐标为(2,2),则点B 关于x 轴对称点P 的坐标为(2,-2). ……1分直线AP 的解析式是5433y x =-+.……1分 令y =0,得45x =.即所求点Q 的坐标是(45,0).……1分(2)① 解法1:CQ =︱-2-45︱=145,……1分故将抛物线212y x =向左平移145个单位时,A ′C +CB ′最短,……2分此时抛物线的函数解析式为2114()25y x =+.……1分解法2:设将抛物线212y x =向左平移m 个单位,则平移后A ′,B ′的坐标分别为A ′(-4-m ,8)和B ′(2-m ,2),点A ′关于x 轴对称点的坐标为A ′′(-4-m ,-8).直线A ′′B ′的解析式为554333y x m =+-. (1)分要使A ′C +CB ′最短,点C 应在直线A ′′B ′上, ……1分 将点C (-2,0)代入直线A ′′B ′的解析式,解得145m =.……1分故将抛物线212y x =向左平移145个单位时A ′C +CB ′最短,此时抛物线的函数解析式为2114()25y x =+.……1分② 左右平移抛物线212y x =,因为线段A ′B ′和CD 的长是定值,所以要使四边形A ′B ′CD 的周长最短,只要使A ′D +CB ′最短; ……1分第一种情况:如果将抛物线向右平移,显然有A ′D +CB ′>AD +CB ,因此不存在某个位置,使四边形A ′B ′CD 的周长最短.……1分第二种情况:设抛物线向左平移了b 个单位,则点A ′和点B ′的坐标分别为A ′(-4-b ,8)和B ′(2-b ,2).因为CD =2,因此将点B ′向左平移2个单位得B ′′(-b ,2),要使A ′D +CB ′最短,只要使A ′D +DB ′′最短. ……1分(第1题)4 x2 2A8 -2 O-2 -4 y 6 B CD -44(第1题(1)) 4 x2 2A8 -2 O -2 -4 y 6 BCD -44Q P (第1题(2)①)4 x2 2 A ′8-2 O -2 -4 y 6B ′C D-4 4 A ′′(第1题(2)②)4 x 2 2A ′8-2 O-2 -4 y6B ′CD -4 4 A ′′B ′′点A ′关于x 轴对称点的坐标为A ′′(-4-b ,-8), 直线A ′′B ′′的解析式为55222y x b =++.要使A ′D +DB ′′最短,点D 应在直线A ′′B ′′上,将点D (-4,0)代入直线A ′′B ′′的解析式,解得165b =. 故将抛物线向左平移时,存在某个位置,使四边形A ′B ′CD 的周长最短,此时抛物线的函数解析式为2116()25y x =+.……1分2.如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
专题16 二次函数与最短路径问题-备战2022年中考数学母题题源解密(解析版)

专题16 二次函数与最短路径问题考向1 利用轴对称求线段之和的最小值【母题来源】2021年中考山东省东营卷【母题题文】如图,抛物线y =−12x 2+bx+c 与x 轴交于A 、B 两点,与y 轴交于点C ,直线y =−12x+2过B 、C 两点,连接AC .(1)求抛物线的解析式;(2)求证:△AOC ∽△ACB ;(3)点M (3,2)是抛物线上的一点,点D 为抛物线上位于直线BC 上方的一点,过点D 作DE ⊥x 轴交直线BC 于点E ,点P 为抛物线对称轴上一动点,当线段DE 的长度最大时,求PD+PM 的最小值.【答案】(1)∵直线y =−12x+2过B 、C 两点,当x =0时,代入y =−12x+2,得y =2,即C (0,2),当y =0时,代入y =−12x+2,得x =4,即B (4,0),把B (4,0),C (0,2)分别代入y =−12x 2+bx+c ,得{−8+4b +c =0c =2, 解得{b =32c =2, ∴抛物线的解析式为y =−12x 2+32x+2;(2)∵抛物线y =−12x 2+32x+2与x 轴交于点A ,∴−12x 2+32x+2=0,解得x 1=﹣1,x 2=4,∴点A 的坐标为(﹣1,0),∴AO =1,AB =5,在Rt △AOC 中,AO =1,OC =2,∴AC=√5,∴AOAC=√5=√55,∵ACAB=√55,∴AOAC=ACAB,又∵∠OAC=∠CAB,∴△AOC∽△ACB;(3)设点D的坐标为(x,−12x2+32x+2),则点E的坐标为(x,−12x+2),∴DE=−12x2+32x+2﹣(−12x+2)=−12x2+32x+2+12x﹣2 =−12x2+2x=−12(x﹣2)2+2,∵−12<0,∴当x=2时,线段DE的长度最大,此时,点D的坐标为(2,3),∵C(0,2),M(3,2),∴点C和点M关于对称轴对称,连接CD交对称轴于点P,此时PD+PM最小,连接CM交直线DE于点F,则∠DFC=90°,点F的坐标为(2,2),∴CD=√CF2+DF2=√5,∵PD+PM=PC+PD=CD,∴PD+PM的最小值为√5.【试题解析】(1)直线y=−12x+2过B、C两点,可求B、C两点坐标,把B(4,0),C(0,2)分别代入y=−12x2+bx+c,可得解析式.(2)抛物线y=−12x2+32x+2与x轴交于点A,即y=0,可得点A的横坐标,由相似三角形的判定得:△AOC∽△ACB.(3)设点D的坐标为(x,−12x2+32x+2),则点E的坐标为(x,−12x+2),由坐标得DE=−12x2+2x,当x=2时,线段DE的长度最大,此时,点D的坐标为(2,3),即点C和点M关于对称轴对称,连接CD交对称轴于点P,此时PD+PM最小,连接CM交直线DE于点F,则∠DFC=90°,由勾股定理得CD=√5,根据PD+PM =PC+PD=CD,即可求解.【命题意图】函数思想;应用意识.【命题方向】主要为解答题,一般为压轴题,具有很强的甄别性.【得分要点】已知:在直线l同恻有A.B两点,在l上找一点P,使得AP+PB最小.作法:如图.作点A关于直线l的对称点A’,连结A'B,与直线,的交点就是点P考向2 利用三点共线求线段之和的最小值【母题来源】2021年中考湖北省恩施卷【母题题文】如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c 经过点B,D(﹣4,5)两点,且与直线DC交于另一点E.(1)求抛物线的解析式;(2)F为抛物线对称轴上一点,Q为平面直角坐标系中的一点,是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由;(3)P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为M,连接ME,BP,探究EM+MP+PB是否存在最小值.若存在,请求出这个最小值及点M的坐标;若不存在,请说明理由.BAPlABl【答案】(1)由点D 的纵坐标知,正方形ABCD 的边长为5,则OB =AB ﹣AO =5﹣4=1,故点B 的坐标为(1,0),则{1+b +c =016−4b +c =5,解得{b =2c =−3故抛物线的表达式为y =x 2+2x ﹣3; (2)存在,理由:∵点D 、E 关于抛物线对称轴对称,故点E 的坐标为(2,5),由抛物线的表达式知,其对称轴为直线x =﹣1,故设点F 的坐标为(﹣1,m ),由点B 、E 的坐标得,BE 2=(2﹣1)2+(5﹣0)2=26,设点Q 的坐标为(s ,t ),∵以点Q ,F ,E ,B 为顶点的四边形是以BE 为边的菱形,故点B 向右平移1个单位向上平移5个单位得到点E ,则Q (F )向右平移1个单位向上平移5个单位得到点F (Q ),且BE =EF (BE =EQ ),则{s +1=−1t +5=m 26=(2+1)2+(m −5)2或{s −1=−1t −5=m 26=(s −2)2+(t −5)2, 解得{m =5±√17s =−2t =±√17或{s =0t =5±√22m =±√22,故点F 的坐标为(﹣1,5+√17)或(﹣1,5−√17)或(﹣1,√22)或(﹣1,−√22);(3)存在,理由:由题意抛物线的对称轴交x 轴于点B ′(﹣1,0),将点B ′向左平移1个单位得到点B ″(﹣2,0),连接B″E,交函数的对称轴于点M,过点M作MP⊥y轴,则点P、M为所求点,此时EM+MP+PB为最小,理由:∵B′B″=PM=1,且B′B″∥PM,故四边形B″B′PM为平行四边形,则B″M=B′P=BP,则EM+MP+PB=EM+1+MB″=B″E+1为最小,由点B″、E的坐标得,直线B″E的表达式为y=54(x+2),当x=﹣1时,y=54(x+2)=54,故点M的坐标为(﹣1,54),则EM+MP+PB的最小值B″E+1=1+√(−2−2)2+(0−5)2=√41+1.【试题解析】(1)求出点B的坐标为(1,0),再用待定系数法即可求解;(2)以点Q,F,E,B为顶点的四边形是以BE为边的菱形,故点B向右平移1个单位向上平移5个单位得到点E,则Q(F)向右平移1个单位向上平移5个单位得到点F(Q),且BE=EF(BE=EQ),即可求解;(3)由题意抛物线的对称轴交x轴于点B′(﹣1,0),将点B′向左平移1个单位得到点B″(﹣2,0),连接B″E,交函数的对称轴于点M,过点M作MP⊥y轴,则点P、M为所求点,此时EM+MP+PB为最小,进而求解.【命题意图】考查代数几何综合题;分类讨论;矩形菱形正方形;数据分析观念.【命题方向】解答题,一般设定为试卷压轴题.【得分要点】利用转化思想得三点共线,进而利用三点共线求线段的最小值.1.(2021•湖北南漳县模拟)在平面直角坐标系xOy中,矩形OABC的顶点A,C的坐标分别为(0,3),(2,0),顶点为M的抛物线y=﹣x2+bx+c经过点A,B,且与x轴交于点D,E(点D在点E的左侧).(1)求点B 的坐标,抛物线的解析式及顶点M 的坐标;(2)点P 是(1)中抛物线对称轴上一动点,求△PAD 的周长最小时点P 的坐标;(3)平移抛物线y =﹣x 2+bx+c ,使抛物线的顶点始终在直线AM 上移动,在平移的过程中,当抛物线与线段BM 有公共点时,求抛物线顶点的横坐标a 的取值范围.解:(1)∵A ,C 点的坐标分别为(0,3),(2,0),并且四边形ABCD 是矩形,∴B 点的坐标是(2,3),把A 、B 代入抛物线解析式,则{c =3−4+2b +c =3, 解得{c =3b =2, ∴抛物线的解析式为y =﹣x 2+2x+3,∴y =﹣(x ﹣1)2+4,即顶点M 为(1,4);(2)在对称轴上取一点P ,连接PA ,PB ,PD ,由抛物线及矩形的轴对称性可知点A ,B 关于抛物线的对称轴对称,∴PA =PB ,∴当点P ,B ,D 在一条直线上时△PAD 的周长最小,当﹣x 2+2x+3=0时,解得x 1=﹣1,x 3=3,∴点D (﹣1,0),设直线BD 的解析式为y =kx+q ,代入B 点、D 点坐标得({2k +q =3−k +q =0, 解得{k =1q =1, ∴直线BD 的解析式为y =x+1,当x =1时,y =2,∴P 点的坐标为(1,2);(3)设直线AM 的解析式为:y AM =mx+n ,代入点A 和点M 的坐标得{n =3m +n =4, 解得{m =1n =3, ∴直线AM 的解析式为y AM =x+3,同理得直线BM 的解析式为y BM =﹣x+5,∵抛物线y =﹣x 2+bx+c 的顶点在直线y AM =x+3上,∴设平移中的抛物线的解析式为y =﹣(x ﹣a )2+a+3,当a =1时,抛物线y =﹣(x ﹣a )2+a+3即y =﹣x 2+2x+3,此时抛物线y =﹣(x ﹣a )2+a+3与线段AB 有两个交点,当a >1时,①抛物线y =﹣(x ﹣a )2+a+3经过点M 时,有﹣(1﹣a )2+a+3=4,解得:a 1=1(舍去),a 2=2,②当抛物线y =﹣(x ﹣a )2+a+3经过点B 时,有﹣(2﹣a )2+a+3=3,解得:a 1=1(舍去),a 2=4,综上可得2≤a ≤4,当a <1,抛物线y =﹣(x ﹣a )2+a+3与直线y BA =﹣x+5有公共点时,则方程﹣(x ﹣a )2+a+3=﹣x+5即x 2﹣(2a+1)x+a 2﹣a+2=0有实数根,∴(2a+1)2﹣4(a 2﹣a+2)≥0,即a ≥78,∴1>a ≥78,综上可得1>a ≥78或2≤a ≤4时,平移后的抛物线与线段BA 有公共点.2. (2021•江苏省江阴市模拟)如图,菱形ABCD 的对角线AC ,BD 交于点O ,AB =4.BD =5.点P 是线段AO 上一动点(不与A ,O 重合).点E 与点P 在AD 所在直线的两侧.AE ⊥AB .AE =BD .点F 在AD 边上,DF =AP .连接PE ,BF .(1)补全图形,求PE :BF 的值;(2)连接BP ,点P 在何处时BP+BF 取得最小值?并求出这个最小值.解:(1)图形如图所示:∵四边形ABCD是菱形,∴AC⊥BD,∠DAO=∠BAO,∴∠AOD=90°,∵EA⊥AB,∴∠EAP+∠BAO=90°,∵∠DAO+∠ADO=90°,∴∠EAP=∠BDF,∵AE=DB,AP=DF,∴△EAP≌△BDF(SAS),∴PE=BF,∴PE:BF=1.(2)∵PE=BF,∴BP+BF=BP+PE≥BE,∴当点P在BE与OA的交点处时,BP+BF的值最小,最小值BE=√AE2+AB2=√52+42=√41.。
二次函数之距离最小(思维)

二次函数之最短路径问题例1.(广东)已知二次函数y=x 2-2mx+m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式;(2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.例2.(甘肃兰州)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线y =23x 2+bx +c 经过点B ,且顶点在直线x =52上.(1)求抛物线对应的函数关系式;(2)若把△ABO 沿x 轴向右平移得到△DCE ,点A 、B 、O 的对应点分别是D 、C 、E ,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD ,已知对称轴上存在一点P 使得△PBD 的周长最小,求出P 点的坐标;例3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例4.(湖南郴州)已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.例5.(辽宁)如图16,在平面直角坐标系中,直线y=x轴交于点A,与y轴交于点C,抛物线2(0)y ax c a=+≠经过A B C,,三点.(1)求过A B C,,三点抛物线的解析式并求出顶点F的坐标;(2)在抛物线上是否存在点P,使ABP△为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由;(3)试探究在直线AC上是否存在一点M,使得MBF△的周长最小,若存在,求出M点的坐标;若不存在,请说明理由.xx例6.(山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.例7.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使∠CPN=90°?若存在,请直接写出点P的坐标.例8.(德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.练习:(烟台)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B 两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=1.5(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.例10.已知抛物线y=ax2+bx+1经过点A(1,3)和点B(2,1)。
二次函数压轴题最短路径问题

最短路径问题一一和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题)•如图所示,在直线 丨上找一点P 使得P%PB 最小•当点P 为直线AB 与直线丨的交点时,PA + PB 最小.B-r | P ,B'B4 P .B'③如图所示,在/ AOB 勺边AO B0上分别找一点 C D 使得PO C 戻PD 最小•过点P 分别作关于 AO BO 的对称点E ,F ,连接EF,并与AO B0分别交于点C, D,此时PO C 戻PD 最小,则点C D 即为所求.④如图所示,在/ AOB 勺边AO BO 上分别找一点 E F 使得D 可EF + CF 最小•分别过点 C , D 作关于AO BO 的对称点D ; C ;连接DC,并与AO BC 分别交于点E, F ,此时DE^EF + CF 最小,则点E, F 即为所求.⑤如图所示,长度不变的线段 CD 在直线丨上运动,在直线丨上找到使得AO BD 最小的CD 的位置•分别过 点A ,D 作AA// CD DA// AC AA 与 DA 交于点A ;再作点B 关于直线丨的对称点B',连接A'B 与直线丨交于【方法归纳】在直线丨上找一点B 使得线段AB 最小•过点A 作AB1丨,垂足为B,则线段AB 即为所求.在直线 ②如图所示,点P ,此时PA^ PB 最小,则点P 即为所求.丨上找一点P 使得PA^ PB 最小•过点B 作关于直线丨的对称点B',BB'与直线丨交于BFB点D ,此时点D 即为所求.1⑥如图所示,在平面直角坐标系中,点P 为抛物线(y = 4X 1 2)上的一点,点A ( 0, 1)在y 轴正半轴.点P在什么位置时PA+PB 最小?过点B 作直线I : y =— 1的垂线段BH, BH 与抛物线交于点 P ,此时PA+ PB最小,则点P 即为所求.【思路点拨】 (1)由二次函数的图象经过坐标原点 0(0,0),直接代入求出 m 的值即可;1 (13广东)已知二次函数 y = x2 — 2m 灶卅一1. (1)当二次函数的图象经过坐标原点 0(0, 0)时,求二次函数的解析式;(2) 如图,当m= 2时,该抛物线与y 轴交于点C ,顶点为D 求C 、D 两点的坐标;(3) 在(2)的条件下,x 轴上是否存在一点 P ,使得PO PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.BBB'(2) 把m= 2代入求出二次函数解析式,令 X = o ,求出y 的值,得出点C 的坐标;利用配方法或顶点坐标 公式求岀顶点坐标即可; (3) 根据当P C 、D 共线时根据"两点之间,线段最短"得出PC +PD 最短,求出CD 的直线解析式,令y=0,求出x 的值,即可得出P 点的坐标. 【解题过程】解:(1)T 二次函数的图象经过坐标原点0(0,0),•••代入二次函数y = X 3 4 5-2m 对m — 1,得出:m — 1 = 0,解得:m=± 1, •••二次函数的解析式为:y =x 2— 2x 或y = X 2 + 2x ;(2) v m= 2, •二次函数 y = x 2 — 2m 灶 m - 1 得:y = x 2— 4x + 3=( x — 2) 2 — 1,•抛物线的顶点为:D (2,— 1),当 x = 0 时,y = 3,• C 点坐标为:(0, 3),• C (0, 3)、D( 2,— 1 ); (3) 当P 、C D 共线时PO PD 最短,【方法一】:C ( 0, 3)、D( 2,— 1),设直线CD 的解析式为y = kx + 3,代入得:2k + 3=— 1 ,• k =— 2, • y = — 2x + 3, 3 3当y = 0时,一2x + 3= 0,解得x = 2,二PO PD 最短时,P 点的坐标为:P ( 2,0). 【方法二】过点D 作DEL y 轴于点E ,3• PO PD 最短时,P 点的坐标为:P (2,0).12. (11菏泽)如图,抛物线 y = 2x 2 + bx - 2与x 轴交于A , B 两点,与y 轴交于C 点,且A (- 1, 0).3 求抛物线的解析式及顶点 D 的坐标;4 判断△ ABC 勺形状,证明你的结论;5 点M(m 0)是x 轴上的一个动点,当 M G MD 的值最小时,求 m 的值.v PO/ DEPO =CODE" CE P0=32 = 4,解得:3 P0=2,【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标;(2) 观察发现A ABC 是直角三角形,可以通过勾股定理的逆定理证明. 由抛物线的解析式,分别求出点B , C 的坐标,再得出AB AC BC 的长度,易得AC + BC = AB ,得出△ ABC 是直角三角形; (3) 作出点C 关于x 轴的对称点C ;连接C D 交x 轴于点M 根据“两点之间,线段最短”可知 MO MD 的值最小•求岀直线 C D 的解析式,即可得岀点 M 的坐标,进而求岀 m 的值. 【解题过程】1 2 1 23解:(1) v 点 A (- 1, 0)在抛物线 y =於 + bx — 2 上, /• 2^ (- 1 ) + b x (- 1) — 2= 0,解得 b =- ,1 2 31 32 25 一3 25二抛物线的解析式为 y =—必—2= 2 (x — 2)— 8,二顶点D 的坐标为 (2,— 8)•(2)当 x = 0 时 y = — 2,「. C (0,— 2),OC= 2•, 亠 1 2 3当 y = 0 时,2X — q x — 2 = 0,二 X 1=— 1, X 2= 4,•: B (4, 0),「• OA= 1, OB= 4, AB= 5.V A B = 25, A C = oA + oC = 5, B C = OC + OB = 20,「. A C + B C = A B • •••△ ABO 直角三角形. (3) 作出点C 关于x 轴的对称点C',则C'(0, 2), OC = 2,连接C'D 交x 轴于点M 根据轴对称性及两点之间线段最短可知, MO MD 勺值最小.【方法一】设直线C'D 的解析式为y = kx +n ,则3丄=_ 25,解得:2k + n = — ~8 41 24 24.当 y = 0 时,一12x + 2 = 0, x = 41 • . n== 41 • 【方法二】设抛物线的对称轴交x 轴于点E.v ED/ y 轴,OCM=/ EDM /C‘OM= / DEM .△ C’Og DEM .OM =OC . = 2 . 24…EM = E D 3 = 25,n 41 •2 — m 百n = 2十4141 .. y = — —x + 2 k =— • y 12x 十 23. (11福州)已知,如图,二次函数 y = ax 2+ 2ax - 3a (a H))图象的顶点为 H,与x 轴交于A B 两点(B 在A 点右侧),点H B 关于直线丨:y=£x +冷3对称.(1 )求A 、B 两点坐标,并证明点 A 在直线丨上; (2) 求二次函数解析式;(3) 过点B 作直线BK// AH 交直线丨于K 点,M N 分别为直线AH 和直线丨上的两个动点,连接 HN NM MK 求HN^ NMF MK 和的最小值.【思路点拨】(1 )二次函数y = ax 2+ 2ax - 3a(a 旳)中只有一个未知参数 a ,令y = 0,解出方程ax 2 + 2ax - 3a = 0(a ^D ), 即可得到点A ,B 的坐标•把点A 的坐标代入直线丨的解析式即可判断 A 是否在直线上;(2) 根据点H B 关于过A 点的直线丨:y = jx + 3对称,得出AH= AB= 4,过顶点H 作HCL AB 交AB 于1C 点,得AC= 2AB= 2,利用勾股定理求出 HC 的长,即可得出点 H 的坐标,代入二次函数解析式,求出 a ,即可得到二次函数解析式;(3) 直线BK// AH 易得直线BK 的解析式,联立直线 丨的解析式方程组,即可求出 K 的坐标•因为点 H B 关于直线AK 对称,所以HN= BN 所以根据“两点之间,线段最短"得出 HN b MN 的最小值是MB 作点K 关 于直线AH 的对称点Q 连接QK 交直线AH 于 E ,所以Ql = KM 易得BW MK 的最小值为BQ 即BQ 的长是 HN F NMF MK 勺最小值,求出 QB 的长即可. 【解题过程】解:(1)依题意,得 ax' + 2ax - 3a = 0 ( a®,解得 X 1=- 3,X 2 = 1,v B 点在A 点右侧,A 点坐标为(-3,0),B 点坐标为(1,0),丁直线丨:y =3,当x =- 3时,y = X - 3) + 3 = 0,点A 在直线丨上.过顶点 H 作 HCLAB 交 AB 于 C 点,贝U AC= 2AB= 2, HC= 2 3, 顶点H ( — 1, 2寸3),代入二次函数解析式,解得 a =—芈 二次函数解析式为y = — 2^x 2 — ^ 3x + ~2^,(2) v 点H 、B 关于过A 点的直线丨:二 AH= AB= 4,(3)直线AH 的解析式为y = »:;3x + 3 3,直线BK 的解析式为y =-J 3x + 3寸3, 由y=老X 十护,解得x- 3即K ( 3, 2、0,则BK= 4,y - 3x - 3 y - 6 7 3T 点H B 关于直线 AK 对称,••• HW M N 勺最小值是 MB KD= KE - 2*3,过点K 作直线AH 的对称点 Q 连接QK 交直线AH 于巳_则QM= MK QE F EK= ^-3, AE 1QK 二B 冊 MK 勺最小值是 BQ 即BQ 的长是HN b NM- MK 勺最小值, v BK// AHBK —/HE(- 90° ° 由勾股定理得 QB= 8 , 二HN - NM- MK 勺最小值为8.当a -1时,求四边形 MEFP 勺面积的最大值,并求此时点 P 的坐标;若厶PCM!以点P 为顶点的等腰三角形,求 a 为何值时,四边形 PMEF 周长最小?请说明理由.(2) (3)4. (14海南) 如图,对称轴为直线x - 2的抛物线经过A (- 1 , 0), C(0 , 5)两点,与x 轴另一交点为 B-已知 M (0, 1),E (a , 0),F (a +1, 0),点P 是第一象限内的抛物线上的动点.(1) 求此抛物线的解析式;【思路点拨】(1 )由对称轴为直线x = 2,可以得出顶点横坐标为 2,设二次函数的解析式为 y = a (x -2) 2+ k ,再把点 A , B 的代入即可求出抛物线的解析式; (2) 求四边形MEF 的面积的最大值,要先表示出四边形MEF 面积•直接求不好求,可以考虑用割补法来求,过点P 作PN4L y 轴于点N,由S 四边形MEFP = S 梯形OFP — S ^PM — S OM 即可得出;(3) 四边形PMEF 勺四条边中,线段 PM EF 长度固定,当M H PF 取最小值时,四边形 PMEF 勺周长取得最 小值•将点M 向右平移1个单位长度(EF 的长度),得到点M (1,1),作点M 关于x 轴的对称点M (1, —1),连接PM ,与x 轴交于F 点,此时MB PF = PM 最小.【解题过程】解:(1 )v 对称轴为直线x = 2,.••设抛物线解析式为 y = a (x — 2) °+ k .2 2.y = —( x — 2) + 9= — x +4x + 5.(2)当 a = 1 时,E (1 , 0) , F ( 2, 0) , OE= 1 , OF= 2•设 P( x , — x 2 + 4x + 5), 如答图2,过点P 作PNL y 轴于点N,则PNhx , O = — x 2+ 4x + 5,.Mf = ONF OM= — x 2 + 4x + 4.1 1 1MEF= S梯形 OFP— S A PM — ® OM =2 ( PI H OF ?O — 2PN?M — 2OMOE1 1 1=2 (x + 2) (— x +4x + 5) — ?x ?( — x + 4x + 4) —1 X 19 153 9 153•••当x = 4时,四边形MEFP 勺面积有最大值为16,此时点P 坐标为(4, 16 .(3)v M( 0, 1), C (0, 5) ,△ PCM!以点P 为顶点的等腰三角形,•点 P 的纵坐标为3 . 令 y =— X 2 + 4X + 5 =3,解得 x = 2± 6.T 点 P 在第一象限,• P (2 + 6, 3). 四边形PMEF 勺四条边中,PM EF 长度固定, 因此只要MH PF 最小,则PMEF 勺周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M (1, 1); 作点M 关于x 轴的对称点M ,则M (1,- 1);连接PM,与x 轴交于 F 点,此时 M 曰PF = PM 最小.设直线PM 的解析式为y = m>H n ,将P(2 + 6, 3) , M ( 1,- 1)代入得:将 A (— 1, 0), C (0, 5 )代入得:9a + k = 04a + k = 5,解得a =— 1 k = 9 S四边形9 =-(X -4)153 16(m +n =6—T n = 3,解得:m =呼6+ 5当y = 0时,解得x = 4,0). 丁 a +1 =•斗咛1时,四边形PME 周长最小.4 6+ 4 n =5 ,顶点为D 了.(1) 求点A B , D 的坐标;(2) 连接CD 过原点O 作O 吐CD 垂足为H, OE 与抛物线的对称轴交于点 E,连接AE AD 求证:/ AEO=Z ADC(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点 切点为Q,当PQ 的长最小时,求点 P 的坐标,并直接写岀点 Q 的坐标.【思路点拨】1(1) 由顶点式直接得出点 D 的坐标,再令y = 0,得2(x 3)2 1 = 0解出方程,即可得出点 A B 的坐标; (2) 设HD 与AE 相交于点F ,可以发现厶ADF 组成一个“ 8字型” •对顶角/ HFE=Z AFD 只要/ FHE=/FAD 即可•因为/ EHF= 90 °,只需证明/ EAD= 90°即可•由勾股定理的逆定理即可得出△ ADE 为 直角三角形,得/FHE=Z FAD= 90°即可得出结论;(3) 先画出图形.因为PQ 为。
中考二次函数压轴题解题技巧

中考二次函数压轴题解题技巧在解题过程中,我们需要借助函数解析式来表示动点坐标。
首先,我们可以设定动点P在某条直线上,其坐标为(t,f(t))。
然后,我们可以通过计算两个线段的长度,利用代数式证明它们相等。
这种方法适用于各种类型的线段相等问题,如求证两个三角形的周长相等等。
2.求解“定三角形内一点到三边距离之和〞的问题:对于定三角形内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到定理的结论。
这种方法适用于各种类型的定三角形内点距离之和问题。
3.求解“定直线与定点之间的距离〞的问题:对于一个定点A和一条定直线L,我们可以利用点到直线的距离公式来求解它们之间的距离。
具体来说,我们可以设定一个动点P在直线L上,然后计算点P到点A的距离,即可得到定点与定直线之间的距离。
这种方法适用于各种类型的定直线与定点之间的距离问题。
4.求解“定点到定线段的最短距离〞的问题:对于一个定点A和一条定线段BC,我们可以利用点到线段的最短距离公式来求解它们之间的最短距离。
具体来说,我们可以设定一个动点P在线段BC上,然后计算点A到线段BP和线段CP的距离,取其中较小值即可得到定点到定线段的最短距离。
这种方法适用于各种类型的定点到定线段的最短距离问题。
5.求解“动三角形内一点到三边距离之和〞的问题:对于一个动三角形ABC内的一个点P,我们可以利用动点的方法来求解其到三边距离之和。
具体来说,我们可以将点P的坐标表示为(x,y),然后通过计算P到三条边的距离,再将它们相加,得到结论。
这种方法适用于各种类型的动三角形内点距离之和问题。
1.证明两线段相等的方法:首先确定两线段的距离类型(点点距离、点轴距离或点线距离),然后利用距离公式计算出两线段的长度,并进行化简,从而证明它们相等。
2.平行于y轴的动线段长度的最大值问题:对于平行于y轴的线段,可以利用端点的函数图象解析式,将两个端点的纵坐标表示为含有字母t的代数式。
中考专题复习:二次函数压轴题分类训练 最大最小问题(含答案)

中考压轴题专练(一)——二次函数综合考点一:距离之和最小问题 1.如图,抛物线y =21x 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,且A (一1,0). ⑴求抛物线的解析式及顶点D 的坐标; ⑵判断△ABC 的形状,证明你的结论;⑶点M (m ,0)是x 轴上的一个动点,当CM +DM 的值最小时,求m 的值. 解:(1)b =23-解析式y =21x 2-23x -2. 顶点D (23, -825).(2)当x = 0时y = -2, ∴C (0,-2),OC = 2。
∴B (4,0) ∴OA = 1, OB = 4, AB = 5. △ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C ′,则C ′(0,2),OC ′=2,连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC + MD 的值最小。
解法一:设抛物线的对称轴交x 轴于点E .∵ED ∥y 轴, ∴∠OC ′M =∠EDM ,∠C ′O M =∠DEM ∴△C ′O M ∽△DEM . ∴EDC O EM OM '=∴825223=-m m ,∴m =4124. 解法二:设直线C ′D 的解析式为y = kx + n ,则⎪⎩⎪⎨⎧-=+=825232n k n ,解得n = 2, 1241-=k .∴21241+-=x y . ∴当y = 0时, 021241=+-x , 4124=x . ∴4124=m .2.(2016河池第26题)在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,顶点为D . (1)请直接写出点A ,C ,D 的坐标;(2)如图(1),在x 轴上找一点E ,使得△CDE 的周长最小,求点E 的坐标;(3)如图(2),F 为直线AC 上的动点,在抛物线上是否存在点P ,使得△AFP 为等腰直角三角形?若存在,求出点P 的坐标,若不存在,请说明理由.解析:(1)当223y x x =--+中y =0时,有2230x x --+=,解得:1x =﹣3,2x =1,∵A 在B 的左侧,∴A (﹣3,0),B (1,0).当223y x x =--+中x =0时,则y =3,∴C (0,3). ∵223y x x =--+=2(1)4x -++,∴顶点D (﹣1,4).(3)设直线AC 的解析式为y =ax +c ,则有:330c a c =⎧⎨-+=⎩,解得:13a c =⎧⎨=⎩,∴直线AC 的解析式为y =x +3.假设存在,设点F (m ,m +3),△AFP 为等腰直角三角形分三种情况(如图2所示):①当∠P AF =90°时,P (m ,﹣m ﹣3),∵点P 在抛物线223y x x =--+上,∴2323m m m --=--+,解得:m 1=﹣3(舍去),m 2=2,此时点P 的坐标为(2,﹣5);②当∠AFP =90°时,P (2m +3,0)∵点P 在抛物线223y x x =--+上,∴20(23)2(23)3m m =-+-++,解得:m 3=﹣3(舍去),m 4=﹣1,此时点P 的坐标为(1,0);③当∠APF =90°时,P (m ,0),∵点P 在抛物线223y x x =--+上,∴2023m m =--+,解得:m 5=﹣3(舍去),m 6=1,此时点P 的坐标为(1,0).综上可知:在抛物线上存在点P ,使得△AFP 为等腰直角三角形,点P 的坐标为(2,﹣5)或(1,0).3.(2016铜仁第25题)如图,抛物线21y ax bx =+-(a ≠0)经过A (-1,0),B (2,0)两点,与y 轴交于点C .(1)求抛物线的解析式及顶点D 的坐标;(2)点P 在抛物线的对称轴上,当△ACP 的周长最小时,求出点P 的坐标;(3) 点N 在抛物线上,点M 在抛物线的对称轴上,是否存在以点N 为直角顶点的Rt △DNM 与Rt △BOC 相似,若存在,请求出所有符合条件的点N 的坐标;若不存在,请说明理由.解析:(1)由于抛物线21y ax bx =+- (a ≠0)经过A (-1,0),B (2,0)两点,因此把A 、B 两点的坐标代入21y ax bx =+- (a ≠0),可得:104210a b a b --=⎧⎨+-=⎩;解方程组可得:1212a b ⎧=⎪⎪⎨⎪=-⎪⎩,故抛物线的解析式为:211122y x x =--,∵211122y x x =--=2119()228x --,所以D 的坐标为(12,98-). (2)如图1,设P (12,k ),∵211122y x x =--,∴C (0,-1),∵A (-1,0),B (2,0),∴A 、B 两点关于对称轴对称,连接CB 交对称轴于点P ,则△ACP 的周长最小.设直线BC 为y =kx +b ,则:201k b b +=⎧⎨=-⎩,解得:121k b ⎧=⎪⎨⎪=-⎩,∴直线BC 为:112y x =-.当x =12时,11122y =⨯-=34-,∴P (12,34-); (3)存在.如图2,过点作NF ⊥DM ,∵B (2,0),C (0,﹣1),∴OB =2,OC =1,∴tan ∠OBC =12OC OB =,tan ∠OCB =OBOA=2,设点N (m ,211122m m --),∴FN =|m ﹣12|,FD =|21191228m m --+|=|2111228m m -+|,∵Rt △DNM 与Rt △BOC 相似,∴∠MDN =∠OBC ,或∠MDN=∠OCB;①当∠MDN=∠OBC时,∴tan∠MDN=FNFD=12,∴21121112228mm m-=-+,∴m=12(舍)或m=92或m=72-,∴N(92,558)或(72-,558);②当∠MDN=∠OCB时,∴tan∠MDN=FNFD=2,∴2122111228mm m-=-+,∴m=12(舍)或m=32或m=12-,∴N(32,58-)或(12-,58-);∴符合条件的点N的坐标(92,558)或(72-,558)或(32,58-)或(12-,58-).考点:二次函数综合题;相似三角形的判定与性质;分类讨论;压轴题.4.(2016湘西州第26题)如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.(1)求抛物线的解析式;(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.(2)如图1所示;∵BD⊥DE,∴∠BDE=90°.∴∠BDC+∠EDO=90°.又∵∠ODE+∠DEO=90°,∴∠BDC=∠DE0.在△BDC和△DOE中,,∴△BDC≌△DEO.。
二次函数线段和最值--最短路径
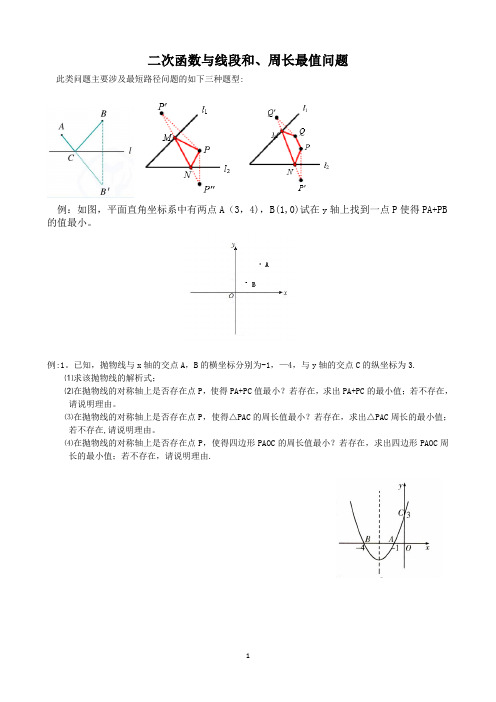
二次函数与线段和、周长最值问题此类问题主要涉及最短路径问题的如下三种题型:例:如图,平面直角坐标系中有两点A(3,4),B(1,0)试在y轴上找到一点P使得PA+PB 的值最小。
例:1。
已知,抛物线与x轴的交点A,B的横坐标分别为-1,—4,与y轴的交点C的纵坐标为3.⑴求该抛物线的解析式;⑵在抛物线的对称轴上是否存在点P,使得PA+PC值最小?若存在,求出PA+PC的最小值;若不存在,请说明理由。
⑶在抛物线的对称轴上是否存在点P,使得△PAC的周长值最小?若存在,求出△PAC周长的最小值;若不存在,请说明理由。
⑷在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长值最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.2。
如图,直线5+-=x y 与x 轴交于点B ,与y 轴交于点C,抛物线c bx x y ++-=2与直线5+-=x y 交于B 、C 两点.已知点D 的坐标为(0,3).⑴求该抛物线的解析式;⑵点M 、N 分别是直线BC 和x 轴上的动点,则当△DMN 的周长最小时,求点M ,N 的坐标,并写出△DMN 周长的最小值.3。
如图,二次函数)0(2>++=a c bx ax y 图像的顶点为D ,与x 轴的交点为A (—1,0),B(3,0),与y 轴负半轴交于点C.⑴若△ABD 为等腰直角三角形,求该抛物线的解析式; ⑵在⑴的条件下,抛物线与直线4-45x y =交于M 、N 两点(点M 在点N 的左侧),动点P 从M 点出发,先到达抛物线对称轴上的某点E ,再到达x 轴上的某点F ,最后运动到点N ,若使点P 运动的总路径最短,求点P 运动的总路径的长.。
二次函数中求线段和差最短

二次函数压轴题专项练习(一) 由运动产生的线段和差问题一、线段的和最短问题例1、如图,已知抛物线的方程C 1:()()1y x 2(x m)m 0m=-+->与x 轴相交于点B 、C ,与y 轴相交 于点E ,且点B 在点C 的左侧.(1)若抛物线C 1过点M(2,2),求实数m 的值.(2)在(1)的条件下,求△BCE的面积.(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使BH+EH 最小,并求出点H 的坐标.对应练习:1、如图,已知抛物线2y ax bx c =++经过A (4,0),B (2,3),C (0,3)三点.(1)求抛物线的解析式及对称轴.(2)在抛物线的对称轴上找一点M ,使得MA+MB 的值最小,并求出点M 的坐标.变一:已知:抛物线的对称轴为与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.1、如图,抛物线2y ax bx c=++的顶点P的坐标为13⎛⎫-⎪⎪⎝⎭,,交x轴于A、B两点,交y轴于点(0C,.、(1)求抛物线的表达式.(2)把△ABC绕AB的中点E旋转180°,得到四边形ADBC.判断四边形ADBC的形状,并说明理由.(3)试问在线段AC上是否存在一点F,使得△FBD的周长最小,若存在,请写出点F的坐标;若不存在,请说明理由.变二:如图,已知抛物线223y x x=-++与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)求A、B、C三点的坐标;(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;(3)在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
二次函数之距离最小(思维)

二次函数之最短路径问题例1.(广东)已知二次函数y=x 2-2mx+m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m=2时,该抛物线与y 轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.例2.(甘肃兰州)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线y =23x 2+bx +c 经过点B ,且顶点在直线x =52上.(1)求抛物线对应的函数关系式;(2)若把△ABO 沿x 轴向右平移得到△DCE ,点A 、B 、O 的对应点分别是D 、C 、E ,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连接BD ,已知对称轴上存在一点P 使得△PBD 的周长最小,求出P 点的坐标;例3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.例4.(湖南郴州)已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.(1)求这条抛物线的解析式;(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.例5.(辽宁)如图16,在平面直角坐标系中,直线y=x轴交于点A,与y轴交于点C,抛物线2(0)y ax c a=+≠经过A B C,,三点.(1)求过A B C,,三点抛物线的解析式并求出顶点F的坐标;(2)在抛物线上是否存在点P,使ABP△为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由;(3)试探究在直线AC上是否存在一点M,使得MBF△的周长最小,若存在,求出M点的坐标;若不存在,请说明理由.xx例6.(山西)综合与实践:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.例7.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P 是∠AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使∠CPN=90°?若存在,请直接写出点P的坐标.例8.(德州)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式;(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.练习:(烟台)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧上的点F作FH⊥AD于点H,且FH=1.5(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.例10.已知抛物线y=ax2+bx+1经过点A(1,3)和点B(2,1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路径问题——和最小【方法说明】“和最小”问题常见的问法是,在一条直线上面找一点,使得这个点与两个定点距离的和最小(将军饮马问题).如图所示,在直线l 上找一点P 使得PA +PB 最小.当点P 为直线AB ′与直线l 的交点时,PA +PB 最小.【方法归纳】①如图所示,在直线l 上找一点B 使得线段AB 最小.过点A 作AB ⊥l ,垂足为B ,则线段AB 即为所求.②如图所示,在直线l 上找一点P 使得PA +PB 最小.过点B 作关于直线l 的对称点B ′,BB ′与直线l 交于点P ,此时PA +PB 最小,则点P 即为所求.③如图所示,在∠AOB 的边AO ,BO 上分别找一点C ,D 使得PC +CD +PD 最小.过点P 分别作关于AO ,BO 的对称点E ,F ,连接EF ,并与AO ,BO 分别交于点C ,D ,此时PC +CD +PD 最小,则点C ,D 即为所求.`④如图所示,在∠AOB 的边AO ,BO 上分别找一点E ,F 使得DE +EF +CF 最小.分别过点C ,D 作关于AO ,BO 的对称点D ′,C ′,连接D ′C ′,并与AO ,BO 分别交于点E ,F ,此时DE +EF +CF 最小,则点E ,F 即为所求.lBAlAllAlOBOBBOB O⑤如图所示,长度不变的线段CD 在直线l 上运动,在直线l 上找到使得AC +BD 最小的CD 的位置.分别过点A ,D 作AA ′∥CD ,DA ′∥AC ,AA ′与DA ′交于点A ′,再作点B 关于直线l 的对称点B ′,连接A ′B ′与直线l 交于点D ′,此时点D ′即为所求.⑥如图所示,在平面直角坐标系中,点P 为抛物线(y =14x 2)上的一点,点A (0,1)在y 轴正半轴.点P在什么位置时PA +PB 最小过点B 作直线l :y =-1的垂线段BH ′,BH ′与抛物线交于点P ′,此时PA +PB 最小,则点P 即为所求.1.(13广东)已知二次函数y =x 2-2mx +m 2-1.(1)当二次函数的图象经过坐标原点O (0,0)时,求二次函数的解析式; (2)如图,当m =2时,该抛物线与y轴交于点C ,顶点为D ,求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P ,使得PC +PD 最短若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.$ll【思路点拨】(1)由二次函数的图象经过坐标原点O(0,0),直接代入求出m的值即可;(2)把m=2代入求出二次函数解析式,令x=0,求出y的值,得出点C的坐标;利用配方法或顶点坐标公式求出顶点坐标即可;(3)根据当P、C、D共线时根据“两点之间,线段最短”得出PC+PD最短,求出CD的直线解析式,令y =0,求出x的值,即可得出P点的坐标.【解题过程】解:(1)∵二次函数的图象经过坐标原点O(0,0),∴代入二次函数y=x2-2mx+m2-1,得出:m2-1=0,解得:m=±1,∴二次函数的解析式为:y=x2-2x或y=x2+2x;(2)∵m=2,∴二次函数y=x2-2mx+m2-1得:y=x2-4x+3=(x-2)2-1,∴抛物线的顶点为:D(2,-1),!当x=0时,y=3,∴C点坐标为:(0,3),∴C(0,3)、D(2,-1);(3)当P、C、D共线时PC+PD最短,【方法一】∵C(0,3)、D(2,-1),设直线CD的解析式为y=kx+3,代入得:2k+3=-1,∴k=-2,∴y=-2x+3,当y=0时,-2x+3=0,解得x=32,∴PC+PD最短时,P点的坐标为:P(32,0).【方法二】过点D作DE⊥y轴于点E,∵PO∥DE,∴PODE=COCE,∴PO2=34,解得:PO=32,∴PC+PD最短时,P点的坐标为:P(32,0)./2.(11菏泽)如图,抛物线y=12x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,证明你的结论;(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.【思路点拨】(1)把点A 的坐标代入求出b 的值,即可得出抛物线的解析式,通过配方法即可求出顶点D 的坐标; (2)观察发现△ABC 是直角三角形,可以通过勾股定理的逆定理证明.由抛物线的解析式,分别求出点B ,C 的坐标,再得出AB ,AC ,BC 的长度,易得AC 2+BC 2=AB 2,得出△ABC 是直角三角形;(3)作出点C 关于x 轴的对称点C ′,连接C 'D 交x 轴于点M ,根据“两点之间,线段最短”可知MC +MD 的值最小.求出直线C 'D 的解析式,即可得出点M 的坐标,进而求出m 的值. 【解题过程】解:(1)∵点A (-1,0)在抛物线y =12x 2+bx -2上,∴12×(-1 )2+b ×(-1)-2=0,解得b =-32,:∴抛物线的解析式为y =12x 2-32x -2=12(x -32)2-258,∴顶点D 的坐标为 (32,-258).(2)当x =0时y =-2,∴C (0,-2),OC =2.当y =0时,12x 2-32x -2=0,∴x 1=-1,x 2=4,∴B (4,0),∴OA =1,OB =4,AB =5.∵AB 2=25,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2. ∴△ABC 是直角三角形.(3)作出点C 关于x 轴的对称点C ′,则C ′(0,2),OC ′=2,连接C ′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC +MD 的值最小. 【方法一】设直线C ′D 的解析式为y =kx +n ,则⎩⎨⎧n =232k +n =-258,解得:⎩⎨⎧n =2k =-4112.∴y =-4112x +2. ∴当y =0时,-4112x +2=0,x =2441.∴m =2441.【方法二】 (设抛物线的对称轴交x 轴于点E .∵ED ∥y 轴,∴∠OC ′M =∠EDM ,∠C ′OM =∠DEM ,∴△C ′OM ∽△DEM . ∴OM EM =OC ′ED ,∴m 32-m =2258,∴m =2441.3.(11福州)已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=33x+3对称.(1)求A、B两点坐标,并证明点A在直线l上;(2)求二次函数解析式;(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.(【思路点拨】(1)二次函数y=ax2+2ax﹣3a(a≠0)中只有一个未知参数a,令y=0,解出方程ax2+2ax﹣3a=0(a≠0),即可得到点A,B的坐标.把点A的坐标代入直线l的解析式即可判断A是否在直线上;(2)根据点H、B关于过A点的直线l:y=33x+3对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,得AC=12AB=2,利用勾股定理求出HC的长,即可得出点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)直线BK∥AH易得直线BK的解析式,联立直线l的解析式方程组,即可求出K的坐标.因为点H,B 关于直线AK对称,所以HN=BN,所以根据“两点之间,线段最短”得出HN+MN的最小值是MB.作点K关于直线AH的对称点Q,连接QK,交直线AH于E,所以QM=KM,易得BM+MK的最小值为BQ,即BQ的长是HN+NM+MK的最小值,求出QB的长即可.【解题过程】解:(1)依题意,得ax2+2ax﹣3a=0(a≠0),解得x1=﹣3,x2=1,∵B点在A点右侧,∴A点坐标为(﹣3,0),B点坐标为(1,0),∵直线l:y=33x+3,当x=﹣3时,y=33×(-3)+3=0,∴点A在直线l上.(2)∵点H、B关于过A点的直线l:y=33x+3对称,∴AH=AB=4,(过顶点H作HC⊥AB交AB于C点,则AC=12AB=2,HC=23,∴顶点H (-1,23),代入二次函数解析式,解得a =-32, ∴二次函数解析式为y =-32x 2-3x +332, (3)直线AH 的解析式为y =3x +33,直线BK 的解析式为y =3x +33,由⎩⎪⎨⎪⎧y =33x +3y =3x -3,解得⎩⎨⎧x =3y =23,即K (3,23),则BK =4,∵点H 、B 关于直线AK 对称,∴HN +MN 的最小值是MB ,KD =KE =23,过点K 作直线AH 的对称点Q ,连接QK ,交直线AH 于E ,则QM =MK ,QE =EK =23,AE ⊥QK , ∴BM +MK 的最小值是BQ ,即BQ 的长是HN +NM +MK 的最小值, ∵BK ∥AH ,∴∠BKQ =∠HEQ =90°,由勾股定理得QB =8, ∴HN +NM +MK 的最小值为8.#4.(14海南)如图,对称轴为直线x =2的抛物线经过A (-1,0),C (0,5)两点,与x 轴另一交点为B .已知M (0,1),E (a ,0),F (a +1,0),点P 是第一象限内的抛物线上的动点. (1)求此抛物线的解析式;(2)当a =1时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若△PCM 是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小请说明理由.【思路点拨】(1)由对称轴为直线x =2,可以得出顶点横坐标为2,设二次函数的解析式为y =a (x -2)2+k ,再把点A ,B 的代入即可求出抛物线的解析式;(2)求四边形MEFP 的面积的最大值,要先表示出四边形MEFP 面积.直接求不好求,可以考虑用割补法来求,过点P 作PN ⊥y 轴于点N ,由S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME 即可得出;@(3)四边形PMEF 的四条边中,线段PM ,EF 长度固定,当ME +PF 取最小值时,四边形PMEF 的周长取得最小值.将点M 向右平移1个单位长度(EF 的长度),得到点M 1(1,1),作点M 1关于x 轴的对称点M 2(1,-1),连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小. 【解题过程】解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =a (x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎨⎧9a +k =04a +k =5,解得⎩⎨⎧a =-1k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)当a =1时,E (1,0),F (2,0),OE =1,OF =2.设P (x ,-x 2+4x +5),如答图2,过点P 作PN ⊥y 轴于点N ,则PN =x ,ON =-x 2+4x +5, ∴MN =ON -OM =-x 2+4x +4.S 四边形MEFP =S 梯形OFPN -S △PMN -S △OME =12(PN +OF )•ON -12PN •MN -12OM •OE=12(x +2)(-x 2+4x +5)-12x •(-x 2+4x +4)-12×1×1 =-x 2+92x +92【=-(x -94)2+15316∴当x =94时,四边形MEFP 的面积有最大值为15316,此时点P 坐标为(94,15316).(3)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3). 四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则PMEF 的周长将取得最小值.如答图3,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1); 作点M 1关于x 轴的对称点M 2,则M 2(1,-1); 连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得: ⎩⎨⎧(2+6)m +n =3m +n =-1,解得:m =46-45 ,n =46+45,∴y =46-45x -46+45.;当y =0时,解得x =6+54.∴F (6+54,0).∵a +1=6+54,∴a =6+14. ∴a =6+14时,四边形PMEF 周长最小.图1 图2 2.(14福州)如图,抛物线y =12(x3)21与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D 了.(1)求点A ,B ,D 的坐标;(2)连接CD ,过原点O 作OE ⊥CD ,垂足为H ,OE 与抛物线的对称轴交于点E ,连接AE ,AD .求证:∠AEO =∠ADC ;(3)以(2)中的点E 为圆心,1为半径画圆,在对称轴右侧的抛物线上有一动点P ,过点P 作⊙E 的切线,切点为Q ,当PQ 的长最小时,求点P 的坐标,并直接写出点Q 的坐标.yxFEMACBOPN yxF EM 2M 1M ACOP【思路点拨】(1)由顶点式直接得出点D 的坐标,再令y =0,得12(x3)21=0解出方程,即可得出点A ,B 的坐标;\(2)设HD 与AE 相交于点F ,可以发现△HEF 与△ADF 组成一个“8字型”.对顶角∠HFE =∠AFD ,只要∠FHE =∠FAD 即可.因为∠EHF =90°,只需证明∠EAD =90°即可.由勾股定理的逆定理即可得出△ADE 为直角三角形,得∠FHE =∠FAD =90°即可得出结论;(3)先画出图形.因为PQ 为⊙E 的切线,所以△PEQ 为直角三角形,半径EQ 长度不变,当斜边PE 最小时,PQ 的长度最小.设出点P 的坐标,然后表示出PE ,求出PE 的最小值,得到点P 的坐标,再求出点Q 的坐标即可. 【解题过程】解:(1)顶点D 的坐标为(3,1).令y =0,得12(x3)21=0,解得x 1=3+2,x 2=32.∵点A 在点B 的左侧,∴A 点坐标(32,0),B 点坐标(32,0).(2)过D 作DG ⊥y 轴,垂足为G .则G (0,1),GD =3.令x =0,则y =72,∴C 点坐标为(0,72).∴GC =72(1) = 92.设对称轴交x 轴于点M .∵OE ⊥CD ,∴∠GCD +∠COH =90.∵∠MOE +∠COH =90,∴∠MOE =∠GCD .又∵∠CGD =∠OMN =90,∴△DCG ∽△EOM . ∴CG OM =DGEM ,即923=3EM .∴EM =2,即点E 坐标为(3,2),ED =3. 由勾股定理,得AE 2=6,AD 2=3,∴AE 2+AD 2=6+3=9=ED 2. ∴△AED 是直角三角形,即∠DAE =90.,设AE 交CD 于点F .∴∠ADC +∠AFD =90.又∵∠AEO +∠HFE =90, ∴∠AFD =∠HFE ,∴∠AEO =∠ADC .(3)由⊙E 的半径为1,根据勾股定理,得PQ 2=EP 2-1.要使切线长PQ 最小,只需EP 长最小,即EP 2最小.设P 坐标为(x ,y ),由勾股定理,得EP 2=(x -3)2+(y -2)2.xy HAEDBCOxyADBCO∵y =12(x -3)2-1,∴(x -3)2=2y +2.∴EP 2=2y +2+y 2-4y +4=(y -1)2+5.当y =1时,EP 2最小值为5.把y =1代入y =12(x -3)2-1,得12(x -3)21=1,解得x 1=1,x 2=5.又∵点P 在对称轴右侧的抛物线上,∴x 1=1舍去.∴点P 坐标为(5,1). 此时Q 点坐标为(3,1)或(195,135).【6.(14遂宁)已知:直线l :y =﹣2,抛物线y =ax 2+bx +c 的对称轴是y 轴,且经过点(0,﹣1),(2,0).(1)求该抛物线的解析式;(2)如图①,点P 是抛物线上任意一点,过点P 作直线l 的垂线,垂足为Q ,求证:PO =PQ . (3)请你参考(2)中结论解决下列问题:(i )如图②,过原点作任意直线AB ,交抛物线y =ax 2+bx +c 于点A 、B ,分别过A 、B 两点作直线l 的垂线,垂足分别是点M 、N ,连结ON 、OM ,求证:ON ⊥OM .(ii )已知:如图③,点D (1,1),试探究在该抛物线上是否存在点F ,使得FD +FO 取得最小值若存在,求出点F 的坐标;若不存在,请说明理由.【思路点拨】#(1)因为抛物线的对称轴是y 轴,所以b =0,再代入点(0,﹣1),(2,0)即可求出抛物线的解析式; xyFH ADBCO GE xyE Q 1ADBCOPQ 2yxEOPQyxBAO N MyxDOF(2)由(1)设出P 的坐标,分别表示出PE ,PQ 的长度,即可得出结论;(3)(i )因为BN ∥AM ,所以∠ABN +∠BAM =180°.由(2)的结论可得BO =BN ,AO =AM ,可得出∠BON =∠BNO ,∠AOM =∠AMO ,易得∠BON +∠AOM =90°再得到∠MON =90°即可;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,由(2)的结论根据矩形的性质可以得出结论. 【解题过程】解:(1)由题意,得⎩⎪⎨⎪⎧-b 2a =0-1=c 0=4a +2b +c ,解得:⎩⎪⎨⎪⎧a =14b =0c =-1,∴抛物线的解析式为:y =14x 2-1;(2)如图①,设P (a ,14a 2﹣1),就有OE =a ,PE =14a 2﹣1,∵PQ ⊥l ,∴EQ =2,∴QP =14a 2+1.在Rt△POE 中,由勾股定理,得PO =a 2+(14a 2-1)2=14a 2+1,∴PO =PQ ;(3)(i )如图②,∵BN ⊥l ,AM ⊥l ,∴BN =BO ,AM =AO ,BN ∥AM ,∴∠BNO =∠BON ,∠AOM =∠AMO ,∠ABN +∠BAM =180°. ∵∠BNO +∠BON +∠NBO =180°,∠AOM +∠AMO +∠OAM =180°,{∴∠BNO +∠BON +∠NBO +∠AOM +∠AMO +∠OAM =360°,∴2∠BON +2∠AOM =180°, ∴∠BON +∠AOM =90°,∴∠MON =90°,∴ON ⊥OM ;(ii )如图③,作F ′H ⊥l 于H ,DF ⊥l 于G ,交抛物线与F ,作F ′E ⊥DG 于E ,∴∠EGH =∠GHF ′=∠F ′EG =90°,FO =FG ,F ′H =F ′O ,∴四边形GHF ′E 是矩形,FO +FD =FG +FD =DG ,F ′O +F ′D =F ′H +F ′D ,∴EG =F ′H ,∴DE <DF ′, ∴DE +GE <HF ′+DF ′,∴DG <F ′O +DF ′,∴FO +FD <F ′O +DF ′,∴F 是所求作的点. ∵D (1,1),∴F 的横坐标为1,∴F (1,54).【举一反三】1.(12滨州)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 经过A (﹣2,﹣4),O (0,0),B (2,0)三点.(1)求抛物线y =ax 2+bx +c 的解析式;)(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.l@2.(13成都)在平面直角坐标系中,已知抛物线y=﹣12x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;(ii)取BC的中点N,连接NP,BQ.试探究PQNP+BQ是否存在最大值若存在,求出该最大值;若不存在,请说明理由."》【3.(11眉山)如图,在直角坐标系中,已知点A (0,1),B (﹣4,4),将点B 绕点A 顺时针方向90°得到点C ;顶点在坐标原点的拋物线经过点B . (1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为d 1,点P 到点A 的距离为d 2,试说明d 2=d 1+1; (3)在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出△PAC 的周长的最小值.?{%¥【参考答案】1.解:(1)把A (﹣2,﹣4),O (0,0),B (2,0)三点的坐标代入y =ax 2+bx +c 中,得⎩⎨⎧4a -2b +c =-44a +2b +c =0c =0,解得a =﹣12,b =1,c =0,∴解析式为y =﹣12x 2+x .(2)由y =﹣12x 2+x =﹣12(x ﹣1)2+12,可得抛物线的对称轴为x =1,并且对称轴垂直平分线段OB ,∴OM =BM , ∴OM +AM =BM +AM ,连接AB 交直线x =1于M 点,则此时OM +AM 最小, 过点A 作AN ⊥x 轴于点N ,在Rt△ABN 中,AB =AN 2+BN 2=42+42=42,^∴OM +AM 最小值为42.2.解:(1)∵等腰直角三角形ABC 的顶点A 的坐标为(0,-1),C 的坐标为(4,3),∴点B 的坐标为(4,-1).∵抛物线过A (0,-1),B (4,-1)两点,∴ ⎩⎨⎧c =-1-12×16+4b +c =-1,解得:b =2,c =-1,∴抛物线的函数表达式为:y =-12x 2+2x -1.(2)(i )∵A (0,-1),C (4,3),∴直线AC 的解析式为:y =x -1.设平移前抛物线的顶点为P 0,则由(1)可得P 0的坐标为(2,1),且P 0在直线AC 上. ∵点P 在直线AC 上滑动,∴可设P 的坐标为(m ,m -1), 则平移后抛物线的函数表达式为:y =-12(x -m )2+m -1.解方程组:⎩⎨⎧y =x -1y =-12(x -m )2+(m -1),解得⎩⎨⎧x 1=m y 1=m -1, ⎩⎨⎧x 2=m -2y 2=m -3, ^∴P (m ,m -1),Q (m -2,m -3).过点P 作PE ∥x 轴,过点Q 作QF ∥y 轴,则PE =m -(m -2)=2,QF =(m -1)-(m -3)=2.∴PQ =22=AP 0.若以M 、P 、Q 三点为顶点的等腰直角三角形,则可分为以下两种情况: ①当PQ 为直角边时:点M 到PQ 的距离为22(即为PQ 的长). 由A (0,-1),B (4,-1),P 0(2,1)可知, △ABP 0为等腰直角三角形,且BP 0⊥AC ,BP 0=22.如答图1,过点B 作直线l 1∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 1的解析式为:y =x +b 1,∵B (4,-1),∴-1=4+b 1,解得b ==-5,∴直线l 1的解析式为:y =x -5.解方程组 ⎩⎨⎧y =x -5y =-12x 2+2x -1,得:⎩⎨⎧x 1=4y 1=-1,⎩⎨⎧x 2=-2y 2=-7, ∴M 1(4,-1),M 2(-2,-7).|②当PQ 为斜边时:MP =MQ =2,可求得点M 到PQ 的距离为 2 . 如答图2,取AB 的中点F ,则点F 的坐标为(2,-1). 由A (0,-1),F (2,-1),P 0(2,1)可知:△AFP 0为等腰直角三角形,且点F 到直线AC 的距离为 2 .过点F 作直线l 2∥AC ,交抛物线y =-12x 2+2x -1于点M ,则M 为符合条件的点.∴可设直线l 2的解析式为:y =x +b 2,∵F (2,-1),∴-1=2+b 2,解得b 2=-3,∴直线l 2的解析式为:y =x -3.解方程组⎩⎨⎧y =x -3y =-12x 2+2x -1,得:⎩⎨⎧x 1=1+5y 1=-2+5,⎩⎨⎧x 1=1-5y 1=-2-5, ∴M 3(1+5,-2+5),M 4(1-5,-2-5). 综上所述,所有符合条件的点M 的坐标为:M 1(4,-1),M 2(-2,-7),M 3(1+5,-2+5),M 4(1-5,-2-5).(ii )PQNP +BQ存在最大值.理由如下:由i )知PQ =22为定值,则当NP +BQ 取最小值时,PQNP +BQ有最大值. 如答图2,取点B 关于AC 的对称点B ′,易得点B ′的坐标为(0,3),BQ =B ′Q . 连接QF ,FN ,QB ′,易得FN ∥PQ ,且FN =PQ ,∴四边形PQFN 为平行四边形.∴NP =FQ . ∴NP +BQ =FQ +B ′Q ≥FB ′=22+42=25.∴当B ′、Q 、F 三点共线时,NP +BQ 最小,最小值为25.∴PQ NP +BQ 的最大值为2225=105.3.解:(1)设抛物线的解析式:y =ax 2,∵拋物线经过点B (﹣4,4),∴4=a •42,解得a =14,所以抛物线的解析式为:y =14x 2;F过点B作BE⊥y轴于E,过点C作CD⊥y轴于D,如图,∵点B绕点A顺时针方向90°得到点C,∴Rt△BAE≌Rt△ACD,∴AD=BE=4,CD=AE=OE﹣OA=4﹣1=3,∴OD=AD+OA=5,∴C点坐标为(3,5);(2)设P点坐标为(a,b),过P作PF⊥y轴于F,PH⊥x轴于H,如图,∵点P在抛物线y=14x2上,∴b=14a2,∴d1=14a2,∵AF=OF﹣OA=PH﹣OA=d1﹣1=14a2﹣1,PF=a,在Rt△PAF中,PA=d2=AF2+PF2=(14a2-1)2+a2=14a2+1,∴d2=d1+1;(3)由(1)得AC=5,∴△PAC的周长=PC+PA+5=PC+PH+6,要使PC+PH最小,则C、P、H三点共线,∴此时P点的横坐标为3,把x=3代入y=14x2,得到y=94,即P点坐标为(3,94),此时PC+PH=5,∴△PAC的周长的最小值=5+6=11.。
