高中物理公式大全(学考用)

合集下载

学考物理公式大全

学考物理公式大全以下列出了一些高中物理中常用的重要公式：力学：1. 位移公式：$s=vt+\dfrac{1}{2}at^2$2. 速度公式：$v=u+at$3. 加速度公式：$a=\dfrac{v-u}{t}$4. 位移、速度、加速度之间的关系：$v^2=u^2+2as$5. 牛顿第二定律：$F=ma$6. 牛顿第三定律：$F_{12}=-F_{21}$7. 功公式：$W=Fs$8. 功率公式：$P=\dfrac{W}{t}$9. 动能公式：$E_k=\dfrac{1}{2}mv^2$10. 动能定理：$W=F\times s=E_k$11. 弹性势能（弹性应变能）：$E_p=\dfrac{1}{2}kx^2$12. 势能公式：$E_p=mgh$13. 动能和势能之间的转换关系：$E_k+E_p=E$14. 阻力公式：$F=kv$15. 滑动摩擦力公式：$f_s=\mu_sN$光学：1. 光速公式：$c=\lambda f$，其中$c$为光速，$\lambda$为波长，$f$为频率。

2. 焦距公式：$\dfrac{1}{f}=\dfrac{1}{p}+\dfrac{1}{q}$，其中$f$为焦距，$p$为物距，$q$为像距。

3. 物距像距公式：$m=-\dfrac{q}{p}$，其中$m$为放大率。

4. 折射定律：$\dfrac{\sin i}{\sin r}=\dfrac{n_2}{n_1}$，其中$n_1$为第一介质的折射率，$n_2$为第二介质的折射率。

5. 分辨本领：$\sin\theta=\dfrac{1.22\lambda}{D}$，其中$\theta$为最小分辨角，$\lambda$为波长，$D$为孔径直径。

电学：1. 电荷量公式：$Q=It$，其中$Q$为电荷量，$I$为电流强度，$t$为时间。

2. 欧姆定律：$U=IR$，其中$U$为电压，$I$为电流强度，$R$为电阻。

3. 焦耳定律：$W=UIt=I^2Rt=\dfrac{U^2}{R}t$，其中$W$为电功，$U$为电压，$I$为电流强度，$R$为电阻，$t$为时间。

物理高中学考重点公式

物理高中学考重点公式在高中物理学考试中，掌握重要的公式对于解题和计算非常重要。

以下是一些物理高中学考重点公式的例子：1. 运动学公式：- 位移公式：S = V0 * t + 1/2 * a * t^2- 速度公式：V = V0 + a * t- 加速度公式：a = (V - V0) / t- 两点间距离公式：S = (V + V0) / 2 * t- 自由落体高度公式：h = 1/2 * g * t^22. 动力学公式：- 力的定义：F = m * a- 动量公式：p = m * v- 动量变化公式：Δp = F * Δt- 冲力公式：F = Δp / Δt- 动能公式：KE = 1/2 * m * v^2- 功率公式：P = W / t3. 电学公式：- 电流强度公式：I = Q / t- 电压公式：V = I * R- 电阻公式：R = V / I- 等效电阻公式：1/R = 1/R1 + 1/R2 + ...- 欧姆定律：V = I * R4. 光学公式：- 光速公式：c = λ * f- 光的折射定律：n1 * sinθ1 = n2 * sinθ2- 焦距公式：1/f = 1/o + 1/i- 放大率公式：m = -i / o这些公式覆盖了物理学的基本概念和常见问题。

在考试中，掌握这些公式并理解它们的应用非常重要。

同时，理解物理背后的概念和原理也是解题的关键。

除了这些公式，还应该熟悉单位制和符号的使用，以确保计算的准确性。

最重要的是，通过大量的练习和实践，将这些公式应用到实际问题中，以提高解题的能力。

高中物理学考公式大全

高中物理学考公式大全一、运动学基本公式1．匀变速直线运动基本公式：速度公式：(无位移)at v v t +=0 位移公式：（无末速度）2021at t v x += 推论公式（无时间）：ax v v t2202=- （无加速度）t v v x t 20+=2、计算平均速度txv ∆∆=【计算所有运动的平均速度】 20tv v v +=【只能算匀变速运动的平均速度】3、打点计时器 (1)两种打点计时器（a ）电磁打点计时器：工作电压（6V 以下）交流电频率50HZ （b ）电火花打点计时器：工作电压（220v ）交流电频率50HZ【计数点要看清是相邻的打印点（间隔0.02s ）还是每隔5个点取一个计数点(间隔0.1s)】（2）纸带分析（a ）求加速度公式： (b)求某点速度公式：tx v v t22==【会根据纸带计算某个计数点的瞬时速度】二、力学基本规律1、不同种类的力的特点（1）．重力：mg G =（2rGMg ∝，↓↑g r ,，在地球两极g 最大，在赤道g 最小） (2). 弹力: x k F ⋅= 【弹簧的劲度系数k 是由它的材料，粗细等元素决定的，与它受不受力以及在弹性线度内受力的大小无关】 (3).滑动摩擦力 N F F ⋅=μ；【在平面地面上，FN=mg ，在斜面上等于重力沿着斜面的分力】静摩擦力F 静 :0～F max ,【用力的平衡观点来分析】2．合力：2121F F F F F +≤≤-合力的合成与分解：满足平行四边形定则三、牛顿运动定律（1）惯性：只和质量有关（2）F 合=ma 【用此公式时，要对物体做受力分析】(3)作用力和反作用力：大小相等、方向相反、性质相同、同时产生同时消失，作用在不同的物体上（这是与平衡力最明显的区别）特殊规律：匀变速直线运动的中间时刻速度公式：202tt t v v v v +== 22)(T n m x x T xa n m--=∆= 自由落体运动公式：速度公式：gt v=位移公式：221gt h =位移和速度的公式：gh v 22=受力分析顺序：1.重力2.弹力（看接触的物体）3.摩擦力4.其他力（4）运用牛顿运动定律解题四、曲线运动1．曲线运动的速度：与曲线的切线方向相同曲线运动的条件：合外力与速度不在同一直线上（合外力指向轨迹凹侧） 2．平抛运动：（特点：初速度沿水平方向，物体只受重力，加速度a=g 恒定不变，平抛运动是匀变速曲线运动）水平方向：00 ,v v t v x x == 竖直方向：221gt y =, gh gt v y 2== , 经时间t 的速度：22022)(gt v v v v y x t +=+= 、位移22y x s +=平抛运动时间：ght 2=（取决下落高度，与初速度无关） 3．匀速圆周运动（1）线速度：T rt s v ⋅==π2 （2）角速度：Tt πφω2==（3）r v ⋅=ω（4）向心加速度：v r r v a ⋅===ωω22 周期：ωπ2=T （5）向心力：r Tm r m r v m a m F 22224πω===⋅= 【匀速圆周运动中保持不变的物理量】：角速度、周期、频率、线速度的大小（线速度变化，因为它的方向变化）（匀速圆周运动是变加速曲线运动，因为它的加速度方向在不断变化）五、万有引力与航天【学考要求】：会算天体的质量，会判断线速度、角速度、周期、向心加速度随轨道半径变化的关系万有引力定律：221rm m GF = （1）应用：把天体运动看成是匀速圆周运动，其所需向心力由万有引力提供。

高中物理学考公式(纯公式4页word版)

知识像烛光，能照亮一个人，也能照亮无数的人。

--培根高二物理新课程会考公式汇总（精简版）《必修1》1、匀速直线运动的速度：txv = 2、加速度：tv v a 0-=⇒3、匀变速直线运动：（1）速度与时间公式：v = v 0 + at（2）位移与时间公式: x = v o t +12at 2（3）速度与位移关系：ax vv 2202=-（4）面积公式：tvv x )2(0+=注意：公式应用时各矢量的方向⇒正、负的取值以v 0的方向为正方向，v 、a 、x 的方向与v 0相同取正值，相反取负值（5）研究匀变速直线运动（纸带模型）常用两个推论：（1）△x = aT 2（2））v t 2⁄=v 0+v 2(中点时刻)< v x 2⁄=√v 02+v 22（中点位置）4、胡克定律：F = kx ⇒{5、滑动摩擦力的公式：μ=f F N6、静摩擦力： 0<F 静≤F ma =μsF N7、两个共点力的合力F=√F 12+F 22+2F 1F 2cosθ tan θ=F 2sinθF 1+F 2cosθ合力范围：|F 1－F 2| ≤ F 合≤ F 1＋F 2注意：1.两个分力的大小一定时，合力随着夹角的增大而减小 2.合力不一定大于分力 8、牛顿第二定律: F 合=ma伸长量 x=L-L 0压缩量 x=L 0-L自由落体运动⇒v 0=0{v =+ at x =12at 2 v 2=2ax⇒{已知（求）物体受力情况求（已知）物体运动情况牛顿第二定律运动学公式加速度 a9. 动力学有两类问题： F=ma ⟺ 《必修2》1、曲线运动（1）运动轨迹（2）匀变速运动（3）曲线运动的条件：①有一定初速度；②所受合外力与速度不共线注意：共线为直线运动（4）两个匀变速直线运动的合运动①合初速度方向与合加速度方向共线匀变速直线运动合初速度方向与合加速度方向不共线匀变速曲线运动2、平抛运动规律：水平位移：x= v o t 竖直位移：h =21g t 2 合(实际)位移： r=√x 2+y 2 夹角：tan α=gt 2v 0水平速度：v x = v o 竖直分速度：v y = g t 合（实际）速度：v=√v 02+(gt)2 夹角：tan θ=gt v 03、匀速圆周运动：（1）线速度: v =Trt s π2==r ω （2）角速度：ωT t πθ2== （3）向心加速度：a =22ωr r v =（4）向心力：F=ma= m 22ωmr r v ==m （2πT ）2r=m (2πn)2r（注意：做圆周运动的物体必须必须提供向心力，而不是受到向心力）4、天体运动（1）开普勒三大定律：第一定律（轨道定律）：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上第二定律（面积定律）：对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。

高中物理学业水平测试公式大全

高中物理学业水平测试公式大全在高中物理学中，有很多重要的公式可以帮助我们理解和解决问题。

下面是一些常见的高中物理公式：1.速度公式：v=Δx/Δt。

它表示速度等于位移与时间的比值。

2.加速度公式：a=Δv/Δt。

它表示加速度等于速度变化与时间的比值。

3. 动力学公式：F = ma。

它表示力等于物体质量乘以加速度。

4. 动能公式：KE = 1/2mv^2、它表示动能等于物体质量乘以速度的平方的一半。

5. 势能公式：PE = mgh。

它表示势能等于物体质量、重力加速度和高度的乘积。

6.机械能守恒公式：E=KE+PE。

它表示机械能等于动能和势能之和。

7. 弹性势能公式：PE = 1/2kx^2、它表示弹性势能等于弹簧常数和位移平方的乘积的一半。

8.冲量公式：J=FΔt。

它表示冲量等于力乘以时间。

9.牛顿第一定律：F=0。

它表示当物体处于平衡状态时，合力等于零。

10. 牛顿第二定律：F = ma。

它表示物体的加速度等于物体的质量乘以合力。

11.牛顿第三定律：F₁₂=-F₂₁。

它表示两个物体之间的作用力和反作用力大小相等，方向相反。

12.简单机械的杠杆原理：F₁d₁=F₂d₂。

它表示杠杆上两个力和其对应的力臂的乘积相等。

13.摩擦力公式：Ff=μN。

它表示摩擦力等于摩擦系数和法向压力的乘积。

14.能量守恒公式：E₁+W=E₂。

它表示能量之和等于外界对物体做的功。

15.电阻公式：R=V/I。

它表示电阻等于电压与电流的比值。

16.电路中的欧姆定律：V=IR。

它表示电压等于电流乘以电阻。

17.电功公式：W=VIt。

它表示电功等于电压乘以电流乘以时间。

这些公式是高中物理学的基础，通过运用它们，我们可以更好地理解物理现象和解决与力学、运动、能量、电路等相关的问题。

它们是我们在物理学习中的重要工具，帮助我们进行分析和计算，从而加深我们对物理学的理解。

高二物理学考公式

高二物理学考公式高二物理的学考公式主要有以下几个部分：1. 平抛运动：水平方向速度公式：Vx=Vo竖直方向速度公式：Vy=gt水平方向位移公式：Sx=Vot竖直方向位移公式：Sy=gt^2/2运动时间公式：t=(2Sy/g)^(1/2)合速度公式：Vt=(Vx^2+Vy^2)^(1/2)=[Vo^2+(gt)^2]^(1/2) 合速度方向与水平夹角公式：tgβ=Vy/Vx=gt/Vo合位移公式：S=(Sx^2+Sy^2)^(1/2)位移方向与水平夹角公式：tgα=Sy/Sx=gt/2Vo2. 匀速圆周运动：线速度公式：V=s/t=2πR/T角速度公式：ω=Φ/t=2π/T=2πf向心加速度公式：a=V^2/R=ω^2R=(2π/T)^2R向心力公式：F心=Mv^2/R=mω^2R=m(2π/T)^2R周期与频率关系公式：T=1/f角速度与线速度关系公式：V=ωR角速度与转速关系公式：ω=2πn（此处频率与转速意义相同）3. 其他常用公式：匀速直线运动的位移公式：x=vt匀变速直线运动的速度公式：v=v0+at匀变速直线运动的位移公式：x=v0t+at^2/2向心加速度与半径关系公式：a=v^2/r=4π^2r/T^2动能定理公式：W=mvt^2/2-mv0^2/2重力势能计算公式：Ep=mgh库仑定律的数学表达式：F=kQq/r^2电场强度的定义式：E=F/q电势差的定义式：U=W/q欧姆定律：I=U/R电功率的计算公式：P=UI焦耳定律：Q=I^2Rt磁感应强度的定义式：B=F/IL安培力的计算式：F=BIL洛伦兹力的计算式：f=qvb法拉第电磁感应定律：E=φ/t导体切割磁感线产生的感应电动势公式：E=Blv。

高中物理学考必背公式

高中物理学考必背公式高中物理是一门重要的科目，对于理解自然界的运行规律具有重要的作用。

在高中物理学习中，掌握一些必背公式是很重要的，下面将介绍一些高中物理学考试中常见的必背公式。

1.加速度公式：加速度a=(v-u)/t其中，a表示加速度，v表示最终速度，u表示初始速度，t表示时间。

2.动力公式：力F=m*a其中，F表示力，m表示物体的质量，a表示加速度。

3.动能公式：动能E=1/2*m*v^2其中，E表示动能，m表示物体的质量，v表示物体的速度。

4.位移公式：位移s=1/2*(v+u)*t其中，s表示位移，v表示最终速度，u表示初始速度，t表示时间。

5.动量公式：动量p=m*v其中，p表示动量，m表示物体的质量，v表示物体的速度。

6.弹性势能公式：弹性势能Ep=1/2*k*x^2其中，Ep表示弹性势能，k表示弹性系数，x表示弹性变形的位移。

7.万有引力公式：万有引力Fg=G*(m1*m2)/r^2其中，Fg表示万有引力，G表示万有引力常数，m1和m2分别表示两个物体的质量，r表示两个物体的距离。

8.简谐振动的周期公式：周期T = 2π * sqrt(m / k)其中，T表示周期，m表示物体的质量，k表示弹性系数。

9.柯尼希定律：U=R*I其中，U表示电压，R表示电阻，I表示电流。

10.等效电阻的计算公式：1/Rt=1/R1+1/R2+1/R3+...其中，Rt表示等效电阻，R1、R2、R3等表示电阻的取值。

以上是高中物理学中较为常见的一些必背公式，掌握这些公式将有助于顺利完成物理学的学习和考试。

除了背诵这些公式，理解公式的物理意义和适当的运用也非常重要，通过练习和实践巩固公式的应用。

2022年高中物理学业水平合格考公式大全

2、自由落体运动：
①初速度 Vo＝0
②末速度 V＝gt
③下落高度 h＝gt2/2（从 Vo 位置向下计算）
④推论 V2＝2gh
注:(1)自由落体运动是初速度为零的匀加速直线运动，遵循匀变速直线运动规律；
(2)a＝g＝9.8m/s2≈10m/s2（重力加速度在赤道附近较小,在高山处比平地小，方向竖直向下）。
7、电场线从正电荷出发终止于负电荷,电场线不相交,切线方向为场强方向,电场线密处场强大。 8、电子伏(eV)是能量的单位，1eV＝1.60×10-19J。
9、电流：I＝Q/t｛I:电流(A)，q:在时间 t 内通过导体横截面的电量(C)，t:(s)｝
10、欧姆定律：I＝U/R｛I:导体电流(A)，U:导体两端电压(V)，R:导体电阻(Ω)｝
5、国际单位制中的力学基本单位（符号~单位）：时间（t）~s，长度（l）~m，质量（m）~kg
四、机械能及其守恒定律：
1、功：W＝Flcosα（定义式）｛W:功(J)，F:恒力(N)，l:位移(m)，α:F、l 间的夹角｝
2、功率：P＝W/t(定义式)｛P:功率[瓦(W)]，W:t 时间内所做的功(J)，t:做功所用时间(s)｝
小相等。
六、电场·电流：
1、电荷守恒定律、元电荷：(e＝1.60×10-19C)；带电体所带电荷量等于元电荷的整数倍 2、库仑定律：F＝kQ1Q2/r2（在真空中）｛F:点电荷间的作用力(N)，k:静电力常量 k＝9.0×109N•m2/C2，Q1、 Q2:两点电荷的电量(C)，r:两点电荷间的距离(m)，方向在它们的连线上，是作用力与反作用力，同种电荷互相排斥，异种电荷互相吸引｝
二、相互作用：
1、重力 G＝mg（方向竖直向下，g＝9.8m/s2≈10m/s2，作用点在重心，适用地球表面附近）

高中物理会考学业水平考试公式及知识点归纳总结(超详细)

一、力学部分1. 运动学公式速度公式：v = Δx / Δt加速度公式：a = Δv / Δt位移公式：Δx = v0 Δt + 1/2 a Δt^2速度时间图像：vt图像中的斜率表示加速度，面积表示位移2. 动力学公式牛顿第一定律：物体静止或匀速直线运动时，合外力为零牛顿第二定律：F = m a牛顿第三定律：作用力与反作用力大小相等、方向相反动能定理：ΔK = W = F Δx势能公式：Ep = m g h3. 动能和势能动能：K = 1/2 m v^2势能：Ep = m g h机械能守恒：在没有非保守力做功的情况下，机械能守恒二、热学部分1. 温度与热量温度：表示物体热冷程度的物理量热量：物体间传递的热能比热容：单位质量的物质升高1摄氏度所需的热量2. 热力学第一定律ΔU = Q W内能：物体内部所有分子动能和势能的总和热量传递：热传导、热对流、热辐射3. 热力学第二定律熵：表示系统无序程度的物理量熵增原理：孤立系统的熵总是增加或保持不变三、电磁学部分1. 静电场库仑定律：F = k (q1 q2) / r^2电场强度：E = F / q电势：V = k Q / r电势差：ΔV = Vb Va2. 电流与电阻欧姆定律：I = V / R电阻：R = ρ L / A电阻率：ρ = R A / L3. 磁场与电磁感应洛伦兹力：F = q (v × B)法拉第电磁感应定律：ε = N ΔΦ / Δt楞次定律：感应电流的方向总是使得它产生的磁场与原磁场的变化相反四、光学部分1. 几何光学反射定律：入射角等于反射角折射定律：n1 sinθ1 = n2 sinθ2薄透镜公式：1/f = 1/u + 1/v2. 波动光学干涉：两束相干光波叠加产生明暗相间的条纹衍射：光波绕过障碍物或通过狭缝后发生弯曲现象偏振：光波振动方向具有特定方向性的现象五、近代物理部分1. 相对论时间膨胀：Δt' = Δt / √(1 v^2 / c^2)长度收缩：L' = L √(1 v^2 / c^2)质能方程：E = mc^22. 量子力学波函数：描述微观粒子状态的数学函数不确定性原理：Δx Δp ≥ h / 4π能级量子化：微观粒子的能量只能取离散的值六、振动与波动1. 简谐振动振幅：A = Δx_max周期：T = 2π / ω频率：f = 1 / T速度：v = Aωcos(ωt)加速度：a = Aω^2cos(ωt)2. 机械波波速：v = fλ波长：λ = v / f波动方程：y = A cos(ωt kx)能量密度：u = 1/2 ω^2 A^2能量传输速率：P = u v S七、原子物理1. 原子结构氢原子能级：E_n = 13.6 / n^2 eV波尔半径：a_0 = 0.529 Å粒子自旋：微观粒子自旋角动量的大小和方向2. 核物理质量亏损：Δm = (m_核 m_质子 m_中子)核结合能：ΔE = Δmc^2放射性衰变：α衰变、β衰变、γ衰变核反应方程：质量数守恒、电荷数守恒八、实验技能1. 实验误差分析系统误差：由于测量仪器或方法不准确引起的误差偶然误差：由于测量过程中随机因素引起的误差误差传递：实验结果误差的传递和合成2. 实验数据处理有效数字：表示测量结果的精确程度图像处理：通过图像处理方法分析实验数据数据拟合：利用数学模型对实验数据进行拟合，得出规律简洁明了地概括实验内容引言：介绍实验背景、目的和意义实验原理：阐述实验原理和所用公式实验步骤：详细描述实验过程和操作方法数据处理：对实验数据进行处理和分析讨论：对实验结果进行讨论，提出改进建议九、解题技巧1. 分析题目理解题意：仔细阅读题目，明确题目要求解决的问题。

高中学考物理公式总结表

高中学考物理公式总结表一、运动学1. 匀速直线运动公式匀速直线运动的位移与速度成正比，位移与时间成正比，速度与时间无关。

公式为：位移Δx = v × t2. 匀加速直线运动公式匀加速直线运动的位移与速度成正比，位移与时间的平方成正比，速度与时间成正比。

公式为：位移Δx = v0 × t + 1/2 × a × t^23. 初速度、末速度与加速度的关系匀加速直线运动的末速度与初速度和加速度成正比。

公式为：v = v0 + a × t4. 速度、加速度和位移的关系匀加速直线运动的位移与初速度、时间和加速度成正比。

公式为：Δx = v0 × t + 1/2 × a × t^25. 速度、加速度和时间的关系匀加速直线运动的末速度与初速度、加速度和时间成正比。

公式为：v^2 = v0^2 + 2 × a × Δx6. 自由落体运动公式自由落体运动是指物体只受重力作用的运动。

在自由落体运动中，物体的位移与时间的平方成正比。

公式为：Δx = 1/2 × g × t^27. 匀变速圆周运动公式匀变速圆周运动的角速度与时间成正比，角度与时间成正比，角速度与角度无关。

公式为：θ = ω × t8. 匀变速圆周运动的速度公式匀变速圆周运动的速度与角速度和半径成正比。

公式为：v = ω × r二、力学1. 牛顿第一定律牛顿第一定律也称为惯性定律，它指出：物体如果没有外力作用，将保持静止或匀速直线运动的状态。

2. 牛顿第二定律牛顿第二定律描述了物体受力后的加速度与作用力成正比的关系。

公式为：F = m × a3. 牛顿第三定律牛顿第三定律指出：任何两个物体之间都存在相等且反向的作用力。

即：作用力与反作用力大小相等，方向相反。

4. 动量定理动量定理描述了物体的动量变化与作用力和时间的乘积成正比的关系。

高中物理学业水平考试公式及知识点总结

高中物理学业水平考试公式及知识点总结力=kx（k为弹性系数，x为伸长或压缩的长度，方向与伸长或压缩的方向相反，作用点在物体的接触点上）3、摩擦力：静摩擦力和动摩擦力，静摩擦力的大小不超过物体间的正压力与静摩擦系数的乘积，动摩擦力的大小与物体间的正压力成正比，与动摩擦系数有关。

4、牛顿第三定律：作用力与反作用力大小相等，方向相反，作用在不同的物体上。

三、牛顿运动定律：1、牛顿第一定律：惯性定律，物体在无外力作用下静止或匀速直线运动。

2、牛顿第二定律：运动定律，物体所受合外力等于物体的质量乘以加速度，F=ma。

3、牛顿第三定律：作用力与反作用力大小相等，方向相反，作用在不同的物体上。

四、功和能量：1、功：力沿着位移方向所做的功，W=Fs。

2、功率：单位时间内所做的功，P=W/t。

3、动能：物体由于运动而具有的能量，Ek=1/2mv2.4、势能：物体由于位置而具有的能量，Ep=mgh。

5、机械能守恒定律：在没有非弹性碰撞和摩擦力的情况下，机械能守恒。

五、电学基础：1、电荷：带电物体所具有的属性，同种电荷相斥，异种电荷相吸。

2、库仑定律：两个电荷之间的电力与它们的电荷量成正比，与它们之间的距离平方成反比。

3、电场：电荷周围的空间中存在电场，电荷在电场中受到电力作用。

4、电势：单位正电荷所具有的电势能，电势差为两点间电势的差值，V=U/Q。

5、欧姆定律：电流强度与电压成正比，与电阻成反比，I=U/R。

六、磁学基础：1、磁场：磁荷周围的空间中存在磁场，磁荷在磁场中受到磁力作用。

2、洛伦兹力：带电粒子在磁场中受到的力，F=qvBsinθ。

3、安培定律：电流元在磁场中所受的力与电流元、磁场和它们之间的夹角有关，F=BILsinθ。

4、法拉第电磁感应定律：磁通量的变化率与电磁感应电动势成正比，ε=-dΦ/dt。

5、楞次定律：感应电流的方向使得磁场的变化量减小。

以上是高中物理学考试中的重点知识点，掌握这些知识点可以有效提高物理学考试的成绩。

学考必背公式

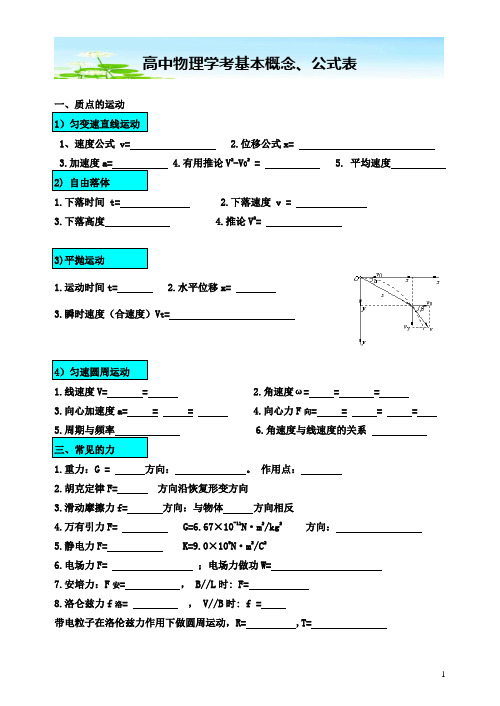
高中物理学考基本概念、公式表1、速度公式 v= 2.位移公式x=有用推论V2-V02 = 5. 平均速度1.下落时间 t=2.下落速度 v =3.下落高度4.推论V2=1.运动时间t=2.水平位移x=3.瞬时速度（合速度）V t=1.线速度V= =2.角速度ω= = =3.向心加速度a= = =4.向心力F向= = = =角速度与线速度的关系1.重力：G = 方向：。

作用点：2.胡克定律F= 方向沿恢复形变方向3.滑动摩擦力f= 方向：与物体方向相反4.万有引力F= G=6.67×10-11N·m2/kg2 方向：5.静电力F= K=9.0×109N·m2/C26.电场力F= ；电场力做功W=7.安培力：F安= ， B//L时: F=8.洛仑兹力f洛= ， V//B时: f =带电粒子在洛伦兹力作用下做圆周运动，R= ,T=1.两共点力F1F2，同向: F合= 反向：F合= (F1>F2)任意夹角合力大小范围≤F合≤2.互成角度力的合成F1⊥F2时: F合=3. 如图，G1= G2=五、动力学（运动和力）1.第二运动定律：F合= a由合外力决定,与合外力方向一致。

2.超重：F N = G + ma 失重：F N =G - ma3、功W = Ɵ的含义3.重力做功W ab= 重力做正功，重力势能，重力做负功，重力势能。

4.瞬时功率P瞬 = 平均功率P5.汽车牵引力的功率 P= ；汽车最大行驶速度V max=7.动能E k= ；重力势能E P= 机械能E=应用：1.一对作反力的特点：F= -F´特点：2.共点力的平衡条件：F合= ，二力平衡特点：3、不论超重还是失重，物体的重力（填“不变”或“变”）4.做功是能量转化的，功和能的单位都是，功和能都是是量（填“标”或“矢”）5.动能定理公式表述：6、机械能守恒条件：选修3-1 （占学考总分15%左右）1.元电荷e =2.库仑定律：F库= ，适用条件：3.电场强度E= （普适） = （点电荷） = （匀强电场）4.电场力F=5、电势差 U AB= = .电场力做功W AB= 电场力做功与无关；电场力做正功，电势能，电场力做负功，电势能。

高中物理学考公式大全总结

高中物理学考公式大全总结高中物理学考试中，掌握并熟练运用各种公式是非常重要的。

下面是一份总结了常见物理学公式的大全，供同学们复习备考使用。

1. 运动学公式- 位移公式：s = v0t + 1/2at^2- 速度公式：v = v0 + at- 加速度公式：a = (v - v0) / t2. 动力学公式- 牛顿第二定律：F = ma- 动量公式：p = mv- 冲量公式：I = Ft3. 能量与功公式- 功公式：W = Fs- 功率公式：P = W/t- 动能公式：E = 1/2mv^2- 位能公式：Ep = mgh- 动能定理：W = ΔE4. 万有引力公式- 引力公式：F = G(m1m2/r^2)- 万有引力定律：F = G(m1m2/r^2)5. 光学公式- 光速公式：c = λf- 折射定律：n1sinθ1 = n2sinθ2- 焦距公式：1/f = 1/v + 1/u6. 电学公式- 电流公式：I = Q/t- 电阻公式：R = V/I- 电压公式：V = IR- 等效电阻公式（串联电路）：1/Rt = 1/R1 + 1/R2 + ...- 等效电阻公式（并联电路）：1/Rt = 1/R1 + 1/R2 + ...7. 磁学公式- 洛伦兹力公式：F = qvBsinθ- 安培定理：B = μ0I/2πr这只是一部分常见的物理学公式，不同的教材和地区可能会有些许差异。

在备考过程中，建议同学们结合自己所使用的教材和学校教学要求进行复习，并多做相关的习题来加深对公式的理解和应用能力。

希望这份物理学公式大全能够帮助到你，在考试中取得好成绩！如果还有其他问题，欢迎继续提问。

高中物理会考公式

高中物理会考公式
高中物理会考的公式内容主要涵盖以下几个方面：
1. 运动学公式：
- 位移公式（s = v0 * t + 0.5 * a * t^2）
- 速度公式（v = v0 + a * t）
- 物体平均速度公式
- 物体加速度公式
2. 动力学公式：
- 牛顿第二定律（F = m * a）
- 力的合成与分解
- 弹性力公式（F = k * x）
3. 能量和功公式：
- 功公式（W = F * s * cosθ）
- 功率公式（P = W / t）
- 动能公式（K = 0.5 * m * v^2）
- 势能公式（Ep = m * g * h）
4. 链轮与滑轮公式：
- 钟摆公式（T = 2π * (l / g)^0.5）
- 质点转动惯量公式（I = m * r^2）
- 固体转动惯量公式（I = 0.5 * m * r^2）
5. 波动公式：
- 波速公式（v = f * λ）
- 光速公式（c = f * λ）
- 声强公式（I = P / A）
6. 静电学公式：
- 库仑定律（F = k * q1 * q2 / r^2）
- 电场强度公式（E = F / q）
- 电压公式（V = U / q）
- 电容公式（C = Q / V）
7. 电磁感应公式：
- 法拉第电磁感应定律（ε = -N * ΔΦ / Δt）- 感应电动势公式（ε = B * l * v * sinθ）
- 比奥萨伐尔定律（B = μ * H）
- 荷质比公式（e/m = ε / B^2 * v^2 * sinθ）
这些公式是高中物理课程中常见的考点，希望对你的学习有所帮助。

高中物理会考学业水平考试公式及知识点归纳总结(超详细)

一、力学1. 速度与加速度平均速度：v = Δx/Δt瞬时速度：v = lim(Δt→0) Δx/Δt加速度：a = Δv/Δt2. 运动学公式匀速直线运动：x = vt匀变速直线运动：x = v0t + 1/2at²自由落体运动：h = 1/2gt² (g = 9.8 m/s²) 3. 牛顿运动定律第一定律：惯性定律第二定律：F = ma第三定律：作用力与反作用力4. 功与能功：W = Fd cosθ动能：K = 1/2mv²势能：Ep = mgh机械能守恒：E = K + Ep5. 冲量与动量冲量：J = FΔt动量：p = mv动量守恒：Δp = J6. 转动角速度：ω = Δθ/Δt角加速度：α = Δω/Δt转动惯量：I = ∑mr²动能：K = 1/2Iω²二、热学1. 温度与热传递温度：T (单位：K)热传递：Q = mcΔT2. 理想气体状态方程PV = nRT3. 热力学第一定律ΔU = Q W4. 热力学第二定律熵增加原理5. 物态变化熔化、凝固、汽化、液化、升华、凝华三、电磁学1. 静电场库仑定律：F = kQq/r²电场强度：E = F/q电势：V = kQ/r2. 电流与电路电流：I = Q/t欧姆定律：V = IR串联电路：V = V1 + V2 + + Vn并联电路：I = I1 + I2 + + In3. 磁场毕奥萨伐尔定律安培力：F = BIL sinθ洛伦兹力：F = qvB4. 电磁感应法拉第电磁感应定律：ε = NΔΦ/Δt自感：L = NΦ/I四、光学1. 光的反射与折射反射定律：入射角 = 反射角折射定律：n1sinθ1 = n2sinθ22. 透镜成像凸透镜：1/f = 1/u + 1/v凹透镜：1/f = 1/u 1/v3. 光的干涉与衍射双缝干涉：Δx = λD/d单缝衍射：Δθ = λ/a五、原子物理1. 波尔模型能级：En = 13.6/n² eV光谱：E = hf2. 量子力学波函数：ψ海森堡不确定性原理：ΔxΔp ≥ h/4π3. 放射性半衰期：T1/2放射性衰变：N(t) = N0e^(λt)。

高中物理学考必记公式

高中物理学考必记公式一、物理量及单位1.长度：米（m）2.质量：千克（kg）3.时间：秒（s）4.电流强度：安培（A）5.物质的量：摩尔（mol）6.温度：开尔文（K）7.光强度：坎德拉（cd）二、力学1.牛顿第一定律：物体在不受外力作用时保持静止或匀速直线运动。

2.牛顿第二定律：物体的加速度与作用在物体上的力成正比，与物体的质量成反比。

3.牛顿第三定律：作用在两个物体之间的力大小相等，方向相反。

4.动量定理：物体受到的冲量等于物体动量的变化量。

5.动能定理：物体动能的变化量等于物体所受合外力沿位移方向所做的功。

6.位能定理：物体的位能变化量等于重力做的功。

7.机械能守恒：一个系统中，只要合外力做功为零，机械能守恒。

8.弹性碰撞：在碰撞中，动量守恒且动能守恒。

9.非弹性碰撞：在碰撞中，动量守恒但动能不守恒。

10.重力势能：物体在重力场中由于高度差而具有的能量。

三、热学1.理想气体状态方程：PV=nRT，其中P为气压，V为体积，T为温度，n为物质的量，R为气体常数。

2.热力学第一定律：热一定会流动，但热能的总量在一个封闭系统中是不变的。

3.热机效率：热机输出功与输入热量之比的最大值为理论效率。

4.热传导定律：热量的传导速率正比于传导面积和温度差，反比于传导距离和材料导热系数。

5.热辐射定律：辐射能流密度与温度的第四次方成正比。

6.热容量：物体吸收的热量与物体温度的升降量之比为热容量，单位为焦耳/开尔文。

四、电学1.库仑定律：两点间电力与它们间距离的平方成反比。

2.欧姆定律：电流强度与电势差成正比，与电阻成反比。

3.基尔霍夫定律：一个电路中的任意闭合回路上的各电动势之和等于各电势降之和。

4.电磁感应定律：磁通量的变化引起感应电动势，大小与磁通量变化率成正比。

5.麦克斯韦方程组：电学与磁学基本方程组。

6.电容器的电容：电容器两极板之间的电势差与板间距和板面积成反比。

7.电感器的电感：电感器中的感应电动势与电流变化率成正比，与电感系数成正比。

高中物理学考必记公式

高中物理学考必记公式一、力学1. 动量公式运动物体的动量等于质量乘以速度：p = mv2. 动能公式运动物体的动能等于其质量与速度平方的乘积的一半：E_k = 1/2mv^23. 势能公式一个物体具有的势能等于其所受的力沿位移方向所做的功：E_p = Fs4. 冲量公式一个力作用于一个物体上改变它的动量量的量叫做冲量：J = FΔt5. 合力公式合力等于物体受到的所有力的矢量和：F_net = ΣF6. 牛顿第一定律一个物体保持静止或匀速直线运动，当且仅当它所受到的合外力等于零。

7. 牛顿第二定律一个物体受到的加速度与所受合外力成正比例，与物体的质量成反比例：F_net = ma8. 牛顿第三定律对于每一个作用力都存在一个同大小但方向相反的反作用力。

9. 滑动摩擦力公式一个物体在另一个物体表面上滑动时所受到的摩擦力的大小与周围环境有关：f_k = μ_k F_n10. 静摩擦力公式两个表面间相互嵌套的力称为静摩擦力，它的结果是物体在表面上保持静止：f_s = μ_s F_n二、运动学11. 速度公式速度是描述物体移动状态的物理量，表示单位时间内物体的位移量：v = Δx/Δt12. 速度变化公式一个物体速度变化的加速度可以通过计算它得到的速度增量与时间增量的比值来确定：a = Δv/Δt13. 加速度公式当一个物体在加速之间，距离与加速度之间的关系可以由以下公式来描述：d = 1/2at^214. 自由落体公式自由落体是独立于质量的物体在重力的影响下的运动状态：y = -1/2gt^2 + v_ot + y_o三、电学15. 欧姆定律欧姆定律描述了电流、电阻和电压之间的关系：V = IR16. 电阻公式一个电导体的电阻可以用以下公式来计算：R = ρl/A17. 电功率公式电功率是电流与电压的乘积：P = IV18. 法拉第电容公式法拉第电容描述了一个电容器可以蓄电的能力：C = Q/V四、光学19. 光速公式光在真空中传播的速度是固定的：c = 3.00×10^8 m/s20. 透镜公式透镜公式描述了一个透镜如何通过聚焦光线集成一个点：1/f = 1/d_i + 1/d_o21. 折射定律折射定律描述了光线在穿过介质时在方向和速度上的变化：n_1 sinθ_1 = n_2 sinθ_222. 反射公式反射公式描述了光源在反射一个表面时反射角和入射角之间的关系：θ_i = θ_r五、核物理学23. 裂变公式在核反应中，裂变可以使用以下公式来描述：E = mc^224. 合成公式核反应的合成可以用以下公式来描述：p + n → D + γ25. 半衰期公式半衰期是放射性同位素数量下降到一半所需的时间：N(t) = N_0 (1/2)^(t/T_1/2)。

高中物理公式大全(学考用)

力学一、力1、重力：G=mg，方向竖直向下，g=9.8m/s 2≈10m/s2，作用点在物体重心。

2、静摩擦力：0≤ f静≤≤ f m ，与物体相对运动趋势方向相反，f m 为最大静摩擦力。

3、滑动摩擦力：f= μN，与物体运动或相对运动方向相反，μ是动摩擦因数，N是正压力。

4、弹力：F = kx （胡克定律），x 为弹簧伸长量（m），k 为弹簧的劲度系数（N/m ）。

5、力的合成与分解：①两个力方向相同， F 合=F1＋F2，方向与F1、F2 同向②两个力方向相反， F 合=F1－F2，方向与F1（F1 较大）同向互成角度（0<θ<180o）：θ增大→F 减少θ减小→F 增大θ=90o，F= 2 2F1 F ，F 的方向：tgφ=2 F2F1。

F1=F2，θ=60o，F=2F1cos30o， F 与F1，F2 的夹角均为30o，即φ=30oθ=120o，F=F1=F2，F 与F1，F2 的夹角均为60o，即φ=60o由以上讨论，合力既可能比任一个分力都大，也可能比任一个分力都小，它的大小依赖于两个分力之间的夹角。

合力范围：（F1－F2）≤F≤(F1＋F2)求F1、F2两个共点力的合力大小的公式（F1与F2夹角为θ）：F2 2F1 F 2F1F22cos二、直线运动xv匀速直线运动：位移x vt 。

平均速度t匀变速直线运动：1、位移与时间的关系，公式：x v o t 122 at2、速度与时间的关系，公式：v t v o at2 23、位移与速度的关系：v t v o 2ax ，适合不涉及时间时的计算公式。

4、平均速度vvovt 22vtxt，即为中间时刻的速度。

5、中间位移处的速度大小2 2v vo tv ，并且x22v x vt2 2匀变速直线运动的推理：1、匀变速直线运动的物体，在任意两个连续相等的时间里的位移之差是个恒量，即△s=s n+1 —s n=aT2=恒量2、初速度为零的匀加速直线运动（设T为等分时间间隔）：①1T 末、2T 末、3T 末⋯⋯瞬时速度的比值为v1:v2:v3......:v n=1:2:3......:n②1T 内、2T 内、3T 内⋯⋯的位移之比为s1:s2:s3:⋯⋯:s n=12:22:32⋯⋯:n2③第一个T 内、第二个T 内、第三个T 内⋯⋯位移之比为S I:S II :S III :⋯⋯:S n=1:3:5⋯⋯:(2n-1)④从静止开始通过连续相等的位移所用时间的t1:t2:t3:......:t n=1:( 2 1) :( 3 2): ......:( n n 1)自由落体运动(1) 位移公式: h 12gt 2- 1 -(2) 速度公式 : vgtt2(3) 位移—速度关系式 : v 2gh三、牛顿运动定律1、牛顿第一定律 (惯性定律）：物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止。

高中学业考试物理公式大全

高中物理公式（一）力学匀变速直线运动：V t = V 0+a t S =V 0t+12a t 2 V t 2 = V 02+2as —v =t s =2v v t0+匀速圆周运动：线速度：V= 2πRT =2πR n 角速度：ω=n T t ππφ22==V=ω R n: 转速(r/s) ω: rad/s共点力作用下物体的平衡条件： F 合=0万有引力： F=G m m r 122 (G 为引力恒量:卡文迪什测得)牛顿第二定律： F 合 = ma (受力分析)功： W = Fs cos θ (适用于恒力的功的计算)动能： E k = 221mV重力势能：E p = mgh (h 与零势能面的选择有关)机械能守恒定律：条件:只有重力做功: mgh 1 +121212222m V m gh m V =+ 功率： P = Wt (平均功率) P = FV=fV m (F:牵引力)波长、波速、频率的关系： V =λT =λf f =1/T波速由介质决定/频率由波源决定波在同种介质中匀速传播：S=Vt（二）气体玻意耳定律：一定质量气体，T 不变 (等温变化)P 1V 1 = P 2V 2 (p 和V 反比)查理定律：一定质量气体，V 不变 (等容变化)P T P T 1122= (T=t+273 △T=△t) (p 和T 正比)盖·吕萨克定律：一定质量气体，P 不变 (等压变化)2211V V T T = (V 和T 成正比)（三）电学电场强度E(牛/库)：E=F/q （E 与F 、q 无关）磁感应强度B (特T)：B=F/IL （B 与F 、I 、L 无关）磁场对电流的作用力:（安培力）：F=BIL （I ⊥B ）; F=0（I ∥B ）方向:左手定则磁通量ϕ(韦伯wb) ：ϕ=Bs （s ⊥B ）; ϕ=0（s ∥B ）电流强度：I = Qt 串联(分压)：I 1=I 2=I U=U 1+U 2 R=R 1+R 2并联(分流)：U 1=U 2=U I=I 1+I 2 11112R R R =+ 或：R=R R R R 1212+欧姆定律：I UR =电功(J)：W=UIt=I Rt U R t 22==Pt 电功率(w) ：P=t W =UI=I R U R 22=1. 电动机：效率：η=入出PP =UIt mgh （测量）2. 输入功率 P 入=UI3. 发热功率：P 热=I 2r4. P 入=P 出+P 热高中物理概念规律1. 加速度是表示速度变化快慢的物理量，速度变化越快，加速度越大；功率是表示做功快慢的物理量，做功越快，功率越大。