全国省会城市经纬度
中国各省各市经纬度查询

直辖市各市经纬度查询北京市北纬39.55 东经116.24上海市北纬31.14 东经121.29天津市北纬39.02 东经117.12重庆市北纬29.35 东经106.33香港特别行政区北纬21.23 东经115.12 澳门特别行政区北纬21.33 东经115.07 安徽省各市经纬度查询合肥北纬31.52 东经117.17安庆北纬30.31 东经117.02蚌埠北纬32.56 东经117.21亳州北纬33.52 东经115.47巢湖北纬31.36 东经117.52滁州北纬32.18 东经118.18阜阳北纬32.54 东经115.48贵池北纬30.39 东经117.28淮北北纬33.57 东经116.47淮南北纬32.37 东经116.58黄山北纬29.43 东经118.18界首北纬33.15 东经115.21六安北纬31.44 东经116.28马鞍山北纬31.43 东经118.28明光北纬32.47 东经117.58宿州北纬33.38 东经116.58天长北纬32.41 东经118.59铜陵北纬30.56 东经117.48芜湖北纬31.19 东经118.22宣州北纬30.57 东经118.44福建省各市经纬度查询福州北纬26.05 东经119.18长乐北纬25.58 东经119.31福安北纬27.06 东经119.39福清北纬25.42 东经119.23建瓯北纬27.03 东经118.20建阳北纬27.21 东经118.07晋江北纬24.49 东经118.35龙海北纬24.26 东经117.48龙岩北纬25.06 东经117.01南安北纬24.57 东经118.23南平北纬26.38 东经118.10宁德北纬26.39 东经119.31莆田北纬24.26 东经119.01三明北纬26.13 东经117.36 邵武北纬27.20 东经117.29 石狮北纬24.44 东经118.38 武夷山北纬27.46 东经118.02 厦门北纬24.27 东经118.06 永安北纬25.58 东经117.23 漳平北纬25.17 东经117.24 漳州北纬24.31 东经117.39 吉林省各市经纬度查询长春北纬43.54 东经125.19 白城北纬45.38 东经122.50 白山北纬41.56 东经126.26 大安北纬45.30 东经124.18 德惠北纬44.32 东经125.42 敦化北纬43.22 东经128.13 公主岭北纬43.31 东经124.49 和龙北纬42.32 东经129.00 桦甸北纬42.58 东经126.44 珲春北纬42.52 东经130.22 集安北纬41.08 东经126.11 蛟河北纬43.42 东经127.21 吉林北纬43.52 东经126.33 九台北纬44.09 东经125.51 辽源北纬42.54 东经125.09 临江北纬41.49 东经126.53 龙井北纬42.46 东经129.26 梅河口北纬42.32 东经125.40 舒兰北纬44.24 东经126.57 四平北纬43.10 东经124.22 松原北纬45.11 东经124.49 洮南北纬45.20 东经122.47 通化北纬41.43 东经125.56 图们北纬42.57 东经129.51 延吉北纬42.54 东经129.30 愉树北纬44.49 东经126.32 辽宁省各市经纬度查询沈阳北纬41.48 东经123.25 鞍山北纬41.07 东经123.00 北票北纬41.48 东经120.47 本溪北纬41.18 东经123.46 朝阳北纬41.34 东经120.27 大连北纬38.55 东经121.36 丹东北纬40.08 东经124.22东港北纬39.53 东经124.08凤城北纬40.28 东经124.02抚顺北纬41.51 东经123.54阜新北纬42.01 东经121.39盖州北纬40.24 东经122.21海城北纬40.51 东经122.43葫芦岛北纬40.45 东经120.51 锦州北纬41.07 东经121.09开原北纬42.32 东经124.02辽阳北纬41.16 东经123.12凌海北纬41.10 东经121.21凌源北纬41.14 东经119.22盘锦北纬41.07 东经122.03普兰店北纬39.23 东经121.58 铁法北纬42.28 东经123.32铁岭北纬42.18 东经123.51瓦房店北纬39.37 东经122.00 兴城北纬40.37 东经120.41新民北纬41.59 东经122.49营口北纬40.39 东经122.13庄河北纬39.41 东经122.58黑龙江省各市经纬度查询哈尔滨北纬45.44 东经126.36 阿城北纬45.32 东经126.58安达北纬46.24 东经125.18北安北纬48.15 东经126.31大庆北纬46.36 东经125.01富锦北纬47.15 东经132.02海林北纬44.35 东经129.21海伦北纬47.28 东经126.57鹤岗北纬47.20 东经130.16黑河北纬50.14 东经127.29佳木斯北纬46.47 东经130.22 鸡西北纬45.17 东经130.57密山北纬45.32 东经131.50牡丹江北纬44.35 东经129.36 讷河北纬48.29 东经124.51宁安北纬44.21 东经129.28齐齐哈尔北纬47.20 东经123.57 七台河北纬45.48 东经130.49 双城北纬45.22 东经126.15尚志北纬45.14 东经127.55双鸭山北纬46.38 东经131.11绥化北纬46.38 东经126.59铁力北纬46.59 东经128.01同江北纬47.39 东经132.30五常北纬44.55 东经127.11五大连池北纬48.38 东经126.07 伊春北纬47.42 东经128.56肇东北纬46.04 东经125.58河北省各市经纬度查询石家庄北纬38.02 东经114.30 安国北纬38.24 东经115.20保定北纬38.51 东经115.30霸州北纬39.06 东经116.24泊头北纬38.04 东经116.34沧州北纬38.18 东经116.52承德北纬40.59 东经117.57定州北纬38.30 东经115.00丰南北纬39.34 东经118.06高碑店北纬39.20 东经115.51 蒿城北纬38.02 东经114.50邯郸北纬36.36 东经114.28河间北纬38.26 东经116.05衡水北纬37.44 东经115.42黄骅北纬38.21 东经117.21晋州北纬38.02 东经115.02冀州北纬37.34 东经115.33廓坊北纬39.31 东经116.42鹿泉北纬38.04 东经114.19南宫北纬37.22 东经115.23秦皇岛北纬39.55 东经119.35 任丘北纬38.42 东经116.07三河北纬39.58 东经117.04沙河北纬36.51 东经114.30深州北纬38.01 东经115.32唐山北纬39.36 东经118.11武安北纬36.42 东经114.11邢台北纬37.04 东经114.30辛集北纬37.54 东经115.12新乐北纬38.20 东经114.41张家口北纬40.48 东经114.53 涿州北纬39.29 东经115.59遵化北纬40.11 东经117.58河南省各市经纬度查询郑州北纬34.46 东经113.40长葛北纬34.12 东经113.47 登封北纬34.27 东经113.02 邓州北纬32.42 东经112.05 巩义北纬34.46 东经112.58 鹤壁北纬35.54 东经114.11 辉县北纬35.27 东经113.47 焦作北纬35.14 东经113.12 济源北纬35.04 东经112.35 开封北纬34.47 东经114.21 灵宝北纬34.31 东经110.52 林州北纬36.03 东经113.49 漯河北纬33.33 东经114.02 洛阳北纬34.41 东经112.27 南阳北纬33.00 东经112.32 平顶山北纬33.44 东经113.17 濮阳北纬35.44 东经115.01 沁阳北纬35.05 东经112.57 汝州北纬34.09 东经112.50 三门峡北纬34.47 东经111.12 商丘北纬34.26 东经115.38 卫辉北纬35.24 东经114.03 舞钢北纬33.17 东经113.30 项城北纬33.26 东经114.54 荥阳北纬34.46 东经113.21 新密北纬34.31 东经113.22 新乡北纬35.18 东经113.52 信阳北纬32.07 东经114.04 新郑北纬34.24 东经113.43 许昌北纬34.01 东经113.49 偃师北纬34.43 东经112.47 义马北纬34.43 东经111.55 禹州北纬34.09 东经113.28 周口北纬33.37 东经114.38 驻马店北纬32.58 东经114.01 浙江省各市经纬度查询杭州北纬30.16 东经120.10 慈溪北纬30.11 东经121.15 东阳北纬29.16 东经120.14 奉化北纬29.39 东经121.24 富阳北纬30.03 东经119.57 海宁北纬30.32 东经120.42 湖州北纬30.52 东经120.06 建德北纬29.29 东经119.16嘉兴北纬30.46 东经120.45 金华北纬29.07 东经119.39 兰溪北纬29.12 东经119.28 临海北纬28.51 东经121.08 丽水北纬28.27 东经119.54 龙泉北纬28.04 东经119.08 宁波北纬29.52 东经121.33 平湖北纬30.42 东经121.01 衢州北纬28.58 东经118.52 瑞安北纬27.48 东经120.38 上虞北纬30.01 东经120.52 绍兴北纬30.00 东经120.34 台州北纬28.41 东经121.27 桐乡北纬30.38 东经120.32 温岭北纬28.22 东经121.21 温州北纬28.01 东经120.39 萧山北纬30.09 东经120.16 义乌北纬29.18 东经120.04 乐清北纬28.08 东经120.58 余杭北纬30.26 东经120.18 余姚北纬30.02 东经121.10 永康北纬29.54 东经120.01 舟山北纬30.01 东经122.06 诸暨北纬29.43 东经120.14 海南省各市经纬度查询海口北纬20.02 东经110.20 儋州北纬19.31 东经109.34 琼海北纬19.14 东经110.28 琼山北纬19.59 东经110.21 三亚北纬18.14 东经109.31 通什北纬18.46 东经109.31 江西省各市经纬度查询南昌北纬28.40 东经115.55 德兴北纬28.57 东经117.35 丰城北纬28.12 东经115.48 赣州北纬28.52 东经114.56 高安北纬28.25 东经115.22 吉安北纬27.07 东经114.58 景德镇北纬29.17 东经117.13 井冈山北纬26.34 东经114.10 九江北纬29.43 东经115.58 乐平北纬28.58 东经117.08 临川北纬27.59 东经116.21瑞昌北纬29.40 东经115.38 瑞金北纬25.53 东经116.01 上饶北纬25.27 东经117.58 新余北纬27.48 东经114.56 宜春北纬27.47 东经114.23 鹰潭北纬28.14 东经117.03 樟树北纬28.03 东经115.32 云南省各市经纬度查询昆明北纬25.04 东经102.42 保山北纬25.08 东经99.10楚雄北纬25.01 东经101.32 大理北纬25.34 东经100.13 东川北纬26.06 东经103.12 个旧北纬23.21 东经103.09 景洪北纬22.01 东经100.48 开远北纬23.43 东经103.13 曲靖北纬25.30 东经103.48 瑞丽北纬24.00 东经97.50思茅北纬22.48 东经100.58 畹町北纬24.06 东经98.04宣威北纬26.13 东经104.06 玉溪北纬24.22 东经102.32 昭通北纬27.20 东经103.42 江苏省各市经纬度查询南京北纬32.03 东经118.46 常熟北纬31.39 东经120.43 常州北纬31.47 东经119.58 丹阳北纬32.00 东经119.32 东台北纬32.51 东经120.19 高邮北纬32.47 东经119.27 海门北纬31.53 东经121.09 淮安北纬33.30 东经119.09 淮阴北纬33.36 东经119.02 江都北纬32.26 东经119.32 姜堰北纬32.34 东经120.08 江阴北纬31.54 东经120.17 靖江北纬32.02 东经120.17 金坛北纬31.46 东经119.33 昆山北纬31.23 东经120.57 连去港北纬34.36 东经119.10 溧阳北纬31.26 东经119.29 南通北纬32.01 东经120.51 邳州北纬34.19 东经117.59如皋北纬32.23 东经120.33 宿迁北纬33.58 东经118.18 苏州北纬31.19 东经120.37 太仓北纬31.27 东经121.06 泰兴北纬32.10 东经120.01 泰州北纬32.30 东经119.54 通州北纬32.05 东经121.03 吴江北纬31.10 东经120.39 无锡北纬31.34 东经120.18 兴化北纬32.56 东经119.50 新沂北纬34.22 东经118.20 徐州北纬34.15 东经117.11 盐在北纬33.22 东经120.08 扬中北纬32.14 东经119.49 扬州北纬32.23 东经119.26 宜兴北纬31.21 东经119.49 仪征北纬32.16 东经119.10 张家港北纬31.52 东经120.32 镇江北纬32.11 东经119.27 四川省各市经纬度查询成都北纬30.40 东经104.04 巴中北纬31.51 东经106.43 崇州北纬30.39 东经103.40 达川北纬31.14 东经107.29 德阳北纬31.09 东经104.22 都江堰北纬31.01 东经103.37 峨眉山北纬29.36 东经103.29 涪陵北纬29.42 东经107.22 广汉北纬30.58 东经104.15 广元北纬32.28 东经105.51 华蓥北纬30.26 东经106.44 简阳北纬30.24 东经104.32 江油北纬31.48 东经104.42 阆中北纬31.36 东经105.58 乐山北纬29.36 东经103.44 泸州北纬28.54 东经105.24 绵阳北纬31.30 东经104.42 南充北纬30.49 东经106.04 内江北纬29.36 东经105.02 攀枝花北纬26.34 东经101.43 彭州北纬30.59 东经103.57 邛崃北纬30.26 东经103.28 遂宁北纬30.31 东经105.33万源北纬32.03 东经108.03 西昌北纬27.54 东经102.16 雅安北纬29.59 东经102.59 宜宾北纬28.47 东经104.34 自贡北纬29.23 东经104.46 资阳北纬30.09 东经104.38 湖南省各市经纬度查询长沙北纬28.12 东经112.59 常德北纬29.02 东经111.51 郴州北纬25.46 东经113.02 衡阳北纬26.53 东经112.37 洪江北纬27.07 东经109.59 怀化北纬27.33 东经109.58 津市北纬29.38 东经111.52 吉首北纬28.18 东经109.43 耒阳北纬26.24 东经112.51 冷水江北纬27.42 东经111.26 冷水滩北纬26.26 东经111.35 涟源北纬27.41 东经111.41 醴陵北纬27.40 东经113.30 临湘北纬29.29 东经113.27 浏阳北纬28.09 东经113.37 娄底北纬27.44 东经111.59 汨罗北纬28.49 东经113.03 韶山北纬27.54 东经112.29 邵阳北纬27.14 东经111.28 武冈北纬26.43 东经110.37 湘潭北纬27.52 东经112.53 湘乡北纬27.44 东经112.31 益阳北纬28.36 东经112.20 永州北纬26.13 东经111.37 沅江北纬28.50 东经112.22 岳阳北纬29.22 东经113.06 张家界北纬29.08 东经110.29 株洲北纬27.51 东经113.09 资兴北纬25.58 东经113.13 湖北省各市经纬度查询武汉北纬30.35 东经114.17 安陆北纬31.15 东经113.41 当阳北纬30.50 东经111.47 丹江口北纬32.33 东经108.30 大冶北纬30.06 东经114.58 恩施北纬30.16 东经109.29广水北纬31.37 东经113.48 洪湖北纬29.48 东经113.27 黄石北纬30.12 东经115.06 黄州北纬30.27 东经114.52 荆门北纬31.02 东经112.12 荆沙北纬30.18 东经112.16 老河口北纬32.23 东经111.40 利川北纬30.18 东经108.56 麻城北纬31.10 东经115.01 浦圻北纬29.42 东经113.51 潜江北纬30.26 东经112.53 石首北纬29.43 东经112.24 十堰北纬32.40 东经110.47 随州北纬31.42 东经113.22 天门北纬60.39 东经113.10 武穴北纬29.51 东经115.33 襄樊北纬32.02 东经112.08 咸宁北纬29.53 东经114.17 仙桃北纬30.22 东经113.27 孝感北纬30.56 东经113.54 宜昌北纬30.42 东经111.17 宜城北纬31.42 东经112.15 应城北纬30.57 东经113.33 枣阳北纬32.07 东经112.44 枝城北纬30.23 东经111.27 钟祥北纬31.10 东经112.34 山东省各市经纬度查询济南北纬36.40 东经117.00 安丘北纬36.25 东经119.12 滨州北纬37.22 东经118.02 昌邑北纬39.52 东经119.24 德州北纬37.26 东经116.17 东营北纬37.27 东经118.30 肥城北纬36.14 东经116.46 高密北纬36.22 东经119.44 菏泽北纬35.14 东经115.26 胶南北纬35.53 东经119.58 胶州北纬36.17 东经120.00 即墨北纬36.22 东经120.28 济宁北纬35.23 东经116.33 莱芜北纬36.12 东经117.40 莱西北纬36.52 东经120.31 莱阳北纬36.58 东经120.42乐陵北纬37.44 东经117.12 聊城北纬36.26 东经115.57 临清北纬36.51 东经115.42 临沂北纬35.03 东经118.20 龙口北纬37.39 东经120.21 蓬莱北纬37.48 东经120.45 平度北纬36.47 东经119.58 青岛北纬36.03 东经120.18 青州北纬36.42 东经118.28 曲阜北纬35.36 东经116.58 日照北纬35.23 东经119.32 荣成北纬37.10 东经122.25 乳山北纬36.54 东经121.31 寿光北纬36.53 东经118.44 泰安北纬36.11 东经117.08 滕州北纬35.06 东经117.09 潍坊北纬36.43 东经119.06 威海北纬37.31 东经122.07 文登北纬37.12 东经122.03 新泰北纬35.54 东经117.45 烟台北纬37.32 东经121.24 兖州北纬35.32 东经116.49 禹城北纬36.56 东经116.39 枣庄北纬34.52 东经117.33 章丘北纬36.43 东经117.32 招远北纬37.21 东经120.23 诸城北纬35.59 东经119.24 淄博北纬36.48 东经118.03 邹城北纬35.24 东经116.58 山西省各市经纬度查询太原北纬37.54 东经112.33 长治北纬36.11 东经113.06 大同北纬40.06 东经113.17 高平北纬35.48 东经112.55 古交北纬37.54 东经112.09 河津北纬35.35 东经110.41 侯马北纬35.37 东经111.21 霍州北纬36.34 东经111.42 介休北纬37.02 东经111.55 晋城北纬35.30 东经112.51 临汾北纬36.05 东经111.31 潞城北纬36.21 东经113.14 朔州北纬39.19 东经112.26忻州北纬38.24 东经112.43阳泉北纬37.51 东经113.34永济北纬34.52 东经110.27原平北纬38.43 东经112.42榆次北纬37.41 东经112.43运城北纬35.02 东经110.59新疆维吾尔自治区各市经纬度查询乌鲁木齐北纬43.45 东经87.36 阿克苏北纬41.09 东经80.19阿勒泰北纬47.50 东经88.12阿图什北纬39.42 东经76.08博乐北纬44.57 东经82.08昌吉北纬44.02 东经87.18阜康北纬44.09 东经87.58哈密北纬42.50 东经93.28和田北纬37.09 东经79.55克拉玛依北纬45.36 东经84.51 喀什北纬39.30 东经75.59库尔勒北纬41.46 东经86.07奎屯北纬44.27 东经84.56石河子北纬44.18 东经86.00塔城北纬46.46 东经82.59吐鲁番北纬42.54 东经89.11伊宁北纬43.55 东经81.20贵州省各市经纬度查询贵阳北纬26.35 东经106.42安顺北纬26.14 东经105.55毕节北纬27.18 东经105.18赤水北纬28.34 东经105.42都匀北纬26.15 东经107.31凯里北纬26.35 东经107.58六盘水北纬26.35 东经104.50清镇北纬26.33 东经106.27铜仁北纬27.43 东经109.12兴义北纬25.05 东经104.53遵义北纬27.42 东经106.55陕西省各市经纬度查询西安北纬34.17 东经108.57安康北纬32.41 东经109.01宝鸡北纬34.22 东经107.09韩城北纬35.28 东经110.27汉中北纬33.04 东经107.01华阴北纬34.34 东经110.05铜川北纬35.06 东经109.07渭南北纬34.30 东经109.30咸阳北纬34.20 东经108.43兴平北纬34.18 东经108.29延安北纬36.35 东经109.28榆林北纬38.18 东经109.47重庆市各区经纬度查询合川市北纬30.02 东经106.15 江津市北纬29.18 东经106.16 南川市北纬29.10 东经107.05 永川市北纬29.23 东经105.53 甘肃省各市经纬度查询兰州北纬36.04 东经103.51白银北纬36.33 东经104.12敦煌北纬40.08 东经94.41嘉峪关北纬39.48 东经98.14金昌北纬38.28 东经102.10酒泉北纬39.44 东经98.31临夏北纬35.37 东经103.12平凉北纬35.32 东经106.40天水北纬34.37 东经105.42武威北纬37.56 东经102.39西峰北纬35.45 东经107.40玉门北纬39.49 东经97.35张掖北纬38.56 东经100.26宁夏回族自治区各市经纬度查询银川北纬38.27 东经106.16青铜峡北纬37.56 东经105.59 石嘴山北纬39.02 东经106.22 吴忠北纬37.59 东经106.11内蒙古自治区各市经纬度查询呼和浩特北纬40.48 东经111.41 包头北纬40.39 东经109.49赤峰北纬42.17 东经118.58东胜北纬39.48 东经109.59二连浩特北纬43.38 东经111.58 额尔古纳北纬50.13 东经120.11 丰镇北纬40.27 东经113.09根河北纬50.48 东经121.29海拉尔北纬49.12 东经119.39 霍林郭勒北纬45.32 东经119.38 集宁北纬41.02 东经113.06临河北纬40.46 东经107.22通辽北纬43.37 东经122.16乌兰浩特北纬46.03 东经122.03 乌海北纬39.40 东经106.48锡林浩特北纬43.57 东经116.03 牙克石北纬49.17 东经120.40 扎兰屯北纬48.00 东经122.47 青海省各市经纬度查询西宁北纬36.38 东经101.48德令哈北纬37.22 东经97.23格尔木北纬36.26 东经94.55广东省各市经纬度查询广州北纬23.08 东经113.14潮阳北纬23.16 东经116.36潮州北纬23.40 东经116.38澄海北纬23.28 东经116.46从化北纬23.33 东经113.33东莞北纬23.02 东经113.45恩平北纬22.12 东经112.19佛山北纬23.02 东经113.06高明北纬22.53 东经112.50高要北纬23.02 东经112.26高州北纬21.54 东经110.50鹤山北纬22.46 东经112.57河源北纬23.43 东经114.41花都北纬23.23 东经113.12化州北纬21.39 东经110.37惠阳北纬22.48 东经114.28惠州北纬23.05 东经114.22江门北纬22.35 东经113.04揭阳北纬22.32 东经116.21开平北纬22.22 东经112.40乐昌北纬25.09 东经113.21雷州北纬20.54 东经110.04廉江北纬21.37 东经110.17连州北纬24.48 东经112.23罗定北纬22.46 东经111.33茂名北纬21.40 东经110.53梅州北纬24.19 东经116.07南海北纬23.01 东经113.09番禺北纬22.57 东经113.22普宁北纬23.18 东经116.10清远北纬23.42 东经113.01三水北纬23.10 东经112.52汕尾北纬22.47 东经115.21韶关北纬24.48 东经113.37深圳北纬22.33 东经114.07顺德北纬22.50 东经113.15四会北纬23.21 东经112.41台山北纬22.15 东经112.48吴川北纬21.26 东经110.47新会北纬22.32 东经113.01兴宁北纬24.09 东经115.43阳春北纬22.10 东经111.48阳江北纬21.50 东经111.58英德北纬24.10 东经113.22云浮北纬22.57 东经112.02增城北纬23.18 东经113.49湛江北纬21.11 东经110.24肇庆北纬23.03 东经112.27中山北纬22.31 东经113.22珠海北纬22.17 东经113.34广西壮族自治区各市经纬度查询南宁北纬22.48 东经108.19北海北纬21.28 东经109.07北流北纬22.42 东经110.21百色北纬23.54 东经106.36防城港北纬21.37 东经108.20贵港北纬23.06 东经109.36桂林北纬25.17 东经110.17桂平北纬23.22 东经110.04河池北纬24.42 东经108.03合山北纬23.47 东经108.52柳州北纬23.19 东经109.24赁祥北纬22.07 东经106.44钦州北纬21.57 东经108.37梧州北纬23.29 东经111.20玉林北纬22.38 东经110.09宜州北纬24.28 东经108.40台湾省各市经纬度查询台北市北纬25.03 东经121.30西藏自治区各市经纬度查询拉萨北纬29.39 东经91.08日喀则北纬29.16 东经88.511 后盾资料。
中国城市经纬度汇总

中国城市经纬度汇总北京市市中心经纬度:(116.41667,39.91667)上海市区经纬度:(121.43333,34.50000)天津市区经纬度:(117.20000,39.13333)香港经纬度:(114.10000,22.20000)广州经纬度:(113.23333,23.16667)珠海经纬度:(113.51667,22.30000)深圳经纬度:(114.06667,22.61667)杭州经纬度:(120.20000,30.26667)重庆市区经纬度:(106.45000, 29.56667)青岛经纬度:(120.33333,36.06667)厦门经纬度:(118.10000,24.46667)福州经纬度:(119.30000,26.08333)兰州经纬度:(103.73333,36.03333)贵阳经纬度:(106.71667,26.56667)长沙经纬度:(113.00000,28.21667)南京经纬度:(118.78333,32.05000)南昌经纬度:(115.90000,28.68333)沈阳经纬度:(123.38333,41.80000)太原经纬度:(112.53333,37.86667)成都经纬度:(104.06667,30.66667)拉萨经纬度:(91.00000,29.60000)乌鲁木齐经纬度:(87.68333,43.76667)昆明经纬度:(102.73333,25.05000)西安经纬度:(108.95000,34.26667)西宁经纬度:(101.75000,36.56667)银川经纬度:(106.26667,38.46667)兰浩特经纬度:(122.08333,46.06667)哈尔滨经纬度:(126.63333,45.75000)长春经纬度:(125.35000,43.88333)武汉经纬度:(114.31667,30.51667)郑州经纬度:(113.65000,34.76667)石家庄经纬度:(114.48333,38.03333)三亚经纬度:(109.50000,18.20000)海口经纬度:(110.35000,20.01667)澳门经纬度:(113.50000,22.20000)2、中国主要城市经纬度查询(精确到二级省市):所在省城市名纬度经度安徽省合肥北纬31.52 东经117.17安徽省安庆北纬30.31 东经117.02安徽省蚌埠北纬32.56 东经117.21安徽省亳州北纬33.52 东经115.47安徽省巢湖北纬31.36 东经117.52安徽省滁州北纬32.18 东经118.18安徽省贵池北纬30.39 东经117.28 安徽省淮北北纬33.57 东经116.47 安徽省淮南北纬32.37 东经116.58 安徽省黄山北纬29.43 东经118.18 安徽省界首北纬33.15 东经115.21 安徽省六安北纬31.44 东经116.28 安徽省马鞍山北纬31.43 东经118.28 安徽省明光北纬32.47 东经117.58 安徽省宿州北纬33.38 东经116.58 安徽省天长北纬32.41 东经118.59 安徽省铜陵北纬30.56 东经117.48 安徽省芜湖北纬31.19 东经118.22 安徽省宣州北纬30.57 东经118.44 澳门澳门市北纬21.33 东经115.07 北京市北京市北纬39.55 东经116.24 福建省福州北纬26.05 东经119.18 福建省长乐北纬25.58 东经119.31 福建省福安北纬27.06 东经119.39 福建省福清北纬25.42 东经119.23 福建省建瓯北纬27.03 东经118.20 福建省建阳北纬27.21 东经118.07 福建省晋江北纬24.49 东经118.35 福建省龙海北纬24.26 东经117.48 福建省龙岩北纬25.06 东经117.01 福建省南安北纬24.57 东经118.23 福建省南平北纬26.38 东经118.10 福建省宁德北纬26.39 东经119.31 福建省莆田北纬24.26 东经119.01 福建省泉州北纬24.56 东经118.36 福建省三明北纬26.13 东经117.36 福建省邵武北纬27.20 东经117.29 福建省石狮北纬24.44 东经118.38 福建省武夷山北纬27.46 东经118.02 福建省厦门北纬24.27 东经118.06 福建省永安北纬25.58 东经117.23 福建省漳平北纬25.17 东经117.24 福建省漳州北纬24.31 东经117.39 甘肃省兰州北纬36.04 东经103.51 甘肃省白银北纬36.33 东经104.12 甘肃省敦煌北纬40.08 东经94.41甘肃省嘉峪关北纬39.48 东经98.14 甘肃省金昌北纬38.28 东经102.10 甘肃省酒泉北纬39.44 东经98.31甘肃省平凉北纬35.32 东经106.40 甘肃省天水北纬34.37 东经105.42 甘肃省武威北纬37.56 东经102.39 甘肃省西峰北纬35.45 东经107.40 甘肃省玉门北纬39.49 东经97.35 甘肃省张掖北纬38.56 东经100.26 广东省广州北纬23.08 东经113.14 广东省潮阳北纬23.16 东经116.36 广东省潮州北纬23.40 东经116.38 广东省澄海北纬23.28 东经116.46 广东省从化北纬23.33 东经113.33 广东省东莞北纬23.02 东经113.45 广东省恩平北纬22.12 东经112.19 广东省佛山北纬23.02 东经113.06 广东省高明北纬22.53 东经112.50 广东省高要北纬23.02 东经112.26 广东省高州北纬21.54 东经110.50 广东省鹤山北纬22.46 东经112.57 广东省河源北纬23.43 东经114.41 广东省花都北纬23.23 东经113.12 广东省化州北纬21.39 东经110.37 广东省惠阳北纬22.48 东经114.28 广东省惠州北纬23.05 东经114.22 广东省江门北纬22.35 东经113.04 广东省揭阳北纬22.32 东经116.21 广东省开平北纬22.22 东经112.40 广东省乐昌北纬25.09 东经113.21 广东省雷州北纬20.54 东经110.04 广东省廉江北纬21.37 东经110.17 广东省连州北纬24.48 东经112.23 广东省罗定北纬22.46 东经111.33 广东省茂名北纬21.40 东经110.53 广东省梅州北纬24.19 东经116.07 广东省南海北纬23.01 东经113.09 广东省番禺北纬22.57 东经113.22 广东省普宁北纬23.18 东经116.10 广东省清远北纬23.42 东经113.01 广东省三水北纬23.10 东经112.52 广东省汕头北纬23.22 东经116.41 广东省汕尾北纬22.47 东经115.21 广东省韶关北纬24.48 东经113.37 广东省深圳北纬22.33 东经114.07 广东省顺德北纬22.50 东经113.15广东省台山北纬22.15 东经112.48广东省吴川北纬21.26 东经110.47广东省新会北纬22.32 东经113.01广东省兴宁北纬24.09 东经115.43广东省阳春北纬22.10 东经111.48广东省阳江北纬21.50 东经111.58广东省英德北纬24.10 东经113.22广东省云浮北纬22.57 东经112.02广东省增城北纬23.18 东经113.49广东省湛江北纬21.11 东经110.24广东省肇庆北纬23.03 东经112.27广东省中山北纬22.31 东经113.22广东省珠海北纬22.17 东经113.34广西自治区南宁北纬22.48 东经108.19 广西自治区北海北纬21.28 东经109.07 广西自治区北流北纬22.42 东经110.21 广西自治区百色北纬23.54 东经106.36 广西自治区防城港北纬21.37 东经108.20 广西自治区贵港北纬23.06 东经109.36 广西自治区桂林北纬25.17 东经110.17 广西自治区桂平北纬23.22 东经110.04 广西自治区河池北纬24.42 东经108.03 广西自治区合山北纬23.47 东经108.52 广西自治区柳州北纬23.19 东经109.24 广西自治区赁祥北纬22.07 东经106.44 广西自治区钦州北纬21.57 东经108.37 广西自治区梧州北纬23.29 东经111.20 广西自治区玉林北纬22.38 东经110.09 广西自治区宜州北纬24.28 东经108.40 贵州省贵阳北纬26.35 东经106.42贵州省安顺北纬26.14 东经105.55贵州省毕节北纬27.18 东经105.18贵州省赤水北纬28.34 东经105.42贵州省都匀北纬26.15 东经107.31贵州省凯里北纬26.35 东经107.58贵州省六盘水北纬26.35 东经104.50贵州省清镇北纬26.33 东经106.27贵州省铜仁北纬27.43 东经109.12贵州省兴义北纬25.05 东经104.53贵州省遵义北纬27.42 东经106.55海南省海口北纬20.02 东经110.20海南省儋州北纬19.31 东经109.34海南省琼海北纬19.14 东经110.28海南省三亚北纬18.14 东经109.31 海南省通什北纬18.46 东经109.31 河北省石家庄北纬38.02 东经114.30 河北省安国北纬38.24 东经115.20 河北省保定北纬38.51 东经115.30 河北省霸州北纬39.06 东经116.24 河北省泊头北纬38.04 东经116.34 河北省沧州北纬38.18 东经116.52 河北省承德北纬40.59 东经117.57 河北省定州北纬38.30 东经115.00 河北省丰南北纬39.34 东经118.06 河北省高碑店北纬39.20 东经115.51 河北省蒿城北纬38.02 东经114.50 河北省邯郸北纬36.36 东经114.28 河北省河间北纬38.26 东经116.05 河北省衡水北纬37.44 东经115.42 河北省黄骅北纬38.21 东经117.21 河北省晋州北纬38.02 东经115.02 河北省冀州北纬37.34 东经115.33 河北省廓坊北纬39.31 东经116.42 河北省鹿泉北纬38.04 东经114.19 河北省南宫北纬37.22 东经115.23 河北省秦皇岛北纬39.55 东经119.35 河北省任丘北纬38.42 东经116.07 河北省三河北纬39.58 东经117.04 河北省沙河北纬36.51 东经114.30 河北省深州北纬38.01 东经115.32 河北省唐山北纬39.36 东经118.11 河北省武安北纬36.42 东经114.11 河北省邢台北纬37.04 东经114.30 河北省辛集北纬37.54 东经115.12 河北省新乐北纬38.20 东经114.41 河北省张家口北纬40.48 东经114.53 河北省涿州北纬39.29 东经115.59 河北省遵化北纬40.11 东经117.58 河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21 河南省长葛北纬34.12 东经113.47 河南省登封北纬34.27 东经113.02 河南省邓州北纬32.42 东经112.05 河南省巩义北纬34.46 东经112.58 河南省鹤壁北纬35.54 东经114.11 河南省辉县北纬35.27 东经113.47河南省济源北纬35.04 东经112.35河南省开封北纬34.47 东经114.21河南省灵宝北纬34.31 东经110.52河南省林州北纬36.03 东经113.49河南省漯河北纬33.33 东经114.02河南省洛阳北纬34.41 东经112.27河南省南阳北纬33.00 东经112.32河南省平顶山北纬33.44 东经113.17 河南省濮阳北纬35.44 东经115.01河南省沁阳北纬35.05 东经112.57河南省汝州北纬34.09 东经112.50河南省三门峡北纬34.47 东经111.12 河南省商丘北纬34.26 东经115.38河南省卫辉北纬35.24 东经114.03河南省舞钢北纬33.17 东经113.30河南省项城北纬33.26 东经114.54河南省荥阳北纬34.46 东经113.21河南省新密北纬34.31 东经113.22河南省新乡北纬35.18 东经113.52河南省信阳北纬32.07 东经114.04河南省新郑北纬34.24 东经113.43河南省许昌北纬34.01 东经113.49河南省偃师北纬34.43 东经112.47河南省义马北纬34.43 东经111.55河南省禹州北纬34.09 东经113.28河南省周口北纬33.37 东经114.38河南省驻马店北纬32.58 东经114.01 黑龙江省哈尔滨北纬45.44 东经126.36 黑龙江省阿城北纬45.32 东经126.58 黑龙江省安达北纬46.24 东经125.18 黑龙江省北安北纬48.15 东经126.31 黑龙江省大庆北纬46.36 东经125.01 黑龙江省富锦北纬47.15 东经132.02 黑龙江省海林北纬44.35 东经129.21 黑龙江省海伦北纬47.28 东经126.57 黑龙江省鹤岗北纬47.20 东经130.16 黑龙江省黑河北纬50.14 东经127.29 黑龙江省佳木斯北纬46.47 东经130.22 黑龙江省鸡西北纬45.17 东经130.57 黑龙江省密山北纬45.32 东经131.50 黑龙江省牡丹江北纬44.35 东经129.36 黑龙江省讷河北纬48.29 东经124.51 黑龙江省宁安北纬44.21 东经129.28黑龙江省齐齐哈尔北纬47.20 东经123.57 黑龙江省七台河北纬45.48 东经130.49 黑龙江省双城北纬45.22 东经126.15黑龙江省尚志北纬45.14 东经127.55黑龙江省双鸭山北纬46.38 东经131.11 黑龙江省绥芬河北纬44.25 东经131.11 黑龙江省绥化北纬46.38 东经126.59黑龙江省铁力北纬46.59 东经128.01黑龙江省同江北纬47.39 东经132.30黑龙江省五常北纬44.55 东经127.11黑龙江省五大连池北纬48.38 东经126.07 黑龙江省伊春北纬47.42 东经128.56黑龙江省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省广水北纬31.37 东经113.48湖北省洪湖北纬29.48 东经113.27湖北省黄石北纬30.12 东经115.06湖北省黄州北纬30.27 东经114.52湖北省荆门北纬31.02 东经112.12湖北省荆沙北纬30.18 东经112.16湖北省老河口北纬32.23 东经111.40湖北省利川北纬30.18 东经108.56湖北省麻城北纬31.10 东经115.01湖北省浦圻北纬29.42 东经113.51湖北省潜江北纬30.26 东经112.53湖北省石首北纬29.43 东经112.24湖北省十堰北纬32.40 东经110.47湖北省随州北纬31.42 东经113.22湖北省天门北纬60.39 东经113.10湖北省武穴北纬29.51 东经115.33湖北省襄樊北纬32.02 东经112.08湖北省咸宁北纬29.53 东经114.17湖北省仙桃北纬30.22 东经113.27湖北省孝感北纬30.56 东经113.54湖北省宜昌北纬30.42 东经111.17湖北省宜城北纬31.42 东经112.15湖北省应城北纬30.57 东经113.33湖北省枣阳北纬32.07 东经112.44湖北省钟祥北纬31.10 东经112.34 湖南省长沙北纬28.12 东经112.59 湖南省常德北纬29.02 东经111.51 湖南省郴州北纬25.46 东经113.02 湖南省衡阳北纬26.53 东经112.37 湖南省洪江北纬27.07 东经109.59 湖南省怀化北纬27.33 东经109.58 湖南省津市北纬29.38 东经111.52 湖南省吉首北纬28.18 东经109.43 湖南省耒阳北纬26.24 东经112.51 湖南省冷水江北纬27.42 东经111.26 湖南省冷水滩北纬26.26 东经111.35 湖南省涟源北纬27.41 东经111.41 湖南省醴陵北纬27.40 东经113.30 湖南省临湘北纬29.29 东经113.27 湖南省浏阳北纬28.09 东经113.37 湖南省娄底北纬27.44 东经111.59 湖南省汨罗北纬28.49 东经113.03 湖南省韶山北纬27.54 东经112.29 湖南省邵阳北纬27.14 东经111.28 湖南省武冈北纬26.43 东经110.37 湖南省湘潭北纬27.52 东经112.53 湖南省湘乡北纬27.44 东经112.31 湖南省益阳北纬28.36 东经112.20 湖南省永州北纬26.13 东经111.37 湖南省沅江北纬28.50 东经112.22 湖南省岳阳北纬29.22 东经113.06 湖南省张家界北纬29.08 东经110.29 湖南省株洲北纬27.51 东经113.09 湖南省资兴北纬25.58 东经113.13 吉林省长春北纬43.54 东经125.19 吉林省白城北纬45.38 东经122.50 吉林省白山北纬41.56 东经126.26 吉林省大安北纬45.30 东经124.18 吉林省德惠北纬44.32 东经125.42 吉林省敦化北纬43.22 东经128.13 吉林省公主岭北纬43.31 东经124.49 吉林省和龙北纬42.32 东经129.00 吉林省桦甸北纬42.58 东经126.44 吉林省珲春北纬42.52 东经130.22 吉林省集安北纬41.08 东经126.11 吉林省蛟河北纬43.42 东经127.21 吉林省吉林北纬43.52 东经126.33吉林省辽源北纬42.54 东经125.09 吉林省临江北纬41.49 东经126.53 吉林省龙井北纬42.46 东经129.26 吉林省梅河口北纬42.32 东经125.40 吉林省舒兰北纬44.24 东经126.57 吉林省四平北纬43.10 东经124.22 吉林省松原北纬45.11 东经124.49 吉林省洮南北纬45.20 东经122.47 吉林省通化北纬41.43 东经125.56 吉林省图们北纬42.57 东经129.51 吉林省延吉北纬42.54 东经129.30 吉林省愉树北纬44.49 东经126.32 江苏省南京北纬32.03 东经118.46 江苏省常熟北纬31.39 东经120.43 江苏省常州北纬31.47 东经119.58 江苏省丹阳北纬32.00 东经119.32 江苏省东台北纬32.51 东经120.19 江苏省高邮北纬32.47 东经119.27 江苏省海门北纬31.53 东经121.09 江苏省淮安北纬33.30 东经119.09 江苏省淮阴北纬33.36 东经119.02 江苏省江都北纬32.26 东经119.32 江苏省姜堰北纬32.34 东经120.08 江苏省江阴北纬31.54 东经120.17 江苏省靖江北纬32.02 东经120.17 江苏省金坛北纬31.46 东经119.33 江苏省昆山北纬31.23 东经120.57 江苏省连去港北纬34.36 东经119.10 江苏省溧阳北纬31.26 东经119.29 江苏省南通北纬32.01 东经120.51 江苏省邳州北纬34.19 东经117.59 江苏省启乐北纬31.48 东经121.39 江苏省如皋北纬32.23 东经120.33 江苏省宿迁北纬33.58 东经118.18 江苏省苏州北纬31.19 东经120.37 江苏省太仓北纬31.27 东经121.06 江苏省泰兴北纬32.10 东经120.01 江苏省泰州北纬32.30 东经119.54 江苏省通州北纬32.05 东经121.03 江苏省吴江北纬31.10 东经120.39 江苏省无锡北纬31.34 东经120.18 江苏省兴化北纬32.56 东经119.50 江苏省新沂北纬34.22 东经118.20江苏省盐在北纬33.22 东经120.08 江苏省扬中北纬32.14 东经119.49 江苏省扬州北纬32.23 东经119.26 江苏省宜兴北纬31.21 东经119.49 江苏省仪征北纬32.16 东经119.10 江苏省张家港北纬31.52 东经120.32 江苏省镇江北纬32.11 东经119.27 江西省南昌北纬28.40 东经115.55 江西省德兴北纬28.57 东经117.35 江西省丰城北纬28.12 东经115.48 江西省赣州北纬28.52 东经114.56 江西省高安北纬28.25 东经115.22 江西省吉安北纬27.07 东经114.58 江西省景德镇北纬29.17 东经117.13 江西省井冈山北纬26.34 东经114.10 江西省九江北纬29.43 东经115.58 江西省乐平北纬28.58 东经117.08 江西省临川北纬27.59 东经116.21 江西省萍乡北纬27.37 东经113.50 江西省瑞昌北纬29.40 东经115.38 江西省瑞金北纬25.53 东经116.01 江西省上饶北纬25.27 东经117.58 江西省新余北纬27.48 东经114.56 江西省宜春北纬27.47 东经114.23 江西省鹰潭北纬28.14 东经117.03 江西省樟树北纬28.03 东经115.32 辽宁省沈阳北纬41.48 东经123.25 辽宁省鞍山北纬41.07 东经123.00 辽宁省北票北纬41.48 东经120.47 辽宁省本溪北纬41.18 东经123.46 辽宁省朝阳北纬41.34 东经120.27 辽宁省大连北纬38.55 东经121.36 辽宁省丹东北纬40.08 东经124.22 辽宁省大石桥北纬40.37 东经122.31 辽宁省东港北纬39.53 东经124.08 辽宁省凤城北纬40.28 东经124.02 辽宁省抚顺北纬41.51 东经123.54 辽宁省阜新北纬42.01 东经121.39 辽宁省盖州北纬40.24 东经122.21 辽宁省海城北纬40.51 东经122.43 辽宁省葫芦岛北纬40.45 东经120.51 辽宁省锦州北纬41.07 东经121.09 辽宁省开原北纬42.32 东经124.02辽宁省凌海北纬41.10 东经121.21辽宁省凌源北纬41.14 东经119.22辽宁省盘锦北纬41.07 东经122.03辽宁省普兰店北纬39.23 东经121.58辽宁省铁法北纬42.28 东经123.32辽宁省铁岭北纬42.18 东经123.51辽宁省瓦房店北纬39.37 东经122.00辽宁省兴城北纬40.37 东经120.41辽宁省新民北纬41.59 东经122.49辽宁省营口北纬40.39 东经122.13辽宁省庄河北纬39.41 东经122.58内自治区呼和浩特北纬40.48 东经111.41 内自治区包头北纬40.39 东经109.49内自治区赤峰北纬42.17 东经118.58内自治区东胜北纬39.48 东经109.59内自治区二连浩特北纬43.38 东经111.58 内自治区额尔古纳北纬50.13 东经120.11 内自治区丰镇北纬40.27 东经113.09内自治区根河北纬50.48 东经121.29内自治区海拉尔北纬49.12 东经119.39 内自治区霍林郭勒北纬45.32 东经119.38 内自治区集宁北纬41.02 东经113.06内自治区临河北纬40.46 东经107.22内自治区满洲里北纬49.35 东经117.23 内自治区通辽北纬43.37 东经122.16内自治区乌兰浩特北纬46.03 东经122.03 内自治区乌海北纬39.40 东经106.48内自治区锡林浩特北纬43.57 东经116.03 内自治区牙克石北纬49.17 东经120.40 内自治区扎兰屯北纬48.00 东经122.47 宁夏自治区银川北纬38.27 东经106.16 宁夏自治区青铜峡北纬37.56 东经105.59 宁夏自治区石嘴山北纬39.02 东经106.22 宁夏自治区吴忠北纬37.59 东经106.11 青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55山东省济南北纬36.40 东经117.00山东省安丘北纬36.25 东经119.12山东省滨州北纬37.22 东经118.02山东省昌邑北纬39.52 东经119.24山东省德州北纬37.26 东经116.17山东省东营北纬37.27 东经118.30山东省高密北纬36.22 东经119.44 山东省菏泽北纬35.14 东经115.26 山东省胶南北纬35.53 东经119.58 山东省胶州北纬36.17 东经120.00 山东省即墨北纬36.22 东经120.28 山东省济宁北纬35.23 东经116.33 山东省莱芜北纬36.12 东经117.40 山东省莱西北纬36.52 东经120.31 山东省莱阳北纬36.58 东经120.42 山东省莱州北纬37.10 东经119.57 山东省乐陵北纬37.44 东经117.12 山东省聊城北纬36.26 东经115.57 山东省临清北纬36.51 东经115.42 山东省临沂北纬35.03 东经118.20 山东省龙口北纬37.39 东经120.21 山东省蓬莱北纬37.48 东经120.45 山东省平度北纬36.47 东经119.58 山东省青岛北纬36.03 东经120.18 山东省青州北纬36.42 东经118.28 山东省曲阜北纬35.36 东经116.58 山东省日照北纬35.23 东经119.32 山东省荣成北纬37.10 东经122.25 山东省乳山北纬36.54 东经121.31 山东省寿光北纬36.53 东经118.44 山东省泰安北纬36.11 东经117.08 山东省滕州北纬35.06 东经117.09 山东省潍坊北纬36.43 东经119.06 山东省威海北纬37.31 东经122.07 山东省文登北纬37.12 东经122.03 山东省新泰北纬35.54 东经117.45 山东省烟台北纬37.32 东经121.24 山东省兖州北纬35.32 东经116.49 山东省禹城北纬36.56 东经116.39 山东省枣庄北纬34.52 东经117.33 山东省章丘北纬36.43 东经117.32 山东省招远北纬37.21 东经120.23 山东省诸城北纬35.59 东经119.24 山东省淄博北纬36.48 东经118.03 山东省邹城北纬35.24 东经116.58 山西省太原北纬37.54 东经112.33 山西省长治北纬36.11 东经113.06 山西省大同北纬40.06 东经113.17 山西省高平北纬35.48 东经112.55山西省河津北纬35.35 东经110.41 山西省侯马北纬35.37 东经111.21 山西省霍州北纬36.34 东经111.42 山西省介休北纬37.02 东经111.55 山西省晋城北纬35.30 东经112.51 山西省临汾北纬36.05 东经111.31 山西省潞城北纬36.21 东经113.14 山西省朔州北纬39.19 东经112.26 山西省孝义北纬37.08 东经111.48 山西省忻州北纬38.24 东经112.43 山西省阳泉北纬37.51 东经113.34 山西省永济北纬34.52 东经110.27 山西省原平北纬38.43 东经112.42 山西省榆次北纬37.41 东经112.43 山西省运城北纬35.02 东经110.59 陕西省西安北纬34.17 东经108.57 陕西省安康北纬32.41 东经109.01 陕西省宝鸡北纬34.22 东经107.09 陕西省韩城北纬35.28 东经110.27 陕西省汉中北纬33.04 东经107.01 陕西省华阴北纬34.34 东经110.05 陕西省商州北纬33.52 东经109.57 陕西省铜川北纬35.06 东经109.07 陕西省渭南北纬34.30 东经109.30 陕西省咸阳北纬34.20 东经108.43 陕西省兴平北纬34.18 东经108.29 陕西省延安北纬36.35 东经109.28 陕西省榆林北纬38.18 东经109.47 上海市上海市北纬31.14 东经121.29 四川省成都北纬30.40 东经104.04 四川省巴中北纬31.51 东经106.43 四川省崇州北纬30.39 东经103.40 四川省达川北纬31.14 东经107.29 四川省德阳北纬31.09 东经104.22 四川省都江堰北纬31.01 东经103.37 四川省峨眉山北纬29.36 东经103.29 四川省涪陵北纬29.42 东经107.22 四川省广汉北纬30.58 东经104.15 四川省广元北纬32.28 东经105.51 四川省华蓥北纬30.26 东经106.44 四川省简阳北纬30.24 东经104.32 四川省江油北纬31.48 东经104.42 四川省阆中北纬31.36 东经105.58四川省泸州北纬28.54 东经105.24四川省绵阳北纬31.30 东经104.42四川省南充北纬30.49 东经106.04四川省内江北纬29.36 东经105.02四川省攀枝花北纬26.34 东经101.43四川省彭州北纬30.59 东经103.57四川省邛崃北纬30.26 东经103.28四川省遂宁北纬30.31 东经105.33四川省万县北纬30.50 东经108.21四川省万源北纬32.03 东经108.03四川省西昌北纬27.54 东经102.16四川省雅安北纬29.59 东经102.59四川省宜宾北纬28.47 东经104.34四川省自贡北纬29.23 东经104.46四川省资阳北纬30.09 东经104.38台湾省台北市北纬25.03 东经121.30天津市天津市北纬39.02 东经117.12西藏自治区拉萨北纬29.39 东经91.08西藏自治区日喀则北纬29.16 东经88.51 香港香港市北纬21.23 东经115.12新疆自治区乌鲁木齐北纬43.45 东经87.36 新疆自治区阿克苏北纬41.09 东经80.19 新疆自治区阿勒泰北纬47.50 东经88.12 新疆自治区阿图什北纬39.42 东经76.08 新疆自治区博乐北纬44.57 东经82.08新疆自治区昌吉北纬44.02 东经87.18新疆自治区阜康北纬44.09 东经87.58新疆自治区哈密北纬42.50 东经93.28新疆自治区和田北纬37.09 东经79.55新疆自治区克拉玛依北纬45.36 东经84.51 新疆自治区喀什北纬39.30 东经75.59新疆自治区库尔勒北纬41.46 东经86.07 新疆自治区奎屯北纬44.27 东经84.56新疆自治区石河子北纬44.18 东经86.00 新疆自治区塔城北纬46.46 东经82.59新疆自治区吐鲁番北纬42.54 东经89.11 新疆自治区伊宁北纬43.55 东经81.20云南省昆明北纬25.04 东经102.42云南省保山北纬25.08 东经99.10云南省楚雄北纬25.01 东经101.32云南省大理北纬25.34 东经100.13云南省东川北纬26.06 东经103.12云南省个旧北纬23.21 东经103.09云南省开远北纬23.43 东经103.13 云南省曲靖北纬25.30 东经103.48 云南省瑞丽北纬24.00 东经97.50云南省思茅北纬22.48 东经100.58 云南省畹町北纬24.06 东经98.04云南省宣威北纬26.13 东经104.06 云南省玉溪北纬24.22 东经102.32 云南省昭通北纬27.20 东经103.42 浙江省杭州北纬30.16 东经120.10 浙江省慈溪北纬30.11 东经121.15 浙江省东阳北纬29.16 东经120.14 浙江省奉化北纬29.39 东经121.24 浙江省富阳北纬30.03 东经119.57 浙江省海宁北纬30.32 东经120.42 浙江省湖州北纬30.52 东经120.06 浙江省建德北纬29.29 东经119.16 浙江省江山北纬28.45 东经118.37 浙江省嘉兴北纬30.46 东经120.45 浙江省金华北纬29.07 东经119.39 浙江省兰溪北纬29.12 东经119.28 浙江省临海北纬28.51 东经121.08 浙江省丽水北纬28.27 东经119.54 浙江省龙泉北纬28.04 东经119.08 浙江省宁波北纬29.52 东经121.33 浙江省平湖北纬30.42 东经121.01 浙江省衢州北纬28.58 东经118.52 浙江省瑞安北纬27.48 东经120.38 浙江省上虞北纬30.01 东经120.52 浙江省绍兴北纬30.00 东经120.34 浙江省台州北纬28.41 东经121.27 浙江省桐乡北纬30.38 东经120.32 浙江省温岭北纬28.22 东经121.21 浙江省温州北纬28.01 东经120.39 浙江省萧山北纬30.09 东经120.16 浙江省义乌北纬29.18 东经120.04 浙江省乐清北纬28.08 东经120.58 浙江省余杭北纬30.26 东经120.18 浙江省余姚北纬30.02 东经121.10 浙江省永康北纬29.54 东经120.01 浙江省舟山北纬30.01 东经122.06 浙江省诸暨北纬29.43 东经120.14 重庆市重庆市北纬29.35 东经106.33 重庆市合川市北纬30.02 东经106.15重庆市南川市北纬29.10 东经107.05 重庆市永川市北纬29.23 东经105.53。
全国经纬度

省份 地市 区县 经度 纬度北京市 北京市 北京市 116.4 39.9天津市 天津市 天津市 117.2 39.12河北省 石家庄市 石家庄市 114.52 38.05河北省 唐山市 唐山市 118.2 39.63河北省 秦皇岛市 秦皇岛市 119.6 39.93河北省 邯郸市 邯郸市 114.48 36.62河北省 邢台市 邢台市 114.48 37.07河北省 保定市 保定市 115.47 38.87河北省 张家口市 张家口市 114.88 40.82河北省 承德市 承德市 117.93 40.97河北省 沧州市 沧州市 116.83 38.3河北省 廊坊市 廊坊市 116.7 39.52河北省 衡水市 衡水市 115.68 37.73山西省 太原市 太原市 112.55 37.87山西省 大同市 大同市 113.3 40.08山西省 阳泉市 阳泉市 113.57 37.85山西省 长治市 长治市 113.12 36.2山西省 晋城市 晋城市 112.83 35.5山西省 朔州市 朔州市 112.43 39.33山西省 晋中市 晋中市 112.75 37.68山西省 运城市 运城市 110.98 35.02山西省 忻州市 忻州市 112.73 38.42山西省 临汾市 临汾市 111.52 36.08山西省 临汾市 尧都区 111.52 36.08山西省 吕梁市 吕梁市 111.13 37.52内蒙古自治区 呼和浩特市 呼和浩特市 111.73 40.83 内蒙古自治区 包头市 包头市 109.83 40.65内蒙古自治区 乌海市 乌海市 106.82 39.67内蒙古自治区 赤峰市 赤峰市 118.92 42.27内蒙古自治区 通辽市 通辽市 122.27 43.62内蒙古自治区 鄂尔多斯市 鄂尔多斯市 109.8 39.62 内蒙古自治区 呼伦贝尔市 呼伦贝尔市 119.77 49.22 内蒙古自治区 巴彦淖尔市 巴彦淖尔市 107.42 40.75 内蒙古自治区 乌兰察布市 乌兰察布市 113.12 40.98 内蒙古自治区 兴安盟 兴安盟 122.05 46.08内蒙古自治区 锡林郭勒盟 锡林郭勒盟 116.07 43.95 内蒙古自治区 阿拉善盟 阿拉善盟 105.67 38.83辽宁省 沈阳市 沈阳市 123.43 41.8辽宁省 大连市 大连市 121.62 38.92辽宁省 鞍山市 鞍山市 122.98 41.1辽宁省 抚顺市 抚顺市 123.98 41.88辽宁省 本溪市 本溪市 123.77 41.3辽宁省 丹东市 丹东市 124.38 40.13辽宁省 锦州市 锦州市 121.13 41.1辽宁省 营口市 营口市 122.23 40.67辽宁省 阜新市 阜新市 121.67 42.02辽宁省 辽阳市 辽阳市 123.17 41.27辽宁省 盘锦市 盘锦市 122.07 41.12辽宁省 铁岭市 铁岭市 123.83 42.28辽宁省 朝阳市 朝阳市 120.45 41.57辽宁省 葫芦岛市 葫芦岛市 120.83 40.72吉林省 长春市 长春市 125.32 43.9吉林省 吉林市 吉林市 126.55 43.83吉林省 四平市 四平市 124.35 43.17吉林省 辽源市 辽源市 125.13 42.88吉林省 通化市 通化市 125.93 41.73吉林省 白山市 白山市 126.42 41.93吉林省 松原市 松原市 124.82 45.13吉林省 白城市 白城市 122.83 45.62吉林省 延边朝鲜族自治州 延边朝鲜族自治州 129.5 42.88 黑龙江省 哈尔滨市 哈尔滨市 126.53 45.8黑龙江省 齐齐哈尔市 齐齐哈尔市 123.95 47.33黑龙江省 鸡西市 鸡西市 130.97 45.3黑龙江省 鹤岗市 鹤岗市 130.27 47.33黑龙江省 双鸭山市 双鸭山市 131.15 46.63黑龙江省 大庆市 大庆市 125.03 46.58黑龙江省 伊春市 伊春市 128.9 47.73黑龙江省 佳木斯市 佳木斯市 130.37 46.82黑龙江省 七台河市 七台河市 130.95 45.78黑龙江省 牡丹江市 牡丹江市 129.6 44.58黑龙江省 黑河市 黑河市 127.48 50.25黑龙江省 绥化市 绥化市 126.98 46.63黑龙江省 大兴安岭地区 大兴安岭地区 124.12 50.42上海市 上海市 上海市 121.47 31.23江苏省 南京市 南京市 118.78 32.07江苏省 无锡市 无锡市 120.3 31.57江苏省 徐州市 徐州市 117.18 34.27江苏省 常州市 常州市 119.95 31.78江苏省 苏州市 苏州市 120.58 31.3江苏省 南通市 南通市 120.88 31.98江苏省 连云港市 连云港市 119.22 34.6江苏省 淮安市 淮安市 119.02 33.62江苏省 盐城市 盐城市 120.15 33.35江苏省 扬州市 扬州市 119.4 32.4江苏省 镇江市 镇江市 119.45 32.2江苏省 泰州市 泰州市 119.92 32.45江苏省 宿迁市 宿迁市 118.28 33.97浙江省 杭州市 杭州市 120.15 30.28浙江省 宁波市 宁波市 121.55 29.88浙江省 温州市 温州市 120.7 28.0浙江省 嘉兴市 嘉兴市 120.75 30.75浙江省 湖州市 湖州市 120.08 30.9浙江省 绍兴市 绍兴市 120.57 30.0浙江省 金华市 金华市 119.65 29.08浙江省 衢州市 衢州市 118.87 28.93浙江省 舟山市 舟山市 122.2 30.0浙江省 台州市 台州市 121.43 28.68浙江省 丽水市 丽水市 119.92 28.45安徽省 合肥市 合肥市 117.25 31.83安徽省 芜湖市 芜湖市 118.38 31.33安徽省 蚌埠市 蚌埠市 117.38 32.92安徽省 淮南市 淮南市 117.0 32.63安徽省 马鞍山市 马鞍山市 118.5 31.7 安徽省 淮北市 淮北市 116.8 33.95安徽省 铜陵市 铜陵市 117.82 30.93安徽省 安庆市 安庆市 117.05 30.53安徽省 黄山市 黄山市 118.33 29.72安徽省 滁州市 滁州市 118.32 32.3安徽省 阜阳市 阜阳市 115.82 32.9安徽省 阜阳市 颍州区 115.8 32.88安徽省 宿州市 宿州市 116.98 33.63安徽省 巢湖市 巢湖市 117.87 31.6安徽省 六安市 六安市 116.5 31.77安徽省 亳州市 亳州市 115.78 33.85安徽省 池州市 池州市 117.48 30.67安徽省 宣城市 宣城市 118.75 30.95福建省 福州市 福州市 119.3 26.08福建省 厦门市 厦门市 118.08 24.48福建省 莆田市 莆田市 119.0 25.43福建省 三明市 三明市 117.62 26.27福建省 泉州市 泉州市 118.67 24.88福建省 漳州市 漳州市 117.65 24.52福建省 南平市 南平市 118.17 26.65福建省 南平市 延平区 118.17 26.65福建省 龙岩市 龙岩市 117.03 25.1福建省 宁德市 宁德市 119.52 26.67江西省 南昌市 南昌市 115.85 28.68江西省 景德镇市 景德镇市 117.17 29.27 江西省 萍乡市 萍乡市 113.85 27.63江西省 九江市 九江市 116.0 29.7江西省 新余市 新余市 114.92 27.82江西省 鹰潭市 鹰潭市 117.07 28.27江西省 赣州市 赣州市 114.93 25.83江西省 吉安市 吉安市 114.98 27.12江西省 宜春市 宜春市 114.38 27.8江西省 抚州市 抚州市 116.35 28.0江西省 上饶市 上饶市 117.97 28.45山东省 济南市 济南市 116.98 36.67山东省 青岛市 青岛市 120.38 36.07山东省 淄博市 淄博市 118.05 36.82山东省 枣庄市 枣庄市 117.32 34.82山东省 枣庄市 市中区 117.0 36.65山东省 东营市 东营市 118.67 37.43山东省 烟台市 烟台市 121.43 37.45山东省 潍坊市 潍坊市 119.15 36.7山东省 济宁市 济宁市 116.58 35.42山东省 泰安市 泰安市 117.08 36.2山东省 威海市 威海市 122.12 37.52山东省 日照市 日照市 119.52 35.42山东省 莱芜市 莱芜市 117.67 36.22山东省 临沂市 临沂市 118.35 35.05山东省 德州市 德州市 116.3 37.45山东省 聊城市 聊城市 115.98 36.45山东省 滨州市 滨州市 117.97 37.38山东省 牡丹区 牡丹区 115.43 35.25河南省 郑州市 郑州市 113.62 34.75河南省 开封市 开封市 114.3 34.8河南省 洛阳市 洛阳市 112.45 34.62河南省 平顶山市 平顶山市 113.18 33.77河南省 安阳市 安阳市 114.38 36.1河南省 鹤壁市 鹤壁市 114.28 35.75河南省 新乡市 新乡市 113.9 35.3河南省 焦作市 焦作市 113.25 35.22河南省 濮阳市 濮阳市 115.03 35.77河南省 许昌市 许昌市 113.85 34.03河南省 漯河市 漯河市 114.02 33.58河南省 三门峡市 三门峡市 111.2 34.78河南省 南阳市 南阳市 112.52 33.0河南省 商丘市 商丘市 115.65 34.45河南省 信阳市 信阳市 114.07 32.13河南省 周口市 周口市 114.65 33.62河南省 驻马店市 驻马店市 114.02 32.98湖北省 武汉市 武汉市 114.3 30.6湖北省 黄石市 黄石市 115.03 30.2湖北省 十堰市 十堰市 110.78 32.65湖北省 宜昌市 宜昌市 111.28 30.7湖北省 襄樊市 襄樊市 112.15 32.02湖北省 鄂州市 鄂州市 114.88 30.4湖北省 荆门市 荆门市 112.2 31.03湖北省 孝感市 孝感市 113.92 30.93湖北省 荆州市 荆州市 112.23 30.33湖北省 黄冈市 黄冈市 114.87 30.45湖北省 咸宁市 咸宁市 114.32 29.85湖北省 随州市 随州市 113.37 31.72湖北省 恩施土家族苗族自治州 恩施土家族苗族自治州 109.47 30.3 湖北省 仙桃市 仙桃市 113.45 30.37湖南省 长沙市 长沙市 112.93 28.23湖南省 株洲市 株洲市 113.13 27.83湖南省 湘潭市 湘潭市 112.93 27.83湖南省 衡阳市 衡阳市 112.57 26.9湖南省 邵阳市 邵阳市 111.47 27.25湖南省 岳阳市 岳阳市 113.12 29.37湖南省 常德市 常德市 111.68 29.05湖南省 张家界市 张家界市 110.47 29.13湖南省 益阳市 益阳市 112.32 28.6湖南省 益阳市 资阳区 112.32 28.6湖南省 益阳市 赫山区 112.37 28.6湖南省 益阳市 南县 112.4 29.38湖南省 益阳市 桃江县 112.12 28.53湖南省 郴州市 郴州市 113.02 25.78湖南省 永州市 永州市 111.62 26.43湖南省 怀化市 怀化市 110.0 27.57湖南省 娄底市 娄底市 112.0 27.73湖南省 湘西土家族苗族自治州 湘西土家族苗族自治州 109.73 28.32 广东省 广州市 广州市 113.27 23.13广东省 广州市 荔湾区 113.23 23.13广东省 韶关市 韶关市 113.6 24.82广东省 深圳市 深圳市 114.05 22.55广东省 珠海市 珠海市 113.57 22.27广东省 汕头市 汕头市 116.68 23.35广东省 佛山市 佛山市 113.12 23.02广东省 江门市 江门市 113.08 22.58广东省 湛江市 湛江市 110.35 21.27广东省 茂名市 茂名市 110.92 21.67广东省 肇庆市 肇庆市 112.47 23.05广东省 惠州市 惠州市 114.42 23.12广东省 梅州市 梅州市 116.12 24.28广东省 汕尾市 汕尾市 115.37 22.78广东省 河源市 河源市 114.7 23.73广东省 阳江市 阳江市 111.98 21.87广东省 清远市 清远市 113.03 23.7广东省 东莞市 东莞市 113.75 23.05广东省 中山市 中山市 113.38 22.52广东省 潮州市 潮州市 116.62 23.67广东省 揭阳市 揭阳市 116.37 23.55广东省 云浮市 云浮市 112.03 22.92广西壮族自治区 南宁市 南宁市 108.37 22.82广西壮族自治区 柳州市 柳州市 109.42 24.33广西壮族自治区 桂林市 桂林市 110.28 25.28广西壮族自治区 桂林市 阳朔县 110.48 24.78广西壮族自治区 梧州市 梧州市 111.27 23.48广西壮族自治区 北海市 北海市 109.12 21.48广西壮族自治区 防城港市 防城港市 108.35 21.7广西壮族自治区 钦州市 钦州市 108.62 21.95广西壮族自治区 贵港市 贵港市 109.6 23.1广西壮族自治区 玉林市 玉林市 110.17 22.63广西壮族自治区 百色市 百色市 106.62 23.9广西壮族自治区 贺州市 贺州市 111.55 24.42广西壮族自治区 河池市 河池市 108.07 24.7广西壮族自治区 来宾市 来宾市 109.23 23.73广西壮族自治区 崇左市 崇左市 107.37 22.4海南省 海口市 海口市 110.32 20.03海南省 三亚市 三亚市 109.5 18.25海南省 五指山市 五指山市 109.52 18.78重庆市 重庆市 重庆市 106.55 29.57四川省 成都市 成都市 104.07 30.67四川省 自贡市 自贡市 104.78 29.35四川省 攀枝花市 攀枝花市 101.72 26.58四川省 泸州市 泸州市 105.43 28.87四川省 德阳市 德阳市 104.38 31.13四川省 绵阳市 绵阳市 104.73 31.47四川省 广元市 广元市 105.83 32.43四川省 遂宁市 遂宁市 105.57 30.52四川省 内江市 内江市 105.05 29.58四川省 乐山市 乐山市 103.77 29.57四川省 南充市 南充市 106.08 30.78四川省 眉山市 眉山市 103.83 30.05四川省 宜宾市 宜宾市 104.62 28.77四川省 广安市 广安市 106.63 30.47四川省 达州市 达州市 107.5 31.22四川省 雅安市 雅安市 103.0 29.98四川省 巴中市 巴中市 106.77 31.85四川省 资阳市 资阳市 104.65 30.12四川省 阿坝藏族羌族自治州 阿坝藏族羌族自治州 102.22 31.9四川省 甘孜藏族自治州 甘孜藏族自治州 101.97 30.05四川省 凉山彝族自治州 凉山彝族自治州 102.27 27.9四川省 凉山彝族自治州 西昌市 102.27 27.9贵州省 贵阳市 贵阳市 106.63 26.65贵州省 六盘水市 六盘水市 104.83 26.6贵州省 遵义市 遵义市 106.92 27.73贵州省 安顺市 安顺市 105.95 26.25贵州省 铜仁地区 铜仁地区 109.18 27.72贵州省 兴义市 兴义市 104.9 25.08贵州省 毕节地区 毕节地区 105.28 27.3贵州省 黔东南苗族侗族自治州 黔东南苗族侗族自治州 107.97 26.58 贵州省 黔南布依族苗族自治州 黔南布依族苗族自治州 107.52 26.27 云南省 昆明市 昆明市 102.72 25.05云南省 曲靖市 曲靖市 103.8 25.5云南省 曲靖市 麒麟区 103.8 25.5云南省 玉溪市 玉溪市 102.55 24.35云南省 保山市 保山市 99.17 25.12云南省 昭通市 昭通市 103.72 27.33云南省 丽江市 丽江市 100.23 26.88云南省 墨江哈尼族自治县 墨江哈尼族自治县 101.68 23.43云南省 临沧市 临沧市 100.08 23.88云南省 楚雄彝族自治州 楚雄彝族自治州 101.55 25.03云南省 红河哈尼族彝族自治州 红河哈尼族彝族自治州 103.4 23.37 云南省 文山壮族苗族自治州 文山壮族苗族自治州 104.25 23.37云南省 西双版纳傣族自治州 西双版纳傣族自治州 100.8 22.02云南省 大理白族自治州 大理白族自治州 100.23 25.6云南省 德宏傣族景颇族自治州 德宏傣族景颇族自治州 98.58 24.43 云南省 怒江傈僳族自治州 怒江傈僳族自治州 98.85 25.85云南省 迪庆藏族自治州 迪庆藏族自治州 99.7 27.83西藏自治区 拉萨市 拉萨市 91.13 29.65西藏自治区 昌都地区 昌都地区 97.18 31.13西藏自治区 山南地区 山南地区 91.77 29.23西藏自治区 日喀则地区 日喀则地区 88.88 29.27西藏自治区 日喀则地区 日喀则市 88.88 29.27西藏自治区 那曲地区 那曲地区 92.07 31.48西藏自治区 阿里地区 阿里地区 80.1 32.5西藏自治区 林芝地区 林芝地区 94.37 29.68陕西省 西安市 西安市 108.93 34.27陕西省 铜川市 铜川市 108.93 34.9陕西省 宝鸡市 宝鸡市 107.13 34.37陕西省 咸阳市 咸阳市 108.7 34.33陕西省 渭南市 渭南市 109.5 34.5陕西省 延安市 延安市 109.48 36.6陕西省 汉中市 汉中市 107.02 33.07陕西省 榆林市 榆林市 109.73 38.28陕西省 安康市 安康市 109.02 32.68陕西省 商洛市 商洛市 109.93 33.87甘肃省 兰州市 兰州市 103.82 36.07甘肃省 嘉峪关市 嘉峪关市 98.27 39.8甘肃省 金昌市 金昌市 102.18 38.5甘肃省 白银市 白银市 104.18 36.55甘肃省 天水市 天水市 105.72 34.58甘肃省 武威市 武威市 102.63 37.93甘肃省 张掖市 张掖市 100.45 38.93甘肃省 平凉市 平凉市 106.67 35.55甘肃省 酒泉市 酒泉市 98.52 39.75甘肃省 庆阳市 庆阳市 107.63 35.73甘肃省 定西市 定西市 104.62 35.58甘肃省 陇南市 陇南市 104.92 33.4甘肃省 临夏回族自治州 临夏回族自治州 103.22 35.6甘肃省 甘南藏族自治州 甘南藏族自治州 102.92 34.98青海省 西宁市 西宁市 101.78 36.62青海省 海东地区 海东地区 102.12 36.5青海省 海北藏族自治州 海北藏族自治州 100.9 36.97青海省 黄南藏族自治州 黄南藏族自治州 102.02 35.52青海省 黄南藏族自治州 同仁县 102.02 35.52青海省 海南藏族自治州 海南藏族自治州 100.62 36.28青海省 果洛藏族自治州 果洛藏族自治州 100.23 34.48青海省 玉树藏族自治州 玉树藏族自治州 97.02 33.0青海省 海西蒙古族藏族自治州 海西蒙古族藏族自治州 97.37 37.37 宁夏回族自治区 银川市 银川市 106.28 38.47宁夏回族自治区 石嘴山市 石嘴山市 106.38 39.02宁夏回族自治区 吴忠市 吴忠市 106.2 37.98宁夏回族自治区 固原市 固原市 106.28 36.0宁夏回族自治区 中卫市 中卫市 105.18 37.52新疆维吾尔 乌鲁木齐市 乌鲁木齐市 87.62 43.82新疆维吾尔 克拉玛依市 克拉玛依市 84.87 45.6新疆维吾尔 吐鲁番地区 吐鲁番地区 89.17 42.95新疆维吾尔 哈密地区 哈密地区 93.52 42.83新疆维吾尔 昌吉回族自治州 昌吉回族自治州 87.3 44.02新疆维吾尔 博尔塔拉蒙古自治州 博尔塔拉蒙古自治州 82.07 44.9 新疆维吾尔 巴音郭楞蒙古自治州 巴音郭楞蒙古自治州 86.15 41.77 新疆维吾尔 阿克苏地区 阿克苏地区 80.27 41.17新疆维吾尔 阿图什市 阿图什市 76.17 39.72新疆维吾尔 喀什地区 喀什地区 75.98 39.47新疆维吾尔 和田地区 和田地区 79.92 37.12新疆维吾尔 伊犁哈萨克自治州 伊犁哈萨克自治州 81.32 43.92新疆维吾尔 塔城地区 塔城地区 82.98 46.75新疆维吾尔 阿勒泰地区 阿勒泰地区 88.13 47.85新疆维吾尔 石河子市 石河子市 86.03 44.3港澳台 港澳台 香港 114.08 22.2港澳台 港澳台 澳门 113.33 22.13港澳台 港澳台 台北市 121.5 25.03港澳台 港澳台 高雄市 120.28 22.62港澳台 港澳台 基隆市 121.73 25.13港澳台 港澳台 台中市 120.67 24.15港澳台 港澳台 台南市 120.2 23.0港澳台 港澳台 新竹市 120.95 24.82港澳台 港澳台 嘉义市 120.43 23.48。
各地经纬度汇总

各地经纬度汇总直辖市各市经纬度查询北京市北纬39.55 东经116.24天津市北纬39.02 东经117.12上海市北纬31.14 东经121.29重庆市北纬29.35 东经106.33香港特别行政区北纬21.23 东经115.12 澳门特别行政区北纬21.33 东经115.07 台湾省各市经纬度查询台北市北纬25.03 东经121.30西藏自治区各市经纬度查询拉萨北纬29.39 东经91.08日喀则北纬29.16 东经88.51湖北省各市经纬度查询武汉北纬30.35 东经114.17安陆北纬31.15 东经113.41当阳北纬30.50 东经111.47丹江口北纬32.33 东经108.30大冶北纬30.06 东经114.58恩施北纬30.16 东经109.29鄂州北纬30.23 东经114.52广水北纬31.37 东经113.48洪湖北纬29.48 东经113.27黄石北纬30.12 东经115.06黄州北纬30.27 东经114.52荆门北纬31.02 东经112.12荆沙北纬30.18 东经112.16老河口北纬32.23 东经111.40利川北纬30.18 东经108.56浦圻北纬29.42 东经113.51 潜江北纬30.26 东经112.53 石首北纬29.43 东经112.24 十堰北纬32.40 东经110.47 随州北纬31.42 东经113.22 天门北纬60.39 东经113.10 武穴北纬29.51 东经115.33 襄樊北纬32.02 东经112.08 咸宁北纬29.53 东经114.17 仙桃北纬30.22 东经113.27 孝感北纬30.56 东经113.54 宜昌北纬30.42 东经111.17 宜城北纬31.42 东经112.15 应城北纬30.57 东经113.33 枣阳北纬32.07 东经112.44 枝城北纬30.23 东经111.27 钟祥北纬31.10 东经112.34 湖南省各市经纬度查询长沙北纬28.12 东经112.59 常德北纬29.02 东经111.51 郴州北纬25.46 东经113.02 衡阳北纬26.53 东经112.37 洪江北纬27.07 东经109.59 怀化北纬27.33 东经109.58 津市北纬29.38 东经111.52 吉首北纬28.18 东经109.43 耒阳北纬26.24 东经112.51 冷水江北纬27.42 东经111.26 冷水滩北纬26.26 东经111.35醴陵北纬27.40 东经113.30 临湘北纬29.29 东经113.27 浏阳北纬28.09 东经113.37 娄底北纬27.44 东经111.59 汨罗北纬28.49 东经113.03 韶山北纬27.54 东经112.29 邵阳北纬27.14 东经111.28 武冈北纬26.43 东经110.37 湘潭北纬27.52 东经112.53 湘乡北纬27.44 东经112.31 益阳北纬28.36 东经112.20 永州北纬26.13 东经111.37 沅江北纬28.50 东经112.22 岳阳北纬29.22 东经113.06 张家界北纬29.08 东经110.29 株洲北纬27.51 东经113.09 资兴北纬25.58 东经113.13 广东省各市经纬度查询广州北纬23.08 东经113.14 潮阳北纬23.16 东经116.36 潮州北纬23.40 东经116.38 澄海北纬23.28 东经116.46 从化北纬23.33 东经113.33 东莞北纬23.02 东经113.45 恩平北纬22.12 东经112.19 佛山北纬23.02 东经113.06 高明北纬22.53 东经112.50 高要北纬23.02 东经112.26 高州北纬21.54 东经110.50河源北纬23.43 东经114.41 花都北纬23.23 东经113.12 化州北纬21.39 东经110.37 惠阳北纬22.48 东经114.28 惠州北纬23.05 东经114.22 江门北纬22.35 东经113.04 揭阳北纬22.32 东经116.21 开平北纬22.22 东经112.40 乐昌北纬25.09 东经113.21 雷州北纬20.54 东经110.04 廉江北纬21.37 东经110.17 连州北纬24.48 东经112.23 罗定北纬22.46 东经111.33 茂名北纬21.40 东经110.53 梅州北纬24.19 东经116.07 南海北纬23.01 东经113.09 番禺北纬22.57 东经113.22 普宁北纬23.18 东经116.10 清远北纬23.42 东经113.01 三水北纬23.10 东经112.52 汕头北纬23.22 东经116.41 汕尾北纬22.47 东经115.21 韶关北纬24.48 东经113.37 深圳北纬22.33 东经114.07 顺德北纬22.50 东经113.15 四会北纬23.21 东经112.41 台山北纬22.15 东经112.48 吴川北纬21.26 东经110.47 新会北纬22.32 东经113.01阳春北纬22.10 东经111.48 阳江北纬21.50 东经111.58 英德北纬24.10 东经113.22 云浮北纬22.57 东经112.02 增城北纬23.18 东经113.49 湛江北纬21.11 东经110.24 肇庆北纬23.03 东经112.27 中山北纬22.31 东经113.22 珠海北纬22.17 东经113.34 广西壮族自治区各市经纬度查询南宁北纬22.48 东经108.19 北海北纬21.28 东经109.07 北流北纬22.42 东经110.21 百色北纬23.54 东经106.36 防城港北纬21.37 东经108.20 贵港北纬23.06 东经109.36 桂林北纬25.17 东经110.17 桂平北纬23.22 东经110.04 河池北纬24.42 东经108.03 合山北纬23.47 东经108.52 柳州北纬23.19 东经109.24 赁祥北纬22.07 东经106.44 钦州北纬21.57 东经108.37 青塘北纬22.26 东经108.82 梧州北纬23.29 东经111.20 玉林北纬22.38 东经110.09 宜州北纬24.28 东经108.40 四川省各市经纬度查询成都北纬30.40 东经104.04崇州北纬30.39 东经103.40 达川北纬31.14 东经107.29 德阳北纬31.09 东经104.22 都江堰北纬31.01 东经103.37 峨眉山北纬29.36 东经103.29 涪陵北纬29.42 东经107.22 广汉北纬30.58 东经104.15 广元北纬32.28 东经105.51 华蓥北纬30.26 东经106.44 简阳北纬30.24 东经104.32 江油北纬31.48 东经104.42 阆中北纬31.36 东经105.58 乐山北纬29.36 东经103.44 泸州北纬28.54 东经105.24 绵阳北纬31.30 东经104.42 南充北纬30.49 东经106.04 内江北纬29.36 东经105.02 攀枝花北纬26.34 东经101.43 彭州北纬30.59 东经103.57 邛崃北纬30.26 东经103.28 遂宁北纬30.31 东经105.33 万县北纬30.50 东经108.21 万源北纬32.03 东经108.03 西昌北纬27.54 东经102.16 雅安北纬29.59 东经102.59 宜宾北纬28.47 东经104.34 自贡北纬29.23 东经104.46 资阳北纬30.09 东经104.38 浙江省各市经纬度查询慈溪北纬30.11 东经121.15 东阳北纬29.16 东经120.14 奉化北纬29.39 东经121.24 富阳北纬30.03 东经119.57 海宁北纬30.32 东经120.42 湖州北纬30.52 东经120.06 建德北纬29.29 东经119.16 江山北纬28.45 东经118.37 嘉兴北纬30.46 东经120.45 金华北纬29.07 东经119.39 兰溪北纬29.12 东经119.28 临海北纬28.51 东经121.08 丽水北纬28.27 东经119.54 龙泉北纬28.04 东经119.08 宁波北纬29.52 东经121.33 平湖北纬30.42 东经121.01 衢州北纬28.58 东经118.52 瑞安北纬27.48 东经120.38 上虞北纬30.01 东经120.52 绍兴北纬30.00 东经120.34 台州北纬28.41 东经121.27 桐乡北纬30.38 东经120.32 温岭北纬28.22 东经121.21 温州北纬28.01 东经120.39 萧山北纬30.09 东经120.16 义乌北纬29.18 东经120.04 乐清北纬28.08 东经120.58 余杭北纬30.26 东经120.18 余姚北纬30.02 东经121.10舟山北纬30.01 东经122.06 诸暨北纬29.43 东经120.14 陕西省各市经纬度查询西安北纬34.17 东经108.57 安康北纬32.41 东经109.01 宝鸡北纬34.22 东经107.09 韩城北纬35.28 东经110.27 汉中北纬33.04 东经107.01 华阴北纬34.34 东经110.05 商州北纬33.52 东经109.57 铜川北纬35.06 东经109.07 渭南北纬34.30 东经109.30 咸阳北纬34.20 东经108.43 兴平北纬34.18 东经108.29 延安北纬36.35 东经109.28 榆林北纬38.18 东经109.47 甘肃省各市经纬度查询兰州北纬36.04 东经103.51 白银北纬36.33 东经104.12 敦煌北纬40.08 东经94.41 嘉峪关北纬39.48 东经98.14 金昌北纬38.28 东经102.10 酒泉北纬39.44 东经98.31 临夏北纬35.37 东经103.12 平凉北纬35.32 东经106.40 天水北纬34.37 东经105.42 武威北纬37.56 东经102.39 西峰北纬35.45 东经107.40 玉门北纬39.49 东经97.35重庆市各区经纬度查询合川市北纬30.02 东经106.15 江津市北纬29.18 东经106.16 南川市北纬29.10 东经107.05 永川市北纬29.23 东经105.53 宁夏回族自治区各市经纬度查询银川北纬38.27 东经106.16青铜峡北纬37.56 东经105.59 石嘴山北纬39.02 东经106.22 吴忠北纬37.59 东经106.11内蒙古自治区各市经纬度查询呼和浩特北纬40.48 东经111.41 包头北纬40.39 东经109.49赤峰北纬42.17 东经118.58东胜北纬39.48 东经109.59二连浩特北纬43.38 东经111.58 额尔古纳北纬50.13 东经120.11 丰镇北纬40.27 东经113.09根河北纬50.48 东经121.29海拉尔北纬49.12 东经119.39 霍林郭勒北纬45.32 东经119.38 集宁北纬41.02 东经113.06临河北纬40.46 东经107.22满洲里北纬49.35 东经117.23 通辽北纬43.37 东经122.16乌兰浩特北纬46.03 东经122.03 乌海北纬39.40 东经106.48锡林浩特北纬43.57 东经116.03 牙克石北纬49.17 东经120.40青海省各市经纬度查询西宁北纬36.38 东经101.48 德令哈北纬37.22 东经97.23 格尔木北纬36.26 东经94.55 江西省各市经纬度查询南昌北纬28.40 东经115.55 德兴北纬28.57 东经117.35 丰城北纬28.12 东经115.48 赣州北纬28.52 东经114.56 高安北纬28.25 东经115.22 吉安北纬27.07 东经114.58 景德镇北纬29.17 东经117.13 井冈山北纬26.34 东经114.10 九江北纬29.43 东经115.58 乐平北纬28.58 东经117.08 临川北纬27.59 东经116.21 萍乡北纬27.37 东经113.50 瑞昌北纬29.40 东经115.38 瑞金北纬25.53 东经116.01 上饶北纬25.27 东经117.58 新余北纬27.48 东经114.56 宜春北纬27.47 东经114.23 鹰潭北纬28.14 东经117.03 樟树北纬28.03 东经115.32 安徽省各市经纬度查询合肥北纬31.52 东经117.17 安庆北纬30.31 东经117.02 蚌埠北纬32.56 东经117.21 亳州北纬33.52 东经115.47滁州北纬32.18 东经118.18 阜阳北纬32.54 东经115.48 贵池北纬30.39 东经117.28 淮北北纬33.57 东经116.47 淮南北纬32.37 东经116.58 黄山北纬29.43 东经118.18 界首北纬33.15 东经115.21 六安北纬31.44 东经116.28 马鞍山北纬31.43 东经118.28 明光北纬32.47 东经117.58 宿州北纬33.38 东经116.58 天长北纬32.41 东经118.59 铜陵北纬30.56 东经117.48 芜湖北纬31.19 东经118.22 宣州北纬30.57 东经118.44 贵州省各市经纬度查询贵阳北纬26.35 东经106.42 安顺北纬26.14 东经105.55 毕节北纬27.18 东经105.18 赤水北纬28.34 东经105.42 都匀北纬26.15 东经107.31 凯里北纬26.35 东经107.58 六盘水北纬26.35 东经104.50 清镇北纬26.33 东经106.27 铜仁北纬27.43 东经109.12 兴义北纬25.05 东经104.53 遵义北纬27.42 东经106.55 辽宁省各市经纬度查询沈阳北纬41.48 东经123.25北票北纬41.48 东经120.47 本溪北纬41.18 东经123.46 朝阳北纬41.34 东经120.27 大连北纬38.55 东经121.36 丹东北纬40.08 东经124.22 大石桥北纬40.37 东经122.31 东港北纬39.53 东经124.08 凤城北纬40.28 东经124.02 抚顺北纬41.51 东经123.54 阜新北纬42.01 东经121.39 盖州北纬40.24 东经122.21 海城北纬40.51 东经122.43 葫芦岛北纬40.45 东经120.51 锦州北纬41.07 东经121.09 开原北纬42.32 东经124.02 辽阳北纬41.16 东经123.12 凌海北纬41.10 东经121.21 凌源北纬41.14 东经119.22 盘锦北纬41.07 东经122.03 普兰店北纬39.23 东经121.58 铁法北纬42.28 东经123.32 铁岭北纬42.18 东经123.51 瓦房店北纬39.37 东经122.00 兴城北纬40.37 东经120.41 新民北纬41.59 东经122.49 营口北纬40.39 东经122.13 庄河北纬39.41 东经122.58 河北省各市经纬度查询石家庄北纬38.02 东经114.30保定北纬38.51 东经115.30 霸州北纬39.06 东经116.24 泊头北纬38.04 东经116.34 沧州北纬38.18 东经116.52 承德北纬40.59 东经117.57 定州北纬38.30 东经115.00 丰南北纬39.34 东经118.06 高碑店北纬39.20 东经115.51 蒿城北纬38.02 东经114.50 邯郸北纬36.36 东经114.28 河间北纬38.26 东经116.05 衡水北纬37.44 东经115.42 黄骅北纬38.21 东经117.21 晋州北纬38.02 东经115.02 冀州北纬37.34 东经115.33 廓坊北纬39.31 东经116.42 鹿泉北纬38.04 东经114.19 南宫北纬37.22 东经115.23 秦皇岛北纬39.55 东经119.35 任丘北纬38.42 东经116.07 三河北纬39.58 东经117.04 沙河北纬36.51 东经114.30 深州北纬38.01 东经115.32 唐山北纬39.36 东经118.11 武安北纬36.42 东经114.11 邢台北纬37.04 东经114.30 辛集北纬37.54 东经115.12 新乐北纬38.20 东经114.41 张家口北纬40.48 东经114.53遵化北纬40.11 东经117.58 河南省各市经纬度查询郑州北纬34.46 东经113.40 安阳北纬36.06 东经114.21 长葛北纬34.12 东经113.47 登封北纬34.27 东经113.02 邓州北纬32.42 东经112.05 巩义北纬34.46 东经112.58 鹤壁北纬35.54 东经114.11 辉县北纬35.27 东经113.47 焦作北纬35.14 东经113.12 济源北纬35.04 东经112.35 开封北纬34.47 东经114.21 灵宝北纬34.31 东经110.52 林州北纬36.03 东经113.49 漯河北纬33.33 东经114.02 洛阳北纬34.41 东经112.27 南阳北纬33.00 东经112.32 平顶山北纬33.44 东经113.17 濮阳北纬35.44 东经115.01 沁阳北纬35.05 东经112.57 汝州北纬34.09 东经112.50 三门峡北纬34.47 东经111.12 商丘北纬34.26 东经115.38 卫辉北纬35.24 东经114.03 舞钢北纬33.17 东经113.30 项城北纬33.26 东经114.54 荥阳北纬34.46 东经113.21 新密北纬34.31 东经113.22信阳北纬32.07 东经114.04 新郑北纬34.24 东经113.43 许昌北纬34.01 东经113.49 偃师北纬34.43 东经112.47 义马北纬34.43 东经111.55 禹州北纬34.09 东经113.28 周口北纬33.37 东经114.38 驻马店北纬32.58 东经114.01 山东省各市经纬度查询济南北纬36.40 东经117.00 安丘北纬36.25 东经119.12 滨州北纬37.22 东经118.02 昌邑北纬39.52 东经119.24 德州北纬37.26 东经116.17 东营北纬37.27 东经118.30 肥城北纬36.14 东经116.46 高密北纬36.22 东经119.44 菏泽北纬35.14 东经115.26 胶南北纬35.53 东经119.58 胶州北纬36.17 东经120.00 即墨北纬36.22 东经120.28 济宁北纬35.23 东经116.33 莱芜北纬36.12 东经117.40 莱西北纬36.52 东经120.31 莱阳北纬36.58 东经120.42 莱州北纬37.10 东经119.57 乐陵北纬37.44 东经117.12 聊城北纬36.26 东经115.57 临清北纬36.51 东经115.42龙口北纬37.39 东经120.21 蓬莱北纬37.48 东经120.45 平度北纬36.47 东经119.58 青岛北纬36.03 东经120.18 青州北纬36.42 东经118.28 曲阜北纬35.36 东经116.58 日照北纬35.23 东经119.32 荣成北纬37.10 东经122.25 乳山北纬36.54 东经121.31 寿光北纬36.53 东经118.44 泰安北纬36.11 东经117.08 滕州北纬35.06 东经117.09 潍坊北纬36.43 东经119.06 威海北纬37.31 东经122.07 文登北纬37.12 东经122.03 新泰北纬35.54 东经117.45 烟台北纬37.32 东经121.24 兖州北纬35.32 东经116.49 禹城北纬36.56 东经116.39 枣庄北纬34.52 东经117.33 章丘北纬36.43 东经117.32 招远北纬37.21 东经120.23 诸城北纬35.59 东经119.24 淄博北纬36.48 东经118.03 邹城北纬35.24 东经116.58。
中国各省省会城市经纬度
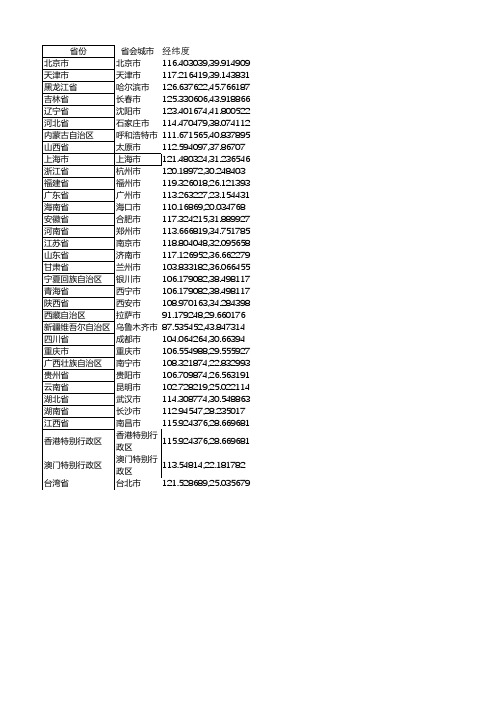
广东省
广州市 113.263227,23.154431
海南省
海口市 110.16869,20.034768
安徽省
合肥市 117.324215,31.889927
河南省
郑州市 113.666819,34.751785
江苏省
南京市 118.804048,32.095658
山东省
济南市 117.126952,36.662279
石家庄市 114.470479,38.074112
内蒙古自治区 呼和浩特市 111.671565,40.837895
山西省
太原市 112.594097,37.86707
上海市
上海市 121.480324,31.236546
浙江省
杭州市 120.18972,30.248403
福建省
福州市 119.326018,26.121393
省份
省会城市 经纬度
北京市
北京市 116.403039,39.914909
天津市
天津市 117.216419,39.143831
黑龙江省
哈尔滨市 126.637622,45.766187
吉林省
长春市 125.330606,43.918866
辽宁省
沈阳市 123.401674,41.800522
河北省
四川省
成都市 104.064264,30.66394
重庆市
重庆市 106.554988,29.555927
广西壮族自治区 南宁市 108.321874,22.832993
贵州省
贵阳市 106.709874,26.563191
云南省
昆明市 102.728219,25.022114
全国各城市经纬度

全国各城市经纬度全国各城市经纬度城市经度纬度城市经度纬度北京116:28E 39:54N 青岛120:19E 36:04N天津117:10E 39:10N 郑州113:42E 34:44N石家庄114:26E 38:03N 开封114:23E 34:52N 保定115:28E 38:53N 洛阳112:26E 34:43N唐山118:09E 39:37N 许昌113:48E 34:00N秦皇岛119:37E 39:54N 新乡113:54E 35:18N 张家口114:55E 40:51N 武汉114:20E 30:37N 承德117:52E 40:59N 宜昌111:15E 30:42N太原112:33E 37:51N 沙市112:17E 30:16N大同113:13E 40:07N 长沙112:55E 28:12N临汾111:31E 36:05N 衡阳112:34E 26:55N长治113:13E 36:05N 湘潭112:51E 27:54N呼和浩特111:38E 40:48N 常德111:39E 29:00N 包头110:00E 40:35N 广州113:18E 23:10N海拉尔119:43E 49:14N 汕头116:40E 23:21N沈阳123:23E 41:48N 韶关113:33E 24:48N大连121:38E 38:54N 海口110:10E 20:03N鞍山123:00E 41:04N 南宁108:21E 22:47N锦州121:09E 41:09N 桂林110:10E 25:18N长春125:18E 43:55N 柳州109:19E 24:20N吉林126:36E 43:48N 悟州111:18E 23:28N哈尔滨126:38E 45:45N 成都104:04E 30:39N 齐齐哈尔123:55E 47:22N 重庆106:33E 29:33N 牡丹江129:36E 44:35N 内江105:03E 29:35N 上海121:26E 31:12N 泸州105:27E 28:54N南京118:46E 32:03N 万县108:22E 30:48N无锡120:18E 31:35N 贵阳106:43E 26:34N苏州120:39E 31:20N 遵义106:53E 27:45N徐州117:12E 34:16N 昆明102:42E 25:03N杭州120:10E 30:15N 拉萨91:02E 29:39N宁波121:34E 29:53N 日喀则88:49E 29:16N温州120:38E 28:00N 西安108:55E 34:15N金华119:49E 29:10N 宝鸡107:09E 34:21N合肥117:16E 31:51N 延安109:26E 36:35N芜湖118:20E 31:21N 兰州103:50E 36:03N安庆117:02E 30:32N 天水105:33E 34:35N福州119:19E 26:02N 酒泉98:30E 39:44N厦门118:04E 24:26N 西宁101:49E 36:37N泉州118:37E 24:54N 银川106:13E 38:28N南昌115:53E 28:41N 乌鲁木齐87:36E 43:46N 九江115:59E 29:43N 哈密93:27E 42:50N赣州114:56E 25:51N 喀什75:59E 39:27N济南117:02E 36:40N 和田79:55E 37:07N烟台121:20E 37:33N 台北121:31E 25:02N所在省城市名纬度经度安徽省合肥北纬31.52 东经117.17安徽省安庆北纬30.31 东经117.02安徽省蚌埠北纬32.56 东经117.21安徽省亳州北纬33.52 东经115.47安徽省巢湖北纬31.36 东经117.52安徽省滁州北纬32.18 东经118.18安徽省阜阳北纬32.54 东经115.48安徽省贵池北纬30.39 东经117.28安徽省淮北北纬33.57 东经116.47安徽省淮南北纬32.37 东经116.58安徽省黄山北纬29.43 东经118.18安徽省界首北纬33.15 东经115.21安徽省六安北纬31.44 东经116.28安徽省马鞍山北纬31.43 东经118.28安徽省宿州北纬33.38 东经116.58 安徽省天长北纬32.41 东经118.59 安徽省铜陵北纬30.56 东经117.48安徽省芜湖北纬31.19 东经118.22 安徽省宣州北纬30.57 东经118.44 澳门澳门市北纬21.33 东经115.07 北京市北京市北纬39.55 东经116.24福建省福州北纬26.05 东经119.18 福建省长乐北纬25.58 东经119.31 福建省福安北纬27.06 东经119.39 福建省福清北纬25.42 东经119.23 福建省建瓯北纬27.03 东经118.20 福建省建阳北纬27.21 东经118.07福建省龙海北纬24.26 东经117.48 福建省龙岩北纬25.06 东经117.01 福建省南安北纬24.57 东经118.23 福建省南平北纬26.38 东经118.10 福建省宁德北纬26.39 东经119.31 福建省莆田北纬24.26 东经119.01 福建省泉州北纬24.56 东经118.36 福建省三明北纬26.13 东经117.36 福建省邵武北纬27.20 东经117.29 福建省石狮北纬24.44 东经118.38 福建省武夷山北纬27.46 东经118.02 福建省厦门北纬24.27 东经118.06 福建省永安北纬25.58 东经117.23 福建省漳平北纬25.17 东经117.24 福建省漳州北纬24.31 东经117.39甘肃省兰州北纬36.04 东经103.51 甘肃省白银北纬36.33 东经104.12 甘肃省敦煌北纬40.08 东经94.41甘肃省嘉峪关北纬39.48 东经98.14 甘肃省金昌北纬38.28 东经102.10甘肃省临夏北纬35.37 东经103.12 甘肃省平凉北纬35.32 东经106.40 甘肃省天水北纬34.37 东经105.42 甘肃省武威北纬37.56 东经102.39 甘肃省西峰北纬35.45 东经107.40 甘肃省玉门北纬39.49 东经97.35 甘肃省张掖北纬38.56 东经100.26广东省广州北纬23.08 东经113.14 广东省潮阳北纬23.16 东经116.36 广东省潮州北纬23.40 东经116.38 广东省澄海北纬23.28 东经116.46 广东省从化北纬23.33 东经113.33 广东省东莞北纬23.02 东经113.45 广东省恩平北纬22.12 东经112.19 广东省佛山北纬23.02 东经113.06 广东省高明北纬22.53 东经112.50 广东省高要北纬23.02 东经112.26 广东省高州北纬21.54 东经110.50 广东省鹤山北纬22.46 东经112.57 广东省河源北纬23.43 东经114.41广东省化州北纬21.39 东经110.37广东省惠阳北纬22.48 东经114.28广东省惠州北纬23.05 东经114.22广东省江门北纬22.35 东经113.04广东省揭阳北纬22.32 东经116.21广东省开平北纬22.22 东经112.40广东省乐昌北纬25.09 东经113.21广东省雷州北纬20.54 东经110.04广东省廉江北纬21.37 东经110.17广东省连州北纬24.48 东经112.23广东省罗定北纬22.46 东经111.33广东省茂名北纬21.40 东经110.53广东省梅州北纬24.19 东经116.07广东省南海北纬23.01 东经113.09 广东省番禺北纬22.57 东经113.22广东省普宁北纬23.18 东经116.10广东省三水北纬23.10 东经112.52 广东省汕头北纬23.22 东经116.41 广东省汕尾北纬22.47 东经115.21 广东省韶关北纬24.48 东经113.37 广东省深圳北纬22.33 东经114.07 广东省顺德北纬22.50 东经113.15 广东省四会北纬23.21 东经112.41 广东省台山北纬22.15 东经112.48 广东省吴川北纬21.26 东经110.47 广东省新会北纬22.32 东经113.01 广东省兴宁北纬24.09 东经115.43 广东省阳春北纬22.10 东经111.48 广东省阳江北纬21.50 东经111.58 广东省英德北纬24.10 东经113.22 广东省云浮北纬22.57 东经112.02 广东省增城北纬23.18 东经113.49 广东省湛江北纬21.11 东经110.24 广东省肇庆北纬23.03 东经112.27 广东省中山北纬22.31 东经113.22 广东省珠海北纬22.17 东经113.34广西自治区南宁北纬22.48 东经108.19 广西自治区北海北纬21.28 东经109.07 广西自治区北流北纬22.42 东经110.21 广西自治区百色北纬23.54 东经106.36 广西自治区防城港北纬21.37 东经108.20 广西自治区贵港北纬23.06 东经109.36 广西自治区桂林北纬25.17 东经110.17 广西自治区桂平北纬23.22 东经110.04 广西自治区河池北纬24.42 东经108.03 广西自治区合山北纬23.47 东经108.52 广西自治区柳州北纬23.19 东经109.24 广西自治区赁祥北纬22.07 东经106.44 广西自治区钦州北纬21.57 东经108.37 广西自治区梧州北纬23.29 东经111.20 广西自治区玉林北纬22.38 东经110.09 广西自治区宜州北纬24.28 东经108.40贵州省贵阳北纬26.35 东经106.42贵州省安顺北纬26.14 东经105.55贵州省毕节北纬27.18 东经105.18贵州省赤水北纬28.34 东经105.42贵州省都匀北纬26.15 东经107.31贵州省凯里北纬26.35 东经107.58 贵州省六盘水北纬26.35 东经104.50 贵州省清镇北纬26.33 东经106.27 贵州省铜仁北纬27.43 东经109.12 贵州省兴义北纬25.05 东经104.53 贵州省遵义北纬27.42 东经106.55海南省海口北纬20.02 东经110.20 海南省儋州北纬19.31 东经109.34 海南省琼海北纬19.14 东经110.28 海南省琼山北纬19.59 东经110.21 海南省三亚北纬18.14 东经109.31 海南省通什北纬18.46 东经109.31河北省石家庄北纬38.02 东经114.30 河北省安国北纬38.24 东经115.20 河北省保定北纬38.51 东经115.30 河北省霸州北纬39.06 东经116.24 河北省泊头北纬38.04 东经116.34 河北省沧州北纬38.18 东经116.52 河北省承德北纬40.59 东经117.57 河北省定州北纬38.30 东经115.00河北省丰南北纬39.34 东经118.06 河北省高碑店北纬39.20 东经115.51 河北省蒿城北纬38.02 东经114.50 河北省邯郸北纬36.36 东经114.28河北省河间北纬38.26 东经116.05 河北省衡水北纬37.44 东经115.42 河北省黄骅北纬38.21 东经117.21 河北省晋州北纬38.02 东经115.02 河北省冀州北纬37.34 东经115.33 河北省廓坊北纬39.31 东经116.42 河北省鹿泉北纬38.04 东经114.19 河北省南宫北纬37.22 东经115.23 河北省秦皇岛北纬39.55 东经119.35 河北省任丘北纬38.42 东经116.07 河北省三河北纬39.58 东经117.04 河北省沙河北纬36.51 东经114.30 河北省深州北纬38.01 东经115.32河北省武安北纬36.42 东经114.11 河北省邢台北纬37.04 东经114.30 河北省辛集北纬37.54 东经115.12 河北省新乐北纬38.20 东经114.41 河北省张家口北纬40.48 东经114.53 河北省涿州北纬39.29 东经115.59 河北省遵化北纬40.11 东经117.58 河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21 河南省长葛北纬34.12 东经113.47 河南省登封北纬34.27 东经113.02 河南省邓州北纬32.42 东经112.05 河南省巩义北纬34.46 东经112.58 河南省鹤壁北纬35.54 东经114.11 河南省辉县北纬35.27 东经113.47 河南省焦作北纬35.14 东经113.12 河南省济源北纬35.04 东经112.35 河南省开封北纬34.47 东经114.21 河南省灵宝北纬34.31 东经110.52 河南省林州北纬36.03 东经113.49 河南省漯河北纬33.33 东经114.02河南省南阳北纬33.00 东经112.32 河南省平顶山北纬33.44 东经113.17 河南省濮阳北纬35.44 东经115.01 河南省沁阳北纬35.05 东经112.57 河南省汝州北纬34.09 东经112.50 河南省三门峡北纬34.47 东经111.12 河南省商丘北纬34.26 东经115.38 河南省卫辉北纬35.24 东经114.03 河南省舞钢北纬33.17 东经113.30 河南省项城北纬33.26 东经114.54 河南省荥阳北纬34.46 东经113.21 河南省新密北纬34.31 东经113.22 河南省新乡北纬35.18 东经113.52 河南省信阳北纬32.07 东经114.04 河南省新郑北纬34.24 东经113.43 河南省许昌北纬34.01 东经113.49 河南省偃师北纬34.43 东经112.47 河南省义马北纬34.43 东经111.55 河南省禹州北纬34.09 东经113.28 河南省周口北纬33.37 东经114.38 河南省驻马店北纬32.58 东经114.01黑龙江省哈尔滨北纬45.44 东经126.36 黑龙江省阿城北纬45.32 东经126.58 黑龙江省安达北纬46.24 东经125.18 黑龙江省北安北纬48.15 东经126.31 黑龙江省大庆北纬46.36 东经125.01黑龙江省富锦北纬47.15 东经132.02 黑龙江省海林北纬44.35 东经129.21 黑龙江省海伦北纬47.28 东经126.57 黑龙江省鹤岗北纬47.20 东经130.16 黑龙江省黑河北纬50.14 东经127.29黑龙江省佳木斯北纬46.47 东经130.22 黑龙江省鸡西北纬45.17 东经130.57 黑龙江省密山北纬45.32 东经131.50 黑龙江省牡丹江北纬44.35 东经129.36 黑龙江省讷河北纬48.29 东经124.51 黑龙江省宁安北纬44.21 东经129.28黑龙江省齐齐哈尔北纬47.20 东经123.57 黑龙江省七台河北纬45.48 东经130.49 黑龙江省双城北纬45.22 东经126.15黑龙江省尚志北纬45.14 东经127.55黑龙江省双鸭山北纬46.38 东经131.11 黑龙江省绥芬河北纬44.25 东经131.11 黑龙江省绥化北纬46.38 东经126.59黑龙江省铁力北纬46.59 东经128.01黑龙江省同江北纬47.39 东经132.30黑龙江省五常北纬44.55 东经127.11黑龙江省五大连池北纬48.38 东经126.07 黑龙江省伊春北纬47.42 东经128.56黑龙江省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省广水北纬31.37 东经113.48湖北省黄石北纬30.12 东经115.06 湖北省黄州北纬30.27 东经114.52 湖北省荆门北纬31.02 东经112.12 湖北省荆沙北纬30.18 东经112.16 湖北省老河口北纬32.23 东经111.40 湖北省利川北纬30.18 东经108.56 湖北省麻城北纬31.10 东经115.01 湖北省浦圻北纬29.42 东经113.51 湖北省潜江北纬30.26 东经112.53 湖北省石首北纬29.43 东经112.24 湖北省十堰北纬32.40 东经110.47 湖北省随州北纬31.42 东经113.22 湖北省天门北纬60.39 东经113.10 湖北省武穴北纬29.51 东经115.33 湖北省襄樊北纬32.02 东经112.08 湖北省咸宁北纬29.53 东经114.17 湖北省仙桃北纬30.22 东经113.27 湖北省孝感北纬30.56 东经113.54 湖北省宜昌北纬30.42 东经111.17 湖北省宜城北纬31.42 东经112.15 湖北省应城北纬30.57 东经113.33湖北省枝城北纬30.23 东经111.27湖北省钟祥北纬31.10 东经112.34湖南省长沙北纬28.12 东经112.59湖南省常德北纬29.02 东经111.51湖南省郴州北纬25.46 东经113.02湖南省衡阳北纬26.53 东经112.37湖南省洪江北纬27.07 东经109.59湖南省怀化北纬27.33 东经109.58湖南省津市北纬29.38 东经111.52湖南省吉首北纬28.18 东经109.43 湖南省耒阳北纬26.24 东经112.51湖南省冷水江北纬27.42 东经111.26湖南省冷水滩北纬26.26 东经111.35湖南省涟源北纬27.41 东经111.41湖南省醴陵北纬27.40 东经113.30湖南省临湘北纬29.29 东经113.27湖南省浏阳北纬28.09 东经113.37 湖南省娄底北纬27.44 东经111.59 湖南省汨罗北纬28.49 东经113.03 湖南省韶山北纬27.54 东经112.29 湖南省邵阳北纬27.14 东经111.28 湖南省武冈北纬26.43 东经110.37 湖南省湘潭北纬27.52 东经112.53 湖南省湘乡北纬27.44 东经112.31 湖南省益阳北纬28.36 东经112.20 湖南省永州北纬26.13 东经111.37 湖南省沅江北纬28.50 东经112.22 湖南省岳阳北纬29.22 东经113.06 湖南省张家界北纬29.08 东经110.29 湖南省株洲北纬27.51 东经113.09 湖南省资兴北纬25.58 东经113.13吉林省长春北纬43.54 东经125.19 吉林省白城北纬45.38 东经122.50 吉林省白山北纬41.56 东经126.26 吉林省大安北纬45.30 东经124.18 吉林省德惠北纬44.32 东经125.42吉林省敦化北纬43.22 东经128.13 吉林省公主岭北纬43.31 东经124.49 吉林省和龙北纬42.32 东经129.00 吉林省桦甸北纬42.58 东经126.44 吉林省珲春北纬42.52 东经130.22 吉林省集安北纬41.08 东经126.11 吉林省蛟河北纬43.42 东经127.21 吉林省吉林北纬43.52 东经126.33 吉林省九台北纬44.09 东经125.51 吉林省辽源北纬42.54 东经125.09 吉林省临江北纬41.49 东经126.53 吉林省龙井北纬42.46 东经129.26 吉林省梅河口北纬42.32 东经125.40 吉林省舒兰北纬44.24 东经126.57 吉林省四平北纬43.10 东经124.22 吉林省松原北纬45.11 东经124.49 吉林省洮南北纬45.20 东经122.47 吉林省通化北纬41.43 东经125.56 吉林省图们北纬42.57 东经129.51 吉林省延吉北纬42.54 东经129.30 吉林省愉树北纬44.49 东经126.32江苏省南京北纬32.03 东经118.46 江苏省常熟北纬31.39 东经120.43 江苏省常州北纬31.47 东经119.58 江苏省丹阳北纬32.00 东经119.32 江苏省东台北纬32.51 东经120.19 江苏省高邮北纬32.47 东经119.27 江苏省海门北纬31.53 东经121.09 江苏省淮安北纬33.30 东经119.09 江苏省淮阴北纬33.36 东经119.02 江苏省江都北纬32.26 东经119.32 江苏省姜堰北纬32.34 东经120.08 江苏省江阴北纬31.54 东经120.17 江苏省靖江北纬32.02 东经120.17 江苏省金坛北纬31.46 东经119.33 江苏省昆山北纬31.23 东经120.57 江苏省连去港北纬34.36 东经119.10 江苏省溧阳北纬31.26 东经119.29 江苏省南通北纬32.01 东经120.51 江苏省邳州北纬34.19 东经117.59江苏省启乐北纬31.48 东经121.39 江苏省如皋北纬32.23 东经120.33 江苏省宿迁北纬33.58 东经118.18 江苏省苏州北纬31.19 东经120.37 江苏省太仓北纬31.27 东经121.06 江苏省泰兴北纬32.10 东经120.01 江苏省泰州北纬32.30 东经119.54 江苏省通州北纬32.05 东经121.03江苏省吴江北纬31.10 东经120.39 江苏省无锡北纬31.34 东经120.18 江苏省兴化北纬32.56 东经119.50 江苏省新沂北纬34.22 东经118.20 江苏省徐州北纬34.15 东经117.11 江苏省盐在北纬33.22 东经120.08 江苏省扬中北纬32.14 东经119.49 江苏省扬州北纬32.23 东经119.26 江苏省宜兴北纬31.21 东经119.49 江苏省仪征北纬32.16 东经119.10 江苏省张家港北纬31.52 东经120.32江西省南昌北纬28.40 东经115.55 江西省德兴北纬28.57 东经117.35 江西省丰城北纬28.12 东经115.48 江西省赣州北纬28.52 东经114.56 江西省高安北纬28.25 东经115.22 江西省吉安北纬27.07 东经114.58 江西省景德镇北纬29.17 东经117.13 江西省井冈山北纬26.34 东经114.10 江西省九江北纬29.43 东经115.58 江西省乐平北纬28.58 东经117.08 江西省临川北纬27.59 东经116.21 江西省萍乡北纬27.37 东经113.50 江西省瑞昌北纬29.40 东经115.38 江西省瑞金北纬25.53 东经116.01 江西省上饶北纬25.27 东经117.58 江西省新余北纬27.48 东经114.56 江西省宜春北纬27.47 东经114.23 江西省鹰潭北纬28.14 东经117.03 江西省樟树北纬28.03 东经115.32辽宁省鞍山北纬41.07 东经123.00 辽宁省北票北纬41.48 东经120.47 辽宁省本溪北纬41.18 东经123.46 辽宁省朝阳北纬41.34 东经120.27 辽宁省大连北纬38.55 东经121.36 辽宁省丹东北纬40.08 东经124.22 辽宁省大石桥北纬40.37 东经122.31 辽宁省东港北纬39.53 东经124.08 辽宁省凤城北纬40.28 东经124.02 辽宁省抚顺北纬41.51 东经123.54 辽宁省阜新北纬42.01 东经121.39 辽宁省盖州北纬40.24 东经122.21 辽宁省海城北纬40.51 东经122.43 辽宁省葫芦岛北纬40.45 东经120.51 辽宁省锦州北纬41.07 东经121.09 辽宁省开原北纬42.32 东经124.02 辽宁省辽阳北纬41.16 东经123.12 辽宁省凌海北纬41.10 东经121.21 辽宁省凌源北纬41.14 东经119.22 辽宁省盘锦北纬41.07 东经122.03 辽宁省普兰店北纬39.23 东经121.58辽宁省铁岭北纬42.18 东经123.51辽宁省瓦房店北纬39.37 东经122.00辽宁省兴城北纬40.37 东经120.41辽宁省新民北纬41.59 东经122.49辽宁省营口北纬40.39 东经122.13 辽宁省庄河北纬39.41 东经122.58内蒙古自治区呼和浩特北纬40.48 东经111.41内蒙古自治区包头北纬40.39 东经109.49内蒙古自治区赤峰北纬42.17 东经118.58内蒙古自治区东胜北纬39.48 东经109.59内蒙古自治区二连浩特北纬43.38 东经111.58内蒙古自治区额尔古纳北纬50.13 东经120.11内蒙古自治区丰镇北纬40.27 东经113.09内蒙古自治区根河北纬50.48 东经121.29内蒙古自治区海拉尔北纬49.12 东经119.39内蒙古自治区霍林郭勒北纬45.32 东经119.38 内蒙古自治区集宁北纬41.02 东经113.06内蒙古自治区临河北纬40.46 东经107.22内蒙古自治区满洲里北纬49.35 东经117.23 内蒙古自治区通辽北纬43.37 东经122.16内蒙古自治区乌兰浩特北纬46.03 东经122.03 内蒙古自治区乌海北纬39.40 东经106.48内蒙古自治区锡林浩特北纬43.57 东经116.03 内蒙古自治区牙克石北纬49.17 东经120.40 内蒙古自治区扎兰屯北纬48.00 东经122.47宁夏自治区银川北纬38.27 东经106.16宁夏自治区青铜峡北纬37.56 东经105.59宁夏自治区石嘴山北纬39.02 东经106.22宁夏自治区吴忠北纬37.59 东经106.11青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55山东省济南北纬36.40 东经117.00山东省安丘北纬36.25 东经119.12山东省昌邑北纬39.52 东经119.24 山东省德州北纬37.26 东经116.17 山东省东营北纬37.27 东经118.30 山东省肥城北纬36.14 东经116.46 山东省高密北纬36.22 东经119.44 山东省菏泽北纬35.14 东经115.26 山东省胶南北纬35.53 东经119.58 山东省胶州北纬36.17 东经120.00 山东省即墨北纬36.22 东经120.28 山东省济宁北纬35.23 东经116.33 山东省莱芜北纬36.12 东经117.40 山东省莱西北纬36.52 东经120.31 山东省莱阳北纬36.58 东经120.42 山东省莱州北纬37.10 东经119.57 山东省乐陵北纬37.44 东经117.12 山东省聊城北纬36.26 东经115.57 山东省临清北纬36.51 东经115.42 山东省临沂北纬35.03 东经118.20 山东省龙口北纬37.39 东经120.21 山东省蓬莱北纬37.48 东经120.45 山东省平度北纬36.47 东经119.58山东省青州北纬36.42 东经118.28山东省曲阜北纬35.36 东经116.58山东省日照北纬35.23 东经119.32山东省荣成北纬37.10 东经122.25山东省乳山北纬36.54 东经121.31山东省寿光北纬36.53 东经118.44山东省泰安北纬36.11 东经117.08山东省滕州北纬35.06 东经117.09山东省潍坊北纬36.43 东经119.06 山东省威海北纬37.31 东经122.07山东省文登北纬37.12 东经122.03山东省新泰北纬35.54 东经117.45山东省烟台北纬37.32 东经121.24山东省兖州北纬35.32 东经116.49山东省禹城北纬36.56 东经116.39山东省枣庄北纬34.52 东经117.33山东省章丘北纬36.43 东经117.32。
中国各城市的地理位置经纬度

中国各城市的地理位置经纬度【直辖市】 北京市 北纬 39°55 东经 116°24 上海市 北纬 31°14 东经 121°29 天津市 北纬 39°02 东经 117°12 重庆市 北纬 29°35 东经 106°33 (重庆市各区) 合川市 北纬 30°02 东经 106°15 江津市 北纬 29°18 东经 106°16 南川市 北纬 29°10 东经 107°05 永川市 北纬 29°23 东经 105°53【安徽省】 合肥 北纬 31°52 东经 117°17 安庆 北纬 30°31 东经 117°02 蚌埠 北纬 32°56 东经 117°21 亳州 北纬 33°52 东经 115°47 巢湖 北纬 31°36 东经 117°52 滁州 北纬 32°18 东经 118°18 阜阳 北纬 32°54 东经 115°48 贵池 北纬 30°39 东经 117°28 淮北 北纬 33°57 东经 116°47 淮南 北纬 32°37 东经 116°58 黄山 北纬 29°43 东经 118°18 界首 北纬 33°15 东经 115°21 六安 北纬 31°44 东经 116°28 马鞍山 北纬 31°43 东经 118°28 明光 北纬 32°47 东经 117°58 宿州 北纬 33°38 东经 116°58 天长 北纬 32°41 东经 118°59 铜陵 北纬 30°56 东经 117°48 芜湖 北纬 31°19 东经 118°22 宣州 北纬 30°57 东经 118°44【福建省】 福州 北纬 26°05 东经 119°18 长乐 北纬 25°58 东经 119°31 福安 北纬 27°06 东经 119°39 福清 北纬 25°42 东经 119°23 建瓯 北纬 27°03 东经 118°20 建阳 北纬 27°21 东经 118°07 晋江 北纬 24°49 东经 118°35 龙海 北纬 24°26 东经 117°48 龙岩 北纬 25°06 东经 117°01 南安 北纬 24°57东经 118°23 南平 北纬 26°38 东经 118°10 宁德 北纬 26°39 东经 119°31 莆田 北纬 24°26 东经 119°01 泉州 北纬 24°56 东经 118°36 三明 北纬 26°13 东经 117°36 邵武 北纬 27°20 东经 117°29 石狮 北纬 24°44 东经 118°38 武夷山 北纬 27°46 东经 118°02 厦门 北纬 24°27 东经 118°06 永安 北纬 25°58 东经 117°23 漳平 北纬 25°17 东经 117°24 漳州 北纬 24°31 东经 117°39【广东省】 广州 北纬 23°08 东经 113°14 潮阳 北纬 23°16 东经 116°36 潮州 北纬 23°40 东经 116°38 澄海 北纬 23°28 东经 116°46 从化 北纬 23°33 东经 113°33 东莞 北纬 23°02 东经 113°45 恩平 北纬 22°12 东经 112°19 佛山 北纬 23°02 东经 113°06 高明 北纬 22°53 东经 112°50 高要 北纬 23°02 东经 112°26 高州 北纬 21°54 东经 110°50 鹤山 北纬 22°46 东经 112°57 河源 北纬 23°43 东经 114°41 花都 北纬 23°23 东经 113°12 化州 北纬 21°39 东经 110°37 惠阳 北纬 22°48 东经 114°28 惠州 北纬 23°05 东经 114°22 江门 北纬 22°35 东经 113°04 揭阳 北纬 22°32 东经 116°21 开平 北纬 22°22 东经 112°402 乐昌 北纬 25°09 东经 113°21 雷州 北纬 20°54 东经 110°04 廉江 北纬 21°37 东经 110°17 连州 北纬 24°48 东经 112°23 罗定 北纬 22°46 东经 111°33 茂名 北纬 21°40 东经 110°53 梅州 北纬 24°19 东经 116°07 南海 北纬 23°01 东经 113°09 番禺 北纬 22°57 东经 113°22 普宁 北纬23°18 东经 116°10 清远 北纬 23°42 东经 113°01 三水 北纬 23°10 东经 112°52 汕头 北纬 23°22 东经 116°41 汕尾 北纬 22°47 东经 115°21 韶关 北纬 24°48 东经 113°37 深圳 北纬 22°33 东经 114°07 顺德 北纬 22°50 东经 113°15 四会 北纬 23°21 东经 112°41 台山 北纬 22°15 东经 112°48 吴川 北纬 21°26 东经 110°47 新会 北纬 22°32 东经 113°01 兴宁 北纬 24°09 东经 115°43 阳春 北纬 22°10 东经 111°48 阳江 北纬 21°50 东经 111°58 英德 北纬 24°10 东经 113°22 云浮 北纬 22°57 东经 112°02 增城 北纬 23°18 东经 113°49 湛江 北纬 21°11 东经 110°24 肇庆 北纬 23°03 东经 112°27 中山 北纬 22°31 东经 113°22 珠海 北纬 22°17 东经 113°34【广西壮族自治区】 南宁 北纬 22°48 东经 108°19 北海 北纬 21°28 东经 109°07 北流 北纬 22°42 东经 110°21 百色 北纬 23°54 东经 106°36 防城港 北纬 21°37 东经 108°20 贵港 北纬 23°06 东经 109°36 桂林 北纬 25°17 东经 110°17 桂平 北纬 23°22 东经 110°04 河池 北纬 24°42 东经 108°03 合山 北纬 23°47 东经 108°52 柳州 北纬 23°19 东经 109°24 赁祥 北纬 22°07 东经 106°44 钦州 北纬 21°57 东经 108°37 梧州 北纬 23°29 东经 111°20 玉林 北纬 22°38 东经 110°09 宜州 北纬 24°28 东经 108°40【贵州省】 贵阳 北纬 26°35 东经 106°42 安顺 北纬 26°14 东经 105°55 毕节 北纬 27°18 东经 105°18 赤水 北纬 28°34东经 105°42 都匀 北纬 26°15 东经 107°31 凯里 北纬 26°35 东经 107°58 六盘水 北纬 26°35 东经 104°50 清镇 北纬 26°33 东经 106°27 铜仁 北纬 27°43 东经 109°12 兴义 北纬 25°05 东经 104°53 遵义 北纬 27°42 东经 106°55【甘肃省】 兰州 北纬 36°04 东经 103°51 白银 北纬 36°33 东经 104°12 敦煌 北纬 40°08 东经 94°41 嘉峪关 北纬 39°48 东经 98°14 金昌 北纬 38°28 东经 102°10 酒泉 北纬 39°44 东经 98°31 临夏 北纬 35°37 东经 103°12 平凉 北纬 35°32 东经 106°40 天水 北纬 34°37 东经 105°42 武威 北纬 37°56 东经 102°39 西峰 北纬 35°45 东经 107°40 玉门 北纬 39°49 东经 97°35 张掖 北纬 38°56 东经 100°26 【湖北省】 武汉 北纬 30°35 东经 114°17 安陆 北纬 31°15 东经 113°41 当阳 北纬 30°50 东经 111°473 丹江口 北纬 32°33 东经 108°30 大冶 北纬 30°06 东经 114°58 恩施 北纬 30°16 东经 109°29 鄂州 北纬 30°23 东经 114°52 广水 北纬 31°37 东经 113°48 洪湖 北纬 29°48 东经 113°27 黄石 北纬 30°12 东经 115°06 黄州 北纬 30°27 东经 114°52 荆门 北纬 31°02 东经 112°12 荆沙 北纬 30°18 东经 112°16 老河口 北纬 32°23 东经 111°40 利川 北纬 30°18 东经 108°56 麻城 北纬 31°10 东经 115°01 浦圻 北纬 29°42 东经 113°51 潜江 北纬 30°26 东经 112°53 石首 北纬 29°43 东经 112°24 十堰 北纬 32°40 东经 110°47 随州 北纬 31°42 东经113°22 天门 北纬 30°39 东经113°10 武穴 北纬 29°51 东经115°33 襄樊 北纬 32°02 东经112°08 咸宁 北纬 29°53 东经114°17 仙桃 北纬 30°22 东经113°27 孝感 北纬 30°56 东经113°54 宜昌 北纬 30°42 东经111°17 宜城 北纬 31°42 东经112°15 应城 北纬 30°57 东经113°33 枣阳 北纬 32°07 东经112°44 枝城 北纬 30°23 东经111°27 钟祥 北纬 31°10 东经112°34【湖南省】 长沙 北纬 28°12 东经 112°59 常德 北纬 29°02 东经 111°51 郴州 北纬 25°46 东经 113°02 衡阳 北纬 26°53 东经 112°37 洪江 北纬 27°07 东经 109°59 怀化 北纬 27°33 东经 109°58 津市 北纬 29°38 东经 111°52 吉首 北纬 28°18 东经 109°43 耒阳 北纬 26°24 东经 112°51 冷水江 北纬 27°42 东经 111°26 冷水滩 北纬 26°26 东经 111°35 涟源 北纬 27°41 东经 111°41 醴陵 北纬 27°40 东经 113°30 临湘 北纬 29°29 东经 113°27 浏阳 北纬 28°09 东经 113°37 娄底 北纬 27°44 东经 111°59 汨罗 北纬 28°49 东经 113°03 韶山 北纬 27°54 东经 112°29 邵阳 北纬 27°14 东经 111°28 武冈 北纬 26°43 东经 110°37 湘潭 北纬 27°52 东经 112°53 湘乡 北纬 27°44 东经 112°31 益阳 北纬 28°36 东经 112°20 永州 北纬 26°13 东经 111°37 沅江 北纬 28°50 东经 112°22 岳阳 北纬 29°22 东经 113°06 张家界 北纬 29°08 东经 110°29 株洲 北纬 27°51 东经 113°09 资兴 北纬 25°58 东经 113°13 【河北省】 石家庄 北纬 38°02 东经 114°30 安国 北纬 38°24东经 116°24 泊头 北纬 38°04 东经 116°34 沧州 北纬 38°18 东经 116°52 承德 北纬 40°59 东经 117°57 定州 北纬 38°30 东经 115°00 丰南 北纬 39°34 东经 118°06 高碑店 北纬 39°20 东经 115°51 蒿城 北纬 38°02 东经 114°50 邯郸 北纬 36°36 东经 114°28 河间 北纬 38°26 东经 116°05 衡水 北纬 37°44 东经 115°42 黄骅 北纬 38°21 东经 117°21 晋州 北纬 38°02 东经 115°02 冀州 北纬 37°34 东经 115°33 廓坊 北纬 39°31 东经 116°42 鹿泉 北纬 38°04 东经 114°19 南宫 北纬 37°22 东经 115°234 秦皇岛 北纬 39°55 东经 119°35 任丘 北纬 38°42 东经 116°07 三河 北纬 39°58 东经 117°04 沙河 北纬 36°51 东经 114°30 深州 北纬 38°01 东经 115°32 唐山 北纬 39°36 东经 118°11 武安 北纬 36°42 东经 114°11 邢台 北纬 37°04 东经 114°30 辛集 北纬 37°54 东经 115°12 新乐 北纬 38°20 东经 114°41 张家口 北纬 40°48 东经 114°53 涿州 北纬 39°29 东经 115°59 遵化 北纬 40°11 东经 117°58【河南省】 郑州 北纬 34°46 东经 113°40 安阳 北纬 36°06 东经 114°21 长葛 北纬 34°12 东经 113°47 登封 北纬 34°27 东经 113°02 邓州 北纬 32°42 东经 112°05 巩义 北纬 34°46 东经 112°58 鹤壁 北纬 35°54 东经 114°11 辉县 北纬 35°27 东经 113°47 焦作 北纬 35°14 东经 113°12 济源 北纬 35°04 东经 112°35 开封 北纬 34°47 东经 114°21 灵宝 北纬 34°31东经 114°02 洛阳 北纬 34°41 东经 112°27 南阳 北纬 33°00 东经 112°32 平顶山 北纬 33°44 东经 113°17 濮阳 北纬 35°44 东经 115°01 沁阳 北纬 35°05 东经 112°57 汝州 北纬 34°09 东经 112°50 三门峡 北纬 34°47 东经 111°12 商丘 北纬 34°26 东经 115°38 卫辉 北纬 35°24 东经 114°03 舞钢 北纬 33°17 东经 113°30 项城 北纬 33°26 东经 114°54 荥阳 北纬 34°46 东经 113°21 新密 北纬 34°31 东经 113°22 新乡 北纬 35°18 东经 113°52 信阳 北纬 32°07 东经 114°04 新郑 北纬 34°24 东经 113°43 许昌 北纬 34°01 东经 113°49 偃师 北纬 34°43 东经 112°47 义马 北纬 34°43 东经 111°55 禹州 北纬 34°09 东经 113°28 周口 北纬 33°37 东经 114°38 驻马店 北纬 32°58 东经 114°01【黑龙江省】 哈尔滨 北纬 45°44 东经 126°36 阿城 北纬 45°32 东经 126°58 安达 北纬 46°24 东经 125°18 北安 北纬 48°15 东经 126°31 大庆 北纬 46°36 东经 125°01 富锦 北纬 47°15 东经 132°02 海林 北纬 44°35 东经 129°21 海伦 北纬 47°28 东经 126°57 鹤岗 北纬 47°20 东经 130°16 黑河 北纬 50°14 东经 127°29 佳木斯 北纬 46°47 东经 130°22 鸡西 北纬 45°17 东经 130°57 密山 北纬 45°32 东经 131°50 牡丹江 北纬 44°35 东经 129°36 讷河 北纬 48°29 东经 124°51 宁安 北纬 44°21 东经 129°28 齐齐哈尔 北纬 47°20 东经 123°57七台河 北纬 45°48 东经 130°49 双城 北纬 45°22 东经 126°15 尚志 北纬 45°14 东经 127°55 双鸭山 北纬 46°38 东经 131°11 绥芬河 北纬 44°25 东经 131°11 绥化 北纬 46°38 东经 126°59 铁力 北纬 46°59 东经 128°01 同江 北纬 47°39 东经 132°30 五常 北纬 44°55 东经 127°11 五大连池 北纬 48°38 东经 126°07 伊春 北纬 47°42 东经 128°56 肇东 北纬 46°04 东经 125°58【海南省】5 海口 北纬 20°02 东经 110°20 儋州 北纬 19°31 东经 109°34 琼海 北纬 19°14 东经 110°28 琼山 北纬 19°59 东经 110°21 三亚 北纬 18°14 东经 109°31 通什 北纬 18°46 东经 109°31 三沙 北纬 16°50 东经 112°20 【吉林省】 长春 北纬 43°54 东经 125°19 白城 北纬 45°38 东经 122°50 白山 北纬 41°56 东经 126°26 大安 北纬 45°30 东经 124°18 德惠 北纬 44°32 东经 125°42 敦化 北纬 43°22 东经 128°13 公主岭 北纬 43°31 东经 124°49 和龙 北纬 42°32 东经 129°00 桦甸 北纬 42°58 东经 126°44 珲春 北纬 42°52 东经 130°22 集安 北纬 41°08 东经 126°11 蛟河 北纬 43°42 东经 127°21 吉林 北纬 43°52 东经 126°33 九台 北纬 44°09 东经 125°51 辽源 北纬 42°54 东经 125°09 临江 北纬 41°49 东经 126°53 龙井 北纬 42°46 东经 129°26 梅河口 北纬 42°32 东经 125°40 舒兰 北纬 44°24 东经 126°57 四平 北纬 43°10 东经 124°22 松原 北纬 45°11 东经 124°49 洮南 北纬 45°20 东经122°47 通化 北纬 41°43 东经 125°56 图们 北纬 42°57 东经 129°51 延吉 北纬 42°54 东经 129°30 愉树 北纬 44°49 东经 126°32【江西省】 南昌 北纬 28°40 东经 115°55 德兴 北纬 28°57 东经 117°35 丰城 北纬 28°12 东经 115°48 赣州 北纬 28°52 东经 114°56 高安 北纬 28°25 东经 115°22 吉安 北纬 27°07 东经 114°58 景德镇 北纬 29°17 东经 117°13 井冈山 北纬 26°34 东经 114°10 九江 北纬 29°43 东经 115°58 乐平 北纬 28°58 东经 117°08 临川 北纬 27°59 东经 116°21 萍乡 北纬 27°37 东经 113°50 瑞昌 北纬 29°40 东经 115°38 瑞金 北纬 25°53 东经 116°01 上饶 北纬 25°27 东经 117°58 新余 北纬 27°48 东经 114°56 宜春 北纬 27°47 东经 114°23 鹰潭 北纬 28°14 东经 117°03 樟树 北纬 28°03 东经 115°32【江苏省】 南京 北纬 32°03 东经 118°46 常熟 北纬 31°39 东经 120°43 常州 北纬 31°47 东经 119°58 丹阳 北纬 32°00 东经 119°32 东台 北纬 32°51 东经 120°19 高邮 北纬 32°47 东经 119°27 海门 北纬 31°53 东经 121°09 淮安 北纬 33°30 东经 119°09 淮阴 北纬 33°36 东经 119°02 江都 北纬 32°26 东经 119°32 姜堰 北纬 32°34 东经 120°08 江阴 北纬 31°54 东经 120°17 靖江 北纬 32°02 东经 120°17 金坛 北纬 31°46 东经 119°33 昆山 北纬 31°23 东经 120°57 连去港 北纬 34°36 东经 119°10 溧阳 北纬 31°26 东经 119°29 南通 北纬32°01 东经 120°51 邳州 北纬 34°19 东经 117°59 启乐 北纬 31°48 东经 121°39 如皋 北纬 32°23 东经 120°33 宿迁 北纬 33°58 东经 118°18 苏州 北纬 31°19 东经 120°37 太仓 北纬 31°27 东经 121°06 泰兴 北纬 32°10 东经 120°01 泰州 北纬 32°30 东经 119°546 通州 北纬 32°05 东经 121°03 吴江 北纬 31°10 东经 120°39 无锡 北纬 31°34 东经 120°18 兴化 北纬 32°56 东经 119°50 新沂 北纬 34°22 东经 118°20 徐州 北纬 34°15 东经 117°11 盐在 北纬 33°22 东经 120°08 扬中 北纬 32°14 东经 119°49 扬州 北纬 32°23 东经 119°26 宜兴 北纬 31°21 东经 119°49 仪征 北纬 32°16 东经 119°10 张家港 北纬 31°52 东经 120°32 镇江 北纬 32°11 东经 119°27【辽宁省】 沈阳 北纬 41°48 东经 123°25 鞍山 北纬 41°07 东经 123°00 北票 北纬 41°48 东经 120°47 本溪 北纬 41°18 东经 123°46 朝阳 北纬 41°34 东经 120°27 大连 北纬 38°55 东经 121°36 丹东 北纬 40°08 东经 124°22 大石桥 北纬 40°37 东经 122°31 东港 北纬 39°53 东经 124°08 凤城 北纬 40°28 东经 124°02 抚顺 北纬 41°51 东经 123°54 阜新 北纬 42°01 东经 121°39 盖州 北纬 40°24 东经 122°21 海城 北纬 40°51 东经 122°43 葫芦岛 北纬 40°45 东经 120°51 锦州 北纬 41°07 东经 121°09 开原 北纬 42°32 东经 124°02 辽阳 北纬 41°16 东经 123°12 凌海 北纬 41°10 东经 121°21 凌源 北纬 41°14 东经 119°22 盘锦 北纬 41°07 东经 122°03 普兰店 北纬 39°23 东经 121°58 铁法 北纬 42°28 东经 123°32 铁岭 北纬 42°18 东经 123°51 瓦房店 北纬 39°37 东经 122°00 兴城 北纬 40°37 东经 120°41 新民 北纬 41°59 东经 122°49 营口 北纬 40°39 东经 122°13 庄河 北纬 39°41 东经 122°58 【宁夏回族自治区】 银川 北纬 38°27 东经 106°16 青铜峡 北纬 37°56 东经 105°59 石嘴山 北纬 39°02 东经 106°22 吴忠 北纬 37°59 东经 106°11【内蒙古自治区】 呼和浩特 北纬 40°48 东经 111°41 包头 北纬 40°39 东经 109°49 赤峰 北纬 42°17 东经 118°58 东胜 北纬 39°48 东经 109°59 二连浩特 北纬 43°38 东经 111°58 额尔古纳 北纬 50°13 东经 120°11 丰镇 北纬 40°27 东经 113°09 根河 北纬 50°48 东经 121°29 海拉尔 北纬 49°12 东经 119°39 霍林郭勒 北纬 45°32 东经 119°38 集宁 北纬 41°02 东经 113°06 临河 北纬 40°46 东经 107°22 满洲里 北纬 49°35 东经 117°23 通辽 北纬 43°37 东经 122°16 乌兰浩特 北纬 46°03 东经 122°03 乌海 北纬 39°40 东经 106°48 锡林浩特 北纬 43°57 东经 116°03 牙克石 北纬 49°17 东经 120°40 扎兰屯 北纬 48°00 东经 122°47【青海省】 西宁 北纬 36°38 东经 101°48 德令哈 北纬 37°22 东经 97°23 格尔木 北纬 36°26 东经 94°55【四川省】 成都 北纬 30°40 东经 104°04 巴中 北纬 31°51 东经 106°43 崇州 北纬 30°39 东经 103°40 达川 北纬 31°14东经 107°29 德阳 北纬 31°09 东经 104°227 都江堰 北纬 31°01 东经 103°37 峨眉山 北纬 29°36 东经 103°29 涪陵 北纬 29°42 东经 107°22 广汉 北纬 30°58 东经 104°15 广元 北纬 32°28 东经 105°51 华蓥 北纬 30°26 东经 106°44 简阳 北纬 30°24 东经 104°32 江油 北纬 31°48 东经 104°42 阆中 北纬 31°36 东经 105°58 乐山 北纬 29°36 东经 103°44 泸州 北纬 28°54 东经 105°24 绵阳 北纬 31°30 东经 104°42 南充 北纬 30°49 东经 106°04 内江 北纬 29°36 东经 105°02 攀枝花 北纬 26°34 东经 101°43 彭州 北纬 30°59 东经 103°57 邛崃 北纬 30°26 东经 103°28 遂宁 北纬 30°31 东经 105°33 万县 北纬 30°50 东经 108°21 万源 北纬 32°03 东经 108°03 西昌 北纬 27°54 东经 102°16 雅安 北纬 29°59 东经 102°59 宜宾 北纬 28°47 东经 104°34 自贡 北纬 29°23 东经 104°46 资阳 北纬 30°09 东经 104°38【山东省】 济南 北纬 36°40 东经 117°00 安丘 北纬 36°25 东经 119°12 滨州 北纬 37°22 东经 118°02 昌邑 北纬 39°52 东经 119°24 德州 北纬 37°26 东经 116°17 东营 北纬 37°27 东经 118°30 肥城 北纬 36°14 东经 116°46 高密 北纬 36°22 东经 119°44 菏泽 北纬 35°14 东经 115°26 胶南 北纬 35°53 东经 119°58 胶州 北纬 36°17 东经 120°00 即墨 北纬 36°22 东经 120°28 济宁 北纬 35°23 东经 116°33 莱芜 北纬 36°12 东经 117°40 莱西 北纬 36°52 东经 120°31 莱阳 北纬 36°58东经 120°42 莱州 北纬 37°10 东经 119°57 乐陵 北纬 37°44 东经 117°12 聊城 北纬 36°26 东经 115°57 临清 北纬 36°51 东经 115°42 临沂 北纬 35°03 东经 118°20 龙口 北纬 37°39 东经 120°21 蓬莱 北纬 37°48 东经 120°45 平度 北纬 36°47 东经 119°58 青岛 北纬 36°03 东经 120°18 青州 北纬 36°42 东经 118°28 曲阜 北纬 35°36 东经 116°58 日照 北纬 35°23 东经 119°32 荣成 北纬 37°10 东经 122°25 乳山 北纬 36°54 东经 121°31 寿光 北纬 36°53 东经 118°44 泰安 北纬 36°11 东经 117°08 滕州 北纬 35°06 东经 117°09 潍坊 北纬 36°43 东经 119°06 威海 北纬 37°31 东经 122°07 文登 北纬 37°12 东经 122°03 新泰 北纬 35°54 东经 117°45 烟台 北纬 37°32 东经 121°24 兖州 北纬 35°32 东经 116°49 禹城 北纬 36°56 东经 116°39 枣庄 北纬 34°52 东经 117°33 章丘 北纬 36°43 东经 117°32 招远 北纬 37°21 东经 120°23 诸城 北纬 35°59 东经 119°24 淄博 北纬 36°48 东经 118°03 邹城 北纬 35°24 东经 116°58【山西省】 中阳 北纬 37°37 东经 112°17 太原 北纬 37°54 东经 112°33 长治 北纬 36°11 东经 113°06 大同 北纬 40°06 东经 113°17 高平 北纬 35°48 东经 112°55 古交 北纬 37°54 东经 112°09 河津 北纬 35°35 东经 110°41 侯马 北纬 35°37 东经 111°218 霍州 北纬 36°34 东经 111°42 介休 北纬 37°02 东经 111°55 晋城 北纬 35°30 东经 112°51 临汾 北纬36°05 东经 111°31 潞城 北纬 36°21 东经 113°14 朔州 北纬 39°19 东经 112°26 孝义 北纬 37°08 东经 111°48 忻州 北纬 38°24 东经 112°43 阳泉 北纬 37°51 东经 113°34 永济 北纬 34°52 东经 110°27 原平 北纬 38°43 东经 112°42 榆次 北纬 37°41 东经 112°43 运城 北纬 35°02 东经 110°59 【陕西省】西安 北纬 34°17 东经 108°57 安康 北纬 32°41 东经 109°01 宝鸡 北纬 34°22 东经 107°09 韩城 北纬 35°28 东经 110°27 汉中 北纬 33°04 东经 107°01 华阴 北纬 34°34 东经 110°05 商州 北纬 33°52 东经 109°57 铜川 北纬 35°06 东经 109°07 渭南 北纬 34°30 东经 109°30 咸阳 北纬 34°20 东经 108°43 兴平 北纬 34°18 东经 108°29 延安 北纬 36°35 东经 109°28 榆林 北纬 38°18 东经 109°47 【浙江省】 杭州 北纬 30°16 东经 120°10 慈溪 北纬 30°11 东经 121°15 东阳 北纬 29°16 东经 120°14 奉化 北纬 29°39 东经 121°24 富阳 北纬 30°03 东经 119°57 海宁 北纬 30°32 东经 120°42 湖州 北纬 30°52 东经 120°06 建德 北纬 29°29 东经 119°16 江山 北纬 28°45 东经 118°37 嘉兴 北纬 30°46 东经 120°45 金华 北纬 29°07 东经 119°39 兰溪 北纬 29°12 东经 119°28 临海 北纬 28°51 东经 121°08 丽水 北纬 28°27 东经 119°54 龙泉 北纬 28°04 东经 119°08 宁波 北纬 29°52 东经 121°33 平湖 北纬 30°42 东经 121°01 衢州 北纬 28°58 东经 118°52 瑞安 北纬 27°48 东经 120°38 上虞 北纬 30°01 东经 120°52 绍兴 北纬 30°00东经 120°34 台州 北纬 28°41 东经 121°27 桐乡 北纬 30°38 东经 120°32 温岭 北纬 28°22 东经 121°21 温州 北纬 28°01 东经 120°39 萧山 北纬 30°09 东经 120°16 义乌 北纬 29°18 东经 120°04 乐清 北纬 28°08 东经 120°58 余杭 北纬 30°26 东经 120°18 余姚 北纬 30°02 东经 121°10 永康 北纬 29°54 东经 120°01 舟山 北纬 30°01 东经 122°06 诸暨 北纬 29°43 东经 120°14【新疆维吾尔自治区】 乌鲁木齐 北纬 43°45 东经 87°36 阿克苏 北纬 41°09 东经 80°19 阿勒泰 北纬 47°50 东经 88°12 阿图什 北纬 39°42 东经 76°08 博乐 北纬 44°57 东经 82°08 昌吉 北纬 44°02 东经 87°18 阜康 北纬 44°09 东经 87°58 哈密 北纬 42°50 东经 93°28 和田 北纬 37°09 东经 79°55 克拉玛依 北纬 45°36 东经 84°51 喀什 北纬 39°30 东经 75°59 库尔勒 北纬 41°46 东经 86°07 奎屯 北纬 44°27 东经 84°56 石河子 北纬 44°18 东经 86°00 塔城 北纬 46°46 东经 82°59 吐鲁番 北纬 42°54 东经 89°11 伊宁 北纬 43°55 东经 81°20【西藏自治区】拉萨 北纬 29°39 东经 91°08 日喀则 北纬 29°16 东经 88°51【云南省】 昆明 北纬 25°04 东经 102°42 保山 北纬 25°08 东经 99°10 楚雄 北纬 25°01 东经 101°32 大理 北纬 25°34 东经 100°13 东川 北纬 26°06 东经 103°12 个旧 北纬 23°21东经 103°09 景洪 北纬 22°01 东经 100°48 开远 北纬 23°43 东经 103°13 曲靖 北纬 25°30 东经 103°48 瑞丽 北纬 24°00 东经 97°50 思茅 北纬 22°48 东经 100°58 畹町 北纬 24°06 东经 98°04 宣威 北纬 26°13 东经 104°06 玉溪 北纬 24°22 东经 102°32 昭通 北纬 27°20 东经 103°42【台湾省】 台北市 北纬 25°03 东经 121°30 【香港特别行政区】 北纬 21°23 东经 115°12 【澳门特别行政区】 北纬 21°33 东经 115°07 9。
中国各城市的地理位置_经纬度

中国各城市的地理位置经纬度所在省城市名纬度经度安徽省合肥北纬31.52 东经117.17 安徽省安庆北纬30.31 东经117.02 安徽省蚌埠北纬32.56 东经117.21 安徽省亳州北纬33.52 东经115.47 安徽省巢湖北纬31.36 东经117.52 安徽省滁州北纬32.18 东经118.18 安徽省阜阳北纬32.54 东经115.48 安徽省贵池北纬30.39 东经117.28 安徽省淮北北纬33.57 东经116.47 安徽省淮南北纬32.37 东经116.58 安徽省黄山北纬29.43 东经118.18 安徽省界首北纬33.15 东经115.21 安徽省六安北纬31.44 东经116.28 安徽省马鞍山北纬31.43 东经118.28 安徽省明光北纬32.47 东经117.58 安徽省宿州北纬33.38 东经116.58 安徽省天长北纬32.41 东经118.59 安徽省铜陵北纬30.56 东经117.48 安徽省芜湖北纬31.19 东经118.22 安徽省宣州北纬30.57 东经118.44澳门澳门市北纬21.33 东经115.07北京市北京市北纬39.55 东经116.24福建省福州北纬26.05 东经119.18 福建省长乐北纬25.58 东经119.31 福建省福安北纬27.06 东经119.39 福建省福清北纬25.42 东经119.23 福建省建瓯北纬27.03 东经118.20 福建省建阳北纬27.21 东经118.07 福建省晋江北纬24.49 东经118.35 福建省龙海北纬24.26 东经117.48 福建省龙岩北纬25.06 东经117.01 福建省南安北纬24.57 东经118.23 福建省南平北纬26.38 东经118.10 福建省宁德北纬26.39 东经119.31 福建省莆田北纬24.26 东经119.01 福建省泉州北纬24.56 东经118.36 福建省三明北纬26.13 东经117.36 福建省邵武北纬27.20 东经117.29 福建省石狮北纬24.44 东经118.38福建省厦门北纬24.27 东经118.06 福建省永安北纬25.58 东经117.23 福建省漳平北纬25.17 东经117.24 福建省漳州北纬24.31 东经117.39甘肃省白银北纬36.33 东经104.12 甘肃省敦煌北纬40.08 东经94.41 甘肃省嘉峪关北纬39.48 东经98.14 甘肃省金昌北纬38.28 东经102.10 甘肃省酒泉北纬39.44 东经98.31 甘肃省临夏北纬35.37 东经103.12 甘肃省平凉北纬35.32 东经106.40 甘肃省天水北纬34.37 东经105.42 甘肃省武威北纬37.56 东经102.39 甘肃省西峰北纬35.45 东经107.40 甘肃省玉门北纬39.49 东经97.35 甘肃省张掖北纬38.56 东经100.26广东省广州北纬23.08 东经113.14 广东省潮阳北纬23.16 东经116.36 广东省潮州北纬23.40 东经116.38 广东省澄海北纬23.28 东经116.46 广东省从化北纬23.33 东经113.33 广东省东莞北纬23.02 东经113.45 广东省恩平北纬22.12 东经112.19 广东省佛山北纬23.02 东经113.06 广东省高明北纬22.53 东经112.50 广东省高要北纬23.02 东经112.26 广东省高州北纬21.54 东经110.50 广东省鹤山北纬22.46 东经112.57 广东省河源北纬23.43 东经114.41 广东省花都北纬23.23 东经113.12 广东省化州北纬21.39 东经110.37 广东省惠阳北纬22.48 东经114.28 广东省惠州北纬23.05 东经114.22 广东省江门北纬22.35 东经113.04 广东省揭阳北纬22.32 东经116.21 广东省开平北纬22.22 东经112.40 广东省乐昌北纬25.09 东经113.21 广东省雷州北纬20.54 东经110.04 广东省廉江北纬21.37 东经110.17 广东省连州北纬24.48 东经112.23 广东省罗定北纬22.46 东经111.33 广东省茂名北纬21.40 东经110.53 广东省梅州北纬24.19 东经116.07 广东省南海北纬23.01 东经113.09 广东省番禺北纬22.57 东经113.22 广东省普宁北纬23.18 东经116.10广东省三水北纬23.10 东经112.52 广东省汕头北纬23.22 东经116.41 广东省汕尾北纬22.47 东经115.21 广东省韶关北纬24.48 东经113.37 广东省深圳北纬22.33 东经114.07 广东省顺德北纬22.50 东经113.15 广东省四会北纬23.21 东经112.41 广东省台山北纬22.15 东经112.48 广东省吴川北纬21.26 东经110.47 广东省新会北纬22.32 东经113.01 广东省兴宁北纬24.09 东经115.43 广东省阳春北纬22.10 东经111.48 广东省阳江北纬21.50 东经111.58 广东省英德北纬24.10 东经113.22 广东省云浮北纬22.57 东经112.02 广东省增城北纬23.18 东经113.49 广东省湛江北纬21.11 东经110.24 广东省肇庆北纬23.03 东经112.27 广东省中山北纬22.31 东经113.22 广东省珠海北纬22.17 东经113.34广西自治区南宁北纬22.48 东经108.19 广西自治区北海北纬21.28 东经109.07 广西自治区北流北纬22.42 东经110.21 广西自治区百色北纬23.54 东经106.36 广西自治区防城港北纬21.37 东经108.20 广西自治区贵港北纬23.06 东经109.36 广西自治区桂林北纬25.17 东经110.17 广西自治区桂平北纬23.22 东经110.04 广西自治区河池北纬24.42 东经108.03 广西自治区合山北纬23.47 东经108.52 广西自治区柳州北纬23.19 东经109.24 广西自治区赁祥北纬22.07 东经106.44 广西自治区钦州北纬21.57 东经108.37 广西自治区梧州北纬23.29 东经111.20 广西自治区玉林北纬22.38 东经110.09 广西自治区宜州北纬24.28 东经108.40贵州省安顺北纬26.14 东经105.55 贵州省毕节北纬27.18 东经105.18 贵州省赤水北纬28.34 东经105.42 贵州省都匀北纬26.15 东经107.31 贵州省凯里北纬26.35 东经107.58 贵州省六盘水北纬26.35 东经104.50 贵州省清镇北纬26.33 东经106.27 贵州省铜仁北纬27.43 东经109.12 贵州省兴义北纬25.05 东经104.53 贵州省遵义北纬27.42 东经106.55海南省海口北纬20.02 东经110.20 海南省儋州北纬19.31 东经109.34 海南省琼海北纬19.14 东经110.28 海南省琼山北纬19.59 东经110.21 海南省三亚北纬18.14 东经109.31 海南省通什北纬18.46 东经109.31河北省石家庄北纬38.02 东经114.30 河北省安国北纬38.24 东经115.20 河北省保定北纬38.51 东经115.30 河北省霸州北纬39.06 东经116.24 河北省泊头北纬38.04 东经116.34 河北省沧州北纬38.18 东经116.52 河北省承德北纬40.59 东经117.57 河北省定州北纬38.30 东经115.00 河北省丰南北纬39.34 东经118.06 河北省高碑店北纬39.20 东经115.51 河北省蒿城北纬38.02 东经114.50 河北省邯郸北纬36.36 东经114.28 河北省河间北纬38.26 东经116.05 河北省衡水北纬37.44 东经115.42 河北省黄骅北纬38.21 东经117.21 河北省晋州北纬38.02 东经115.02 河北省冀州北纬37.34 东经115.33 河北省廓坊北纬39.31 东经116.42 河北省鹿泉北纬38.04 东经114.19 河北省南宫北纬37.22 东经115.23 河北省秦皇岛北纬39.55 东经119.35 河北省任丘北纬38.42 东经116.07 河北省三河北纬39.58 东经117.04 河北省沙河北纬36.51 东经114.30 河北省深州北纬38.01 东经115.32河北省武安北纬36.42 东经114.11 河北省邢台北纬37.04 东经114.30 河北省辛集北纬37.54 东经115.12 河北省新乐北纬38.20 东经114.41 河北省张家口北纬40.48 东经114.53 河北省涿州北纬39.29 东经115.59 河北省遵化北纬40.11 东经117.58 河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21 河南省长葛北纬34.12 东经113.47 河南省登封北纬34.27 东经113.02 河南省邓州北纬32.42 东经112.05 河南省巩义北纬34.46 东经112.58 河南省鹤壁北纬35.54 东经114.11 河南省辉县北纬35.27 东经113.47 河南省焦作北纬35.14 东经113.12 河南省济源北纬35.04 东经112.35 河南省开封北纬34.47 东经114.21 河南省灵宝北纬34.31 东经110.52 河南省林州北纬36.03 东经113.49 河南省漯河北纬33.33 东经114.02 河南省洛阳北纬34.41 东经112.27 河南省南阳北纬33.00 东经112.32 河南省平顶山北纬33.44 东经113.17 河南省濮阳北纬35.44 东经115.01 河南省沁阳北纬35.05 东经112.57 河南省汝州北纬34.09 东经112.50 河南省三门峡北纬34.47 东经111.12 河南省商丘北纬34.26 东经115.38 河南省卫辉北纬35.24 东经114.03 河南省舞钢北纬33.17 东经113.30 河南省项城北纬33.26 东经114.54 河南省荥阳北纬34.46 东经113.21 河南省新密北纬34.31 东经113.22 河南省新乡北纬35.18 东经113.52 河南省信阳北纬32.07 东经114.04 河南省新郑北纬34.24 东经113.43 河南省许昌北纬34.01 东经113.49 河南省偃师北纬34.43 东经112.47 河南省义马北纬34.43 东经111.55 河南省禹州北纬34.09 东经113.28 河南省周口北纬33.37 东经114.38 河南省驻马店北纬32.58 东经114.01黑龙江省哈尔滨北纬45.44 东经126.36 黑龙江省阿城北纬45.32 东经126.58黑龙江省安达北纬46.24 东经125.18黑龙江省北安北纬48.15 东经126.31黑龙江省大庆北纬46.36 东经125.01黑龙江省富锦北纬47.15 东经132.02黑龙江省海林北纬44.35 东经129.21黑龙江省海伦北纬47.28 东经126.57黑龙江省鹤岗北纬47.20 东经130.16黑龙江省黑河北纬50.14 东经127.29黑龙江省佳木斯北纬46.47 东经130.22 黑龙江省鸡西北纬45.17 东经130.57黑龙江省密山北纬45.32 东经131.50黑龙江省牡丹江北纬44.35 东经129.36 黑龙江省讷河北纬48.29 东经124.51黑龙江省宁安北纬44.21 东经129.28黑龙江省齐齐哈尔北纬47.20 东经123.57 黑龙江省七台河北纬45.48 东经130.49 黑龙江省双城北纬45.22 东经126.15黑龙江省尚志北纬45.14 东经127.55黑龙江省双鸭山北纬46.38 东经131.11 黑龙江省绥芬河北纬44.25 东经131.11 黑龙江省绥化北纬46.38 东经126.59黑龙江省铁力北纬46.59 东经128.01黑龙江省同江北纬47.39 东经132.30黑龙江省五常北纬44.55 东经127.11黑龙江省五大连池北纬48.38 东经126.07 黑龙江省伊春北纬47.42 东经128.56黑龙江省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省广水北纬31.37 东经113.48湖北省洪湖北纬29.48 东经113.27湖北省黄石北纬30.12 东经115.06湖北省黄州北纬30.27 东经114.52湖北省荆门北纬31.02 东经112.12湖北省荆沙北纬30.18 东经112.16湖北省老河口北纬32.23 东经111.40湖北省麻城北纬31.10 东经115.01 湖北省浦圻北纬29.42 东经113.51 湖北省潜江北纬30.26 东经112.53 湖北省石首北纬29.43 东经112.24 湖北省十堰北纬32.40 东经110.47 湖北省随州北纬31.42 东经113.22 湖北省天门北纬60.39 东经113.10 湖北省武穴北纬29.51 东经115.33 湖北省襄樊北纬32.02 东经112.08 湖北省咸宁北纬29.53 东经114.17 湖北省仙桃北纬30.22 东经113.27 湖北省孝感北纬30.56 东经113.54 湖北省宜昌北纬30.42 东经111.17 湖北省宜城北纬31.42 东经112.15 湖北省应城北纬30.57 东经113.33 湖北省枣阳北纬32.07 东经112.44 湖北省枝城北纬30.23 东经111.27 湖北省钟祥北纬31.10 东经112.34湖南省常德北纬29.02 东经111.51 湖南省郴州北纬25.46 东经113.02 湖南省衡阳北纬26.53 东经112.37 湖南省洪江北纬27.07 东经109.59 湖南省怀化北纬27.33 东经109.58 湖南省津市北纬29.38 东经111.52 湖南省吉首北纬28.18 东经109.43 湖南省耒阳北纬26.24 东经112.51 湖南省冷水江北纬27.42 东经111.26 湖南省冷水滩北纬26.26 东经111.35 湖南省涟源北纬27.41 东经111.41 湖南省醴陵北纬27.40 东经113.30 湖南省临湘北纬29.29 东经113.27 湖南省浏阳北纬28.09 东经113.37 湖南省娄底北纬27.44 东经111.59 湖南省汨罗北纬28.49 东经113.03 湖南省韶山北纬27.54 东经112.29 湖南省邵阳北纬27.14 东经111.28 湖南省武冈北纬26.43 东经110.37 湖南省湘潭北纬27.52 东经112.53 湖南省湘乡北纬27.44 东经112.31 湖南省益阳北纬28.36 东经112.20 湖南省永州北纬26.13 东经111.37 湖南省沅江北纬28.50 东经112.22 湖南省岳阳北纬29.22 东经113.06 湖南省张家界北纬29.08 东经110.29 湖南省株洲北纬27.51 东经113.09 湖南省资兴北纬25.58 东经113.13吉林省白城北纬45.38 东经122.50 吉林省白山北纬41.56 东经126.26 吉林省大安北纬45.30 东经124.18 吉林省德惠北纬44.32 东经125.42 吉林省敦化北纬43.22 东经128.13 吉林省公主岭北纬43.31 东经124.49 吉林省和龙北纬42.32 东经129.00 吉林省桦甸北纬42.58 东经126.44 吉林省珲春北纬42.52 东经130.22 吉林省集安北纬41.08 东经126.11 吉林省蛟河北纬43.42 东经127.21 吉林省吉林北纬43.52 东经126.33 吉林省九台北纬44.09 东经125.51 吉林省辽源北纬42.54 东经125.09 吉林省临江北纬41.49 东经126.53 吉林省龙井北纬42.46 东经129.26 吉林省梅河口北纬42.32 东经125.40 吉林省舒兰北纬44.24 东经126.57 吉林省四平北纬43.10 东经124.22 吉林省松原北纬45.11 东经124.49 吉林省洮南北纬45.20 东经122.47 吉林省通化北纬41.43 东经125.56 吉林省图们北纬42.57 东经129.51 吉林省延吉北纬42.54 东经129.30 吉林省愉树北纬44.49 东经126.32江苏省南京北纬32.03 东经118.46 江苏省常熟北纬31.39 东经120.43 江苏省常州北纬31.47 东经119.58 江苏省丹阳北纬32.00 东经119.32 江苏省东台北纬32.51 东经120.19 江苏省高邮北纬32.47 东经119.27 江苏省海门北纬31.53 东经121.09 江苏省淮安北纬33.30 东经119.09 江苏省淮阴北纬33.36 东经119.02 江苏省江都北纬32.26 东经119.32 江苏省姜堰北纬32.34 东经120.08 江苏省江阴北纬31.54 东经120.17 江苏省靖江北纬32.02 东经120.17 江苏省金坛北纬31.46 东经119.33 江苏省昆山北纬31.23 东经120.57 江苏省连去港北纬34.36 东经119.10江苏省南通北纬32.01 东经120.51 江苏省邳州北纬34.19 东经117.59 江苏省启乐北纬31.48 东经121.39 江苏省如皋北纬32.23 东经120.33 江苏省宿迁北纬33.58 东经118.18 江苏省苏州北纬31.19 东经120.37 江苏省太仓北纬31.27 东经121.06 江苏省泰兴北纬32.10 东经120.01 江苏省泰州北纬32.30 东经119.54 江苏省通州北纬32.05 东经121.03 江苏省吴江北纬31.10 东经120.39 江苏省无锡北纬31.34 东经120.18 江苏省兴化北纬32.56 东经119.50 江苏省新沂北纬34.22 东经118.20 江苏省徐州北纬34.15 东经117.11 江苏省盐在北纬33.22 东经120.08 江苏省扬中北纬32.14 东经119.49 江苏省扬州北纬32.23 东经119.26 江苏省宜兴北纬31.21 东经119.49 江苏省仪征北纬32.16 东经119.10 江苏省张家港北纬31.52 东经120.32 江苏省镇江北纬32.11 东经119.27江西省德兴北纬28.57 东经117.35 江西省丰城北纬28.12 东经115.48 江西省赣州北纬28.52 东经114.56 江西省高安北纬28.25 东经115.22 江西省吉安北纬27.07 东经114.58 江西省景德镇北纬29.17 东经117.13 江西省井冈山北纬26.34 东经114.10 江西省九江北纬29.43 东经115.58 江西省乐平北纬28.58 东经117.08 江西省临川北纬27.59 东经116.21 江西省萍乡北纬27.37 东经113.50 江西省瑞昌北纬29.40 东经115.38 江西省瑞金北纬25.53 东经116.01 江西省上饶北纬25.27 东经117.58 江西省新余北纬27.48 东经114.56 江西省宜春北纬27.47 东经114.23 江西省鹰潭北纬28.14 东经117.03 江西省樟树北纬28.03 东经115.32辽宁省鞍山北纬41.07 东经123.00辽宁省北票北纬41.48 东经120.47辽宁省本溪北纬41.18 东经123.46辽宁省朝阳北纬41.34 东经120.27辽宁省大连北纬38.55 东经121.36辽宁省丹东北纬40.08 东经124.22辽宁省大石桥北纬40.37 东经122.31辽宁省东港北纬39.53 东经124.08辽宁省凤城北纬40.28 东经124.02辽宁省抚顺北纬41.51 东经123.54辽宁省阜新北纬42.01 东经121.39辽宁省盖州北纬40.24 东经122.21辽宁省海城北纬40.51 东经122.43辽宁省葫芦岛北纬40.45 东经120.51辽宁省锦州北纬41.07 东经121.09辽宁省开原北纬42.32 东经124.02辽宁省辽阳北纬41.16 东经123.12辽宁省凌海北纬41.10 东经121.21辽宁省凌源北纬41.14 东经119.22辽宁省盘锦北纬41.07 东经122.03辽宁省普兰店北纬39.23 东经121.58辽宁省铁法北纬42.28 东经123.32辽宁省铁岭北纬42.18 东经123.51辽宁省瓦房店北纬39.37 东经122.00辽宁省兴城北纬40.37 东经120.41辽宁省新民北纬41.59 东经122.49辽宁省营口北纬40.39 东经122.13辽宁省庄河北纬39.41 东经122.58内蒙古自治区呼和浩特北纬40.48 东经111.41 内蒙古自治区包头北纬40.39 东经109.49内蒙古自治区赤峰北纬42.17 东经118.58内蒙古自治区东胜北纬39.48 东经109.59内蒙古自治区二连浩特北纬43.38 东经111.58 内蒙古自治区额尔古纳北纬50.13 东经120.11 内蒙古自治区丰镇北纬40.27 东经113.09内蒙古自治区根河北纬50.48 东经121.29内蒙古自治区海拉尔北纬49.12 东经119.39 内蒙古自治区霍林郭勒北纬45.32 东经119.38 内蒙古自治区集宁北纬41.02 东经113.06内蒙古自治区临河北纬40.46 东经107.22内蒙古自治区满洲里北纬49.35 东经117.23 内蒙古自治区通辽北纬43.37 东经122.16内蒙古自治区乌兰浩特北纬46.03 东经122.03 内蒙古自治区乌海北纬39.40 东经106.48内蒙古自治区锡林浩特北纬43.57 东经116.03 内蒙古自治区牙克石北纬49.17 东经120.40 内蒙古自治区扎兰屯北纬48.00 东经122.47宁夏自治区银川北纬38.27 东经106.16 宁夏自治区青铜峡北纬37.56 东经105.59 宁夏自治区石嘴山北纬39.02 东经106.22 宁夏自治区吴忠北纬37.59 东经106.11青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55山东省济南北纬36.40 东经117.00山东省安丘北纬36.25 东经119.12山东省滨州北纬37.22 东经118.02山东省昌邑北纬39.52 东经119.24山东省德州北纬37.26 东经116.17山东省东营北纬37.27 东经118.30山东省肥城北纬36.14 东经116.46山东省高密北纬36.22 东经119.44山东省菏泽北纬35.14 东经115.26山东省胶南北纬35.53 东经119.58山东省胶州北纬36.17 东经120.00山东省即墨北纬36.22 东经120.28山东省济宁北纬35.23 东经116.33山东省莱芜北纬36.12 东经117.40山东省莱西北纬36.52 东经120.31山东省莱阳北纬36.58 东经120.42山东省莱州北纬37.10 东经119.57山东省乐陵北纬37.44 东经117.12山东省聊城北纬36.26 东经115.57山东省临清北纬36.51 东经115.42山东省临沂北纬35.03 东经118.20山东省龙口北纬37.39 东经120.21山东省蓬莱北纬37.48 东经120.45山东省平度北纬36.47 东经119.58山东省青岛北纬36.03 东经120.18山东省青州北纬36.42 东经118.28山东省曲阜北纬35.36 东经116.58山东省日照北纬35.23 东经119.32山东省荣成北纬37.10 东经122.25山东省乳山北纬36.54 东经121.31山东省寿光北纬36.53 东经118.44山东省泰安北纬36.11 东经117.08山东省滕州北纬35.06 东经117.09山东省潍坊北纬36.43 东经119.06山东省威海北纬37.31 东经122.07山东省新泰北纬35.54 东经117.45 山东省烟台北纬37.32 东经121.24 山东省兖州北纬35.32 东经116.49 山东省禹城北纬36.56 东经116.39 山东省枣庄北纬34.52 东经117.33 山东省章丘北纬36.43 东经117.32 山东省招远北纬37.21 东经120.23 山东省诸城北纬35.59 东经119.24 山东省淄博北纬36.48 东经118.03 山东省邹城北纬35.24 东经116.58山西省长治北纬36.11 东经113.06 山西省大同北纬40.06 东经113.17 山西省高平北纬35.48 东经112.55 山西省古交北纬37.54 东经112.09 山西省河津北纬35.35 东经110.41 山西省侯马北纬35.37 东经111.21 山西省霍州北纬36.34 东经111.42 山西省介休北纬37.02 东经111.55 山西省晋城北纬35.30 东经112.51 山西省临汾北纬36.05 东经111.31 山西省潞城北纬36.21 东经113.14 山西省朔州北纬39.19 东经112.26 山西省孝义北纬37.08 东经111.48 山西省忻州北纬38.24 东经112.43 山西省阳泉北纬37.51 东经113.34 山西省永济北纬34.52 东经110.27 山西省原平北纬38.43 东经112.42 山西省榆次北纬37.41 东经112.43 山西省运城北纬35.02 东经110.59陕西省安康北纬32.41 东经109.01 陕西省宝鸡北纬34.22 东经107.09 陕西省韩城北纬35.28 东经110.27 陕西省汉中北纬33.04 东经107.01 陕西省华阴北纬34.34 东经110.05 陕西省商州北纬33.52 东经109.57 陕西省铜川北纬35.06 东经109.07 陕西省渭南北纬34.30 东经109.30 陕西省咸阳北纬34.20 东经108.43 陕西省兴平北纬34.18 东经108.29 陕西省延安北纬36.35 东经109.28 陕西省榆林北纬38.18 东经109.47上海市上海市北纬31.14 东经121.29四川省成都北纬30.40 东经104.04 四川省巴中北纬31.51 东经106.43 四川省崇州北纬30.39 东经103.40 四川省达川北纬31.14 东经107.29 四川省德阳北纬31.09 东经104.22 四川省都江堰北纬31.01 东经103.37 四川省峨眉山北纬29.36 东经103.29 四川省涪陵北纬29.42 东经107.22 四川省广汉北纬30.58 东经104.15 四川省广元北纬32.28 东经105.51 四川省华蓥北纬30.26 东经106.44 四川省简阳北纬30.24 东经104.32 四川省江油北纬31.48 东经104.42 四川省阆中北纬31.36 东经105.58 四川省乐山北纬29.36 东经103.44 四川省泸州北纬28.54 东经105.24 四川省绵阳北纬31.30 东经104.42 四川省南充北纬30.49 东经106.04 四川省内江北纬29.36 东经105.02 四川省攀枝花北纬26.34 东经101.43 四川省彭州北纬30.59 东经103.57 四川省邛崃北纬30.26 东经103.28 四川省遂宁北纬30.31 东经105.33 四川省万县北纬30.50 东经108.21 四川省万源北纬32.03 东经108.03 四川省西昌北纬27.54 东经102.16 四川省雅安北纬29.59 东经102.59 四川省宜宾北纬28.47 东经104.34四川省资阳北纬30.09 东经104.38天津市天津市北纬39.02 东经117.12西藏自治区拉萨北纬29.39 东经91.08西藏自治区日喀则北纬29.16 东经88.51香港香港市北纬21.23 东经115.12新疆自治区乌鲁木齐北纬43.45 东经87.36 新疆自治区阿克苏北纬41.09 东经80.19 新疆自治区阿勒泰北纬47.50 东经88.12 新疆自治区阿图什北纬39.42 东经76.08 新疆自治区博乐北纬44.57 东经82.08新疆自治区昌吉北纬44.02 东经87.18新疆自治区阜康北纬44.09 东经87.58新疆自治区哈密北纬42.50 东经93.28新疆自治区和田北纬37.09 东经79.55新疆自治区克拉玛依北纬45.36 东经84.51 新疆自治区喀什北纬39.30 东经75.59新疆自治区库尔勒北纬41.46 东经86.07 新疆自治区奎屯北纬44.27 东经84.56新疆自治区石河子北纬44.18 东经86.00 新疆自治区塔城北纬46.46 东经82.59新疆自治区吐鲁番北纬42.54 东经89.11 新疆自治区伊宁北纬43.55 东经81.20云南省昆明北纬25.04 东经102.42云南省保山北纬25.08 东经99.10云南省楚雄北纬25.01 东经101.32云南省大理北纬25.34 东经100.13云南省东川北纬26.06 东经103.12云南省个旧北纬23.21 东经103.09云南省景洪北纬22.01 东经100.48云南省开远北纬23.43 东经103.13云南省曲靖北纬25.30 东经103.48云南省瑞丽北纬24.00 东经97.50云南省思茅北纬22.48 东经100.58云南省畹町北纬24.06 东经98.04云南省宣威北纬26.13 东经104.06云南省玉溪北纬24.22 东经102.32云南省昭通北纬27.20 东经103.42浙江省慈溪北纬30.11 东经121.15 浙江省东阳北纬29.16 东经120.14 浙江省奉化北纬29.39 东经121.24 浙江省富阳北纬30.03 东经119.57 浙江省海宁北纬30.32 东经120.42 浙江省湖州北纬30.52 东经120.06 浙江省建德北纬29.29 东经119.16 浙江省江山北纬28.45 东经118.37 浙江省嘉兴北纬30.46 东经120.45 浙江省金华北纬29.07 东经119.39 浙江省兰溪北纬29.12 东经119.28 浙江省临海北纬28.51 东经121.08 浙江省丽水北纬28.27 东经119.54 浙江省龙泉北纬28.04 东经119.08 浙江省宁波北纬29.52 东经121.33 浙江省平湖北纬30.42 东经121.01 浙江省衢州北纬28.58 东经118.52 浙江省瑞安北纬27.48 东经120.38 浙江省上虞北纬30.01 东经120.52 浙江省绍兴北纬30.00 东经120.34 浙江省台州北纬28.41 东经121.27 浙江省桐乡北纬30.38 东经120.32 浙江省温岭北纬28.22 东经121.21 浙江省温州北纬28.01 东经120.39 浙江省萧山北纬30.09 东经120.16 浙江省义乌北纬29.18 东经120.04 浙江省乐清北纬28.08 东经120.58 浙江省余杭北纬30.26 东经120.18 浙江省余姚北纬30.02 东经121.10 浙江省永康北纬29.54 东经120.01 浙江省舟山北纬30.01 东经122.06 浙江省诸暨北纬29.43 东经120.14重庆市重庆市北纬29.35 东经106.33重庆市合川市北纬30.02 东经106.15重庆市江津市北纬29.18 东经106.16重庆市南川市北纬29.10 东经107.05重庆市永川市北纬29.23 东经105.53欢迎您的下载,资料仅供参考!。
中国城市经纬度

2 天津市天津市天津的经纬度北纬39.02东经117.12 3 上海市上海市上海的经纬度北纬31.14东经121.29 4 重庆市重庆市重庆的经纬度北纬29.35东经106.33 重庆市合川的经纬度北纬30.02东经106.15 重庆市江津的经纬度北纬29.18东经106.16 重庆市南川的经纬度北纬29.10东经107.05 重庆市永川的经纬度北纬29.23东经105.53 5 河北省河北省石家庄的经纬度北纬38.02东经114.30 河北省安国的经纬度北纬38.24东经115.20 河北省保定的经纬度北纬38.51东经115.30 河北省霸州的经纬度北纬39.06东经116.24 河北省泊头的经纬度北纬38.04东经116.34 河北省沧州的经纬度北纬38.18东经116.52 河北省承德的经纬度北纬40.59东经117.57 河北省定州的经纬度北纬38.30东经115.00 河北省丰南的经纬度北纬39.34东经118.06 河北省高碑店的经纬度北纬39.20东经115.51 河北省蒿城的经纬度北纬38.02东经114.50河北省邯郸的经纬度北纬36.36东经114.28 河北省河间的经纬度北纬38.26东经116.05 河北省衡水的经纬度北纬37.44东经115.42 河北省黄骅的经纬度北纬38.21东经117.21 河北省晋州的经纬度北纬38.02东经115.02 河北省冀州的经纬度北纬37.34东经115.33 河北省廓坊的经纬度北纬39.31东经116.42 河北省鹿泉的经纬度北纬38.04东经114.19 河北省南宫的经纬度北纬37.22东经115.23 河北省秦皇岛的经纬度北纬39.55东经119.35 河北省任丘的经纬度北纬38.42东经116.07 河北省三河的经纬度北纬39.58东经117.04 河北省沙河的经纬度北纬36.51东经114.30 河北省深州的经纬度北纬38.01东经115.32 河北省唐山的经纬度北纬39.36东经118.11 河北省武安的经纬度北纬36.42东经114.11 河北省邢台的经纬度北纬37.04东经114.30 河北省辛集的经纬度北纬37.54东经115.12 河北省新乐的经纬度北纬38.20东经114.41 河北省张家口的经纬度北纬40.48东经114.53 河北省涿州的经纬度北纬39.29东经115.59 河北省遵化的经纬度北纬40.11东经117.586 山西省山西省太原的经纬度北纬37.54东经112.33 山西省长治的经纬度北纬36.11东经113.06 山西省大同的经纬度北纬40.06东经113.17 山西省高平的经纬度北纬35.48东经112.55 山西省古交的经纬度北纬37.54东经112.09 山西省河津的经纬度北纬35.35东经110.41 山西省侯马的经纬度北纬35.37东经111.21 山西省霍州的经纬度北纬36.34东经111.42 山西省介休的经纬度北纬37.02东经111.55 山西省晋城的经纬度北纬35.30东经112.51 山西省临汾的经纬度北纬36.05东经111.31 山西省潞城的经纬度北纬36.21东经113.14 山西省朔州的经纬度北纬39.19东经112.26 山西省孝义的经纬度北纬37.08东经111.48 山西省忻州的经纬度北纬38.24东经112.43 山西省阳泉的经纬度北纬37.51东经113.34 山西省永济的经纬度北纬34.52东经110.27 山西省原平的经纬度北纬38.43东经112.42 山西省榆次的经纬度北纬37.41东经112.43 山西省运城的经纬度北纬35.02东经110.59 7 内蒙古自治区内蒙古自治区呼和浩特的经纬度北纬40.48东经111.41 内蒙古自治区包头的经纬度北纬40.39东经109.49内蒙古自治区赤峰的经纬度北纬42.17东经118.58内蒙古自治区东胜的经纬度北纬39.48东经109.59内蒙古自治区二连浩特的经纬度北纬43.38东经111.58 内蒙古自治区额尔古纳的经纬度北纬50.13东经120.11 内蒙古自治区丰镇的经纬度北纬40.27东经113.09内蒙古自治区根河的经纬度北纬50.48东经121.29内蒙古自治区海拉尔的经纬度北纬49.12东经119.39 内蒙古自治区霍林郭勒的经纬度北纬45.32东经119.38 内蒙古自治区集宁的经纬度北纬41.02东经113.06内蒙古自治区临河的经纬度北纬40.46东经107.22内蒙古自治区满洲里的经纬度北纬49.35东经117.23 内蒙古自治区通辽的经纬度北纬43.37东经122.16内蒙古自治区乌兰浩特的经纬度北纬46.03东经122.03 内蒙古自治区乌海的经纬度北纬39.40东经106.48内蒙古自治区锡林浩特的经纬度北纬43.57东经116.03 内蒙古自治区牙克石的经纬度北纬49.17东经120.40 内蒙古自治区扎兰屯的经纬度北纬48.00东经122.478 辽宁省辽宁省沈阳的经纬度北纬41.48东经123.25辽宁省鞍山的经纬度北纬41.07东经123.00辽宁省本溪的经纬度北纬41.18东经123.46 辽宁省朝阳的经纬度北纬41.34东经120.27 辽宁省大连的经纬度北纬38.55东经121.36 辽宁省丹东的经纬度北纬40.08东经124.22 辽宁省大石桥的经纬度北纬40.37东经122.31 辽宁省东港的经纬度北纬39.53东经124.08 辽宁省凤城的经纬度北纬40.28东经124.02 辽宁省抚顺的经纬度北纬41.51东经123.54 辽宁省阜新的经纬度北纬42.01东经121.39 辽宁省盖州的经纬度北纬40.24东经122.21 辽宁省海城的经纬度北纬40.51东经122.43 辽宁省葫芦岛的经纬度北纬40.45东经120.51 辽宁省锦州的经纬度北纬41.07东经121.09 辽宁省开原的经纬度北纬42.32东经124.02 辽宁省辽阳的经纬度北纬41.16东经123.12 辽宁省凌海的经纬度北纬41.10东经121.21 辽宁省凌源的经纬度北纬41.14东经119.22 辽宁省盘锦的经纬度北纬41.07东经122.03 辽宁省普兰店的经纬度北纬39.23东经121.58 辽宁省铁法的经纬度北纬42.28东经123.32 辽宁省铁岭的经纬度北纬42.18东经123.51辽宁省兴城的经纬度北纬40.37东经120.41 辽宁省新民的经纬度北纬41.59东经122.49 辽宁省营口的经纬度北纬40.39东经122.13 辽宁省庄河的经纬度北纬39.41东经122.58 9 吉林省吉林省长春的经纬度北纬43.54东经125.19 吉林省白城的经纬度北纬45.38东经122.50 吉林省白山的经纬度北纬41.56东经126.26 吉林省大安的经纬度北纬45.30东经124.18 吉林省德惠的经纬度北纬44.32东经125.42 吉林省敦化的经纬度北纬43.22东经128.13 吉林省公主岭的经纬度北纬43.31东经124.49 吉林省和龙的经纬度北纬42.32东经129.00 吉林省桦甸的经纬度北纬42.58东经126.44 吉林省珲春的经纬度北纬42.52东经130.22 吉林省集安的经纬度北纬41.08东经126.11 吉林省蛟河的经纬度北纬43.42东经127.21 吉林省吉林的经纬度北纬43.52东经126.33 吉林省九台的经纬度北纬44.09东经125.51 吉林省辽源的经纬度北纬42.54东经125.09 吉林省临江的经纬度北纬41.49东经126.53吉林省梅河口的经纬度北纬42.32东经125.40 吉林省舒兰的经纬度北纬44.24东经126.57吉林省四平的经纬度北纬43.10东经124.22吉林省松原的经纬度北纬45.11东经124.49吉林省洮南的经纬度北纬45.20东经122.47吉林省通化的经纬度北纬41.43东经125.56吉林省图们的经纬度北纬42.57东经129.51吉林省延吉的经纬度北纬42.54东经129.30吉林省愉树的经纬度北纬44.49东经126.3210 黑龙江省黑龙江省哈尔滨的经纬度北纬45.44东经126.36 黑龙江省阿城的经纬度北纬45.32东经126.58 黑龙江省安达的经纬度北纬46.24东经125.18 黑龙江省北安的经纬度北纬48.15东经126.31 黑龙江省大庆的经纬度北纬46.36东经125.01 黑龙江省富锦的经纬度北纬47.15东经132.02 黑龙江省海林的经纬度北纬44.35东经129.21 黑龙江省海伦的经纬度北纬47.28东经126.57 黑龙江省鹤岗的经纬度北纬47.20东经130.16 黑龙江省黑河的经纬度北纬50.14东经127.29 黑龙江省佳木斯的经纬度北纬46.47东经130.22黑龙江省密山的经纬度北纬45.32东经131.50黑龙江省牡丹江的经纬度北纬44.35东经129.36 黑龙江省讷河的经纬度北纬48.29东经124.51黑龙江省宁安的经纬度北纬44.21东经129.28黑龙江省齐齐哈尔的经纬度北纬47.20东经123.57 黑龙江省七台河的经纬度北纬45.48东经130.49 黑龙江省双城的经纬度北纬45.22东经126.15黑龙江省尚志的经纬度北纬45.14东经127.55黑龙江省双鸭山的经纬度北纬46.38东经131.11 黑龙江省绥芬河的经纬度北纬44.25东经131.11 黑龙江省绥化的经纬度北纬46.38东经126.59黑龙江省铁力的经纬度北纬46.59东经128.01黑龙江省同江的经纬度北纬47.39东经132.30黑龙江省五常的经纬度北纬44.55东经127.11黑龙江省五大连池的经纬度北纬48.38东经126.07 黑龙江省伊春的经纬度北纬47.42东经128.56黑龙江省肇东的经纬度北纬46.04东经125.5811 江苏省江苏省南京的经纬度北纬32.03东经118.46江苏省常熟的经纬度北纬31.39东经120.43江苏省常州的经纬度北纬31.47东经119.58江苏省东台的经纬度北纬32.51东经120.19 江苏省高邮的经纬度北纬32.47东经119.27 江苏省海门的经纬度北纬31.53东经121.09 江苏省淮安的经纬度北纬33.30东经119.09 江苏省淮阴的经纬度北纬33.36东经119.02 江苏省江都的经纬度北纬32.26东经119.32 江苏省姜堰的经纬度北纬32.34东经120.08 江苏省江阴的经纬度北纬31.54东经120.17 江苏省靖江的经纬度北纬32.02东经120.17 江苏省金坛的经纬度北纬31.46东经119.33 江苏省昆山的经纬度北纬31.23东经120.57 江苏省连去港的经纬度北纬34.36东经119.10 江苏省溧阳的经纬度北纬31.26东经119.29 江苏省南通的经纬度北纬32.01东经120.51 江苏省邳州的经纬度北纬34.19东经117.59 江苏省启乐的经纬度北纬31.48东经121.39 江苏省如皋的经纬度北纬32.23东经120.33 江苏省宿迁的经纬度北纬33.58东经118.18 江苏省苏州的经纬度北纬31.19东经120.37 江苏省太仓的经纬度北纬31.27东经121.06 江苏省泰兴的经纬度北纬32.10东经120.01江苏省通州的经纬度北纬32.05东经121.03 江苏省吴江的经纬度北纬31.10东经120.39 江苏省无锡的经纬度北纬31.34东经120.18 江苏省兴化的经纬度北纬32.56东经119.50 江苏省新沂的经纬度北纬34.22东经118.20 江苏省徐州的经纬度北纬34.15东经117.11 江苏省盐在的经纬度北纬33.22东经120.08 江苏省扬中的经纬度北纬32.14东经119.49 江苏省扬州的经纬度北纬32.23东经119.26 江苏省宜兴的经纬度北纬31.21东经119.49 江苏省仪征的经纬度北纬32.16东经119.10 江苏省张家港的经纬度北纬31.52东经120.32 江苏省镇江的经纬度北纬32.11东经119.27 12 浙江省浙江省杭州的经纬度北纬30.16东经120.10 浙江省慈溪的经纬度北纬30.11东经121.15 浙江省东阳的经纬度北纬29.16东经120.14 浙江省奉化的经纬度北纬29.39东经121.24 浙江省富阳的经纬度北纬30.03东经119.57 浙江省海宁的经纬度北纬30.32东经120.42 浙江省湖州的经纬度北纬30.52东经120.06浙江省江山的经纬度北纬28.45东经118.37 浙江省嘉兴的经纬度北纬30.46东经120.45 浙江省金华的经纬度北纬29.07东经119.39 浙江省兰溪的经纬度北纬29.12东经119.28 浙江省临海的经纬度北纬28.51东经121.08 浙江省丽水的经纬度北纬28.27东经119.54 浙江省龙泉的经纬度北纬28.04东经119.08 浙江省宁波的经纬度北纬29.52东经121.33 浙江省平湖的经纬度北纬30.42东经121.01 浙江省衢州的经纬度北纬28.58东经118.52 浙江省瑞安的经纬度北纬27.48东经120.38 浙江省上虞的经纬度北纬30.01东经120.52 浙江省绍兴的经纬度北纬30.00东经120.34 浙江省台州的经纬度北纬28.41东经121.27 浙江省桐乡的经纬度北纬30.38东经120.32 浙江省温岭的经纬度北纬28.22东经121.21 浙江省温州的经纬度北纬28.01东经120.39 浙江省萧山的经纬度北纬30.09东经120.16 浙江省义乌的经纬度北纬29.18东经120.04 浙江省乐清的经纬度北纬28.08东经120.58 浙江省余杭的经纬度北纬30.26东经120.18浙江省永康的经纬度北纬29.54东经120.01 浙江省舟山的经纬度北纬30.01东经122.06 浙江省诸暨的经纬度北纬29.43东经120.14 13 安徽省安徽省合肥的经纬度北纬31.52东经117.17 安徽省安庆的经纬度北纬30.31东经117.02 安徽省蚌埠的经纬度北纬32.56东经117.21 安徽省亳州的经纬度北纬33.52东经115.47 安徽省巢湖的经纬度北纬31.36东经117.52 安徽省滁州的经纬度北纬32.18东经118.18 安徽省阜阳的经纬度北纬32.54东经115.48 安徽省贵池的经纬度北纬30.39东经117.28 安徽省淮北的经纬度北纬33.57东经116.47 安徽省淮南的经纬度北纬32.37东经116.58 安徽省黄山的经纬度北纬29.43东经118.18 安徽省界首的经纬度北纬33.15东经115.21 安徽省六安的经纬度北纬31.44东经116.28 安徽省马鞍山的经纬度北纬31.43东经118.28 安徽省明光的经纬度北纬32.47东经117.58 安徽省宿州的经纬度北纬33.38东经116.58 安徽省天长的经纬度北纬32.41东经118.59安徽省芜湖的经纬度北纬31.19东经118.22 安徽省宣州的经纬度北纬30.57东经118.44 14 福建省福建省福州的经纬度北纬26.05东经119.18 福建省长乐的经纬度北纬25.58东经119.31 福建省福安的经纬度北纬27.06东经119.39 福建省福清的经纬度北纬25.42东经119.23 福建省建瓯的经纬度北纬27.03东经118.20 福建省建阳的经纬度北纬27.21东经118.07 福建省晋江的经纬度北纬24.49东经118.35 福建省龙海的经纬度北纬24.26东经117.48 福建省龙岩的经纬度北纬25.06东经117.01 福建省南安的经纬度北纬24.57东经118.23 福建省南平的经纬度北纬26.38东经118.10 福建省宁德的经纬度北纬26.39东经119.31 福建省莆田的经纬度北纬24.26东经119.01 福建省泉州的经纬度北纬24.56东经118.36 福建省三明的经纬度北纬26.13东经117.36 福建省邵武的经纬度北纬27.20东经117.29 福建省石狮的经纬度北纬24.44东经118.38 福建省武夷山的经纬度北纬27.46东经118.02福建省永安的经纬度北纬25.58东经117.23 福建省漳平的经纬度北纬25.17东经117.24 福建省漳州的经纬度北纬24.31东经117.39 15 江西省江西省南昌的经纬度北纬28.40东经115.55 江西省德兴的经纬度北纬28.57东经117.35 江西省丰城的经纬度北纬28.12东经115.48 江西省赣州的经纬度北纬28.52东经114.56 江西省高安的经纬度北纬28.25东经115.22 江西省吉安的经纬度北纬27.07东经114.58 江西省景德镇的经纬度北纬29.17东经117.13 江西省井冈山的经纬度北纬26.34东经114.10 江西省九江的经纬度北纬29.43东经115.58 江西省乐平的经纬度北纬28.58东经117.08 江西省临川的经纬度北纬27.59东经116.21 江西省萍乡的经纬度北纬27.37东经113.50 江西省瑞昌的经纬度北纬29.40东经115.38 江西省瑞金的经纬度北纬25.53东经116.01 江西省上饶的经纬度北纬25.27东经117.58 江西省新余的经纬度北纬27.48东经114.56 江西省宜春的经纬度北纬27.47东经114.23江西省樟树的经纬度北纬28.03东经115.32 16 山东省山东省济南的经纬度北纬36.40东经117.00 山东省安丘的经纬度北纬36.25东经119.12 山东省滨州的经纬度北纬37.22东经118.02 山东省昌邑的经纬度北纬39.52东经119.24 山东省德州的经纬度北纬37.26东经116.17 山东省东营的经纬度北纬37.27东经118.30 山东省肥城的经纬度北纬36.14东经116.46 山东省高密的经纬度北纬36.22东经119.44 山东省菏泽的经纬度北纬35.14东经115.26 山东省胶南的经纬度北纬35.53东经119.58 山东省胶州的经纬度北纬36.17东经120.00 山东省即墨的经纬度北纬36.22东经120.28 山东省济宁的经纬度北纬35.23东经116.33 山东省莱芜的经纬度北纬36.12东经117.40 山东省莱西的经纬度北纬36.52东经120.31 山东省莱阳的经纬度北纬36.58东经120.42 山东省莱州的经纬度北纬37.10东经119.57 山东省乐陵的经纬度北纬37.44东经117.12 山东省聊城的经纬度北纬36.26东经115.57山东省临沂的经纬度北纬35.03东经118.20 山东省龙口的经纬度北纬37.39东经120.21 山东省蓬莱的经纬度北纬37.48东经120.45 山东省平度的经纬度北纬36.47东经119.58 山东省青岛的经纬度北纬36.03东经120.18 山东省青州的经纬度北纬36.42东经118.28 山东省曲阜的经纬度北纬35.36东经116.58 山东省日照的经纬度北纬35.23东经119.32 山东省荣成的经纬度北纬37.10东经122.25 山东省乳山的经纬度北纬36.54东经121.31 山东省寿光的经纬度北纬36.53东经118.44 山东省泰安的经纬度北纬36.11东经117.08 山东省滕州的经纬度北纬35.06东经117.09 山东省潍坊的经纬度北纬36.43东经119.06 山东省威海的经纬度北纬37.31东经122.07 山东省文登的经纬度北纬37.12东经122.03 山东省新泰的经纬度北纬35.54东经117.45 山东省烟台的经纬度北纬37.32东经121.24 山东省兖州的经纬度北纬35.32东经116.49 山东省禹城的经纬度北纬36.56东经116.39 山东省枣庄的经纬度北纬34.52东经117.33山东省招远的经纬度北纬37.21东经120.23 山东省诸城的经纬度北纬35.59东经119.24 山东省淄博的经纬度北纬36.48东经118.03 山东省邹城的经纬度北纬35.24东经116.58 17 河南省河南省郑州的经纬度北纬34.46东经11340 河南省安阳的经纬度北纬36.06东经114.21 河南省长葛的经纬度北纬34.12东经113.47 河南省登封的经纬度北纬34.27东经113.02 河南省邓州的经纬度北纬32.42东经112.05 河南省巩义的经纬度北纬34.46东经112.58 河南省鹤壁的经纬度北纬35.54东经114.11 河南省辉县的经纬度北纬35.27东经113.47 河南省焦作的经纬度北纬35.14东经113.12 河南省济源的经纬度北纬35.04东经112.35 河南省开封的经纬度北纬34.47东经114.21 河南省灵宝的经纬度北纬34.31东经110.52 河南省林州的经纬度北纬36.03东经113.49 河南省漯河的经纬度北纬33.33东经114.02 河南省洛阳的经纬度北纬34.41东经112.27 河南省南阳的经纬度北纬33.00东经112.32河南省濮阳的经纬度北纬35.44东经115.01 河南省沁阳的经纬度北纬35.05东经112.57 河南省汝州的经纬度北纬34.09东经112.50 河南省三门峡的经纬度北纬34.47东经111.12 河南省商丘的经纬度北纬34.26东经115.38 河南省卫辉的经纬度北纬35.24东经114.03 河南省舞钢的经纬度北纬33.17东经113.30 河南省项城的经纬度北纬33.26东经114.54 河南省荥阳的经纬度北纬34.46东经113.21 河南省新密的经纬度北纬34.31东经113.22 河南省新乡的经纬度北纬35.18东经113.52 河南省信阳的经纬度北纬32.07东经114.04 河南省新郑的经纬度北纬34.24东经113.43 河南省许昌的经纬度北纬34.01东经113.49 河南省偃师的经纬度北纬34.43东经112.47 河南省义马的经纬度北纬34.43东经111.55 河南省禹州的经纬度北纬34.09东经113.28 河南省周口的经纬度北纬33.37东经114.38 河南省驻马店的经纬度北纬32.58东经114.01 18 湖北省湖北省武汉的经纬度北纬30.35东经114.17湖北省当阳的经纬度北纬30.50东经111.47 湖北省丹江口的经纬度北纬32.33东经108.30 湖北省大冶的经纬度北纬30.06东经114.58 湖北省恩施的经纬度北纬30.16东经109.29 湖北省鄂州的经纬度北纬30.23东经114.52 湖北省广水的经纬度北纬31.37东经113.48 湖北省洪湖的经纬度北纬29.48东经113.27 湖北省黄石的经纬度北纬30.12东经115.06 湖北省黄州的经纬度北纬30.27东经114.52 湖北省荆门的经纬度北纬31.02东经112.12 湖北省荆沙的经纬度北纬30.18东经112.16 湖北省老河口的经纬度北纬32.23东经111.40 湖北省利川的经纬度北纬30.18东经108.56 湖北省麻城的经纬度北纬31.10东经115.01 湖北省浦圻的经纬度北纬29.42东经113.51 湖北省潜江的经纬度北纬30.26东经112.53 湖北省石首的经纬度北纬29.43东经112.24 湖北省十堰的经纬度北纬32.40东经110.47 湖北省随州的经纬度北纬31.42东经113.22 湖北省天门的经纬度北纬60.39东经113.10 湖北省武穴的经纬度北纬29.51东经115.33湖北省咸宁的经纬度北纬29.53东经114.17 湖北省仙桃的经纬度北纬30.22东经113.27 湖北省孝感的经纬度北纬30.56东经113.54 湖北省宜昌的经纬度北纬30.42东经111.17 湖北省宜城的经纬度北纬31.42东经112.15 湖北省应城的经纬度北纬30.57东经113.33 湖北省枣阳的经纬度北纬32.07东经112.44 湖北省枝城的经纬度北纬30.23东经111.27 湖北省钟祥的经纬度北纬31.10东经112.34 19 湖南省湖南省长沙的经纬度北纬28.12东经112.59 湖南省常德的经纬度北纬29.02东经111.51 湖南省郴州的经纬度北纬25.46东经113.02 湖南省衡阳的经纬度北纬26.53东经112.37 湖南省洪江的经纬度北纬27.07东经109.59 湖南省怀化的经纬度北纬27.33东经109.58 湖南省津市的经纬度北纬29.38东经111.52 湖南省吉首的经纬度北纬28.18东经109.43 湖南省耒阳的经纬度北纬26.24东经112.51 湖南省冷水江的经纬度北纬27.42东经111.26 湖南省冷水滩的经纬度北纬26.26东经111.35湖南省醴陵的经纬度北纬27.40东经113.30 湖南省临湘的经纬度北纬29.29东经113.27 湖南省浏阳的经纬度北纬28.09东经113.37 湖南省娄底的经纬度北纬27.44东经111.59 湖南省汨罗的经纬度北纬28.49东经113.03 湖南省韶山的经纬度北纬27.54东经112.29 湖南省邵阳的经纬度北纬27.14东经111.28 湖南省武冈的经纬度北纬26.43东经110.37 湖南省湘潭的经纬度北纬27.52东经112.53 湖南省湘乡的经纬度北纬27.44东经112.31 湖南省益阳的经纬度北纬28.36东经112.20 湖南省永州的经纬度北纬26.13东经111.37 湖南省沅江的经纬度北纬28.50东经112.22 湖南省岳阳的经纬度北纬29.22东经113.06 湖南省张家界的经纬度北纬29.08东经110.29 湖南省株洲的经纬度北纬27.51东经113.09 湖南省资兴的经纬度北纬25.58东经113.13 20 广东省广东省广州的经纬度北纬23.08东经113.14 广东省潮阳的经纬度北纬23.16东经116.36 广东省潮州的经纬度北纬23.40东经116.38广东省从化的经纬度北纬23.33东经113.33 广东省东莞的经纬度北纬23.02东经113.45 广东省恩平的经纬度北纬22.12东经112.19 广东省佛山的经纬度北纬23.02东经113.06 广东省高明的经纬度北纬22.53东经112.50 广东省高要的经纬度北纬23.02东经112.26 广东省高州的经纬度北纬21.54东经110.50 广东省鹤山的经纬度北纬22.46东经112.57 广东省河源的经纬度北纬23.43东经114.41 广东省花都的经纬度北纬23.23东经113.12 广东省化州的经纬度北纬21.39东经110.37 广东省惠阳的经纬度北纬22.48东经114.28 广东省惠州的经纬度北纬23.05东经114.22 广东省江门的经纬度北纬22.35东经113.04 广东省揭阳的经纬度北纬22.32东经116.21 广东省开平的经纬度北纬22.22东经112.40 广东省乐昌的经纬度北纬25.09东经113.21 广东省雷州的经纬度北纬20.54东经110.04 广东省廉江的经纬度北纬21.37东经110.17 广东省连州的经纬度北纬24.48东经112.23 广东省罗定的经纬度北纬22.46东经111.33广东省梅州的经纬度北纬24.19东经116.07 广东省南海的经纬度北纬23.01东经113.09 广东省番禺的经纬度北纬22.57东经113.22 广东省普宁的经纬度北纬23.18东经116.10 广东省清远的经纬度北纬23.42东经113.01 广东省三水的经纬度北纬23.10东经112.52 广东省汕头的经纬度北纬23.22东经116.41 广东省汕尾的经纬度北纬22.47东经115.21 广东省韶关的经纬度北纬24.48东经113.37 广东省深圳的经纬度北纬22.33东经114.07 广东省顺德的经纬度北纬22.50东经113.15 广东省四会的经纬度北纬23.21东经112.41 广东省台山的经纬度北纬22.15东经112.48 广东省吴川的经纬度北纬21.26东经110.47 广东省新会的经纬度北纬22.32东经113.01 广东省兴宁的经纬度北纬24.09东经115.43 广东省阳春的经纬度北纬22.10东经111.48 广东省阳江的经纬度北纬21.50东经111.58 广东省英德的经纬度北纬24.10东经113.22 广东省云浮的经纬度北纬22.57东经112.02 广东省增城的经纬度北纬23.18东经113.49广东省肇庆的经纬度北纬23.03东经112.27广东省中山的经纬度北纬22.31东经113.22广东省珠海的经纬度北纬22.17东经113.3421 广西自治区广西自治区南宁的经纬度北纬22.48东经108.19 广西自治区北海的经纬度北纬21.28东经109.07 广西自治区北流的经纬度北纬22.42东经110.21 广西自治区百色的经纬度北纬23.54东经106.36 广西自治区防城港的经纬度北纬21.37东经108.20 广西自治区贵港的经纬度北纬23.06东经109.36 广西自治区桂林的经纬度北纬25.17东经110.17 广西自治区桂平的经纬度北纬23.22东经110.04 广西自治区河池的经纬度北纬24.42东经108.03 广西自治区合山的经纬度北纬23.47东经108.52 广西自治区柳州的经纬度北纬23.19东经109.24 广西自治区赁祥的经纬度北纬22.07东经106.44 广西自治区钦州的经纬度北纬21.57东经108.37 广西自治区梧州的经纬度北纬23.29东经111.20 广西自治区玉林的经纬度北纬22.38东经110.09 广西自治区宜州的经纬度北纬24.28东经108.40 22 海南省海南省儋州的经纬度北纬19.31东经109.34 海南省琼海的经纬度北纬19.14东经110.28 海南省琼山的经纬度北纬19.59东经110.21 海南省三亚的经纬度北纬18.14东经109.31 海南省通什的经纬度北纬18.46东经109.31 23 四川省四川省成都的经纬度北纬30.40东经104.04 四川省巴中的经纬度北纬31.51东经106.43 四川省崇州的经纬度北纬30.39东经103.40 四川省达川的经纬度北纬31.14东经107.29 四川省德阳的经纬度北纬31.09东经104.22 四川省都江堰的经纬度北纬31.01东经103.37 四川省峨眉山的经纬度北纬29.36东经103.29 四川省涪陵的经纬度北纬29.42东经107.22 四川省广汉的经纬度北纬30.58东经104.15 四川省广元的经纬度北纬32.28东经105.51 四川省华蓥的经纬度北纬30.26东经106.44 四川省简阳的经纬度北纬30.24东经104.32 四川省江油的经纬度北纬31.48东经104.42 四川省阆中的经纬度北纬31.36东经105.58 四川省乐山的经纬度北纬29.36东经103.44四川省绵阳的经纬度北纬31.30东经104.42 四川省南充的经纬度北纬30.49东经106.04 四川省内江的经纬度北纬29.36东经105.02 四川省攀枝花的经纬度北纬26.34东经101.43 四川省彭州的经纬度北纬30.59东经103.57 四川省邛崃的经纬度北纬30.26东经103.28 四川省遂宁的经纬度北纬30.31东经105.33 四川省万县的经纬度北纬30.50东经108.21 四川省万源的经纬度北纬32.03东经108.03 四川省西昌的经纬度北纬27.54东经102.16 四川省雅安的经纬度北纬29.59东经102.59 四川省宜宾的经纬度北纬28.47东经104.34 四川省自贡的经纬度北纬29.23东经104.46 四川省资阳的经纬度北纬30.09东经104.38 24 贵州省贵州省贵阳的经纬度北纬26.35东经106.42 贵州省安顺的经纬度北纬26.14东经105.55 贵州省毕节的经纬度北纬27.18东经105.18 贵州省赤水的经纬度北纬28.34东经105.42 贵州省都匀的经纬度北纬26.15东经107.31 贵州省凯里的经纬度北纬26.35东经107.58。
中国主要城市经纬度

中国主要城市经纬度中国主要城市经纬度北京直辖市116°28′E39°54′N上海直辖市121°29′E31°14′N天津直辖市117°11′E39°09′N重庆直辖市106°32′E29°32′N香港特别行政区114°10′E22°18′N黑龙江省:经度纬度哈尔滨126°41′E45°45′N齐齐哈尔123°54′E47°19′N牡丹江129°34′E44°35′N北安126°30′E48°14′N伊春128°55′E47°42′N鹤岗130°16′E47°23′N鸡西130°58′E45°17′N佳木斯130°22′E46°49′N双鸭山131°21′E46°36′N爱辉127°31′E50°10′N吉林省:经度纬度长春125°19′E43°52′N四平124°20′E43°11′N辽源125°05′E42°55′N通化125°53′E41°46′N吉林126°32′E43°52′N延吉129°29′E42°57′N辽宁省:经度纬度沈阳123°24′E41°50′N朝阳120°25′E41°32′N锦州121°05′E41°07′N阜新121°43′E42°03′N营口122°12′E40°41′N本溪 123°47′E41°18′N鞍山122°56′E41°08′N辽阳123°10′E41°17′N抚顺123°53′E41°50′N丹东124°22′E40°08′N内蒙古自治区:经度纬度呼和浩特111°48′E40°49′N 赤峰119°E42°16′N锡林浩特116°06′E43°57′N 包头109°58′E40°35′N通辽122°13′E33°39′N巴彦浩特105°41′E38°49′N 海拉尔119°40′E49°15′N 牙克石120°41′E49°17′N 河北省:经度纬度石家庄114°28′E38°02′N 保定115°28′E38°52′ N唐山118°12′E39°37′N承德117°51′E40°57′N张家口114°53′E40°50′N 沧县116°51′E38°18′N邢台114°29′E37°03′N邯郸114°27′E36°35′N山西省:经度纬度太原112°34′E37°52′N大同113°16′E40°05′N阳泉113°36′E37°53′N长治113°06′E36°10′N 侯马111°20′E35°37′N 山东省:经度纬度济南117°E 36° 38′N临沂118°22′E38°52′N 聊城115°57′E36°27′N 淄博117°50′E36°30′N 潍坊119°03′E36°42′N 烟台121°20′E37°33′N 青岛120°18′E36°04′N 河南省:经度纬度郑州113°42′E34°48′N 南阳112°31′E33°01′N 陕西省:经度纬度西安108°54′E34°16′N 榆林109°45′E38°17′N 延安109°28′E36°36′N 铜川109°08′E35°03′N 商县109°55′E33°56′N 咸阳108°42′E34°21′N 宝鸡107°08′E34°23′N 安康109°E32°42′N 汉中107°01′E33°03′N 甘肃省:经度纬度兰州103°49′E36°03′N 玉门97°46′E39°51′N 白银104°09′E36°41′N 定西104°36′E35°35′N 天水105°41′E34°14′N张掖100°28′E38°55′N宁夏回族自治区:经度纬度银川106°16′E38°20′N青海省:经度纬度西宁101°45′E36°38′N苏西克94°08′E38°24′N玉树E96°39′E33°01′N新疆自治区:经度纬度乌鲁木齐87°36′E43°48′N 哈密93°32′E42°49′N阿勒泰88°07′E47°55′N若羌88°09′E39° N昌吉87°19′E44°02′N焉耆86°31′E42°03′N塔城83°E46°45′N博乐82°05′E44°53′N伊宁E81°26′E43°57′N阿克苏80°18′E41°09′N和田79°56′E37°05′N喀什76°E 39°31′N安徽省:经度纬度合肥117°18′E31°51′N淮南117°E21°51′N六安116°30′E31°44′N马鞍山118°28′E31°42′N 芜湖118°22′E31°21′N安庆117°01′E 30°31′N屯溪118°16′E29°43′N阜阳115°48′E32°55′N江苏省:经度纬度南京118°50′E32°02′N 连云港119°12′E34°39′N 徐州117°11′E34°15′N 淮阴119°01′E33°34′N 扬州119°25′E32°23′N 镇江119°24′E32°12′N 常州119°58′E31°48′N 南通120°53′E32°03′N 无锡120°17′E31°35′N 苏州120°37′E31°18′N 浙江省:经度纬度杭州120°09′E30°14′N 湖州120°04′E20°52′N 宁波121°31′E29°52′N 金华119°39′E29°06′N 温州120°39′E28°01′N 湖南省:经度纬度长沙113°E28°11′N常德111°41′E29°03′N 湘潭112°54′E27°52′N 株洲113°10′E27°50′N 吉首109°43′E28°29′N 邵阳111°27′E27°12′N 衡阳112°35′E26°56′N 黔阳110°07′E27°20′N 郴州112°59′E25°48′N 江西省:经度纬度南昌115°52′E28°41′N 九江115°58′E29°43′N景德镇117°11′E29°18′N 上饶117°58′E28°27′N 抚州116°19′E28°01′N 宜春114°23′E27°49′N 萍乡113°49′E27°36′N 吉安114°59′E27°05′N 赣州114°55′E25°53′N 湖北省:经度纬度武汉114°21′E30°37′N 恩施109°29′E30°16′N 黄石115°04′E30°12′N 四川省:经度纬度成都104°05′E30°39′N 万县108°20′E30°48′N 达县107°29′E31°13′N 温江103°55′E30°44′N 阿坝101°43′E32°53′N 内江105°03′E29°35′N 马尔康102°20′E31°47′N 自贡104°45′E29°23′N 乐山103°43′E29°35′N 宜宾104°36′E28°46′N 南充106°04′E30°48′N 康定101°58′E30°03′N 甘孜99°58′E31°38′N 昭觉102°51′E28°03′N 西昌102°16′E27°55′N 涪陵107°22′E29°42′N 贵州省:经度纬度遵义106°53′E27°42′N福建省:经度纬度福州119°18′E26°05′N福安119°40′E27°07′N南平118°09′E26°38′N闽侯119°18′E26°N三明117°36′E26°13′N龙岩117°02′E25°08′N泉州118°40′E24°59′N漳州117°39′E24°32′N厦门118°06′E24°29′N台湾省:经度纬度台北121°31′E25°03′N高雄120°19′E22°37′N广东省:经度纬度广州113°15′E23°08′N韶关113°40′E24°53′N汕头116°40′E23°22′N湛江110°23′E21°11′N海南省:经度纬度海口110°20′E20°02′N广西壮族自治区:经度纬度南宁108°20′E22°48′N桂林110°15′E25°18′N柳州109°23′E24°19′N梧州111°20′E23°30′N百色106°36′E23°55′N玉林110°09′E22°39′N云南省:经度纬度昆明102°41′E25°N大理100°10′E25°43′N 下关100°13′E25°35′N 潞西98°32′E24°24′N 景洪100°47′E21°57′N 西藏自治区:经度纬度拉萨91°10′E29°40′N昌都97°14′E31°05′N曼尼87°10′E34°46′ N 日喀则88°53′E29°19′N 亚东88°51′E27°25′N改则85°20′E32°07′N 多木拉E82°26′E34°09′N 噶大克80°21′E31°44′N。
中国各主要城市经纬度坐标

中国各主要城市经纬度坐标中国各主要大城市经纬度数据1、中国各主要大城市经纬度数据:市市中心经纬度:<116.41667,39.91667>##市区经纬度:<121.43333,34.50000>##市区经纬度:<117.20000,39.13333>##经纬度:<114.10000,22.20000>广州经纬度:<113.23333,23.16667>珠海经纬度:<113.51667,22.30000>##经纬度:<114.06667,22.61667>杭州经纬度:<120.20000,30.26667>重庆市区经纬度:<106.45000, 29.56667>青岛经纬度:<120.33333,36.06667>厦门经纬度:<118.10000,24.46667>兰州经纬度:<103.73333,36.03333>贵阳经纬度:<106.71667,26.56667>长沙经纬度:<113.00000,28.21667>南京经纬度:<118.78333,32.05000>##经纬度:<115.90000,28.68333>沈阳经纬度:<123.38333,41.80000>太原经纬度:<112.53333,37.86667>成都经纬度:<104.06667,30.66667>##经纬度:<91.00000,29.60000>乌鲁木齐经纬度:<87.68333,43.76667>昆明经纬度:<102.73333,25.05000>西安经纬度:<108.95000,34.26667>西宁经纬度:<101.75000,36.56667>银川经纬度:<106.26667,38.46667>兰浩特经纬度:<122.08333,46.06667>哈尔滨经纬度:<126.63333,45.75000>武汉经纬度:<114.31667,30.51667>郑州经纬度:<113.65000,34.76667>石家庄经纬度:<114.48333,38.03333>##经纬度:<109.50000,18.20000>海口经纬度:<110.35000,20.01667>澳门经纬度:<113.50000,22.20000>2、中国主要城市经纬度查询<精确到二级省市>:所在省城市名纬度经度##省合肥北纬31.52 东经117.17##省安庆北纬30.31 东经117.02##省蚌埠北纬32.56 东经117.21##省亳州北纬33.52 东经115.47##省巢湖北纬31.36 东经117.52##省滁州北纬32.18 东经118.18##省阜阳北纬32.54 东经115.48##省淮北北纬33.57 东经116.47##省淮南北纬32.37 东经116.58##省黄山北纬29.43 东经118.18##省界首北纬33.15 东经115.21##省六安北纬31.44 东经116.28##省马鞍山北纬31.43 东经118.28 ##省明光北纬32.47 东经117.58##省宿州北纬33.38 东经116.58##省天长北纬32.41 东经118.59##省铜陵北纬30.56 东经117.48##省芜湖北纬31.19 东经118.22##省宣州北纬30.57 东经118.44澳门澳门市北纬21.33 东经115.07市市北纬39.55 东经116.24##省福州北纬26.05 东经119.18##省长乐北纬25.58 东经119.31##省福清北纬25.42 东经119.23##省建瓯北纬27.03 东经118.20##省建阳北纬27.21 东经118.07##省晋江北纬24.49 东经118.35##省龙海北纬24.26 东经117.48##省龙岩北纬25.06 东经117.01##省南安北纬24.57 东经118.23##省南平北纬26.38 东经118.10##省宁德北纬26.39 东经119.31 ##省莆田北纬24.26 东经119.01##省泉州北纬24.56 东经118.36##省三明北纬26.13 东经117.36##省石狮北纬24.44 东经118.38##省武夷山北纬27.46 东经118.02 ##省厦门北纬24.27 东经118.06##省永安北纬25.58 东经117.23##省漳平北纬25.17 东经117.24##省漳州北纬24.31 东经117.39甘肃省兰州北纬36.04 东经103.51甘肃省白银北纬36.33 东经104.12甘肃省敦煌北纬40.08 东经94.41甘肃省嘉峪关北纬39.48 东经98.14甘肃省金昌北纬38.28 东经102.10甘肃省酒泉北纬39.44 东经98.31甘肃省临夏北纬35.37 东经103.12甘肃省平凉北纬35.32 东经106.40甘肃省天水北纬34.37 东经105.42甘肃省武威北纬37.56 东经102.39甘肃省玉门北纬39.49 东经97.35甘肃省张掖北纬38.56 东经100.26广东省广州北纬23.08 东经113.14广东省潮阳北纬23.16 东经116.36广东省潮州北纬23.40 东经116.38广东省澄海北纬23.28 东经116.46广东省从化北纬23.33 东经113.33广东省东莞北纬23.02 东经113.45广东省恩平北纬22.12 东经112.19广东省佛山北纬23.02 东经113.06广东省高明北纬22.53 东经112.50广东省高要北纬23.02 东经112.26广东省高州北纬21.54 东经110.50广东省鹤山北纬22.46 东经112.57广东省河源北纬23.43 东经114.41广东省花都北纬23.23 东经113.12广东省惠阳北纬22.48 东经114.28广东省惠州北纬23.05 东经114.22广东省江门北纬22.35 东经113.04广东省揭阳北纬22.32 东经116.21广东省开平北纬22.22 东经112.40广东省乐昌北纬25.09 东经113.21广东省雷州北纬20.54 东经110.04广东省廉江北纬21.37 东经110.17广东省连州北纬24.48 东经112.23广东省罗定北纬22.46 东经111.33广东省## 北纬21.40 东经110.53广东省梅州北纬24.19 东经116.07广东省南海北纬23.01 东经113.09广东省番禺北纬22.57 东经113.22广东省普宁北纬23.18 东经116.10广东省清远北纬23.42 东经113.01广东省汕头北纬23.22 东经116.41广东省汕尾北纬22.47 东经115.21广东省韶关北纬24.48 东经113.37广东省## 北纬22.33 东经114.07广东省顺德北纬22.50 东经113.15广东省四会北纬23.21 东经112.41广东省台山北纬22.15 东经112.48广东省吴川北纬21.26 东经110.47广东省新会北纬22.32 东经113.01广东省兴宁北纬24.09 东经115.43广东省阳春北纬22.10 东经111.48广东省阳江北纬21.50 东经111.58广东省英德北纬24.10 东经113.22广东省云浮北纬22.57 东经112.02广东省增城北纬23.18 东经113.49广东省湛江北纬21.11 东经110.24广东省肇庆北纬23.03 东经112.27广东省中山北纬22.31 东经113.22广东省珠海北纬22.17 东经113.34##自治区南宁北纬22.48 东经108.19 ##自治区北海北纬21.28 东经109.07 ##自治区北流北纬22.42 东经110.21 ##自治区百色北纬23.54 东经106.36 ##自治区防城港北纬21.37 东经108.20 ##自治区贵港北纬23.06 东经109.36 ##自治区桂林北纬25.17 东经110.17 ##自治区桂平北纬23.22 东经110.04 ##自治区河池北纬24.42 东经108.03 ##自治区合山北纬23.47 东经108.52##自治区赁祥北纬22.07 东经106.44 ##自治区钦州北纬21.57 东经108.37 ##自治区梧州北纬23.29 东经111.20 ##自治区玉林北纬22.38 东经110.09 ##自治区宜州北纬24.28 东经108.40贵州省贵阳北纬26.35 东经106.42贵州省安顺北纬26.14 东经105.55贵州省毕节北纬27.18 东经105.18贵州省赤水北纬28.34 东经105.42贵州省都匀北纬26.15 东经107.31贵州省凯里北纬26.35 东经107.58贵州省六盘水北纬26.35 东经104.50贵州省清镇北纬26.33 东经106.27贵州省铜仁北纬27.43 东经109.12贵州省兴义北纬25.05 东经104.53贵州省遵义北纬27.42 东经106.55海南省儋州北纬19.31 东经109.34海南省琼海北纬19.14 东经110.28海南省琼山北纬19.59 东经110.21海南省## 北纬18.14 东经109.31海南省通什北纬18.46 东经109.31 ##省石家庄北纬38.02 东经114.30 ##省安国北纬38.24 东经115.20 ##省保定北纬38.51 东经115.30 ##省霸州北纬39.06 东经116.24 ##省泊头北纬38.04 东经116.34 ##省沧州北纬38.18 东经116.52 ##省承德北纬40.59 东经117.57 ##省定州北纬38.30 东经115.00 ##省丰南北纬39.34 东经118.06 ##省高碑店北纬39.20 东经115.51 ##省蒿城北纬38.02 东经114.50##省河间北纬38.26 东经116.05 ##省衡水北纬37.44 东经115.42 ##省黄骅北纬38.21 东经117.21 ##省晋州北纬38.02 东经115.02 ##省冀州北纬37.34 东经115.33 ##省廓坊北纬39.31 东经116.42 ##省鹿泉北纬38.04 东经114.19 ##省南宫北纬37.22 东经115.23 ##省秦皇岛北纬39.55 东经119.35 ##省任丘北纬38.42 东经116.07 ##省三河北纬39.58 东经117.04 ##省沙河北纬36.51 东经114.30 ##省深州北纬38.01 东经115.32 ##省唐山北纬39.36 东经118.11 ##省武安北纬36.42 东经114.11 ##省邢台北纬37.04 东经114.30##省新乐北纬38.20 东经114.41 ##省## 北纬40.48 东经114.53##省涿州北纬39.29 东经115.59 ##省遵化北纬40.11 东经117.58河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21河南省长葛北纬34.12 东经113.47河南省登封北纬34.27 东经113.02河南省邓州北纬32.42 东经112.05河南省巩义北纬34.46 东经112.58河南省鹤壁北纬35.54 东经114.11河南省## 北纬35.27 东经113.47河南省济源北纬35.04 东经112.35河南省开封北纬34.47 东经114.21河南省灵宝北纬34.31 东经110.52河南省## 北纬36.03 东经113.49河南省漯河北纬33.33 东经114.02河南省洛阳北纬34.41 东经112.27河南省南阳北纬33.00 东经112.32河南省平顶山北纬33.44 东经113.17河南省濮阳北纬35.44 东经115.01河南省沁阳北纬35.05 东经112.57河南省汝州北纬34.09 东经112.50河南省三门峡北纬34.47 东经111.12河南省商丘北纬34.26 东经115.38河南省卫辉北纬35.24 东经114.03河南省舞钢北纬33.17 东经113.30河南省项城北纬33.26 东经114.54河南省新密北纬34.31 东经113.22河南省新乡北纬35.18 东经113.52河南省信阳北纬32.07 东经114.04河南省新郑北纬34.24 东经113.43河南省许昌北纬34.01 东经113.49河南省偃师北纬34.43 东经112.47河南省义马北纬34.43 东经111.55河南省## 北纬34.09 东经113.28河南省周口北纬33.37 东经114.38河南省驻马店北纬32.58 东经114.01 ##省哈尔滨北纬45.44 东经126.36 ##省阿城北纬45.32 东经126.58##省安达北纬46.24 东经125.18##省北安北纬48.15 东经126.31##省大庆北纬46.36 东经125.01##省富锦北纬47.15 东经132.02##省海伦北纬47.28 东经126.57##省鹤岗北纬47.20 东经130.16##省黑河北纬50.14 东经127.29##省佳木斯北纬46.47 东经130.22 ##省鸡西北纬45.17 东经130.57##省密山北纬45.32 东经131.50##省牡丹江北纬44.35 东经129.36 ##省讷河北纬48.29 东经124.51##省宁安北纬44.21 东经129.28##省齐齐哈尔北纬47.20 东经123.57 ##省七台河北纬45.48 东经130.49 ##省双城北纬45.22 东经126.15##省尚志北纬45.14 东经127.55##省双鸭山北纬46.38 东经131.11 ##省绥芬河北纬44.25 东经131.11 ##省绥化北纬46.38 东经126.59##省同江北纬47.39 东经132.30##省五常北纬44.55 东经127.11##省五大连池北纬48.38 东经126.07##省伊春北纬47.42 东经128.56##省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省洪湖北纬29.48 东经113.27湖北省黄石北纬30.12 东经115.06湖北省黄州北纬30.27 东经114.52湖北省荆门北纬31.02 东经112.12湖北省荆沙北纬30.18 东经112.16湖北省老河口北纬32.23 东经111.40湖北省利川北纬30.18 东经108.56湖北省麻城北纬31.10 东经115.01湖北省浦圻北纬29.42 东经113.51湖北省潜江北纬30.26 东经112.53湖北省石首北纬29.43 东经112.24湖北省十堰北纬32.40 东经110.47湖北省随州北纬31.42 东经113.22湖北省天门北纬60.39 东经113.10湖北省武穴北纬29.51 东经115.33湖北省襄樊北纬32.02 东经112.08湖北省仙桃北纬30.22 东经113.27湖北省孝感北纬30.56 东经113.54湖北省宜昌北纬30.42 东经111.17湖北省宜城北纬31.42 东经112.15湖北省应城北纬30.57 东经113.33湖北省枣阳北纬32.07 东经112.44湖北省枝城北纬30.23 东经111.27湖北省钟祥北纬31.10 东经112.34湖南省长沙北纬28.12 东经112.59湖南省常德北纬29.02 东经111.51湖南省郴州北纬25.46 东经113.02湖南省衡阳北纬26.53 东经112.37湖南省洪江北纬27.07 东经109.59湖南省怀化北纬27.33 东经109.58湖南省津市北纬29.38 东经111.52湖南省吉首北纬28.18 东经109.43湖南省冷水江北纬27.42 东经111.26湖南省冷水滩北纬26.26 东经111.35湖南省涟源北纬27.41 东经111.41湖南省醴陵北纬27.40 东经113.30湖南省临湘北纬29.29 东经113.27湖南省浏阳北纬28.09 东经113.37湖南省娄底北纬27.44 东经111.59湖南省汨罗北纬28.49 东经113.03湖南省韶山北纬27.54 东经112.29湖南省邵阳北纬27.14 东经111.28湖南省武冈北纬26.43 东经110.37湖南省湘潭北纬27.52 东经112.53湖南省湘乡北纬27.44 东经112.31湖南省益阳北纬28.36 东经112.20湖南省永州北纬26.13 东经111.37湖南省沅江北纬28.50 东经112.22湖南省张家界北纬29.08 东经110.29湖南省株洲北纬27.51 东经113.09湖南省资兴北纬25.58 东经113.13##省长春北纬43.54 东经125.19##省白城北纬45.38 东经122.50##省白山北纬41.56 东经126.26##省大安北纬45.30 东经124.18##省德惠北纬44.32 东经125.42##省敦化北纬43.22 东经128.13 ##省公主岭北纬43.31 东经124.49##省和龙北纬42.32 东经129.00##省桦甸北纬42.58 东经126.44##省集安北纬41.08 东经126.11 ##省蛟河北纬43.42 东经127.21 ##省## 北纬43.52 东经126.33##省九台北纬44.09 东经125.51 ##省辽源北纬42.54 东经125.09 ##省临江北纬41.49 东经126.53 ##省龙井北纬42.46 东经129.26 ##省梅河口北纬42.32 东经125.40 ##省舒兰北纬44.24 东经126.57 ##省四平北纬43.10 东经124.22 ##省松原北纬45.11 东经124.49 ##省洮南北纬45.20 东经122.47 ##省通化北纬41.43 东经125.56 ##省图们北纬42.57 东经129.51 ##省延吉北纬42.54 东经129.30 ##省愉树北纬44.49 东经126.32##省常熟北纬31.39 东经120.43 ##省常州北纬31.47 东经119.58 ##省丹阳北纬32.00 东经119.32 ##省东台北纬32.51 东经120.19 ##省高邮北纬32.47 东经119.27 ##省海门北纬31.53 东经121.09 ##省淮安北纬33.30 东经119.09 ##省淮阴北纬33.36 东经119.02 ##省江都北纬32.26 东经119.32 ##省姜堰北纬32.34 东经120.08 ##省江阴北纬31.54 东经120.17 ##省靖江北纬32.02 东经120.17 ##省金坛北纬31.46 东经119.33 ##省## 北纬31.23 东经120.57##省连去港北纬34.36 东经119.10 ##省## 北纬31.26 东经119.29##省邳州北纬34.19 东经117.59 ##省启乐北纬31.48 东经121.39 ##省如皋北纬32.23 东经120.33 ##省宿迁北纬33.58 东经118.18 ##省苏州北纬31.19 东经120.37 ##省太仓北纬31.27 东经121.06 ##省泰兴北纬32.10 东经120.01 ##省泰州北纬32.30 东经119.54 ##省通州北纬32.05 东经121.03 ##省吴江北纬31.10 东经120.39 ##省无锡北纬31.34 东经120.18 ##省兴化北纬32.56 东经119.50 ##省新沂北纬34.22 东经118.20 ##省徐州北纬34.15 东经117.11 ##省盐在北纬33.22 东经120.08 ##省扬中北纬32.14 东经119.49##省宜兴北纬31.21 东经119.49 ##省仪征北纬32.16 东经119.10 ##省张家港北纬31.52 东经120.32 ##省镇江北纬32.11 东经119.27 ##省## 北纬28.40 东经115.55##省德兴北纬28.57 东经117.35 ##省丰城北纬28.12 东经115.48 ##省赣州北纬28.52 东经114.56 ##省高安北纬28.25 东经115.22 ##省吉安北纬27.07 东经114.58 ##省景德镇北纬29.17 东经117.13 ##省井冈山北纬26.34 东经114.10 ##省九江北纬29.43 东经115.58 ##省乐平北纬28.58 东经117.08 ##省临川北纬27.59 东经116.21##省萍乡北纬27.37 东经113.50##省瑞昌北纬29.40 东经115.38##省瑞金北纬25.53 东经116.01##省上饶北纬25.27 东经117.58##省新余北纬27.48 东经114.56##省宜春北纬27.47 东经114.23##省鹰潭北纬28.14 东经117.03##省樟树北纬28.03 东经115.32##省沈阳北纬41.48 东经123.25##省鞍山北纬41.07 东经123.00##省北票北纬41.48 东经120.47##省本溪北纬41.18 东经123.46##省朝阳北纬41.34 东经120.27##省大连北纬38.55 东经121.36##省大石桥北纬40.37 东经122.31 ##省东港北纬39.53 东经124.08 ##省凤城北纬40.28 东经124.02 ##省抚顺北纬41.51 东经123.54 ##省阜新北纬42.01 东经121.39 ##省盖州北纬40.24 东经122.21 ##省海城北纬40.51 东经122.43 ##省葫芦岛北纬40.45 东经120.51 ##省锦州北纬41.07 东经121.09 ##省开原北纬42.32 东经124.02 ##省辽阳北纬41.16 东经123.12 ##省凌海北纬41.10 东经121.21 ##省凌源北纬41.14 东经119.22 ##省盘锦北纬41.07 东经122.03 ##省普兰店北纬39.23 东经121.58 ##省铁法北纬42.28 东经123.32##省瓦房店北纬39.37 东经122.00##省兴城北纬40.37 东经120.41##省新民北纬41.59 东经122.49##省营口北纬40.39 东经122.13##省庄河北纬39.41 东经122.58内自治区呼和浩特北纬40.48 东经111.41内自治区包头北纬40.39 东经109.49内自治区赤峰北纬42.17 东经118.58内自治区东胜北纬39.48 东经109.59内自治区二连浩特北纬43.38 东经111.58内自治区额尔古纳北纬50.13 东经120.11内自治区丰镇北纬40.27 东经113.09内自治区根河北纬50.48 东经121.29内自治区海拉尔北纬49.12 东经119.39内自治区霍林郭勒北纬45.32 东经119.38内自治区集宁北纬41.02 东经113.06内自治区临河北纬40.46 东经107.22内自治区满洲里北纬49.35 东经117.23内自治区通辽北纬43.37 东经122.16内自治区乌兰浩特北纬46.03 东经122.03内自治区乌海北纬39.40 东经106.48内自治区锡林浩特北纬43.57 东经116.03内自治区牙克石北纬49.17 东经120.40内自治区扎兰屯北纬48.00 东经122.47宁夏自治区银川北纬38.27 东经106.16宁夏自治区青铜峡北纬37.56 东经105.59宁夏自治区石嘴山北纬39.02 东经106.22宁夏自治区吴忠北纬37.59 东经106.11青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55##省济南北纬36.40 东经117.00##省安丘北纬36.25 东经119.12 ##省滨州北纬37.22 东经118.02 ##省昌邑北纬39.52 东经119.24 ##省德州北纬37.26 东经116.17 ##省东营北纬37.27 东经118.30 ##省肥城北纬36.14 东经116.46 ##省高密北纬36.22 东经119.44 ##省菏泽北纬35.14 东经115.26 ##省胶南北纬35.53 东经119.58 ##省胶州北纬36.17 东经120.00 ##省即墨北纬36.22 东经120.28 ##省济宁北纬35.23 东经116.33 ##省莱芜北纬36.12 东经117.40 ##省莱西北纬36.52 东经120.31##省莱州北纬37.10 东经119.57 ##省乐陵北纬37.44 东经117.12 ##省聊城北纬36.26 东经115.57 ##省临清北纬36.51 东经115.42 ##省临沂北纬35.03 东经118.20 ##省龙口北纬37.39 东经120.21 ##省蓬莱北纬37.48 东经120.45 ##省平度北纬36.47 东经119.58 ##省青岛北纬36.03 东经120.18 ##省青州北纬36.42 东经118.28 ##省曲阜北纬35.36 东经116.58 ##省日照北纬35.23 东经119.32 ##省荣成北纬37.10 东经122.25 ##省乳山北纬36.54 东经121.31 ##省寿光北纬36.53 东经118.44 ##省泰安北纬36.11 东经117.08##省潍坊北纬36.43 东经119.06 ##省威海北纬37.31 东经122.07 ##省文登北纬37.12 东经122.03 ##省新泰北纬35.54 东经117.45 ##省烟台北纬37.32 东经121.24 ##省兖州北纬35.32 东经116.49 ##省禹城北纬36.56 东经116.39 ##省枣庄北纬34.52 东经117.33 ##省章丘北纬36.43 东经117.32 ##省招远北纬37.21 东经120.23 ##省诸城北纬35.59 东经119.24 ##省淄博北纬36.48 东经118.03 ##省邹城北纬35.24 东经116.58 ##省太原北纬37.54 东经112.33 ##省长治北纬36.11 东经113.06 ##省大同北纬40.06 东经113.17##省古交北纬37.54 东经112.09 ##省河津北纬35.35 东经110.41 ##省侯马北纬35.37 东经111.21 ##省霍州北纬36.34 东经111.42 ##省介休北纬37.02 东经111.55 ##省晋城北纬35.30 东经112.51 ##省临汾北纬36.05 东经111.31 ##省潞城北纬36.21 东经113.14 ##省朔州北纬39.19 东经112.26 ##省孝义北纬37.08 东经111.48 ##省忻州北纬38.24 东经112.43 ##省阳泉北纬37.51 东经113.34 ##省永济北纬34.52 东经110.27 ##省原平北纬38.43 东经112.42 ##省榆次北纬37.41 东经112.43 ##省运城北纬35.02 东经110.59陕西省安康北纬32.41 东经109.01陕西省宝鸡北纬34.22 东经107.09陕西省韩城北纬35.28 东经110.27陕西省汉中北纬33.04 东经107.01陕西省华阴北纬34.34 东经110.05陕西省商州北纬33.52 东经109.57陕西省铜川北纬35.06 东经109.07陕西省渭南北纬34.30 东经109.30陕西省咸阳北纬34.20 东经108.43陕西省兴平北纬34.18 东经108.29陕西省延安北纬36.35 东经109.28陕西省榆林北纬38.18 东经109.47四川省成都北纬30.40 东经104.04四川省巴中北纬31.51 东经106.43四川省崇州北纬30.39 东经103.40四川省达川北纬31.14 东经107.29四川省德阳北纬31.09 东经104.22四川省都江堰北纬31.01 东经103.37四川省峨眉山北纬29.36 东经103.29四川省涪陵北纬29.42 东经107.22四川省广汉北纬30.58 东经104.15四川省广元北纬32.28 东经105.51四川省华蓥北纬30.26 东经106.44四川省简阳北纬30.24 东经104.32四川省江油北纬31.48 东经104.42四川省阆中北纬31.36 东经105.58四川省乐山北纬29.36 东经103.44四川省泸州北纬28.54 东经105.24四川省## 北纬30.49 东经106.04四川省内江北纬29.36 东经105.02四川省攀枝花北纬26.34 东经101.43四川省彭州北纬30.59 东经103.57四川省邛崃北纬30.26 东经103.28四川省遂宁北纬30.31 东经105.33四川省万县北纬30.50 东经108.21四川省万源北纬32.03 东经108.03四川省西昌北纬27.54 东经102.16四川省雅安北纬29.59 东经102.59四川省宜宾北纬28.47 东经104.34四川省自贡北纬29.23 东经104.46四川省资阳北纬30.09 东经104.38 ##省台北市北纬25.03 东经121.30 ##市##市北纬39.02 东经117.12##自治区## 北纬29.39 东经91.08##自治区## 北纬29.16 东经88.51## ##市北纬21.23 东经115.12##自治区乌鲁木齐北纬43.45 东经87.36 ##自治区阿克苏北纬41.09 东经80.19 ##自治区阿勒泰北纬47.50 东经88.12 ##自治区阿图什北纬39.42 东经76.08 ##自治区博乐北纬44.57 东经82.08##自治区昌吉北纬44.02 东经87.18##自治区阜康北纬44.09 东经87.58##自治区哈密北纬42.50 东经93.28##自治区和田北纬37.09 东经79.55##自治区克拉玛依北纬45.36 东经84.51 ##自治区喀什北纬39.30 东经75.59##自治区库尔勒北纬41.46 东经86.07 ##自治区奎屯北纬44.27 东经84.56##自治区石河子北纬44.18 东经86.00 ##自治区塔城北纬46.46 东经82.59##自治区吐鲁番北纬42.54 东经89.11 ##自治区伊宁北纬43.55 东经81.20云南省昆明北纬25.04 东经102.42云南省保山北纬25.08 东经99.10云南省楚雄北纬25.01 东经101.32云南省大理北纬25.34 东经100.13云南省东川北纬26.06 东经103.12云南省个旧北纬23.21 东经103.09云南省景洪北纬22.01 东经100.48云南省开远北纬23.43 东经103.13云南省曲靖北纬25.30 东经103.48云南省瑞丽北纬24.00 东经97.50云南省思茅北纬22.48 东经100.58云南省畹町北纬24.06 东经98.04云南省宣威北纬26.13 东经104.06云南省玉溪北纬24.22 东经102.32云南省昭通北纬27.20 东经103.42 ##省杭州北纬30.16 东经120.10 ##省慈溪北纬30.11 东经121.15 ##省东阳北纬29.16 东经120.14 ##省## 北纬29.39 东经121.24##省富阳北纬30.03 东经119.57 ##省## 北纬30.32 东经120.42##省湖州北纬30.52 东经120.06 ##省建德北纬29.29 东经119.16 ##省江山北纬28.45 东经118.37 ##省嘉兴北纬30.46 东经120.45 ##省金华北纬29.07 东经119.39 ##省兰溪北纬29.12 东经119.28 ##省临海北纬28.51 东经121.08##省龙泉北纬28.04 东经119.08 ##省宁波北纬29.52 东经121.33 ##省平湖北纬30.42 东经121.01 ##省衢州北纬28.58 东经118.52 ##省瑞安北纬27.48 东经120.38 ##省## 北纬30.01 东经120.52 ##省绍兴北纬30.00 东经120.34 ##省台州北纬28.41 东经121.27 ##省桐乡北纬30.38 东经120.32 ##省温岭北纬28.22 东经121.21 ##省温州北纬28.01 东经120.39 ##省萧山北纬30.09 东经120.16 ##省义乌北纬29.18 东经120.04 ##省乐清北纬28.08 东经120.58 ##省余杭北纬30.26 东经120.18 ##省余姚北纬30.02 东经121.10##省舟山北纬30.01 东经122.06##省## 北纬29.43 东经120.14重庆市重庆市北纬29.35 东经106.33重庆市合川市北纬30.02 东经106.15重庆市江津市北纬29.18 东经106.16重庆市南川市北纬29.10 东经107.05重庆市永川市北纬29.23 东经105.53。
中国各城市经纬度数据

中国各城市经纬度数据中国各城市经纬度数据1、中国各主要大城市经纬度数据:北京市市中心经纬度:(116.41667, 39.91667) 上海市区经纬度 :(121.43333, 34.50000) 天津市区经纬度 :(117.20000, 39.13333) 香港经纬度:(114.10000,22.20000) 广州经纬度:(113.23333,23.16667) 珠海经纬度:(113.51667, 22.30000) 深圳经纬度:(114.06667, 22.61667) 杭州经纬度:(120.20000, 30.26667) 重庆市区经纬度 :(106.45000, 29.56667) 青岛经纬度:(120.33333, 36.06667) 厦门经纬度:(118.10000, 24.46667) 福州经纬度:(119.30000, 26.08333) 兰州经纬度:(103.73333, 36.03333) 贵阳经纬度:(106.71667, 26.56667) 长沙经纬度:(113.00000, 28.21667) 南京经纬度:(118.78333,32.05000)南昌经纬度 :(115.90000, 28.68333) 沈阳经纬度 :(123.38333, 41.80000) 太原经纬度 :(112.53333, 37.86667) 成都经纬度 :(104.06667, 30.66667) 拉萨经纬度 :( 91.00000, 29.60000) 乌鲁木齐经纬度 :( 87.68333, 43.76667) 昆明经纬度:(102.73333, 25.05000) 西安经纬度:(108.95000, 34.26667) 西宁经纬度:(101.75000, 36.56667) 银川经纬度 :(106.26667, 38.46667) 兰浩特经纬度 :(122.08333, 46.06667) 哈尔滨经纬度:(126.63333, 45.75000) 长春经纬度:(125.35000, 43.88333) 武汉经纬度:(114.31667, 30.51667) 郑州经纬度 :(113.65000, 34.76667) 石家庄经纬度:(114.48333, 38.03333) 三亚经纬度:(109.50000, 18.20000) 海口经纬度:(110.35000, 20.01667) 澳门经纬度:(113.50000, 22.20000) 2、中国主要城市经纬度查询(精确到二级省市):所在省城市名纬度经度安徽省合肥北纬 31.52 东经 117.17 安徽省安庆北纬 30.31 东经 117.02 安徽省蚌埠北纬 32.56 东经 117.21 安徽省亳州北纬 33.52 东经 115.47 安徽省巢湖北纬 31.36 东经 117.52 安徽省滁州北纬 32.18 东经 118.18 安徽省阜阳北纬 32.54 东经 115.48 安徽省贵池北纬 30.39 东经 117.28 安徽省淮北北纬 33.57 东经 116.47 安徽省淮南北纬 32.37 东经 116.58 安徽省黄山北纬 29.43 东经 118.18 安徽省界首北纬 33.15 东经 115.21 安徽省六安北纬 31.44 东经 116.28 安徽省马鞍山北纬 31.43 东经 118.28 安徽省明光北纬 32.47 东经 117.58 安徽省宿州北纬 33.38 东经 116.58 安徽省天长北纬 32.41 东经 118.59 安徽省铜陵北纬 30.56 东经 117.48 安徽省芜湖北纬 31.19 东经 118.22 安徽省宣州北纬 30.57 东经 118.44 澳门澳门市北纬 21.33 东经 115.07 北京市北京市北纬 39.55 东经 116.24福建省福州北纬 26.05 东经 119.18 福建省长乐北纬 25.58 东经 119.31 福建省福安北纬 27.06 东经 119.39 福建省福清北纬 25.42 东经 119.23 福建省建瓯北纬 27.03 东经 118.20 福建省建阳北纬 27.21 东经 118.07 福建省晋江北纬 24.49 东经 118.35 福建省龙海北纬 24.26 东经 117.48 福建省龙岩北纬 25.06东经 117.01福建省南安北纬 24.57 东经 118.23 福建省南平北纬 26.38 东经 118.10福建省宁德北纬 26.39 东经 119.31 福建省莆田北纬 24.26 东经 119.01福建省泉州北纬 24.56 东经 118.36 福建省三明北纬 26.13 东经 117.36福建省邵武北纬 27.20 东经 117.29福建省石狮北纬 24.44 东经 118.38 福建省厦门北纬 24.27 东经 118.06 福福建省武夷山北纬 27.46 东经 118.02建省永安北纬 25.58 东经 117.23 福建省漳平北纬 25.17 东经 117.24 福建省漳州北纬 24.31 东经 117.39 甘肃省兰州北纬 36.04 东经 103.51 甘肃省白银北纬 36.33 东经 104.12 甘肃省敦煌北纬 40.08 东经 94.41 甘肃省嘉峪关北纬 39.48 东经 98.14 甘肃省金昌北纬 38.28 东经 102.10 甘肃省酒泉北纬 39.44 东经 98.31 甘肃省临夏北纬 35.37 东经 103.12 甘肃省平凉北纬 35.32 东经 106.40 甘肃省天水北纬 34.37 东经 105.42 甘肃省武威北纬 37.56 东经 102.39 甘肃省西峰北纬 35.45 东经 107.40 甘肃省玉门北纬 39.49 东经 97.35 甘肃省张掖北纬 38.56 东经 100.26 广东省广州北纬 23.08 东经 113.14 广东省潮阳北纬 23.16 东经 116.36 广东省潮州北纬 23.40 东经 116.38 广东省澄海北纬 23.28 东经 116.46广东省从化北纬 23.33 东经 113.33广东省东莞北纬 23.02 东经113.45广东省 梅州 北纬 24.19东经116.07广东省恩平 北纬 22.12东经 112.19 广东省佛山 北纬 23.02东经 113.06 广东省高明 北纬 22.53东经 112.50 广东省高要 北纬 23.02东经 112.26 广东省 高州北纬 21.54东经 110.50 广东省 鹤山 北纬 22.46东经112.57 广东省 河源 北纬 23.43东经114.41 广东省 花都 北纬 23.23东经113.12 广东省 化州北纬 21.39东经 110.37 广东省 惠阳 北纬 22.48东经114.28 广东省 惠州北纬 23.05东经 114.22 广东省 江门 北纬 22.35东经113.04 广东省 揭阳北纬 22.32东经 116.21 广东省 开平 北纬 22.22东经112.40 广东省 乐昌北纬 25.09东经 113.21 广东省 雷州 北纬 20.54东经 110.04 广东省 廉江 北纬 21.37东经110.17 广东省 连州 北纬 24.48东经112.23 广东省 罗定 北纬 22.46东经 111.33 广东省 茂名 北纬 21.40东经110.53广东省南海北纬 23.01 东经 113.09广东省番禺北纬 22.57 东经 113.22广东省普宁北纬 23.18 东经 116.10广东省清远北纬 23.42 东经 113.01广东省三水北纬 23.10 东经 112.52广东省汕头北纬 23.22 东经 116.41广东省汕尾北纬 22.47 东经 115.21广东省韶关北纬 24.48 东经 113.37广东省深圳北纬 22.33 东经 114.07广东省顺德北纬 22.50 东经 113.15广东省四会北纬 23.21 东经 112.41广东省台山北纬 22.15 东经 112.48广东省吴川北纬 21.26 东经 110.47广东省新会北纬 22.32 东经 113.01广东省兴宁北纬 24.09 东经 115.43广东省阳春北纬 22.10 东经 111.48广东省阳江广东省英德北纬 24.10 东经 113.22北纬 21.50 东经 111.58广西自治区 宜州 北纬 24.28 东经108.40112.02 广东省 增城 北纬 23.18 东经 113.49 广东省 湛江 北纬 21.11 东经 110.24 广东省 肇庆 北纬 23.03 东经 112.27 广东省 中山 北纬 22.31 东经 113.22 广东省 珠海 北纬 22.17 东经 113.34 广西自治区 南宁 北纬 22.48 东经 108.19 广西自治区 北海 北纬 21.28 东经 109.07 广西自治区 北流 北纬 22.42 东经 110.21 广西自治区 百色 北纬 23.54 东经 106.36 广西自治区 防城港 北纬 21.37 东经 108.20 广西自治区 贵港 北纬 23.06 东经 109.36 广西自治区 桂林 北纬 25.17 东经 110.17 广西自治区 桂平 北纬 23.22 东经 110.04 广西自治区 河池 北纬 24.42 东经 108.03 广西自治区 合山 北纬 23.47 东经 108.52 广西自治区 柳州 北纬 23.19 东经 109.24 广西自治区 赁祥 北纬 22.07 东经 106.44 广西自治区 钦州 北纬 21.57 东经 108.37 广西自治区 梧州 北纬 23.29 东经 111.20 广西自治区 玉林 北纬 22.38 东经 110.09106.42 贵州省安顺北纬 26.14东经 105.55贵州省毕节北纬 27.18 东经105.18 贵州省赤水北纬 28.34东经 105.42贵州省都匀北纬 26.15 东经107.31贵州省凯里北纬 26.35 东经107.58贵州省六盘水北纬 26.35 东经 104.50 贵州省清镇北纬 26.33 东经106.27贵州省铜仁北纬 27.43 东经109.12贵州省兴义北纬 25.05 东经104.53贵州省遵义北纬 27.42 东经106.55海南省海口北纬 20.02 东经110.20海南省儋州北纬19.31 东经109.34海南省琼海北纬19.14 东经110.28海南省琼山北纬19.59 东经110.21海南省三亚北纬18.14 东经109.31海南省通什北纬18.46 东经109.31河北省石家庄北纬 38.02 东经 114.30 河北省安国北纬 38.24 东经115.20河北省保定北纬 38.51 东经115.30 河北省霸州北纬 39.06 东经 116.24河北省泊头北纬 38.04 东经116.340O ∙9LL ≡⅛0o o ∂e抵氓 =2二≡⅛N ooe抵氓B «綁氓回 0 寸Io LL ≡⅛寸寸l<e抵 ⅛90∙9 LL ≡⅛90oo e抵氓I& 寸二≡⅛979"抵氓W 岳09•寸二≡⅛0o oo e抵氓 L9∙9LL ≡⅛O0∙6e抵氓 辿雲恤9000LL ≡⅛寸 e ∙6e抵氓W卅O O ∙9L L ≡⅛0e oo e抵氓-,-S卜 92LL ≡⅛690寸抵氓1 09∙9L L ≡⅛8L oo e抵氓-,-S寸∙9e抵氓1L L oo L L ≡⅛9e ∙6e 抵氓 m ⅛0e ∙9LL≡⅛s o ∂e抵氓 W ≡O e寸二≡⅛抵S寸O I<L L ≡⅛89∙6e抵氓回川縛氓回 卜O∙9二≡⅛0 寸oo e抵氓W史976二≡⅛99∙6e抵氓W S &9二≡⅛00l<e抵氓te w6L ∙寸二≡⅛寸 000"抵⅛ 0寸∙9二≡⅛o ∙6e抵氓 6 co e ∙9河南省济源北纬 35.04 东经 112.35河南省开封 北纬 34.47 东经 114.212 东经 114.11 河北省 邢台 北纬 37.04 东经 114.30 河北省 辛集北纬 37.54 东经 115.12河北省 新乐 北纬 38.20 东经 114.41 河北省 张家口 北纬 40.48 东经 114.53 河北省 涿州 北纬 39.29 东经 115.59 河北省 遵化 北纬 40.11 东经 117.58 河南省 郑州 北纬 34.46 东经 11340 河南省 安阳 北纬 36.06 东经 114.21 河南省 长葛 北纬 34.12 东经 113.47 河南省 登封 北纬 34.27 东经 113.02 河南省 邓州 北纬 32.42 东经 112.05 河南省 巩义 北纬 34.46 东经 112.58 河南省 鹤壁 北纬 35.54 东经114.11 河南省 辉县 北纬 35.27 东经 113.47 河南省 焦作 北纬 35.14 东经 113.12 河南省灵宝 北纬 34.31 东经110.52河南省林州北纬 36.03 东经 113.49河南省漯河北纬 33.33 东经 114.02河南省洛阳北纬 34.41 东经 112.27河南省南阳北纬 33.00 东经 112.32河南省平顶山北纬 33.44 东经113.17 河南省濮阳北纬 35.44 东经115.01 河南省沁阳北纬 35.05 东经112.57 河南省汝州北纬 34.09 东经112.50 河南省三门峡北纬 34.47 东经 111.12 河南省商丘北纬 34.26 东经 115.38河南省卫辉北纬 35.24 东经 114.03 河南省舞钢北纬 33.17 东经 113.30河南省项城北纬 33.26 东经 114.54 河南省荥阳北纬 34.46 东经 113.21河南省新密北纬 34.31 东经 113.22河南省新乡北纬 35.18 东经 113.52 河南省信阳北纬 32.07 东经 114.04河南省新郑北纬 34.24 东经 113.43 河南省许昌北纬 34.01 东经 113.49河南省偃师北纬 34.43 东经 112.47河南省义马北纬 34.43 东经 111.55河南省禹州北纬 34.09 东经 113.28河南省周口北纬 33.37 东经 114.38 河南省驻马店北纬 32.58 东经114.01 黑龙江省哈尔滨北纬 45.44 东经 126.36 黑龙江省阿城北纬45.32 东经 126.58 黑龙江省安达北纬 46.24 东经 125.18 黑龙江省北安北纬 48.15 东经 126.31 黑龙江省大庆北纬 46.36 东经 125.01 黑龙江省富锦北纬 47.15 东经 132.02 黑龙江省海林北纬 44.35 东经 129.21 黑龙江省海伦北纬 47.28 东经 126.57 黑龙江省鹤岗北纬 47.20 东经 130.16 黑龙江省黑河北纬 50.14 东经127.29 黑龙江省佳木斯北纬 46.47 东经 130.22 黑龙江省鸡西北纬45.17 东经 130.57 黑龙江省密山北纬 45.32 东经 131.50 黑龙江省牡丹江北纬 44.35 东经 129.36 黑龙江省讷河北纬 48.29 东经 124.51 黑龙江省宁安北纬 44.21 东经 129.28 黑龙江省齐齐哈尔北纬 47.20 东经123.57 黑龙江省七台河北纬 45.48 东经 130.49 黑龙江省双城北纬45.22 东经 126.15 黑龙江省尚志北纬 45.14 东经 127.55黑龙江省双鸭山北纬 46.38 东经131.11 黑龙江省绥芬河北纬 44.25 东经 131.11 黑龙江省绥化北纬46.38 东经 126.59 黑龙江省铁力北纬 46.59 东经 128.01 黑龙江省同江北纬 47.39 东经 132.30黑龙江省五常北纬 44.55 东经127.11 黑龙江省五大连池北纬 48.38 东经 126.07 黑龙江省伊春北纬47.42 东经 128.56 黑龙江省肇东北纬 46.04 东经 125.58 湖北省武汉北纬 30.35 东经 114.17 湖北省安陆北纬 31.15 东经 113.41 湖北省当阳北纬 30.50 东经 111.47 湖北省丹江口北纬 32.33 东经 108.30 湖北省大冶北纬 30.06 东经 114.58 湖北省恩施北纬 30.16 东经 109.29 湖北省鄂州湖北省洪湖北纬 29.48 东经 113.27北纬 30.23 东经 114.52 湖北省广水北纬 31.37 东经 113.48湖北省洪湖北纬 29.48 东经 113.27湖北省黄石北纬 30.12 东经 115.06湖北省黄州北纬 30.27 东经 114.52 湖北省荆门北纬 31.02 东经 112.12 湖北省荆沙北纬 30.18 东经 112.16 湖北省老河口北纬 32.23 东经111.40 湖北省利川北纬 30.18 东经108.56湖北省麻城北纬 31.10 东经 115.01湖北省浦圻北纬 29.42 东经 113.51 湖北省潜江北纬 30.26 东经 112.53湖北省石首北纬 29.43 东经 112.24湖北省十堰北纬 32.40 东经 110.47 湖北省随州北纬 31.42 东经 113.22湖北省天门北纬 60.39 东经 113.10 湖北省武穴北纬 29.51 东经 115.33湖北省襄樊北纬 32.02 东经 112.08湖北省咸宁北纬 29.53 东经 114.17 湖北省仙桃北纬 30.22 东经 113.27湖北省孝感北纬 30.56 东经 113.54 湖北省宜昌北纬 30.42 东经 111.17湖北省宜城北纬 31.42 东经 112.15湖北省应城北纬 30.57 东经 113.33 湖北省枣阳北纬 32.07 东经 112.44 湖北省枝城北纬 30.23 东经 111.27湖北省钟祥北纬 31.10 东经 112.34湖南省长沙北纬 28.12 东经 112.59 湖南省常德北纬 29.02 东经 111.51湖南省郴州北纬 25.46 东经 113.02湖南省衡阳北纬 26.53 东经 112.37 湖南省洪江北纬 27.07 东经 109.59湖南省怀化北纬 27.33 东经 109.58 湖南省津市北纬 29.38 东经 111.52湖南省吉首北纬 28.18 东经 109.43湖南省耒阳北纬 26.24 东经 112.51 湖南省冷水江北纬 27.42 东经111.26湖南省冷水滩北纬 26.26 东经111.35 湖南省涟源北纬 27.41 东经111.41湖南省醴陵北纬 27.40 东经 113.30湖南省临湘北纬 29.29 东经 113.27 湖南省浏阳北纬 28.09 东经 113.37湖南省娄底北纬 27.44 东经 111.59 湖南省汨罗北纬 28.49 东经 113.03 湖南省韶山北纬 27.54 东经 112.29 湖南省邵阳北纬 27.14 东经 111.28 湖南省武冈北纬 26.43 东经 110.37 湖南省湘潭北纬 27.52 东经 112.53 湖南省湘乡北纬 27.44 东经 112.31 湖南省益阳北纬 28.36 东经 112.20 湖南省永州北纬 26.13 东经 111.37 湖南省沅江北纬 28.50 东经 112.22湖南省岳阳北纬 29.22 东经 113.06 湖南省张家界北纬 29.08 东经110.29 湖南省株洲北纬 27.51 东经113.09 湖南省资兴北纬 25.58 东经113.13 吉林省长春北纬 43.54 东经125.19 吉林省白城北纬 45.38 东经122.50 吉林省白山北纬 41.56 东经126.26吉林省大安北纬 45.30 东经 124.18 吉林省德惠北纬 44.32 东经 125.42 吉林省敦化北纬 43.22 东经 128.13 吉林省公主岭北纬 43.31 东经 124.49 吉林省和龙北纬 42.32 东经 129.00 吉林省桦甸北纬 42.58 东经 126.44江苏省常熟北纬 31.39 东经120.43130.22 吉林省 集安 北纬 41.08 东经 126.11 吉林省 蛟河 北纬 43.42 东经 127.21吉林省 吉林 北纬 43.52 东经 126.33 吉林省 九台 北纬 44.09 东经 125.51 吉林省 辽源 北纬 42.54 东经 125.09 吉林省 临江 北纬 41.49 东经 126.53吉林省 龙井 北纬 42.46 东经 129.26 吉林省 梅河口 北纬 42.32 东经 125.40 吉林省 舒兰 北纬 44.24 东经 126.57 吉林省 四平 北纬 43.10 东经 124.22 吉林省 松原 北纬 45.11 东经 124.49吉林省 洮南 北纬 45.20 东经 122.47 吉林省 通化 北纬 41.43 东经 125.56 吉林省 图们 北纬 42.57 东经 129.51 吉林省 延吉 北纬 42.54 东经 129.30吉林省 愉树 北纬 44.49 东经126.32 江苏省 南京 北纬 32.03 东经 118.46江苏省 常州 北纬 31.47 东经 119.58 江苏省 丹阳 北纬 32.00 东经 119.32 江苏省 东台 北纬 32.51 东经 120.19江苏省太仓北纬 31.27 东经121.06119.27 江苏省 海门 北纬 31.53 东经 121.09江苏省 淮安 北纬 33.30 东经 119.09江苏省 淮阴 北纬 33.36 东经 119.02 江苏省 江都 北纬 32.26 东经 119.32 江苏省 姜堰 北纬 32.34 东经 120.08 江苏省 江阴 北纬 31.54 东经 120.17江苏省 靖江 北纬 32.02 东经 120.17 江苏省 金坛 北纬 31.46 东经 119.33 江苏省 昆山 北纬 31.23 东经 120.57 江苏省 连去港 北纬 34.36 东经 119.10 江苏省 溧阳 北纬 31.26 东经 119.29江苏省 南通 北纬 32.01 东经 120.51 江苏省 邳州 北纬 34.19 东经 117.59 江苏省 启乐 北纬 31.48 东经 121.39 江苏省 如皋 北纬 32.23 东经 120.33江苏省 宿迁 北纬 33.58 东经 118.18江苏省 苏州 北纬 31.19 东经 120.37江苏省 泰兴 北纬 32.10 东经 120.01 江苏省 泰州 北纬 32.30 东经 119.54 江苏省 通州 北纬 32.05 东经 121.03江西省 景德镇 北纬 29.17 东经 117.13 江苏省 吴江 北纬 31.10 东经 120.39 江苏省 无锡 北纬 31.34 东经 120.18 江苏省 兴化 北纬 32.56 东经 119.50 江苏省 新沂 北纬 34.22 东经 118.20 江苏省 徐州 北纬 34.15 东经 117.11 江苏省 盐在 北纬 33.22 东经 120.08 江苏省 扬中 北纬 32.14 东经 119.49 江苏省 扬州 北纬 32.23 东经 119.26 江苏省 宜兴 北纬 31.21 东经 119.49 江苏省 仪征 北纬 32.16 东经 119.10 江苏省 张家港 北纬 31.52 东经 120.32 江苏省 镇江 北纬 32.11 东经 119.27江西省 南昌 北纬 28.40 东经 115.55 江西省 德兴 北纬 28.57 东经 117.35江西省 丰城 北纬 28.12 东经 115.48江西省 赣州 北纬 28.52 东经 114.56 江西省 高安 北纬 28.25 东经 115.22江西省吉安北纬27.07 东经114.58江西省江西省景德镇北纬 29.17 东经117.13井冈山 北纬 26.34 东经 114.10辽宁省丹东 北纬 40.08 东经124.22江西省 九江 北纬 29.43 东经 115.58 江西省 乐平 北纬 28.58 东经 117.08 江西省 临川 北纬 27.59 东经 116.21 江西省 萍乡 北纬 27.37 东经 113.50 江西省 瑞昌 北纬 29.40 东经 115.38 江西省 瑞金 北纬 25.53 东经 116.01 江西省 上饶 北纬 25.27 东经 117.58江西省 新余 北纬 27.48 东经 114.56 江西省 宜春 北纬 27.47 东经 114.23 江西省 鹰潭 北纬 28.14 东经 117.03 江西省 樟树 北纬 28.03 东经 115.32 辽宁省 沈阳 北纬 41.48 东经 123.25辽宁省 鞍山 北纬 41.07 东经 123.00 辽宁省 北票 北纬 41.48 东经 120.47 辽宁省 本溪 北纬 41.18 东经 123.46 辽宁省 朝阳 北纬 41.34 东经 120.27 辽宁省 大连 北纬 38.55 东经 121.36辽宁省 大石桥北纬 40.37 东经 122.31辽宁省 东港 北纬 39.53 东经124.08辽宁省凤城北纬 40.28 东经 124.02 辽宁省抚顺北纬 41.51 东经 123.54辽宁省阜新北纬 42.01 东经 121.39 辽宁省盖州北纬 40.24 东经 122.21辽宁省海城北纬 40.51 东经 122.43 辽宁省葫芦岛北纬 40.45 东经120.51 辽宁省锦州北纬 41.07 东经121.09辽宁省开原北纬 42.32 东经 124.02 辽宁省辽阳北纬 41.16 东经 123.12辽宁省凌海北纬 41.10 东经 121.21辽宁省凌源北纬 41.14 东经 119.22 辽宁省盘锦北纬 41.07 东经 122.03 辽宁省普兰店北纬 39.23 东经121.58 辽宁省铁法北纬 42.28 东经123.32辽宁省铁岭北纬 42.18 东经 123.51辽宁省瓦房店北纬 39.37 东经122.00 辽宁省兴城北纬 40.37 东经120.41辽宁省新民北纬 41.59 东经 122.49 辽宁省营口北纬 40.39 东经 122.13辽宁省庄河北纬 39.41 东经 122.58 内自治区呼和浩特北纬 40.48 东经111.41内自治区包头北纬 40.39 东经109.49内自治区赤峰北纬 42.17 东经118.58 内自治区东胜北纬 39.48 东经 109.59 内自治区二连浩特北纬43.38 东经 111.58 内自治区额尔古纳北纬 50.13 东经 120.11 内自治区丰镇北纬 40.27 东经 113.09 内自治区根河北纬 50.48 东经 121.29 内自治区海拉尔北纬 49.12 东经 119.39 内自治区霍林郭勒北纬 45.32 东经119.38 内自治区集宁北纬 41.02 东经 113.06 内自治区临河北纬 40.46 东经 107.22 内自治区满洲里北纬49.35 东经 117.23 内自治区通辽北纬 43.37 东经 122.16 内自治区乌兰浩特北纬 46.03 东经 122.03 内自治区乌海北纬 39.40 东经 106.48 内自治区锡林浩特北纬 43.57 东经116.03 内自治区牙克石北纬 49.17 东经 120.40 内自治区扎兰屯北纬48.00 东经 122.47 宁夏自治区银川北纬 38.27 东经 106.16 宁夏自治区青铜峡北纬 37.56 东经 105.59 宁夏自治区石嘴山北纬 39.02 东经106.22 宁夏自治区吴忠北纬 37.59 东经 106.11青海省德令哈北纬 37.22 东经 97.23 青海省格尔木青海省西宁北纬 36.38 东经 101.48北纬 36.26 东经 94.55 山东省济南北纬 36.40 东经 117.00 山东省安丘北纬 36.25 东经 119.12 山东省滨州北纬 37.22 东经 118.02 山东省昌邑北纬 39.52 东经 119.24 山东省德州北纬 37.26 东经 116.17 山东省东营北纬 37.27 东经 118.30 山东省肥城北纬 36.14 东经 116.46 山东省高密北纬 36.22 东经 119.44 山东省菏泽北纬 35.14 东经 115.26 山东省胶南北纬 35.53 东经 119.58 山东省胶州北纬 36.17 东经 120.00 山东省即墨北纬 36.22 东经 120.28 山东省济宁北纬 35.23 东经 116.33 山东省莱芜北纬 36.12 东经 117.40 山东省莱西北纬 36.52 东经 120.31山东省莱阳北纬 36.58 东经 120.42山东省乐陵北纬 37.44 东经 117.12 山东省聊城北纬 36.26 东经 115.57 山东省临清北纬 36.51 东经 115.42 山东省临沂北纬 35.03 东经 118.20 山东省龙口北纬 37.39 东经 120.21 山东省蓬莱北纬 37.48 东经 120.45 山东省平度北纬 36.47 东经 119.58 山东省青岛北纬 36.03 东经 120.18 山东省青州北纬 36.42 东经 118.28 山东省曲阜北纬 35.36 东经 116.58 山东省日照北纬 35.23 东经 119.32 山东省荣成北纬 37.10 东经 122.25 山东省乳山北纬 36.54 东经 121.31 山东省寿光北纬 36.53 东经 118.44 山东省泰安北纬 36.11 东经 117.08 山东省滕州北纬 35.06 东经 117.09 山东省潍坊北纬 36.43 东经 119.06 山东省威海北纬 37.31 东经 122.07 山东省文登北纬 37.12 东经 122.03 山东省新泰北纬 35.54 东经 117.45 山东省烟台北纬 37.32 东经 121.24山西省孝义北纬 37.08 东经 111.48山东省禹城北纬 36.56 东经 116.39 山东省枣庄北纬 34.52 东经 117.33 山东省章丘北纬 36.43 东经 117.32 山东省招远北纬 37.21 东经 120.23 山东省诸城北纬 35.59 东经 119.24 山东省淄博北纬 36.48 东经 118.03 山东省邹城北纬 35.24 东经 116.58 山西省太原北纬 37.54 东经 112.33 山西省长治北纬 36.11 东经 113.06 山西省大同北纬 40.06 东经 113.17 山西省高平北纬 35.48 东经 112.55 山西省古交北纬 37.54 东经 112.09 山西省河津北纬 35.35 东经 110.41 山西省侯马北纬 35.37 东经 111.21 山西省霍州北纬 36.34 东经 111.42 山西省介休北纬 37.02 东经 111.55 山西省晋城北纬 35.30 东经 112.51 山西省临汾北纬 36.05 东经 111.31 山西省潞城北纬 36.21 东经 113.14 山西省朔州北纬 39.19 东经 112.26*≡⅛<6020L≡⅛& 寸e 抵氓震w*≡堡 LO ∙60 L≡⅛L寸 Ze 抵氓 S⅛B卜900OL ≡⅛卜 L•寸e 抵氓 M ≡⅛B690二≡⅛抵氓S⅛≡3Co寸 ZLL ≡⅛L寸l<e抵S *≡m寸 ZLL ≡⅛Co寸oo e抵氓粧M*≡m卜00LL ≡⅛29•寸 C 抵氓1 ⅛≡3寸e o L L ≡⅛L 9l<e 抵氓*E *≡m80∙6oL ≡⅛9e ∙9e 抵6000OL ≡⅛8 LGe抵J ⅛BCo寸Oo OL ≡⅛00•寸 e抵 ms ⅛1 O O o O -≡⅛O eG e抵氓w ≡⅛B卜 O ∙60L≡⅛90lo e抵氓三W ⅛B卜 9∙60L≡⅛09∙co e抵氓 W ≡900LL ≡⅛寸7寸 C抵氓≡<卜 00LL≡⅛80∙9e抵氓 I陕西省榆林北纬 38.18 东经 109.47 上海市上海市北纬 31.14 东经 121.29 四川省成都北纬 30.40 东经 104.04四川省巴中北纬 31.51 东经 106.43 四川省崇州北纬 30.39 东经 103.40 四川省达川北纬 31.14 东经 107.29 四川省德阳北纬 31.09 东经 104.22 四川省都江堰北纬 31.01 东经 103.37 四川省峨眉山北纬 29.36 东经 103.29 四川省涪陵北纬 29.42 东经 107.22 四川省广汉北纬 30.58 东经 104.15 四川省广元北纬 32.28 东经 105.51 四川省华蓥北纬 30.26 东经 106.44 四川省简阳北纬 30.24 东经 104.32 四川省江油北纬 31.48 东经 104.42 四川省阆中北纬 31.36 东经 105.58 四川省乐山北纬 29.36 东经 103.44 四川省泸州北纬 28.54 东经 105.24 四川省绵阳北纬 31.30 东经 104.42 四川省南充北纬 30.49 东经 106.04 四川省内江北纬 29.36 东经 105.02四川省彭州北纬 30.59 东经 103.57 四川省邛崃北纬 30.26 东经 103.28 四川省遂宁北纬 30.31 东经 105.33 四川省万县北纬 30.50 东经 108.21 四川省万源北纬 32.03 东经 108.03 四川省西昌北纬 27.54 东经 102.16 四川省雅安北纬 29.59 东经 102.59 四川省宜宾北纬 28.47 东经 104.34 四川省自贡北纬 29.23 东经 104.46 四川省资阳北纬 30.09 东经 104.38 台湾省台北市北纬 25.03 东经 121.30 天津市天津市北纬 39.02 东经 117.12 西藏自治区拉萨北纬 29.39 东经91.08 西藏自治区日喀则北纬 29.16 东经 88.51 香港香港市北纬 21.23 东经 115.12 新疆自治区乌鲁木齐北纬43.45 东经 87.36 新疆自治区阿克苏北纬 41.09 东经 80.19 新疆自治区阿勒泰北纬 47.50 东经 88.12 新疆自治区阿图什北纬 39.42 东经 76.08 新疆自治区博乐北纬 44.57 东经 82.08 新疆自治区昌吉北纬 44.02 东经 87.18 新疆自治区阜康北纬 44.09 东经87.58四川省攀枝花北纬 26.34 东经新疆自治区哈密北纬 42.50 东经93.28 新疆自治区和田北纬 37.09 东经 79.55 新疆自治区克拉玛依北纬45.36 东经 84.51 新疆自治区喀什北纬 39.30 东经 75.59 新疆自治区库尔勒北纬 41.46 东经 86.07 新疆自治区奎屯北纬 44.27 东经 84.56 新疆自治区石河子北纬 44.18 东经 86.00 新疆自治区塔城北纬 46.46 东经 82.59 新疆自治区吐鲁番北纬 42.54 东经89.11 新疆自治区伊宁北纬 43.55 东经 81.20 云南省昆明北纬 25.04 东经102.42 云南省保山北纬 25.08 东经99.10 云南省楚雄北纬 25.01 东经101.32 云南省大理北纬 25.34 东经 100.13 云南省东川北纬 26.06 东经 103.12 云南省个旧北纬 23.21 东经 103.09 云南省景洪北纬 22.01 东经 100.48云南省曲靖北纬 25.30 东经 103.48 云南省瑞丽北纬 24.00 东经 97.50 云南省思茅北纬 22.48 东经 100.58 云南省畹町北纬 24.06 东经 98.04 云南省云南省开远北纬 23.43 东经 103.13宣威北纬 26.13 东经 104.06 云南省玉溪北纬 24.22 东经 102.32 云南省昭通北纬 27.20 东经 103.42 浙江省杭州北纬 30.16 东经 120.10 浙江省慈溪北纬 30.11 东经 121.15 浙江省东阳北纬 29.16 东经 120.14 浙江省奉化北纬 29.39 东经 121.24 浙江省富阳北纬 30.03 东经 119.57 浙江省海宁北纬 30.32 东经 120.42 浙江省湖州北纬 30.52 东经 120.06 浙江省建德北纬 29.29 东经 119.16 浙江省江山北纬 28.45 东经 118.37 浙江省嘉兴北纬 30.46 东经 120.45 浙江省金华北纬 29.07 东经 119.39 浙江省兰溪北纬 29.12 东经 119.28 浙江省临海北纬 28.51 东经 121.08 浙江省丽水北纬 28.27 东经 119.54浙江省宁波北纬 29.52 东经 121.33 浙江省平湖北纬 30.42 东经 121.01 浙江省衢州北纬 28.58 东经 118.52 浙江省瑞安北纬 27.48 东经 120.38 浙浙江省龙泉北纬 28.04 东经 119.08江省上虞北纬 30.01 东经 120.52 浙江省绍兴北纬 30.00 东经 120.34 浙江省台州北纬 28.41 东经 121.27 浙江省桐乡北纬 30.38 东经 120.32 浙江省温岭北纬 28.22 东经 121.21 浙江省温州北纬 28.01 东经 120.39 浙江省萧山北纬 30.09 东经 120.16 浙江省义乌北纬 29.18 东经 120.04 浙江省乐清北纬 28.08 东经 120.58 浙江省余杭北纬 30.26 东经 120.18 浙江省余姚北纬 30.02 东经 121.10 浙江省永康北纬 29.54 东经 120.01 浙江省舟山北纬 30.01 东经 122.06 浙江省诸暨北纬 29.43 东经 120.14 重庆市重庆市北纬 29.35 东经 106.33 重庆市合川市北纬 30.02 东经 106.15 重庆市江津市北纬 29.18 东经 106.16 重庆市永川市北纬 29.23 东经 105.53浙江省龙泉北纬 28.04 东经 119.08。
中国主要城市经纬度查询

中国主要城市经纬度查询2021-03-261 中国主要城市经纬度查询【直辖市】北京市北纬39°55 东经116°24 上海市北纬31°14 东经121°29 天津市北纬39°02 东经117°12 重庆市北纬29°35 东经106°33 (重庆市各区)合川市北纬30°02东经106°15 江津市北纬29°18 东经106°16 南川市北纬29°10 东经107°05 永川市北纬29°23 东经105°53【安徽省】合肥北纬31°52 东经117°17 安庆北纬30°31 东经117°02 蚌埠北纬32°56 东经117°21 亳州北纬33°52 东经115°47 巢湖北纬31°36 东经117°52 滁州北纬32°18 东经118°18 阜阳北纬32°54 东经115°48 贵池北纬30°39 东经117°28 淮北北纬33°57 东经116°47 淮南北纬32°37 东经116°58 黄山北纬29°43 东经118°18 界首北纬33°15 东经115°21 六安北纬31°44 东经116°28 马鞍山北纬31°43 东经118°28 明光北纬32°47 东经117°58 宿州北纬33°38 东经116°58 天长北纬32°41 东经118°59 铜陵北纬30°56 东经117°48 芜湖北纬31°19 东经118°22 宣州北纬30°57 东经118°44【福建省】福州北纬26°05 东经119°18 长乐北纬25°58 东经119°31 福安北纬27°06 东经119°39 福清北纬25°42 东经119°23 建瓯北纬27°03 东经118°20 建阳北纬27°21 东经118°07 晋江北纬24°49 东经118°35 龙海北纬24°26 东经117°48 龙岩北纬25°06 东经117°01 南安北纬24°57 东经118°23 南平北纬26°38 东经118°10 宁德北纬26°39 东经119°31 莆田北纬24°26 东经119°01 泉州北纬24°56 东经118°36 三明北纬26°13 东经117°36 邵武北纬27°20 东经117°29 石狮北纬24°44 东经118°38 武夷山北纬27°46 东经118°02 厦门北纬24°27 东经118°06 永安北纬25°58 东经117°23 漳平北纬25°17 东经117°24 漳州北纬24°31 东经117°39【广东省】广州北纬23°08 东经113°14 潮阳北纬23°16 东经116°36 潮州北纬23°40 东经116°38 澄海北纬23°28 东经116°46 从化北纬23°33 东经113°33 东莞北纬23°02 东经113°45 恩平北纬22°12 东经112°19 佛山北纬23°02 东经113°06 高明北纬22°53 东经112°50 高要北纬23°02 东经112°26 高州北纬21°54 东经110°50 鹤山北纬22°46东经112°57 河源北纬23°43 东经114°41 花都北纬23°23 东经113°12 化州北纬21°39 东经110°37 惠阳北纬22°48 东经114°28 惠州北纬23°05 东经114°22 江门北纬22°35 东经113°04 揭阳北纬22°32 东经116°21 开平北纬22°22 东经112°402 乐昌北纬25°09 东经113°21 雷州北纬20°54 东经110°04 廉江北纬21°37 东经110°17 连州北纬24°48 东经112°23 罗定北纬22°46 东经111°33 茂名北纬21°40 东经110°53 梅州北纬24°19 东经116°07 南海北纬23°01 东经113°09 番禺北纬22°57 东经113°22 普宁北纬23°18 东经116°10 清远北纬23°42 东经113°01 三水北纬23°10 东经112°52 汕头北纬23°22 东经116°41 汕尾北纬22°47 东经115°21 韶关北纬24°48 东经113°37 深圳北纬22°33 东经114°07 顺德北纬22°50 东经113°15 四会北纬23°21 东经112°41 台山北纬22°15 东经112°48 吴川北纬21°26 东经110°47 新会北纬22°32 东经113°01 兴宁北纬24°09 东经115°43 阳春北纬22°10 东经111°48 阳江北纬21°50 东经111°58 英德北纬24°10 东经113°22 云浮北纬22°57 东经112°02 增城北纬23°18 东经113°49 湛江北纬21°11 东经110°24 肇庆北纬23°03 东经112°27 中山北纬22°31 东经113°22 珠海北纬22°17 东经113°34【广西壮族自治区】南宁北纬22°48 东经108°19 北海北纬21°28 东经109°07 北流北纬22°42 东经110°21 百色北纬23°54 东经106°36 防城港北纬21°37 东经108°20 贵港北纬23°06 东经109°36 桂林北纬25°17 东经110°17 桂平北纬23°22 东经110°04 河池北纬24°42 东经108°03 合山北纬23°47 东经108°52 柳州北纬23°19 东经109°24 赁祥北纬22°07 东经106°44 钦州北纬21°57东经108°37 梧州北纬23°29 东经111°20 玉林北纬22°38 东经110°09 宜州北纬24°28 东经108°40【贵州省】贵阳北纬26°35 东经106°42 安顺北纬26°14 东经105°55 毕节北纬27°18 东经105°18 赤水北纬28°34 东经105°42 都匀北纬26°15 东经107°31 凯里北纬26°35 东经107°58 六盘水北纬26°35 东经104°50 清镇北纬26°33 东经106°27 铜仁北纬27°43 东经109°12 兴义北纬25°05 东经104°53 遵义北纬27°42 东经106°55【甘肃省】兰州北纬36°04 东经103°51 白银北纬36°33 东经104°12敦煌北纬40°08 东经94°41 嘉峪关北纬39°48 东经98°14 金昌北纬38°28 东经102°10 酒泉北纬39°44 东经98°31 临夏北纬35°37 东经103°12 平凉北纬35°32 东经106°40 天水北纬34°37 东经105°42 武威北纬37°56 东经102°39 西峰北纬35°45 东经107°40 玉门北纬39°49 东经97°35 张掖北纬38°56 东经100°26 【湖北省】武汉北纬30°35 东经114°17 安陆北纬31°15 东经113°41 当阳北纬30°50 东经111°473 丹江口北纬32°33 东经108°30 大冶北纬30°06 东经114°58 恩施北纬30°16 东经109°29 鄂州北纬30°23 东经114°52 广水北纬31°37 东经113°48 洪湖北纬29°48 东经113°27 黄石北纬30°12 东经115°06 黄州北纬30°27 东经114°52 荆门北纬31°02 东经112°12荆沙北纬30°18 东经112°16 老河口北纬32°23 东经111°40 利川北纬30°18 东经108°56 麻城北纬31°10 东经115°01 浦圻北纬29°42 东经113°51 潜江北纬30°26 东经112°53 石首北纬29°43 东经112°24 十堰北纬32°40 东经110°47 随州北纬31°42 东经113°22 天门北纬30°39 东经113°10 武穴北纬29°51 东经115°33 襄樊北纬32°02 东经112°08 咸宁北纬29°53 东经114°17 仙桃北纬30°22 东经113°27 孝感北纬30°56 东经113°54 宜昌北纬30°42 东经111°17 宜城北纬31°42 东经112°15 应城北纬30°57 东经113°33 枣阳北纬32°07 东经112°44 枝城北纬30°23 东经111°27 钟祥北纬31°10 东经112°34【湖南省】长沙北纬28°12 东经112°59 常德北纬29°02 东经111°51 郴州北纬25°46 东经113°02 衡阳北纬26°53 东经112°37 洪江北纬27°07 东经109°59 怀化北纬27°33 东经109°58 津市北纬29°38 东经111°52 吉首北纬28°18 东经109°43 耒阳北纬26°24 东经112°51 冷水江北纬27°42 东经111°26 冷水滩北纬26°26 东经111°35 涟源北纬27°41 东经111°41 醴陵北纬27°40 东经113°30 临湘北纬29°29 东经113°27 浏阳北纬28°09 东经113°37 娄底北纬27°44 东经111°59 汨罗北纬28°49 东经113°03 韶山北纬27°54 东经112°29 邵阳北纬27°14 东经111°28 武冈北纬26°43 东经110°37 湘潭北纬27°52 东经112°53 湘乡北纬27°44 东经112°31 益阳北纬28°36 东经112°20 永州北纬26°13 东经111°37 沅江北纬28°50 东经112°22 岳阳北纬29°22 东经113°06 张家界北纬29°08 东经110°29 株洲北纬27°51 东经113°09 资兴北纬25°58 东经113°13 【河北省】石家庄北纬38°02 东经114°30 安国北纬38°24 东经115°20 保定北纬38°51 东经115°30 霸州北纬39°06 东经116°24 泊头北纬38°04 东经116°34 沧州北纬38°18 东经116°52 承德北纬40°59 东经117°57 定州北纬38°30 东经115°00 丰南北纬39°34 东经118°06 高碑店北纬39°20 东经115°51 蒿城北纬38°02 东经114°50 邯郸北纬36°36 东经114°28 河间北纬38°26 东经116°05 衡水北纬37°44 东经115°42 黄骅北纬38°21 东经117°21 晋州北纬38°02 东经115°02 冀州北纬37°34 东经115°33 廓坊北纬39°31 东经116°42 鹿泉北纬38°04 东经114°19 南宫北纬37°22 东经115°234 秦皇岛北纬39°55 东经119°35 任丘北纬38°42 东经116°07 三河北纬39°58 东经117°04 沙河北纬36°51 东经114°30 深州北纬38°01 东经115°32 唐山北纬39°36 东经118°11 武安北纬36°42 东经114°11 邢台北纬37°04 东经114°30 辛集北纬37°54 东经115°12 新乐北纬38°20 东经114°41 张家口北纬40°48 东经114°53 涿州北纬39°29 东经115°59 遵化北纬40°11 东经117°58【河南省】郑州北纬34°46 东经113°40 安阳北纬36°06 东经114°21 长葛北纬34°12 东经113°47 登封北纬34°27 东经113°02 邓州北纬32°42 东经112°05 巩义北纬34°46 东经112°58 鹤壁北纬35°54 东经114°11 辉县北纬35°27 东经113°47 焦作北纬35°14 东经113°12 济源北纬35°04 东经112°35 开封北纬34°47 东经114°21 灵宝北纬34°31 东经110°52 林州北纬36°03 东经113°49 漯河北纬33°33 东经114°02 洛阳北纬34°41 东经112°27 南阳北纬33°00 东经112°32 平顶山北纬33°44 东经113°17 濮阳北纬35°44 东经115°01 沁阳北纬35°05 东经112°57 汝州北纬34°09 东经112°50 三门峡北纬34°47 东经111°12 商丘北纬34°26 东经115°38 卫辉北纬35°24 东经114°03 舞钢北纬33°17 东经113°30 项城北纬33°26 东经114°54 荥阳北纬34°46 东经113°21 新密北纬34°31 东经113°22 新乡北纬35°18 东经113°52 信阳北纬32°07 东经114°04 新郑北纬34°24 东经113°43 许昌北纬34°01 东经113°49 偃师北纬34°43 东经112°47 义马北纬34°43 东经111°55 禹州北纬34°09 东经113°28 周口北纬33°37 东经114°38 驻马店北纬32°58 东经114°01【黑龙江省】哈尔滨北纬45°44 东经126°36 阿城北纬45°32 东经126°58 安达北纬46°24 东经125°18 北安北纬48°15 东经126°31 大庆北纬46°36 东经125°01 富锦北纬47°15 东经132°02 海林北纬44°35 东经129°21 海伦北纬47°28 东经126°57 鹤岗北纬47°20 东经130°16 黑河北纬50°14 东经127°29 佳木斯北纬46°47 东经130°22 鸡西北纬45°17 东经130°57 密山北纬45°32 东经131°50 牡丹江北纬44°35 东经129°36 讷河北纬48°29 东经124°51 宁安北纬44°21 东经129°28 齐齐哈尔北纬47°20 东经123°57 七台河北纬45°48 东经130°49 双城北纬45°22东经126°15 尚志北纬45°14 东经127°55 双鸭山北纬46°38 东经131°11 绥芬河北纬44°25 东经131°11 绥化北纬46°38 东经126°59 铁力北纬46°59 东经128°01 同江北纬47°39 东经132°30 五常北纬44°55 东经127°11 五大连池北纬48°38 东经126°07 伊春北纬47°42 东经128°56 肇东北纬46°04 东经125°58【海南省】5 海口北纬20°02 东经110°20 儋州北纬19°31 东经109°34 琼海北纬19°14 东经110°28 琼山北纬19°59 东经110°21 三亚北纬18°14 东经109°31 通什北纬18°46 东经109°31 三沙北纬16°50 东经112°20 【吉林省】长春北纬43°54 东经125°19 白城北纬45°38 东经122°50 白山北纬41°56 东经126°26 大安北纬45°30 东经124°18 德惠北纬44°32 东经125°42敦化北纬43°22 东经128°13 公主岭北纬43°31 东经124°49 和龙北纬42°32 东经129°00 桦甸北纬42°58 东经126°44 珲春北纬42°52 东经130°22 集安北纬41°08 东经126°11 蛟河北纬43°42 东经127°21 吉林北纬43°52 东经126°33 九台北纬44°09 东经125°51 辽源北纬42°54 东经125°09 临江北纬41°49 东经126°53 龙井北纬42°46 东经129°26 梅河口北纬42°32 东经125°40 舒兰北纬44°24 东经126°57 四平北纬43°10 东经124°22 松原北纬45°11 东经124°49 洮南北纬45°20 东经122°47 通化北纬41°43 东经125°56 图们北纬42°57 东经129°51 延吉北纬42°54 东经129°30 愉树北纬44°49 东经126°32【江西省】南昌北纬28°40 东经115°55 德兴北纬28°57 东经117°35 丰城北纬28°12 东经115°48 赣州北纬28°52 东经114°56 高安北纬28°25 东经115°22 吉安北纬27°07 东经114°58 景德镇北纬29°17 东经117°13 井冈山北纬26°34 东经114°10 九江北纬29°43 东经115°58 乐平北纬28°58 东经117°08 临川北纬27°59 东经116°21 萍乡北纬27°37 东经113°50 瑞昌北纬29°40 东经115°38 瑞金北纬 25°53 东经116°01 上饶北纬25°27 东经117°58 新余北纬27°48 东经114°56 宜春北纬27°47 东经114°23 鹰潭北纬28°14 东经117°03 樟树北纬28°03 东经115°32【江苏省】南京北纬32°03 东经118°46 常熟北纬31°39 东经120°43 常州北纬31°47 东经119°58 丹阳北纬32°00 东经119°32 东台北纬32°51 东经120°19 高邮北纬32°47 东经 119°27 海门北纬31°53 东经121°09 淮安北纬33°30 东经119°09 淮阴北纬33°36 东经119°02 江都北纬32°26 东经119°32 姜堰北纬32°34 东经120°08 江阴北纬31°54 东经120°17 靖江北纬32°02 东经120°17 金坛北纬31°46 东经119°33 昆山北纬31°23 东经120°57 连去港北纬34°36 东经119°10 溧阳北纬31°26 东经119°29 南通北纬32°01 东经120°51 邳州北纬34°19 东经117°59 启乐北纬31°48 东经121°39 如皋北纬32°23 东经120°33 宿迁北纬33°58 东经118°18 苏州北纬31°19 东经120°37 太仓北纬31°27 东经121°06 泰兴北纬32°10 东经120°01 泰州北纬32°30 东经119°546 通州北纬32°05 东经121°03 吴江北纬31°10 东经120°39 无锡北纬31°34 东经120°18 兴化北纬32°56 东经119°50 新沂北纬34°22 东经118°20 徐州北纬34°15 东经117°11 盐在北纬33°22 东经120°08 扬中北纬32°14 东经119°49 扬州北纬32°23 东经119°26 宜兴北纬31°21 东经119°49 仪征北纬32°16 东经119°10 张家港北纬31°52 东经120°32 镇江北纬32°11 东经119°27【辽宁省】沈阳北纬41°48 东经123°25 鞍山北纬41°07 东经123°00 北票北纬41°48 东经120°47 本溪北纬41°18 东经123°46 朝阳北纬41°34 东经120°27 大连北纬38°55 东经121°36 丹东北纬40°08 东经124°22 大石桥北纬40°37 东经122°31 东港北纬39°53 东经124°08 凤城北纬40°28 东经124°02 抚顺北纬41°51 东经123°54 阜新北纬42°01 东经121°39 盖州北纬40°24 东经122°21 海城北纬40°51 东经122°43 葫芦岛北纬40°45 东经120°51 锦州北纬41°07 东经121°09 开原北纬42°32 东经124°02 辽阳北纬41°16 东经123°12 凌海北纬41°10 东经121°21 凌源北纬41°14 东经119°22 盘锦北纬41°07 东经122°03 普兰店北纬39°23 东经121°58 铁法北纬42°28 东经123°32 铁岭北纬42°18 东经123°51 瓦房店北纬39°37 东经122°00 兴城北纬40°37 东经120°41 新民北纬41°59 东经122°49 营口北纬40°39 东经122°13 庄河北纬39°41 东经122°58 【宁夏回族自治区】银川北纬38°27 东经106°16 青铜峡北纬37°56 东经105°59 石嘴山北纬39°02 东经106°22 吴忠北纬37°59 东经106°11【内蒙古自治区】呼和浩特北纬40°48 东经111°41 包头北纬40°39 东经 109°49 赤峰北纬42°17 东经118°58 东胜北纬39°48 东经109°59 二连浩特北纬43°38 东经111°58 额尔古纳北纬50°13 东经120°11 丰镇北纬40°27 东经113°09 根河北纬50°48 东经121°29 海拉尔北纬49°12 东经119°39 霍林郭勒北纬45°32 东经119°38 集宁北纬41°02 东经113°06 临河北纬40°46 东经107°22 满洲里北纬49°35 东经117°23 通辽北纬43°37 东经122°16 乌兰浩特北纬46°03 东经122°03 乌海北纬39°40 东经106°48 锡林浩特北纬43°57 东经116°03 牙克石北纬49°17 东经120°40 扎兰屯北纬48°00 东经122°47【青海省】西宁北纬36°38 东经101°48 德令哈北纬37°22 东经97°23 格尔木北纬36°26 东经94°55【四川省】成都北纬30°40 东经104°04 巴中北纬31°51 东经106°43 崇州北纬30°39 东经103°40 达川北纬31°14 东经107°29 德阳北纬31°09 东经104°227 都江堰北纬31°01 东经103°37 峨眉山北纬29°36 东经103°29 涪陵北纬29°42 东经107°22 广汉北纬30°58 东经104°15 广元北纬32°28 东经105°51 华蓥北纬30°26 东经106°44 简阳北纬30°24 东经104°32 江油北纬31°48 东经104°42 阆中北纬 31°36 东经105°58 乐山北纬29°36 东经103°44 泸州北纬28°54 东经105°24 绵阳北纬31°30 东经104°42 南充北纬30°49 东经106°04 内江北纬29°36 东经105°02 攀枝花北纬26°34 东经101°43 彭州北纬30°59 东经103°57 邛崃北纬30°26 东经103°28 遂宁北纬30°31 东经105°33 万县北纬30°50 东经108°21 万源北纬32°03 东经108°03 西昌北纬27°54 东经102°16 雅安北纬29°59 东经102°59 宜宾北纬28°47 东经104°34 自贡北纬29°23 东经104°46 资阳北纬30°09 东经104°38【山东省】济南北纬36°40 东经117°00 安丘北纬36°25 东经119°12 滨州北纬37°22 东经118°02 昌邑北纬39°52 东经119°24 德州北纬37°26 东经116°17 东营北纬37°27 东经118°30 肥城北纬36°14 东经116°46 高密北纬36°22 东经119°44 菏泽北纬35°14 东经115°26 胶南北纬35°53 东经119°58 胶州北纬36°17 东经120°00 即墨北纬36°22 东经120°28 济宁北纬35°23 东经116°33 莱芜北纬36°12 东经117°40 莱西北纬36°52 东经120°31 莱阳北纬36°58 东经120°42 莱州北纬37°10 东经119°57 乐陵北纬37°44 东经117°12 聊城北纬36°26 东经115°57 临清北纬36°51 东经115°42 临沂北纬35°03 东经118°20 龙口北纬37°39 东经120°21 蓬莱北纬37°48 东经120°45 平度北纬36°47 东经119°58 青岛北纬36°03 东经120°18 青州北纬36°42 东经118°28 曲阜北纬35°36 东经116°58 日照北纬35°23 东经119°32 荣成北纬37°10 东经122°25 乳山北纬36°54东经121°31 寿光北纬36°53 东经118°44 泰安北纬36°11 东经117°08 滕州北纬35°06 东经117°09 潍坊北纬36°43 东经119°06 威海北纬37°31 东经122°07 文登北纬37°12 东经122°03 新泰北纬35°54 东经117°45 烟台北纬37°32 东经121°24 兖州北纬35°32 东经116°49 禹城北纬36°56 东经116°39 枣庄北纬34°52 东经117°33 章丘北纬36°43 东经117°32 招远北纬37°21 东经120°23 诸城北纬35°59 东经119°24 淄博北纬36°48 东经118°03 邹城北纬35°24 东经116°58【山西省】中阳北纬37°37 东经112°17 太原北纬37°54 东经112°33 长治北纬36°11 东经113°06 大同北纬40°06 东经113°17 高平北纬35°48 东经112°55 古交北纬37°54 东经112°09 河津北纬35°35 东经110°41 侯马北纬35°37 东经111°218 霍州北纬36°34 东经111°42 介休北纬37°02 东经111°55 晋城北纬35°30 东经112°51 临汾北纬36°05 东经111°31 潞城北纬36°21 东经113°14 朔州北纬39°19 东经112°26 孝义北纬37°08 东经111°48 忻州北纬38°24 东经112°43 阳泉北纬37°51 东经113°34 永济北纬34°52 东经110°27 原平北纬38°43 东经112°42 榆次北纬37°41 东经112°43 运城北纬35°02 东经110°59 【陕西省】西安北纬34°17 东经108°57 安康北纬32°41 东经109°01 宝鸡北纬34°22 东经107°09 韩城北纬35°28 东经110°27 汉中北纬33°04 东经107°01 华阴北纬34°34 东经110°05 商州北纬33°52 东经109°57 铜川北纬35°06 东经109°07 渭南北纬34°30 东经109°30 咸阳北纬34°20 东经108°43 兴平北纬34°18 东经108°29 延安北纬36°35 东经109°28 榆林北纬38°18 东经109°47 【浙江省】杭州北纬30°16 东经120°10 慈溪北纬30°11 东经121°15 东阳北纬29°16 东经120°14 奉化北纬29°39 东经121°24 富阳北纬30°03 东经119°57 海宁北纬30°32 东经120°42 湖州北纬30°52 东经 120°06 建德北纬29°29 东经119°16 江山北纬28°45 东经118°37 嘉兴北纬30°46 东经120°45 金华北纬29°07 东经119°39 兰溪北纬29°12 东经119°28 临海北纬28°51 东经121°08 丽水北纬28°27 东经119°54 龙泉北纬28°04 东经119°08 宁波北纬29°52 东经121°33 平湖北纬30°42 东经121°01 衢州北纬28°58 东经118°52 瑞安北纬27°48 东经120°38 上虞北纬30°01 东经120°52 绍兴北纬30°00 东经120°34 台州北纬28°41 东经121°27 桐乡北纬30°38 东经120°32 温岭北纬28°22 东经121°21 温州北纬28°01 东经120°39 萧山北纬30°09 东经120°16 义乌北纬29°18 东经120°04 乐清北纬28°08 东经120°58 余杭北纬30°26 东经120°18 余姚北纬30°02 东经121°10 永康北纬29°54 东经120°01 舟山北纬30°01 东经122°06 诸暨北纬29°43 东经120°14【新疆维吾尔自治区】乌鲁木齐北纬43°45 东经87°36 阿克苏北纬41°09 东经80°19 阿勒泰北纬47°50 东经88°12 阿图什北纬39°42 东经76°08 博乐北纬44°57 东经82°08 昌吉北纬44°02 东经87°18 阜康北纬44°09 东经87°58 哈密北纬42°50 东经93°28 和田北纬37°09 东经79°55 克拉玛依北纬45°36 东经84°51 喀什北纬39°30 东经75°59 库尔勒北纬41°46 东经86°07 奎屯北纬44°27 东经84°56 石河子北纬44°18 东经86°00 塔城北纬46°46 东经82°59 吐鲁番北纬42°54 东经89°11 伊宁北纬43°55 东经81°20【西藏自治区】拉萨北纬29°39 东经91°08 日喀则北纬29°16 东经88°51【云南省】昆明北纬25°04东经102°42 保山北纬25°08 东经99°10 楚雄北纬25°01 东经101°32 大理北纬25°34 东经100°13 东川北纬26°06 东经103°12 个旧北纬23°21 东经103°09 景洪北纬22°01 东经100°48 开远北纬23°43 东经103°13 曲靖北纬25°30 东经103°48 瑞丽北纬24°00 东经97°50 思茅北纬22°48 东经100°58 畹町北纬24°06 东经98°04 宣威北纬26°13 东经104°06 玉溪北纬24°22 东经102°32 昭通北纬27°20 东经103°42【台湾省】台北市北纬25°03 东经121°30 【香港特别行政区】北纬21°23 东经115°12 【澳门特别行政区】北纬21°33 东经115°07 9本站是提供个人知识管理的网络存储空间,所有内容均由用户发布,不代表本站观点。
中国城市经纬度表

中国城市经纬度表城市经度纬度城市经度纬度北京116:28E 39:54N 青岛120:19E 36:04N天津117:10E 39:10N 郑州113:42E 34:44N石家庄114:26E 38:03N 开封114:23E 34:52N保定115:28E 38:53N 洛阳112:26E 34:43N唐山118:09E 39:37N 许昌113:48E 34:00N秦皇岛119:37E 39:54N 新乡113:54E 35:18N张家口114:55E 40:51N 武汉114:20E 30:37N承德117:52E 40:59N 宜昌111:15E 30:42N太原112:33E 37:51N 沙市112:17E 30:16N大同113:13E 40:07N 长沙112:55E 28:12N临汾111:31E 36:05N 衡阳112:34E 26:55N长治113:13E 36:05N 湘潭112:51E 27:54N呼和浩特111:38E 40:48N 常德111:39E 29:00N 包头110:00E 40:35N 广州113:18E 23:10N海拉尔119:43E 49:14N 汕头116:40E 23:21N沈阳123:23E 41:48N 韶关113:33E 24:48N大连121:38E 38:54N 海口110:10E 20:03N鞍山123:00E 41:04N 南宁108:21E 22:47N锦州121:09E 41:09N 桂林110:10E 25:18N长春125:18E 43:55N 柳州109:19E 24:20N吉林126:36E 43:48N 悟州111:18E 23:28N哈尔滨126:38E 45:45N 成都104:04E 30:39N 齐齐哈尔123:55E 47:22N 重庆106:33E 29:33N 牡丹江129:36E 44:35N 内江105:03E 29:35N 上海121:26E 31:12N 泸州105:27E 28:54N南京118:46E 32:03N 万县108:22E 30:48N无锡120:18E 31:35N 贵阳106:43E 26:34N苏州120:39E 31:20N 遵义106:53E 27:45N徐州117:12E 34:16N 昆明102:42E 25:03N杭州120:10E 30:15N 拉萨91:02E 29:39N宁波121:34E 29:53N 日喀则88:49E 29:16N温州120:38E 28:00N 西安108:55E 34:15N金华119:49E 29:10N 宝鸡107:09E 34:21N合肥117:16E 31:51N 延安109:26E 36:35N芜湖118:20E 31:21N 兰州103:50E 36:03N安庆117:02E 30:32N 天水105:33E 34:35N福州119:19E 26:02N 酒泉98:30E 39:44N厦门118:04E 24:26N 西宁101:49E 36:37N泉州118:37E 24:54N 银川106:13E 38:28N南昌115:53E 28:41N 乌鲁木齐87:36E 43:46N 九江115:59E 29:43N 哈密93:27E 42:50N赣州114:56E 25:51N 喀什75:59E 39:27N 济南117:02E 36:40N 和田79:55E 37:07N 烟台121:20E 37:33N 台北121:31E 25:02N 1601825668。
中国所有城市坐标表

中国所有城市坐标表所在省城市名纬度经度省北纬31.52 东经117.17省北纬30.31 东经117.02省北纬32.56 东经117.21省亳州北纬33.52 东经115.47省北纬31.36 东经117.52省北纬32.18 东经118.18省北纬32.54 东经115.48省北纬30.39 东经117.28省北纬33.57 东经116.47省北纬32.37 东经116.58省北纬29.43 东经118.18省界首北纬33.15 东经115.21省北纬31.44 东经116.28省马北纬31.43 东经118.28省明光北纬32.47 东经117.58省北纬33.38 东经116.58省天长北纬32.41 东经118.59省北纬30.56 东经117.48省北纬31.19 东经118.22省宣州北纬30.57 东经118.44澳门澳门市北纬21.33 东经115.07市市北纬39.55 东经116.24省北纬26.05 东经119.18省长乐北纬25.58 东经119.31 省福安北纬27.06 东经119.39 省福清北纬25.42 东经119.23 省建瓯北纬27.03 东经118.20 省建阳北纬27.21 东经118.07 省北纬24.49 东经118.35省龙海北纬24.26 东经117.48 省北纬25.06 东经117.01省南安北纬24.57 东经118.23 省北纬26.38 东经118.10省北纬26.39 东经119.31省北纬24.26 东经119.01省北纬24.56 东经118.36省北纬26.13 东经117.36省邵武北纬27.20 东经117.29 省石狮北纬24.44 东经118.38 省武夷山北纬27.46 东经118.02 省北纬24.27 东经118.06 省永安北纬25.58 东经117.23 省漳平北纬25.17 东经117.24 省北纬24.31 东经117.39省北纬36.04 东经103.51省北纬36.33 东经104.12省敦煌北纬40.08 东经94.41 省嘉峪关北纬39.48 东经98.14 省金昌北纬38.28 东经102.10 省北纬39.44 东经98.31省北纬35.37 东经103.12省北纬35.32 东经106.40省北纬34.37 东经105.42省北纬37.56 东经102.39省北纬35.45 东经107.40省玉门北纬39.49 东经97.35 省北纬38.56 东经100.26省北纬23.08 东经113.14省北纬23.16 东经116.36省北纬23.40 东经116.38省澄海北纬23.28 东经116.46 省从化北纬23.33 东经113.33 省北纬23.02 东经113.45省恩平北纬22.12 东经112.19 省北纬23.02 东经113.06省高明北纬22.53 东经112.50 省高要北纬23.02 东经112.26 省高州北纬21.54 东经110.50 省鹤山北纬22.46 东经112.57 省北纬23.43 东经114.41省花都北纬23.23 东经113.12 省化州北纬21.39 东经110.37 省惠阳北纬22.48 东经114.28 省北纬23.05 东经114.22省江门北纬22.35 东经113.04 省揭阳北纬22.32 东经116.21 省开平北纬22.22 东经112.40 省乐昌北纬25.09 东经113.21 省雷州北纬20.54 东经110.04 省廉江北纬21.37 东经110.17 省连州北纬24.48 东经112.23 省罗定北纬22.46 东经111.33 省北纬21.40 东经110.53 省北纬24.19 东经116.07省南海北纬23.01 东经113.09 省番禺北纬22.57 东经113.22 省普宁北纬23.18 东经116.10省北纬23.42 东经113.01省三水北纬23.10 东经112.52省北纬23.22 东经116.41省北纬22.47 东经115.21省北纬24.48 东经113.37省北纬22.33 东经114.07省北纬22.50 东经113.15省四会北纬23.21 东经112.41省台山北纬22.15 东经112.48省吴川北纬21.26 东经110.47省新会北纬22.32 东经113.01省兴宁北纬24.09 东经115.43省阳春北纬22.10 东经111.48省北纬21.50 东经111.58省英德北纬24.10 东经113.22省北纬22.57 东经112.02省增城北纬23.18 东经113.49省北纬21.11 东经110.24省北纬23.03 东经112.27省北纬22.31 东经113.22省北纬22.17 东经113.34广西自治区北纬22.48 东经108.19广西自治区北纬21.28 东经109.07广西自治区北流北纬22.42 东经110.21 广西自治区北纬23.54 东经106.36广西自治区北纬21.37 东经108.20广西自治区贵港北纬23.06 东经109.36 广西自治区北纬25.17 东经110.17广西自治区桂平北纬23.22 东经110.04 广西自治区北纬24.42 东经108.03广西自治区合山北纬23.47 东经108.52 广西自治区北纬23.19 东经109.24广西自治区赁祥北纬22.07 东经106.44 广西自治区北纬21.57 东经108.37广西自治区北纬23.29 东经111.20广西自治区北纬22.38 东经110.09广西自治区宜州北纬24.28 东经108.40 省北纬26.35 东经106.42 省北纬26.14 东经105.55省北纬27.18 东经105.18省赤水北纬28.34 东经105.42省都匀北纬26.15 东经107.31省北纬26.35 东经107.58省六盘水北纬26.35 东经104.50省北纬27.43 东经109.12省北纬25.05 东经104.53省北纬27.42 东经106.55省北纬20.02 东经110.20省北纬19.31 东经109.34省琼海北纬19.14 东经110.28 省琼山北纬19.59 东经110.21 省北纬18.14 东经109.31省通什北纬18.46 东经109.31 省北纬38.02 东经114.30省安国北纬38.24 东经115.20 省北纬38.51 东经115.30省霸州北纬39.06 东经116.24 省泊头北纬38.04 东经116.34 省北纬38.18 东经116.52省北纬40.59 东经117.57省定州北纬38.30 东经115.00 省丰南北纬39.34 东经118.06 省高碑店北纬39.20 东经115.51 省蒿城北纬38.02 东经114.50 省北纬36.36 东经114.28省北纬37.44 东经115.42省黄骅北纬38.21 东经117.21 省晋州北纬38.02 东经115.02 省冀州北纬37.34 东经115.33 省廓坊北纬39.31 东经116.42 省鹿泉北纬38.04 东经114.19 省南宫北纬37.22 东经115.23 省北纬39.55 东经119.35省任丘北纬38.42 东经116.07 省三河北纬39.58 东经117.04 省沙河北纬36.51 东经114.30 省深州北纬38.01 东经115.32 省北纬39.36 东经118.11省武安北纬36.42 东经114.11 省北纬37.04 东经114.30省辛集北纬37.54 东经115.12 省新乐北纬38.20 东经114.41 省北纬40.48 东经114.53省涿州北纬39.29 东经115.59 省遵化北纬40.11 东经117.58 省北纬34.46 东经11340省北纬36.06 东经114.21省长北纬34.12 东经113.47 省登封北纬34.27 东经113.02 省邓州北纬32.42 东经112.05 省巩义北纬34.46 东经112.58 省北纬35.54 东经114.11省北纬35.27 东经113.47省北纬35.14 东经113.12省济源北纬35.04 东经112.35 省北纬34.47 东经114.21省灵宝北纬34.31 东经110.52 省林州北纬36.03 东经113.49 省北纬33.33 东经114.02省北纬34.41 东经112.27省北纬33.00 东经112.32省北纬33.44 东经113.17省北纬35.44 东经115.01省沁阳北纬35.05 东经112.57 省汝州北纬34.09 东经112.50 省北纬34.47 东经111.12省北纬34.26 东经115.38省卫辉北纬35.24 东经114.03省舞钢北纬33.17 东经113.30 省项城北纬33.26 东经114.54 省荥阳北纬34.46 东经113.21 省新密北纬34.31 东经113.22 省北纬35.18 东经113.52省北纬32.07 东经114.04省新北纬34.24 东经113.43 省北纬34.01 东经113.49省偃师北纬34.43 东经112.47 省义马北纬34.43 东经111.55 省禹州北纬34.09 东经113.28 省北纬33.37 东经114.38省北纬32.58 东经114.01省北纬45.44 东经126.36省北纬45.32 东经126.58省安达北纬46.24 东经125.18 省北安北纬48.15 东经126.31 省北纬46.36 东经125.01省富锦北纬47.15 东经132.02 省海林北纬44.35 东经129.21 省海伦北纬47.28 东经126.57 省鹤岗北纬47.20 东经130.16 省北纬50.14 东经127.29省北纬46.47 东经130.22省鸡西北纬45.17 东经130.57 省密山北纬45.32 东经131.50 省北纬44.35 东经129.36省讷河北纬48.29 东经124.51 省宁安北纬44.21 东经129.28 省北纬47.20 东经123.57省七台河北纬45.48 东经130.49 省双城北纬45.22 东经126.15 省尚志北纬45.14 东经127.55 省双鸭山北纬46.38 东经131.11 省绥芬河北纬44.25 东经131.11 省北纬46.38 东经126.59省铁力北纬46.59 东经128.01 省同江北纬47.39 东经132.30 省五常北纬44.55 东经127.11 省五池北纬48.38 东经126.07 省北纬47.42 东经128.56省肇东北纬46.04 东经125.58 省北纬30.35 东经114.17省安陆北纬31.15 东经113.41省当阳北纬30.50 东经111.47 省丹江口北纬32.33 东经108.30 省大冶北纬30.06 东经114.58 省北纬30.16 东经109.29 省北纬30.23 东经114.52省广水北纬31.37 东经113.48 省洪湖北纬29.48 东经113.27 省北纬30.12 东经115.06省北纬30.27 东经114.52省北纬31.02 东经112.12省荆沙北纬30.18 东经112.16 省老河口北纬32.23 东经111.40 省利川北纬30.18 东经108.56 省麻城北纬31.10 东经115.01 省浦圻北纬29.42 东经113.51 省潜江北纬30.26 东经112.53 省石首北纬29.43 东经112.24 省北纬32.40 东经110.47省随州北纬31.42 东经113.22 省天门北纬60.39 东经113.10 省武穴北纬29.51 东经115.33 省襄樊北纬32.02 东经112.08 省北纬29.53 东经114.17省仙桃北纬30.22 东经113.27 省北纬30.56 东经113.54省北纬30.42 东经111.17省宜城北纬31.42 东经112.15 省应城北纬30.57 东经113.33 省枣阳北纬32.07 东经112.44 省枝城北纬30.23 东经111.27 省钟祥北纬31.10 东经112.34 省北纬28.12 东经112.59省北纬29.02 东经111.51省北纬25.46 东经113.02省北纬26.53 东经112.37省洪江北纬27.07 东经109.59 省北纬27.33 东经109.58省津市北纬29.38 东经111.52 省北纬28.18 东经109.43省耒阳北纬26.24 东经112.51 省冷水江北纬27.42 东经111.26 省冷水滩北纬26.26 东经111.35 省涟源北纬27.41 东经111.41 省醴陵北纬27.40 东经113.30省临湘北纬29.29 东经113.27 省浏阳北纬28.09 东经113.37 省北纬27.44 东经111.59省汨罗北纬28.49 东经113.03 省韶山北纬27.54 东经112.29 省北纬27.14 东经111.28省武冈北纬26.43 东经110.37 省北纬27.52 东经112.53省湘乡北纬27.44 东经112.31 省北纬28.36 东经112.20省永州北纬26.13 东经111.37 省沅江北纬28.50 东经112.22 省北纬29.22 东经113.06省北纬29.08 东经110.29省株洲北纬27.51 东经113.09 省资兴北纬25.58 东经113.13 省北纬43.54 东经125.19省北纬45.38 东经122.50省白山北纬41.56 东经126.26 省大安北纬45.30 东经124.18 省德惠北纬44.32 东经125.42 省北纬43.22 东经128.13省公主岭北纬43.31 东经124.49 省和龙北纬42.32 东经129.00 省桦甸北纬42.58 东经126.44 省北纬42.52 东经130.22 省集安北纬41.08 东经126.11 省蛟河北纬43.42 东经127.21 省北纬43.52 东经126.33省九台北纬44.09 东经125.51 省北纬42.54 东经125.09省临江北纬41.49 东经126.53 省龙井北纬42.46 东经129.26 省梅河口北纬42.32 东经125.40 省舒兰北纬44.24 东经126.57 省北纬43.10 东经124.22省北纬45.11 东经124.49省洮南北纬45.20 东经122.47 省北纬41.43 东经125.56省图们北纬42.57 东经129.51 省北纬42.54 东经129.30省愉树北纬44.49 东经126.32 省北纬32.03 东经118.46省常熟北纬31.39 东经120.43省北纬31.47 东经119.58省丹阳北纬32.00 东经119.32 省东台北纬32.51 东经120.19 省高邮北纬32.47 东经119.27 省海门北纬31.53 东经121.09 省北纬33.30 东经119.09省北纬33.36 东经119.02省江都北纬32.26 东经119.32 省堰北纬32.34 东经120.08省江阴北纬31.54 东经120.17 省靖江北纬32.02 东经120.17 省金坛北纬31.46 东经119.33 省昆山北纬31.23 东经120.57 省连去港北纬34.36 东经119.10 省北纬31.26 东经119.29省北纬32.01 东经120.51省邳州北纬34.19 东经117.59 省启乐北纬31.48 东经121.39 省如皋北纬32.23 东经120.33 省宿迁北纬33.58 东经118.18 省北纬31.19 东经120.37省太仓北纬31.27 东经121.06省泰兴北纬32.10 东经120.01 省北纬32.30 东经119.54省通州北纬32.05 东经121.03 省吴江北纬31.10 东经120.39 省北纬31.34 东经120.18省兴化北纬32.56 东经119.50 省新沂北纬34.22 东经118.20 省北纬34.15 东经117.11省盐在北纬33.22 东经120.08 省扬中北纬32.14 东经119.49 省北纬32.23 东经119.26省宜兴北纬31.21 东经119.49 省仪征北纬32.16 东经119.10 省家港北纬31.52 东经120.32 省北纬32.11 东经119.27省北纬28.40 东经115.55省德兴北纬28.57 东经117.35 省丰城北纬28.12 东经115.48 省北纬28.52 东经114.56省高安北纬28.25 东经115.22 省北纬27.07 东经114.58省北纬29.17 东经117.13省井冈山北纬26.34 东经114.10 省北纬29.43 东经115.58省乐平北纬28.58 东经117.08 省北纬27.59 东经116.21省北纬27.37 东经113.50省瑞昌北纬29.40 东经115.38 省瑞金北纬25.53 东经116.01 省北纬25.27 东经117.58省新余北纬27.48 东经114.56 省北纬27.47 东经114.23省北纬28.14 东经117.03省樟树北纬28.03 东经115.32 省北纬41.48 东经123.25省北纬41.07 东经123.00省北票北纬41.48 东经120.47 省北纬41.18 东经123.46省北纬41.34 东经120.27省北纬38.55 东经121.36省北纬40.08 东经124.22省大石桥北纬40.37 东经122.31 省东港北纬39.53 东经124.08 省凤城北纬40.28 东经124.02省北纬41.51 东经123.54省北纬42.01 东经121.39省盖州北纬40.24 东经122.21省海城北纬40.51 东经122.43省北纬40.45 东经120.51省北纬41.07 东经121.09省开原北纬42.32 东经124.02省北纬41.16 东经123.12省凌海北纬41.10 东经121.21省凌源北纬41.14 东经119.22省北纬41.07 东经122.03省普兰店北纬39.23 东经121.58省铁法北纬42.28 东经123.32省北纬42.18 东经123.51省瓦房店北纬39.37 东经122.00省兴城北纬40.37 东经120.41省新民北纬41.59 东经122.49省北纬40.39 东经122.13省庄河北纬39.41 东经122.58自治区呼和浩特北纬40.48 东经111.41 自治区北纬40.39 东经109.49自治区北纬42.17 东经118.58。
全国主要城市经纬度

所在省城市名纬度经度安徽省合肥北纬31.52 东经117.17 安徽省安庆北纬30.31 东经117.02 安徽省蚌埠北纬32.56 东经117.21 安徽省亳州北纬33.52 东经115.47 安徽省巢湖北纬31.36 东经117.52 安徽省滁州北纬32.18 东经118.18 安徽省阜阳北纬32.54 东经115.48 安徽省贵池北纬30.39 东经117.28 安徽省淮北北纬33.57 东经116.47 安徽省淮南北纬32.37 东经116.58 安徽省黄山北纬29.43 东经118.18 安徽省界首北纬33.15 东经115.21 安徽省六安北纬31.44 东经116.28 安徽省马鞍山北纬31.43 东经118.28 安徽省明光北纬32.47 东经117.58 安徽省宿州北纬33.38 东经116.58 安徽省天长北纬32.41 东经118.59 安徽省铜陵北纬30.56 东经117.48 安徽省芜湖北纬31.19 东经118.22 安徽省宣州北纬30.57 东经118.44澳门澳门市北纬21.33 东经115.07北京市北京市北纬39.55 东经116.24福建省福州北纬26.05 东经119.18 福建省长乐北纬25.58 东经119.31 福建省福安北纬27.06 东经119.39 福建省福清北纬25.42 东经119.23 福建省建瓯北纬27.03 东经118.20 福建省建阳北纬27.21 东经118.07 福建省晋江北纬24.49 东经118.35 福建省龙海北纬24.26 东经117.48 福建省龙岩北纬25.06 东经117.01 福建省南安北纬24.57 东经118.23 福建省南平北纬26.38 东经118.10 福建省宁德北纬26.39 东经119.31 福建省莆田北纬24.26 东经119.01 福建省泉州北纬24.56 东经118.36 福建省三明北纬26.13 东经117.36 福建省邵武北纬27.20 东经117.29 福建省石狮北纬24.44 东经118.38 福建省武夷山北纬27.46 东经118.02福建省永安北纬25.58 东经117.23 福建省漳平北纬25.17 东经117.24 福建省漳州北纬24.31 东经117.39甘肃省兰州北纬36.04 东经103.51 甘肃省白银北纬36.33 东经104.12 甘肃省敦煌北纬40.08 东经94.41 甘肃省嘉峪关北纬39.48 东经98.14 甘肃省金昌北纬38.28 东经102.10 甘肃省酒泉北纬39.44 东经98.31 甘肃省临夏北纬35.37 东经103.12 甘肃省平凉北纬35.32 东经106.40 甘肃省天水北纬34.37 东经105.42 甘肃省武威北纬37.56 东经102.39 甘肃省西峰北纬35.45 东经107.40 甘肃省玉门北纬39.49 东经97.35 甘肃省张掖北纬38.56 东经100.26广东省广州北纬23.08 东经113.14 广东省潮阳北纬23.16 东经116.36 广东省潮州北纬23.40 东经116.38 广东省澄海北纬23.28 东经116.46 广东省从化北纬23.33 东经113.33 广东省东莞北纬23.02 东经113.45 广东省恩平北纬22.12 东经112.19 广东省佛山北纬23.02 东经113.06 广东省高明北纬22.53 东经112.50 广东省高要北纬23.02 东经112.26 广东省高州北纬21.54 东经110.50 广东省鹤山北纬22.46 东经112.57 广东省河源北纬23.43 东经114.41 广东省花都北纬23.23 东经113.12 广东省化州北纬21.39 东经110.37 广东省惠阳北纬22.48 东经114.28 广东省惠州北纬23.05 东经114.22 广东省江门北纬22.35 东经113.04 广东省揭阳北纬22.32 东经116.21 广东省开平北纬22.22 东经112.40 广东省乐昌北纬25.09 东经113.21 广东省雷州北纬20.54 东经110.04 广东省廉江北纬21.37 东经110.17 广东省连州北纬24.48 东经112.23 广东省罗定北纬22.46 东经111.33广东省梅州北纬24.19 东经116.07广东省南海北纬23.01 东经113.09广东省番禺北纬22.57 东经113.22广东省普宁北纬23.18 东经116.10广东省清远北纬23.42 东经113.01广东省三水北纬23.10 东经112.52广东省汕头北纬23.22 东经116.41广东省汕尾北纬22.47 东经115.21广东省韶关北纬24.48 东经113.37广东省深圳北纬22.33 东经114.07广东省顺德北纬22.50 东经113.15广东省四会北纬23.21 东经112.41广东省台山北纬22.15 东经112.48广东省吴川北纬21.26 东经110.47广东省新会北纬22.32 东经113.01广东省兴宁北纬24.09 东经115.43广东省阳春北纬22.10 东经111.48广东省阳江北纬21.50 东经111.58广东省英德北纬24.10 东经113.22广东省云浮北纬22.57 东经112.02广东省增城北纬23.18 东经113.49广东省湛江北纬21.11 东经110.24广东省肇庆北纬23.03 东经112.27广东省中山北纬22.31 东经113.22广东省珠海北纬22.17 东经113.34广西自治区南宁北纬22.48 东经108.19 广西自治区北海北纬21.28 东经109.07 广西自治区北流北纬22.42 东经110.21 广西自治区百色北纬23.54 东经106.36 广西自治区防城港北纬21.37 东经108.20 广西自治区贵港北纬23.06 东经109.36 广西自治区桂林北纬25.17 东经110.17 广西自治区桂平北纬23.22 东经110.04 广西自治区河池北纬24.42 东经108.03 广西自治区合山北纬23.47 东经108.52 广西自治区柳州北纬23.19 东经109.24 广西自治区赁祥北纬22.07 东经106.44 广西自治区钦州北纬21.57 东经108.37 广西自治区梧州北纬23.29 东经111.20 广西自治区玉林北纬22.38 东经110.09 广西自治区宜州北纬24.28 东经108.40贵州省安顺北纬26.14 东经105.55 贵州省毕节北纬27.18 东经105.18 贵州省赤水北纬28.34 东经105.42 贵州省都匀北纬26.15 东经107.31 贵州省凯里北纬26.35 东经107.58 贵州省六盘水北纬26.35 东经104.50 贵州省清镇北纬26.33 东经106.27 贵州省铜仁北纬27.43 东经109.12 贵州省兴义北纬25.05 东经104.53 贵州省遵义北纬27.42 东经106.55海南省海口北纬20.02 东经110.20 海南省儋州北纬19.31 东经109.34 海南省琼海北纬19.14 东经110.28 海南省琼山北纬19.59 东经110.21 海南省三亚北纬18.14 东经109.31 海南省通什北纬18.46 东经109.31河北省石家庄北纬38.02 东经114.30 河北省安国北纬38.24 东经115.20 河北省保定北纬38.51 东经115.30 河北省霸州北纬39.06 东经116.24 河北省泊头北纬38.04 东经116.34 河北省沧州北纬38.18 东经116.52 河北省承德北纬40.59 东经117.57 河北省定州北纬38.30 东经115.00 河北省丰南北纬39.34 东经118.06 河北省高碑店北纬39.20 东经115.51 河北省蒿城北纬38.02 东经114.50 河北省邯郸北纬36.36 东经114.28 河北省河间北纬38.26 东经116.05 河北省衡水北纬37.44 东经115.42 河北省黄骅北纬38.21 东经117.21 河北省晋州北纬38.02 东经115.02 河北省冀州北纬37.34 东经115.33 河北省廓坊北纬39.31 东经116.42 河北省鹿泉北纬38.04 东经114.19 河北省南宫北纬37.22 东经115.23 河北省秦皇岛北纬39.55 东经119.35 河北省任丘北纬38.42 东经116.07 河北省三河北纬39.58 东经117.04 河北省沙河北纬36.51 东经114.30 河北省深州北纬38.01 东经115.32河北省武安北纬36.42 东经114.11 河北省邢台北纬37.04 东经114.30 河北省辛集北纬37.54 东经115.12 河北省新乐北纬38.20 东经114.41 河北省张家口北纬40.48 东经114.53 河北省涿州北纬39.29 东经115.59 河北省遵化北纬40.11 东经117.58 河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21 河南省长葛北纬34.12 东经113.47 河南省登封北纬34.27 东经113.02 河南省邓州北纬32.42 东经112.05 河南省巩义北纬34.46 东经112.58 河南省鹤壁北纬35.54 东经114.11 河南省辉县北纬35.27 东经113.47 河南省焦作北纬35.14 东经113.12 河南省济源北纬35.04 东经112.35 河南省开封北纬34.47 东经114.21 河南省灵宝北纬34.31 东经110.52 河南省林州北纬36.03 东经113.49 河南省漯河北纬33.33 东经114.02 河南省洛阳北纬34.41 东经112.27 河南省南阳北纬33.00 东经112.32 河南省平顶山北纬33.44 东经113.17 河南省濮阳北纬35.44 东经115.01 河南省沁阳北纬35.05 东经112.57 河南省汝州北纬34.09 东经112.50 河南省三门峡北纬34.47 东经111.12 河南省商丘北纬34.26 东经115.38 河南省卫辉北纬35.24 东经114.03 河南省舞钢北纬33.17 东经113.30 河南省项城北纬33.26 东经114.54 河南省荥阳北纬34.46 东经113.21 河南省新密北纬34.31 东经113.22 河南省新乡北纬35.18 东经113.52 河南省信阳北纬32.07 东经114.04 河南省新郑北纬34.24 东经113.43 河南省许昌北纬34.01 东经113.49 河南省偃师北纬34.43 东经112.47 河南省义马北纬34.43 东经111.55 河南省禹州北纬34.09 东经113.28 河南省周口北纬33.37 东经114.38 河南省驻马店北纬32.58 东经114.01黑龙江省哈尔滨北纬45.44 东经126.36 黑龙江省阿城北纬45.32 东经126.58黑龙江省安达北纬46.24 东经125.18黑龙江省北安北纬48.15 东经126.31黑龙江省大庆北纬46.36 东经125.01黑龙江省富锦北纬47.15 东经132.02黑龙江省海林北纬44.35 东经129.21黑龙江省海伦北纬47.28 东经126.57黑龙江省鹤岗北纬47.20 东经130.16黑龙江省黑河北纬50.14 东经127.29黑龙江省佳木斯北纬46.47 东经130.22 黑龙江省鸡西北纬45.17 东经130.57黑龙江省密山北纬45.32 东经131.50黑龙江省牡丹江北纬44.35 东经129.36 黑龙江省讷河北纬48.29 东经124.51黑龙江省宁安北纬44.21 东经129.28黑龙江省齐齐哈尔北纬47.20 东经123.57 黑龙江省七台河北纬45.48 东经130.49 黑龙江省双城北纬45.22 东经126.15黑龙江省尚志北纬45.14 东经127.55黑龙江省双鸭山北纬46.38 东经131.11 黑龙江省绥芬河北纬44.25 东经131.11 黑龙江省绥化北纬46.38 东经126.59黑龙江省铁力北纬46.59 东经128.01黑龙江省同江北纬47.39 东经132.30黑龙江省五常北纬44.55 东经127.11黑龙江省五大连池北纬48.38 东经126.07 黑龙江省伊春北纬47.42 东经128.56黑龙江省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省广水北纬31.37 东经113.48湖北省洪湖北纬29.48 东经113.27湖北省黄石北纬30.12 东经115.06湖北省黄州北纬30.27 东经114.52湖北省荆门北纬31.02 东经112.12湖北省荆沙北纬30.18 东经112.16湖北省利川北纬30.18 东经108.56 湖北省麻城北纬31.10 东经115.01 湖北省浦圻北纬29.42 东经113.51 湖北省潜江北纬30.26 东经112.53 湖北省石首北纬29.43 东经112.24 湖北省十堰北纬32.40 东经110.47 湖北省随州北纬31.42 东经113.22 湖北省天门北纬60.39 东经113.10 湖北省武穴北纬29.51 东经115.33 湖北省襄樊北纬32.02 东经112.08 湖北省咸宁北纬29.53 东经114.17 湖北省仙桃北纬30.22 东经113.27 湖北省孝感北纬30.56 东经113.54 湖北省宜昌北纬30.42 东经111.17 湖北省宜城北纬31.42 东经112.15 湖北省应城北纬30.57 东经113.33 湖北省枣阳北纬32.07 东经112.44 湖北省枝城北纬30.23 东经111.27 湖北省钟祥北纬31.10 东经112.34湖南省长沙北纬28.12 东经112.59 湖南省常德北纬29.02 东经111.51 湖南省郴州北纬25.46 东经113.02 湖南省衡阳北纬26.53 东经112.37 湖南省洪江北纬27.07 东经109.59 湖南省怀化北纬27.33 东经109.58 湖南省津市北纬29.38 东经111.52 湖南省吉首北纬28.18 东经109.43 湖南省耒阳北纬26.24 东经112.51 湖南省冷水江北纬27.42 东经111.26 湖南省冷水滩北纬26.26 东经111.35 湖南省涟源北纬27.41 东经111.41 湖南省醴陵北纬27.40 东经113.30 湖南省临湘北纬29.29 东经113.27 湖南省浏阳北纬28.09 东经113.37 湖南省娄底北纬27.44 东经111.59 湖南省汨罗北纬28.49 东经113.03 湖南省韶山北纬27.54 东经112.29 湖南省邵阳北纬27.14 东经111.28 湖南省武冈北纬26.43 东经110.37 湖南省湘潭北纬27.52 东经112.53 湖南省湘乡北纬27.44 东经112.31 湖南省益阳北纬28.36 东经112.20湖南省沅江北纬28.50 东经112.22 湖南省岳阳北纬29.22 东经113.06 湖南省张家界北纬29.08 东经110.29 湖南省株洲北纬27.51 东经113.09 湖南省资兴北纬25.58 东经113.13吉林省长春北纬43.54 东经125.19 吉林省白城北纬45.38 东经122.50 吉林省白山北纬41.56 东经126.26 吉林省大安北纬45.30 东经124.18 吉林省德惠北纬44.32 东经125.42 吉林省敦化北纬43.22 东经128.13 吉林省公主岭北纬43.31 东经124.49 吉林省和龙北纬42.32 东经129.00 吉林省桦甸北纬42.58 东经126.44 吉林省珲春北纬42.52 东经130.22 吉林省集安北纬41.08 东经126.11 吉林省蛟河北纬43.42 东经127.21 吉林省吉林北纬43.52 东经126.33 吉林省九台北纬44.09 东经125.51 吉林省辽源北纬42.54 东经125.09 吉林省临江北纬41.49 东经126.53 吉林省龙井北纬42.46 东经129.26 吉林省梅河口北纬42.32 东经125.40 吉林省舒兰北纬44.24 东经126.57 吉林省四平北纬43.10 东经124.22 吉林省松原北纬45.11 东经124.49 吉林省洮南北纬45.20 东经122.47 吉林省通化北纬41.43 东经125.56 吉林省图们北纬42.57 东经129.51 吉林省延吉北纬42.54 东经129.30 吉林省愉树北纬44.49 东经126.32江苏省南京北纬32.03 东经118.46 江苏省常熟北纬31.39 东经120.43 江苏省常州北纬31.47 东经119.58 江苏省丹阳北纬32.00 东经119.32 江苏省东台北纬32.51 东经120.19 江苏省高邮北纬32.47 东经119.27 江苏省海门北纬31.53 东经121.09 江苏省淮安北纬33.30 东经119.09 江苏省淮阴北纬33.36 东经119.02江苏省姜堰北纬32.34 东经120.08 江苏省江阴北纬31.54 东经120.17 江苏省靖江北纬32.02 东经120.17 江苏省金坛北纬31.46 东经119.33 江苏省昆山北纬31.23 东经120.57 江苏省连去港北纬34.36 东经119.10 江苏省溧阳北纬31.26 东经119.29 江苏省南通北纬32.01 东经120.51 江苏省邳州北纬34.19 东经117.59 江苏省启乐北纬31.48 东经121.39 江苏省如皋北纬32.23 东经120.33 江苏省宿迁北纬33.58 东经118.18 江苏省苏州北纬31.19 东经120.37 江苏省太仓北纬31.27 东经121.06 江苏省泰兴北纬32.10 东经120.01 江苏省泰州北纬32.30 东经119.54 江苏省通州北纬32.05 东经121.03 江苏省吴江北纬31.10 东经120.39 江苏省无锡北纬31.34 东经120.18 江苏省兴化北纬32.56 东经119.50 江苏省新沂北纬34.22 东经118.20 江苏省徐州北纬34.15 东经117.11 江苏省盐在北纬33.22 东经120.08 江苏省扬中北纬32.14 东经119.49 江苏省扬州北纬32.23 东经119.26 江苏省宜兴北纬31.21 东经119.49 江苏省仪征北纬32.16 东经119.10 江苏省张家港北纬31.52 东经120.32 江苏省镇江北纬32.11 东经119.27江西省南昌北纬28.40 东经115.55 江西省德兴北纬28.57 东经117.35 江西省丰城北纬28.12 东经115.48 江西省赣州北纬28.52 东经114.56 江西省高安北纬28.25 东经115.22 江西省吉安北纬27.07 东经114.58 江西省景德镇北纬29.17 东经117.13 江西省井冈山北纬26.34 东经114.10 江西省九江北纬29.43 东经115.58 江西省乐平北纬28.58 东经117.08 江西省临川北纬27.59 东经116.21 江西省萍乡北纬27.37 东经113.50 江西省瑞昌北纬29.40 东经115.38江西省上饶北纬25.27 东经117.58江西省新余北纬27.48 东经114.56江西省宜春北纬27.47 东经114.23江西省鹰潭北纬28.14 东经117.03江西省樟树北纬28.03 东经115.32辽宁省沈阳北纬41.48 东经123.25辽宁省鞍山北纬41.07 东经123.00辽宁省北票北纬41.48 东经120.47辽宁省本溪北纬41.18 东经123.46辽宁省朝阳北纬41.34 东经120.27辽宁省大连北纬38.55 东经121.36辽宁省丹东北纬40.08 东经124.22辽宁省大石桥北纬40.37 东经122.31辽宁省东港北纬39.53 东经124.08辽宁省凤城北纬40.28 东经124.02辽宁省抚顺北纬41.51 东经123.54辽宁省阜新北纬42.01 东经121.39辽宁省盖州北纬40.24 东经122.21辽宁省海城北纬40.51 东经122.43辽宁省葫芦岛北纬40.45 东经120.51辽宁省锦州北纬41.07 东经121.09辽宁省开原北纬42.32 东经124.02辽宁省辽阳北纬41.16 东经123.12辽宁省凌海北纬41.10 东经121.21辽宁省凌源北纬41.14 东经119.22辽宁省盘锦北纬41.07 东经122.03辽宁省普兰店北纬39.23 东经121.58辽宁省铁法北纬42.28 东经123.32辽宁省铁岭北纬42.18 东经123.51辽宁省瓦房店北纬39.37 东经122.00辽宁省兴城北纬40.37 东经120.41辽宁省新民北纬41.59 东经122.49辽宁省营口北纬40.39 东经122.13辽宁省庄河北纬39.41 东经122.58内蒙古自治区呼和浩特北纬40.48 东经111.41 内蒙古自治区包头北纬40.39 东经109.49内蒙古自治区赤峰北纬42.17 东经118.58内蒙古自治区东胜北纬39.48 东经109.59内蒙古自治区二连浩特北纬43.38 东经111.58 内蒙古自治区额尔古纳北纬50.13 东经120.11 内蒙古自治区丰镇北纬40.27 东经113.09内蒙古自治区根河北纬50.48 东经121.29内蒙古自治区海拉尔北纬49.12 东经119.39 内蒙古自治区霍林郭勒北纬45.32 东经119.38 内蒙古自治区集宁北纬41.02 东经113.06内蒙古自治区临河北纬40.46 东经107.22内蒙古自治区满洲里北纬49.35 东经117.23 内蒙古自治区通辽北纬43.37 东经122.16内蒙古自治区乌兰浩特北纬46.03 东经122.03 内蒙古自治区乌海北纬39.40 东经106.48内蒙古自治区锡林浩特北纬43.57 东经116.03 内蒙古自治区牙克石北纬49.17 东经120.40 内蒙古自治区扎兰屯北纬48.00 东经122.47宁夏自治区银川北纬38.27 东经106.16宁夏自治区青铜峡北纬37.56 东经105.59宁夏自治区石嘴山北纬39.02 东经106.22宁夏自治区吴忠北纬37.59 东经106.11青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55山东省济南北纬36.40 东经117.00山东省安丘北纬36.25 东经119.12山东省滨州北纬37.22 东经118.02山东省昌邑北纬39.52 东经119.24山东省德州北纬37.26 东经116.17山东省东营北纬37.27 东经118.30山东省肥城北纬36.14 东经116.46山东省高密北纬36.22 东经119.44山东省菏泽北纬35.14 东经115.26山东省胶南北纬35.53 东经119.58山东省胶州北纬36.17 东经120.00山东省即墨北纬36.22 东经120.28山东省济宁北纬35.23 东经116.33山东省莱芜北纬36.12 东经117.40山东省莱西北纬36.52 东经120.31山东省莱阳北纬36.58 东经120.42山东省莱州北纬37.10 东经119.57山东省乐陵北纬37.44 东经117.12山东省聊城北纬36.26 东经115.57山东省临清北纬36.51 东经115.42山东省临沂北纬35.03 东经118.20山东省龙口北纬37.39 东经120.21山东省平度北纬36.47 东经119.58 山东省青岛北纬36.03 东经120.18 山东省青州北纬36.42 东经118.28 山东省曲阜北纬35.36 东经116.58 山东省日照北纬35.23 东经119.32 山东省荣成北纬37.10 东经122.25 山东省乳山北纬36.54 东经121.31 山东省寿光北纬36.53 东经118.44 山东省泰安北纬36.11 东经117.08 山东省滕州北纬35.06 东经117.09 山东省潍坊北纬36.43 东经119.06 山东省威海北纬37.31 东经122.07 山东省文登北纬37.12 东经122.03 山东省新泰北纬35.54 东经117.45 山东省烟台北纬37.32 东经121.24 山东省兖州北纬35.32 东经116.49 山东省禹城北纬36.56 东经116.39 山东省枣庄北纬34.52 东经117.33 山东省章丘北纬36.43 东经117.32 山东省招远北纬37.21 东经120.23 山东省诸城北纬35.59 东经119.24 山东省淄博北纬36.48 东经118.03 山东省邹城北纬35.24 东经116.58山西省太原北纬37.54 东经112.33 山西省长治北纬36.11 东经113.06 山西省大同北纬40.06 东经113.17 山西省高平北纬35.48 东经112.55 山西省古交北纬37.54 东经112.09 山西省河津北纬35.35 东经110.41 山西省侯马北纬35.37 东经111.21 山西省霍州北纬36.34 东经111.42 山西省介休北纬37.02 东经111.55 山西省晋城北纬35.30 东经112.51 山西省临汾北纬36.05 东经111.31 山西省潞城北纬36.21 东经113.14 山西省朔州北纬39.19 东经112.26 山西省孝义北纬37.08 东经111.48 山西省忻州北纬38.24 东经112.43 山西省阳泉北纬37.51 东经113.34 山西省永济北纬34.52 东经110.27 山西省原平北纬38.43 东经112.42 山西省榆次北纬37.41 东经112.43陕西省西安北纬34.17 东经108.57 陕西省安康北纬32.41 东经109.01 陕西省宝鸡北纬34.22 东经107.09 陕西省韩城北纬35.28 东经110.27 陕西省汉中北纬33.04 东经107.01 陕西省华阴北纬34.34 东经110.05 陕西省商州北纬33.52 东经109.57 陕西省铜川北纬35.06 东经109.07 陕西省渭南北纬34.30 东经109.30 陕西省咸阳北纬34.20 东经108.43 陕西省兴平北纬34.18 东经108.29 陕西省延安北纬36.35 东经109.28 陕西省榆林北纬38.18 东经109.47上海市上海市北纬31.14 东经121.29四川省成都北纬30.40 东经104.04 四川省巴中北纬31.51 东经106.43 四川省崇州北纬30.39 东经103.40 四川省达川北纬31.14 东经107.29 四川省德阳北纬31.09 东经104.22 四川省都江堰北纬31.01 东经103.37 四川省峨眉山北纬29.36 东经103.29 四川省涪陵北纬29.42 东经107.22 四川省广汉北纬30.58 东经104.15 四川省广元北纬32.28 东经105.51 四川省华蓥北纬30.26 东经106.44 四川省简阳北纬30.24 东经104.32 四川省江油北纬31.48 东经104.42 四川省阆中北纬31.36 东经105.58 四川省乐山北纬29.36 东经103.44 四川省泸州北纬28.54 东经105.24 四川省绵阳北纬31.30 东经104.42 四川省南充北纬30.49 东经106.04 四川省内江北纬29.36 东经105.02 四川省攀枝花北纬26.34 东经101.43 四川省彭州北纬30.59 东经103.57 四川省邛崃北纬30.26 东经103.28 四川省遂宁北纬30.31 东经105.33 四川省万县北纬30.50 东经108.21 四川省万源北纬32.03 东经108.03 四川省西昌北纬27.54 东经102.16四川省宜宾北纬28.47 东经104.34四川省自贡北纬29.23 东经104.46四川省资阳北纬30.09 东经104.38台湾省台北市北纬25.03 东经121.30天津市天津市北纬39.02 东经117.12西藏自治区拉萨北纬29.39 东经91.08西藏自治区日喀则北纬29.16 东经88.51香港香港市北纬21.23 东经115.12新疆自治区乌鲁木齐北纬43.45 东经87.36 新疆自治区阿克苏北纬41.09 东经80.19 新疆自治区阿勒泰北纬47.50 东经88.12 新疆自治区阿图什北纬39.42 东经76.08 新疆自治区博乐北纬44.57 东经82.08新疆自治区昌吉北纬44.02 东经87.18新疆自治区阜康北纬44.09 东经87.58新疆自治区哈密北纬42.50 东经93.28新疆自治区和田北纬37.09 东经79.55新疆自治区克拉玛依北纬45.36 东经84.51 新疆自治区喀什北纬39.30 东经75.59新疆自治区库尔勒北纬41.46 东经86.07 新疆自治区奎屯北纬44.27 东经84.56新疆自治区石河子北纬44.18 东经86.00 新疆自治区塔城北纬46.46 东经82.59新疆自治区吐鲁番北纬42.54 东经89.11 新疆自治区伊宁北纬43.55 东经81.20云南省昆明北纬25.04 东经102.42云南省保山北纬25.08 东经99.10云南省楚雄北纬25.01 东经101.32云南省大理北纬25.34 东经100.13云南省东川北纬26.06 东经103.12云南省个旧北纬23.21 东经103.09云南省景洪北纬22.01 东经100.48云南省开远北纬23.43 东经103.13云南省曲靖北纬25.30 东经103.48云南省瑞丽北纬24.00 东经97.50云南省思茅北纬22.48 东经100.58云南省畹町北纬24.06 东经98.04云南省玉溪北纬24.22 东经102.32 云南省昭通北纬27.20 东经103.42浙江省杭州北纬30.16 东经120.10 浙江省慈溪北纬30.11 东经121.15 浙江省东阳北纬29.16 东经120.14 浙江省奉化北纬29.39 东经121.24 浙江省富阳北纬30.03 东经119.57 浙江省海宁北纬30.32 东经120.42 浙江省湖州北纬30.52 东经120.06 浙江省建德北纬29.29 东经119.16 浙江省江山北纬28.45 东经118.37 浙江省嘉兴北纬30.46 东经120.45 浙江省金华北纬29.07 东经119.39 浙江省兰溪北纬29.12 东经119.28 浙江省临海北纬28.51 东经121.08 浙江省丽水北纬28.27 东经119.54 浙江省龙泉北纬28.04 东经119.08 浙江省宁波北纬29.52 东经121.33 浙江省平湖北纬30.42 东经121.01 浙江省衢州北纬28.58 东经118.52 浙江省瑞安北纬27.48 东经120.38 浙江省上虞北纬30.01 东经120.52 浙江省绍兴北纬30.00 东经120.34 浙江省台州北纬28.41 东经121.27 浙江省桐乡北纬30.38 东经120.32 浙江省温岭北纬28.22 东经121.21 浙江省温州北纬28.01 东经120.39 浙江省萧山北纬30.09 东经120.16 浙江省义乌北纬29.18 东经120.04 浙江省乐清北纬28.08 东经120.58 浙江省余杭北纬30.26 东经120.18 浙江省余姚北纬30.02 东经121.10 浙江省永康北纬29.54 东经120.01 浙江省舟山北纬30.01 东经122.06 浙江省诸暨北纬29.43 东经120.14重庆市重庆市北纬29.35 东经106.33 重庆市合川市北纬30.02 东经106.15 重庆市江津市北纬29.18 东经106.16 重庆市南川市北纬29.10 东经107.05 重庆市永川市北纬29.23 东经105.53。
中国各大城市经纬度

1、中国各主要大城市经纬度数据:北京市市中心经纬度:(116.41667,39.91667)上海市区经纬度:(121.43333,34.50000)天津市区经纬度:(117.20000,39.13333)香港经纬度:(114.10000,22.20000)广州经纬度:(113.23333,23.16667)珠海经纬度:(113.51667,22.30000)深圳经纬度:(114.06667,22.61667)杭州经纬度:(120.20000,30.26667)重庆市区经纬度:(106.45000, 29.56667)青岛经纬度:(120.33333,36.06667)厦门经纬度:(118.10000,24.46667)福州经纬度:(119.30000,26.08333)兰州经纬度:(103.73333,36.03333)贵阳经纬度:(106.71667,26.56667)长沙经纬度:(113.00000,28.21667)南京经纬度:(118.78333,32.05000)南昌经纬度:(115.90000,28.68333)沈阳经纬度:(123.38333,41.80000)太原经纬度:(112.53333,37.86667)成都经纬度:(104.06667,30.66667)拉萨经纬度:(91.00000,29.60000)乌鲁木齐经纬度:(87.68333,43.76667)昆明经纬度:(102.73333,25.05000)西安经纬度:(108.95000,34.26667)西宁经纬度:(101.75000,36.56667)银川经纬度:(106.26667,38.46667)兰浩特经纬度:(122.08333,46.06667)哈尔滨经纬度:(126.63333,45.75000)长春经纬度:(125.35000,43.88333)武汉经纬度:(114.31667,30.51667)郑州经纬度:(113.65000,34.76667)石家庄经纬度:(114.48333,38.03333)三亚经纬度:(109.50000,18.20000)海口经纬度:(110.35000,20.01667)澳门经纬度:(113.50000,22.20000)2、中国主要城市经纬度查询(精确到二级省市):所在省城市名纬度经度安徽省合肥北纬31.52 东经117.17安徽省安庆北纬30.31 东经117.02安徽省蚌埠北纬32.56 东经117.21安徽省亳州北纬33.52 东经115.47安徽省巢湖北纬31.36 东经117.52安徽省滁州北纬32.18 东经118.18安徽省阜阳北纬32.54 东经115.48安徽省贵池北纬30.39 东经117.28安徽省淮北北纬33.57 东经116.47安徽省淮南北纬32.37 东经116.58安徽省黄山北纬29.43 东经118.18安徽省界首北纬33.15 东经115.21安徽省六安北纬31.44 东经116.28安徽省马鞍山北纬31.43 东经118.28安徽省明光北纬32.47 东经117.58安徽省宿州北纬33.38 东经116.58安徽省天长北纬32.41 东经118.59安徽省铜陵北纬30.56 东经117.48安徽省芜湖北纬31.19 东经118.22安徽省宣州北纬30.57 东经118.44澳门澳门市北纬21.33 东经115.07北京市北京市北纬39.55 东经116.24福建省福州北纬26.05 东经119.18福建省长乐北纬25.58 东经119.31福建省福安北纬27.06 东经119.39福建省福清北纬25.42 东经119.23福建省建瓯北纬27.03 东经118.20福建省建阳北纬27.21 东经118.07福建省晋江北纬24.49 东经118.35福建省龙海北纬24.26 东经117.48福建省龙岩北纬25.06 东经117.01福建省南安北纬24.57 东经118.23福建省南平北纬26.38 东经118.10福建省宁德北纬26.39 东经119.31福建省莆田北纬24.26 东经119.01 福建省泉州北纬24.56 东经118.36福建省邵武北纬27.20 东经117.29 福建省石狮北纬24.44 东经118.38 福建省武夷山北纬27.46 东经118.02 福建省厦门北纬24.27 东经118.06 福建省永安北纬25.58 东经117.23 福建省漳平北纬25.17 东经117.24 福建省漳州北纬24.31 东经117.39 甘肃省兰州北纬36.04 东经103.51 甘肃省白银北纬36.33 东经104.12 甘肃省敦煌北纬40.08 东经94.41甘肃省嘉峪关北纬39.48 东经98.14 甘肃省金昌北纬38.28 东经102.10 甘肃省酒泉北纬39.44 东经98.31甘肃省临夏北纬35.37 东经103.12 甘肃省平凉北纬35.32 东经106.40 甘肃省天水北纬34.37 东经105.42 甘肃省武威北纬37.56 东经102.39 甘肃省西峰北纬35.45 东经107.40 甘肃省玉门北纬39.49 东经97.35甘肃省张掖北纬38.56 东经100.26 广东省广州北纬23.08 东经113.14 广东省潮阳北纬23.16 东经116.36 广东省潮州北纬23.40 东经116.38 广东省澄海北纬23.28 东经116.46 广东省从化北纬23.33 东经113.33 广东省东莞北纬23.02 东经113.45 广东省恩平北纬22.12 东经112.19 广东省佛山北纬23.02 东经113.06 广东省高明北纬22.53 东经112.50 广东省高要北纬23.02 东经112.26 广东省高州北纬21.54 东经110.50 广东省鹤山北纬22.46 东经112.57 广东省河源北纬23.43 东经114.41 广东省花都北纬23.23 东经113.12 广东省化州北纬21.39 东经110.37 广东省惠阳北纬22.48 东经114.28 广东省惠州北纬23.05 东经114.22 广东省江门北纬22.35 东经113.04 广东省揭阳北纬22.32 东经116.21 广东省开平北纬22.22 东经112.40广东省雷州北纬20.54 东经110.04广东省廉江北纬21.37 东经110.17广东省连州北纬24.48 东经112.23广东省罗定北纬22.46 东经111.33广东省茂名北纬21.40 东经110.53广东省梅州北纬24.19 东经116.07广东省南海北纬23.01 东经113.09广东省番禺北纬22.57 东经113.22广东省普宁北纬23.18 东经116.10广东省清远北纬23.42 东经113.01广东省三水北纬23.10 东经112.52广东省汕头北纬23.22 东经116.41广东省汕尾北纬22.47 东经115.21广东省韶关北纬24.48 东经113.37广东省深圳北纬22.33 东经114.07广东省顺德北纬22.50 东经113.15广东省四会北纬23.21 东经112.41广东省台山北纬22.15 东经112.48广东省吴川北纬21.26 东经110.47广东省新会北纬22.32 东经113.01广东省兴宁北纬24.09 东经115.43广东省阳春北纬22.10 东经111.48广东省阳江北纬21.50 东经111.58广东省英德北纬24.10 东经113.22广东省云浮北纬22.57 东经112.02广东省增城北纬23.18 东经113.49广东省湛江北纬21.11 东经110.24广东省肇庆北纬23.03 东经112.27广东省中山北纬22.31 东经113.22广东省珠海北纬22.17 东经113.34广西自治区南宁北纬22.48 东经108.19 广西自治区北海北纬21.28 东经109.07 广西自治区北流北纬22.42 东经110.21 广西自治区百色北纬23.54 东经106.36 广西自治区防城港北纬21.37 东经108.20 广西自治区贵港北纬23.06 东经109.36广西自治区桂林北纬25.17 东经110.17 广西自治区桂平北纬23.22 东经110.04 广西自治区河池北纬24.42 东经108.03 广西自治区合山北纬23.47 东经108.52 广西自治区柳州北纬23.19 东经109.24 广西自治区赁祥北纬22.07 东经106.44 广西自治区钦州北纬21.57 东经108.37 广西自治区梧州北纬23.29 东经111.20 广西自治区玉林北纬22.38 东经110.09 广西自治区宜州北纬24.28 东经108.40 贵州省贵阳北纬26.35 东经106.42贵州省安顺北纬26.14 东经105.55贵州省毕节北纬27.18 东经105.18贵州省赤水北纬28.34 东经105.42贵州省都匀北纬26.15 东经107.31贵州省凯里北纬26.35 东经107.58贵州省六盘水北纬26.35 东经104.50 贵州省清镇北纬26.33 东经106.27贵州省铜仁北纬27.43 东经109.12贵州省兴义北纬25.05 东经104.53贵州省遵义北纬27.42 东经106.55海南省海口北纬20.02 东经110.20海南省儋州北纬19.31 东经109.34海南省琼海北纬19.14 东经110.28海南省琼山北纬19.59 东经110.21海南省三亚北纬18.14 东经109.31海南省通什北纬18.46 东经109.31河北省石家庄北纬38.02 东经114.30 河北省安国北纬38.24 东经115.20河北省保定北纬38.51 东经115.30河北省霸州北纬39.06 东经116.24河北省泊头北纬38.04 东经116.34河北省沧州北纬38.18 东经116.52河北省承德北纬40.59 东经117.57河北省定州北纬38.30 东经115.00河北省丰南北纬39.34 东经118.06河北省高碑店北纬39.20 东经115.51 河北省蒿城北纬38.02 东经114.50河北省邯郸北纬36.36 东经114.28河北省河间北纬38.26 东经116.05河北省衡水北纬37.44 东经115.42河北省晋州北纬38.02 东经115.02 河北省冀州北纬37.34 东经115.33 河北省廓坊北纬39.31 东经116.42 河北省鹿泉北纬38.04 东经114.19 河北省南宫北纬37.22 东经115.23 河北省秦皇岛北纬39.55 东经119.35 河北省任丘北纬38.42 东经116.07 河北省三河北纬39.58 东经117.04 河北省沙河北纬36.51 东经114.30 河北省深州北纬38.01 东经115.32 河北省唐山北纬39.36 东经118.11 河北省武安北纬36.42 东经114.11 河北省邢台北纬37.04 东经114.30 河北省辛集北纬37.54 东经115.12 河北省新乐北纬38.20 东经114.41河北省张家口北纬40.48 东经114.53 河北省涿州北纬39.29 东经115.59 河北省遵化北纬40.11 东经117.58 河南省郑州北纬34.46 东经11340河南省安阳北纬36.06 东经114.21 河南省长葛北纬34.12 东经113.47 河南省登封北纬34.27 东经113.02 河南省邓州北纬32.42 东经112.05 河南省巩义北纬34.46 东经112.58 河南省鹤壁北纬35.54 东经114.11 河南省辉县北纬35.27 东经113.47 河南省焦作北纬35.14 东经113.12 河南省济源北纬35.04 东经112.35 河南省开封北纬34.47 东经114.21 河南省灵宝北纬34.31 东经110.52 河南省林州北纬36.03 东经113.49 河南省漯河北纬33.33 东经114.02 河南省洛阳北纬34.41 东经112.27 河南省南阳北纬33.00 东经112.32 河南省平顶山北纬33.44 东经113.17 河南省濮阳北纬35.44 东经115.01河南省汝州北纬34.09 东经112.50河南省三门峡北纬34.47 东经111.12河南省商丘北纬34.26 东经115.38河南省卫辉北纬35.24 东经114.03河南省舞钢北纬33.17 东经113.30河南省项城北纬33.26 东经114.54河南省荥阳北纬34.46 东经113.21河南省新密北纬34.31 东经113.22河南省新乡北纬35.18 东经113.52河南省信阳北纬32.07 东经114.04河南省新郑北纬34.24 东经113.43河南省许昌北纬34.01 东经113.49河南省偃师北纬34.43 东经112.47河南省义马北纬34.43 东经111.55河南省禹州北纬34.09 东经113.28河南省周口北纬33.37 东经114.38河南省驻马店北纬32.58 东经114.01黑龙江省哈尔滨北纬45.44 东经126.36 黑龙江省阿城北纬45.32 东经126.58黑龙江省安达北纬46.24 东经125.18黑龙江省北安北纬48.15 东经126.31黑龙江省大庆北纬46.36 东经125.01黑龙江省富锦北纬47.15 东经132.02黑龙江省海林北纬44.35 东经129.21黑龙江省海伦北纬47.28 东经126.57黑龙江省鹤岗北纬47.20 东经130.16黑龙江省黑河北纬50.14 东经127.29黑龙江省佳木斯北纬46.47 东经130.22 黑龙江省鸡西北纬45.17 东经130.57黑龙江省密山北纬45.32 东经131.50黑龙江省牡丹江北纬44.35 东经129.36 黑龙江省讷河北纬48.29 东经124.51黑龙江省宁安北纬44.21 东经129.28黑龙江省齐齐哈尔北纬47.20 东经123.57 黑龙江省七台河北纬45.48 东经130.49 黑龙江省双城北纬45.22 东经126.15黑龙江省尚志北纬45.14 东经127.55黑龙江省双鸭山北纬46.38 东经131.11 黑龙江省绥芬河北纬44.25 东经131.11 黑龙江省绥化北纬46.38 东经126.59黑龙江省同江北纬47.39 东经132.30黑龙江省五常北纬44.55 东经127.11黑龙江省五大连池北纬48.38 东经126.07 黑龙江省伊春北纬47.42 东经128.56黑龙江省肇东北纬46.04 东经125.58湖北省武汉北纬30.35 东经114.17湖北省安陆北纬31.15 东经113.41湖北省当阳北纬30.50 东经111.47湖北省丹江口北纬32.33 东经108.30湖北省大冶北纬30.06 东经114.58湖北省恩施北纬30.16 东经109.29湖北省鄂州北纬30.23 东经114.52湖北省广水北纬31.37 东经113.48湖北省洪湖北纬29.48 东经113.27湖北省黄石北纬30.12 东经115.06湖北省黄州北纬30.27 东经114.52湖北省荆门北纬31.02 东经112.12湖北省荆沙北纬30.18 东经112.16湖北省老河口北纬32.23 东经111.40湖北省利川北纬30.18 东经108.56湖北省麻城北纬31.10 东经115.01湖北省浦圻北纬29.42 东经113.51湖北省潜江北纬30.26 东经112.53湖北省石首北纬29.43 东经112.24湖北省十堰北纬32.40 东经110.47湖北省随州北纬31.42 东经113.22湖北省天门北纬60.39 东经113.10湖北省武穴北纬29.51 东经115.33湖北省襄樊北纬32.02 东经112.08湖北省咸宁北纬29.53 东经114.17湖北省仙桃北纬30.22 东经113.27湖北省孝感北纬30.56 东经113.54湖北省宜昌北纬30.42 东经111.17湖北省宜城北纬31.42 东经112.15湖北省应城北纬30.57 东经113.33湖北省枣阳北纬32.07 东经112.44湖北省钟祥北纬31.10 东经112.34 湖南省长沙北纬28.12 东经112.59 湖南省常德北纬29.02 东经111.51 湖南省郴州北纬25.46 东经113.02 湖南省衡阳北纬26.53 东经112.37 湖南省洪江北纬27.07 东经109.59 湖南省怀化北纬27.33 东经109.58 湖南省津市北纬29.38 东经111.52 湖南省吉首北纬28.18 东经109.43 湖南省耒阳北纬26.24 东经112.51 湖南省冷水江北纬27.42 东经111.26 湖南省冷水滩北纬26.26 东经111.35 湖南省涟源北纬27.41 东经111.41 湖南省醴陵北纬27.40 东经113.30 湖南省临湘北纬29.29 东经113.27 湖南省浏阳北纬28.09 东经113.37 湖南省娄底北纬27.44 东经111.59 湖南省汨罗北纬28.49 东经113.03 湖南省韶山北纬27.54 东经112.29 湖南省邵阳北纬27.14 东经111.28 湖南省武冈北纬26.43 东经110.37 湖南省湘潭北纬27.52 东经112.53 湖南省湘乡北纬27.44 东经112.31 湖南省益阳北纬28.36 东经112.20 湖南省永州北纬26.13 东经111.37 湖南省沅江北纬28.50 东经112.22 湖南省岳阳北纬29.22 东经113.06 湖南省张家界北纬29.08 东经110.29 湖南省株洲北纬27.51 东经113.09 湖南省资兴北纬25.58 东经113.13 吉林省长春北纬43.54 东经125.19 吉林省白城北纬45.38 东经122.50 吉林省白山北纬41.56 东经126.26 吉林省大安北纬45.30 东经124.18 吉林省德惠北纬44.32 东经125.42 吉林省敦化北纬43.22 东经128.13 吉林省公主岭北纬43.31 东经124.49 吉林省和龙北纬42.32 东经129.00吉林省桦甸北纬42.58 东经126.44吉林省珲春北纬42.52 东经130.22吉林省集安北纬41.08 东经126.11吉林省蛟河北纬43.42 东经127.21吉林省吉林北纬43.52 东经126.33吉林省九台北纬44.09 东经125.51吉林省辽源北纬42.54 东经125.09吉林省临江北纬41.49 东经126.53吉林省龙井北纬42.46 东经129.26吉林省梅河口北纬42.32 东经125.40吉林省舒兰北纬44.24 东经126.57吉林省四平北纬43.10 东经124.22吉林省松原北纬45.11 东经124.49吉林省洮南北纬45.20 东经122.47吉林省通化北纬41.43 东经125.56吉林省图们北纬42.57 东经129.51吉林省延吉北纬42.54 东经129.30吉林省愉树北纬44.49 东经126.32江苏省南京北纬32.03 东经118.46江苏省常熟北纬31.39 东经120.43江苏省常州北纬31.47 东经119.58江苏省丹阳北纬32.00 东经119.32江苏省东台北纬32.51 东经120.19江苏省高邮北纬32.47 东经119.27江苏省海门北纬31.53 东经121.09江苏省淮安北纬33.30 东经119.09江苏省淮阴北纬33.36 东经119.02江苏省江都北纬32.26 东经119.32江苏省姜堰北纬32.34 东经120.08江苏省江阴北纬31.54 东经120.17江苏省靖江北纬32.02 东经120.17江苏省金坛北纬31.46 东经119.33江苏省昆山北纬31.23 东经120.57江苏省连去港北纬34.36 东经119.10江苏省溧阳北纬31.26 东经119.29江苏省南通北纬32.01 东经120.51江苏省邳州北纬34.19 东经117.59江苏省启乐北纬31.48 东经121.39江苏省如皋北纬32.23 东经120.33江苏省苏州北纬31.19 东经120.37江苏省太仓北纬31.27 东经121.06江苏省泰兴北纬32.10 东经120.01江苏省泰州北纬32.30 东经119.54江苏省通州北纬32.05 东经121.03江苏省吴江北纬31.10 东经120.39江苏省无锡北纬31.34 东经120.18江苏省兴化北纬32.56 东经119.50江苏省新沂北纬34.22 东经118.20江苏省徐州北纬34.15 东经117.11江苏省盐在北纬33.22 东经120.08江苏省扬中北纬32.14 东经119.49江苏省扬州北纬32.23 东经119.26江苏省宜兴北纬31.21 东经119.49江苏省仪征北纬32.16 东经119.10江苏省张家港北纬31.52 东经120.32江苏省镇江北纬32.11 东经119.27江西省南昌北纬28.40 东经115.55江西省德兴北纬28.57 东经117.35江西省丰城北纬28.12 东经115.48江西省赣州北纬28.52 东经114.56江西省高安北纬28.25 东经115.22江西省吉安北纬27.07 东经114.58江西省景德镇北纬29.17 东经117.13江西省井冈山北纬26.34 东经114.10江西省九江北纬29.43 东经115.58江西省乐平北纬28.58 东经117.08江西省临川北纬27.59 东经116.21 江西省萍乡北纬27.37 东经113.50江西省瑞昌北纬29.40 东经115.38江西省瑞金北纬25.53 东经116.01江西省上饶北纬25.27 东经117.58江西省新余北纬27.48 东经114.56江西省宜春北纬27.47 东经114.23江西省鹰潭北纬28.14 东经117.03江西省樟树北纬28.03 东经115.32辽宁省鞍山北纬41.07 东经123.00辽宁省北票北纬41.48 东经120.47辽宁省本溪北纬41.18 东经123.46辽宁省朝阳北纬41.34 东经120.27辽宁省大连北纬38.55 东经121.36辽宁省丹东北纬40.08 东经124.22辽宁省大石桥北纬40.37 东经122.31辽宁省东港北纬39.53 东经124.08辽宁省凤城北纬40.28 东经124.02辽宁省抚顺北纬41.51 东经123.54辽宁省阜新北纬42.01 东经121.39辽宁省盖州北纬40.24 东经122.21辽宁省海城北纬40.51 东经122.43辽宁省葫芦岛北纬40.45 东经120.51辽宁省锦州北纬41.07 东经121.09辽宁省开原北纬42.32 东经124.02辽宁省辽阳北纬41.16 东经123.12辽宁省凌海北纬41.10 东经121.21辽宁省凌源北纬41.14 东经119.22辽宁省盘锦北纬41.07 东经122.03辽宁省普兰店北纬39.23 东经121.58辽宁省铁法北纬42.28 东经123.32辽宁省铁岭北纬42.18 东经123.51辽宁省瓦房店北纬39.37 东经122.00辽宁省兴城北纬40.37 东经120.41辽宁省新民北纬41.59 东经122.49辽宁省营口北纬40.39 东经122.13辽宁省庄河北纬39.41 东经122.58内自治区呼和浩特北纬40.48 东经111.41 内自治区包头北纬40.39 东经109.49内自治区赤峰北纬42.17 东经118.58内自治区东胜北纬39.48 东经109.59内自治区二连浩特北纬43.38 东经111.58 内自治区额尔古纳北纬50.13 东经120.11 内自治区丰镇北纬40.27 东经113.09内自治区根河北纬50.48 东经121.29内自治区海拉尔北纬49.12 东经119.39 内自治区霍林郭勒北纬45.32 东经119.38 内自治区集宁北纬41.02 东经113.06内自治区临河北纬40.46 东经107.22内自治区满洲里北纬49.35 东经117.23 内自治区通辽北纬43.37 东经122.16内自治区乌兰浩特北纬46.03 东经122.03 内自治区乌海北纬39.40 东经106.48内自治区锡林浩特北纬43.57 东经116.03 内自治区牙克石北纬49.17 东经120.40 内自治区扎兰屯北纬48.00 东经122.47 宁夏自治区银川北纬38.27 东经106.16 宁夏自治区青铜峡北纬37.56 东经105.59 宁夏自治区石嘴山北纬39.02 东经106.22 宁夏自治区吴忠北纬37.59 东经106.11 青海省西宁北纬36.38 东经101.48青海省德令哈北纬37.22 东经97.23青海省格尔木北纬36.26 东经94.55山东省济南北纬36.40 东经117.00山东省安丘北纬36.25 东经119.12山东省滨州北纬37.22 东经118.02山东省昌邑北纬39.52 东经119.24山东省德州北纬37.26 东经116.17山东省东营北纬37.27 东经118.30山东省肥城北纬36.14 东经116.46山东省高密北纬36.22 东经119.44山东省菏泽北纬35.14 东经115.26山东省胶南北纬35.53 东经119.58山东省胶州北纬36.17 东经120.00山东省即墨北纬36.22 东经120.28山东省济宁北纬35.23 东经116.33山东省莱芜北纬36.12 东经117.40山东省莱西北纬36.52 东经120.31山东省莱阳北纬36.58 东经120.42山东省莱州北纬37.10 东经119.57山东省乐陵北纬37.44 东经117.12山东省聊城北纬36.26 东经115.57山东省临清北纬36.51 东经115.42山东省临沂北纬35.03 东经118.20山东省龙口北纬37.39 东经120.21山东省蓬莱北纬37.48 东经120.45山东省青岛北纬36.03 东经120.18 山东省青州北纬36.42 东经118.28 山东省曲阜北纬35.36 东经116.58 山东省日照北纬35.23 东经119.32 山东省荣成北纬37.10 东经122.25 山东省乳山北纬36.54 东经121.31 山东省寿光北纬36.53 东经118.44 山东省泰安北纬36.11 东经117.08 山东省滕州北纬35.06 东经117.09 山东省潍坊北纬36.43 东经119.06 山东省威海北纬37.31 东经122.07 山东省文登北纬37.12 东经122.03 山东省新泰北纬35.54 东经117.45 山东省烟台北纬37.32 东经121.24 山东省兖州北纬35.32 东经116.49 山东省禹城北纬36.56 东经116.39 山东省枣庄北纬34.52 东经117.33 山东省章丘北纬36.43 东经117.32 山东省招远北纬37.21 东经120.23 山东省诸城北纬35.59 东经119.24 山东省淄博北纬36.48 东经118.03 山东省邹城北纬35.24 东经116.58 山西省太原北纬37.54 东经112.33 山西省长治北纬36.11 东经113.06 山西省大同北纬40.06 东经113.17 山西省高平北纬35.48 东经112.55 山西省古交北纬37.54 东经112.09 山西省河津北纬35.35 东经110.41 山西省侯马北纬35.37 东经111.21 山西省霍州北纬36.34 东经111.42 山西省介休北纬37.02 东经111.55 山西省晋城北纬35.30 东经112.51 山西省临汾北纬36.05 东经111.31 山西省潞城北纬36.21 东经113.14 山西省朔州北纬39.19 东经112.26 山西省孝义北纬37.08 东经111.48 山西省忻州北纬38.24 东经112.43 山西省阳泉北纬37.51 东经113.34 山西省永济北纬34.52 东经110.27 山西省原平北纬38.43 东经112.42山西省运城北纬35.02 东经110.59陕西省西安北纬34.17 东经108.57陕西省安康北纬32.41 东经109.01陕西省宝鸡北纬34.22 东经107.09陕西省韩城北纬35.28 东经110.27陕西省汉中北纬33.04 东经107.01陕西省华阴北纬34.34 东经110.05陕西省商州北纬33.52 东经109.57 陕西省铜川北纬35.06 东经109.07陕西省渭南北纬34.30 东经109.30陕西省咸阳北纬34.20 东经108.43陕西省兴平北纬34.18 东经108.29陕西省延安北纬36.35 东经109.28陕西省榆林北纬38.18 东经109.47上海市上海市北纬31.14 东经121.29四川省成都北纬30.40 东经104.04四川省巴中北纬31.51 东经106.43四川省崇州北纬30.39 东经103.40四川省达川北纬31.14 东经107.29四川省德阳北纬31.09 东经104.22四川省都江堰北纬31.01 东经103.37四川省峨眉山北纬29.36 东经103.29四川省涪陵北纬29.42 东经107.22四川省广汉北纬30.58 东经104.15四川省广元北纬32.28 东经105.51四川省华蓥北纬30.26 东经106.44四川省简阳北纬30.24 东经104.32四川省江油北纬31.48 东经104.42四川省阆中北纬31.36 东经105.58四川省乐山北纬29.36 东经103.44四川省泸州北纬28.54 东经105.24四川省绵阳北纬31.30 东经104.42四川省南充北纬30.49 东经106.04四川省内江北纬29.36 东经105.02四川省攀枝花北纬26.34 东经101.43四川省彭州北纬30.59 东经103.57四川省遂宁北纬30.31 东经105.33四川省万县北纬30.50 东经108.21四川省万源北纬32.03 东经108.03四川省西昌北纬27.54 东经102.16四川省雅安北纬29.59 东经102.59四川省宜宾北纬28.47 东经104.34四川省自贡北纬29.23 东经104.46四川省资阳北纬30.09 东经104.38台湾省台北市北纬25.03 东经121.30天津市天津市北纬39.02 东经117.12西藏自治区拉萨北纬29.39 东经91.08西藏自治区日喀则北纬29.16 东经88.51 香港香港市北纬21.23 东经115.12新疆自治区乌鲁木齐北纬43.45 东经87.36 新疆自治区阿克苏北纬41.09 东经80.19 新疆自治区阿勒泰北纬47.50 东经88.12 新疆自治区阿图什北纬39.42 东经76.08 新疆自治区博乐北纬44.57 东经82.08新疆自治区昌吉北纬44.02 东经87.18新疆自治区阜康北纬44.09 东经87.58新疆自治区哈密北纬42.50 东经93.28新疆自治区和田北纬37.09 东经79.55新疆自治区克拉玛依北纬45.36 东经84.51 新疆自治区喀什北纬39.30 东经75.59新疆自治区库尔勒北纬41.46 东经86.07 新疆自治区奎屯北纬44.27 东经84.56新疆自治区石河子北纬44.18 东经86.00 新疆自治区塔城北纬46.46 东经82.59新疆自治区吐鲁番北纬42.54 东经89.11 新疆自治区伊宁北纬43.55 东经81.20云南省昆明北纬25.04 东经102.42云南省保山北纬25.08 东经99.10云南省楚雄北纬25.01 东经101.32云南省大理北纬25.34 东经100.13云南省东川北纬26.06 东经103.12云南省个旧北纬23.21 东经103.09云南省景洪北纬22.01 东经100.48云南省开远北纬23.43 东经103.13 云南省曲靖北纬25.30 东经103.48 云南省瑞丽北纬24.00 东经97.50 云南省思茅北纬22.48 东经100.58 云南省畹町北纬24.06 东经98.04 云南省宣威北纬26.13 东经104.06 云南省玉溪北纬24.22 东经102.32 云南省昭通北纬27.20 东经103.42 浙江省杭州北纬30.16 东经120.10 浙江省慈溪北纬30.11 东经121.15 浙江省东阳北纬29.16 东经120.14 浙江省奉化北纬29.39 东经121.24 浙江省富阳北纬30.03 东经119.57 浙江省海宁北纬30.32 东经120.42 浙江省湖州北纬30.52 东经120.06 浙江省建德北纬29.29 东经119.16 浙江省江山北纬28.45 东经118.37 浙江省嘉兴北纬30.46 东经120.45 浙江省金华北纬29.07 东经119.39 浙江省兰溪北纬29.12 东经119.28 浙江省临海北纬28.51 东经121.08 浙江省丽水北纬28.27 东经119.54 浙江省龙泉北纬28.04 东经119.08 浙江省宁波北纬29.52 东经121.33 浙江省平湖北纬30.42 东经121.01 浙江省衢州北纬28.58 东经118.52 浙江省瑞安北纬27.48 东经120.38 浙江省上虞北纬30.01 东经120.52 浙江省绍兴北纬30.00 东经120.34 浙江省台州北纬28.41 东经121.27 浙江省桐乡北纬30.38 东经120.32 浙江省温岭北纬28.22 东经121.21 浙江省温州北纬28.01 东经120.39 浙江省萧山北纬30.09 东经120.16 浙江省义乌北纬29.18 东经120.04 浙江省乐清北纬28.08 东经120.58 浙江省余杭北纬30.26 东经120.18 浙江省余姚北纬30.02 东经121.10 浙江省永康北纬29.54 东经120.01 浙江省舟山北纬30.01 东经122.06浙江省诸暨北纬29.43 东经120.14 重庆市重庆市北纬29.35 东经106.33 重庆市合川市北纬30.02 东经106.15 重庆市江津市北纬29.18 东经106.16 重庆市南川市北纬29.10 东经107.05 重庆市永川市北纬29.23 东经105.53。
中国各省市经纬度

中国各省市经纬度北京市位于北纬39度54分,东经116度23分。
雄踞华北大平原北端。
北京的西、北和东北天津市北纬38°34′-40°15′之间,东经116°43′-118°194′之间上海市北纬31°14’,东经121°29’。
重庆市位于东经105°17'-110°11'、北纬28°10'-32°13'之间河北省位于东经113°04'至119°53',北纬36°01'至42°37'山西省地理坐标为北纬34°34'——40°43'、东经110°14'——114°33'。
辽宁省东经118°53′至125°46′, 北纬38°43′至43°26′之间吉林省北纬40°52′~46°18′,东经121°38′~131°19′之间黑龙江省东经121°11′-135°05′,北纬43°25′-53°33′江苏省东经116°18′-121°57′,北纬30°45′-35°20′之间浙江省浙杭州安徽省位于东经114°54′一119°37′与北纬29°41′—34°38′之间福建省介于北纬23度30分至28度22分,东经115度50分至120度40分之间江西省赣南昌山东省东经114度19分- 122度43分纬度:北纬34度22分- 38度23分河南省东经110°21′~116°39′,北纬31°23′~36°22′之间湖北省北纬29°05′~33°20′,东经108°21′~116°07′湖南省湘长沙广东省粤广州海南省位于东经108度37分,-111度05分,北纬18度10分,-20度10分之间四川省介于东经97°21′-108°31′和北纬26°03′-34°19′之间贵州省介于东经103°36′~109°35′、北纬24°37′~29°13′之间云南省陕西省东经105°29′~111°15′和北纬31°42′~39°35′之间甘肃省介于北纬32°11′~42°57′、东经92°13′~108°46′之间青海省青西宁西藏自治区藏拉萨广西壮族自治区位于北纬20°54′~26°23′,东经104°29′~112°04′内蒙古自治区东起东经126度29分,西北东经97度10分宁夏回族自治区位于北纬35’14,-39‘23,东经104’17,~107‘39,之间新疆维吾尔自治区新乌鲁木齐香港特别行政区位于东经114°15′,北纬22°15′澳门地区简称澳,1999年12月20MACAO MACAU,别名濠江、濠海、濠镜、马交、濠澳、香山澳等台湾省地处东经119°18′03〃至124°34′30〃,北纬20°45′25〃至25°56′30〃之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国省会城市经纬度
2010-04-25 18:19
北京E116°28'N39°54'
上海E121°29'N31°14'
天津E117°11'N39°09'
重庆E106°32'N29°32'
哈尔滨E126°41'N45°45'
长春E125°19'N43°52'
沈阳E123°24'N41°50'
呼和浩特E111°48'N40°49'
石家庄E114°28'N38°02'
太原E112°34'N37°52'
济南E117°N36°38'
郑州E113°42'N34°48'
西安E108°54'N34°16'
兰州E103°49'N36°03'
银川E106°16'N38°20'
西宁E101°45'N36°38'
乌鲁木齐E87°36'N43°48'
合肥E117°18'N31°51'
南京E118°50'N32°02'
杭州E120°09'N30°14'
长沙E113°N28°11'
南昌E115°52'N28°41'
武汉E114°21'N30°37'
成都E104°05'N30°39'
贵阳E106°42'N26°35'
福州E119°18'N26°05'
台北E121°31'N25°03'
广州E113°15'N23°08'
海口E110°20'N20°02'
南宁E108°20'N22°48'
昆明E102°41'N25°
拉萨E90°08' N29°39'
香港E114°10'N22°18'
澳门E113°35'N22°14'
台北E121°31'N25°03'
把地球当作一个正常的球体(其实它是椭球)来说,球面两点之间的距离计算并不复杂,运用球坐标很容易就能计算出两点之间的弧长。
当然这都是高中的知识,我和你一样,也没有那个耐心来将其推导,所以我就利用google map的经纬度到距离计算的js脚本,将球面
弧长的公式给还原出来(估计这个公式是经过部分修正的),还原出来的公式如下:
公式解释如下:
公式中经纬度均用弧度表示,角度到弧度的转化应该是很简单的了吧,若不会,依然请参考这个这个经纬度算距离的工具;
Lat1 Lung1 表示A点经纬度,Lat2 Lung2 表示B点经纬度;
a=Lat1 – Lat2 为两点纬度之差 b=Lung1 -Lung2 为两点经度之差;
6378.137为地球半径,单位为公里;
matlab代码:
adress={'北京';
'上海';
'天津';
'重庆';
'哈尔滨';
'长春';
'沈阳';
'呼和浩特';
'石家庄';
'太原';
'济南';
'郑州';
'西安';
'兰州';
'银川';
'西宁';
'乌鲁木齐';
'合肥';
'南京';
'杭州';
'长沙';
'南昌';
'武汉';
'成都';
'贵阳';
'福州';
'台北';
'广州';
'海口';
'南宁';
'昆明';
'拉萨';
'香港';
'香港';
'澳门';
'台北'};
%经纬度,第一列是东经E,第二列是北纬N EN=[116.28,39.54;
121.29,31.14;
117.11,39.09;
106.32,29.32;
126.41,45.45;
125.19,43.52;
123.24,41.5;
111.48,40.49;
114.28,38.02;
112.34,37.52;
117,36.38;
113.42,34.48;
108.54,34.16;
103.49,36.03;
106.16,38.2;
101.45,36.38;
87.36,43.48;
117.18,31.51;
118.5,32.02;
120.09,30.14;
113,28.11;
115.52,28.41;
114.21,30.37;
104.05,30.39;
106.42,26.35;
119.18,26.05;
121.31,25.03;
113.15,23.08;
110.2,20.02;
108.2,22.48;
102.41,25;
90.08,29.39;
114.1,22.18;
114.1,22.18;
113.35,22.14;
121.31,25.03];
%计算任意两点间的直线距离
ENNew(:,1)=(floor(EN(:,1))+(EN(:,1)-floor(EN(:,1)))/60)*pi/180;
ENNew(:,2)=(floor(EN(:,2))+(EN(:,2)-floor(EN(:,2)))/60)*pi/180;
%计算任意两点的距离,使用公式
$2*6378.137*\arcsin\sqrt{sin^2(a)+cos(Lat2)*cos(Lat2)*sin^2(b/2)}$
%Lat1 Lung1 表示A点经纬度,Lat2 Lung2 表示B点经纬度;
%a=Lat1 – Lat2 为两点纬度之差 b=Lung1 -Lung2 为两点经度之差;
%Lat1 Lung1 表示A点经纬度,Lat2 Lung2 表示B点经纬度;
SizeEN=size(EN,1);
Dis=zeros(SizeEN,SizeEN);
for i=1:SizeEN
for j=1:SizeEN
WeiDuCha=EN(i,2)-EN(j,2);
JingDuCha=EN(i,1)-EN(j,1);
Dis(i,j)=
2*6378.137*asin(sqrt(sin(WeiDuCha/2)^2+sin(JingDuCha/2)^2*cos(EN(i,2))*cos(EN(j ,2))));
end
end。
