折半插入排序
排序大全

(共八种排序方法:直接插入排序,折半插入排序,冒泡排序,简单选择排序,希尔排序,快速排序,堆排序,归并排序)一.简单排序1.直接插入排序:a)思想:每次从后面无序表中取出第一个元素,通过循环比较把它插入到前面有序表的合适位置,使前面有序表仍然有序。
b)稳定性:稳定c)时空效率:时间复杂度:O(n^2) 空间复杂度:O(1)d)代码:/******************************************function: InsertSort 直接插入排序paramaters: list[] 形参数组length 数组长度(并非最大下标)******************************************/void InsertSort(int list[],int length){int temp,i,j;for(i=1;i<length;i++){if(list[i]<list[i-1]){temp=list[i];//保存小值list[i]=list[i-1];//大值向后移一位for(j=i-1;j>=1&&temp<list[j-1];j--){list[j]=list[j-1];}list[j]=temp;}}}2.折半插入排序:a) 思想:在插入第i个元素时,对前面的0~i-1元素进行折半,先跟他们中间的那个元素比,如果小,则对前半再进行折半,否则对后半进行折半,直到low>hight,找到插入位置low,然后把low到i-1的所有元素均后移一位,再把第i个元素放在目标位置low上。
b) 稳定性:稳定c) 时空效率:时间复杂度:O(n^2) 空间复杂度:O(1)d) 代码:/******************************************function: BInsertSort 折半插入排序又叫二分法插入排序paramaters: list[] 形参数组length 数组长度(并非最大下标)******************************************/void BInsertSort(int p[],int length){int i,j,low,high,m,temp;for(i=1;i<length;i++){temp=p[i];low=0;high=i-1;while(low<=high){m=(low+high)/2;if(p[i]<p[m])//插入点是high+1,而非m,因为有的循环m变化了,而m与high没有发生关系,//循环就结束了,他们的关系还保留在上一层,因此插入点应该用high来保存{high=m-1;}else low=m+1;}// 其实用low更方便点,不用再对low做任何改变/*for(j=i-1;j>=high+1;j--){p[j+1]=p[j];}p[high+1]=temp;*/for(j=i-1;j>=low;j--){p[j+1]=p[j];}p[low]=temp;}}3.冒泡排序:a) 思想:依次比较相邻的两个数,将小数放在前面,大数放在后面。
数据结构之排序---折半插入排序(时间复杂度O(nlog2n))

数据结构之排序---折半插⼊排序(时间复杂度O(nlog2n))排序Time Limit: 1000MS Memory limit: 32678K题⽬描述给你N(N<=100)个数,请你按照从⼩到⼤的顺序输出。
输⼊输⼊数据第⼀⾏是⼀个正整数N,第⼆⾏有N个整数。
输出输出⼀⾏,从⼩到⼤输出这N个数,中间⽤空格隔开。
⽰例输⼊51 4 32 5⽰例输出1 2 3 4 5#include <math.h>#include <string.h>#include <stdio.h>#include <iostream>#include <string>#include <algorithm>using namespace std;//折半插⼊排序void B_insertsort(int a[], int n){int i, j;int mid, low, high;for(i=2; i<=n; i++){a[0]=a[i]; //a[0] 只是我写的这个算法模板的“中转站”,实际数据存在下标: 1--->n ⾥⾯low=1; high=i-1;while(low <= high){mid = (low+high)/2;if(a[0]>a[mid]) // 此语句将决定是“由⼤到⼩” 还是 “由⼩到⼤”排序的顺序!low=mid+1;elsehigh=mid-1;}for(j=i-1; j>=high+1; j--){a[j+1]=a[j];}a[high+1]=a[0];}}int main(){int a[200];int i, j;int n;while(~scanf("%d", &n)){for(i=1; i<=n; i++){cin>>a[i];}B_insertsort(a, n);for(j=1; j<=n; j++){if(j==1)cout<<a[j];elsecout<<" "<<a[j]; }cout<<endl;}return 0;}。
源代码--数据结构与算法(Python版)chap10 排序

交换类
(2)快速排序 快速排序采用分而治之(Divide and Conquer)
的策略将问题分解成若干个较小的子问题,采用 相同的方法一一解决后,再将子问题的结果整合 成最终答案。快速排序的每一轮处理其实就是将 这一的基准数定位,直到所有的数都排序完成 为止。
21
快速排序的基本步骤:
1. 选定一个基准值(通常可选第一个元素); 2. 将比基准值小的数值移到基准值左边,形
14
• 交换类
交换类排序的基本思想是:通过交换无序序列 中的记录得到其中关键字最小或最大的记录,并将 其加入到有序子序列中,最终形成有序序列。交换 类排序可分为冒泡排序和快速排序等。
15
交换类
(1)冒泡排序 两两比较待排序记录的关键字,发现两
个记录的次序相反时即进行交换,直到没有 反序的记录为止。因为元素会经由交换慢慢 浮到序列顶端,故称之为冒泡排序。
3. 最后对这个组进行插入排序。步长的选法 一般为 d1 约为 n/2,d2 为 d1 /2, d3 为 d2/2 ,…, di = 1。
11
【例】给定序列(11,9,84,32,92,26,58,91,35, 27,46,28,75,29,37,12 ),步长设为d1 =5、d2 =3、 d3 =1,希尔排序过程如下:
for i in range(1,len(alist)):
#外循环n-1
for j in range(i,0,-1):
#内循环
if alist[j]<alist[j-1]:
alist[j],alist[j-1]=alist[j-1],alist[j] #交换
li=[59,12,77,64,72,69,46,89,31,9] print('before: ',li) insert_sort(li) print('after: ',li)
c#实现的几种排序方法

c#实现的⼏种排序⽅法1.经典排序算法 – 插⼊排序Insertion sort插⼊排序就是每⼀步都将⼀个待排数据按其⼤⼩插⼊到已经排序的数据中的适当位置,直到全部插⼊完毕。
插⼊排序⽅法分直接插⼊排序和折半插⼊排序两种,这⾥只介绍直接插⼊排序,折半插⼊排序留到“查找”内容中进⾏。
图1演⽰了对4个元素进⾏直接插⼊排序的过程,共需要(a),(b),(c)三次插⼊。
public void Sort(int[] arr){for (int i = 1; i < arr.Length; i++){int t = arr[i];int j = i;while ((j > 0) && (arr[j - 1] > t)){arr[j] = arr[j - 1];//交换顺序--j;}arr[j] = t;}}折半排序算法是对直接插⼊算法的⼀种优化,优化的核⼼是:通过折半查看有序数组中间位置的数值(a)与待插⼊的数值(temp)的⼤⼩,如果a>=temp,则转向折半的左区间继续折半查找;如果a<temp,则转向折半后的右区间继续折半查找。
直到左右下标相同时,此时折半的下标也指向相同的位置,再做最后⼀次循环,最终的结果是:左右下标相差1,并且原来左侧的下标指向⼤于temp的位置,原来右侧的下标指向了⼩于temp的位置,即:array[biggerIndex] < temp < array[smallerIndex]。
//折半排序算法(传递待排数组名,即:数组的地址。
故形参数组的各种操作反应到实参数组上)private static void BinaryInsertionSortFunction(int[] array){try{int smallerIndex = 0; //记录有序数组的起始位置int biggerIndex = 0; //记录有序数组的终⽌位置int midIndex = 0; //记录获取有序数组的中间位置(折半法的关键:折半的位置)int temp; //记录带排的数值for (int i = 1; i < array.Length; i++) //循环向有序数组中插⼊数值(i从1开始,因为操作的是同⼀个数组){temp = array[i]; //记录待插⼊有序数组的数值biggerIndex = i - 1;//当smallerIndex==biggerIndex时,进⼊最后⼀次循环:smallerIndex指向⼤于temp的数组位置,biggerIndex指向⼩于temp的数组位置while (smallerIndex <= biggerIndex){midIndex = (smallerIndex + biggerIndex) / 2; //确定折半的位置if(array[midIndex] >= temp) //折半位置的数值 >= temp{biggerIndex = midIndex - 1; //biggerIndex以midIndex为基础向前移动⼀位}else{smallerIndex = midIndex + 1; //smallerIndex以midIndex为基础向后移动⼀位}}for (int j = i - 1; j >biggerIndex; j--) //将有序数组中⼤于temp的数值分别向后移动⼀位{array[j + 1] = array[j]; //}array[biggerIndex + 1] = temp; //将temp插⼊biggerIndex + 1,因为此时array[biggerIndex]<temp<array[smallerIndex]}}catch (Exception ex){ }}2. //选择排序public static void SelectionSort(int[] num){int min, temp;for (int i = 0; i < num.Length-1; i++){min = i;for (int j =i+1; j < num.Length; j++){if (num[j] < num[min]){min = j;}}temp = num[i];num[i] = num[min];num[min] = temp;}}3. //冒泡排序(Bubble Sort)的基本思想是:将相邻的记录的关键码进⾏⽐较,若前⾯记录的关键码⼤于后⾯记录的关键码,则将它们交换,否则不交换。
排序算法:折半插入排序

排序算法:折半插⼊排序算法分析:(1)时间复杂度 从时间上⽐较,折半查找⽐顺序查找快,所以就平均性能来说,折半插⼊排序优于直接插⼊排序。
折半插⼊排序所需要的关键字⽐较次数与待排序序列的初始排列⽆关,仅依赖于记录的个数。
不论初始序列情况如何,在插⼊第i个记录时,需要经过logi+1(向下取整+1)次⽐较,才能确定它插⼊的位置。
所以当记录的初始排列为正序或接近正序时,直接插⼊排序⽐折半插⼊排序执⾏的关键字⽐较次数要少。
折半插⼊排序的对象移动次数与直接插⼊排序相同,依赖于对象的初始排列。
在平均情况下,折半插⼊排序仅减少了关键字的⽐较次数,⽽记录的移动次数不变。
因此,折半插⼊排序的时间复杂度仍然为O(n^2)。
(2)空间复杂度 折半插⼊排序所需附加存储空间和直接插⼊排序相同,只需要⼀个记录的辅助空间r[0],所以空间复杂度为O(1)算法特点:(1)是稳定排序。
(2)因为要进⾏折半插⼊查找,所以只能⽤于顺序结构,不能⽤于链式结构。
(3)适合初始记录⽆序、n较⼤的情况。
#include<iostream>#include<vector>using namespace std;void BSort(int a[],int n){for (int i = 1; i < n; i++)//数组中的第⼀个元素最为已经排好的序列,所以从数组的第⼆个元素开始排{int key = a[i];//带插⼊元素int low = 0, high = i - 1;while (low <= high){int mid = (low + high) / 2;if (key < a[mid]){high = mid - 1;}else{low = mid + 1;}}for (int j = i - 1; j >= high + 1; j--){//i-1是已经排好序的序列的数量,high+1是待插⼊的的位置,元素后移腾出high+1这个位置a[j + 1] = a[j];}a[high + 1] = key;}}int main(){int a [11] = { 2,6,4,5,54,53,53,5,34,34,32};BSort(a, 11);for (int i = 0; i < 11; i++){cout << a[i] << " ";}return 0;}。
数据结构之各种排序的实现与效率分析

各种排序的实现与效率分析一、排序原理(1)直接插入排序基本原理:这是最简单的一种排序方法,它的基本操作是将一个记录插入到已排好的有序表中,从而得到一个新的、记录增1的有序表。
效率分析:该排序算法简洁,易于实现。
从空间来看,他只需要一个记录的辅助空间,即空间复杂度为O(1).从时间来看,排序的基本操作为:比较两个关键字的大小和移动记录。
当待排序列中记录按关键字非递减有序排列(即正序)时,所需进行关键字间的比较次数达最小值n-1,记录不需移动;反之,当待排序列中记录按关键字非递增有序排列(即逆序)时,总的比较次数达最大值(n+2)(n-1)/2,记录移动也达到最大值(n+4)(n-2)/2.由于待排记录是随机的,可取最大值与最小值的平均值,约为n²/4.则直接插入排序的时间复杂度为O(n²).由此可知,直接插入排序的元素个数n越小越好,源序列排序度越高越好(正序时时间复杂度可提高至O(n))。
插入排序算法对于大数组,这种算法非常慢。
但是对于小数组,它比其他算法快。
其他算法因为待的数组元素很少,反而使得效率降低。
插入排序还有一个优点就是排序稳定。
(2)折半插入排序基本原理:折半插入是在直接插入排序的基础上实现的,不同的是折半插入排序在将数据插入一个有序表时,采用效率更高的“折半查找”来确定插入位置。
效率分析:由上可知该排序所需存储空间和直接插入排序相同。
从时间上比较,折半插入排序仅减少了关键字间的比较次数,为O(nlogn)。
而记录的移动次数不变。
因此,折半查找排序的时间复杂度为O(nlogn)+O(n²)= O(n²)。
排序稳定。
(3)希尔排序基本原理:希尔排序也一种插入排序类的方法,由于直接插入排序序列越短越好,源序列的排序度越好效率越高。
Shell 根据这两点分析结果进行了改进,将待排记录序列以一定的增量间隔dk 分割成多个子序列,对每个子序列分别进行一趟直接插入排序, 然后逐步减小分组的步长dk,对于每一个步长dk 下的各个子序列进行同样方法的排序,直到步长为1 时再进行一次整体排序。
双向交替折半插入排序法

收稿日期:2019-07-31 修回日期:2019-11-29基金项目:贵州省自然科学基金(黔科合基础[2019]1130号)作者简介:王代星(1969-),男,工程师,硕士,研究方向为数据库技术㊁现代教育技术㊂双向交替折半插入排序法王代星1,袁琳琳2(1.贵州大学教育教学评估中心㊁高等教育研究所,贵州贵阳550025;2.贵州职业技术学院,贵州贵阳550023)摘 要:提出了一种2-路插入排序法的改进算法㊂首先在分析2-路插入排序算法和其他改进算法的基础上,给出了改进算法的思想㊁算法描述㊁算法分析㊂改进算法通过在待排序序列的两端交替地插入排序,有效地减少了数据移动次数㊂同时保证两端的有序序列同步增长,排序在序列的中间点结束,有效地避免了2-路插入排序效率受分界元素影响的缺点㊂算法的空间复杂度为O (1)㊂实验数据证明,在对随机序列排序时,数据移动次数比折半插入排序降低了50%㊁比2-路插入排序降低了25%;在对正序序列排序时,数据比较次数为2n –3次,数据移动次数为0次,而2-路插入排序的数据比较次数为n log 2n 次,移动数据为2n 次;在对逆序数据排序时,相比2-路插入排序而言,数据比较次数降低了47.37%,数据移动次数降低了25%㊂关键词:插入排序;双向;交替;折半插入;算法改进中图分类号:TP 301 文献标识码:A 文章编号:1673-629X (2020)07-0025-05doi :10.3969/j.issn.1673-629X.2020.07.006A Bidirectional Alternating Binary Insertion Sort AlgorithmWANG Dai -xing 1,YUAN Lin -lin 2(1.Higher Education Evaluation Center &Institute of Higher Education ,Guizhou University ,Guiyang 550025,China ;2.Guizhou Vocational Technology Institute ,Guiyang 550023,China )Abstract :A new improved 2-way insertion sort algorithm is put forward.Firstly ,based on the analysis of the traditional insertion sorting algorithm ,2-way insertion sorting algorithm and other improved algorithms ,the idea ,description and analysis of the proposed algorithm are given.The proposed algorithm effectively reduces the number of data movement by alternately inserting at both ends of the sequence to be sorted.At the same time ,it ensures that the ordered sequence at both ends grows synchronously ,and the ordering action ends at the middle point of the sequence ,and it avoids the disadvantage that the sorting efficiency of 2-way insertion sorting algorithm is affected by the first element.The spatial complexity of the proposed algorithm is O (1).The experimental data shows that when sorting a random sequence ,the number of data moves is 50%less than the binary insertion sort and 25%less than the 2-way insertion sort ;when sorting sorted sequence data ,the number of data comparisons is 2n -3times ,the number of data movement is 0times ,while the number of data comparisons of 2-way insertion sort is n log 2n times ,and its number of data movement is 2n times ;when ordering an inverse ordered se⁃quence ,compared with 2-way insertion sort ,the number of data comparisons and data movement decreases by 47.37%and 25%.Key words :insertion sort ;bidirectional ;alternating ;binary insertion sort ;improved algorithm0 引 言插入排序是计算机内部排序中最简单的排序算法之一㊂它的基本思想是把第一个元素当作初始有序序列,从第二个元素开始,逐个将所有元素向前插入到该序列之中㊂插入排序主要有两个基本操作,即查找插入位置时的数据比较和插入时的数据移动,通常把数据比较次数和数据移动次数作为算法的时间复杂度㊂根据查找插入位置方式的不同,又分为直接插入排序和折半插入排序㊂折半插入排序也可视为直接插入排序的改进算法,通过折半查找方式,减少了数据比较次数,但数据移动次数没有改变㊂2-路插入排序[1]是折半插入排序的改进算法,能相对减少排序过程中数据的移动次数,但空间复杂度从O (1)增加到了O (n ),时间复杂度受第一个元素影响㊂当第一个元素是最大或最小的元素时,算法的时间复杂度变得与折半插入排序一致㊂针对这些不足,文中提出一种改进算法,即第30卷 第7期2020年7月 计算机技术与发展COMPUTER TECHNOLOGY AND DEVELOPMENT Vol.30 No.7July 2020双向交替折半插入排序算法㊂通过在待排序序列的两端交替地插入排序,使数据移动次数比折半插入排序降低了50%㊁比2-路插入排序降低了25%,避免了2-路插入排序效率受分界元素影响的缺点,排序在序列的中间点结束,空间复杂度恢复为O(1)㊂1 2-路插入排序算法简介对于长度为n的待排序序列r[0 n-1],另设置等长的同类型数组d,将r[0]赋给d[0],将数组d视为一个循环向量,排序在d中进行㊂将d[0]视作有序序列的中间元素,从r[1]开始,逐个将r中的元素插入到d中㊂具体插入方法是:对于待插元素r[i],若r[i]<d[0],则将r[i]插入到d[0]之前的有序序列中;反之,则插入到d[0]之后的有序序列中㊂在排序过程中,需要设置两个指针first和final分别指向有序序列的第一个元素和最后一个元素㊂排序结束后,需要从d中,从first指针位置开始,把数据移回r中㊂具体排序过程如图1所示㊂图1 2-路插入排序示例2 具有代表性的其他改进算法2.1 有分界元素的改进算法文献[2]提出了一种名为 双向插入排序法”的改进算法㊂其基本思想是:对于长度为n的待排序序列r[0 n-1],排序在两端进行㊂取r[0]㊁r[n/2]㊁r[n-1]三个元素中大小在中间的元素为分界元素,分别从右向左扫描和从左向右扫描待排序序列㊂在从右向左扫描时,将不小于分界元素的元素,向右侧有序序列插入;当遇到小于分界元素的元素时,停止向左扫描,将该元素插入左侧有序序列,然后开始从左向右扫描㊂在从左向右扫描时,将不大于分界元素的元素,向左侧有序序列插入,当遇到大于分界元素的元素时,停止向右扫描,将该元素插入右侧有序序列,然后又开始从右向左扫描㊂如此交替扫描和插入,直到处理完所有待排序元素为止㊂双向插入排序法优于2-路排序法,空间复杂度为O(1),最终排序结果顺序存储在原序列中㊂但使用分界元素的不足之处仍未能避免㊂当分界元素碰巧为待排序序列的最大㊁最小,或次最大㊁次最小时,算法退化为单路插入,排序效率跟折半插入排序一致㊂与文献[2]类似的还有文献[3-5]提出的算法㊂2.2 无分界元素的改进算法文献[6]提出了 循环插入排序法”㊂其算法的基本思想是:对于长度为n的待排序序列r[0 n-1],把r[n/2]元素作为初始有序序列,即把有序序列安排在整个序列的中部,待排序元素两侧,插入在中部有序序列的两端循环进行㊂设置两个指针,分别指向中部有序序列的低端和高端㊂扫描待排序元素,当待排序元素大于有序序列中间的元素时,在有序序列的高端插入,高端指针向右移动加1;否则,在有序序列的低端插入,低端指针向左移动减1㊂直到所有持排序元素扫描结束为止㊂该算法的优点是每次数据移动的次数都不大于有序序列长度的一半,能够有效减少数据的移动次数㊂但美中不足的是在排序过程指针越界时,要作循环处理;排序结束后,需要重新整理移动数据,需要1到n/2个数量不等的元素辅助空间㊂文献[7-8]与文献[6]的思路完全一样,只是有序序列安排在循环序列的两端㊂文献[9]提出了 一种新的2路插入排序算法”,排序在序列的两端进行,待排序元素先与后端的最小元素比较,若大,则在后端插入;反之,则在前端插入㊂其他的多路插入排序算法,有的增加了空间复杂度,有的增加了数据的比较次数,有的设置了一个或多个分界元素,比如文献[10-16]等,此处不再详述㊂3 双向交替折半插入排序在没有特别说明或不影响理解的情况下,算法即指双向交替折半插入排序算法㊂3.1 算法思想以数据非递减排序为例㊂对于给定长度为n的待排序序列r[0 n-1],为不增加辅助空间,排序在原序列中进行,即原地排序;为有效减少数据移动次数,保证数据最终按非递减排列,先在序列的左右两端按非递减排序,再逐渐向中间靠拢,同时保证右端有序序列的数据不小于左端有序序列的数据;为让大的数据尽早向右移,让小的数据尽早向左移,在扫描待排序数据时,采取从右向左和从左向右双向交替扫描的方式,分别将大的数据插入右部有序序列和将小的数据插入左部有序序列,保证左右两端的有序序列等长,排序最终在序列的中间点结束;在排序过程中,既要随时保证㊃62㊃ 计算机技术与发展 第30卷右端有序序列数据不小于左端有序序列数据,同时也要充分利用这一特性,减少数据的比较和移动次数㊂在两端有序序列中插入元素时,采用折半插入法,以减少数据的比较次数㊂具体做法如下:初始化左右两端有序序列,比较r [0]与r [n -1],若r [0]>r [n -1],则交换r [0]与r [n -1],保证左端的初始有序序列不大于右端的初始有序序列㊂设置两个指针left 与right ,分别指向左端有序序列的最后一个元素和右端有序序列的第一个元素㊂初始时,left =0,right =n -1㊂首先,从右端向左端扫描,比较r [right -1]与r [right ],若r [right -1]>r [right ],则r [right -1]向右端插入,指针right 减1;若r [right -1]<r [right ],则指针right 减1,此时,为保证指针right 所指元素不小于left 所指元素,则比较r[right ]与r [left ],若r [right ]<r [left ],则r [right ]向左端插入,r [left ]移动到right 位置㊂接着,开始从左端向右端扫描,比较r [left ]与r [left +1],若r [left ]>r [left +1],则r [left +1]向左端插入,指针left 加1;若r [left ]<r [left +1],则指针left 加1,此时,为保证指针left 所指元素不大于指针right 所指元素,则比较r [left ]与r [right ],若r [left ]>r [right ],则r [left ]向右端插入,r [right ]移动到left 位置㊂此后,不断重复左右交替扫描,直到left =right ,算法结束㊂具体排序过程如图2所示㊂图2 双向交替折半插入排序示例3.2 算法描述算法:双向交替折半插入排序输入:随机序列r [0 n -1]输出:非递减序列r [0 n -1]方法:Step 1:初始化㊂若r [0]>r [n -1],则r [0]与r [n -1]交换;左端有序序列指针left =0;右端有序序列指针right =n -1;Step 2:从右端向左扫描㊂若r [right -1]>r[right ],则r [right -1]向右端插入,right --;若r [right -1]<r [right ],则right --,比较r [right ]与r [left ],若r [right ]<r [left ],则r [right ]向左端插入,然后r [right ]=r [left ]㊂Step 3:从左端向右扫描㊂若r [left ]>r [left +1],则r [left +1]向左端插入,left ++;若r [left ]<r [left +1],则left ++,比较r [left ]与r [right ],若r [left ]>r [right ],则r [left ]向右端插入,然后r [left ]=r [right ]㊂Step 4:若left <right ,重复Step 2㊁Step 3㊂Step 5:输出r [0 n -1],算法结束㊂3.3 算法分析以下的分析,皆以随机序列为例㊂3.3.1 时间复杂度算法的排序时间主要消耗在数据的比较和移动上㊂由于计算机硬件环境和程序语言的差别,一般不用绝对运行时间来衡量排序算法的效率,而采用排序过程中所发生的数据比较次数和数据移动次数来衡量㊂算法的数据比较次数,主要发生在查找数据插入位置时㊂本算法在排序过程中,把有序序列均等地分布在序列的两端,数据插入在两端进行,减少了后半部分元素在插入有序序列时数据的比较次数,平均每个元素减少了1次,总的比较次数减少了约n /2次㊂传统折半插入法平均数据比较次数为n log 2n ,则本算法的平均数据比较次数不高于n log 2n -n /2㊂后文的实验数据也证明了这一点㊂算法的数据移动次数,主要发生在数据插入时㊂同样,由于数据插入是在两端等长的有序序列中进行,每一端有序序列的长度,都相当于传统的折半插入法排序时的有序序列长度的一半,故平均数据移动次数减半㊂传统的折半插入法的平均数据移动次数约为n 2/4,则本算法的平均数据移动次数约为n 2/8㊂后文的实验数据证明了,本算法的平均数据移动次数比传统的折半插入法下降了50%,比2-路插入法下降了25%㊂3.3.2 空间复杂度从前面的算法分析和算法描述可以得知,本算法只需要一个元素辅助空间,作为数据交换时的临时存储空间,故空间复杂度为O (1)㊂3.3.3 算法的稳定性由于插入排序是在序列的两端交替进行,同时为了保证右端的有序序列不小于左端的有序序列,元素会在两端移动,即序列左半部分的数据,有可能插入到右端的有序序列中,右半部分数据也可能插入到左端有序序列中,因此,算法是不稳定的㊂㊃72㊃ 第7期 王代星等:双向交替折半插入排序法4 实验数据与结果通过实际测试,得出实验数据与结果,其中随机序列的统计数据,是执行了100次的平均数㊂另外,两数据交换位置,按两次数据移动统计㊂4.1 算法的数据比较和移动次数表1给出了算法在不同的排序规模和三种主要数据序列状态下进行排序时实际的数据比较次数㊂当原序列为随机时,比较次数不超过n log2n–n/2次;正序时,为2n–3次;逆序时,为n log2n/1.9次㊂表1 双向交替折半插入排序法的数据比较次数排序量n随机序列正序序列逆序序列10001000012393619997718072000026789539997153602300004196085999723860240000575839799973272455000073622599997417217 表2给出了算法在不同的排序规模和三种主要数据序列状态下进行排序时实际的数据移动次数㊂当原序列为随机时,移动次数约为n2/8次;正序时,为0次;逆序时,为1.5n次㊂表2 双向交替折半插入排序法的数据移动次数排序量n随机序列正序序列逆序序列100010000125068160149972000050032020029994300001126083690449944000019997749106000050000312448058074994 4.2 几种算法的比较下面比较了直接插入㊁折半插入㊁2-路插入和双向交替折半插入排序的实验数据㊂在图表中,双向交替折半插入排序简称双向交替㊂实验数据分别按随机㊁正序和逆序序列,给出数据比较次数和数据移动次数的对比㊂4.2.1 对随机序列排序对比表3给出了4种排序算法数据比较次数的对比㊂直接插入法的数据比较次数约为n2/4;折半插入㊁双向交替和2-路插入不超过n log2n㊂由于双向交替法需要保证右端有序序列不小于左端有序序列,所以数据比较次数比2-路插入法要约高㊂通过表中数据计算,平均约高1.6%㊂表4给出了4种算法数据移动次数的对比㊂直接插入和折半插入的数据移动次数是一样的,约为n2/4;2-路插入约为n2/6;双向交替约为n2/8㊂双向交替比2-路插入约减少了25%㊂图3显示了数据移动次数随着排序规模变化的趋势图,直接插入与折半插入重叠一致,双向交替增长最缓慢㊂表3 对随机序列排序时的数据比较次数对比排序量n直接插入折半插入双向交替2-路插入10000 1000025009218128915123936121594 2000099945526277899267895263314 30000224893320434586419608412797 40000399835284595856575839568414 50000625036158761212736225725394表4 对随机序列排序时的数据移动次数对比排序量n直接插入折半插入2-路插入双向交替10000 1000025029180250291801638930612506816 2000099985485999854856605452750032020 30000224953274224953274149071772112608369 40000399915233399915233273143604199977491 50000625136105625136105418134859312448058图3 随机序列数据移动次数对比4.2.2 对正序序列排序对比表5给出了4种排序算法数据比较次数的对比㊂2-路插入法不仅是4种算法中数据比较次数最多的,而且通过与表3比较,数据比较次数还要约高于在随机序列排序时,同样约为n log2n次;双向插入为2n–3次;直接插入和折半插入为n–1次㊂表5 对正序序列排序时的数据比较次数对比排序量n2-路插入双向交替直接插入折半插入10000 100001336021999799999999 20000287217399971999919999 30000447217599972999929999 40000614448799973999939999 50000784448999974999949999 表6给出了4种算法的数据移动次数的对比㊂2-路插入法需要移动数据2n次;其他算法无需移动数据㊂表6 对正序序列排序时的数据移动次数对比排序量n2-路插入双向交替直接插入折半插入10000 1000020000000 2000040000000 3000060000000㊃82㊃ 计算机技术与发展 第30卷续表6排序量n2-路插入双向交替直接插入折半插入4000080000000 500001000000004.2.3 对逆序序列排序对比表7给出了4种排序算法数据比较次数的对比㊂此时,直接插入的数据比较次数达到最高,约为(n-1)(n+2)/2次;2-路插入和折半插入相近,约为n log2n次,跟随机序列排序时的比较次数悬殊不大;双向插入比较次数最少,约为n log2n/1.9次,比2-路插入排序降低了47.37%㊂表7 对逆序序列排序时的数据比较次数对比排序量n直接插入折半插入2-路插入双向交替10000 100004999619612515312361771807 20000199978796272023267219153602 30000449949197427002417206238602 40000799910278587566574436327245 500001249860210751744734436417217 表8给出了4种算法的数据移动次数的对比㊂此时,直接插入和折半插入的数据移动次数达到最高,为(n-1)(n+2)/2次;2-路插入为2n次;双向交替约为1.5n次,比2-路插入排序降低了25%㊂表8 对逆序序列排序时的数据移动次数对比排序量n直接插入折半插入2-路插入双向交替10000 1000050009893500098932000014997 200002000101282000101284000029994 300004499997364499997366000044994 400007999804247999804248000060000 500001249950260124995026010000074994 4.3 结 论通过 3.3算法分析”和 4实验数据与结果”得出,文章提出的双向交替折半插入排序法,在对随机序列进行排序时,数据比较次数不超过n log2n–n/2次,数据移动次数约为n2/8次;在对正序序列进行排序时,比较次数为2n–3次,数据移动次数为0次;在对逆序序列进行排序时,比较次数约为n log2n/1.9次,数据移动次数约为1.5n㊂与2-路插入法对比,在对随机序列进行排序时,数据比较次数约增1.6%,数据移动次数约减25%;在对初始序列为正序或逆序序列排序时,也有比2-路插入法良好的表现;空间复杂度为O(1),也比2-路插入法的O(n)少;且在排序时,当第一个元素为序列中最小或最大值的元素时, 2-路插入法退化为单路插入,排序效率与折半插入排序一致,而双向交替折半插入排序法则没有这样的缺点㊂综上所述,双向交替折半插入排序法的综合性能优于2-路插入排序法㊂5 结束语总的来说,2-路插入排序及其改进算法,其数据的移动次数跟直接插入排序法还是一个数量级的,要彻底有所改进,只有改顺序存储结构为链式存储结构,比如文献[17]所述算法,但数据的比较次数又难以兼顾㊂实际应用应综合考虑数据比较和移动的代价㊂参考文献:[1] 严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,1997:265-268.[2] 唐开山.双向插入排序法[J].微计算机应用,2003,24(2):107-111.[3] 黄橡丽,王 兵.2-路插入排序的一种新算法[J].天津纺织工学院学报,1996,15(1):36-40.[4] 张连堂,牛全营.一种新的2-路插入排序算法[J].河南大学学报:自然科学版,2004,34(2):73-75.[5] 王 昱,杨小萍,陈延文,等.一种非循环2路插入排序算法[J].工业仪表与自动化装置,2012(2):66-68. [6] 唐开山.循环插入排序法[J].计算机工程与应用,2005,41(12):88-91.[7] 王 昱,杨小萍,陈延文,等.一种改进的循环2路插入排序算法[J].工业仪表与自动化装置,2011(6):79-81. [8] 胡圣荣.一个改进的循环2路插入排序算法[J].计算机应用与软件,2008,25(2):248-249.[9] 王 昱,杨小萍,陈延文,等.一种新的2路插入排序算法[J].现代计算机,2013(1):26-28.[10]唐开山.4路插入排序法[J].计算机工程,2006,32(1):51-53.[11]李胜华.多路插入排序算法[J].湖北大学学报:自然科学版,2008,30(2):145-148.[12]王 昱,杨小萍,陈延文,等.一种4路插入排序算法[J].工业仪表与自动化装置,2013(6):76-79. [13]王 昱,杨小萍,陈延文,等.一种3路插入排序算法[J].计算机应用与软件,2014,31(7):275-276. [14]MOHAMMED A S,AMRAHOV S E,ÇELEBI F V.Bidirec⁃tional conditional insertion sort algorithm;an efficient pro⁃gress on the classical insertion sort[J].Future GenerationComputer Systems,2017,71:102-112.[15]WANG MIN.Analysis on2-element insertion sort algorithm[C]//2010international conference on computer design andapplications.Washington:IEEE,2010:143-146. [16]NENWANI K,MANE V,BHARNE S,et al.Enhancing a⁃daptability of Insertion sort through2-Way expansion[C]//20145th international conference-confluence the next gener⁃ation information technology summit:20145th internationalconference-confluence the next generation information tech⁃nology summit(confluence).Noida,India:IEEE,2014:843-847.[17]陈黎静.一种新的表插入排序算法[J].计算机技术与发展,2010,20(8):33-36.㊃92㊃ 第7期 王代星等:双向交替折半插入排序法。
24种插入法

24种插入法24种插入法是一种优化排序算法,它的基本思想是将一个列表分为已排序区间和未排序区间,每次从未排序区间取出一个元素,插入到已排序区间的正确位置,使已排序区间保持有序。
在这个过程中,相邻元素的比较和交换次数都很少,所以可以提高排序的效率。
此外,24种插入法还有一些变体,可以根据不同情况选用相应的插入法,达到更好的排序效果。
以下是24种插入法的详细介绍:1. 直接插入排序直接插入排序是最简单的插入法,它将未排序元素插入到已排序区间合适的位置。
时间复杂度为O(n²),空间复杂度为O(1)。
2. 折半插入排序折半插入排序是对直接插入排序的优化,它采用二分查找的方式找到插入位置。
时间复杂度为O(n²),空间复杂度为O(1)。
3. 希尔排序希尔排序是一种针对直接插入排序的改进,它将列表按照一定步长分组,每个子列表采用直接插入排序,随着步长逐渐缩小,最终变为一组,完成排序。
时间复杂度为O(nlogn),空间复杂度为O(1)。
4. 二路插入排序二路插入排序是对直接插入排序的改进,它采用两个指针,在有序区间之前和之后分别插入未排序元素。
时间复杂度为O(n²),空间复杂度为O(1)。
5. 多关键词插入排序多关键词插入排序是针对多关键词排序的优化,它将排序条件拆分为多个关键词,分别进行插入排序。
时间复杂度为O(nlogn),空间复杂度为O(1)。
6. 基数插入排序基数插入排序是对基数排序的优化,它使用插入法对每个桶内的元素进行排序,并合并桶内已排序的元素。
时间复杂度为O(dn),空间复杂度为O(max)。
7. 大小插入排序大小插入排序是对多关键词排序的优化,它根据元素的大小关系建立排序树,对树进行遍历并插入已排序区间。
时间复杂度为O(nlogn),空间复杂度为O(nlogn)。
8. 块插入排序块插入排序是对桶排序的优化,它将待排序元素分为若干块,分别进行插入排序,再将已排序块合并。
折半插入排序

折半插入排序
折半插入排序法,又称四舍五入排序法。
是按照折半法和插入法交替进行逐步排除错误的一种方法,也叫“舍弃小的,保留大的”或“用全排出去,用缺补上来”排序法.它适合于成对象形的数据,也就是说要求将某些对象先看作一组,然后再把它们每一对当作两个来排列,这样容易产生正确的结果。
常见的排序问题,通常包含多对对象,而且要求所选择的对象都必须有相同的特征值。
由于相邻的两个单元可能互为相反数,故在实际操作过程中往往需要将两者按互为倒数来处理,这就引申出一系列简便计算,即求整数部分的个位数字,因此排序也是很容易解决的。
下面举例说明其思路和方法。
例如有10名学生参加考试,前8人平均成绩为80分,最后2人平均成绩为90分,则求出平均成绩为81分的2人平均成绩的值。
应用该方法时要注意以下几点:1、运算符号、公式及各种运算之间不能混淆;2、在用这种方法时还需进一步分析原来顺序中有无矛盾,是否具备等价性(平均成绩相等),排除非同质的现象(比如全为80分,或全为90分);3、用该方法解决的问题,只要求得到最终结果,不要求知道开始时的情况,但要求知道结束时的情况。
在用这种方法时还需进一步分析原来顺序中有无矛盾,是否具备等价性(平均成绩相等),排除非同质的现象(比如全为80分,或全为90分)。
3、使用了这种方法后,若遇到不能直接利用上述方法解决的问
题,可采取折半插入排序法。
例如,已知某班男女生人数分别为20人和21人,求男生人数占总人数的百分比。
4、用该方法解决的问题,只要求得到最终结果,不要求知道开始时的情况,但要求知道结束时的情况。
2016年考研核心题型【数据结构部分】【第7章 排序】

温馨提示:快速排序主要考查两点:1、快速排序算法的特点;2、快速排序算法实现; 3、快速排序的过程或者一趟排序的结果。本考点历年考查很多,是复习的重点,请同学们 务必掌握。
接插入排序每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍
然有序。
折半插入排序是对直接插入排序算法的一种改进。由于前半部分为已排好序的数列,
这样我们可以不用按顺序依次寻找插入点,而是采用折半查找的方法来加快寻找插入点的
速度。折半查找的方法来寻找插入位置,可以减少比较次数。但不影响排序的趟数(仍然
本题只剩下希尔排序了,事实上,本题是利用增量为 d=5、3、1 来对关键字{50 , 26 , 38 , 80 , 70 , 90 , 8 , 30 , 40 , 20 }进行希尔排序。其排序过程如图 7.2 所示。
我方慎重声明,各盈利机构若采用我方资料,必追究法律责任
102
2016 年考研核心考点命题思路解密 数据结构 梦享团队主编
1. 对一待排序序列分别进行折半插入排序和直接插入排序,两者之间可能的不同之处是
(
)。
A. 排序的总趟数
B. 元素的移动次数
C. 使用辅助空间的数量
D. 元素之间的比较次数
【2012 年统考——第 11 题】
【考查内容】直接插入排序和折半插入排序的区别。
【解析】所谓排序算法过程,就是不断的依次将元素插入前面已排好序的序列中。直
一趟冒泡排序结束。
整个排序过程如下图所示。
其过程如图 7.1 所示。
50 40 95 20 15 70 60 45 80
50>40,50和40交换
40 50 95 20 15 70 60 45 80
排序问题与算法的多样性-高中数学知识点讲解

排序问题与算法的多样性1.排序问题与算法的多样性【知识点的认识】排序问题与算法的多样性1.对于一个有序列:,欲将新数据A 插入到有序列中,形成新的有序列,其做法是:将数据A 与原有序列中的数据从右到左依次进行比较,直到发现某一数据a i 使得a i≤A,把A 插入到a i 的右边;如果数据A 小于原有序列中的所有数据,则将A 插入到原序列的最左边.这种排序算法通常称为有序列直接插入排序的算法.2.折半插入排序的基本思想是:先将新数据与有序列中“中间位置”的数据进行比较.若有序列有 2n+1 个数据则“中间位置”的数据指的是第n+1 个数,或有序列有 2n 个数据则“中间位置”的数据指的是第n 个数.如果新数据小于“中间位置”的数据,则新数据插入的位置应该在靠左边的一半;如果新数据大于“中间位置”的数据,则新数据插入的位置应该在靠右边的一半;也就是说,一次比较就排除了数据列中一半的位置.反复进行这种比较直到确定新数据的位置,像这样的插入排序方法我们称之为折半插入排序方法.3.冒泡排序:冒泡排序是一种交换排序,顺次相邻位置的两个数据,如果逆序,则交换顺序,直到将最后两个数据比较完毕.这样,完成一趟冒泡,如果数据已经有序化则停止排序.否则,继续进行.4.当n 比较小时,冒泡排序用起来比较简单;但是当n 很大时,它耗费的时间是很惊人的.著名的英国计算机科学家霍尔(C.A.R.Hoare)对其进行改进,得到了一种新的交换排序算法,由于性能突出,被称为快速排序法(Quicksort).快速排序所基于的事实是:为了得到更好的效果,交换应跨过较长的距离进行.这是对冒泡排序算法的改进.将待排序的数组分割成两部分是快速排序的关键.我们总是以某种方式选一个值,然后以它为参照将数组分为两部分,一部分包含的元素大于这个值,一部分包含的元素小于这个值.快速排序算法的核心是分而治之,这和前面介绍的二分法的思想是一致的.1/ 1。
字符串排序c语言

字符串排序c语言
1字符串排序
字符串的排序是电脑科学中一个基础的操作,它可以为程序查询提供便利,并同时也具有现实实际意义。
C语言中,可以采用冒泡排序、快速排序、折半插入排序等多种算法来实现字符串的排序。
1.1冒泡排序
冒泡排序是一种经典的排序算法,其时间复杂度为O(n2)。
冒泡排序方法简单地比较相邻两个字符串,如果顺序错误,就将它们换位。
从而每一趟排序,都把其中最小的字符串放到最前面。
最多需要n-1趟排序,就可以使所有的字符串符合指定的次序。
1.2快速排序
快速排序是一种分治策略的排序算法,其时间复杂度的期望是
O(nlogn)。
快速排序首先选择一个“基准”元素,经过一趟排序后,将原序列分为两个子序列,测试结果比基准元素小的放在基准元素左边,大的放在右边。
递归地重复这个过程,即可排序好所有的字符串。
1.3折半插入排序
折半插入排序是一种效率较高的排序算法,它的时间复杂度为
O(nlogn)。
折半插入排序首先将要排序的序列分成两部分,先进行折半查找,将原序列中的每一个元素插入到它应该插入到的位置,最终
获得排序后的序列。
这样可以节省大量的逐一比较时间,使排序变得更加高效。
2结论
字符串的排序是一种基本操作,C语言中一般采用冒泡排序、快速排序、折半插入排序等算法来实现排序功能,其中,冒泡排序的时间复杂度为O(n2),快速排序和折半插入排序的时间复杂度均为
O(nlogn)。
选择合适的排序算法,可有效提高字符串排序的效率。
详解排序算法(一)之3种插入排序(直接插入、折半插入、希尔)

详解排序算法(⼀)之3种插⼊排序(直接插⼊、折半插⼊、希尔)直接插⼊排序打过牌的⼈都知道,当我们拿到⼀张新牌时,因为之前的牌已经经过排序,因此,我们只需将当前这张牌插⼊到合适的位置即可。
⽽直接插⼊排序,正是秉承这⼀思想,将待插⼊元素与之前元素⼀⼀⽐较,从⽽找到合适的插⼊位置。
那么使⽤直接插⼊排序,具体是怎样操作的呢?我们取 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 来进⾏⽰范。
(1)第1轮排序,3之前⽆可⽐较值,因此我们从44开始操作,取44和3⽐较,⼤于3,顺序保持不变。
得数据3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48(2)第2轮排序,取38和44⽐较,38 < 44,再将38与3⽐较,38 > 3,故将38放于第2位,得数据3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48(3)第3轮排序,取5与44⽐较,5 < 44,再将5与38⽐较,5 < 38,再将5与3⽐较,5 > 3, 置于第2位,得数据3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48(4)如此经过14轮排序后,得到最终结果2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50动态图javascript实现function directInsertSort (arr) {let compare, // 对⽐元素下标current // 待插⼊元素值for (let i = 1; i < arr.length; i++) {current = arr[i]compare = i - 1while (current < arr[compare] && compare >= 0) {arr[compare + 1] = arr[compare]compare--}arr[compare + 1] = current}return arr}折半插⼊排序细⼼的同学可能已经注意到,当我们要将⼀个元素插⼊合适的位置时,其之前的元素是有序的,因此,我们可以⽤折半查找的⽅式来⽐对并插⼊元素,也就是所谓的折半插⼊排序。
折半插入排序报告
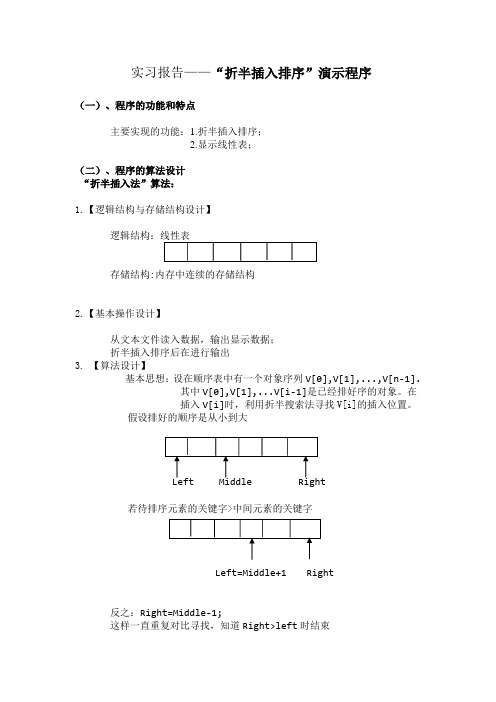
实习报告——“折半插入排序”演示程序(一)、程序的功能和特点主要实现的功能:1.折半插入排序;2.显示线性表;(二)、程序的算法设计“折半插入法”算法:1.【逻辑结构与存储结构设计】逻辑结构:线性表存储结构:内存中连续的存储结构2.【基本操作设计】从文本文件读入数据,输出显示数据;折半插入排序后在进行输出3. 【算法设计】基本思想:设在顺序表中有一个对象序列V[0],V[1],...,V[n-1].其中V[0],V[1],...V[i-1]是已经排好序的对象。
在插入V[i]时,利用折半搜索法寻找V[i]的插入位置。
假设排好的顺序是从小到大Left Middle Right若待排序元素的关键字>中间元素的关键字Left=Middle+1 Right反之:Right=Middle-1;这样一直重复对比寻找,知道Right>left时结束找到插入位置Left后,依次移动后边的每个元素,空开插入位置,进行插入;4.【高级语言代码】//成员方法:折半插入法排序public void BineryInsSort(){Record temp;//临时存放记录int Left,Right,Middle;//指向待排序列两端的下标/** 第一个数据已经排好,从第二个数据起* 逐个插入到已经排好的序列*/for(int i=1;i<CurrentSize;i++){Left=0;Right=i-1;temp=Vector[i];//备份要插入的数据//寻找插入位置Middlewhile(Left<=Right){//折半,插入中点Middle=(Left+Right)/2;if(temp.key>Vector[Middle].key)Right=Middle-1;//在左半区间找else Left=Middle+1;//在右半区间找}//结束时Left>Right//找到插入位置Left,后移空开插入位置for(int k=i-1;k>=Left;k--)Vector[k+1]=Vector[k];Vector[Left]=temp;//插入空位}//循环结束,所有数据读入}//显示线性表public void display(){double s=0.0;for(int i=0;i<CurrentSize;i++){//其余数据列System.out.print(Vector[i].other.stu_num+" ");System.out.print(Vector[i]+" ");System.out.print(Vector[i].other.sex+" ");System.out.print(Vector[i].other.age+" ");//排序关键字System.out.println(Vector[i].key+" ");s+=Vector[i].key;}System.out.println("平均分="+s/CurrentSize);}(三)、程序中类的设计“DataList”类:1.【主要成员变量说明】private static int DefaultSize=100;private Record Vector[];//线性表private int MaxSize,CurrentSize;//最大长度与当前长度2.【主要成员方法说明】//交换两记录public void swap(int i,int j){}//成员方法:折半插入法排序public void BineryInsSort(){}//成员方法:折半插入法排序public void BineryInsSort(){}//显示线性表public void display(){}4.【高级语言代码】package study_3;import java.io.*;//"待排表"类(多行数据构成的线性表)public class DataList {private static int DefaultSize=100;private Record Vector[];//线性表private int MaxSize,CurrentSize;//最大长度与当前长度//构造函数:从文件建表public DataList (String filename){MaxSize=DefaultSize;CurrentSize=0;Vector=new Record[MaxSize];//对象数组for(int i=0;i<MaxSize;i++)Vector[i]=new Record();//数组元素初始化try{//创建文件输入流File f=new File(filename);FileInputStream fin=new FileInputStream(f);//创建数据输入流,二者关联DataInputStream din=new DataInputStream(fin);byte c=0;byte temp[]=new byte[100];int len=0;String s;len=0;while((c=din.readByte())!=13){//遇到回车符temp[len]=c;//记录数是文本,非二进制数len++;//读取长度加1}s=new String(temp,0,len);int rs=Integer.parseInt(s);//字符串转整数din.skipBytes(1);//跳过换行符(ASII码11)while(CurrentSize<rs){//输入流结束时len=0;while((c=din.readByte())!='\t'){//读取字符temp[len]=c;//接收内容len++;//读取长度加1}s=new String(temp,0,len);//学号装入数组Vector[CurrentSize].other.stu_num=new String(temp,0,len);len=0;while((c=din.readByte())!='\t'){ // 读取字符temp[len] = c;// 接收内容len++ ;// 读取长度加1}s=new String(temp,0,len);//姓名装入数组Vector[CurrentSize]= s;len=0;while((c=din.readByte())!='\t'){ // 读取字符temp[len] = c;// 接收内容len++ ;// 读取长度加1}s=new String(temp,0,len);//性别装入数组Vector[CurrentSize].other.sex= s;//读出年龄len=0;while((c=din.readByte())!='\t'){ // 读取字符temp[len] = c;// 接收内容len++ ;// 读取长度加1}s=new String(temp,0,len); //字符串转整数Vector[CurrentSize].other.age=Integer.parseInt(s);//读出考试分数len=0;while((c=din.readByte())!=13){ // 读取字符temp[len] = c;// 接收内容len++ ;// 读取长度加1}s=new String(temp,0,len);din.skipBytes(1); //跳过换行字符Vector[CurrentSize].key=Double.parseDouble(s);CurrentSize++; //字符串转实数}//输入流结束din.close();//关闭数据流同时关闭文件流}catch(IOException e){System.out.println("文件异常");}}//交换两记录public void swap(int i,int j){Record temp=Vector[i];Vector[i]=Vector[j];Vector[j]=temp;}//成员方法:折半插入法排序public void BineryInsSort(){Record temp;//临时存放记录int Left,Right,Middle;//指向待排序列两端的下标/** 第一个数据已经排好,从第二个数据起* 逐个插入到已经排好的序列*/for(int i=1;i<CurrentSize;i++){Left=0;Right=i-1;temp=Vector[i];//备份要插入的数据//寻找插入位置Middlewhile(Left<=Right){//折半,插入中点Middle=(Left+Right)/2;if(temp.key>Vector[Middle].key)Right=Middle-1;//在左半区间找else Left=Middle+1;//在右半区间找}//结束时Left>Right//找到插入位置Left,后移空开插入位置for(int k=i-1;k>=Left;k--)Vector[k+1]=Vector[k];Vector[Left]=temp;//插入空位}//循环结束,所有数据读入}//显示线性表public void display(){double s=0.0;for(int i=0;i<CurrentSize;i++){//其余数据列System.out.print(Vector[i].other.stu_num+" ");System.out.print(Vector[i]+" ");System.out.print(Vector[i].other.sex+" ");System.out.print(Vector[i].other.age+" ");//排序关键字System.out.println(Vector[i].key+" ");s+=Vector[i].key;}System.out.println("平均分="+s/CurrentSize);}public static void main(String[] args) {//读入数据,把成绩作为排序关键字DataList D=new DataList("student.txt");D.display();//显示线性表D.BineryInsSort();//折半插入法排序D.display();}}(四)、程序的输入输出和运行结果截屏。
详解折半插入排序算法

详解折半插⼊排序算法折半插⼊排序算法的时间复杂度:O(nlogn)折半插⼊排序利⽤⼆分法的思想,在⼀个有序的序列中,找到新元素在该序列中的位置,然后插⼊。
如图1所⽰,共有n个元素,前i个元素已经是有序序列,现在要将第i个元素插⼊其中。
折半插⼊排序需要做两步⼯作:找到待插⼊元素的位置、插⼊。
图1 插⼊排序⽰意图⾸先要定义两个指针(不是语法⾥⾯的指针,是下标的意思)low和high⽤于寻找a[i]的插⼊位置,low指向a[0],high指向a[i-1],中点mid=(low+high)/2,图2 “折半”⽰意图如图2所⽰⼆分法的思想是,⽐较a[i]与a[mid]的⼤⼩,若a[i]>a[mid],说明a[i]的位置应该在mid~high之间,将区间[low,high]缩短为[mid+1,high],令指针low=mid+1;若a[i]<=a[mid],说明a[i]的位置应该在low~mid之间,将区间压缩为[low,mid-1],令指针high=mid-1。
每次折半之后,a[i]的位置应该在[low,high]之间。
如此循环,low与high渐渐靠近,直到low>high跳出循环,a[i]的位置找到,low即为a[i]应该放置的位置。
找到a[i]的位置之后进⾏插⼊,先将a[low]~a[i-1]这些元素向后平移⼀个元素的位置,然后将a[i]放到low位置。
⽤Dev-C++编写的C++代码:#include <iostream>using namespace std;void BinSort(int *a,int n) //对int数组进⾏从⼩到⼤的排序{for(int i=1;i<n;i++) //开始以a[0]作为有序序列,从a[1]开始找到当前元素a[i]应该放置的位置{int low=0,high = i-1,mid;//每次寻找a[i]的位置,都要更新这些数据while(low<=high) //⼆分思想循环寻找a[i]的位置{mid = (low+high) / 2;if(a[i]<=a[mid])high = mid - 1; //high指针减⼩elselow = mid + 1; //low指针增加} //循环结束,low就是a[i]应该放置的位置int temp = a[i];for(int j=i;j>low;j--) //将元素向后平移a[j] = a[j-1];a[low] = temp; //将元素temp = a[i] 放置到low位置}}int main() //举例说明{int n = 10;int a[10] = {5,8,9,4,7,5,6,3,1,11};BinSort(a,n);for(int i=0;i<n;i++)cout << a[i] << " ";cout << endl;return 0;}⼀个细节:为什么内层的循环while(low<=high){...}结束之后以low作为a[i]应该放置的位置?观察指针low与high重合之前与之后⼆者位置变化情况。
排序的详细分类

排序的详细分类排序分为外部排序和内部排序,其中平时主要学习的是内部排序。
内部排序主要分为5⼤类:(ps:其中计数排序⼀般不做分析)1. 插⼊排序:1. 直接插⼊排序:每次处理就是将⽆序的数列中第⼀个元素与有序数列的元素从后到前⽐较,找到插⼊位置,将该元素插⼊到有序数列的适当的最终的位置上(稳定排序)。
算法过程/*直接插⼊排序*/#include<stdio.h>void insertSort(int arr[], int length);int main() {int a[5] = { 5,2,3,4,1 };insertSort(a, 5);for (int i = 0; i < 5; i++)printf("%5d", a[i]);}void insertSort(int arr[], int length) {int i, j, k;for (i = 1; i < length; i++) {if (arr[i] < arr[i - 1]) {k = arr[i];for (j = i - 1; arr[j] > k && j >= 0; j--) {//待插元素⼩于当前元素arr[j + 1] = arr[j];}arr[j + 1] = k;}}} 2.折半插⼊排序 算法过程/*折半插⼊排序:将⼀个新元素插⼊打已经拍好像的数组的过程,mid=(low+high)/2,判断插⼊元素是否⼩于参考元素,若是则选择low-high(high=mid-1)为插⼊区间,反之则选择low(low=mid+1)-high,直到low>high时,即将此位置之后所有元素后移⼀位,并将新元素插⼊a[high+1]*/#include<stdio.h>int main() {void BinSort(int a[], int n);void put(int r[], int n);int arr[] = { 9,8,7,6,5,4,3,2,1 };BinSort(arr, 9);put(arr, 9);}void BinSort(int a[], int n) {int i, j, high,low, mid,t;for (i = 1; i < n; i++) {low = 0;high = i - 1;t = a[i];while (low<=high){mid = (low + high) / 2;if (t < a[mid]) {high = mid - 1;}else{low = mid + 1;}}for (j = i - 1; j >=high+1; j--) {//high+1的元素后移a[j + 1] = a[j];}a[j + 1] = t;//插⼊选定的地点}}。
C语言最常用的六种排序方法详解
1.冒泡排序:
2.简单选择排序:
3.快速排序:
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。
4.直接插入排序:
5.折半插入排序:
折半插入排序(binary insertion sort)是对插入排序算法的一种改进,在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为
a[high],则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小,则选择a[low]到a[m-1]为新的插入区域(即high=m-1),否则选择a[m+1]到a[high]为新的插入区域(即low=m+1),如此直至low<=high不成立,即将此位置之后所有元素后移一位,并将新元素插入a[high+1]。
代码:
6.希尔排序:。
Python理解折半插入排序

Python理解折半插入排序引言插入排序中有直接插入排序,善于思考的能够发现该算法在进插入的时候是采用了顺序查找的方法,而在要查找的表中数据本身有序的前提下可以使用折半查找来代替顺序查找,这种排序的算法就是折半插入排序算法。
算法描述本篇文章描述的是折半插入排序算法,折半插入排序算法的原理就是利用折半查找的方法来查找插入的位置,然后直接将需要的数据插入该位置就可以了。
第一步:先将需要排序的序列中的第一个数据看成是一个有序序列。
第二步:从第二个元素开始,逐个进行插入。
第三步:在插入的时候先使用折半查找在有序序列中找到该数据应该插入的位置,比较该数据与有序序列中的中间值大小。
给定一个序列为a[0], a[1], a[2]……a[i-1], a[i], a[i+1]……a[n-1]。
假设前面i个元素已经是有序序列,现在将第i个元素插入其中,首先需要做的是找到插入元素的位置,然后再插入。
此时定义两个指针为low和high,low指向a[0],high指向a[i-1],使用折半查找,前面有序序列的中间值为a[mid],mid=(low+high)/2,则前面序列为a[0], a[1], a[2]…a[mid]…a[i-1]。
将a[i]与a[mid]进行比较,若a[i]>a[mid] ,说明a[i]的位置就应该在mid和high之间,再在mid和high之间用相同方法进行查找。
若a[i]< a[mid], 说明a[i]的位置就应该在mid和low之间,再在mid和low之间用相同方法进行查找。
找到相应位置后就将该数据插入到该位置,这样就进行了一次折半插入排序。
例题:给定序列[5,2,6,0,9],对其进行排序首先把5当成有序序列1.此时mid为5,将2与5做比较,2比5小,插在5前面则为[2,5, 6,0,9]2.将6先与2比较,再与6比较得[2,5, 6,0,9]3.将0先与5作比较,比5小,则位置在5左边,再与2比较,比2小,则再2左边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折半插入排序
描述
用函数实现折半插入排序,并输出每趟排序的结果.
Input
第一行:键盘输入待排序关键的个数n
第二行:输入n个待排序关键字,用空格分隔数据Output
每行输出一趟排序结果,数据之间用一个空格分隔
#include"stdio.h"
#define MAXSIZE 20//一个用作示例的小顺序表的最大长度typedef int KeyType;//定义关键字类型为整数类型
typedef struct
{ int key;
float info;
}JD;
void bsort(JD r[],int n)
{//作折半插入排序
int i,j,low,high,mid;
for(i=2;i<=n;i++)
{
r[0]=r[i]; //r[0]用作哨兵单元
low=1;high=i-1;
while(low<=high) //在r[low...high]中折半查找插入的位置
{
mid=(low+high)/2; //折半
if(r[0].key<r[mid].key) //插入点在低半区
high=mid-1;
else //插入点在高半区
low=mid+1;
}//while
j=i-1;
while(j>=high+1)
{ r[j+1]=r[j]; //记录后移
--j;
}//while
r[high+1]=r[0]; //插入到正确位置
for(j=1;j<=n;j++) //输出每趟排序的结果
{
printf("%d ",r[j].key);
}//for
printf("\n");
}//for
}//straisort
void main()
{
int n,i; //待排序的关键字个数
JD r[MAXSIZE];
scanf("%d",&n);
for(i=1;i<=n;i++)//输入待排序的关键字
scanf("%d",&r[i].key);
bsort(r,n);
}。
