2019年安徽省初中学业水平考试数学阶段检测试卷一(含答案)

合集下载

安徽省2019年初中学业水平考试数学卷及答案解析

11. 计算 18 2 的结果是
。
12 命题“如果 a+b=0，那么 a，b 互为相反数”的逆命题为____________________________.
13.如图，△ABC 内接于☉O，∠CAB=30°，∠CBA=45°，
D，若☉O 的半径为 2，则 CD 的长为
。
CD⊥AB 于点
14.在平面直角坐标系中，垂直于 x 轴的直线 l 分别于函数
安徽省 2019 年初中学业水平考试
数学卷
试卷满分为 150 分，考试时间为 120 分钟。[来源:学+科+网]
一、选择题（本大题共 10 小题，每小题 4 分，满分 40 分）每小题都给出 A，B，C，D 四个选项，其中只有一个是正确的。
1.在-2,-1,0,1 这四个数中，最小的数是
A.-2
B.-1
检结束后，检测员将测得的个数据按从小到大的顺序整理成如下表格：
编号
①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮
尺寸（cm）8.72 8.88 8.92 8.93 8.94 8.96 8.97 8.98a 9.03 9.04 9.06 9.07 9.08b
按照生产标准，产品等次规定如下：
尺寸（单位：cm）
产品等次
8.97≤x≤9.03
（1）将线段 AB 向右平移 5 个单位，再向上平移 3 个单位得到线段 CD，请画出线段 CD.
2
（2）以线段 CD 为一边，作一个菱形 CDEF，且点 E，F 也为格点.（作出一个菱形即可）
四、(本大题共 2 小题，每小题 8 分，满分 16 分)
17.为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路.其中一段长为 146 米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作 2 天后，乙工程队加入，两工程队又联合工作了 1 天，这 3 天共掘进 26 米.已知甲工程队每天比乙工程队多掘进 2 米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？

安徽省2019年初中学业水平考试中考数学真题试卷(含答案)

安徽省2019年初中学业水平考试中考数学真题试卷（含答案）数学（试题卷）注意事项：1.你拿到的试卷满分为150分,考试时间为120分钟。

2.试卷包括”试题卷“和“答题卷”两部分,“试题卷”共4页,“答题卷“共6页；3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的；4.考试结束后,请将”试题卷”和“答题卷”一井交回。

一、选择题（本大题共10小题,每小题4分,满分40分）每小超都给出A,B,C,D 四个选项,其中只有一个是正确的。

1.8-的绝对值是（）A.-8B.8C.±8D.2.2017年我赛粮食总产量为635.2亿斤,其中635.2亿科学记数法表示（）3.下列运算正确的是（） A.()4.一个由圆柱和圆锥组成的几何体如图水平放置，其主（正）视图为（）5.下列分解因式正确的是（）6.据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%假定2018年的平均增长率保持不变，2016年和2018年我省有效发明专利分别为a 万件和b 万件，则（）7.若关于x 的一元二次方程x (x +1)+ax =0有两个相等的实数根,则实数a 的值为（）A. 1-B.1C.2或-2D.1或-38. 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲,乙两组数据,如下表：类于以上数据,说法正确的是（）A.甲、乙的众数相同B.甲、乙的中位数相同C.甲的平均数小于乙的平均数D.甲的方差小于乙的方差9.□ABCD 中，E 、F 是对角线BD 上不同的两点，下列条件中，不能得出四边形AECF 一定为平行四边形的是（）A.BE=DFB.AE=CFC.AF//C ED.∠BAE =∠DCF10.如图,直线21l l 、都与直线l 垂直,垂足分别为M,N,MN =1正方形ABCD 的边长为3，对角线AC 在直线l 上,且点C 位于点M 处,将正方形ABCD 沿l 向右平移,直到点A 与点N 重合为止，记点C 平移的距离为x ,正方形ABCD 的边位于21l l 、之间分的长度和为y ，则y 关于x 的函数图象太致为（）二、填空题(本大共4小题,每小题5分,满分30分)11.不等式>的解集是。

2019年安徽中考数学试卷及答案

精心整理2019年安徽省初中学业水平考试数学试卷一、选择题（本大题共10小题，每小题4分，满分40分）1、在—2，—1，0，1这四个数中，最小的数是（）A、—2B、—1 C.、0D、12、计算a3·(—a)的结果是（）A、a2B、—a2C、a4D、—a43、一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是（）4、2019A、5A、3B6、则这50A、7上，E F⊥ACA、3.6B8A、20199A、b＞0C、b10A、0B、4 C、6D、8二、填空题（本大题共4小题，每小题5分，满分20分）11的结果是.12、命题“如果a+b=0，那么a，b互为相反数”的逆命题为.13、如图，△ABC内接于⊙O，∠CAB＝30O，∠CBA＝45O，CD⊥AB于点D，若⊙O的半径为2，则CD的长为.精心整理14、在平面直角坐标系中，垂直于x 轴的直线l 分别与函数y=x-a+1和y=x 2-2ax 的图像交于P ，Q两点，若平移直线l ，可以使P ，Q 都在x 轴的下方，则实数a 的取值范围是.三、（本大题共2小题，每小题8分，满分16分）15、解方程（x —1）2=4.16、如图，在边长为1的单位长度的小正方形组的12×12风格中，给出了以格点（风格线的交点）为端点的线段AB 。

（1）将线段AB 向右平移5个单位，再向上平移3个单位得到线段CD ，请画出线段CD 。

（2）也为格四、17、米的米，已18（1）求证：△BC E ≌△ADF ；（2）设□ABCD 的面积为S ，四边形AEDF 的面积为T ，求S T的值。

六、（本题满分12分）21、为监控某条生产线上产品的质量，检测员每隔相同时间抽取一件产品，并测量其尺寸，在一天的抽检结束后，检测员将测得的15个数据按从小到大的顺序整（1）已知此次抽检的合格率为80，请判断编号为的产品是否为合格品，并说明理由。

二、填空题11、312、如果a ，b 互为相反数，那么a+b=01314、a>1或a<-1三、（本大题共2小题，第小题8分，满分16分）15、解：（x-1）2=4，所以x-1=2，或x-1=-2，即x=3或x=-1。

[名师推荐]2019年安徽省初中学业水平考试数学模拟试卷(1)附参考答案

2019 年安徽省初中学业水平考试数学模拟试卷(一)一、选择题(本大题共10小题，每小题4分，满分40分) 1．合肥市某日的气温是－2 ℃～6 ℃，则该日的温差是( A ) A ．8 ℃ B ．5 ℃ C ．2 ℃D ．－8 ℃2．计算x 2·4x 3的结果是( C ) A ．4x 3 B ．4x 4 C ．4x 5D ．4x 6 3．如图，一个水平放置的六棱柱，这个六棱柱的左视图是( C )A B C D4．地球上陆地的面积约为150 000 000 km 2把“150 000 000用科学记数法表示为( A ) A ．1.5×108 B ．1.5×107 C ．1.5×109D ．1.5×1065．如图，已知AB ∥CD ，直线EF 分别交AB ，CD 于点E ，F ，EG 平分∠BEF ，若∠1＝48°，则∠2的度数是( C )A ．64°B ．65°C ．66°D ．67°6．不等式组⎩⎪⎨⎪⎧1－x ＜0，6＞3x 的解集是( C )A ．x ＞1B ．x ＜2C ．1＜x ＜2D ．无解7．小明为了解本市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图(部分信息未给出)．根据以上信息，如下结论错误的是( D ) A ．被抽取的天数为50天B ．空气轻微污染的所占比例为10%C ．扇形统计图中表示优的扇形的圆心角度数57.6°D ．估计该市这一年(365天)达到优和良的总天数不多于290天8．市政府计划两年内将该市人均住房面积由现在的10 m 2提高到14.4 m 2，设每年人均住房面积增长率为x ，则所列方程正确的是( A )A ．10(1＋x )2＝14.4B ．10(1－x )2＝14.4C ．10(1＋x )＝14.4D ．10＋10(1＋x )＋10(1＋x )2＝14.49．若函数y ＝ax －c 与函数y ＝bx的图象如图所示，则函数y ＝ax 2＋bx ＋c 的大致图象为( D )A B C D10．如图，在矩形ABCD 中，AB ＝3，BC ＝3，将△ABC 沿对角线AC 折叠，点B 恰好落在点P 处，CP 与AD 交于点F ，连接BP 交AC 于点G ，交AD 于点E ，下列结论不正确的是( D )A ．AC ＝2APB ．△PBC 是等边三角形 C ．S △BGC ＝3S △AGPD ．PG CG ＝13二、填空题(本大题共4小题，每小题5分，满分20分) 11.84.1的整数部分是__9__.12．因式分解：a 3－4ab 2＝__a (a ＋2b )(a －2b )__.13．如图，一个边长为4 cm 的等边三角形ABC 的高与⊙O 的直径相等．⊙O 与BC 相切于点C ，与AC相交于点E ，则CE ＝3cm __.14．在△ABC 中，AB ＝6 cm ，点P 在AB 上，且∠ACP ＝∠B ，若点P 是AB 的三等分点，则AC 的长是三、(本大题共2小题，每小题8分，满分16分) 15．计算：9＋(π－3)0－|－5|＋(－1)2 018＋⎝⎛⎭⎫12－2解：原式＝3＋1－5－1＋4＝4.16．先化简，再求值：⎝⎛⎭⎫x x ＋1－3x x －1÷xx 2－1，其中x ＝－2.解：原式＝x (x －1)－3x (x ＋1)(x ＋1)(x －1)·(x ＋1)(x －1)x ＝－2x 2－4xx ＝－2x －4，把x ＝－2代入，得－2×(－2)－4＝0.四、(本大题共2小题，每小题8分，满分16分)17．如图，在正方形网格中，△ABC 为格点三角形，每个小正方形的边长均为1个单位． (1)画出△ABC 关于y 轴对称的△A ′B ′C ′； (2)求AC 边上的高．解：(1)如图所示，△A ′B ′C ′为所求；(2)△ABC 中，AB ＝32＋32＝32，BC ＝22＋22＝22，AC ＝12＋52＝26；∵AB 2＋BC 2＝(32)2＋(22)2＝26＝AC 2，∴△ABC 为直角三角形，设AC 边上的高为x ，则有12AC·x ＝12AB·BC ，∴x ＝32×2226＝62613.18．两位数相乘：19×11＝209,18×12＝216,25×25＝625,34×36＝1 224，47×43＝2 021，…(1)认真观察，分析上述各式中两因数的个位数字、十位数字分别有什么联系，找出因数与积之间的规律，并用字母表示出来；(2)验证你得到的规律．解：(1)上述等式的规律是：两因数的十位数字相等，个位数字相加等于10，而积后两位是两因数个位数字相乘、前两位是十位数字相乘，乘积再加上这个十位数字之和；如果用m 表示十位数字，n 表示个位数字的话，则第一个因数为10m ＋n ，第二个因数为10m ＋(10－n )，积为100m (m ＋1)＋n (10－n )；表示出来为：(10m ＋n )[10m ＋(10－n )]＝100m (m ＋1)＋n (10－n )；(2)∵左边＝(10m ＋n )(10m －n ＋10)＝(10m ＋n )[10(m ＋1)－n ]＝100m (m ＋1)－10mn ＋10n (m ＋1)－n 2＝100m (m ＋1)－10mn ＋10mn ＋10n －n 2＝100m (m ＋1)＋n (10－n )＝右边，∴(10m ＋n )[10m ＋(10－n )]＝100m (m ＋1)＋n (10－n )，成立．五、(本大题共2小题，每小题10分，满分20分)19．如图所示，巨型广告牌AB 背后有一看台CD ，台阶每层高0.3 m ，且AC ＝17 m ，小明坐在台阶的FG 这层上晒太阳，设太阳光线与水平地面的夹角为α，当α＝60°时，测得广告牌AB 在地面上的影长AE ＝10 m ，过了一会，当α＝45°，问小明在FG 这层是否还能晒到太阳？请说明理由(3取1.73)．解：当α＝45°时，小明仍可以晒到太阳．理由如下：假设没有台阶，当α＝45°时，从点B 射下的光线与地面AD 的交点为点M ，与MC 的交点为点H.当α＝60°时，在Rt △ABE 中，∵tan 60°＝AB AE ＝AB 10，∴AB ＝10·tan 60°＝103≈10×1.73＝17.3(m )，∵∠BFA ＝45°，∴tan 45°＝ABAM ＝1，此时的影长AM ＝AB ＝17.3(m )，∴CM ＝AM －AC ＝17.3－17＝0.3(m )，∴CM ＝CF ＝0.3(m )，∴大楼的影子落在台阶FC 这个侧面上，∴小明能晒到太阳．20．商店只有雪碧、可乐、果汁、红茶四种饮料，赵敏同学去该店购买饮料，每种饮料被选中的可能性相同．(1)若他去买一瓶饮料，则他买到红茶的概率是多少？(2)若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和红茶的概率．解：(1)∵商店只有雪碧、可乐、果汁、红茶四种饮料，每种饮料被选中的可能性相同，∴他去买一瓶饮料，则他买到红茶的概率是14；(2)画树状图得：∵共有12种等可能的结果，他恰好买到雪碧和红茶的有2种情况，∴他恰好买到雪碧和红茶的概率P ＝212＝16. 六、(本题满分12分)21．如图，C ，D 两点在以AB 为直径的半圆O 上，AD 平分∠BAC ，AB ＝20，AD ＝415，DE ⊥AB 于E .(1)求DE 的长； (2)求证：AC ＝2OE .(1)解：连接BD ，∵AB 为直径，∴∠ADB ＝90°，在Rt △ADB 中，BD ＝AB 2－AD 2＝202－(415)2＝410，∵S △ADB ＝12AD·BD ＝12AB·DE ，∴AD·BD ＝AB·DE ，∴DE ＝AD·BD AB ＝415×41020＝46，即DE ＝46；(2)证明：连接OD ，作OF ⊥AC 于点F .∵OF ⊥AC ，∴AC ＝2AF ，∵AD 平分∠BAC ，∴∠BAC ＝2∠BAD ，又∵∠BOD ＝2∠BAD ，∴∠BAC ＝∠BOD ，Rt △OED 和Rt △AFO 中，∵⎩⎨⎧∠BAC ＝∠BOD ，∠AFO ＝∠OED ＝90°，OA ＝OD ，∴△AFO ≌△OED ，∴AF ＝OE ，∵AC ＝2AF ，∴AC ＝2OE.七、(本题满分12分)22．安徽凤凰城建材市场为某工厂代销一种建筑材料．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．(1)当每吨售价是240元时，计算此时的月销售量；(2)在遵循“薄利多销”的原则下，问每吨材料售价为多少时，该经销店的月利润为9 000元？ (3)小明说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．解：(1)当每吨售价是240元时，此时的月销售量为：45＋260－24010×7.5＝60(吨)；(2)设当售价定为每吨x 元时，由题意，可列方程(x －100)⎝⎛⎭⎫45＋260－x 10×7.5＝9 000，化简得x 2－420x ＋44 000＝0.解得x 1＝200，x 2＝220，当售价定为每吨200元时，销量更大，所以售价应定为每吨200元；(3)小明说的不对．∵由(2)知，x 2－420x ＋44 000＝0，∴当月利润最大时，x 为210元，理由：方法一：当月利润最大时，x 为210元，而对于月销售额W ＝x ⎝⎛⎭⎫45＋260－x 10×7.5＝－34(x －160)2＋19 200来说，当x为160元时，月销售额W 最大，∴当x 为210元时，月销售额W 不是最大，∴小明说的不对．方法二：当月利润最大时，x 为210元，此时，月销售额为17 325元；而当x 为200元时，月销售额为18 000元．∵17 325元＜18 000元，∴当月利润最大时，月销售额W 不是最大．∴小明说的不对．八、(本题满分14分)23．如图，在菱形ABCD 中，E ，F 为边BC ，CD 上的点，且CE ＝CF ，连接AE ，AF ，∠ABC 的平分线交AE 于点G ，连接CG .(1)求证：AG ＝CG ； (2)求证：CG ∥AF ；(3)若BG ＝CG ，则△ABE 与△BGE 是否相似？若相似，写出证明过程；若不相似，请说明理由． (1)证明：在菱形ABCD 中，AB ＝BC ，∵BG 平分∠ABC ，∴∠ABG ＝∠CBG ，在△ABG 和△CBG 中，⎩⎨⎧AB ＝BC ，∠ABG ＝∠CBG ，BG ＝BG ，∴△ABG ≌△CBG ，∴AG ＝CG ；(2)证明：连接AC ，∵AC 是菱形ABCD 的对角线，∴∠ACE ＝∠ACF ，在△ACE 和△ACF 中，⎩⎨⎧CE ＝CF ，∠ACE ＝∠ACF ，AC ＝AC ，∴△ACE ≌△ACF ，∴∠CAE ＝∠CAF ，由(1)知，AG ＝CG ，∴∠CAE ＝∠ACG ，∴∠ACG ＝∠CAF ，∴CG ∥AF ；(3)解：△ABE ∽△BGE.理由如下：由(1)知，△ABG ≌△CBG ，∴∠BAG ＝∠BCG ，∵BG ＝CG ，∴∠CBG ＝∠BCG ，∴∠BAG ＝∠CBG ，又∵∠AEB ＝∠BEG ，∴△ABE ∽△BGE.。

2019年安徽省初中学业水平考试数学试卷(解析卷)

如果您喜欢这份文档，欢迎下载！祝您成绩进步，学习愉快！2019年安徽省初中学业水平考试数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是正确的．1．（4分）在﹣2，﹣1，0，1这四个数中，最小的数是（）A．﹣2B．﹣1C．0D．1解：根据有理数比较大小的方法，可得﹣2＜﹣1＜0＜1，∴在﹣2，﹣1，0，1这四个数中，最小的数是﹣2．故选：A．2．（4分）计算a3•（﹣a）的结果是（）A．a2B．﹣a2C．a4D．﹣a4解：a3•（﹣a）＝﹣a3•a＝﹣a4．故选：D．3．（4分）一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是（）A．B．C．D．解：几何体的俯视图是：故选：C．4．（4分）2019年“五一”假日期间，我省银联网络交易总金额接近161亿元，其中161亿用科学记数法表示为（）A．1.61×109B．1.61×1010C．1.61×1011D．1.61×1012解：根据题意161亿用科学记数法表示为1.61×1010．故选：B．5．（4分）已知点A（1，﹣3）关于x轴的对称点A'在反比例函数y＝的图象上，则实数k 的值为（）A．3B．C．﹣3D．﹣解：点A（1，﹣3）关于x轴的对称点A'的坐标为（1，3），把A′（1，3）代入y＝得k＝1×3＝3．故选：A．6．（4分）在某时段由50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这50辆车的车速的众数（单位：km/h）为（）A．60B．50C．40D．15解：由条形图知，50个数据的中位数为第25、26个数据的平均数，即中位数为＝＝40，故选：C．7．（4分）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝12，点D在边BC上，点E 在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G．若EF＝EG，则CD的长为（）A．3.6B．4C．4.8D．5解：作DH∥EG交AB于点H，则△AEG∽△ADH，∴，∵EF⊥AC，∠C＝90°，∴∠EFA＝∠C＝90°，∴EF∥CD，∴△AEF∽△ADC，∴，∴，∵EG＝EF，∴DH＝CD，设DH＝x，则CD＝x，∵BC＝12，AC＝6，∴BD＝12﹣x，∵EF⊥AC，EF⊥EG，DH∥EG，∴EG∥AC∥DH，∴△BDH∽△BCA，∴，即，解得，x＝4，∴CD＝4，故选：B．8．（4分）据国家统计局数据，2018年全年国内生产总值为90.3万亿，比2017年增长6.6%．假设国内生产总值的年增长率保持不变，则国内生产总值首次突破100万亿的年份是（）A．2019年B．2020年C．2021年D．2022年解：2019年全年国内生产总值为：90.3×（1+6.6%）＝96.2598（万亿），2020年全年国内生产总值为：96.2598×（1+6.6%）≈102.6（万亿），∴国内生产总值首次突破100万亿的年份是2020年，故选：B．9．（4分）已知三个实数a，b，c满足a﹣2b+c＝0，a+2b+c＜0，则（）A．b＞0，b2﹣ac≤0B．b＜0，b2﹣ac≤0C．b＞0，b2﹣ac≥0D．b＜0，b2﹣ac≥0解：∵a﹣2b+c＝0，a+2b+c＜0，∴a+c＝2b，b＝，∴a+2b+c＝（a+c）+2b＝4b＜0，∴b＜0，∴b2﹣ac＝＝﹣ac＝＝≥0，即b＜0，b2﹣ac≥0，故选：D．10．（4分）如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12，点P在正方形的边上，则满足PE+PF＝9的点P的个数是（）A．0B．4C．6D．8解：如图，作点F关于BC的对称点M，连接FM交BC于点N，连接EM，∵点E，F将对角线AC三等分，且AC＝12，∴EC＝8，FC＝4，∵点M与点F关于BC对称∴CF＝CM＝4，∠ACB＝∠BCM＝45°∴∠ACM＝90°∴EM＝＝4则在线段BC存在点N到点E和点F的距离之和最小为4＜9∴在线段BC上点N的左右两边各有一个点P使PE+PF＝9，同理在线段AB，AD，CD上都存在两个点使PE+PF＝9．即共有8个点P满足PE+PF＝9，故选：D．二、填空题（共4小题，每小题5分，满分20分）11．（5分）计算÷的结果是3．解：．故答案为：312．（5分）命题“如果a+b＝0，那么a，b互为相反数”的逆命题为如果a，b互为相反数，那么a+b＝0．解：命题“如果a+b＝0，那么a，b互为相反数”的逆命题为：如果a，b互为相反数，那么a+b＝0；故答案为：如果a，b互为相反数，那么a+b＝0．13．（5分）如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为．解：连接CO并延长交⊙O于E，连接BE，则∠E＝∠A＝30°，∠EBC＝90°，∵⊙O的半径为2，∴CE＝4，∴BC＝CE＝2，∵CD⊥AB，∠CBA＝45°，∴CD＝BC＝，故答案为：．14．（5分）在平面直角坐标系中，垂直于x轴的直线l分别与函数y＝x﹣a+1和y＝x2﹣2ax 的图象相交于P，Q两点．若平移直线l，可以使P，Q都在x轴的下方，则实数a的取值范围是a＞1或a＜﹣1．解：y＝x﹣a+1与x轴的交点为（1﹣a，0），∵平移直线l，可以使P，Q都在x轴的下方，∴当x＝1﹣a时，y＝（1﹣a）2﹣2a（1﹣a）＜0，∴a2﹣1＞0，∴a＞1或a＜﹣1；故答案为a＞1或a＜﹣1；三、（本大题共2小题，每小题8分，满分16分）15．（8分）解方程：（x﹣1）2＝4．解：两边直接开平方得：x﹣1＝±2，∴x﹣1＝2或x﹣1＝﹣2，解得：x1＝3，x2＝﹣1．16．（8分）如图，在边长为1个单位长度的小正方形组成的12×12的网格中，给出了以格点（网格线的交点）为端点的线段AB．（1）将线段AB向右平移5个单位，再向上平移3个单位得到线段CD，请画出线段CD．（2）以线段CD为一边，作一个菱形CDEF，且点E，F也为格点．（作出一个菱形即可）解：（1）如图所示：线段CD即为所求；（2）如图：菱形CDEF即为所求，答案不唯一．四、（本大题共2小题，每小题8分，满分16分）17．（8分）为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路．其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工．甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进26米．已知甲工程队每天比乙工程队多掘进2米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？解：设甲工程队每天掘进x米，则乙工程队每天掘进（x﹣2）米，由题意，得2x+（x+x﹣2）＝26，解得x＝7，所以乙工程队每天掘进5米，（天）答：甲乙两个工程队还需联合工作10天．18．（8分）观察以下等式：第1个等式：＝+，第2个等式：＝+，第3个等式：＝+，第4个等式：＝+，第5个等式：＝+，……按照以上规律，解决下列问题：（1）写出第6个等式：；（2）写出你猜想的第n个等式：（用含n的等式表示），并证明．解：（1）第6个等式为：，故答案为：；（2）证明：∵右边＝＝左边．∴等式成立，故答案为：．五、（本大题共2小题，每小题10分，满分20分）19．（10分）筒车是我国古代发明的一种水利灌溉工具．如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．如图2，筒车盛水桶的运行轨迹是以轴心O 为圆心的圆．已知圆心在水面上方，且圆被水面截得的弦AB长为6米，∠OAB＝41.3°，若点C为运行轨道的最高点（C，O的连线垂直于AB），求点C到弦AB所在直线的距离．（参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88）解：连接CO并延长，与AB交于点D，∵CD⊥AB，∴AD＝BD＝AB＝3（米），在Rt△AOD中，∠OAB＝41.3°，∴cos41.3°＝，即OA＝＝＝4（米），tan41.3°＝，即OD＝AD•tan41.3°＝3×0.88＝2.64（米），则CD＝CO+OD＝4+2.64＝6.64（米）．20．（10分）如图，点E在▱ABCD内部，AF∥BE，DF∥CE．（1）求证：△BCE≌△ADF；（2）设▱ABCD的面积为S，四边形AEDF的面积为T，求的值．解：（1）∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴∠ABC+∠BAD＝180°，∵AF∥BE，∴∠EAB+∠BAF＝180°，∴∠CBE＝∠DAF，同理得∠BCE＝∠ADF，在△BCE和△ADF中，∵，∴△BCE≌△ADF（ASA）；（2）∵点E在▱ABCD内部，+S△AED＝S▱ABCD，∴S△BEC由（1）知：△BCE≌△ADF，∴S△BCE＝S△ADF，∴S四边形AEDF＝S△ADF+S△AED＝S△BEC+S△AED ＝S▱ABCD，∵▱ABCD的面积为S，四边形AEDF的面积为T，∴＝＝2．六、（本题满分12分）21．（12分）为监控某条生产线上产品的质量，检测员每个相同时间抽取一件产品，并测量其尺寸，在一天的抽检结束后，检测员将测得的个数据按从小到大的顺序整理成如下表格：编号①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮尺寸（cm）8.728.888.928.938.948.968.978.98a9.039.049.069.079.08b按照生产标准，产品等次规定如下：尺寸（单位：cm）产品等次8.97≤x≤9.03特等品8.95≤x≤9.05优等品8.90≤x≤9.10合格品x＜8.90或x＞9.10非合格品注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）计算在内．（1）已知此次抽检的合格率为80%，请判断编号为⑮的产品是否为合格品，并说明理由．（2）已知此次抽检出的优等品尺寸的中位数为9cm．（i）求a的值；（ii）将这些优等品分成两组，一组尺寸大于9cm，另一组尺寸不大于9cm，从这两组中各随机抽取1件进行复检，求抽到的2件产品都是特等品的概率．解：（1）不合格．因为15×80%＝12，不合格的有15﹣12＝3个，给出的数据只有①②两个不合格；（2）（i）优等品有⑥～⑪，中位数在⑧8.98，⑨a之间，∴，解得a＝9.02（ii）大于9cm的有⑨⑩⑪，小于9cm的有⑥⑦⑧，其中特等品为⑦⑧⑨⑩画树状图为：共有九种等可能的情况，其中抽到两种产品都是特等品的情况有4种．∴抽到两种产品都是特等品的概率P＝．七、（本题满分12分）22．（12分）一次函数y＝kx+4与二次函数y＝ax2+c的图象的一个交点坐标为（1，2），另一个交点是该二次函数图象的顶点（1）求k，a，c的值；（2）过点A（0，m）（0＜m＜4）且垂直于y轴的直线与二次函数y＝ax2+c的图象相交于B，C两点，点O为坐标原点，记W＝OA2+BC2，求W关于m的函数解析式，并求W 的最小值．解：（1）由题意得，k+4＝﹣2，解得k＝﹣2，又∵二次函数顶点为（0，4），∴c＝4把（1，2）带入二次函数表达式得a+c＝2，解得a＝﹣2（2）由（1）得二次函数解析式为y＝﹣2x2+4，令y＝m，得2x2+m﹣4＝0∴，设B，C两点的坐标分别为（x1，m）（x2，m），则，∴W＝OA2+BC2＝∴当m＝1时，W取得最小值7八、（本题满分14分）23．（14分）如图，Rt△ABC中，∠ACB＝90°，AC＝BC，P为△ABC内部一点，且∠APB ＝∠BPC＝135°．（1）求证：△PAB∽△PBC；（2）求证：PA＝2PC；（3）若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证h12＝h2•h3．解：（1）∵∠ACB＝90°，AB＝BC，∴∠ABC＝45°＝∠PBA+∠PBC又∠APB＝135°，∴∠PAB+∠PBA＝45°∴∠PBC＝∠PAB又∵∠APB＝∠BPC＝135°，∴△PAB∽△PBC（2）∵△PAB∽△PBC∴在Rt△ABC中，AB＝AC，∴∴∴PA＝2PC（3）如图，过点P作PD⊥BC，PE⊥AC交BC、AC于点D，E，∴PF＝h1，PD＝h2，PE＝h3，∵∠CPB+∠APB＝135°+135°＝270°∴∠APC＝90°，∴∠EAP+∠ACP＝90°，又∵∠ACB＝∠ACP+∠PCD＝90°∴∠EAP＝∠PCD，∴Rt△AEP∽Rt△CDP，∴，即，∴h3＝2h2∵△PAB∽△PBC，∴，∴∴．即：h12＝h2•h3．。

2019年安徽省初中学业水平考试数学阶段检测试卷一(含答案)

2019年安徽省初中学业水平考试阶段检测卷一代数综合检测(时间：120分钟，满分：150分)一、选择题(本大题共10小题，每小题4分，满分40分)每小题都给出A 、B 、C 、D 四个选项，其中只有一个是正确的．1．2的倒数是( )A ．－2 B.12 C ．－12D ．2 2．下列实数中的无理数是( )A ．0.7 B.12C ．πD ．－8 3．温度由－4 ℃上升7 ℃是( )A. 3 ℃B. －3 ℃C. 11 ℃D. －11 ℃4．一条数学信息在一周内被转发了2 180 000次，将数据2 180 000用科学记数法表示为( )A ．2.18×106B ．2.18×105C ．21.8×106D ．21.8×1055．下列算式中，结果等于a 6的是( )A ．a 3＋a 4B ．a 2＋a 2＋a 2C ．a 2·a 3D ．a 2·a 2·a 26．下列分解因式正确的是( )A ．－ma －m ＝－m (a －1)B ．a 2－1＝(a －1)2C ．a 2－6a ＋9＝(a －3)2D ．a 2＋3a ＋9＝(a ＋3)27．不等式组⎩⎪⎨⎪⎧2x ＜6，x ＋1≥－4的解集是( ) A ．－5＜x ≤3 B ．－5≤x ＜3C ．x ≥－5D ．x ＜38．已知关于x 的一元二次方程4mx 2－4(m ＋2)x ＋m ＝0有两个不相等的实数根，则m 的值可以是( )A ．2或－1B ．－1C ．2D ．不存在9．某小区为了排污，需铺设一段全长为720米的排污管道，为减少施工对居民生活的影响，需缩短施工时间，实际施工时每天的工作效率比原计划提高20%，结果提前2天完成任务，设原计划每天铺设x 米，下面所列方程正确的是( )A.720x －720（1＋20%）x ＝2B.720（1－20%）x －720x＝2 C.720（1＋20%）x －720x ＝2 D.720x ＋2＝720（1＋20%）x10．如图，菱形ABCD 的边长是4 cm ，∠B＝60°，动点P 以1 cm/s 的速度自A 点出发沿AB 方向运动至B 点停止，动点Q 以2 cm/s 的速度自B 点出发沿折线BCD 运动至D 点停止．若点P 、Q 同时出发运动了t s ，记△B PQ 的面积为S cm 2，下面图象中能表示S 与t 之间的函数关系的是( )二、填空题(本大题共4小题，每小题8分，满分20分)11．计算：12×3＝________．12．方程组⎩⎪⎨⎪⎧x －y ＝4，2x ＋y ＝－1的解是____________．13．方程12x ＝1x ＋1的解是__________． 14．如图，正比例函数y ＝x 的图象与反比例函数y ＝k x的图象相交于A ，B 两点，且点B 的横坐标为－2.若点E 是反比例函数在第一象限内图象上一点，S △A OE ＝3，则点E 的坐标为__________________________．三、(本大题共2小题，每小题8分，满分16分)15．计算：π0＋2cos 30°＋︱2－3︱－(12)－2.16．先化简，再求值：x 2＋2x ＋1x 2－1－x x －1，其中x ＝2.四、(本大题共2小题，每小题8分，满分16分)17．先化简，再求值：(－x 2＋3－7x )＋(5x －7＋2x 2)，其中x ＝2＋1.18．《九章算术》中有一题：今有二马、一牛价过一万，如半马之价．一马、二牛价不满一万，如半牛之价．向牛、马价各几何？译文为：现有二匹马加一头牛的价钱超过一万，超过的部分正好是半匹马的价钱；一匹马加上二头牛的价钱则不到一万，不足部分正好是半头牛的价钱，求一匹马、一头牛各多少钱．请解答上述问题．五、(本大题共2小题，每小题10分，满分20分)19．阅读下列材料解决问题：材料：古希腊著名数学家毕达哥拉斯发现把数1，3，6，10，15，21…这些数量的(石子)，都可以排成三角形，则称像这样的数为三角形数．把数 1，3，6，10，15，21…换一种方式排列，即1＝11＋2＝31＋2＋3＝61＋2＋3＋4＝101＋2＋3＋4＋5＝15…从上面的排列方式看，把1，3，6，10，15…叫做三角形数“名副其实”．(1)设第一个三角形数a1＝1，第二个三角形数为a2＝3，第三个三角形数为a3＝6，请直接写出第n个三角形数为a n的表达式(其中n为正整数)；(2)根据(1)的结论判断66是三角形数吗？若是，请说出66是第几个三角形数？若不是，请说明理由；(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由．20．某校为打造书香校园，计划购进甲乙两种规格的书柜放置新购买的图书，调查发现，若购买甲种书柜3个，乙种书柜2个，共需资金1 020元；若购买甲种书柜4个，乙种书柜3个，共需资金1 440元．(1)甲乙两种书柜每个的价格分别是多少元？(2)若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多提供资金4 320元，请设计几种购买方案供这个学校选择．六、(本题满分12分)21．如图，点M 在函数y ＝3x(x ＞0)的图象上，过点M 分别作x 轴和y 轴的平行线交函数y ＝1x(x ＞0)的图象于点B 、C. (1)若点M 坐标为(1，3)．①求B 、C 两点的坐标；②求直线BC 的表达式．(2)求△B M C 的面积．七、(本题满分12分)22．如图，已知点O(0，0)，A(－5，0)，B(2，1)，抛物线l：y＝－(x－h)2＋1(h为常数)与y轴的交点为C.(1)当l经过点B，求它的表达式，并写出此时l的对称轴及顶点坐标；(2)当线段O A被l只分为两部分，且这两部分的比是1∶4时，求h的值．第22题图八、(本题满分14分)23．为响应某市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18 m ，另外三边由36 m 长的栅栏围成．设矩形ABCD 空地中，垂直于墙的边AB ＝x m ，面积为y m 2(如图)．(1)求y 与x 之间的函数关系式，并写出自变量x 的取值范围；(2)若矩形空地的面积为160 m 2，求x 的值；(3)若该单位用8 600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表)．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．参考答案1．B 2.C 3.A 4.A 5.D 6.C 7.B 8.C 9.A 10.D11．6 12.⎩⎪⎨⎪⎧x ＝1，y ＝－313.x ＝1 14.(4，1)或(1，4) 15．解：原式＝－2.16．解：原式＝1x －1.当x ＝2时，原式＝12－1＝1.17．解：原式＝x 2－2x －4.当x ＝2＋1时，原式＝(2＋1)2－2(2＋1)－4＝－3.18．解：一匹马的价钱为6 00011，一头牛的价钱是20 00011. 19．解：(1)a n ＝n （n ＋1）2(n 为正整数)； (2)66是三角形数，理由如下：当n （n ＋1）2＝66时，解得：n ＝11或n ＝－12(舍去)，则66是第11个三角形数；(2)T ＝11＋13＋16＋115＋…＋2n （n ＋1）＝21×2＋22×3＋23×4＋24×5＋…＋2n （n ＋1）＝2(1－12＋12－13＋13－14＋…＋1n －1n ＋1)＝2n n ＋1∵n 为正整数，∴0＜n n ＋1＜1，则T ＜2. 20．解：(1)甲种书柜单价为180元，乙种书柜单价为240元，(2)学校的购买方案有以下三种：方案一：甲种书柜8个，乙种书柜12个，方案二：甲种书柜9个，乙种书柜11个，方案三：甲种书柜10个，乙种书柜10个．21．解：(1)①点C 坐标为(1，1)，点B 坐标为(13，3)． ②直线BC 的表达式为：y ＝－3x ＋4.(2)设点M 坐标为(a ，t)，∵点M 在函数y ＝3x(x ＞0)的图象上，∴at＝3.由(1)知C 点坐标为(a ，1a )，B 点坐标为(1t，t)， ∴BM＝a －1t ＝at －1t ，MC ＝t －1a ＝at －1a， ∴S △BMC ＝12·at －1t ·at －1a ＝23. 22．解：(1)把B(2，1)代入y ＝－(x －h)2＋1，得h ＝2，∴函数表达式为y ＝－(x －2)2＋1，∴对称轴为x ＝2，顶点坐标为B(2，1)．(2)把OA 分为1∶4两部分的点为(－1，0)或(－4，0)，把x ＝－1，y ＝0代入y ＝－(x －h)2＋1，得h ＝0或h ＝－2，但h ＝－2时，OA 被分为三部分，不合题意，舍去，同样，把x ＝－4，y ＝0代入y ＝－(x －h)2＋1，得h ＝－5或h ＝－3(舍去)， ∴h 的值为0或－5.23．解：(1)∵四边形ABCD 是矩形，垂直于墙的边AB ＝x ，∴CD＝AB ＝x ，BC ＝(36－2x)，∴y＝x(36－2x)，即y ＝－2x 2＋36x ，由矩形的任一边都大于0，⎩⎪⎨⎪⎧36－2x ＞0，36－2x≤18，解得9≤x＜18， ∴y 与x 之间的函数关系式为y ＝－2x 2＋36x(9≤x＜18)．(2)∵矩形空地的面积为160 m 2，即y ＝160，∴－2x 2＋36x ＝160，解得x 1＝10，x 2＝8，∵9≤x＜18，∴x 2＝8舍去，答：x 的值为10.(3)设甲、乙、丙三种植物分别购买了m 棵、n 棵、k 棵，由题意得：⎩⎪⎨⎪⎧m ＋n ＋k ＝400 ①，14m ＋16n ＋28k ＝8 600②，①×16－②得：m ＝6k －1 100.②－①×14得：n ＝1 500－7k ，∵m、n 、k 分别表示三种植物的数量，∴m、n 、k 为正整数，∴⎩⎪⎨⎪⎧6k －1 100＞0，1 500－7k ＞0，解得5503＜k ＜1 5007， ∵k 为正整数，∴k 能取的最大正整数为214，即丙种植物最多可以购买214棵，当k ＝214时，m ＝6k －1 100＝6×214－1 100＝184，n ＝1 500－7k ＝1 500－7×214＝2，∵y＝－2x 2＋36x ＝－2(x －9)2＋162，∴当x ＝9时，y 有最大值，最大值为162，即当垂直于墙的一边长为9 m 时，矩形空地的面积最大，最大为162 m 2.∵0.4×184＋2＋0.4×214＝161.2＜162，∴这批植物可以全部栽种到这块空地上．。

2019 年安徽省初中学业水平考试(一)

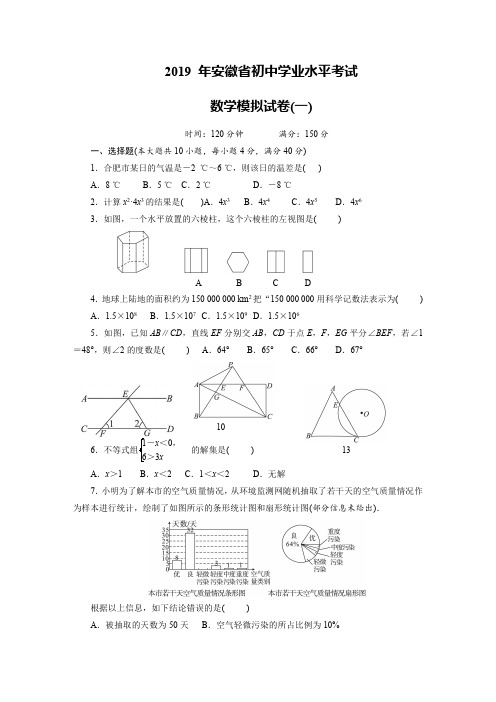
2019年安徽省初中学业水平考试数学模拟试卷(一)时间：120分钟满分：150分一、选择题(本大题共10小题，每小题4分，满分40分)1．合肥市某日的气温是－2℃～6℃，则该日的温差是()A ．8℃B ．5℃C ．2℃D ．－8℃2．计算x 2·4x 3的结果是()A ．4x 3B ．4x 4C ．4x 5D ．4x 63．如图，一个水平放置的六棱柱，这个六棱柱的左视图是()AB C D4．地球上陆地的面积约为150000000km 2把“150000000用科学记数法表示为()A ．1.5×108B ．1.5×107C ．1.5×109D ．1.5×1065．如图，已知AB ∥CD ，直线EF 分别交AB ，CD 于点E ，F ，EG 平分∠BEF ，若∠1＝48°，则∠2的度数是()A ．64°B ．65°C ．66°D ．67°5106－x ＜0，＞3x 的解集是()13A ．x ＞1B ．x ＜2C ．1＜x ＜2D ．无解7．小明为了解本市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图(部分信息未给出)．根据以上信息，如下结论错误的是()A ．被抽取的天数为50天B ．空气轻微污染的所占比例为10%C ．扇形统计图中表示优的扇形的圆心角度数57.6°D ．估计该市这一年(365天)达到优和良的总天数不多于290天8．市政府计划两年内将该市人均住房面积由现在的10m 2提高到14.4m 2，设每年人均住房面积增长率为x ，则所列方程正确的是()A ．10(1＋x )2＝14.4B ．10(1－x )2＝14.4C ．10(1＋x )＝14.4D ．10＋10(1＋x )＋10(1＋x )2＝14.49．若函数y ＝ax －c 与函数y ＝bx 的图象如图所示，则函数y ＝ax 2＋bx ＋c 的大致图象为()A B C D10．如图，在矩形ABCD 中，AB ＝3，BC ＝3，将△ABC 沿对角线AC 折叠，点B 恰好落在点P 处，CP 与AD 交于点F ，连接BP 交AC 于点G ，交AD 于点E ，下列结论不正确的是()A ．AC ＝2AP B ．△PBC 是等边三角形C ．S △BGC ＝3S △AGPD ．PG CG ＝13二、填空题(本大题共4小题，每小题5分，满分20分)11.84.1的整数部分是____.12．因式分解：a 3－4ab 2＝__.13．如图，一个边长为4cm 的等边三角形ABC 的高与⊙O 的直径相等．⊙O 与BC 相切于点C ，与AC 相交于点E ，则CE ＝____.14．在△ABC 中，AB ＝6cm ，点P 在AB 上，且∠ACP ＝∠B ，若点P 是AB 的三等分点，则AC 的长是__三、(本大题共2小题，每小题8分，满分16分)15．计算：9＋(π－3)0－|－5|＋(－1)2018216÷xx2－1，其中x＝－2.四、(本大题共2小题，每小题8分，满分16分)17．如图，在正方形网格中，△ABC为格点三角形，每个小正方形的边长均为1个单位．(1)画出△ABC关于y轴对称的△A′B′C′；(2)求AC边上的高．18．两位数相乘：19×11＝209,18×12＝216,25×25＝625,34×36＝1224，47×43＝2021，…(1)认真观察，分析上述各式中两因数的个位数字、十位数字分别有什么联系，找出因数与积之间的规律，并用字母表示出来；(2)验证你得到的规律．五、(本大题共2小题，每小题10分，满分20分)19．如图所示，巨型广告牌AB背后有一看台CD，台阶每层高0.3m，且AC＝17m，小明坐在台阶的FG这层上晒太阳，设太阳光线与水平地面的夹角为α，当α＝60°时，测得广告牌AB在地面上的影长AE＝10m，过了一会，当α＝45°，问小明在FG这层是否还能晒到太阳？请说明理由(3取1.73)．20．商店只有雪碧、可乐、果汁、红茶四种饮料，赵敏同学去该店购买饮料，每种饮料被选中的可能性相同．(1)若他去买一瓶饮料，则他买到红茶的概率是多少？(2)若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和红茶的概率．六、(本题满分12分)21．如图，C，D两点在以AB为直径的半圆O上，AD平分∠BAC，AB＝20，AD＝415，DE⊥AB于E.(1)求DE的长；(2)求证：AC＝2OE.七、(本题满分12分)22．安徽凤凰城建材市场为某工厂代销一种建筑材料．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用100元．(1)当每吨售价是240元时，计算此时的月销售量；(2)在遵循“薄利多销”的原则下，问每吨材料售价为多少时，该经销店的月利润为9000元？(3)小明说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．八、(本题满分14分)23．如图，在菱形ABCD中，E，F为边BC，CD上的点，且CE＝CF，连接AE，AF，∠ABC的平分线交AE于点G，连接CG.(1)求证：AG＝CG；(2)求证：CG∥AF；(3)若BG＝CG，则△ABE与△BGE是否相似？若相似，写出证明过程；若不相似，请说明理由．。

2019年安徽省初中毕业水平考试(有答案)

2019年安徽省初中毕业水平考试数学（满分150分，考试时间120分钟）一、选择程（本大题共10小题，每小题4分，满分40分）1.在12--，，0，1这四个数中，最小的数是（）A.2- B.1- C.0 D.12.计算)(3a a -•的结果是（）A.2a B.2a - C.4a D.4a -3.一个由圆柱和长方体组成的几间体如题水平故置，它的俯视图是（）4.2019年“五一”假日期间，我省银联网络交易总金额接近161亿，其中161亿用科学记数法表示为（）A.91061.1⨯ B.101061.1⨯ C.111061.1⨯D.121061.1⨯ 5.已知点A （1，3-）关于x 轴的对称点A ’在反比例函数xk y =的图象上，实数k 的值为（） A.3 B.31 C.3- D.31- 6.在某时段有50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这50辆车的车速的众数（单位：km/h ）为（）A.60B. 50C.40D.15 7.如图，在Rt △ABC 中，090=∠ACB ，AC=6，BC=12，点D 在边BC 上，点E 在线段AD 上.EF ⊥AC 点F ， EG ⊥EF ，交AB 于点G ，若EF=EG ，则CD 的长为（）A.3.6B.4C.4.8D.58.据国家统计局数据，2018年全年国内生产总值为90.03万亿元，比3017年增长6.6%，假设国内生产总值的年增长率保持不变，则国内生产总值首次突破100万亿元的年份是（）A.2019年B.2020年C.2021年 D2022年9.已知三个实数c b a ，，满足02=+-c b a ，02<++c b a ，则（）A.0402≤->ac b b ，B.0402≤-<ac b b ，C.0402≥->ac b b ，D.0402≥-<ac b b ，10.如图，在正方形ABCD 中，点E ，F 将对角线AC 三等分，且AC=12，点P 在正方形边上，则满足9=+PF PE 的点P 的个数是（）A.0 B.4 C.6 D.8第6题图第7题图第10题图二、填空题（本大题共4小题，每小题5分，满分20分）11.计算218÷的结果是_______________.12.命题“如果0=+b a ，那么b a ，互为相反数”的逆命题为_______________________.13.如图，△ABC 内内接于⊙O ，030=∠CAB ，045=∠CBA ，AB CD ⊥于点D ，若⊙O 的直经为2，则CD 的长为________________.14.在平面直角坐标系中，垂直于x 轴的直线l 分别与函数1+-=a x y 和ax x y 22-=的图象交于P ，Q 两点都在x 轴的下方，则实数a 的取值范围是____________________.三、（本大题共2小题，每小题8分，满分16分）15.解方程：4)1(2=-x16.如图，在边长为1个单位长度的小正方形组成的12x12网格中，给出了以格点（网格线的交点）为端点的线段AB.（1）将线段ABA 先向右平移5个单位长度，再向上平移3个单位长度，得到线段CD （点A ，B 的对应点分别为点C ，D ）,请画出线段CD ；（2）以线段CD 为一边，作一个菱形CDEF ，且点E ，F 也为格点.（作出一个菱形即可）四、（本大题共2小题，每小题8分，满分16分）17.为实施乡村振兴战略，解决某山区老百姓出行难问题，当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲，乙两个工程队负责施工. 甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进26米. 已知甲工程队每天比乙工程队多掘进2米，按此速度完成这项隧道贯穿工程，甲、乙两个工程队还需联合工作多少天？18.观察以下等式：第1个等式：111112+=；第2个等式：612132+=；第3个等式：1513152+=；第4个等式：2814172+=；第5个等式：4515192+=；…… 按照以上规律，解决下列问题：（1）写出第6个等式：_________________；（2）写出你猜想的的第n 个等式：____________ （用含n 的等式表示），并证明.五、（本大题共2小题，每小题8分，满分16分）19.筒车是我国古代发明的一种水利灌溉工具.如图（1），明朝科学家徐光启在《农政全书》中用图描绘了筒车的工作原理. 如图（2），筒车盛水桶的运行轨迹是以轴心O 为圆心的圆.已知圆心在水面上方，且圆被水面截得的弦AB 的长为6米，03.41=∠OAB ，若点C 为运行轨迹的最高点（C ，D 的连线垂直于AB ），求点C 到弦AB 所在直线的距离.（参考数据：66.03.41sin 0≈，75.03.41cos 0≈，88.03.41tan 0≈）20如图，点E 在口AB CD 内部，A//BFE ，DF//CE ，连接AE ，DE.（1）求证：△BCE ≌△ADF ；（2）设口ABCD 的面为S ，四边形AEDP 的面积为T ，求TS 的值.六、（本题满分12分）21.为监控某条生产线上产品的质量，检验员每隔相同的时间抽检一件产品，并测量其尺寸.在一天的抽检结束后，检验员将测得的15个数据按从小到大的顺序整理成如下表格：（1）已知此次抽检的合格率为80%，请判断编号为○15的产品是否为合格品，并说明理由.（2）已知此次抽检出的优等品尺寸的中位数为9 cm.①求a 的值；②将这些优等品分成两组，一组尺寸大于9cm ，另一组尺寸不太于9cm ，从这两组中各随机抽取1件进行复检，求抽取到的2件产品都是特等品的概率.七、（本题满分12分）22.已知一次函数4+=kx y 与二次函数c ax y +=2的图象的一个交点坐标为(1，2)，另一个交点是请二次函数的顶点.（1）求k ，c a ，的值;（2）过点A(o ，m) （40<<m ）且垂直于y 轴的直线与二次函数c ax y +=2的图象交于B ，C 两点，点O 为坐标为原点，记22BC OA W +=，求W 关于m 的函数解析式，并求W 的最小值.八、（本题满分14分）23.如圆，在Rt △A BC 中，090=∠ACB ，AC=BC ， P 为△A BC 内部一点，且0135=∠=∠BPC APB .（1）求证：△PAB ∽△PBC ；（2）求证：PA=2PC ；（3）若点P 到三角形的边AB ，BC ，CA 的距离分别为321h h h ，，，求证：3221h h h •=.。

2019年安徽中考数学试卷及答案

2019年安徽省初中学业水平考试数学试卷一、选择题（本大题共10小题，每小题4分，满分40分）1、在—2，—1，0，1这四个数中，最小的数是（）A 、—2B 、—1 C.、0 D 、12、计算a 3·(—a)的结果是（）A 、a 2B 、—a 2C 、a 4D 、—a 43、一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是（）4、2019年“五一”假日期间，我省银联网络交易总金额接近161亿元，其中161亿用科学计数法表示为（）A 、1.61×109B 、1.61×1010C 、1.61×1011D 、1.61×10125、已知点A （1，—3）关于x 轴的对称点A/在反比例函数k y x的图像上，则实数k 的值为（）A 、3B 、13C 、—3D 、－136、在某时段有50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这50辆车的车速的众数（单位：km/h ）为（）A 、60B 、50 C 、40 D 、157、如图，在R t △ABC 中，∠ACB=900，AC=6，BC=12，点D 在边BC 上，点E 在线段AD 上，E F ⊥AC 于点F ，EG ⊥EF 交AB 于G ，若EF=EG ，则CD 的长为（）A 、3.6B 、4C 、4.8D 、58、据国家统计局数据，2018年全年国内生产总值为90.3万亿，比2017年增长6.6﹪，假设国内生产总值增长率保持不变，则国内生产总值首次突破100万亿的年份为（）A 、2019年B 、2020年C 、2021年D 、2022年9、已知三个实数a，b，c满足a-2b+c=0，a+2b+c<0，则（）A、b＞0，b2-a c≤0B、b＜0，b2-a c≤0C、b＞0，b2-a c≥0D、b＜0，b2-a c≥010、如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC=12，点P正方形的边上，则满足PE+PF=9的点P个数是（）A、0B、4C、6D、8二、填空题（本大题共4小题，每小题5分，满分20分）11的结果是.12、命题“如果a+b=0，那么a，b互为相反数”的逆命题为.13、如图，△ABC内接于⊙O，∠CAB＝30O，∠CBA＝45O，CD⊥AB于点D，若⊙O的半径为2，则CD的长为 .14、在平面直角坐标系中，垂直于x轴的直线l分别与函数y=x-a+1和y=x2-2ax的图像交于P，Q两点，若平移直线l，可以使P，Q都在x轴的下方，则实数a的取值范围是.三、（本大题共2小题，每小题8分，满分16分）15、解方程（x—1）2=4.16、如图，在边长为1的单位长度的小正方形组的12×12风格中，给出了以格点（风格线的交点）为端点的线段AB。

2019年安徽省初中学业水平模拟考试数学试卷(一)

子．问上等稻子和下等稻子一捆各能结多少？（十升为一斗）
请解答上述问题．
四、（本大题共２小题，每小题８分，满分１６分）
１７．观察下列等式：
１＋３×２＋１＝８，
１＋６×３＋８＝２７，
１＋９×４＋２７＝６４，
…
按照以上规律，解决下列问题：
（１）写出第４个等式：；
（２）写出你猜想的第ｎ个等式：（用含ｎ的式子表示），并证明．
（参考数据：ｓｉｎ７５°≈０．９７，槡２≈１．４１）
第１９题图
逆袭诊断卷·数学第３页（共４页）
２０．如图，ＡＢ是⊙Ｏ的直径，ＡＢ＝６．
（１）用尺规作图作出半径ＯＢ的垂直平分线，并标出它与⊙Ｏ的交点Ｃ、Ｄ（保留作图痕
迹，不写作法）；
（２）在（１）的条件下，连接ＡＣ，求弦ＡＣ的长．六、（本题满分１２分）
第１３题图
１４．矩形ＡＢＣＤ中，ＡＢ＝１５，ＢＣ＝２０，Ｅ是边ＡＤ上一动点，点Ｆ在矩形ＡＢＣＤ的内部，将△ＡＢＥ沿ＢＥ折叠，使点Ａ落
在点Ｆ处，过点Ｆ作ＦＧ⊥ＢＣ于点Ｇ，若△ＢＦＧ与△ＢＣＤ相似，则ＣＦ的长为．
逆袭诊断卷·数学第２页（共４页）
三、（本大题共２小题，每小题８分，满分１６分）
１５．计算：－１２０１９＋槡８－｜－２槡２｜．１６．《九章算术》中记载了这样一个问题，原文如下：
今有上禾五秉，损实一斗一升，当下禾七秉；上禾七秉，损实二斗五升，当下禾五秉．问上、下禾实一秉
各几何？
大意是：
５捆上等稻子少结一斗一升，相当于７捆下等稻子；７捆上等稻子少结二斗五升，相当于５捆下等稻
２０１９年安徽省初中学业水平考试数学
（试题卷）

2019年安徽省初中学业水平考试数学试卷(解析卷)

2019年安徽省初中学业水平考试数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A，B，C，D四个选项，其中只有一个是正确的．1．（4分）在﹣2，﹣1，0，1这四个数中，最小的数是（）A．﹣2B．﹣1C．0D．1解：根据有理数比较大小的方法，可得﹣2＜﹣1＜0＜1，∴在﹣2，﹣1，0，1这四个数中，最小的数是﹣2．故选：A．2．（4分）计算a3•（﹣a）的结果是（）A．a2 B．﹣a2C．a4D．﹣a4解：a3•（﹣a）＝﹣a3•a＝﹣a4．故选：D．3．（4分）一个由圆柱和长方体组成的几何体如图水平放置，它的俯视图是（）A．B．C．D．解：几何体的俯视图是：故选：C．4．（4分）2019年“五一”假日期间，我省银联网络交易总金额接近161亿元，其中161亿用科学记数法表示为（）A．1.61×109 B．1.61×1010 C．1.61×1011 D．1.61×1012解：根据题意161亿用科学记数法表示为1.61×1010 ．故选：B．5．（4分）已知点A（1，﹣3）关于x轴的对称点A'在反比例函数y＝的图象上，则实数k 的值为（）A．3B．C．﹣3D．﹣解：点A（1，﹣3）关于x轴的对称点A'的坐标为（1，3），把A′（1，3）代入y＝得k＝1×3＝3．故选：A．6．（4分）在某时段由50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这50辆车的车速的众数（单位：km/h）为（）A．60B．50C．40D．15解：由条形图知，50个数据的中位数为第25、26个数据的平均数，即中位数为＝＝40，故选：C．7．（4分）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝12，点D在边BC上，点E 在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G．若EF＝EG，则CD的长为（）A．3.6B．4C．4.8D．5解：作DH∥EG交AB于点H，则△AEG∽△ADH，∴，∵EF⊥AC，∠C＝90°，∴∠EF A＝∠C＝90°，∴EF∥CD，∴△AEF∽△ADC，∴，∴，∵EG＝EF，∴DH＝CD，设DH＝x，则CD＝x，∵BC＝12，AC＝6，∴BD＝12﹣x，∵EF⊥AC，EF⊥EG，DH∥EG，∴EG∥AC∥DH，∴△BDH∽△BCA，∴，即，解得，x＝4，∴CD＝4，故选：B．8．（4分）据国家统计局数据，2018年全年国内生产总值为90.3万亿，比2017年增长6.6%．假设国内生产总值的年增长率保持不变，则国内生产总值首次突破100万亿的年份是（）A．2019年B．2020年C．2021年D．2022年解：2019年全年国内生产总值为：90.3×（1+6.6%）＝96.2598（万亿），2020年全年国内生产总值为：96.2598×（1+6.6%）≈102.6（万亿），∴国内生产总值首次突破100万亿的年份是2020年，故选：B．9．（4分）已知三个实数a，b，c满足a﹣2b+c＝0，a+2b+c＜0，则（）A．b＞0，b2﹣ac≤0B．b＜0，b2﹣ac≤0C．b＞0，b2﹣ac≥0D．b＜0，b2﹣ac≥0解：∵a﹣2b+c＝0，a+2b+c＜0，∴a+c＝2b，b＝，∴a+2b+c＝（a+c）+2b＝4b＜0，∴b＜0，∴b2﹣ac＝＝﹣ac＝＝≥0，即b＜0，b2﹣ac≥0，故选：D．10．（4分）如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12，点P在正方形的边上，则满足PE+PF＝9的点P的个数是（）A．0B．4C．6D．8解：如图，作点F关于BC的对称点M，连接FM交BC于点N，连接EM，∵点E，F将对角线AC三等分，且AC＝12，∴EC＝8，FC＝4，∵点M与点F关于BC对称∴CF＝CM＝4，∠ACB＝∠BCM＝45°∴∠ACM＝90°∴EM＝＝4则在线段BC存在点N到点E和点F的距离之和最小为4＜9∴在线段BC上点N的左右两边各有一个点P使PE+PF＝9，同理在线段AB，AD，CD上都存在两个点使PE+PF＝9．即共有8个点P满足PE+PF＝9，故选：D．二、填空题（共4小题，每小题5分，满分20分）11．（5分）计算÷的结果是3．解：．故答案为：312．（5分）命题“如果a+b＝0，那么a，b互为相反数”的逆命题为如果a，b互为相反数，那么a+b＝0．解：命题“如果a+b＝0，那么a，b互为相反数”的逆命题为：如果a，b互为相反数，那么a+b＝0；故答案为：如果a，b互为相反数，那么a+b＝0．13．（5分）如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为．解：连接CO并延长交⊙O于E，连接BE，则∠E＝∠A＝30°，∠EBC＝90°，∵⊙O的半径为2，∴CE＝4，∴BC＝CE＝2，∵CD⊥AB，∠CBA＝45°，∴CD＝BC＝，故答案为：．14．（5分）在平面直角坐标系中，垂直于x轴的直线l分别与函数y＝x﹣a+1和y＝x2﹣2ax 的图象相交于P，Q两点．若平移直线l，可以使P，Q都在x轴的下方，则实数a的取值范围是a＞1或a＜﹣1．解：y＝x﹣a+1与x轴的交点为（1﹣a，0），∵平移直线l，可以使P，Q都在x轴的下方，∴当x＝1﹣a时，y＝（1﹣a）2﹣2a（1﹣a）＜0，∴a2﹣1＞0，∴a＞1或a＜﹣1；故答案为a＞1或a＜﹣1；三、（本大题共2小题，每小题8分，满分16分）15．（8分）解方程：（x﹣1）2＝4．解：两边直接开平方得：x﹣1＝±2，∴x﹣1＝2或x﹣1＝﹣2，解得：x1＝3，x2＝﹣1．16．（8分）如图，在边长为1个单位长度的小正方形组成的12×12的网格中，给出了以格点（网格线的交点）为端点的线段AB．（1）将线段AB向右平移5个单位，再向上平移3个单位得到线段CD，请画出线段CD．（2）以线段CD为一边，作一个菱形CDEF，且点E，F也为格点．（作出一个菱形即可）解：（1）如图所示：线段CD即为所求；（2）如图：菱形CDEF即为所求，答案不唯一．四、（本大题共2小题，每小题8分，满分16分）17．（8分）为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路．其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工．甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进26米．已知甲工程队每天比乙工程队多掘进2米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？解：设甲工程队每天掘进x米，则乙工程队每天掘进（x﹣2）米，由题意，得2x+（x+x﹣2）＝26，解得x＝7，所以乙工程队每天掘进5米，（天）答：甲乙两个工程队还需联合工作10天．18．（8分）观察以下等式：第1个等式：＝+，第2个等式：＝+，第3个等式：＝+，第4个等式：＝+，第5个等式：＝+，……按照以上规律，解决下列问题：（1）写出第6个等式：；（2）写出你猜想的第n个等式：（用含n的等式表示），并证明．解：（1）第6个等式为：，故答案为：；（2）证明：∵右边＝＝左边．∴等式成立，故答案为：．五、（本大题共2小题，每小题10分，满分20分）19．（10分）筒车是我国古代发明的一种水利灌溉工具．如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．如图2，筒车盛水桶的运行轨迹是以轴心O 为圆心的圆．已知圆心在水面上方，且圆被水面截得的弦AB长为6米，∠OAB＝41.3°，若点C为运行轨道的最高点（C，O的连线垂直于AB），求点C到弦AB所在直线的距离．（参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88）解：连接CO并延长，与AB交于点D，∵CD⊥AB，∴AD＝BD＝AB＝3（米），在Rt△AOD中，∠OAB＝41.3°，∴cos41.3°＝，即OA＝＝＝4（米），tan41.3°＝，即OD＝AD•tan41.3°＝3×0.88＝2.64（米），则CD＝CO+OD＝4+2.64＝6.64（米）．20．（10分）如图，点E在▱ABCD内部，AF∥BE，DF∥CE．（1）求证：△BCE≌△ADF；（2）设▱ABCD的面积为S，四边形AEDF的面积为T，求的值．解：（1）∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴∠ABC+∠BAD＝180°，∵AF∥BE，∴∠EAB+∠BAF＝180°，∴∠CBE＝∠DAF，同理得∠BCE＝∠ADF，在△BCE和△ADF中，∵，∴△BCE≌△ADF（ASA）；（2）∵点E在▱ABCD内部，∴S△BEC+S△AED＝S▱ABCD，由（1）知：△BCE≌△ADF，∴S△BCE＝S△ADF，∴S四边形AEDF＝S△ADF+S△AED＝S△BEC+S△AED＝S▱ABCD，∵▱ABCD的面积为S，四边形AEDF的面积为T，∴＝＝2．六、（本题满分12分）21．（12分）为监控某条生产线上产品的质量，检测员每个相同时间抽取一件产品，并测量其尺寸，在一天的抽检结束后，检测员将测得的个数据按从小到大的顺序整理成如下表格：编号①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮8.728.888.928.938.948.968.978.98a9.039.049.069.079.08b尺寸（cm）按照生产标准，产品等次规定如下：尺寸（单位：cm）产品等次8.97≤x≤9.03特等品8.95≤x≤9.05优等品8.90≤x≤9.10合格品x＜8.90或x＞9.10非合格品注：在统计优等品个数时，将特等品计算在内；在统计合格品个数时，将优等品（含特等品）计算在内．（1）已知此次抽检的合格率为80%，请判断编号为⑮的产品是否为合格品，并说明理由．（2）已知此次抽检出的优等品尺寸的中位数为9cm．（i）求a的值；（ii）将这些优等品分成两组，一组尺寸大于9cm，另一组尺寸不大于9cm，从这两组中各随机抽取1件进行复检，求抽到的2件产品都是特等品的概率．解：（1）不合格．因为15×80%＝12，不合格的有15﹣12＝3个，给出的数据只有①②两个不合格；（2）（i）优等品有⑥～⑪，中位数在⑧8.98，⑨a之间，∴，解得a＝9.02（ii）大于9cm的有⑨⑩⑪，小于9cm的有⑥⑦⑧，其中特等品为⑦⑧⑨⑩画树状图为：共有九种等可能的情况，其中抽到两种产品都是特等品的情况有4种．∴抽到两种产品都是特等品的概率P＝．七、（本题满分12分）22．（12分）一次函数y＝kx+4与二次函数y＝ax2+c的图象的一个交点坐标为（1，2），另一个交点是该二次函数图象的顶点（1）求k，a，c的值；（2）过点A（0，m）（0＜m＜4）且垂直于y轴的直线与二次函数y＝ax2+c的图象相交于B，C两点，点O为坐标原点，记W＝OA2+BC2，求W关于m的函数解析式，并求W的最小值．解：（1）由题意得，k+4＝﹣2，解得k＝﹣2，又∵二次函数顶点为（0，4），∴c＝4把（1，2）带入二次函数表达式得a+c＝2，解得a＝﹣2（2）由（1）得二次函数解析式为y＝﹣2x2+4，令y＝m，得2x2+m﹣4＝0∴，设B，C两点的坐标分别为（x1，m）（x2，m），则，∴W＝OA2+BC2＝∴当m＝1时，W取得最小值7八、（本题满分14分）23．（14分）如图，Rt△ABC中，∠ACB＝90°，AC＝BC，P为△ABC内部一点，且∠APB ＝∠BPC＝135°．（1）求证：△P AB∽△PBC；（2）求证：P A＝2PC；（3）若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证h12＝h2•h3．解：（1）∵∠ACB＝90°，AB＝BC，∴∠ABC＝45°＝∠PBA+∠PBC又∠APB＝135°，∴∠P AB+∠PBA＝45°∴∠PBC＝∠P AB又∵∠APB＝∠BPC＝135°，∴△P AB∽△PBC（2）∵△P AB∽△PBC∴在Rt△ABC中，AB＝AC，∴∴∴P A＝2PC（3）如图，过点P作PD⊥BC，PE⊥AC交BC、AC于点D，E，∴PF＝h1，PD＝h2，PE＝h3，∵∠CPB+∠APB＝135°+135°＝270°∴∠APC＝90°，∴∠EAP+∠ACP＝90°，又∵∠ACB＝∠ACP+∠PCD＝90°∴∠EAP＝∠PCD，∴Rt△AEP∽Rt△CDP，∴，即，∴h3＝2h2∵△P AB∽△PBC，∴，∴∴．即：h12＝h2•h3．。