机械原理习题答案新
机械原理习题册答案

参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
机械原理简答题答案(新)

三、简答题1、什么叫机械零件的计算准则?常用的机械零件的计算准则有那些?答:机械零件的计算准则就是为了防止机械零件的失效而制定的判定条件,常用的准则有:强度准则、刚度准则、寿命准则、振动稳定性规则、可靠性准则。
2、影响机械零件疲劳强度的主要因素有哪些?提高机械零件疲劳强度的措施?答:主要因素有:应力集中,零件尺寸,表面状态,措施:①降低应力集中的影响;②选用疲劳强度高的材料或规定能够提高材料疲劳强度的热处理方法及强化工艺,③提高零件的表面质量;④尽可能的减小或消除零件表面可能发生的初始裂纹的尺寸3、画图表示机械零件的正常磨损过程,并指出正常磨损过程通常经历哪几个磨损阶段?答:经历①磨合磨损阶段②稳定磨损阶段③剧烈磨损阶段磨合稳定剧烈4、根据磨损机理的不同,磨损通常可分为哪几种类型?它们各有什么主要特点?答:①粘着磨损:由于干摩擦,在有油,无油的表面,都需要切向力使吸附膜和脏污膜破裂后,由新表面直接接触才能发生粘着,载荷越大,表面温度越高,粘着现象也越严重;②表面疲劳磨损:受交变接触应力的摩擦副,在其表面上将形成疲劳点蚀,有小块金属剥落;③磨粒磨损:硬质颗粒或摩擦表面上的硬质突出物,在摩擦过程中引起材料脱落,与摩擦材料的硬度,磨粒的硬度有关;④腐蚀磨损:与周围介质发生化学反应或电化学反应。
5、何谓螺纹联接的预紧,预紧的目的是什么?预紧力的最大值如何控制?答:螺纹连接的预紧:螺纹连接的预紧是指在装配时拧紧,是连接在承受工作载荷之前预先受到预紧力的作用。
目的:增强连接的可靠性与紧密性,以防受载后被连接件间出现间隙或者发生相对滑移。
6、螺纹联接有哪些基本类型?适用于什么场合?答:①螺栓联接:用于被联接件不太厚且两边有足够的安装空间的场合。
②螺钉联接:用于不能采用螺栓联接,如被联接件之一太厚不宜制成通孔,或没有足够的装配空间,又不需要经常拆卸的场合。
③双头螺柱联接:用于不能采用螺栓联接且又需要经常拆卸的场合。
机械原理习题及答案(1-1至4-3)

2-1 试求出下列图示机构中的全部瞬心。
2-2 图示铰链四杆机构中,已知:
l BC = 50 mm, lCD = 35 mm, l AD = 30 mm,AD为机架。
1. 2. 3.
若若若此此此机机机构构构为为为曲双双柄曲摇摇柄杆杆机机机构构,构,,求求且llAAABBB的为的最曲数小柄值值,范;求围l。AB
3-1 5-9 渐开线主动齿轮I逆时针转动,已知两轮的齿顶
圆 ra ,齿根圆 r f ,基圆 rb 以及中心距如图所
示。试在图上画出:
1)理论啮合线N1N2 ;
2)啮合开始点 B 2 及啮合
终止点 B 1 ,标出实
际啮合线;
' 3)啮合角 ,一对节圆,
注出其半径 r1 及 r2 ,
4)徒手画出在节点P啮合的一对 齿的齿廓工作段(用双线表示)。
2-3
1-4b (答案)
(答案a)(答案b)
1-4c (答案)
(答案c)(答案d)
(答案e)(答案f)
2-4 (答案a)(答案b)
3-1 (答案) 3-2(答案a)(答案b) 3-3 (答案)
2-5 (答案) 2-6答案 2-7答案
3-4 (答案)
(答案) (答案) (答案)
1-1 试画出下列各机构的运动简图, 并分别计算其自由度。
1-2b
解: 依次拆下6-7,4-5,2-3 三个II级组,故为II级机构。 C为复合铰链。
n 7 ,p L 1,0 p H 0 ,
F 3 7 2 1 1 0 .
1-3 图示椭圆画器机构, 已知AB=BC=BD, 试证滑块4对连杆CD的约 束是虚约束, 去掉构件4之后计算此机构的自由度。
(完整版)机械原理课后全部习题答案

机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征?机器通常由哪三部分组成?各部分的功能是什么?2)、机器与机构有什么异同点?3)、什么叫构件?什么叫零件?什么叫通用零件和专用零件?试各举二个实例。
4)、设计机器时应满足哪些基本要求?试选取一台机器,分析设计时应满足的基本要求。
2、填空题1)、机器或机构,都是由组合而成的。
2)、机器或机构的之间,具有确定的相对运动。
3)、机器可以用来人的劳动,完成有用的。
4)、组成机构、并且相互间能作的物体,叫做构件。
5)、从运动的角度看,机构的主要功用在于运动或运动的形式。
6)、构件是机器的单元。
零件是机器的单元。
7)、机器的工作部分须完成机器的动作,且处于整个传动的。
8)、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9)、构件之间具有的相对运动,并能完成的机械功或实现能量转换的的组合,叫机器。
3、判断题1)、构件都是可动的。
()2)、机器的传动部分都是机构。
()3)、互相之间能作相对运动的物件是构件。
()4)、只从运动方面讲,机构是具有确定相对运动构件的组合。
()5)、机构的作用,只是传递或转换运动的形式。
()6)、机器是构件之间具有确定的相对运动,并能完成有用的机械功或实现能量转换的构件的组合。
()7)、机构中的主动件和被动件,都是构件。
()2 填空题答案1)、构件2)、构件3)、代替机械功4)、相对运动5)、传递转换6)、运动制造7)、预定终端8)、中间环节9)、确定有用构件3判断题答案1)、√2)、√3)、√4)、√5)、×6)、√7)、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
机械原理练习题库(附答案)

机械原理练习题库(附答案)一、单选题(共50题,每题1分,共50分)1、冲压机采用的是()机构。
A、摆动导杆B、曲柄滑块C、移动导杆正确答案:B2、具有结构简单、定位可靠、能承受较大的轴向力等特点,广泛应用于各种轴上零件的轴向固定是()。
A、紧定螺钉B、轴肩与轴环C、紧定螺钉与挡圈正确答案:B3、从动件作等速运动规律的位移曲线形状是()。
A、斜直线B、双曲线C、抛物线正确答案:A4、10.V带顶面应与带轮外缘表面()一些。
A、平齐B、平齐或略高C、略高D、略低正确答案:B5、从动件作等加速等减速运动规律的位移曲线是()。
A、双曲线B、抛物线C、斜直线正确答案:B6、传动比大且准确的传动是()。
A、蜗轮蜗杆传动B、齿轮传动C、链传动正确答案:A7、基圆上的压力角等于()。
A、40︒B、20︒C、0︒正确答案:C8、内燃机的配气机构采用了()机构。
A、铰链四杆B、齿轮C、凸轮正确答案:C9、在轮系中,()即可以是主动轮又可以是从动轮,对总传动比没有影响,起改变齿轮副中从动轮回转方向的作用。
A、惰轮B、蜗轮蜗杆C、锥齿轮正确答案:A10、国家标准规定,斜齿圆柱齿轮的()模数和压力角为标准值。
A、端面B、法面和端面C、法面正确答案:C11、在键连接中,对中性好的是()。
A、切向键B、平键C、楔键正确答案:B12、在一般机械传动中,常用于数控机床、纺织机械的带传动是()。
A、平带传动B、普通V带传动C、同步带传动正确答案:C13、下列连接中属于不可拆连接的是()。
A、焊接B、螺纹连接C、销连接正确答案:A14、铰链四杆机构中,各构件之间均以()相连接。
A、螺旋副B、移动副C、转动副正确答案:C15、()花键形状简单、加工方便,应用较为广泛。
A、渐开线B、三角形C、矩形齿正确答案:C16、在闭式传动中,()润滑适用于中速机器中轴承的润滑。
A、油环B、压力C、润滑脂正确答案:B17、两被连接件上均为通孔且有足够装配空间的场合应采用()。
机械原理习题(附标准答案)

第二章一、单项选择题:1.两构件组成运动副的必备条件是。
A.直接接触且具有相对运动; B.直接接触但无相对运动;C.不接触但有相对运动; D.不接触也无相对运动。
2.当机构的原动件数目小于或大于其自由度数时,该机构将确定的运动。
A.有; B.没有; C.不一定3.在机构中,某些不影响机构运动传递的重复部分所带入的约束为。
A.虚约束; B.局部自由度; C.复合铰链4.用一个平面低副联二个做平面运动的构件所形成的运动链共有个自由度。
A.3; B.4; C.5; D.65.杆组是自由度等于的运动链。
A.0; B.1; C.原动件数6.平面运动副所提供的约束为A.1; B.2; C.3; D.1或27.某机构为Ⅲ级机构,那么该机构应满足的必要充分条件是。
A.含有一个原动件组; B.至少含有一个基本杆组;C.至少含有一个Ⅱ级杆组; D.至少含有一个Ⅲ级杆组。
8.机构中只有一个。
A.闭式运动链; B.原动件; C.从动件; D.机架。
9.要使机构具有确定的相对运动,其条件是。
A.机构的自由度等于1; B.机构的自由度数比原动件数多1;C.机构的自由度数等于原动件数二、填空题:1.平面运动副的最大约束数为_____,最小约束数为______。
2.平面机构中若引入一个高副将带入_______个约束,而引入一个低副将带入_____个约束。
3.两个做平面平行运动的构件之间为_______接触的运动副称为低副,它有_______个约束;而为_______接触的运动副为高副,它有_______个约束。
4.在平面机构中,具有两个约束的运动副是_______副或_______副;具有一个约束的运动副是_______副。
5.组成机构的要素是________和________;构件是机构中的_____单元体。
6.在平面机构中,一个运动副引入的约束数的变化范围是_______。
7.机构具有确定运动的条件是____________________________________________。
机械原理习题答案新
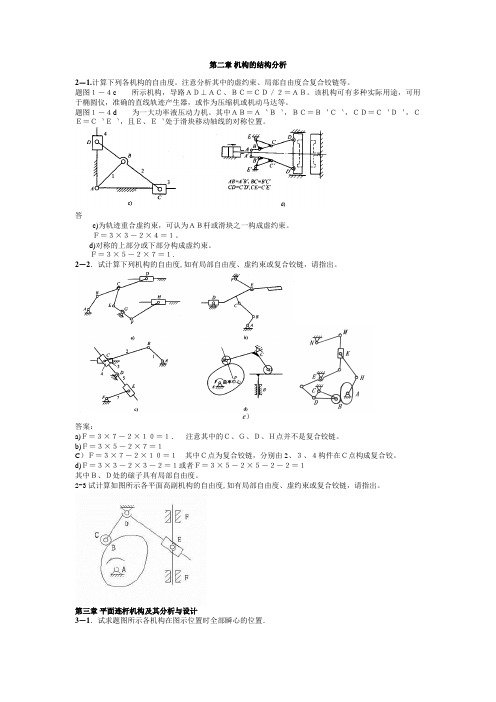
第二章机构的结构分析2-1.计算下列各机构的自由度。
注意分析其中的虚约束、局部自由度合复合铰链等。
题图1-4c所示机构,导路AD⊥AC、BC=CD/2=AB。
该机构可有多种实际用途,可用于椭圆仪,准确的直线轨迹产生器,或作为压缩机或机动马达等。
题图1-4d为一大功率液压动力机。
其中AB=A`B`,BC=B`C`,CD=C`D`,CE=C`E`,且E、E`处于滑块移动轴线的对称位置。
答c)为轨迹重合虚约束,可认为AB杆或滑块之一构成虚约束。
F=3×3-2×4=1。
d)对称的上部分或下部分构成虚约束。
F=3×5-2×7=1.2-2.试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
e)答案:a)F=3×7-2×10=1.注意其中的C、G、D、H点并不是复合铰链。
b)F=3×5-2×7=1C)F=3×7-2×10=1其中C点为复合铰链,分别由2、3、4构件在C点构成复合铰。
d)F=3×3-2×3-2=1或者F=3×5-2×5-2-2=1其中B、D处的磙子具有局部自由度。
2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
第三章平面连杆机构及其分析与设计3-1.试求题图所示各机构在图示位置时全部瞬心的位置.答案:瞬心P 12在A 点瞬心P 23、 P 24均在B 点 瞬心P 34在C 点P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中,试用瞬心法求齿轮1与齿轮3的传动比31/ωω。
答案:此题关键是找到相对瞬心P13. 3-6在图示凸轮机构中,已知mm r 50=,mm l OA 22=,mm l AC 80=,οϕ901=,凸轮,凸轮以角速度s rad /101=ω逆时针方向转动。
机械原理基础复习题(含答案)

机械原理基础复习题(含答案)一、单选题(共70题,每题1分,共70分)1、周转轮系传动比的计算通常采用()。
:A、反转法B、阻抗力法C、摩擦力法D、正转法正确答案:A2、()的自由度等于2,两个中心轮都运动,给定2个原动件机构的运动才是确定的。
:A、差动轮系B、定轴轮系C、行星轮系D、周转轮系正确答案:A3、一对标准齿轮,其安装距离大于标准安装中心距时,压力角()。
:A、不一定B、变大C、变小D、不变正确答案:B4、平面机构自由度的计算公式为F=3n-2PL-PH,其中n为活动构件个数,PL为低副个数,PH为()个数。
:A、活动构件B、低副C、高副D、机架正确答案:C5、对于满足杆长条件的四杆机构,若最短杆为机架,为()。
:A、曲柄滑块机构B、曲柄摇杆机构C、双摇杆机构D、双曲柄机构正确答案:D6、2K-H型周转轮系是具有()个太阳轮()个行星架的周转轮系。
:A、2、2B、1、1C、1、2D、2、1正确答案:D7、齿轮轮廓是()齿廓,此齿廓的提出已有近两百多年的历史,目前还没有其它曲线可以替代。
主要在于它具有很好的传动性能,而且便于制造、安装、测量和互换使用等优点。
:A、抛物线B、渐开线C、直线D、五次曲线正确答案:B8、()是指由于摩擦的原因,机构有效驱动力总是小于等于其摩擦力,使得机构无法运动的现象。
这种机构的自由度大于零。
:A、自由度F小于等于零B、死点C、自锁正确答案:C9、()机构用来传递任意两轴间的运动和动力,是机械中应用最广泛的一种传动机构。
:A、齿轮B、连杆C、间歇运动D、凸轮正确答案:A10、()接触面积大,表面接触应力小,润滑方便,不易磨损,制造较为容易,但能实现的相对运动少,适用于载荷较大、运动不是很复杂的场合。
:A、空间副B、高副C、平面副D、低副正确答案:D11、一对标准齿轮,模数为4,齿数分别为20,80,则其顶隙为()mm。
:A、2B、3C、4D、1正确答案:D12、对于满足杆长条件的四杆机构,最短杆的邻边为机架,得到()。
机械原理课后习题答案

《机械原理》课后习题答案第2章(P27)2-2 计算下列机构的自由度,如遇有复合铰链、局部自由度、虚约束等加以说明。
(a)n=3,p l=3 F=3*3-2*3=3(b)n=3,p l=3,p h=2 F=3*3-2*3-2=1 (B处有局部自由度)(c)n=7,p l=10 F=3*7-2*10=1(d)n=4,p l=4,p h=2 F=3*4-2*4-2=2 (A处有复合铰链)(e)n=3,p l=4 F=3*3-2*4=1 (A或D处有虚约束)(f)n=3,p l=4 F=3*3-2*4=1 (构件4和转动副E、F引入虚约束)(g)n=3,p l=5 F=(3-1)*3-(2-1)*5=1 (有公共约束)(h)n=9,p l=12,p h=2 F=3*9-2*12-2=1 (M处有复合铰链,C处有局部自由度)2-3 计算下列机构的自由度,拆杆组并确定机构的级别。
(a)n=5,p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组,故此机构为Ⅱ级机构。
(b)n=5,p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
(c)n=5,p l=7 F=3*5-2*7=1拆分时只须将主动件拆下,其它构件组成一个Ⅲ级杆组,故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定,并提出具有确定运动的修改方案。
(a)n=3,p l=4,p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示:(b)n=4,p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示:或第3章(P42)3-2 下列机构中,已知机构尺寸,求在图示位置时的所有瞬心。
(a)(b)(c)(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中,三个圆互作纯滚,试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章(P80)5-2 一铰接四杆机构(2)机构的两极限位置如下图:(3)传动角最大和最小位置如下图:5-3题略解:若使其成为曲柄摇杆机构,则最短杆必为连架杆,即a 为最短杆。
《机械原理》第二版(刘会英 杨志强 张明勤 著)课后习题答案 机械工业出版社

D1D圆弧的中间. 5)曲柄应增长到 400mm. 2-6 答案:1)机构处在图示位置时,其机构的传动角γ如图所示.
γ=∠CBE
COSγ=BE/BC
即 COSγ=(γSinα+e)/L
……①
从上式可知,r↑,e↑均可使传动角γ↓;L↑使γ↑。
2)从上式可知,最小传动角出现在AB杆垂直于导路时.(即α=900时)
综上分析:AB 杆的取值为: 15<lAB<45 或者者 55<lAB<115
2-3 答案:由于lAB+lAD≤lBC+lCD,且以最短杆AB的邻边为机架。故该铰链四杆机构 为曲柄摇杆机构。AB为曲柄。
1)以曲柄AB为主动件,作业摇杆CD的极限位置如图所示。
∴AC1=lAB+lBC=80 AC2=lBC-lAB=24 极位夹角θ: θ=COS-1∠C2AD-COS-1∠C1AD =COS-1[(AC 2 2+AD2-C 2 D2)/2AC 2 *AD]-COS-1[(AC 1 2+AD2-C 1 D2)/
为机架,则只能最短杆即为 AD=30,则最长杆可能为 BC 杆,也可能是 AB 杆。
1)1) 若AB杆为最长杆:lAD+lAB≤lBC+lCD∴lAB≤55 即50<lAB≤55 2)2) 若BC杆为最长杆:lAD+lBC≤lAB+lCD∴lAB≥45 即45≤lAB<50 ∴若该机构为双曲柄机构,则AB杆杆长的取值范围为:45≤lAB≤55 3)3) 欲使该机构为双摇杆机构,则最短杆与最长杆之和应大于另外二杆之和。现在
以EF为原动件时:
由2个Ⅱ级基本杆组组成,机构级别为2级。 C)F=3×7-2×10=1 其中C点为复合铰链,分别由 2、3、4构件在C点构成 复合铰。以AB为原动件时:
机械原理习题及课后答案(图文并茂)

2
1 5
解答:原机构自由度 F=33- 2 4-1 = 0,不合理 , 改为以下几种结构均可:
2-3 图 2-39 所示为一小型压力机,其中,1 为滚子;2 为摆杆;3 为滑块;4 为滑杆;5 为齿轮及凸轮;6 为连杆;7 为齿轮及偏心轮;8 为机架;9 为压头。试绘制 其机构运动简图,并计算其自由度。
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料1荷试试下卷卷高问总中题体资2配2料,置试而时卷且,调可需控保要试障在验各最;类大对管限设路度备习内进题来行到确调位保整。机使在组其管高在路中正敷资常设料工过试况程卷下中安与,全过要,度加并工强且作看尽下护可都关能可于地以管缩正路小常高故工中障作资高;料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高,核中或对资者定料对值试某,卷些审弯异核扁常与度高校固中对定资图盒料纸位试,置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高,技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术,、以术来管及避架系免等统不多启必项动要方方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
机械原理习题集答案

机械原理习题集答案第一章:机械运动学1. 问题:简述平面运动的基本概念。
答案:平面运动是指物体在平面内的运动,其轨迹可以是直线或曲线。
在平面运动中,物体的每一个点都在同一平面内移动。
2. 问题:什么是四杆机构的运动规律?答案:四杆机构是最基本的机械机构之一,其运动规律取决于杆的长度和连接方式。
常见的四杆机构有双曲柄机构、曲柄滑块机构等。
第二章:机械动力学1. 问题:牛顿运动定律在机械设计中的应用是什么?答案:牛顿运动定律是描述物体运动的基本定律,包括惯性定律、力的作用与反作用定律和作用力与加速度的关系。
在机械设计中,这些定律用于预测和计算机械系统的运动状态和受力情况。
2. 问题:简述达朗贝尔原理。
答案:达朗贝尔原理是动力学中的一个基本原理,它指出在没有外力作用的系统中,系统内各部分的动量守恒。
在机械设计中,这一原理常用于分析和计算机械系统的动态平衡。
第三章:机构设计与分析1. 问题:什么是机构的自由度?答案:机构的自由度是指在没有约束的情况下,机构能够独立进行的运动的数量。
自由度的计算公式为:\( F = 3n - 2j - h \),其中\( n \)是机构中杆件的数量,\( j \)是铰链的数量,\( h \)是高副的数量。
2. 问题:如何确定一个机构的运动类型?答案:确定机构的运动类型需要分析机构的几何形状和连接方式。
例如,如果机构中存在曲柄和滑块,它可能是一个曲柄滑块机构,其运动类型为往复直线运动。
第四章:机械结构设计1. 问题:机械结构设计中需要考虑哪些因素?答案:在机械结构设计中,需要考虑的因素包括材料的选择、强度和刚度的计算、尺寸的确定、成本控制、维护的便利性等。
2. 问题:什么是疲劳强度?答案:疲劳强度是指材料在反复加载和卸载过程中抵抗断裂的能力。
在机械结构设计中,需要考虑疲劳强度以确保结构的可靠性和耐久性。
第五章:机械传动1. 问题:什么是齿轮传动?答案:齿轮传动是一种利用齿轮啮合来传递运动和动力的机械传动方式。
机械原理考试题及答案

机械原理考试题及答案一、单项选择题(每题2分,共20分)1. 机械原理中,机构的自由度是指()。
A. 机构中独立运动的数目B. 机构中运动副的数目C. 机构中构件的数目D. 机构中高副的数目答案:A2. 凸轮机构中,从动件的位移规律有()。
A. 直线运动规律B. 匀速运动规律C. 匀加速运动规律D. 以上都是答案:D3. 四杆机构中,若最短杆长度为Lmin,最长杆长度为Lmax,则Lmin与Lmax之比应满足()。
A. Lmin/Lmax < 0.5B. Lmin/Lmax ≥ 0.5C. Lmin/Lmax > 0.5D. Lmin/Lmax = 0.5答案:B4. 齿轮传动中,齿数比是指()。
A. 两个齿轮的齿数之和B. 两个齿轮的齿数之差C. 两个齿轮的齿数之比D. 两个齿轮的直径之比答案:C5. 机械系统中,惯性力的平衡是指()。
A. 惯性力与外力平衡B. 惯性力与重力平衡C. 惯性力与摩擦力平衡D. 惯性力与惯性力平衡答案:D6. 机构中,若存在高副,则机构的自由度会()。
A. 增加B. 减少C. 不变D. 无法确定答案:B7. 机械系统中,若要实现运动的合成,需要满足的条件是()。
B. 运动方向相反C. 运动方向垂直D. 运动方向任意答案:D8. 齿轮传动中,若要实现减速,应选择()。
A. 小齿轮带动大齿轮B. 大齿轮带动小齿轮C. 两个齿轮直径相同D. 两个齿轮齿数相同答案:A9. 机械系统中,若要实现运动的分解,需要满足的条件是()。
A. 运动方向相同B. 运动方向相反D. 运动方向任意答案:D10. 四杆机构中,若最短杆长度为Lmin,最长杆长度为Lmax,则Lmin与Lmax之比应满足()。
A. Lmin/Lmax < 0.5B. Lmin/Lmax ≥ 0.5C. Lmin/Lmax > 0.5D. Lmin/Lmax = 0.5答案:B二、填空题(每题2分,共20分)1. 机械原理中,机构的自由度是指机构中独立运动的数目,其计算公式为:自由度 = 3n - 2pl - ph,其中n为构件数目,pl为低副数目,ph为高副数目。
机械原理试题及答案试卷答案

机械原理试题及答案试卷答案一、选择题(每题2分,共20分)1. 下列哪个选项不属于机械的基本组成要素?A. 零件B. 部件C. 机构D. 系统答案:D2. 下列哪种机构属于高副机构?A. 齿轮机构B. 曲柄滑块机构C. 螺旋机构D. 摇杆机构答案:A3. 下列哪个选项不是机械设计的基本要求?A. 实用性B. 安全性C. 经济性D. 艺术性答案:D4. 下列哪种材料不适合用作机械零件?A. 钢B. 铝C. 塑料D. 橡胶答案:D5. 下列哪个选项不是机械传动的基本形式?A. 齿轮传动B. 摩擦传动C. 液压传动D. 磁悬浮传动答案:D二、填空题(每题2分,共20分)6. 机械原理是研究机械的______、______和______等方面的基本理论和方法的科学。
答案:结构、运动、力学7. 机械零件的疲劳破坏是由于______引起的。
答案:交变应力8. 机械零件的强度计算方法主要有______、______和______。
答案:安全系数法、许用应力法、极限载荷法9. 齿轮传动的失效形式主要有______、______和______。
答案:点蚀、齿面磨损、轮齿折断10. 机械系统的平衡条件是______、______和______。
答案:力平衡、力矩平衡、功率平衡三、判断题(每题2分,共20分)11. 零件和部件是机械的基本组成要素。
()答案:√12. 机械设计的基本要求不包括可靠性。
()答案:×13. 机械传动中的摩擦力总是有害的。
()答案:×14. 机械零件的疲劳破坏只与材料性能有关,与应力状态无关。
()答案:×15. 机械系统的平衡条件只包括力平衡和力矩平衡。
()答案:×四、简答题(每题10分,共30分)16. 简述机械原理的主要研究内容。
答案:机械原理的主要研究内容包括:机械的基本组成要素、机械的运动、机械的力学性能、机械零件的强度计算、机械传动、机械系统设计等。
最新机械原理习题及答案教学文案

第二章 平面机构的结构分析2-1 绘制图示机构的运动简图。
B解:大腿 小腿213456(b)ACB FEDB解:ABC DE FGH解:2-3 计算图示机构的自由度,并指出复合铰链、局部自由度和虚约束。
ABCDE(a)ABDCE(b)ABCDE(c)(e)(f)H(g)解:(a) C 处为复合铰链。
7,n =p h =0,p l =10。
自由度 323721001W l h F n p p =--=⨯-⨯-=。
(b) B 处为局部自由度,应消除。
3n =, p h =2,p l =2自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。
(c) B 、D 处为局部自由度,应消除。
3n =, p h =2,p l =2。
自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。
(d) CH 或DG 、J 处为虚约束,B 处为局部自由度,应消除。
6n =,p h =1,p l =8。
自由度 32362811W l h F n p p =--=⨯-⨯-=。
(e) 由于采用对称结构,其中一边的双联齿轮构成虚约束,在连接的轴颈处,外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。
其中的一边为复合铰链。
其中4n =,p h =2,p l =4。
自由度 32342422W l h F n p p =--=⨯-⨯-=。
(f) 其中,8n =,p h =0,p l =11。
自由度 323821102W l h F n p p =--=⨯-⨯-=。
(g) ① 当未刹车时,6n =,p h =0,p l =8,刹车机构自由度为 32362802W l h F n p p =--=⨯-⨯-=② 当闸瓦之一刹紧车轮时,5n =,p h =0,p l =7,刹车机构自由度为 32352701W l h F n p p =--=⨯-⨯-=③ 当两个闸瓦同时刹紧车轮时,4n =,p h =0,p l =6,刹车机构自由度为32342602W l h F n p p =--=⨯-⨯-=2-3 判断图示机构是否有确定的运动,若否,提出修改方案。
机械原理课后习题解答(最新)
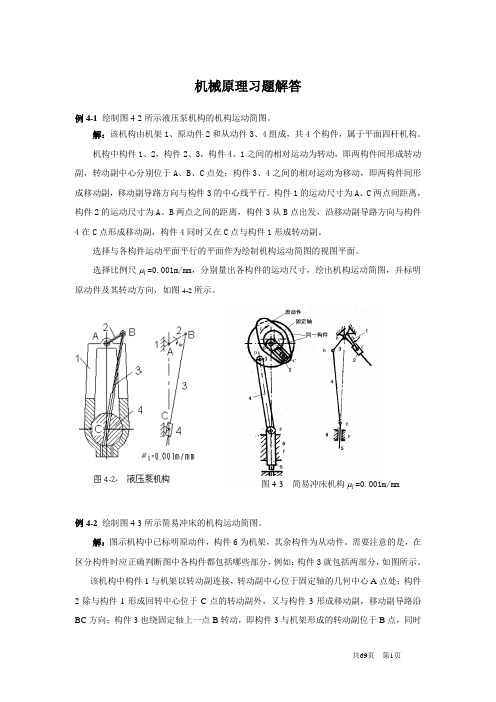
式中 和 可直接从所作的图中量取。由上式可解出
由绝对速度 方向,得出ω2方向为顺时针方向。
同理,在速度瞬心点P13有
由绝对速度 的方向,可知其为逆时针方向。
例5-2在图5-4所示的凸轮机构,已知该机构的结构尺寸和凸轮1的角速度 。利用瞬心法,求机构在图示位置时从动件2的线速度 。机构运动简图的比例尺为 。
按照以上分析,自由度分别为1、2和3的Ⅲ级机构最简单的结构分别如图中(a)、(b)和(c)所示。
4-12确定图4-19a所示机构当构件8为原动件时机构的级别。
解:确定机构的级别关键是要拆出机构中所含的基本杆组。当构件8为原动件时,拆基本杆组首先应当从最远离原动件的构件1拆起,可以拆出Ⅱ级基本杆组ABC,然后,又依次可以拆出Ⅱ级基本杆组DEF和GHI。如下图示。所以该机构为Ⅱ级机构。
(e)、 ,机构没有确定的运动。没有局部自由度、复合铰链、虚约束。
4-7计算题4-7图所示齿轮-连杆机构的自由度。
解:(a)、 ,铰链点A为复合铰链,齿轮副为高副。
(b)、 ,铰链点B、C、D均为复合铰链。
4-8题4-8图所示为缝纫机中的送料机构。计算该机构的自由度,该机构在什么条件下具有确定的运动?
则机构自由度为:
4-6在题4-6图所示所有机构中,原动件数目均为1时,判断图示机构是否有确定的运动。如有局部自由度、复合铰链和虚约束请予以指出。
解:(a)、 ,机构有确定的运动。其中:F、D、B、C四处均为复合铰链,没有局部自由度、虚约束;
(b)、 ,机构没有确定的运动。其中:A处为复合铰链,K处为局部自由度,没有虚约束;
去掉机构中的虚约束,则机构中活动构件数为 ,机构中低副数 ,得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章机构的结构分析2-1.计算下列各机构的自由度。
注意分析其中的虚约束、局部自由度合复合铰链等。
题图1-4c所示机构,导路AD⊥AC、BC=CD/2=AB。
该机构可有多种实际用途,可用于椭圆仪,准确的直线轨迹产生器,或作为压缩机或机动马达等。
题图1-4d为一大功率液压动力机。
其中AB=A`B`,BC=B`C`,CD=C`D`,CE=C`E`,且E、E`处于滑块移动轴线的对称位置。
答c)为轨迹重合虚约束,可认为AB杆或滑块之一构成虚约束。
F=3×3-2×4=1;d)对称的上部分或下部分构成虚约束。
F=3×5-2×7=1.2-2.试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
e)答案:a)F=3×7-2×10=1.注意其中的C、G、D、H点并不是复合铰链。
b)F=3×5-2×7=1C)F=3×7-2×10=1其中C点为复合铰链,分别由2、3、4构件在C点构成复合铰。
d)F=3×3-2×3-2=1或者F=3×5-2×5-2-2=1其中B、D处的磙子具有局部自由度。
2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链,请指出。
第三章平面连杆机构及其分析与设计3-1.试求题图所示各机构在图示位置时全部瞬心的位置.答案:瞬心P 12在A 点 瞬心P 23、 P 24均在B 点 瞬心P 34在C 点 P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点 穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中,试用瞬心法求齿轮1与齿轮3的传动比31/ωω。
答案:此题关键是找到相对瞬心P13. 3-6在图示凸轮机构中,已知mm r50=,mm l OA 22=,mm l AC 80=,οϕ901=,凸轮,凸轮以角速度s rad /101=ω逆时针方向转动。
试用瞬心法求从动件2的角速度2ω。
答案:找到1,2构件的相对瞬心P12 即有:ω1×AP12=ω2×CP12……①现在的关键是求出AP12的值。
设AP12为 x , 则OP12=(222+x 2)1/2BP12=50+(222+x2)1/2,CP12=80+x△P12AO∽△P12BC 则有:x/[50+(222+x2)1/2]=(222+x2)1/2/(80+x)求解出x=37.4 由①式可得:ω2=ω1×AP12/CP12=4.675rad/m第六章6-2.题图6-2所示的盘形转子中,有4个不平衡质量,它们的大小及其质心到回转轴的距离分别为:m1=10kg,r1=100mm,m2=8kg,r2=150mm,m3=7kg,r3=200mm,m4=5kg,r4=100mm.试对该转子进行平衡设计.答案:各质径积的大小分别为:m1r1=1000kg·mm m2r2=1200kg·mmm3r3=1400kg·mm m4r4=500kg·mm现取1:20作出质径积的向量多边形,以平衡质径积m e r e构成封闭的向量多边形.从上面的向量多边形中可知:平衡质径积大小m e r e=40×20=800kg/mm,方向与x向成60o角.欲平衡有2种方法:在m e r e方向配质量,若在r e=100mm,则m e=8kg;可在m e r e反方向挖去一块,使其径积为800kg/mm.6-3.题图6-3所示为一均匀圆盘转子,工艺要求在圆盘上钻4个圆孔,圆孔直径及孔心到转轴O的距离分别为:d1=40mm,r1=120mm,d2=60mm,r2=100mm,d3=50mm,r3=110mm,d4=70mm,r4=90mm,方位如图.试对该转子进行平衡设计.设单位面积的质量为1,其4个孔的质径比分别为:m1r1=π(d1/2) 2120=48000π;m2r2=π(d2/2)2100=90000πm3r3=π(d3/2)2110=68750π;m4r4=π(d4/2)290=108450π现取1:2000π作向量多边形:从向量图中可知:m e r e=43×2000π=86000π若在半径r e=100mm且与x轴正向成θ=46o的位置上.挖圆孔的直径d5=(3440)1/2mm即可平衡.6-4 在图示的转子中,已知各偏心质量m 1=10kg ,m 2=15kg ,m 3=20kg ,m 4=10kg ;它们的回转半径分别为r 1=300mm ,r 2=r 4=150mm ,r 3=100mm ,又知各偏心质量所在的回转平面间的距离为l 1=l 2=l 3=200mm ,各偏心质量间的方位角为α1120=,α260=,α390=,α430=。
若置于平衡基面I 及II 中的平衡质量m I 和m II 的回转半径均为400mm ,试求m I 及m II 的大小和方位。
6-5.题图6-5所示曲柄摇杆机构中,已知各构件:l 1=75mm ,l 2=300mm ,l 3=150mm ;各杆的质量为m 1=0.3kg ,m 2=0.6kg ,m 3=0.9kg ,其质心位置l AS1=25mm ,l BS2=100mm ,l BS3=100mm . 1) 试用质量静替代法将各杆质量替代到A ,B ,C ,D 四点;2) 若在曲柄,摇杆上加平衡质量m e1及m e3使机构惯性力平衡,当取平衡质量的回转半径为r e1=r e3=75mm 时,m e1,m e3各为多少?答案:1)m 1用A,B两点替代 m 2用B ,C 两点替代 AS1=50×0.3/75=0.2kgm BS1=25×0.3/75=0.1kg m 3用C ,D 两点替代 CS3=100×0.9/150=0.6kg m DS3=50×0.9/150=0.3kg ∴m A =m AS1=0.2kgm B = m BS1+m BS2=0.5kg m C = m CS2+m CS3=0.8kg m D =m DS2=0.3kg2)m e1×r e1=m B ×l AB e1=0.5×75/75=0.5kg m e3×r e3=m C ×l CD e3=0.8×150/75=16kg6-6.在题图6-6所示曲柄滑块机构中,已知各杆长度:l AB =100mm ,l BC =300mm ;曲柄和连杆的质心S 1,S 2的位置分别为l AS1=100mm=l AS2,滑块3的质量m 3=0.4kg ,试求曲柄滑块机构惯性完全平衡时的曲柄质量m 1和连杆质量m 2的大小.答案:m2×l BC=m3×l BS2 m2=m3×l BS2/l BC=0.133kgm B=m2+m3=0.533kgm1×l AB=m B×l AS11=0.533kg第八章8-1.已知图所示铰链四杆机构ABCD中,l BC=50mm,l CD=35mm,l AD=30mm,取AD为机架.1)如果该机构能成为曲柄摇杆机构,且AB是曲柄,求l AB的取值范围;2)如果该机构能成为双曲柄杆构,求l AB的取值范围;3)如果该机构能成为双摇杆机构,求l AB的取值范围.答案:1)该机为曲柄摇杆机构,且AB为曲柄,则AB应为最短杆。
其中已知BC杆为最长杆50。
∴l AB+l BC≤l AD+l CD∴l AB≤152)该机构欲成为双曲柄机构,同样应满足曲柄存在的条件,且应以最短杆为机架。
现AD为机架,则只能最短杆即为AD=30,则最长杆可能为BC杆,也可能是AB杆。
1)若AB杆为最长杆:l AD+l AB≤l BC+l CD∴l AB≤55 即50<l AB<552)若BC杆为最长杆:l AB+l BC≤l AB+l CD∴l AB≤45 即45≤l AB<50∴若该机构为双曲柄机构,则AB杆杆长的取值范围为:45≤l AB≤503)欲使该机构为双摇杆机构,则最短杆与最长杆之和应大于另外二杆之和。
现在的关键是谁是最短、最长杆?1) 若AB杆最短,则最长杆为BC:∴l AB+l BC>l CD+l AD∴l AB>152)若AD杆最短,BC杆最长:l AD+l AB>l BC+l CD∴l AB<45AB杆最长:l AD+l AB>l BC+l CD l AB>55l AB<l AD+l CD+l BC l AB<115综上分析:AB杆的取值为:15<l AB<45 或者55<l AB<1158-3.已知两连架杆的三组对应位置如题图所示为:φ1=60o,ψ1=30o,φ2=90o,ψ2=50o,φ3=120o,ψ3=80o,若取机架AD长度l AD=100mm,l CD=100mm,试用图解法计算此铰链四杆机构各杆长度。
假定连架杆CD 与机架夹角ψ1,ψ2,ψ3正好定CD的连线与机架所成形的角。
现假象把连架杆AB固定在第一位置,转动机架AD ,使AD 分别与AD 的固定位置分别成φ1,φ2,φ3,从而可找到另一连架杆C 2D ,C 3D 位置。
即转化为已知连杆的三位置而设计铰链四杆机构,A 是不用设计,其值只有C 1,C 2,C 3的转动中心B 1(作C 1C 2,C 2C 2的垂线)连接CB 1C 1D ,即得铰链四杆机构。
8-4.如图2-31所示的铰链四杆机构。
设已知其摇杆CD 的长度为 75mm ,行程时间比系数K =1.5,机架AD 的长度为80mm,又已知摇杆的一个极限位置与机架的夹角φ=45o ,试求其曲柄的长度l AB 和连杆的长度l BC 。
答案:选尺寸比例画出机架AD ,即极限位置的CD 极位夹角θ=(k-1)/(k+1)×180°=36°此题有2组解,因为CD 位置既可认为最近极限位置。
又可按最远极限位置来设计。
1CD 为最近极限位置,则最远极限位置在C 2D 则有 l AB +l BC 2×μl BC -l AB =AC 2×μ即可求l AB ,l BC 亦可用作用在AC 2上截去AC ,剩余段的一半即为l AB ,AF 即代表l BC 。
2CD 为最远极限位置,则最近极限位置在C 1D 。
则有 l AB +l BC 2×μ l BC —l AB =AC 2×μ即可求l AB ,l BC (亦可用作图法,同上)。
8-5设计一曲柄摇杆机构,已知其摇杆CD 的长度mm l CD 290=,摇杆两极限位置间的夹角οψ32=,行程速比系数25.1=K ,若曲柄的长度mm l AB 75=,试用图解法求连杆的长度BC l 和机架的长度AD l 。
