R语言 House Price 预测房价数据挖掘分析报告附代码数据

合集下载

房地产数据R语言分析

-Exclude the Order, PID, and of course SalesPrice variables from your predictors.在变量中要去除Order, PID, 当然SalesPrice也要去掉。

AmesHousing=AmesHousing[,-c(1,2 )]一个class是大于USD 200，000，另一类小于USD 20,000>=200000 :1<200000 :0AmesHousing$SalePrice <-ifelse(AmesHousing$SalePrice>200000,1,0)看看线性关系如何，如果不够好那么就要做变换（transformation）head(AmesHousing2)MS.SubClass Lot.Frontage Lot.Area Overall.Qual Overall.Cond Year.Bui lt1 20 141 31770 6 5 19 602 20 80 11622 5 6 19 613 20 81 14267 6 6 19 584 20 93 11160 75 19 685 60 74 13830 5 5 19 976 60 78 9978 6 6 19 98Year.Remod.Add Mas.Vnr.Area BsmtFin.SF.1 BsmtFin.SF.2 Bsmt.Unf.SF1 1960 112 639 0 4412 1961 0 468 144 2703 1958 108 923 0 4064 1968 0 1065 0 10455 1998 0 791 0 1376 1998 20 602 0 324Total.Bsmt.SF X1st.Flr.SF X2nd.Flr.SF Low.Qual.Fin.SF Gr.Liv.Area1 1080 1656 0 0 16562 882 896 0 0 8963 1329 1329 0 0 13294 2110 2110 0 0 21105 928 928 701 0 16296 926 926 678 0 1604Bsmt.Full.Bath Bsmt.Half.Bath Full.Bath Half.Bath Bedroom.AbvGr1 1 0 1 0 32 0 0 1 0 23 0 0 1 1 34 1 0 2 1 35 0 0 2 1 36 0 0 2 1 3Kitchen.AbvGr TotRms.AbvGrd Fireplaces Garage.Yr.Blt Garage.Cars1 1 72 1960 22 1 5 0 1961 13 1 6 0 1958 14 1 8 2 1968 25 16 1 1997 26 17 1 1998 2Garage.Area Wood.Deck.SF Open.Porch.SF Enclosed.Porch X3Ssn.Porch1 528 210 62 0 02 730 140 0 0 03 312 393 36 0 04 522 0 0 0 05 482 212 34 0 06 470 360 36 0 0Screen.Porch Pool.Area Misc.Val Mo.Sold Yr.Sold SalePrice1 0 0 0 5 2010 12 120 0 0 6 2010 03 0 0 12500 6 2010 04 0 0 0 4 2010 15 0 0 0 3 2010 06 0 0 0 6 2010 0有一些变量可能需要整合合并关键词"Flr"，"Porch"，"Bath"，"Overall"，"Sold"，SF"，"Year"，"AbvGr"，"Garag e"，"Area"MS.SubClass Lot.Frontage Fireplaces Misc.Val SalePrice Flr Porch Ba th1 20 1412 0 1 1656 62 22 20 80 0 0 0 896 120 13 20 81 0 12500 0 1329 36 24 20 93 2 0 1 2110 0 45 60 74 1 0 0 1629 34 36 60 78 1 0 0 1604 36 3Overall Sold SF Year AbvGr Garage Area1 11 2015 2370 3920 11 2490 335382 11 2016 1904 3922 8 2692 125183 12 2016 3051 3916 10 2271 157044 12 2014 4220 3936 12 2492 132705 10 2013 2068 3995 10 2481 154596 12 2016 2212 3996 11 2470 11602plot(AmesHousing2)4.跑logistic regression, GAM, LDA, KNN这几个模型logistic regressionprint(paste('Accuracy',1-misClasificError))[1] "Accuracy 0.932166301969365"library("mgcv")gam建模misClasificError <-mean(fitted.results !=Ames.test$SalePrice,na.rm=T) print(paste('Accuracy',1-misClasificError))[1] "Accuracy 0.911062906724512"Knnlibrary(kknn)print(paste('Accuracy',1-misClasificError))[1] "Accuracy 0.585284280936455"LDAmisClasificError <-mean(fitted.results !=Ames.test$SalePrice,na.rm=T) print(paste('Accuracy',1-misClasificError))[1] "Accuracy 0.923413566739606"。

【原创】R语言数据挖掘统计预测模型课件教案讲义(附代码数据)

IS 6489: Statistics and Predictive Analytics
Class 8
Jeﬀ Webb
Jeﬀ Webb
IS 6489: Statistics and Predictive Analytics
1 / report expectations Homework discussion Class 8 topics:
Jeﬀ Webb
IS 6489: Statistics and Predictive Analytics
7 / 51
Logistic regression: the model
The logistic regression model can be written in terms of log odds: log Pr(yi = 1|xi ) Pr(yi = 0|xi ) = Xi β
2 / 51
Final Report Expectations
Jeﬀ Webb
IS 6489: Statistics and Predictive Analytics
3 / 51
Final report
PDF of the project assignment is available at Canvas Length: 5 pages of text plus additional pages, if necessary, for relevant plots and tables. Expectation: a client-ready report using best practices of technical writing and statistical communication, using graphs when possible, labeling and explaining them, and interpreting statistical results using language and quantities that non-statisticians can understand. Elements:

R语言房价回归预测案例报告附代码数据

【原创】R语言报告论文（附代码数据）
有问题到淘宝找“大数据部落”就可以了
R语言房价回归预测案例报告首先，我们加载数据和必要的软件包：
1
1.
上面绘制的房屋年龄分布是非常正确的。

2.我们看到三个峰值，表明分布是多模态的。

这个数据集中的大部分房子（约140个）都是
10-15岁。

第二类房屋（约80人）年龄在55-60岁之间，分布右边的第三类房屋（约37户）的年龄在90-95岁之间。

这可能表示指定期间房地产业务的繁荣。

3.分配表明，超过45％的房屋建于不到45年前。

2
【原创】R语言报告论文（附代码数据）
有问题到淘宝找“大数据部落”就可以了
##计算由邻居分组并存储在数据框中的所有中央和传播统计数据。

ames_stats<-ames_train%>%group_by(Neighborhood)%>%summarise(Min=min(price, na.rm=TRUE), Mean=me。

用R语言进行数据挖掘与分析

用R语言进行数据挖掘与分析
一、前言
数据挖掘和分析是当今社会中非常重要的研究方向，因为大量的数据产生和存储已经成为我们的日常，而如何从这些数据中获取有益信息和规律是非常重要的。

而R语言作为数据科学领域中最重要的编程语言之一，受到了广泛的认可，并在越来越多的领域中应用起来。

本文就用R语言来进行数据挖掘和分析。

二、数据的获取
数据的获取是进行数据分析和挖掘的第一步。

这里我们选择了一个房价数据集来进行分析。

数据集包括了所统计城市的房屋信息、售价、建筑面积、交通情况、商业情况、房间数量和面积等信息。

我们可以使用R语言中的read.csv函数读取该csv格式的数据集，并将其存储在一个变量中。

```
house_data <- read.csv(\。

r语言去除极值并统计

r语言去除极值并统计R语言是一种用于数据分析和统计的编程语言。

在进行数据分析时，经常需要处理极值（outliers），即远离其他数据点的异常值。

去除极值可以帮助我们更准确地分析数据，避免异常值对结果的影响。

本文将介绍如何使用R语言去除极值，并对去除后的数据进行统计分析。

我们需要导入数据。

假设我们有一组表示某城市房价的数据集，并存储在一个名为"house_price"的数据框中。

我们可以使用read.csv()函数从CSV文件中导入数据，也可以使用其他类似的函数导入其他类型的数据文件。

接下来，我们可以使用summary()函数对数据进行初步的统计分析。

该函数会输出数据的最小值、最大值、均值、中位数等统计量，帮助我们对数据的整体情况有一个初步的了解。

然后，我们需要判断数据中是否存在极值。

常用的一种方法是使用箱线图（boxplot）来可视化数据分布。

箱线图可以显示数据的中位数、上下四分位数以及可能的极值点。

通过观察箱线图，我们可以判断数据中是否存在离群点。

如果数据中存在极值，我们可以使用R语言的一些函数来去除这些异常值。

一种常用的方法是使用Z-score（标准化分数）来判断数据点是否为离群点。

Z-score表示一个数据点与均值的偏差程度，如果Z-score超过一个阈值（通常为3），则被认为是离群点。

我们可以使用scale()函数对数据进行标准化，然后使用abs()函数计算Z-score，最后使用which()函数找出Z-score大于阈值的数据点的索引，即离群点的位置。

可以使用这些索引来删除离群点。

另一种常用的方法是使用四分位距（IQR）来判断数据点是否为离群点。

IQR是上四分位数与下四分位数之差，它可以衡量数据的离散程度。

通常将低于下四分位数减去1.5倍IQR或高于上四分位数加上1.5倍IQR的数据点视为离群点。

我们可以使用quantile()函数计算四分位数，然后根据公式计算离群点的位置，并使用which()函数找出这些位置，最后删除这些离群点。

r语言回归分析案例

r语言回归分析案例R语言回归分析案例。

回归分析是统计学中常用的一种方法，它用于探究变量之间的关系，并对未来的变量进行预测。

R语言作为一种强大的统计分析工具，被广泛应用于回归分析中。

本文将通过一个实际案例，介绍如何使用R语言进行回归分析。

首先，我们需要准备一些数据。

假设我们有一个数据集，包括了房屋的面积、房龄和售价。

我们想要分析房屋的售价与其面积、房龄之间的关系。

接下来，我们将使用R语言进行回归分析。

在R语言中，我们可以使用lm()函数来进行线性回归分析。

首先，我们需要加载我们的数据集，并创建一个线性模型。

代码如下：```R。

# 加载数据集。

data <read.csv("house_data.csv")。

# 创建线性模型。

model <lm(price ~ area + age, data = data)。

```。

在上面的代码中，我们使用lm()函数创建了一个线性模型，其中price是我们要预测的变量，而area和age是我们用来预测的自变量。

接下来，我们可以使用summary()函数来查看我们的线性回归模型的结果。

```R。

# 查看回归分析结果。

summary(model)。

```。

summary()函数将输出我们线性回归模型的各项统计指标，包括回归系数、残差标准差、R平方等。

通过这些指标，我们可以评估我们的回归模型的拟合程度和预测能力。

除了线性回归分析，R语言还支持其他类型的回归分析，如多元回归、逻辑回归等。

对于不同类型的回归分析，我们可以使用不同的函数来创建模型，并使用不同的方法来评估模型的拟合程度。

总之，R语言是一种强大的统计分析工具，它提供了丰富的函数和包，支持各种类型的回归分析。

通过本文介绍的案例，我们可以看到R语言在回归分析中的应用，希望对大家有所帮助。

【原创】R语言数据可视化分析报告(附代码数据)

echo=TRUE
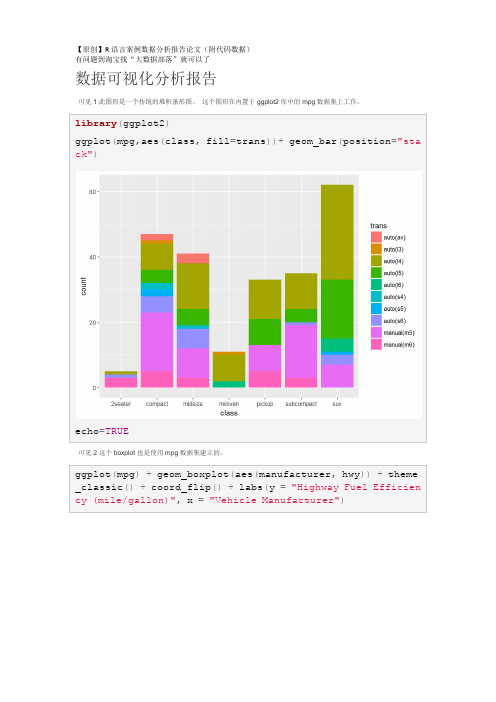
Vis 3这个图形是用另一个数据集菱形建立的，也是内置在ggplot2包中的数据集。
library(ggthemes)
ggplot(diamonds)+geom_density(aes(price,fill=cut,color=cut),alpha=0.4,size=0.5)+labs(title='Diamond Price Density',x='Diamond Price (USD)',y='Density')+theme_economist()
library(ggplot2)
ggplot(mpg,aes(class,fill=trans))+geom_bar(position="stack")
echo=TRUE
可见2这个boxplot也是使用mpg数据集建立的。
ggplot(mpg)+geom_boxplot(aes(manufacturer,hwy))+theme_classic()+coord_flip()+labs(y="Highway Fuel Efficiency (mile/gallon)",x="Vehicle Manufacturer")
echo=TRUE
另外，我正在使用ggplot2软件包来将线性模型拟合到框架内的所有数据上。
ggplot(iris,aes(Sepal.Length,Petal.Length))+geom_point()+geom_smooth(method=lm)+theme_minimal()+theme(panel.grid.major=element_line(size=1),panel.grid.minor=element_line(size=0.7))+labs(title='relationship between Petal and Sepal Length',x='Iris Sepal Length',y='Iris Petal Length')

【原创】r语言房价回归分析代码

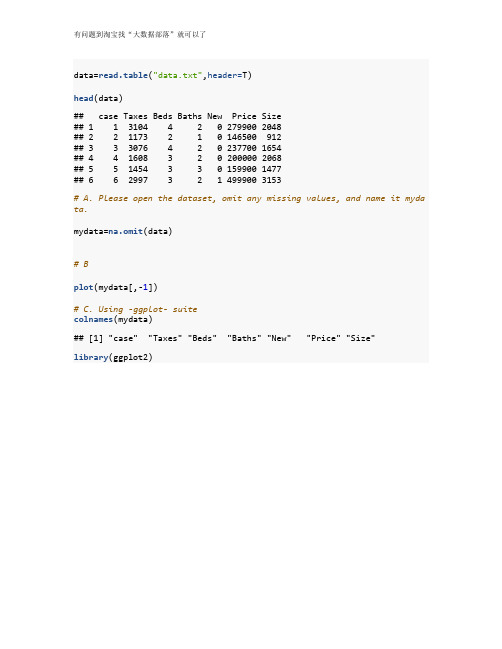
data=read.table("data.txt",header=T)head(data)## case Taxes Beds Baths New Price Size## 1 1 3104 4 2 0 279900 2048## 2 2 1173 2 1 0 146500 912## 3 3 3076 4 2 0 237700 1654## 4 4 1608 3 2 0 200000 2068## 5 5 1454 3 3 0 159900 1477## 6 6 2997 3 2 1 499900 3153# A. Please open the dataset, omit any missing values, and name it myda ta.mydata=na.omit(data)# Bplot(mydata[,-1])# C. Using -ggplot- suitecolnames(mydata)## [1] "case""Taxes""Beds""Baths""New""Price""Size"library(ggplot2)ggplot(mydata, aes(x = Size, y = Price)) + geom_point(aes( )) +geom_smooth()ggplot(mydata, aes(x = Taxes, y = Price)) +geom_point(aes( )) +geom_smooth()# D. Do your visualizations show a positive, negative,# or no relationship?# E. Is there evidence that you may need to transform any of your varia bles? Why? Motivate# your answer by showing any relevant statistics or graphsggplot(mydata, aes(x =(Size) , y =log(Price))) +geom_point(aes( )) +geom_smooth()ggplot(mydata, aes(x = (Taxes), y =log(Price))) + geom_point(aes( )) +geom_smooth()attach(mydata)cor(Taxes,Price)## [1] 0.8419802cor( (Taxes)^2 , (Price))## [1] 0.856277# F. Transform any variables as necessary. Explain your decisions. If y ou transformed any# of the variables, make additional visualizations of the relationship between the new# variable and the dependent variableggplot(mydata, aes(x = (Taxes^2), y =log(Price))) +geom_point(aes( )) +geom_smooth()# G. Estimate the correlation between any continuous independent variab les and the dependent variable.# What do they mean?cor(data[,-1])## Taxes Beds Baths New Price Size ## Taxes 1.0000000 0.47392873 0.5948543 0.38087410 0.8419802 0.8187958 ## Beds 0.4739287 1.00000000 0.4922224 0.04931556 0.3939570 0.5447831## Baths 0.5948543 0.49222235 1.0000000 0.25148095 0.5582533 0.6582247 ## New 0.3808741 0.04931556 0.2514810 1.00000000 0.4732608 0.3843277 ## Price 0.8419802 0.39395702 0.5582533 0.47326080 1.0000000 0.8337848 ## Size 0.8187958 0.54478311 0.6582247 0.38432773 0.8337848 1.0000000 # H. Fit a multiple regression to the data. Notice that your coefficien ts are really large, as# the dependent variable is measured in dollars. The norm is to rescale such dependent# variables (divide price by 1000), so that the coefficients are smalle r.summary(lm(Price~.,data=data[,-1]))#### Call:## lm(formula = Price ~ ., data = data[, -1])#### Residuals:## Min 1Q Median 3Q Max## -182112 -24377 -2046 21306 161870#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 4525.753 24474.054 0.185 0.8537## Taxes 38.135 6.815 5.596 2.16e-07 ***## Beds -11259.061 9115.003 -1.235 0.2198## Baths -2114.372 11465.113 -0.184 0.8541## New 41711.428 16887.196 2.470 0.0153 *## Size 68.350 13.936 4.904 3.92e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 47240 on 94 degrees of freedom## Multiple R-squared: 0.7934, Adjusted R-squared: 0.7824## F-statistic: 72.19 on 5 and 94 DF, p-value: < 2.2e-16summary(lm(Price/1000~.,data=data[,-1]))#### Call:## lm(formula = Price/1000 ~ ., data = data[, -1])#### Residuals:## Min 1Q Median 3Q Max## -182.112 -24.377 -2.046 21.306 161.870#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 4.525753 24.474054 0.185 0.8537## Taxes 0.038135 0.006815 5.596 2.16e-07 ***## Beds -11.259061 9.115003 -1.235 0.2198## Baths -2.114372 11.465113 -0.184 0.8541## New 41.711428 16.887196 2.470 0.0153 *## Size 0.068350 0.013936 4.904 3.92e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 47.24 on 94 degrees of freedom## Multiple R-squared: 0.7934, Adjusted R-squared: 0.7824## F-statistic: 72.19 on 5 and 94 DF, p-value: < 2.2e-16# I. Interpret the intercept and each of the coefficients.# J. Do the results make sense theoretically? Why or why not? If you fi nd that some of the# result do not make sense theoretically# K. Regress Price on Beds and Newsummary(mk<-lm(Price~Baths +New,data=data[,-1]))#### Call:## lm(formula = Price ~ Baths + New, data = data[, -1])#### Residuals:## Min 1Q Median 3Q Max## -154619 -52868 -9093 29513 287907#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) -21355 28228 -0.757 0.451## Baths 83724 14143 5.920 4.87e-08 ***## New 114425 25506 4.486 1.99e-05 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 77240 on 97 degrees of freedom## Multiple R-squared: 0.4299, Adjusted R-squared: 0.4182## F-statistic: 36.58 on 2 and 97 DF, p-value: 1.454e-12predict(mk,data.frame(Baths=1:5,New=1),interval="confidence",level =0.9 )## fit lwr upr## 1 176794.4 126578.3 227010.5## 2 260518.5 220910.7 300126.4## 3 344242.6 302778.9 385706.3## 4 427966.7 373441.3 482492.2## 5 511690.8 438683.0 584698.6predict(mk,data.frame(Baths=1:5,New=0),interval="confidence",level =0.9 )## fit lwr upr## 1 62369.07 37034.79 87703.35## 2 146093.18 132333.24 159853.11## 3 229817.28 200831.47 258803.10## 4 313541.39 262606.62 364476.16## 5 397265.50 323428.81 471102.19# L. Repeat the steps in the previous answer to make a graph of predict ed values and the# 90% confidence interval around them for each number of bedrooms, assu ming that the# house is an old construction.# M. Put the two graphs side-by-side in your text document. What do the y tell you?preds=predict(mk,data.frame(Baths=1:5,New=1),interval="confidence", level =0.9 )plot( 1:5, preds[ ,1],xlab="Baths",type="l",main="Predicted Prices for New Consruction")# intervalslines(1:5, preds[ ,3], lty ='dashed', col ='red')lines(1:5, preds[ ,2], lty ='dashed', col ='red')preds=predict(mk,data.frame(Baths=1:5,New=0),interval="confidence", level =0.9 )# plotplot( 1:5, preds[ ,1],xlab="Baths",type="l",main="Predicted Prices for Old Consruction")# model# intervalslines(1:5, preds[ ,3], lty ='dashed', col ='red')lines(1:5, preds[ ,2], lty ='dashed', col ='red')# N. Make graphs that look exactly like the ones presented in Figure 1.。

Kaggle竞赛——房价预测（HousePrices）

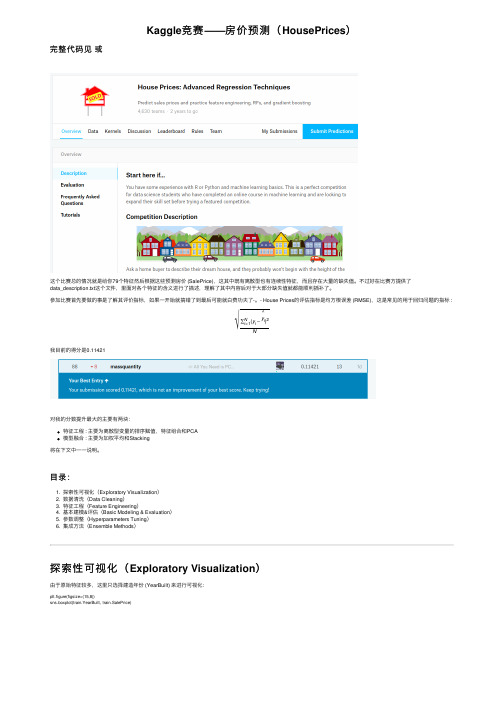
Kaggle 竞赛——房价预测（HousePrices ）完整代码见或这个⽐赛总的情况就是给你79个特征然后根据这些预测房价 (SalePrice)，这其中既有离散型也有连续性特征，⽽且存在⼤量的缺失值。

不过好在⽐赛⽅提供了data_description.txt 这个⽂件，⾥⾯对各个特征的含义进⾏了描述，理解了其中内容后对于⼤部分缺失值就都能顺利插补了。

参加⽐赛⾸先要做的事是了解其评价指标，如果⼀开始就搞错了到最后可能就⽩费功夫了-。

- House Prices 的评估指标是均⽅根误差 (RMSE)，这是常见的⽤于回归问题的指标 :∑N i =1(y i −^y i )2N 我⽬前的得分是0.11421对我的分数提升最⼤的主要有两块：特征⼯程 : 主要为离散型变量的排序赋值，特征组合和PCA模型融合 : 主要为加权平均和Stacking将在下⽂中⼀⼀说明。

⽬录：1. 探索性可视化（Exploratory Visualization ）2. 数据清洗（Data Cleaning ）3. 特征⼯程（Feature Engineering ）4. 基本建模&评估（Basic Modeling & Evaluation ）5. 参数调整（Hyperparameters Tuning ）6. 集成⽅法（Ensemble Methods ）探索性可视化（Exploratory Visualization ）由于原始特征较多，这⾥只选择建造年份 (YearBuilt) 来进⾏可视化：plt.figure(figsize=(15,8))sns.boxplot(train.YearBuilt, train.SalePrice)√⼀般认为新房⼦⽐较贵，⽼房⼦⽐较便宜，从图上看⼤致也是这个趋势，由于建造年份 (YearBuilt) 这个特征存在较多的取值 (从1872年到2010年)，直接one hot encoding会造成过于稀疏的数据，因此在特征⼯程中会将其进⾏数字化编码 (LabelEncoder) 。

r语言时间序列预测实例 -回复

r语言时间序列预测实例-回复R语言时间序列预测实例本文将以R语言为工具，介绍一个时间序列预测的实例。

我们将从数据收集、数据处理、建模和预测等几个步骤来进行讲解。

第一步：数据收集首先，我们需要收集一组时间序列数据。

本实例中，我们将使用一个公开可获得的数据集，即美国某地区的房价指数数据。

我们可以从美国统计局或房产相关网站上找到这些数据。

第二步：数据处理在开始时间序列预测之前，我们需要对数据进行处理和准备。

通常，时间序列数据在收集过程中会有一些缺失值、异常值或离群值。

因此，在进行模型训练之前，我们需要对数据进行清洗和处理。

首先，我们需要将数据导入到R中，并检查数据的完整性和一致性。

可以使用read.csv()或read.table()等函数将数据导入R。

导入数据后，我们需要对数据进行可视化，以了解数据的基本特征。

使用plot()函数可以绘制时间序列的图形，观察序列的趋势、季节性和周期性等。

如果存在缺失值或异常值，我们需要对其进行处理。

可以使用na.omit()、na.approx()或na.interp()等函数来填充缺失值，或者使用outliers()等函数来识别和处理异常值。

第三步：建模在数据处理完成后，我们可以开始进行时间序列预测建模。

进行时间序列预测的一种常用方法是使用自回归移动平均模型（ARIMA模型）。

在R中，可以使用forecast包中的auto.arima()函数来自动选择最佳ARIMA模型。

该函数会根据给定的时间序列数据和其他参数，选择出最优的ARIMA模型。

除此之外，我们还可以尝试其他的时间序列模型，如指数平滑法、季节性分解法、灰色预测法等等。

根据实际情况和数据特点，选择合适的模型进行预测。

第四步：预测构建好ARIMA模型后，我们可以使用模型对未来的数据进行预测。

在R 中，可以使用forecast包中的forecast()函数来进行预测。

使用forecast()函数可以得到模型的预测结果，包括预测值、置信区间和预测误差等。

原创R语言线性回归案例数据分析可视化报告附代码数据

原创R语言线性回归案例数据分析可视化报告附代码数据在数据分析领域，线性回归是一种常用的数据建模和预测方法。

本文将使用R语言进行一个原创的线性回归案例分析，并通过数据可视化的方式呈现分析结果。

下面是我们的文本分析报告，同时包含相关的代码数据（由于篇幅限制，只呈现部分相关代码和数据）。

请您详细阅读以下内容。

1. 数据概述本次案例我们选用了一个关于房屋价格的数据集，数据包含了房屋面积、房间数量、地理位置等多个维度的信息。

我们的目标是分析这些因素与房屋价格之间的关系，并进行可视化展示。

2. 数据预处理在开始回归分析之前，我们需要对数据进行预处理，包括数据清洗和特征选择。

在这个案例中，我们通过删除空值和异常值来清洗数据，并选择了面积和房间数量两个特征作为自变量进行回归分析。

以下是示例代码：```R# 导入数据data <- read.csv("house_data.csv")# 清洗数据data <- na.omit(data)# 删除异常数据data <- data[data$area < 5000 & data$rooms < 10, ]# 特征选择features <- c("area", "rooms")target <- "price"```3. 线性回归模型建立我们使用R语言中的lm()函数建立线性回归模型，并通过summary()函数输出模型摘要信息。

以下是相关代码：```R# 线性回归模型建立model <- lm(data[, target] ~ ., data = data[, features])# 输出模型摘要信息summary(model)```回归模型摘要信息包含了拟合优度、自变量系数、截距等重要信息，用于评估模型的拟合效果和各个因素对因变量的影响程度。

【最新】R语言分段回归数据分析案例报告

【最新】R语言分段回归数据分析案例报告在当今数据驱动的时代，数据分析成为了揭示事物内在规律、做出明智决策的关键手段。

R 语言作为一种强大的统计分析工具，在数据分析领域发挥着重要作用。

其中，分段回归作为一种特殊的回归分析方法，能够处理数据中的非线性关系，为我们提供更深入、更准确的洞察。

接下来，我们将通过一个具体的案例来深入探讨 R 语言中的分段回归分析。

假设我们正在研究某地区的房价与房屋面积之间的关系。

我们收集了一系列的数据，包括房屋的面积以及对应的售价。

初步观察数据，我们发现房价与房屋面积之间的关系并非简单的线性关系，可能存在着分段的特征。

首先，我们使用 R 语言中的相关函数读取数据，并对数据进行初步的处理和探索性分析。

通过绘制散点图，我们可以直观地看到数据的分布情况。

从散点图中，我们发现当房屋面积较小时，房价随着面积的增加而快速上升；然而，当面积超过一定阈值后，房价的增长速度逐渐放缓。

为了进行分段回归分析，我们需要确定分段的节点。

这可以通过观察数据的特征、结合实际的业务知识或者使用一些统计方法来确定。

在这个案例中，我们根据经验和数据的分布，将分段节点设定为 150 平方米。

接下来，我们使用 R 语言中的`lm`函数来构建分段回归模型。

对于面积小于 150 平方米的部分，我们建立一个线性回归模型；对于面积大于等于 150 平方米的部分，建立另一个线性回归模型。

｀｀｀R读取数据data ＜ readcsv(＂house_pricecsv"）提取面积小于 150 平方米的数据subset1 ＜ datadata$area ＜ 150,构建第一段回归模型model1 ＜ lm(price ～ area, data ＝ subset1)提取面积大于等于 150 平方米的数据subset2 ＜ datadata$area ＞＝ 150,构建第二段回归模型model2 ＜ lm(price ～ area, data ＝ subset2)｀｀｀在构建好分段回归模型后，我们需要对模型进行评估和诊断。

【原创】R语言概率与分布数据分析数据挖掘案例报告(附代码

【原创】定制代写开发 r/python/spss/matlab/WEKA/sas/sql/C++/stata/eviews 数据挖掘和统计分析可视化调研报告程序等服务（附代码数据）,咨询：3025393450@ 有问题到淘宝找“大数据部落”就可以了
3.1 随机抽样 sample(1:52, 4) sample(c("H", "T"), 10, replace=T) sample(1:6, 10, replace=T) sample(c(" 成功", " 失败"), 10, replace=T, prob=c(0.9,0.1)) sample(c(1,0), 10, replace=T, prob=c(0.9,0.1)) 1/prod(52:49) 1/choose(52,4) qnorm(0.025) qnorm(0.975) 1 - pchisq(3.84, 1) 2*pt(-2.43, df = 13) ###二项分布: op <- par(mfrow=c(2,2)) limite.central(rbinom, distpar=c(10 ,0.1), m=1, s=0.9) par(op) ###泊松分布： op <- par(mfrow=c(2,2)) limite.central(rpois, distpar=1, m=1, s=1, n=c(3, 10, 30 ,50)) par(op) ###均匀分布: op <- par(mfrow=c(2,2)) limite.central( ) par(op) ###指数分布: op <- par(mfrow=c(2,2)) limite.central(rexp, distpar=1, m=1, s=1) par(op) ###正态混合分布: op <- par(mfrow=c(2,2)) mixn <- function (n, a=-1, b=1) {rnorm(n, sample(c(a,b),n,replace=T))} limite.central(r=mixn, distpar=c(-3,3), m=0, s=sqrt(10), n=c(1,2,3,10)) par(op) limite.central <- function (r=runif, distpar=c(0,1), m=.5,s=1/sqrt(12), n=c(1,3,10,30), N=1000) { for (i in n) { if (length(distpar)==2){ x <- matrix(r(i*N, distpar[1],distpar[2]),nc=i) }

【原创附代码数据】R语言隐马尔科夫模型(HMM)模型股指预测代码

R语言隐马尔科夫模型(HMM)模型股指预测代码了解不同的股市状况，改变交易策略，对股市收益有很大的影响。

有些策略在波澜不惊的股市中表现良好，而有些策略可能适合强劲增长或长期下跌的情况。

弄清楚何时开始或合适止损，调整风险和资金管理技巧，都取决于股市的当前状况。

在本文中，我们将通过使用一类强大的机器学习算法“隐马尔可夫模型”（HMM）来探索如何识别不同的股市状况。

▍隐马尔可夫模型马尔科夫模型是一个概率过程，查看当前状态来预测下一个状态。

一个简单的例子就是看天气。

假设我们有三种天气情况：下雨、多云、阳光明媚。

如果今天下雨，马尔科夫模型就会寻找每种不同天气的概率。

例如，明天可能会持续下雨的可能性较高，变得多云的可能性略低，而会变得晴朗的几率很小。

▍构建模型基于以上背景，然后我们可以用来找到不同的股市状况优化我们的交易策略。

我们使用2004年至今的上证指数（000001.ss）来构建模型。

首先，我们得到上证指数的收盘价数据，计算得到收益率数据，并建立HMM模型比较模型的预测结果。

library(depmixS4)library(TTR)library(ggplot2)library(reshape2)library(plotly)# create the returns stream from thisshdata<-getSymbols( "000001.ss", from="2004-01-01",auto.assign=F )gspcRets = diff( log( Cl( shdata ) ) )returns = as.numeric(gspcRets)write.csv(as.data.frame(gspcRets),"gspcRets.csv")shdata=na.omit(shdata)df <- data.frame(Date=index(shdata),coredata(shdata))p <- df %>%plot_ly(x = ~Date, type="candlestick",open = ~X000001.SS.Open, close = ~X000001.SS.Close,high = ~X000001.SS.High, low = ~X000001.SS.Low, name = "000001.SS",increasing = i, decreasing = d) %>%add_lines(y = ~up , name = "B Bands",line = list(color = '#ccc', width = 0.5),legendgroup = "Bollinger Bands",hoverinfo = "none") %>%add_lines(y = ~dn, name = "B Bands",line = list(color = '#ccc', width = 0.5),legendgroup = "Bollinger Bands",showlegend = FALSE, hoverinfo = "none") %>%add_lines(y = ~mavg, name = "Mv Avg",line = list(color = '#E377C2', width = 0.5),hoverinfo = "none") %>%layout(yaxis = list(title = "Price"))绘制上证指数的收盘价和收益率数据，我们看到2004年和2017年期间股市的波动情况。

房地产价格指数的R语言

南京理工大学课程考核论文课程名称：应用时间序列分析-1 - / 16前言近十年来，国内的房地产业发展迅速，开发的面积和规模也越来越大。

大多数国人对房地产这个话题的热情是经久不衰，房地产业内任何重大的政策和举措都对普通老百姓的生活产生深刻的影响。

本文选择的比较对象是一篇关于1998年初-2009年底的房地产销售价格指数的时间序列论文。

原作者使用的是SAS软件，而我将使用R语言软件对数据进行观察研究并预测其走势。

通过两者的过程及结果，比较其优劣。

目录一、时间序列概述 (4)1、 ........................................................ 槪念42、 ........................................................ 定义43、 ................................................ 主要分析方法44、 .................................................... 研究意义4二、时间序列的预处理 (5)1、 ...................................................... 平稳性52、 .................................................... 纯随机性5三、时间序列分析的主要方法及模型 (6)1、 ...................................... 平稳时间序列分析的模型62、 .............................................. 非平稳序列分析63、 ............................................ 非平稳序列的模型7四、实例分析 (9)1、 .................................................. 平稳性检验92、 ........................................ 拟合及残差白噪声检验113、 .............................................. 预测效果及比对13完整的程序 (16)参考文献 (16)时间序列概述1.概念所谓时间疗;列就是按照时间的顺序记录的一列有序数据。