2013华二自招试题
华二初中自招培优讲义之自主招生考试数学试题

自主招生考试数学试题一、选择题(每小题3分)1、已知81cos sin =⋅αα,且︒<<︒9045α,则ααsin cos -的值为( ) A. 23 B. 23- C. 43 D. 23± 2、若c b a ,,为正数,已知关于x 的一元二次方程02=++c bx ax 有两个相等的实根,则方程()()01212=+++++c x b x a 的根的情况是( )A.没有实根B.有两个相等的实根C.有两个不等的实根D.根的情况不确定3、已知半径为1和2的两个圆外切与点P ,则点P 到两圆外公切线的距离为( )A. 43B. 34C. 23 D. 3 4、下图的长方体是由A ,B ,C ,D 四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )二、填空题(每小题4分)5、某次数学测验共有20题,每题答对得5分,不答得0分,答错得-2分,若小丽这次测验得分是质数,则小丽这次最多答对 题6、已知⊙O 的直径AB=20,弦CD 交AB 于G ,AG>BG ,CD=16,AE ⊥CD 于E ,BF ⊥CD 于F ,则 AE -BF=7、如图,两个反比例函数x k y 1=和xk y 2=在第一象限内的图像依次是1C 和2C ,设点P 在1C 上,PC ⊥x 轴于点C ,交2C 于点A ,PD ⊥x 轴于点D ,交2C 于点B ,则四边形PAOB 的面积为8、若二次方程组⎪⎩⎪⎨⎧+-==-1)2(122x k y y x 有唯一解,则k 的所有可能取值为 9、设正△ABC 的边长为2,M 是AB 中点,P 是BC 边上任意一点,PA+PM 的最大值和最小值分别为s 和t ,则22t s -=10、在△ABC 中, AC=2011,BC=2010,AB=20112010+,则C A cos sin ⋅=11、已知c b a ,,为实数,且514131=+=+=+c a ac c b bc b a ab ,,,则=++cabc ab abc 12、已知Rt △ABC 的三个顶点A ,B ,C 均在抛物线2x y =上,且斜边AB 平行于x 轴,设斜边上的高为h ,则h 的取值为13、方程xx x 222=-的正根个数为 14、已知,124=+=+ab n b a ,,若221914919b ab a ++的值为2011,则n=15、任意选择一个三位正整数,其中恰好为2的幂的概率为16、勾股定理有着悠久的历史,它曾引起很多人的兴趣。
华师大二附中自主招生2013真题及答案解析

2013华二自主招生试卷1、在,,90b AC a AB A ABC Rt ==︒=∠∆,中,在AC 上有一点E ,在BC 上有一点F ,x AE EF BE =⊥,,,y S EFC =∆求x y 与的函数关系。
2、定义○1111=*,○2()1111+=+**n n ,求=*1n ;3、()()()()41128231)(22-+++--++++=a x a x a a x a x a x f 定义域为D,0)(>x f 在定义域D 内恒成立,求a 的取值范围?4、已知:2222411b a b a +=+,求20132012⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛b a a b =__________.5、如图,有棋子摆成这样,求第n 幅图有_________颗棋子。
∙∙∙∙∙∙(3)(2)(1)冲刺2019年华师大二附中自主招生真题及答案解析6、如图,在矩形ABCD 中,2AE=BE,将=∠︒=∠∆∆ECB EA D EC BE DEC ABE ,求翻折,、分别沿、15''____.7.1,2,2,3,3,3,4,4,4,4,…..,第2013个数是_____________.8.已知:y x 、为有理数,且满足,33421y x +=+求._________),(=y xADCB-2-121Oyx2013华二自主招生数学试题B1.寒山寺每隔9秒敲一此钟,第一次敲钟时,甲乙两船分别向上、下游驶去,速度分别为3m/s ,9m/s ,当甲船听到第108声时,乙船只能听见第_______声.(V 声=300m/s) 2.9名同学分别投票给“杨坤组”5票,“那英组”4票,问“杨坤组”的票数始终压过“那英组”的概率为__________.3.(x-3)2+(y-3)2=6的所有实数对(x ,y) 使yx 最大,则这个最大值为______.4.a x 12有三个整数解,则a =______.5.若方程x 2+2(a+1)x+2a+1=0有个小于1的正数根,a 的范围_______6.n 为正整数,S=1+2+3+,+n 为一个由同一数字组成的三位数,则n =______.7.在一个8×8的正方形格子中,一角剪去一个2×2的小正方形,问其余部分可否剪成15块“L ” 型纸片?若能剪,给出剪切方法,若不能剪,请说明理由.8.正方形ABCD 中有一点E ,使E 到A 、B 、C 的距离之和最小为62,求正方形边长.9.“帽子函数”(1)求函数解析式(2)若有抛物线y=-x 2+a(a<43),求它与“帽子函数”交点个数;(3)请试写一个抛物线,使它与“帽子函数”有且只有2个交点,横坐标分别为27,25.答案十。
2013高中自主招生考试选拔试题(含答案)

(2)根据对对阵形式的分析可以知道:天忌赢得比赛的概率为 (得4分)
解(115、(本小题满分10分)
解:解:(1)集合 不是好的集合, 是好的集合。(每个判断正确得2分)
(2)集合 、 、 、 等都可以举。(每举出一个得3分)
16、(本小题满分10分)
证明: ,且 为 三等分点, 为 中点
我们观察操作,将某次操作前的三个数记为 .因为 对称,不妨设操作 .则操作后的三个数为 , , .不难发现
也就是说,操作前后平方和不改变,所以经过有限此操作后,三个数的平方和为10不为2014.(得4分)
A.20分钟B.22分钟
C.24分钟D.26分钟
5.二次函数 的图象如何移动就得到 的图象( )
A. 向左移动1个单位,向上移动3个单位。
B. 向右移动1个单位,向上移动3个单位。
C. 向左移动1个单位,向下移动3个单位。
D. 向右移动1个单位,向下移动3个单位。
6.下列名人中:①比尔 盖茨②高斯③刘翔④诺贝尔⑤陈景润⑥陈省身⑦高尔基⑧爱因斯坦,其中是数学家的是()
13.如果有2007名学生排成一列,按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、1……的规律报数,那么第2007名学生所报的数是.
三、解答题:(本题有4个小题,共38分)解答应写出文字说明,证明过程或推演步骤。
14.(本小题满分8分)【田忌赛马】
齐王和他的大臣田忌均有上、中、下马各一匹,每场比赛三匹马各出场一次,共赛三次,以胜的次数多者为赢.已知田忌的马较齐王的马略有逊色,即:田忌的上马不敌齐王的上马,但胜过齐王的中马;田忌的中马不敌齐王的中马,但胜过齐王的下马; 田忌的下马不敌齐王的下马. 田忌在按图1的方法屡赛屡败后,接受了孙膑的建议,用图2的方法,结果田忌两胜一负,赢了比赛.假如在不知道齐王出马顺序的情况下:
华二自招练习题(5)---内部资料

练习五
1. 已知:E 是正方形ABCD 的BC 边中点,过点D B .分别作AE 垂线,垂足分别是G F ..求角FBG ∠.
2. 若k 为整数,使得关于x 的方程03)32(2=++-x k kx 有有理数根,则称k 为“好数”,求这个好数k 的个数。
3. 在ABC Rt ∆中,已知6=AC ,点E 在AC 边上,满足AE CE 2=,D 为斜边AB 中点,F 为线段BC 一动点,满足ο90=∠EDF ,求FC BF -最大值。
4. 已知n (3≥n )个实数数n 的最小值。
5.已知o为锐角三角形ABC的外心,ο
∠BAC,延长CO,与AB交于点D,延长BO与AC交于点E,
60
=
6.
7.
8.
9. 已知二次函数b x ax y ++=421与 a x bx y ++=422均有最小值,记1y 与2y 的最小值是 n m ,。
(1)若0=+n m ,证明:任意的实数x ,均有021≥+y y ;
(2)若n m ,均大于0,且 2=mn 记M 为n m ,中较大者,求M 的值。
10. 如图,在三角形ABC 中,AC AB =,D 为边AC 上一动点,过点D 作AB DE //,DE 与BC 交于点E ,F 为BD 中点,1o 与2o 是CDE ∆和BDE ∆外接圆圆心,证明:
(1)ο90=∠AFO ;
(2)2
1FO FO FD FA =。
2013华约自主招生数学试题及答案详解

2013“华约”自主招生试题2013-03-16(时间90分钟,满分100分)1.(10分)集合{|10,}A x x x N *=≥∈,B 为A 的子集,若集合B 中元素满足以下条件:①任意数字都不相等;②任意两个数之和不为9 (1)B 中两位数有多少?三位数有多少? (2)B 中是否有五位数?六位数?(3)若将集合B 的元素按从小到大的顺序排列,第1081个数为多少?【解】将0,1,2,…,9这10个数字按照和为9进行配对,考虑(0,9),(1,8),(2,7),(3,6), (4,5),B 中元素的每个数位只能从上面五对数中每对至多取一个数构成.(1)两位数有22215242272C A C ⨯⨯-⨯=个; 三位数有333222534222432C A C A ⨯⨯-⨯⨯=个;(2)存在五位数,只需从上述五个数对中每对取一个数即可构成符合条件的五位数;不存在六位数,由抽屉原理易知,若存在,则至少要从一个数对中取出两个数,则该两个数字之和为9,与B 中任意一个元素的任意两个数位的数字之和不等于矛盾,因此不存在六位数;(3)四位数共有4443335443221728C A C A ⨯⨯-⨯⨯=个,因此第1081个元素是四位数,且是第577个四位数,我们考虑千位,千位为1,2,3的四位数有3334332576C A ⨯⨯⨯=个,因此第1081个元素是4012.2.(15分)1sin sin 3x y +=,1cos cos 5x y -=,求sin()x y -与cos()x y +的值 【解】由1sin sin 3x y +=……①,1cos cos 5x y -=……②,平方相加得208cos()225x y +=;另一方面由①可得12sincos 223x y x y +-=……③ 由②式可得12sin sin 225x y x y +--=……④,由③/④式得3tan 25x y -=-,也所以22tan152sin()171tan 2x y x y x y --==--+即求.3.点A 在y kx =上,点B 在y kx =-上,其中0k >,2||||1OA OB k ⋅=+,且A B 、在y 轴同侧. (1)求AB 中点M 的轨迹C ;(2)曲线C 与22(0)x py p =>相切,求证:切点分别在两条定直线上,并求切线方程. 【解】(1)设1122(,),(,)A x y B x y ,(,)M x y ,则1212121122(),,,222x x y y k x x y kx y kx x y ++-==-===, 由2||||1OA OB k ⋅=+得,121x x =,显然22121212()()44x x x x x x +--==,于是得2221(0)y x k k-=>,于是AB 中点M 的轨迹C是焦点为(,实轴长为2的双曲线.(2)将22(0)x py p =>与2221(0)y x k k-=>联立得22220y pk y k -+=,由曲线C 与抛物线相切,故242440p k k ∆=-=,即1pk =,所以方程可化为2220y ky k -+=,即切点的纵从标均为y k =,代入曲线C 得横坐标为.因此切点分别在定直线x x ==,两切点为),()D k E k ,又因为xy p'=,于是在)D k处的切线方程为y k x p -=,即1y x p p=-;同理在()E k处的切线方程为1y x p p=--. 4. (15分)7个红球,8个黑球,从中任取4个球.(1)求取出的球中恰有1个是红球的概率;(2)求所取出球中黑球个数X 的分布列及期望()E X ; (3)若所取出的4个球颜色相同,求恰好全黑的概率;【解】(1)由题知恰有一个红球的概率为137841556195C C C =; (2)易知X 的所有可能取值为0,1,2,3,4,则由古典概型知,474155(0)195C P X C ===,137841540(1)195C C P X C ===,227841584(2)195C C P X C ===,137841556(3)195C C P X C ===, 4841510(4)195C P X C ===,即X 的分布列为:所以其数学期望为 540845610320123419519519519519515EX =⨯+⨯+⨯+⨯+⨯=(事实上由超几何分布期望公式可以直接得出期望为83241515EX =⨯=,无须繁杂计算) (3)取出四个球同色,全为黑色的概率为48447823C C C =+即求. 5. (15分)数列{}n a 均为正数,且对任意*n N ∈满足21(0n nn a ca a c +=+>为常数). (1) 求证:对任意正数M ,存在N *N ∈,当n N >时有n a M >; (2)设11n n b ca =+,n S 是数列{}n b 的前n 项和,求证:对任意0d >,存在*N N ∈,当n N >时,110||n S d ca <-<. 【证明】:(1)因为对任意的*n N ∈满足0n a >,所以21n n n n a ca a a +=+>,又因为0c >, 所以22111121()n n n n n n n n a a c a a a a a a a a +----=-+->->>-,所以2112211211()(1)()(1)n n n n n a a a a a a a a n a a n a ---=-+-++-+>--=-故对任意的正整数M ,存在*21{1,[]2}MN N a =+∈,当n N >时有n a M >; (注:21M a ⎡⎤⎢⎥⎣⎦表示不超过21Ma 的最大正整数.) (2)由21(1)n n n n n a ca a a ca +=+=+可得,111n n n a ca a +=+,所以211111111n n n n n n n n n n ca a a ca ca a ca a ca ca ++++-===-+; 也所以11111nn i i n S b ca ca =+==-∑,即11110n n S ca ca +-=> 且由(1)知211n a na +>,所以21111n ca nca +<, 即对任意0d >,存在211max 1,N dca ⎧⎫⎡⎤⎪⎪=⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭,当n N >时,有110||n S d ca <-<. 6. (15分)已知,,x y z 是互不相等的正整数,|(1)(1)(1)xyz xy xz yz ---,求,,x y z . 【解】本题等价于求使(1)(1)(1)1()xy xz yz xy yz zx xyz x y z xyz xyz---++-=-+++为整数的正整数,,x y z ,由于,,x y z 是互不相等的正整数,因此|1xyz xy yz zx ++-,不失一般性不妨设x y z >>,则13xyz xy yz zx yx ≤++-<,于是3z <,结合z 为正整数,故1,2z =, 当1z =时,|1xy xy y x ++-,即|1xy y x +-,于是12xy xy y x x ≤++-<,所以2y <, 但另一方面y z >,且为正整数,所以2y ≥矛盾,不合题意.所以2z =,此时2|221xy xy y x ++-,于是2221xy xy y x ≤++-,即221xy y x ≤+-, 也所以224xy y x x <+<,所以4y <,又因为2y z >=,所以3y =; 于是6|55x x +,所以655x x ≤+,即5x ≤,又因为3x y >=,所以4,5x =, 经检验5x =符合题意,于是符合题意的正整数,,x y z 有(,,)x y z =(2,3,5)、(2,5,3)、(3,2,5)、(3,5,2)、(5,2,3)、(5,3,2)注:该题与2011年福建省高一数学竞赛试题雷同. 7. (15分)已知()(1)1x f x x e =-- 求证:(1)当0x >,()0f x <;(2)数列{}n x 满足111,1n n x x n x e e x +=-=,求证:数列{}n x 单调递减且12n n x >.【解】(1)当0x >时,()0xf x xe '=-<,所以()f x 在(0,)+∞上递减,所以()(0)0f x f <=. (2)由11n nx x n x ee +=-得11n n x x ne ex +-=,结合11x =,及对任意0,1xx e x >>+,利用数学归纳法易得0n x >对任意正整数n 成立,由(1)知()0n f x <,即1n n xxn e x e -<, 即1n n x x n n x ex e +<,因为0n x >,所以1n n x x e e +<,即1n n x x +>,所以数列{}n x 递减,下面证明12n n x >,用数学归纳法证,设1()x e g x x -=,则221()()x x xe e f x g x x x -+'==-,由(1)知当0x >时,()0f x <,即()0g x '>,故()g x 在(0,)+∞递增,由归纳假设12n n x >得1()()2n n g x g >,要证明1112n n x ++>只需证明1112n n xe e ++>,即112()n n g x e +>,故只需证明1121()2n n g e +>,考虑函数2()()x h x xg x xe =-,因为当0x >时212x x e >+,所以222()(1)[(1)]022x x xxx x h x e e e e =-+=-+>,故()h x 在(0,)+∞上递增,又102n >,所以1()02n h >,即1121()2n n g e +>,由归纳法知,12n n x >对任意正整数n 成立.注:此题的函数模型与2012年清华大学保送生考试试题的函数模型相似.。
华二自招模拟训练卷(二)

华二自招训练题〔二〕Part 1 Words and phrasesI. Choice:1. A person’s _________ body temperature is about 37C.(A :ordinary, B:normal, C: common,D:usual)2.When I opened the door, a parcel on the floor___________ my eye.(A: met, B: caught, C:drew,D: attracted)3.Many foreigners_____________the Great Wall as the World’s Seventh Wonder.(A: look at ,B: look for,C: look around,D: look on)4. A piece of ______________music will make you happy. (A:fond ,B: pleased, C: merry,D: glad)5.It has been ten years now since the Labour Party came to____________ in that country.(A:power ,B: control ,C: force,D: charge)6.Have you finished your report yet? No, I'll finish in _________ten minutes. (A:other,B:another, C:more,D: less )7.You are __________your time trying to persuade him; He'll never join us. (A:spending,B: losing, C: missing, D: wasting )8.It's nearly seven o'clock. Jack ___________be here at any moment. (A:need,B: must,C: can,D: s hould )9.What did you think of her speech? She ____________for an hour but didn't ____________much . (A:spoke …say;B: said …speak;C: said …say ;D:spoke …speak )11.He was expected to ___________at the meeting but he failed to come. (A:come across, B:show out,C: turn up,D: present out )12.The information ______________on the mystery of Mary's sudden death. (A:threw light,B: ga ve light,C: made light ,D:too light )13.It's necessary for us to ______________our bad habits. (A:break with,B:break out of, C:break away with, D:break up )14._______________her clothing,the woman must be from an Arabian country. (A:Looking at, B: Seen fron,C: Observe by, D:Judging by )15.As we all know, our living conditions can only be ____________step by step. (A:improved, B: raised, C:turned, D:corrected )16. What he said will ____________.(A:realize, B:complete,C: come true, D: finish )17.It will further strengthen the exchange between ___________and thus lead _____________bett er understanding. (A:peoples ……to;B: people ……into; C:peoples ……/ ;D:people ……/)18..This photo ___________me of what we did together during our holiday. (A:reminds,B: recogn izes,C: remembers D :causes ).19.Students in that area learn how to ______________food and animals besides subjects. (A:feed, B:plant, C:grow, D:raise )20.I went to Hangzhou last summer vacation with my brother and visited many _______________ ______.(A:places of interests, B:places of interest, C:place of interest, D: place of interests )21 .Please ________________this little gift as your souvenir. (A:receive, B:get,C:accept, D:gain ).22.We have ______________some victories despite these difficulties. (A:finished, B:completed,C : achieved, D:accomplished )23. All this ____________me that she was innocent. (convinced, persuaded, advised, taught )24 .A daughter's marriage is quite a(n) _____________for a father. (A:incident, B:accident, C:eve nt,D: thing )25.He ran into the burning house and saved the child, which was really a brave ______________. (A:motion,B: action, C:deed, D:act )26.The girl kept a cat as a __________.(A:animal.B: beast, C:pet,D: creature )27. She has no ___________in him. ( A: belief ;B: faith, C: hope, D: trust )28.I was not ____________to see the difference between them. (A: capable, B: able, C: qualified, D: enabled )29. Gold is ___________ , wealth is abstract. (A: real, B: actual, C: concrete, D: exact )30.The town was __________in the early hours of the morning. (A: ever,B: still, C: yet, D: never )31.Is it __________for you to buy so many dresses at a time? (A: vital,B: necessary, C: essential, D: imperative )32.Her behavior is _________of great praises. (A: worthy, B: worth,C: worthwhile ,D: valuable )33.Are we allowed to take __________in the museum? (A: drawings, B: paintings,C: portraits, D: pictures )34.You'd better ___________the holiday arrangement once more before you leave tomorrow. (A: go round, B: go into, C: go after,D: go over )35.Her outstanding ____________in the competition proved that she was a worthy winner. (A: per formance, B: activity, C: behavior, D: personality )36.___________your step, or you might fall into the poll. (A: Feel, B: See, C: Watch, D: Look )37. As we know, there are four ___________of blood. (A: kinds, B: sorts, C: types, D: shapes )38.Please __________that you won't make such a mistake. (A: make sure, B: make out, C: make u p,D: make in )39.There 'll be some baby birds in the nest, these eggs are ready to ____________.(A: search, B: match, C: clench, D: hatch )40.The close _____________are not allowed to get married. (A:relationships,B: relatives,C: rela tions,D: relatives )II. Phrases1.As a whole2.As far as3.As usual4.Ask a favor of6.Ask after7.Associate A with B8.Assure …of/assure sb.that…9.At a loss / at sea10.At all costs / at any cost11.At first sight12.At one time13.At present14.At the cost of15.At the mercy of16.At the moment17.At the risk of one’s life18.At times19.Attach… to20.Attach importance toIII. Put the following into English or vice versa: 1.你最好从整体来看待这个问题。
2010-2013“华约”自主招生物理试题及参考解答
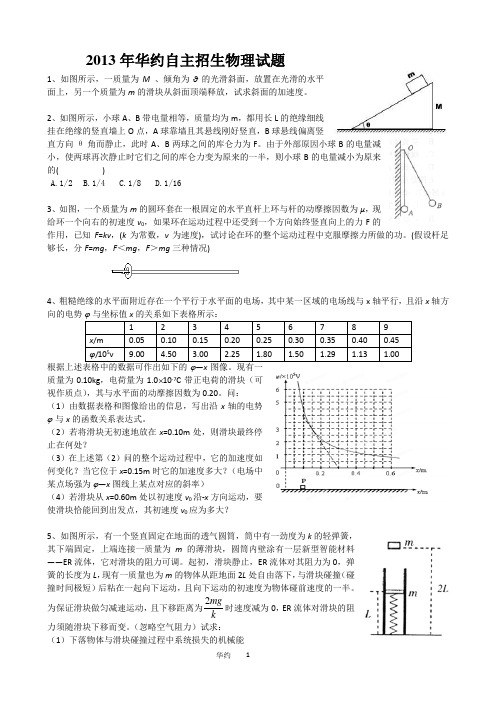
2013年华约自主招生物理试题1、如图所示,一质量为M 、倾角为θ的光滑斜面,放置在光滑的水平面上,另一个质量为m 的滑块从斜面顶端释放,试求斜面的加速度。
2、如图所示,小球A 、B 带电量相等,质量均为m ,都用长L 的绝缘细线挂在绝缘的竖直墙上O 点,A 球靠墙且其悬线刚好竖直,B 球悬线偏离竖直方向θ角而静止,此时A 、B 两球之间的库仑力为F 。
由于外部原因小球B 的电量减小,使两球再次静止时它们之间的库仑力变为原来的一半,则小球B 的电量减小为原来的( )A.1/2B.1/4C.1/8D.1/163、如图,一个质量为m 的圆环套在一根固定的水平直杆上环与杆的动摩擦因数为μ,现给环一个向右的初速度v 0,如果环在运动过程中还受到一个方向始终竖直向上的力F 的作用,已知F =kv ,(k 为常数,v 为速度),试讨论在环的整个运动过程中克服摩擦力所做的功。
(假设杆足够长,分F =mg ,F <mg ,F >mg 三种情况)4、粗糙绝缘的水平面附近存在一个平行于水平面的电场,其中某一区域的电场线与x 轴平行,且沿x 轴方向的电势根据上述表格中的数据可作出如下的—x 图像。
现有一质量为0.10kg ,电荷量为1.0⨯10-7C 带正电荷的滑块(可视作质点),其与水平面的动摩擦因数为0.20。
问: (1)由数据表格和图像给出的信息,写出沿x 轴的电势ϕ与x 的函数关系表达式。
(2)若将滑块无初速地放在x =0.10m 处,则滑块最终停止在何处?(3)在上述第(2)问的整个运动过程中,它的加速度如何变化?当它位于x =0.15m 时它的加速度多大?(电场中某点场强为ϕ—x 图线上某点对应的斜率)(4)若滑块从x =0.60m 处以初速度v 0沿-x 方向运动,要使滑块恰能回到出发点,其初速度v 0应为多大?5、如图所示,有一个竖直固定在地面的透气圆筒,筒中有一劲度为k 的轻弹簧,其下端固定,上端连接一质量为m 的薄滑块,圆筒内壁涂有一层新型智能材料——ER 流体,它对滑块的阻力可调。
2013华约、北约自主招生数学、物理试题和答案详解

2013“华约”自主招生试题2013-03-16(时间90分钟,满分100分)1.(10分)集合{|10,}A x x x N *=≥∈,B 为A 的子集,若集合B 中元素满足以下条件:①任意数字都不相等;②任意两个数之和不为9(1)B 中两位数有多少?三位数有多少? (2)B 中是否有五位数?六位数?(3)若将集合B 的元素按从小到大的顺序排列,第1081个数为多少?【解】将0,1,2,…,9这10个数字按照和为9进行配对,考虑(0,9),(1,8),(2,7),(3,6), (4,5),B 中元素的每个数位只能从上面五对数中每对至多取一个数构成.(1)两位数有22215242272C A C ⨯⨯-⨯=个; 三位数有333222534222432C A C A ⨯⨯-⨯⨯=个;(2)存在五位数,只需从上述五个数对中每对取一个数即可构成符合条件的五位数;不存在六位数,由抽屉原理易知,若存在,则至少要从一个数对中取出两个数,则该两个数字之和为9,与B 中任意一个元素的任意两个数位的数字之和不等于矛盾,因此不存在六位数;(3)四位数共有4443335443221728C A C A ⨯⨯-⨯⨯=个,因此第1081个元素是四位数,且是第577个四位数,我们考虑千位,千位为1,2,3的四位数有3334332576C A ⨯⨯⨯=个,因此第1081个元素是4012.2.(15分)1sin sin 3x y +=,1cos cos 5x y -=,求sin()x y -与cos()x y +的值 【解】由1sin sin 3x y +=……①,1cos cos 5x y -=……②,平方相加得208cos()225x y +=;另一方面由①可得12sincos 223x y x y +-=……③ 由②式可得12sin sin 225x y x y +--=……④,由③/④式得3tan 25x y -=-,也所以22tan152sin()171tan 2x y x y x y --==--+即求.3.点A 在y kx =上,点B 在y kx =-上,其中0k >,2||||1OA OB k ⋅=+,且A B 、在y 轴同侧. (1)求AB 中点M 的轨迹C ;(2)曲线C 与22(0)x py p =>相切,求证:切点分别在两条定直线上,并求切线方程. 【解】(1)设1122(,),(,)A x y B x y ,(,)M x y ,则1212121122(),,,222x x y y k x x y kx y kx x y ++-==-===, 由2||||1OA OB k ⋅=+得,121x x =,显然22121212()()44x x x x x x +--==,于是得2221(0)y x k k-=>,于是AB 中点M 的轨迹C是焦点为(,实轴长为2的双曲线.(2)将22(0)x py p =>与2221(0)y x k k-=>联立得22220y pk y k -+=,由曲线C 与抛物线相切,故242440p k k ∆=-=,即1pk =,所以方程可化为2220y ky k -+=,即切点的纵从标均为y k =,代入曲线C 得横坐标为.因此切点分别在定直线x x ==,两切点为),()D k E k ,又因为xy p'=,于是在)D k处的切线方程为y k x -=,即1y x p=-;同理在()E k处的切线方程为1y x p p=--. 4. (15分)7个红球,8个黑球,从中任取4个球.(1)求取出的球中恰有1个是红球的概率;(2)求所取出球中黑球个数X 的分布列及期望()E X ; (3)若所取出的4个球颜色相同,求恰好全黑的概率;【解】(1)由题知恰有一个红球的概率为137841556195C C C =; (2)易知X 的所有可能取值为0,1,2,3,4,则由古典概型知,474155(0)195C P X C ===,137841540(1)195C C P X C ===,227841584(2)195C C P X C ===,137841556(3)195C C P X C ===, 4841510(4)195C P X C ===,即X 的分布列为:所以其数学期望为 540845610320123419519519519519515EX =⨯+⨯+⨯+⨯+⨯=(事实上由超几何分布期望公式可以直接得出期望为83241515EX =⨯=,无须繁杂计算) (3)取出四个球同色,全为黑色的概率为48447823C C C =+即求. 5. (15分)数列{}n a 均为正数,且对任意*n N ∈满足21(0n nn a ca a c +=+>为常数).(1) 求证:对任意正数M ,存在N *N ∈,当n N >时有n a M >; (2)设11n n b ca =+,n S 是数列{}n b 的前n 项和,求证:对任意0d >,存在*N N ∈,当n N >时,110||n S d ca <-<. 【证明】:(1)因为对任意的*n N ∈满足0n a >,所以21n n n n a ca a a +=+>,又因为0c >, 所以22111121()n n n n n n n n a a c a a a a a a a a +----=-+->->>-,所以2112211211()(1)()(1)n n n n n a a a a a a a a n a a n a ---=-+-++-+>--=-故对任意的正整数M ,存在*21{1,[]2}MN N a =+∈,当n N >时有n a M >; (注:21M a ⎡⎤⎢⎥⎣⎦表示不超过21Ma 的最大正整数.)(2)由21(1)n n n n n a ca a a ca +=+=+可得,111n n n a ca a +=+,所以211111111n n n n n n n n n n ca a a ca ca a ca a ca ca ++++-===-+; 也所以11111nn i i n S b ca ca =+==-∑,即11110n n S ca ca +-=> 且由(1)知211n a na +>,所以21111n ca nca +<, 即对任意0d >,存在211max 1,N dca ⎧⎫⎡⎤⎪⎪=⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭,当n N >时,有110||n S d ca <-<. 6. (15分)已知,,x y z 是互不相等的正整数,|(1)(1)(1)xyz xy xz yz ---,求,,x y z . 【解】本题等价于求使(1)(1)(1)1()xy xz yz xy yz zx xyz x y z xyz xyz---++-=-+++为整数的正整数,,x y z ,由于,,x y z 是互不相等的正整数,因此|1xyz xy yz zx ++-,不失一般性不妨设x y z >>,则13xyz xy yz zx yx ≤++-<,于是3z <,结合z 为正整数,故1,2z =,当1z =时,|1xy xy y x ++-,即|1xy y x +-,于是12xy xy y x x ≤++-<,所以2y <, 但另一方面y z >,且为正整数,所以2y ≥矛盾,不合题意.所以2z =,此时2|221xy xy y x ++-,于是2221xy xy y x ≤++-,即221xy y x ≤+-,也所以224xy y x x <+<,所以4y <,又因为2y z >=,所以3y =; 于是6|55x x +,所以655x x ≤+,即5x ≤,又因为3x y >=,所以4,5x =, 经检验5x =符合题意,于是符合题意的正整数,,x y z 有(,,)x y z =(2,3,5)、(2,5,3)、(3,2,5)、(3,5,2)、(5,2,3)、(5,3,2)注:该题与2011年福建省高一数学竞赛试题雷同. 7. (15分)已知()(1)1x f x x e =-- 求证:(1)当0x >,()0f x <;(2)数列{}n x 满足111,1n n x x n x e e x +=-=,求证:数列{}n x 单调递减且12n nx >. 【解】(1)当0x >时,()0xf x xe '=-<,所以()f x 在(0,)+∞上递减,所以()(0)0f x f <=. (2)由11n nx x n x ee +=-得11n n x x ne ex +-=,结合11x =,及对任意0,1xx e x >>+,利用数学归纳法易得0n x >对任意正整数n 成立,由(1)知()0n f x <,即1n n xxn e x e -<, 即1n n x x n n x ex e +<,因为0n x >,所以1n n x x e e +<,即1n n x x +>,所以数列{}n x 递减,下面证明12n n x >,用数学归纳法证,设1()x e g x x -=,则221()()x x xe e f x g x x x -+'==-,由(1)知当0x >时,()0f x <,即()0g x '>,故()g x 在(0,)+∞递增,由归纳假设12n n x >得1()()2n n g x g >,要证明1112n n x ++>只需证明1112n n xe e ++>,即112()n n g x e +>,故只需证明1121()2n n g e +>,考虑函数2()()x h x xg x xe =-,因为当0x >时212x x e >+,所以222()(1)[(1)]022x x xxx x h x e e e e =-+=-+>,故()h x 在(0,)+∞上递增,又102n >,所以1()02n h >,即1121()2n n g e +>,由归纳法知,12n n x >对任意正整数n 成立.注:此题的函数模型与2012年清华大学保送生考试试题的函数模型相似.2013“北约”自主招生试题2013-03-16(时间90分钟,满分120分)一、选择题(每题8分,共48分)1.和1( ) A. 2 B. 3 C. 5 D. 6【解】由1x =可知22x =,同理由1x 可知3(1)2x -=; 所以方程23(2)[(1)2]0x x ---=的次数最小,其次数为5,故选C.2.在66⨯的表中停放3辆完全相同的红色和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车只占一格,共有 种停放方法.A. 720B. 20C. 518400D. 14400 【解】红色车选3列有3620C =种方法,再从这三列中选三行有3620C =种方法,另外将红色车放在已选好的三列三行中有326⨯=种方法,同理黑色车只能从剩下的三行三列九个格中选,也有326⨯=种方法,因此方法数有(20206)614400⨯⨯⨯=种.故选D.3.已知225x y =+,225y x =+(x y ≠),则32232x x y y -+值为( ) A. 10- B. 12- C. 14- D. 16-【解】由225x y =+与225y x =+两式作差得2()x y x y +=-≠,代入两式中分别化出 2210x x +-=、2210y y +-=,所以,x y 是方程2210t t +-=的两个不等实根,于是 2,1x y x y +=-=-,也所以 3223222()[()3]2()(2)7216x x y y x y x y x y x y -+=++--=-⨯-=-.故选D. 4.在数列{}n a 中,11a =,142n n S a +=+(1n ≥),则2013a 值为( )A. 201230192⨯B. 201330192⨯C. 201230182⨯D. 无法确定 【解】由11a =,142n n S a +=+(1n ≥)……①可知,当1n =时,2142S a =+,所以25a =;当2n ≥时,有142(2)n n S a n -=+≥……②,由①-②式得,1144(2)n n n a a a n +-=-≥,即1122()(2)n n n n a a a a n +--=-≥,且2123a a -=所以11232n n n a a -+-=⨯(*n N ∈),同除以2n 得,113222n n n n a a +--=,且1012a =;所以13122n n a n +=+,故令2012n =时,得2012201323019a =⨯,故选A. 5.在ABC ∆中,D 为BC 中点,DM 平分ADB ∠交AB 于点M ,DN 平分ADC ∠交AC 于N ,则BM CN +与MN 的关系为( ) A.BM CN MN +> B.MN CN MN +< C.BM CN MN +=D.无法确定【解】如图,在DA 取DE DB =,连接,,ME NE MN则显然可证,ME MB EN NC ==,且有ME NE MN +≥,即BM CN MN +≥, 上述不等式当且仅当180MED DEN ∠+∠=, 也即180B C ∠+∠=,这显然与三角形内角和定理矛盾,故等号取不到, 也即选A.6.模长都为1的复数,,A B C 满足0A B C ++≠,则BC AC ABA B C++++的模长为( )A. 12- B. 1 C. 2 D. 无法确定 【解】由题知1AA BB CC ===,所以2BC AC AB BC AC AB BC AC ABA B C A B C A B C ++++++=⨯++++++,也即2BC AC AB BC AC AB BC AC ABA B C A B C A B C++++++=⨯++++++313BA C A AB CB AC BCAB AC BA BC C A CB++++++==++++++,故选B.二、解答题(每题18分,共72分)7.最多能找多少个两两不相等的正整数使其任意三个数之和为质数,并证明你的结论.【解】:至多有4个.首先可以取1,3,7,9这四个数,它们任意三个数之和分别为11,13,17,19符合质数定义.下面再证明5个正整数是不符合题意的.若有5个正整数,则考虑质数被3除的余数,如果有一个数的余数为0,那么考虑余下的4个数被3除的余数,如果余数既有1也有2,那么这两个数与前面余数为0的数的和刚好为3的倍数,故不符合题意,如果余下四个数的余数均相等,显然取余下四个数中的三个数,则这三个数的和为3的倍数不是质数,也不符合题意,如果这5个数被3除的余数都不等于3,则由抽屉原理,至少有3个数被3除的余数相同,这三个数的和是3的倍数不是质数,也不符合题意.综上可知,不存在5个正整数符合题意,即至多有4个正整数符合题意. 8.已知12320130a a a a ++++=,且122320131|2||2||2|a a a a a a -=-==-证明:12320130a a a a =====.【证明】:观察可知12320130a a a a ++++=,即21322013201212013(2)(2)(2)(2)0a a a a a a a a -+-++-+-=……① 又122320131|2||2||2|a a a a a a -=-==-,不妨设12|2|a a t -=,M ACDBE则①可写为(2013)0(02013,)kt k t k k N --=≤≤∈,即(22013)0k t -=, 又显然220130k -≠,则有0t =,于是有122320122013201312,2,,2,2a a a a a a a a ====,所以2013112a a =,即10a =.也所以12320130a a a a =====,即证.9.对于任意θ,求632cos cos66cos415cos2θθθθ---的值. 【解】632cos cos66cos415cos2θθθθ--- 31c o s 232()c o s 66c o s 415c o s 22θθθθ+=--- 3234(1c o s 23c o s 23c o s 2)(3c o s 24c o s 2)6c o s 415c o s2θθθθθθθ=+++---- 2412c o s 26c o s 446(1c o s 4)6c o s 410θθθθ=+-=++-=即求. 10.有一个m n ⨯的数表,已知每一行的数均是由小到大排列.现在将每一列的数由小到大重新排列,则新的数表中每一行的数满足什么样的关系?请证明你的结论.〖原题叙述〗:已知有m n ⋅个实数,排列成m n ⨯阶数阵,记作{}ij m n a ⨯,使得数阵中的每一行从左到右都是递增的,即对意的1,2,3,,i m =,当12j j <时,都有12ij ij a a <.现将{}ij m n a ⨯的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的m n ⨯阶数阵,记作{}ijm n a ⨯',即对任意的1,2,3,,i n =,当12i i <时,都有12i ji j a a ''<.试判断{}ijm n a ⨯'中每一行的n 个数的大小关系,并说明理由. 【解】:数阵{}ijm n a ⨯'中每一行的n 个数从左到右都是递增的,理由如下: 显然,我们要证明数阵{}ijm n a ⨯'中每一行的n 个数从左到右都是递增的,我们只需证明, 对于任意1,2,3,,i m =,都有(1)iji j a a +''<,其中1,2,3,,(1)j n =-. 若存在一组(1)pq p q a a +''>,令(1)(1)k k q i q a a ++'=,其中121,2,3,,,{,,,}{1,2,,}k k m i i i m ==,则当t p ≤时,都有(1)(1)(1)t t i q i q t q p q pq a a a a a +++'''≤=≤<.也即在(1,2,,)iq a i m =中,至少有p 个数小于pq a ',也即pq a '在数阵{}ij m n a ⨯'中的第q 列中,至少排在第1p +行,与pq a '排在第p 行矛盾.所以对于任意的1,2,,i m =,都有(1)iji j a a +''<,即数阵{}ij m n a ⨯'中每一行的n 个数从左到右都是递增的.2013年高水平大学(华约)自主选拔学业能力测试物理探究注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
上海市华东师范大学第二附属中自主招生英语试题 含答案

华二自招试卷(八)Lecture NineWords and phrasesChoice:1.What you said just now________me of that American professor.(mentioned,informed,reminded,memorized)2.Fred is second to none in maths in our class,but believe it or not,he_______passed the last exam.(easily,hardly,actually,successfully)3.She is______to leave as soon as possible.(hurried,worried,anxious,nervous)4.Mary has______a difficult question to me.(put,asked,made up,set)5.Will you_____me a favor,please?(give,make,do,bring)6.Some of the houses on the hillside are________to cars.(impossible,inconvenient,inadequate,inaccessible)7.If you are_______about Australian cities,just read the book written by Dr.Johnson.(interested,curious,anxious,upset)8.Many countries are increasing their use of natural gas,wind and other forms of_________.(source,power,material,energy)9.The cars give off a great deal of waste gas in the streets.Yes.But I’m sure something will be done to _______air pollution.(remove,reduce,warn,collect)10.The thing that_______is not whether you fail or not,but whether you try or not.(cares,considers,matters,minds)11.Although she has taken the medicine for two months,she can’t_______the cold.(take off,do away,get rid of,put away)12.We had a few _______days of rest in the mountain area.(quiet,silent,calm,still)13.Two important secrets of long life are regular exercise and_____from worry.(feelings,motion,freedom,process)14.If you disobey traffic rules,I think it will______you much trouble.(offer,take,give,cause.)15.What does she is often contrary________what she says.(against,for,to,on)16.I would rather stay at home_______swim.(than,to ,for,instead of)17.We all find that Mr.White seems to be_________these days.(more thankful,more considerate,more personal,more surprising)18.In the field of medicine,nowadays,the new______of psychology seems to be more popular.(application,reply,relief,practice)19.The bedroom was in a state of______because of these naughty boys.(dirty,disorder,mind,confidence)20.The special service____all the members of the club.(is needed to,is needed for,is available to,is available with)21.You are so kind to me that I wonder how i can_________you your help.(award,reward,grant,deserve)22.People used to_______that the earth was flat.(trust,believe,believe in, assure)23.Can i ______this novel for three weeks?(take,lend,borrow,keep)24.His brother will be____to work in the countryside.(taken,brought,sent,carried)25.She said she______the countryside to the city.(picked,chose,preferred,selected)26.The Chinese nation_______more than 50 national minorities besides theHans.(includes,holds,contains,involves)27.Perhaps i can not ______any time except on Sunday.(spend,take,cost,spare)28.Her honesty and willingness to work are the_________of her success.29.He gave away several______of old newspapers and magazines.(parcels,bunches,bundles,packages)30.I’m glad to tell you that your______for the job is tomorrow morning.(conversation,dialogue,interview,chat)31.For a reception male guests usually wear black_______and white shirts.(suits,dresses,garments,clothes.)32.The Victorian______of the English history is the time when Victoria was queen.(time,period,ages,day)33His parents felt very happy because he had passed the college_______examination.(gate,door,exit,entrance)34.His novel is perhaps the_______one of his century.(biggest,largest,greatest,hugest)35.She looked________while she was lying there.(quiet,silent,still,peaceful)36.He started his______life as an actor at the age of 20.(experienced,professional,qualified,practiced)37.There are usually at least two_______of looking at every question.(ways,views,means,directions)38.She has searched_______for the ring but can not find it.(hardly,deeply,heavily,thoroughly.)39.His mother often complains________the music he plays because it’s too______(of...aloud,about...loudly,of...loudly,about...loud)40.Wilson tried hard to_______a new world record.(set up,set out,set about,set)Phrases:bine...withe acrosse down withe into existence/beinge oute to(oneself)e into powere to/arrive at a conclusione up withe upment onmit a crimemon sensepare A to Bpare A with Bpete with sb. For sth.17.Concentrate on18.Conduct a survey19.Confuse A with B20.Congratulate sb.on sth.Underlined the following sentences:1.When they are allowed to combine with oxygen,this energy is released as heat and light.2.When you come across something important,write it down.3.What should I do when I come across situations like these again?4.Scientists are really interested in this idea that if you infect people with the virus,everyone will get infected,but only 75%of the people will actually come down with the cold.5.In Australia on Saturday,health officials said a person in Queensland who had been travelling in the U.S. had come down with the disease but had fully recovered.6.The implication is that these are jobs that would not otherwise have come into existence without the bridge.7.New products would be developed,new companies would come into existence and retailers would increase their sales.8.What he said came out to be true.9.The patient came to himself with the help of the doctors.10.Half a year later,no matter how significant their achievements are,2 new successors will take place of them and come into power after the reelection.11.We can’t come to any conclusion before we do any investigation.12.I am going to discuss this topic and strive to give the arguments of both sides.I will then come to a conclusion based on what i have learned.13.You would take things as they came.All you had to do was think a little harder and come up with a new conclusion.14.With theentire team gathered together,each team member must come up with something positive from the past three months and something negative from the past three months.15.You should see all the services come up on the backup machine in under a minute.16.The little boy came up to the singer and presented the flowers to him.17.You’d better keep silent and don’t comment on anything.18.The young who break the law and commit a crime are both vermin and victims19.It’s common sense to dress more warmly when it gets cold20.These are all common sense treatments.21.Nurses are compared to angels in white.22.How does the US compare to Canada,Russia,India-other populous nations?23.Weeds compete with plantings for water and nutrients.24.In spite of this,however,women in many places are still denied the right to compete with men for jobs on equal terms and the right to equal opportunities for promotion.25.He can hardly concentrate himself on his study.26.If you concentrate on the project,you can finish it on time.27.To understand our target customers’ needs better,we would like to conduct a survey.28.In accordance with the standard for students healthy condition,we conduct a survey on 13033 students in Nantong University.29.They do original reporting,they do not confuse fact with opinion or rumor,and they make sound editorial decisions.30.The twins are so much alike that i often confuse one with the other.31.I come here to congratulate on your promotion.32.Congratulate on their new position and please kindly support them for the coming new termas always!Part TwoReading:Reading SkillsII.如何阅读记叙文1.夹叙夹议阅读此类文体时一定要在通读全文的基础上弄清文章的结构。
2013年自主招生考试化学试卷

化学试卷(满分60分)可能用到的相对原子质量:O—16 Cl—35.5 K—39 Mn—55一、本大题包括10小题,每小题2分,共20分。
每小题4个备选答得分评卷人案中只有一个答案符合题意,请将选出的答案序号填在下列答题表内。
1.日常生活中的下列变化,其中一种变化与其余三种变化类型不同的是A.酒精挥发B.铁棒磨成针C.食品腐烂D.花香四溢2.下列不属于氢氧化钾的化学性质的是A.能和碳酸钠溶液反应B.可使酚酞溶液变红色C.能和二氧化碳反应D.能和硫酸反应3.食醋中含有醋酸,食醋除作调味剂外,生活中还有些妙用,下列使用食醋肯定不能达到目的的是A.除去菜刀上的铁锈B.除去水壶壁上的水垢C.清洗溅到皮肤上的碱液D.鉴别黄金饰品中是否含有铜4.聚四氟乙烯(C2F4)的耐热性和化学稳定性超过其他塑料,被称为“塑料王”。
其中F元素的化合价是—1价,则C元素的化合价与下列哪种物质中C元素的化合价相同A.CB.CH4C.COD.CO25.苯甲酸(C6H5COOH)是一种酸,可用于食品防腐,下列说法正确的是A.苯甲酸属无机物B.苯甲酸能使湿润的红色石蕊试纸变蓝C.苯甲酸能与氢氧化钠溶液反应生成盐和水D.在食品中大量添加苯甲酸以延长保质期6.下列变化中,溶液中原溶质的溶解度和溶质分量分数都发生变化的是A.常温下密闭容器中硝酸钾稀溶液升温10 ℃B.氯化铁溶液中加入少量生石灰C.硫酸锌溶液中加入少量铜粉D.稀释硫酸钠溶液7.下列除杂选用试剂正确的是A.用过量的O2除去CO2中COB.用过量的FeSO4溶液除去Zn中FeC.用过量的NaOH除去CaCl2溶液中HClD.用过量的HCl溶液除去Cu中CuO8.下列各组溶液,不用其他试剂就能鉴别出来的是A.K2SO4,稀HCl,NaNO3B.K2SO4,NaOH,稀HClC.Na2SO4,BaCl2,KNO3D.NaOH,NaCl,FeCl39.下列物质的转变,不能一步实现的是A.KCl → KNO3B. Fe(NO3)2→AgNO3C.SO3→ Na2SO4D.H2→Cu10.如图为甲、乙.两种固体物质在水中的溶解度曲线.下列说法错误的是A.将甲从甲、乙混和物中分离出来可以将它们加热水溶解后降温结晶B.在t1℃时,甲溶液和乙溶液的溶质质量分数相等C.在t2℃时,N点表示的溶液是甲物质的不饱和溶液D.在t1℃时,100g乙物质的饱和溶液中溶质的质量肯定小于25g答题表:二、本大题包括5小题,共34分。
