大学物理下18章习题参考答案中国石油大学
中国石油大学大学物理下册历年考题

2012—2013学年第一学期《大学物理(2-2)》期末试卷专业班级姓名学号开课系室物理与光电工程系考试日期 20XX年1月13日 14:30-16:301.请在试卷正面答题,反面及附页可作草稿纸;2.答题时请注意书写清楚,保持卷面整洁;3.本试卷共三道大题,满分100分;试卷本请勿撕开,否则作废;4. 本试卷正文共9页。
一、选择题(共10小题,每小题3分,共计30分)1、(本题3分) 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中,正确的是(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零. (B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零.(C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(D) 闭合面上各点场强均为零时,闭合面内一定处处无电荷. [ ] 2、(本题3分)两个完全相同的电容器C 1和C 2,串联后与电源连接.现将一各向同性均匀电介质板插入C 1中,如图所示,则(A) 电容器组总电容减小.(B) C 1上的电荷大于C 2上的电荷. (C) C 1上的电压高于C 2上的电压 . (D) 电容器组贮存的总能量增大.[ ] 3、(本题3分)如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理可知(A) 0d =⎰⋅Ll B,且环路上任意一点B = 0. (B) 0d =⎰⋅Ll B ,且环路上任意一点B ≠0. (C) 0d ≠⎰⋅L l B,且环路上任意一点B ≠0.(D) 0d ≠⎰⋅Ll B,且环路上任意一点B =常量. [ ]4、(本题3分)如图所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度(A) 方向垂直环形分路所在平面且指向纸内. (B) 方向垂直环形分路所在平面且指向纸外. (C) 方向在环形分路所在平面,且指向b . (D) 方向在环形分路所在平面内,且指向a .(E) 为零. [ ]5、(本题3分)如图,无限长载流直导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将(A) 向着长直导线平移. (B) 离开长直导线平移.(C) 转动. (D) 不动.[ ]6、(本题3分)自感为0.25 H 的线圈中,当电流在(1/16) s 内由2 A 均匀减小到零时,线圈中自感电动势的大小为(A) 7.8 ×10-3 V . (B) 3.1 ×10-2V .(C) 8.0 V . (D) 12.0 V . [ ] 7、(本题3分)两个通有电流的平面圆线圈相距不远,如果要使其互感系数近似为零,则应调整线圈的取向使(A) 两线圈平面都平行于两圆心连线. (B) 两线圈平面都垂直于两圆心连线.(C) 一个线圈平面平行于两圆心连线,另一个线圈平面垂直于两圆心连线.(D) 两线圈中电流方向相反. [ ] 8、(本题3分)对位移电流,有下述四种说法,请指出哪一种说法正确.(A) 位移电流是由变化的电场产生的. (B) 位移电流是由线性变化磁场产生的. (C) 位移电流的热效应服从焦耳─楞次定律.(D) 位移电流的磁效应不服从安培环路定理. [ ] 9、(本题3分)如果(1)锗用锑(五价元素)掺杂,(2)硅用铝(三价元素)掺杂,则分别获得的半导体属于下述类型(A) (1),(2)均为n 型半导体. (B) (1)为n 型半导体,(2)为p 型半导体. (C) (1)为p 型半导体,(2)为n 型半导体.(D) (1),(2)均为p 型半导体. [ ] 10、(本题3分)在激光器中利用光学谐振腔 (A) 可提高激光束的方向性,而不能提高激光束的单色性. (B) 可提高激光束的单色性,而不能提高激光束的方向性.I 1(C) 可同时提高激光束的方向性和单色性.(D) 既不能提高激光束的方向性也不能提高其单色性. [ ]二、简单计算与问答题(共6小题,每小题5分,共计30分) 1、(本题5分)图示为一半径为a 、不带电的导体球,球外有一内半径为b 、外半径为c 的同心导体球壳,球壳带正电荷+Q .今将内球与地连接,设无限远处为电势零点,大地电势为零,球壳离地很远,试求导体球上的感生电荷.2、(本题5分)边长为b 的立方盒子的六个面,分别平行于xOy 、yOz 和xOz 平面.盒子的一角在坐标原点处.在此区域有一静电场,场强为j i E300200+= .试求穿过各面的电通量.3、(本题5分)如图,均匀磁场B可绕通过环心O 与环面垂直的转轴旋转.当圆环以角速度受到的磁力矩.4、(本题5分) 均匀磁场B被限制在半径R =10 cm 的无限长圆柱空间内,方向垂直纸面向里.取一固定的等腰梯形回路abcd ,梯形所在平面的法向与圆柱空间的轴平行,位置如图所示.设磁感强度以d B /d t =1 T/s 匀速率增加,已知π=31θ,cm 6==Ob Oa ,求等腰梯形回路中感生电动势的大小和方向.5、(本题5分)(1) 试述德国物理学家海森伯提出的不确定关系.(2) 粒子(a)、(b)的波函数分别如图所示,试用不确定关系解释哪一粒子动量的不确定量较大.6、(本题5分)根据量子力学理论,氢原子中电子的运动状态可由那几个量子数来描述?试说明它们各自确定什么物理量?三.计算题(共5小题,共计40分)x (a)x(b)c1、(本题10分)一半径为R 的均匀带电导体球面,其表面总电量为Q .球面外部充满了相对电容率为r ε 的各向同性电介质. 试求:(1)球面内外D 和E 的 大小分布.(3) 导体球面的电势.(4) (3)整个空间的电场能量W e . 2、(本题10分)一无限长圆柱形铜导体(磁导率μ),半径为R ,通有均匀分布的电流I . 试求:(1)圆柱内外B 和H 的大小分布.(2) 今取一矩形平面S (长为1 m ,宽为2 R ),位置如右图中画斜线部分所示,试求通过该矩形平面磁感应强度B 的通量.3、(本题10分)如图所示,一根长为L 的金属细杆ab 处在磁感应强度为B 的均匀磁场当中,若金属杆绕竖直轴O 1O 2以角速度ω在水平面内旋转.轴O 1O 2在离细杆a 端L /5处.试求ab 两端间的电势差b a U U -.1 m4(本题5分)已知从铝金属逸出一个电子至少需要A = 4.2 eV 的能量,若用可见光(400 nm~760 nm )投射到铝的表面,能否产生光电效应?为什么?(普朗克常量h =6.63×10-34 J ·s ,基本电荷e =1.60×10-19 C)5、(本题5分)Ψ =c x ( L – x ) ,其中c 是待定常数,试求在 0 ~L / 3率.b2012—2013学年第一学期 《大学物理(2-2)》期末试卷A 卷答案一、选择题1、C2、D3、B4、E5、A6、C7、C8、A9、B 10、C 二、简答题1、解:内球接地时,其上将出现负的感生电荷,设为-q .而球壳内表面将出现正的感生电荷+q ,这可用高斯定理证明.球壳外表面的电荷成为Q -q (电荷守恒定律).这些电荷在球心处产生的电势应等于零,即0000444q q Q qa b c e e e --++=πππ 3分 1111q Q abc c 骣÷ç-+=÷ç÷ç桫 解出 abq Q ab bc ac=+- 2分 2、解:由题意知E x =200 N/C , E y =300 N/C ,E z =0平行于xOy 平面的两个面的电场强度通量 01=±==⋅S E S E z eΦ 1分平行于yOz 平面的两个面的电场强度通量2002±=±==⋅S E S E x eΦ b 2N ·m 2/C 2分“+”,“-”分别对应于右侧和左侧平面的电场强度通量 平行于xOz 平面的两个面的电场强度通量3003±=±==⋅S E S E y eΦ b 2 N ·m 2/C 2分“+”,“-”分别对应于上和下平面的电场强度通量. 3、解:带电圆环旋转等效成的圆形电流强度为:2π2πq R I R Tλλωω=== 1分圆形电流的磁矩为:23ππp I S R R R m λωλω=== 方向垂直于纸面向外 2分 磁力矩为:3M P B R B m λω=⨯=π 方向在图面中竖直向上 2分4、解:大小: =⎪d Φ /d t ⎪= S d B / d t1分= S d B / d t =t B Oa R d /d )sin 2121(22θθ⋅- 2分=3.68mV 1分 方向:沿adcb 绕向. 1分c5、答:(1)不确定关系是指微观粒子的位置坐标和动量不能同时准确确定,两者不确定量之间的关系满足:x p x ∆∆≥2hπ。
智慧树答案物理化学(下)(中国石油大学(华东))知到课后答案章节测试2022年

第一章1.当一定的直流电通过一含有金属离子的电解质溶液时,在阴极上析出金属的量正比于答案:通过的电量2.下列哪个方法不能用来测量离子的迁移数答案:电导法3.对相同温度下无限稀释的硫酸、盐酸和硝酸中的氢离子而言,下列说法不正确的是答案:迁移数均相同4.在用对消法测量电池的电动势的实验中,必须用到答案:韦斯登电池5.因正、负离子迁移数不同引起的两溶液界面处的电势差称为答案:液接电势6.pH计是利用哪种电学性质测定水溶液中氢离子的活度?答案:电动势7.“若要比较各种电解质的导电能力的大小,用电解质的电导率值大小进行比较是合理的方法。
” 这种说法对吗?答案:错8.“在实验中测定溶液的电导实际上是测量溶液的电流强度。
”这种说法对吗?答案:错9.“在饱和 AgCl 溶液中加入 NaNO3,AgCl 的饱和浓度变大。
”这种说法对吗?答案:对10.“无限稀电解质溶液的摩尔电导率可以看成是正、负离子无限稀摩尔电导率之和,这一规律适用于强电解质,也用于弱电解质” ,这种说法对吗?答案:对第二章1.下列各系统中属于独立粒子系统的是答案:理想气体混合物2.系统的微观性质和宏观性质是通过_______联系起来的答案:统计力学3.对于一个粒子数N、体积V和内能U确定的系统,其微观状态数最大的那套分布就是最概然分布,得出这一结论的依据是________答案:等概率假定4.对三原子分子H2O(g)和CO2(g),下面关于它们各种运动形式自由度的描述正确的是________答案:平动自由度相同,转动和振动自由度不同5.三个可别粒子分布于同一能级的两个不同量子态上时,下列说法中正确的是____答案:分布方式有4种6.对热力学性质(U、V、N)确定的系统,下面描述中不对的是__________答案:体系中粒子在各能级上的分布数一定7.下面的说法中,错误的是___________答案:最概然分布随系统中粒子数的增多而出现的几率增大8.某双原子分子AB取振动基态能量为零,在温度T时的振动配分函数为2.0,则粒子分布在基态上的分布分数N0/N应为_______答案:0.59.从统计热力学的观点看,对理想气体封闭系统在非体积功为零、体积不变的情况下吸热时体系中粒子________答案:能级不变,但各能级上的粒子分布数发生变化10.经典粒子的零点能规定不同时,必定影响________答案:配分函数第三章1.关于反应速率,表达不正确的是答案:可为正值也可为负值2.某反应进行时,反应物浓度与时间成线性关系,则此反应的半衰期与反应物初始浓度答案:成正比3.某反应的半衰期与其初始浓度成正比,则该反应是答案:零级反应4.化学反应速率系数的Arrhenius关系式能成立的范围是答案:某些反应在一定温度范围内5.下面不属于平行反应特点的是答案:各产物的百分数与时间有关6.稳态近似法常用于处理下列哪种动力学问题答案:连串反应7.反应级数可以是正整数、分数或负数。
中国石油大学(华东)__大学物理课后习题答案

ax
az 0
d2 x r 2 cost 2 dt
ay
d2 y r 2 s i n t 2 dt
7-2
所以
a ax i a y j az k r 2 costi r 2 sin tj
(3) 由式(1) 、 (2) 、 (3)得运动方程的矢量式 r xi yj zk r costi r sin tj ctk 1-8 质点沿 x 轴运动,已知 v 8 2t 2 ,当 t 8 s 时,质点在原点左边 52m 处(向右为 x 轴正向) .试求: (1)质点的加速度和运动学方程; (2)初速度和初位置; (3)分析质点的 运动性质. [解] (1) 质点的加速度 a d v /d t 4t 又 v d x /d t 所以 d x vdt 对上式两边积分,并考虑到初始条件得
vx dx r sin t dt
dy r cost dt dz vz c dt vy
所以
v vx i v y j vz k r sin ti r costj ck
由式(1) 、 (2) 、 (3)两边对时间求二阶导数,可得质点的加速度
所以, t 时刻齿尖 P 的加速度为
2 a a t2 an b2
(v0 bt) 4 R2
1-17 火车在曲率半径 R=400m 的圆弧轨道上行驶. 已知火车的切向加速度 a t 0.2 m s 2 , 求火车的瞬时速率为 10 m s 时的法向加速度和加速度. [解] 火车的法向加速度 火车的总加速度
y x2
7-4
对时间 t 求导数
vy
dy dx 2x 2 xvx dt dt
(1)
大学物理第18章答案

《大学物理》参考答案第18章 原子核物理与粒子物理简介18-1 如果原子核半径按公式11531.210R A -=⨯确定(式中A 为质量数),试计算核物质密度以及核物质的单位体积内的核子数.解:原子核的体积 334R V π=,1u =1.660 5402×10-27kg 所以核物质密度为 3034334r u R Au V M ππρ===31527)102.1(4106605402.13--⨯⨯⨯⨯=π=2.29×1017kg ·m -3 单位体积内的核子数3043r u N πρ===1.38×104418-2 计算2个2H 原子核结合成1个4He 原子核时释放的能量(以MeV 为单位). 解: m D =2.014102u; m He =4.002603u .质量亏损:∆m=2⨯m D -m He =0.025601 0u释放的能量: 2ΔΔmc E ==0.025601 0⨯931.441=23.85 MeV18-3 2个氢原子结合成氢分子时释放的能量为4.73eV ,试计算由此发生的质量亏损.解: ∆mc 2=4.73eV质量亏损 5.9311073.46-⨯=∆m = 5.07×10-9u18-4 11p 和10n 的质量分别为1.007276u 和1.008665u ,试计算126C 中每个核子的平均结合能(1u =931.5MeV 2).解:质量亏损 ∆m =(6×1.007276u+6×1.008665u)-12.00000u= 0.095646u平均结合能 125.93100956462⨯=∆=A mc E = 7.42452075MeV18-5 226Ra 和222Rn 原子质量分别为226.02536u 和222.01753u ,4He 原子质量为4.002603u ,试求226Ra 衰变为222Rn 时的衰变能.解:质量亏损 ∆m =226.02536u –(222.01753u+4.002603u)= 0.005227u衰变能 Q=0.005227931.5=4.8689505MeV18-6 在铍(94Be)核内每个核子的平均结合能等于6.45MeV ,而在42He 内每个核子的平均结合能为7.06Mev ,要把94Be 分裂为2个α粒子和1个中子时,必须耗费多少能量?解: 94B e →242He+n∆E=9×6.45MeV -8×7.06Mev =1.57MeV18-7 32P 的半衰期是14.3d ,试计算它的衰变常数λ和平均寿命,1μg 纯32P 的放射性活度是多少贝可?解:衰变常数: λλ693.02ln 2/1==T d3.14693.0=λ= 0.048d -1平均寿命: λτ1==20.6d 放射性活度: 23610022.632101⨯⨯⨯=-N =1.88×1016161088.16060243.14693.0693.0⨯⨯⨯⨯⨯===N T N I λ=1.05×1010Bq18-8 131I 的半衰期是8.04d ,问在某月12日上午9:00测量时131I 的放射性活度为5.6×108Bq ,到同月30日下午3:00,放射性活度还有多少?解:I 0=5.6×108Bq t T t eI e I t I 693.000)(--==λ 25.1804.8693.08106.5)(⨯-⨯⨯=e t I =1.16×108Bq18-9 131I 的半衰期是193h ,试计算它的衰变常数和平均寿命.今有一个放射强度为108Bq 的放射源,只有131I 具有放射性,问其中的131I 的质量是多少?解: λλ693.02ln 2/1==T 2/1693.0T =λ=9.976×10-7s -1 λτ1==278.5h A AN m m N =, λN t I =)( 237831002.610976.91010131⨯⨯⨯⨯⨯==--A A N I m m λ=2.18×10-11kg18-10 利用131I 的溶液作甲状腺扫描,在溶液出厂时,只需注射0.5ml 就够了(131I 的半衰期是8.04d),如溶液出厂后贮存了11d ,作同样的扫描需要多少毫升的溶液?解: t T e I t I 693.00)(-=要求 131I 的数量相同 V 0I 0=VI1104.8693.0693.00005.0⨯⨯===e e V V II V t T 0.65ml18-11 24Na 的半衰期为14.8h ,现需要100μCi 的24Na ,从产地到使用处需用6h ,问应从生产地取多少μCi 的24Na ? 解:t T e I t I 693.00)(-=68.14693.0693.00100⨯⨯==eIe I t T = 132.4μCi18-12 32P 的半衰期为14.3d ,问1μg 32P 在1h 中放出多少个β-粒子? 解:t Te I t I 693.00)(-= t T e N N 693.00-= )1()1(693.0693.000t T A At T e N m m e N N N N ---=-=-=∆ )1(10022.610321011243.14693.02339⨯⨯----⨯⨯⨯⨯⨯=∆e N =3.75×101318-13 一个含3H 的样品,其放射性强度为3.7×102Bq ,问样品中3H 的含量有多少克?解:3H 半衰期为12.33y2/1693.0T =λ60602436533.12693.0⨯⨯⨯⨯==1.78×10-9s -1 A AN m m N =, λN t I =)( 2392310022.61078.1107.31032⨯⨯⨯⨯⨯⨯==--A A N I m m λ=1.1×10-14kg=1.1×10-11g18-14 已知U 3O 8中铀为放射性核素,今有5.0g 的U 3O 8,试求其放射性活度. 解:238U 半衰期为4.47×109y2/1693.0T =λ 23910022.623856060243651047.4693.0693.0⨯⨯⨯⨯⨯⨯⨯=⨯==A A N M m T N I λ I=6.21×104Bq18-15 放射性活度为3.7×109Bq 的放射性核素32P ,在制剂后10d 、20d 、30d 的放射性活度各是多少?解:32P 半衰期为14.26d , I 0 =3.7×109Bqt T eI t I 693.00)(-= 10d: 1026.14693.09107.3⨯-⨯⨯=e I = 2.28×109Bq20d: 2026.14693.09107.3⨯-⨯⨯=e I =1.40×109Bq30d: 3026.14693.09107.3⨯-⨯⨯=e I = 0.86×109Bq18-16 样品最初放射性为每分钟800次衰变,24min 后,放射性为每分钟640次衰变,求衰变常数和半衰期. 解:t T e I t I 693.00)(-=24693.0800640⨯-=T e , 0.2231=24693.0⨯T2/1693.0T =λ=1.55×10-4s -1T 1/2= 74.565min。
大学物理下17章习题参考答案中国石油大学

17章习题参考答案17-3 如图所示,通过回路的磁场与线圈平面垂直且指出纸里,磁通量按如下规律变化()Wb 1017632-⨯++=Φt t式中t 的单位为s 。
问s 0.2=t 时,回路中感应电动势的大小是多少? R 上的电流方向如何?[解] ()310712d d -⨯+=Φ-=t tε ()23101.3107212--⨯=⨯+⨯=V根据楞次定律,R 上的电流从左向右。
17-4如图所示,两个半径分别为R 和r 的同轴圆形线圈,相距x ,且,R >>r ,x >>R 。
若大线圈有电流I 而小线圈沿x 轴方向以速度v 运动。
试求x =NR 时(N >0),小线圈中产生的感应电动势的大小。
[解] 因R>>r 可将通过小线圈的B 视为相等,等于在轴线上的B()2322202xR IR B +=μ由于x >>R ,有 3202x IR B μ=所以 t xxIS R t d d 32d d 420μ=Φ-=ε 而v t x=d d 因此 x =NR 时, 242023R N v r I πμ=ε17-5 如图所示,半径为R 的导体圆盘,它的轴线与外磁场平行,并以角速度ω转动(称为法拉第发电机)。
求盘边缘与中心之间的电势差,何处电势高?当R =0.15m ,B =0.60T ,rad 30=ω时,U 等于多大?[解] 圆盘可看成无数由中心向外的导线构成的,每个导线切割磁力线运动且并联,因此有2021d d )(BR r rB R L ωω==⋅⨯=⎰⎰l B v 感ε因电动势大于零,且积分方向由圆心至边缘,所以边缘处电位高(或由右手定则判断)代入数据得201506030212...=⨯⨯⨯==εU V 17-6 一长直导线载有电流强度I =5.0A 的直流电,在近旁有一与它共面的矩形线圈,线圈长l =20cm ,宽a =10cm ,共1000匝,如图所示。
石油大学(北京)18春《大学物理(含模拟实验)》第二阶段在线作业100分答案

中国石油大学(北京)15秋《大学物理(含模拟实验)》第二阶段在线作业单选题(共27道题)3.题目见图片•A、.•B、.•C、.•D、.我的答案:D 此题得分:2.5分4.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分5.题目见图片•A、.•B、.•C、.•D、.我的答案:D 此题得分:2.5分6.题目见图片•A、.•B、.•C、.•D、.我的答案:B 此题得分:2.5分7.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分8.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分9.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分10.题目见图片•B、.•C、.•D、.我的答案:D 此题得分:2.5分11.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分12.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分13.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分14.题目见图片•A、.•B、.•C、.•D、.我的答案:B 此题得分:2.5分15.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分16.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分17.题目见图片•A、.•B、.•D、.我的答案:B 此题得分:2.5分18.题目见图片•A、.•B、.•C、.•D、.•E、.•F、.我的答案:D 此题得分:2.5分19.题目见图片•A、.•B、.•C、.•D、.•E、.我的答案:C 此题得分:2.5分20.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分21.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分22.题目见图片•A、.•B、.•C、.•D、.我的答案:A 此题得分:2.5分23.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分24.题目见图片•A、.•C、.•D、.我的答案:C 此题得分:2.5分25.题目见图片•A、.•B、.•C、.•D、.我的答案:B 此题得分:2.5分26.题目见图片•A、.•B、.•C、.•D、.我的答案:B 此题得分:2.5分27.题目见图片•A、.•B、.•C、.•D、.我的答案:C 此题得分:2.5分判断题(共13道题)收起28.题目见图片电势高的地方,场强一定大•正确•错误我的答案:错误此题得分:2.5分29.题目见图片电势相等处,场强一定相等•正确•错误我的答案:错误此题得分:2.5分30.题目见图片已知某一点的电势,可求出该点的场强•正确•错误我的答案:错误此题得分:2.5分31.题目见图片已知某一点的电场,可求出该点的电势•正确•错误我的答案:错误此题得分:2.5分32.题目见图片刚体的转动惯量取决于质量、质量分布和轴的位置•正确•错误我的答案:正确此题得分:2.5分33.题目见图片质点和刚体相互作用系统角动量守恒的条件是系统受到的合外力为零•正确•错误我的答案:错误此题得分:2.5分34.题目见图片刚体的势能可以认为是其质量集中到质心上的质点的势能•正确•错误我的答案:正确此题得分:2.5分35.题目见图片两共轴刚体系统所受合外力矩为零,系统角动量守恒•正确•错误我的答案:正确此题得分:2.5分36.题目见图片包含刚体在内的质点系的机械能守恒条件是系统中只有保守内力做功•正确•错误我的答案:正确此题得分:2.5分37.题目见图片质点与刚体相互作用系统动量守恒的条件与角动量守恒的条件等价•正确•错误我的答案:错误此题得分:2.5分38.题目见图片质点与刚体相互作用系统机械能守恒时,该系统角动量也守恒•正确•错误我的答案:错误此题得分:2.5分39.题目见图片库仑定律的适用于任意形状的带电体之间•正确•错误我的答案:错误此题得分:2.5分40.题目见图片场强为零的地方,电势不一定为零•正确•错误我的答案:正确此题得分:2.5分。
大学物理习题答案第十八章

[习题解答]18-1 一个来自衰变的能量为4.7 MeV的α粒子,与金核发生正碰,求此α粒子最接近金核中心处的距离为多大?解 在α粒子与金核()发生正碰的情况下,设在相距甚远时a粒子的动能为E k ,当两者相距r时,α粒子的瞬时速度变为零。
所以,a粒子将自身的动能E k全部用于克服它与金核之间的斥力而作功,根据动能定理,斥力对质点所作的功等于质点动能的增量,故有,其中A为斥力对α粒子所作的功。
同时,根据势能的规律,保守力(在此是斥力)所作的功等于势能增量的负值,即.由以上两式,得,所以.18-2 试计算核物质的密度。
解 解答见上面[例题分析]中的例题18-1 。
18-3 在、和中各有多少质子和中子?解:Z = 7, N = 6;:Z = 8, N = 9 ;:Z = 30, N = 34 。
18-6 如果原子核的自旋量子数为j,那么该原子核的核磁矩的大小如何表示?此核处于磁感应强度为B的磁场中,核磁矩与磁场的相互作用能为多大?分裂后的能级间距为多大?解 核磁矩的大小为.核磁矩与外磁场的相互作用能为, .分裂后的能级间距为.18-13 计算原子核的核子平均结合能。
已知的原子质量为232.03821 u,氢原子M H和中子n的质量分别为1.007830 u和1.008665 u。
解 核的质量亏损为,其中, , , , 。
将这些数据代入上式可算的质量亏损,为.核子的平均结合能为.18-14 已知氢原子M H和中子n的质量分别为1.007830 u和1.008665 u,的原子质量为12.000000 u,计算核的核子平均结合能。
解 核的质量亏损为.核子的平均结合能为.18-16 计算在聚变反应中所释放出来的能量, 分别用J和MeV为单位表示结果。
已知氘原子的质量为2.01410 u,氦原子的质量为4.00260 u。
解 已知氘原子和氦原子的质量分别为2.01410 u和4.00260 u,根据题意所要求的聚变反应,可以得出氦核的质量亏损为.释放的能量为,或者.18-17 试计算1 mol的氘气(双原子分子)在上题的聚变反应中,所释放出来的总能量是多少?解 释放出来的总能量为..18-18 在核和核内核子的平均结合能分别为6.45 MeV和7.07 MeV,要把核分裂为两个 粒子和一个中子,必须耗费多大能量?解 反应过程可以写为.若将核分散为9个核子,外界需提供的能量为,将其中8个核子结合成2个核所释放出来的能量为.所以,要把核分裂为两个a粒子和一个中子外界必须耗费的能量为.18-20 已知放射性碘()的半衰期为8.0 d,问:(1)衰变常量为多大?(2) 1 mCi的放射性活度需要多少质量的碘同位素?解(1)衰变常量.(2)因为,所以,要达到3.7⨯107 Bq的放射性活度所需母核的数目为个.1 mol碘同位素的质量为0.131 kg,其中包含的核的数目等于N A = 6.022⨯1023,于是需要碘同位素的质量为.18-21 已知镭的半衰期是1600 a,求衰变常量和镭核的平均寿命。
大学物理18章重点习题解答

18.3.8 设想地球上有一观察者测得一宇宙飞船以0.6 测得速率向东飞行,5.0s后该飞船与一个以0.8c的速率 向西飞行的彗星相碰撞。试问: 1、飞船中的人测得彗星将以多大的速率向它运动? 2、从飞船中的钟来看,还有多少时间容许它离开航线, 以避免与彗星碰撞? /
解:1、如右图,取地球为S系,飞 船A为S/系,则S/系相对于S系的速 度u=0.6c,彗星B相对S系的速度 vx=-0.8c,则B相对S/系(A)的速 度为
l 0.6ct 3c
飞船上测得地以0.6c朝飞船运动,根据长度收缩效应,
2 v l' l 1 2 3c 1 0.62 2.4c c
飞船上测得两事件的时间间隔为 即:所剩逃避时间为 4s
l t 4s 0.6c
18.3.10半人马座 星是距离太阳系最近的恒星,它 16 4 . 3 10 m ,设有一宇宙飞船自地球往返于 距离地球 半人马座 星之间,若宇宙飞船相对地球的速度为 0.999c,按地球上的时钟计算,飞船往返一次需要用 多少时间?如以飞船上的时钟计算,所需时间又为多 少?
解:按地球上的时钟计算,飞船往返一次所需时间为
2s 2 4.3 1016 t 9.1年 8 v 0.999 3 10 365 24 3600
若用飞船上的钟测量,飞船往返所需时间为
1t 1 0.9992 9.1 0.4年
c 情况下,粒子的动量等于非相 18.1.5、在速度υ= 3 对论动量的两倍;在速度υ= 2 c 情况下,粒子的 动能等于它静止能量。
解:1、粒子的动量为
3 2
p
m0 v
2
c2
1
m0 v 2m0 v
大学物理(2-1)(山东联盟)智慧树知到课后章节答案2023年下中国石油大学(华东)

大学物理(2-1)(山东联盟)智慧树知到课后章节答案2023年下中国石油大学(华东)中国石油大学(华东)绪论单元测试1.大学物理是面向理工科大学生的一门重要的必修基础课,该课程讲授的物理学知识、思想和方法是构成学生科学素养的重要组成部分.答案:对第一章测试1.质点由一点运动到另外一点,则下列说法正确的是答案:位移是唯一的2.以下关于加速度的说法中错误的是答案:物体速度大,加速度一定大3.质点沿半径为R的圆周作匀速率运动,每T秒转一圈。
在2T时间间隔中,其平均速度大小与平均速率大小分别为答案:0 ,2πR/T4.气球正在上升,气球下系有一重物,当气球上升到离地面100m高处,系绳突然断裂,重物下落,这重物下落到地面的运动与另一个物体从100m 高处自由落到地面的运动相比,下列哪一个结论是正确的答案:下落的位移相同5.某人骑自行车以速率v向正西方向行驶,遇到由北向南刮的风(设风速大小也是v),则他感到风是从答案:西北方向吹来6.电子很小可以视为质点,而太阳很大不能视为质点.答案:错7.质点做匀加速运动,其轨迹一定是直线.答案:错8.物体具有恒定的速度,但仍有变化的速率是不可能的.答案:对9.质点作匀速圆周运动时速度一定不变.答案:错10.同一物体的运动,如果选取的参考系不同,对它的运动描述也不同.答案:对第二章测试1.在下列关于力与运动关系的叙述中,正确的是答案:若质点从静止开始,所受合力恒定,则一定作匀加速直线运动2.质量为m的物体自空中落下,它除受重力外,还受到一个与速度平方成正比的阻力的作用,比例系数为k,k为正值常量.该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是答案:3.体重、身高相同的甲乙两人,分别用双手握住跨过无摩擦轻滑轮的绳子各一端.他们从同一高度由初速为零向上爬,经过一定时间,甲相对绳子的速率是乙相对绳子速率的两倍,则到达顶点的情况是答案:同时到达4.功的概念有以下几种说法:1)保守力作正功时,系统内相应的势能增加.2)质点运动经一闭合路径,保守力对质点做的功为零.3)作用力与反作用力大小相等,方向相反,所以两者所做功的代数和必为零.上列说法中答案:2)正确5.在下列关于动量的表述中,不正确的是答案:内力对系统内各质点的动量没有影响6.物体只有作匀速直线运动和静止时才有惯性.答案:错7.摩擦力总和物体运动的方向相反.答案:错8.质量为m的质点以速度v沿一直线运动,则它对空间任一点的角动量都为零.答案:错9.牛顿运动定律在任何参考系中都成立.答案:错10.一个不受外力作用的系统,它的动量和机械能都守恒.答案:错第三章测试1.下面几种运动属于定轴转动的是答案:电风扇叶片的运动2.刚体绕定轴作匀变速转动时,刚体上距轴为r的任一点的答案:切向加速度的大小恒定,法向加速度的大小变化3.刚体角动量守恒的充分而必要的条件是答案:刚体所受合外力矩为零4.有两个力作用在一个有固定转轴的刚体上(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中答案:(1) 、(2)正确,(3) 、(4) 错误5.一个人站在有光滑固定转轴的转动平台上,双臂水平地拿着二哑铃.在该人把此二哑铃水平收缩到胸前的过程中,人、哑铃与转动平台组成的系统的答案:机械能不守恒,角动量守恒6.刚体的转动惯量只与转轴和刚体总质量有关.答案:错7.一均匀细直棒,可绕通过其一端的光滑固定轴在竖直平面内转动.使棒从水平位置自由下摆,棒作匀角加速转动.答案:错8.刚体定轴转动时所有质点的角速度和角加速度都相同.答案:对9.刚体作定轴转动时,刚体角动量守恒的条件是刚体所受的合外力等于零.答案:错10.一个质量为m的小虫,在有光滑竖直固定中心轴的水平圆盘边缘上,此时圆盘转动的角速度为ω.若小虫沿着半径向圆盘中心爬行,则圆盘的角速度变大.答案:对第四章测试1.有下列几种说法:(1)所有惯性系对物理基本规律都是等价的;(2)在真空中,光的速度与光的频率、光源的运动状态无关;(3)在任何惯性系中,光在真空中沿任何方向的传播速率都相同.其中说法是正确的是答案:全部说法都是正确的2.在狭义相对论中,下列说法中正确的是:(1)一切运动物体相对于观察者的速度都不能大于真空中的光速;(2)质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的;(3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的;(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些.答案:(1),(2),(4)3.宇宙飞船相对于地面以速度0.8c直线飞行,一光脉冲从船尾传到船头.飞船的静止长度是100m,则地球观察者测出光脉冲从船尾到船头两个事件的空间间隔为答案:300m4.在某地发生两件事,静止位于该地的甲测得时间间隔为4 s,若相对于甲作匀速直线运动的乙测得时间间隔为5 s,则乙相对于甲的运动速度是(c表示真空中光速)答案:(3/5)c5.粒子在加速器中被加速,当其质量为静止质量的3倍时,其动能为静止能量的答案:2倍6.经典力学中的所有基本定律,如动量守恒定律,角动量守恒定律,机械能守恒定律都具有伽利略变换不变性.答案:对7.狭义相对论的两条基本原理是狭义相对性原理和光速不变原理.答案:对8.我们把与物体保持静止的参考系所测得的长度称为物体的固有长度.答案:对9.光子的静止质量为零.答案:对10.在某个惯性系中有两个同时同地发生的事件,在对该系有相对运动的其他惯性系中,这两个事件不一定是同时同地发生的.答案:错第五章测试1.一质量为m的物体挂在劲度系数为k的轻弹簧下面,振动角频率为f ,若把此弹簧分割成四等份,将物体m挂在分割后的一根弹簧上,则振动角频率是答案:2f2.一质点作简谐振动,周期为T. 质点由平衡位置向x轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为答案:T/123.一弹簧振子,当把它水平放置时,它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上,试判断下面哪种情况是正确的答案:两种情况都可作简谐振动4.一弹簧振子作简谐振动,总能量为E,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量变为答案:4E5.一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的答案:3/46.质点作简谐振动时,从平衡位置运动到最远点需时1/4周期,因此走过该距离的一半需时1/8周期.答案:错7.一个作简谐振动的物体,其位移与加速度的相位始终相差π.答案:对8.一个作简谐振动的物体处于平衡位置处时具有最大的速度和最大的加速度.答案:错9.简谐运动的动能和势能都随时间作周期性的变化,且变化频率与位移变化频率相同.答案:错10.两个相同的弹簧挂着质量不同的物体,当它们以相同的振幅作简谐振动时,振动总能量相同.对第六章测试1.在相同的时间内,某种波长的单色光在空气中和在玻璃中答案:传播的路程不相等,走过的光程相等2.用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则答案:不产生干涉条纹3.在双缝干涉实验中,两条缝的宽度原来是相等的,若其中一缝的宽度略变窄(缝中心位置不变),则答案:干涉条纹的间距不变4.在光栅衍射实验中,与缺级级数有关的量为光栅常数5.一束白光垂直照射在一光栅上,在形成的同一级光栅光谱中,偏离中央明纹最远的是答案:红光6.获得相干光源只能用波阵面分割和振幅分割这两种方法来实现.答案:错7.发光的本质是原子、分子等从具有较高能级的激发态到较低能级的激发态跃迁过程中释放能量的一种形式.答案:对8.光波的相干叠加服从波的叠加原理,不相干叠加不服从波的叠加原理.答案:错9.光程是将光在不同介质中走过的实际路程折合成在真空中走过的路程.答案:错10.双折射现象是光从光疏介质进入光密介质时发生的一种现象.答案:错第七章测试1.水蒸气分解成同温度的氢气和氧气,内能增加了答案:25%2.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们答案:温度相同,但氦气的压强大于氮气的压强3.关于温度的意义,有下列几种说法:(1)气体的温度是分子平均平动动能的量度.(2)气体的温度是大量气体分子热运动的集体表现,具有统计意义.(3)温度的高低反映物质内部分子热运动剧烈程度的不同.(4)从微观上看,气体的温度表示每个气体分子的冷热程度.这些说法中正确的是答案:(1)、(2)、(3)4.下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线答案:5.玻尔兹曼分布律表明:在某一温度的平衡态,(1)分布在某一区间(坐标区间和速度区间)的分子数,与该区间粒子的能量成正比.(2)在同样大小的各区间(坐标区间和速度区间)中,能量较大的分子数较少;能量较小的分子数较多.(3)在大小相等的各区间(坐标区间和速度区间)中比较,分子总是处于低能态的概率大些.(4)分布在某一坐标区间内、具有各种速度的分子总数只与坐标区间的间隔成正比,与粒子能量无关.以上四种说法中答案:只有(2)、(3)是正确的6.只有对大量分子的集体,温度的微观意义才成立.答案:对7.物体的熔解、凝固、蒸发等现象都属于热现象.答案:对8.一切互为热平衡的热力学系统不一定具有相同的温度.答案:错9.表征系统热平衡的宏观性质的物理量为压强.答案:错10.每个分子的质量、速度和能量属于微观量.答案:对第八章测试1.关于可逆过程和不可逆过程的判断:(1)可逆热力学过程一定是准静态过程.(2)准静态过程一定是可逆过程.(3)不可逆过程就是不能向相反方向进行的过程.(4)凡有摩擦的过程,一定是不可逆过程.以上四种判断,其中正确的是答案:(1)、(4)2.质量一定的理想气体,从相同状态出发,分别经历等温过程、等压过程和绝热过程,使其体积增加一倍,那么气体温度的改变(绝对值)在答案:等压过程中最大,等温过程中最小3.两个相同的容器,容积固定不变,一个盛有氨气,另一个盛有氢气(看成刚性分子的理想气体),它们的压强和温度都相等,现将5J的热量传给氢气,使氢气温度升高,如果使氨气也升高同样的温度,则应向氨气传递的热量是答案:3J4.1mol的单原子分子理想气体从状态A变为状态B,如果不知是什么气体,变化过程也不知道,但A、B两态的压强、体积和温度都知道,则可求出答案:气体内能的变化5.一定量的某种理想气体起始温度为T,体积为V,该气体在下面循环过程中经过三个平衡过程:(1)绝热膨胀到体积为2V,(2)等体变化使温度恢复为T,(3)等温压缩到原来体积V,则此整个循环过程中答案:气体向外界放热6.用旋转的叶片使绝热容器中的水温上升(焦耳热功当量实验),这一过程是可逆的.答案:错7.不规则地搅拌盛于绝热容器中的液体,液体温度在升高,若将液体看作系统,则外界对系统作功,系统的内能增加.答案:对8.热力学系统的状态发生变化时,其内能的改变量只决定于初末态的温度而与过程无关.答案:对9.不作任何热交换也可以使系统温度发生变化.答案:对10.对物体加热也可以不致升高物体的温度.答案:对。
中国石油大学大学物理实验课后习题_答案

Gb 第一章误差估算与数据处理方法课后习题答案1.指出下列各量有效数字的位数。
(1)kV 有效位数:4(2)mm 有效位数:3 (3)kg 有效位数:5(4)自然数有效位数:无限位2.判断下列写法是否正确,并加以改正。
(1)A mA错,0.0350A 有效位数为3位,而35mA 有效位数为2位,二者物理意义不同,不可等同,应改为A mA 。
(2)kg错,测量结果(即最佳估计值)有效数字的最后一位应与不确定度的末位对齐。
测量结果有效数字取位时,应遵循“四舍六入五凑偶”的原则;而且,不确定度应记为“”的形式。
故应将上式改成kg 。
(3)km 错,当采用科学计数法表示测量结果时,最佳估计值与不确定度应同时用科学计数法表示,并且10的指数应取一致,还要保证最佳估计值的最后一位与不确定度的末位对齐。
因此,上式应改为。
(4)A正确。
3.试按有效数字修约规则,将下列各数据保留三位有效数字。
3.8547,2.3429,1.5451,3.8750,5.4349,7.6850,3.6612,6.26383.85 2.34 1.54 3.88 5.43 7.68 3.66 6.26 4.按有效数字的确定规则,计算下列各式。
(1)000.1=U 000123.0=L 010.10=m 40350.0=I 35=0350.0=I 11050.3⨯=()3.0270.53+=m 270.53=m ±()3.03.53±=m ()2000103.274±⨯=h ()km h 4102.03.27⨯±=()004.0325.4±=x ?6386.08.7537.343=++解:原式 (2)解:原式 (3)解:原式(4)解:原式5.分别写出下列各式的不确定度传播公式。
(1)(K 为常数)解:(a )绝对不确定度:(b )相对不确定度:其中,、分别表示A 、B 量的合成不确定度。
中国石油大学《大学物理(一)》实验报告

中国石油大学(华东)现代远程教育实验报告课程名称:大学物理(一)实验名称:速度、加速度的测定和牛顿运动定律的验证实验形式:在线模拟+现场实践提交形式:在线提交实验报告学生姓名:学号:年级专业层次:网络秋机电一体化学习中心:石化学习中心提交时间:2021 年6月14 日一、实验目的1.了解气垫导轨的构造和性能,熟悉气垫导轨的调节和使用方法。
2.了解光电计时系统的基本工作原理,学会用光电计时系统测量短暂时间的方法。
3.掌握在气垫导轨上测定速度、加速度的原理和方法。
4.从实验上验证F=ma的关系式,加深对牛顿第二定律的理解。
5.掌握验证物理规律的基本实验方法。
二、实验原理1.速度的测量一个作直线运动的物体,如果在t~t+Δt时间内通过的位移为Δx(x~x+Δx),则该物体在Δt时间内的平均速度为,Δt越小,平均速度就越接近于t时刻的实际速度。
当Δt→0时,平均速度的极限值就是t时刻(或x位置)的瞬时速度(1)实际测量中,计时装置不可能记下Δt→0的时间来,因而直接用式(1)测量某点的速度就难以实现。
但在一定误差范围内,只要取很小的位移Δx,测量对应时间间隔Δt,就可以用平均速度近似代替t时刻到达x点的瞬时速度。
本实验中取Δx为定值(约10mm),用光电计时系统测出通过Δx所需的极短时间Δt,较好地解决了瞬时速度的测量问题。
2.加速度的测量在气垫导轨上相距一定距离S的两个位置处各放置一个光电门,分别测出滑块经过这两个位置时的速度v1和v2。
对于匀加速直线运动问题,通过加速度、速度、位移及运动时间之间的关系,就可以实现加速度a的测量。
(1)由测量加速度在气垫导轨上滑块运动经过相隔一定距离的两个光电门时的速度分别为v1和v2,经过两个光电门之间的时间为t21,则加速度a为(2)根据式(2)即可计算出滑块的加速度。
(2)由测量加速度设v1和v2为滑块经过两个光电门的速度,S是两个光电门之间距离,则加速度a为(3)根据式(3)也可以计算出作匀加速直线运动滑块的加速度。
中国石油大学油层物理习题答案
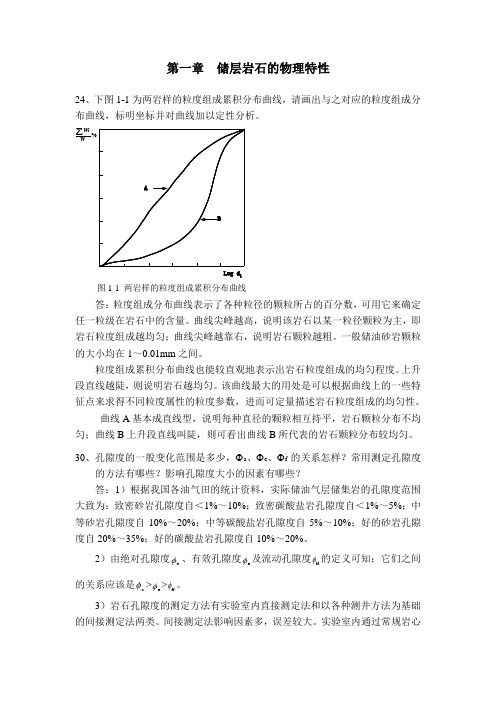
第一章 储层岩石的物理特性24、下图1-1为两岩样的粒度组成累积分布曲线,请画出与之对应的粒度组成分布曲线,标明坐标并对曲线加以定性分析。
∑Log d iWWi图1-1 两岩样的粒度组成累积分布曲线答:粒度组成分布曲线表示了各种粒径的颗粒所占的百分数,可用它来确定任一粒级在岩石中的含量。
曲线尖峰越高,说明该岩石以某一粒径颗粒为主,即岩石粒度组成越均匀;曲线尖峰越靠右,说明岩石颗粒越粗。
一般储油砂岩颗粒的大小均在1~0.01mm 之间。
粒度组成累积分布曲线也能较直观地表示出岩石粒度组成的均匀程度。
上升段直线越陡,则说明岩石越均匀。
该曲线最大的用处是可以根据曲线上的一些特征点来求得不同粒度属性的粒度参数,进而可定量描述岩石粒度组成的均匀性。
曲线A 基本成直线型,说明每种直径的颗粒相互持平,岩石颗粒分布不均匀;曲线B 上升段直线叫陡,则可看出曲线B 所代表的岩石颗粒分布较均匀。
30、孔隙度的一般变化范围是多少,Φa 、Φe 、Φf 的关系怎样?常用测定孔隙度的方法有哪些?影响孔隙度大小的因素有哪些?答:1)根据我国各油气田的统计资料,实际储油气层储集岩的孔隙度范围大致为:致密砂岩孔隙度自<1%~10%;致密碳酸盐岩孔隙度自<1%~5%;中等砂岩孔隙度自10%~20%;中等碳酸盐岩孔隙度自5%~10%;好的砂岩孔隙度自20%~35%;好的碳酸盐岩孔隙度自10%~20%。
2)由绝对孔隙度a φ、有效孔隙度e φ及流动孔隙度ff φ的定义可知:它们之间的关系应该是a φ>e φ>ff φ。
3)岩石孔隙度的测定方法有实验室内直接测定法和以各种测井方法为基础的间接测定法两类。
间接测定法影响因素多,误差较大。
实验室内通过常规岩心分析法可以较精确地测定岩心的孔隙度。
4)对于一般的碎屑岩 (如砂岩),由于它是由母岩经破碎、搬运、胶结和压实而成,因此碎屑颗粒的矿物成分、排列方式、分选程度、胶结物类型和数量以及成岩后的压实作用(即埋深)就成为影响这类岩石孔隙度的主要因素。
智慧树知道网课《物理化学(下)(中国石油大学(华东))》课后章节测试满分答案

绪论单元测试1【判断题】(10分)物理化学课程是建立在数学、物理学、基础化学等学科上的一门理论化学A.错B.对2【判断题】(10分)物理化学主要涉及研究过程发生后能量的转化、反应的方向和限度等问题。
A.错B.对3【判断题】(10分)物理化学课程学习过程中需要注意例题的演练、公式概念的应用条件和高等数学微积分知识的应用。
A.对B.错第一章测试1【判断题】(10分)低温低压的真实气体可以认为是理想气体A.错B.对2【判断题】(10分)分子间无作用力,分子本身无体积的气体一定是理想气体A.错B.对3【判断题】(10分)道尔顿分压定律和阿玛伽分体积定律只适用于理想气体混合物A.对B.错4【判断题】(10分)对于不同的真实气体,范德华方程中的特性常数也不同A.对B.错5【判断题】(10分)理想气体在一定温度、压力下也能液化A.对B.错6【判断题】(10分)不同的真实气体,只要处于相同的对应状态,就具有相同的压缩因子A.错B.对7【单选题】(10分)已知某气体的临界温度为304.15K,临界压力为7.375Mpa。
钢瓶中储存着302.15K的这种气体,则该气体()状态A.一定为气体B.数据不足,无法确定C.一定为气液共存D.一定为液体8【多选题】(10分)对临界点性质的描述中,正确的是A.固、液、气三相共存B.液相与气相界面消失C.当真实气体的温度低于临界点温度时,是真实气体液化的必要条件D.液相摩尔体积与气相摩尔体积相等9【单选题】(10分)理想气体的压缩因子ZA.随所处状态而定B.z>1C.z<1D.z=110【单选题】(10分)恒温300K下,某一带隔板的容器中,两侧分别充入压力相同的3dm3氮气和1dm3二氧化碳的理想气体,当抽调隔板后混合气体中氮气和二氧化碳的压力之比为()A.1:3B.3:1C.1:4D.4:1第二章测试1【判断题】(10分)状态函数的变化值只与始态和末态的状态有关,与具体的实现途径无关A.错B.对2【判断题】(10分)据焦耳实验可知,理想气体的内能只是温度的函数A.错B.对3【判断题】(10分)液态水和水蒸气的标准摩尔燃烧焓的值均为0A.错B.对4【判断题】(10分)A.错B.对5【判断题】(10分)热力学第一定律可表述为隔离系统中的热力学能守恒A.错B.对6【判断题】(10分)气体的节流膨胀过程一定是绝热不可逆过程A.错B.对7【多选题】(10分)关于热力学可逆过程,下列表述正确的是A.一般化学都是热力学可逆过程B.可逆压缩过程环境对系统做最小功C.可逆过程是一种理想的过程,实际过程只能无限接近它D.可逆过程发生后,系统和环境一定同时复原8【单选题】(10分)A.理想气体在101325Pa恒定外压下从101325Pa膨胀到10132.5PaB.气体从373K,10132.5Pa可逆变化到298K,101325PaC.在一定温度、压力下电解CuSO4水溶液D.在一定温度、压力下,冰融化成水9【多选题】(10分)下列关于焓的说法,正确的是A.焓是人为定义的一种具有能量量纲的物理量B.焓是系统能与环境进行交换的能量C.焓是系统的状态函数D.焓变只有在特定条件下,才与过程热数值相等10【单选题】(10分)下列关于绝热过程的说法正确的是A.其余选项均不正确B.绝热的恒外压过程也可能是绝热可逆过程C.绝热可逆压缩过程的末态温度可能会升高,也可能不变D.绝热可逆过程始末态压力、体积之间符合过程方程第三章测试1【判断题】(10分)热不可能全部转换成功。
大学物理下18章习题参考答案中国石油大学

18章习题参考答案18-3 当波长为3000Å的光照射在某金属表面时,光电子的能量范围从0到J 100.419-⨯。
在做上述光电效应实验时遏止电压是多大?此金属的红限频率是多大?[解] 由Einstien 光电效应方程()02max 21νν-=h mv 2max 2max 02121mv hc mv h h -=-=λνν19191910626.2100.410626.6---⨯=⨯-⨯=红限频率 Hz 1097.3140⨯=ν 遏止电压a U 满足 J 100.421192max a -⨯==mv eU 所以 V 5.2106.1100.41919a a =⨯⨯==--e eU U 18-4 图中所示为一次光电效应实验中得出的遏止电压随入射光频率变化的实验曲线。
(1)求证对不同的金属材料,AB 线的斜率相同;(2)由图上数据求出普朗克常量h 的值。
[解] (1) 由Einstien 光电效应方程得 A h U e -=νa 即 eA e hU -=νa 仅A 与金属材料有关,故斜率eh与材料无关。
(2)()s V 100.4100.50.100.21514⋅⨯=⨯-=-e h 所以 s J 104.6106.1100.4341915⋅⨯=⨯⨯⨯=---h18-6 在康普顿散射中,入射光子的波长为0.03Å,反冲电子的速度为光速的60%。
求散射光子的波长和散射角。
[解] (1) 电子能量的增加ννh h E -=∆0min λ ()⎪⎪⎭⎫ ⎝⎛--=-=160.01122020c m c m m2025.0c m =0434.025.011200=⎪⎪⎭⎫⎝⎛-=-h c m λλÅ(2) 由于 )cos 1(0φλ-=∆cm h所以 554.0cos 100=-=-cm h λλφ解得 0463.=φ18-7 已知X 射线光子的能量为0.60MeV ,若在康普顿散射中散射光子的波长变化了20%,试求反冲电子的动能。
中国石油大学09-10大物下册期中题目和答案

v0
α
q I
qRµ0nI 2msinα
,
18、电子在磁感强度B = 0.1 T的匀强磁场中沿圆周运动,电 、电子在磁感强度 的匀强磁场中沿圆周运动, 的匀强磁场中沿圆周运动 4.48×10-10 A . × 子运动形成的等效圆电流强度I 子运动形成的等效圆电流强度 =_____________. (电子电荷 =1.60×10-19 C,电子质量 = 9.11×10-31 kg) 电子电荷e 电子电荷 × ,电子质量m ×
I O a r O′
b I 2
O a I e c
17、半径为R的空心载流无限长螺线管,单 、半径为 的空心载流无限长螺线管 的空心载流无限长螺线管, 位长度有n匝线圈 导线中电流为I. 匝线圈, 位长度有 匝线圈,导线中电流为 .今在螺 线管中部以与轴成a 线管中部以与轴成 角的方向发射一个质量 的粒子(如图 为m,电荷为 的粒子 如图 .则该粒子初 ,电荷为q的粒子 如图). 速v0必须小于或等于 才能保证它不与螺线管壁相撞. 才能保证它不与螺线管壁相撞.
√
qa (C) 2 πε 0 x 3
1
(D)
q 4 πε 0 x 2
-q -a
O
+q +a
P (x,0)
x x
q q E= [ ] − 2 2 4πε 0 ( x − a ) ( x + a )
qa xa = = 2 2 2 πε0 ( x − a ) πε0 x3
q
2、图示为一具有球对称性分布的静电场的E~r关系 、图示为一具有球对称性分布的静电场的 关系 曲线. 曲线.请指出该静电场是由下列哪种带电体产生 选球心O处为坐标原点 的.(选球心 处为坐标原点 选球心 处为坐标原点) (A) 半径为 的均匀带电球面. 半径为R的均匀带电球面 的均匀带电球面. (B) 半径为R的均匀带电球体. 半径为 的均匀带电球体. 的均匀带电球体 (C) 半径为 、电荷体密度 =Ar (A为常数)的非 半径为R 电荷体密度r= 为常数) 为常数
石油炼制工程_中国石油大学(华东)中国大学mooc课后章节答案期末考试题库2023年

石油炼制工程_中国石油大学(华东)中国大学mooc课后章节答案期末考试题库2023年1.下列指标中反映柴油蒸发性能的是。
参考答案:馏程_闪点2.轴向和径向重整反应器的总压降主要取决于其中催化剂床层的压降。
参考答案:错误3.焦化过程中发生的主要反应包括?参考答案:加氢反应_缩合反应_裂解反应_环化反应4.催化裂化装置中,催化剂属于稀相输送的部位是。
参考答案:提升管5.石油烃类组成的表示方法包括?参考答案:族组成_单体烃组成_结构族组成6.从安全防火角度来说,轻质油品防明火,重质油品防高温泄漏。
参考答案:正确7.减压渣油馏分的沸点范围一般是?参考答案:500℃以上8.煤柴油馏分的沸点范围一般是?参考答案:200-350℃9.催化裂化反再系统中催化剂的循环量由决定。
参考答案:再生器热平衡10.石油常压蒸馏塔的回流比是由确定的。
参考答案:全塔热平衡11.在常压塔的操作中,若降低回流比,则会引起塔内各点温度?参考答案:升高12.当催化重整以生产BTX为目的时一般用的馏分做原料。
参考答案:60~130℃13.催化裂化催化剂的失活原因不包括。
参考答案:氯含量变化引起的失活14.在分子结构和分子大小相近的情况下,加氢反应过程中杂原子脱除速率最快的是。
参考答案:加氢脱硫15.在催化裂化的吸收稳定系统中,稳定塔的塔底出___产品。
参考答案:汽油16.一般将原油中沸点在350-500℃之间的馏分称为?参考答案:润滑油馏分17.重整过程的原料预处理过程包括?参考答案:预脱砷_预加氢_预分馏18.石油馏分与对应石油产品的组成和性质一样。
参考答案:错误19.催化重整过程的芳烃转化率可以大于100%。
参考答案:正确20.加氢催化剂和重整催化剂在使用之前需要预硫化的目的是相同的。
参考答案:错误21.催化裂化分馏塔的特征包括?参考答案:全塔剩余热量很大。
_塔顶一般不使用冷回流。
_塔底设人字形挡板。
22.随着石油馏分的沸点升高,下列物理性质的数值变大的是?参考答案:粘度_密度23.催化裂化再生器中的催化剂藏量是由决定的?参考答案:再生器烧焦24.汽油馏程的10%馏出温度偏低,则汽油在使用中。
2014年中国石油大学大学物理-课后习题解答汇总

解:对地: 对带:
考虑一对功对地: ,物体对传送带做功:
总功 。对带 也成立,不受参考系不同选择的影响。
5、如图4.2所示,M沿光滑斜面下滑,滑轮的质量不计,摩擦力可忽略。试判断:
(1)取M和地球为系统,机械能守恒吗?
图4.2
(2)取M、m和地球为系统,机械能守恒吗?
(3)取M、m绳和地球为一系统,机械能守恒吗?
注意:斜劈在碰撞瞬间受到桌面的冲力。
(2)令斜劈左右位置互换,如右图
A、m的物体放在水平传送带上,与传送带一起以恒定的加速度 前进,当物体被传送一段距离 时,传送带对物体作功是多少?物体对传送带作功多少?请分别以地面和皮带为参照系考虑问题。在两个参照系中它们互相所做的功的总和是否改变?
(2)如图4.4所示,细线一端固定在竖直圆柱上端,给另一端连接的
小球一个初速,使细线逐渐缠绕于柱上;
(3)如图4.5所示,桌面光滑,物体A、B一起运动至使绳子绷紧,从而带动物体C运动的前后过程。
图4.3
图4.4
图4.5
答:(1)系统的动量不守恒,角动量的竖直分量守恒,动能和机械能守恒。
(2)动量不守恒,角动量不守恒,动能不守恒,机械能守恒。
1)、A、B为均质球体,如图2.1静止放置。
图2.1
2)、A、B被水平方向的力 压在竖直的粗糙平面上保持静止(如图2.2);如F增为原来2倍,受力如何变化?
图2.2
解:如下图所示。
力 增大后,水平方向的力同比例增大,竖直方向不变。
图2.3
3)、A与B叠放在一起(如图2.3),分以下几种情况讨论:a、A、B静止;b、A、B一起自由下落;c、一起匀速上升。
解:子弹以初速 射入小木块过程中,两者得
新版中国石油大学(华东)物理学考研经验考研参考书考研真题

考研是一项小火慢炖的工程,切不可操之过急,得是一步一个脚印,像走长征那样走下来。
在过去的一年中,我几乎从来没有在12点之前睡去过。
也从来也没有过睡到自然醒的惬意生活,我总是想着可能就因为这一时的懒惰,一切都不同了。
所以,我非常谨小慎微,以至于有时会陷入自我纠结中,像是强迫症那样。
如今想来,这些都是不应该的,首先在心态上尽量保持一个轻松的状态,不要给自己过大的压力。
虽然考研是如此的重要,但它并不能给我们的人生下一个定论。
所以在看待这个问题上不可过于极端,把自己逼到一个退无可退的地步。
而在备考复习方面呢,好多学弟学妹们都在问我备考需要准备什么,在我看来考研大工程,里面的内容实在实在是太多了。
首先当你下定决心准备备考的时候,要根据自己的实际情况、知识准备、心理准备、学习习惯做好学习计划,学习计划要细致到每日、每周、每日都要规划好,这样就可以很好的掌握自己的学习进度,稳扎稳打步步为营。
另外,复试备考计划融合在初试复习中。
在进入复习之后,自己也可以根据自己学习情况灵活调整我们的计划。
总之,定好计划之后,一定要坚持下去。
最近我花费了一些时间,整理了我的一些考研经验供大家参考。
篇幅比较长,希望大家能够有耐心读完,文章结尾处会附上我的学习资料供大家下载。
中国石油大学(华东)物理学的初试科目为:(101)思想政治理论和(201)英语一(705)普通物理和(843)量子力学或(844)电动力学参考书目为:1.《大学物理教程》(上、下册)任兰亭等编,石油大学出版社1998 年版。
2.《大学物理教程》(上、下册),贾瑞皋主编,科学出版社,2009 年版。
3.门福殿《量子力学》,中国石油大学出版社,2005.12;4.周世勋《量子力学教程》,高等教育出版社,1979.2;5.关洪《量子力学基础》,高等教育出版社,1999.6跟大家先说一下英语的复习吧。
学英语免不了背单词这个难关,词汇量上不去,影响的不仅是考试成绩,更是整体英语能力的提升;背单词也是学习者最感到头痛的过程,不是背完了转身就忘,就是背的单词不会用,重点单词主要是在做阅读的时候总结的,我把不认识不熟悉的单词全都挑出来写到旁边,记下来反复背直至考前,总之单词这一块贵在坚持,背单词的日程一定要坚持到考研前一天。
大学物理下18章习题参考答案中国石油大学-推荐下载

n≤3.688 所以 n = 3 可产生从 n = 3 到 n = 2,n = 1 及 n = 2 到 n = 1 三条谱线。
由公式
给出波长分别为 31 1027 Å
c nm
m0e4
8
2 0
h
3
1 m2
1 n2
1 n2
32 6571 Å
18-10 试求:(1)红光( 7 105 cm );(2)X 射线( 0.25 Å)的光子的能量、动量和
V s
2.5 V
2 max
即
Ua
h e
A e
(2) 由于 所以 解得
1 0
m
0.25m0c 2
0.25m0c 2 h
h (1 cos ) m0c
1 cos 0 0.554 h
m0c 63.40
m0
c 2
1
在氢原子能级图中表示出来,并指明波长最短的是哪一条谱
线。
[解] (1) h h c
1.988 1015 4.58 1019 J 2.86eV 4340
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18章习题参考答案
18-3 当波长为3000Å
的光照射在某金属表面时,光电子的能量范围从0到
J 100.419-⨯。
在做上述光电效应实验时遏止电压是多大?此金属的红限频率是多大?
[解] 由Einstien 光电效应方程
()02
max 21νν-=h mv 2
max 2max 02
121mv hc mv h h -=-=λνν
19191910626.2100.410626.6---⨯=⨯-⨯=
红限频率 Hz 1097.3140⨯=ν 遏止电压a U 满足 J 100.42
1192
max a -⨯==
mv eU 所以 V 5.2106.1100.419
19
a a =⨯⨯==--e eU U 18-4 图中所示为一次光电效应实验中得出的遏止电压随入射光频率变化的实验曲线。
(1)求证对不同的金属材料,AB 线的斜率相同;
(2)由图上数据求出普朗克常量h 的值。
[解] (1) 由Einstien 光电效应方程得 A h U e -=νa 即 e
A e h
U -=νa 仅A 与金属材料有关,故斜率
e
h
与材料无关。
(2)
()s V 100.4100.50.100.21514
⋅⨯=⨯-=-e h 所以 s J 104.6106.1100.4341915⋅⨯=⨯⨯⨯=---h
18-6 在康普顿散射中,入射光子的波长为0.03Å,反冲电子的速度为光速的60%。
求散射光子的波长和散射角。
[解] (1) 电子能量的增加ν
νh h E -=∆0
min λ ()⎪⎪⎭⎫ ⎝⎛--=-=160.011
22020c m c m m
2025.0c m =
0434.025.011
2
00
=⎪⎪⎭
⎫
⎝⎛-=-h c m λλÅ
(2) 由于 )cos 1(0φλ-=
∆c
m h
所以 554.0cos 100
=-=
-c
m h λλφ
解得 0463.=φ
18-7 已知X 射线光子的能量为0.60MeV ,若在康普顿散射中散射光子的波长变化了20%,试求反冲电子的动能。
[解] 020.0λλ=∆ MeV 60.00=νh
0020.1λλλλ=∆+= 20
.120.100νλλ
ν==
=
c
c
反冲电子动能 ()MeV 1.020.11100k =⎪⎭
⎫ ⎝⎛
-=-=νννh h E
18-8 氢原子光谱的巴耳末线系中,有一光谱线的波长为 4340Å,试求: (1)与这一谱线相应的光子能量为多少电子伏特?
(2)该谱线是氢原子由能级n E 跃迁到k E 产生的,n 和k 各等于多少?
(3)若有大量氢原子处于能级为5E 的激发态,最多可以发射几个线系?共几条谱线?请在氢原子能级图中表示出来,并指明波长最短的是哪一条谱线。
[解] (1) λ
νc
h
h =
eV
86.2J 1058.44340
10988.11915
=⨯=⨯=--min λ
(2) 86.21416.1311
36.122
2=⎪⎭
⎫
⎝⎛-=⎪⎭⎫ ⎝⎛-=n n k h ν 因此 n =5 k =2
(3) 共四个线系:赖曼系、巴耳末系、帕邢系、布喇开系。
共十条谱线。
波长最短的是从n =5到n =1跃迁发射的谱线。
18-9以动能为12.5eV 的电子通过碰撞使处于基态氢原子激发,最高能激发到哪一级?
当回到基态时能产生哪些谱线?并求出其波长。
[解] 处于基态的电子吸收轰击电子最多能激发到量子数为n 的轨道上,则应有
eV 512k .=E ≥eV 116.132⎪⎭
⎫ ⎝⎛-
n n ≤3.688 所以 n = 3
可产生从n = 3到n = 2,n = 1及n = 2到n = 1三条谱线。
由公式
⎪⎭
⎫
⎝⎛-=2232040nm
118n m h e m c
ελ (见书363页) 给出波长分别为102731=λÅ 657132=λÅ 121721=λÅ 18-10 试求:(1)红光(cm 1075-⨯=λ);(2)X 射线(=λ0.25 Å)的光子的能量、动量和质量。
[解] (1)J 1084.210
710988.119
725---⨯=⨯⨯==λhc
E s m kg 1047.928⋅⨯==
-c E
p kg 1016.3362-⨯==c E
m
(2) J 1096.710
25.010988.1151025---⨯=⨯⨯==λhc
E s m kg 1065.223⋅⨯==
-c E
p kg 1084.8322-⨯==c E
m
18-11 求下列各自由粒子的德布罗意波长:(1)被400V 电压由静止加速的电子;(2)能量为100eV 、质量为kg 103-的质点。
[解] (1)
eU v m =202
1
s m 1019.110
11.9400106.122731
190⨯=⨯⨯⨯⨯==--m eU v 61000.v
c c m h v m h p h ====
λÅ (2) m
p E 22
k = 即 k 2mE p =
1419
334k 107.3106.110010210626.62----⨯=⨯⨯⨯⨯⨯===mE h p h λÅ
18-12 若电子的总能量为静止能量的2倍,求电子的德布罗意波长。
[解] 202
202
21c m c v c m mc =⎪⎭
⎫
⎝⎛-=
c v 2
3=
014.0310====
c
m h mv h p h λ Å 18-14 试证明自由粒子的不确定[度]关系可以写成
λ∆⋅∆x ≥2λ (提示:根据p x ∆⋅∆≥h 求解。
)
[证明] 自由粒子λ
h
p =
λλ∆=
∆2
h
p
由不确定度关系p x ∆⋅∆≥h ,上式可写成
λ∆⋅∆x ≥2λ
18-15 光子的波长为=λ5000 Å,如果确定此波长的精确度达到λλ610-=∆,试求此光子位置的不确定量x ∆ (按p x ∆⋅∆≥h 求解)。
[解] 根据上题x ∆≥
9662210510
5000
10---⨯===∆λλλλ Å=0.5m 18-16 已知粒子在无限深势阱中运动,其波函数为
()⎪⎭
⎫ ⎝⎛=
a x a x πϕ3sin 2 (0≤x ≤a ) 求:(1)粒子在43a x =处出现的概率密度;
(2)发现粒子概率最大的位置; (3)画出粒子概率分布的示意图。
[解] 粒子在x 处的概率密度()()⎪⎭
⎫ ⎝⎛=
=a x a x x πψρ3sin 222
(1) a
a a a a 1
433sin 2432=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛πρ
(2)令
()0=∂∂x x ρ得,06sin =a x π,即ππn a
x
=6 (n =0,1,……,6) 所以极值点在6na x = (n =0,1,……,6)处。
n 为奇数时a a a x 6
5
,63,61=为()x ρ极
大点处,而当n 为偶数时对应()x ρ极小值。
18-17 原子中一电子的主量子数为n =2,它可能具有的状态数为多少?分别用一组量子数表示出各种可能的状态。
[解] 可能状态数822222=⨯=n ,它们分别是(2,0,0,21±)、(2,1,1,2
1
±)、(2,1,0,21±
)、(2,1,-1,2
1
±) 18-18 在原子的壳层结构中,为什么n =3的壳层最多只能容纳18个电子? [解]由于泡利不相容原理,不允许有两个电子具有同一量子态,即同一组()s l m ,m ,l .n 量子数。
给定n ,l 只可取0,1,……,n -1,给定n 、l 后,l m 只能取-l ,-l +1,……,l 等2l +1个值,给定n 、l 、l m 后,s m 只可取2
1
±
=s m ,故对于一定的n 只能有 ()()222
1222122n n n l =⨯-+=
+∑
个不同的态。
当每个量子态都被一个电子占据时n 壳层电子数最多。
n =3,它为1822=n
18-19 试说明绝缘体和半导体能带结构的相同点和不同点。
18-20 已知T =0 K 时纯硅晶体能吸收的辐射最长的波长是1.09 m ,试求纯硅晶体的禁带宽度。
(用eV 表示)。
18-21 什么叫粒子数的反转?实现粒子数反转的条件是什么?
[答] 从一般情况的高能级上的原子数2n 大于低能级上的原子数1n 转变为2n >1n 的分布称为粒子数的反转。
实现粒子数反转的条件: 激励能源:提供能量。
激活物质:有适当的能级结构(亚稳态)。
18-22 试简述谐振腔的作用。
[答] (1)产生并维持光振荡,使光得到加强放大。
(2)提高激光的方向性。
(3)具有选频作用,提高激光的单色性。
.。
