数值计算-利用Python程序绘制的函数图像-精品课程

合集下载

数值计算PPT课件

x1=(-b+math.sqrt(d))/(2*a) x2=(-b-math.sqrt(d))/(2*a) print("方程有两个不同的解",x1,x2) elif d==0: x1=-b/(2*a) print("方程有两个相同的解",x1) else: print("方程无解")
用辗转相除法求解两个正整数的最大公约数
在Python中，绘制函数图像一般要用到numpy和matplotlib两个模块，这两个模块需要另外安装。
Numpy模块简介 numpy是一个科学计算包，其中包括很多数学函数，如三角函数、矩阵计算方法等
import numpy as np
#加载numpy模块并取一个简洁的别名为np
x=np.arrange(0,2*np.pi,0.01) # x在0到2π之间，每隔0.01取一个点
表4.2.1 函数计算
x
1
0
2
30
3
60
…
…
14 360
sin(x) 0 0.5
0.866025404
…
0
sin(-x) 0
-0.5 -0.866025404
…
0
sin(2x)/2 0 0.5
0.866025404
…
0
利用wps绘制的函数图像
利用WPS表格画图
2x2+x-6=0
利用python绘制正弦曲线
参考答案： num1=int(input('请输入第一个正整数：')) num2=int(input('请输入第二个正整数：')) m=max(num1,num2) n=min(num1,num2) r=m % n while r!=0:

高教社2024Python数据可视化教学课件04章Matplotlib统计图表绘制

ax.plot(theta, r2, c='y', marker='d', mfc='r', ms=10, lw=2)
说明：以上两种方法绘图效果相同。第二种方法使用的绘图函数是ax.plot()，该方ห้องสมุดไป่ตู้原本是绘制折线图，但因为ax采用极坐标系，所以原来的x和y位置的参数被理解为了极角和极径。
# 代码1 x = np.linspace(0.1, 0.8, 10) y = np.exp(x) plt.errorbar(x, y, fmt="ro:", yerr=0.15, xerr=0.03)
# 代码2
x = np.linspace(0.1, 0.8, 10)
for patch, color in zip(box['boxes'], colors):
# 遍历box['boxes'], 设置不同的箱体颜色
patch.set_facecolor(color)
plt.axhline(np.mean(y1), c='#FFF68F')
# 均值水平参考线
plt.axhline(np.mean(y2), c='#9999ff')
三、极坐标参数设置
左图绘制了一个整圆和渐开的曲线，同时清空了圆内的标注数字。plt.rgrids()设置同心栅格的极径大小和文字标注的角度，因此右图中的虚线圆圈只有两个，极径为0.3和1，圆圈上的标注沿45°线排列。函数 plt.thetagrids()设置放射线栅格的角度，因此右图中只有两条放射线，角度为0°和 45°。
极坐标系中点的坐标用弧度(theta)和极径(r)描述，绘制极线图需提供两个相同长度的参数数组theta和r，对应极角和极径。极线图的绘制有如下两种方法：

python编程教学三阶第17课-Tkinter绘图课件 (26张PPT).ppt

新知教授
1、创建按钮 2、绘制图形 3、设置颜色
4、课堂总结
创建按钮
新知教授ห้องสมุดไป่ตู้
作为我们的第一个例子，我们要用tkinter 创建一个带按钮的简单程序。
编玩边学
from tkinter import * def printStr():
print('hello world!') windows1 = Tk() button1 = Button(windows1, text='点击我', command=printStr)
用海龟画图的问题是海龟……太……慢……了。就算海龟以它最快的速度跑也还是太慢。对海龟来讲这不是个问题，但是对于计算机绘图来讲就是个问题了。
计算机绘图，尤其是在游戏里，通常都要求能快速移动。
情境引入
用海龟画图的问题是海龟……太……慢……了。就算海龟以它最快的速度跑也还是太慢。对海龟来讲这不是个问题，但是对于计算机绘图来讲就是个问题了。
实践创作
完成本节课的程序，尝试使用 tkinter绘图来重绘海龟画图的
作品
课堂总结
1、创建按钮
button1 = Button(windows1, text='点击我', command=printStr)
2、绘制图形
canvas = Canvas(object1, width=600, height=500) canvas.create_rectangle(30, 30, 150, 150)
编玩边学
from tkinter import * object1 = Tk() canvas = Canvas(object1, width=800, height=500) # 画布大小 canvas.pack() object1.mainloop()

基于Python的画图工具课件PPT

动态交互式图表展示，支持在线编辑和分享
Matplotlib基础
1
创建图形
创建画布和子图，设置样式风格和标签
添加元素
2
添加坐标轴、图例、文本标注等元素
3
绘图
绘制线图、散点图、饼图、直方图等图形
基本图表绘制
折线图
适用于展示时间序列类数据变化趋势
条形图
适用于展示不同类别数据的数量或大小差异
饼图
适用于展示数据所占比例，不宜展示过多类别
力图、小提琴图、琴形图等
式、配色方案和标注选项，
更具特色的图表类型
可大大降低自定义的难度
3 更容易加入统计学元素
S eaborn内置了许多统计学元素，如直方图中的核密度估计线和散点图中的回归拟合线等
Seaborn常见图形展示
热力图
适用于展示变量之间的相关性和大小关系
密度图
适用于展示变量的频率分布情况和变化规律
适用于展示不同类别的变化趋势及其贡献度
3 D绘图
三维散点图
适用于展示三个变量之间的关系和规律
三维曲面图
根据三个变量的数值绘制具有高度的曲面图
Seaborn简介
1 提供更丰富的图形类型 2 支持更丰富的自定义选
项除了Βιβλιοθήκη atplotlib中的基本图表类型外，Seaborn还提供了热
S eaborn提供了更多的图表样
开源免费
Python不仅语言本身是开源免费，许多强大的Python库也是开源免费。
画图工具概述
画图工具 Matplotlib S eaborn Plotly
功能描述
可用于制作线图、散点图、条形图、饼图、直方图等各种静态图表

(完整版)Python学习课件

100%
浮点数类型
浮点数用于表示实数，即带有小数点的数字。Python中的浮点数类型通常是双精度浮点数。
80%
数字类型的运算
Python支持基本的数学运算，如加、减、乘、除和取余等。
字符串类型及操作
字符串定义
字符串是由零个或多个字符组成的一种数据类型，用引号括起来表示。
字符串操作
Python提供了丰富的字符串操作方法，如连接、截取、查找、替换等。
(完整版)Python学习课件
汇报人:
2023-12-21
目
CONTENCT
录
• Python基础知识 • Python数据类型与运算符 • Python流程控制语句 • Python函数与模块 • Python面向对象编程思想 • Python文件操作与数据处理
01
Python基础知识
Python简介与发展历程
字符串格式化
可以使用格式化字符串来插入变量或表达式的值，生成动态的字符串内容。
列表、元组和字典等数据结构
列表
列表是一种有序的数据结构，可以包含任意类型的元素，且元素
之间可以重复。
元组
元组与列表类似，也是一种有序的数据结构，但元组是不可变的，即创建后不能修改。
字典
字典是一种无序的数据结构，用于存储键值对，其中键必须是不可变类型（如整数、字符串或元组）。
03
Python流程控制语句
条件语句：if-else结构
if语句
elif语句
用于根据条件判断执行相应的代码块。
用于在if语句中添加额外的条件判断。
else语句
与if语句配合使用，当if语句条件不满足时执行else代码块。

初中信息技术_《巧用python绘制数学图形》教学设计学情分析教材分析课后反思

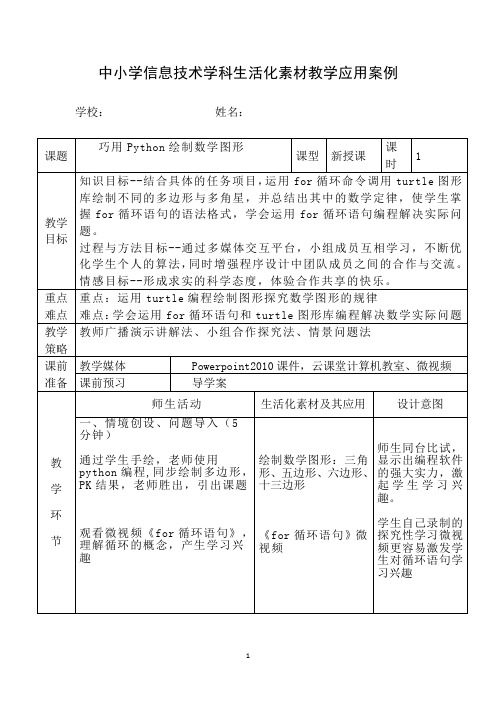
学 PK 结果，老师胜出，引出课题十三边形
起学生学习兴趣。
环
学生自己录制的
节
观看微视频《for 循环语句》，《for 循环语句》微探究性学习微视
理解循环的概念，产生学习兴视频
频更容易激发学
趣
生对循环语句学
习兴趣
1
二、新课探究（33 分钟）
教
1.小组合作探究从任务 1《三角
从绘制三角形入手，运用数学规律，寻找
三、数学图形中的数学规律
课后反思
生活化素材使用效果
使用的生活化素材都是与学生学习生活息息相关的事例，贴近学生日常，容易引起共鸣，帮助学生很好地理解抽象的循环概念和数学图形绘制过程与方法，能更好地激发学生学习和使用编程来解决生活上问题的热情。
（表格不够可以加页）习编程语言会感到十分吃力，看不懂代码。他们对形象生动、形式多样动手实践的学习内容更有兴趣，他们爱探索、爱动手实践。《巧用 Python 绘制数学图形》一课，结合运用 Python 编程教学中《for 循环语句》与 turtle 图形库图形绘制以及数学图形的规律三方面的内容，通过运用 for 循环命令调用 turtlel 图形库绘制不同的数学图形多边形与多角星，让学生从一些单纯的程序代码入手运行结果，既可以观摩数学图形详细的绘制过程，同时显示结果也是彩色的形式各样的图形，还可以同时验证平时所学的数学定律。这些实践操作将可以引起所有学生的主动创作意愿，极大地激发学习兴趣。
4
同学们的创新设计思维、提升了编程能力，提高了活动中自我管理、自我创新的能力。
Python 教程第九节教材分析
《巧用 Python 绘制数学图形》一课，结合 Python 编程教学中第九节《for 循环语句》与 turtle 图形库图形绘制以及数学图形的规律三方面的内容。for 循环命令在 python 教学中，是一个非常重要的语句命令，但对于七年级、八年级学生来说，是一个比较抽象的概念，难于理解。如果只是单纯讲代码编写，学生容易产生畏难情绪。通过运用 for 循环命令调用 turtlel 图形库绘制不同的数学图形---多边形与多角星，这些实践操作可以引起所有学生的主动创作意愿，可以极大地激发学习兴趣，化难为易。

用计算机绘制函数的图像(王伟)

《用计算机绘制函数的图像》教案设计学校：西丰职专教师：王伟一、教案背景1、面向学生：中职生一年级2、学科：数学语文出版社中等职业教育课程改革国家规划教材基础模块上册3、课时：第3课时4、学生课前准备：（1）预习本课时教学内容。

（2）利用网络搜索几何画板5.01软件及简明教程，进行自学。

二、教学课题教养方面：1、认识并掌握几何画板5.01软件的界面组成，并能够进行简单的绘图操作。

2、掌握二次函数y=x2 与y=-x2图像及性质，抛物线的定义，理解并掌握二次函数y=ax2的图像及性质，并能解释解决一些简单的抛物线的现象和问题。

教育方面：1、培养学生观察、思考身边的事物、现象的习惯和能力，体会实际生活与数学的紧密联系。

2、培养学生数形结合的思想和方法，类比的思想和方法，实验的思想和方法。

提高学生分析问题、解决问题的能力。

发展方面：培养学生自主学习的态度和能力，动手操作的实践能力，大胆的想象力和合作交流的能力。

三、教材分析《用计算机绘制函数的图像》是语文出版社出版，中等职业教育课程改革国家规划教材基础模块上册63页的教学内容。

需要运用的软件是几何画板5.01。

几何画板一个通用的数学、物理教学环境，提供丰富而方便的创造功能使用户可以随心所欲地编写出自己需要的教学课件，是最出色的教学软件之一。

它主要以点、线、圆为基本元素，通过对这些基本元素的变换、构造、测算、计算、动画、跟踪轨迹等，构造出其它较为复杂的图形，是数学、物理教学中强有力的工具。

《用计算机绘制函数的图像》是学生们在系统的学习了函数的概念及表示法后，利用函数的图像，系统的学习研究二次函数y=ax2的图像和性质。

教学重点是二次函数y=ax2的图像及性质。

教学难点是通过系统的学习研究二次函数y=ax2的图像和性质培养学生数形结合的思想和方法，类比的思想和方法，提高学生分析问题、解决问题的能力，丰富他们的想象力，增强他们对数学的兴趣。

教学之前用百度在网上搜索二次函数的图像和性质的相关教学材料，在百度上搜索到《数学实验二次函数的图像和性质》课件，教学软件几何画板5.01，几何画板5.01中文最强版，画版实例 5.x平抛运动课件，视频《被苹果砸中的牛顿》。

python中绘制sin、cos函数图像

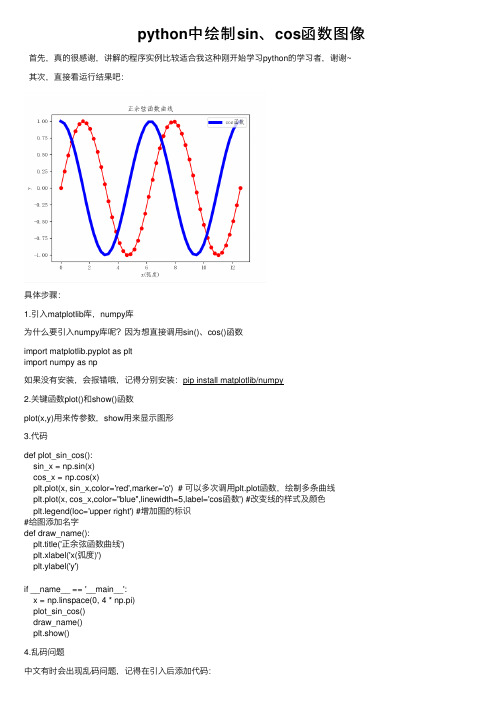
python中绘制sin、cos函数图像⾸先，真的很感谢，讲解的程序实例⽐较适合我这种刚开始学习python的学习者，谢谢~其次，直接看运⾏结果吧：具体步骤：1.引⼊matplotlib库，numpy库为什么要引⼊numpy库呢？因为想直接调⽤sin()、cos()函数import matplotlib.pyplot as pltimport numpy as np如果没有安装，会报错哦，记得分别安装：pip install matplotlib/numpy2.关键函数plot()和show()函数plot(x,y)⽤来传参数，show⽤来显⽰图形3.代码def plot_sin_cos():sin_x = np.sin(x)cos_x = np.cos(x)plt.plot(x, sin_x,color='red',marker='o') # 可以多次调⽤plt.plot函数，绘制多条曲线plt.plot(x, cos_x,color="blue",linewidth=5,label='cos函数') #改变线的样式及颜⾊plt.legend(loc='upper right') #增加图的标识#给图添加名字def draw_name():plt.title('正余弦函数曲线')plt.xlabel('x(弧度)')plt.ylabel('y')if __name__ == '__main__':x = np.linspace(0, 4 * np.pi)plot_sin_cos()draw_name()plt.show()4.乱码问题中⽂有时会出现乱码问题，记得在引⼊后添加代码：plt.rcParams['font.sans-serif']=['FangSong'] plt.rcParams['axes.unicode_minus']=False ⼤家有问题，可以相互交流学习~。

python语言基础(数据类型运算符)课件(共40张PPT)高中信息技术浙教版(2019)必修1

运算符优先级
算术运算符
关系运算符
赋值运算符
逻辑运算符
运算符优先级规则：算术运算符优先级最高，其次是成员测试运算符、关系运算符、赋值运算符、逻辑运算符等，算术运算符遵循“先乘除，后加减”的基本运算原则。
高中信息技术
• 变量：用于存储一个数据 • Python的赋值语句：<变量>=<表达式>
例如表示姓名的变量可以是 name xingming xm
试一试：判断变量名是否合法
count_1 HelloWorld ans#1 姓名 print 1ans
算术运算符逻辑运算符关系运算符赋值运算符
教学目标：
1、熟悉Python数据类型 2、熟悉并会使用算术运算符、关系运算符、逻辑运算符、字符串运算符
课堂练习
3.设a=8、b=6、c=5、d=3，表达式 a == c and b != c or c > d的值是( B ) A.1 B.True C.False D.2
Thanks
资料
高中信息技术
2020年7月23日12时41分，长征五号运载火箭在中国文昌航天发射场发射升空，火箭飞行2167秒后，成功将执行我国首次火星任务的探测器——“天问一号”送入预定轨道。请你编写程序，把以秒为单位的火箭飞行时间，转换为用“H : M : S”的格式来表示。
课堂练习
1.判断x是否在区间[a,b]上，哪个逻辑表达式是正确的？( A ) A. x >= a and x <= b B. x≥a and x≤b C. a≤x≤b D. a <= x or x <= b
课堂练习
2.有一个四位整数x，要得到该整数的百位，代码应如何写？

python画图程序课程设计

python画图程序课程设计一、教学目标本课程的学习目标旨在让学生掌握Python基本画图程序的编写方法，培养学生的编程思维和实际操作能力。

具体目标如下：1.知识目标：使学生了解Python画图程序的基本概念和原理，包括turtle库的使用方法，以及基本绘图函数如circle()、dot()等。

2.技能目标：培养学生能够运用Python编写简单的画图程序，如绘制图形、绘制函数图像等。

同时，培养学生能够通过查阅资料和文档，自主学习和解决问题的能力。

3.情感态度价值观目标：培养学生对计算机编程的兴趣，增强其对科学和技术的热爱，培养其创新精神和团队合作意识。

二、教学内容本课程的教学内容主要包括以下几个部分：1.Python画图程序的基本概念和原理，如turtle库的使用方法。

2.基本绘图函数的学习，如circle()、dot()等。

3.典型画图程序的编写和分析，如绘制图形、绘制函数图像等。

4.实际操作练习，让学生通过编写程序，实现自己的创意画图。

三、教学方法本课程的教学方法主要包括讲授法、案例分析法和实验法。

1.讲授法：用于讲解Python画图程序的基本概念、原理和绘图函数。

2.案例分析法：通过分析典型画图程序，让学生了解实际应用中如何运用Python进行画图。

3.实验法：让学生动手编写程序，进行实际操作，培养其实际操作能力和解决问题的能力。

四、教学资源本课程的教学资源主要包括以下几个部分：1.教材：Python编程基础教材，用于为学生提供理论知识的学习。

2.参考书：Python画图程序相关书籍，用于为学生提供更多的学习资料。

3.多媒体资料：包括教学PPT、视频教程等，用于为学生提供生动、直观的学习资源。

4.实验设备：计算机、投影仪等，用于进行实验教学，让学生动手实践。

五、教学评估为了全面、客观地评估学生的学习成果，本课程将采用多种评估方式，包括平时表现、作业、考试等。

1.平时表现：通过学生在课堂上的参与度、提问回答、小组讨论等表现，评估其对课程内容的理解和掌握程度。

4.2 数值计算(第1课时)课件-2023—2024学年高中信息技术教科版(2019)必修1

用WPS表格绘制函数图像还是不太方便，我们还可以用什么样的方法实现函数的绘制呢？
可以借助计算机程序描点绘制函数来达到速度快且精度高的效果。
任务：绘制数学函数曲线
➢ 活动2 利用Python绘制正弦曲线
• 4.2 数值计算
借助计算机程序描点，可以达到速度快且精确度高的效果。下面我们尝试利用Python编写程序绘制正弦曲线。
课堂小结
• 4.2 数值计算
绘制数学函数曲线
wps绘制 Python绘制
numpy模块
matplotlib 模块
课后作业
• 4.2 数值计算
➢ 利用Python绘制x5+x4+x-3=0在区间【-1,2】的函数图像。
感谢观看
学无பைடு நூலகம்境永攀高峰
① 利用课本上间隔30的数据； ② 利用间隔1度的数据，绘制正弦函数图像。
任务：绘制数学函数曲线
➢ 活动1 用WPS表格绘制正弦曲线
• 4.2 数值计算
仔细观察图像，会发现图像的关键点太少，精度不够，图像不光滑。要想提高图像的光滑程度，就要减小角度间隔，但间隔增加，工作量也会随之增加：每隔1°画一个点，数据表上就会增加300多行新数据；如果以0.1°为间隔，将有3000多行数据。
上机实践4
课堂小测
• 4.2 数值计算
填空题
1．numpy是一个科学计算包，其中包括很多________，如________、矩阵计算方法、________、线性代数等。通过numpy模块中的________函数可以创建一个等差数列。如在0-2π之间每隔0.01取个值，则可以用_ _______表示，其中numpy.pi表示________。 2．matplotlib模块是一个________。matplotlib的绘图原理很简单，利用________画线函数就可以在直角平面内轻松地将________坐标点对连接成平滑曲线。

教你如何绘制数学函数图像——numpy和matplotlib的简单应用

教你如何绘制数学函数图像——numpy和matplotlib的简单应⽤numpy和matplotlib的简单应⽤⼀、numpy库1.什么是numpyNumPy系统是Python的⼀种开源的数值计算扩展。

这种⼯具可⽤来存储和处理⼤型矩阵，⽐Python⾃⾝的嵌套列表（nested list structure)结构要⾼效的多（该结构也可以⽤来表⽰矩阵（matrix））。

numpy是科学计算包，⽀持N维数组运算、处理⼤型矩阵、成熟的⼴播函数库、⽮量运算、线性代数、傅⾥叶变换、随机数⽣成，并可与C++/Fortran语⾔⽆缝结合。

2.numpy的安装在Python v3中默认安装已经包含了numpy如果没有安装，可以在命令⾏（ctrl+R，输⼊cmd）中输⼊pip install numpy即可⾃动安装使⽤3.numpy的使⽤注意：这⾥的矩阵跟线性代数（⾼等代数）中的矩阵⼀致，运算⽅法⼀致（1）导⼊模块import numpy as np #⽤np来代替numpy（2）⽣成数组(创建数组）1import numpy as np2print(np.array([1, 2, 3, 4, 5])) # 把列表转换为数组3print(np.array((1, 2, 3, 4, 5))) # 把元组转换成数组4print(np.array(range(5))) # 把range对象转换成数组5print(np.array([[1, 2, 3], [4, 5, 6]])) # ⼆维数组6print(np.arange(8)) # 类似于内置函数range()7print(np.arange(1, 10, 2))8print(np.linspace(0, 10, 11)) # 等差数组，包含11个数9print(np.linspace(0, 10, 11, endpoint=False)) # 不包含终点10print(np.logspace(0, 100, 10)) # 对数数组11print(np.logspace(1,6,5, base=2)) # 对数数组，相当于2 ** np.linspace(1,6,5)12print(np.zeros(3)) # 全0⼀维数组13print(np.ones(3)) # 全1⼀维数组14print(np.zeros((3,3))) # 全0⼆维数组，3⾏3列15print(np.zeros((3,1))) # 全0⼆维数组，3⾏1列16print(np.zeros((1,3))) # 全0⼆维数组，1⾏3列17print(np.ones((1,3))) # 全1⼆维数组18print(np.ones((3,3))) # 全1⼆维数组19print(np.identity(3)) # 单位矩阵20print(np.identity(2))21print(np.empty((3,3))) # 空数组，只申请空间⽽不初始化，元素值是不确定的结果如图所⽰（因为是⼀次性输出全部，所以显⽰不是很好）（3）数组的运算1/ 数组与数值的运算x=np.array((1,2,3,4,5)) #创建数组x*2 #乘法x/2 #除法x//2 #整除x**3 #幂次⽅x+2 #加法x%3 #求余2**x #2的（x中的每⼀个元素）次⽅，同时⽣成另⼀个数组2/x #2除以x中的每⼀个元素，同时⽣成另外⼀个数组63//x #63除以x中的每⼀个元素，取整数，同时⽣成另外⼀个数组2/ 数组与数组的运算a= np.array((1,2,3)) #先创建两个数组b=np.array(([1,2,3],[4,5,6],[7,8,9]))数组之间的基本运算c=a*b c/ba+aa*ac-ac/ab=np.array(([1,2,3],[4,5,6],[7,8,9]))b.T #转置值得注意的是：⼀维数组转置以后和原来是⼀样的（5）点积和内积a = np.array((5, 6, 7)) #创建数组ab = np.array((6, 6, 6)) #创建数组ba.dot(b) #向量内积np.dot(a,b)c = np.array(([1,2,3],[4,5,6],[7,8,9])) # ⼆维数组c.dot(a) # ⼆维数组的每⾏与⼀维向量计算内积a.dot(c) # ⼀维向量与⼆维向量的每列计算内积（6）元素访问b = np.array(([1,2,3],[4,5,6],[7,8,9]))b[0] # 第0⾏b[0][0] # 第0⾏第0列的元素值b[0,2] # 第0⾏第2列的元素值b[[0,1]] # 第0⾏和第1⾏b[[0,1], [1,2]] #第0⾏第1列的元素和第1⾏第2列的元素 x = np.arange(0,100,10,dtype=np.floating)x[[1, 3, 5]] # 同时访问多个位置上的元素x[[1, 3, 5]] = 3 # 把多个位置上的元素改为相同的值x[[1, 3, 5]] = [34, 45, 56] # 把多个位置上的元素改为不同的值（7）数组⽀持函数运算np.sin(x) #求正弦值np.cos(x) #求余弦值np.round(_) #四舍五⼊x = np.random.rand(10) * 10 # 包含10个随机数的数组np.floor(x) # 所有元素向下取整np.ceil(x) # 所有元素向上取整a = np.arange(1, 11, 1) #创建⼀维数组a.shape = 2, 5 #将数组改为2⾏5列a.shape = 5, -1 #将元素分成5列， -1表⽰⾃动计算，原地修改b = a.reshape(2,5) # reshape()⽅法返回新数组（9）切⽚操作a[::-1] # 反向切⽚a[::2] # 隔⼀个取⼀个元素a[:5] # 前5个元素c[0, 2:5] # 第0⾏中下标[2,5)之间的元素值c[1] # 第1⾏所有元素c[2:5, 2:5] # ⾏下标和列下标都介于[2,5)之间的元素值（10）布尔运算（结果⼀般是True或者False显⽰)x > 0.5 # ⽐较数组中每个元素值是否⼤于0.5x[x>0.5] # 获取数组中⼤于0.5的元素，可⽤于检测和过滤异常值x < 0.5np.all(x<1) # 测试是否全部元素都⼩于1np.any([1,2,3,4]) # 是否存在等价于True的元素a >b # 两个数组中对应位置上的元素⽐较a[a>b] #输出相对应元素a>b的元素位置（11）取整运算x = np.random.rand(10)*50 # 10个随机数np.int64(x) # 取整np.int32(x)（12）⼴播a = np.arange(0,60,10).reshape(-1,1) # 创建列向量b = np.arange(0,6) # 创建⾏向量a[0] + b # 数组与标量的加法a + b #⾏向量与列向量的相加a*b #⾏向量与列向量的相乘（13）计算唯⼀值以及出现的次数x = np.random.randint(0, 10, 7) #创建0到10之间的随机数，个数为7np.bincount(x) #计算元素出现的次数，由最⼩的元素开始，到最⼤值np.sum(_) # 所有元素出现次数之和等于数组长度np.unique(x) # 返回唯⼀元素值（14）矩阵运算a_list = [3, 5, 7]a_mat = np.matrix(a_list) # 创建矩阵a_mat.T # 矩阵转置a_mat.shape # 矩阵形状a_mat.size # 元素个数a_mat.mean() # 元素平均值a_mat.sum() # 所有元素之和a_mat.max() # 最⼤值a_mat.max(axis=1) # 横向最⼤值a_mat.max(axis=0) # 纵向最⼤值a_mat * b_mat.T # 矩阵相乘c_mat = np.matrix([[1, 5, 3], [2, 9, 6]]) # 创建⼆维矩阵c_mat.argsort(axis=0) # 纵向排序后的元素序号c_mat.argsort(axis=1) # 横向排序后的元素序号d_mat.diagonal() # 矩阵对⾓线元素x = np.matrix(np.random.randint(0, 10, size=(3,3)))x.std() # 标准差x.std(axis=1) # 横向标准差x.std(axis=0) # 纵向标准差x.var(axis=0) # 纵向⽅差⼆、matplotlib库1.什么是matplotlib库matplotlib模块依赖于numpy模块和tkinter模块，可以绘制多种形式的图形，包括线图、直⽅图、饼状图、散点图、误差线图等等。

如何用Python绘制函数图像

要使用Python 绘制函数图像，最常用的库是Matplotlib ，特别是它的pyplot 模块。

Matplotlib 是一个非常强大的Python 绘图库，可以用来绘制各种静态、动态、交互式的图表。

下面介绍如何使用Matplotlib 来绘制函数图像的基本原理和步骤，并给出一些例子。

原理1. 导入库：首先需要导入matplotlib.pyplot ，通常简写为plt 。

如果没有安装matplotlib 库，需要先使用pip 安装：pip install matplotlib 。

2. 准备数据：根据函数表达式，生成一系列的x 值和相应的y 值。

这通常通过numpy 库完成，因为numpy 提供了大量的数学函数和操作数组的功能，非常适合进行数学计算。

3. 绘制图像：使用plt.plot(x, y)函数绘制出x 和y 值的图像。

4. 展示图像：使用plt.show()函数展示图像。

步骤以下是一个使用matplotlib 绘制函数y = x^2图像的简单例子：更多例子绘制正弦波和余弦波：import matplotlib .pyplot as plt import numpy as np # 1. 准备数据x = np .linspace (-10, 10, 400) # 生成一个包含400个点的x 值数组，范围从-10到10y = x ** 2 # 计算对应的y 值# 2. 绘制图像plt .plot (x , y )# 3. 设置图表标题和坐标轴标签plt .title ("y = x^2")plt .xlabel ("x")plt .ylabel ("y")# 4. 展示图像plt .show ()1234567891011121314151617import matplotlib .pyplot as plt import numpy as np x = np .linspace (-2 * np .pi , 2 * np .pi , 1000) # x 值范围y_sin = np .sin (x ) # 正弦值y_cos = np .cos (x ) # 余弦值plt .plot (x , y_sin , label ='sin(x)')plt .plot (x , y_cos , label ='cos(x)')plt .title ("Sin and Cos Function")plt .xlabel ("x")plt .ylabel ("y")12345678910111213绘制多项式函数：通过这些例子，你可以看到使用Matplotlib 和Numpy 绘制函数图像是一个相对直接和简单的过程。

python绘图教程

python绘图教程Python是一种功能强大的编程语言，其绘图库提供了丰富且多样化的工具，可以帮助您以各种方式可视化数据。

本教程将向您介绍一些常用的Python绘图库，以及如何使用它们创建图表、图形和其他可视化内容。

首先，我们将介绍最流行的Python绘图库之一——Matplotlib。

Matplotlib提供了广泛的绘图工具，包括散点图、折线图、柱状图、饼图等多种类型的图表。

使用Matplotlib可以轻松地创建各种静态图表，并为其添加标题、标签和其他美化效果。

下面是使用Matplotlib创建一个简单的折线图的示例代码：```pythonimport matplotlib.pyplot as plt# 创建 x 和 y 坐标轴的数据x = [1, 2, 3, 4, 5]y = [1, 4, 9, 16, 25]# 创建折线图plt.plot(x, y)# 添加标题和坐标轴标签plt.title("Square Numbers")plt.xlabel("x")plt.ylabel("y")# 显示图表plt.show()```运行上述代码，您将看到一个简单的折线图，其中 x 坐标轴显示从 1 到 5 的值，y 坐标轴显示相应的平方值。

您可以使用Matplotlib的其他函数和方法自定义图表的样式和外观。

接下来，我们将介绍另一个常用的Python绘图库——Seaborn。

Seaborn是建立在Matplotlib之上的库，它提供了更高级的统计绘图功能，可以用于创建散点图、箱线图、热力图等多种类型的图表。

Seaborn的优点之一是其美观的默认风格，可以帮助您更轻松地创建专业水平的图表。

下面是使用Seaborn创建一个简单箱线图的示例代码：```pythonimport seaborn as sns# 创建数据data = [10, 20, 30, 40, 50]# 创建箱线图sns.boxplot(data)# 显示图表plt.show()```运行上述代码，您将看到一个简单的箱线图，它显示了数据的中位数、四分位数和异常值。

Python绘制参数方程图

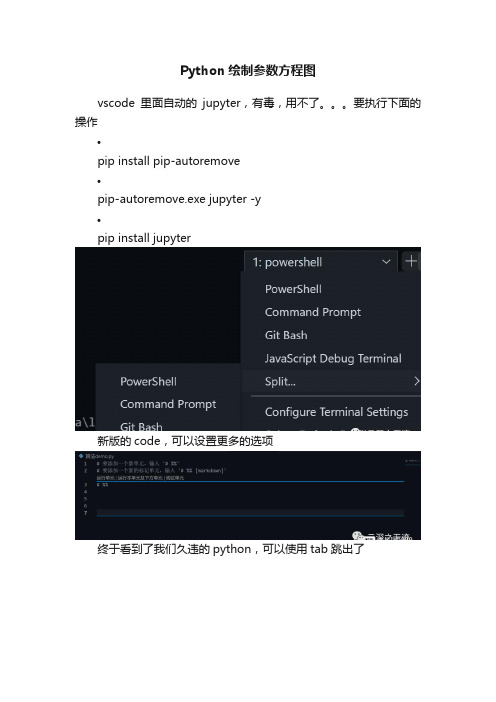
Python绘制参数方程图vscode里面自动的jupyter，有毒，用不了。

要执行下面的操作•pip install pip-autoremove•pip-autoremove.exe jupyter -y•pip install jupyter新版的code，可以设置更多的选项终于看到了我们久违的python，可以使用tab跳出了shift+EnterMarkdown也正常使用••••••••••••••••••••••import matplotlib.pyplot as plt from matplotlib import animation import numpy as np import math def xin(): t = np.linspace(0, math.pi*2, 1000) # 参数方程的范围 x = np.cos(3*t) y = np.sin(2*t) # 参数式 plt.plot(x, y, color='blue', linewidth=2, label='圆') # 传入x，y，颜色是蓝色，线宽，plt.xlabel('t') plt.ylabel('h') # y，x轴的名字 plt.ylim(-1, 1) plt.xlim(-1.5,1.5) # 坐标轴的长度 plt.legend() plt.show() xin()先完整的绘制一个图1.取x点2.书写表达式3.绘制4.美化••x = np.cos(50*t) y = np.sin(39*t)将参数改变，再绘制一次接下来绘制圆的参数方程••••••••#半径r = 2.0# 圆心a, b = (0., 0.)#参数方程theta = np.arange(0, 2*np.pi, 0.01)x = a + r * np.cos(theta)y = b + r * np.sin(theta)很完美•••••••••••••••from math import pi from numpy import cos, sin from matplotlib import pyplot as pltif __name__ == '__main__': '''plot data margin''' angles_circle = [i * pi / 180for i in range(0, 360)] # i先转换成double x = cos(angles_circle) y = sin(angles_circle) plt.plot(x, y, 'r') plt.axis('equal') plt.axis('scaled') plt.show()另外一种绘制圆形的方法~ •••••••••••••••import numpy as npfrom matplotlib import pyplot as pltr=2.0a,b=0.0,0.0# 标准方程x = np.arange(a-r, a+r, 0.01)y = b + np.sqrt(r**2 - (x - a)**2)fig = plt.figure() axes = fig.add_subplot(111)axes.plot(x, y) # 上半部axes.plot(x, -y) # 下半部axes.axis('equal')plt.show()这里是使用的圆的标准方程进行绘制••••••••••import matplotlib.pyplot as pltimport numpy as np# create 1000 equally spaced points between -10 and 10x = np.linspace(-10, 10, 1000)# calculate the y value for each element of the x vectory = x**2 + 2*x + 2fig, ax = plt.subplots()ax.plot(x, y)抛物线••••••••••••••••import matplotlib.pyplot as plta=[]b=[]# y=0# x=-50for x in range(-50,50,1): y=x**2+2*x+2 a.append(x) b.append(y) #x= x+1fig=plt.figure()axes=fig.add_subplot(111)axes.plot(a,b)plt.show() 三个参数，分别代表子图的行数，列数，图索引号因为频繁的出现add_asubplot（）•https:///stable/api/_as_gen/matplotlib.pyplot. subplot.html••••••••••••••••••••import matplotlib.pyplot as plt import numpy as np'''Set the values in the variable xThe function arange helps to generate an array with the following parameters arange(start,end,increment)'''x = np.arange(-100,100,1)'''Now set the formula in the variable y'''y = x**2'''Then add the pair (x,y) to the plot'''plt.plot(x,y)'''Finally show the graph'''plt.show()•••••••••••••import numpy as np import matplotlib.pyplot as pltx = np.arange(0, 100)plt.subplot(221)plt.plot(x, x)plt.subplot(222)plt.plot(x, -x)plt.subplot(223)plt.plot(x, x ** 2)plt.subplot(224)plt.plot(x, np.log(x))plt.show()•••••••••••••••••••••import numpy as npimport matplotlib.pyplot as pltx = np.arange(0, 100)# 首先就是生成点列，xfig = plt.figure()# 创建一个大的画布ax1 = fig.add_subplot(221)ax1.plot(x, x)# 第一个图，直接221的位置ax2 = fig.add_subplot(222)ax2.plot(x, -x)# 222的位置，-的斜率ax3 = fig.add_subplot(223)ax3.plot(x, x ** 2)# 二次函数ax4 = fig.add_subplot(224)ax4.plot(x, np.log(x))# 对数形式plt.show()pyplot的方式中plt.subplot()参数和面向对象中的add_subplot()参数和含义都相同这里针对，子图的绘制函数做了一个简单的绘制~。

Python数据处理——绘制函数图形以及数据拟合

Python数据处理——绘制函数图形以及数据拟合1.多项式拟合对散点进⾏多项式拟合并打印出拟合函数以及拟合后的图形import matplotlib.pyplot as pltimport numpy as npx=np.arange(1,17,1) #⽣成散点列表作为x的值y=np.array([4.00, 6.40, 8.00, 8.80, 9.22, 9.50, 9.70, 9.86, 10.00, 10.20, 10.32, 10.42, 10.50, 10.55, 10.58, 10.60]) #给定y的散点值#⽤3次多项式拟合z1=np.polyfit(x,y,3)p1=np.poly1d(z1)print(p1) #打印拟合的多项式yvals=p1(x) #拟合后的y值plot1=plt.plot(x,y,'r*',label='original values')plot2=plt.plot(x,yvals,'b',label='polyfit values')plt.xlabel('X ')plt.ylabel('Y')# 'best' : 0, (only implemented for axes legends)(⾃适应⽅式)# 'upper right' : 1,# 'upper left' : 2,# 'lower left' : 3,# 'lower right' : 4,# 'right' : 5,# 'center left' : 6,# 'center right' : 7,# 'lower center' : 8,# 'upper center' : 9,# 'center' : 10,plt.legend(loc=3) #设置图⽰的位置plt.title('polyfitting') #设置标题plt.show() #显⽰图⽚plt.savefig('p1.png')2.指定函数拟合#使⽤⾮线性最⼩⼆乘法拟合import matplotlib.pyplot as pltfrom scipy.optimize import curve_fitimport numpy as np#⽤指数形式来拟合x = np.arange(1, 17, 1)y = np.array([4.00, 6.40, 8.00, 8.80, 9.22, 9.50, 9.70, 9.86, 10.00, 10.20, 10.32, 10.42, 10.50, 10.55, 10.58, 10.60]) def func(x,a,b):return a*np.exp(b/x)popt, pcov = curve_fit(func, x, y)a=popt[0]#popt⾥⾯是拟合系数，读者可以⾃⼰help其⽤法b=popt[1]yvals=func(x,a,b)plot1=plt.plot(x, y, '*',label='original values')plot2=plt.plot(x, yvals, 'r',label='curve_fit values')plt.xlabel('x axis')plt.ylabel('y axis')plt.legend(loc=4)#指定legend的位置,读者可以⾃⼰help它的⽤法plt.title('curve_fit')plt.show()plt.savefig('p2.png')。

Python绘制你想要的数学函数图形

Python绘制你想要的数学函数图形Python ⾮常热门，但除⾮⼯作需要没有刻意去了解更多，直到有个函数图要绘制，想起了它。

结果发现，完全⽤不着明⽩什么是编程，就可以使⽤它完成很多数学函数图的绘制。

通过以下两个步骤，就可以进⾏数学函数的绘制了。

两个步骤（1）安装 AnacondaAnaconda 包含了 Python 的运⾏环境、诸多科学计算库以及好些实⽤⼯具，安装它，有当前所需的⼀切。

看它们的翻译，的确也是同类。

下载地址：直接运⾏安装即可，有点⼤。

（2）编织代码运⾏运⾏ Anaconda Navigator，打开界⾯中的 Spyder，如下图：进⼊编辑界⾯，我们以⼀个最简单的 y = x 函数为例输⼊以下代码：import numpy as npimport matplotlib.pyplot as pltx = np.linspace(1, 10, 1000)y = xplt.plot(x,y,'r',linewidth=2)运⾏它就能看到已经有我们想要的结果。

关键解析这⼏⾏代码中，前两⾏是引⼊相应的功能库，Anaconda 已经包含了这些库，复制代码上去即可。

最后⼀⾏是执⾏绘制。

所以关键的代码以下两⾏。

x = np.linspace(1, 10, 1000)y = x⽽第⼀⾏指明的是 x 的取值范围，x = np.linspace(1, 10, 1000)表⽰ x 的取值范围为 1 ⾄ 10，后边那个 1000 指的是细粒度，线是由点构成的，但点是⽆穷的，我们通过有限的点形成线，理论上点定义得越细线越精确。

则我们只剩下第⼆⾏ y = x 的函数部分了，对于 y = f(x) 的函数，仅此⼀处写函数即可。

试试：y = np.sin(x)是不是完全只需要关⼼数据函数，如果你需要的就是这些，⾄此就可以了。

更多控制若需要进⼀步的对坐标进⾏修饰，设置坐标轴标签，精准刻度等，可以参考：更多库功能：numpy 库基础信息可参考：matplotlib.pyplot 库操作可参考：不得不提Anoconda 除了提供 Spyder 编辑⼯具，还提供 Jupyter notebook ⼯具，即所谓有⽂学编程⼯具（左⼿程序员，右⼿作家），了解它可参阅此⽂章：以下为本⽂介绍的⼏个函数通过 Jupyter notebook 形成⽂档的⼀个⽰例：效果如下：。

初中信息技术_《巧用python绘制数学图形》教学课件设计

72°
144° 72°
80°
钝9角星
锐9角星 160°
160
°
已知：正九边形转角度数==360/9=40 钝九角星移动转角度数= （ 40+40 ） = （ 80 ）锐九角星移动转角度数= （ 80+80 ） = （ 160 ）
九边形
turtle right (40) =360/9=40
钝九边星
八边形
turtle right (45） =360/8=45
°
任意多边形的外角和都等于
360度
135°
turtle right (135) =180-45=90+45=135 （180-锐角内角度数）
锐八角星
锐八角星内角=360/8=45
三角形外角等于不相邻的两
个内角和
奇数多角星内角=180/n
turtle.right（ 120 ）顺时针移动120度数。顺时针移动度数=180-多边形内角
思考：在绘制三角形时，小乌龟每次顺时针移动多少度？你能够利用已知的多边形内角计算公式计算出来吗？
A
B
C 多边形内角=（n-2）*180/n
多边形角计算公式
72 转角度数=360/N
想一想，如何让五边形变成五角星呢？
巧用python绘制数学图形
多边形绘制
12 边形
for i in range(1,101) turtle.forward(150) turtle.right(120)
range（）也可以直接写入循环次数，例如range（3），表示循环3次。
绘制三角形时，循环范围值是（ 3 ），又可以写作（ 1 ， 4 ）
偶数多角星内角=360/n