2019年广东省初中学业水平考试数学试卷及答案

2019年广东省中考数学试题(含答案,解析版)

2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用像皮檫干净后，再选涂其他答案，答案不能答在试题上．4．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．﹣2的绝对值是A ．2B ．﹣2C ．21 D ．±2 【答案】A【解析】正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0.【考点】绝对值2．某网店2019年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为A．2.21×106B．2.21×105 C．221×103 D．0.221×106【答案】B【解析】a×10n形式，其中0≤|a|＜10.【考点】科学记数法3．如图，由4个相同正方体组合而成的几何体，它的左视图是【答案】A【解析】从左边看，得出左视图.【考点】简单组合体的三视图4．下列计算正确的是A．b6÷b3=b2B．b3·b3=b9C．a2+a2=2a2D．(a3)3=a6【答案】C【解析】合并同类项：字母部分不变，系数相加减.【考点】同底数幂的乘除，合并同类项，幂的乘方5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是【答案】C【解析】轴对称与中心对称的概念.【考点】轴对称与中心对称6．数据3、3、5、8、11的中位数是A ．3B ．4C ．5D ．6【答案】C【解析】按顺序排列，中间的数或者中间两个数的平均数.【考点】中位数的概念 7．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是A ．a>bB ．|a| < |b|C ．a+b>0D ．ba <0【答案】D【解析】a 是负数，b 是正数，异号两数相乘或相除都得负.【考点】数与代数式的大小比较，数轴的认识8．化简24的结果是A ．﹣4B ．4C ．±4D ．2【答案】B【解析】公式aa2 .【考点】二次根式9．已知x1、x2是一元二次方程了x2﹣2x=0的两个实数根，下列结论错误的是A．x1≠x2B．x12﹣2x1=0 C．x1+x2=2 D．x1·x2=2 【答案】D【解析】因式分解x（x-2）=0，解得两个根分别为0和2，代入选项排除法. 【考点】一元二次方程的解的概念和计算10．如图，正方形ABCD的边长为4，延长CB至E使EB=2，以EB为边在上方作正方形EFGB，延长FG交DC于M，连接AM、AF，H为AD的中点，连接FH分别与AB、AM交于点N、K．则下列结论：①△ANH≌△GNF；②∠AFN=∠HFG；③FN=2NK；④S△AFN: S△ADM =1 : 4．其中正确的结论有A．1个B．2个C．3个D．4个【答案】C【解析】AH=GF=2，∠ANH=∠GNF，∠AHN=∠GFN，△ANH≌△GNF（AAS），①正确；由①得AN=GN=1，∵NG⊥FG，NA不垂直于AF，∴FN不是∠AFG的角平分线，∴∠AFN≠∠HFG，②错误；由△AKH∽△MKF，且AH:MF=1:3，∴KH:KF=1:3，又∵FN=HN，∴K为NH的中点，即FN=2NK，③正确；S△AFN =21AN·FG=1，S△ADM =21DM·AD=4，∴S△AFN : S△ADM =1 :4，④正确.【考点】正方形的性质，平行线的应用，角平分线的性质，全等三角形，相似三角形，三角形的面积二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算20190+(31)﹣1=____________．【答案】4【解析】1+3=4【考点】零指数幂和负指数幂的运算12．如图，已知a ∥b ，∠l=75°，则∠2 =________．【答案】105°【解析】180°-75°=105°.【考点】平行线的性质 13．一个多边形的内角和是1080°，这个多边形的边数是_________．【答案】8【解析】（n-2）×180°=1080°，解得n=8.【考点】n 边形的内角和=（n-2）×180°14．已知x=2y+3，则代数式4x ﹣8y+9的值是___________．【解析】由已知条件得x-2y=3，原式=4（x-2y）+9=12+9=21.【考点】代数式的整体思想15米，在实验楼的15．如图，某校教学楼AC与实验楼BD的水平间距CD=3顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是_________________米（结果保留根号）．【答案】15+153【解析】AC=CD·tan30°+CD·tan45°=15+153.【考点】解直角三角形，特殊三角函数值16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是_____________________（结果用含a、b代数式表示）．【解析】每个接触部分的相扣长度为（a-b ），则下方空余部分的长度为a-2（a-b ）=2b-a ，3个拼出来的图形有1段空余长度，总长度=2a+（2b-a ）=a+2b ；5个拼出来的图形有2段空余长度，总长度=3a+2（2b-a ）=a+4b ；7个拼出来的图形有3段空余长度，总长度=4a+3（2b-a ）=a+6b ；9个拼出来的图形有4段空余长度，总长度=5a+4（2b-a ）=a+8b.【考点】规律探究题型三、解答题（一）（本大题3小题，每小题6分，共18分）17．解不等式组：【答案】解：由①得x ＞3，由②得x ＞1，∴原不等式组的解集为x ＞3.【考点】解一元一次不等式组18．先化简，再求值：4-x x -x 2-x 1-2-x x 22÷⎪⎭⎫ ⎝⎛ ，其中x=2．【答案】解：原式=2-x 1-x 4-x x -x 22÷ =2-x 1-x ×()()()1-x x 2-x 2x + =x 2x +当x=2，原式=222+=2222+=1+2. 【考点】分式的化简求值，包括通分、约分、因式分解、二次根式计算19．如图，在△ABC 中，点D 是AB 边上的一点．（1）请用尺规作图法，在△ABC 内，求作∠ADE ．使∠ADE=∠B ，DE 交AC于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若DB AD=2，求EC AE的值．【答案】解：（1）如图所示，∠ADE 为所求.（2）∵∠ADE=∠B∴DE ∥BC ∴EC AE =DB AD∵DB AD =2 ∴ECAE =2 【考点】尺规作图之作一个角等于已知角，平行线分线段成比例四、解答题（二）（本大题3小题，毎小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x =________，y =_______，扇形图中表示C 的圆心角的度数为_______度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．【答案】解：（1）y=10÷25%=40，x=40-24-10-2=4，C 的圆心角=360°×404=36° （2）画树状图如下：一共有6种可能结果，每种结果出现的可能性相同，其中同时抽到甲、乙的结果有2种∴P （甲乙）=62=31 答：同时抽到甲、乙两名学生的概率为31. 【考点】数据收集与分析，概率的计算21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，己知每个篮球的价格为70元，毎个足球的价格为80元．（1）若购买这两类球的总金额为4600元，篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，最多可购买多少个篮球？【答案】解：（1）设购买篮球x 个，则足球（60-x ）个.由题意得70x+80（60-x ）=4600，解得x=20则60-x=60-20=40.答：篮球买了20个，足球买了40个.（2）设购买了篮球y 个.由题意得 70y ≤80（60-x ），解得y ≤32答：最多可购买篮球32个.【考点】一元一次方程的应用，一元一次不等式的应用22．在如图所示的网格中，每个正方形的连长为1，每个小正方形的顶点叫格点，△ABC 的三个顶点均在格点上，以点A 为圆心的⌒EF 与BC 相切于点D ，分别交AB 、AC 于点E 、F ．（1）求△ABC 三边的长；（2）求图中由线段EB 、BC 、CF 及⌒FE 所围成的阴影部分的面积．【答案】解：（1）由题意可知，AB=2262+=102，AC=2262+=102， BC=2284+=54（2）连接AD由（1）可知，AB2+AC2=BC2，AB=AC∴∠BAC=90°，且△ABC 是等腰直角三角形∵以点A 为圆心的⌒EF 与BC 相切于点D∴AD ⊥BC∴AD=21BC=52 （或用等面积法AB ·AC=BC ·AD 求出AD 长度） ∵S 阴影=S △ABC －S 扇形EAFS △ABC =21×102×102=20 S 扇形EAF =()25241π =5π ∴S 阴影=20－5π【考点】勾股定理及其逆定理，阴影面积的计算包括三角形和扇形的面积公式五、解答题（三）（本大题3小题，毎小题7分，共21分）23．如图，一次函数y=k 1x+b 的图象与反比例函数y=xk 2的图象相交于A 、B 两点，其中点A 的坐标为（﹣1，4），点B 的坐标为（4，n ）．（1）根据函数图象，直接写出满足k 1x+b>xk 2的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且S △AOP : S △BOP =1 : 2，求点P 的坐标．【答案】解：（1）x ＜-1或0＜x ＜4（2）∵反比例函数y=xk 2图象过点A （﹣1，4） ∴4=1-k 2，解得k 2=﹣4 ∴反比例函数表达式为x4-y = ∵反比例函数x4-y =图象过点B （4，n ） ∴n=44-=﹣1，∴B （4，﹣1） ∵一次函数y=k 1x+b 图象过A （﹣1，4）和B （4，﹣1）∴⎩⎨⎧+=+=bk 41-b -k 411，解得⎩⎨⎧==3b 1-k 1 ∴一次函数表达式为y=﹣x+3（3）∵P 在线段AB 上，设P 点坐标为（a ，﹣a+3）∴△AOP 和△BOP 的高相同∵S △AOP : S △BOP =1 : 2∴AP : BP=1 : 2过点B 作BC ∥x 轴，过点A 、P 分别作AM ⊥BC ，PN ⊥BC 交于点M 、N∵AM ⊥BC ，PN ⊥BC ∴BNMN BP AP = ∵MN=a+1，BN=4-a ∴21a -41a =+，解得a=32 ∴-a+3=37 ∴点P 坐标为（32，37）（或用两点之间的距离公式AP=()()224-3a -1a +++，BP=()()223-a 1-a -4++，由21BP AP =解得a 1=32，a 2=-6舍去）【考点】一次函数和反比例函数的数形结合，会比较函数之间的大小关系，会求函数的解析式，同高的三角形的面积比与底边比的关系24．如题24-1图，在△ABC 中，AB=AC ，⊙O 是△ABC 的外接圆，过点C 作∠BCD=∠ACB 交⊙O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF=AC ，连接AF ．（1）求证：ED=EC ；（2）求证：AF是⊙O的切线；（3）如题24-2图，若点G是△ACD的内心，BC·BE=25，求BG的长．【答案】（1）证明：∵AB=AC∴∠B==∠ACB∵∠BCD=∠ACB∴∠B=∠BCD∵⌒AC=⌒AC∴∠B=∠D∴∠BCD=∠D ∴ED=EC （2）证明：连接AO并延长交⊙O于点G，连接CG 由（1）得∠B=∠BCD∴AB∥DF∵AB=AC，CF=AC∴AB=CF∴四边形ABCF是平行四边形∴∠CAF=∠ACB∵AG为直径∴∠ACG=90°，即∠G+∠GAC=90°∵∠G=∠B，∠B=∠ACB∴∠ACB+∠GAC=90°∴∠CAF+∠GAC=90°即∠OAF=90°∵点A在⊙O上∴AF是⊙O的切线（3）解：连接AG∵∠BCD=∠ACB ，∠BCD=∠1∴∠1=∠ACB∵∠B=∠B∴△ABE ∽△CBA ∴BCAB AB BE ∵BC ·BE=25∴AB 2=25∴AB=5∵点G 是△ACD 的内心∴∠2=∠3∵∠BGA=∠3+∠BCA=∠3+∠BCD=∠3+∠1=∠3+∠2=∠BAG∴BG=AB=5【考点】圆的综合应用，等弧等弦等角的转换，切线的证明，垂径定理的逆应用，内心的概念，相似三角形的应用，外角的应用，等量代换的意识25．如题25-1图，在平面直角坐标系中，抛物线y=837 -x 433x 832+与x 轴交于点A 、B(点A 在点B 右侧)，点D 为抛物线的顶点．点C 在y 轴的正半轴上，CD 交x 轴于点F ，△CAD 绕点C 顺时针旋转得到△CFE ，点A 恰好旋转到点F ，连接BE ．（1）求点A 、B 、D 的坐标；（2）求证：四边形BFCE 是平行四边形；（3）如题25-2图，过顶点D 作DD 1⊥x 轴于点D 1，点P 是抛物线上一动点，过点P 作PM ⊥ x 轴，点M 为垂足，使得△PAM 与△DD 1A 相似（不含全等）．①求出一个满足以上条件的点P 的横坐标；②直接回答．．．．这样的点P 共有几个？【答案】（1）解：由y=837 -x 433x 832+=()32-3x 83+得点D 坐标为（﹣3，32）令y=0得x 1=﹣7，x 2=1∴点A 坐标为（﹣7，0），点B 坐标为（1，0）（2）证明：过点D 作DG ⊥y 轴交于点G ，设点C 坐标为（0，m ）∴∠DGC=∠FOC=90°，∠DCG=∠FCO∴△DGC ∽△FOC ∴COCG FO DG = 由题意得CA=CF ，CD=CE ，∠DCA=∠ECF ，OA=1，DG=3，CG=m+32 ∵CO ⊥FA∴FO=OA=1 ∴m 32m 13+=，解得m=3 （或先设直线CD 的函数解析式为y=kx+b ，用D 、F 两点坐标求出y=3x+3，再求出点C 的坐标）∴点C 坐标为（0，3）∴CD=CE=()223233++=6 ∵tan ∠CFO=FO CO =3∴∠CFO=60°∴△FCA 是等边三角形∴∠CFO=∠ECF∴EC ∥BA∵BF=BO －FO=6∴CE=BF∴四边形BFCE 是平行四边形（3）解：①设点P 坐标为（m ，837-m 433m 832+），且点P 不与点A 、B 、D 重合．若△PAM 与△DD 1A 相似，因为都是直角三角形，则必有一个锐角相等．由（1）得AD 1=4，DD 1=32（A ）当P 在点A 右侧时，m ＞1 （a ）当△PAM ∽△DAD 1，则∠PAM=∠DAD 1，此时P 、A 、D 三点共线，这种情况不存在（b ）当△PAM ∽△ADD 1，则∠PAM=∠ADD 1，此时11DD AD AM PM = ∴3241-m 837-m 433m 832=+，解得m 1=35-（舍去），m 2=1（舍去），这种不存在（B ）当P 在线段AB 之间时，﹣7＜m ＜1 （a ）当△PAM ∽△DAD 1，则∠PAM=∠DAD 1，此时P 与D 重合，这种情况不存在第 21 页（共 21 页）（b ）当△PAM ∽△ADD 1，则∠PAM=∠ADD 1，此时11DD AD AM PM = ∴3241-m 837-m 433m 832=+，解得m 1=35-，m 2=1（舍去）（C ）当P 在点B 左侧时，m ＜﹣7（a ）当△PAM ∽△DAD 1，则∠PAM=∠DAD 1，此时11AD DD AM PM = ∴﹣3241-m 837-m 433m 832=+432，解得m 1=﹣11，m 2=1（舍去）（b ）当△PAM ∽△ADD 1，则∠PAM=∠ADD 1，此时11DD AD AM PM = ∴﹣3241-m 837-m 433m 832=+，解得m 1=337-，m 2=1（舍去）综上所述，点P 的横坐标为35-，﹣11，337-，三个任选一个进行求解即可． ②一共存在三个点P ，使得△PAM 与△DD 1A 相似．【考点】二次函数的综合应用，旋转的性质，相似三角形的的应用，等边三角形的性质，平行四边形的证明，平面直角坐标的灵活应用，动点问题，分类讨论思想。

(完整版)2019年广东省初中学业水平考试(数学)试卷及答案

2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动，用橡皮擦干净后,再选涂其他答案,答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时,将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分,共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．-2的绝对值是（A）A．2 B．-2 C．12D．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为（B）A．2。

21×106 B．2。

21×105 C．221×103 D．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是（A）4．下列计算正确的是(C ） A ．632b b b ÷=B ．339b b b ⋅=C ．2222a a a +=D ．()363a a =5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C ）6．数据3、3、5、8、11的中位数是（C ） A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是（D ）A ．a b >B ．a b <C ．0a b +>D ．0a b<824的结果是(B ) A ．-4B ．4C ．±4D ．29．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（D ） A ．12x x ≠ B ．2112=0x x - C ．12=2x x +D ．12=2x x ⋅10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：ANH GNF ①≌△△ ;AFN HFG ∠=∠② ；2FN NK =③；:1:4AFN ADM S S =④△△．其中正确的结论有（C ）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题6小题,每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算：1120193-⎛⎫+ ⎪⎝⎭= ．答案：4解析：本题考查了零次幂和负指数幂的运算12．如图，已知a b ，175∠=°，则∠2＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算13．一个多边形的内角和是1080︒ ，这个多边形的边数是．答案：8解析:本题考查了多边形内角和的计算公式14．已知23x y =+，则代数式489x y -+的值是．答案：21解析：整体思想，考查了整式的运算15．如图,某校教学楼AC 与实验楼BD 的水平间距CD=153米，在实验楼顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是米（结果保留根号) ．答案：()15153+解析：本题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角,长度如图所示，小明按题16—2图所示方法玩拼图游戏,两两相扣,相互间不留空隙，那么小明用9个这样的图形(题16-1图）拼出来的图形的总长度是（结果用含a 、b 代数式表示）．答案:8a b +解析：本题考查了轴对称图形的性质,根据题目找规律三、解答题（一)（本大题3小题，每小题6分，共18分）17．解不等式组：()12214x x ->⎧⎨+>⎩①②解 ①21>-x x >3 ②4)1(2>+x 422>+x 22>x 1>x∴该不等式组的解集是x >318．先化简,再求值：221224xx x x x x -⎛⎫-÷ ⎪---⎝⎭,其中x 解原式=)1()2)(2(21--+⋅--x x x x x x =xx 2+ 当2=x原式=222+ =2222+ =21+19．如图，在ABC △中，点D 是AB 边上的一点．（1)请用尺规作图法，在ABC △内,求作∠ADE ，使∠ADE =∠B ，DE 交AC 于E ;（不要求写作法，保留作图痕迹)（2)在（1)的条件下，若2AD DB =,求AEEC的值．解（1）如图（2）A A B ADE ∠=∠∠=∠,ADE ∆∴∽ABC ∆ 2==∴DBADEC AE四、解答题（二）（本大题3小题，每小题7分，共21分)20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示,根据图表信息解答下列问题:（1）x = ，y = ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法,求同时抽到甲、乙两名学生的概率．解 (1) 4x = ； 40y = ; 36（2）解：由题意可知树状图为由树状图可知,同时抽到甲、乙两名学生的概率为21 = 63答:同时抽到甲、乙两名学生的概率为13。

2019年广东省初中学业水平考试(数学)试卷及答案

2019年广东省初中学业水平考试数学说明：．全卷共页，满分为 分，考试用时为 分钟．．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用 铅笔把对应该号码的标号涂黑．．选择题每小题选出答案后，用 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题 小题，每小题分，共 分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．． 的绝对值是（✌）✌．．  ．12．±．某网店 年母亲节这天的营业额为 元，将数 用科学记数法表示为（）✌．  ．  ． ． ．如图，由个相同正方体组合而成的几何体，它的左视图是（✌）．下列计算正确的是（）✌．632b b b ÷= ．339b b b ⋅= ．2222a a a += ．()363a a =．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（）．数据、、、、 的中位数是（）✌．．．．．实数♋、♌在数轴上的对应点的位置如图所示，下列式子成立的是（）✌．a b > ．a b <．0a b +> ．0ab< 24（）✌．  ．．  ．．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（） ✌．12x x ≠ ．2112=0x x -．12=2x x + ．12=2x x ⋅．如图，正方形✌的边长为，延长 至☜使☜，以☜为边在上方作正方形☜☞☝，延长☞☝交于，连接✌、✌☞，☟为✌的中点，连接☞☟分别与✌、✌交于点☠、．则下列结论：ANH GNF ①≌△△ ；AFN HFG ∠=∠② ；2FN NK =③；:1:4AFN ADM S S =④△△．其中正确的结论有（）✌．个．个．个．个二、填空题（本大题小题，每小题分，共 分）请将下列各题的正确答案填写在答题卡相应的位置上．．计算：1120193-⎛⎫+ ⎪⎝⎭ ．答案：解析：本题考查了零次幂和负指数幂的运算．如图，已知a b ，175∠=°，则∠ ＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算．一个多边形的内角和是1080︒ ，这个多边形的边数是．答案：解析：本题考查了多边形内角和的计算公式．已知23-+的值是．x yx y=+，则代数式489答案： 解析：整体思想，考查了整式的运算．如图，某校教学楼✌与实验楼 的水平间距 153米，在实验楼顶部点测得教学楼顶部✌点的仰角是 °，底部点的俯角是 °，则教学楼✌的高度是米（结果保留根号）．答案：()+15153解析：本题利用了特殊三角函数值解决实际问题．如题 图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题 图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用个这样的图形（题 图）拼出来的图形的总长度是（结果用含♋、♌代数式表示）．答案：8a b +解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题小题，每小题分，共 分）．解不等式组：()12214x x ->⎧⎨+>⎩①②解 ①21>-x⌧  ②4)1(2>+x 422>+x 22>x 1>x∴该不等式组的解集是⌧ ．先化简，再求值：221224xx x x x x -⎛⎫-÷ ⎪---⎝⎭，其中x 解原式)1()2)(2(21--+⋅--x x x x x x xx 2+ 当2=x原式222+2222+ 21+．如图，在ABC △中，点是✌边上的一点．（）请用尺规作图法，在ABC △内，求作∠✌☜，使∠✌☜ ∠ ， ☜交✌于☜；（不要求写作法，保留作图痕迹）（）在（）的条件下，若2AD DB =，求AEEC的值．解（）如图（2）A A B ADE ∠=∠∠=∠,ADE ∆∴∽ABC ∆2==∴DBADEC AE四、解答题（二）（本大题小题，每小题分，共 分）．为了解某校九年级全体男生 米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为✌、、、四个等级，绘制如下不完整的统计图表，如题 图表所示，根据图表信息解答下列问题：（）⌧ ，⍓ ，扇形图中表示的圆心角的度数为度；（）甲、乙、丙是✌等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．解 ☎✆ 4x = ； 40y =  ☎✆解：由题意可知树状图为由树状图可知，同时抽到甲、乙两名学生的概率为21 =63答：同时抽到甲、乙两名学生的概率为13。

(完整版)2019广东省中考数学试卷及答案

2019 年广东省初中学业水平考试数学说明：1．全卷共 4 页，满分为120 分，考试用时为100 分钟．2. 答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3. 选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；准使用铅笔和涂改液．按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10 小题，每小题 3 分，共30 分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1. -2 的绝对值是A ．2B ．-2 C．12D ．±22. 某网店2019 年母亲节这天的营业额为221000 元，将数221000 用科学记数法表示为A ．2.21 ×160B ．2.21 ×150 C．221 ×130 D ．0.221 ×1603. 如图，由 4 个相同正方体组合而成的几何体，它的左视图是4. 下列计算正确的是6 3 2 3 3 9 2 2 2 3 36A ．b b bB ．b b b C．a a 2a D ． a a5. 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是221 212 1 16. 数据 3、3、5、8、 11 的中位数是A ． 3B ． 4C ． 5D ． 67．实数 a 、b 在数轴上的对应点的位置如图所示，下列式孑成立的是A ． a bB ． a bC. a b 0D.a 0b8. 化简 4 的结果是A ． -4B ． 4C ． ± 4D ． 29. 己知 x 、 x 是一元二次方程 x 2x 0 的两个实数根，下列结论错误．．的是A ． x xB ． x 22 x =0C ． x 1 x 2 =2D ． x 1 x 2 =210. 如图，正方形 ABCD 的边长为 4，延长 CB 至 E 使 EB=2 ，以 EB 为边在上方作正方形 EFGB ，延长 FG交 DC 于 M ，连接 AM 、 AF ， H 为 AD 的中点，连接 FH 分别与 AB 、AM 交于点 N 、K ．则下列结论：① V ANH ≌VGNF ； ② AFNHFG ； ③FN2NK ； ④S V AFN : S VADM 1: 4 ．其中正确的结论有A ． 1 个B ． 2 个C ． 3 个D ． 4 个二、填空题（本大题 6 小题，每小题 4 分，共 24 分）请将下列各题的正确答案填写在答题卡相应的位置上．11. 计算： 1201901 = ．312．如图，己知 a Pb ， 1 75 °，则∠2＝．13. 一个多边形的内角和是1080 ，这个多边形的边数是．14. 己知x 2 y 3 ，则代数式 4 x 8y 9 的值是．15. 如图，某校教学楼AC 与实验楼BD 的水平间距CD= 15 3 米，在实验楼顶部 B 点测得教学楼顶部 A 点的仰角是30°，底部 C 点的俯角是45°，则教学楼AC 的高度是米（结果保留根号）．16. 如题16-1 图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2 图所示方法玩拼图游戏，两两相扣，相互间留空隙，那么小明用9 个这样的图形（题16-1 图）拼出来的图形的总长度是（结果用含a、b 代数式表示）．三、解答题（一）（本大题 3 小题，每小题 6 分，共18 分）17. 解等式组：x 1 2 ①2 x 1 4 ②18. 先化简，再求值：x 1x 2 x 2x2 xx2 4，其中x= 2 ．19. 如图，在VABC 中，点D 是AB 边上的一点．（1）请用尺规作图法，在VABC 内，求作∠ ADE ，使∠ ADE =∠B，DE 交AC 于E；（要求写作法，保留作图痕迹）AD（2）在（1）的条件下，若 2 ，求DB AE的值．EC四、解答题（二）（本大题 3 小题，每小题7 分，共21 分）20. 为了解某校九年级全体男生1000 米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A、B、C、D 四个等级，绘制如下完整的统计图表，如题20 图表所示，根据图表信息解答下列问题：（1）x= ，y= ，扇形图中表示 C 的圆心角的度数为度；（2）甲、乙、丙是 A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．21. 某校为了开展“阳光体育运动”，计划购买篮球、足球共60 个，己知每个篮球的价格为70 元，每个足球的价格为80 元．（1）若购买这两类球的总金额为4600 元，求篮球、足球各买了多少个？（2）若购买篮球的总金额超过购买足球的总金额，求最多可购买多少个篮球？22. 在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，在格点上，以点 A 为圆心的?EF 与BC 相切于点 D ，分别交AB、AC 于点E、F．VABC 的三个顶点均（1）求VABC 三边的长；（2）求图中由线段EB 、BC、CF 及F?E 所围成的阴影部分的面积．五、解答题（三）（本大题 3 小题，每小题9 分，共27 分）k2 23. 如图，一次函数y=k1x+b 的图象与反比例函数y 4），点 B 的坐标为（4，n）．的图象相交于A、B 两点，其中点 A 的坐标为（-1，x（1）根据图象，直接写出满足（2）求这两个函数的表达式；k1x bk2的x 的取值范围；x（3）点P 在线段AB 上，且S AOP : S B OP 1: 2 ，求点P 的坐标．24. 如题24-1 图，在VABC 中，AB =AC，⊙O 是VABC 的外接圆，过点 C 作∠BCD =∠ACB 交⊙O 于点D ，连接AD 交BC 于点E，延长DC 至点F，使CF=AC，连接AF．（1）求证：ED =EC；（2）求证：AF 是⊙ O 的切线；（3）如题24-2 图，若点G 是VACD 的内心，BC BE 25，求BG 的长．25. 如题25-1 图，在平面直角坐标系中，抛物线y3x2 3 3 x7 3与x 轴交于点A、B（点 A 在点 B 8 4 8右侧），点 D 为抛物线的顶点．点 C 在y 轴的正半轴上，CD 交x 轴于点F，VCAD 绕点 C 顺时针旋转得到VCFE ，点A 恰好旋转到点F，连接BE．（1）求点A、B、D 的坐标；（2）求证：四边形BFCE 是平行四边形；（3）如题25-2 图，过顶点 D 作DD1 x 轴于点D1，点P 是抛物线上一动点，过点P 作PM x 轴，点M 为垂足，使得VPAM 与VDD1 A 相似（含全等）．①求出一个满足以上条件的点P 的横坐标；②直．接．回．答．这样的点P 共有几个？二、填空题11、答案：4解析：本题考查了零次幂和负指数幂的运算12、答案：105解析：本题考查了平行线的性质，互为补角的计算13、答案：8解析：本题考查了多边形内角和的计算公式14、答案：21解析：整体思想，考查了整式的运算15、答案：15 15 3解析：本题利用了特殊三角函数值解决实际问题16、答案： a 8b三解答题（一）17、解：①得：x 3①得：x 1① 等式组的解集为：x 318、解：原式=xx 12( x 2)( x 2)x( x 1)= x 2x当x 2 时原式= 2 222=222=1 22019 广东省中考数学答案一、选择题1 2 3 4 5 6 7 8 9 10A B A C C C D B D C19、解：（1）如图所示：①ADE 即为所求。

2019年广东省初中学业水平考试(数学)试卷及答案(可编辑修改word版)

2019 年广东省初中学业水平考试数学说明：1．全卷共4 页，满分为120 分，考试用时为100 分钟．2.答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10 小题，每小题3 分，共30 分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．-2 的绝对值是（A）A．2 B．-2 C．12D．±22.某网店2019 年母亲节这天的营业额为221000 元，将数221000 用科学记数法表示为（B）A．2.21×106 B．2.21×105 C．221×103 D．0.221×1063.如图，由4 个相同正方体组合而成的几何体，它的左视图是（A）4.下列计算正确的是（C）A.b6÷b3=b2B.b3⋅b3=b9C．a2+a2= 2a2D．(a3 )3 =a642 5. 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C ）6. 数据 3、3、5、8、11 的中位数是（C ）A ．3B ．4C ．5D ．67. 实数 a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是（D ）A ． a > bB ． a < bC ． a + b > 0D ． a < 0b8. 化简的结果是（B ）A ．-4B ．4C ．±4D ．29. 已知 x 、 x 是一元二次方程 x 2 - 2x = 0 的两个实数根，下列结论错误的是（D ） 1 2A. x ≠ x B ． x 2 - 2x =0 1 2 1 1C ． x 1 + x 2 =2D ． x 1 ⋅ x 2 =210. 如图，正方形 ABCD 的边长为 4，延长 CB 至 E 使 EB=2，以 EB 为边在上方作正方形 EFGB ，延长 FG 交 DC 于 M ，连接 AM 、AF ，H 为 AD 的中点，连接 FH 分别与 AB 、AM 交于点 N 、K ．则下列结论： ①△ANH ≌△GNF； ②∠AFN = ∠HFG ； ③FN = 2NK ； ④S △AFN : S △ADM = 1: 4 ．其中正确的结论有（C ）3 A.1 个 B ．2 个 C ．3 个 D ．4 个二、填空题（本大题 6 小题，每小题 4 分，共 24 分）请将下列各题的正确答案填写在答题卡相应的位置上． ⎛ 1 ⎫-111．计算： 20190 + ⎪ ⎝ 3 ⎭答案：4= ．解析：本题考查了零次幂和负指数幂的运算12．如图，已知 a b ，∠1 = 75 °，则∠2＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算13. 一个多边形的内角和是1080︒答案：8，这个多边形的边数是．解析：本题考查了多边形内角和的计算公式14. 已知 x = 2 y + 3 ，则代数式4x - 8 y + 9 的值是．答案：21解析：整体思想，考查了整式的运算15. 如图，某校教学楼 AC 与实验楼 BD 的水平间距 CD=15 米，在实验楼顶部 B 点测得教学楼顶部 A 点的仰角是 30°，底部 C 点的俯角是 45°，则教学楼 AC 的高度是米（结果保留根号）．答案： (15 + 15 3 )⎩ 解析：本题利用了特殊三角函数值解决实际问题16. 如题 16-1 图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题 16-2 图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用 9 个这样的图形（题 16-1图）拼出来的图形的总长度是（结果用含 a 、b 代数式表示）．答案： a + 8b解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题 3 小题，每小题 6 分，共 18 分）⎧x -1 > 2 ① 17．解不等式组： ⎨2 ( x +1) > 4 ②解 ① x -1 > 2x >3② 2(x +1) > 42x + 2 > 42x > 2x > 12 ∴该不等式组的解集是 x >3⎛ x - 1⎫÷ x 2- x 18. 先化简，再求值： x - 2 x - 2 ⎪ x 2 - 4 ，其中 x = ．⎝ ⎭解原式= x -1 ⋅ (x + 2)(x - 2)x - 2= x + 2xx (x -1)当 x =原式== 2 + 2 22=1+19. 如图，在△ABC 中，点 D 是 AB 边上的一点．（1）请用尺规作图法，在△ABC 内，求作∠ADE ，使∠ADE =∠B ，DE 交 AC 于 E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若 AD = 2 ，求 AE 的值．DB EC22 + 222解（1）如图（2） ∠ADE =∠B, ∠A =∠A ∴∆ADE ∽∆ABC∴AE=AD= 2 EC DB四、解答题（二）（本大题3 小题，每小题7 分，共21 分）20.为了解某校九年级全体男生1000 米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A、B、C、D 四个等级，绘制如下不完整的统计图表，如题20 图表所示，根据图表信息解答下列问题：（1）x= ，y= ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．⎩⎩ 解 (1) x = 4 ；y = 40 ; 36(2)解：由题意可知树状图为由树状图可知，同时抽到甲、乙两名学生的概率为 1答：同时抽到甲、乙两名学生的概率为。

2019年广东省中考数学试卷-答案

广东省2019年初中毕业生学业水平考试数学答案解析第Ⅰ卷一、选择题1.【答案】A【解析】根据数轴上某个数与原点的距离叫做这个数的绝对值的定义，在数轴上，点2-到原点的距离是2，所以2-的绝对值是2，【考点】绝对值的概念。

2.【答案】B【解析】科学记数法的表示形式为10n a ⨯的形式，其中110a ≤＜，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值1＞时，n 是正数；当原数的绝对值1＜时，n 是负数．221 000的小数点向左移动5位得到2.21，所以221 000用科学记数法表示为52.2110⨯，【考点】科学记数法的表示方法。

3.【答案】A【解析】根据左视图是从左面看得到的图形，结合所给图形以及选项进行求解即可.观察图形，从左边看得到两个叠在一起的正方形，如下图所示：，【考点】简单几何体的三视图。

4.【答案】C【解析】根据同底数幂除法法则、同底数幂乘法法则、合并同类项法则、幂的乘方法则逐一进行计算即可得.A.633b b b ÷=，故A 选项错误；B.336b b b ⋅=，故B 选项错误；C.2222a a a +=，正确；D.()339a a =，故D 选项错误，【考点】同底数幂的乘除法，幂的乘方等运算。

5.【答案】C【解析】根据轴对称图形和中心对称图形的概念逐一进行判断即可得.A 、是轴对称图形，不是中心对称图形，故不符合题意；B 、是轴对称图形，不是中心对称图形，故不符合题意；C 、是轴对称图形，也是中心对称图形，故符合题意；D 、是轴对称图形，不是中心对称图形，故不符合题意，【考点】轴对称图形和中心对称图形。

6.【答案】C【解析】根据中位数的定义进行求解即可。

从小到大排序：3、3、5、8、11，位于最中间的数是5，所以这组数据的中位数是5，【考点】中位数。

7.【答案】D【解析】先由数轴上a ，b 两点的位置确定A ，b 的取值范围，再逐一验证即可求解．由数轴上a ，b 两点的位置可知21a --＜＜，01b ＜＜，所以a b ＜，故A 选项错误；a b ＞，故B 选项错误；0a b +＜，故C 选项错误；0a b＜，故D 选项正确，【考点】实数与数轴，实数的大小比较、实数的运算等。

2019年广东省初中毕业生学业考试数学试题及答案(Word版)

2019年广东省初中毕业生学业考试数学试题及答案（Word 版）一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑. 1. 2的相反数是 A.21-B. 21C.－2D.22.下列几何体中,俯视图为四边形的是3.据报道,2018年第一季度,广东省实现地区生产总值约1 260 000 000 000元,用科学记数法表示为 A. 0.126×2018元 B. 1.26×2018元 C. 1.26×2018元 D. 12.6×2018元4.已知实数a 、b ，若a >b ，则下列结论正确的是 A.55-<-b a B.b a +<+22 C.33ba < D.b a 33> 5.数据1、2、5、3、5、3、3的中位数是A.1B.2C.3D.56.如题6图,AC ∥DF,AB ∥EF,点D 、E 分别在AB 、AC 上，若∠2=50°，则∠1的大小是 A.30° B.40° C.50° D.60°7.下列等式正确的是A.1)1(3=-- B. 1)4(0=- C. 6322)2()2(-=-⨯- D. 2245)5()5(-=-÷-8.不等式5215+>-x x 的解集在数轴上表示正确的是9.下列图形中,不是．．轴对称图形的是10.已知210k k <<,则是函数11-=x k y 和xk y 2=的图象大致是二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上.11.分解因式：92-x =________________.12.若实数a 、b 满足042=-++b a ，则=ba 2________. 13.一个六边形的内角和是__________.14.在Rt △ABC 中,∠ABC=90°,AB=3,BC=4,则sinA=________.15.如题15图，将一张直角三角板纸片ABC 沿中位线DE 剪开后,在平面上将△BDE 绕着CB 的中点D 逆时针旋转180°,点E 到了点E ′位置, 则四边形ACE ′E 的形状是________________.16.如题16图,三个小正方形的边长都为1,则图中阴影部分面积的和是__________(结果保留π). 三、解答题（本大题3小题，每小题5分，共15分）17.解方程组⎩⎨⎧=++=821y x y x 18.从三个代数式：①222b ab a +-，②b a 33-，③22b a -中任意选择两个代数式构造成分式，然后进行化简，并求当3,6==b a 时该分式的值.19.如题19图，已知□ABCD.(1)作图:延长BC,并在BC 的延长线上截取线段CE,使得CE=BC (用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,不连结AE,交CD 于点F,求证:△AFD ≌△EFC.四、解答题（本大题3小题，每小题8分，共24分）20.某校教导处为了解该校七年级同学对排球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情况（每位同学必须且只能选择最喜爱的一项运动项目），进行了随机抽样调查，并将调查结果统计后绘制成了如【表1】和题20图所示的不完整统计图表. (1)请你补全下列样本人数分布表（【表1】）和条形统计图（题20图）；（2）若七年级学生总人数为920人，请你估计七年级学生喜爱羽毛球运动项目的人数.21.雅安地震牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动.第一天收到捐款10 000元，第三天收到捐款12 100元.①②（1）如果第二天、第三天收到捐款的增长率相同，求捐款增长率；（2）按照（1）中收到捐款的增长速度，第四天该单位能收到多少捐款？22.如题22图，矩形ABCD 中,以对角线BD 为一边构造一个矩形BDEF,使得另一边EF 过原矩形的顶点C.(1)设Rt △CBD 的面积为S 1, Rt △BFC 的面积为S 2, Rt △DCE 的面积为S 3 , 则S 1______ S 2+ S 3(用“>”、“=”、“<”填空)；（2）写出题22图中的三对相似三角形，并选择其中一对进行证明.五、解答题（本大题3小题，每小题9分，共27分）23. 已知二次函数1222-+-=m mx x y .（1）当二次函数的图象经过坐标原点O(0,0)时,求二次函数的解析式; (2)如题23图,当2=m 时,该抛物线与y 轴交于点C,顶点为D, 求C 、D 两点的坐标;(3)在(2)的条件下,x 轴上是否存在一点P,使得PC+PD 最短?若P 点存在,求出P 点的坐标;若P 点不存在,请说明理由.24.如题24图,⊙O 是Rt △ABC 的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5, BE ⊥DC 交DC 的延长线于点E. (1)求证：∠BCA=∠BAD; (2)求DE 的长;(3)求证:BE 是⊙O 的切线.25.有一副直角三角板,在三角板ABC 中,∠BAC=90°,AB=AC=6,在三角板DEF 中,∠FDE=90°,DF=4,DE=34.将这副直角三角板按如题25图(1)所示位置摆放,点B 与点F 重合,直角边BA 与FD 在同一条直线上.现固定三角板ABC,将三角板DEF 沿射线BA 方向平行移动,当点F 运动到点A 时停止运动.(1)如题25图(2),当三角板DEF 运动到点D 与点A 重合时,设EF 与BC 交于点M, 则∠EMC=______度； (2)如题25图（3），在三角板DEF 运动过程中,当EF 经过点C 时,求FC 的长;(3)在三角板DEF 运动过程中,设BF=x ,两块三角板重叠部分面积为y ,求y 与x 的函数解析式,并求出对应的x 取值范围.FED CBA参考答案一、C D B D C C B A C A二、11.)3)(3(-+x x ；12. 1；13. 720°；14.54；15.平行四边形；16.83π 三、17.⎩⎨⎧==23y x ；18.选取①、②得3)(3)(332222b a b a b a b a b ab a -=--=-+-，当3,6==b a 时，原式=1336=-（有6种情况）. 19. (1)如图所示,线段CE 为所求;(2)证明:在□ABCD 中,AD ∥BC,AD=BC.∴∠CEF=∠DAF ∵CE=BC,∴AD=CE,又∵∠CFE=∠DFA,∴△AFD ≌△EFC. 20.(1)30%、10、50；图略；（2）276（人）. 21.（1）10%；（2）20180×（1+0.1）=20180（元）. 22.（1） S 1= S 2+ S 3；（2）△BCF ∽△DBC ∽△CDE; 选△BCF ∽△CDE证明:在矩形ABCD 中,∠BCD=90°且点C 在边EF 上,∴∠BCF+∠DCE=90° 在矩形BDEF 中,∠F=∠E=90°,∴在Rt △BCF 中，∠CBF+∠BCF=90° ∴∠CBF=∠DCE,∴△BCF ∽△CDE.23.(1)m=±1,二次函数关系式为x x y x x y 2222-=+=或；（2）当m=2时，1)2(3422--=+-=x x x y ，∴D(2,－1);当0=x 时，3=y ，∴C(0,3). (3)存在.连结C 、D 交x 轴于点P,则点P 为所求,由C(0,3)、D(2,－1)求得直线CD 为32+-=x y 当0=y 时,23=x ,∴P(23,0). 24.(1)∵AB=DB,∴∠BDA=∠BAD,又∵∠BDA=∠BCA,∴∠BCA=∠BAD. (2)在Rt △ABC 中，AC=135122222=+=+BC AB ,易证△ACB ∽△DBE,得ACBDAB DE =, ∴DE=13144131212=⨯ (3)连结OB,则OB=OC,∴∠OBC=∠OCB,∵四边形ABCD 内接于⊙O,∴∠BAC+∠BCD=180°,NA FD BA 又∵∠BCE+∠BCD=180°,∴∠BCE=∠BAC,由(1)知∠BCA=∠BAD,∴∠BCE=∠OBC,∴OB ∥DE ∵BE ⊥DE,∴OB ⊥BE,∴BE 是⊙O 的切线.25. 解：（1）15；（2）在Rt △CFA 中,AC=6,∠ACF=∠E=30°,∴FC=30cos AC=6÷3423=(3)如图(4),设过点M 作MN ⊥AB 于点N,则MN ∥DE,∠NMB=∠B=45°,∴NB=NM,NF=NB-FB=MN-x∵MN ∥DE ∴△FMN ∽FED,∴FD FNDE MN =,即434x MN MN -=，∴x MN 233+= ①当20≤≤x 时,如图(4) ,设DE 与BC 相交于点G ,则DG=DB=4+x ∴x x x MN BF DG DB S S y BMF BGD 23321)4(2121212+⋅⋅-+=⋅⋅-⋅⋅=-=∆ 即844312+++-=x x y ; ②当3262-≤<x 时,如图(5), x MN BF AC S S y BMF BCA 23321362121212+⋅-⨯=⋅⋅-⋅=-=∆即184332++-=x y ; ③当4326≤<-x 时, 如图(6) 设AC 与EF 交于点H ，∵AF=6－x ，∠AHF=∠E=30° ∴AH=)6(33x AF -=2)6(23)6(3)6(21x x x S y FHA -=-⋅-==∆ 综上所述，当20≤≤x 时，844312+++-=x x y 当3262-≤<x ，184332++-=x y 当4326≤<-x 时，2)6(23x y -=。

2019年广东省中考数学真题试题(含答案)

2019年广东省初中学业水平考试数学(含答案)说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用像皮檫干净后，再选涂其他答案，答案不能答在试题上．4．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．﹣2的绝对值是A ．2B ．﹣2C ．21 D ．±2 2．某网店2019年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为A ．2.21×106B ．2.21×105C ．221×103D ．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是4．下列计算正确的是A ．b 6÷b 3=b 2B ．b 3·b 3=b 9C ．a 2+a 2=2a 2D ．(a 3)3=a 65．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是6．数据3、3、5、8、11的中位数是A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是A ．a>bB ．|a|<|b|C ．a+b>0D ．ba <08．化简24的结果是A ．﹣4B ．4C ．±4D ．29．已知x 1、x 2是一元二次方程了x 2﹣2x=0的两个实数根，下列结论错误的是A ．x 1≠x 2B ．x 12﹣2x 1=0C ．x 1+x 2=2D ．x 1·x 2=210．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：①△ANH ≌△GNF ；②∠AFN=∠HFG ；③FN=2NK ；④S △AFN :S △ADM =1:4．其中正确的结论有A ．1个B ．2个C ．3个D ．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算20190+(31)﹣1=____________． 12．如图，已知a ∥b ，∠l=75°，则∠2 =________．13．一个多边形的内角和是1080°，这个多边形的边数是_________．14．已知x=2y+3，则代数式4x ﹣8y+9的值是___________．15．如图，某校教学楼AC 与实验楼BD 的水平间距CD=315米，在实验楼的顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是_________________米（结果保留根号）．16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是_____________________（结果用含a 、b 代数式表示）．三、解答题（一）（本大题3小题，每小题6分，共18分）17．解不等式组：18．先化简，再求值：4-x x -x 2-x 1-2-x x 22÷⎪⎭⎫ ⎝⎛ ，其中x=2． 19．如图，在△ABC 中，点D 是AB 边上的一点．（1）请用尺规作图法，在△ABC 内，求作∠ADE ．使∠ADE=∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若DB AD =2，求ECAE 的值．四、解答题（二）（本大题3小题，毎小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A、B、C、D四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x =________，y =_______，扇形图中表示C的圆心角的度数为_______度；（2）甲、乙、丙是A等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，己知每个篮球的价格为70元，毎个足球的价格为80元．（1）若购买这两类球的总金额为4600元，篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，最多可购买多少个篮球？22．在如图所示的网格中，每个正方形的连长为1，每个小正方形的顶点叫格点，△ABC 的三个顶点均在格点上，以点A 为圆心的⌒EF 与BC 相切于点D ，分别交AB 、AC 于点E 、F ．（1）求△ABC 三边的长；（2）求图中由线段EB 、BC 、CF 及⌒FE 所围成的阴影部分的面积．五、解答题（三）（本大题3小题，毎小题7分，共21分）23．如图，一次函数y=k 1x+b 的图象与反比例函数y=xk 2的图象相交于A 、B 两点，其中点A 的坐标为（﹣1，4），点B 的坐标为（4，n ）．（1）根据函数图象，直接写出满足k 1x+b>xk 2的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且S △AOP :S △BOP =1 : 2，求点P 的坐标．24．如题24-1图，在△ABC 中，AB=AC ，⊙O 是△ABC 的外接圆，过点C 作∠BCD=∠ACB 交⊙O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF=AC ，连接AF ．（1）求证：ED=EC ；（2）求证：AF 是⊙O 的切线；（3）如题24-2图，若点G 是△ACD 的内心，BC ·BE=25，求BG 的长．25．如题25-1图，在平面直角坐标系中，抛物线y=837 -x 433x 832 与x 轴交于点A 、B(点A 在点B 右侧)，点D 为抛物线的顶点．点C 在y 轴的正半轴上，CD 交x 轴于点F ，△CAD 绕点C 顺时针旋转得到△CFE ，点A 恰好旋转到点F ，连接BE ．（1）求点A 、B 、D 的坐标；（2）求证：四边形BFCE 是平行四边形；（3）如题25-2图，过顶点D 作DD 1⊥x 轴于点D 1，点P 是抛物线上一动点，过点P 作PM⊥ x 轴，点M 为垂足，使得△PAM 与△DD 1A 相似（不含全等）．①求出一个满足以上条件的点P 的横坐标；②直接回答．．．．这样的点P 共有几个？解析卷1．﹣2的绝对值是A ．2B ．﹣2C ．D ．±2 【答案】A【解析】正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0.【考点】绝对值2．某网店2019年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为A ．2.21×106B ．2.21×105C ．221×103D ．0.221×106【答案】B【解析】a ×10n 形式，其中0≤|a|＜10.【考点】科学记数法213．如图，由4个相同正方体组合而成的几何体，它的左视图是【答案】A【解析】从左边看，得出左视图.【考点】简单组合体的三视图4．下列计算正确的是A．b6÷b3=b2 B．b3·b3=b9 C．a2+a2=2a2 D．(a3)3=a6【答案】C【解析】合并同类项：字母部分不变，系数相加减.【考点】同底数幂的乘除，合并同类项，幂的乘方5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是【答案】C【解析】轴对称与中心对称的概念.【考点】轴对称与中心对称6．数据3、3、5、8、11的中位数是A ．3B ．4C ．5D ．6【答案】C【解析】按顺序排列，中间的数或者中间两个数的平均数.【考点】中位数的概念7．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是A ．a>bB ．|a|<|b|C ．a+b>0D ．<0【答案】D【解析】a 是负数，b 是正数，异号两数相乘或相除都得负.【考点】数与代数式的大小比较，数轴的认识8．化简的结果是A ．﹣4B ．4C ．±4D ．2【答案】B【解析】公式.【考点】二次根式9．已知x 1、x 2是一元二次方程了x 2﹣2x=0的两个实数根，下列结论错误的是A ．x 1≠x 2B ．x 12﹣2x 1=0 C ．x 1+x 2=2 D ．x 1·x 2=2【答案】Db a24a a 2【解析】因式分解x （x-2）=0，解得两个根分别为0和2，代入选项排除法.【考点】一元二次方程的解的概念和计算10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：①△ANH ≌△GNF ；②∠AFN=∠HFG ；③FN=2NK ；④S △AFN :S △ADM =1:4．其中正确的结论有A ．1个B ．2个C ．3个D ．4个【答案】C【解析】AH=GF=2，∠ANH=∠GNF ，∠AHN=∠GFN ，△ANH ≌△GNF （AAS ），①正确；由①得AN=GN=1，∵NG ⊥FG ，NA 不垂直于AF ，∴FN 不是∠AFG 的角平分线，∴∠AFN ≠∠HFG ，②错误；由△AKH ∽△MKF ，且AH:MF=1:3，∴KH:KF=1:3，又∵FN=HN ，∴K 为NH 的中点，即FN=2NK ，③正确；S △AFN =AN ·FG=1，S △ADM =DM ·AD=4，∴S △AFN :S △ADM =1:4，④正确. 【考点】正方形的性质，平行线的应用，角平分线的性质，全等三角形，相似三角形，三角形的面积二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算20190+()﹣1=____________．【答案】4212131【解析】1+3=4【考点】零指数幂和负指数幂的运算12．如图，已知a ∥b ，∠l=75°，则∠2 =________．【答案】105°【解析】180°-75°=105°.【考点】平行线的性质13．一个多边形的内角和是1080°，这个多边形的边数是_________．【答案】8【解析】（n-2）×180°=1080°，解得n=8.【考点】n 边形的内角和=（n-2）×180°14．已知x=2y+3，则代数式4x ﹣8y+9的值是___________．【答案】21【解析】由已知条件得x-2y=3，原式=4（x-2y ）+9=12+9=21.【考点】代数式的整体思想15．如图，某校教学楼AC 与实验楼BD 的水平间距CD=米，在实验楼的顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是_________________米（结果保留根号）．315【答案】15+15【解析】AC=CD ·tan30°+CD ·tan45°=15+15.【考点】解直角三角形，特殊三角函数值16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是_____________________（结果用含a 、b 代数式表示）．【答案】a+8b【解析】每个接触部分的相扣长度为（a-b ），则下方空余部分的长度为a-2（a-b ）=2b-a ，3个拼出来的图形有1段空余长度，总长度=2a+（2b-a ）=a+2b ；5个拼出来的图形有2段空余长度，总长度=3a+2（2b-a ）=a+4b ；7个拼出来的图形有3段空余长度，总长度=4a+3（2b-a ）=a+6b ；9个拼出来的图形有4段空余长度，总长度=5a+4（2b-a ）=a+8b.【考点】规律探究题型三、解答题（一）（本大题3小题，每小题6分，共18分）3317．解不等式组：【答案】解：由①得x ＞3，由②得x ＞1，∴原不等式组的解集为x ＞3.【考点】解一元一次不等式组18．先化简，再求值：，其中x=．【答案】解：原式==×=当x=，原式===1+.【考点】分式的化简求值，包括通分、约分、因式分解、二次根式计算 19．如图，在△ABC 中，点D 是AB 边上的一点．（1）请用尺规作图法，在△ABC 内，求作∠ADE ．使∠ADE=∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若=2，求的值．4-x x-x 2-x 1-2-x x22÷⎪⎭⎫⎝⎛22-x 1-x 4-x x-x 22÷2-x 1-x ()()()1-x x 2-x 2x +x 2x +2222+2222+2DB ADEC AE【答案】解：（1）如图所示，∠ADE 为所求.（2）∵∠ADE=∠B∴DE ∥BC∴= ∵=2 ∴=2 【考点】尺规作图之作一个角等于已知角，平行线分线段成比例四、解答题（二）（本大题3小题，毎小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将EC AE DB AD DB AD EC AE测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x =________，y =_______，扇形图中表示C 的圆心角的度数为_______度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．【答案】解：（1）y=10÷25%=40，x=40-24-10-2=4，C 的圆心角=360°×=36° （2）画树状图如下：一共有6种可能结果，每种结果出现的可能性相同，其中同时抽到甲、乙的结果有2种404∴P （甲乙）== 答：同时抽到甲、乙两名学生的概率为. 【考点】数据收集与分析，概率的计算21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，己知每个篮球的价格为70元，毎个足球的价格为80元．（1）若购买这两类球的总金额为4600元，篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，最多可购买多少个篮球？【答案】解：（1）设购买篮球x 个，则足球（60-x ）个.由题意得70x+80（60-x ）=4600，解得x=20则60-x=60-20=40.答：篮球买了20个，足球买了40个.（2）设购买了篮球y 个.由题意得 70y ≤80（60-x ），解得y ≤32答：最多可购买篮球32个.【考点】一元一次方程的应用，一元一次不等式的应用22．在如图所示的网格中，每个正方形的连长为1，每个小正方形的顶点叫格点，△ABC 的623131三个顶点均在格点上，以点A 为圆心的⌒EF 与BC 相切于点D ，分别交AB 、AC 于点E 、F ．（1）求△ABC 三边的长；（2）求图中由线段EB 、BC 、CF 及⌒FE 所围成的阴影部分的面积．【答案】解：（1）由题意可知，AB==，AC==，BC==（2）连接AD由（1）可知，AB2+AC2=BC2，AB=AC∴∠BAC=90°，且△ABC 是等腰直角三角形∵以点A 为圆心的⌒EF 与BC 相切于点D∴AD ⊥BC∴AD=BC= （或用等面积法AB ·AC=BC ·AD 求出AD 长度）∵S 阴影=S △ABC －S 扇形EAFS △ABC =××=202262+1022262+1022284+54215221102102S 扇形EAF ==5π ∴S 阴影=20－5π【考点】勾股定理及其逆定理，阴影面积的计算包括三角形和扇形的面积公式五、解答题（三）（本大题3小题，毎小题7分，共21分）23．如图，一次函数y=k 1x+b 的图象与反比例函数y=的图象相交于A 、B 两点，其中点A 的坐标为（﹣1，4），点B 的坐标为（4，n ）．（1）根据函数图象，直接写出满足k 1x+b>的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且S △AOP :S △BOP =1 : 2，求点P 的坐标．【答案】解：（1）x ＜-1或0＜x ＜4（2）∵反比例函数y=图象过点A （﹣1，4） ()25241π xk 2xk2xk 2∴4=，解得k 2=﹣4∴反比例函数表达式为∵反比例函数图象过点B （4，n ）∴n==﹣1，∴B （4，﹣1）∵一次函数y=k 1x+b 图象过A （﹣1，4）和B （4，﹣1） ∴，解得 ∴一次函数表达式为y=﹣x+3（3）∵P 在线段AB 上，设P 点坐标为（a ，﹣a+3）∴△AOP 和△BOP 的高相同∵S △AOP :S △BOP =1 : 2∴AP : BP=1 : 2过点B 作BC ∥x 轴，过点A 、P 分别作AM ⊥BC ，PN ⊥BC 交于点M 、N∵AM ⊥BC ，PN ⊥BC1-k 2x 4-y =x 4-y =44-⎩⎨⎧+=+=b k 41-b -k 411⎩⎨⎧==3b1-k1∴ ∵MN=a+1，BN=4-a∴，解得a= ∴-a+3= ∴点P 坐标为（，）（或用两点之间的距离公式AP=，BP=，由解得a 1=，a 2=-6舍去）【考点】一次函数和反比例函数的数形结合，会比较函数之间的大小关系，会求函数的解析式，同高的三角形的面积比与底边比的关系24．如题24-1图，在△ABC 中，AB=AC ，⊙O 是△ABC 的外接圆，过点C 作∠BCD=∠ACB 交⊙O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF=AC ，连接AF ．（1）求证：ED=EC ；（2）求证：AF 是⊙O 的切线；（3）如题24-2图，若点G 是△ACD 的内心，BC ·BE=25，求BG 的长．BNMN BP AP =21a -41a =+32373237()()224-3a -1a +++()()223-a 1-a -4++21BP AP =32【答案】（1）证明：∵AB=AC∴∠B==∠ACB∵∠BCD=∠ACB∴∠B=∠BCD∵⌒AC=⌒AC∴∠B=∠D∴∠BCD=∠D∴ED=EC（2）证明：连接AO并延长交⊙O于点G，连接CG 由（1）得∠B=∠BCD∴AB∥DF∵AB=AC，CF=AC∴AB=CF∴四边形ABCF是平行四边形∴∠CAF=∠ACB∵AG为直径∴∠ACG=90°，即∠G+∠GAC=90°∵∠G=∠B，∠B=∠ACB∴∠ACB+∠GAC=90°∴∠CAF+∠GAC=90°即∠OAF=90°∵点A在⊙O上∴AF是⊙O的切线（3）解：连接AG∵∠BCD=∠ACB ，∠BCD=∠1∴∠1=∠ACB∵∠B=∠B∴△ABE ∽△CBA∴ ∵BC ·BE=25∴AB 2=25∴AB=5∵点G 是△ACD 的内心∴∠2=∠3∵∠BGA=∠3+∠BCA=∠3+∠BCD=∠3+∠1=∠3+∠2=∠BAG∴BG=AB=5【考点】圆的综合应用，等弧等弦等角的转换，切线的证明，垂径定理的逆应用，内心的概念，相似三角形的应用，外角的应用，等量代换的意识 25．如题25-1图，在平面直角坐标系中，抛物线y=与x 轴交于点A 、B(点A 在点B 右侧)，点D 为抛物线的顶点．点C 在y 轴的正半轴上，CD 交x 轴于点F ，△CAD 绕点C 顺时针旋转得到△CFE ，点A 恰好旋转到点F ，连接BE ．（1）求点A 、B 、D 的坐标；（2）求证：四边形BFCE 是平行四边形；BCAB AB BE =837 -x 433x 832+（3）如题25-2图，过顶点D 作DD 1⊥x 轴于点D 1，点P 是抛物线上一动点，过点P 作PM⊥ x 轴，点M 为垂足，使得△PAM 与△DD 1A 相似（不含全等）．①求出一个满足以上条件的点P 的横坐标；②直接回答．．．．这样的点P 共有几个？【答案】（1）解：由y==得点D 坐标为（﹣3，）令y=0得x 1=﹣7，x 2=1∴点A 坐标为（﹣7，0），点B 坐标为（1，0）（2）证明：837 -x 433x 832+()32-3x 83+32过点D 作DG⊥y 轴交于点G ，设点C 坐标为（0，m ）∴∠DGC=∠FOC=90°，∠DCG=∠FCO∴△DGC∽△FOC∴ 由题意得CA=CF ，CD=CE ，∠DCA=∠ECF，OA=1，DG=3，CG=m+∵CO⊥FA ∴FO=OA=1∴，解得m= （或先设直线CD 的函数解析式为y=kx+b ，用D 、F 两点坐标求出y=x+，再求出点C 的坐标）∴点C 坐标为（0，） ∴CD=CE==6∵tan∠CFO== ∴∠CFO=60°∴△FCA 是等边三角形∴∠CFO=∠ECF∴EC∥BA∵BF=BO－FO=6∴CE=BFCOCG FO DG =32m32m 13+=3333()223233++FOCO 3∴四边形BFCE 是平行四边形（3）解：①设点P 坐标为（m ，），且点P 不与点A 、B 、D 重合．若△PAM 与△DD 1A 相似，因为都是直角三角形，则必有一个锐角相等．由（1）得AD 1=4，DD 1=（A ）当P 在点A 右侧时，m ＞1 （a ）当△PAM∽△DAD 1，则∠PAM=∠DAD 1，此时P 、A 、D 三点共线，这种情况不存在（b ）当△PAM∽△ADD 1，则∠PAM=∠ADD 1，此时 ∴，解得m 1=（舍去），m 2=1（舍去），这种不存在（B ）当P 在线段AB 之间时，﹣7＜m ＜1（a ）当△PAM∽△DAD 1，则∠PAM=∠DAD 1，此时P 与D 重合，这种情况不存在（b ）当△PAM∽△ADD 1，则∠PAM=∠ADD 1，此时 ∴，解得m 1=，m 2=1（舍去）（C ）当P 在点B 左侧时，m ＜﹣7（a ）当△PAM∽△DAD 1，则∠PAM=∠DAD 1，此时 ∴﹣，解得m 1=﹣11，m 2=1（舍去） 837-m 433m 832+3211DD AD AM PM =3241-m 837-m 433m 832=+35-11DD AD AM PM =3241-m 837-m 433m 832=+35-11AD DD AM PM =3241-m 837-m 433m 832=+432（b ）当△PAM∽△ADD 1，则∠PAM=∠ADD 1，此时 ∴﹣，解得m 1=，m 2=1（舍去）综上所述，点P 的横坐标为，﹣11，，三个任选一个进行求解即可． ②一共存在三个点P ，使得△PAM 与△DD 1A 相似．【考点】二次函数的综合应用，旋转的性质，相似三角形的的应用，等边三角形的性质，平行四边形的证明，平面直角坐标的灵活应用，动点问题，分类讨论思想11DD AD AM PM =3241-m 837-m 433m 832=+337-35-337-。

2019年广东省中考数学试卷-答案

，
【考点】简单几何体的三视图。 4.【答案】C 【解析】根据同底数幂除法法则、同底数幂乘法法则、合并同类项法则、幂的乘方法则逐一进行计算即可得. A. b6 b3 b3 ，故 A 选项错误； B. b3 b3 b6 ，故 B 选项错误； C. a2 a2 2a2 ，正确；
D. a3 3 a9 ，故 D 选项错误，
【考点】同底数幂的乘除法，幂的乘方等运算。 5.【答案】C
1 / 14
【解析】根据轴对称图形和中心对称图形的概念逐一进行判断即可得. A、是轴对称图形，不是中心对称图形，故不符合题意； B、是轴对称图形，不是中心对称图形，故不符合题意； C、是轴对称图形，也是中心对称图形，故符合题意； D、是轴对称图形，不是中心对称图形，故不符合题意，【考点】轴对称图形和中心对称图形。 6.【答案】C 【解析】根据中位数的定义进行求解即可。从小到大排序：3、3、5、8、11，位于最中间的数是 5，所以这组数据的中位数是 5，【考点】中位数。 7.【答案】D 【解析】先由数轴上 a，b 两点的位置确定 A，b 的取值范围，再逐一验证即可求解．由数轴上 a，b 两点的位置可知 2＜a＜1， 0＜b＜1 ，所以 a＜b ，故 A 选项错误； a ＞ b ，故 B 选项错误； a b＜0 ，故 C 选项错误； a ＜0 ，故 D 选项正确， b 【考点】实数与数轴，实数的大小比较、实数的运算等。 8.【答案】B 【解析】根据算术平方根的定义进行求解即可.由题意知， 42 16 4 . 【考点】算术平方根。 9.【答案】D 【解析】根据一元二次方程的根的判别式、一元二次方程根的定义、一元二次方程根与系数的关系逐一进行分析即可。 x1 、 x2 是一元二次方程 x2 2x 0 的两个实数根，这里 a 1， b 2 ， c 0 ，

2019年广东省初中学业水平考试(数学)试卷及答案

．实数、在数轴上的对应点的位置如图所示，下列式子成立的是（）
． a b ． a b ． a b 0 ． a 0
b
．化简 42 的结果是（）
．．．．
．已知 x1 、 x2 是一元二次方程 x2 2x 0 的两个实数根，下列结论错．误．的是（）
、如图，在中，，，：：，点从点出发沿方向向点运动，速度为，同时点从点出发沿方向向点运动，速度为，当一个运动点到达终点时，另一个运动点也随之停止运动．
又∵以点A为圆心的圆与BC相切于点D
AD BC， CD BD AD 1 BC 2 5
2
SABC
12 2
10 2
10 20
、如图，在中，，，：：，点从点出发沿方向向点运动，速度为，同时点从点出发沿方向向点运动，速度为，当一个运动点到达终点时，另一个运动点也随之停止运动．
S阴
20
1 4
解（） ∵ ∴弧弧∠∠ ∴∠∠ 又∵∠∠ ∴∠∠ ∴ （）证明：连接交于点 ∵ ∴为弧中点 ∴⊥ ∵∠∠＋∠ 又∵∠∠∠∠ ∴∠∠ ∴∥
、如图，在中，，，：：，点从点出发沿方向向点运动，速度为，同时点从点出发沿方向向点运动，速度为，当一个运动点到达终点时，另一个运动点也随之停止运动．
∴∠∠° 即⊥ 又∵ A 在圆上， ∴为⊙ O 的切线（）连接由（）知∥ ∴∠∠ ∵为△的内心 ∴平分∠ ∴∠∠ 又∵∠∠∠ ∴∠∠∠∠ ∴∠∠ ∴ ∵∠∠∠∠ ∴△∽△
x 4
，其中
x=
2．
、如图，在中，，，：：，点从点出发沿方向向点运动，速度为，同时点从点出发沿方向向点运动，速度为，当一个运动点到达终点时，另一个运动点也随之停止运动．
解原式 x 1 (x 2)( x 2) x 2 x(x 1)

2019年广东省初中学业水平考试(数学)试卷及答案

2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑． 1．-2的绝对值是（A ） A ．2B ．-2C ．12D ．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为（B ） A ．×106B ．×105C ．221×103D ．×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是（A ）4．下列计算正确的是（C ） A ．632b b b ÷=B ．339b b b ⋅=C ．2222a a a +=D ．()363a a =5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C ）6．数据3、3、5、8、11的中位数是（C ） A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是（D ）A ．a b >B ．a b <C ．0a b +>D ．0ab<8（B ） A ．-4B ．4C ．±4D ．29．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（D ） A ．12x x ≠B ．2112=0x x -C ．12=2x x +D ．12=2x x ⋅10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：ANH GNF ①≌△△ ；AFN HFG ∠=∠② ；2FN NK =③；:1:4AFN ADM S S =④△△．其中正确的结论有（C ）A ．1个B ．2个C ．3个D ．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算：1120193-⎛⎫+ ⎪⎝⎭= ．答案：4解析：本题考查了零次幂和负指数幂的运算12．如图，已知a b，175∠=°，则∠2＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算13．一个多边形的内角和是1080︒，这个多边形的边数是．答案：8解析：本题考查了多边形内角和的计算公式14．已知23x y=+，则代数式489x y-+的值是．答案：21解析：整体思想，考查了整式的运算15．如图，某校教学楼AC与实验楼BD的水平间距CD=米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是米（结果保留根号）．答案：(15+解析：本题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是（结果用含a 、b 代数式表示）．答案：8a b +解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题3小题，每小题6分，共18分）17．解不等式组：()12214x x ->⎧⎨+>⎩①②解 ①21>-x x >3 ②4)1(2>+x 422>+x 22>x 1>x∴该不等式组的解集是x >318．先化简，再求值：221224x x x x x x -⎛⎫-÷ ⎪---⎝⎭，其中x 解原式=)1()2)(2(21--+⋅--x x x x x x =xx 2+ 当2=x原式=222+ =2222+ =21+19．如图，在ABC △中，点D 是AB 边上的一点．（1）请用尺规作图法，在ABC △内，求作∠ADE ，使∠ADE =∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2AD DB =，求AEEC的值．解（1）如图（2）A A B ADE ∠=∠∠=∠,ADE ∆∴∽ABC ∆ 2==∴DBADEC AE四、解答题（二）（本大题3小题，每小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x = ，y = ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．解 (1) 4x = ； 40y = ; 36(2)解：由题意可知树状图为由树状图可知，同时抽到甲、乙两名学生的概率为21=63答：同时抽到甲、乙两名学生的概率为13。

(完整版)2019广东省中考数学试卷及答案

2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑． 1．-2的绝对值是 A ．2B ．-2C ．12D ．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为 A ．2.21×106B ．2.21×105C ．221×103D ．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是4．下列计算正确的是 A ．632b b b ÷=B ．339b b b ⋅=C ．2222a a a +=D ．()363a a =5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是6．数据3、3、5、8、11的中位数是 A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是A ．a b >B ．a b <C ．0a b +>D ．0ab<8的结果是 A ．-4B ．4C ．±4D ．29．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是 A ．12x x ≠ B ．2112=0x x - C ．12=2x x +D ．12=2x x ⋅10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：ANH GNF ①≌ ；AFN HFG ∠=∠② ；2FN NK =③；:1:4AFNADMSS=④．其中正确的结论有A ．1个B ．2个C ．3个D ．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算：1120193-⎛⎫+ ⎪⎝⎭= ．12．如图，已知a b ，175∠=°，则∠2＝．13．一个多边形的内角和是1080︒ ，这个多边形的边数是． 14．已知23x y =+ ，则代数式489x y -+ 的值是．15．如图，某校教学楼AC 与实验楼BD 的水平间距CD=米，在实验楼顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是米（结果保留根号）．16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是（结果用含a 、b 代数式表示）．三、解答题（一）（本大题3小题，每小题6分，共18分） 17．解不等式组：()12214x x ->⎧⎨+>⎩①②18．先化简，再求值：221224xx x x x x -⎛⎫-÷ ⎪---⎝⎭，其中x19．如图，在ABC 中，点D 是AB 边上的一点．（1）请用尺规作图法，在ABC 内，求作∠ADE ，使∠ADE =∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2AD DB ，求AEEC的值．四、解答题（二）（本大题3小题，每小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x = ，y = ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，已知每个篮球的价格为70元，每个足球的价格为80元．（1）若购买这两类球的总金额为4600元，求篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，求最多可购买多少个篮球？22．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，ABC 的三个顶点均在格点上，以点A 为圆心的EF 与BC 相切于点D ，分别交AB 、AC 于点E 、F ．（1）求ABC 三边的长；（2）求图中由线段EB 、BC 、CF 及FE 所围成的阴影部分的面积．五、解答题（三）（本大题3小题，每小题9分，共27分） 23．如图，一次函数y =k 1x +b 的图象与反比例函数2k y x=的图象相交于A 、B 两点，其中点A 的坐标为（-1，4），点B 的坐标为（4，n ）．（1）根据图象，直接写出满足21k k x b x+>的x 的取值范围；（2）求这两个函数的表达式；（3）点P 在线段AB 上，且:1:2AOP BOP S S ∆∆=，求点P 的坐标．24．如题24-1图，在ABC 中，AB =AC ，⊙O 是ABC 的外接圆，过点C 作∠BCD =∠ACB 交⊙O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF =AC ，连接AF ．（1）求证：ED =EC ；（2）求证：AF 是⊙O 的切线；（3）如题24-2图，若点G 是ACD 的内心，25BC BE ⋅=，求BG 的长．25．如题25-1图，在平面直角坐标系中，抛物线2y x 与x 轴交于点A 、B （点A 在点B 右侧），点D 为抛物线的顶点．点C 在y 轴的正半轴上，CD 交x 轴于点F ，CAD 绕点C 顺时针旋转得到CFE ，点A 恰好旋转到点F ，连接BE ．（1）求点A 、B 、D 的坐标；（2）求证：四边形BFCE 是平行四边形；（3）如题25-2图，过顶点D 作1DD x ⊥轴于点D 1，点P 是抛物线上一动点，过点P 作PM x ⊥轴，点M 为垂足，使得PAM 与1DD A 相似（不含全等）． ①求出一个满足以上条件的点P 的横坐标； ②直接回答．．．．这样的点P 共有几个？2019广东省中考数学答案一、选择题二、填空题 11、答案：4解析：本题考查了零次幂和负指数幂的运算 12、答案：︒105解析：本题考查了平行线的性质，互为补角的计算 13、答案：8解析：本题考查了多边形内角和的计算公式 14、答案：21解析：整体思想，考查了整式的运算 15、答案：31515+解析：本题利用了特殊三角函数值解决实际问题16、答案：b a 8+三解答题（一）17、解： ①得：3>x ①得：1>x①不等式组的解集为：3>x18、解：原式=)1()2)(2(21--+⋅--x x x x x x =xx 2+ 当2=x 时原式=222+ =2222+ =21+19、解：（1）如图所示：①ADE 即为所求。

2019年广东省中考数学试题((含答案)

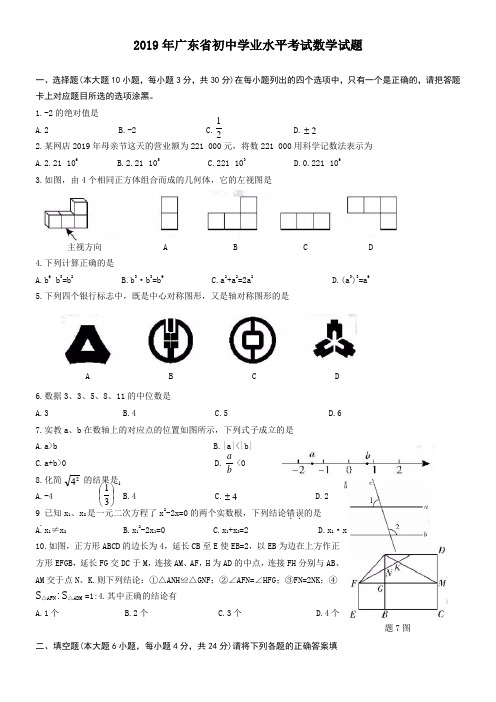
2019年广东省初中学业水平考试数学试题一、选择题(本大题10小题，每小题3分，共30分)在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑。

1.-2的绝对值是A.2B.-2C. D. 2.某网店2019年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为A.2.21×106B.2.21×105C.221×103D.0.221×1063.如图，由4个相同正方体组合而成的几何体，它的左视图是4.下列计算正确的是A.b 6÷b 3=b 2B.b 3·b 3=b 9C.a 2+a 2=2a 2D.(a 3)3=a 65.下列四个银行标志中，既是中心对称图形，又是轴对称图形的是6.数据3、3、5、8、11的中位数是A.3B.4C.5D.6 7.实教a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是 A.a>bB.|a|<|b|C.a+b>0D. <0 8.化简的结果是 A.-4 B.4 C. D.2 9.已知x 1、x 2是一元二次方程了x 2-2x=0的两个实数根，下列结论错．误．的是 A.x 1≠x 2 B.x 12-2x 1=0 C.x 1+x 2=2 D.x 1·x 2=2 10.如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K.则下列结论：①△ANH≌△GNF；②∠AFN=∠HFG；③FN=2NK ；④S △AFN :S △ADM =1:4.其中正确的结论有A.1个B.2个C.3个D.4个二、填空题(本大题6小题，每小题4分，共24分)请将下列各题的正确答案填2±21主视方向 A B C DA B C Dba题7图4±题7图131-⎪⎭⎫ ⎝⎛24题15图写在答题卡相应的位置上.11.计算20190+ = .12.如图，已知a//b ，∠l=75°，则∠2 = .13.一个多边形的内角和是1080°，这个多边形的边数是 . 14.已知x=2y+3，则代数式4x-8y+9的值是 .15.如图，某校教学楼AC 与实验楼BD 的水平间距CD= 米，在实验楼顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是米(结果保留根号)。

2019年广东省初中学业水平考试数学试卷及答案

2019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B 铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．-2的绝对值是（A ）A ．2B ．-2C ．12 D ．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为（B ）A ．2.21×106B ．2.21×105C ．221×103D ．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是（A ）4．下列计算正确的是（C ）A ．632b b b ÷=B ．339b b b ⋅=C ．2222a a a +=D ．()363a a =5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C ）6．数据3、3、5、8、11的中位数是（C ）A ．3B ．4C ．5D ．67．实数a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是（D ）A ．a b >B ．a b <C ．0a b +>D ．0a b< 8．化简24的结果是（B ）A ．-4B ．4C ．±4D ．29．已知1x 、2x 是一元二次方程220x x -=的两个实数根，下列结论错误．．的是（D ） A ．12x x ≠ B ．2112=0x x -C ．12=2x x +D ．12=2x x ⋅10．如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K ．则下列结论：ANH GNF ①≌△△ ；AFN HFG ∠=∠② ；2FN NK =③；:1:4AFN ADM S S =④△△．其中正确的结论有（C ）A．1个B．2个C．3个D．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算：1120193-⎛⎫+ ⎪⎝⎭= ．答案：4解析：本题考查了零次幂和负指数幂的运算12．如图，已知a b，175∠=°，则∠2＝．答案：105︒解析：本题考查了平行线的性质，互为补角的计算13．一个多边形的内角和是1080︒，这个多边形的边数是．答案：8解析：本题考查了多边形内角和的计算公式14．已知23x y=+，则代数式489x y-+的值是．答案：21解析：整体思想，考查了整式的运算15．如图，某校教学楼AC与实验楼BD的水平间距CD=153米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是米（结果保留根号）．答案：(15153+解析：本题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是（结果用含a 、b 代数式表示）．答案：8a b +解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题3小题，每小题6分，共18分）17．解不等式组：()12214x x ->⎧⎨+>⎩①② 解 ①21>-xx >3②4)1(2>+x422>+x22>x1>x∴该不等式组的解集是x >318．先化简，再求值：221224x x x x x x -⎛⎫-÷ ⎪---⎝⎭，其中=2x ．解原式=)1()2)(2(21--+⋅--x x x x x x =x x 2+ 当2=x原式=222+ =2222+ =21+19．如图，在ABC △中，点D 是AB 边上的一点．（1）请用尺规作图法，在ABC △内，求作∠ADE ，使∠ADE =∠B ，DE 交AC 于E ；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2AD DB =，求AE EC的值．解（1）如图（2）A A B ADE ∠=∠∠=∠,ADE ∆∴∽ABC ∆2==∴DBAD EC AE四、解答题（二）（本大题3小题，每小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A 、B 、C 、D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x = ，y = ，扇形图中表示C 的圆心角的度数为度；（2）甲、乙、丙是A 等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．解 (1) 4x = ； 40y = ; 36(2)解：由题意可知树状图为由树状图可知，同时抽到甲、乙两名学生的概率为21=63答：同时抽到甲、乙两名学生的概率为13。

2019广东省中考数学试题(含答案)

2019年广东省初中学业水平考试数学试题一、选择题(本大题10小题，每小题3分，共30分)在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑。

1.-2的绝对值是A.2B.-2C. D. 2.某网店2019年母亲节这天的营业额为221 000元，将数221 000用科学记数法表示为A.2.21×106B.2.21×105C.221×103D.0.221×1063.如图，由4个相同正方体组合而成的几何体，它的左视图是4.下列计算正确的是A.b 6÷b 3=b 2B.b 3·b 3=b 9C.a 2+a 2=2a 2D.(a 3)3=a 65.下列四个银行标志中，既是中心对称图形，又是轴对称图形的是6.数据3、3、5、8、11的中位数是A.3B.4C.5D.6 7.实教a 、b 在数轴上的对应点的位置如图所示，下列式子成立的是 A.a>bB.|a|<|b|C.a+b>0D. <0 8.化简的结果是 A.-4 B.4 C. D.2 9.已知x 1、x 2是一元二次方程了x 2-2x=0的两个实数根，下列结论错．误．的是 A.x 1≠x 2 B.x 12-2x 1=0 C.x 1+x 2=2 D.x 1·x 2=2 10.如图，正方形ABCD 的边长为4，延长CB 至E 使EB=2，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K.则下列结论：①△ANH≌△GNF；②∠AFN=∠HFG；③FN=2NK ；④S △AFN :S △ADM =1:4.其中正确的结论有A.1个B.2个C.3个D.4个二、填空题(本大题6小题，每小题4分，共24分)请将下列各题的正确答案填2±21主视方向 A B C DA B C Dba题7图4±题7图131-⎪⎭⎫ ⎝⎛24题15图写在答题卡相应的位置上.11.计算20190+ = .12.如图，已知a//b ，∠l=75°，则∠2 = .13.一个多边形的内角和是1080°，这个多边形的边数是 . 14.已知x=2y+3，则代数式4x-8y+9的值是 .15.如图，某校教学楼AC 与实验楼BD 的水平间距CD= 米，在实验楼顶部B 点测得教学楼顶部A 点的仰角是30°，底部C 点的俯角是45°，则教学楼AC 的高度是米(结果保留根号)。

2019年广东省初中学业水平考试(数学)试卷与答案

2021年XX省初中学业水平考试数学说明：1．全卷共4页，总分值为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的XX号、XX、考场号、座位号．用2B铅笔把对应该的标号涂黑．3．选择题每题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试完毕时，将试卷和答题卡一并交回．一、选择题〔本大题10小题，每题3分，共30分〕在每题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．-2的绝对值是〔A〕A．2B．-2C．12D．±22．某网店2021年母亲节这天的营业额为221000元，将数221000用科学记数法表示为〔B〕6B．2.21×105C．221×103D．0.221×106A．2.21×103．如图，由4个一样正方体组合而成的几何体，它的左视图是〔A〕4．以下计算正确的选项是〔C〕A．632bbbB．339bbbC．2222aaaD．336aa5．以下四个银行标志中，既是中心对称图形，又是轴对称图形的是〔C〕6．数据3、3、5、8、11的中位数是〔C〕A．3B．4C．5D．67．实数a、b在数轴上的对应点的位置如下图，以下式子成立的是〔D〕1A．abB．aba C．ab0D．0b28．化简4的结果是〔B〕A．-4B．4C．±4D．29．x1、x2是一元二次方程2xx的两个实数根，以下结论错误．．的是〔D〕20A．x1x2B．2x12x1=0C．x1x2=2D．x1x2=210．如图，正方形A BCD的边长为4，延长C B至E使EB=2，以EB为边在上方作正方形E FGB，延长F G交DC于M，连接A M、AF，H为AD的中点，连接F H分别与A B、AM交于点N、K．那么以下结论：①△ANH≌△GNF；△△．其中正确的结论有〔C〕②；③FN2NK；S:S1:4AFNHFG④AFNADMA．1个B．2个C．3个D．4个二、填空题〔本大题6小题，每题4分，共24分〕请将以下各题的正确答案填写在答题卡相应的位置上．0120213111．计算：=．答案：4解析：此题考察了零次幂和负指数幂的运算12．如图，ab，175°，那么∠2＝．答案：105解析：此题考察了平行线的性质，互为补角的计算213．一个多边形的内角和是1080，这个多边形的边数是．答案：8解析：此题考察了多边形内角和的计算公式14．x2y3，那么代数式4x8y9的值是．答案：21解析：整体思想，考察了整式的运算15．如图，某校教学楼AC与实验楼BD的水平间距CD=153米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，那么教学楼AC的高度是米〔结果保存根号〕．答案：15153解析：此题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如下图，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形〔题16-1图〕拼出来的图形的总长度是〔结果用含a、b代数式表示〕．答案：a8b解析：此题考察了轴对称图形的性质，根据题目找规律三、解答题〔一〕〔本大题3小题，每题6分，共18分〕317．解不等式组： x 12 2x14① ②解①x12x>3 ②2(x1)4 2x 24 2x2 x1∴该不等式组的解集是x>318．先化简，再求值：2x1xx2x2x2x4，其中x=2．解原式= x x 1 2 (x 2)( x(x x 1)2)=x 2 x当x222原式=2=2 2 22 =1219．如图，在△ABC 中，点D 是AB 边上的一点．〔1〕请用尺规作图法，在△ABC 内，求作∠ADE ，使∠ADE=∠B ，DE 交AC 于E ；〔不要求写作法，保存作图痕迹〕AD〔2〕在〔1〕的条件下，假设2DB，求A E EC的值． 4解〔1〕如图〔2〕ADEB,AAADE ∽ABC AE ECA D DB2四、解答题〔二〕〔本大题3小题，每题7分，共21分〕20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了局部男生进展测试，并将测试成绩分为A 、B 、C 、 D 四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答以下问题：〔1〕x=，y=，扇形图中表示C 的圆心角的度数为度；〔2〕甲、乙、丙是A 等级中的三画树状图法，求同时抽到甲、乙两名解(1)x4；y40;36 (2)解：由题意可知树状图为 5由树状图可知，同时抽到甲、乙两名学生的概率为21 = 63答：同时抽到甲、乙两名学生的概率为13。