江西省萍乡市数学高三文数第二次联考试卷

合集下载

江西省重点中学盟校2023届高三第二次联考数学(文)试题及参考答案

江西省重点中学盟校2023届高三第二次联考数学（文）试题一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}22,3,4,5,6,8120A B xx x ==-+>∣，则()RA B ⋂=（）A.{}2,3,4,5B.{}2,3,4,5,6C.{}3,4,5D.{}3,4,5,62.如果一个复数的实部和虚部相等，则称这个复数为“等部复数”，若复数()()23i i (z a =++其中)a R ∈为“等部复数”，则复数i z a +在复平面内对应的点在（） A.第一象限 B.第二象限 C.第三象限 D.第四象限3.“x y >”的一个充分条件可以是（） A.12x ye-> B.44x y > C.1xy> D.22xt yt > 4.已知两个非零向量,a b 满足(2)a a b ⊥-，且3a b a b+=-，则,a b 的夹角为（）A.3π B.2π C.23π D.4π5.在区间()1,5-与()1,5内各随机取1个整数，设两数之和为M ，则2log 2M >成立的概率为（） A.35 B.58 C.815 D.7156.函数()3sin x x f x x x+=-的大致图象为（）A. B.C. D.7.作为惠民政策之一，新农合是国家推出的一项新型农村合作医疗保险政策，极大地解决了农村人看病难的问题.为了检测此项政策的落实情况，现对某地乡镇医院随机抽取100份住院记录作出频率分布直方图如图：已知该医院报销政策为：花费400元及以下的不予报销；花费超过400元不超过6000元的，超过400元的部分报销65%；花费在6000元以上的报销所花费费用的80%.则下列说法中，正确的是（） A.0.0018a =B.若某病人住院花费了4300元，则报销后实际花费为2235元C.根据频率分布直方图可估计一个病人在该医院报销所花费费用为80%的概率为310D.这100份花费费用的中位数是4200元8.过双曲线222x y -=上任意一点(),P x y 分别作两条渐近线的垂线，垂足分别为,A B ，则四边形OAPB 的面积为（） A.12B.1C.2D.4 9.被誉为“中国现代数学之父”的著名数学家华罗庚先生于1946年9月应普林斯顿大学邀请去美国讲学，之后又被美国伊利诺依大学聘为终身教授.新中国成立的消息使华罗庚兴奋不已，他放弃了在美国的优厚待遇，克服重重困难，终于回到祖国怀抱，投身到我国数学科学研究事业中去.这种赤子情怀，使许多年轻人受到感染､受到激励，其中他倡导的“0.618优选法”在生产和科研实践中得到了非常广泛的应用，0.618就是黄金分割比51t -=的近似值，黄金分割比还可以表示成2sin1822427sin 27t t --的值为（）A.-4B.4C.-2D.210.已知正项数列{}n a 的前n 项和为n S ，且()()1112,33nn n n nna S S S S++=-=+，则2023S =（） A.202331- B.202331+ C.2023312+ D.2022312+ 11.若球O 是正三棱锥A BCD -的外接球，3,BC AB ==E 在线段BA 上，3BA BE =，过点E 作球O 的截面，则所得的截面中面积最小的截面的面积为（）A.83π B.2π C.43π D.π12.已知函数()222ln 1xx ax f x e x++=-，当()0,x ∞∈+时，()0f x ≥恒成立，则实数a 的取值范围是（）A.(],1∞-B.(2,1e ∞⎤--⎦ C.(],e ∞- D.(],2∞-二､填空题：本大题共4小题，每小题5分，共20分.13.若前n 项和为n S 的等差数列{}n a 满足712812a a a +=-，则17S =__________.14.已知变量x y ､满足约束条件11y xx y y ≤⎧⎪+≤⎨⎪≥-⎩，则32x y +的最大值__________.15.已知圆221:1O x y +=，圆222:(2)4O x y -+=.请写出一条与两圆都相切的直线方程：__________.16.函数()f x 和()g x 的定义域均为R ，且()33y f x =+为偶函数，()32y g x =++为奇函数，对x ∀∈R ，均有()()21f x g x x +=+，则()()77f g =__________.三､解答题：共70分，解答应写出文字说明､证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答，第22､23题为选做题，考生根据要求作答. （一）必考题：共60分.17.（12分）近年来随着新能源汽车的逐渐普及，传统燃油车市场的竞争也愈发激烈.近日，各地燃油车市场出现史诗级大降价的现象，引起了广泛关注.2023年3月以来，各地政府和车企打出了汽车降价促销“组合拳”，被誉为“史上最卷”的汽车降价促销潮从南到北，不断在全国各地蔓延，据不完全统计，十几家车企的近40个传统燃油车品牌参与了此次降价，从几千元到几万元助力汽车消费复苏.记发放的补贴额度为x （千元），带动的销量为y （千辆）.某省随机抽查的一些城市的数据如下表所示.y10 12 13 18 19 21 24 27（1）根据表中数据，求出y 关于x 的线性回归方程.（2）（i ）若该省A 城市在2023年4月份准备发放额度为1万元的补贴消费券，利用（1）中求得的线性回归方程，预计可以带动多少销量？（ii ）当实际值与估计值的差的绝对值与估计值的比值不超过10%时，认为发放的该轮消费券助力消费复苏是理想的.若该省A 城市4月份发放额度为1万元的消费补贴券后，经过一个月的统计，发现实际带动的消费为3万辆，请问发放的该轮消费券助力消费复苏是否理想？若不理想，请分析可能存在的原因.参考公式：()()()()()()()11222111ˆˆˆ,,nniiiii i nnni iii i i x x y y x x y y r ba y bx x x x x y y =====----===----∑∑∑∑∑.参考数据：()()()8821169,20i i i i i x x y y x x ==--=-=∑∑.18.（12分）在ABC 中，角,,A B C 所对的边分别为,,a b c 已知222sin sin cos cos sin 2A B A B C +++=（1）求角C ；（2）若ABC 为锐角三角形，且2b =，求ABC 面积的取值范围.19.（12分）如图所示，圆锥的高3PO =，底面圆O 的半径为1，延长直径AB 到点C ，使得1BC =，分别过点,A C 作底面圆O 的切线，两切线相交于点E ，点D 是切线CE 与圆O 的切点.（1）证明：平面PDE ⊥平面POD ；（2）点E 到平面PAD 的距离为1d ，求1d 的值. 20.（12分）已知函数()313f x ax x =+，函数()2sin x g x e x x =-+. （1）求函数()g x 的单调区间；（2）记()()()F x g x f x =-'，对任意的()0,0x F x ≥≥恒成立，求实数a 的取值范围.21.（12分）已知椭圆方程：22221(0)x y a b a b +=>>，其离心率为22e =，且,P Q 分别是其左顶点和上顶点，坐标原点O 到直线PQ 的距离为233. （1）求该椭圆的方程；（2）已知直线:2l y kx =+交椭圆于,A B 两点，双曲线：22142x y -=的右顶点,E EA 与EB交双曲线左支于,C D 两点，求证：直线CD 的斜率为定值，并求出定值.（二）选考题：共10分.请考生在第22､23题中选定一题作答，并用2B 铅笔在答题卡上将所选题目对应的题号方框涂黑.按所涂题号进行评分，不涂､多涂均按所答第一题评分；多答按所答第一题评分.22.（10分）选修4-4：坐标系与参数方程下图所示形如花瓣的曲线G 称为四叶玫瑰线，并在极坐标系中，其极坐标方程为2sin2ρθ=.（1）若射线:6l πθ=与G 相交于异于极点O 的点P ，求OP ；（2）若,A B 为G 上的两点，且23AOB π∠=，求AOB 面积S 的最大值. 23.（10分）选修4-5：不等式选讲已知函数()322f x x x x =+---. （1）求()f x 的最小值m ；（2）若,a b 为正实数，且20a b m ++=，证明不等式22111a b b a +≥++.江西省重点中学盟校2023届高三第二次联考数学（文）参考答案一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.二､填空题：本大题共4小题，每小题5分，共20分.13.68 14.5 15.20(x +=或20)x += 16.61616.由函数()33f x +为偶函数，则()()3333f x f x +=-，即函数()f x 关于直线3x =对称，故()()6f x f x =-；由函数()32g x ++为奇函数，则()()3232g x g x ++=--+-，整理可得()()334g x g x ++-+=-，即函数()g x 关于()3,2-对称，故()()46g x g x =---；由()()21f x g x x +=+，则，可得()()266(6)1f x g x x -+-=-+，得()()24(6)1f x g x x +-=-+故()()()()2214(6)1f xg x x f x g x x ⎧+=+⎪⎨--=-+⎪⎩，解得()()2621,620f x x x g x x =-+=-， ()()772822616f g =⨯=.故答案为：616.三､解答题：共70分，解答应写出文字说明､证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答，第22､23题为选做题，考生根据要求作答.17.（1）3345566810121318192124275,1888x y ++++++++++++++====.经计算可得()()()8182169ˆˆˆ3.45,18 3.4550.7520iii i i x x y y bay bx x x ==--====-=-⨯=-∑∑. 所以所求线性回归方程为ˆ 3.450.75yx =+. （2）（i ）当10x =时，ˆ 3.45100.7535.25y=⨯+=，所以预计能带动的消费达3.525万辆.（ii ）因为3035.2510%35.25->，所以发放的该轮消费补贴助力消费复苏不是理想的.发放消费券只是影响消费的其中一个因素，还有其他重要因素，比如：A 城市经济发展水平不高，居民的收入水平直接影响了居民的消费水平；A 城市人口数量有限､商品价格水平､消费者偏好､消费者年龄构成等因素一定程度上影响了消费总量.年轻人开始更加注重出行的舒适性和环保性，而传统燃油车的排放和能耗等问题也逐渐成为了消费者们考虑的重点.（只要写出一个原因即可）. 18.（1）因为222sin sin cos cos sin 2A B A B C +++= 所以()()2222sin sin sin 1sin 1sin C A B A B -=+-+-可得222sin sin sin sin sin A B C A B +-=由正弦定理可得：222a b c ab +-=.由余弦定理知，2221cos 222a b c ab C ab ab +-===因为()0,C π∈，所以3C π=（2），由（1）知，3C π=所以23A B π+=又ABC 是锐角三角形，可得02B π<<且2032B ππ<-<解得62B ππ<< 由正弦定理知：sin sin b c B C =又2b =可得sin sin b C c B ⋅==所以2sin 11233sin 2sin 223sin 2tan ABCB Sbc A B B B ππ⎛⎫- ⎪⎛⎫⎝⎭==⨯-== ⎪⎝⎭因为62B ππ<<所以tan B >ABCS<<故ABC面积的取值范围为⎝.19.（1）由题设，PO ⊥平面,ABD D 又是切线CE 与圆O 的切点，CE ∴⊂平面ABD ，则PO CE ⊥，且OD CE ⊥，又,,PO OD O PO OD ⋂=⊂平面,POD CE ∴⊥平面POD ，又CE ⊂平面PDE ，所以平面PDE ⊥平面POD . （2）,30,OD CE CD OCD AE CE ∠⊥∴==∴==1111111333332P ADE ADE E PAD PAD V S PO V S d d --=⋅===⋅=⋅113d ∴=20.（1）()2sin xg x e x x =-+则()'2cos xg x e x =-+且()00g =，令()()()()()(),'sin ,0,,'sin 1sin 0,x x x g x x e x x x e x x x ϕϕ∞ϕϕ'==-∈+=->-≥在()0,∞+上单调递增，所以()()()00x g x g ϕ''=>=，所以()g x 的单调递增区间为()0,∞+，()(),0,'2cos cos 10x x g x e x x ∞∈-=-+<-≤，所以()g x 的单调递减区间为(),0∞-.（2）()()()22sin 1xF x g x f x e x x x =-'=-+--，且()00F =，()[)cos 22,0,,x F x e x ax x ∞='+--∈+令()()()','sin 2,x G x F x G x e x a ==--令()()()','cos 1cos 0xH x G x H x e x x ==-≥-≥，所以()'G x 在[)0,+∞上单调递增， ①若()()1,''01202a G x G a ≤≥=-≥，所以()'F x 在[)0,+∞上单调递增，所以()()'00F x F '≥=，所以()()00F x F ≥=恒成立. ②若()1,'01202a G a >=-< ()()()'ln 222sin 220G a a +=-+>，所以存在()()00,ln 22x a ∈+，使()0'0G x =，故存在()00,x x ∈，使得()0G x '<，此时()G x 单调递减，即()F x '在()00,x 上单调递减，所以()()00F x F ''=，故()F x 在()00,x 上单调递减，所以此时()()00F x F =，不合题意.综上，12a.21.（1）由已知可知：()(),0,0,P a Q b -，所以PQ =POQ 中，等面积可得：1122ab =2,a b ==所以该椭圆方程为22142x y +=.（2）设()()()()11223344,,,,,,,A x y B x y C x y D x y 由()2,0E 可设直线AE 方程：1122x x y y -=+直线BE 方程：2222x x y y -=+ 将直线AE 与双曲线22142x y -=联立可得：()2212111211424420x x x y y y y y --+-+=. 又因为2211142x y -=代入上式中可得：()()111221122420x x x y y y y --+= 解得：1312y y x =-代入直线AE 方程：314x x =所以C 点坐标为11124,y x x ⎛⎫- ⎪⎝⎭ 同理可得D 点坐标为：22224,y x x ⎛⎫- ⎪⎝⎭所以直线CD 的斜率()()2112122112121212222222441444444CD kx kx y y x x x x x x k x x x x x x ⎛⎫++-----+ ⎪⎝⎭====----.所以直线CD 的斜率为定值该定值为-122.（1）62sin2πϕρρθ⎧=⎪⇒=⎨⎪=⎩（2）设()[)2,,0,23A B A B πρθρθθπ⎛⎫+∈ ⎪⎝⎭ 2sin2A ρθ= 42sin 23B πρθ⎛⎫=+⎪⎝⎭12sin 23AOBA B Sπρρ=⋅⋅142sin22sin 223πθθ⎛⎫=⋅+ ⎪⎝⎭1sin2sin2cos222θθθ⎛⎫=+ ⎪ ⎪⎝⎭11sin 4264πθ⎛⎫=-+ ⎪⎝⎭ 当462ππθ-=时即6πθ=时AOBS23.（1）()min 1102101()251313x x x f x f x x x x =-<⎧⎪+≤≤⎪=∴⎨-+≤<⎪⎪-≥⎩（2）由（1）可知2a b +=()()()()222222221111111211144114a ab b a b a b a b ab a b b a b a ⎡⎤++⎛⎫++++=+++≥++=⎢⎥ ⎪++++⎝⎭⎣⎦或由柯西不等式114≥=当且仅当1a b ==时取等号.。

部编版江西省萍乡市高三下学期4月第二次模拟考试(二模)数学(文)试卷

准考证号姓名绝密★启用前（在此卷上答题无效）萍乡市2020－2021学年度高三二模考试试卷文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至4页．满分150分，考试时间120分钟．注意事项：1．答卷前，考生务必将自已的准考证号、姓名填写在答题卡上．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人的准考证号、姓名是否一致．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号．第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答题无效． 3．考试结束后，监考员将试题卷、答题卡一并收回．第Ⅰ卷一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．（1）已知全集{}1,2,3,4,5,6U =，{}1,2,4M =，{}2,5,6N =，则图中阴影部分表示的集合是A.{}1 B. {}1,4 C. {}5,6 D. {}1,2,4,5,6（2）已知复数满足()1234i z i -=+(i 为虚数单位)，则z=A.2B. 5C.52D. 5 （3）下列函数中,在()0,+∞上单调递增的是A. 21y x =-+B.1y x =- C. 3y x = D. 2x y -=（4）已知a ，b 均为单位向量，它们的夹角为120︒，则|3|a b +=A. 7B. 7C. 13D. 13 （5）已知tan 2α=-，则2sin 2cos αα+的值为A. 45B. 45- C. 35 D. 35-（6）2021年3月12日是全国第43个植树节，为提高大家爱劳动的意识，某中学组织开展植树活动，并收集了高三年级1～11班植树量的数据(单位:棵)，绘制了下面的折线图.根据折线图，下列结论不正确．．．的是A. 各班植树的棵数不是逐班增加的B. 4班植树的棵数低于11个班的平均值C. 各班植树棵数的中位数为6班对应的植树棵数D. 1至5班植树的棵数相对于6至11班，波动更小，变化比较平稳（7）函数1sin 2y x =-的图像沿轴向右平移个单位(0a >)，所得图像关于y 轴对称，则的最小值为A. πB. 34πC. 2πD. 4π（8）执行如图所示的程序框图，则输出的y 值为A.201812 B.201912 C.202012 D.202112（9）已知抛物线()220:yp C x p =>，以()2,0M -为圆心，半径为5的圆与抛物线C 交于,A B 两点，若8AB =，则p =A. 4B. 8C. 10D. 16（10）已知球O 夹在一个二面角l αβ--之间，与两个半平面分别相切于点,A B .若2AB =，球心O 到该二面角的棱l 的距离为2，则球O 的表面积为A. 8πB. 6πC. 4πD. 2π（11）2021年是中国共产党百年华诞，3月24日，中宣部发布中国共产党成立100周年庆祝活动标识（图1），标识由党徽、数字“100”“1921”“2021”和56根光芒线组成，生动展现中国共产党团结带领中国人民不忘初心、牢记使命、艰苦奋斗的百年光辉历程.其中“100”的两个“0”设计为两个半径为R 的相交大圆，分别内含一个半径为的同心小圆，且同心小圆均与另一个大圆外切（图2）.已知21R r =+（），则在两个大圆的区域内随机取一点，则该点取自两大圆公共部分的概率为图1 图2A.121ππ-+ B. 232ππ-+ C. 343ππ-+ D. 454ππ-+ （12）若22x t e lnx t +≥-对一切正实数恒成立，则实数的取值范围是A. 1(,]e -∞B. 1(,]2-∞C. 1+2⎡⎫-∞⎪⎢⎣⎭， D. (,]e -∞ 第Ⅱ卷本卷包括必考题和选考题两部分.第13题～第21题为必考题，每个试题考生都必须做答.第22，23题为选考题，考生根据要求做答.二、填空题:本大题共4小题,每小题5分．（13）在平面直角坐标系中，直线3430x y ++=被圆()()22214x y -++=截得的弦长为 .（14）函数1y x =在点1(2,)2处的切线与直线10ax y ++=垂直，则实数的值为 . （15）在ABC ∆中，58,60a c B ==︒，其内切圆半径为3，则其外接圆半径为 .（16）在ABC ∆中，tan :tan 1:3B C =，以,B C 为焦点的双曲线的一支经过顶点A ，另一支交线段AB 于点M ，BMMA λ=，e 为双曲线的离心率. 设2BC c =，当()2,3e ∈时，λ的取值范围是 .三、解答题：解答应写出文字说明、证明过程或演算步骤．（17）（本小题满分12分）某中学高三共男生800人，女生1200人.现学校某兴趣小组为研究学生日均消费水平是否与性别有关，采用分层抽样的方式从高三年级抽取男女生若干人.记录其日均消费，得到如图所示男生日均消费的茎叶图和女生日均消费的频率分布直方图.将所抽取女生的日均消费分为以下五组：(](](](](]15,20,20,25,25,30,30,35,35,40，规定日均消费不超过25元的人为“节俭之星”.（1）请完成下面22⨯的列联表；“节俭之星”非“节俭之星” 总计男生女生总计根据以上22⨯的列联表，能否有90%的把握认为学生是否为“节俭之星”与性别有关？（2）现已知学校某小组有6名“节俭之星”，其中男生2人，女生4人.现从中选取2人在学校做勤俭节约宣讲活动报告，求选取的2人中至少有一名男生的概率.附：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.0()P K k ≥ 0.15 0.100.05 0.025 0.01 0.0050k2.0722.7063.841 5.0246.6357.829（18）（本小题满分12分）已知等比数列{}n a 各项均为正数，n S 为其前n 项和.若对任意正整数n ，有24+3n n S S +=恒成立，且22log n n b a =.（1）求数列{}n a 的通项公式；（2）令11nn n c b b +=，求数列{}n c 的前n 项和n T ．（19）（本小题满分12分）在如图所示的空间几何体中，两等边三角形ACD ∆与ABC ∆互相垂直，4AC BE ==，BE 和平面ABC 所成的角为60︒，且点E 在平面ABC 上的射影落在ABC ∠的平分线上．（1）求证：DE 平面ABC ；（2）求点B 到平面ADE 的距离．（20）（本小题满分12分）已知椭圆2222:1(0)x y E a b a b+=>>，,A B 为其左右顶点，G 点坐标为(,1)c ，c 为椭圆的半焦距，且有0AG BG ⋅=.椭圆E 的离心率32e =. （1）求椭圆E 的标准方程；（2）已知O 为坐标原点，,M N 为椭圆上不重合两点，且,M N 的中点H 落在直线12y x =上，求MNO ∆面积的最大值. （21）（本小题满分12分）已知21()sin 2f x x x a x =-+，且0x >.（1）当1a =时，求证：()0f x >恒成立；（2）令21()()2ln(1)2g x f x x x x =-+-+，当()0,x π∈时，()g x 无零点，求a 的取值范围.请考生在第22，23两题中任选一题做答.只能做所选定的题目.如果多做，则按所做的第一个题记分.做答时用2B 铅笔在答题卡上把所选题号后方框涂黑. （22）（本小题满分10分）选修4—4：坐标系与参数方程在平面直角坐标系中，P 为曲线122cos :sin x C y αα=+⎧⎨=⎩（α为参数）上的动点，将P 点纵坐标不变，横坐标变为原来的一半得Q 点，记Q 点轨迹为2C ，以坐标原点O 为极点，x轴非负半轴为极轴建立极坐标系. （1）求曲线2C 的极坐标方程；（2）,A B 是曲线2C 上异于极点的两点，且6AOB π∠=，求OA 的取值范围.（23）（本小题满分10分）选修4—5：不等式选讲已知()3544f x x x =-++．（1）关于的不等式()2f x a a ≤-有解，求实数的取值范围；（2）设,m n R +∈，且22m n +=萍乡市2020－2021学年度高三二模考试试卷文科数学试题参考答案及评分标准一、选择题（12×5=60分）：CDCAD ； CDDBA ；BC ．二、填空题（4×5=20分）：13．23 14．4-； 1573 16．18,211⎛⎫⎪⎝⎭．三、解答题（共75分）：17. （1）由茎叶图可知此次抽样男生共20人，由于采用分层抽样的方式，抽取女生人数为30人.“节俭之星”非“节俭之星”总计男生 7 13 20 女生 18 12 30 总计252550…………………2分从而2250(1813127) 3.000 2.70625252030K ⨯-⨯==>⨯⨯⨯ ………………………………………………5分故有90％把握认为学生是否为“节俭之星”与性别有关. ………………………………………6分（2）记2名男生分别为A1,A2,记4名女生为B1,B2,B3,B4,则从这6名“节俭之星”选取2名的所有可能有：（A1,A2）（A1,B1）（A1,B2）（A1,B3）（A1,B4）（A2,B1）（A2,B2）（A2,B3）（A2,B4）（B1,B2）（B1,B3）（B1,B4）（B2,B3）（B2,B4）（B3,B4）………………………………………………………………………………9分共15种，其中至少有1名男生的情况有9种，因此，所求概率为3.5P =……………………12分18. （1）设等比数列{}n a 的公比为q ，首项为1a由2211434243n n n n n n S S a a q S S +++-=+⎧⇒=⇒=⎨=+⎩，……………………………………………………2分由于2121(21),(21)n n nn S a S a ++=-=-，所以211124233n n a a a +-==，故11a =，故12n n a -=…………………………………………6分（2）22log 21n n b a n ==-，则111111()(21)(21)22121n n n C b b n n n n +===--+-+………9分故12111111(1)2335212121n n nT C C C n n n =+++=-+-++-=-++…………………12分19. （1）取AC 中点O ，连接,BO DO ，由题知，BO 为ABC ∠的平分线，,BO AC DO AC ⊥⊥设点F 是点E 在平面ABC 上的射影，由题知，点F 在BO 上连接EF ，则EF ⊥平面ABC .平面ACD ⊥平面ABC ，平面ACD 平面ABC AC =，DO ⊂平面,ACD DO AC ⊥，DO ∴⊥平面ABC//DO EF ∴……………………………………………………………2分BE 和平面ABC 所成的角为60︒，即60EBF ∠=︒，23EF ∴=又23DO =，∴四边形EFOD为平行四边形，//DE BO ∴…………………………………5分BO ⊆平面ABC ，DE ⊄平面ABC ，DE ∴平面ABC (6)分（2）设点B 到平面ADE 的距离为d 由B ADE A BDE V V --=得：11233ADE BDE d S S ∆∆⋅=⋅…………………………………………………8分111123232AD DE d ED DO ⋅⋅⋅⋅=⋅⋅⋅⋅………………………………………………………………10分解得3d =…………………………………………………………………………………………12分20. （1）依题意：(,0),(,0)A a B a -，则(,1),(,1)AG c a BG c a =+=-……………………1分2210AG BG c a ∴=-+=，即21b =，又32c a =，解得3,2,1c a b ===………………3分所以椭圆方程为：2214x y +=………………………………………………………………………4分（2）设112200(,),(,),(,)M x y N x y H x y ，则002y x =，因为,M N 在椭圆上，有：2211021122221120224414()4244MN x y x y y x x k x x y y y x y ⎧+=-+⎪⇒==-=-=-⎨-++=⎪⎩………………………………6分设直线MN ：1(0)2y x m m =-+≠，联立 2221212221244402,22244y x m x mx m x x m x x m x y ⎧=-+⎪⇒-+-=⇒+==-⎨⎪+=⎩………………8分又232160m ∆=->，得(m ∈所以12x x MN -===原点O 到直线MN的距离d ==……………………………………………………10分故2212122MNO m m S d MN ∆+-===………………………………………11分当且仅当222m m =-，即1m =±时等号成立，故MNO ∆面积的最大值为1. ……………12分21. （1）依题意：当1a =时，21()sin 2f x x x x =-+，则'()1cos f x x x =-+.…………1分令()1cos x x x ϕ=-+，则'()1sin 0x x ϕ=-≥恒成立.()x ϕ∴在R 上单调递增………………3分()(0)0x ϕϕ∴≥=，即'()0f x ≥恒成立，()f x ∴在R 上单增，()(0)0f x f ∴≥=即证…5分（2）[解法1]：21()()2ln(1)sin ln(1)2g x f x x x x x a x x =-+-+=+-+ 1()1+cos 1g x a x x '=-+……………………………………………………………………………6分○1当0a <时， ()g x '在()0π，递增，(0)0g '<，1()=101g a ππ'-->+，所以存在()00x π∈，使0()=0g x '……………………………………8分当()00x x ∈，，()g x 单调递减，当()0x x π∈，，()g x 单调递增又(0)=0g ，()=ln(+1)>0g πππ-故存在唯一的零点0(,)t x π∈使()=0g t …………………………………………………………10分○2当0a ≥时，由()0x π∈，得()ln(1)g x x x ≥-+，可证：ln(1)0((0,))x x x π-+>∈ ()0g x >在()0x π∈，上恒成立。

江西省萍乡市2019-2020学年高考第二次大联考数学试卷含解析

江西省萍乡市2019-2020学年高考第二次大联考数学试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()()3cos 0f x x x ωωω+>，对任意的1x ，2x ，当()()1212f x f x =-时，12min 2x x π-=，则下列判断正确的是（）A ．16f π⎛⎫=⎪⎝⎭ B ．函数()f x 在,62ππ⎛⎫⎪⎝⎭上递增 C ．函数()f x 的一条对称轴是76x π= D ．函数()f x 的一个对称中心是,03π⎛⎫⎪⎝⎭【答案】D 【解析】【分析】利用辅助角公式将正弦函数化简，然后通过题目已知条件求出函数的周期T ，从而得到ω，即可求出解析式，然后利用函数的性质即可判断. 【详解】Q ()3cos 3f x x x x πωωω⎛⎫=+=+ ⎪⎝⎭，又sin 13x πω⎛⎫-≤+≤ ⎪⎝⎭Q ，即3x πω⎛⎫-≤+≤ ⎪⎝⎭， ∴有且仅有12-=-满足条件；又12min2x x π-=，则22T T ππ=⇒=， 22T πω∴==，∴函数()23f x x π⎛⎫=+ ⎪⎝⎭，对于A ，2363f ππ⎛⎫== ⎪⎝⎭，故A 错误；对于B ，由()222232k x k k Z πππππ-+≤+≤+∈，解得()51212k x k k Z ππππ-+≤≤+∈，故B 错误；对于C ，当76x π=时，7726333f ππππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，故C 错误；对于D ，由20333f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，故D 正确. 故选：D本题考查了简单三角恒等变换以及三角函数的性质，熟记性质是解题的关键，属于基础题. 2．在边长为1的等边三角形ABC 中，点E 是AC 中点，点F 是BE 中点，则AF AB ⋅=u u u r u u u r（） A ．54B ．34C ．58D ．38【答案】C 【解析】【分析】根据平面向量基本定理，用,AB AC u u u r u u u r 来表示AF u u u r，然后利用数量积公式，简单计算，可得结果.【详解】由题可知：点E 是AC 中点，点F 是BE 中点()12AF AB AE =+u u u r u u u r u u u r ，12AE AC =u u u r u u u r所以1124AF AB AC =+u u u r u u u r u u u r又11cos 1122AB AC AB AC A ⋅=∠=⨯⨯=u u u r u u u r u u u r u u u r所以1124AF AB AB AC AB ⎛⎫⋅=+⋅ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r则2115248AF AB AB AC AB ⋅=+⋅=u u u r u u u r u u u r u u u r u u u r故选：C 【点睛】本题考查平面向量基本定理以及数量积公式，掌握公式，细心观察，属基础题.3．已知()f x 为定义在R 上的奇函数，若当0x ≥时，()2xf x x m =++（m 为实数），则关于x 的不等式()212f x -<-<的解集是（） A ．()0,2 B ．()2,2-C ．()1,1-D ．()1,3【答案】A 【解析】【分析】先根据奇函数求出m 的值，然后结合单调性求解不等式. 【详解】据题意，得()010f m =+=，得1m =-，所以当0x ≥时，()21xf x x =+-.分析知，函数()f x 在R上为增函数.又()12f =，所以()12f -=-.又()212f x -<-<，所以111x -<-<，所以02x <<，【点睛】本题主要考查函数的性质应用，侧重考查数学抽象和数学运算的核心素养. 4．设复数z 满足()117i z i +=-，则z 在复平面内的对应点位于（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】C 【解析】【分析】化简得到34z i =--，得到答案. 【详解】()117i z i +=-，故()()()()1711768341112i i i iz i i i i -----====--++-，对应点在第三象限.故选：C . 【点睛】本题考查了复数的化简和对应象限，意在考查学生的计算能力. 5．已知52i 12ia =+-（a ∈R ），i 为虚数单位，则a =（） AB ．3C ．1D ．5【答案】C 【解析】【分析】利用复数代数形式的乘法运算化简得答案. 【详解】由52i 12ia =+-，得12i 2i a +=+，解得1a =. 故选:C. 【点睛】本题考查复数代数形式的乘法运算,是基础题. 6．已知数列1a ，21a a ，32a a ，…，1n n a a -是首项为8，公比为12得等比数列，则3a 等于（）A ．64B ．32C ．2D ．4【答案】A 【解析】【分析】根据题意依次计算得到答案. 【详解】根据题意知：18a =，214a a =，故232a =，322a a =，364a =. 故选：A . 【点睛】本题考查了数列值的计算，意在考查学生的计算能力.7．如图是国家统计局公布的年入境游客（单位：万人次）的变化情况，则下列结论错误的是（）A ．2014年我国入境游客万人次最少B ．后4年我国入境游客万人次呈逐渐增加趋势C ．这6年我国入境游客万人次的中位数大于13340万人次D ．前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差【答案】D 【解析】【分析】ABD 可通过统计图直接分析得出结论，C 可通过计算中位数判断选项是否正确. 【详解】A ．由统计图可知：2014年入境游客万人次最少，故正确；B ．由统计图可知：后4年我国入境游客万人次呈逐渐增加趋势，故正确；C ．入境游客万人次的中位数应为13340.13与13604.33的平均数，大于13340万次，故正确；D ．由统计图可知：前3年的入境游客万人次相比于后3年的波动更大，所以对应的方差更大，故错误. 故选：D. 【点睛】本题考查统计图表信息的读取以及对中位数和方差的理解，难度较易.处理问题的关键是能通过所给统计图，分析出对应的信息，对学生分析问题的能力有一定要求.8．已知等差数列{}n a 中，468a a +=则34567a a a a a ++++=（）A ．10B ．16C ．20D ．24【答案】C 【解析】【分析】根据等差数列性质得到46582a a a +==，再计算得到答案. 【详解】已知等差数列{}n a 中，4655824a a a a +==⇒=345675520a a a a a a ++++==故答案选C 【点睛】本题考查了等差数列的性质，是数列的常考题型. 9．已知数列{}n a 中，12a =，111n n a a -=-(2n ≥)，则2018a 等于（） A ．12B ．12-C ．1-D ．2【答案】A 【解析】【分析】分别代值计算可得，观察可得数列{}n a 是以3为周期的周期数列，问题得以解决. 【详解】解：∵12a =，111n n a a -=-(2n ≥)， 211122a ∴=-=， 3121a =-=-，41(1)2a =--=，511122a =-=， …，∴数列{}n a 是以3为周期的周期数列，201836722=⨯+Q ，2018212a a ∴==，故选：A. 【点睛】本题考查数列的周期性和运用：求数列中的项，考查运算能力，属于基础题.10．二项式52x ⎫-⎪⎭的展开式中，常数项为（）A ．80-B ．80C ．160-D ．160【答案】A 【解析】【分析】求出二项式52x ⎫-⎪⎭的展开式的通式，再令x 的次数为零，可得结果.【详解】解：二项式52x ⎫-⎪⎭展开式的通式为()()55225215512rrr rrr rrr T C x C x---+-+=-=-，令5202rr --+=，解得1r =，则常数项为()11451280C -=-.故选：A. 【点睛】本题考查二项式定理指定项的求解，关键是熟练应用二项展开式的通式，是基础题. 11．已知复数,z a i a R =+∈，若||2z =，则a 的值为（） A ．1 BC ．±1D．【答案】D 【解析】由复数模的定义可得：2z ==，求解关于实数a的方程可得：a =.本题选择D 选项.12．已知:|1|2p x +> ，:q x a >，且p ⌝是q ⌝的充分不必要条件，则a 的取值范围是（） A ．1a ≤ B ．3a ≤-C ．1a ≥-D ．1a ≥【答案】D 【解析】“p ⌝是q ⌝的充分不必要条件”等价于“q 是p 的充分不必要条件”，即q 中变量取值的集合是p 中变量取值集合的真子集. 【详解】由题意知：:|1|2p x +>可化简为{|31}x x x <->或，:q x a >，所以q 中变量取值的集合是p 中变量取值集合的真子集，所以1a ≥. 【点睛】利用原命题与其逆否命题的等价性，对p ⌝是q ⌝的充分不必要条件进行命题转换，使问题易于求解. 二、填空题：本题共4小题，每小题5分，共20分。

江西省萍乡市2022届高三数学第二次模拟考试试题文(解析版)

如图，当直线在阴影处运动时，直线与圆没有公共点，当直线在非阴影处运动时，直线与圆有公共点，
故事件“直线与圆有公共点”发生的概率
故答案选：C
10. 已知函数，则的所有零点之和为（）
A. B. C. D.
【10题答案】
【答案】D
【解析】
【分析】根据零点定义求出零点后可得．
【详解】时，由得，
【详解】由题意当是圆切线时，取得最大值，而当时，，
所以由在圆上总存在点，使得，得，
即，解得．
故答案为：．
三、解答题：解答应写出文字说明、证明过程或演算步骤．
17. 第24届冬奥会于2022年2月4日至2月20日在北京举行，组委会为普及冬奥知识，面向全市征召名志愿者成立冬奥知识宣传小组，现把该小组成员按年龄分成这组，得到的频率分布直方图如图所示，已知年龄在内的人数为．
A. B.
C. D.
【9题答案】
【答案】C
【解析】
【分析】根据题意，设出直线，利用圆心到直线位置关系，作图，即可计算出所求概率
【详解】
根据题意，直线为绕原点转动的任一直线，可设，设圆心到直线的距离为，
所以，，若与圆相交或相切，则，化简得，，得，
所以，，可以用原点为圆心， (半径长度可随意取)，作圆，
故选：A.
8. 已知椭圆，圆，若的重心在椭圆上，则椭圆的离心率为（）
A. B. C. D.
【8题答案】
【答案】A
【解析】
【分析】先表示出的重心，代入椭圆可得出，即可求出离心率.
【详解】由题可得，则的重心为，
将代入椭圆可得，即，

江西省萍乡市数学高三上学期文数第二次联考试卷

江西省萍乡市数学高三上学期文数第二次联考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共12分)1. （1分） (2019高一上·大庆期中) 设函数的定义域，函数y=ln(1-x)的定义域为 ,则（）A . （1,2）B . （1,2]C . （-2,1）D . [-2,1)2. （1分）复数在复平面的对应的点位于（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限3. （1分） (2018高一下·大连期末) 已知，不共线，，，其中 .设点是直线，的交点，则（）A .B .C .D .4. （1分）设x,y满足约束条件，则目标函数z=x+2y的最大值是（）A . 3B . 4C . 5D . 65. （1分）(2020·重庆模拟) 已知AB是圆的任意一条直径，点P在直线上运动，若的最小值为4，则实数a的值为（）A . 2B . 4C . 5D . 66. （1分）(2017·东莞模拟) 己知函数f（x）是定义在R上的偶函数，f（x+1）为奇函数，f（0）=0，当x∈（0，1]时，f（x）=log2x，则在区间（8，9）内满足方f（x）程f（x）+2=f（）的实数x为（）A .B .C .D .7. （1分） (2016高一上·铜仁期中) 函数y=logax，y=logbx，y=logcx，y=logdx的图象如图所示，则a，b，c，d的大小顺序是（）A . 1＜d＜c＜a＜bB . c＜d＜1＜a＜bC . c＜d＜1＜b＜aD . d＜c＜1＜a＜b8. （1分）(2017·金华模拟) 在△ABC中，角A，B，C的对边分别为a，b，c，已知∠B=30°，△ABC的面积为，且sinA+sinC=2sinB，则b的值为（）A . 4+2B . 4﹣2C . ﹣1D . +19. （1分）已知一个三角形的三边长构成等比数列，其公比为，则函数的值域为（）A .B .C .D .10. （1分） (2018高一下·攀枝花期末) 已知数列满足：， .设，，且数列是单调递增数列，则实数的取值范围是（）A .B .C .D .11. （1分） (2015高二下·永昌期中) 设f（n）= + + +…+ （n∈N+）则f（k+1）﹣f （k）=（）A .B .C .D .12. （1分） (2018高二下·集宁期末) 函数f(x)= (e为自然对数的底数)在区间[-1,1]上的最大值是（）A . 1+B . 1C . e+1D . e-1二、填空题 (共4题；共4分)13. （1分） (2015高三上·临川期末) 已知△ABC中，AB=7，AC=8，BC=9，P点在平面ABC内，且 +7=0，则| |的最大值为________ ．14. （1分） (2017高二上·西华期中) 已知等差数列{an}，{bn}前n项和分别为Sn和Tn ，若 = ，则 =________．15. （1分） (2018高一上·西宁期末) 已知，则 ________．16. （1分） (2017高一上·中山月考) 函数在区间上的值域是________.三、解答题 (共6题；共13分)17. （2分）已知数列{an}的通项公式为an=2n﹣1（1）求证：{an}是等差数列；（2）求{an}的前n项和Sn18. （3分） (2018高三上·黑龙江月考) 已知，且（1）求的值；（2）求的值.19. （2分） (2016高一下·漳州期末) 已知△ABC的外接圆半径为1，角A，B，C的对边分别为a，b，c，且2acosA=ccosB+bcosC．（1）求cosA及a的值；（2）若b2+c2=4，求△ABC的面积．20. （2分） (2017高一下·蚌埠期中) 在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b+c=2acosB．（Ⅰ）证明：A=2B（Ⅱ）若△ABC的面积S= ，求角A的大小．21. （2分） (2018高三上·丰台期末) 已知函数 .（Ⅰ）求函数的单调区间；（Ⅱ）当时，若在上有零点，求实数的取值范围.22. （2分） (2017高二下·合肥期中) 请您设计一个帐篷．它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥（如图所示）．试问当帐篷的顶点O到底面中心O1的距离为多少时，帐篷的体积最大？参考答案一、单选题 (共12题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共13分)17-1、18-1、18-2、19-1、19-2、20-1、21-1、22-1、第11 页共11 页。

江西省七校高三第二次联考数学文科试卷及答案

1 / 6江西省七校第二次联考高三年级数学试卷（文科）一、选择题(本大题共12小题，每小题5分，共60分。

每小题给出四个选项中，只有一项是符合题目要求的。

)1、若集合P ＝{－2, 0, 2}，i 是虚数单位，则A ．2i ∈PB ．2i∈P C ．(2i)2∈P D ．32i∈P 2、点A(sin °, cos °)位于 A ．第一象限 B ．第二象限C ．第三象限D ．第四象限3、已知函数f(x)＝ln(2116x +－4x)＋1，则f(lg3)＋f(lg 13)＝A ．2B ．1C ．0D ．－1 4、设α,β是空间两个平面，m, n 是空间两条直线，则下列选项不正确．．．的是 A ．当m ⊂α时，“n ∥α”是“m ∥n ”的必要不充分条件 B ．当m ⊂α时，“m ⊥β”是“α⊥β”的充分不必要条件 C ．当n ⊥α时，“n ⊥β”是“α∥β”的充要条件D ．当m ⊂α时，“n ⊥α”是“m ⊥n ”的充分不必要条件5、已知椭圆22163x y +=上有一点P ，F 1, F 2是椭圆的左、右焦点，若△F 1PF 2为直角三角形，则这样的点P 有 A ．8个 B ．6个 C ．4个 D ．2个6、现有四个函数：①y ＝xsinx, ②y ＝xcosx, ③y ＝x |cosx|, ④y ＝x ·2x 的部分图象如下，但顺序被打乱了，则按照从左到右将图像对应的函数序号排列正确的一组是A ．①②③④B ．②①③④C ．③①④②D ．①④②③7、在区间[－2π, 2π]内随机取两个数分别记为a, b, 则使得函数 f(x)＝4x 2＋4ax －b 2＋π有零点的概率为A ．34B ．1516C ．78D ．1168、一个几何体的三视图如图所示，则这个几何体的外接球的体积为A ．23π B ．2πC ．2πD ．223π9、设双曲线)0,0(12222>>=-b a by a x 的右焦点为F(c, 0), 方程ax 2＋bx －c ＝0的两个实根分别为x 1, x 2，则点P(x 1, x 2) A ．必在圆x 2＋y 2＝2内 B ．必在圆x 2＋y 2＝2外 C ．必在圆x 2＋y 2＝2上 D ．以上三种情况都有可能 10、定义某种运算S ＝a ⊗b ，运算原理如图所示，设函数f(x)＝(x 2―2)⊗(x ―x 2), x ∈R , 若函数y ＝f(x)－c 的图象与x 轴恰有两个公共点，则实数c 的取值范围为A ．(－∞, －2)∪(－1,32)B ．(－∞, －2]∪(―1, ―34) C ．(－1,14)∪(14, ＋∞)D ．(―1, ―34)∪[14, ＋∞) 11、某同学在纸上画出如下若干个三角形：△▲△△▲△△△▲△△△△▲△△△△△▲…… 若依此规律，得到一系列的三角形，则在前个三角形中共有▲的个数是 A ．64 B ．63 C ．62 D ．6112、若0,2sin cos ,x x y x π⎧≤≤⎪⎨⎪≤≤⎩则z ＝x ＋2y 的取值范围是A ．(0,6π] B ．[0, 3] C ．[0, 3－6π] D ．[0, 3＋6π] 二、填空题（本大题共4小题，每小题5分，共20分。

江西省萍乡市2022届高三数学第二次模拟考试试题文(解析版)

1江西省萍乡市2022届高三数学第二次模拟考试试题文本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至4页．满分150分，考试时间120分钟．注意事项：1．答卷前，考生务必将自已的准考证号、姓名填写在答题卡上．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人的准考证号、姓名是否一致．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号．第Ⅱ卷用0．5毫米的黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答题无效．3．考试结束后，监考员将试题卷、答题卡一并收回．第Ⅰ卷一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知，，则（）A. B. C. D. 【1题答案】【答案】C 【解析】【分析】根据集合元素的形式可得关于的不等式，从而可求.【详解】令，则，而，故，故，故选：C.2. 已知复数满足(为虚数单位)，则=（）B.C.D. 【2题答案】{}+|17A x N x =∈-≤≤{}|31,B x x n n N ==+∈A B = {}1,4{}4,7{}1,4,7{}1,1,4,7-n A B 1317n -≤+≤223n -≤≤n N ∈0,1,2n ={}1,4,7A B = z 32i (1i)z =+i z 21122【解析】【分析】先化简复数z ，再利用复数的模公式求解.【详解】解：因为，所以，故选：D3. 北京2022年冬奥会的成功举办，带动了我国冰雪产业快速发展，冰雪运动市场需求得到释放．下图是2012-2019年我国已投入运营的室内滑雪场数量（家）与同比增长率（与上一年相比）的统计情况，则下面说法错误的是（）A. 2012-2019年，我国室内滑雪场的数量总体呈增长态势B. 2013-2019年，我国室内滑雪场的增速逐渐加快C. 2013-2019年，我国室内滑雪场的增速在2017年触底D. 2013-2019年，我国室内滑雪场的增速在2018年首次出现正增长【3题答案】【答案】B32i i 1(1i)2i 2z ==-=-+12z =3【分析】根据图表中的柱状图的高低变化和同比增长率的曲线图可得错误的说法.【详解】图表中的室内滑雪场的数量的柱状图逐年升高，故总体呈增长态势，故A 正确.2013-2017年，我国室内滑雪场的增速逐年降低，2018年，我国室内滑雪场的增速有所提高，而2019年的增速有小幅回落.故B 错误，CD 正确.故选：B.4. 已知，则（）A. B. C. D. 【4题答案】【答案】A 【解析】【分析】利用二倍角的余弦公式求解.【详解】因为，所以，，，故选：A 5. 若函数的图象在处的切线斜率为，则()A. B. C. D. 【5题答案】【答案】A1sin 62πα⎛⎫+= ⎪⎝⎭cos 23πα⎛⎫+= ⎪⎝⎭12212-21sin 62πα⎛⎫+= ⎪⎝⎭cos 2cos 236ππαα⎡⎤⎛⎫⎛⎫+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦212sin 6πα⎛⎫=-+ ⎪⎝⎭2111222⎛⎫=-= ⎪⎝⎭()ln f x x a x=-1x =3=a 2-1-124【分析】求f (x )导数，由题可知即可求a 的取值．【详解】∵，∴，若函数的图象在处的切线斜率为，则．故选：A ．6. 在中，为边上的中线，在线段上，，则（）A. B. C. D. 【6题答案】【答案】B 【解析】【分析】由向量的线性运算法则计算．【详解】由题意，故选：B ．7. 如图，在正方体中，E ，F 分别为BC ，的中点，过点A ，E ，F 作一截面，该截面将正方体分成上下两部分，则下部分几何体的正视图为（）(1)3f '=()ln f x x a x =-()1af x x'=-()ln f x x a x=-1x =3(1)1321af a '=-=⇒=-ABCADBCEAD2AE ED=EB =3144AB AC -2133AB AC -2233AB AC -3144AB AC +22121()33233EB AB AE AB AD AB AB AC AB AC =-=-=-⨯+=-1111ABCD A B C D -1CC5A. B. C. D.【7题答案】【答案】A 【解析】【分析】由，可得截面为，得到几何体，进而得正视图.【详解】如图由于，，由题意得此截面为，由图可知正视图应为A 选项，故选：A.8. 已知椭圆，圆，若的重心在椭圆上，则椭圆的离心率为（）A. B. C. D. 【8题答案】【答案】A 【解析】【分析】先表示出的重心，代入椭圆可得出，即可求出离心率.【详解】由题可得，则的重心为，将代入椭圆可得，即，1//EF AD 1AEFD 1//EF AD 1AEFD 2222:1(0)x y C a b a b+=>>22:630M x y bx ay +-+=12F MF △CC21223412F MF △222a b =()()123,0,,0,3,2F c F c M b a ⎛⎫-- ⎪⎝⎭12F MF △,2a b ⎛⎫- ⎪⎝⎭,2a b ⎛⎫- ⎪⎝⎭222214b a a b +=4224440b a b a -+=6即，则，所以.故选：A.9. 已知圆，直线为绕原点转动的任一直线，则事件“直线与圆有公共点”发生的概率为（）A. B. C. D. 【9题答案】【答案】C 【解析】【分析】根据题意，设出直线，利用圆心到直线位置关系，作图，即可计算出所求概率【详解】根据题意，直线为绕原点转动的任一直线，可设，设圆心到直线的距离为，所以，，若与圆相交或相切，则，化简得，，得，所以，，可以用原点为圆心，(半径长度可随意取)，作圆，()22220ba-=222a b=2c e a ===()22:21C x y -+=l l C 3π6π1316:l y kx=l:l y kx=dd =l C 1d ≤2241k k≤+33k -≤≤60AOB ∠=︒O3r =7如图，当直线在阴影处运动时，直线与圆没有公共点，当直线在非阴影处运动时，直线与圆有公共点，故事件“直线与圆有公共点”发生的概率故答案选：C10. 已知函数，则的所有零点之和为（）A. B. C. D. 【10题答案】【答案】D 【解析】【分析】根据零点定义求出零点后可得．【详解】时，由得，时，由得或，所以四个零点和为．故选：D ．11. 已知四棱锥的底面四边形是正方形，侧棱平面，，且直线与平面所成的角的正切值为，则四棱锥的体积为（）A.B.C.D.【11题答案】【答案】Cl l Cl l Cl C 12013603P ︒==︒()()21,01,0x x f x x x ⎧-≥⎪=⎨+<⎪⎩1()2y f x =-1212-2x ≥21(1)02x --=12x =±0x <1102x +-=12x =-32x =-131102222++---=P ABCD-ABCDPA ⊥ABCD3PA =PCPAB 3P ABCD -3918278【解析】【分析】利用直线与平面所成的角的正切值，求出的边长，进一步利用体积公式求出答案.【详解】设的边长为∵平面∴又∵，∴平面∴直线与平面所成的角即为角∴解得四棱锥的体积为.故选：C.PCPABABCDABCDaPA ⊥ABCDPA ⊥BCBC AB⊥PA AB A⋂=BC ⊥PABPCPABCPB∠3BC PB =3=a =P ABCD -213183V a =⨯=912. 设函数在区间上的最大值为，最小值为，则的最小值为（）A. B. C. D. 【12题答案】【答案】B 【解析】【分析】求出的范围，把它作为整体，结合正弦函数性质得最大值与最小值并分析它们的差最小时结论．【详解】时，，令，，则问题转化为在上的最大值是，最小值是，由正弦函数性质，的周期是，要使得最小，则的最大值或最小值点是区间的中点，由周期性，不妨取或，，或，时，，，，时，，，，()sin 24f x x π⎛⎫=+ ⎪⎝⎭,3a a π⎡⎤+⎢⎥⎣⎦M m M m-21212-12-24x π+M m [,]3x a a π∈+22,24443x a a ππππ2⎡⎤+∈+++⎢⎥⎣⎦24x t π+=24a h π+=()sin g t t =2[,]3t t π+M m ()sin g t t=2πM m-()g t 2[,3h h π+23h h ππ++=233h h ππ++=6h π=76h π=6h π=1M =1sin 62m π==12M m -=76h π=1m =-71sin 62M π==-12M m -=10故选：B ．第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22，23题为选考题，考生根据要求做答．二、填空题:本大题共4小题，每小题5分．13. 已知函数是上的奇函数，且，若非零正实数满足，则的小值是_______．【13题答案】【答案】【解析】【分析】由函数为奇函数，得到，结合函数的单调性，得到，得到，利用基本不等式，即可求解.【详解】因为函数为奇函数，可得，由，可得，又因为，可得，所以函数为单调递增函数，所以，即，即，则，当且仅当，即时，等号成立，()f x R ()33f x x x=+,m n ()()20f m mn f n -+=11m n +2()f x ()2()f m mn f n -=-2m mn n -=-111111()()(2)22n m m n m n m n m n +=⋅++=⋅++()f x ()()f x f x -=-()()20f m mn f n -+=()()2()f m mn f n f n -=-=-()33f x x x =+()2330f x x '=+>()f x 2m mn n -=-2m n mn +=112m n +=1111111()()(2(22222n m m n m n m n m n +=⋅++=⋅++≥⋅+=n mm n =1m n ==11所以的小值是.故答案为：14. 若实数、满足约束条件，则目标函数的最小值为________．【14题答案】【答案】【解析】【分析】作出可行域，平移直线，找出使得目标函数在轴上截距最小时对应的最优解，代入目标函数即可得解.【详解】作出不等式组所表示的可行域如下图所示：联立，解得，即点，平移直线，当该直线经过可行域的顶点时，直线在轴上的截距最小，此时取最小值，即.故答案为：.15. 中，角的对边分别为，若，则________．11m n +22x y1002310x x y x y +≥⎧⎪-≤⎨⎪+-≥⎩3z x y =+2-3z x y=+3z x y=+y1002310x x y x y +≥⎧⎪-≤⎨⎪+-≥⎩102310x x y +=⎧⎨+-=⎩11x y =-⎧⎨=⎩()1,1A -3z x y=+A3z x y=+yz ()min 3112z =⨯-+=-2-ABC ,,A B C ,,a bc ,cos cos 2o c s a b cc B C a A +=+=b =12【15题答案】【答案】【解析】【分析】由正弦定理化边为角，然后由两角差的正弦公式变形，结合正弦函数性质求得，再用余弦定理列方程解得．【详解】因为，由正弦定理得，，，，是三角形内角，，所以，所以，所以，由余弦定理得，解得（舍去），故答案为：．16. 已知圆，对直线上一点，在圆上总存在点，使得23C π=bcos cos cos a b c A B C +=+sin sin sin cos cos cos A B CA B C +=+sin cos sin cos sin cos sin cos A C B C C A C B +=+sin cos sin cos sin cos sin cos A C C A C B B C-=-sin()sin()A C C B -=-,,A B C(,)A C CB A B ππ-+-=-∈-AC C B-=-2A B C +=3C π=2222cos c a b ab C =+-2243cos33b b π=+-=+-2b=2b=222:2O x y +=340x y +-=(),P t k O A13，则实数的取值范围为________．【16题答案】【答案】【解析】【分析】在圆上，当是圆切线时，取得最大值，由题意这个最大值不小于即满足题意，利用圆心到点的距离与半径的2倍比较可得．【详解】由题意当是圆切线时，取得最大值，而当时，，所以由在圆上总存在点，使得，即，解得．故答案为：．三、解答题：解答应写出文字说明、证明过程或演算步骤．17. 第24届冬奥会于2022年2月4日至2月20日在北京举行，组委会为普及冬奥知识，面向全市征召名志愿者成立冬奥知识宣传小组，现把该小组成员按年龄分成这组，得到的频率分布直方图如图所示，已知年龄在内的人数为．30OPA ∠=︒k2,25⎡⎤⎢⎥⎣⎦A OPAOOPA∠30°P PA O OPA ∠30OPA ∠=︒2OP R ==O A 30OPA ∠=︒≤22(43)8k k -+≤225k ≤≤2,25⎡⎤⎢⎥⎣⎦a [20,25),[25,30),[30,35),[35,40),[40,45]5[25,30)3514（1）求和的值，并估计该冬奥知识宣传小组成员年龄的中位数（中位数精确到）；（2）若用分层抽样的方法从年龄在内的志愿者中抽取名参加某社区的宣传活动，再从这名志愿者中随机抽取名志愿者去该社区的一所高中组织一次冬奥知识宣讲，求这志愿者中至少有1人年龄在内的概率．【17题答案】【答案】（1），，31.7（2）【解析】【分析】（1）先计算各组的频率，再根据频率和为1计算出的值，然后再根据段的人数和对应的频率计算出总人数；利用面积法求出中位数；（2）先计算出年龄在内的志愿者人数；再求从这6名志愿者中随机抽取2名志愿者的基本事件总数和至少有一名志愿者年龄在内的事件数，代入古典概型概率计算公式，可得答案【小问1详解】由频率分布直方图知：，解得…因为年龄在内的人数为，所以设冬奥知识宣传小组成员年龄的中位数的估计值为，则内，且满足，解得【小问2详解】ma 0.1[30,35),[35,40),[40,45]6622名[35,40)0.07m =100a =35m[25,30)[30,35),[35,40),[40,45][35,40)(0.010.060.040.02)51m ++++⨯=0.07m =[25,30)3535(0.075)100a =÷⨯=x[30,35)x ∈0.0150.075(30)0.060.5x ⨯+⨯+-⨯=23131.73x =≈15由频率分布直方图知：小组成员年龄在的人数之比为，故抽取的6名志愿者中，在区间中分别抽取了人，人，人记中的名志愿者为，中的名志愿者为，中的名志愿者为，则从人中再随机抽取人的所有可能有；共种，至少有1人年龄在内的情形有种，故所求概率为19. 如图，一半圆的圆心为，是它的一条直径，，延长至，使得，设该半圆所在平面为，平面外有一点，满足平面平面，且，该半圆上点满足．（1）求证：平面平面；．（2）若线段与半圆交于，求三棱锥的体积．【19题答案】【答案】（1）证明见解析（2）[30,35),[35,40),[40,45]3:2:1[30,35),[35,40),[40,45]321[30,35)3123,,A A A [35,40)212,B B [40,45]1C 62121311121(,),(,),(,),(,),(,),A A A A AB A B AC 2321222313231212(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)A A AB A B AC A B A B A C B B B C B C 15[35,40)993155P ==OAB2AB =ABCBC OB=ααP POC ⊥αOP CP ==Q PQ =POQ ⊥POCCQRO PQR-41516【解析】【分析】（1）连接，结合面面垂直得平面，进而得，再结合勾股定理得，进而证明平面即可证明结论；（2）过点作于，则为的中点，进而根据几何关系，结合体积公式求解即可.【小问1详解】证明：连接，又平面平面，平面平面，平面，，∵，平面，又平面，，由平面平面，且平面平面，平面，又平面，∴平面平面.【小问2详解】解：过点作于，则为的中点，PBPB ⊥αPB OQ⊥PO OQ⊥OQ ⊥POCOOD QR⊥DDQRPB ,,OP CP OB CB PB OC==∴⊥POC ⊥αPOC=OCαPB ∴⊥αPB OQ∴⊥1,OP OQ PQ ∴===222,,OP OQ PQ PO OQ ∴+=∴⊥OP PB P= OQ ∴⊥POCAB ⊆POCOQ AB∴⊥POC ⊥αPOC ⊥ABα=OQ ∴⊥POCOQ ⊆POQPOQ ⊥POCOOD QR⊥DDQR17故在中：，即：又，21. 已知数列中，，令．（1）计算的值，并求数列的通项公式；（2）若，求数列的前项和．【21题答案】【答案】（1）；（2）Rt COQ 1122OC OQ CQ OD ⨯=⨯5OD=5RQ ∴==11222555ORQ S RQ OD ∆∴=⨯=⨯⨯=2PB == 1124233515O PQR P OQR OQR V V S PB --∆∴==⨯=⨯⨯={}n a 111,2n n n a a a +==2nn b a =123,,b b b {}n b ()31n n c n b =+{}n c n n T 1232,4,8b b b ===2nn b =1(32)24n n T n +=-⋅+18【解析】【分析】（1）根据递推关系求出即可得出，再证明为等比数列即可求出通项公式；（2）利用错位相减法可求出.【小问1详解】由得，又，，，由得，两式相除可得，则，是以2 为首项，2 为公比的等比数列，故；【小问2详解】由 (1) 知，则，，两式相减得，故．23. 已知．（1）若，求的极值；246,,a a a 123,,b b b {}n b 12n n n a a +=12nn n a a +=11a =423562,2,4,84,a a a a a ∴=====4612232,4,8b a b a b a ∴======12n n n a a +=1122n n n a a +++=22n na a +=12222n n n nb a b a ++=={}n b ∴2nn b =(31)2nn c n =+()2314272102322(31)2n nn T n n -=⨯+⨯+⨯++-++ ()234124272102322(31)2n n n T n n +=⨯+⨯+⨯++-++ ()2123112283222(31)283(31)212n nn n n T n n +++--=+⨯+++-+=+⨯-+- 1(23)24n n +=-⋅-1(32)24n n T n +=-⋅+21()ln 12a f x x x ax-=+++1a =-()f x19（2）若不等式恒成立，求实数的取值范围．【23题答案】【答案】（1）极大值为；无极小值.（2）【解析】【分析】（1）根据题意，利用导数研究函数的单调性，进而得极值；（2）由题知，进而分和两种情况讨论求解即可.【小问1详解】解：当时，，，当时，递增；当时，递减，的极大值为；无极小值；【小问2详解】解：，当即时，递增；，不合题意，（注：取其它使得的也可）．1()ln 24f x <-a 1ln 24-+(),1a ∞∈--()()()111a x x f x x⎡'⎤-++⎣⎦=10a -≥10a -<1a =-()2ln 1f x x x x =+--()()()121121x x f x x x x+-=-=-'-∴1(0,)2x ∈()()0,f x f x '>1(,)2x ∈+∞()()0,f x f x '<()f x ∴11ln224f ⎛⎫=-+⎪⎝⎭()()()()()21111111a x x a x ax f x a x a x x x⎡⎤-++-++⎣=='⎦+-+=10a -≥1a ≥'()0,()f x f x >311(1)0ln 224a f +=>>-1()ln 24f x ≥-x20当，即时，递增；递减，的最大值恒成立，令，所以，在递增，且，，即25. 已知抛物线，焦点为，过作动直线交抛物线于两点，过作抛物线的切线，过作直线的平行直线交轴于，设线段的垂直平分线为，直线的倾斜角为．已知当时，．（1）求抛物线的方程；（2）证明：直线过轴上一定点，并求该定点的坐标．【25题答案】【答案】（1）（2）证明见解析，【解析】【分析】（1）法一：根据题意，易得直线的方程为：，与抛物线方程联立，求得，代入求解；法二：设抛物线的准线为，过作于，过作10a -<1a <()()10,,0,1x f x f x a ⎛⎫'∈> ⎪-⎝⎭()()1,,0,1x f x f x a ∞⎛⎫∈+< ⎪-⎝⎭'()f x ∴111(ln(1)ln 212(1)4f a a a =--+<---1()ln(1),(1)2(1)g a a a a =--+<-()()()()22211110,(1)12121a g a a a a a -+=+=>-'<--()g a (),1-∞1(1)ln 24g -=-1a ∴<-(),1a ∞∈--2:2(0)C x py p =>F F l C 1122(,),(,)A x yB x y 12()y y ≥B C m A m n y D AD a l α4cos 5α=-14y =Ca y 24x y=(0,1)l 342py x =-+(2,4)-A p 22x py=C b A 1AA b ⊥1A F21于，根据，结合抛物线的定义，得到，再由求解；（2）设的方程为，与抛物线方程联立，用导数法得到切线斜率，由，得到直线的斜率，进而得到直线的方程，令，得到D 的坐标，进而得到线段的垂直平分线的方程求解.【小问1详解】解：法一：当时，直线的斜率为，又过焦点，故直线的方程为：，代入得：，为钝角，，，代入，解得，抛物线的方程为法二：如图：设抛物线的准线为，过作于，过作于，为钝角，在线段上21FA AA ⊥2A 4cos 5α=-22||||sin =∠AA AF AFA 2112||||=-AA AA A A l 1y kx =+m 22=m x k //m n n n 0x =AD a4cos 5α=-l 34-l F l 342p y x =-+22x py =222320x px p +-=12,y y α≥ 12120,0,2,2p x x x p x ∴<>∴=-=(2,4)A p ∴-22x py =2p =∴C 24x y=C b A 1AA b ⊥1A F 21FA AA ⊥2A 12,y y α≥ 2A ∴1AA22，，又，，解得，抛物线的方程为；【小问2详解】直线与抛物线相交，的斜率存在，由（1）知，设的方程为，代入，得，，由，得，则，切线斜率，，243cos ,sin 55AFA α=-∴∠= 223||||sin (425p AA AF AFA ∴=∠=+⨯21121||||422ppAA AA A A y p =-=+-=-3(44252pp∴+⨯=-2p =∴C 24x y = l C l ∴(0,1)F l 1y kx =+24x y =2440x kx --=12124,4x x k x x ∴+==-24x y =24x y =2xy '=∴m 22=m x k //m n23直线斜率，又直线过直线的方程为：，令，得，，的中点，则线段的垂直平分线的斜率，（，否则为轴，与抛物线只有一个交点），直线的方程为：，设与轴交于点，，直线过定点，命题得证．请考生在第22，23两题中任选一题做答．只能做所选定的题目．如果多做，则按所做的第一个题记分．做答时用2B 铅笔在答题卡上把所选题号后方框涂黑．选修4—4：坐标系与参数方程27. 在直角坐标系中，曲线的参数方程为（为参数），以直角坐标原点为极点，轴的正半轴为极轴建立极坐标系．（1）求曲线的极坐标方程；∴n 22n x k =n 11(,),A x y ∴n 211()2x y y x x -=-0x =1212=-D x x y y 1214,2=-∴=+ D x x y y AD ∴11(,1)2x M y +AD a 22a k x =-20x ≠l y ∴a 1122(1)()2x y y x x -+=--a y 0(0,)y 222211111012121111444x x x x x y y x x x ∴=++=++=+-=∴a (0,1)xOy C 12:1x t t C y t t ⎧=+⎪⎪⎨⎪=-⎪⎩t Ox C24（2）若、是曲线上的两点，且，求的最小值．【27题答案】【答案】（1）（2）【解析】【分析】（1）在曲线的参数方程中消去参数，可得出曲线的普通方程，再利用直角坐标方程与极坐标方程之间的转换关系可得出曲线的极坐标方程；（2）因为，所以可设、，利用勾股定理可得出，然后利用三角恒等变换结合正弦型函数的有界性可求得的最小值.【小问1详解】解：在曲线的参数方程中，可得，两式相乘得普通方程为，故曲线的极坐标方程为，即．【小问2详解】解：因为，所以可设、，所以，A B C 0OA OB ⋅= AB 22244cos sin ρθθ=-3C t C C 0OA OB ⋅= (),A A ρθ,2B B πρθ⎛⎫± ⎪⎝⎭2222222444cos sin 4sin cos A B AB ρρθθθθ=+=+-- AB C2222x y t x y t +=⎧⎪⎨-=⎪⎩2244x y -=C 22224cos sin 4ρθρθ-=22244cos sin ρθθ=-0OA OB ⋅= (),A A ρθ,2B B πρθ⎛⎫± ⎪⎝⎭222222222444cos sin 4sin cos A B AB OA OB ρρθθθθ=+=+=+--25，故当且仅当时，的最小值为.选修4—5：不等式选讲29. 已知函数．（1）解不等式；（2）若不等式恒成立，求实数的取值范围．【29题答案】【答案】（1）（2）【解析】【分析】（1）根据题意，分，，三种情况讨论求解；（2）解法一：令，进而分和两种情况讨论，当时，数形结合求解即可；解法二：结合题意，当时，化为，进而结合绝对值三角不等式得，进而得答案.【小问1详解】()()2222224412125cos 15sin 125sin cos 45cos 15sin 1θθθθθθ=+==-----212121625253sin 24444θ=≥=--2sin 21θ=AB3()|1|2||f x x x =+-()12x f x <-()|1|f x a x ≤-a44,,53∞∞⎛⎫⎛⎫--⋃+ ⎪ ⎪⎝⎭⎝⎭[)1,∞+1x <-10x -≤≤0x >()|1|g x a x =-0a ≤0a >0a >1x ≠()|1|f x a x ≤-|1|2|||1|x x a x +-≥-max ()1g x =26解：当时，，则，当时，，则，当时，，则，综上，【小问2详解】解：法一：令当时，，故不合题意，当时，如图所示为的图象，恒过定点，故恒成立，又，则1,0()1231,101,1x x f x x x x x x x -+>⎧⎪=+-=+-≤≤⎨⎪-<-⎩∴1x <-11102x x x -<-⇒<1x <-10x -≤≤1431125x x x +<-⇒<-415x -≤<-0x >141123x x x -+<-⇒>43x >44(,)(,)53x ∈-∞-+∞ ()|1|g x a x =-0a ≤(0)1,(0),(0)(0)f g a f g ==∴>0a ≤0a >(),()f x g x ()g x (1,0)()()f x g x ≤⇔||1a ≥0a >[)1,a ∈+∞27法二：当时，为，显然成立，，当时，化为令，则,当且仅当且时等号成立.，综上知：1x =()|1|f x a x ≤-00≤a R ∈1x ≠()|1|f x a x ≤-|1|2|||1|x x a x +-≥-|1|2||()|1|x x g x x +-=-|1|2|||12|()1|1||1|x x x x g x x x +-+-=≤=--0x ≥1x ≠max ()1,1g x a ∴=∴≥[)1,a ∈+∞。

江西省萍乡市2019-2020学年高考第二次质量检测数学试题含解析

江西省萍乡市2019-2020学年高考第二次质量检测数学试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．在ABC V 中，角,,A B C 所对的边分别为,,a b c ，已知23C π=，1c =．当,a b 变化时，若z b a λ=+存在最大值，则正数λ的取值范围为A ．(0,1)B ．(0,2)C ．1(,2)2D ．(1,3) 【答案】C【解析】【分析】【详解】因为23C π=，1c =，所以根据正弦定理可得sin sin sin a b c A B C ===，所以a A =，b B =，所以sin()])sin32z b a B A B B B λλλπ=+==+-=-+])B B φ=+，其中tan φ=，03B π<<，因为z b a λ=+存在最大值，所以由2,2B k k φπ+=+π∈Z ，可得22,62k k k φπππ+<<π+∈Z ，所以tan φ>>，解得122λ<<，所以正数λ的取值范围为1(,2)2，故选C ． 2．已知双曲线222:1(0)3-=>y x C a a 的一个焦点与抛物线28x y =的焦点重合，则双曲线C 的离心率为（）A ．2B C ．3 D ．4 【答案】A【解析】【分析】根据题意，由抛物线的方程可得其焦点坐标，由此可得双曲线的焦点坐标，由双曲线的几何性质可得234a +=，解可得1a =，由离心率公式计算可得答案．【详解】根据题意，抛物线28x y =的焦点为(0,2)，则双曲线22213y x a -=的焦点也为(0,2)，即2c =，则有234a +=，解可得1a =，双曲线的离心率2c e a==. 故选：A ．【点睛】本题主要考查双曲线、抛物线的标准方程，关键是求出抛物线焦点的坐标，意在考查学生对这些知识的理解掌握水平．3．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（）A ．2-3B ．3-2C ．52D ．25【答案】C【解析】【分析】根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案.【详解】由题意，3,15a n ==，第1次循环，2,23a n =-=，满足判断条件；第2次循环，5,32a n ==，满足判断条件；第3次循环，3,45a n ==，满足判断条件； L L 可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =. 故选：C.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.4．设正项等比数列{}n a 的前n 项和为n S ，若23S =，3412a a +=，则公比q =（）A ．4±B ．4C ．2±D ．2【答案】D【解析】【分析】由23S =得123a a +=，又23412()12a a a a q +=+=，两式相除即可解出q ．【详解】解：由23S =得123a a +=，又23412()12a a a a q +=+=，∴24q =，∴2q =-，或2q =，又正项等比数列{}n a 得0q >，∴2q =，故选：D ．【点睛】本题主要考查等比数列的性质的应用，属于基础题．5．我国古代数学名著《九章算术》有一问题：“今有鳖臑(biē naò)，下广五尺，无袤；上袤四尺，无广；高七尺.问积几何？”该几何体的三视图如图所示，则此几何体外接球的表面积为( )A ．90π平方尺B ．180π平方尺C ．360π平方尺D ．13510π平方尺【答案】A【解析】【分析】根据三视图得出原几何体的立体图是一个三棱锥，将三棱锥补充成一个长方体，此长方体的外接球就是该三棱锥的外接球，由球的表面积公式计算可得选项.【详解】由三视图可得，该几何体是一个如图所示的三棱锥P ABC -，O 为三棱锥外接球的球心，此三棱锥的外接球也是此三棱锥所在的长方体的外接球，所以O 为PC 的中点，设球半径为R ，则()()22222222145+45744211++2R PC AB BC PA ⎛⎫+== ⎪⎝⎭==,所以外接球的表面积24544902R S πππ==⨯=，故选：A ．【点睛】本题考查求几何体的外接球的表面积，关键在于由几何体的三视图得出几何体的立体图，找出外接球的球心位置和半径，属于中档题.6．已知函数()x a f x x e -=+，()()ln 24a x g x x e -=+-，其中e 为自然对数的底数，若存在实数0x ，使()()003f x g x -=成立，则实数a 的值为（） A ．ln21--B ．1ln2-+C ．ln 2-D ．ln 2 【答案】A【解析】令f （x ）﹣g （x ）=x+e x ﹣a ﹣1n （x+1）+4e a ﹣x ，令y=x ﹣ln （x+1），y′=1﹣12x +=12x x ++，故y=x ﹣ln （x+1）在（﹣1，﹣1）上是减函数，（﹣1，+∞）上是增函数，故当x=﹣1时，y 有最小值﹣1﹣0=﹣1，而e x ﹣a +4e a ﹣x ≥4，（当且仅当e x ﹣a =4e a ﹣x ，即x=a+ln1时，等号成立）；故f （x ）﹣g （x ）≥3（当且仅当等号同时成立时，等号成立）；故x=a+ln1=﹣1，即a=﹣1﹣ln1．故选：A ． 7．设1F ，2F 分别为双曲线22221x y a b-=（a ＞0，b ＞0）的左、右焦点，过点1F 作圆222x y b += 的切线与双曲线的左支交于点P ，若212PF PF =，则双曲线的离心率为（）A 2B 3C 5D 6【答案】C【解析】【分析】设过点1F 作圆222x y b += 的切线的切点为T ，根据切线的性质可得1OT PF ⊥，且||OT a =，再由212PF PF =和双曲线的定义可得12||2,||4PF a PF a ==，得出T 为1F P 中点，则有2//OT PF ，得到21PF PF ⊥，即可求解.【详解】设过点1F 作圆222x y b += 的切线的切点为T ，11,||OT PF FT a ∴⊥== 2121212,2,4,2PF PF PF PF a PF a PF a =-===，所以T 是1F P 中点，212//,OT PF PF PF ∴∴⊥，22221212||||20||4PF PF a F F c ∴+===，225,c e a=∴=故选:C.【点睛】本题考查双曲线的性质、双曲线定义、圆的切线性质，意在考查直观想象、逻辑推理和数学计算能力，属于中档题.8．已知正三角形ABC 的边长为2，D 为边BC 的中点，E 、F 分别为边AB 、AC 上的动点，并满足2AE CF =u u u v u u u v ，则DE DF ⋅u u u v u u u v 的取值范围是（）A ．11[,]216-B ．1(,]16-∞C ．1[,0]2- D ．(,0]-∞【答案】A【解析】【分析】建立平面直角坐标系，求出直线:1)AB y x =+，:1)AC y x =-设出点(1)),(,1))E m m F n n +-，通过||2||AE CF =u u u r u u u r ，找出m 与n 的关系．通过数量积的坐标表示，将DE DF ⋅u u u r u u u r 表示成m 与n 的关系式，消元，转化成m 或n 的二次函数，利用二次函数的相关知识，求出其值域，即为DE DF ⋅u u u r u u u r的取值范围．【详解】以D 为原点，BC 所在直线为x 轴，AD 所在直线为y 轴建系，设(1,0),(1,0)A B C -，则直线:1)AB y x =+ ，:1)AC y x =-设点(1)),(,1))E m m F n n +-，10,01m n -≤<<≤所以(),(1,1))AE m CF n n ==--u u u r u u u r由||2||AE CF =u u u r u u u r 得224(1)m n =- ，即2(1)m n =- ，所以22713(1)(1)4734()816DE DF mn m n n n n ⋅=-+-=-+-=--+u u u r u u u r ，由12(1)0m n -≤=-<及01n <≤，解得112n ≤<，由二次函数2714()816y n =--+的图像知，11[,]216y ∈-，所以DE DF ⋅u u u r u u u r 的取值范围是11[,]216-．故选A ．【点睛】本题主要考查解析法在向量中的应用，以及转化与化归思想的运用．9．数列{}n a 的通项公式为()n a n c n N*=-∈．则“2c <”是“{}n a 为递增数列”的（）条件． A ．必要而不充分B ．充要C ．充分而不必要D ．即不充分也不必要【答案】A【解析】【分析】根据递增数列的特点可知10n n a a +->，解得12c n <+，由此得到若{}n a 是递增数列，则32c <，根据推出关系可确定结果.【详解】若“{}n a 是递增数列”，则110n n a a n c n c +-=+--->，即()()221n c n c +->-，化简得：12c n <+，又n *∈N ，1322n ∴+≥，32c ∴<，则2c <¿{}n a 是递增数列，{}n a 是递增数列2c ⇒<，∴“2c <”是“{}n a 为递增数列”的必要不充分条件．故选：A .【点睛】本题考查充分条件与必要条件的判断，涉及到根据数列的单调性求解参数范围，属于基础题.10．已知定义在R 上的奇函数()f x ，其导函数为()f x '，当0x ≥时，恒有())03(x f f x x '+>．则不等式33()(12)(12)0x f x x f x -++<的解集为（）．A ．{|31}x x -<<-B ．1{|1}3x x -<<-C ．{|3x x <-或1}x >-D ．{|1x x <-或1}3x >- 【答案】D【解析】【分析】先通过())03(x f f x x '+>得到原函数()()33x f x g x =为增函数且为偶函数，再利用到y 轴距离求解不等式即可.【详解】构造函数()()33x f x g x =，则()()()()()322'''33x x g x x f x f x x f x f x ⎛⎫=+=+ ⎪⎝⎭ 由题可知())03(x f f x x '+>，所以()()33x f x g x =在0x ≥时为增函数；由3x 为奇函数，()f x 为奇函数，所以()()33x f x g x =为偶函数；又33()(12)(12)0x f x x f x -++<，即33()(12)(12)x f x x f x <++即()()12g x g x <+又()g x 为开口向上的偶函数所以|||12|x x <+，解得1x <-或13x >-故选：D【点睛】此题考查根据导函数构造原函数，偶函数解不等式等知识点，属于较难题目.11．已知i 为虚数单位，若复数12i 12i z +=+-，则z = A ．9i 5+ B ．1i -C ．1i +D ．i - 【答案】B【解析】【分析】【详解】因为212i (12i)(2i)2i 4i 2i 1111i 2i (2i)(2i)5z ++++++=+=+=+=+--+，所以1i z =-，故选B ． 12．若62a x x ⎛⎫+ ⎪⎝⎭的展开式中6x 的系数为150，则2a =（） A ．20B ．15C ．10D ．25【答案】C【解析】【分析】通过二项式展开式的通项分析得到22666150C a x x =，即得解. 【详解】由已知得()62123166()rr rr r r r a T C x C a x x --+⎛⎫== ⎪⎝⎭，故当2r =时，1236r -=，于是有226663150T C a x x ==，则210a =.故选：C【点睛】本题主要考查二项式展开式的通项和系数问题，意在考查学生对这些知识的理解掌握水平.二、填空题：本题共4小题，每小题5分，共20分。

江西省重点中学协作体2023届高三第二次联考数学(文)试题(含解析)

江西省重点中学协作体2023届高三第二次联考数学（文）试题学校:___________姓名：___________班级：___________考号：___________二、填空题三、解答题17．上饶某中学为了解该校高三年级学生数学学习情况，对一模考试数学成绩进行分析，从中抽取了50 名学生的成绩作为样本进行统计（若该校全体学生的成绩均在[)60140,分），按照[)60,70，[)70,80，[)80,90，[)90,100，[)100,110，[)110,120，[)120130,，[)130140,的分组做出频率分布直方图如图所示，若用分层抽样从分数在[)70,90内抽取8人，则抽得分数在[)70,80的人数为3人．(1)求频率分布直方图中的x ，y 的值；并估计本次考试成绩的平均数（以每一组的中间值为估算值）；(2)该高三数学组准备选取数学成绩在前5%的学生进行培优指导，若小明此次数学分数是132，请你估算他能被选取吗？18．已知数列{}n a 满足12a =，1322nn n a a +=+-．(1)令21nb a =+-，证明：数列{}b 为等比数列；(1)证明：四边形ABCD 是正方形；(2)若3PA AB ==，M 为PC 上一点，且满足20．已知函数()ln 1xf x x x=-+(1)求()f x 的单调区间；(2)若对于任意的()0,x ∈+∞，f(1)求抛物线Γ的方程；(2)当直线l 与x 轴垂直时，设C 线AC 、BD 相交于点E ，直线22．在平面直角坐标系xOy 中，直线原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线2sin 2cos ρθθ=+．(1)求直线l 的普通方程和曲线参考答案：【详解】2211612y +=可得4a =，23b =，c 12PF F △的内切圆与三边分别相切与分别为12PF F △的重心和内心．PC ，11F A F C =，22F A F B =，令x y t -=，则直线x y t -=与曲线x x 1x x y y -= 表示的曲线如图，则当表示部分双曲线时，该曲线的渐近线斜率x y t -=平行，0t ∴>；把直线往下移，直到如图与第四象限的圆相切，此时圆心到直线的距离等于半径，22111t ∴=+，解得：2t =±，又是与第四象限圆相切，若直线继续下移，则无交点，不合题意；综上所述：02t <≤，即x y -的取值范围为设P点在平面ABC内的投影的为中，在Rt PDA因为222+=PD AD PAP ABC的外接球半径设三棱锥-==，O D即OP OA R3x -由图可知，两函数有6个交点，不妨设为(12345612345,,,,,,x x x x x x x x x x x x <<<<<根据对称性得1625346x x x x x x +=+=+=，故函数()f x 在113,22⎡⎤-⎢⎥⎣⎦上所有零点之和为1863=⨯．故选B ．（2）∵-1122P ABM C ABM M ABC V V V --==。

2020届江西省萍乡市上栗县高三第二次模拟考试数学(文)试题(解析版)

2020届江西省萍乡市上栗县高三第二次模拟考试数学（文）试题
一、单选题
1．已知集合，，则（）
A． B． C． D．
【答案】C
【解析】根据不等式的写法求解集合B，然后根据交集的定义计算即可.
【详解】
解：∵ ，∴ .
故选：C.
【点睛】
本题考查不等式的计算，考查交集的定义和运算，属于基础题.
2．已知复数z满足，则（）
【详解】
解：依题意得，
则，，，显然该函数为奇函数，且当时，，所以D正确.
故选：D.
【点睛】
本题考查三角函数的图像，考查三角函数的平移变换，涉及利用函数的性质和特殊值的范围判断图像，属于中档题.
7．如图，圆柱的轴截面ABCD为边长为2的正方形，过AC且与截面ABCD垂直的平面截该圆柱表面，所得曲线为一个椭圆，则该椭圆的焦距为（）
A． B． C． D．
【答案】C
【解析】列举法列举出所有可能的情况，利用古典概型的计算方法计算即可.
【详解】
解：依题意得所拨数字可能为610，601，511，160，151，115，106，61，16，共9个，其中有5个是奇数，则所拨数字为奇数的概率为，故选：C.
【点睛】
本题考查概率的实际应用问题，考查古典概型的计算方法，同时考查了学生的阅读能力和文化素养，属于中档题.
A． B． C． D．
【答案】B
【解析】由题意可知，它们的中心滚动一周的运动轨迹都是圆心角为2π的弧长，设半径分别为r1，r2，r3，r4，则半径为中心与顶点的距离，由正方形、正五边形、正六边形得几何特征可知，r1＜r2＜1，r3＝r4＝1，再利用弧长公式即可得到l1＜l2＜l3＝l4．
【详解】

江西省萍乡市2025届高三第二次诊断性检测数学试卷含解析

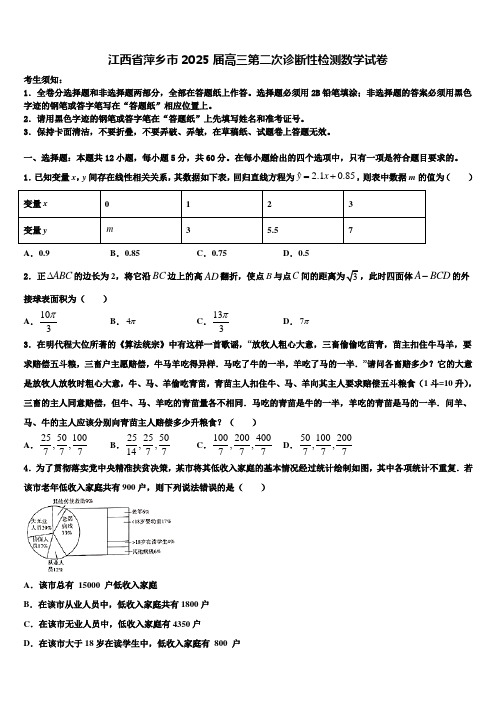
江西省萍乡市2025届高三第二次诊断性检测数学试卷考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知变量x ，y 间存在线性相关关系，其数据如下表，回归直线方程为 2.10.5ˆ8y x =+，则表中数据m 的值为（）变量x 0 1 2 3 变量ym 3 5.5 7 A ．0.9 B ．0.85C ．0.75D ．0.5 2．正ABC ∆的边长为2，将它沿BC 边上的高AD 翻折，使点B 与点C 间的距离为3，此时四面体A BCD -的外接球表面积为（）A ．103πB ．4πC ．133πD ．7π3．在明代程大位所著的《算法统宗》中有这样一首歌谣，“放牧人粗心大意，三畜偷偷吃苗青，苗主扣住牛马羊，要求赔偿五斗粮，三畜户主愿赔偿，牛马羊吃得异样．马吃了牛的一半，羊吃了马的一半．”请问各畜赔多少？它的大意是放牧人放牧时粗心大意，牛、马、羊偷吃青苗，青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食（1斗=10升），三畜的主人同意赔偿，但牛、马、羊吃的青苗量各不相同．马吃的青苗是牛的一半，羊吃的青苗是马的一半．问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食？（）A ．2550100,,777B ．252550,,1477C ．100200400,,777D ．50100200,,7774．为了贯彻落实党中央精准扶贫决策，某市将其低收入家庭的基本情况经过统计绘制如图，其中各项统计不重复．若该市老年低收入家庭共有900户，则下列说法错误的是（）A ．该市总有 15000 户低收入家庭B ．在该市从业人员中，低收入家庭共有1800户C ．在该市无业人员中，低收入家庭有4350户D ．在该市大于18岁在读学生中，低收入家庭有 800 户5．已知命题:p 若1a <，则21a <，则下列说法正确的是（）A ．命题p 是真命题B ．命题p 的逆命题是真命题C ．命题p 的否命题是“若1a <，则21a ≥”D ．命题p 的逆否命题是“若21a ≥，则1a <”6．已知函数()(0)f x x x x =->，()x g x x e =+，()()ln 0h x x x x =+>的零点分别为1x ，2x ，3x ，则（） A ．123x x x <<B ．213x x x <<C ．231x x x <<D ．312x x x <<7．已知集合{}0,1,2,3A =，}{21,B x x n n A ==-∈，P A B =⋂，则P 的子集共有（） A ．2个B ．4个C ．6个D ．8个8．设，则"是""的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件9．已知函数32,1()ln ,1(1)x x x f x a x x x x ⎧-+<⎪=⎨≥⎪+⎩，若曲线()y f x =上始终存在两点A ，B ，使得OA OB ⊥，且AB 的中点在y轴上，则正实数a 的取值范围为（）A ．(0,)+∞B ．10,e ⎛⎤ ⎥⎝⎦C ．1,e ∞⎡⎫+⎪⎢⎣⎭ D ．[e,)+∞10．已知单位向量a ，b 的夹角为34π，若向量2m a =，4n a b λ=-，且m n ⊥，则n =（） A ．2 B ．2 C ．4 D ．611．执行程序框图，则输出的数值为（）A ．12B ．29C ．70D ．16912．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想的内容是：每个大于2的偶数都可以表示为两个素数的和，例如：422=+，633=+，835=+，那么在不超过18的素数中随机选取两个不同的数，其和等于16的概率为（）A ．121B ．221C ．115D ．215二、填空题：本题共4小题，每小题5分，共20分。

江西省重点中学盟校2024届高三第二次联考数学试题及答案

江西省重点中学盟校2024届高三第二次联考数学考生注意：1.本试卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

4.本卷命题范围：高考范围。

一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{}ln 0M x x =<，{}0xN x e a =->，若M N ⊆，则实数a 的取值范围为A ．(],1-∞B ．(),1-∞C ．(],e -∞D ．(),e -∞2.已知a ，b ，c 为非零的平面向量，则“a b a c =⋅⋅ ”是“b c = ”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3.下图是我国2018～2023年纯电动汽车销量统计情况，下列说法错误的是A ．我国纯电动汽车销量呈现逐年增长趋势B ．这六年销量的第60百分位数为536.5万辆C ．这六年增长率最大的为2019年至2020年D ．2020年销量高于这六年销量的平均值4.直线l 过抛物线C ：22y px =（0p >）的焦点，且与C 交于A ，B 两点，若使2AB =的直线l 恰有2条，则p 的取值范围为A ．01p <<B ．02p <<C ．1p >D ．2p >5.已知等差数列{}n a 与等比数列{}n b 的首项均为1-，且2481a b ==，则数列{}n n a b A ．既有最大项又有最小项B ．只有最大项没有最小项C ．只有最小项没有最大项D ．没有最大项也没有最小项6.在平面直角坐标系内，方程22221x y xy +-=对应的曲线为椭圆，则该椭圆的离心率为A ．2B ．2C ．5D ．57.已知定义在R 上的函数()f x 满足()()()2f x f x f x +=-=-，当01x <≤时，()()2log 1f x x =+.若()()1f a f a +>，则实数a 的取值范围是A ．534,422k k ⎛⎫-+-+ ⎪⎝⎭，k Z∈B ．()14,4k k -+，k Z∈C ．114,422k k ⎛⎫-++ ⎪⎝⎭，k Z∈D ．314,422k k ⎛⎫-++ ⎪⎝⎭，k Z∈8.在△ABC 中，若sin 2cos cos A B C =，则22cos cos B C +的取值范围为A ．61,5⎡⎫⎪⎢⎣⎭B ．11,2⎡⎤⎢⎥⎣⎦C ．6,25⎛⎫ ⎪⎝⎭D ．1,22⎫⎪⎪⎣⎭二、选择题：本题共3小题，每小题6分，共18分。

江西省萍乡市数学高三上学期文数第二次调研测试试卷

江西省萍乡市数学高三上学期文数第二次调研测试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知集合M={}，若M R=Ф，则实数m的取值范围是（）A . m<4B . 0<m<4C . 0≤m<4D . m>42. （2分） (2020高三上·贵阳期末) 复数在复平面内对应点的坐标是A .B .C .D .3. （2分）如图是某电视台综艺节目举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）A . 84,4.8B . 84,1.6C . 85,4D . 85,1.6．4. （2分）(2016·青海) 若“x<m”是“(x-2013)(x-2014)>2”的充分不必要条件，则m的最大值是（）A . 2011B . 2012C . 2013D . 20155. （2分） (2019高三上·沈河月考) 函数（，且）的图象恒过定点，且点在角的终边上，则（）A .B .C .D .6. （2分） (2016高二下·南城期末) 在平面直角坐标系中，若不等式组（a为常数）表示的区域面积等于1，则a的值为（）A . -B .C .D . 17. （2分）线性回归直线方程必过定点（）A . (0,0)B .C .D .8. （2分） (2018高二下·河池月考) 函数的最小值（）A .B . 1C . 0D . 不存在9. （2分） (2020高一下·驻马店期末) 已知，是关于的方程的两个根，则的值是（）A .B .C .D .10. （2分）已知是三个不重合的平面，a，b是两条不重合的直线，有下列三个条件：①②③如果命题且_______，则为真命题，则可以在横线处填入的条件是（）A . ①或②B . ②或③C . ①或③D . 只有②11. （2分）双曲线的一个焦点坐标为，则双曲线的渐近线方程为（）A .B .C .D .12. （2分） (2016高一上·武汉期中) 对于0＜a＜1，给出下列四个不等式：①loga（1+a）＜loga（1+ ）；②loga（1+a）＞loga（1+ ）；③a1+a＜a ；④a1+a＞a ；其中成立的是（）A . ①③B . ①④C . ②③D . ②④二、填空题 (共4题；共4分)13. （1分）若直线x+y+m=0与圆x2+y2=m相切，则m为________14. （1分） (2017高二上·牡丹江月考) 在平面直角坐标系中，方程所对应的图形经过伸缩变换后的图形所对应的方程是________。

江西省萍乡市数学高三上学期文数第二次月考试卷

江西省萍乡市数学高三上学期文数第二次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）如果函数的图象向左平移个单位后，所得图象关于原点对称，那么函数的图象（）.A . 关于点对称B . 关于直线对称C . 关于点对称D . 关于直线对称2. （2分） (2019高二下·鹤岗月考) 命题：，的否定是（）A . ，B . ，C . ，D . ，3. （2分）已知为第二象限角，，则的值为（）A .B .C .D .4. （2分）设命题甲:的解集是实数集R;命题乙:,则命题甲是命题乙成的（）A . 充要条件B . 充分非必要条件C . 必要非充分条件D . 既非充分又非必要条件5. （2分）函数f(x)=-（）x-2的零点所在区间为（）A . （3，4）B . （2，3）C . （1，2）D . （0，1）6. （2分） (2018高一上·会泽期中) 计算：的值为（）A .B .C .D .7. （2分）(2019高二上·郑州期中) 在中，则的值等于（）A .B .C .D .8. （2分）设命题p：函数y＝sin2x的最小正周期为；命题q：函数y＝cos x的图像关于直线x＝对称．则下列判断正确的是（）A . p为真B . 为假C . p且q为假D . p或q为真9. （2分） (2015高二下·张掖期中) 函数f（x）的定义域为R，f（1）=3，对任意x∈R，f′（x）＜2，则f（x）＜2x+1的解集为（）A . （1，+∞）B . （﹣1，1）C . （﹣∞，1）D . （﹣∞，+∞）10. （2分）函数y=3sin2x的图象可以看成是将函数y=3sin(2x-)的图象（）A . 向左平移个单位B . 向右平移个单位C . 向左平移个单位D . 向右平移个单位11. （2分） (2019高三上·大同月考) 函数的图象大致为（）A .B .C .D .12. （2分） (2020高三上·泸县期末) 已知定义在上的可导函数的导函数为，满足是偶函数，，则不等式的解集为（）.A .B .C .D .二、填空题 (共4题；共4分)13. （1分）奇函数f（x）定义域是（t，2t+3），则t=________14. （1分）如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的一段图象，则函数的解析式为________．15. （1分） (2019高一上·兴义期中) 设函数则满足的x的取值范围是________.16. （1分）(2018·大新模拟) 若函数有两个极值点，则实数的取值范围是________．三、解答题 (共6题；共55分)17. （10分） (2019高三上·黑龙江月考) 已知函数为的导函数．（1）求函数的单调区间；（2）若函数在上存在最大值0，求函数在[0，＋∞)上的最大值.18. （10分） (2018高一下·上虞期末) 已知，且．（Ⅰ）求的值；（Ⅱ）若，，求的值.19. （10分） (2018高一下·应县期末) 已知，设 .（1）求的解析式及单调递增区间；（2）在中，角所对的边分别为，且，求的面积.20. （10分）(2018·南京模拟) 设函数，（）.（1）当时，若函数与的图象在处有相同的切线，求的值；（2）当时，若对任意和任意，总存在不相等的正实数，使得，求的最小值；（3）当时，设函数与的图象交于两点．求证： .21. （5分） (2019高三上·凉州期中) 的内角，，所对的边分别为，，．向量与平行．（Ⅰ）求；（Ⅱ）若，求的面积．22. （10分）(2017·湖北模拟) 已知函数f（x）=|x+a|+|x﹣2|．（1）若f（x）的最小值为4，求实数a的值；（2）若﹣1≤x≤0时，不等式f（x）≤|x﹣3|恒成立，求实数a的取值范围．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共55分)17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、21-1、22-1、22-2、第11 页共11 页。

江西省萍乡市2024年数学(高考)部编版第二次模拟(提分卷)模拟试卷

江西省萍乡市2024年数学（高考）部编版第二次模拟(提分卷)模拟试卷一、单项选择题（本题包含8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题已知数列为等比数列，，，则数列的前10项和为（）A．352B．401C．625D．913第(2)题已知实数x,y满足不等式组,则z=∣x-最大值为A．0B．3C．9D．11第(3)题在长方体中，与平面相交于点M，则下列结论一定成立的是（）A．B．C．D．第(4)题斐波那契数列满足：.若将数列的每一项按照下图方法放进格子里，每一小格子的边长为1，记前项所占的格子的面积之和为，每段螺旋线与其所在的正方形所围成的扇形面积为，则下列结论错误的是A．B．C．D．第(5)题已知双曲线的中心在原点，以坐标轴为对称轴．则“的离心率为”是“的一条渐近线为”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件第(6)题某校开设A类选修课4门，B类选修课2门，每位同学从中选3门.若要求两类课程中都至少选一门，则不同的选法共有（）A．32种B．20种C．16种D．14种第(7)题如图，圆M为的外接圆，，，N为边BC的中点，则（）A．5B．10C．13D．26第(8)题已知非零实数，满足，则下列不等式中一定成立的是（）A．B．C．D．二、多项选择题（本题包含3小题，每小题6分，共18分。

在每小题给出的四个选项中，至少有两个选项正确。

全部选对的得6分，选对但不全的得3分，有选错或不答的得0分） (共3题)第(1)题已知函数定义域为，是奇函数，，，分别是函数，的导函数，函数在区间上单调递增，则（）A．B．C．D．第(2)题已知函数在上单调，且曲线关于点对称，则（）A．以为周期B ．的图象关于直线对称C．将的图象向右平移个单位长度后对应的函数为偶函数D ．函数在上有两个零点第(3)题对于函数，下列说法正确的是（）A．在处取得极大值B．有两个不同的零点C．D ．若在上恒成立，则三、填空（本题包含3个小题，每小题5分，共15分。

江西省萍乡市2024届高三二模考试数学试卷(含答案与解析)_5254

江西省萍乡市2024届高三二模考试数学本试卷满分150分，考试时间120分钟注意事项：1．答卷前，考生务必将自己的姓名､准考证号填写在答题卡上．2．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．一､单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.1. 集合{12},{2}A xx B x x m =-<<=-<<∣∣，若x B ∈的充分条件是x A ∈，则实数m 的取值范围是（） A. ()1,2-B. [)2,+∞C. (]2,2-D. ()2,+∞2. 复数()()23i 32i z =++，下列说法正确的是（） A. z 实部为12 B. z 的虚部为13i C. 1213i z =-D. 13z =3. 已知随机变量()N 2,9ξ ，且()()12P P a ξξ≤=≥+，则=a （） A. 3B. 2C. 1D. 04. 已知||2a =，b = ，|2|2a b -=，则向量a 与b 的夹角为（）A.π6B.π3C.2π3D.5π65. 陀螺是中国民间的娱乐工具之一，早期陀螺的形状由同底的一个圆柱和一个圆锥组合而成．如图，已知一木制陀螺内接于一表面积为64π的球，其中圆柱的两个底面为球的两个截面，圆锥的顶点在该球的球面上，若圆柱的底面直径为，则该陀螺的体积为（）的A. 48πB. 56πC. 64πD. 72π6. 已知2ln212ln2,,42e ea b c -===，则这三个数大小关系为（） A. c b a << B. a b c << C. a c b <<D. c a b <<7. 点M 将一条线段AB 分为两段AM 和MB，若AM BM AB MA ==M 为线段AB 的黄金分割点.已知直线(11)y a a =-<<与函数()sin y x ωϕ=+的图象相交，,,A B C 为相邻的三个交点，则（）A. 当0a =时，存在ω使点B 为线段AC 黄金分割点B. 对于给定的常数ω，不存在a 使点B 为线段AC 的黄金分割点C. 对于任意的a ，存在ω使点B 为线段AC 的黄金分割点D. 对于任意的ω，存在a 使点B 为线段AC 的黄金分割点8. 如图1，与三角形的一条边以及另外两条边的延长线都相切的圆被称为三角形的旁切圆，旁切圆的圆心被称为三角形的旁心，每个三角形有三个旁心．如图2，已知1F ，2F 是双曲线22221(0,0)x y a b a b -=>>的左、右焦点，P 是双曲线右支上一点，Q 是12PF F △的一个旁心．直线PQ 与x 轴交于点M，若MQQP=，则该双曲线的渐近线方程为（）的的A. 12y x =±B. 2y =±C. y x =±D. y =二､多选题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 数列*{}(N )n a n ∈的前n 项和为n S ，若11a =， 12,1,n n na n a n a +⎧⎪=⎨⎪⎩为奇数为偶数，则下列结论正确的是（） A 32a =B. 1012S =C. {}n S 为递增数列D. 21{}n a -为周期数列10. 已知2510a b ==，则下列关系正确的是（） A e 1a b ->B. a b ab +<C. 49a b +<D. 2211128a b ⎛⎫⎛⎫+++> ⎪ ⎪⎝⎭⎝⎭11. 设O 为坐标原点，直线l 过抛物线2:4C y x =的焦点F 且与C 交于,A B 两点，,M N 满足2,2,MF OF BN ON AM ==与NF 相交于点P ，则下列结论正确的是（）A. AB MNB.111MN AF+= C. 0OP OF ⋅>D. ANP 面积的最大值为1第II 卷三､填空题：本题共3小题，每小题5分，共15分.12. 一种春节吉祥物为分布均匀的正十二面体模型（如图），某兴趣小组在十二个面分别雕刻了十二生肖的..图案.若其中的2个成员将该模型各随机抛出一次，则恰好出现一次龙的图案朝上（即龙的图案在最上面）的概率为__________.13. 在ABC 中，点,D E 分别在边,BC AC 上，3,2BC BD AC AE ==，若,AD BE 交于点I ，则BIIE=__________；当3,4,2BC AC AB ===时，ABI △的面积为__________. 14. 正方体1111ABCD A B C D -的棱长为2,P 为该正方体侧面11CC D D 内的动点（含边界），若,PA PB 分别与直线AD，则四棱锥P ABCD -的体积的取值范围为__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15. 已知函数2()ln f x x x =．（1）求()f x 的单调区间；（2）若存在0x >，使得()f x ax …成立，求实数a 的取值范围．16. 定义两组数据1u ，2(1,2,,)v i n = 的“斯皮尔曼系数”为变量i u 在该组数据中的排名1x 和变量i v 在该组数据中的排名1y 的样本相关系数，记为ρ，其中()()221611ni i i x y n n ρ==---∑．某校15名学生的数学成绩的排名与知识竞赛成绩的排名如下表：i x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 i y 1 5 3 4 9 8 76 10 2 12 14 13 11 15（1）试求这15名学生的数学成绩与知识竞赛成绩的“斯皮尔曼系数”；（2）已知在这15名学生中有10人数学成绩优秀，现从这15人中随机抽取3人，抽到数学成绩优秀的学生有X 人，试求X 的分布列和数学期望．17. 如图所示的几何体是圆锥的一部分，A 为圆锥的顶点，O 是圆锥底面圆的圆心，2π,3BOC P ∠=是弧BC 上一动点（不与,B C 重合），点M 在AB 上，且3AM MB =，OA ==.（1）当π2BOP ∠=时，证明：AB ⊥平面MOP ；（2）若四棱锥M OCPB -. ①求二面角B AO P --的取值范围；②记异面直线AP 与BO 所成的角为α，求cos α的最大值.18. 已知椭圆2222:1(0)y x E a b a b +=>>,A B 是E 上的不同两点，且直线AB 的斜率为1-，当直线AB 过原点时，AB 4=.（1）求椭圆E 的标准方程；（2）设()0,3P ，点,A B 都不在y 轴上，连接,PA PB ，分别交E 于,C D 两点，求点P 到直线CD 的距离的最大值.19. 固定项链的两端，在重力的作用下项链所形成的曲线是悬链线.1691年，莱布尼茨等得出悬链线的方程为e e 2x x cc c y -⎛⎫+ ⎪⎝⎭=，其中c 为参数．当1c =时，该表达式就是双曲余弦函数，记为e e cosh 2x xx -+=，悬链线的原理常运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程．已知三角函数满足性质：①导数：()()sin cos sin cos x x x x''⎧=⎪⎨=-⎪⎩；②二倍角公式：2cos 22cos 1x x =-；③平方关系：22sin cos 1x x +=．定义双曲正弦函数为e e sinh 2x xx --=．（1）写出sinh x ，cosh x 具有的类似于题中①、②、③的一个性质，并证明该性质；（2）任意0x >，恒有sinh 0x kx ->成立，求实数k 的取值范围；（3）正项数列*{}(N )n a n ∈满足11a a =>，2121n n a a +=-，是否存在实数a ，使得2024178a =？若存在，求出a 的值；若不存在，请说明理由．参考答案一､单选题：本题共8小题，每小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.1. 集合{12},{2}A xx B x x m =-<<=-<<∣∣，若x B ∈的充分条件是x A ∈，则实数m 的取值范围是（） A. ()1,2- B. [)2,+∞ C. (]2,2-D. ()2,+∞【答案】B 【解析】【分析】根据题意A 是B 的子集，从而求解.【详解】{12},{2}A xx B x x m =-<<=-<<∣∣，因为x B ∈的充分条件是x A ∈，所以A B ⊆，则2m ≥，故选：B.2. 复数()()23i 32i z =++，下列说法正确的是（） A. z 的实部为12 B. z 的虚部为13i C. 1213i z =- D. 13z =【答案】D 【解析】【分析】先化简复数z ，然后结合选项分析即可求解.【详解】由于复数()()23i 32i 64i 9i 613i z =++=++-=，所以z 的实部为0，虚部为13，故AB 错误；所以13i,13z z =-=，故C 错误，D 正确. 故选：D.3. 已知随机变量()N 2,9ξ ，且()()12P P a ξξ≤=≥+，则=a （） A. 3 B. 2C. 1D. 0【答案】C 【解析】【分析】结合正态分布的性质直接得到答案即可. 【详解】随机变量()N 2,9ξ ，所以()()()132P P P a ξξξ≤=≥=≥+，所以23a +=，故1a =. 故选：C.4. 已知||2a =，b =，|2|2a b -=，则向量a与b的夹角为（） A.π6B.π3C.2π3D.5π6【答案】A 【解析】【分析】首先求出 b ，然后对22a b -= 两边平方即可求出a b ⋅ 的值，然后即可求出cos ,a b 的值，最后得出答案．【详解】因为b = ，所以b ==，又2a =r ，22a b -= ，∴224441244a b a b a b +-⋅=+-⋅= ，解得3⋅= a b ，∴cos ,a b a b a b ⋅=== ，且,[0,π]a b ∈ ，∴π,6a b = ，即向量a 与b的夹角为π6．故选：A ．5. 陀螺是中国民间的娱乐工具之一，早期陀螺的形状由同底的一个圆柱和一个圆锥组合而成．如图，已知一木制陀螺内接于一表面积为64π的球，其中圆柱的两个底面为球的两个截面，圆锥的顶点在该球的球面上，若圆柱的底面直径为，则该陀螺的体积为（）A. 48πB. 56πC. 64πD. 72π【答案】B 【解析】【分析】根据题意易得陀螺的外接球半径4R =，球心为圆柱的中心，再利用球的几何性质，分别求出圆柱与圆锥的高，最后根据体积公式，即可求解．【详解】如图：做陀螺的轴截面，则陀螺的轴截面内接于圆O ，设圆O 的半径为R ，圆柱的底面半径为r .由24π64πR =⇒4R =，球心为圆柱的中心，又圆柱的底面半径r =，所以球心到圆柱底面距离2d ==，所以圆柱的高为24d =，圆锥的高为2h R d =-=，所以该陀螺的体积为221π4π23V r r =⨯+⨯48π8π=+56π=. 故选：B 6. 已知2ln212ln2,,42e e a b c -===，则这三个数的大小关系为（） A. c b a << B. a b c << C. a c b << D. c a b <<【答案】C 【解析】【分析】令()ln 2xf x x=，利用导数可知()f x 在()0,e 上单调递增，在()e,+∞上单调递减，结合2e e 42<<，可得答案.【详解】令()()2ln 22ln ,2(2)x x f x f x x x -=='，所以()f x 在()0,e 上单调递增，在()e,+∞上单调递减，因为22222222e e ln ln 2ln2lne ln2e 22e e e e 2c f ⎛⎫--===== ⎪⎝⎭，且()()ln214,e 42ea fb f ====，则()()2e e 42f f f ⎛⎫>> ⎪⎝⎭，即a c b <<.故选：C.7. 点M 将一条线段AB 分为两段AM 和MB，若AM BM AB MA ==M 为线段AB 的黄金分割点.已知直线(11)y a a =-<<与函数()sin y x ωϕ=+的图象相交，,,A B C 为相邻的三个交点，则（）A. 当0a =时，存在ω使点B 为线段AC 的黄金分割点B. 对于给定的常数ω，不存在a 使点B 为线段AC 的黄金分割点C. 对于任意的a ，存在ω使点B 为线段AC 的黄金分割点D. 对于任意的ω，存在a 使点B 为线段AC 的黄金分割点【答案】D 【解析】【分析】依题意，作出图形，结合题意可分析计算得出答案.【详解】若AM AB =BM MA ==，即AM AB =⇒点M 为线段AB 的黄金分割点，当0a =时，1ABBC=，不存在ω使点B 为线段AC 的黄金分割点，故选项A ，C 错误；如下图，当1a →时，0AB BC →，当1a →-时，AB BC∞→+，则()0,ABBC ∞∈+，则存在一个()01,1a ∈-使得AB BC =，故选项B 错；对于选项D ，若sin y x =与(11)y a a =-<<相交于相邻的三点,,A B C ，其横坐标分别为()123123,,x x x x x x ≤≤，则2131x x AB AC x x -=-，将sin y x =变换成()sin y x ωϕ=+后，点,,A B C 分别对应到点,,A B C '''，且满足312123,,x x x x x x ϕϕϕωωω---'''===，故21213131x x x x A B AB A C x x AC x x ''--===-''-''''，即,ωϕ对比值ABAC无影响，故选项D 正确.故选：D.8. 如图1，与三角形的一条边以及另外两条边的延长线都相切的圆被称为三角形的旁切圆，旁切圆的圆心被称为三角形的旁心，每个三角形有三个旁心．如图2，已知1F ，2F 是双曲线22221(0,0)x y a b a b -=>>的左、右焦点，P 是双曲线右支上一点，Q 是12PF F △的一个旁心．直线PQ 与x 轴交于点M，若MQQP=，则该双曲线的渐近线方程为（）A. 12y x =±B. 2y =±C. y x =±D. y =【答案】D 【解析】【分析】根据双曲线的几何性质，角平分线性质，化归转化思想，即可求解．【详解】解：因为Q 是12PF F △的一个旁心，所以2F Q 平分2PF M ∠，所以22F M MQF P QP==, 又PM 平分12F PF ∠，所以1122PF F M PF MF =,所以121222PF PF F M MF PF MF --=，即2222a c PF MF =，所以22MF c a PF ==所以b a ==y =．故选：D二､多选题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9. 数列*{}(N )n a n ∈的前n 项和为n S ，若11a =， 12,1,nn na n a n a +⎧⎪=⎨⎪⎩为奇数为偶数，则下列结论正确的是（） A. 32a = B. 1012S =C. {}n S 为递增数列D. 21{}n a -为周期数列【答案】BCD【解析】【分析】根据题意，分别求得1a ，2a ，3a ⋯，得到数列{}n a 构成以4为周期的周期数列，逐项判定，即可求解．【详解】解：由题意，数列{}n a 满足11a =， 12,1,n n na n a n a +⎧⎪=⎨⎪⎩为奇数为偶数，当1n =时，2122a a ==，当2n =时，32112a a ==，A 错误；当3n =时，4321a a ==；若n 为奇数，则1n +，3n +为偶数，2n +，4n +为奇数，则12n n a a +=，21112n n n a a a ++==，3212n n n a a a ++==，431n n n a a a ++==；若n 为偶数，则1n +，3n +为奇数，2n +，4n +为偶数，则11n n a a +=，2122n n n a a a ++==，3212n n n a a a ++==，432n n n a a a ++==. 所以数列{}n a 是以4为周期的周期数列.故1012310S a a a a =++++ ()12349102a a a a a a =+++++12121122⎛⎫=+++++ ⎪⎝⎭12=，B 正确：又由0n a >，故{}n S 递增，C 正确；由上述讨论可知，21{}n a -的项为1，12，1，12⋯，故是周期数列，D 正确．故选：BCD ．10. 已知2510a b ==，则下列关系正确的是（） A. e 1a b -> B. a b ab +<C. 49a b +<D. 2211128a b ⎛⎫⎛⎫+++> ⎪ ⎪⎝⎭⎝⎭【答案】AD 【解析】【分析】利用对数的运算法则化简，结合作差法和基本不等式比较大小，依次判断各选项.【详解】因为2510a b ==，所以225511log 101log 5,log 101log 2lg2lg5a b ==+===+=，对A 选项，11lg5lg20lg2lg5lg5lg2a b --=-=>⋅，所以0e e 1a b ->=，故A 正确；对B 选项，1111lg5lg21lg1010lg2lg5lg2lg5lg5lg2lg5lg2a b ab +--+-=+-⋅===⋅⋅，所以a b ab +=，故B 选项不正确；对C 选项，因为,0a b >，11lg 2lg 51a b+=+=，所以()11444559b aa b a b a b a b ⎛⎫+=++=++≥=⎪⎝⎭，而2a b ≠，故上述不等式等号不成立，则49a b +>，故C 不正确；对D 选项，2222221112(lg21)(lg52)(lg21)(1lg22)a b ⎛⎫⎛⎫+++=+++=++-+ ⎪ ⎪⎝⎭⎝⎭222lg 24lg2102(lg21)88=-+=-+>故D 正确.故选：AD11. 设O 为坐标原点，直线l 过抛物线2:4C y x =的焦点F 且与C 交于,A B 两点，,M N 满足2,2,MF OF BN ON AM ==与NF 相交于点P ，则下列结论正确的是（）A. AB MNB.111MN AF+= C. 0OP OF ⋅>D. ANP 面积的最大值为1【答案】ABD 【解析】【分析】根据抛物线标准方程，结合向量关系求选项A ；进而根据四边形B MNF 为平行四边形求选项B ；当AB x ⊥轴时，根据对称性求选项C ；最后设()()1122,,,A x y B x y ，因为l 过焦点F ，则124y y =-，则0MA MB k k +=，求选项D .【详解】因为2MF OF = ，则O 平分线段MF ，又2BN ON =，则O 平分线段BN ，,则四边形BMNF 为平行四边形，故A 对；因为四边形BMNF 为平行四边形，所以MN BF =，对于抛物线可证其有性质112||||AF BF p+=，证明如下：若AB l 斜率存在，设AB l ：()2py k x =-，()()1122,,,A x y B x y ，与方程22y px =联立，得：22222(2)04k p k x p k x -++=，由直线过焦点，0∆>成立，21222k x x p k +∴+=，2124p x x =， 1221212121111||||()2224x x p p pp p AF BF x x x x x x ++∴+=+=+++++ 222222222424k p pk p p k p p k ++==++⋅+，若AB l 斜率不存在，则AB l ：2px =，易求得AF BF p ==， 112||||AF BF p∴+=，故11111||||A AF M F N FB +==+，故B 对；当AB x ⊥轴时，根据对称性，P 在y 轴上，此时0OP OF ⋅=，故C 错；对于抛物线可证其有性质212y y p =-，证明如下：设()()1122,,,A x y B x y ，因为l 过焦点F ，设AB l ：2px my =+，与方程22y px =联立，得：2220y pmy p --=212y y p ∴=-，则124y y =-，则()()2212121212122222121211444164160114444MA MBy y y y y y y y y y k k x x y y y y ++++=+=+==++++++，则AMO BMO ∠=∠，又NFM BMO ∠∠=，则NFM AMO ∠∠=，即PMF △为等腰三角形，且y 轴为MF 的垂直平分线，故P 必在y 轴上，此外，MN AB ，则AMN FMN S S = ，则12ANP FMP S S MF OP OP ==⋅= ，当MA 与抛物线C 相切时，OP 取得最大值1，即ANP S 的最大值为1，故D 对，故选：ABD.【点睛】关键点点睛：若线段AB 是抛物线22y px =的一条过焦点F 的弦，则 112||||AF BF p+=，212y y p =-.第II 卷三､填空题：本题共3小题，每小题5分，共15分.12. 一种春节吉祥物为分布均匀的正十二面体模型（如图），某兴趣小组在十二个面分别雕刻了十二生肖的图案.若其中的2个成员将该模型各随机抛出一次，则恰好出现一次龙的图案朝上（即龙的图案在最上面）的概率为__________.【答案】1172【解析】【分析】利用相互独立事件的概率乘法公式直接计算可得答案.【详解】因为1个人抛出一次时龙的图案在最上面的概率为112，所以2个成员各抛一次，恰好出现一次龙的图案朝上的概率为111111111212121272⨯+⨯=. 故答案为：117213. 在ABC 中，点,D E 分别在边,BC AC 上，3,2BC BD AC AE ==，若,AD BE 交于点I ，则BIIE=__________；当3,4,2BC AC AB ===时，ABI △面积为__________. 【答案】 ①. 1②.【解析】【分析】利用平面向量的基本定理，可得1124AI AB AC =+ ，用待定系数法可得BIIE的值，再结合余弦定理和三角函数值计算出sin A ，利用三角形的面积公式可得答案. 【详解】因为2AC AE =，所以2AC AE =，因3BC BD =，所以3BC BD =，令()()0,1BIIE λλ=∈，所以BI IE λ= ，所以()()111211AI AB BI AB BE AB AE AB AC AB λλλλλλλ=+=+=+-=+++++ ，因为,,B I E 共线，所以()112x AI xAB x AE xAB AC -=+-=+，① 因,,A I D 共线，所以()()()1113BI yBA y BD AI AB y AB y AC AB =+-⇒-=-+-⋅-，所以22133y y AI AB AC --=+②，联立①②，2231123y x x y-⎧=⎪⎪⎨--⎪=⎪⎩，解出14y =，的为为故1124AI AB AC =+ ，所以1121λ=+，解出1λ=，故1BIIE=；在ABI △中，由余弦定理，222416911cos 222416AB AC BC A AB AC +-+-===⋅⨯⨯，因为()0,πA ∈，所以sin A ==，11sin 2422ABC S AB AC A =⋅⋅=⨯⨯=，则14==ABI ABC S S 故答案为：①1. 14. 正方体1111ABCD A B C D -的棱长为2,P 为该正方体侧面11CC D D 内的动点（含边界），若,PA PB 分别与直线AD，则四棱锥P ABCD -的体积的取值范围为__________.【答案】43⎤⎥⎦【解析】【分析】利用空间向量的数量积与角度的关系，列出,PA PB 分别与直线AD 所成角的正切值之和的表达式，从而得到点P 的轨迹为在平面11CC D D 中以点,D C 为焦点的椭圆被平面11CC D D 所截曲线，可得点P 到平面ABCD 的距离h 的取值范围，最后利用棱锥的体积公式计算得到答案即可.【详解】在正方体1111ABCD A B C D -中，以A 为原点，以1,,AB AD AA 所在直线为,,x y z 轴建立空间直角坐标系A xyz -，()()()(),2,,0,0,0,2,0,0,0,2,0P x z A B D ，()()(),2,,2,2,,0,2,0PA x z PB x z AD =---=---=，因为cos ,PA AD，所以sin ,PA AD ==，因为cos ,PB AD，所以sin ,PB AD ==，所以tan ,tan ,PA AD PB AD +==，=+=，整理可得点()2,,P x z 到点()2,0,0D 和点()2,2,0C 的距离之和为所以点P 的轨迹为在平面11CC D D 中以点,D C 为焦点的椭圆被平面11CC D D 所截曲线，则点P 到平面ABCD 的距离h 的最大值为1，此时点P在CD 中点的正上方；时，点P 在点D 或者点C 的正上方，所以四棱锥PABCD -的体积为144333P ABCD ABCD V h S h -⎤=⋅=∈⎥⎦. 故答案为：43⎤⎥⎦.【点睛】关键点点睛：本题考查利用空间向量解决空间角问题，涉及三角函数的计算以及空间点与点之间的距离的转化，其关键是通过计算得出动点P的轨迹方程，即tan ,tan ,PA AD PB AD +==，结合椭圆的性质得出距离的取值范围，再根据锥体的体积公式即可解决问题.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15. 已知函数2()ln f x x x =．（1）求()f x 的单调区间；（2）若存在0x >，使得()f x ax …成立，求实数a 的取值范围．【答案】（1）单调递减区间为120,e -⎛⎫ ⎪⎝⎭，单调递增区间为12e ,∞-⎛⎫+ ⎪⎝⎭；（2）1{|}ea a ≥- 【解析】【分析】（1）先对函数求导，结合导数与单调性关系即可求解；（2）由已知不等式成立，先分离参数，结合成立与最值关系的转化即可求解．【详解】（1）因为()()2ln 1f x x x '=+，0x >，令()0f x '=，解得12e x -=，当120,e x -⎛⎫∈ ⎪⎝⎭时，()0f x '<，()f x 单调递减，当12e ,x ∞-⎛⎫∈+ ⎪⎝⎭时，()0f x '>，()f x 单调递增，则()f x 的单调递减区间为120,e -⎛⎫ ⎪⎝⎭，单调递增区间为12e ,∞-⎛⎫+ ⎪⎝⎭；（2）依题意，存在0x >，使得ln a x x ≥，令()ln g x x x =，则()ln 1g x x ='+，当10,e x ⎛⎫∈ ⎪⎝⎭时，()0g x '<，()g x 单调递减，当1,ex ∞⎛⎫∈+ ⎪⎝⎭时，()0g x '>，()g x 单调递增，故()min 11e e g x g ⎛⎫==-⎪⎝⎭，因此1ea ≥-，故a 的取值范围为1{|}ea a ≥-．16. 定义两组数据1u ，2(1,2,,)v i n = 的“斯皮尔曼系数”为变量i u 在该组数据中的排名1x 和变量i v 在该组数据中的排名1y 的样本相关系数，记为ρ，其中()()221611ni i i x y n n ρ==---∑．某校15名学生的数学成绩的排名与知识竞赛成绩的排名如下表：i x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 i y 1 5 3 4 9 8 7 6 10 2 12 14 13 11 15（1）试求这15名学生的数学成绩与知识竞赛成绩的“斯皮尔曼系数”；（2）已知在这15名学生中有10人数学成绩优秀，现从这15人中随机抽取3人，抽到数学成绩优秀的学生有X 人，试求X 的分布列和数学期望．【答案】（1）0.8；（2）分布列见解析，数学期望为2. 【解析】【分析】（1）根据“斯皮尔曼系数”的计算公式即可求解.（2）X 的值可能为0，1，2，3，计算出各自对应的概率，列出分布列并求出数学期望. 【小问1详解】依题意，61(91644164149)0.815224ρ=-⋅++++++++=⨯，所以这15名学生的数学成绩与知识竞赛成绩的“斯皮尔曼系数”是0.8. 【小问2详解】依题意，X 的值可能为0，1，2，3，3125105331515C C C 220(0),(1)C 91C 91P X P X ======，21310510331515C C C 4524(2),(3)C 91C 91P X P X ======，则X 的分布列为：X 0 1 2 3P291 2091 4591 2491所以X 的数学期望为()2045241232919191E X =⨯+⨯+⨯=． 17. 如图所示的几何体是圆锥的一部分，A 为圆锥的顶点，O 是圆锥底面圆的圆心，2π,3BOC P ∠=是弧BC 上一动点（不与,B C 重合），点M 在AB 上，且3AM MB =，OA ==.（1）当π2BOP ∠=时，证明：AB ⊥平面MOP ；（2）若四棱锥M OCPB -. ①求二面角B AO P --的取值范围；②记异面直线AP 与BO 所成的角为α，求cos α的最大值. 【答案】（1）证明见解析；（2）①ππ,62⎡⎤⎢⎥⎣⎦【解析】【分析】（1）结合余弦定理与勾股定理可证AB OM ⊥，再由OP OB ⊥，AO OP ⊥，可得OP ⊥平面AOB ，从而有OP AB ⊥，再由线面垂直的判定定理，即可得证；（2）①设BOP θ∠=，则二面角B AO P --的平面角即为θ，易得四边形OCPB 的面积π6S θ⎛⎫=+ ⎪⎝⎭，由V ≥，可得ππ,62θ⎡⎤∈⎢⎥⎣⎦，即二面角B AO P --的取值范围； ②以O 为坐标原点建立空间直角坐标系，用含θ的式子表示出点P 的坐标，再利用向量法求异面直线夹角，即可求解. 【小问1详解】由题知2AB =，在MBO △中，1OB =，12MB =,π3MBO ∠=,求得OM =，则222BM OM BO +=，AB OM ∴⊥ 又π2BOP ∠=,AO OP ⊥,AO OP ⊥,OA OB O = ,OA OB ⊂､平面AOB ，故OP ⊥平面AOB ，又AB ⊂平面AOB ，所以OP AB ⊥，又OP OM O ⋂=,OP OM ⊂､平面MOP ，AB ∴⊥平面MOP【小问2详解】①设BOP θ∠=，AO BO ⊥,AO OP ⊥,则二面角B AO P --的平面角即为θ，在OB 上取点N ，使3ON NB =，连接MN ,MN ∴ 1,4OA MN OA ==四棱锥M OCPB -的体积13V S ==，其中S 表示四边形OCPB 的面积，则112πsin sin 223S OP OB OP OC θθ⎛⎫=⋅+⋅- ⎪⎝⎭111sin sin 222θθθ⎫=++⎪⎪⎭3πsin 46θθθ⎛⎫=+=+ ⎪⎝⎭，由V ≥，可得πsin 6θ⎛⎫+≥ ⎪⎝⎭2π03θ<<，则ππ5π666θ<+<，故ππ2π363θ≤+≤，解得ππ,62θ⎡⎤∈⎢⎥⎣⎦，即二面角B AO P --的取值范围为ππ,62⎡⎤⎢⎥⎣⎦；②以OB方向x 轴正方向，在BOC ∠内垂直于OB 的方向为y 轴正方向，OA 方向为z 轴正方向建立空间直角坐标系，则()0,0,0O，(A ,()1,0,0B ,()cos ,sin ,0P θθ(cos ,sin ,AP θθ= ，()1,0,0OB =,1cos cos ,cos 2AP OB αθ∴==ππ,62θ⎡⎤∈⎢⎥⎣⎦,cos θ⎡∈⎢⎣即cos α.18. 已知椭圆2222:1(0)y x E a b a b +=>>,A B 是E 上的不同两点，且直线AB 的斜率为1-，当直线AB 过原点时，AB 4=.（1）求椭圆E 的标准方程；（2）设()0,3P ，点,A B 都不在y 轴上，连接,PA PB ，分别交E 于,C D 两点，求点P 到直线CD 的距离的最大值.【答案】（1）22:163y x E +=；（2. 【解析】【分析】（1）由题，利用弦长公式列出AB 弦长的表达式，结合椭圆的离心率，计算可得答案；（2）联立直线PA ，求出点C 坐标，同理可得B 点坐标，对立CD 方程，可知直线CD 的图象性质，故分析可得结果. 【小问1详解】依题意c e a ==2222212c a b a a -==，因此222a b =，当直线AB 经过原点时，直线AB 的方程为：y x =-，设()()1111,,,A x y B x y --，联立直线AB 与椭圆E 的方程22221y xy x ab =-⎧⎪⎨+=⎪⎩，结合222a b =，得22132x b =，所以4AB =，解得212x =，故223,6b a ==，即椭圆E 的标准方程为22:163y x E +=；【小问2详解】设()()()()11223344,,,,,,,A x y B x y C x y D x y ，可知PA 的斜率存在，设为k ，则()33330y k x x -=≠，直线PA 的方程为3y kx =+，联立直线PA 与椭圆E 的方程，223163y kx y x =+⎧⎪⎨+=⎪⎩，整理得()222630,k x kx +++=其中()()222Δ361222410k k k =-+=->，得1k <-或1k >，13232x x k =+，则()()333122222333333333326952232x x x x y x y y k x y x ====+-+-+-+，又3113125352y y kx y -=+=-，故3333125,5252x y A y y ⎛⎫- ⎪--⎝⎭，同理可得4444125,5252x y B y y ⎛⎫-⎪--⎝⎭，易知CD 的斜率不为0，设CD 的方程为x my n =+，则()()()()()()()()()()4334343421434343525252525252525252my n y my n y m n y y x x x x y y y y y y +--+--+--=-==------，()()334421434312512552525252y y y y y y y y y y ----=-=----，又()()34212134152AB y y y y k x x m n y y --===---+-，则251n m +=，对比CD 的方程可知，直线CD 恒过定点15,22Q ⎛⎫⎪⎝⎭，设点P 到直线CD 的距离为d，则d PQ ≤==，当且仅当PQ CD ⊥时，点P 到直线CD .【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：（1）设直线方程，设交点坐标为()11,x y ，()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆；（3）列出韦达定理；（4）将所求问题或题中的关系转化为1212,x x x x +的形式；（5）代入韦达定理求解.19. 固定项链的两端，在重力的作用下项链所形成的曲线是悬链线.1691年，莱布尼茨等得出悬链线的方程为e e 2x xccc y -⎛⎫+ ⎪⎝⎭=，其中c 为参数．当1c =时，该表达式就是双曲余弦函数，记为e e cosh 2x xx -+=，悬链线的原理常运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程．已知三角函数满足性质：①导数：()()sin cos sin cos x x x x''⎧=⎪⎨=-⎪⎩；②二倍角公式：2cos 22cos 1x x =-；③平方关系：22sin cos 1x x +=．定义双曲正弦函数为e e sinh 2x x x --=．（1）写出sinh x ，cosh x 具有的类似于题中①、②、③的一个性质，并证明该性质；（2）任意0x >，恒有sinh 0x kx ->成立，求实数k 的取值范围；（3）正项数列*{}(N )n a n ∈满足11a a =>，2121n n a a +=-，是否存在实数a ，使得2024178a =？若存在，求出a 的值；若不存在，请说明理由．【答案】（1）答案见解析（2）(-∞，1]（3）存在实数2022202211221222a -⎛⎫=+⎪ ⎪⎝⎭，使得2024178a =成立．【解析】分析】（1）①求导数，②用二倍角公式，③利用平方关系；证明即可；（2）构造函数()sinh F x x kx =-，求导数，利用导数讨论函数的单调性，求k 的取值范围即可；（3）方法一、求出1a ，2a ，3a ，猜想n a ，用数学归纳法证明即可．方法二、构造数列{}n x ，根据()cosh n n a x =，利用递推公式求解即可．【小问1详解】①导数：()()()sinh cosh x x '=，()()()cosh sinh x x '=，证明如下：()()e e e e sin h cos h 22e e e e cos h sin h 22x x x x x x x x x x x x '--''--'⎧⎛⎫-+⎪=== ⎪⎪⎝⎭⎨⎛⎫⎪+-=== ⎪⎪⎝⎭⎩， ②二倍角公式：()()2cosh 22cosh 1x x =-，证明如下：【()()222222e e e 2e e 2cosh 1211cosh 2222e x x x x x xx x ---⎛⎫++++-=⨯-=-== ⎪⎝⎭； ③平方关系：22(cosh )(sinh )1x x -=，证明如下：()()22222222e e e e e e 2e 2e cosh sinh 12244x x x x x x x x x x ----⎛⎫⎛⎫+-++-+-=-=-= ⎪ ⎪⎝⎭⎝⎭；【小问2详解】令()sinh F x x kx =-，,()0x ∈+∞，()cosh F x x k '=-，①当1k ≤时，由e cosh e 21x xx -+=≥=，又因为0x >，所以e e x x -≠，等号不成立，所以()cosh 0F x x k '=->，即()F x 为增函数，此时()(0)0F x F >=，对任意0x >，sinh x kx >恒成立，满足题意；②当1k >时，令()()G x F x ='，,()0x ∈+∞，则()sinh 0G x x '=>，可知()G x 是增函数，由(0)10G k =-<与()1ln204G k k=>可知，存在唯一()00,ln 2x k ∈，使得0()0G x =，所以当0(0,)x x ∈时，0()()()0F x G x G x =<='，则()F x 在0(0,)x 上为减函数，所以对任意0(0,)x x ∈，()(0)0F x F <=，不合题意；综上知，实数k 的取值范围是(],1-∞；【小问3详解】方法一、由11a a =>，函数e e cosh 2x xx -+=的值域为[)1,+∞，对于任意大于1的实数1a ，存在不为0的实数m ，使得1cosh m a =，类比双曲余弦函数的二倍角公式()()2cosh 22cosh 1x x =-，由1cosh m a =，()()222cosh 1cosh 2a m m =-=，()23cosh 2a m =，猜想：()1cosh 2n n a m -=，由数学归纳法证明如下：①当1n =时，()()111cosh 2cosh a a m m -===成立；②假设当(n k k =为正整数）时，猜想成立，即1cosh(2)k k a m -=，则()()()22111212cosh 21cosh 22cosh 2k k k k ka a m m m --+⎡⎤=-=-=⨯=⎣⎦，符合上式，综上知，()1cosh 2n n a m -=；若()2023202417cosh 28a m ==，设20232t m =，则e 17cosh 28e t t t -+==，解得：e 4t =或14，即ln 4t =±，所以2022ln 22m =±，即2022202211221e 1cosh 222e 2m m a m --⎛⎫+===+ ⎪ ⎪⎝⎭．综上知，存在实数2022202211221222a -⎛⎫=+⎪ ⎪⎝⎭，使得2024178a =成立．方法二、构造数列{}(0)n n x x >，且()cosh n n a x =，因为2121n n a a +=-，所以()()212cosh 1cosh 2n n n a x x +=-=，则()()11cosh cosh 2n n n a x x ++==，因为()cosh x 在(0,)+∞上单调递增，所以12n n x x +=，即{}n x 是以2为公比的等比数列，所以2023202412x x =，所以()2023202412eex x =，所以()20232024112e ex x =，又因为()()2024202420242024e 117cosh e 28x x a x -==+=，解得2024e 4x =或14，所以()()2023202320222022111111222211111cosh e 4422222e x x a a x ---⎛⎫⎛⎫===+=+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，综上知，存在实数2022202211221222a -⎛⎫=+ ⎪ ⎪⎝⎭，使得2024178a =成立．【点睛】方法点睛：对于新定义的题目，一定要耐心理解定义，新的定义不但考查的是旧的知识点的延伸，更考查对于新知识的获取理解能力，抓住关键点，解题不是事.。

江西省萍乡市数学高三文数第二次联考试卷

江西省重点中学盟校2023届高三第二次联考数学(文)试题及参考答案

部编版江西省萍乡市高三下学期4月第二次模拟考试(二模)数学(文)试卷

江西省萍乡市2019-2020学年高考第二次大联考数学试卷含解析

江西省萍乡市2022届高三数学第二次模拟考试试题 文(解析版)

江西省萍乡市数学高三上学期文数第二次联考试卷

江西省七校高三第二次联考数学文科试卷及答案

江西省萍乡市2022届高三数学第二次模拟考试试题 文(解析版)

江西省萍乡市2019-2020学年高考第二次质量检测数学试题含解析

江西省重点中学协作体2023届高三第二次联考数学(文)试题(含解析)

2020届江西省萍乡市上栗县高三第二次模拟考试数学(文)试题(解析版)

江西省萍乡市2025届高三第二次诊断性检测数学试卷含解析

江西省重点中学盟校2024届高三第二次联考数学试题及答案

江西省萍乡市数学高三上学期文数第二次调研测试试卷

江西省萍乡市数学高三上学期文数第二次月考试卷

江西省萍乡市2024年数学(高考)部编版第二次模拟(提分卷)模拟试卷

江西省萍乡市2024届高三二模考试数学试卷(含答案与解析)_5254

江西省萍乡市2022届高三数学第二次模拟考试试题文(解析版)

江西省萍乡市2022届高三数学第二次模拟考试试题文(解析版)