2020高考数学立体几何练习题23题

合集下载

高考数学立体几何多选题(讲义及答案)附解析

高考数学立体几何多选题(讲义及答案)附解析一、立体几何多选题1．已知正方体1111 ABCD A B C D -的棱长为2，M 为1DD 的中点，N 为正方形ABCD 所在平面内一动点，则下列命题正确的有（）A ．若2MN =，则MN 的中点的轨迹所围成图形的面积为πB ．若N 到直线1BB 与直线DC 的距离相等，则N 的轨迹为抛物线C ．若1D N 与AB 所成的角为3π，则N 的轨迹为双曲线 D ．若MN 与平面ABCD 所成的角为3π，则N 的轨迹为椭圆【答案】BC 【分析】对于A ，连接MN ，ND ，DP ，得到直角MDN △，且P 为斜边MN 的中点，所以1PD =，进而得到P 点的轨迹为球面的一部分，即可判断选项A 错误；对于B ，可知1NB BB ⊥，即NB 是点N 到直线1BB 的距离，在平面ABCD 中，点N 到定点B 的距离与到定直线DC 的距离相等，利用抛物线定义知B 正确；对于C ，建立空间直角坐标系，设(,,0)N x y ，利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅，化简可知N 的轨迹为双曲线；对于D ，MN 与平面ABCD 所成的角为3MND π∠=，3ND =，可知N 的轨迹是以D 为圆心，33为半径的圆周；【详解】对于A ，如图所示，设P 为MN 的中点，连接MN ，ND ，DP ，由正方体性质知MDN △为直角三角形，且P 为MN 的中点，2MN =，根据直角三角形斜边上的中线为斜边的一半，知MDN △不管怎么变化，始终有1PD =，即P 点的轨迹与正方体的面围城的几何体是一个以D 为球心，1为半径的球的18，其面积214182S ππ=⨯⨯=，故A 错误；对于B ，由正方体性质知，1BB ⊥平面ABCD 由线面垂直的性质定理知1NB BB ⊥，即NB 是点N 到直线1BB 的距离，在平面ABCD 中，点N 到定点B 的距离与到定直线DC 的距离相等，所以点N 的轨迹是以点B 为焦点，直线DC 为准线的抛物线，故B 正确；对于C ，如图以D 为直角坐标系原点，建立空间直角坐标系，(,,0)N x y ，1(0,0,2)D ，(0,2,0)A ，(2,2,0)B ，则1(,,2)D N x y =-，(0,2,0)AB =，利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅，化简整理得：2234y x -=，即221443y x -=，所以N 的轨迹为双曲线，故C 正确；对于D ，由正方体性质知，MN 与平面ABCD 所成的角为MND ∠，即3MND π∠=，在直角MDN △中，3ND =，即N 的轨迹是以D 3D 错误；故选：BC 【点睛】关键点睛：本题考查立体几何与解析几何的综合，解题的关键是抓住解析几何几种特殊曲线的定义，考查学生的逻辑推理能力，转化与划归能力与运算求解能力，属于难题.2．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.3．已知球O 为正方体1111ABCD A B C D -的内切球，平面11A C B 截球O 的面积为24π，下列命题中正确的有（）A ．异面直线AC 与1BC 所成的角为60°B ．1BD ⊥平面11AC B C ．球O 的表面积为36πD ．三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ，1A B ，通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ；通过反证法证明B ；由已知平面11A C B 截球O 的面积为24π求出正方体棱长，进而求出内切球的表面积可判断C ；利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ，连接11A C ，1A B ，由正方体1111ABCD A B C D -，可知11//A C AC ，11AC B ∴∠为异面直线AC 与1BC 所成的角，设正方体边长为a，则1111AC A B BC ==，由等边三角形知1160A C B ∠=，即异面直线AC 与1BC 所成的角为60，故A 正确；对于B ，假设1BD ⊥平面11A C B ，又1A B ⊂平面11A C B ，则11BD B A ⊥，设正方体边长为a ，则11A D a =，1A B =，1BD =，由勾股定理知111A D B A ⊥，与假设矛盾，假设不成立，故1BD 不垂直于平面11A C B ，故B 错误；对于C ，设正方体边长为a，则11AC =，内切球半径为2a，设内切球的球心O 在面11A C B 上的投影为O '，由等边三角形性质可知O '为等边11A C B △的重心，则11123233O A AC a ='=⨯=，又12OA a =，∴球心O 到面11A C B 的距离6a ==，又球心与截面圆心的连线垂直于截面，∴截面圆的半径为223626a a a ⎛⎫⎛⎫ ⎪⎪ ⎪⎝⎭⎝⎭-=，又截面圆的面积26246S a ππ⎛⎫= ⎪ ⎪⎝⎭=，解得12a =，则内切球半径为6，内切球表面积214644S ππ==⨯，故C 错误；对于D ，由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=，故D 正确；故选：AD【点睛】关键点点睛：本题考查了正方体和它的内切球的几何结构特征，关键是想象出截面图的形状，从而求出正方体的棱长，进而求出内切球的表面积及三棱锥的体积，考查了空间想象能力，数形结合的思想，属于较难题.4．如图所示，正三角形ABC 中，D ，E 分别为边AB ，AC 的中点，其中AB ＝8，把△ADE 沿着DE 翻折至A 'DE 位置，使得二面角A '-DE -B 为60°，则下列选项中正确的是（）A ．点A '到平面BCED 的距离为3B ．直线A 'D 与直线CE 所成的角的余弦值为58C ．A 'D ⊥BDD ．四棱锥A '-BCED 237【答案】ABD 【分析】作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .利用线面垂直的判定定理判定CD ⊥平面A'MN ,利用面面垂直的判定定理与性质定理得到'A 到平面面BCED 的高A'H ,并根据二面角的平面角，在直角三角形中计算求得A'H 的值，从而判定A;根据异面直线所成角的定义找到∠A'DN 就是直线A'D 与CE 所成的角，利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N ,在利用外接球的球心的性质进行得到四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,经过计算求解可得半径从而判定D. 【详解】如图所示，作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N . 则A'M ⊥DE ,MN ⊥DE , ,∵'A M ∩MN =M ,∴CD ⊥平面A'MN , 又∵CD ⊂平面ABDC ,∴平面A'MN ⊥平面ABDC , 在平面A'MN 中作A'H ⊥MN ,则A'H ⊥平面BCED , ∵二面角A'-DE -B 为60°，∴∠A'EF =60°，∵正三角形ABC 中，AB =8,∴AN =∴A'M ,∴A'H =A'M sin60°=3，故A 正确；连接DN ,易得DN ‖EC ,DN =EC =4, ∠A'DN 就是直线A'D 与CE 所成的角，DN =DA'=4,A'N =A'M ,cos ∠A'DN =22441252448+-=⨯⨯,故B 正确；A'D =DB =4,==,∴222A D DB A B '≠'+,∴A'D 与BD 不垂直，故C 错误’ 易得NB =NC =ND =NG =4，∴N 为底面梯形BCED 的外接圆的圆心，设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC , 若O 在平面BCED 上方，入图①所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=-+=,解得23x =-,舍去；故O 在平面BCED 下方，如图②所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=++=, 解得23x =,∴244371699R ⨯=+=,R ∴=故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题，涉及二面角问题，异面直线所成的角，用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算，余弦定理等，属综合性较强的题目，关键是利用线面垂直，面面垂直的判定和性质进行空间关系和结构的判定，注意球心在四棱锥的底面上方和下方的讨论与验证.5．在正方体1111ABCD A B C D -中，M 、N 分别是棱AB 、1CC 的中点，1MB P 的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题正确命题的序号是（）A ．平面1MB P 1ND ⊥ B ．平面1MB P ⊥平面11ND AC ．1MB P 在底面ABCD 上的射影图形的面积为定值 D ．1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC【分析】取N 与P 重合，结合勾股定理可判断A 选项的正误；利用面面垂直的判定定理可判断B 选项的正误；分点P 在棱1CC 、11C D 上运动两种情况讨论，利用三角形的面积公式可判断C 选项的正误；取点P 与点1C 重合，判断1MB P 在侧面11D C CD 上射影图形形状，可判断D 选项的正误. 【详解】对于A 选项，设正方体1111ABCD A B C D -的棱长为2，如下图所示：当点P 与点N 重合时，若1ND ⊥平面1MB P ，1B N ⊂平面1MB P ，则11ND B N ⊥，由勾股定理可得2211115D N C N C D =+=，同理可得15B N =，1122B D =，2221111B N D N B D ∴+≠，则1ND 与1B N 不垂直，假设不成立，A 选项错误；对于B 选项，取1BB 的中点E ，连接1A E 、EN ，在正方体1111ABCD A B C D -中，11//BB CC ，且E 、N 分别为1BB 、1CC 的中点，则11//B E C N 且11B E C N =，所以，四边形11B ENC 为平行四边形，则11//EN B C 且11EN B C =，1111//A D B C 且1111A D B C =，所以，11//A D EN 且11A D EN =，所以，四边形11A END 为平行四边形，所以，11//A E D N ，111A B BB =，1B E BM =，11190A B E B BM ∠=∠=，所以，111Rt A B E Rt B BM ≅△△，所以，111B A E BB M ∠=∠，所以，111111190A EB BB M A EB B A E ∠+∠=∠+∠=，190B FE ∴∠=，所以，11B M A E ⊥，11A D ⊥平面11AA B B ，1B M ⊂平面11AA B B ，111B M A D ∴⊥， 1111A D A E A =，11A D 、1A E ⊂平面11ND A ，1MB ∴⊥平面11ND A ，1MB ⊂平面1MB P ，所以，平面1MB P ⊥平面11ND A ，B 选项正确；对于C 选项，设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时，1MB P 在底面ABCD 上的射影为MBC △，此时，射影图形的面积为21224MBCa a S a =⋅=△；若点P 在棱11C D 上运动时，设点P 在底面ABCD 上的射影点为G ，则G CD ∈，且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ，则1MB P 在底面ABCD 内的射影为MBG △，且21224MBGa a S a =⋅⋅=△.综上所述，1MB P 在底面ABCD 内的射影图形的面积为定值，C 选项正确；对于D 选项，当点P 与1C 重合时，P 、1B 两点在平面11D C CD 上的射影重合，此时，1MB P 在侧面11D C CD 上的射影不构成三角形，D 选项错误.故选：BC.【点睛】方法点睛：证明面面垂直常用的方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可.6．已知四面体ABCD 的所有棱长均为2，则下列结论正确的是（）A ．异面直线AC 与BD 所成角为60︒B ．点A 到平面BCD 的距离为3C ．四面体ABCDD ．动点P 在平面BCD 上，且AP 与AC 所成角为60︒，则点P 的轨迹是椭圆【答案】BC【分析】在正四面体中通过线面垂直可证得AC ⊥BD ，通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误.【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误；在四面体ABCD 中，过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心，因为所有棱长均为2,AF ==即点A 到平面BCD ,故B 正确；设O 为正四面体的中心则OF 为内切球的半径，OA 我外接球的半径，因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△，所以4AF OF =，即2=6OF AO =,所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确；建系如图：,A C ⎛⎛⎫ ⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ，则,,0,,333AP x y AC →→⎛⎛=-=- ⎝⎭⎝⎭，因为cos 60AP AC AP AC →→→→⋅=，所以222324812241393972y x y +=++⨯+⨯，即222388=33y x y +++，平方化简可得：22323400399y x y ----，可知点P 的轨迹为双曲线,故D 错误.故选：BC ．【点睛】方法点睛：立体几何中动点轨迹的求解问题，解决此类问题可采用空间向量法，利用空间向量法表示出已知的角度或距离的等量关系，从而得到轨迹方程.7．正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 在侧面11CDD C 上运动，且满足1//B F 平面1A BE .以下命题正确的有（）A ．侧面11CDD C 上存在点F ，使得11B F CD ⊥B ．直线1B F 与直线BC 所成角可能为30︒C ．平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D ．设正方体棱长为1，则过点E ，F ，A 5【答案】AC【分析】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，易证得平面1//B MN 平面1A BE ，可得点F 的运动轨迹为线段MN ．取MN 的中点F ，根据等腰三角形的性质得1B F MN ⊥，即有11B F CD ⊥，A 正确；当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，可判断B 错误；根据平面1//B MN 平面1A BE ，11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，计算可知C 正确；【详解】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，则易证得11//B N A E ，1//MN A B ，从而平面1//B MN 平面1A BE ，所以点F 的运动轨迹为线段MN ．取MN 的中点F ，因为1B MN △是等腰三角形，所以1B F MN ⊥，又因为1//MN CD ，所以11B F CD ⊥，故A 正确；设正方体的棱长为a ，当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，此时11tan C B F ∠=1tan 3023︒<=，所以B 错误；平面1//B MN 平面1A BE ，取F 为MN 的中点，则1MN C F ⊥，1MN B F ⊥，∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，11111tan B C B FC C F ∠==22，所以C 正确；因为当F 为1C E 与MN 的交点时，截面为菱形1AGC E （G 为1BB 的交点），面积为6，故D 错误. 故选：AC.【点睛】本题主要考查线面角，二面角，截面面积的求解，空间几何中的轨迹问题，意在考查学生的直观想象能力和数学运算能力，综合性较强，属于较难题．8．如图，矩形ABCD 中，M 为BC 的中点，将ABM 沿直线AM 翻折成1AB M ，连结1B D ，N 为1B D 的中点，则在翻折过程中，下列说法中所有正确的是（）A ．存在某个位置，使得CN AB ⊥B ．翻折过程中，CN 的长是定值C ．若AB BM =，则1AM BD ⊥D ．若1AB BM ==，当三棱锥1B AMD -的体积最大时，三棱锥1B AMD -的外接球的表面积是4π【答案】BD【分析】对于选项A ，取AD 中点E ，取1AB 中点K ，连结KN ，BK ，通过假设CN AB ⊥，推出AB ⊥平面BCNK ，得到AB BK ⊥，则22AK AB BK AB =+>，即可判断；对于选项B ，在判断A 的图基础上，连结EC 交MD 于点F ，连结NF ，易得1NEC MAB ∠=∠，由余弦定理，求得CN 为定值即可；对于选项C ，取AM 中点O ，1B O ，DO ，由线面平行的性质定理导出矛盾，即可判断；对于选项D ，易知当平面1AB M 与平面AMD 垂直时，三棱锥1B AMD -的体积最大，说明此时AD 中点E 为外接球球心即可.【详解】如图1，取AD 中点E ，取1AB 中点K ，连结EC 交MD 于点F ，连结NF ，KN ，BK ,则易知1//NE AB ，1//NF B M ，//EF AM ，//KN AD ，112NE AB =，EC AM = 由翻折可知，1MAB MAB ∠=∠，1AB AB =，对于选项A ，易得//KN BC ，则K 、N 、C 、B 四点共面，由题可知AB BC ⊥，若CN AB ⊥，可得AB ⊥平面BCNK ，故AB BK ⊥，则22AK AB BK AB =+>，不可能，故A 错误；对于选项B ，易得1NEC MAB ∠=∠，在NEC 中，由余弦定理得222cos CN CE NE NE CE NEC =+-⋅⋅∠，整理得222212422AB AB AB CN AM AM BC AB AM =+-⋅⋅=+，故CN 为定值，故B 正确；如图2，取AD 中点E ，取AM 中点O ，连结1B E ，OE ，1B O ，DO ，，对于选项C ，由AB BM =得1B O AM ⊥，若1AM B D ⊥，易得AM ⊥平面1B OD ，故有AM OD ⊥，从而AD MD =，显然不可能，故C 错误；对于选项D ，由题易知当平面1AB M 与平面AMD 垂直时，三棱锥B 1﹣AMD 的体积最大，此时1B O ⊥平面AMD ，则1B O OE ⊥，由1AB BM ==，易求得122BO =，2DM =22221122122B E OB OE ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，因此1EB EA ED EM ===，E 为三棱锥1B AMD -的外接球球心，此外接球半径为1，表面积为4π，故D 正确.故选：BD.【点睛】本题主要考查了立体几何中的翻折问题以及空间图形的位置关系，考查了空间想象能力，属于较难题.。

高考数学《立体几何》练习题及答案

立体几何1．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学]若某空间几何体的三视图如图所示，则该几何体的体积是A ．2B ．1C ．D ．【答案】B2．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D 【解析】3．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 在正方体1111ABCD A B C D -中，动点E 在棱1BB 上，动点F 在线段11A C 上，O 为底面ABCD 的中心，若1,BE x A F y ==，则四面体O AEF -的体积 A ．与,x y 都有关 B ．与,x y 都无关 C ．与x 有关，与y 无关D ．与y 有关，与x 无关【答案】B4．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]5．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学] 一个圆锥SC的高和底面直径相等，且这个圆锥SC和圆柱OM的底面半径及体积也都相等，则圆锥SC和圆柱OM的侧面积的比值为A．322B．23C．35D．45【答案】C6．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【答案】D【解析】7．[广东省三校（广州真光中学、深圳市第二中学、珠海市第二中学）2020届高三上学期第一次联考数学（理）试题] 在如图直二面角ABDC中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD的中点E，将△ABE 沿BE 翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是A．BC与平面A1BE内某直线平行B．CD∥平面A1BEC．BC与平面A1BE内某直线垂直D．BC⊥A1B【答案】D8．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D【解析】9．[陕西省汉中市2020届高三教学质量第一次检测考试理科数学试题] 圆锥的侧面展开图是半径为R 的半圆，则该圆锥的体积为________. 【答案】33πR 10．[辽宁省本溪高级中学2020届高三一模考试数学（理）试卷]【答案】4π11．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 如图，在棱长为 1 的正方体1111ABCD A B C D -中，点M 是AD 的中点，动点P 在底面ABCD 内（不包括边界），若1B P ∥平面1A BM ，则1C P 的最小值是________．【答案】305【解析】【分析】由面面平行找到点P 在底面ABCD 内的轨迹为线段DN ，再找出点P 的位置，使1C P 取得最小值，即1C P 垂直DN 于点O ，最后利用勾股定理求出最小值. 【详解】取BC 中点N ，连接11,,B D B N DN ，作CO DN ⊥，连接1C O ，因为平面1B DN ∥平面1A BM ，所以动点P 在底面ABCD 内的轨迹为线段DN ，当点P 与点O 重合时，1C P 取得最小值，因为11152225DN CO DC NC CO ⋅=⋅⇒==，所以221min 11130()155C P C O CO CC ==+=+=. 故1C P 的最小值是305. 【点睛】本题考查面面平行及最值问题，求解的关键在于确定点P 的位置，再通过解三角形的知识求最值.12．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]已知某几何体的三视图如图所示，则该几何体的外接球的半径为________．21【答案】【解析】【分析】根据三视图还原几何体，设球心为O，根据外接球的性质可知，O与PAB△和正方形ABCD中心的连线分别与两个平面垂直，从而可得到四边形OGEQ 为矩形，求得OQ和PQ后，利用勾股定理可求得外接球半径.【详解】由三视图还原几何体如下图所示：设PAB△的中心为Q，正方形ABCD的中心为G，外接球球心为O，则OQ⊥平面PAB，OG⊥平面ABCD，E为AB中点，∴四边形OGEQ为矩形，112OQ GE BC ∴===，2233PQ PE ==， ∴外接球的半径：22213R GE PQ =+=. 故答案为21. 【点睛】本题考查多面体外接球半径的求解，关键是能够根据球的性质确定球心的位置，从而根据长度关系利用勾股定理求得结果. 13．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】【解析】14．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]【答案】1 315．[江苏省南通市2020届高三第一学期期末考试第一次南通名师模拟试卷数学试题]如图，在四棱锥P ABCD-中，底面ABCD是平行四边形，平面ABP⊥平面BCP，90APB=，M为CP的中点．求证：∠=︒，BP BC（1）AP//平面BDM；（2）BM ACP⊥平面．【解析】（1）设AC 与BD 交于点O ，连接OM ，因为ABCD 是平行四边形，所以O 为AC 中点，因为M 为CP 的中点，所以AP ∥OM ，又AP ⊄平面BDM ，OM ⊂平面BDM ，所以AP ∥平面BDM ．（2）平面ABP ⊥平面BCP ，交线为BP ，因为90APB ∠=︒，故AP BP ⊥，因为AP ⊂平面ABP ，所以AP ⊥平面BCP ，因为BM ⊂平面BCP ，所以AP ⊥BM ．因为BP BC =，M 为CP 的中点，所以BM CP ⊥．因为AP CP P =I ，AP CP ⊂，平面ACP ，所以BM ⊥平面ACP .16．[河南省新乡市高三第一次模拟考试（理科数学）] 如图，在四棱锥ABCDV -中，二面角D BC V --为︒60，E 为BC 的中点. （1）证明：VE BC =；（2）已知F 为直线VA 上一点，且F 与A 不重合，若异面直线BF 与VE 所成角为︒60，求.VA VFABCDPMABCDPMO【解析】17．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]如图，在底面是菱形的四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=60°，PA=AB=2，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q．（1）已知平面PAB∩平面PCD=l，求证：AB∥l．（2）求直线AQ 与平面PCD 所成角的正弦值．【解析】【分析】（1）证明AB ∥平面PCD ，然后利用直线与平面平行的性质定理证明AB ∥l ；（2）以点A 为原点，直线AE 、AD 、AP 分别为轴建立空间直角坐标系，求出平面PCD 的法向量和直线AQ 的方向向量，然后利用空间向量的数量积求解直线AQ 与平面PCD 所成角的正弦值即可．【详解】（1）证明：∵AB ∥CD ，AB ⊄平面PCD ，CD ⊂平面PCD ． ∴AB ∥平面PCD ，∵AB ⊂平面PAB ，平面PAB ∩平面PCD =l ， ∴AB ∥l ；（2）∵底面是菱形，E 为BC 的中点，且AB =2， ∴13BE AE AE BC ==⊥,,， ∴AE ⊥AD ，又PA ⊥平面ABCD ，则以点A 为原点，直线AE 、AD 、AP 分别为x 、y 、z 轴建立如图所示空间直角坐标系，则()()()()020,002,30,300D P C E,,,,,,,,，∴()0,1,1F ，()()()()3000,11310022AE AF DC DP ===-=-u u u r u u u r u u u r u u u r,,,,,,,,,,，设平面PCD 的法向量为(),,x y z =n ，有0PD ⋅=u u u r n ，0CD ⋅=u u u rn ，得()133=，，n ，设()1AQ AC AP λλ=+-u u u r u u u r u u u r，则()()321AQ λλλ=-u u u r ,,，再设(3,,)AQ mAE n m n n AF =+=u u u r u u u r u u u r，则()3321m n nλλλ⎧=⎪=⎨⎪-=⎩，解之得23m n λ===，∴2223333AQ ⎛⎫=⎪⎝⎭u u u r ,,，设直线AQ 与平面PCD 所成角为α，则3105sin cos ,AQ AQ AQα⋅>=<==u u u r u u u r u u u r n n n ，∴直线AQ 与平面PCD 所成角的正弦值为3105．【点睛】本题考查直线与平面平行的判定定理以及性质定理的应用，直线与平面所成角的向量求法，合理构建空间直角坐标系是解决本题的关键，属中档题.18．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 已知三棱柱111ABC A B C -中，1AB AC AA ==，侧面11ABB A ⊥底面ABC ，D 是BC 的中点，160B BA ∠=︒，1B D AB ⊥.（1）求证：ABC △为直角三角形；（2）求二面角1C AD B --的余弦值．【解析】（1）取AB 中点O ，连接OD ，1B O ，易知1ABB △为等边三角形，从而得到1B O AB ⊥，结合1B D AB ⊥，可根据线面垂直判定定理得到AB ⊥平面1B OD ，由线面垂直的性质知AB OD ⊥，由平行关系可知AB AC ⊥，从而证得结论；（2）以O 为坐标原点可建立空间直角坐标系，根据空间向量法可求得平面1ADC 和平面ADB 的法向量的夹角的余弦值，根据所求二面角为钝二面角可得到最终结果. 【详解】（1）取AB 中点O ，连接OD ，1B O ，在1ABB △中，1AB B B =，160B BA ∠=︒，1ABB ∴△是等边三角形，又O 为AB 中点，1B O AB ∴⊥，又1B D AB ⊥，111B O B D B =I ，11,B O B D ⊂平面1B OD ，AB ∴⊥平面1B OD ，OD ⊂Q 平面1B OD ，AB OD ∴⊥，又OD AC ∥，AB AC ∴⊥， ∴ABC △为直角三角形.（2）以O 为坐标原点，建立如下图所示的空间直角坐标系：令12AB AC AA ===，则()1,2,0C -，()1,0,0A -，()0,1,0D ，()1,0,0B ，()10,0,3B ，()11,0,3BB ∴=-u u u v ，()0,2,0AC =u u u v ，()1,1,0AD =u u u v，()1111,2,3AC AC CC AC BB =+=+=-u u u u v u u u v u u u u v u u u v u u u v，设平面1ADC 的法向量为(),,x y z =m ，10230AD x y AC x y z ⎧⋅=+=⎪∴⎨⋅=++=⎪⎩u u u v u u u u v m m ，令1x =，则1y =-，3z =，()1,1,3∴=-m ，又平面ADB 的一个法向量为()0,0,1=n ，315cos ,5113∴<>==++m n ， Q 二面角1C AD B --为钝二面角，∴二面角1C AD B --的余弦值为15-.【点睛】本题考查立体几何中垂直关系的证明、空间向量法求解二面角的问题，涉及到线面垂直判定定理和性质定理的应用；证明立体几何中线线垂直关系的常用方法是通过证明线面垂直得到线线垂直的关系.19．[江西省宜春市上高二中2020届高三上学期第三次月考数学（理）试题]20．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]21．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【解析】22．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 如图，在四棱锥P ABCD-中，底面ABCD为矩形，平面PCD⊥平面ABCD,2AB=,1BC=，2PC PD==，E为PB中点．（1）求证：PD∥平面ACE；（2）求二面角E AC D--的余弦值；（3）在棱PD上是否存在点M，使得AM⊥BD？若存在，求PMPD的值；若不存在，说明理由．【解析】（1）设BD交AC于点F，连接EF. 因为底面ABCD是矩形，所以F为BD中点 . 又因为E为PB中点，所以EF∥PD.因为PD ⊄平面,ACE EF ⊂平面ACE ，所以PD ∥平面ACE.（2）取CD 的中点O ，连接PO ，FO .因为底面ABCD 为矩形，所以BC CD ⊥.因为PC PD =，O CD 为中点，所以,PO CD OF ⊥∥BC ，所以OF CD ⊥. 又因为平面PCD ⊥平面ABCD ，PO ⊂平面,PCD 平面PCD ∩平面ABCD =CD . 所以PO ⊥平面ABCD ，如图，建立空间直角坐标系O xyz -，则111(1,1,0)(0,1,0)(1,1,0),(0,0,1),(,,)222A C B P E -，,，设平面ACE 的法向量为(,,)x y z =m ，131(1,2,0),(,,)222AC AE =-=-u u u r u u u r ，所以20,2,0,131.00222x y x y AC z y x y z AE -+=⎧⎧=⎧⋅=⎪⇒⇒⎨⎨⎨=--++=⋅=⎩⎩⎪⎩u u u v u u u v m m 令1y =，则2,1x z ==-，所以2,11=-（，）m .平面ACD 的法向量为(0,0,1)OP =u u u r ，则6cos ,OP OP OP⋅<>==-⋅u u u r u u u r u u u r m m |m |. 如图可知二面角E AC D --为钝角，所以二面角E AC D --的余弦值为66-. （3）在棱PD 上存在点M ，使AM BD ⊥.设([0,1]),(,,)PM M x y z PD=∈λλ，则,01,0PM PD D =-u u u u r u u u r λ（，）.因为(,,1)(0,1,1)x y z -=--λ，所以(0,,1)M --λλ. (1,1,1),(1,2,0)AM BD =---=--u u u u r u u u r λλ.因为AM BD ⊥，所以0AM BD ⋅=u u u u r u u u r .所以12(1)0λ--=，解得1=[0,1]2∈λ. 所以在棱PD 上存在点M ，使AM BD ⊥，且12PM PD =。

2020年高考数学立体几何试题分类汇编理

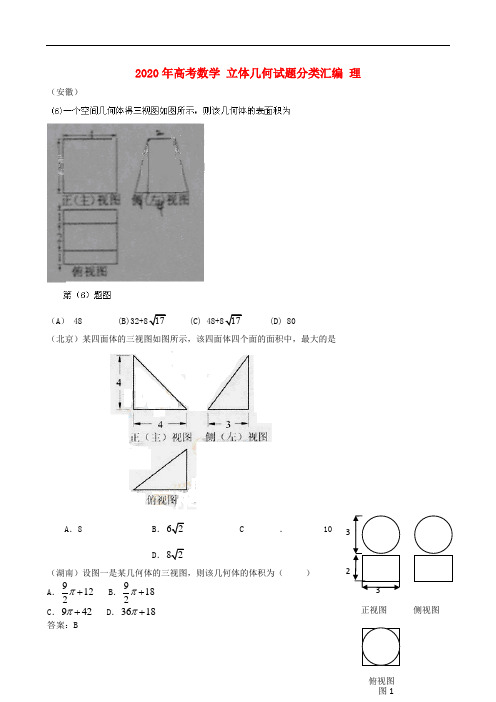
2020年高考数学立体几何试题分类汇编理（安徽）（A ） 48 (B)32+817 (C) 48+817 (D) 80（北京）某四面体的三视图如图所示，该四面体四个面的面积中，最大的是A ．8B ．62C．10D ．82（湖南）设图一是某几何体的三视图，则该几何体的体积为（）A ．9122π+B ．9182π+ C ．942π+ D ．3618π+答案：B3 正视图侧视图解析：有三视图可知该几何体是一个长方体和球构成的组合体，其体积3439+332=18322V ππ=⨯⨯+（）。

（广东）如图l —3．某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为A.63B.93C.123D.183（江西）已知321,,ααα是三个相互平行的平面,平面21,αα之间的距离为1d ,平面32,αα之间的距离为2d .直线l 与321,,ααα分别交于321,,P P P .那么”“3221P P P P =是”“21d d =的 ( ) A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件答案：C解析：平面321,,ααα平行，由图可以得知：如果平面距离相等，根据两个三角形全等可知3221P P P P = 如果3221P P P P =，同样是根据两个三角形全等可知21d d =（辽宁）如图，四棱锥S —ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是 A ．AC ⊥SB B ．AB ∥平面SCDC ．SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D ．AB 与SC 所成的角等于DC 与SA 所成的角（辽宁）已知球的直径SC =4，A ，B 是该球球面上的两点，AB =3，ο30=∠=∠BSC ASC ，则棱锥S —ABC的体积为 A ．33B ．32C ．3D ．1（全国2）已知直二面角l αβ--，点,A AC l α∈⊥,C 为垂足，,,B BD l D β∈⊥为垂足．若AB=2，AC=BD=1，则D 到平面ABC 的距离等于 (A)2 (B)3 (C)6 (D) 1 【思路点拨】本题关键是找出或做出点D 到平面ABC 的距离DE ，根据面面垂直的性质不难证明AC ⊥平面β，进而β⊥平面平面ABC,所以过D 作DE BC ⊥于E ，则DE 就是要求的距离。

高考数学立体几何多选题专项练习及答案

高考数学立体几何多选题专项练习及答案一、立体几何多选题1．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -的高为22222262213⎛⎫--⨯= ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.2．如图，在棱长为2的正方体ABCD A B C D ''''-中，M 为BC 边的中点，下列结论正确的有（）A ．AM 与DB ''所成角的余弦值为1010B ．过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C ．四面体A C BD ''的内切球的表面积为3π D ．正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动并且使MAC PAC ''∠=∠，那么点P 的轨迹是椭圆【答案】AB 【分析】构建空间直角坐标系，由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误；同样设(,,0)P x y 结合向量夹角的坐标表示，22221543y x y +=++⨯P 的轨迹知D 的正误；由立方体的截面为梯形，分别求,,,MN AD AM D N ''，进而得到梯形的高即可求面积，判断B 的正误；由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ，进而求内切球表面积，判断C 的正误.【详解】A ：构建如下图所示的空间直角坐标系：则有：(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D ''， ∴(1,2,0),(2,2,0)AM D B ''==-，10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯，故正确.B ：若N 为CC '的中点，连接MN ，则有//MN AD '，如下图示，∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面，而2,2,5MN AD AM D N ''====322， ∴梯形的面积为132932222S =⨯=，故正确. C ：如下图知：四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积，∴118848323V =-⨯⨯⨯=，而四面体的棱长都为22，有表面积为142222sin 8323S π=⨯⨯⨯⨯=，∴若其内切圆半径为r ，则有188333r ⨯⋅=，即33r =，所以内切球的表面积为2443r ππ=.故错误. D ：正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动且MAC PAC ''∠=∠，即P 的轨迹为面A B C D ''''截以AM 、AP 为母线，AC’为轴的圆锥体侧面所得曲线，如下图曲线GPK ，构建如下空间直角坐标系，232(0,0,2),(2),(0,22,0)22A M C '-，若(,,0)P x y ，则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-，∴15cos ||||512AM AC MAC AM AC '⋅'∠==='⨯222cos ||||43AP AC PAC AP AC x y '⋅'∠=='++⨯22215543x y =++⨯，整理得22(102)9216(0)y x y +-=>，即轨迹为双曲线的一支，故错误.故选：AB 【点睛】关键点点睛：应用向量的坐标表示求异面直线的夹角，并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹，综合立方体的性质求截面面积，分割几何体应用等体积法求内切球半径，进而求内切球的表面积.3．在正方体1111ABCD A B C D -中，M 、N 分别是棱AB 、1CC 的中点，1MB P 的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题正确命题的序号是（）A ．平面1MB P 1ND ⊥ B ．平面1MB P ⊥平面11ND AC ．1MB P 在底面ABCD 上的射影图形的面积为定值 D ．1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC 【分析】取N 与P 重合，结合勾股定理可判断A 选项的正误；利用面面垂直的判定定理可判断B 选项的正误；分点P 在棱1CC 、11C D 上运动两种情况讨论，利用三角形的面积公式可判断C 选项的正误；取点P 与点1C 重合，判断1MB P 在侧面11D C CD 上射影图形形状，可判断D 选项的正误. 【详解】对于A 选项，设正方体1111ABCD A B C D -的棱长为2，如下图所示：当点P 与点N 重合时，若1ND ⊥平面1MB P ，1B N ⊂平面1MB P ，则11ND B N ⊥，由勾股定理可得2211115D N C N C D =+=，同理可得15B N =，1122B D =，2221111B N D N B D ∴+≠，则1ND 与1B N 不垂直，假设不成立，A 选项错误；对于B 选项，取1BB 的中点E ，连接1A E 、EN ，在正方体1111ABCD A B C D -中，11//BB CC ，且E 、N 分别为1BB 、1CC 的中点，则11//B E C N 且11B E C N =，所以，四边形11B ENC 为平行四边形，则11//EN B C 且11EN B C =，1111//A D B C 且1111A D B C =，所以，11//A D EN 且11A D EN =，所以，四边形11A END 为平行四边形，所以，11//A E D N ，111A B BB =，1B E BM =，11190A B E B BM ∠=∠=，所以，111Rt A B E Rt B BM ≅△△，所以，111B A E BB M ∠=∠，所以，111111190A EB BB M A EB B A E ∠+∠=∠+∠=，190B FE ∴∠=，所以，11B M A E ⊥，11A D ⊥平面11AA B B ，1B M ⊂平面11AA B B ，111B M A D ∴⊥， 1111A D A E A =，11A D 、1A E ⊂平面11ND A ，1MB ∴⊥平面11ND A ，1MB ⊂平面1MB P ，所以，平面1MB P ⊥平面11ND A ，B 选项正确；对于C 选项，设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时，1MB P 在底面ABCD 上的射影为MBC △，此时，射影图形的面积为21224MBCa a S a =⋅=△；若点P 在棱11C D 上运动时，设点P 在底面ABCD 上的射影点为G ，则G CD ∈，且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ，则1MB P 在底面ABCD 内的射影为MBG △，且21224MBGa a S a =⋅⋅=△.综上所述，1MB P 在底面ABCD 内的射影图形的面积为定值，C 选项正确；对于D 选项，当点P 与1C 重合时，P 、1B 两点在平面11D C CD 上的射影重合，此时，1MB P 在侧面11D C CD 上的射影不构成三角形，D 选项错误. 故选：BC. 【点睛】方法点睛：证明面面垂直常用的方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可.4．如图，已知正方体1ABCD ABC D -的棱长为a ，E 是棱CD 上的动点.则下列结论中正确的有（）A ．11EB AD ⊥B ．二面角11E A B A --的大小为4π C ．三棱锥11A B D E -体积的最小值为313a D ．1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ，则易证1AD ⊥平面11A DCB ，1EB ⊂平面11A DCB ，则由线面垂直的性质定理可以判断选项A 正确；二面角11E A B A --的平面角为1DA A ∠，易知14DA A π∠=，则可判断选项B 正确；用等体积法，将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积，当点E 与D 重合时，三棱锥11E AB D -的体积最小，此时的值为316a ，则选项C 错误；易知平面11//D DCC 平面11A B BA ，而1D E ⊂平面11D DCC ，则根据面面平行的性质定理可得1//D E 平面11A B BA ，可判断选项D 正确. 【详解】选项A ，连接1A D 、1B C ，则由正方体1ABCD ABC D -可知，11A D AD ⊥，111A B AD ⊥，1111A D A B A =，则1AD ⊥平面11A DCB ，又因为1EB ⊂平面11A DCB ，所以11EB AD ⊥，选项A 正确；选项B ，因为11//DE A B ，则二面角11E A B A --即为二面角11D A B A --，由正方体1ABCD ABC D -可知，11A B ⊥平面1DA A ，则1DA A ∠为二面角11D A B A --的平面角，且14DA A π∠=，所以选项B 正确；选项C ，设点E 到平面11AB D 的距离为d ，则11111113A B D E E AB D AB D V V S d --==⋅，连接1C D 、1C B ，易证平面1//BDC 平面11AB D ，则在棱CD 上，点D 到平面11AB D 的距离最短，即点E 与D 重合时，三棱锥11A B D E -的体积最小，由正方体1ABCD ABC D -知11A B ⊥平面1ADD ，所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=，则选项C 错误；选项D ，由正方体1ABCD ABC D -知，平面11//CC D D 平面11A B BA ，且1D E ⊂平面11CC D D ，则由面面平行的性质定理可知1//D E 平面11A B BA ，则选项D 正确. 故选：ABD. 【点睛】关键点点睛：本题对于选项C 的判断中，利用等体积法求三棱锥的体积是解题的关键.5．正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 在侧面11CDD C 上运动，且满足1//B F 平面1A BE .以下命题正确的有（）A ．侧面11CDD C 上存在点F ，使得11B F CD ⊥ B ．直线1B F 与直线BC 所成角可能为30︒C ．平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D ．设正方体棱长为1，则过点E ，F ，A 5 【答案】AC 【分析】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，易证得平面1//B MN 平面1A BE ，可得点F 的运动轨迹为线段MN ．取MN 的中点F ，根据等腰三角形的性质得1B F MN ⊥，即有11B F CD ⊥，A 正确；当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，可判断B 错误；根据平面1//B MN 平面1A BE ，11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，计算可知C 正确；【详解】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，则易证得11//B N A E ，1//MN A B ，从而平面1//B MN 平面1A BE ，所以点F 的运动轨迹为线段MN ．取MN 的中点F ，因为1B MN △是等腰三角形，所以1B F MN ⊥，又因为1//MN CD ，所以11B F CD ⊥，故A 正确；设正方体的棱长为a ，当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，此时11tan C B F ∠=1tan 3023︒<=，所以B 错误；平面1//B MN 平面1A BE ，取F 为MN 的中点，则1MN C F ⊥，1MN B F ⊥，∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，11111tan B C B FC C F∠==22C 正确；因为当F 为1C E 与MN 的交点时，截面为菱形1AGC E （G 为1BB 的交点），面积为62D 错误.故选：AC.【点睛】本题主要考查线面角，二面角，截面面积的求解，空间几何中的轨迹问题，意在考查学生的直观想象能力和数学运算能力，综合性较强，属于较难题．6．如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且2EF =.则下列结论正确的是（）A ．三棱锥A BEF -的体积为定值B ．当E 向1D 运动时，二面角A EF B --逐渐变小C ．EF 在平面11ABB A 内的射影长为12D ．当E 与1D 重合时，异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图，研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形，11122122BEF S EF BB ∆∴=⋅=⨯⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以，AO 是点A 到平面11BDD B 的距离，即22AO =11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯=A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ，连接11,AD AB ，由正方体性质知11AD AB =,M 是11B D 中点，AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角，在直角三角形1AA M 中，12tan 2MAA ∠=为定值. 选项C:如图，作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中，221cos 45222FT EF =⨯=⨯= 12HG FT ∴==选项D:当E 与1D 重合时，F 与M 重合，连接AC 与BD 交于点R ，连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中，22111132,2AD D R MB BB M B ===+=22AR = 由余弦定理得13cos 6AD R ∠= 故选：AC 【点睛】本题考查空间几何体性质问题.求解思路：关键是弄清(1)点的变化，点与点的重合及点的位置变化；(2)线的变化，应注意其位置关系的变化；(3)长度、角度等几何度量的变化．求空间几何体体积的思路：若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，求三棱锥的体积常用等体积转换法；若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解.7．M ，N 分别为菱形ABCD 的边BC ，CD 的中点，将菱形沿对角线AC 折起，使点D 不在平面ABC 内，则在翻折过程中，下列结论正确的有（）A ．MN ∥平面ABDB ．异面直线AC 与MN 所成的角为定值C ．在二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径先变小后变大D ．若存在某个位置，使得直线AD 与直线BC 垂直，则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ；利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ；借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ，N 分别为菱形ABCD 的边BC ，CD 的中点，所以MN 为BCD ∆的中位线，所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ，所以MN ∥平面ABD ,故选项A 正确；对于选项B ：取AC 的中点O ，连接,DO BO ,作图如下：则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知，AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90，故选项B 正确；对于选项C:借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，球心离开平面ABC ，但是球心在底面的投影仍然是ABC ∆外接圆圆心，故二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径不可能先变小后变大，故选项C 错误；对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角，H 在线段BC 上；若ABC ∠为直角，H 与B 重合；若ABC ∠为钝角，H 在线段BC 的延长线上；若存在某个位置，使得直线AD 与直线BC 垂直，因为AH BC ⊥，所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角，H 与B 重合，所以CB BD ⊥,在CBD ∆中，因为CB CD =, 所以CB BD ⊥不可能成立，即ABC ∠为直角不可能成立；若ABC ∠为钝角，H 在线段BC 的延长线上，则在原平面图菱形ABCD 中，DCB ∠为锐角，由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小，，所以DCB ∠为锐角，CB HD ⊥，故点H 在线段BC 与H 在线段BC 的延长线上矛盾，因此ABC ∠不可能为钝角；综上可知，ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确;故选：ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题；考查空间想象能力和逻辑推理能力；借助极限状态和反证法思想的运用是求解本题的关键；属于综合型强、难度大型试题.8．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ，连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=，连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=， E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴=== N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点，点Q 是线段AD 靠近点D 的三等分点，点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '，做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=，所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体从而平面1D MN 将正方体分成两部分体积比为2∶1.故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.9．如图，正三棱柱11ABC A B C -中，11BC AB ⊥、点D 为AC 中点，点E 为四边形11BCC B 内（包含边界）的动点则以下结论正确的是（）A ．()1112DA A A B A BC =-+ B ．若//DE 平面11ABB A ，则动点E 的轨迹的长度等于22AC C ．异面直线AD 与1BC 6D ．若点E 到平面11ACC A 3EB ，则动点E 的轨迹为抛物线的一部分【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解，逐项判断，进而可得到本题答案. 【详解】解析：对于选项A ，()1112AD A A B A BC =-+，选项A 错误；对于选项B ，过点D 作1AA 的平行线交11A C 于点1D ．以D 为坐标原点，1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz ．设棱柱底面边长为a ，侧棱长为b ，则002a A ⎛⎫⎪⎝⎭,,，3002B a ⎛⎫ ⎪ ⎪⎝⎭,,，130B a b ⎛⎫ ⎪ ⎪⎝⎭,,，102a C b ⎛⎫- ⎪⎝⎭,,，所以1322a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,，1322a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,． ∵11BC AB ⊥，∴110BC AB ⋅=，即222302a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭，解得2b a =．因为//DE 平面11ABB A ，则动点E 的轨迹的长度等于122BB AC =．选项B 正确．对于选项C ，在选项A 的基础上，002a A ⎛⎫⎪⎝⎭,,，3002B a ⎛⎫ ⎪ ⎪⎝⎭,,，()0,0,0D ，12022a C a ⎛⎫- ⎪ ⎪⎝⎭,,，所以002a DA ⎛⎫= ⎪⎝⎭,,，13222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭,-,，因为211162cos ,6||||622a BC DA BC DA BC DA a a ⎛⎫- ⎪⋅⎝⎭<>===-，所以异面直线1,BC DA 所成角的余弦值为6，选项C 正确．对于选项D ，设点E 在底面ABC 的射影为1E ，作1E F 垂直于AC ，垂足为F ，若点E 到平面11ACC A 的距离等于32EB ，即有31E F EB =，又因为在1CE F ∆中，311E F E C =，得1EB E C =，其中1E C 等于点E 到直线1CC 的距离，故点E 满足抛物线的定义，另外点E 为四边形11BCC B 内（包含边界）的动点，所以动点E 的轨迹为抛物线的一部分,故D 正确.故选：BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题，其中涉及到抛物线定义的应用.10．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（）A ．11A C ⊥平面11BB D D B ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2 D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ．【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥，由于四边形1111D C B A 为正方形，则1111AC B D ⊥， 1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ， 1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥，1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角，且111112tan 2C D C BD BC ∠==，故C 错误；对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =，则221cos ,21DA mDA m DA m y z ⋅<>===⋅++， 1122111cos ,221CB m z CB m CB m y z ⋅+<>===⋅⋅++，整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-12z =-由已知可得3z ≤，所以，12z =-+22y =±因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确.故选：ABD.【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．。

2023年新高考数学大一轮复习专题23 立体几何中的压轴小题(原卷版)

专题23 立体几何中的压轴小题【题型归纳目录】题型一：球与截面面积问题题型二：体积、面积、周长、角度、距离定值问题题型三：体积、面积、周长、距离最值与范围问题题型四：立体几何中的交线问题题型五：空间线段以及线段之和最值问题题型六：空间角问题题型七：立体几何装液体问题【典例例题】题型一：球与截面面积问题例1．（2022·河南安阳·模拟预测（文））已知球O 的体积为125π6，高为1的圆锥内接于球O ，经过圆锥顶点的平面α截球O 和圆锥所得的截面面积分别为12,S S ，若125π8S =，则2S =（）A．2 B C D ．例2．（2022·广西·南宁二中高三阶段练习（理））已知正四棱柱1111ABCD A B C D -中，122CC AB ==，E 为1CC 的中点，P 为棱1AA 上的动点，平面α过B ，E ，P 三点，有如下四个命题： ①平面α⊥平面11A B E ；①平面α与正四棱柱表面的交线围成的图形一定是四边形； ①当P 与A 重合时，α截此四棱柱的外接球所得的截面面积为11π8； ①存在点P ，使得AD 与平面α所成角的大小为π3．则正确的命题个数为（）． A ．1 B ．2 C ．3 D ．4例3．（2022·四川资阳·高二期末（理））如图，矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直，2BD =，1DE =，点P 在线段EF 上．给出下列命题：①存在点P ，使得直线//DP 平面ACF ； ①存在点P ，使得直线DP ⊥平面ACF ；①直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦；①三棱锥A CDE -的外接球被平面ACF 所截得的截面面积是9π8．其中所有真命题的序号（） A ．①① B ．①①C ．①①①D ．①①①例4．（2022·全国·高三专题练习）如图所示，圆锥的轴截面PAB △是以P 为直角顶点的等腰直角三角形，2PA =，C 为PA 中点．若底面O 所在平面上有一个动点M ，且始终保持0MA MP ⋅=，过点O 作PM 的垂线，垂足为H ．当点M 运动时，①点H 在空间形成的轨迹为圆 ①三棱锥O HBC -的体积最大值为112①AH HO +的最大值为2①BH 与平面PAB 上述结论中正确的序号为（）． A ．①① B ．①①C ．①①①D ．①①①例5．（2022·安徽省舒城中学一模（理））已知正三棱锥A BCD -的高为3，侧棱AB 与底面BCD 所成的角为3π，E 为棱BD 上一点，且12BE =，过点E 作正三棱锥A BCD -的外接球的截面，则截面面积S 的最小值为（）A ．54π B ．34π C ．4π D ．4π例6．（2022·全国·高三专题练习）已知三棱锥P ABC -的各个顶点都在球O 的表面上，PA ⊥底面ABC ，AB AC ⊥，6AB =，8AC =，D 是线段AB 上一点，且2AD DB =．过点D 作球O 的截面，若所得截面圆面积的最大值与最小值之差为25π，则球O 的表面积为（） A ．128π B ．132π C ．144π D ．156π例7．（2022·全国·高三专题练习）已知直四棱柱1111ABCD A B C D -，其底面ABCD 是平行四边形，外接球体积为36π，若1AC BD ⊥，则其外接球被平面11AB D 截得图形面积的最小值为（） A ．8π B ．24310π C ．8110π D ．6π例8．（2022·全国·高三专题练习（文））已知正三棱锥A BCD -的外接球是球O ，正三棱锥底边3BC =，侧棱AB =点E 在线段BD 上，且BE DE =，过点E 作球O 的截面，则所得截面圆面积的取值范围是（） A ．9,34ππ⎡⎤⎢⎥⎣⎦B ．[]2,3ππC ．11,44ππ⎡⎤⎢⎥⎣⎦ D ．9,44ππ⎡⎤⎢⎥⎣⎦例9．（2022·浙江省江山中学模拟预测）如图，在单位正方体1111ABCD A B C D -中，点P 是线段1AD 上的动点，给出以下四个命题：①异面直线1PC 与直线1B C 所成角的大小为定值； ①二面角1P BC D --的大小为定值；①若Q 是对角线1AC 上一点，则PQ QC +长度的最小值为43； ①若R 是线段BD 上一动点，则直线PR 与直线1A C 不可能平行．其中真命题有（） A ．1个 B ．2个C ．3个D ．4个例10．（2022·北京·人大附中模拟预测）已知正方体1111,ABCD A B C D O -为对角线1AC 上一点（不与点1,A C 重合），过点O 作垂直于直线1AC 的平面α，平面α与正方体表面相交形成的多边形记为M ，下列结论不正确的是（）A ．M 只可能为三角形或六边形B ．平面ABCD 与平面α的夹角为定值C ．当且仅当O 为对角线1AC 中点时，M 的周长最大D ．当且仅当O 为对角线1AC 中点时，M 的面积最大例11．（2022·河南省实验中学高一期中）如图，在正方体1111ABCD A B C D -中，2AB =，M ，N 分别为11A D ，11B C 的中点，E ，F 分别为棱AB ，CD 上的动点，则三棱锥M NEF -的体积（）A ．存在最大值，最大值为83B ．存在最小值，最小值为23C ．为定值43D ．不确定，与E ，F 的位置有关例12．（2022·山西运城·模拟预测（文））如图，正方体1111ABCD A B C D -的棱长为1，线段1CD 上有两个动点E ，F ，且12EF =，点P ，Q 分别为111A B BB ，的中点，G 在侧面11CDD C 上运动，且满足1B G ∥平面1CD PQ ，以下命题错误的是（）A ．1AB EF ⊥B ．多面体1AEFB 的体积为定值C ．侧面11CDD C 上存在点G ，使得1B G CD ⊥ D ．直线1B G 与直线BC 所成的角可能为6π例13．（2022·全国·高三专题练习）如图所示，在正方体1111ABCD A B C D -中，过对角线1BD 的一个平面交1AA 于E ，交1CC 于F ，给出下面几个命题：①四边形1BFD E 一定是平行四边形； ①四边形1BFD E 有可能是正方形； ①平面1BFD E 有可能垂直于平面1BB D ；①设1D F 与DC 的延长线交于M ，1D E 与DA 的延长线交于N ，则M ､N ､B 三点共线； ①四棱锥11B BFD E -的体积为定值．以上命题中真命题的个数为（） A ．2 B ．3C ．4D ．5例14．（2022·陕西·西北工业大学附属中学模拟预测（理））如图，棱长为1的正方体1111ABCD A B C D -中，点P 为线段1A C 上的动点，点,M N 分别为线段111,AC CC 的中点，则下列说法错误．．的是（）A ．11A P AB ⊥ B ．三棱锥1M B NP -的体积为定值C ．[]160,120APD ∠∈︒︒ D ．1AP D P +的最小值为23例15．（2022·全国·高三专题练习）如图，在正方体1111ABCD A B C D -中，点P 为线段11A C 上的动点（点P 与1A ，1C 不重合），则下列说法不正确的是（）A ．BD CP ⊥B ．三棱锥C BPD -的体积为定值C ．过P ，C ，1D 三点作正方体的截面，截面图形为三角形或梯形 D ．DP 与平面1111D C B A 所成角的正弦值最大为13例16．（2022·全国·高三专题练习）已知正方体1111ABCD A B C D -内切球的表面积为π，P 是空间中任意一点： ①若点P 在线段1AD 上运动，则始终有11C P CB ⊥； ①若M 是棱11C D 中点，则直线AM 与1CC 是相交直线； ①若点P 在线段1AD 上运动，三棱锥1D BPC -体积为定值；①E 为AD 中点，过点1B ，且与平面1A BE 以上命题为真命题的个数为（） A ．2 B ．3C ．4D ．5例17．（2022·江西南昌·三模（理））已知长方体1111ABCD A B C D -中，2AB =，BC =13AA =，P 为矩形1111D C B A 内一动点，设二面角P AD C --为α，直线PB 与平面ABCD 所成的角为β，若αβ=，则三棱锥11P A BC -体积的最小值是（） AB．1 CD．2例18．（2022·浙江·高三阶段练习）如图，在四棱锥Q EFGH -中，底面是边长为4QE QF QG QH ====，M 为QG 的中点．过EM 作截面将此四棱锥分成上､下两部分，记上､下两部分的体积分别为1V ，2V ，则12V V 的最小值为（）A ．12B ．13C ．14D ．15例19．（2022·四川省内江市第六中学高二期中（理））已知四面体ABCD,M N 分别为棱,AD BC 的中点，F 为棱AB 上异于,A B 的动点．有下列结论： ①线段MN 的长度为1；①点C 到面MFN的距离范围为⎛ ⎝⎭； ①FMN1；①MFN ∠的余弦值的取值范围为⎡⎢⎣⎭．其中正确结论的个数为（） A ．1 B ．2 C ．3 D ．4例20．（2022·河南省实验中学高一期中）如图，在正方体1111ABCD A B C D -中，2AB =，M ，N 分别为11A D ，11B C 的中点，E ，F 分别为棱AB ，CD 上的动点，则三棱锥M NEF -的体积（）A ．存在最大值，最大值为83B ．存在最小值，最小值为23C ．为定值43D ．不确定，与E ，F 的位置有关例21．（2022·全国·高三专题练习（理），该几何体的表面积最小值是1S ，我们在绘画该表面积最小的几何体的直观图时所画的底面积大小是2S ，则1S 和2S 的值分别是（）A ．3B ．4；12C ．4D ．3；12例22．（2022·全国·高三专题练习）已知棱长为2的正方体1111ABCD A B C D -，棱1DD 中点为M ，动点P 、Q 、R 分别满足：点P 到异面直线BC 、11C D 的距离相等，点Q 使得异面直线1A Q 、BC 点R 使得134A RB π∠=．当动点P 、Q 两点恰好在正方体侧面11CDD C 内时，则多面体1RMPC Q 体积最小值为（）A B C D例23．（2022·全国·高三专题练习）在棱长为2的正方体1111ABCD A B C D -中，点M 是对角线1AC 上的点（点M 与1A C 、不重合），有以下四个结论：①存在点M ，使得平面1A DM ⊥平面1BC D ； ①存在点M ，使得//DM 平面11B D C ；①若1A DM 的周长为L ，则L①若1A DM 的面积为S ，则S ∈⎝．则正确的结论为（） A ．①① B ．①①①C ．①①①D ．①①例24．（2022·河南·模拟预测（文））已知四面体ABCD ，M 、N 分别为棱AD 、BC 的中点，F 为棱AB 上异于A 、B 的动点．有下列结论： ①线段MN 的长度为1；①存在点F ，满足CD ⊥平面FMN ；①MFN ∠的余弦值的取值范围为⎡⎢⎣⎭； ①FMN1．其中所有正确结论的编号为（） A ．①① B ．①① C ．①①① D ．①①①例25．（2022·全国·高三专题练习）在棱长为1的正方体1111ABCD A B C D -中，P 是线段1BC 上的点，过1A 的平面α与直线PD 垂直，当P 在线段1BC 上运动时，平面α截正方体1111ABCD A B C D -所得的截面面积的最小值是（）A ．1B ．54C D例26．（2022·四川省成都市新都一中高二期中（文））如图，正方形EFGH 的中心为正方形ABCD 的中心，AB =截去如图所示的阴影部分后，翻折得到正四棱锥P EFGH -（A ，B ，C ，D 四点重合于点P ），则此四棱锥的体积的最大值为（）A B C ．43D例27．（2022·青海·大通回族土族自治县教学研究室二模（理））在棱长为3的正方体1111ABCD A B C D -中，P 为1ACD △内一点，若1PB D 1DD AP 体积的最大值为（）A BC D例28．（2022·四川省宜宾市第四中学校三模（理））函数()sin 2sin 2π0e 2x x f x x ⎛⎫=<< ⎪⎝⎭，设球O 的半径为()cos 4f x x π⎛⎫- ⎪⎝⎭，则（）A ．球O 的表面积随x 增大而增大B ．球O 的体积随x 增大而减小C ．球O 的表面积最小值为24e π D ．球O 的体积最大值为343e π题型四：立体几何中的交线问题例29．（2022·全国·高三专题练习（理））已知正方体ABCD A B C D ''''-的棱长为4，E ，F 分别为BB '，C D ''的中点，点P 在平面ABB A ''中，=PF N 在线段AE 上，则下列结论正确的个数是（）①点P 的轨迹长度为2π；①线段FP 的轨迹与平面A B CD ''的交线为圆弧；①NP ；①过A 、E 、F 作正方体的截面，则该截面的周长为103A ．4 B ．3C ．2D ．1例30．（2022·全国·高三专题练习）在正四棱锥P ABCD -中，已知2PA AB ==，O 为底面ABCD 的中心，以点O PCD 的交线长度为（）A B C D例31．（2022·全国·高三专题练习）已知正四面体的中心与球心O 重合，正四面体的棱长为A．4π B ．C ．D ．12π例32．（2022·四川成都·模拟预测（理））如图，①ABC 为等腰直角三角形，斜边上的中线AD ＝3，E 为线段BD 中点，将①ABC 沿AD 折成大小为2π的二面角，连接BC ，形成四面体C －ABD ，若P 是该四面体表面或内部一点，则下列说法错误的是（）A ．点P 落在三棱锥E －ABC 内部的概率为12B ．若直线PE 与平面ABC 没有交点，则点P 的轨迹与平面ADCC ．若点P 在平面ACD 上，且满足P A ＝2PD ，则点P 的轨迹长度为23π D ．若点P 在平面ACD 上，且满足P A ＝2PD ，则线段PB 长度为定值例33．（2022·江苏徐州·高二期中）如图1，在正方形ABCD 中，点E 为线段BC 上的动点（不含端点），将ABE △沿AE 翻折，使得二面角B AE D --为直二面角，得到图2所示的四棱锥B AECD -，点F 为线段BD 上的动点（不含端点），则在四棱锥B AECD -中，下列说法正确的是（）A ．B ､E ､C ､F 四点一定共面 B ．存在点F ，使得CF ∥平面BAEC ．侧面BEC 与侧面BAD 的交线与直线AD 相交 D ．三棱锥B ADC -的体积为定值例34．（2022·河南·模拟预测（理））已知正方体1111ABCD A B C D -的棱长是2，E ，F 分别是棱11B C 和1CC 的中点，点P 在正方形11BCC B （包括边界）内，当//AP 平面1A EF 时，AP 长度的最大值为a ．以A 为球心，a 为半径的球面与底面1111D C B A 的交线长为（）A ．2πB ．πC D例35．（2022·湖南·临澧县第一中学高二阶段练习）已知正四棱柱1111ABCD A B C D -中，122CC AB ==，E 为1CC 的中点，P 为棱1AA 上的动点，平面α过B ，E ，P 三点，则（）A ．平面α⊥平面11AB EB ．平面α与正四棱柱表面的交线围成的图形一定是四边形C ．当P 与A 重合时，α截此四棱柱的外接球所得的截面面积为11π8D ．存在点P ，使得AD 与平面α所成角的大小为π3例36．（2022·江苏·南京师大附中模拟预测）如图，圆柱的底面半径和高均为1，线段AB 是圆柱下底面的直径，点O 是下底面的圆心．线段EF 是圆柱的一条母线，且EO AB ⊥．已知平面α经过A ，B ，F 三点，将平面α截这个圆柱所得到的较小部分称为“马蹄体”．记平面α与圆柱侧面的交线为曲线C ．则（）A ．曲线C 是椭圆的一部分B ．曲线C 是抛物线的一部分C ．二面角F AB E --的大小为4πD ．马蹄体的体积为V 满足134V π<<例37．（2022·江苏·南京外国语学校模拟预测）如图，正方形ABCD -A 1B 1C 1D 1边长为1，P 是1A D 上的一个动点，下列结论中正确的是（）A ．BPB ．PA PC + C ．当P 在直线1AD 上运动时，三棱锥1A B PC - 的体积不变D ．以点B 1AB C例38．（2022·全国·高三专题练习）已知正四棱柱1111ABCD A B C D -的底面边为1，侧棱长为a ，M 是1CC 的中点，则（） A ．任意0a >，1A M BD ⊥B ．存在0a >，直线11AC 与直线BM 相交C ．平面1A BM 与底面1111D C B AD ．当2a =时，三棱锥11B A BM -外接球表面积为3π题型五：空间线段以及线段之和最值问题例39．（2022·山东·高一阶段练习）已知三棱锥P ABC -三条侧棱PA ，PB ，PC 两两互相垂直，且6PA PB PC ===，M ､N 分别为该三棱锥的内切球和外接球上的动点，则线段MN 的长度的最小值为（）A ．3B ．6C ．6-D ．例40．（2022·全国·高三专题练习）已知正三棱锥S ABC -外接球表面积为3π，SA <点M ，N 分别是线段AB ，AC 的中点，点P ，Q 分别是线段SN 和平面SCM 上的动点，则AP PQ +的最小值为（）A B C D例41．（2022·全国·高三专题练习）在棱长为3的正方体1111ABCD A B C D -中，点E 满足112A E EB =，点F 在平面1BC D 内，则1A F EF +的最小值为（）A B ．6 C D ．7例42．（2022·全国·高一专题练习）如图所示，在直三棱柱111ABC A B C -中，11AA =，AB BC ==1cos 3ABC ∠=，P 是1A B 上的一动点，则1AP PC +的最小值为（）A B C ．1D ．3例43．（2022·湖北·高一阶段练习）已知正方体1111ABCD A B C D -的棱长为2，E 为线段1AA 的中点，AP AB AD λμ=+，其中,[0,1]λμ∈，则下列选项正确的是（）A ．12μ=时，11A P ED ⊥ B ．14λ=时，1B P PD +C ．1λμ+=时，直线1A P 与面11BDE D ．1λμ+=时，正方体被平面1PAD 截的图形最大面积是例44．（2022·湖南岳阳·三模）如图，在直棱柱1111ABCD A B C D -中，各棱长均为2，π3ABC ∠=，则下列说法正确的是（）A ．三棱锥1A ABC -B ．异面直线1AB 与1BCC ．当点M 在棱1BB 上运动时，1MD MA +最小值为D ．N 是ABCD 所在平面上一动点，若N 到直线1AA 与BC 的距离相等，则N 的轨迹为抛物线例45．（2022·全国·高三专题练习）在棱长为1的正方体1111ABCD A B C D -中，点P 满足1DP DD DA λμ=+，[0,1]λ∈，[0,1]μ∈，则以下说法正确的是（）A ．当λμ=时，//BP 平面11CB D B ．当12μ=时，存在唯一点P 使得DP 与直线1CB 的夹角为3πC ．当1λμ+=时，CPD ．当1λμ+=时，CP 与平面11BCC B 所成的角不可能为3π例46．（2022·全国·模拟预测）如图，点M 是棱长为1的正方体1111ABCD A B C D -中的侧面11ADD A 上的一个动点（包含边界），则下列结论正确的是（）A ．存在无数个点M 满足1CM AD ⊥B ．当点M 在棱1DD 上运动时，1||MA MB +1C ．在线段1AD 上存在点M ，使异面直线1B M 与CD 所成的角是30 D ．满足1||2MD MD =的点M 的轨迹是一段圆弧例47．（2022·浙江绍兴·模拟预测）如图，斜三棱柱111ABC A B C -中，底面ABC 是正三角形，,,E F G 分别是侧棱111,,AA BB CC 上的点，且AE CG BF >>，设直线,CA CB 与平面EFG 所成的角分别为,αβ，平面EFG 与底面ABC 所成的锐二面角为θ，则（）A ．sin sin sin ,cos cos cos θαβθαβ<+≤+B ．sin sin sin ,cos cos cos θαβθαβ≥+<+C ．sin sin sin ,cos cos cos θαβθαβ<+>+D ．sin sin sin ,cos cos cos θαβθαβ≥+≥+例48．（2022·浙江·高三专题练习）在三棱锥P ABC -中，顶点P 在底面的射影为ABC 的垂心O （O 在ABC 内部），且PO 中点为M ，过AM 作平行于BC 的截面α，过BM 作平行于AC 的截面β，记α，β与底面ABC 所成的锐二面角分别为1θ，2θ，若PAM PBM θ∠=∠=，则下列说法错误的是（） A ．若12θθ=，则AC BC = B ．若12θθ≠，则121tan tan 2θθ⋅=C ．θ可能值为6πD ．当θ取值最大时，12θθ=例49．（2022·全国·高三专题练习）在三棱台111BCD B C D -中，1CC ⊥底面BCD ，BC CD ⊥，12BC CD CC ===，111B C =．若A 是BD 中点，点P 在侧面11BDD B 内，则直线1DC 与AP 夹角的正弦值的最小值是（）A ．16B C D例50．（2022·浙江台州·高三期末）已知在正方体1111ABCD A B C D -中，点E 为棱BC 的中点，直线l 在平面1111D C B A 内．若二面角A l E --的平面角为θ，则cos θ的最小值为（）A B ．1121C D ．35例51．（2021·全国·高二课时练习）已知正方体ABCD A B C D ''''-的棱长为3，E 为棱AB 上的靠近点B 的三等分点，点P 在侧面CC D D ''上运动，当平面B EP '与平面ABCD 和平面CC D D ''所成的角相等时，则D P '的最小值为（）A B C D例52．（2021·浙江·瑞安中学模拟预测）已知点P 是正方体ABCD A B C D ''''-上底面A B C D ''''上的一个动点，记面ADP 与面BCP 所成的锐二面角为α，面ABP 与面CDP 所成的锐二面角为β，若αβ>，则下列叙述正确的是（） A ．APC BPD ∠>∠B ．APC BPD ∠<∠C ．{}{}max ,max ,APD BPC APB CPD ∠∠>∠∠ D ．{}{}min ,min ,APD BPC APB CPD ∠∠>∠∠例53．（2022·全国·高三专题练习）如图，将矩形纸片ABCD 折起一角落()EAF △得到EA F '△，记二面角A EF D '--的大小为π04θθ⎛⎫<< ⎪⎝⎭，直线A E '，A F '与平面BCD 所成角分别为α，β，则（）．A ．αβθ+>B ．αβθ+<C ．π2αβ+> D ．2αβθ+>例54．（2022·全国·高三专题练习）如图，在正方体ABCD EFGH -中，P 在棱BC 上，BP x =，平行于BD 的直线l 在正方形EFGH 内，点E 到直线l 的距离记为d ，记二面角为A l P --为θ，已知初始状态下0x =，0d =，则（）A ．当x 增大时，θ先增大后减小B ．当x 增大时，θ先减小后增大C ．当d 增大时，θ先增大后减小D ．当d 增大时，θ先减小后增大题型七：立体几何装液体问题例55．（2022·全国·高二期中）如图，水平桌面上放置一个棱长为4的正方体水槽，水面高度恰为正方体棱长的一半，在该正方体侧面11CDD C 上有一个小孔E ，E 点到CD 的距离为3，若该正方体水槽绕CD 倾斜（CD 始终在桌面上），则当水恰好流出时，侧面11CDD C 与桌面所成角的正切值为（）A B ．12C D ．2例56．（2022·全国·高一课时练习）一个封闭的正三棱柱容器，高为3，内装水若干（如图甲，底面处于水平状态），将容器放倒（如图乙，一个侧面处于水平状态），这时水面与各棱交点11,,,E F F E 分别为所在棱的中点，则图甲中水面的高度为（）A ．32B ．74C ．2D ．94例57．（2022·湖北宜昌·一模（文））已知一个放置在水平桌面上的密闭直三棱柱111ABC A B C -容器，如图1，ABC ∆为正三角形，2AB =，13AA =，里面装有体积为BC 旋转至图2．在旋转过程中，以下命题中正确的个数是（）①液面刚好同时经过A ，1B ，1C 三点；①当平面ABC 1； ①当液面与水平桌面的距离为32时，AB 与液面所成角的正弦值为34．A ．0B ．1C ．2D ．3例58．（2022·全国·高一课时练习）一个密闭且透明的正方体容器中装有部分液体，已知该正方体的棱长为1，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体体积的取值范围为（）A ．15,66⎡⎤⎢⎥⎣⎦B ．15,66⎛⎫ ⎪⎝⎭C ．12,63⎡⎤⎢⎥⎣⎦D ．12,63⎛⎫ ⎪⎝⎭例59．（2022·全国·高一课时练习）一个密闭且透明的正方体容器中装有部分液体，已知该正方体的棱长为2，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体的体积的取值范围为（） A ．202,3⎛⎫ ⎪⎝⎭B ．417,33⎛⎫ ⎪⎝⎭C ．172,3⎛⎫ ⎪⎝⎭D ．420,33⎛⎫ ⎪⎝⎭例60．（2022·重庆·高二期末（文））已知某圆柱形容器的轴截面是边长为2的正方形，容器中装满液体，现向此容器中放入一个实心小球，使得小球完全被液体淹没，则此时容器中所余液体的最小容量为（） A ．π3B ．2π3C ．πD ．4π3例61．（2022·福建厦门·高一期末）如图（1）平行六面体容器1111ABCD A B C D -盛有高度为h 的水，12AB AD AA ===，1A AB ∠=160A AD BAD ∠=∠=︒．固定容器底而一边BC 于地面上，将容器倾斜到图（2）时，水面恰好过A ，1B ，1C ，D 四点，则h 的值为（）A B C D 例62．（2022·福建·厦门市湖滨中学高一期中）如图，透明塑料制成的长方体容器1111ABCD A B C D -内灌进一些水，固定容器一边AB 于地面上，再将容器倾斜，随着倾斜度的不同，有下面几个结论，其中正确的命题是（）A ．水面EFGH 所在四边形的面积为定值B ．随着容器倾斜度的不同，11AC 始终与水面所在平面平行C ．没有水的部分有时呈棱柱形有时呈棱锥形D ．当容器倾斜如图（3）所示时，AE AH ⋅为定值例63．（2022·山东·高三专题练习）一个透明封闭的正四面体容器中，恰好盛有该容器一半容积的水，任意转动这个正四面体，则水面在容器中的形状可能是：①正三角形①直角三形①正方形①梯形，其中正确的个数有（）A ．1个B ．2个C ．3个D ．4个。

2020年高考数学试题分项版—立体几何(解析版)

2020年高考数学试题分项版——立体几何（解析版）一、选择题1.(2020·全国Ⅰ理，3)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析设正四棱锥的底面正方形的边长为a ，高为h ，侧面三角形底边上的高(斜高)为h ′，则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．2．(2020·全国Ⅰ理，10)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆，若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a .由πr 2＝4π，得r ＝2，则33a ＝2，a ＝23，OO 1＝a ＝2 3. 在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.3．(2020·全国Ⅱ理，7)如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为( )A ．EB ．FC ．GD ．H 答案 A解析由三视图还原几何体，如图所示，由图可知，所求端点在侧视图中对应的点为E .4．(2020·全国Ⅱ理，10)已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为( ) A. 3 B.32 C ．1 D.32答案 C 解析如图所示，过球心O 作OO 1⊥平面ABC ，则O 1为等边三角形ABC 的外心．设△ABC 的边长为a ，则34a 2＝934，解得a ＝3， ∴O 1A ＝23×32×3＝ 3.设球O 的半径为r ，则由4πr 2＝16π，得r ＝2，即OA ＝2. 在Rt △OO 1A 中，OO 1＝OA 2－O 1A 2＝1，即O 到平面ABC 的距离为1.5．(2020·全国Ⅲ理，8)下图为某几何体的三视图，则该几何体的表面积是( )A ．6＋4 2B ．4＋4 2C ．6＋2 3D ．4＋2 3答案 C解析如图，该几何体为三棱锥，且其中有三个面是腰长为2的等腰直角三角形，第四个面是边长为22的等边三角形，所以该几何体的表面积为3×12×2×2＋12×22×22×32＝6＋2 3.6.(2020·新高考全国Ⅰ，4)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为( )A ．20°B ．40°C ．50°D ．90° 答案 B解析如图所示，⊙O 为赤道平面，⊙O 1为A 点处的日晷面所在的平面，由点A处的纬度为北纬40°可知∠OAO1＝40°，又点A处的水平面与OA垂直，晷针AC与⊙O1所在的面垂直，则晷针AC与水平面所成角为40°.7.(2020·新高考全国Ⅱ，4)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为()A．20°B．40°C．50°D．90°答案 B解析如图所示，⊙O为赤道平面，⊙O1为A点处的日晷面所在的平面，由点A处的纬度为北纬40°可知∠OAO1＝40°，又点A处的水平面与OA垂直，晷针AC与⊙O1所在的面垂直，则晷针AC与水平面所成角为40°.8．(2020·北京，4)某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为()A．6＋ 3 B．6＋2 3 C．12＋ 3 D．12＋2 3答案 D解析由三视图还原几何体，该几何体为底面是边长为2的正三角形，高为2的直三棱柱， S 底＝2×34×22＝2 3. S 侧＝3×2×2＝12，则三棱柱的表面积为23＋12.9．(2020·北京，10)2020年3月14日是全球首个国际圆周率日(π Day)．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是( ) A ．3n ⎝⎛⎭⎫sin 30°n ＋tan 30°n B ．6n ⎝⎛⎭⎫sin 30°n ＋tan 30°n C ．3n ⎝⎛⎭⎫sin 60°n ＋tan 60°n D ．6n ⎝⎛⎭⎫sin 60°n＋tan 60°n 答案 A解析设内接正6n 边形的周长为C 1，外切正6n 边形的周长为C 2，如图(1)所示，sin 360°12n ＝BC 1， ∴BC ＝sin 30°n，∴AB ＝2sin 30°n ，C 1＝12n sin 30°n.如图(2)所示，tan 360°12n ＝B ′C ′1，∴B ′C ′＝tan 30°n，∴A ′B ′＝2tan 30°n ，C 2＝12n tan 30°n .∴2π＝C 1＋C 22＝6n ⎝⎛⎭⎫sin 30°n ＋tan 30°n ， ∴π＝3n ⎝⎛⎭⎫sin 30°n＋tan 30°n . 10．(2020·天津，5)若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为( )A ．12πB ．24πC ．36πD ．144π 答案 C解析由题意知，正方体的体对角线就是球的直径 ∴2R ＝(23)2＋(23)2＋(23)2＝6， ∴R ＝3，∴S 球＝4πR 2＝36π.11．(2020·浙江，5)某几何体的三视图(单位：cm)如图所示，则该几何体的体积(单位：cm 3)是( )A.73B.143 C ．3 D ．6 答案 A解析如图，三棱柱的体积V 1＝12×2×1×2＝2，三棱锥的体积V 2＝13×12×2×1×1＝13，因此，该几何体的体积V ＝V 1＋V 2＝2＋13＝73.12．(2020·浙江，6)已知空间中不过同一点的三条直线l ，m ，n ，“l ，m ，n 共面”是“l ，m ，n 两两相交”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件答案 B解析如图，直线l ，m ，n 不过同一点，且l ，m ，n 共面有三种情况：①同一平面内三线平行；②两平行线与另一线相交；③三线两两相交．因此，“l ，m ，n 两两相交”是“l ，m ，n 共面”的一种情况，即“l ，m ，n 共面”是“l ，m ，n 两两相交”的必要不充分条件．13.(2020·全国Ⅰ文，3)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析设正四棱锥的底面正方形的边长为a ，高为h ，侧面三角形底边上的高(斜高)为h ′，则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．14．(2020·全国Ⅰ文，12)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆．若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a . 由πr 2＝4π，得r ＝2，则33a ＝2，a ＝23， OO 1＝a ＝2 3.在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.15．(2020·全国Ⅱ文，11)已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为( ) A. 3 B.32 C ．1 D.32答案 C解析如图所示，过球心O 作OO 1⊥平面ABC ，则O 1为等边三角形ABC 的外心．设△ABC 的边长为a ，则34a 2＝934，解得a ＝3， ∴O 1A ＝23×32×3＝ 3.设球O 的半径为r ，则由4πr 2＝16π，得r ＝2，即OA ＝2. 在Rt △OO 1A 中，OO 1＝OA 2－O 1A 2＝1，即O 到平面ABC 的距离为1.16．(2020·全国Ⅲ文，9)下图为某几何体的三视图，则该几何体的表面积是( )A ．6＋4 2B ．4＋4 2C ．6＋2 3D ．4＋2 3答案 C解析如图，该几何体为三棱锥，且其中有三个面是腰长为2的等腰直角三角形，第四个面是边长为22的等边三角形，所以该几何体的表面积为3×12×2×2＋12×22×22×32＝6＋2 3.二、填空题1．(2020·全国Ⅱ理，16)设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内； p 2：过空间中任意三点有且仅有一个平面； p 3：若空间两条直线不相交，则这两条直线平行； p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l . 则下述命题中所有真命题的序号是________． ①p 1∧p 4；②p 1∧p 2；③23p p ⌝∨；④34p p ⌝∨⌝. 答案 ①③④解析 p 1是真命题，两两相交且不过同一点的三条直线必定有三个交点，且这三个交点不在同一条直线上，由平面的基本性质“经过不在同一直线上的三个点，有且只有一个平面”，可知p 1为真命题；p 2是假命题，因为当空间中三点在一条直线上时，有无数个平面过这三个点；p 3是假命题，因为空间两条直线不相交时，它们可能平行，也可能异面；p 4是真命题，因为一条直线垂直于一个平面，那么它垂直于平面内的所有直线．由以上结论知綈p 2，綈p 3，綈p 4依次为真命题、真命题、假命题，从而①③④中命题为真命题，②中命题为假命题．2．(2020·全国Ⅲ理，15)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．答案23π 解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π⎝⎛⎭⎫223＝23π.3．(2020·新高考全国Ⅰ，16)已知直四棱柱ABCD －A 1B 1C 1D 1的棱长均为2，∠BAD ＝60°.以D 1为球心，5为半径的球面与侧面BCC 1B 1的交线长为________．答案2π2解析如图，设B 1C 1的中点为E ，球面与棱BB 1，CC 1的交点分别为P ，Q ，连接DB ，D 1B 1，D 1P ，D 1E ，EP ，EQ ，由∠BAD ＝60°，AB ＝AD ，知△ABD 为等边三角形， ∴D 1B 1＝DB ＝2，∴△D 1B 1C 1为等边三角形，则D 1E ＝3且D 1E ⊥平面BCC 1B 1，∴E 为球面截侧面BCC 1B 1所得截面圆的圆心，设截面圆的半径为r ，则r ＝R 2球－D 1E 2＝5－3＝ 2. 又由题意可得EP ＝EQ ＝2，∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P ＝5，∴B 1P ＝D 1P 2－D 1B 21＝1，同理C 1Q ＝1，∴P ，Q 分别为BB 1，CC 1的中点， ∴∠PEQ ＝π2，知PQ 的长为π2×2＝2π2，即交线长为2π2.4．(2020·新高考全国Ⅱ，13)棱长为2的正方体ABCD －A 1B 1C 1D 1中，M ，N 分别为棱BB 1，AB 的中点，则三棱锥A 1－D 1MN 的体积为________．答案 1解析如图，由正方体棱长为2，得S △A 1MN ＝2×2－2×12×2×1－12×1×1＝32，又易知D 1A 1为三棱锥D 1－A 1MN 的高，且D 1A 1＝2， ∴1111A D MN D A MN V V --=＝13·1A MN S △·D 1A 1＝13×32×2＝1. 5.(2020·江苏，9)如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半径为0.5 cm ，则此六角螺帽毛坯的体积是________cm 3.答案 ⎝⎛⎭⎫123－π2 解析螺帽的底面正六边形的面积 S ＝6×12×22×sin 60°＝63(cm 2)，正六棱柱的体积V 1＝63×2＝123(cm 3)，圆柱的体积V 2＝π×0.52×2＝π2(cm 3)，所以此六角螺帽毛坯的体积 V ＝V 1－V 2＝⎝⎛⎭⎫123－π2cm 3. 6．(2020·浙江，14)已知圆锥的侧面积(单位：cm 2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是________．答案 1解析如图，设圆锥的母线长为l ，底面半径为r ，则圆锥的侧面积S 侧＝πrl ＝2π， ∴r ＝12l .又圆锥侧面展开图为半圆， ∴12πl 2＝2π， ∴l ＝2，∴r ＝1.7．(2020·全国Ⅱ文，16)设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内； p 2：过空间中任意三点有且仅有一个平面； p 3：若空间两条直线不相交，则这两条直线平行； p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l . 则下述命题中所有真命题的序号是________． ①p 1∧p 4；②p 1∧p 2；③23p p ⌝∨；④34p p ⌝∨⌝. 答案 ①③④解析 p 1是真命题，两两相交且不过同一点的三条直线必定有三个交点，且这三个交点不在同一条直线上，由平面的基本性质“经过不在同一直线上的三个点，有且只有一个平面”，可知p 1为真命题；p 2是假命题，因为当空间中三点在一条直线上时，有无数个平面过这三个点；p 3是假命题，因为空间两条直线不相交时，它们可能平行，也可能异面；p 4是真命题，因为一条直线垂直于一个平面，那么它垂直于平面内的所有直线．由以上结论知綈p 2，綈p 3，綈p 4依次为真命题、真命题、假命题，从而①③④中命题为真命题，②中命题为假命题．8．(2020·全国Ⅲ文，16)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．答案23π 解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π⎝⎛⎭⎫223＝23π.三、解答题1.(2020·全国Ⅰ理，18)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE ＝AD .△ABC 是底面的内接正三角形，P 为DO 上一点，PO ＝66DO .(1)证明：P A ⊥平面PBC ； (2)求二面角B －PC －E 的余弦值．(1)证明由题设，知△DAE 为等边三角形，设AE ＝1，则DO ＝32，CO ＝BO ＝12AE ＝12，所以PO ＝66DO ＝24， PC ＝PO 2＋OC 2＝64，PB ＝PO 2＋OB 2＝64，又△ABC 为等边三角形，则BAsin 60°＝2OA ，所以BA ＝32， P A ＝PO 2＋OA 2＝64， P A 2＋PB 2＝34＝AB 2，则∠APB ＝90°，所以P A ⊥PB ，同理P A ⊥PC ，又PC ∩PB ＝P ，所以P A ⊥平面PBC . (2)解过O 作ON ∥BC 交AB 于点N ，因为PO ⊥平面ABC ，以O 为坐标原点，OA 所在直线为x 轴，ON 所在直线为y 轴，OD 所在直线为z 轴，建立如图所示的空间直角坐标系，则E ⎝⎛⎭⎫－12，0，0，P ⎝⎛⎭⎫0，0，24， B ⎝⎛⎭⎫－14，34，0，C ⎝⎛⎭⎫－14，－34，0，PC →＝⎝⎛⎭⎫－14，－34，－24，PB →＝⎝⎛⎭⎫－14，34，－24，PE →＝⎝⎛⎭⎫－12，0，－24，设平面PCB 的一个法向量为n ＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n ·PC →＝0，n ·PB →＝0，得⎩⎨⎧－x 1－3y 1－2z 1＝0，－x 1＋3y 1－2z 1＝0，令x 1＝2，得z 1＝－1，y 1＝0，所以n ＝(2，0，－1)，设平面PCE 的一个法向量为m ＝(x 2，y 2，z 2)，由⎩⎪⎨⎪⎧m ·PC →＝0，m ·PE →＝0，得⎩⎨⎧－x 2－3y 2－2z 2＝0，－2x 2－2z 2＝0，令x 2＝1，得z 2＝－2，y 2＝33，所以m ＝⎝⎛⎭⎫1，33，－2，故cos 〈m ，n 〉＝m ·n|m |·|n |＝223×103＝255，所以二面角B －PC －E 的余弦值为255.2.(2020·全国Ⅱ理，20)如图，已知三棱柱ABC －A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F .(1)证明：AA 1∥MN ，且平面A 1AMN ⊥平面EB 1C 1F ；(2)设O 为△A 1B 1C 1的中心，若AO ∥平面EB 1C 1F ，且AO ＝AB ，求直线B 1E 与平面A 1AMN 所成角的正弦值．(1)证明因为侧面BB 1C 1C 是矩形，且M ，N 分别为BC ，B 1C 1的中点，所以MN ∥CC 1.又由已知得AA 1∥CC 1，故AA 1∥MN . 因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N . 又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)解由已知得AM ⊥BC .以M 为坐标原点，MA →的方向为x 轴正方向，|MB →|为单位长度，建立如图所示的空间直角坐标系，则AB ＝2，AM ＝ 3.连接NP ，则四边形AONP 为平行四边形，故PM ＝233，E ⎝⎛⎭⎫233，13，0.由(1)知平面A 1AMN ⊥平面ABC ，作NQ ⊥AM ，垂足为Q ，则NQ ⊥平面ABC . 设Q (a,0,0)，则NQ ＝4－⎝⎛⎭⎫233－a 2，B 1⎝⎛⎭⎪⎫a ，1，4－⎝⎛⎭⎫233－a 2，故B 1E →＝⎝ ⎛⎭⎪⎫233－a ，－23，－4－⎝⎛⎭⎫233－a 2，|B 1E →|＝2103.又n ＝(0，－1,0)是平面A 1AMN 的一个法向量，故sin ⎝⎛⎭⎫π2－〈n ，B 1E →〉＝cos 〈n ，B 1E →〉＝n ·B 1E →|n ||B 1E →|＝1010.所以直线B 1E 与平面A 1AMN 所成角的正弦值为1010. 3.(2020·全国Ⅲ理，19)如图，在长方体ABCD －A 1B 1C 1D 1中，点E ，F 分别在棱DD 1，BB 1上，且2DE ＝ED 1，BF ＝2FB 1.(1)证明：点C 1在平面AEF 内；(2)若AB ＝2，AD ＝1，AA 1＝3，求二面角A －EF －A 1的正弦值．(1)证明设AB ＝a ，AD ＝b ，AA 1＝c ，如图，以C 1为坐标原点，C 1D 1—→，C 1B 1—→，C 1C —→的方向分别为x 轴，y 轴，z 轴正方向，建立空间直角坐标系C 1－xyz .连接C 1F ，则C 1(0,0,0)，A (a ，b ，c )， E ⎝⎛⎭⎫a ，0，23c ，F ⎝⎛⎭⎫0，b ，13c ， EA →＝⎝⎛⎭⎫0，b ，13c ，C 1F →＝⎝⎛⎭⎫0，b ，13c ，所以EA →＝C 1F →，所以EA ∥C 1F ，即A ，E ，F ，C 1四点共面，所以点C 1在平面AEF 内．(2)解由已知得A (2,1,3)，E (2,0,2)，F (0,1,1)，A 1(2,1,0)，则AE →＝(0，－1，－1)，AF →＝(－2,0，－2)， A 1E →＝(0，－1,2)，A 1F →＝(－2,0,1)．设n 1＝(x 1，y 1，z 1)为平面AEF 的法向量，则⎩⎪⎨⎪⎧n 1·AE →＝0，n 1·AF →＝0，即⎩⎪⎨⎪⎧－y 1－z 1＝0，－2x 1－2z 1＝0，可取n 1＝(－1，－1,1)．设n 2＝(x 2，y 2，z 2)为平面A 1EF 的法向量，则⎩⎪⎨⎪⎧n 2·A 1E →＝0，n 2·A 1F →＝0，即⎩⎪⎨⎪⎧－y 2＋2z 2＝0，－2x 2＋z 2＝0，同理可取n 2＝⎝⎛⎭⎫12，2，1. 因为cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝－77，所以二面角A －EF －A 1的正弦值为427. 4.(2020·新高考全国Ⅰ，20)如图，四棱锥P －ABCD 的底面为正方形，PD ⊥底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明：l ⊥平面PDC ；(2)已知PD ＝AD ＝1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值． (1)证明在正方形ABCD 中，AD ∥BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以AD ∥平面PBC ，又因为AD ⊂平面P AD ，平面P AD ∩平面PBC ＝l ，所以AD ∥l ，因为在四棱锥P －ABCD 中，底面ABCD 是正方形，所以AD ⊥DC ，所以l ⊥DC ，且PD ⊥平面ABCD ，所以AD ⊥PD ，所以l ⊥PD ，因为DC ∩PD ＝D ，所以l ⊥平面PDC .(2)解以D 为坐标原点，DA →的方向为x 轴正方向，如图建立空间直角坐标系D －xyz ，因为PD ＝AD ＝1，则有D (0,0,0)，C (0,1,0)，A (1,0,0)，P (0,0,1)，B (1，1,0)，设Q (m,0,1)，则有DC →＝(0,1,0)，DQ →＝(m,0,1)，PB →＝(1,1，－1)，设平面QCD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧DC →·n ＝0，DQ →·n ＝0，即⎩⎪⎨⎪⎧y ＝0，mx ＋z ＝0，令x ＝1，则z ＝－m ，所以平面QCD 的一个法向量为n ＝(1,0，－m )，则cos 〈n ，PB →〉＝n ·PB →|n ||PB →|＝1＋0＋m 3·m 2＋1. 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB 与平面QCD 所成角的正弦值等于 |cos 〈n ，PB →〉|＝|1＋m |3·m 2＋1＝33·1＋2m ＋m 2m 2＋1＝33·1＋2m m 2＋1≤33·1＋2|m |m 2＋1≤33·1＋1＝63，当且仅当m ＝1时取等号，所以直线PB 与平面QCD 所成角的正弦值的最大值为63. 5.(2020·新高考全国Ⅱ，20)如图，四棱锥P －ABCD 的底面为正方形，PD ⊥底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明：l ⊥平面PDC ；(2)已知PD ＝AD ＝1，Q 为l 上的点，QB ＝2，求PB 与平面QCD 所成角的正弦值． (1)证明在正方形ABCD 中，AD ∥BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以AD ∥平面PBC ，又因为AD ⊂平面P AD ，平面P AD ∩平面PBC ＝l ，所以AD ∥l ，因为在四棱锥P －ABCD 中，底面ABCD 是正方形，所以AD ⊥DC ，所以l ⊥DC ，且PD ⊥平面ABCD ，所以AD ⊥PD ，所以l ⊥PD ，因为DC ∩PD ＝D ，所以l ⊥平面PDC .(2)解以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系D －xyz ，则D (0,0,0)，C (0,1,0)， B (1,1,0)，P (0,0,1)，DC →＝(0,1,0)，PB →＝(1,1，－1)．由(1)设Q (a,0,1)，则BQ →＝(a －1，－1,1)．由题意知(a －1)2＋2＝2， ∴a ＝1，∴DQ →＝(1,0,1)．设n ＝(x ，y ，z )是平面QCD 的一个法向量，则⎩⎪⎨⎪⎧n ·DQ →＝0，n ·DC →＝0，即⎩⎪⎨⎪⎧x ＋z ＝0，y ＝0，可取n ＝(1,0，－1)，∴cos 〈n ，PB →〉＝n ·PB →|n |·|PB →|＝63，故PB 与平面QCD 所成角的正弦值为63. 6.(2020·北京，16)如图，在正方体ABCD －A 1B 1C 1D 1中，E 为BB 1的中点．(1)求证：BC 1∥平面AD 1E ；(2)求直线AA 1与平面AD 1E 所成角的正弦值． (1)证明在正方体ABCD －A 1B 1C 1D 1中， AB ∥A 1B 1且AB ＝A 1B 1，A 1B 1∥C 1D 1且A 1B 1＝C 1D 1， ∴AB ∥C 1D 1且AB ＝C 1D 1，∴四边形ABC 1D 1为平行四边形，则BC 1∥AD 1， ∵BC 1⊄平面AD 1E ，AD 1⊂平面AD 1E ， ∴BC 1∥平面AD 1E .(2)解以点A 为坐标原点，AD ，AB ，AA 1所在直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系A －xyz ，设正方体ABCD －A 1B 1C 1D 1的棱长为2，则A (0,0,0)，A 1(0,0,2)，D 1(2,0,2)，E (0,2,1)， AD 1→＝(2,0,2)，AE →＝(0,2,1)，AA 1→＝(0,0,2)，设平面AD 1E 的法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·AD 1→＝0，n ·AE →＝0，得⎩⎪⎨⎪⎧2x ＋2z ＝0，2y ＋z ＝0，令z ＝－2，得x ＝2，y ＝1，则n ＝(2,1，－2)． cos 〈n ，AA 1→〉＝n ·AA 1→|n |·|AA 1→|＝－43×2＝－23.因此，直线AA 1与平面AD 1E 所成角的正弦值为23.7.(2020·天津，17)如图，在三棱柱ABC －A 1B 1C 1中，CC 1⊥平面ABC ，AC ⊥BC ，AC ＝BC ＝2，CC 1＝3，点D ，E 分别在棱AA 1和棱CC 1上，且AD ＝1，CE ＝2，M 为棱A 1B 1的中点．(1)求证：C 1M ⊥B 1D ；(2)求二面角B －B 1E －D 的正弦值；(3)求直线AB 与平面DB 1E 所成角的正弦值．(1)证明依题意，以C 为坐标原点，分别以CA →，CB →，CC 1→的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)，可得C (0,0,0)，A (2,0,0)，B (0,2,0)，C 1(0,0,3)，A 1(2,0,3)，B 1(0,2,3)，D (2,0,1)，E (0,0,2)，M (1,1,3)．则C 1M →＝(1,1,0)，B 1D →＝(2，－2，－2)， ∵C 1M →·B 1D →＝2－2＋0＝0，∴C 1M ⊥B 1D .(2)解依题意，CA →＝(2,0,0)是平面BB 1E 的一个法向量，EB 1→＝(0,2,1)，ED →＝(2,0，－1)．设n ＝(x ，y ，z )为平面DB 1E 的法向量，则⎩⎪⎨⎪⎧n ·EB 1→＝0，n ·ED →＝0，即⎩⎪⎨⎪⎧2y ＋z ＝0，2x －z ＝0.不妨设x ＝1，可得n ＝(1，－1,2)．∴cos 〈CA →，n 〉＝CA →·n |CA →||n |＝66，∴sin 〈CA →，n 〉＝1－16＝306. ∴二面角B －B 1E －D 的正弦值为306. (3)解依题意，AB →＝(－2,2,0)，由(2)知，n ＝(1，－1,2)为平面DB 1E 的一个法向量， ∴cos 〈AB →，n 〉＝AB →·n |AB →||n |＝－33，∴直线AB 与平面DB 1E 所成角的正弦值为33. 8.(2020·江苏，15)在三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．(1)求证：EF ∥平面AB 1C 1； (2)求证：平面AB 1C ⊥平面ABB 1.证明 (1)因为E ，F 分别是AC ，B 1C 的中点，所以EF ∥AB 1.又EF ⊄平面AB 1C 1，AB 1⊂平面AB 1C 1，所以EF ∥平面AB 1C 1.(2)因为B 1C ⊥平面ABC ，AB ⊂平面ABC ，所以B 1C ⊥AB .又AB ⊥AC ，B 1C ⊂平面AB 1C ，AC ⊂平面AB 1C ， B 1C ∩AC ＝C ，所以AB ⊥平面AB 1C . 又因为AB ⊂平面ABB 1，所以平面AB 1C ⊥平面ABB 1.9.(2020·江苏，22)在三棱锥A －BCD 中，已知CB ＝CD ＝5，BD ＝2，O 为BD 的中点，AO ⊥平面BCD ，AO ＝2，E 为AC 的中点．(1)求直线AB 与DE 所成角的余弦值；(2)若点F 在BC 上，满足BF ＝14BC ，设二面角F －DE －C 的大小为θ，求sin θ的值．解 (1)如图，连接OC ，因为CB ＝CD ，O 为BD 的中点，所以CO ⊥BD .又AO ⊥平面BCD ，所以AO ⊥OB ，AO ⊥OC .以{OB →，OC →，OA →}为基底，建立空间直角坐标系O －xyz . 因为BD ＝2，CB ＝CD ＝5，AO ＝2，所以B (1,0,0)，D (－1,0,0)，C (0,2,0)，A (0,0,2)．因为E 为AC 的中点，所以E (0,1,1)．所以AB →＝(1,0，－2)，DE →＝(1,1,1)，所以|cos 〈AB →，DE →〉|＝|AB →·DE →||AB →|·|DE →|＝|1＋0－2|5×3＝1515.因此，直线AB 与DE 所成角的余弦值为1515. (2)因为点F 在BC 上，BF ＝14BC ，BC →＝(－1,2,0)．所以BF →＝14BC →＝⎝⎛⎭⎫－14，12，0. 又DB →＝(2,0,0)，故DF →＝DB →＋BF →＝⎝⎛⎭⎫74，12，0.设n 1＝(x 1，y 1，z 1)为平面DEF 的一个法向量，则⎩⎪⎨⎪⎧ DE →·n 1＝0，DF →·n 1＝0，即⎩⎪⎨⎪⎧x 1＋y 1＋z 1＝0，74x 1＋12y 1＝0，令x 1＝2，得y 1＝－7，z 1＝5，所以n 1＝(2，－7,5)．设n 2＝(x 2，y 2，z 2)为平面DEC 的一个法向量，又DC →＝(1,2,0)，则⎩⎪⎨⎪⎧DE →·n 2＝0，DC →·n 2＝0，即⎩⎪⎨⎪⎧x 2＋y 2＋z 2＝0，x 2＋2y 2＝0，令x 2＝2，得y 2＝－1，z 2＝－1，所以n 2＝(2，－1，－1)．故|cos θ|＝|n 1·n 2||n 1|·|n 2|＝|4＋7－5|78×6＝1313. 所以sin θ＝1－cos 2θ＝23913. 10.(2020·浙江，19)如图，在三棱台ABC －DEF 中，平面ACFD ⊥平面ABC ，∠ACB ＝∠ACD ＝45°，DC ＝2BC .(1)证明：EF ⊥DB ；(2)求直线DF 与平面DBC 所成角的正弦值．(1)证明如图(1)，过点D 作DO ⊥AC ，交直线AC 于点O ，连接OB .由∠ACD ＝45°，DO ⊥AC ，得CD ＝2CO . 由平面ACFD ⊥平面ABC ，得DO ⊥平面ABC ，所以DO ⊥BC .由∠ACB ＝45°，BC ＝12CD ＝22CO ，得BO ⊥BC .所以BC ⊥平面BDO ，故BC ⊥DB . 由ABC －DEF 为三棱台，得BC ∥EF ，所以EF ⊥DB .(2)解方法一如图(2)，过点O 作OH ⊥BD ，交直线BD 于点H ，连接CH .由ABC －DEF 为三棱台，得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角．由BC ⊥平面BDO ，得OH ⊥BC ，故OH ⊥平面DBC ，所以∠OCH 为直线CO 与平面DBC 所成角．设CD ＝22，则DO ＝OC ＝2，BO ＝BC ＝2，得BD ＝6，OH ＝233，所以sin ∠OCH ＝OH OC ＝33.因此，直线DF 与平面DBC 所成角的正弦值为33. 方法二由ABC －DEF 为三棱台，得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角，记为θ.如图(3)，以O 为原点，分别以射线OC ，OD 为y ，z 轴的正半轴，建立空间直角坐标系O－xyz .设CD ＝22，由题意知各点坐标如下：O (0,0,0)，B (1,1,0)，C (0,2,0)，D (0,0,2)．因此OC →＝(0,2,0)，BC →＝(－1,1,0)，CD →＝(0，－2,2)．设平面DBC 的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·BC →＝0，n ·CD →＝0，即⎩⎪⎨⎪⎧－x ＋y ＝0，－2y ＋2z ＝0，可取n ＝(1,1,1)，所以sin θ＝|cos 〈OC →，n 〉|＝|OC →·n ||OC →|·|n |＝33.因此，直线DF 与平面DBC 所成角的正弦值为33. 11.(2020·全国Ⅰ文，19)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 是底面的内接正三角形，P 为DO 上一点，∠APC ＝90°.(1)证明：平面P AB ⊥平面P AC ；(2)设DO ＝2，圆锥的侧面积为3π，求三棱锥P －ABC 的体积． (1)证明 ∵D 为圆锥顶点，O 为底面圆心， ∴OD ⊥平面ABC ，∵P 在DO 上，OA ＝OB ＝OC ， ∴P A ＝PB ＝PC ，∵△ABC 是圆内接正三角形， ∴AC ＝BC ，△P AC ≌△PBC ，∴∠APC ＝∠BPC ＝90°，即PB ⊥PC ，P A ⊥PC ， P A ∩PB ＝P ，∴PC ⊥平面P AB ，PC ⊂平面P AC ，∴平面P AB ⊥平面P AC .(2)解设圆锥的母线为l ，底面半径为r ，圆锥的侧面积为πrl ＝3π，rl ＝3，OD 2＝l 2－r 2＝2，解得r ＝1，l ＝3，AC ＝2r sin 60°＝3，在等腰直角三角形APC 中， AP ＝22AC ＝62，在Rt △P AO 中，PO ＝AP 2－OA 2＝64－1＝22， ∴三棱锥P －ABC 的体积为V P －ABC ＝13PO ·S △ABC ＝13×22×34×3＝68.12.(2020·全国Ⅱ文，20)如图，已知三棱柱ABC －A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F .(1)证明：AA 1∥MN ，且平面A 1AMN ⊥平面EB 1C 1F ；(2)设O 为△A 1B 1C 1的中心．若AO ＝AB ＝6，AO ∥平面EB 1C 1F ，且∠MPN ＝π3，求四棱锥B－EB 1C 1F 的体积．(1)证明因为侧面BB 1C 1C 是矩形，且M ，N 分别为BC ，B 1C 1的中点，所以MN ∥CC 1.又由已知得AA 1∥CC 1，故AA 1∥MN . 因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N . 又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)解因为AO ∥平面EB 1C 1F ，AO ⊂平面A 1AMN ，平面A 1AMN ∩平面EB 1C 1F ＝PN ，所以AO ∥PN ，又AP ∥ON ，故四边形APNO 是平行四边形，所以PN ＝AO ＝6，AP ＝ON ＝13AM ＝3，PM ＝23AM ＝23，EF ＝13BC ＝2.因为BC ∥平面EB 1C 1F ，所以四棱锥B －EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离．如图，作MT ⊥PN ，垂足为T ，则由(1)知，MT ⊥平面EB 1C 1F ，故MT ＝PM sin ∠MPN ＝3. 底面EB 1C 1F 的面积为12(B 1C 1＋EF )·PN ＝12×(6＋2)×6＝24. 所以四棱锥B －EB 1C 1F 的体积为13×24×3＝24.13.(2020·全国Ⅲ文，19)如图，在长方体ABCD －A 1B 1C 1D 1中，点E ，F 分别在棱DD 1，BB 1上，且2DE ＝ED 1，BF ＝2FB 1.证明：(1)当AB ＝BC 时，EF ⊥AC ； (2)点C 1在平面AEF 内．证明 (1)如图，连接BD ，B 1D 1. 因为AB ＝BC ，所以四边形ABCD 为正方形，故AC ⊥BD .又因为BB 1⊥平面ABCD ，AC ⊂平面ABCD ，于是AC ⊥BB 1.又BD ∩BB 1＝B ，BD ，BB 1⊂平面BB 1D 1D ，所以AC ⊥平面BB 1D 1D .又因为EF ⊂平面BB 1D 1D ，所以EF ⊥AC .(2)如图，在棱AA 1上取点G ，使得AG ＝2GA 1，连接GD 1，FC 1，FG ，因为ED 1＝23DD 1，AG ＝23AA 1，DD 1∥AA 1且DD 1＝AA 1，所以ED 1∥AG 且ED 1＝AG ，所以四边形ED 1GA 为平行四边形，故AE ∥GD 1.因为B 1F ＝13BB 1，GA 1＝13AA 1，BB 1∥AA 1且BB 1＝AA 1，所以B 1F ∥GA 1，且B 1F ＝GA 1，所以四边形B 1FGA 1是平行四边形，所以FG ∥A 1B 1且FG ＝A 1B 1，所以FG ∥C 1D 1且FG ＝C 1D 1，所以四边形FGD 1C 1为平行四边形，故GD 1∥FC 1. 所以AE ∥FC 1.所以A ，E ，F ，C 1四点共面，即点C 1在平面AEF 内．。

【新高考数学】23个立体几何与空间向量专题

是圆的直径，ADB 60o ，BDC 45o ，PD 垂直于底面 ABCD ，PD 2 2R ，E, F
分别是 PB,CD 上的点，且 PE DF ，过点 E 作 BC 的平行线交 PC 于G ． EB FC
⑴求 BD 与平面 ABP 所成角的正弦值 sin ；
P
⑵当 PE 1 时，求 EFG 的面积 S ． EB 2
是 CD 的中点， PA 底面 ABCD ， PA 3 . ⑴证明：平面 PBE 平面 PAB ； ⑵求二面角 A BE P 的大小.
F P
E
G
H
D
C
E
A
图 21
B
A
D
B
C 图 22
例 22 、如图 22，平面 ABEF 平面 ABCD ，四边形 ABEF 与四边形 ABCD 都是直角梯形，
D
PE
A
C
C
A
O
F
B 图1
D O
B
图2 E
C
例 2 、如图 2，四面体 ABCD 中， O, E 分别是 BD, BC 的中点， CA CB CD BD 2 ，
AB AD 2 ⑴ 求异面直线 AB 与 CD 所成角的余弦值 cos ；
⑵ 求点 E 到平面 ACD 的距离 d .
例 3 、如图 3 所示，四棱锥 P ABCD 的底面 ABCD 是半径为 R 的圆的内接四边形，其中 BD
例 19 、如图 19 ，直三棱柱 ABC A1B1C1 中， D、E 分别是 AB、BB1 的中点 .
AA1 AC CB
2 2
AB ，求二面角 D
A1C
E 的正弦值 sin
.

2023-2024学年高考数学空间向量与立体几何专项练习题(附答案)

A ．B ．223．若直线的方向向量为，平面l bA ．()(1,0,0,2,0,0b n ==-()(0,2,1,1,0,1b n ==--A ．B ．5136．如图，在平行六面体ABCDA．1122a b c -++C．1122a b c --+7．如图，在四面体OABC中，1-16．已知四棱锥P ABCDPC棱上运动，当平面1．C【分析】根据已知结合向量的坐标运算可得出，且.然后根据向量的数量积a b a +=- 14a = 运算求解，即可得出答案.【详解】由已知可得，且.()1,2,3a b a+=---=-14a =又，()7a b c +⋅= 所以，即有，7a c -⋅= cos ,14cos ,7a c a c a c -⋅=-=所以，.1cos ,2a c =-又，所以.0,180a c ≤≤ ,120a c =︒ 故选：C.2．C【分析】利用中点坐标公式求出中点的坐标，根据空间两点间的距离公式即可得出中线BC 长.【详解】由图可知：，，，(0,0,1)A (2,0,0)B (0,2,0)C 由中点坐标公式可得的中点坐标为，BC (1,1,0)根据空间两点间距离公式得边上的中线的长为.BC 22211(1)3++-=故选：C 3．D【分析】若直线与平面平行，则直线的方向向量与平面的法向量垂直，利用向量数量积检验.【详解】直线的方向向量为，平面的法向量为，l bαn 若可能，则，即.//l αb n ⊥r r 0b n ⋅=r r A 选项，；()1220b n =⨯-⋅=-≠B 选项，；11305160b n =⨯⨯⋅+⨯+=≠C 选项，；()()01201110b n =⨯-+⨯+⨯-⋅=-≠D 选项，；()1013310b n =⨯+-⨯=⋅+⨯因为，，3AB =4BC =2PA =所以()()(0,0,2,3,0,0,0,0,1P B Q 设平面的法向量为BQD (m x =()(),,3,0,1m BQ x y z ⎧设，2AB AD AS ===则()()()0,0,0,0,0,2,2,2,0,A S C P 设，()0,,2M t t -(1,1,2OM t =--所以1120OM AP t t ⊥=-+-+-=点到平面与平面的距离和为为定值，D 选项正确.M ABCD SAB 22t t -+=，，()2,0,0B ()()2,0,2,0,2,0SB BC =-=设平面的法向量为，SBC (),,n x y z =则，故可设，22020n SB x z n BC y ⎧⋅=-=⎪⎨⋅==⎪⎩()1,0,1n = 要使平面，又平面，//OM SBC OM ⊄SBC 则，()()1,1,21,0,11210OM n t t t t ⋅=---⋅=-+-=-=解得，所以存在点，使平面，B 选项正确.1t =M //OM SBC 若直线与直线所成角为，又，OM AB 30︒()2,0,0AB =则，()()222213cos3022661122OM ABOM ABt t t t ⋅-︒====⋅-++-+-⨯ 整理得，无解，所以C 选项错误.23970,8143730t t -+=∆=-⨯⨯=-<故选：ABD.10．BCD【分析】根据向量的多边形法则可知A 正确；根据向量的三角不等式等号成立条件可知，B 错误；根据共线向量的定义可知，C 错误；根据空间向量基本定理的推论可知，D 错误．【详解】对A ，四点恰好围成一封闭图形，根据向量的多边形法则可知，正确；对B ，根据向量的三角不等式等号成立条件可知，同向时，应有，即必要,a b a b a b+=+ 性不成立，错误；对C ，根据共线向量的定义可知，所在直线可能重合，错误；,a b对D ，根据空间向量基本定理的推论可知，需满足x +y +z =1，才有P 、A 、B 、C 四点共面，错误．故选：BCD ．11．AB【分析】以，，作为空间的一组基底，利用空间向量判断A ，C ，利用空间向量法ABAD AA 可得面，再用向量法表示，即可判断B ，利用割补法判断D ；1AC ⊥PMN AH【详解】依题意以，，作为空间的一组基底，ABAD AA 则，，11AC AB AD AA =++ ()1122MN BD AD AB ==-因为棱长均为2，，11π3A AD A AB ∠=∠=所以，，224AB AD == 11π22cos 23AA AD AA AB ⋅=⋅=⨯⨯= 所以()()1112D A A C MN AD A A B AA B++⋅⋅=- ，()2211102AB AD AB AD AB AD AA AD AA AB ⋅-+-⋅+==⋅+⋅故，即，故A 正确；1AC MN ⊥1AC MN ⊥同理可证，，面，面，PN AC ⊥MN PN N ⋂=MN ⊂PMN PN ⊂PMN 所以面，即面，即为正三棱锥的高，1AC ⊥PMN AH ⊥PMN AH A PMN -所以()()1133AH AN NH AN NP NM AN AP AN AM AN=+=++=+-+- ，()13AP AM AN =++又，，分别是，，的中点，，P M N 1AA AB AD π3PAM PAN MAN ∠=∠=∠=所以，则三棱锥是正四面体，1PA AM AN PM MN PN ======P AMN -所以()11111133222AH AP AM AN AA AB AD ⎛⎫=++=⨯++ ⎪⎝⎭ ，()111166AA AB AD AC =++=所以，故B 正确；116AH AC =因为()211AC AB AD AA =++ ()()()222111222AB ADAA AB AD AB AA AD AA =+++⋅+⋅+⋅ ，2426==()21111111=AC AA AB AD AA AA AB AA AD AA AA ⋅=++⋅⋅+⋅+ ，11222222=822=⨯⨯+⨯⨯+⨯设直线和直线所成的角为，1AC 1BB θ则，故C 错误；1111111186cos cos ,cos ,3262AC AA AC BB AC AA AC AA θ⋅=====⨯ ，11111111111111A B D C ABCD A B C D A B D A C B D A B ABC D ADCV V V V V V ------=----其中，1111111111116ABCD A B C D A B D A C B D C B ABC D ADC V V V V V -----====所以，故D 错误.1111113A B D C ABCD A B C D V V --=故选：AB.关键点睛：本题解决的关键点是利用空间向量的基底法表示出所需向量，利用空间向量的数量积运算即可得解.12．AC【分析】对于A ，根据即可算出的值；对于B ，根据计算；对于C ，根据||2a = m a b ⊥ m 计算即可；对于D ，根据求出，从而可计算出.a b λ= 1a b ⋅=- m a b + 【详解】对于A ，因为，所以，解得，故A 正确；||2a = 2221(1)2m +-+=2m =±对于B ，因为，所以，所以，故B 错误；a b ⊥ 2120m m -+-+=1m =对于C ，假设，则，a b λ= (1,1,)(2,1,2)m m λ-=--所以，该方程组无解，故C 正确；()12112m m λλλ=-⎧⎪-=-⎨⎪=⎩对于D ，因为，所以，解得，1a b ⋅=- 2121m m -+-+=-0m =所以，，所以，故D 错误.(1,1,0)a =- (2,1,2)b =-- (1,2,2)+=-- a b 故选：AC.13．15【分析】根据线面垂直，可得直线的方向向量和平面的法向量共线，由此列式计算，即得答案.【详解】∵，∴，∴，解得，l α⊥u n ∥ 3123a b ==6,9a b ==∴，15a b +=故1514．2【分析】根据垂直得到，得到方程，求出.()0a a b λ⋅-= 2λ=【详解】，()()()2,1,31,2,12,12,3a b λλλλλ-=---=--- 因为，所以，()a a b λ⊥- ()0a a b λ⋅-= 即，()()2,12,3241293702,1,134λλλλλλλ----=-++-+-=+⋅-=解得.2λ=故215．17【分析】利用向量的加法，转化为，直接求模长即可.CD CA AB BD =++ 【详解】因为.CD CA AB BD =++ 所以()22CD CA AB BD =++ 222222CA CA AB AB AB BD BD CA BD=+⋅++⋅++⋅ 222132022042342⎛⎫=+⨯++⨯++⨯⨯⨯- ⎪⎝⎭17=所以.17CD = 故答案为.1716．33【分析】首先建立空间直角坐标系，分别求平面和平面的法向量，利用法向量垂MBD PCD 直求点的位置，并利用向量法求异面直线所成角的余弦值，即可求解正弦值.M 【详解】如图，以点为原点，以向量为轴的正方向，建立空间直角坐标A ,,AB AD AP ,,x y z 系，设，2AD AP ==，，，，()2,0,0B ()0,2,0D ()002P ,,()2,2,0C 设,()()()0,2,22,2,22,22,22DM DP PM DP PC λλλλλ=+=+=-+-=-- ，，，()2,2,0BD =-u u u r ()2,0,0DC =u u u r ()0,2,2DP =- 设平面的法向量为，MBD ()111,,m x y z =r ，()()11111222220220DM m x y z DM m x y λλλ⎧⋅=+-+-=⎪⎨⋅=-+=⎪⎩33故。

高考数学立体几何大题训练

高考数学立体几何大题训练1．如图，平面ABCD ⊥平面ADEF ，其中ABCD 为矩形，ADEF 为梯形，//AF DE ，AF FE ⊥，2AF AD DE ==，G 为BF 中点．（Ⅰ）求证：//EG 平面ABCD ；（Ⅱ）求证：AF DG ⊥．2．如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，底面ABCD 是菱形，60BAD ∠= ，2,6AB PD ==,O为AC 与BD 的交点，E 为棱PB 上一点．（Ⅰ）证明：平面EAC ⊥平面PBD ；（Ⅱ）若PD ∥平面EAC ,求三棱锥P EAD -的体积．3．如图，已知四边形ABCD 是正方形，PD ⊥平面ABCD ，CD=PD=2EA,PD//EA ，F ，G ，H 分别为PB ，BE ，PC 的中点. GA EF D B C P A B C DEO（Ⅰ）求证：GH//平面PDAE ；（Ⅱ）求证：平面FGH ⊥平面PCD.4．如图，在矩形ABCD 中，点E 为边AD 上的点，点F 为边CD 的中点， 234A E D B A A ===,现将ABE ∆沿BE 边折至PBE ∆位置，且平面PBE ⊥平面BCDE .（Ⅰ）求证：平面PBE ⊥平面PEF ；（Ⅱ）求四棱锥P BCFE -的体积．5．如图，AB 为圆O 的直径，点E 、F 在圆O 上，AB ∥EF ，矩形ABCD 所在的平面和圆O 所在的平面互相垂直，且AB=2，AD=EF=1. A B C D E B CDE FP（Ⅰ）求证：AF ⊥平面CBF ；（Ⅱ）设FC 的中点为M ，求证：OM ∥平面DAF ；（Ⅲ）设平面CBF 将几何体EFABCD 分成的两个锥体的体积分别为,F ABCD F CBE V V --，求:F ABCD F CBE V V --.6．如图所示，在正方体1111ABCD A B C D -中，E F 、分别是棱111D C DD 、的中点．（Ⅰ）证明：平面11ADC B ⊥平面1A BE ；（Ⅱ）证明：F B 1//平面BE A 1；7．如图，四棱锥P ABCD -中，PAB ∆是正三角形，四边形ABCD 是矩形，且平面PAB ⊥平面ABCD ，2PA =，4PC =．E AB C D B 1 A 1D 1C 1F（Ⅰ）若点E 是PC 的中点，求证：//PA 平面BDE ；（Ⅱ）若点F 在线段PA 上，且FA PA λ=，当三棱锥B AFD -的体积为43时，求实数λ的值．8．如图，三棱柱111ABC A B C -中，侧棱垂直底面，︒=∠90ACB ，112AC BC AA ==，D 是棱1AA 的中点.（1）证明：1DC ⊥平面BDC ；（2）若12AA =，求三棱锥1C BDC -的体积.9．已知平行四边形ABCD ，4AB =，2AD =，60o DAB ∠=，E 为AB 的中点，把三角形ADE 沿DE 折起至1A DE位置，使得14AC =，F 是线段1AC 的中点.（1）求证：1//BF A DE 面；（2）求证：面1A DE ⊥面DEBC ；（3）求四棱锥1A DEBC -的体积.10．如图, 已知边长为2的的菱形ABCD 与菱形ACEF 全等，且FAC ABC ∠=∠,平面ABCD ⊥平面ACEF ，点G 为CE 的中点. G EOB D A CF（Ⅰ）求证：//AE 平面DBG ；（Ⅱ）求证：FC BG ⊥；（Ⅲ）求三棱锥E BGD -的体积.11．如图,三棱柱111ABC A BC -中,112AB AC AA BC ====,1160AAC ∠=︒,平面1ABC ⊥平面11AAC C ,1AC 与1AC 相交于点D .D C B AE CD A 1FB E（Ⅰ）求证:BD ⊥平面11AAC C ；（Ⅱ）求二面角1C AB C --的余弦值.12．如图，已知四边形ABCD 为正方形，⊥EA 平面ABCD ，CF ∥EA ，且222===CF AB EA（1）求证：⊥EC 平面BDF ；（2）求二面角E BD F --的余弦值.13．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧面PAB ⊥底面ABCD ， PA AB =，点E 是PB 的中点，点F 在边BC 上移动． CC 1 B 1AA 1B D（Ⅰ）若F 为BC 中点，求证：EF //平面PAC ；（Ⅱ）求证：AE PF ⊥；（Ⅲ）若2PB AB =，二面角E AF B --的余弦值等于1111，试判断点F 在边BC 上的位置，并说明理由.14．已知几何体A BCDE -的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（1）求此几何体的体积V 的大小；（2）求异面直线DE 与AB 所成角的余弦值；（3）求二面角A-ED-B 的正弦值．15．如图，在直三棱柱111ABC A B C -中，平面1A BC ⊥侧面11A ABB ，且12AA AB ==（1）求证：AB BC ⊥；（2）若直线AC 与平面1A BC 所成的角为6π，求锐二面角1A AC B --的大小.16．如图所示，正方形与矩形所在平面互相垂直，，点为的中点.（1）求证：∥平面；（2）求证：；（3）在线段上是否存在点，使二面角的大小为？若存在，求出的长；若不存在，请说明理由.17．如图，在三棱柱111ABC A B C -中，1A A ⊥平面ABC ，90BAC ︒∠=，F 为棱1AA 上的动点，14,2A A AB AC ===. ⑴当F 为1A A 的中点，求直线BC 与平面1BFC 所成角的正弦值； ⑵当1AF FA 的值为多少时，二面角1B FC C --的大小是45︒. 22==AD AB D D AA 11ABCD E AB 1BD DE A 1E D 1⊥D A 1AB M D MC D --16πAM18．如图，在四棱锥BCDE A -中，平面⊥ABC 平面======∠=∠AC BE DE CD AB BED CDE BCDE ,1,2,90,02.（1）证明：⊥DE 平面ACD ;（2）求二面角E AD B --的大小4681012141618E DC B A19．如图，正方形ADEF 与梯形ABCD 所在的平面互相垂直，AD CD ⊥，AB ∥CD ，2AB AD ==，4CD =，M 为CE 的中点．（1）求证：BM ∥平面ADEF ；（2）求证：平面BDE ⊥平面BEC ；（3）求平面BEC 与平面ADEF 所成锐二面角的余弦值.AF1ABC1B 1C20．在如图所示的几何体中，四边形ABCD 为平行四边形，90ACB ∠=，EA ⊥平面ABCD ，//EF AB ，//FG BC ，//EG AC ，2AB EF =.（1）若M 是线段AD 的中点，求证：//GM 平面ABFE ；（2）若22AC BC AE ===，求二面角A BF C --的余弦值. MEFCD B A参考答案1．（Ⅰ）详见解析; （Ⅱ）详见解析【解析】试题分析：证明：（Ⅰ）取AB 的中点O ，连接OD ，可得OG = 12AF ，又因为 //AF DE ，2AF DE =所以OG =DE ，四边形ODEG 为平行四边形，所以//EG OD ，在根据线面平行的判定定理，即可证明结果．（Ⅱ）取AF 的中点H ，连接DH 、GH ，可得//GH AB ，因为平面ABCD ⊥平面ADEF ，AB AD ⊥，所以AB ⊥平面ADEF ，AB AF ⊥，所以AF GH ⊥，因为 //AF DE ，2AF DE =所以四边形EFHD 为平行四边形，//EF DH ，又AF FE ⊥，所以AF DH ⊥ ，根据线面垂直的判定定理，即可证明结果．试题解析：证明：（Ⅰ）取AB 的中点O ，连接OD因为,O G 分别是AB ,BF 的中点，所以OG =12AF ， 2分又因为 //AF DE ，2AF DE = 所以OG =DE ，四边形ODEG 为平行四边形所以//EG OD 4分因为OD ⊂平面ABCD ，EG ⊄平面ABCD所以//EG 平面ABCD 5分（Ⅱ）取AF 的中点H ，连接DH 、GH因为,G H 分别是BF ,AF 的中点，所以//GH AB ， 7分因为平面ABCD ⊥平面ADEF ，AB AD ⊥所以AB ⊥平面ADEF ，AB AF ⊥所以AF GH ⊥ 9分因为//AF DE ，2AF DE = 所以四边形EFHD 为平行四边形，//EF DH又AF FE ⊥，所以AF DH ⊥ 11分因为GH DH H = GA E F DB CHO所以AF ⊥平面DGH所以AF DG ⊥ 12分考点： 1．线面平行的判定定理；2．线面垂直的判定定理．2．（Ⅰ）证明见解析；（Ⅱ）22P EAD V -=．【解析】试题分析：（Ⅰ）要证面面垂直需证线面垂直，根据题意，需证AC ⊥平面PBD ，因为底面为菱形对角线互相垂直，又因为PD ⊥平面ABCD ，所以AC ⊥平面PBD 得证；（Ⅱ）根据线面平行的性质定理可知：PD 平行平面PBD 与平面ACE 的交线EO ,同时O 为BD 中点,所以E 为PB 中点，所以三棱锥P EAD -的体积等于三棱锥E PAD -即为三棱锥B PAD -体积的一半,进而求得三棱锥P EAD -的体积．试题解析：（Ⅰ）PD ⊥ 平面ABCD ,AC ⊂平面ABCD ,AC PD ∴⊥．四边形ABCD 是菱形,AC BD ∴⊥,又PD BD D = ,AC ⊥平面PBD ．而AC ⊂平面EAC ,∴平面EAC ⊥平面PBD ． 6分（Ⅱ） PD ∥平面EAC ,平面EAC 平面PBD OE =,PD OE ∴∥,O 是BD 中点,E ∴是PB 中点．取AD 中点H ,连结BH , 四边形ABCD 是菱形,60BAD ∠= ,BH AD ∴⊥,又,BH PD AD PD D ⊥= ,BD ∴⊥平面PAD ,332BH AB ==． 9分 12P EAD E PAD B PAD V V V ---==1123PAD S BH =⨯⨯⨯△ 112263622=⨯⨯⨯⨯=． 12分 PA B C DEOH考点：1．面面平行的判定定理;2．线面平行的性质定理;3．三棱锥的体积公式．3．（1）证明详见解析；（2）证明详见解析.【解析】试题分析：本题主要考查线线平行、线面平行、线线垂直、线面垂直等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力.第一问，取PD 、EA 中点，利用中位线得1//2MN CD ==，1//2NG AB ==，而//AB CD ==，∴//MN NG ==，∴说明GHMN 是平行四边形，∴//GH MN ，∴利用线面平行的判定//GH 平面PDAE ；第二问，先利用线面垂直的性质得PD BC ⊥，再利用线面垂直的判定得BC ⊥平面PCD ，即FH ⊥平面PCD ，最后利用面面垂直的判定得平面FGH ⊥平面PCD . 试题解析：（1）分别取PD 的中点M EA ,的中点.N 连结MH NG MN ,,.因为G H ,分别为BE PC ,的中点，所以1//2MN CD == . 因为//AB CD ==，所以//MN NG ==, 故四边形GHMN 是平行四边形.所以//GH MN . 4分又因为GH ⊄平面PDAE ，MN ⊂平面PDAE ，所以//GH 平面PDAE . 6分（2）证明：因为PD ⊥平面ABCD ，BC ⊂平面ABCD ，所以PD BC ⊥.因为,,BC CD PD CD D ⊥= 所以BC ⊥平面PCD .因为F H ,分别为PB PC 、的中点，所以//FH BC所以FH ⊥平面.PCD因为FH ⊂平面FGH ，所以平面FGH ⊥平面PCD . 12分考点：线线平行、线面平行、线线垂直、线面垂直.4．（Ⅰ）见解析（Ⅱ）2823【解析】试题分析：对于第一问要证明面面垂直，关键是把握住面面垂直的判定定理，在其中一个平面内找出另一个平面的垂线即可，而在找线面垂直时，需要把握住线面垂直的判定定理的内容，注意做好空间中的垂直转化工作，对于第二问，注意在求棱锥的体积时，注意把握住有关求体积的量是多少，底面积和高弄清楚后就没有问题.试题解析：（Ⅰ）证明：在Rt ΔDEF 中,45ED DF DEF =∴∠=oQ ,在Rt ΔABE 中，,45AE AB AEB =∴∠=o Q ,90BEF ∴∠=o ,EF BE ∴⊥. 3分平面PBE ⊥平面BCDE ，且平面PBE 平面BCDE BE =∴ EF ⊥平面PBE ,EF ⊂Q 平面PEF ，∴平面PBE ⊥平面PEF . 6分（Ⅱ）解：过P 做PO BE ⊥,PO ⊂平面,PBE 平面PBE ⊥平面BCDE 且平面PBE 平面BCDE BE =∴ PO ⊥平面BCDE ,四棱锥P BCFE -的高22h PO ==. 8分ABE DEF S S S S ∆∆=--矩形ABCD 四边形BCFE116444221422=⨯-⨯⨯-⨯⨯=， 10分则112821422333P BCFE BCFE V S h -=⋅=⨯⨯=四边形. 12分考点：面面垂直的判定，棱锥的体积.5．（Ⅰ）参考解析；（Ⅱ）参考解析；（Ⅲ）4:1【解析】试题分析：（Ⅰ）要证线面垂直等价转化为线线垂直，由圆周角所对的弦为直径即可得AF 与BF 垂直，再根据面面垂直的性质即可得CB 与AF 垂直.由此即可得到结论.（Ⅱ）线面平行等价转化为线线平行，通过做DF 的中点即可得到一个平行四边形，由此即可得到线线平行，即可得到结论.（Ⅲ）根据四棱锥的体积公式，以及三棱锥的体积公式，其中有些公共的线段，由此即可求出两个体积的比值.试题解析：（Ⅰ）证明：∵平面ABCD ⊥平面ABEF ，CB ⊥AB ，平面ABCD ∩平面ABEF=AB ， ∴CB ⊥平面ABEF ，∵AF ⊂平面ABEF ，∴AF ⊥CB ，又∵AB 为圆O 的直径，∴AF ⊥BF ，∴AF ⊥平面CBF.（Ⅱ）设DF 的中点为N ，则MN ∥12CD ，又12AO CD ∥，则MN AO ∥，MNAO 为平行四边形， DB C E F PO∴OM ∥AN ，又AN ⊂平面DAF ，PM ⊄平面DAF ，∴OM ∥平面DAF.（Ⅲ）过点F 作FG ⊥AB 于G ，∵平面ABCD ⊥平面ABEF ，∴FG ⊥平面ABCD ，∴1233F ABCD ABCD V S FG FG -=⋅=， ∵CB ⊥平面ABEF ，∴11113326F CBEC BFE BFE V V S CB EF FG CB FG --∆==⋅=⋅⋅⋅=， ∴:4:1F ABCD F CBE V V --=考点：1.线面垂直.2.线面平行.3.棱锥的体积公式. 6．（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）16【解析】试题分析：Ⅰ）证明面面垂直，一般利用面面垂直判定定理，即从证明线面垂直出发：因为11B C ⊥面11ABB A 所以111B C A B ⊥．又11A B AB ⊥，所以1A B ⊥面11ADC B ,所以平面11ADC B ⊥面1A BE .（Ⅱ）证明线面平行，一般利用线面平行判定定理，即从证明线线平行出发，这一般可利用平面几何知识得以证明：设11AB A B O = ，则易得四边形1B OEF 为平行四边形，所以1B F //OE .所以F B 1//面BE A 1 （Ⅲ）求棱锥体积，关键在于确定其高。

高考数学立体几何大题30题

高考数学立体几何大题30题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN立体几何大题1．如下图，一个等腰直角三角形的硬纸片ABC 中，∠ACB ＝90°，AC ＝4cm ，CD 是斜边上的高沿CD 把△ABC 折成直二面角．（1）如果你手中只有一把能度量长度的直尺，应该如何确定A ，B 的位置，使二面角A －CD －B 是直二面角？证明你的结论．（2）试在平面ABC 上确定一个P ，使DP 与平面ABC 内任意一条直线都垂直，证明你的结论．（3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值．解：（1）用直尺度量折后的AB 长，若AB ＝4cm ，则二面角A －CD －B 为直二面角．∵ △ABC 是等腰直角三角形，(),cm 22DB AD ==∴又∵ AD ⊥DC ，BD ⊥DC ．∴ ∠ADC 是二面角A －CD －B 的平面角．有时当,cm 4AB ,22DB AD ===.90ADB .AB DB AD 222︒=∠∴=+（2）取△ABC 的中心P ，连DP ，则DP 满足条件 ∵ △ABC 为正三角形，且 AD ＝BD ＝CD ．∴ 三棱锥D －ABC 是正三棱锥，由P 为△ABC 的中心，知DP ⊥平面ABC ， ∴ DP 与平面内任意一条直线都垂直．（3）当小球半径最大时，此小球与三棱锥的4个面都相切，设小球球心为0，半径为r ，连结OA ，OB ，OC ，OD ，三棱锥被分为4个小三棱锥，且每个小三棱锥中有一个面上的高都为r ，故有ABC O ABD O ADC O BCD O BCD A V V V V V -----+++=代入得3623r -=，即半径最大的小球半径为3623-．A B C 第1题图 AB CD 第1题图2．如图，已知正四棱柱ABCD —A 1B 1C 1D 1的底面边长为3，侧棱长为4，连结A 1B ，过A 作AF ⊥A 1B 垂足为F ，且AF 的延长线交B 1B 于E 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020高考数学之立体几何解答題23 題
一．解答题（共 23 小题）
1．在如图所示的几何体中，四边形 ABCD 是菱形， ADNM 是矩形，平面 ADNM ⊥平面 ABCD ，
∠DAB=60 °，AD=2 ， AM=1 ， E 为 AB 的中点．
（Ⅰ）求证： AN ∥平面 MEC；
（Ⅱ）在线段 AM 上是否存在点 P，使二面角 P﹣ EC﹣D 的大小为？若存在，求出 AP 的长 h；若不存在，请说明理由．
2．如图，三棱柱中 ABC ﹣A1B1C1 中，点 A1 在平面 ABC 内的射影 D 为棱 AC 的中点，侧面 A1ACC 1为边长为 2 的菱形， AC⊥CB，BC=1 ．
（Ⅰ）证明： AC 1⊥平面 A 1BC；（Ⅱ）求二面角 B﹣ A1C﹣B1的大小．
3．如图，已知四棱锥 P﹣ABCD ，PB⊥AD 侧面 PAD 为边长等于 2的正三角形，底面 ABCD 为菱形，侧面PAD 与底面 ABCD 所成的二面角为 120°．
（I）求点 P 到平面 ABCD 的距离，
（II ）求面 APB 与面 CPB 所成二面角的大小．
4．在正三棱锥 P﹣ABC 中，底面正△ ABC 的中心为 O，D 是 PA 的中点， PO=AB=2 ，求 PB 与平面 BDC 所成角的正弦值．
5．如图，正三棱锥 O ﹣ABC 的三条侧棱 OA 、OB 、 OC 两两垂直，且长度均为 2．E 、F 分别是 AB 、AC 的中点， H 是 EF 的中点，过 EF 作平面与侧棱 OA 、OB 、OC 或其延长线分别相交于 A 1、B 1、C 1，已知．（ 1）求证： B 1C 1⊥平面 OAH ；
（ 2）求二面角 O ﹣A 1B 1﹣C 1 的大小．
6．如图，在三棱锥 A ﹣ BCD 中，侧面 ABD 、ACD 是全等的直角三角形， AD 是公共的斜边，且AD= ，BD=CD=1 ，另一个侧面是正三角形．
1）求证： AD ⊥BC ．
E ，使 ED 与面 BCD 成 30°角？若存在，确定
E 的位置；若不存在，说明理由． 2）求二面角 B ﹣AC ﹣D 的大
小．
7．如图，在四棱锥 P ﹣ ABCD 中， AD ∥ BC ，∠ ADC= ∠ PAB=90 °， BC=CD=
PA 与CD 所成的角为 90°．
（Ⅰ）在平面 PAB 内找一点 M ，使得直线 CM ∥平面 PBE ，并说明理由；（Ⅱ）若二面角 P ﹣CD ﹣A 的大小为 45°，求直线 PA 与平面 PCE 所成角的正弦值．
8．如图，在三棱台 ABC ﹣DEF 中，平面 BCFE ⊥平面 ABC ，∠ ACB=90 °，BE=EF=FC=1
， BC=2 ， AC=3 ．（ Ⅰ ）求证： BF ⊥平面 ACFD ；
（ Ⅱ ）求直线 BD 与平面 ACFD 所成角的余弦值．
9．如图，在以 A ，B ，C ，D ，E ，F 为顶点的五面体中，面 ABEF 为正方形， AF=2FD ，∠
AFD=90 °，且二面角 D ﹣AF ﹣E 与二面角 C ﹣BE ﹣ F 都是 60°．
（Ⅰ）证明平面 ABEF ⊥平面 EFDC ；（Ⅱ）求二面角 E ﹣ BC ﹣A 的余弦值．
AD ．E 为棱 AD 的中点，异面直线
10．如图，已知边长为 6的菱形 ABCD ，∠ ABC=120 °，AC 与BD 相交于 O ，将菱形 ABCD 沿对角线 AC 折起，使 BD=3 ．
（1）若 M 是 BC 的中点，求证：在三棱锥 D ﹣ABC 中，直线 OM 与平面 ABD 平行；
（2）求二面角 A ﹣BD ﹣O 的余弦值；
（ 3）在三棱锥 D ﹣ ABC 中，设点 N 是 BD 上的一个动点，试确定 N 点的位置，使得 CN=4 ．
11．如图所示的多面体 ABCDE 中，已知 AB ∥DE ，AB ⊥AD ，△ACD 是正三角形， AD=DE=2AB=2 ，BC= ，F 是 CD 的中点．
（ 1）求证： AF ∥平面 BCE ；
（ 2）求直线 CE 与平面 ABED 所成角的余弦值；
（ 3）求多面体 ABCDE 的体积．
12．如图，已知矩形 ABCD 所在平面垂直于直角梯形 ABPE 所在平面于直线 AB ，且 AB=BP=2 ，
AD=AE=1 ，AE ⊥AB ，且 AE ∥BP ．
Ⅰ）设点 M 为棱 PD 中点，求证： EM ∥平面 ABCD ；
若不存在，请说明理由．
Ⅱ ）线段 PD 上是否存在一点 N ，使得直线 BN 与平面 PCD 所成角的正弦值等于？若存在，
试确定点 N 的位置；
13．如图，在三棱锥 P ﹣ABC 中，∠ PAB= ∠PAC=∠ ACB=90 °．
（ 1）求证：平面 PBC ⊥平面 PAC ；
（2）若 PA=1，AB=2 ， BC= ，在直线 AC 上是否存在一点 D ，使得直线 BD 与平面 PBC 所成角为 30°？若存在，求出 CD 的长；若不存在，说明理由．
14．如图，在四棱锥 P ﹣ABCD 中，底面 ABCD 是平行四边形， ∠BCD=135 °，侧面 PAB ⊥底面 ABCD ，∠ BAP=90 °， AB=AC=PA=2 ， E ，F 分别为 BC ，AD 的中点，点 M 在线段 PD 上．
（ Ⅰ ）求证： EF ⊥平面 PAC ；
（ Ⅱ ）如果直线 ME 与平面 PBC 所成的角和直线 ME 与平面 ABCD 所成的角相等，求的值．
Ⅰ）求证： CD ⊥AM ；
AM 与平面 BDM
所成角的正弦值．
15．如图，在多面体 ABCDM 平面 BCD ， AB ⊥平面 BCD ．中，△ BCD 是等边三角形，△ CMD 是等腰直角三角形，∠ CMD=90 °，平面 CMD ⊥
Ⅱ ）若 AM=BC=2 ，求直
16．如图，矩形ABCD 所在的平面和平面ABEF 互相垂直，等腰梯形ABEF 中，AB ∥EF，AB=2 ，AD=AF=1 ，∠ BAF=60°，O，P分别为 AB，CB的中点， M为底面△ OBF的重心．
（Ⅰ）求证： PM ∥平面 AFC；
（Ⅱ ）求直线 AC 与平面 CEF 所成角的正弦值．
17．已知菱形 ABCD ，AB=2 ，∠BAD= ，半圆 O 所在平面垂直于平面 ABCD ，点 P 在半圆弧上．（不同于B ，C）．
（1）若 PA与平面 ABCD 所成角的正弦值为，求出点 P 的位置；
（2）是否存在点 P，使得 PC⊥ BD ，若存在，求出点 P 的位置，若不存在，说明理由．
18．如图，菱形 ABCD 中，∠ ABC=60 °，AC 与BD相交于点 O，AE ⊥平面 ABCD，CF∥AE，
AB=AE=2 ．（Ⅰ）求证： BD ⊥平面 ACFE ；
（Ⅱ）当直线 FO与平面 BED 所成角的大小为 45°时，求 CF 的长度．
19．如图，在四棱锥 P﹣ ABCD 中，等边△ PAD 所在的平面与正方形 ABCD 所在的平面
O为 AD 的中点，互相垂直， E 为 DC 的中点，且 AD=2 ．
（Ⅰ ）求证： PO⊥平面 ABCD ；
（Ⅱ）求二面角 P﹣EB﹣ A 的余弦值；
（Ⅲ）在线段 AB 上是否存在点 M，使线段 PM 与△PAD 所在平面成 30°角．若存在，求出 AM 的长，若不存在，请说明理由．
20．在斜三棱柱 ABC ﹣ A 1B 1C1中，底面 ABC 是正三角形， E 是 AB 中点， A 1E⊥平
面 ABC．（ I）证明： BC1∥平面 A1EC；
（II）若 A1A⊥A1B，且 AB=2 ．
① 求点 B 到平面 ACC 1A1 的距离；
② 求直线 CB1 与平面 ACC 1A 1 所成角的正弦值．
1）求证： DF ⊥平面 ABCD ；
2）若△ ABD 是边长为 2 的等边三角形，且 BF 与平面 ABCD 所成角的正切值为 1，求点 E 到平面 BDF 的距离．
22．如图，在三棱柱 ABC ﹣A 1B 1C 1中，G 为ABC 的重心，
（ 1）求证： GE ∥平面 AA 1B 1B ；
（2）若侧面 ABB 1A 1⊥底面 ABC ，∠ A 1AB= ∠BAC=60
°，AA 1=AB=AC=2 ，求直线 A 1B 与平面 B 1GE 所成角正弦值．
21．如图，在多面体 EF ﹣ABCD 中， ABCD ， ABEF 均为直角梯
形，∠ 平面 DCEF ⊥平面 ABCD ．
ABE= ∠ABC= DCEF 为平行四边形，
θ的
BC 1．
23．如图，在四棱锥 P﹣ABCD 中， PA⊥底面 ABCD，AD∥BC，AD⊥CD，BC=2，AD=CD=1，M是 PB的中点．（Ⅰ ）求证： AM ∥平面 PCD；
（Ⅱ ）求证：平面 ACM ⊥平面 PAB；。