编译原理第五章
编译原理chapter5

若S+ …X,则X•>#。
第五章 优先分析法
第二节 简单优先分析方法
三、简单优先分析的基本思想
根据优先关系的定义,将简单优先文法中各 文法符号之间的这种关系用一个矩阵表示,称 作简单优先矩阵。PDA读入一个单词后,比较 栈顶符号和该单词的优先级,若栈顶符号优先 级低于该单词,继续读入;若栈顶符号优先级 高于或等于读入符号,则找句柄进行归约,找 不到句柄就继续读入。直到最后栈内只剩下开 始符号,输入串读到“#”为止。此时识别正 确。
1、自下而上归约
2、规定算符(更一般地说,指终结符)的优先级 及结合规则,以使得分析过程唯一
3、比较相邻两个算符而决定动作
注:1)这里的关键是对所有算符定义某种优先 关系
2)算符优先分析法是仿效四则运算的计算过 程而构造的一种语法分析方法
第五章 优先分析法 第三节 算符优先分析方法 一、基本思想
4、实例 表达式文法:
第五章 优先分析法 第二节 简单优先分析方法
四、简单优先矩阵
用于表示文法符号之间的简单优先关系的矩阵。
注:简单优先矩阵的构造可通过Warshall算法实 现。
第五章 优先分析法 第二节 简单优先分析方法
五、简单优先分析法的优缺点
优点:技术简单 缺点:适用范围小,分析表尺寸太大。
第五章 优先分析法 第三节 算符优先分析方法 一、基本思想
设A1A2…Ai-1AiAi+1…An是文法G的一个句型, 1)、若AiVN,则Ai-1、Ai+1 VT,即不许出现相继两个
非终结符;
第五章 优先分析法
第三节 算符优先分析方法 四、算符优先文法及优先表的构造 3、算符文法和算符优先文法定义的意义
编译原理课件Chapter_5

•
结点N的属性值由N的产生式所关联的语义规则来定义 通过N的子结点或N本身的属性值来定义
结点N的属性值由N的父结点所关联的语义规则来定义 依赖于N的父结点、N本身和N的兄弟结点上的属性值 不允许N的继承属性通过N的子结点上的属性来定义, 但允许N的综合属性依赖于N本身的继承属性 终结符号有综合属性 (来自词法分析),但无继承属性
–
每个语义规则都根据产生式体中的属性值来计算头部 非终结符号的属性值
栈中的状态/文法符号可以附加相应的属性值 归约时,按照语义规则计算归约得到的符号的属性值 要求副作用不影响其它属性的求值 没有副作用的SDD称为属性文法
•
S属性的SDD可以和LR语法分析器一起实现
– –
•
语义规则不应该有复杂的副作用
•
•
•
抽象语法树的表示方法
– –
叶子结点中只存放词法值 内部结点中存放了op值和参数 (通常指向其它结点)
30
构造简单表达式的抽象语法树的SDD
属性E.node指向E对应的抽象语法树的根结点
31
表达式抽象语法树的构造过程
•
输入
•
a–4+c
•
步骤
p1 = new Leaf(id, entry_a); p2 = new Leaf(num, 4); p3 = new Node('–', p1, p2); p4 = new Leaf(id, entry_c); p5 = new Node('+', p3, p4);
–
–
9
语法分析树上的SDD求值 (1)
•
•
实践中很少先构造语法分析树再进行SDD求值, 但在分析树上求值有助于翻译方案的可视化,便 于理解 注释语法分析树
编译原理第五章 (1)

简单优先分析算法要点
找第一个使Sj⊳Sj+1的Sj 从Sj开始往前(左)找第一个使Si-1⊲Si的Si
用SiSi+1…Sj去查产生式的右部,并用相应 的左部符号代替句柄SiSi+1…Sj (归约) 。
重复上述过程,直至输入符结束。如果归 约出文法的开始符号则成功。否则失败。
简单优先分析实例
优先关系矩阵 一个文法的全部优先关系可以用矩阵来表示,Biblioteka 称作优先关系矩阵。
例: Z bMb Ma M (L L Ma)
Z FIRST b LAST b M a, ( a ,L, ) L M, ( , a )
Z FIRST b 例: Z bMb LAST b
文法优先关系的确定 FIRST(W) ={S | W + S…,S(VNVT)} LAST(W) ={S | W + …S,S(VN VT)}
若有U…SiSj…: 则有Si Sj ; 若有U…SiW…:任SjFIRST(W),有Si ⊲ Sj 若有U…VW…:任SiLAST(V), Sj(FIRST(W) {W})则有Si ⊳ Sj 输入流的开始和结束标志 ‘#’,文法的开始符为Z, SFIRST(Z),有# ⊲ S,; 且# ⊲ Z SLAST(Z),有S ⊳ #,; 且Z ⊳ #
符号栈 # #b #b( 关系 输入流 b(aa)b# (aa)b# aa)b#
#b(a #b(M #b(Ma #b(Ma)
#b(L #bM
⊲ ⊲ ⊲ ⊳
a)b# a)b# )b# b#
b# b#
例: Z bMb Ma M (L L Ma)
编译原理第5章

二.算符优先分析法的基本思路
是仿照算术表达式的四则运算过程而设计的一 种语法分析方法。
终结符号 运算符 非终结符号 运算对象 算符优先分析法的关键在于用合适的方法去定义 任何两个可能相继出现的结符号a和b(它们之间 可能插有一个非终结符号)之间的优先级。然后利 用这种关系比较相邻运算符之间的优先级来确定 可归约串并进行归约。
bcde#
归约Ab
4
#aA
bcde#
移进
5
#aAb
cde#
归约AAb
6
#aA
cde#
移进
7
#aAc
de#
移进
8
#aAcd
e#
归约Bd
9
#aAcB
e#
移进
10
#aAcBe
# 归约SaAcBe
11
#S
#
接受
5.2算符优先分析法 概述 一. 算符文法的定义 二. 算符优先分析法的基本思想
算符优先分析法概述
第五章 自底向上分析
P94
概论
▪ 思想
• 自下而上的语法分析过程是最右推导的逆过
程(最左归约);即从输入串开始,朝着文 法开始符号进行归约,直至到达文法开始符 号为止的过程。
▪ 核心
• 寻找句型中的“句柄”进行归约,用不同的
方法寻找句柄,就可获得不同的分析方法
5.1 自底向上分析
一、规范归约
•归约 G=(VT,VN,S,P),α, β ∈(VT∪VN)*,A→β∈P,
规范句型的特点:
生式如下:
①S→aAcBe
②A→b
句柄后不会出现非终结符号。
③A→Ab
④B→d
对输入串abbcde#进行分析
编译原理第5章

语法分析-自下而上分析 语法分析-
E E T | E+T T F | T*F F i | (E) E + T 短语有:i, T * F, E+T * F, E + T * F + i 直接短语有: i, T * F 句柄是:T * F
第7页
E + T F
T *
F
i
编译原理
语法分析-自下而上分析 语法分析-
接短语
*
位于一个句型最左边的直接短语称为句柄. 句型最左边的直接短语称为 位于 句型---> 短语 ---> 直接短语 --->句柄 句型 句柄
注: 每次归约的部分必须是称之为句柄 句柄的字符串(最右 句柄 推导)。 关键的问题是如何识别句柄 如何识别句柄
第6页
编译原理
例:下述文法的另一个句型: 下述文法的另一个句型: E+T * F + i 其短语、直接短语、句柄分别是? 其短语、直接短语、句柄分别是?
第17页
T *
F
i
编译原理 算符优先分析法小结
优点 简单、效率高 能够处理部分二义性文法 缺点 文法书写限制大 占用内存空间大 不规范、存在查不到的语法错误
语法分析-自下而上分析 语法分析-
第18页
编译原理
语法分析-自下而上分析 语法分析-
LR分析法 LR分析法
L表示从左到右扫描输入串,R表示构造一个 表示从左到右扫描输入串, 表示构造一个 表示从左到右扫描输入串 最右推导的逆过程。 最右推导的逆过程。 大多数用上下文无关文法描述的程序语言都 可用LR分析器予以识别 分析器予以识别。 可用 分析器予以识别。 能用I.R分析器分析的文法类 包含能用LL(1) 分析器分析的文法类, 能用 分析器分析的文法类,包含能用 分析器分析的全部文法类, 分析法在自左 分析器分析的全部文法类,LR分析法在自左 至右扫描输入串时就能发现其中的任何错 并能准确地指出出错地点。 误.并能准确地指出出错地点。
编译原理 第五章

一个文法符号串的开始符号集合定义如下: 定义5.1 设G=(VT,VN,S,P)是上下文无关文法 FIRST(α)={a|α aβ,a∈VT,α,β∈V*} 若α ε,则规定ε∈FIRST(α).
不难求出在例5.2文法G2中 FIRST(Ap)={a,c} FIRST(Bq)={b,d} 因此有 FIRST(A)∩(FIRST(B)= 这样文法G2中,关于S的两个产生式的右部虽然都以非 终结符开始,但它们右部的符号串可能推导出的首符号集 合不相交,因而可以根据当前的输入符号是属于哪个产生 式右部的首符号集合而决定选择相应产生式进行推导,因 此仍能构造确定的自顶向下分析。
定义5.4 一个上下文无关文法是LL(1)文法的充分 必要条件是:对每个非终结符A的两个不同产生式, A→α, A→β,满足 SELECT(A→α)∩SELECT(A→β)= 其中α,β不同时能 ε。
LL(1)文法也可定义为: 一个文法G是LL(1)的,当且仅当对于G的每 一个非终结符A的任何两个不同产生式 A→α|β, 下面的条件成立: ① FIRST(α)∩FIRST(β)= ,也就是α和 β推导不出以某个相同的终结符a为首的符号串; 它们不应该都能推出空字ε. ② 假若β ε那么, FIRST(α)∩ FOLLOW(A)= 也就是,若β ε 则α所能推出的串的首符号不应在FOLLOW(A) 中(如例5.3)。这种表示与定义5.4相比计算步骤 少,但不如定义5.4清晰。
编译原理 第9讲第五章 优质课件

LL(1)文法判别
LL(1)文法(充分必要条件) 一个上下文无关文法G是LL(1)的,当且仅当对于G的每一个非终结符
A的任何两个不同产生式A α β ,下面的条件成立: 1.FIRST(α )∩FIRST(β )=,也就是α 和β 推导不出以同一个终结
符a为首的符号串;它们不应该都能推出空字. 2.假若β =>* ,那么,FIRST(α )∩FOLLOW(A)=.
识别输入串w=ccap是否为该文法的句子 试探,推导过程:
S=>Ap=>cAp=>ccAp=>ccap 试探成功
文法特点: 产生式的右部不全是由终结符开始 如果两个产生式有相同的左部,那么它们右部由不同的终结符或非终结符开始 没有空产生式
12
例子(3)
例:文法G1: S → aA | d
A → bAS | ε
3
语法分析
在语言的编译实现中,把句子分析的过程
称为语法分析,即完成这个任务的程序 称为语法分析程序或称为识别程序。分 析算法又称识别算法。 从左到右的分析算法,即总是从左到右地
识别输入符号串,首先识别符号串中的
最左符号,进而依次识别右边的一个符
号,直到分析结束。
4
分析算法分类
自上而下分析法:
从文法的开始符号出发,寻找与输入符 号串匹配的推导,或者说,为输入串寻 找一个最左推导。
这时
w的第二个符号可以与叶子 结点a得以匹配,但第三个 符号d却不能与下一叶子结 点b匹配
怎么办?-查看A有无另一个选 择,有!回溯,把A为根的 子树剪掉,扫描过的输入串 中的a吐出来,再试探用产生 式(3)构造推导S cAd cad
识别输入串w=caa的过程: 1.S cAd 2.选择(2)扩展A,得到推导S cAd
编译原理-第五章习题答案

上一页
下一页
11
例:5.3 文法:SaAcBe A bAb B d 句子:abbcde
步骤 (1) (2) (3) (4) (5) (6)
栈
# #a #ab #aA #aAb #aA #aAc #aAcd #aAcB #aAcBe #S
输入 abbcde# bbcde# bcde# bcde# cde# cde#
上一页
下一页
20
5)构造算符优先文法G的优先表的算法
思路:对文法中的每一个产生式的候选式检查,判断句型中相邻符号之间 的关系 来构造优先表; 具体算法: FOR 每条产生式P→X1X2…Xn FOR i=1 TO n-1 IF Xi,Xi+1∈VT,THEN Xi=Xi+1; IF i ≤n-2且Xi,Xi+2∈VT,Xi+1∈VN THEN Xi=Xi+2; IF Xi∈VT,Xi+1∈VN THEN FOR FIRSTVT(Xi+1)中的每个a Xi <. a; NEXT IF Xi∈VN,Xi+1∈VT THEN FOR LASTVT(Xi)中的每个a DO a .> Xi+1; NEXT NEXT NEXT
上一页
下一页
8
例:5.1 P85 文法: E→T|E+T T→F|T*F F→i|(E) 句型:i1*i2+i3其中:短语有i1、i2、i3、i1*i2、 i1*i2+i3 直接短语:i1、i2、i3;句柄:i1 例:5.2 P85 文法如上 E 句型:E+T*F+i 短语:E+T*F+i,E+T*F,T*F,i 直接短语:T*F和i E + 句柄:T*F
编译原理 第五章 语法分析-自下而上分析

5.2.2 算符优先分析算法
• 素短语:
–是一个短语,它至少含有一个终结符,并且,除 它自身之外不再含任何更小的素短语。
• 最左素短语:
–最左边的素短语是最左素短语。
• 例子:
– 对文法(5.3)p*p和i是句型p*p+i的素短语,而p*p+i 本身也是素短语。
பைடு நூலகம்
• 算符优先文法:
算符优先文法,我们把句型(括在两个#之间) 的一般形式写成: #N1a1N2a2…NnanNn+1# 其中,每个ai都是终结符,Ni是可有可无的非终结 符。 文法G的任何短语是满足如下条件的最左子串 Njaj…NiaiNi+1 aj-1⋖ aj aj ≖ aj+1 , …,aj-1 ≖ ai ai ⋗ ai+1
– 对于每个终结符a(包括#)令其对应两个符号fa 和ga ,画一张以fa 和ga 所有符号为结点的方向图, 如 果 a⋗≖b, 那 么 , 就 从 fa 画 一 箭 弧 至 gb ; 如 果 a ⋖≖b,就画一条从gb到fa的箭弧。 – 对每个结点都赋予一个数,此数等于从该结点能 到达结点(包括出发结点自身在内)的个数。赋 给fa的数作为f(a),赋给gb的数作为g(b)。 –检查所构造出来的函数f和g,看它们 同原来的关 系表是否有矛盾。如果没有矛盾,则f和g就是所 要的优先函数。如果有矛盾,那么,就不存在优 先函数。
• 例子:假定文法G
S→aAcBe A→b A→Ab B→d 输入串abbcde归约到S过程。
图5.1 规约中符号栈的变迁
步骤 动作
1 进 a
2 进 b
3 归 (2)
4 进 b
5 归 (3)
6 进 c
7 进 d d
编译原理 第5章--代码优化

(2) 确定满足以下条件的出口语句: 确定满足以下条件的出口语句 出口语句: 下一个入口语句的前导语句 入口语句的前导语句; ① 下一个入口语句的前导语句; 转移语句 包括转移语句自身); 语句(包括转移语句自身 ② 转移语句 包括转移语句自身 ; 停语句 包括停语句自身 包括停语句自身)。 ③ 停语句(包括停语句自身 。
第5章
代码优化
(3) 图中各个结点上可能附加一个或多个标识符,表示这些 图中各个结点上可能附加一个或多个标识符 附加一个或多个标识符, 变量具有该结点所代表的值。 变量具有该结点所代表的值。
一个基本块由一个四元式 序列组成 四元式都可以用相应的 一个 基本块由一个四元式序列 组成 , 且 每一个 四元式都可以用 相应的 基本块 由一个四元式序列组成, 每一个四元式都可以用 DAG结点表示。 结点表示。 结点表示 给出了不同四元式和与其对应的DAG结点形式。图中,各结点圆圈 结点形式。 图5–1给出了不同四元式和与其对应的 给出了不同四元式和与其对应的 结点形式 图中, 中的ni是构造 构造DAG过程中各结点的编号, 过程中各结点的编号, 中的 过程中各结点的编号 而各结点下面的符号(运算符、标识符或常数)是各结点的标记, 是各结点的标记 而各结点下面的符号 运算符、标识符或常数 是各结点的标记,各结点右 运算符 边的标识符是结点上的附加标识符。 边的标识符是结点上的附加标识符。 附加标识符 除了对应转移语句的结点右边可附加一语句位置来指示转移目标外, 除了对应转移语句的结点右边可附加一语句位置来指示转移目标外,其余 对应转移语句的结点右边可附加一语句位置来指示转移目标外 各类结点的右边只允许附加标识符。 各类结点的右边只允许附加标识符。 除对应于数组元素赋值的结点 标记为 继外, 除对应于数组元素赋值的结点(标记为 ]=)有三个后继外,其余结点最多只 应于数组元素赋值的结点 标记为[ 有三个后继外 有两个后继。 两个后继。 后继
编译原理chapter5

•22
a < b, b < c a<c
|– M : int, |– N : int
|– M + N : int
5.2 描述类型系统的语言
类型系统的形式化 类型表达式 定型断言 定型规则
•23
5.2 描述类型系统的语言
5.2.1 断言
断言的形式 |– S S的所有自由变量都声明在中 其中 是一个静态定型环境,如x1:T1, …, xn:Tn S的形式随断言形式的不同而不同 断言有三种具体形式
•30
5.3 简单类型检查器的说明
例: i : integer; j : integer; j := i mod 2000
•31
5.3 简单类型检查器的说明
5.3.2 类型系统 环境规则
(Env )
•32
|– |T, id dom () , id : T |
(Decl Var)
5.1.2 类型化语言和类型系统 类型化的语言
变量的类型 类型化的语言 未类型化的语言 显式类型化语言 类型是语法的一部分
•10
5.1 类型在程序设计语言中的作用
5.1.2 类型化语言和类型系统 类型化的语言
变量的类型 类型化的语言 未类型化的语言 显式类型化语言 隐式类型化的语言
类型系统的形式化 类型系统是一种逻辑系统
有关自然数的逻辑系统 -自然数表达式(需要定义它的语法) a+b, 3 - 合适公式(断言,需要定义它的语法) a+b=3, (d=3)(c<10) - 推理规则
•19
a < b, b < c a<c
5.2 描述类型系统的语言
类型系统的形式化 类型系统是一种逻辑系统
编译原理答案第五章
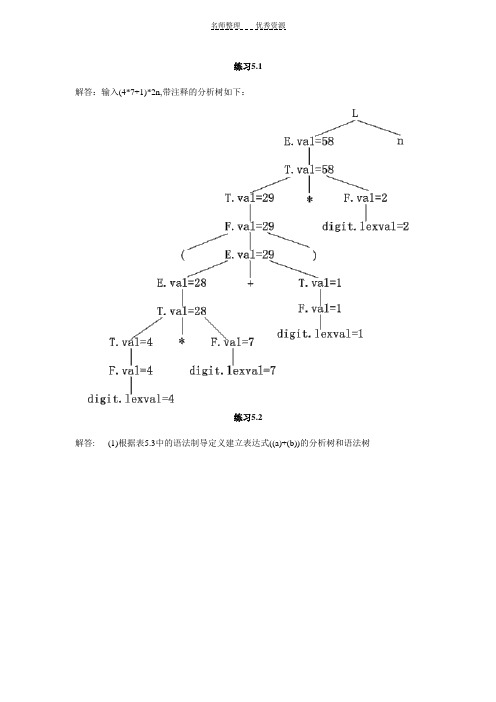
练习5.1解答:输入(4*7+1)*2n,带注释的分析树如下:练习5.2解答: (1)根据表5.3中的语法制导定义建立表达式((a)+(b))的分析树和语法树(2)根据图5.17的翻译模式构造((a)+(b))的分析树和语法树练习5.3解答:设置下面的函数和属性:expr1||expr2:把表达式expr2拼写在表达式expr1后面。
deletep(expr):去掉表达式expr左端的‘(’和右端的‘)’。
E.expr,T.expr,F.expr:属性变量,分别表示E,T,F的表达式。
E.add,T.add,F.add,属性变量,若为true,则表示其表达式中外层有‘+’号,否则无‘+’号。
E.pmark,T.pmark,F.pmark,属性变量,若为true,表示E,T,F的表达式中左端为‘(’,右端是‘)’。
语法制导定义如下:产生式语义规则E -> E1 +T if(T.pmark==true)THEN E.expr=E1.expr||'+'||deletep(T.expr) ELSE E.expr:=E1.expr||'+'||T.expr;E.add:=true;E.pmark:=false;E -> T if(T.pmark==true)THEN E.expr:=deletep(T.expr)ELSE E.expr:=T.expr;E.add:=T.add;E.pmark:=false;T -> T1*F T.expr:=T1.expr||'*'||F.expr; T.add:=false;T.pmark:=false;T -> F T.expr:=F.expr; T.add:=F.add;T.pmark:=F.pmark;F -> (E) if(E.add==false)THEN BEGINF.expr:=E.expr;F.add:=false;F.pmark:=false;ENDELSE BEGINF.expr:='('||E.expr||')';F.add:=true;F.pmark:=true;END;F -> id F.expr:=id.lexval;F.add:=false;F.pmark:=false;练习5.4解答: (1)语法制导定义如下:产生式语义规则E -> E1+T if(E1.type==int) AND (T.type==int) THEN E.type:=intELSE E.type:=real;E -> T E.type:=T.type;T -> num T.type:=int;T -> num.num T.type:=real;(2)设E.pf和T.pf分别是E和T的前缀形式,||是两个字符串的连接,语法制导定义如下:产生式语义规则E -> E1+T if(E1.type==int) AND (T.type==int)THEN E.type:=intELSE BEGINE.type:=real;if(E1.type==int) AND (T.type==real)THEN E1.pf:='inttoreal'||E1.pfELSE if(E1.type==real)AND(T.type==int)THEN T.pf:='inttoreal'||T.pfEND;E.pf:='+'||E1.pf||T.pf;E -> T E.type:=T.type; E.pf:=T.pf;T -> num T.type:=int; T.pf:=int.lexval;T ->num.numT.type:=real; T.pf:=real.lexval;练习5.5解答: (1)用综合属性决定s.val的语法制导定义:产生式语义规则S -> L S.val:=L.val;S ->L1.L2S.val:=L1.val+L2.val*L2.p;L -> B L.val:=B.val; L.p:=2-1;L -> L1B L.val:=L1.val*2+B.val; L.p:=L.p*2-1;B -> 0 B.val:=0;B -> 1 B.val:=1;注:L.p表示恢复L.val的因子。
编译原理_第5章(清华大学)

学习目标: ➢掌握:LL(1)文法的判别,预测分析
法,递归子程序的构造方法 ➢理解:LL(1)文法 ➢了解:不确定的自顶向下分析
语法分析的作用是识别由词法分析给出的单词序 列是否是给定文法的正确句子
分类:
语法分析
自顶向下分析 自底向上分析
确定的
不确定的 算法优先分析(第六章)
进行推导,类似地LL(k)文法需要向前看K个符号才 可以确定选用哪个产生式。
例 有文法G[S]为:
S→aAS
SELECT(S→aAS)= {a}
S→b
SELECT(S→b)= {b}
A→bA
SELECT(A→bA)= {b}
A→ε
SELECT(A→ε)=Follow(A)= {a,b}
Hale Waihona Puke 由于SELECT(A→bA)∩SELECT(A→ε)={b}≠Φ,
此外若可能导出空串,A自动获得匹配,输入符a 有可能与A后的一个符号匹配,所以当a应属于 Follow(A)时,选择产生式A→也是可以的。
直观上说某产生式A→α的选择集合是指遇到哪些输 入符号(包括#)时选用该产生式向下推导。
例 G3[S]: 若α≠>*ε,则SELECT(A→α)=FIRST(α) S→aA 若α=>*ε, 则SELECT(A→α)
例文法G2[S]: S→Ap FIRST(Ap)={a,c}
S→Bq FIRST(Bq)={b,d}
A→a
FIRST(a)={a }
A→cA FIRST(cA)={c}
B→b
FIRST(b)={b}
B→dB FIRST(dB)={d}
由于同一非终结符的两个产生式的右部推导出来的 开始符号集不相交,因此可根据当前输入符属于哪 个产生式右部的开始符号集而决定选哪个产生式进 行推导,可以进行确定的自顶向下分析
编译原理 第五章 词法分析

三、LEX编译程序的工作过程:
1.根据每条识别规则Pi {ACTION i}构造相应的非确 定有限自动机NFA,分别画出它们的状态转换图; 2.将所有的状态转换图连接成一个完整的状态转换图; 3.由状态转换图构造状态转换矩阵; 4.将状态转换矩阵确定化; 5.根据DFA,构造词法分析器;
预处理 子程序 扫描器 单词符号
输入 列表 输入缓冲区
扫描缓冲区
词法分析器的结构
三、设置缓冲器的必要性
之所以要设置缓冲器,是因为对于许多源程序而言,有 时词法分析器为了得到某个单词符号的确切性质,只从该符 号本身所含有的字符不能作出判定,还需要超前扫描若干字 符之后,才能作出确切的分析。 例如:有合法的Fortran语句: DO99K=1,10 和 DO99K=1.10 前者是循环语句,后者是赋值语句,两者的区别在于等 号后的第一个界符不同,前者是逗号,后者是句号,因此为 了识别前者中的关键字‘“DO”,必须超前扫描若干字符之 后,才能作出确切的判定。
3、词法分析器和语法分析器作为协同程序 如果两个或两个以上的程序,他们之间交叉执行,这些程序称为协同程 序。词法分析器和语法分析器也可协工作的方式安排在同一遍中,以生产 者和消费者的关系同步运行。
1.词法分析单独作为一遍
S.P.(字符串)
第一 遍 词法分析 单词 串 S.P.(符号串) 第二 遍 语法分析
例如:
%{ int wordCount = 0; int noCount = 0; %} chars [A-za-z] numbers ([0-9])+ words {chars}+ 注意:凡是对已经定义的正则表达式的名字的引用,都必须用花括 号将它们括起来。在LEX源程序中,起标识作用的符号%%,%{以及%}都 必须处在所在行的最左字符位置。
编译原理 第5章

例:有文法G(S):
S→bAb A→( B | a B→Aa ) 解:文法符号优先关系推导如下: (1) 求=· 关系: 由S→bAb , A→( B, B→Aa ) b =· A, A =· b, (=· B , A =· a, a =· )
自底向上的语法分析
• 核心问题
– 寻找可归约串。对“可归约串”概念的不同定义, 就形成了不同的自底向上的分析方法。在算符优 先分析法中我们用“最左素短语”来刻画“可归 约串”,在“规范归约”中,则用“句柄”来刻 画“可归约串”
分析方法
• 输入串:
abbcde
S → a A c B e A → A b|b B → d
S
b
>·
=· <·
>·
A
(
=·
<· <· =·
=·
<·
B
a
>·
>·
>·
>· =· =·
)
#
寻找句柄
>·
<· <·
>·
简单优先文法的定义: (1)在文法符号集中,任意两个符号之间最多只有 一种优先关系; (2)在文法中任意两个产生式没有相同的右部。
语法树结构如下:
S S S b S b
b
A b
B
b
U S0…Sj-1SjSj+1Sj+2… …Si-1SiSi+1…Sn
算符优先分析
• 我们要通过两个相邻符号SiSi+1之间的关系来找到句 柄: – SiSi+1在句柄内:必然有规则U …SiSi+1… – Si在句柄内部,但是Si+1在句柄之后:必然有规则 U …Si,且存在规范句型…USi+1…。 – 如果Si+1在句柄内,而Si在句柄外,那么必然存在 规范句型…SiU…,且U Si+1…。
编译原理-第五章

利用下面的两条规则,可把包含直接左递归的产生式转换成 用扩展BNF表示法表示的产生式。
❖ ① 提公因子
每当一条产生式中有公因子可提的时候,就把它提出来,若
原产生式是
A→x|xy
则可写成 A→x(y|ε),这里把ε当作最后一个候选式。
❖ ② 若 A→x|y|…|z|Av
是一组产生式,且它只有一个直接左递归的右部位于最后,
如果x是一个终结符串,而且h中至多最左符号是终 结符,那么,(q,y,h)是该NDPDA的一个构形,而且
(q,xy,S)├*(q,y,h)
5.2 消除左递归方法
5.2.1 文法的左递归性
❖ 文法的左递归性属文法递归性的一种,在一文法中,所有形
如
A→xAy x,y ∈(∑∪N) *,A∈N
称为递归产生式(或自嵌入产生式)。
U→1|1|…|n
都有 SELECT (U→i)∩SELECT(U→j)= (ij, i, j=1, 2, …, n),则文法G是一个LL(1)文法。
5.3造
1. 设X(VN∪VT),FIRST(X)的构造
❖ ① 若XVT,则FIRST(X)={X};
(可空)。 ❖ δ 是一个转换函数,它将三元组(q,a,Z)映象成对偶集
{(p1,h1),(p2,h2),…},即,δ(q,a,Z)= {(p1,h1),(p2,h2),…} .
5.1.2 PDA的 构形和移动
PDA的一个构形是一个三元组:(q,w,h) ❖ 其中,q∈Q;w∈∑*是尚待扫描的输入串,包括读
第五章 自上而下语法分析
❖ 语法分析是继词法分析之后编译过程的第2阶段。 它的主要任务是对词法分析的输出结果——单词序 列进行分析,识别合法的语法单位。
编译原理chapter5

struct expty expTy (Tr_exp exp; Ty_ty ty) { struct expty e; e.exp=exp; e.ty=ty; return e; }
5.2 Type-Checking Expressions
• 举例:在Tiger语言中,加法表达式e1+e2
– 两个操作数都必须是整型的(类型检查器必须对此检查) – 结果是整型(类型检查器将返回这种类型)
• 用散列表对字典操作(插入、搜索和删除)的平均时间 为Θ(1),此操作在最坏情况下的操作正比于元素个数n。 • 二叉搜索树对字典的基本操作能在O(logn)的时间内完成。
5.1.3 Efficient Functional Symbol Tables
• 二叉搜索树:
m1={bat→1, camel→2, dog→3} m2=m1+{mouse→4}
• 当σ′= σ + { a→τ },是通过以a 作为键值将τ 插入散 列表来实现的。
void insert ( string key, void *binding) { int index = hash(key) % SIZE table[index] = Bucket ( key, binding, table[index]); } unsigned int hash ( char *s0) { unsigned int h=0; char *s; for ( s=s0; *s; s++) h=h*65599 + *s; return h; }
– formals:各个形式参数的类型;
– result:该函数返回的结果的类型(或Void)。
5.2 Tiger编译器的绑定
编译原理第五章语法分析——自下而上分析

第五章语法分析——自下而上分析要紧内容:[1]自下而上分析的大体问题[2]算符优先分析法[3]算符优先分析表和优先函数的构造[4]LR分析器的大体原理大体要求:[1]明白得自下而上分析法的大体思想[2]明白得有关归约、短语、句柄、标准归约等概念[3]把握算符优先分析法[4]了解算符优先表和优先函数的构造技术[5]了解LR 分析器大体原理和工作方式教学要点:本章介绍自下而上语法分析方式。
所谓自下而上分析法确实是从输入串开始,慢慢进行“归约”,直至归约到文法的开始符号;或说,从语法树的结尾开始,步步向上“归约”,直到根结。
讲义摘要:5.1 自下而上分析大体问题自下而上分析法的大体思想:从输入串开始,慢慢进行“归约”,直到文法的开始符号。
即从树结尾开始,构造语法树。
所谓归约,是指依照文法的产生式规那么,把产生式的右部替换成左部符号。
自上而下分析的核心问题是:如何判定符号串的可归约性,和如何归约。
即,识别可归约串的问题。
归约自下而上分析法事实上确实是一种“移进-归约”法,即,采纳“移进-归约”思想进行。
实现思想是:对输入符号串自左向右进行扫描,并将输入符逐个移入一个后进先出栈中,边移入边分析,一旦栈顶符号串形成某个句型的句柄时,(该句型对应某产生式的右部,即栈顶生成了某产生式的右部的文法符号串),就将栈顶的这一部份替换成 (归约为) 该产生式的左部符号,这称为归约。
重复这一进程直到归约到栈中只剩文法的开始符号时那么为分析成功,也就确认输入串是文法的句子。
现举例说明。
例1:设文法G[S]为:(1) S→aAcBe(2) A→b(3) A→Ab(4) B→d试对abbcde进行“移进-归约”分析。
步骤: 1 2 3 4 5 6 7 8 9 10解:动作: 进a 进b 归(2) 进b 归(3) 进c 进d 归(4) 进e 归(1)表1符合栈的转变进程自下而上语法分析的进程也可看成自底向上构造语法树的进程,每步归约都是构造一棵子树,最后当输入串终止时恰好构造出整个语法树,如图1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章
2.对下面的文法G:
E→TE/
E/→+E|ε
T→FT/
T/→T|ε
F→PF/
F/→*F/|ε
P→(E)|a|b|^
(1)计算这个文法的每个非终结符的FIRST集和FOLLOW集。
(2)证明这个方法是LL(1)的。
(3)构造它的预测分析表。
(4)构造它的递归下降分析程序。
解:
(1)计算这个文法的每个非终结符的FIRST集和FOLLOW集。
FIRST集合有:
FIRST(E)=FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^};
FIRST(E/)={+,ε}
FIRST(T)=FIRST(F)=FIRST(P)={(,a,b,^};
FIRST(T/)=FIRST(T)∪{ε}={(,a,b,^,ε};
FIRST(F)=FIRST(P)={(,a,b,^};
FIRST(F/)=FIRST(P)={*,ε};
FIRST(P)={(,a,b,^};
FOLLOW集合有:
FOLLOW(E)={),#};
FOLLOW(E/)=FOLLOW(E)={),#};
FOLLOW(T)=FIRST(E/)∪FOLLOW(E)={+,),#};//不包含ε
FOLLOW(T/)=FOLLOW(T)=FIRST(E/)∪FOLLOW(E)={+,),#};
FOLLOW(F)=FIRST(T/)∪FOLLOW(T)={(,a,b,^,+,),#};//不包含εFOLLOW(F/)=FOLLOW(F)=FIRST(T/)∪FOLLOW(T)={(,a,b,^,+,),#};
FOLLOW(P)=FIRST(F/)∪FOLLOW(F)={*,(,a,b,^,+,),#};//不包含ε(2)证明这个方法是LL(1)的。
各产生式的SELECT集合有:
SELECT(E→TE/)=FIRST(T)={(,a,b,^};
SELECT(E/→+E)={+};
SELECT(E/→ε)=FOLLOW(E/)={),#}
SELECT(T→FT/)=FIRST(F)={(,a,b,^};
SELECT(T/→T)=FIRST(T)={(,a,b,^};
SELECT(T/→ε)=FOLLOW(T/)={+,),#};
SELECT(F→PF/)=FIRST(P)={(,a,b,^};
SELECT(F/→*F/)={*};
SELECT(F/→ε)=FOLLOW(F/)={(,a,b,^,+,),#};
SELECT(P→(E))={(}
SELECT(P→a)={a}
SELECT(P→b)={b}
SELECT(P→^)={^}
可见,相同左部产生式的SELECT集的交集均为空,所以文法G[E]是LL(1)文法。
(3)构造它的预测分析表。
文法G[E]的预测分析表如下:
(4)构造它的递归下降分析程序。
对每个非终结符写出不带回溯的递归子程序如下:
char CH;//存放当前的输入符号
void P_E()//非终结符E的子程序
{
if(IsIn(CH,FIRST_TEP)) //FIRST_TEP为T→TE/ 的右部的FIRST集合,产生式E→TE/
{
P_T();
P_EP();
}
else ERR;
}
void P_EP()//非终结符E/的子程序
{
if(CH==’+’) //产生式E/→+E
{
READ(CH);
P_E();
}
else//产生式E/→ε
{
if(IsIn(CH,FOLLOW_EP)) //FOLLOW_EP为E/的FOLLOW集合
return ;
else ERR;
}
}
void P_T()//非终结符T的子程序
{
if(IsIn(CH,FIRST_FTP)) //FIRST_TEP为T→FT/ 的右部的FIRST集合,产生式T→FT/
{
P_F();
P_TP();
}
else ERR;
}
void P_TP()//非终结符T/的子程序
{
if(IsIn(CH,FIRST_T)) //FIRST_T为产生式T/→T的右部的FIRST集合,产生式T/→T
{
P_T();
}
else//产生式T/→ε
{
if(IsIn(CH,FOLLOW_TP)) //FOLLOW_TP为T/的FOLLOW集合
return ;
else ERR;
}
}
void P_F()//非终结符F的子程序
{
if(IsIn(CH,FIRST_PFP)) //FIRST_PFP为F→PF/ 的右部的FIRST集合,产生式F→PF/
{
P_P();
P_FP();
}
else ERR;
}
void P_FP()//非终结符F/的子程序
{
if(CH==’*’) //产生式F/→*F/
{
READ(CH);
P_FP();
}
else//产生式F/→ε
{
if(IsIn(CH,FOLLOW_FP)) //FOLLOW_FP为F/的FOLLOW集合
return ;
else ERR;
}
}
void P_P()//非终结符P的子程序
{
if(CH==’(‘)
{
READ(CH);
P_E();
if(CH==’)’) READCH(CH);
else
ERR;
}
else if(CH==’a’) READ(CH);
else if(CH==’b’) READ(CH);
else if(CH==’^’) READ(CH);
else ERR;
}
4证明下述文法不是LL(1)的。
S->C$ C->bA|aB A->a|aC|bAA B->b|bC|aBB 你能否构造一等价的文法,使其是LL (1)的,并给出判断过程。
【解】因为SELECT(A->a)∩SELECT(A->aC)≠Ф,根据LL(1)文法的判定条件:(1)文法不含左递归(2)对于文法U的任意两个不同的规则有: Select(U→α) ∩Select(U→)=Φ一个文法若满足以上条件,称该文法G为LL(1)文法。
得出该文法不是LL(1)文法。
该文法含公共因子,消除后的文法为:S->C$ C-> bA|aB A->aA'|bAA A’->C|εB->bB'| aBB
B’->C|ε【证明】因为SELECT(C-> bA) ∩SELECT(C->aB)= ΦSELECT(A->Aa) ∩SELECT(A->bAA) = ΦSELECT(A’->C) ∩SELECT(A’->ε)=(FIRST(C)-{ ε})∩FOLLOW(A’) ≠Ф因此消除公共因子后得到文法也不是LL(1)文法。
