向心力实例分析之汽车转弯
合集下载
2019-2020学年高中物理 4.3 向心力的实例分析课件 鲁科版必修2
名师指点
一、理解火车转弯问题 1．火车轮缘结构：火车的车轮有凸出的轮缘，且火车在轨道上运行时，有凸 出轮缘的一边在两轨道内侧，如图甲所示．
甲
乙
2．向心力的来源：转弯时所需的向心力由重力和弹力的合力提供．如乙图．
3．明确圆周平面 虽然外轨高于内轨，但整个外轨是等高的，整个内轨是等高的．因而火车在 行驶的过程中，重心的高度不变，即火车重心的轨迹在同一水平面内．故火车的 圆周平面是水平面，而不是斜面．即火车的向心加速度和向心力均是沿水平面指 向圆心．
对竖直平面内的圆周运动： (1)要明确运动的模型，即绳或杆． (2)由不同模型的临界条件分析受力，找到向心力的来源． (3)结合机械能守恒定律列方程．
3－1：长 L＝0.5 m，质量可忽略的杆，其下端固定于 O 点，上端连 有质量 m＝2 kg 的小球，它绕 O 点在竖直平面内做圆周运动．当通过最高点时， 如图所示，求下列情况下杆受到的力(计算出大小，并说明是拉力还是压力，g 取 10 m/s2)：
2.如图所示，用细绳拴着质量为 m 的小球，在竖直平面内做圆周运动，圆周 半径为 R，则下列说法正确的是( )
A．小球过最高点时，绳子张力不可能为零 B．小球过最高点时的最小速度为零 C．小球刚好过最高点时的速度为 Rg D．小球过最高点时，绳子对小球的作用力可以与球所受的重力方向相反
解析： 小球在最高点时，受重力 mg、绳子竖直向下的拉力 F(注意：绳子 不能产生竖直向上的支持力)．
(1)外轨对车轮的侧压力提供火车转弯所需的向心力，所以有 N＝mvr2＝1054×00202 N＝105 N 由牛顿第三定律可知铁轨受到的侧压力大小等于 105 N.
(2)火车过弯道，重力和铁轨对火车的支持力的合力正好提供向心力，即 mgtan θ＝mvr2 所以 tan θ＝vrg2 ＝4002×02 10＝0.1. 答案： (1)105 N (2)0.1
向心力实例分析
一、转弯时的向心力实例分析1、汽车、自行车转弯问题汽车在水平路面上转弯，靠的是轮胎与路面间的静摩擦力。
设汽车以速率v 转弯，要转的弯的半径为R ，则需要的侧向静摩擦力Rv m F 2=。
如该汽车与地面间侧向最大静摩擦力为F max ，有R v m F 2max =得，转弯的最大速率mRF v max max =，超过这个速率，汽车就会侧向滑动。
2、火车转弯问题火车在转弯处，外侧的轨道高于内侧轨道，火车的受力分析如图所示，其转弯时所需向心力由重力和弹力的合力提供。
Rv M Mg 2tan =θ解得：v ＝θtan gR 拓展：①当火车行驶速率v 等于v 规定时，即v ＝θtan gR 时，支持力和重力的合力恰好充当所需的向心力，则内、外轨都不受挤压（此时为临界条件）．②当火车行驶速率v 大于v 规定时，即v ＞θtan gR 时，支持力和重力的合力不足以提供所需向心力，则此时需要外轨提供一部分向心力，即此时外轨受挤压．③当火车行驶速率小于v 规定时，即v ＜θtan gR 时，支持力和重力的合力大于所需的向心力，二、竖直平面内的圆周运动实例分析1、汽车过拱桥问题在汽车过拱桥时，汽车的向心力是由汽车的重力和路面的支持力来提供的。
当路面对汽车的支持力为零时，汽车将脱离路面，因此，必须保证支持力N ＞0，即汽车在最高点时速度的最大值是刚好重力提供向心力，即mg＝m rυ2，即该圆周运动的最大速度为v ＝gr，当速度为该值时，汽车将由沿桥面切线方向上的速度（水平速度）和只受重力作用，而做平抛运动。
因此，汽车过拱桥时，速度应小于gr 。
2、汽车过凹型桥3、小球在绳和杆的作用下通过最高点问题（1）在最低点，不论是线拉物体还是杆连物体，线或杆的弹力指向圆心（竖直向上），物体的重力竖直向下，二者的合力提供向心力，则有mg ＋T ＝mr ω2＝m rυ2；（2）在最高点时，线拉物体的临界状态是T ＝0，重力提供向心力mg ＝m rυ2，即v ＝gr 。
4.3 向心力的实例分析 4.4 离心运动 课件(鲁科版必修2)解析
(2)小球 A 在最低点时，对球受力分析：重力 mg、拉力 F，设向上为正方向 根据小球做圆周运动的条件，合外力等于向心力， F－ v2 mg＝ m L v2 解得 F＝ mg＋m ＝7mg， L v2 故球的向心加速度 a＝ ＝6g. L
【答案】 (1) 2gL 或 0 (2)7mg 6g
易错案例警示——对向心力分析不清 导致错误
(1)v＝ gr时，拉力或压力为零． (2)v> gr时，物体受向下的拉力或压力，并且随速度的 增大而增大． (3)v< gr时，物体不能达到最高点．(实际上球未到最高 点就脱离了轨道 ) 即绳类的临界速度为 v 临＝ gr .
2．杆类 如图 4－ 3－ 7 所示，在细轻杆上固定的小球或在管形轨 道内运动的小球，由于杆和管能对小球产生向上的支持力， 所以小球能在竖直平面内做圆周运动的条件是在最高点的速 度大于或等于零，小球的受力情况为：
4.3 向心力的实例分析
4.4 离心运动
向心力的实例分析
转弯时的向心力实例分析
路面种类 汽车在水平路面 汽车、火车在内低 分析 转弯 外高的路面上转弯
受力分析
向心力来源
静摩擦力 f
重力和支持力的合 力
路面种类 汽车在水平路面转 汽车、火车在内低 分析 向心力 关系式 弯
v2 f＝ m R
外高的路面上转弯
火车及汽车转弯时，运动的圆周面是水平面，而不是斜 面，其向心力沿水平方向指向圆心，而不沿斜面方向．
如图所示， 某游乐场里的赛车场地为圆形， 半径为 100 m， 一赛车的总质量为 100 kg，车轮与地面 间的最大静摩擦力为 600 N. (1)若赛车的速度达到 72 km/h，这 辆车在运动过程中会不会发生侧移？
3．探究交流 除了火车弯道具有内低外高的特点外，你还了解哪些道 路具有这样的特点？
向心力实例分析之汽车转弯ppt课件
N
F
f静
G
11
若v gr tan
N
f静
F
G
12
同类模型还有：
F
F合
G
13
鸟 飞 行 转 弯
飞 机 转 弯
F F合
G
14
小 结
1、分析圆周运动的基本思路。 2、实例分析：汽车转弯。 3、圆周运动问题的解题步骤。
15
16
思考：火车转弯时，什么力提供向心力？
17
18
4
向心力的来源
“供”
m rw2 m v2 r
向心力的表达式
“需”
F向
做圆周 运动
=5Βιβλιοθήκη 解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。
2.受力分析，找到向心力。
3.列出向心力表达式方程。
6
汽车转弯（水平面内的圆周运动）
7
汽车转弯
N F牵
俯视图:
F牵
f静
v
f静
G
f切
f切
汽车在水平路面上转弯的向心力由哪个力提供？
8
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽
车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽
车拐弯时的最大安全速度？
f max
v
v m g m r
v2 f max m r 2
v gr
9
N
v m g tan m r
F
2
v gr tan
G
10
若v gr tan
重庆市黔江中学校 QianJiang Middle School of ChongQing
F
f静
G
11
若v gr tan
N
f静
F
G
12
同类模型还有：
F
F合
G
13
鸟 飞 行 转 弯
飞 机 转 弯
F F合
G
14
小 结
1、分析圆周运动的基本思路。 2、实例分析：汽车转弯。 3、圆周运动问题的解题步骤。
15
16
思考：火车转弯时，什么力提供向心力？
17
18
4
向心力的来源
“供”
m rw2 m v2 r
向心力的表达式
“需”
F向
做圆周 运动
=5Βιβλιοθήκη 解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。
2.受力分析，找到向心力。
3.列出向心力表达式方程。
6
汽车转弯（水平面内的圆周运动）
7
汽车转弯
N F牵
俯视图:
F牵
f静
v
f静
G
f切
f切
汽车在水平路面上转弯的向心力由哪个力提供？
8
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽
车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽
车拐弯时的最大安全速度？
f max
v
v m g m r
v2 f max m r 2
v gr
9
N
v m g tan m r
F
2
v gr tan
G
10
若v gr tan
重庆市黔江中学校 QianJiang Middle School of ChongQing
向心力实例分析之汽车转弯
做圆周 运动
解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。 2.受力分析，找到向心力。 3.列出向心力表达式方程。
汽车转弯（水平面内的圆周运动）
汽车转弯
N
F牵
f静
f切
G
F牵 俯视图:
v
f静
f切
汽车在水平路面上转弯的向心力由哪个力提供？
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽 车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽车 拐弯时的最大安全速度？
向心力实例分析之
—汽车转弯
回顾向心力的表达式：
F mv2 mr2
r
需求量
回顾向心力的来源
N
T G
T F合
G
T T1 T2
G
向心力的来源： 可以是某一个力, 也可以是某些力的合力, 也可以是某个力的分力.
解决圆周运动的基本思路
向心力的来源 “供”
向心力的表达式 “需”
mrw2 m v2 r
F向 =
作业：实地考察或查资料，认识火车车 轮与铁轨的构造
思考：火车转弯时，什么力提供向心力？
v
fmax
f max
m
v2 r
m g m v2
r
v gr
赛道的设计——外高内低
N
mgtan mv2
r
F
v grtan
G
若v grtan
N
F
f静
G
பைடு நூலகம் 若v grtan
N
F
f静
G
同类模型还有：
F
F合
G
鸟
飞
行
转
飞
弯
解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。 2.受力分析，找到向心力。 3.列出向心力表达式方程。
汽车转弯（水平面内的圆周运动）
汽车转弯
N
F牵
f静
f切
G
F牵 俯视图:
v
f静
f切
汽车在水平路面上转弯的向心力由哪个力提供？
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽 车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽车 拐弯时的最大安全速度？
向心力实例分析之
—汽车转弯
回顾向心力的表达式：
F mv2 mr2
r
需求量
回顾向心力的来源
N
T G
T F合
G
T T1 T2
G
向心力的来源： 可以是某一个力, 也可以是某些力的合力, 也可以是某个力的分力.
解决圆周运动的基本思路
向心力的来源 “供”
向心力的表达式 “需”
mrw2 m v2 r
F向 =
作业：实地考察或查资料，认识火车车 轮与铁轨的构造
思考：火车转弯时，什么力提供向心力？
v
fmax
f max
m
v2 r
m g m v2
r
v gr
赛道的设计——外高内低
N
mgtan mv2
r
F
v grtan
G
若v grtan
N
F
f静
G
பைடு நூலகம் 若v grtan
N
F
f静
G
同类模型还有：
F
F合
G
鸟
飞
行
转
飞
弯
第三节 向心力的实例分析分解
v2 F向 T mg m r
15
三、竖直面轨道圆周运动——线模型
(1)临界条件：绳子或轨道对小球没有力的作用：
mg ＝m v
2
临界 ⇒v R
＝ 临界
gR。
(2)能过最高点的条件：v≥ gR，当 v> gR时，绳对 球产生拉力或轨道对球产生压力。
(3)不能过最高点的条件：v<v 临界(实际上球还没到最 高点时就脱离了轨道)。
那么当汽车的速度为多少时汽车对桥毫无附着力，会完全失控？Fra bibliotekv gR
10
三、竖直面轨道圆周运动——汽车过桥（凹底问题）
若是凹形圆桥面汽车对桥的压力等于多少？
N
mg
v2 m
N
R
N mg m v2 mg R
G
由牛顿第三定律可知，汽车对桥及轮胎的压力都大于重力， 汽车有爆胎的危险！
对比上面的研究可以看出来，不同圆桥能够
在最高点处对过山车受力分析： 重力G与压力N为过山车提供向心力
mg N m v2 R
思考：当车速度为多少时，对轨道无挤 压？
Nv
G
R
N’
G
13
三、竖直面轨道圆周运动——过山车
过山车：(在最高点和最低点) (1)向心力来源：受力如图所示，重力和支持力的合力提 供向心力。
(2)向心力方程：
在最高点：
行驶 v gr ，否则将发生事故。
思考
在现实生活中，公路和铁路的弯道通 常是外高内低，为什么这样设计呢？
6
二、倾斜轨道圆周运动——赛车拐弯
拐弯情景： N
受力分析：
h
G 可得：F mg tan m v2
r
N
若倾角θ很小时，可
(竖直面)向心力的实例分析
(竖直面)
过山车
复习：
向心力可能是 重 力，可能是 弹 力， 也可能是 摩擦 力，还可能是它们的 合力 。
N T
G O
ω
Ｆ
N
Ｇ
f G
【 思考】： 1.汽车驶过拱桥顶部和驶过凹形桥底部时 向心力由哪些力来提供？
2.“过山车”驶过轨道最高点时
向心力由哪些力来提供？
【问题1】：
汽车过拱形桥时， 汽车对拱形桥的压力等于汽车所受的重力吗？ 汽车行驶在拱形桥容易爆胎 还是行驶在凹形桥容易爆胎呢
在杂技水流星表演中， 水在最高点时都没有流出来， 这是为什么呢？
简化的模型 ——轻绳系着一小球在竖直平面内做圆周运动。
背景问题2：水流星
杂技表演中有一个“水流星”的节目：在一只水杯 中装上水，然后让桶在竖直平面内做圆周运动，水不会 洒出来。这是为什么？
解析： 当水杯运动到最高点的时候，如果水没有洒 出来，那么在其他位置上水也不会洒出来。 所以选取最高点为研究对象。
B
车速至少为(
A.15m/s C.25m/s
)
B.20m/s D.30m/s
N
G
解析：当v= 10m / s 时，对车受力分析如图所示 v2 mg - N = m 解得：R=40m R 当汽车对顶部恰好没有压力时，重力提供汽车做圆周运动的向心力
2 mv1 mg 解得：v1= 20 m s R
【问题2】：
rg
—小球能过最高点的最小速度
（临界速度）
v rg
（脱离原轨道）
想一想：游乐园里的过山车用的又是什么原理呢？
4.过山车：
在游乐场里，惊险有趣的项目之一就是过山车， 如右图，当你看到乘客头朝下高速飞行的时候， 为什么不用担心乘客会从过山车上栽下来
过山车
复习：
向心力可能是 重 力，可能是 弹 力， 也可能是 摩擦 力，还可能是它们的 合力 。
N T
G O
ω
Ｆ
N
Ｇ
f G
【 思考】： 1.汽车驶过拱桥顶部和驶过凹形桥底部时 向心力由哪些力来提供？
2.“过山车”驶过轨道最高点时
向心力由哪些力来提供？
【问题1】：
汽车过拱形桥时， 汽车对拱形桥的压力等于汽车所受的重力吗？ 汽车行驶在拱形桥容易爆胎 还是行驶在凹形桥容易爆胎呢
在杂技水流星表演中， 水在最高点时都没有流出来， 这是为什么呢？
简化的模型 ——轻绳系着一小球在竖直平面内做圆周运动。
背景问题2：水流星
杂技表演中有一个“水流星”的节目：在一只水杯 中装上水，然后让桶在竖直平面内做圆周运动，水不会 洒出来。这是为什么？
解析： 当水杯运动到最高点的时候，如果水没有洒 出来，那么在其他位置上水也不会洒出来。 所以选取最高点为研究对象。
B
车速至少为(
A.15m/s C.25m/s
)
B.20m/s D.30m/s
N
G
解析：当v= 10m / s 时，对车受力分析如图所示 v2 mg - N = m 解得：R=40m R 当汽车对顶部恰好没有压力时，重力提供汽车做圆周运动的向心力
2 mv1 mg 解得：v1= 20 m s R
【问题2】：
rg
—小球能过最高点的最小速度
（临界速度）
v rg
（脱离原轨道）
想一想：游乐园里的过山车用的又是什么原理呢？
4.过山车：
在游乐场里，惊险有趣的项目之一就是过山车， 如右图，当你看到乘客头朝下高速飞行的时候， 为什么不用担心乘客会从过山车上栽下来
高一物理课件：4.3向心力的实例分析
h
θ
m g
例题
例4、质量为m的小球，用一条绳子系着在
竖直平面内做圆周运动，小球到最高点时 2 的速度为 v，到达最低点时的速度为 4gR+v ，则小球通过上述两位置处时绳子所受的 A 张力之差是( )
A.6mg C.4mg B.5mg
mg T1 m
( 4 gR v ) T2 mg m R
训练巩固
3. 有一列重为100 t的火车，以72 km/h的速率匀速通过
一个内外轨一样高的弯道，轨道半径为400 m.(g取10
m/s2)
(1)试计算铁轨受到的侧压力； (2)若要使火车以此速率通过弯道，且使铁轨受到的侧 压力为零，我们可以适当倾斜路基，试计算路基倾斜角 [解析] 度(1) θ的正切值 . 外轨对轮缘的侧压力提供火车转弯所需要的向心力，
第 三 节 向心力的实 例分析
第四章 匀速圆周 运动
一、转弯时的向心力 实例分析
生活中的向心力
弯道上行驶的汽车
一、转弯时的向心力 实例分析
一、转弯时的向心力 实例分析 外 轨 内 轨
火车在水平轨 道（内外轨道 一样高）上转 弯时，所需的 向心力由谁提 供？
外轨 对轮 缘的 弹力 F
FN
G
4
一、转弯时的向心力 实例分析 在转弯处 外轨略高 于内轨
v FN mg m R
2
m ag 由牛顿第三定律得，汽车通过桥的最高点时对桥的压力：
FN ＜ mg
v mg m R
2
若汽车通过拱 桥的速度增大 ，会出现什么
三、竖直平面内的圆周运动实 例分析
2 v FN ＝mg－ R
FN
m
m g 当FN = 0 时，汽车脱离桥面，做平 抛运动，汽车及其中的物体处于完 全失重状态. mg＝ R m
赛车在弯道的受力分析原理
赛车在弯道的受力分析原理赛车在弯道中的受力分析是理解赛车运动的重要一环。
赛车经过弯道时，会受到多种力的作用，包括向心力、重力、摩擦力等。
下面我将详细解释这些受力原理。
首先，我们需要了解向心力的概念。
向心力是赛车在弯道中朝向中心的力，使得赛车保持在曲线路径上。
当车辆以一定速度通过弯道时，其本身具有向直线运动的惯性，而弯道的曲率会将车辆的运动改变为弯曲路径。
为了维持这种路径，向心力就产生了。
向心力的大小与车辆的质量、速度以及弯道的曲率有关。
当车辆速度增加或曲率增大时，向心力也会增大。
赛车的动力系统为驱动力，这个力与速度和车辆的传动系统有关。
当赛车在弯道中运行时，驱动力可以被分解为两个分量：垂直于地面的重力分量和平行于地面的向心力分量。
重力分量会使车辆受到向内的压力，增大了轮胎与地面的接触力，提供了附着力。
而向心力分量则是赛车通过弯道时所需的。
其次是重力对赛车的影响。
重力是指地球对赛车的吸引力。
在弯道中，由于向心力的作用，车辆偏离重力作用的中心轴线。
因此，净作用力是一个向内的向心力，这个力与重力之间的差值。
这个差值越大，车辆受向内的力就越大，能够保持在弯道的路径上。
此外，还有摩擦力对赛车的作用。
赛车在弯道中的前轮和后轮需要保持与地面的摩擦力，以维持车辆的稳定性和操控性能。
当车辆向内运动时，前轮处于转向状况，向内倾斜，而后轮则偏离中心轴线向外倾斜。
这种倾斜会使轮胎与地面之间的摩擦力，具有对抗车辆径向运动的作用。
因此，摩擦力对车辆行驶在弯道中的稳定性和控制性能至关重要。
综上所述，赛车在弯道中的受力分析原理主要包括向心力、重力和摩擦力。
通过合理的控制这些力的大小和方向，车辆能够保持在弯道上，并具备较好的操控性能和稳定性。
这对赛车运动中的竞技表现有着重要的影响。
向心力实例分析
生活中的圆周运动： 生活中的圆周运动：水平面内的圆周运动 汽 车 转 弯
பைடு நூலகம்
火 车 转 弯
生活中的圆周运动---竖直面内的圆周运动 生活中的圆周运动 竖直面内的圆周运动
汽车过拱形桥 汽车过拱形桥
一。水平面内的圆周运动 1.汽车转弯 汽车转弯
想一想： 想一想：
若一辆汽车以速度V=50m/s转弯，此 转弯， 若一辆汽车以速度 转弯 过程可以看作匀速圆周运动。已知此处路面与轮 过程可以看作匀速圆周运动。 胎之间的动摩擦因数为0.5，这个人转弯的半径R 胎之间的动摩擦因数为 ，这个人转弯的半径 最小是多大？ 最小是多大？ 最大静摩擦力近似等于滑动摩擦力） （最大静摩擦力近似等于滑动摩擦力）
v F = mg tan θ = m r ∴ v = gr tan θ 又tanθ ≈ sin θ = h / l = 0.1
∴ v = 30m / s
h θ l
2
FN
F
mg
生活中的圆周运动---竖直面内的圆周运动 生活中的圆周运动 竖直面内的圆周运动
汽车过拱形桥 汽车过拱形桥
可见如果在平直路面上， 可见如果在平直路面上，高速转弯动摩擦因数一 定的前提下，需要很大的转弯半径。 定的前提下，需要很大的转弯半径。
Ｆ１赛车转弯
赛道的设计
你观察过高速公路 转弯处的路面情况 吗?
点击播放
高速公路转弯处也 是外高内底 （并且超车道比主 车道更加倾斜） 车道更加倾斜）
一。水平面内的圆周运动 1.汽车转弯 汽车转弯
2.火车转弯 火车转弯
火车转弯：
m转弯 转弯， 2、火车以半径r= 900 m转弯，火车质量为 轨道宽为l=1.4m 1.4m， 8×105kg ，轨道宽为 1.4m，外轨比内轨高 h=14cm，为了使铁轨不受轮缘的挤压， h=14cm，为了使铁轨不受轮缘的挤压，火车的 速度应为多大？ 很小时， 速度应为多大？ 很小时，可认为 tan θ ≈ sin θ θ
பைடு நூலகம்
火 车 转 弯
生活中的圆周运动---竖直面内的圆周运动 生活中的圆周运动 竖直面内的圆周运动
汽车过拱形桥 汽车过拱形桥
一。水平面内的圆周运动 1.汽车转弯 汽车转弯
想一想： 想一想：
若一辆汽车以速度V=50m/s转弯，此 转弯， 若一辆汽车以速度 转弯 过程可以看作匀速圆周运动。已知此处路面与轮 过程可以看作匀速圆周运动。 胎之间的动摩擦因数为0.5，这个人转弯的半径R 胎之间的动摩擦因数为 ，这个人转弯的半径 最小是多大？ 最小是多大？ 最大静摩擦力近似等于滑动摩擦力） （最大静摩擦力近似等于滑动摩擦力）
v F = mg tan θ = m r ∴ v = gr tan θ 又tanθ ≈ sin θ = h / l = 0.1
∴ v = 30m / s
h θ l
2
FN
F
mg
生活中的圆周运动---竖直面内的圆周运动 生活中的圆周运动 竖直面内的圆周运动
汽车过拱形桥 汽车过拱形桥
可见如果在平直路面上， 可见如果在平直路面上，高速转弯动摩擦因数一 定的前提下，需要很大的转弯半径。 定的前提下，需要很大的转弯半径。
Ｆ１赛车转弯
赛道的设计
你观察过高速公路 转弯处的路面情况 吗?
点击播放
高速公路转弯处也 是外高内底 （并且超车道比主 车道更加倾斜） 车道更加倾斜）
一。水平面内的圆周运动 1.汽车转弯 汽车转弯
2.火车转弯 火车转弯
火车转弯：
m转弯 转弯， 2、火车以半径r= 900 m转弯，火车质量为 轨道宽为l=1.4m 1.4m， 8×105kg ，轨道宽为 1.4m，外轨比内轨高 h=14cm，为了使铁轨不受轮缘的挤压， h=14cm，为了使铁轨不受轮缘的挤压，火车的 速度应为多大？ 很小时， 速度应为多大？ 很小时，可认为 tan θ ≈ sin θ θ
向心力实例分析
第三节 向心力的 实例分析
知识回顾
• 物体做圆周运动时，需要 受到指向圆心的等效力的 作用 • 向心力的特点
–方向：总是指向圆心
F向 m v
2
r
m r
2
向心力公式的理解
提供物体做圆 周运动的力
F
=m
v
2
r
物体做圆周 运动所需的 向心力
“供”、“需”平衡 物体做圆周运动
向心力实例分析
N
外高 F向 θ
O
内低 θ
r
V= gr tanθ
（弯道设计速度）
G
V设计= g rtanα
当V实际> V设计时： 路面对车轮有沿斜面 向内侧的静摩擦力 当V实际<V设计时： 路面对车轮有沿斜面 向外侧的静摩擦力 外高
N
O
F向
θ 内低 θ
G
赛道的设计
观看图片
注意观察 铁轨弯道的特点
火车水平转弯时情况分析
又因为 F向 m v
2
小球运动
v G T r T1
v
2
所以 T m
r
mg
点
G
所以要使小球经过最高 小球速度 v
2
r
gr
小球又如何呢
即 ：G
T m
v
r
游乐场的过山车
v r
过山车分析：
可见，v越大时，N越大，v越小时，N
越小
当v很小并趋近于零时，则
很小并趋近于 零，由于重力一定，重力大于小球所需向心力， 小球偏向圆心方向，不能达到最高点，在到最高 点之前已做斜抛运动离开圆轨道。 当N=0时，
汽车
受力分析
N
f
知识回顾
• 物体做圆周运动时，需要 受到指向圆心的等效力的 作用 • 向心力的特点
–方向：总是指向圆心
F向 m v
2
r
m r
2
向心力公式的理解
提供物体做圆 周运动的力
F
=m
v
2
r
物体做圆周 运动所需的 向心力
“供”、“需”平衡 物体做圆周运动
向心力实例分析
N
外高 F向 θ
O
内低 θ
r
V= gr tanθ
（弯道设计速度）
G
V设计= g rtanα
当V实际> V设计时： 路面对车轮有沿斜面 向内侧的静摩擦力 当V实际<V设计时： 路面对车轮有沿斜面 向外侧的静摩擦力 外高
N
O
F向
θ 内低 θ
G
赛道的设计
观看图片
注意观察 铁轨弯道的特点
火车水平转弯时情况分析
又因为 F向 m v
2
小球运动
v G T r T1
v
2
所以 T m
r
mg
点
G
所以要使小球经过最高 小球速度 v
2
r
gr
小球又如何呢
即 ：G
T m
v
r
游乐场的过山车
v r
过山车分析：
可见，v越大时，N越大，v越小时，N
越小
当v很小并趋近于零时，则
很小并趋近于 零，由于重力一定，重力大于小球所需向心力， 小球偏向圆心方向，不能达到最高点，在到最高 点之前已做斜抛运动离开圆轨道。 当N=0时，
汽车
受力分析
N
f
高中物理汽车转弯时向心力的分析
高中物理汽车转弯时向心力的分析一、题目及解析汽车沿半径为R的圆跑道匀速行驶，设跑道的路面是水平的，路面作用于车的最大静摩擦力是车重的0。
10倍，要使汽车不至于冲出圆跑道，车速最大不能超过多少？解析：汽车在圆跑道匀速行驶时，轮胎所受的静摩擦力F（方向指向圆心）提供向心力。
车速越大，所需向心力也越大，则静摩擦力F也越大，向心力不可能超过路面与车间的最大静摩擦力F m，设车速的最大值为，则得：汽车沿半径为R的圆跑道匀速行驶时的速率不能超过，不然会冲出圆跑道，因为这时最大静摩擦力不足以提供汽车做圆周运动所需的向心力，汽车就脱离原来的圆跑道做离心运动了。
二、问题的提出在书本上和资料上有很多类似题，解题依据都是最大静摩擦力提供向心力。
最大静摩擦力只提供向心力吗？三、问题的分析1．汽车在平直路面运动受力情况分析一般情况下汽车的后轮是驱动轮或称主动轮，前轮是导向轮或称被动轮。
后轮在发动机驱动力矩作用下发生转动，在轮缘与路面接触处，轮将对地面施加一个作用力，方向与运动方向相反，同时路面对轮产生一个向前的反作用力，在反作用力的作用下使得汽车向前运动，而前轮在轮轴推动下将作平动，同样道理路面对前轮产生一个反作用力，方向向后，在反作用力力矩的作用下，前轮发生转动。
两对作用力与反作用力都是静摩擦力，施加在后轮的驱动力矩随着汽车发动机输出功率的改变而相应地改变。
后轮的静摩擦力是由路面作用产生的，在给定的硬路面和汽车的情况下，路面所提供的最大静摩擦力是一定的，因此汽车的输出功率的大小将受到限制，即存在着临界状态。
沿路面自由滚动的车轮，具有不断变化的瞬时转动中心，车轮和路面的各个接触点在它们接触的瞬间是没有相对运动的，轮胎与公路之间的纵向水平作用力就是物理学所说的静摩擦力。
静摩擦力最大值被定义为“最大静摩擦力”，是一个与运动状态无关的常量，它等于路面对车轮的垂直支持力与静摩擦系数的乘积。
可能实现的牵引力最大值约为轮胎与公路间的最大静摩擦力。
向心力的实例分析
如果 v gr ，轻绳对 小球存在拉力。 如果 v gr ，小球无法 到达圆周的最高点
例：如图，在“水流星”表演中，绳长为1m， 水桶的质量为2kg,若水桶通过最高点的速度 为4m/s，求此时绳受到的拉力大小。
v r
2、轻杆作用下的竖直面的圆周运动（杆的模型）
如图所示轻杆栓一小球,在竖直面做圆周运动。求： 经过最高点的线速度需要多大?
问题情境：
汽车过拱桥
质量为m的汽车在拱形桥上以速度v行驶，若桥面的圆 弧半径为r，试画出受力分析图，分析汽车通过桥的最高 点时对桥面的压力？
a：选汽车为研究对象 b：对汽车进行受力分析：受到重力和桥 对车的支持力
c：上述两个力的合力提供向心力、 且向心力 方向向下
d：建立关系式：
2 v F向 mg N 即mg N m r
1、轻绳作用下的竖直面的圆周运动（绳的模型）
如图所示轻绳栓一小球,在竖直面做圆周运动。求： 经过最高点的线速度至少需要多大?
解：在最高点F向=G+T, 即G+T=mv2/r T=mv2/r-mg≥0 小球经过最高点的速度：
线或绳
v0 ≥ gr
线或绳
当 v gr时，细绳对 小球没有拉力作用。向心 力只由小球所受重力提供。
e:又根据牛顿第三定律，所以
2 v N N mg m r
且
N mg
v N mg m r
2
失重现象
试讨论上面情况中，汽车行驶的速度越大，汽车对桥的压力 如何变化；当汽车对桥的压力刚好减为零时，汽车的速度有 多大．当汽车的速度大于这个速度时，会发生什么现象?
2、请你根据上面分析汽车通过凸形桥的思路，分析 一下汽车通过凹形桥最低点时对桥的压力（如图）。 这时的压力比汽车的重力大还是小？
向心力的实例分析
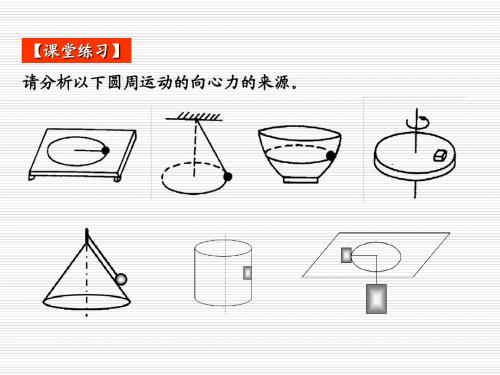
光滑的圆轨道AB部分平直，BC部分是处于 竖直平面内半径为R的半圆，圆管截面半径 r<<R,有一质量为m，半径比r略小的光滑 小球以水平初速度v0射入圆管。（1）若要 小球能从C端出来，初速度v0 是多少？（2） 小球从C端从来瞬间，对管壁压力有哪几种 典型情况，初速度v0应各满足什么条件
生活中的圆周运动：
N+mg=mv2/r
∵N≥0
①当
∴v≥
gr
v gr 时，Ｎ＝０，水在杯中刚好不流出
gr 时，Ｎ>０
② 当v
③
当
v gr 时，Ｎ<０，此时水将会流出杯子。
实例6:轻杆与球：如图所示，一 质量为m的小球，用长为L轻杆固 定住，使其在竖直面内作圆周运 动。 (1)小球做的是什么运动？
(2)小球在运动过程中，受到哪 些力？有哪些力对物体做功？ 小球的运动过程有什么特点？ (3)小球能在竖直平面内作圆周 运动，必须满足的条件是什么？
gr
汽车飞出去了。
汽车质量为1.5x104kg, 以不变的速率驶过 凹形路面和凸行路面，路面圆弧半径为15m 如果路面承受的最大压力不得超过2x105N， 汽车允许的最大速率是多少？汽车以此速率 驶过路面的最小压力是多少？
实例3:细绳与球：如图所示，一质量为 m的小球，用长为L细绳系住，使其在竖 直面内作圆周运动。 (1)小球做的是什么运动？ mg
(2)小球在运动过程中，受到哪 些力？有哪些力对物体做功？ 小球的运动过程有什么特点？
O
(3)小球能在竖直平面内作圆周 运动，必须满足的条件是什么？
如图所示，一质量为m的小球，用长 为L细绳系住，使其在竖直面内作圆周运 动。
(1)若过小球恰好能通过最高点， 则小球在最高点和最低点的速度 分别是多少？小球的受力情况分 别如何？
第四章 第3节 向心力的实例分析
首页
上一页
下一页
末页
2．轻杆模型
结束
如图 4-3-10 所示，在细轻杆上固定的小球或在管形轨道内
运动的小球，由于杆和管能对小球产生向上的支持力，所以小
球能在竖直平面内做圆周运动的条件是在最高点的速度大于或
等于零，小球的受力情况为：
图 4-3-10
首页
上一页
下一页
末页
结束
(1)v＝0 时，小球受向上的支持力 N＝mg。 (2)0<v< gr时，小球受向上的支持力且随速度的增大而减小。 (3)v＝ gr时，小球只受重力。 (4)v> gr时，小球受向下的拉力或压力，并且随速度的增大 而增大。 即杆类的最高点的临界速度为 v 临＝0。
转弯时有 mgtan α＝mRv02
①
当火车以实际速率 v 转弯时，车轮对外轨的侧压力与外轨
对车轮的侧压力是一对相互作用力，此时有
Nsin α＋Fcos α＝mRv2
②
Ncos α－Fsin α＝mg
③
联立①②③式，解得 F＝vv2－04＋v0g22mRg2 。
[答案]
v2－v02mg v04＋g2R2
结束
(2)如图 4-3-4 所示，滑冰运动员转弯时为什么要向转弯处的内 侧倾斜身体？
图 4-3-4 提示：倾斜身体是为了获得冰面对运动员向内侧的静摩擦 力，从而获得做圆周运动所需要的向心力。
首页
上一页
下一页
末页
结束
(3)过山车和乘客在轨道上的运动是圆周运动，如图 4-3-5 所示， 过山车驶至轨道的顶部，车与乘客在轨道的下方，为什么车 与乘客不会掉下来？
图 4-3-3
首页
上一页
下一页
2.3匀速圆周运动的案例分析---物体转弯时的向心力PPT优秀课件
N
f静
G
F合
G
θ
F向 = f静
F向 = F合=mg•tan6θ
在倾斜路面上转弯
N
F合
G
θ
问题2、如图拐弯路段 是半径为R的圆弧，要 使车速为V时车轮与路 面之间横向摩擦力等于 零，则θ应为多大？
F向 = F合= mg•tanθ
7
二、汽车过桥
问题3：如图所示，汽车以一定的速度经过一个圆弧 桥面的顶点时，关于汽车的受力及汽车对桥面的 压力情况，以下说法正确的是（ ）
Ｎ=mg－ mv2/r<mg
O
N
r
mg
F向 = N–mg
N>mg
问题2：如图所示，汽车以一定的速度经过一个圆弧 桥面的顶点时，关于汽车的受力及汽车对桥面的
压力情况，以下说法正确的是（ B）
A．在竖直方向汽车受到三个力： 重力、桥面的支持力和向心力 B. 在竖直方向汽车只受两个力： 重力和桥面的支持力 C.汽车对桥面的压力等于汽车的重力 D.汽车对桥面的压力大于汽车的重力
2.3匀速圆周运动 的实例分析（2） ---物体的转弯
1
知识回顾
物体做匀速圆周运动时，受力有何共同点？
物体要受到指向圆心的合外力——向心力
向心力的特点：
方向：总是指向圆心
大小： F=mrω2
或：F=m
v2 r
向心力公式的理解
提供物体做
匀速圆周运 动的力
F=m
v2 r
物体做匀速 圆周运动所
需的力
“供需”平衡 物体做匀速圆周运动
• 向心力公式、向心加速度公式虽然是从匀 速圆周运动这一特例得出，但它同样适用 于变速圆周运动．
24
11
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重庆市黔江中学校 QianJiang Middle School of ChongQing
作业：实地考察或查资料，认识火车车轮与 铁轨的构造
重庆市黔江中学校 QianJiang Middle School of ChongQing
思考：火车转弯时，什么力提供向心力？
重庆市黔江中学校 QianJiang Middle School of ChongQing
同类模型还有：
F
F合
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
鸟
飞
行
转
飞
弯
机
F
转
F合
弯
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
小结
1、分析圆周运动的基本思路。 2、实例分析：汽车转弯。 3、圆周运动问题的解题步骤。
重庆市黔江中学校 QianJiang Middle School of ChongQing
向心力实例分析之
—汽车转弯
黔江中学： 曾 芳
QianJiang Middle School of ChongQing
回顾向心力的表达式：
F m v2 mr2
r
需求量
重庆市黔江中学校 QianJiang Middle School of ChongQing
N
mg tan m v2
r
F
v gr tan
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
若v gr tan
N
F
f静
G 重庆市黔江中学校 QianJiang Middle School of ChongQing
若v gr tan
N
F
f静
G 重庆市黔江中学校 QianJiang Middle School of ChongQing
mrw 2 m v2 r
重庆市黔江中学校 QianJiang Middle School of ChongQing
解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。 2.受力分析，找到向心力。 3.列出向心力表达式方程。
重庆市黔江中学校 QianJiang Middle School of ChongQing
重庆市黔江中学校 QianJiang Middle School of ChongQing
回顾向心力的来源
N
T G
T F合
G
T T1 T2
G
向心力的来源： 可以是某一个力, 也可以是某些力的合力, 也可以是某个力的分力.
重庆市黔江中学校 QianJiang Middle School of ChongQing
解决圆周运动的基本思路
向心力的来源 “供”
汽车转弯（水平面内的圆周运动）
重庆市黔江中学校 QianJiang Middle School of ChongQing
汽车转弯
N
F牵
f静
f切
G
F牵 俯视图:
v
f静
f切
汽车在水平路面上转弯的向心力由哪个力提供？
重庆市黔江中学校 QianJiang Middle School of ChongQing
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽 车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽车拐 弯时的最大安全速度？
v
fmax
fmax
m
v2 r
mg m v2
r
v gr
重庆市黔江中学校 QianJiang Middle School of ChongQing
赛道的设计——外高内低
作业：实地考察或查资料，认识火车车轮与 铁轨的构造
重庆市黔江中学校 QianJiang Middle School of ChongQing
思考：火车转弯时，什么力提供向心力？
重庆市黔江中学校 QianJiang Middle School of ChongQing
同类模型还有：
F
F合
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
鸟
飞
行
转
飞
弯
机
F
转
F合
弯
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
小结
1、分析圆周运动的基本思路。 2、实例分析：汽车转弯。 3、圆周运动问题的解题步骤。
重庆市黔江中学校 QianJiang Middle School of ChongQing
向心力实例分析之
—汽车转弯
黔江中学： 曾 芳
QianJiang Middle School of ChongQing
回顾向心力的表达式：
F m v2 mr2
r
需求量
重庆市黔江中学校 QianJiang Middle School of ChongQing
N
mg tan m v2
r
F
v gr tan
G
重庆市黔江中学校 QianJiang Middle School of ChongQing
若v gr tan
N
F
f静
G 重庆市黔江中学校 QianJiang Middle School of ChongQing
若v gr tan
N
F
f静
G 重庆市黔江中学校 QianJiang Middle School of ChongQing
mrw 2 m v2 r
重庆市黔江中学校 QianJiang Middle School of ChongQing
解决圆周运动问题的一般步骤：
1.确定圆轨道，圆心和半径。 2.受力分析，找到向心力。 3.列出向心力表达式方程。
重庆市黔江中学校 QianJiang Middle School of ChongQing
重庆市黔江中学校 QianJiang Middle School of ChongQing
回顾向心力的来源
N
T G
T F合
G
T T1 T2
G
向心力的来源： 可以是某一个力, 也可以是某些力的合力, 也可以是某个力的分力.
重庆市黔江中学校 QianJiang Middle School of ChongQing
解决圆周运动的基本思路
向心力的来源 “供”
汽车转弯（水平面内的圆周运动）
重庆市黔江中学校 QianJiang Middle School of ChongQing
汽车转弯
N
F牵
f静
f切
G
F牵 俯视图:
v
f静
f切
汽车在水平路面上转弯的向心力由哪个力提供？
重庆市黔江中学校 QianJiang Middle School of ChongQing
汽车转弯
例1：在一段半径为r的圆形水平轨道上，已知路面对汽 车轮胎的最大静摩擦力是车重的μ倍（μ＜1），求汽车拐 弯时的最大安全速度？
v
fmax
fmax
m
v2 r
mg m v2
r
v gr
重庆市黔江中学校 QianJiang Middle School of ChongQing
赛道的设计——外高内低