优化并行计算的性能评价
并行计算综述

并行计算综述姓名:尹航学号:S131020012 专业:计算机科学与技术摘要:本文对并行计算的基本概念和基本理论进行了分析和研究。
主要内容有:并行计算提出的背景,目前国内外的研究现状,并行计算概念和并行计算机类型,并行计算的性能评价,并行计算模型,并行编程环境与并行编程语言。
关键词:并行计算;性能评价;并行计算模型;并行编程1. 前言网络并行计算是近几年国际上并行计算新出现的一个重要研究方向,也是热门课题。
网络并行计算就是利用互联网上的计算机资源实现其它问题的计算,这种并行计算环境的显著优点是投资少、见效快、灵活性强等。
由于科学计算的要求,越来越多的用户希望能具有并行计算的环境,但除了少数计算机大户(石油、天气预报等)外,很多用户由于工业资金的不足而不能使用并行计算机。
一旦实现并行计算,就可以通过网络实现超级计算。
这样,就不必要购买昂贵的并行计算机。
目前,国内一般的应用单位都具有局域网或广域网的结点,基本上具备网络计算的硬件环境。
其次,网络并行计算的系统软件PVM是当前国际上公认的一种消息传递标准软件系统。
有了该软件系统,可以在不具备并行机的情况下进行并行计算。
该软件是美国国家基金资助的开放软件,没有版权问题。
可以从国际互联网上获得其源代码及其相应的辅助工具程序。
这无疑给人们对计算大问题带来了良好的机遇。
这种计算环境特别适合我国国情。
近几年国内一些高校和科研院所投入了一些力量来进行并行计算软件的应用理论和方法的研究,并取得了可喜的成绩。
到目前为止,网络并行计算已经在勘探地球物理、机械制造、计算数学、石油资源、数字模拟等许多应用领域开展研究。
这将在计算机的应用的各应用领域科学开创一个崭新的环境。
2. 并行计算简介[1]2.1并行计算与科学计算并行计算(Parallel Computing),简单地讲,就是在并行计算机上所作的计算,它和常说的高性能计算(High Performance Computing)、超级计算(Super Computing)是同义词,因为任何高性能计算和超级计算都离不开并行技术。
层次聚类 评价指标

层次聚类评价指标
层次聚类的评价指标主要包括以下几个方面:
1. 凝聚层次聚类和分裂层次聚类的评价指标:
内部评价指标:用于评估聚类结果内部的紧密程度或一致性。
常见的内部
评价指标包括:轮廓系数、DB指数、CH指数等。
外部评价指标:用于评估聚类结果与外部参考标准(如真实标签)的一致性。
常见的外部评价指标包括:调整兰德指数、兰德指数、纯度等。
2. 层次聚类中的距离度量:
距离度量是层次聚类中的重要概念,用于衡量数据点或簇之间的相似性或
差异性。
常见的距离度量方法包括:欧氏距离、曼哈顿距离、余弦相似度等。
3. 层次聚类中的分裂和合并策略:
分裂层次聚类:将数据集不断分裂成更小的簇,直到满足停止条件(如达
到预设的簇数量或簇大小)。
分裂层次聚类的评价指标主要关注簇的紧凑性和分离性。
分裂层次聚类:将数据集不断合并成更大的簇,直到满足停止条件(如达
到预设的簇数量或簇大小)。
分裂层次聚类的评价指标主要关注簇的紧凑性和分离性。
4. 层次聚类中的并行计算和优化方法:
层次聚类中的并行计算和优化方法可以提高聚类的效率和性能。
这些方法包括:动态规划、贪心算法、遗传算法等。
综上所述,层次聚类的评价指标需要根据具体的应用场景和需求选择合适的指标进行评估。
同时,在层次聚类中还需要注意距离度量的选择、分裂和合并策略的权衡以及并行计算和优化方法的运用等方面的问题。
随机矩阵特征值分解算法在机器学习中的应用优化与效果评估

随机矩阵特征值分解算法在机器学习中的应用优化与效果评估随机矩阵特征值分解算法(Random Matrix Eigenvalue Decomposition Algorithm,RMEDA)是一种在机器学习领域中被广泛应用的算法。
该算法通过对特征矩阵进行分解,能够提取出关键的特征值和特征向量,以便用于数据降维、聚类分析、特征提取等任务中。
本文将介绍RMEDA算法的优化方法,并进行效果评估。
一、算法原理介绍RMEDA算法的核心思想是利用随机矩阵来逼近原始矩阵,从而快速求解特征值和特征向量。
在传统的特征值分解算法中,由于需要计算矩阵的特征多项式,计算复杂度较高。
而RMEDA算法则通过使用随机矩阵,将特征值和特征向量的计算转化为一个优化问题,从而大大降低了计算复杂度。
二、算法应用优化为了提高RMEDA算法的性能和效率,研究者们进行了一系列的优化工作。
以下是一些常用的算法应用优化技术:1. 并行计算:将RMEDA算法中的计算过程进行并行化,利用多核处理器或分布式计算平台来加速算法的执行速度。
通过合理的任务划分和数据交换,可以充分利用计算资源,提高算法的并行效率。
2. 迭代收敛:传统的RMEDA算法可能会出现迭代收敛速度较慢的问题,为了加快算法的收敛速度,研究者们提出了各种改进方法,如使用快速迭代算法、引入加速技术等。
这些方法都旨在减少迭代次数,从而提高算法的执行效率。
3. 参数调优:RMEDA算法中存在一些可调节的参数,如随机矩阵的大小、迭代收敛的阈值等。
通过对这些参数进行调优,可以进一步提高算法的性能。
常用的参数调优方法包括网格搜索、遗传算法等。
4. 数据预处理:在实际应用中,原始数据往往存在噪声和异常值,为了提高RMEDA算法的鲁棒性,可以对数据进行预处理。
例如,可以使用数据平滑技术、异常值检测算法等,从而提高算法在噪声数据上的效果。
三、算法效果评估为了评估RMEDA算法在机器学习任务中的效果,研究者们通常使用各种评价指标对算法进行评估。
【计算机科学】_开放体系结构_期刊发文热词逐年推荐_20140724
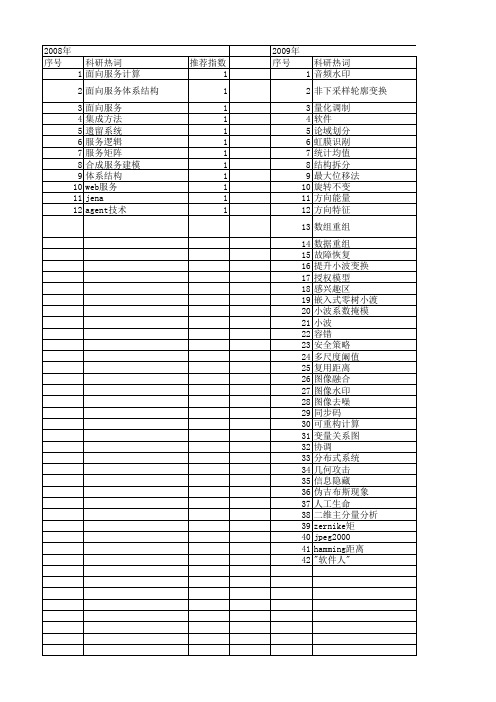
科研热词 性质分析 变迁指标 petri网分解 重构 遥感影像 软件演化 积木化 硬件 矢量映射 模型检测 模型 最少侵入 方法学 操作系统 开放服务网关协议 开放性 建模 应用服务器 多光谱 可重构 变化检测 变化性分离 动态演化 功能进化 信息隐藏 信任基 产生式规则 主成分变换 xyz/re xyz/adl web服务组合 uppaal em delta-grammar bigraph反应系统 bigraph aodsa
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 面向服务计算 面向服务体系结构 面向服务 集成方法 遗留系统 服务逻辑 服务矩阵 合成服务建模 体系结构 web服务 jena agent技术
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
2011年 科研热词 进程环境 运行时监测 软件老化 软件再生 资源动态重配置 能耗优化 网络安全 结构化 模型检测 时间属性 时间优化 无干扰 操作系统 性能优化 态势感知 异步通信 异构计算 异构混合 异构传感器 应用服务器 可扩展 协同并行计算 体系结构 任务执行 xyz/adl web服务组合 gpu计算 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
《基于并行空洞卷积的2.5D胸腔CT气道自动分割》

《基于并行空洞卷积的2.5D胸腔CT气道自动分割》一、引言在医学影像处理领域,胸腔CT(Computed Tomography)图像分析是诊断呼吸系统疾病的重要手段。
其中,气道分割是CT 图像处理的关键任务之一。
传统的气道分割方法主要依赖于手动标记或半自动方法,但这些方法效率低下且易受人为因素影响。
近年来,随着深度学习技术的发展,基于深度学习的自动分割方法在医学影像处理中得到了广泛应用。
本文提出了一种基于并行空洞卷积的2.5D胸腔CT气道自动分割方法,以提高分割的准确性和效率。
二、相关工作在医学影像处理领域,深度学习已被广泛应用于图像分割任务。
其中,卷积神经网络(CNN)因其强大的特征提取能力在图像分割中得到了广泛应用。
在气道分割方面,基于U-Net架构的模型已被证明具有较好的性能。
然而,传统的卷积操作在提取上下文信息方面存在局限性,这可能导致在处理CT图像时出现细节丢失的问题。
为了解决这一问题,本文引入了并行空洞卷积(Atrous Convolution)来提高特征提取的准确性。
三、方法本文提出的基于并行空洞卷积的2.5D胸腔CT气道自动分割方法主要包括以下步骤:1. 数据预处理:对原始CT图像进行预处理,包括去噪、归一化等操作,以便于后续的模型训练。
2. 构建模型:采用U-Net架构作为基础模型,通过引入并行空洞卷积来提高特征提取能力。
在卷积层中,采用不同膨胀率的空洞卷积来扩大感受野,从而更好地捕捉上下文信息。
3. 训练模型:使用标注的CT图像作为训练数据,通过优化损失函数来训练模型。
损失函数采用交叉熵损失和Dice损失的组合,以平衡正负样本的不均衡性并提高分割准确性。
4. 模型评估与优化:使用测试数据集对模型进行评估,根据评估结果对模型进行优化。
同时,采用并行计算技术来加速模型的训练和推理过程。
四、实验与结果为了验证本文方法的性能,我们进行了以下实验:1. 数据集:使用公开的胸腔CT图像数据集进行实验,包括正常和异常气道的数据。
高性能计算机群的性能评测与优化

要 :高性能计算机群 的性 能评测大致可分为机 器级 、 算法级 和程序级 的性能评测 怎样
评测一套高性能计算机群的性能 , 与测试者 的出发点有关 。从 购买前 的机器级 评测、 实程序评 真
测, 购买后试运行期间的机器级评测 、 户程序评测介绍有效评测机 群性能 的方法 , 用 在性能评测基
多地运 行不 同的应 用 程 序 。使 用 标 准 测 试 程 序 如 Ln AC 来 进 行 性 能 评 测 。在 实 际 评 测 iP K 中, 我们使用 机群 的 8节点 1C U 进行 Ln ak性能 测试 。使 用 Itl 6P ipr ne C和 F rrn编译 器 、 ot a MK L数学 库及 G C和 Gfrrn . . 编译 器 、 C ota4 4 1 ATL s .. 学库 在 8节 点 1C U 的 Ln A 3 60数 6P i—
2 1 购 买 前评测 .
首 先进行 机器 级 的性 能 评测 。比较各 厂商 提供 的各 种 机 群节 点 机 的 C U 和 存储 器 的 某 P 些基 本性 能 指标 。根据性 价 比和 计 划 经 费确 定所 选 节 点机 的 性 能指 标 , 主要 是 C U、 存 的 P 内 指标 。然 后在 预选 厂商 的节点 机上 进行 程序 级性 能评 测 。主要是 运行 一些 真实 的应 用程 序或 小 测试程 序 , 看是 否能够 调试 通过 , 到一个 好 的 结果 。这 一 步很 重 要 , 为不 同 的应用 需 要 得 因 不 同性能 和架 构的 机群 。如计 算密 集型 应用 问题重 点关 注机 群 的 C U; P 网络 密集 型应用 问题 重 点关注 机群 的 网络性能 ; 据密集 型应 用 问题 重点 关 注存 储 器 和 IO通 道 性 能 。这两 步测 数 /
并行计算--第2章-并行计算性能评价

加速比的几个问题
绝对加速
对于给定的问题,最佳串行算法能使用的时间除以 同一问题的并行算法所使用的时间
相对加速
同一问题的求解算法在单处理机上运行的时间除以 在多个处理机上的运行时间
超线性加速
一般的讲,线性加速已很难达到,超线性加速则是 难上加难。但在某些算法中,可能出现超线性加速 现象。
概念
可扩放性包括哪些方面?
机器规模的可扩放性
系统性能是如何随着处理机数目的增加而改善的
问题规模的可扩放性
系统的性能是如何随着数据规模和负载规模的增 加而改善
技术的可扩放性
系统的性能上如何随着技术的改变而改善
概念
可扩放性研究的目的是什么?
确定解决某类问题时何种并行算法与何种并 行体系结构的组合,可以有效的利用大量的 处理器;
等效率度量标准(ISO-efficiency)
优点
等效率函数是一种用分析方法处理工作负载 增长率与处理机增长率之间关系的有用的工 具,可用简单的、可定量计算的、少量的参 数就能计算出等效率函数,并由其复杂性可 指出算法的可扩放程度
如果W与p呈线性关系,则系统是可扩放的 如果W与p呈指数关系,则系统是不可扩放的
Sun and Ni’s 定理
Sun and Ni’s 定理
Sun and Ni’s 定理
Sun and Ni’s 定理几何意义
处理能力随处理器 数目的增加而增加
处理器的增加,执 行时间随之增加
2.1 加速比性能定律
2.1.1 Amdahl定律 2.1.2 Gustafson’s定理 2.1.3 Sun and Ni’s 定理 2.1.4 加速比的几个问题 小结
小结
影响加速比的因素:
ABAQUS钢筋混凝土有限元分析

ABAQUS钢筋混凝土有限元分析钢筋混凝土作为一种常见的建筑材料,在建筑、交通、水利等领域得到了广泛应用。
然而,钢筋混凝土结构在服役期间会受到多种复杂荷载的作用,导致结构性能退化甚至破坏。
因此,对钢筋混凝土结构进行精确的分析和模拟至关重要。
ABAQUS是一款强大的工程仿真软件,能够模拟各种材料和结构的力学行为。
本文将介绍如何使用ABAQUS 对钢筋混凝土进行有限元分析。
ABAQUS是一款专业的有限元分析软件,它提供了丰富的材料模型库和边界条件设置功能,可以模拟各种复杂结构的力学行为。
ABAQUS具有强大的前后处理功能,用户可以通过直观的界面进行模型构建、材料属性设置、边界条件施加等操作。
同时,ABAQUS还提供了强大的数据分析和可视化工具,方便用户对模拟结果进行详细分析。
钢筋混凝土是由钢筋和混凝土两种材料组成的复合材料。
混凝土是一种抗压强度高、抗拉强度低的材料,而钢筋具有较高的抗拉强度和塑性。
将钢筋嵌入混凝土中,可以提高结构的抗拉强度、抗压强度和韧性。
钢筋混凝土还具有较好的耐久性和防火性能。
在有限元分析中,需要对钢筋混凝土的力学性能进行适当简化。
通常假定混凝土为各向同性材料,钢筋为弹塑性材料。
同时,还应考虑混凝土的裂缝、损伤以及钢筋与混凝土之间的粘结和滑移等因素。
在ABAQUS中,可以对钢筋混凝土结构进行详细的有限元分析。
需要建立合适的计算模型,包括几何模型、材料属性、边界条件和荷载等。
模型建立完成后,可以通过ABAQUS的求解器进行计算,得到各节点位移、应力、应变等结果。
通过对计算结果的分析,可以评价结构的性能和安全性。
例如,可以通过应力和应变分布情况,分析结构的整体和局部稳定性、裂缝分布及扩展等。
还可以观察钢筋与混凝土之间的粘结性能以及评估结构的耐久性。
本文介绍了如何使用ABAQUS对钢筋混凝土进行有限元分析。
通过建立合适的计算模型,设置材料属性和边界条件,以及进行求解计算,可以得到结构的详细应力、应变和位移分布情况。
高性能计算导论:并行计算性能评价

如流水线技术、分治算法等,通过将任务划分为多个子任 务,分配给不同的处理单元并行执行,从而实现任务的快 速完成。
消息传递并行算法
如MPI(Message Passing Interface)算法,通过进程 间通信来协调不同处理单元上的任务执行,适用于分布式 内存系统。
算法优化策略与方法探讨
结果分析和改进建议
结果分析
对实验结果进行深入分析,找出性能 瓶颈和影响性能的关键因素。
改进建议
根据分析结果提出针对性的改进建议,如优 化算法、改进系统结构、提高硬件性能等。 同时,也可以对实验方法和流程进行反思和 改进,以提高评估的准确性和有效性。
05 案例分析:并行计算性能 评价实践
案例背景和目标设定
加速比
并行算法相对于串行算法 的执行速度提升倍数。
效率
用于衡量并行系统中处理 器利用率的指标,通常表 示为加速比与处理器数量 的比值。
可扩展性与规模性指标
1 2
等效性
在增加处理器数量时,保持问题规模和计算复杂 度不变的情况下,系统性能的提升能力。
弱可扩展性
在增加处理器数量的同时,增加问题规模,保持 每个处理器的负载不变,系统性能的提升能力。
功耗与能效比指标
功耗
01
并行计算系统在运行过程中的总功率消耗。
能效比
02
用于衡量并行计算系统每消耗一单位能量所能完成的计算量或
任务量的指标。
节能技术
03
采用低功耗处理器、动态电压频率调整、节能算法等技术降低
并行计算系统的功耗。
03 并行算法设计与优化策略
典型并行算法介绍及原理剖析
数据并行算法
如数组运算、矩阵乘法等,通过将数据划分为多个部分, 在多个处理单元上并行执行相同的操作来提高性能。
程序性能评价与优化

代码优化库
提供一些经过优化的函 数和算法,用于替换标 准库中的对应函数和算
法。
重构工具
自动或半自动地帮助开 发者改进代码结构,提 高可读性和可维护性。
缓存技术
数据缓存
将频繁访问的数据存储在缓存中,减 少对数据库或其他存储设备的访问次 数。
对象缓存
通过代理服务器缓存请求和响应,减 少网络传输时间。
选择评价方法
根据评价目标和需求选择合适的评价 方法,如基准测试、压力测试等。
收集数据
通过实际运行程序或模拟运行,收集 相关数据,如响应时间、CPU占用率 等。
分析数据
对收集到的数据进行整理和分析,找 出程序中的瓶颈和优化潜力。
制定优化方案
根据分析结果,制定相应的优化方案, 如算法改进、代码优化等。
实施优化并验证
算法改进
根据实际情况,选择更高效的算法或改进现有算法,降低计算复杂度。
算法并行化
将串行算法转化为并行算法,利用多核处理器或分布式计算资源提高计算效率。
数据结构优化
选择合适的数据结构
根据实际需求选择合适的数据结构,如哈希表、二叉树、堆等, 以减少数据访问和操作的时间。
数据结构优化
对常见的数据结构进行优化,如使用平衡二叉树、红黑树等自平衡 数据结构,提高查找、插入和删除操作的效率。
数据压缩与编码
采用数据压缩和编码技术,减少数据存储和传输的开销,提高数据 处理速度。
系统架构优化
分布式架构
01
将系统拆分成多个独立的子系统,通过分布式部署和负载均衡
技术提高系统整体性能。
缓存技术
02
利用缓存技术减少对数据库等存储设备的访问次数,提高系统
响应速度。
本人使用FEKO进行并行计算的经验总结

本人使用FEKO进行并行计算的经验总结(血泪史)作者: 尘谖(站内联系TA)发布: 2008-11-14项目需要,老师考虑要购进一台高性能计算机。
有公司主动上门推荐我们试用他们的产品。
师兄们都忙,稀里糊涂地让我做了实验员。
说明白一点儿,我的任务就是拿着我们的模型,去人家的机子上面装软件,然后对模型进行计算,记下计算时间,拷回计算结果。
目的一是试试机子性能,二是帮我们快速计算,赶一下实验进度。
使用的高性能计算机是曙光公司的PHPC100,5个节点,10个CPU,每个CPU是8个核。
计算软件用的是FEKO5.2,在网上下载的盗版,自行破解之后使用。
计算模型是几个不同情况的天线。
我自己虽然也做天线的仿真,但是我用的是HFSS,至于FEKO我并没有用过。
师兄事无巨细地给我写了安装步骤,又手把手地教我操作了两遍。
我拿着师兄写的步骤记录和网上下载的安装过程,信心百倍的和公司的人一起去试用了。
呵呵,原来就在我们实验室的楼上,简单地说。
满以为半天就能搞定。
机子好大啊,近一米长,半米高,30公分厚,呼呼地散发着热风。
坐在它旁边就想打盹,因为无论从各个方面都感觉它像一个壁炉。
殊不知,装软件就出了各种各样的问题。
软件安装的时候,会弹出一个提示页面,让输入用户名和密码。
这时如果你是以管理员的身份进行计算的话,千万不能输入用户名,密码也不能胡乱输入。
用户名要默认,回车,密码也一定要是最初进入节点使用的初始密码。
公司的人也是一知半解,指示我随便输入一个用户名,随便设置一个密码,后来接了各电话干脆闪人了。
我一个人吭哧吭哧在那里装软件。
一上午终于装好了软件,下午开始计算,肯定搞不定啦。
到了人家的下班时间,才算了1%。
因为,只能在一个节点上串行计算,不能并行计算。
晚上去了之后,认识了那里实验室的一个研一小美女,开朗活泼,勤奋好学,着实招人喜欢。
看我操作,呵呵,还小小地崇拜了我一把,确切地说是盲目崇拜。
因为我在更换节点的时候,死活进不去了计算机了。
利用并行计算方法实现地震活动速率变化参数 Z 值的空间扫描处理及其计算效能评价

并行计算是提高计算机系统计算速度和处理能力的一种有效手段。它的基本思想是用 多个处理器来协同求解同一问题,即将被求解的问题分解成若干个部分,各部分均由一个 独立的处理机进行计算。
并行计算系统既可以是专门设计的、含有多个处理器的超级计算机,也可以是以某种 方式互连的若干台独立计算机构成的集群。从1972年第一台并行计算机ILLIAC—IV的产
为了检验Z值的结果是否可靠,将相同计算条件下利用并行计算方法获取的结果图和 利用ZMAP软件获取的结果图进行比较。假没如下相同的计算条件:纬度最小值Brain一 20度,纬度最大值Bmax=40度,经度最小值Lmin=100度,经度最大值Lmax—120度。 经度上和纬度上空间扫描的滑动步长为dL—dB一0.05度。起始时间T。=1985年,结束时 间Te一2005年,时间窗的起始时间Tc=1997年,窗长rw 3年。震级约束条件为M(大 于等于2.0,震源深度约束条件为小于等于50 km,采样时间间隔参数step一15d,选取等 地震数为N_--100作为格点计算的空间统计窗口,计算函数是LTA函数。
相比于利用确定的空间窗口(圆形窗口或方形窗口)计算Z值,选择等地震数窗口的处 理方式无疑大大增加了生成Z值图的计算量。目前,国内地震活动性分析软件MapSis中 空间扫描步长可以设置的最小值为0.1度,这无法满足针对局部地区的高分辨率扫描处理 的实际需求。另外,笔者在Intel酷睿2双核E6550上用ZMAP软件计算生成16万格点的 Z值图需要花费几十分钟、甚至几个小时。可以推测计算百万、甚至千万级别格点数的Z 值图,花费的时间将是几个小时,甚至几天,这很难满足日常快速处理分析的要求。为了 解决这个问题,本文采用了并行计算的方法来处理Z值的空间扫描,并且可以进一步将此 方法推广应用于其他地震活动性参数空间扫描处理中去,以提高处理的精度和效率。
计算机并行计算的基本问题及现状

计算机并行计算的基本问题及现状作者:张悦来源:《文存阅刊》2017年第12期(哈尔滨广厦学院黑龙江哈尔滨 150025)摘要:工作中,我们总是希望我们自己工作更有效率,用更少的时间解决更多的问题。
在计算机里,这就是并行计算的基本初衷。
全世界第一台计算机ENIAC中就己经出现了并行计算的概念。
它有20个累加器,可以并发执行多个加减运算,可谓开并行计算的先河。
在随后的20世纪五六十年代,由于晶体管和集成电器的发明,出现了更多更快的计算机。
20世纪70年代,随着微电子技术的发展,出现了微型处理器(CPU),接着,1974年,全世界第一台个人电脑—牛郎星顺利出炉。
紧随其后,看到市场前景的苹果和IBM推波助澜,计算机开始进入个人时代。
个人计算机同时又催生了软件业的高速发展,软件又带动CPU不断升级换代。
这为并行计算摆脱高端路线,进入平民化时代打下了基础。
关键词:并行计算、累加器、微电子技术、微型处理器一、并行计算的意义与功能1.1并行计算的功能在个人计算机诞生后的几十年里,程序员们编写了大量的应用软件,这些软件决大部分了采用串行计算方法。
所谓串行,是指软件在PC上执行,在进入CPU前被分解为一个个指令,指令在CPU中一条条顺序执行。
任一时间内,CPU只能够运行一条指令。
这种方式很符合我们对现实世界的思考习惯。
至于软件的运行速度,则依赖硬件的处理能力,尤其CPU的处理速度。
这种思维方式到了2005年遇到了挑战。
在那一年,受限于制造CPU的半导体材料限制,左右CPU发展的摩尔定律开始失效了。
但芯片业很快找到了一个变通的办法:在一块芯片中植入多个处理核心,通过多核的共同运算,提高运行速度。
1.2并行计算的意义并行计算目前还是一门发展中的学科。
并行计算是相对串行计算而言的,并行计算可以分为时间上的并行计算和空间上的并行计算。
时间上的并行计算就是流水线技术,即采用指令预取技术,将每个指令分成多步,各步间叠加操作,当前指令完成前,后一指令准备就绪,缩小指令执行的时钟周期。
第2章并行硬件和并行软件

ASIC在比特币挖矿、网络通信等领域有广泛应用。
10
现场可编程门阵列(FPGA)
FPGA是一种可编程的集成电路,可以通过编程实 现不同的逻辑功能。
FPGA具有高度的灵活性和可重构性,可以根据需 要动态配置硬件资源。
FPGA在嵌入式系统、数字信号处理等领域有广泛 应用。
2024/1/25
11
2024/1/25
第2章并行硬件和并 行软件
2024/1/25
1
目录
2024/1/25
• 并行计算概述 • 并行硬件基础 • 并行软件基础 • 并行硬件与软件交互方式 • 并行计算性能评价与优化 • 未来发展趋势与挑战
2
2024/1/25
01
CATALOGUE
并行计算概述
3
并行计算定义与分类
2024/1/25
定义
同步与互斥
为了避免数据冲突和保证一致性,需要使用同步 机制(如锁、信号量等)来实现对共享资源的互 斥访问。
编程复杂度
3
共享内存模型编程相对简单,但需要注意数据一 致性和同步问题,否则可能导致程序错误或性能 下降。
2024/1/25
18
消息传递模型
2024/1/25
独立的内存空间
01
每个并行线程拥有自己的私有内存空间,线程之间通过发送和
容错性
设计并行算法时需要考虑容错性,以 便在某个处理单元出现故障时,整个 系统仍能继续运行。
15
典型并行软件介绍
Hadoop
CUDA
一个开源的分布式计算框架,支持大规模 数据处理和分析,广泛应用于大数据领域 。
NVIDIA推出的并行计算平台和编程模型, 允许开发人员使用C/C语言编写高性能的 GPU加速程序。
施瓦茨-克里斯托弗反变换的快速收敛算法及其应用

施瓦茨-克里斯托弗反变换是一种常用的数值计算算法,广泛应用于信号处理、图像处理、地球物理勘探、量子力学等领域。
在实际应用中,快速收敛是评价该算法优劣的重要指标之一。
本文将对施瓦茨-克里斯托弗反变换的快速收敛算法及其应用进行探讨。
一、施瓦茨-克里斯托弗反变换的基本原理施瓦茨-克里斯托弗反变换是一种离散傅里叶变换的快速算法,能够将时域信号转换为频域信号。
其基本原理是通过迭代计算,将离散傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn),大大提高了计算效率。
二、快速收敛算法的原理及优化针对施瓦茨-克里斯托弗反变换算法的快速收敛问题,研究者们提出了多种优化算法,包括剪枝算法、加速收敛算法、块状矩阵分解算法等。
这些算法在不同场景下有不同的适用性,能够有效提高算法的收敛速度,降低计算成本。
三、施瓦茨-克里斯托弗反变换在信号处理中的应用在信号处理领域,施瓦茨-克里斯托弗反变换广泛应用于音频处理、语音识别、图像处理等方面。
通过快速收敛的算法,可以实现对信号的快速、准确的频域分析,为信号处理提供了重要的技术支持。
四、施瓦茨-克里斯托弗反变换在地球物理勘探中的应用在地球物理勘探领域,施瓦茨-克里斯托弗反变换被广泛应用于地震数据处理、地下水资源勘探、油气勘探等方面。
通过快速收敛的算法,可以实现对地下介质的高分辨率成像,为地球物理勘探提供了重要的技术支持。
五、施瓦茨-克里斯托弗反变换在量子力学中的应用在量子力学领域,施瓦茨-克里斯托弗反变换被广泛应用于量子态的描述、哈密顿量的计算等方面。
通过快速收敛的算法,可以实现对量子系统的快速模拟和计算,为量子力学研究提供了重要的技术支持。
总结:施瓦茨-克里斯托弗反变换的快速收敛算法在各个领域都有重要的应用,通过不断优化算法,可以进一步提高算法的计算速度和精度,推动相关领域的发展和进步。
希望本文的介绍能够为相关领域的研究和应用提供一定的参考和借鉴。
六、算法的改进和未来展望随着计算机硬件性能的不断提升和算法优化的深入研究,施瓦茨-克里斯托弗反变换的快速收敛算法将会迎来更大的改进空间和发展机遇。
并行程序实用优化方法讨论

并行算法性能简析

d u l f d u l a) tm ( . obe ( obe f u e r 40/(. aa )) 1 0+ * ) ;
定 义 被 积 函 数 fx) ( 。
以计算 盯的近似值 为例 : 1 4(慨 d 设 T =I /1 )x的近似值 ,
很 容 易 就 想 到 如 何 完 成 一 个 并 行 程 序 来 实 现 这 个 题 目。 即 h
果 的误 差 。
对这 些子 区间 的计算 值求 和 , 到计算 结果 。代码 中计 算 区间 即得
p-I
采 用 循 环 分 配 的方 式 , 将 计 算 公 式 写 成 : h 1 即 、
,鼍 ()
d u l myi p , , u x /m p : 程 中所 有 小 区 间 obe p, i h sm, ;* y i进 面 积 的 求 和 值 ;i最 终 的 计 算 叮值 ; : 区 间宽 度 ; u 进 p: r h小 sm:
-
何 怡芝
d u l trw i . e d tme o be s t t a me n w i :
并行 算 法性 能 简析
】
定 义 变 量 开 始 时 间
srt e t t i 和结 束时间 e d t e aw m n w i 。均为 MP_ i e ) m I Wt ( 的返 回值 。 m
# n l d sd oh i cu e< t i - >
足 计 算 机 计 算 速 度 的 惟 一 可行Байду номын сангаас途 径 嘲 所 谓 并 行 计 算 [ 就 是 。 1 1 ,
将 一 个 任 务 分 解 成 多 个 子 任 务 , 时 分 配 给 几 个 不 同 的 处 理 同 器 , 个 处 理 器 之 间 相 互 协 同 , 行 地 执 行 子 任 务 , 而 能 够 各 并 从 加 速 求 解 问 题 的 速 度 , 者 扩 大 求 解 应 用 问题 的 规 模 。 或
(2024年)并行计算机程序设计导论

02
根据任务的依赖关系和可用资源,动态地分配任务到不同的处
理单元,以最大化并行度和减少总执行时间。
任务粒度
03
选择合适的任务粒度,以平衡通信开销和计算开销,实现高效
的并行执行。
13
数据划分与映射策略
2024/3/26
数据划分
将数据集划分为多个子集,每个子集可以在单独的处理单元上进 行并行处理。
数据映射
将数据子集映射到相应的处理单元,以减少数据移动和通信开销 。
数据局部性
优化数据布局和访问模式,以提高缓存利用率和数据访问速度。
14
负载均衡与性能优化策略
1 2
负载均衡
动态地分配任务和数据到处理单元,以保持各处 理单元的负载平衡,避免某些处理单元空闲而其 他处理单元过载。
性能优化
采用各种优化技术,如循环展开、向量化、并行 化库等,以提高并行程序的执行效率。
并行计算机程序设计导论
2024/3/26
ห้องสมุดไป่ตู้
1
contents
目录
2024/3/26
• 并行计算概述 • 并行编程模型与语言 • 并行算法设计策略 • 典型并行算法案例分析 • 并行计算性能评价与优化 • 现代并行计算技术展望
2
01
并行计算概述
2024/3/26
3
并行计算定义与发展
定义
并行计算是指同时使用多种计算资源 解决计算问题的过程,其主要目的是 快速解决大型且复杂的计算问题。
3
资源利用
充分利用计算资源,如多核处理器、GPU、分布 式集群等,以加速并行程序的执行。
2024/3/26
15
04
典型并行算法案例分析
系统集成与优化方法研究

常用系统集成策略比较
单一系统集成策略
1.系统内部的模块化设计:通过模块化的系统设计,可以实现单一系统的可扩展性和灵活性。 2.统一的数据接口和协议:单一系统集成策略需要统一的数据接口和通信协议,以保证各个子系统 之间的数据交换和信息共享。 3.单点故障的风险管理:由于所有功能都集中在单一系统中,因此需要采取有效的风险管理措施, 防止单点故障导致整个系统的瘫痪。
▪ 遗传算法
1.个体编码:遗传算法通过将待优化问题的解表示为二进制字符串或其他形式的编 码,实现个体在种群中的表示和交换。 2.遗传操作:遗传算法采用选择、交叉和突变三种基本遗传操作,模拟自然选择和 进化过程,不断生成新的个体群体,以期接近最优解。 3.停止准则:遗传算法通过设置一定的停止准则(如达到预设代数或满足预定精度 ),来确定算法结束的时间点。
多目标优化问题的研究进展
▪ 多目标优化问题的求解策略
1.分级搜索、精英保留等基本策略 2.基于参考点和指示器的排序方法 3.考虑问题特定性质的定制化求解策略
▪ 多目标优化的实际应用案例
1.工程设计优化问题的应用实例 2.生物医学领域中的应用示例 3.社会经济系统中的多目标优化问题
多目标优化问题的研究进展
常用系统集成策略比较
面向服务架构(SOA)集成策略
1.服务化和模块化的设计理念:SOA将业务功能划分为一系列 的服务,每个服务都是独立的、可重用的,可以根据需求进行 组合。 2.服务发现和调用机制:在SOA中,服务消费者需要能够发现 并调用所需的服务,这需要相应的服务注册中心和服务代理来 实现。 3.异构系统间的互操作性:SOA支持异构系统之间的互操作性 ,可以通过Web服务技术实现不同系统之间的通信和数据交换 。
并 行 计 算

并行计算之基本概念
主要内容:
●并行计算?(PWT投影片)
⏹并行机体系结构;
⏹并行计算机环境建设与管理;
⏹并行算法设计;
⏹并行程序设计;
⏹并行性能优化与评价;
⏹并行应用是并行计算的最终目的。
●并行算法设计原则:
⏹并行算法设计:将一个任务分解为多个可同时执行的子任务,
这些子任务分别运行在不同的处理器上,通过相互之间的数据
交换完成同一个任务。
⏹并行算法设计的分类:
◆独立并行计算(MC、生物序列比对、数据库查询、遗传算
法、数据并行处理等;
◆大粒度的同步并行算法(数值并行算法解PDE方程区域分
解、数据分解、空间分解、时间分解?);
◆大粒度的异步并行算法(数据驱动类并行算法,大分子生
物计算)
⏹大粒度并行:计算通信比;
●并行程序设计:
⏹独立并行计算;
⏹大粒度的同步并行计算;
⏹大粒度的异步并行计算;
●并行性能评价
⏹加速比;
⏹效率;
⏹峰值性能与实际浮点性能;
⏹超线性加速比;
⏹性能评价的主要目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V01.2 1 No.6
计算tn.T程与设计
COMPUTER ENGINEERING AND DESIGN 中图分类号:TP301
2000年12月
Dcc. 2000
文章编号:1000-7024(2000)06-0004-04
文献标识码:A
优化并行计算的性能评价
刘杰,迟利华,胡庆丰
(国防科学技术大学计算机学院,长沙410073)
128
仉53 0.7
37.1 53
l l l 44 l 3
3.3l
3.53 4.46 3.53
699
76.1
NPB2
NPBl NPB2
92J 76.1
化就是要得到更高的优化加速比,而不是更高的加速比。
5结柬语
并行计算性能的评价在并行处理中显得越来越重要.通过性能评价可以揭示并行算法及并行机的 性能瓶颈,指导算法和并行机的设计与改进。目前,常用加速比来评价并行算法的性能,而加速比有 许多缺点和不足,需要有新的性能评价模型来克服加速比的缺点和不足。本文将加速比和优化加速因 子结合起来定义了优化加速比,充分考虑了算法和机器两者的性能,能充分反映并行算法的计算性 能。在设计一个并行算法的过程中,如果得到较好的加速比,那么就要进一步优化程序使得处理速度 变快,相应地增加优化加速比,以达到改进和优化并行算法的目的。
叫辑赫
;孵
(4)式中的不同取法就得到不同的加速比性能评价模型:①W=ZW,保持不变.此时得到周定规模加速
圪模型;②耳(聊b;罢吲+口c尸)保持不变,此时得到固定时间加速比模型;③降t;孵表示达到Jp台处
理机总存储容量问题规模,此时得到固定存储容量加速比。 显然.在固定时间加速比和固定存储容量加速比中问题的规模随处理机处理速度的变化而变化, 特别是固定时间加速比模型中,问题的规模只随处理机处理速度的变化而变化。 通常使用并行机求解一个应用问题都有其周有的最佳的通信模式,而并行机的网络性能是不变 的,因此我们在下述讨论中,设总开销Qc一保持不变.我们对并行算法采用诸如数据的合理划分,负 载平衡,充分利用Cache,编译等优化手段使得单个处理机对一应用问题的处理速度加快,即△增大, 此时加速比的变化情况见定理1。 定理l设Q(一保持不变.对并行算法进行优化,单个处理机的处理速度△’>△,设优化以后问题规模
"
P
△'△。则优化后并行程序在P台处理机上的优化加速比叩∽有:叮(尸)=—争—争
J J,
个
(10)
设优化前并行程序的优化因子c喱尸卜l,则优化前并行程序的优化加速比
珂㈣=尉一-[ⅨPbs(P)
即优化前并行程序的优化加速比就等于加速比。
(II)
假设P,。咭l,2,…,Ⅳ)表示另一个优化程序在尸台处理机上的计算时间,单机处理机速度为△”.且
;彤
根据(4),设吲专,有
而耳=古£景斗QcP)保持不变,从而z=z—}保持不变.即:s缸'=墨(P),证毕.
由定理1可知当问题的求解速度加快以后,加速比反而下降.这说明加速比不能充分揭示并行计 算的性能。表l中给出了NPB中的FT(问题规模为A)NPB2和NPBl并行程序在IBMSP2(66mhz/wn) 上的测试结果.NAS并行基准测试程序集(NPB)旧是由美国NASA Ames研究中心于1991年开发、 以”pencil andpaper"方式给出、以数值空气动力学模拟为主要内容的高度并行计算机系统基准测试程序 集。NPB包括NPBI和NPB2,NPB2基于Fortran77和MPI,实现时极小或不作微调(无厂家优化), NPBI针对特定的目标系统,设计并行算法,进行程序优化,可得到目标系统的最好性能。 从表l可以看 出NPBl FT的计算 时间比NPB2 Fr大 约短1.5倍.而相应 的加速比比NPB2 FT要小。计算时问 长说明处理速度 慢,从而也说明了
△”>△’,优化加速比矿【P)。此时优化后并行程序的优化加速比_㈣和叩”(P)与优化以前的并行程序的优
化加速比械尸)之间的关系由定理2给出。
定理2设gP)保持不变.并设并行计算总时间大于通信总开销,单机处理速度满足△”>7△>△,则优
化加速比rl(P)、平仰和々“(功,和满足:节(P)q蜘”(聊
(12)
参考文献:
【1]1 computer【J】IEEE Speetrtma,1972,9(3):84-91 【2]GustMson j.Reevaluating Amdahl’s law川.Commtmication ofACM,1988,31(5):532-533 【3]Stm X.and
Ni L Scalable
在一般的实际应用问题中,定理2中的假设并行计算总时间大于通信总开销是很容易满足的,因
为只有大规模的问题才会用并行机来进行计算,对于~般小规模的问题只用单个处理机就行了,而大 规模的问题大都满足上述条件。从定理2可看出,具有较快单机处理速度可以得到更高的优化加速比。
在我们的讨论中一直假设烈P)保持不变,在实际应用中是不现实的,但这种情况确实存在:另一方面,
C叩ud“g,1993,19:27・37.
摘要:传统的并行计算的性能评价模型是加速比,文中讨论了加速比的缺点和不足,在此基 础上提出了一种新的优化并行计算的性能评价模型(我们称之为优化加速比).利用优化加速 比分析了NAS基准测试程序MG和FT在IBM SP2(66mhz/wn)上的・巨能. 关键词:加速比;优化并行计算;性能评价模型;NAS基准测试程序集 1引言
随着并行机和并行算法研究的深入t并行计算性能评价日益成为研究热点,使用和研究最多的评 价模型是加速比。Ware II]首先总结了Amdahl的观点.提出加速比公式,此公式固定问题规模。不能 满足实际需要,Gustafson“提出了固定时间加速比,但问题规模的增加受到内存限制,Stm和Ni“提 出了内存受限加速比。上述3个加速比存在一个共同的缺点.就是当并行计算数据划分不合理、Cache 没得到充分利用、并行程序设计不合理、编译优化低效等情况时并行处理的速度变慢.而加速比反而 增加,快的并行处理速度和好的加速比看起来是矛盾的,这显然不能揭示并行计算的性能,因此需要 有新的评价标准来对并行计算作出合理的评价。为了改进加速比中的缺点和不足,文M提出了新的 并行计算时间模型,但依然存在上述问题。 本文首先分析了加速比的缺点和不足。指出低的并行处理速度会带来高的加速比,然后我们将加
假设对并行算法进行优化使得烈P)减小而其它条件不变,由加速比定义可知。加速比增大,相应地优
化加速比增大,从而可看出尽管定理2假设匹P)保持不变,对舻)发生变化的情形,(12)式依然成立-
从而利用优化加速比可以报好地刻划优化并行计算的性能。
4倒子
表2给出了NPBIMG和NPB2MG在IBMSP2(“mII刀伽)上的铡试结果。从表1和表2的测试结 万方数据
——6一
果可看出,当对并行程序进 行优化时,程序的执行时间 缩短。而相应的加速比却在 减小,因此显然不能充分反 映并行算法的性能;而此时 相应的优化加速比增大,说 明NPBl并行程序的计算性 能好于NPB2,这是符合事实 的。我们对并行程序进行优
加速比 优化 加速比 处理机台教 时问 (秒)
NPBl NPB2 NPBl
证明:先证明叮(P)‘_tP)。因为并行计算总时间大于通信总开销,所以
Q(肛掣
至旱嘲
(13)
I}+堕凹r
04)
从而有:
△・△。F吾亭芦f
(△>△’((;孚旧卜△嘻争吲+△口㈣
(13)式成立且△'△,所以:(△一△,((霎孚J軎k一(dP)r△△'<o
从而
眦磋萼霄tX+△㈣r<(;孚吲td面t"
n升
在(14)式两边同乘以彤,即得到:耔彘,从而有叩(_P>qtP)成立・同理可证_tP)勺”(P)a证毕・
速比和优化加速因子结合起来提出了一种新的并行计算性能评价模型,即优化加速比.能给出并行计
算性能合理的评价,为设计高效并行算法和并行机提供指导。最后利用优化加速比分析了NAS基准 测试程序集MG和FT在SP2上的性能。
2加速比性能评价模型
下面讨论固定负载、固定时间和固定存储加速比性能评价模型.首先给出并行度定义。 定义1算法的并行度是指该算法中可并行执行的操作数. 设甲表示一个应用问题工作量.常用浮点数来表示,P表示处理机台数,胂表示最大并行度,孵表 示并行度为f时的工作量,△表示一台处理机对相应并行算法的计算性能,常用Mflops/s来表示,对同 一问题的不同并行算法,△不同。此时有:矸,-=孵 (1)
加速比 优化 加速比 处理机台数 时间 (秒)
I
s喃
表1 NⅧl
NPB2NPBl㈣霹耘∑孵NTBFT在IBMSP2上的鬻试结果
2
45 87 6950 1.856 4 24 7i 37ll 3.446 8 13.3 J 19 92 6 390 6 543 16 7.Ol lOll 12.0l 13.02 17.14 13.02
Wave w
The ultimate
problems and memory-bounded speedup闭.Journal ofParallel and Distributed Wilson S.Heterogeneous computing machines and Amdahl's law闭.Parallel
28 24
9 550
6.543
25.04
46北
慢的处理速度带来高的加速比.
万方数据
5一
3新的优化并行计算的性能评价模型
通过第2部分的讨论可知.加速比模型不能充分揭示优化并行计算的性能.有对得到的结论可能 是错的.那么是否可用并行执行时间来刻化并行计算的性能呢?回答是否定的,因为采用并行时间时 没有充分考虑并行机的处理速度,因此需要有新的并行计算性能评价模型。定义2给出了优化加速因 子的定义。 定义2一个优化并行程序在尸台处理机上的优化加速因子
