六年级数学计算组合图形周长和面积
小学六年级【小升初】数学《平面图形的测量专题课程》含答案
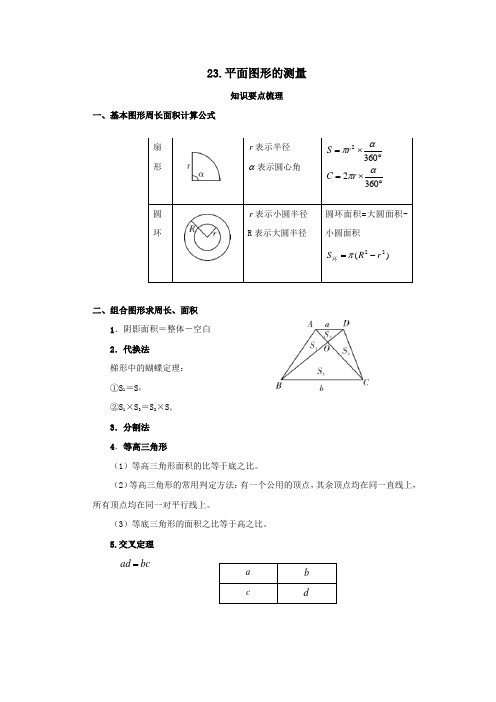
23.平面图形的测量知识要点梳理一、基本图形周长面积计算公式二、组合图形求周长、面积 1.阴影面积=整体-空白 2.代换法梯形中的蝴蝶定理: ①S 1=S 4 ②S 1×S 3=S 2×S 4 3.分割法 4.等高三角形(1)等高三角形面积的比等于底之比。
(2)等高三角形的常用判定方法:有一个公用的顶点,其余顶点均在同一直线上,所有顶点均在同一对平行线上。
(3)等底三角形的面积之比等于高之比。
5.交叉定理 bc ad =扇形r 表示半径α表示圆心角︒⨯=3602απr S ︒⨯=3602απr C圆环 r 表示小圆半径R 表示大圆半径圆环面积=大圆面积-小圆面积)(22r R S -=π环a bcd考点精讲分析典例精讲考点1组合图形的周长和面积【例1】 求下面图形的周长和面积。
(单位:米) 【精析】 要求它的周长,可用长方形的2个长+1个宽+圆的周长的一半;要求它的面积,可用图中长方形的面积加上半圆的面积即可。
【答案】 周长:2.5×2+2+3.14×2÷2 =5+2+3.14 =10.14(米)面积:2.5×2+3.14×2)22(÷2 =5+3.14×1÷2 =5+1.57 =6.57(平方米)答:这个图形的周长是10.14米,面积是6.57平方米【归纳总结】 组合图形的计算,一般都要把它分割成规则图形再进行计算。
考点2 等积变换法求面积【例2】 如图,ABCD 是直角梯形,AB =3厘米,AD =4厘米,BC =6厘米,求阴影部分的面积。
【精析】 阴影部分的面积为三角形ABE 和三角形DEC 的面积之和,利用△ABE 和△DEC 是等高三角形则阴影部分的面积可以变换为BC 边的长乘以高,再除以2。
【答案】 6×3÷2=9(平方厘米)【归纳总结】 高一定,阴影部分面积=底之和×高÷2。
六年级数学上册组合图形的周长和面积讲解

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级数学《组合图形面积》经典习题

1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF 的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
六年级第二次课平面组合图形的面积计算
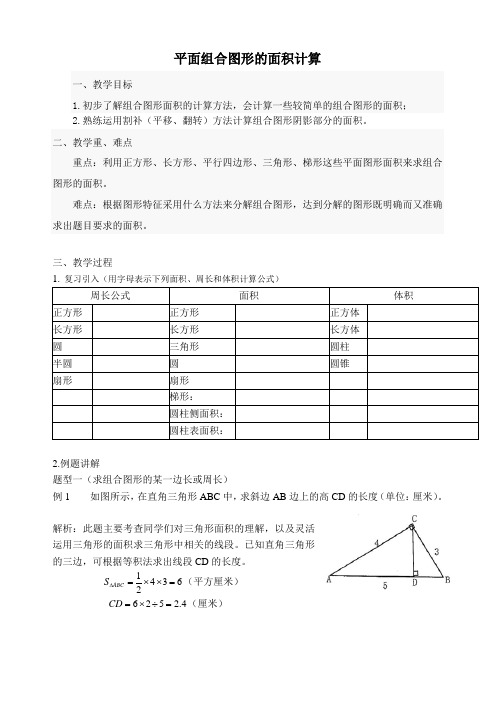
平面组合图形的面积计算一、教学目标1.初步了解组合图形面积的计算方法,会计算一些较简单的组合图形的面积;2.熟练运用割补(平移、翻转)方法计算组合图形阴影部分的面积。
二、教学重、难点重点:利用正方形、长方形、平行四边形、三角形、梯形这些平面图形面积来求组合图形的面积。
难点:根据图形特征采用什么方法来分解组合图形,达到分解的图形既明确而又准确求出题目要求的面积。
三、教学过程1. 复习引入(用字母表示下列面积、周长和体积计算公式)周长公式面积 体积正方形 正方形 正方体 长方形 长方形 长方体 圆 三角形 圆柱 半圆 圆 圆锥 扇形 扇形 梯形:圆柱侧面积:圆柱表面积:2.例题讲解题型一(求组合图形的某一边长或周长)例1 如图所示,在直角三角形ABC 中,求斜边AB 边上的高CD 的长度(单位:厘米)。
解析:此题主要考查同学们对三角形面积的理解,以及灵活运用三角形的面积求三角形中相关的线段。
已知直角三角形的三边,可根据等积法求出线段CD 的长度。
14362ABC S ∆=⨯⨯=(平方厘米)625 2.4CD =⨯÷=(厘米)DCBE A练习一(1)图中,王叔叔上班有两条路可走,他走哪条路近?(2) 公园里有一个半圆的花圃,花圃周围要围上竹篱笆,竹篱笆长多少米?题型二(求组合图形的面积)例2 如图,已知梯形ABCD 的面积是560平方厘米,ABCE 是正方形,:5:4CE ED =。
求三角形的面积。
解析:因为:5:4CE ED =,所以正方形和三角形的面积比是25:105:2=,三角形的面积为25601607⨯=(平方厘米)练习二(1) 如图,是由4个相同的半圆形组合的,已知图形的周长是50.24厘米,求图形的面积。
(2) 如图所示,长方形的长12 cm ,宽8 cm ,DE=5 cm ,求△ABC 的面积。
题型三(利用平移法求阴影部分面积)555555例3 求下图阴影部分的面积。
(单位:厘米)解:将阴影部分进行平移,合并成一个简单图形,再求它们的面积,如上右图。
(完整版)六年级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级数学思维:组合图形的面积计算,例题解析!

六年级数学思维:组合图形的面积计算,例题解析!主要题型:一、求不规则图形面积(阴影部分面积);二、求不能直接利用公式计算的图形面积;三、求规则图形的面积,但条件比较隐蔽,用常规思路无法解答。
基本解题思路:解题的基本思路是,先通过分割、切拼、旋转、平移、翻折、缩放、等积替换等方法,把不规则图形转化为规则图形(或规则图形面积的和差),让隐蔽条件明朗化,再合理运用面积公式,巧求不规则图形面积。
解题技巧:这一块分六讲,以后会陆续更新,每一块各有侧重地介绍了六种求面积的计算方法,但每一种解题方法并不是孤立存在的,在实际解题时一道题常常需要综合运用多种方法,才能巧妙解题。
例如加减法求面积常需要对图形进行割补,而用割补法求面积常需要添加辅助线、平移、旋转、进行加减运算等。
在解答图形面积问题时,关键就是要注意寻找不同图形或同一个图形的各个部分之间的内在联系,可以变换角度或适当添加辅助线帮助观察,特别要注意观察图形边角的形状、长度和角度,及是否隐藏有等底等高之类的条件。
从而根据图形的形状特征,合理地进行分割重组,化不规则为规则,巧妙地运用题目给出的各种条件。
小学阶段常见的面积公式:长方形的面积=长×宽S=ab正方形的面积=边长×边长S=a.a=a2三角形的面积=底×高÷2S=ah÷2平行四边形的面积=底×高S=ah梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2圆的面积=圆周率×半径×半径S=πr2今天我们讲第一块内容:加减法求面积方法介绍:根据组合图形的形状特征,从整体上观察,将不规则图形分解转化成几个基本规则图形,分别计算它们的面积。
再变化角度思考,通过相加或相减求出所求图形的面积。
例题1:求下图中阴影部分的面积(最后结果保留一位小数)。
(单位:厘米)【解析】:上图阴影部分可以分割成3个完全相同的弓形,先求出其中一个弓形的面积,再求出3个弓形的总面积就是所求阴影部分的面积。
北师大版六年级上册数学圆的周长和面积组合图形计算

专题01 圆的周长和面积(组合图形)注意事项:1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.所有题目必须在答题卡上作答,在试卷上作答无效。
3.考试结束后将试卷和答题卡一并交回。
一.计算题(共20小题)1.计算下面图形阴影部分的周长和面积。
(单位:厘米)2.如图中,大圆的半径等于小圆的直径。
请计算阴影部分的周长。
3.计算下面图形的周长与面积。
4.计算下边图形的周长和面积。
5.计算如图形阴影部分的周长和面积。
(单位:dm)6.求下面各图中阴影部分的周长和面积。
(1)(2)7.求阴影部分的周长。
(单位:)cm8.计算图中阴影部分的面积。
(单位:)cm9.求阴影部分的周长。
10.求如图阴影部分的周长(单位:厘米).11.求阴影部分的周长。
(大圆 4.5R =,小圆2r =,单位:)cm12.求图中形阴影部分的面积.(可以直接用π表示,也可以π取3.14)13.如图,求阴影部分的周长。
(π取3.14)14.计算右图的面积(单位:)dm 。
15.已知三角形的面积是29m,求圆的面积。
16.按要求计算下列各题。
(1)求图中图形的周长。
(2)求图中阴影部分的面积。
17.求阴影部分的面积:(单位:)cm18.求阴影部分的周长。
(单位:)cm19.求下列阴影部分的面积.20.求如图阴影部分面积。
(单位:厘米)专题01 圆的周长和面积(组合图形)答案解析一.计算题(共20小题)1.计算下面图形阴影部分的周长和面积。
(单位:厘米)【分析】根据题意,圆的直径为(4×3)厘米,阴影部分的周长等于圆的周长的一半加上5条4厘米长的线段之和,利用圆的周长公式:C=πd,代入数据即可求出阴影部分的周长;阴影部分的面积等于圆的面积的一半减去边长为4厘米的正方形面积,分别利用圆的面积和正方形的面积公式求出这两个图形的面积,再相减即可得解。
××÷+×【解答】3.14(43)245×÷+=3.1412220+=18.8420=38.84(厘米)2××÷÷−×3.14(432)244=2×÷−3.146216×÷−=3.1436216−=56.5216=40.52(平方厘米)即阴影部分的周长是38.84厘米,面积是40.52平方厘米。
六年级上册数学教案-第九讲组合图形的周长与面积人教版

六年级上册数学教案第九讲组合图形的周长与面积人教版教学内容本讲主要介绍组合图形的周长与面积的计算方法。
学生需要掌握组合图形的构成,理解组合图形可以分解为简单的几何图形,如三角形、矩形、圆形等。
学生需要学习如何计算组合图形的周长和面积,包括分解图形、计算各部分周长和面积、求和等步骤。
本讲还将介绍一些常见的组合图形的周长与面积的求解技巧和注意事项。
教学目标1. 理解组合图形的构成,能够将组合图形分解为简单的几何图形。
2. 学会计算组合图形的周长和面积,能够熟练运用相关公式和定理。
3. 掌握一些常见的组合图形的周长与面积的求解技巧和注意事项。
4. 培养学生的观察能力、分析能力和解决问题的能力。
教学难点1. 如何正确地将组合图形分解为简单的几何图形。
2. 如何准确地计算组合图形的周长和面积,特别是涉及到多个几何图形的情况。
3. 如何灵活运用求解技巧和注意事项,解决实际问题。
教具学具准备1. 教师准备:组合图形的模型或图片,用于讲解和演示。
2. 学生准备:直尺、圆规、计算器等学习工具。
教学过程1. 导入:通过展示一些组合图形的图片或模型,引起学生的兴趣和好奇心,激发他们的学习欲望。
2. 讲解:讲解组合图形的构成,如何分解为简单的几何图形,以及如何计算组合图形的周长和面积。
通过示例和练习,让学生理解和掌握相关的概念和计算方法。
3. 练习:让学生进行一些练习题,巩固所学知识,提高计算能力。
同时,教师可以给予指导和解答,帮助学生解决遇到的问题。
4. 应用:通过解决实际问题,让学生将所学知识应用到实际中,提高解决问题的能力。
同时,教师可以给予指导和评价,帮助学生提高解题能力。
板书设计1. 组合图形的周长与面积2. 内容:包括组合图形的构成、分解方法、周长和面积的计算公式、示例和练习题等。
作业设计1. 基础题:计算给定组合图形的周长和面积。
2. 提高题:解决实际问题,应用所学知识。
3. 挑战题:探索一些特殊的组合图形的周长和面积的计算方法。
六年级数学《组合图形面积》经典习题

六年级数学《组合图形面积》经典习题
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF
的面积,各占长方形ABCD的1/3,求三角形AEF的
面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
六年级数学 分数应用题及组合图形的周长与面积的计算

六年级数学上册校本教材(B )班级: 姓名:训练内容:分数应用题及组合图形的周长与面积的计算。
知识要点:1、灵活掌握分数与比的应用题的解题技巧;2、巧解组合图形部分的周长及面积;典型例题:有两根蜡烛,一根长8cm ,另一根长6cm ,把两根都燃烧掉同样长的一部分后,短的一根剩下的长度是长的一根剩下的35 。
每段燃掉多少厘米?解题思路:这两根蜡烛的差没有变。
两根都燃掉同样长的一部分,两根燃烧后的长度都相差8-6=2(厘米),2厘米相当于长的一段所剩的1-35 =25 ,(8-6)÷(1-35 )=5(厘米)8-5=3(厘米) 答:每段燃掉3厘米。
巩固练习1、上层书架上有40本书,下层书架上有30本书。
从两层书架上取同样本数的书以后,下层书架上剩下的书是上层书架上所剩书的本数的35 。
每层书架上各取走多少本书?2、上下两层书架放书本数之比为4:3。
如果从上层取出80本放到下层,则本数之比为4:5。
那么上、下两层书架现在分别放有图书多少本?3、甲乙两车分别从A 、B 两地同时相对而行,甲车每小时行40千米,乙车每小时行45千米,当甲行了全程的25 时,乙车离中点还有8千米,A 、B 两地相距多少千米?(提示:当行驶时间相同时,两车行驶的路程比等于它们的速度比)4、甲、乙两根绳子共长22米,甲绳截去15后,乙绳和甲绳的长度比是3:2,甲、乙两根绳原来各长多少米?(2011年升中试题)5、6、求阴影部分的周长和面积。
7、把一个圆平均分成若干等份后,能拼成一个周长为20.7分米的长方形,这个圆的面积是多少?8、一种压路机的前轮直径是2.5米,前轮每分钟转5周,它每分钟前进多少米?如果压路机车轮的宽度是2.2米,则10分钟压路机压过的路面时多少平方米?9、一块长方形铁片,长50厘米,宽40厘米,剪下最大直径的圆盘后,还剩下多少平方厘米?剩下的铁片还能剪出几个直径是10厘米的圆盘?8163。
六级数学上册组合图形地周长和面积.doc

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级数学《组合图形面积》经典习题

1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18。
84cm,求阴影部分面积.
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长. AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积.
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF 的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
