《整流滤波电路》PPT课件
单相全波整流和滤波电路

第一节 单相全波整流和滤波电路
3.复合滤波电路 (1)LC 滤波电路 电感与电容组成 LC 滤波器,可进一步减小输出电压的脉动程 度。
第8页/共28页
第一节 单相全波整流和滤波电路
(2)RC 滤波器 由于电感体积大,在输出电流不很大的场合,常用电阻代替 电感,组成 RC- 形滤波器。
第2页/共28页
第一节 单相全波整流和滤波电路
3.波形图 将4个二极管组合封装在一起, 制成单相桥式整流器,如图所示。
第3页/共28页
第一节 单相全波整流和滤波电路
二、滤波电路
1.电容滤波电路
第4页/共28页
第一节 单相全波整流和滤波电路
(1)工作原理 ① v2 为正半周,且 v2 > vC 时,VD1、VD3 管导通, v2 向 C 充电。 ② 直到 v2 < vC 时,VD1、 VD3 管截止,C 上电压通过负 载放电。 ③ 同理, v2 负半周 -v2 > vC 时,VD2、VD4 管导通, v2 向 C 充电。
④ 直到 -v2 < vC 时,VD2、VD4 管截止,C 上电压通过负载 放电。
⑤ 如此不断地充放电,维持着输出电压的锯齿状波动。
第5页/共28页
第一节 单相全波整流和滤波电路
(2)波形图
1.2
(3)输出电压
VO 1.2 V2
第6页/共28页
第一节 单相全波整流和滤波电路
2.电感滤波电路 在整流电路的输出端接上一个电感,利用其限制电流变化 的特点,能使通过整流管的电流平滑。电感滤波适用于负载电 流较大的场合。
二、开关电源的工作原理
1.工作原理 (1)开关调整管饱和导通时,有大电流通过,其饱和管压降 很小,因而管耗不大。
整流滤波全桥电路

在工业自动化领域,整流滤波全桥电路的应用促进了电机 驱动技术的进步,为实现精确控制和提高生产效率提供了 有力支持。
02 整流滤波全桥电路的组成
整流器
整流器是整流滤波全桥电路的核心组成部分,其作用是将 交流电转换为直流电。
整流器通常由四个二极管组成,采用全桥或半桥的连接方 式,根据输入交流电的相位变化,二极管会交替导通和截 止,从而将交流电转换为直流电。
整流效率
整流效率
整流滤波全桥电路的整流效率是指整流器将交流电转换为直流电的效率,通常以 百分比表示。整流效率越高,电路的能量转换效率就越高,能够减少能源的浪费 。
影响因素
整流效率受到多种因素的影响,包括整流器元件的性能、电路设计、工作电压和 电流等。为了提高整流效率,需要选择性能良好的整流器元件,优化电路设计, 以及合理调整工作电压和电流。
滤波效果
滤波效果
滤波效果是指整流滤波全桥电路对交流电中杂波的滤除能力。滤波效果越好,输出的直流电质量就越高,能够减 少对用电设备的影响。
影响因素
滤波效果受到滤波电容和滤波电感的影响。滤波电容和滤波电感的选择和配置直接影响到滤波效果。为了提高滤 波效果,需要选择适当的电容和电感元件,并合理配置它们的参数。
工业控制
在工业控制系统中,整流滤波全桥电路用于将交流电机驱动器转换为 直流电机驱动器,实现精确的速度和位置控制。
整流滤波全桥电路的重要性
提高能源利用效率
整流滤波全桥电路能够将交流电高效地转换为直流电,减 少能源的浪费,提高能源利用效率。
保证电子设备正常运行
整流滤波全桥电路为电子设备提供稳定的直流电源,保证 设备的正常运行和延长使用寿命。
全桥电路的工作原理
01
单相整流滤波电路

第二节 单相整流滤波电路整流电路是利用二极管的单向导电性将交流电变换为脉动直流电的电路。
根据交流电的相数,整流电路可分为单相整流电路与三相整流电路等,在小功率电路中(1kV A 以下)一般采用单相整流,常见的有单相半波、全波和桥式整流。
本节重点讨论单相半波和桥式整流电路。
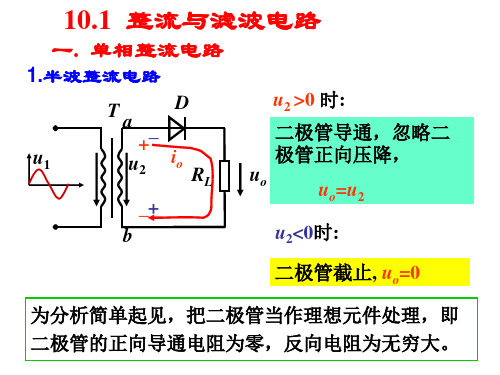
一、单相整流电路1.单相半波整流 电路由整流变压器Tr 、整流二极管VD 以及负载电阻R L 组成,如图6-2-1(a )所示。
VD图6-2-1 单相半波整流电路 a )b ) (a )电路图 (b )波形图图6-2-1(a )中,设电源变压器次级电压u 2为t U u ω=sin 222式中,U 2为次级电压的有效值。
当u 2的波形为正半周时,A 端为正,B 端为负,二极管正向导通,忽略二极管的正向导通压降时,负载电压为u o =u 2;当u 2为负半周时,A 端为负,B 端为正,二极管反向截止,电路中电流为零,负载电压u o =0,u 2全部加在二极管两端。
各电压波形如图6-2-1(b )所示,由图可知,负载上得到的是单相脉动直流电压和电流。
由于输出电压u o 仅为电源电压u 2的正半波,所以称为半波整流。
负载上脉动直流电压的大小用平均值Uo 来示,根据数学推导有2U 450U .O ≈ (6-5) 通过负载的电流Io 为L LO O .R U 450R U I 2≈= (6-6) 二极管与负载串联,因此流经二极管的平均电流为L.R U 450I I 2O D == (6-7) 此外,由图6-3(b )可知,二极管反向截止时,管子两端承受的最高反向电压就是u 2的最大值,即2DRM 2U U = (6-8) 在选择二极管时,所选管子的最大整流电流I F 和最高反向工作电压U RM 应大于式(6-7)和式(6-8)的计算值,即L.R U 450I I 2D F =≥ (6-9) 2RM U 2U U =≥DRM (6-10) 实际应用中,应根据I F 和U RM 的计算值查阅半导体器件手册,选择合适的二极管型号。
单相桥式整流滤波电路

选择合适的电感
选择适当的电感值,以控 制电流和电压的波形,从 而减小电压脉动。
提高输出电压稳定性
调整元件参数
优化电路布局
通过调整整流二极管、滤波电容和电 感的参数,可以改善输出电压的稳定 性。
合理布置元件和布线,减小线路阻抗 和干扰对输出电压的影响。
采用稳压器
在整流滤波电路之后加入稳压器,进 一步稳定输出电压,使其不受输入电 压和负载变化的影响。
单相桥式整流滤波电路
目录
• 电路概述 • 工作原理分析 • 电路参数计算 • 电路优化与改进 • 应用实例
01 电路概述
定义与工作原理
定义
单相桥式整流滤波电路是一种将 交流电转换为直流电的电路,通 常由四个整流二极管和滤波电容 组成。
工作原理
利用四个整流二极管的单向导电 性,将交流电的正负半波整流成 直流电,并通过滤波电容滤除交 流成分,得到平滑的直流输出。
直流电源
单相桥式整流滤波电路常用于将 交流电转换为直流电,为各种电
子设备提供稳定的电源。
电池充电器
在充电电池的充电过程中,单相 桥式整流滤波电路能够将交流电 转换为直流电,为电池提供充电
电流。
太阳能充电器
在太阳能充电器中,单相桥式整 流滤波电路用于将太阳能电池产 生的交流电转换为直流电,为电
子设备充电。
在电力系统的应用
电网监控
在电网监控系统中,单相桥式整流滤波电路用于将交流电转换为直流电,为各种传感器和仪表提供电 源。
分布式发电系统
在分布式发电系统中,单相桥式整流滤波电路用于将风能、太阳能等可再生能源产生的交流电转换为 直流电,为电力储存和分配系统提供电源。
THANKS FOR WATCHING
整流滤波电路ppt课件

作业:
1. 测量直流稳压电源纹波电压时,发现接入负载和负载开 路测得的纹波电压大小相差很多,这种现象是否正常? 为什么?
答:正常。 当负载开路时,滤波电容放电速度很慢,故输出电
压比较平稳,纹波电压很小;当接入负载电阻后,滤波 电容放电加快,使输出电压波动增大,所以纹波电压较 大。因此纹波电压大小的测量,应在额定负载下进行。
L
C1
C2 RL
C1、C2 对交流容抗小 L 对交流感抗很大
负载电流小时,
可用R 代替L。
*讨论
1. 测量直流稳压电源纹波电压时,发现接入负载和负载开 路测得的纹波电压大小相差很多,这种现象是否正常? 为什么? 答案
*2. 试比较电容滤波、电感滤波、π型滤波电路的特点与应用 场合。 答案
讨论小结
(3) 选择整流二极管
T 1 f 150 s 0.02 s
取
RLC
4T 2
0.04 s
则得 C 0.04s 1 000 F 40
可选取 1 000 F、耐压 50 V 的电解电容。
二、其它形式的滤波电路
1. 电感滤波 +
~ u2
2. 型滤波 +
~ u2
L RL
L 通直流阻交流
L 越大,负载电阻越小, 滤波效果越好。
0.45 U2
RL
URM 2U2
二、桥式整流电路 续
5. 桥式整流电路的简化画法
~
6. 整流桥
+
RL uo
~~
9.1.2 滤波电路
利用电容、电感的储能 作用,滤除纹波,得到
平滑的直流输出电压。
一、电容滤波电路 1. 工作原理 2. 输出电压
当 RL = 时:
整流滤波电路
由UO(AV)的表达式可看出,C越大, UO(AV)也越 的表达式可看出, 越大, 越大 也会增大,而整流管的通电时间却越短, 大,IO(AV)也会增大,而整流管的通电时间却越短, 整流管的导通电流加大,如果C太大则初始充电时 整流管的导通电流加大,如果 太大则初始充电时 间要长,整流管中通过的冲击电流时间加长, 间要长,整流管中通过的冲击电流时间加长,长时 间会影响整流管使用寿命。所以一般选择整流管时 间会影响整流管使用寿命。 ID(AV)>(2~3) IO(AV) 。 改变RLC会对 O(AV)和S有影响,将UO(AV)和IO(AV) 会对U 有影响, 改变 会对 有影响 的关系曲线称为输出特性 输出特性, 的关系曲线称为输出特性,将S和IO(AV)的关系曲线 和 称为滤波特性 如果R 越小 滤波特性, 越小, 越低, 称为滤波特性,如果 LC越小,UO(AV)越低,则S 越低 越大,而加大C可使滤波效果和负载能力增强 可使滤波效果和负载能力增强, 越大,而加大 可使滤波效果和负载能力增强,但 C不能无限增大。 不能无限增大。 不能无限增大 所以电容滤波形式电路一般适用于输出电流较 小且负载变化不大的场合。 小且负载变化不大的场合。
(1)整流输出电压的平均值 整流输出电压的平均值 的平均值为: 负载电压 Uo的平均值为 uo
0 π ωt 2π π
1 Uo = 2π
∫
2π
0
ω uod ( t )
负载上的(平均 电流 负载上的 平均)电流 平均 电流:
Uo Io = RL
(2)脉动系数S )
uo
0 π ωt 2π π
S定义:整流输出电压的基波峰值Uo1M与Uo平均值之比。S 定义:整流输出电压的基波峰值 平均值之比。 定义 越小越好。 越小越好。 分解后可得: 用傅氏级数对全波整流的输出 uo 分解后可得
整流滤波与稳压电路

物理实验中心实验指导书整流、滤波与稳压电路ﻬ整流、滤波与稳压电路整流电路是将工频交流电转为具有直流电成分的脉动直流电.整流电路由整流器件组成。
滤波电路是将脉动直流中的交流成分滤除,减少交流成分,增加直流成分。
滤波电路直接接在整流电路后面,通常由电容器,电感器和电阻器按照一定的方式组合而成.作用是把脉动的直流电变为平滑的直流电供给负载.稳压电路对整流后的直流电压采用负反馈技术进一步稳定直流电压。
直流电源的方框图如图1所示。
滤波电路利用电抗性元件对交、直流阻抗的不同,实现滤波。
电容器C对直流开路,对交流阻抗小,所以CL对直流阻抗小,对交流阻抗大,因此L 应与负载串联.经过滤波电路后,既可保留直流分量、又可滤掉一部分交流分量,改变了交直流成分的比例,减小了电路的脉动系数,改善了直流电压的质量。
一、实验目的1。
了解整流、滤波电路的作用.2。
进一步熟悉示波器的使用.3。
观察单相半波、单相桥式及单相桥式整流电容滤波电路的输入、输出电压波形。
二、实验原理为方便分析,把二极管当作理想器件,即认为它加上正向电压导通时电阻为零,加上反向电压截止时电阻为无穷大.电容器在电路中有储存和释放能量的作用,电源供给的电压升高时,它把部分能量储存起来,而当电源电压降低时,就把能量释放出来,从而减少脉动成分,使负载电压比较平滑。
1。
单相半波整流电路电路如图2所示。
设在输入交流电压正半周:A端为正、B端为负,二极管因承受正向电压而导通,电流I L通路是A-V1—RL-B。
忽略二极管正向压降时,输入电压全部加在负载R L上。
在输入交流电压负半周:B端为正、A端为负,二极管因承受反向电压而截止。
输入电压几乎全部降落在二极管V上,负载RL上电压基本为零。
图1 直流稳压电路方框图由图5可见,在交流电一个周期内,二极管半个周期导通半个周期截止,以后周期重复上述过程.2.单相桥式整流电路电路如图3所示。
设在输入交流电压正半周:A端为正、B端为负,即A点电位高于B点电位。
单相半波整流滤波电路

1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办
()
A.打破了外商对中国航运业的垄断
B.阻止了外国对中国的经济侵略
C.标志着中国近代化的起步
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵 制了列强的经济侵略,但是并未能阻止其侵略。故B、C、D 三项表述都有错误。 答案:A
UO
t
总结
交流电 直流电
整流
+电容
滤波
脉动电压
较平滑的直流电
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材·填要点]
一、铁路,更多的铁路 1.地位 铁路是 交通建运设输的重点,便于国计民生,成为国民经济 发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 至开胥平各庄铁 路建成通车。 1888年,宫廷专用铁路落成。
[串点成面·握全局]
一、近代交通业发展的原因、特点及影响 1.原因 (1)先进的中国人为救国救民,积极兴办近代交通业,促 进中国社会发展。 (2)列强侵华的需要。为扩大在华利益,加强控制、镇压 中国人民的反抗,控制和操纵中国交通建设。 (3)工业革命的成果传入中国,为近代交通业的发展提供 了物质条件。
筹办航空事宜
处
三、从驿传到邮政 1.邮政 (1)初办邮政: 1896年成立“大清邮政局”,此后又设 , 邮传邮正传式部脱离海关。 (2)进一步发展:1913年,北洋政府宣布裁撤全部驿站; 1920年,中国首次参加 万国。邮联大会
滤波电路详细解析ppt课件

L 一阶滤波
+
CL 二阶滤波
+
LC 二阶滤波
+
LCL T型三阶滤波
+
+
CLC π三阶滤波
D1
L
+ C1
D2
DLC 型二阶滤波器
+
C 一阶滤波
+
RC 二阶滤波
+
RCR T型三阶滤波
+
+
CRC π三阶滤波
X 0.1
8mH
X
L 0.1
8mH
Y 2.2
Y 2.2
开关电源 单级低通滤波回路
8mH
8mH
X 0.2
L
Y 2.2
X
L
பைடு நூலகம்
0.2
Y 2.2
8mH
8mH
开关电源 双级串联式低通滤波回路
1
1、工作原理介绍
CLC П型滤波器
LL
正 脉 冲
+
+ RL
输 入
iC1
iC2
iRL
图1: CLC П型 滤波器正脉冲输入电流方向
a.输入正脉冲时,先给C1充电,充电电流为ic1,迅速充到脉冲的峰值电压Vi,同时电 感器L中也有线性增长的电流,并在L中储存了磁能,随着电流的增长,储存的磁 能越来越多,电容器C2通过电感L也充上了电压,充电电流为ic2,C2和C1上的电
求输出电压脉动较小的场合。
3.弱点:用在没有稳压电路的电源中,负载能力差。
2
4. CLC П型滤波器常用在脉幅式开关稳压电源,电容和电感值越大,滤波效果越好
1、工作原理介绍
单相全波整流和滤波电路

第一节 单相全波整流和滤波电路
3.波形图
将4个二极管组合封装在一起, 制成单相桥式整流器,如图所示。
第一节 单相全波整流和滤波电路
二、滤波电路
1.电容滤波电路
第一节 单相全波整流和滤波电路
第七章 直流电源电路
第一节 单相全波整流和滤波电路 第二节 连续调整型直流稳压电路 第三节 开关调整型直流稳压电源 本章小结
第一节 单相全波整流和滤波电路
一、单相全波整流电路
1.电路组成
因为与电桥结构类似,故又称为桥式整流电路。
第一节 单相全波整流和滤波电路
2.工作原理
(1)v2 为正半周,如图(c) 所示,VD1、VD3 导通,VD2、 VD4 截止,RL 上产生压降 vO。
图示电路可提供 5 V 电压的稳压电源。两个 24 V 的电源变 压器二次电压分别提供给两个格式整流器,两个 1000 F 电容器 分别为两个桥式整流电路的滤波电容。
第二节 连续调整型直流稳压电路
3.输出电压可调的稳压电路
CW317 的基准电压是 1.25 V。
VO1.25V(1 RP R)第三节 开关调整型直流稳压电源
第一节 单相全波整流和滤波电路
3.复合滤波电路 (1)LC 滤波电路 电感与电容组成 LC 滤波器,可进一步减小输出电压的脉动 程度。
第一节 单相全波整流和滤波电路
(2)RC 滤波器 由于电感体积大,在输出电流不很大的场合,常用电阻代替 电感,组成 RC- 形滤波器。
第二节 连续调整型直流稳压电路
一、串联调整型直流稳压电路的基本原理
1.工作原理 ① 输入电压 VI 增大,致使 VO 增大,增大 RP ,其上压降增大, VO 的增大也受到了限制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、电容滤波电路
电容滤波电路是使用最多也是最简单的滤波电路。 其结构为在整流电路的输出端并联一较大容量的电解 电容,利用电容对电压的充放电作用使输出电压趋于 平滑。该形式电路多用于小功率电源电路中。
1.电容滤波原理
以单向 桥式整流电 u1 容滤波为例 进行分析, 其电路如图 所示。 u1
a
u2
D4 D3
1 2 ( R // RL ) ( ) C2 1 ( R // RL ) 通常选择滤波元件的参数使得: C2
2
U o1m
RL = R RL
1 C2
U'o1m
U o1m
RL 1 U'o1m R RL C2 ( R // RL )
uo的脉动系数S与uo1的脉动系数S´的关系:
U o1m U'o1m 1 1 S= = S' Uo C2 ( R // RL ) U'o C2 ( R // RL )
2、 L-C 型滤波电路
L
u1
u2 uo1
C
RL
uo
设uo1的直流分量为U´O,交流分量的基波的幅 值为U´O1m,: S' = 0.67 U U' = 0.9U
o o 2
T
+
b
–
+
u2
+
– +
u1
u2–
–
a
D1 io uo D2 RL
原理:
变压器副边中心抽头, 感应出两个相等的电压u2 当u2正半周时, D1导通,
D2截止。
当u2负半周时, D2导通,
D1截止。
单相全波整流电压波形 T
a
D1
+
u2
0 2 3 t 4
u1
u2 –
u2 b
+ –
io uo D2
单相半波整流电压波形 u2 T uD D
0 2 3 t 4
a u2 b
u1
uo
RL uo uD
输出电压平均值(Uo),输出电流平均值(Io ): uD D T a io u o u1 u2 RL uo
0 2
t
1 1 2 Uo = uo d (t ) = 2 2 0 2U2 = 0.45U2 =
RL+
uo uD1
忽略二极管正向压降 0 ~ : uD2
uD2 = 2u2
输出电压平均值(Uo),输出电流平均值(Io ): D1 T a uo i o u1 u2 RL u2 b D2 1 1 Uo = uo d (t ) = uo
0 2
t
0
0
2U2 sin td ( t)
实际uo的波动没有近似波形误差大,故实际S比 计算值要小。
(a) 输出电压 平均值Uo与时间常数 RLC 有关
RLC 愈大 电容器放电愈慢 Uo(平均值)愈大 T 一般取 = RLC ( 3 ~ 5 ) = ( 1.5 ~ 2.5 )T 2 近似估算: Uo(AV)≈1.2U2 (b) 流过二极管瞬时电流很大
二、电感滤波电路
电路结构: 在桥式整流电路与负载间串入一电感L 就构成了电感滤波电路。 L
u1
u2
RL
uo
电感滤波原理
L
u1
u2
RL
uo
对直流分量: XL=0 相当于短路,电压大部分降在RL上
对谐波分量: f 越高,XL 越大,电压大部分降在XL上。
因此,在输出端得到比较平滑的直流电压。 当忽略电感线圈的直流电阻时,输出平均电压:
四. 倍压整流电路
利用滤波电容的充放电作用,将多个电容和二极 管组合可获得倍数于变压器附边电压的输出电压。
1、二倍压整流电路
–
a
uo C2 – +
+
u2的正半周时:D1导通, D2截止,理想情况下,电 容C1的电压:
UC 1 =
2U 2
u1
b
u2D1 – + C1
D2
u2的负半周时:D2导通, D1截止,理想情况下,电 容C2的电压:
3. 桥式整流电路
组成:由四个二极管组成桥路
T D3 D1 D4 D2
u1
u2
RL
uo
D1
u2 D3
D2 D4
RL uo
u2
uo
u2正半周时电流通路
T u1
+
u2 D3 D1 D4 D2 RL uo
–
D1 、D4导通, D2、D3截止
u2负半周时电流通路
T u1
u2 D3 D1 D4 D2
RL
=
2 2U2
= 0. 9 U2
Io= Uo /RL =0.9 U2 / RL
二极管上的平均电流及承受的最高反向电压: D1 T a 二极管上的平均电流: io u1 u2 RL 1 u2 b D2 uo uD
t 0 2
ID = I o 2
二极管承受的最高反向电压: U DRM = 2 2U2
基波峰值
U o1M S= Uo
4 2U 2 2 3 π = = 0.67 3 2 2U 2 输出电压平均值 π
(3)二极管平均电流与反向峰值电压
平均电流(ID)与反向峰值电压(UDRM)是选择整流管 的主要依据。
例如: 在桥式整流电路中,每个二极管只有半周导通。 因此,流过每只整流二极管的平均电流 ID 是负载平均电 流的一半。
Uo(AV)≈0.9U2
三、其他形式的滤波电路
改善滤波特性的方法:采取多级滤波。如: RC– 型滤波电路:在电容滤波后再接一级RC滤 波电路。
L-C 型滤波电路:在电感滤波后面再接一电容。 LC – 型滤波电路:在电容滤波后面再接L-C 型 滤波电路。
性能及应用场合分别与电容滤波和电感滤波相似。
u1
u1
u2
D4
D3 b u2
只有整流电路输出 电压大于uc时,才 有充电电流。因此 二极管中的电流是 脉冲波。
D1
S C uo RL
D2
t
uo
二极管中的 电流
t
u1
u1
u2
D4
D3 b RL接入(且RLC较大)时 u2 电容充电时, 电容电压滞后 于u2。 uo RLC越小,输 出电压越低。
D1
uo的脉动系数S与uo1的脉动系数S´的关系:
U o1m U'o1m 1 1 S= = S' 2 2 Uo 1 LC U'o 1 LC
3、LC – 型滤波电路
L
uo1
u1
u2
C1
C2
RL
uo
显然, LC – 型滤波电路输出电压的脉动系 数比只有LC滤波时更小,波形更加平滑;由 于在输入端接入了电容,因而较只有LC滤波 时,提高了输出电压。 请自行分析LC – 型滤波电路的输出 电压和脉动系数等基本参数。
S C uo RL
D2
t
t
2.电容滤波的主要参数
因为滤波的过程中含有正弦波、指数曲线及谐 波成分,一般很难用精确的数学表达式进行计算, 所以一般使用中多采用近似估算来确定其参数。 输出电压可以近似看成 锯齿波,如图所示。 设uc每次充电到峰值 Uomax= 2 U2后按RLC放电的 初始斜率线性下降,经过 T τ=RLC放电结束交于横轴; 并令在 2 (T为正弦波周 期)处为电容充放电转换时的电压值Uomin。 则: U U
RLC 越大 Uo越高负载电流的平均值越大 ;
整流管导电时间越短 iD的峰值电流越大 (c) 二极管承受的最高反向电压:U RM =
2U 2
(d) 滤波电容应选用耐压>1.1 2U 2 的电解电容。
由UO(AV)的表达式可看出,C越大, UO(AV)也越 大,IO(AV)也会增大,而整流管的通电时间却越短, 整流管的导通电流加大,如果C太大则初始充电时 间要长,整流管中通过的冲击电流时间加长,长时 间会影响整流管使用寿命。所以一般选择整流管时 ID(AV)>(2~3) IO(AV) 。 改变RLC会对UO(AV)和S有影响,将UO(AV)和IO(AV) 的关系曲线称为输出特性,将S和IO(AV)的关系曲线 称为滤波特性,如果RLC越小,UO(AV)越低,则S 越大,而加大C可使滤波效果和负载能力增强,但 C不能无限增大。 所以电容滤波形式电路一般适用于输出电流较 小且负载变化不大的场合。
U O ( AV ) =
Omax
Omin
2
由相似三角形关系可得:
U Omax U Omin U Omax
则: U O ( AV )
T = 2 RL C
Ux 2 4RLC
U Omax U Omin U Omax U Omin = = U Omax 2 2 T = U Omax ( 1 ) 4RLC
1 I = I D 2 o
(选购时:二极管额定电流 2ID)
二极管截止时两端承受的最大反向电压:
U RM = 2U 2
(选购时:最大反向电压 2URM)
§10.3
交流 电压
滤波电路
整流
脉动 直流电压
滤波
直流 电压
经过整流后的电源电压虽然没有交流变化成分, 但其脉动较大,需要经过滤波电路消除其脉动成分, 使其更接近于直流。 滤波的方法一般采用无源元件电容或电感,利 用其对电压、电流的储能特性达到滤波的目的。
即: U O(AV)
T = 2U 2 ( 1 ) 4RLC
Io(AV)= Uo(AV)/RL
脉动系数S:采用近似波形计算。 以(Uomax-Uomin)为基波峰-峰值,则
