CFD讲义-湍流模型
CFD湍流模型使用技巧培训
k-kl-w Transition Model (3 eq.) SST Transition Model (4 eq.) 4-Equation v2f Model Reynolds Stress Model Detached Eddy Simulation
DES (Detached Eddy Simulation)
First industrial-strength model for high-Re with LEScontent
Increased complexity (grid sensitivity) due to explicit mix of to modelling concepts
嵌入式大涡模拟
– 可以和DES/SAS模型联用
E-LES: Spatially decaying turbulence
E-LES: Fully developed channel flow
RANS
Re=395
LES
Viscosity ratio on iso-surfaces of
q-criterion (-500)
Correlation based model Reasonably accurate Correlations can be found for many different transition mechanisms (e.g. FSTI, dp/dx, Roughness) Not compatible with 3D flows and unstructured/parallel CFD codes – non-local
cfd中湍流模型与控制方程
CFD中湍流模型与控制方程在计算流体动力学（CFD）中，湍流模型和控制方程是非常重要的概念。
湍流模型：湍流是一种高度复杂、非线性的流体运动状态，其特点是流体中的速度、压力等物理量随时间和空间发生随机变化。
为了模拟湍流，需要采用湍流模型。
湍流模型通常分为两类：直接数值模拟（DNS）和非直接数值模拟。
1.直接数值模拟（DNS）：DNS直接求解Navier-Stokes方程，不需要对湍流进行任何假设或简化。
然而，由于湍流的多尺度特性，DNS需要极高的计算资源，因此在实际应用中受到限制。
2.非直接数值模拟：为了降低计算成本，非直接数值模拟方法被广泛应用。
这些方法包括雷诺平均法（RANS）、大涡模拟（LES）和统计平均法（SAS）等。
这些方法通过对湍流进行某种程度的平均或滤波，将湍流分解为可解析的大尺度运动和需要模型化的小尺度运动。
控制方程：在CFD中，流体的运动遵循基本的物理定律，如质量守恒定律、动量守恒定律和能量守恒定律。
这些定律在数学上表现为一系列偏微分方程，称为控制方程。
1.质量守恒方程（连续性方程）：描述流体微元的质量不随时间变化，即流体微元的质量流入率等于其质量流出率。
在不可压缩流体中，连续性方程简化为速度场的散度为零。
2.动量守恒方程（Navier-Stokes方程）：描述流体微元的动量不随时间变化，即流体微元的动量流入率加上外力等于其动量流出率。
Navier-Stokes方程是流体动力学的基本方程，描述了流体运动的基本规律。
3.能量守恒方程：描述流体微元的能量不随时间变化，即流体微元的能量流入率加上外力做功和热源等于其能量流出率。
在不可压缩流体中，能量守恒方程通常简化为温度场的热传导方程。
在求解这些控制方程时，需要选择合适的湍流模型来封闭方程组，以便进行数值求解。
不同的湍流模型和控制方程组合可以适用于不同的流体流动场景，如层流、湍流、可压缩流体、不可压缩流体等。
3天了解CFD——湍流、多相流的方程推导和数值解法(上)
如果为大量固定质量的流体微元他就是有限控制体，少量流体微团（但足够表现流体宏观量）的就是流动微元（fluid
element），但是体积和面积会变化。之所以守恒和不守恒是因为空间位置固定的微元或者控制体可以应用质量守恒
方程来推导，空间位置随流因为质量固定不能应用与质量守恒因此成为非守恒形式。
1.2 动量方程
+
�������������
+
������������������������ ������������
�������������������������
������������������������������������������������
−
������������
������������������������������������������������������������������������
�������������������������
������������������������������������������������
−
������������
������������������������������������������������������������������������
+
������������
∙
∇�
+
�������������������������������������
+
∇
∙
(������������������������)�
=
������������
������������������������ ������������
(仅供参考)CFD湍流模型使用技巧培训
Integration Platform w-equation
2-equation models • k-w, BSL, SST
Transition Model • g-ReQ model
Unsteady models • SST-SAS • SST-DES
w-equation
Wall Treatment • Automatic wall treatment
Eddy Simulation Models:
Large Eddy Simulation (LES) [transient]
Detached Eddy Simulation (DES)* Scale Adaptive Simulation SST (SAS)*
* Not available in the ANSYS CFD-Flo product
RNG k-ε model.
Stress
Standard k-ω model.
SMC-ω model
Baseline (BSL) zonal k-ω based model. Baseline (BSL) Reynolds' Stress model
SST zonal k-ω based model. (k-ε)1E model.
SAS – globally unstable flows DDES – globally and locally unstable flows ELES/WMLES marginally unstable flows
ANSYS Fluent 湍流模型
RANS Models
One-Equation Model Spalart-Allmaras
DES (Detached Eddy Simulation)
湍流模型及其在CFD中的应用
(5)
将（5）代入瞬时状态下的连续性方程（1）和动量方 程（2），并对时间取平均，得到湍流时均流动的控制 方程如下：
湍流时均流动的控制方程
divu 0
(6)
u '2 u ' v' u ' w' u 1 p div(u u ) vdiv(gradu ) (7a) t x y z x
u p u '2 u ' v' ( u ' w') div( uu ) div( gradu ) Su t x x y z v p u ' v' v' ( v' w') div( vu ) div( gradv) Sv t y x y z
u ' ' v' ' w' ' ( ) div( u ) divgrad t x y z
S
（11）
张量形式的时均输运方程
u i 0 t xi u p i ui uiu j ui ' u j ' S i t xi xi x j x j u j t x j x j u j ' ' S x j
2、湍流的基本方程
无论湍流运动多么复杂，非稳态的连续方程和N-S方程对 于湍流的瞬时运动仍然是适用的。在此，考虑不可压流 动，使用笛卡尔坐标系，速度矢量在x、y和z方向的分量 分别为u、v和w，写出湍流瞬时控制方程如下：
第三章_湍流模型
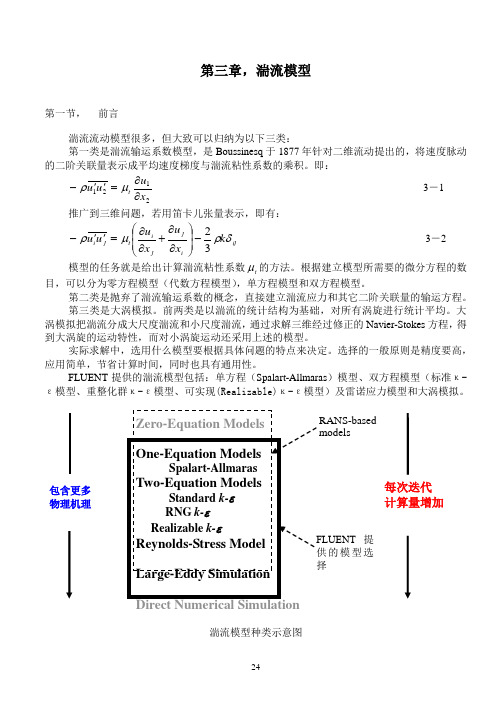
第三章 湍流模型第一节 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。
实际求解中，选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。
湍流模型种类示意图Direct Numerical Simulation包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节 平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。
CFD讲义-湍流模型
第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。
实际求解中，选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。
湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。
CFD课件动力工程专业软件应用5-湍流模型
第五章：湍流模型授课教师：张金亚湍流模型简介湍流的特征从NS方程到雷诺平均NS模型（RANS） 雷诺应力和封闭问题湍动能方程（k）涡粘模型(EVM)雷诺应力模型SRS模型Generalized k-w（GEKO）模型近壁面处理及网格要求进口边界条件总结: 湍流模型湍流的特征湍流本质是非稳态的、三维的、非周期的、中及高雷诺数流动中的漩涡运动（脉动），湍流会加强混合、传热和剪切时空域的瞬间脉动是随机的（不可预测的），但湍流脉动的统计平均可量化为输运机理所有的湍流中都存在大范围的长度尺度（涡尺度）对初场敏感注：工程流动一般以低粘度流体为基础，因此几乎所有的流动都是湍流。
后台阶流时间平均的速度分布瞬时速度分布横风中的射流左图是抓拍的瞬态羽流图，右图是延时的光滑掉细节（涡）的平均图。
横风中的射流From Su and Mungal in Durbin and Medic (2008)层流Laminar(低雷诺数)转捩Transition(逐渐增大雷诺数)湍流Turbulent(高雷诺数)雷诺观察的试验如何判断是否为湍流外流内流自然对流along a surface around an obstaclewherewhereOther factors such as free-stream turbulence, surfaceconditions, blowing, suction, and other disturbances etc. maycause transition to turbulence atlower Reynolds numbers(Rayleigh number)etc.,,,h d d x L (Prandtl number)雷诺数的效果Re > 3.5×10640 < Re < 150150 < Re < 3×1055-15 < Re < 40 Re < 5 湍流涡街，但涡间距离更近边界层转捩为湍流分离点前为层流边界层，尾迹为湍流层流涡街尾迹区有一对稳定涡蠕动流（无分离）3×105< Re < 3.5×106湍流结构SmallStructuresLargeStructuresEnergy Cascade (after Richardson, 1922)Injectionof energyDissipationof energyDissipating eddies Large-scale eddiesFlux of energy守恒方程模拟湍流的方法•直接数值模拟(DNS)理论上，所有湍流(和层流/转捩)都可以通过求解完全的Navier-Stokes方程进行数值求解 求解整个尺度谱. 无模型要求计算代价过大! 对工业流动并不实际•大涡模拟(LES)类模型求解空间平均的N-S方程直接模拟大的涡, 而比网格小的涡通过模型模化较DNS计算代价小, 但是对大多数运用来说，计算资源及计算代价依然较高•雷诺平均Navier-Stokes (RANS)模型求解时均的Navier-Stokes方程在RANS中模拟湍流的所有长度尺度•多种模型可以选用对工业流动计算，这是最为广泛采用的方法•现在没有一种紊流模型能够可靠的预测出具有充分精度的所有紊流流动时均的思想是将瞬时量分解为时均量与脉动量，并抽取出时均量雷诺应力张量R ij对称二阶应力; 由对动量方程的输运加速度项平均得来雷诺应力提供了湍流（随机脉动）输运的平均效应，是高度扩散的 RANS方程中的雷诺应力张量代表湍流脉动的混合和平均带来的光顺RANS 模型-封闭问题为了封闭RANS 方程组，必须对雷诺应力张量进行模拟 涡粘模型(EVM) –基于Boussinesq 假设，即雷诺应力正比于时均速度的应变，比例常数为涡粘系数（湍流粘性）雷诺应力模型(RSM): 求解六个雷诺应力项（加上耗散率方程）的偏微分输运方程组Eddy viscosity量纲分析表明，如果我们知道必要的几个尺度（如速度尺度、长度尺度），涡粘系数就可以确定出来例如，给定速度尺度和长度尺度，或速度尺度和时间尺度，涡粘系数就被确定，RANS方程也就封闭了只有非常简单的流动才能预测出这些尺度（如充分发展的管流或粘度计里的流动对一般问题，我们需要导出偏微分输运方程组来计算涡粘系数湍动能k启发了求解涡粘模型的物理机理涡粘系数类似于动量扩散效应中的分子粘性涡粘系数不是流体的属性，是一个湍流的特征量，随着流体流动的位置而改变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。
实际求解中，选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。
湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。
把上面的表达式代入瞬时的连续与动量方程，并取平均（去掉平均速度i u 上的横线），我们可以把连续与动量方程写成如下的笛卡儿坐标系下的张量形式：0)(=∂∂+∂∂i iu x t ρρ 3－5 ()j i jl l ij i j j i ji i u u x x u x u x u x x p Dt Du ''-∂∂+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+∂∂∂∂+∂∂-=ρδμρ32 3－6 上面两个方程称为雷诺平均的Navier-Stokes （RANS ）方程。
他们和瞬时Navier-Stokes 方程有相同的形式，只是速度或其它求解变量变成了时间平均量。
额外多出来的项j i u u ''-ρ是雷诺应力，表示湍流的影响。
如果要求解该方程，必须模拟该项以封闭方程。
如果密度是变化的流动过程如燃烧问题，我们可以用法夫雷（Favre ）平均。
这样才可以求解有密度变化的流动问题。
法夫雷平均就是出了压力和密度本身以外，所有变量都用密度加权平均。
变量的密度加权平均定义为：ρρ/~Φ=Φ 3－7符号～表示密度加权平均；对应于密度加权平均值的脉动值用Φ''表示，即有：Φ''+Φ=Φ~。
很显然，这种脉动值的简单平均值不为零，但它的密度加权平均值等于零，即：0≠Φ''， 0=Φ''ρBoussinesq 近似与雷诺应力输运模型为了封闭方程，必须对额外项雷诺应力j i u u ''-ρ进行模拟。
一个通常的方法是应用Boussinesq 假设，认为雷诺应力与平均速度梯度成正比，即：ij i i t ijj i t j i x u k x u xu u u δμρμρ)(32∂∂+-⎪⎪⎭⎫⎝⎛∂∂+∂∂=''- 3－8 Boussinesq 假设被用于Spalart-Allmaras 单方程模型和ε-k 双方程模型。
Boussinesq 近似的好处是与求解湍流粘性系数有关的计算时间比较少，例如在Spalart-Allmaras 单方程模型中，只多求解一个表示湍流粘性的输运方程；在ε-k 双方程模型中，只需多求解湍动能k 和耗散率ε两个方程，湍流粘性系数用湍动能k 和耗散率ε的函数。
Boussinesq 假设的缺点是认为湍流粘性系数t μ是各向同性标量，对一些复杂流动该条件并不是严格成立，所以具有其应用限制性。
另外的方法是求解雷诺应力各分量的输运方程。
这也需要额外再求解一个标量方程，通常是耗散率ε方程。
这就意味着对于二维湍流流动问题，需要多求解4个输运方程，而三维湍流问题需要多求解7个方程，需要比较多的计算时间，对计算机内存也有更高要求。
在许多问题中，Boussinesq 近似方法可以得到比较好的结果，并不一定需要花费很多时间来求解雷诺应力各分量的输运方程。
但是，如果湍流场各向异性很明显，如强旋流动以及应力驱动的二次流等流动中，求解雷诺应力分量输运方程无疑可以得到更好的结果。
第三节， 湍流模型3.3.1 单方程（Spalart-Allmaras ）模型Spalart-Allmaras 模型的求解变量是ν~，表征出了近壁（粘性影响）区域以外的湍流运动粘性系数。
ν~的输运方程为： ννννρννρμσνρY x C x x G Dt D j b j j -⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∂∂+∂∂+=~~)~(1~2~ 3－9 其中，νG 是湍流粘性产生项；νY 是由于壁面阻挡与粘性阻尼引起的湍流粘性的减少；νσ~和2b C 是常数；ν是分子运动粘性系数。
湍流粘性系数用如下公式计算：1~ννρμf t = 其中，1νf 是粘性阻尼函数，定义为：31331ννχχC f +=，并且ννχ~≡。
湍流粘性产生项，νG 用如下公式模拟：νρν~~1S C G b = 3－10 其中，222~~ννf dk S S +≡，而1211ννχχf f +-=。
其中，1b C 和k 是常数，d 是计算点到壁面的距离；S ij ij ΩΩ≡2。
ij Ω定义为：⎪⎪⎭⎫⎝⎛∂∂-∂∂=Ωji i j ij x u x u 21 3－11 由于平均应变率对湍流产生也起到很大作用，FLUENT 处理过程中，定义S 为：),0min(ij ij prod ij S C S Ω-+Ω≡ 3－12其中，0.2=prod C ，ij ij ij ΩΩ≡Ω，ij ij ij S S S 2≡，平均应变率ij S 定义为：⎪⎪⎭⎫⎝⎛∂∂+∂∂=ji i j ij x u x u S 21 3－13在涡量超过应变率的计算区域计算出来的涡旋粘性系数变小。
这适合涡流靠近涡旋中心的区域，那里只有“单纯”的旋转，湍流受到抑止。
包含应变张量的影响更能体现旋转对湍流的影响。
忽略了平均应变，估计的涡旋粘性系数产生项偏高。
湍流粘性系数减少项νY 为：21~⎪⎭⎫ ⎝⎛=d f C Y w w νρν 3－14其中，6/1636631⎥⎦⎤⎢⎣⎡++=w w w C g C g f 3－15 )(62r r C r g w -+= 3－1622~~dk S r ν≡ 3－17其中，1w C ，2w C ，3w C 是常数，222~~ννf dk S S +≡。
在上式中，包括了平均应变率对S的影响，因而也影响用S ~计算出来的r 。
上面的模型常数在FLUENT 中默认值为：1335.01=b C ，622.02=b C ，3/2~=νσ，1.71=νC ，νσ~2211/)1(/b b w C k C C ++=，3.02=w C ，0.23=w C ，41.0=k 。
壁面条件在壁面，湍流运动粘性ν~设置为零。
当计算网格足够细，可以计算层流底层时，壁面切应力用层流应力－应变关系求解，即：μρττy u u u= 3－18 如果网格粗错不能用来求解层流底层，则假设与壁面近邻的网格质心落在边界层的对数区，则根据壁面法则：⎪⎪⎭⎫ ⎝⎛=μρττy u E k u u ln 13－19 其中，k=0.419，E=9.793。
对流传热传质模型在FLUENT 中，用雷诺相似湍流输运的概念来模拟热输运过程。
给出的能量方程为：h eff ij j i t p i i i S u x T t c k x p E u x E t +⎥⎥⎦⎤⎢⎢⎣⎡+∂∂⎪⎪⎭⎫ ⎝⎛+∂∂=+∂∂+∂∂)(Pr )]([)(τμρρ 3－20 式中，E 是总能量，eff ij )(τ是偏应力张量，定义为：ij ii eff j i ij eff eff ij x u x u x u δμμτ∂∂-∂∂+∂∂=32)()( 3－21 其中，eff ij )(τ表示粘性加热，耦合求解。
如果默认为分开求解，FLUENT 不求解处eff ij )(τ。
但是可以通过变化“粘性模型”面板上的湍流普朗特数（Prt ），其默认值为0.85。
湍流质量输运与热输运类似，默认的Schmidt 数是0.7，该值同样也可以在“粘性模型”面板上调节。
标量的壁面处理与动量壁面处理类似，分别选用合适的壁面法则。
综上所述，Spalart-Allmaras 模型是相对简单的单方程模型，只需求解湍流粘性的输运方程，并不需要求解当地剪切层厚度的长度尺度。
该模型对于求解有壁面影响流动及有逆压力梯度的边界层问题有很好模拟效果，在透平机械湍流模拟方面也有较好结果。
Spalart-Allmaras 模型的初始形式属于对低雷诺数湍流模型，这必须很好解决边界层的粘性影响区求解问题。
在FLUENT 中，当网格不是很细时，采用壁面函数来解决这一问题。
当网格比较粗糙时，网格不满足精确的湍流计算要求，用壁面函数也许是最好的解决方案。
另外，该模型中的输运变量在近壁处的梯度要比ε-k 中的小，这使得该模型对网格粗糙带来数值误差不太敏感。
但是，Spalart-Allmaras 模型不能预测均匀各向同性湍流的耗散。
并且，单方程模型没有考虑长度尺度的变化，这对一些流动尺度变换比较大的流动问题不太适合。
比如，平板射流问题，从有壁面影响流动突然变化到自由剪切流，流场尺度变化明显。
3.3.2 标准ε-k 模型标准ε-k 模型需要求解湍动能及其耗散率方程。
湍动能输运方程是通过精确的方程推导得到，但耗散率方程是通过物理推理，数学上模拟相似原形方程得到的。
该模型假设流动为完全湍流，分子粘性的影响可以忽略。
因此，标准ε-k 模型只适合完全湍流的流动过程模拟。
标准ε-k 模型的湍动能k 和耗散率ε方程为如下形式：M b k i k t iY G G x k x Dt Dk --++⎥⎦⎤⎢⎣⎡∂∂⎪⎪⎭⎫ ⎝⎛+∂∂=ρεσμμρ3－22 kC G C G k C x x DtD b k i k t i 2231)(ερεεσμμερεεε-++⎥⎦⎤⎢⎣⎡∂∂⎪⎪⎭⎫ ⎝⎛+∂∂= 3－23 在上述方程中，k G 表示由于平均速度梯度引起的湍动能产生，b G 是用于浮力影响引起的湍动能产生；M Y 可压速湍流脉动膨胀对总的耗散率的影响。