Projection pursuit regression(PPR)
统计学专业英语词汇

log-log 对数
log-normal distribution 对数正态分布
longitudinal 经度的,纵的
loss function 损失函数
M
Mahalanobis\' generalized distance Mahalanobis广义距离
drop out 脱落例
Durbin-Watson statistic(ratio) Durbin-Watson统计量(比)
E
efficient, efficiency 有效的、有效性
* Engel\'s coefficient 恩格尔系数
entropy 熵
epidemiology 流行病学
* error 误差
item 项
J
Jacknife 刀切法
K
Kaplan-Meier estimate Kaplan-Meier估计
* Kendall\'s rank correlation coefficients 肯德尔等级相关系数
Kullback-Leibler information number 库尔贝克-莱布勒信息函数
model, -ing 模型(建模)
moment 矩
moving average 移动平均
multicolinear, -ity 多重共线(性)
multidimensional scaling(MDS) 多维换算
multiple answer 重复回答
multiple choice 多重选择
multiple comparison 多重比较
* histogram 直方图
大数据通用模型算法介绍

通用模型算法介绍为方便用户使用,系统预制了大量通用的模型算法,可供用户直接调用。
系统已提供机器学习算法、统计模型如下所示:1)机器学习算法机器学习常用算法分类:•ID3ID3算法是一种贪心算法,用来构造决策树。
ID3算法起源于概念学习系统(CLS),以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准,然后继续这个过程,直到生成的决策树能完美分类训练样例。
ID3算法使用了信息熵和信息增益。
信息熵,是随机变量的期望,度量信息的不确定程度。
信息熵越大,信息越混乱。
计算公式如下:H(S)=−∑p(x)log2p(x)x∈X其中,S –当前数据集,X – S中的类,p(x) - 概率密度函数,以2为底。
信息增益,用于度量属性A降低样本集合X熵的贡献大小。
信息增益越大,越适于对X分类。
计算公式如下。
IG(A,S)=H(S)−∑p(t)H(t)t∈T其中,H(S) – S的信息熵,T – S被属性A分割的子集,p(t) –子集t在集合S中的比例,H(t) –子集t的信息熵。
ID3算法通过信息增益构建决策树,适用于离散型的分类问题。
•C4.5C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。
它的目标是监督学习:给定一个数据集,其中的每一个元组都能用一组属性值来描述,每一个元组属于一个互斥的类别中的某一类。
C4.5的目标是通过学习,找到一个从属性值到类别的映射关系,并且这个映射能用于对新的类别未知的实体进行分类。
C4.5算法依据信息增益率构建决策树,信息增益率定义如下:GainRatio(S,A)=Gain(S,A) Splitinfo(S,A)其中,Gain(S,A)与ID3算法中的信息增益相同。
分裂信息SplitInfo(S,A)代表了按照属性A分裂样本集S的广度和均匀性。
分裂信息计算公式如下:Splitinfo(S,A)=∑|S i| Sci=1log2(|S i|S)其中,S1到Sc是c个不同值的属性A分割S而形成的c个样本子集。
基于PPR_建模的固废材料固化戈壁土抗压强度计算模型

72
38 卷
粉煤灰综合利用
材料科学
脱硫石膏的化学成分见表 3。
表 2 矿物掺合料技术指标
Table 2 Technical index of mineral admixture
密度 比表面积 需水量 活性指数 / %
矿物掺 细度 /
合料 (m2 / kg) / (g / cm3 ) / (m2 / kg) 比 / %
∗基金项目: 新疆维吾尔自治区自然科学基金项目 (2021D01A100) ; 新疆农业大学大学生创新训练计划项目 ( dxscx2022370) 。
作者简介: 宋紫裕 (2003—) , 男, 本科, 主要研究方向: 水利水电与水工结构工程。
通信作者: 何建新 (1973—) , 男, 硕士, 教授, 主要研究方向: 水利水电工程。
(1 College of Water Conservancy and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052, China;
2 Key Laboratory of Safety and Water Disaster Prevention of Xinjiang Water Conservancy Engineering,
solidified Gobi soil was analyzed. The results showed that the PPR calculation model is reliable, and the weight coefficients of each
influence factor to compressive strength were ranked as the sequence of content of dosage of curing agent>age>flyash mixed>dosage of
投影寻踪模型

投影寻踪方法及应用内容摘要:本文从投影寻踪的研究背景出发,给出了投影寻踪的定义和投影指标,在此基础上得出了投影寻踪聚类模型,随后简单介绍了遗传算法。
最后结合上市公司的股价进行实证分析,并给出结论和建议。
关键词:投影寻踪投影寻踪聚类模型遗传算法一、简介(一)产生背景随着科技的发展,高维数据的统计分析越来越普遍,也越来越重要。
多元分析方法是解决高维数据这类问题的有力工具。
但传统的多元分析方法是建立在总体服从正态分布这个假定基础之上的。
不过实际问题中有许多数据不满足正态假定,需要用稳健的或非参数的方法来解决。
但是,当数据的维数很高时,即使用后两种方法也面临以下困难:第一个困难是随着维数增加,计算量迅速增大。
第二个困难是对于高维数据,即使样本量很大,仍会存在高维空间中分布稀疏的“维数祸根”。
对于核估计,近邻估计之类的非参数法很难使用。
第三个困难是对低维稳健性好的统计方法,用到高维时则稳健性变差。
另一方面,传统的数据分析方法的一个共同点是采用“对数据结构或分布特征作某种假定——按照一定准则寻找最优模拟——对建立的模型进行证实”这样一条证实性数据分析思维方法〔简称CDA法)。
这种方法的一个弱点是当数据的结构或特征与假定不相符时,模型的拟合和预报的精度均差,尤其对高维非正态、非线性数据分析,很难收到好的效果。
其原因是证实性数据分析思维方法过于形式化、数学化,受束缚大。
它难以适应千变万化的客观世界,无法真正找到数据的内在规律,远不能满足高维非正态数据分析的需要。
针对上述困难,近20年来,国际统计界提出采用“直接从审视数据出发—通过计算机分析模拟数据—设计软件程序检验”这样一条探索性数据分析新方法,而PP就是实现这种新思维的一种行之有效的方法。
(二)发展简史PP最早由Kruskal于70年初建议和试验。
他把高维数据投影到低维空间,通过数值计算得到最优投影,发现数据的聚类结构和解决化石分类问题。
1974年Frledman和Tukey加以改正,提出了一种把整体上的散布程度和局部凝聚程度结合起来的新指标进行聚类分析,正式提出了PP概念,并于1976年编制了计算机图像系统PRIM——9。
【国家自然科学基金】_闪速熔炼_基金支持热词逐年推荐_【万方软件创新助手】_20140802
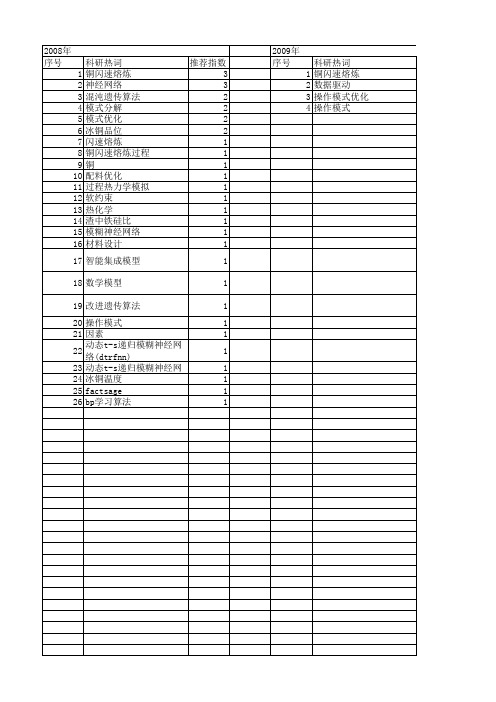
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 推荐指数 铜闪速熔炼 3 神经网络 3 混沌遗传算法 2 模式分解 2 模式优化 2 冰铜品位 2 闪速熔炼 1 铜闪速熔炼过程 1 铜 1 配料优化 1 过程热力学模拟 1 软约束 1 热化学 1 渣中铁硅比 1 模糊神经网络 1 材料设计 1 智能集成模型 1 数学模型 1 改进遗传算法 1 操作模式 1 因素 1 动态t-s递归模糊神经网络(dtrfnn) 1 动态t-s递归模糊神经网络 1 冰铜温度 1 factsage 1 bp学习算法 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 铜闪速熔炼 操作模式 铜闪速连续炼铜 铜闪速熔炼过程 过渡过程 过渡代价函数 热力学分析 热力学 炉型结构 模式匹配 柯西不等式 数据驱动 数值模拟 操作参数轨迹优化 挂渣 投影寻踪回归 反应塔 动态模型 优化控制 主元分析 legendre伪谱法 fe3o4
2009年 序号 1 2 3 4
科研热词 铜闪速熔炼 数据驱动 操作模式优化 操作模式
推荐指数 1 1 1 1
2010年 序号 1 2 3 4
科研热词 配料 遗传算法 软约束 优化模型
推荐指数 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 推荐指数 铜闪速熔炼过程 2 预测模型 1 铅闪速熔炼 1 相似性度量 1 模型 1 最小吉布斯自由能 1 最小二乘支持向量机 1 故障检测 1 投影寻踪回归 1 小波变换 1 委员会投票选择算法 1 多相平衡 1 加速遗传算法 1 代价敏感支持向量机 1 主动学习 1 similarity measure 1 projection pursuit regression 1 copper flash smelting process 1 acceleration genetic algorithm1
预测回归的九大类算法

预测回归的九大类算法包括以下几种:1. 线性回归(Linear Regression):它是预测中最简单也是最直观的方法。
通过找到一个线性方程来最小化预测值和实际值之间的平方差。
2. 逻辑回归(Logistic Regression):虽然称为“回归”,但它实际上是一种分类算法。
逻辑回归通过Sigmoid函数将输入特征映射到0和1之间,用于估计某个事件发生的概率。
3. 多项式回归(Polynomial Regression):它是线性回归的扩展,允许模型具有非线性的特征。
通过将特征转换为多项式形式,可以捕捉到数据中的非线性关系。
4. 决策树回归(Decision Tree Regression):决策树是一种树形结构,用于对数据进行分类或回归。
在回归任务中,决策树通过预测连续值来预测结果。
5. 随机森林回归(Random Forest Regression):随机森林是由多个决策树组成的集成学习方法。
每个树都独立地进行预测,最终结果是所有树预测值的平均值。
6. 支持向量机回归(Support Vector Regression, SVR):SVR是一种监督学习算法,用于回归分析。
它的目标是找到一个最佳的超平面,以最大化数据点与超平面的距离。
7. 人工神经网络回归(Artificial Neural Network Regression):人工神经网络是一种模仿人脑工作方式的计算模型,用于处理复杂的非线性关系。
8. 梯度提升机回归(Gradient Boosting Regression):梯度提升机是一种强大的集成学习算法,通过逐步构建模型来最小化损失函数,提高预测准确性。
9. 弹性网回归(Elastic Net Regression):弹性网是一种线性回归模型,它结合了L1和L2正则化,以解决数据集中的多重共线性问题。
这些算法各有优势和局限性,适用于不同类型的数据和问题。
在实际应用中,通常需要根据具体问题和对数据的理解来选择合适的算法。
基于人工鱼群算法的南宁市内河水质综合评价的投影寻踪回归分析

文章编号:1007-2284(2010)02-0008-05基于人工鱼群算法的南宁市内河水质综合评价的投影寻踪回归分析方 崇,张春乐,陆克芬(广西水利电力职业技术学院,南宁530023)摘 要:针对目前我国城市内河普遍遭到污染的问题,在分析影响内河水质因素的基础上,选取BO D 5(5日生化需氧量)、CO D cr (化学需氧量)、石油类、挥发酚、NH 3O N (氨氮)、总磷等6个主要因素作为评价因子,建立了城市内河水质评价的投影寻踪分析模型,采用人工鱼群算法对评价模型进行优化,并将该模型应用于南宁市10条内河水质的评价与排序。
研究表明,用投影寻踪回归分析法进行水质评价,避免了传统评价方法由于主观原因造成的误差,评价结果合理可信、方法简单,为我国城市内河水质的评价提供了新途径。
关键词:投影寻踪;人工鱼群算法;南宁市;内河;水质评价 中图分类号:T U 992.3 文献标识码:AAn Evaluation of Water Quality Projection Pursuit Based on Artificial Fish O swarm Algorithm in Inland River in NanningFANG Chong,ZHANG C hun O le,LU Ke O fen(G uang xi Hy dr aulic and Electr ic Po ly technic,Nanning 530023,China)Abstract:Po llut ion is g etting w or se in China's ur ban rivers at pr esent.In this paper,by analy zing facto rs affect ing inland r iver water qualit y,choo sing BO D 5,CO D cr ,petro leum,v olatile pheno l,N H 3O N and tot al phospho rus for evaluation factor s,a w ater qualit y e -v aluatio n method is established,and the model is applied to inland r iver s in N anning.T he evaluation results a re accur ate and so me erro rs ar e eliminated because o f the subjective facto rs of tr aditional methods.P roject ion pur suit is a new evaluation metho d of urban inland r iver wat er quality,it w ill be widely used in the fut ur e.Key words:pr ojection pursuit;artificial fish O sw arm algo rithm;N anning ;inland river;water quality assessment 收稿日期:2009-05-13基金项目:广西壮族自治区水利厅科技专项基金(No.200806)。
【国家自然科学基金】_度量投影_基金支持热词逐年推荐_【万方软件创新助手】_20140730
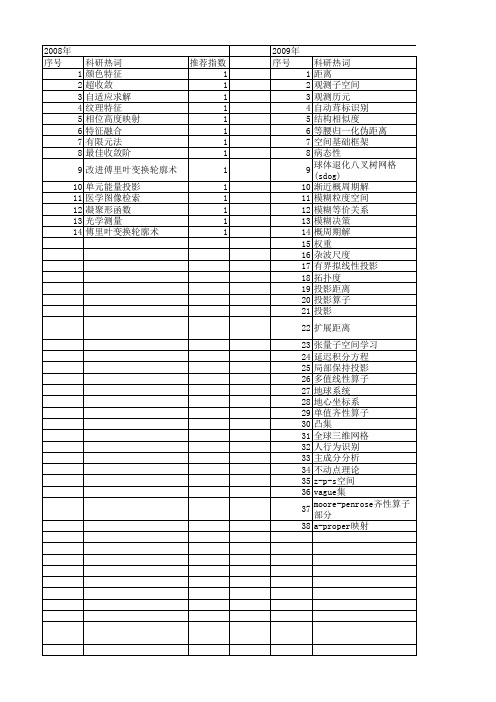
2011年 科研热词 超收敛 自适应 流形学习 有限元线法 单元能量投影 二维边值问题 高通形状调控 预警指标 预算松驰 非支配解 非对称失真 逼近紧性 近可凹性 近严格凸性 资源共享 虚拟手写数字 联盟有效 编辑距离 综合评价 立体图像质量评价 相似内容 特征提取 特征匹配 混凝土坝 模型显著域 样本单元 有限元法 旋转特征 方向投影 数据包络分析 拓扑相似性约束 形状调控 张量分析 度量投影算子 度量 平面划分 带权值的主成分分析 局部保持投影 小波图像融合 头部姿态估计 大坝监测 增强形状调控 变形熵 协同学 偏置距离 低通形状调控 人脸识别 主观调查法 上半连续 三轴加速度信号 k近邻 推荐指数 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 颜色特征 超收敛 自适应求解 纹理特征 相位高度映射 特征融合 有限元法 最佳收敛阶 改进傅里叶变换轮廓术 单元能量投影 医学图像检索 凝聚形函数 光学测量 傅里叶变换轮廓术
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 人脸识别 高光谱遥感 非负矩阵分解 非监督判别映射 非扩张映像 零空间 闭超平面 邻域 逼近理想解排序法 距离 端元 相空间同步 相对贴近度 相对熵 相关分析 相似度量 特征提取 流形学习 流形 核正交非监督判别映射 核函数 投影 强收敛 度量投影 差异离散度 局部离散度 局域预测 小波变换 子空间 夹角度量法 多属性决策 多变量混沌序列 单形体 医疗诊断 分裂可行性问题 分类算法 光谱解混 修正的mann迭代算法 人工免疫识别系统 乳腺癌 不动点 上半连续性 vague集 banach空间
Orthogonal matching pursuit recursive function approximation with

2 Orthogonal Matching Pursuit
Assume we have the following kth-order model for f 2 H,
1 Introduction Fra biblioteknd Background
Given space H,
a collection of let us de ne
vectors
D
=
fxig
in
a
Hilbert
V = Spanfxng; and W = V? (in H):
We shall refer to D as a dictionary, and will assume the vectors xn, are normalized (kxnk = 1). In 3] Mallat and Zhang proposed an iterative algorithm that they termed Matching Pursuit (MP) to construct representations of the form
/ To appear in Proc. of the 27th Annual Asilomar Conference on Signals Systems and Computers, Nov. 1{3, 1993 /
35种原点回归模式

35种原点回归模式详解在数据分析与机器学习的领域中,回归分析是一种重要的统计方法,用于研究因变量与自变量之间的关系。
以下是35种常见的回归分析方法,包括线性回归、多项式回归、逻辑回归等。
1.线性回归(Linear Regression):最简单且最常用的回归分析方法,适用于因变量与自变量之间存在线性关系的情况。
2.多项式回归(Polynomial Regression):通过引入多项式函数来扩展线性回归模型,以适应非线性关系。
3.逻辑回归(Logistic Regression):用于二元分类问题的回归分析方法,其因变量是二元的逻辑函数。
4.岭回归(Ridge Regression):通过增加一个正则化项来防止过拟合,有助于提高模型的泛化能力。
5.主成分回归(Principal Component Regression):利用主成分分析降维后进行线性回归,减少数据的复杂性。
6.套索回归(Lasso Regression):通过引入L1正则化,强制某些系数为零,从而实现特征选择。
7.弹性网回归(ElasticNet Regression):结合了L1和L2正则化,以同时实现特征选择和防止过拟合。
8.多任务学习回归(Multi-task Learning Regression):将多个任务共享部分特征,以提高预测性能和泛化能力。
9.时间序列回归(Time Series Regression):专门针对时间序列数据设计的回归模型,考虑了时间依赖性和滞后效应。
10.支持向量回归(Support Vector Regression):利用支持向量机技术构建的回归模型,适用于小样本数据集。
11.K均值聚类回归(K-means Clustering Regression):将聚类算法与回归分析相结合,通过对数据进行聚类后再进行回归预测。
12.高斯过程回归(Gaussian Process Regression):基于高斯过程的非参数贝叶斯方法,适用于解决非线性回归问题。
二分类问题常用的模型

二分类问题常用的模型二分类问题是监督学习中的一种常见问题,其中目标是根据输入数据将其分为两个类别。
以下是一些常用的二分类模型:1. 逻辑回归(Logistic Regression):逻辑回归是一种经典的分类模型,它通过拟合一个逻辑函数来预测一个样本属于某个类别。
逻辑回归适用于线性可分的数据,对于非线性问题可以通过特征工程或使用核函数进行扩展。
2. 支持向量机(Support Vector Machine,SVM):支持向量机是一种强大的分类器,它试图找到一个最优超平面来分隔两个类别。
通过最大化超平面与最近数据点之间的距离,SVM 可以在高维空间中有效地处理非线性问题。
3. 决策树(Decision Tree):决策树是一种基于树结构的分类模型,通过递归地分割数据来创建决策规则。
决策树在处理非线性和混合类型的数据时表现良好,并且易于解释。
4. 随机森林(Random Forest):随机森林是一种集成学习方法,它结合了多个决策树以提高预测性能。
通过随机选择特征和样本进行训练,随机森林可以减少过拟合,并在处理高维数据时表现出色。
5. 朴素贝叶斯(Naive Bayes):朴素贝叶斯是一种基于贝叶斯定理的分类模型,它假设特征之间是相互独立的。
对于小型数据集和高维数据,朴素贝叶斯通常具有较高的效率和准确性。
6. K 最近邻(K-Nearest Neighbors,KNN):K 最近邻是一种基于实例的分类方法,它将新样本分配给其最近的 k 个训练样本所属的类别。
KNN 适用于处理非线性问题,但对大规模数据集的效率可能较低。
7. 深度学习模型(Deep Learning Models):深度学习模型,如卷积神经网络(Convolutional Neural Network,CNN)和循环神经网络(Recurrent Neural Network,RNN),在处理图像、语音和自然语言处理等领域的二分类问题时非常有效。
用于回归问题算法

用于回归问题算法回归问题是一种常见的机器学习问题,其主要目标是根据已知数据的特征来预测连续值的输出。
在处理回归问题时,我们通常需要选择合适的算法来构建模型,以便准确预测输出值。
以下是一些常用于回归问题的算法:1. 线性回归(Linear Regression):线性回归是一种基本的回归算法,它试图建立特征与输出之间的线性关系。
通过最小化实际值与预测值之间的误差来拟合直线,从而找到最佳拟合线。
线性回归在数据特征与输出之间存在线性关系时效果很好,但在数据非线性关系时表现不佳。
2. 多项式回归(Polynomial Regression):多项式回归是在线性回归的基础上,通过增加特征的高次项来拟合非线性关系的回归算法。
通过引入多项式特征,可以更好地拟合数据中的曲线关系。
但是,多项式回归容易出现过拟合的问题,需要谨慎选择多项式的阶数。
3. 决策树回归(Decision Tree Regression):决策树是一种树形结构的模型,通过不断将数据分割成更小的子集来预测输出值。
决策树回归适用于非线性关系的数据,并且易于解释。
但是,决策树容易出现过拟合问题,需要进行剪枝操作。
4. 随机森林回归(Random Forest Regression):随机森林是一种集成学习算法,通过多个决策树的组合来提高预测的准确性。
随机森林回归通常比单个决策树的回归效果更好,且具有较好的泛化能力。
随机森林能够处理大量的数据和高维特征,且不易过拟合。
5. 支持向量机回归(Support Vector Machine Regression):支持向量机是一种强大的机器学习算法,可以用于回归问题。
支持向量机回归通过构建一个最优的超平面来拟合数据,以最大化间隔来提高预测的准确性。
支持向量机适用于小样本的回归问题,但需要调节参数以获得最佳的性能。
6. 神经网络回归(Neural Network Regression):神经网络是一种深度学习模型,可以用于回归问题。
logisticregression各参数

logisticregression各参数Logistics Regression和Logistic RegressionCVlogistic RegressionCV使⽤交叉验证来计算正则化系数C1、penalty默认为L2(1)在调参时,如果是为了解决过拟合问题,⼀般⽤L2就可以了。
但如果选择L2后发现还是过拟合,则需要⽤L1(2)如果模型特征特别多,希望减少⼀些特征,让模型系数稀疏化,也选择L1penalty参数的选择会影响损失函数优化算法的选择L2可选的算法有 ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’L1可选的算法有liblinear’(L1正则化的损失函数不是连续可导)2、优化算法solver的选择 solver参数决定了我们对逻辑回归损失函数的优化⽅法,有4种算法可以选择,分别是: a) liblinear:使⽤了开源的liblinear库实现,内部使⽤了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟⽜顿法的⼀种,利⽤损失函数⼆阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是⽜顿法家族的⼀种,利⽤损失函数⼆阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅⽤⼀部分的样本来计算梯度,适合于样本数据多的时候。
liblinear也有⾃⼰的弱点:逻辑回归有⼆元逻辑回归和多元逻辑回归。
对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。
⽽MvM⼀般⽐OvR分类相对准确⼀些。
liblinear只⽀持OvR,不⽀持MvM,这样如果我们需要相对精确的多元逻辑回归时,就不能选择liblinear了。
也意味着如果我们需要相对精确的多元逻辑回归不能使⽤L1正则化了。
3、multi-class :ovr 和multinomial4、class-weight 类型权重参数⽤于标识分类模型中各类型的权重,可以不选择,也可以⾃⼰指定,可以选择balanced让类库⾃⼰指定5、样本权重参数 sample_weight调节样本权重的⽅法有两种,第⼀种是在class_weight使⽤balanced。
S-PLUS介绍

2
3
0.S-Plus简介
TIBCO 公司的 Spotfire 系列产品 S-PLUS 自 1987 年来在各行各业广泛使用。 她 曾获得著名的“美国计算机协会优秀软件奖” ,而其它获此殊荣的是大名鼎鼎的 TCP/IP,UNIX 与网上浏览器的创始者 MOSAIC 等。S-PLUS 具有开放的平台、最 完备的分析工具库与多样化的价格设计,非常适合中国用户。可惜由于该软件的初 始创始国的出口限制,导致她直到 2002 年才正式许可进入中国大陆市场。 S-PLUS 主要是针对金融、生物医药、制造、环境、教育科研等行业设计开发 的。
1.数据访问
可读取和输出的文件格式包括: ASCII文件:fixed format, comma-separated, 以及 tab-delimited等 特定软件格式:
Lotus 1-2-3 Excel Dbase FoxPro Access Epi Info Bloomberg Quattro Pro Paradox FAME LIM MATLAB SAS 7/8/9 SPSS Minitab Sysstat Gauss STATA
1
S-PLUS 介绍
北京宏能畅然数据应用有限公司
2008-09
1
0.S-Plus简介 ........................................................................................................................................ 3 1.数据访问...............................................................................
投影寻踪和熵权法

投影寻踪和熵权法
投影寻踪(Projection Pursuit)是一种用于高维数据降维和发现数据内在结构的方法。
它的目标是在保持数据关键特征的同时实现降维,帮助揭示数据集的主要结构。
投影寻踪的基本原理是通过对数据进行线性或非线性投影,将数据从高维空间投影到低维空间,并选择最具信息量的投影方向。
最常见的投影方法是优化具有特定目标函数的投影方向,这个目标函数通常与数据内在结构的特征有关。
熵权法(Entropy Weight Method)是一种多指标综合评价方法,常用于多指标决策问题。
它基于信息熵的概念,通过计算各指标的权重,将多个指标的评价结果综合为一个综合指标。
具体而言,熵权法使用信息熵来衡量各指标的不确定性,越大的不确定性对应的指标权重越小。
熵权法的步骤如下:
1.根据具体问题,确定评价指标集合。
2.对每个指标,收集样本数据,计算各指标的数学期望和方
差。
3.计算每个指标的熵值,熵的计算公式为:熵= - Σ (p(i) *
log2(p(i))),其中p(i)表示第i个指标的频率。
4.计算每个指标的权重,权重的计算公式为:权重 = (1-熵) /
Σ (1-熵),确保权重之和为1。
5.进行指标综合评价,根据权重对每个指标的评价结果进行
加权求和,得到综合评价结果。
熵权法在多指标决策、综合评价和排名等领域广泛应用。
它能够从信息熵的角度,系统地考虑各指标的重要性和贡献度,帮助决策者更准确地进行决策和评价。
统计学词汇对照

统计学词汇对照统计学词汇 Aacceptance region接受区域adjusted校正的allocation配置、布局alternative hypothesis 备择假设 * analysis of variance 方差分析 * analysis of covariance 协方差分析 ANOCOVA =Analysis of covariance * ANOVA =Analysis of variance arithmetic mean算术平均值 association 关联性* assumed mean假定平均值* asymmetric distribution非对称分布autoregressive 自回归(的) averages 平均量B bar chart 条线图 Bartlett's test 巴特利特检验 * Bayes, -ian 贝叶斯的、贝叶斯 beta function 贝塔函数 between (间)内 bias 偏倚 biased question 有偏质问* binomial distribution二项分布binomial theorem二项定理bioassay 生物鉴定法 bivariate normal distribution 二元正态分布 blind test 盲检法 Bonferroni's inequality Bonferroni不等式 bootstrap 自助法 Box-Cox transformation Box-Cox变换C canonical correlation典型相关case control study案例对照研究categorization 分类 categorize 分类 category 类别 causality 因果关系 central limit theorem 中心极限定理 Chebyshev's inequality 切比雪夫不等式χ2-statistic χ2统计量χ2-test χ2检验classification分类cluster analysis 聚类分析 coding 编码 coefficient of concordance 一致性系数 coefficient of determination 可决系数 cohort 同辈 common factors 公共因子,公因数 communality 公因子方差、公共因子方差 comparison 比较component 成分 * conditional probability 条件概率 * confidence coefficient 置信系数 * confidence interval 置信区间 * confidence limits 置信界限 * confound, -ing 混杂、混杂法 * confounding design 混杂设计 * consumer's price index消费物价指数consumer's risk用方风险* contribution基值confirmatory 确定的 consistent, consistency 一致(的)、一致性 contingency table 列联表 continuous distribution 连续分布 control(group)控制、控制(群) convergence in probability 概率收敛 convergence in law (distribution)依法则收敛(依分布收敛) correction 校正、修正 correction factor 校正因子correction for continuity连续校正correlation相关correlation coefficient相关系数correlation ratio相关比correlogram相关图covariate共变向量covariation共变criterion variable基准变量critical region 判别区域 * cross-section 横截面 * cross-tabulation 交叉表 * cumulative frequency 累积频率 cumulative distribution function 累积分布函数 * cumulative relative frequency 累积频率 curvilinear 曲线(的)D * data 数据 * data analysis 数据分析 * degree of freedom 自由度 density 密度 density function 密度函数 * dependent variable 应变数 * descriptive statistics 描述性统计 deviate 偏差 deviation 偏、偏差(cf. standard -- , mean --) dichotomous question 二分搜索法 discriminant analysis 判別分析discriminant function 判別函数 discrimination 判別 discrete distribution 离散分布distribution分布 D.K.(Don't Know)dose-response curve (relationship)用量反应曲线(关系) double blind test 二重盲检法 * downward trend下降倾向drop out脱落例Durbin-Watson statistic(ratio)Durbin-Watson统计量(比)E efficient, efficiency 有效的、有效性 * Engel's coefficient 恩格尔系数entropy 熵 epidemiology 流行病学 * error 误差 error margin 误差幅度error of the first kind(type I error)第1类误差 error of the second kind (type II error)第2类误差 error term 误差项 estimable 可估的 estimate 估计量 * estimation 估计 estimator 估计量 event 事件 exact probability test直接概率法* expectation期望 * expected frequency期待度数experimental design 试验设计 * explanatory variable 说明变量 exploratory 探索的 exponential distribution 指数分布F face sheet factor 因子 * factor analysis 因子分析 * factor loadings 因子输入量(系数) factorial effects 析因效应 factorial experiment 析因试验 fiducial probability 置信概率 filter, -ing 滤子 finite population 有限总体 Fisher information 费希尔信息 * fitting 拟合 fixed-effect model 固定效应模型 follow-up study 追跡研究 force of mortality 死力 fractional factorial design分步实施计划设计free-answer question自由回答法* frequency 频率 * frequency distribution 频率分布 F statistic(ratio, test)F 统计量(F 比、F 检验)G Gauss, Gaussian高斯(的)* genetic algorithm遗传算法geometric distribution 几何分布 geometric mean 几何平均值 goodness of fit 拟合优度 Greco-Latin square 正交拉丁方H harmonic mean 调和平均 hazard function 故障率函数 heteroscedastic, -ity 异方差(性)* histogram直方图homoscedastic, -ity同方差(性)hypergeometric distribution 超几何分布 hypothesis 假说I * independence 独立 * independent variable 独立变量 infinite population 无限总体 input 入力 inspection 检查 interaction 相互作用 intercept 切片 * interval estimation 区间推定 * interval scale 间隔尺度 interviewee 被调査者 interviewer 调査员 interviewing method 面试调查法 item 项J Jacknife 刀切法K Kaplan-Meier estimate Kaplan-Meier估计* Kendall's rank correlation coefficients 肯德尔等级相关系数 Kullback-Leibler information number 库尔贝克-莱布勒信息函数 * kurtosis 峰度L lag 时间滞后 large sample 大样本 Latin square 拉丁方 law of large numbers 大数定律(strong -, weak- :強定律、弱定律) least significant difference, LSD. 最低显著性差异 * least square 最小二乘法 * level of significance 显著水平 life table 生命表 likelihood 似然 linear discriminant function 线形判别函数 local control 局部控制 logistic function 逻辑斯蒂函数 logit analysis(transformation)分对数分析(变换) log-linear model 对数线性模型 log-log 对数 log-normal distribution 对数正态分布 longitudinal 经度的,纵的 loss function 损失函数M Mahalanobis' generalized distance Mahalanobis广义距离 mail survey 邮送调査 main effect 主效应 marginal 边缘(的) Markov, -ian 马尔科夫(的)mathematical statistics 数理统计学 * maximum 最大(pl. maxima) maximuim likelihood estimate(estimation)最大似然估计(估计法)McNemar's test McNemar测试 * mean 平均(值) * mean deviation 平均偏差 mean effect 平均效应 * median 中位数 meta-analysis 元分析 * minimum 最小(pl. minima)missing value 缺区值 * mode 众数 model, -ing 模型(建模) moment 矩moving average 移动平均 multicolinear, -ity 多重共线(性) multidimensional scaling(MDS)多维换算 multiple answer 重复回答 multiple choice 多重选择 multiple comparison 多重比较 * multiple correlation coefficient 多重相关系数 * multiple regression 多重回归 multi-stage sampling 多阶段抽样 * multivariate analysis 多变量分析 Multivariate analysis of variance 多元方差分析 multivariate normal distribution 多变量正态分布* MANOVA =Multivariate analysis of variance * multiway table 多路表N * n×m tablen×m表 * nominal scale 额定尺度 non-central 无心nonparametric 非参数的 normal approximation 正态近似 * normal distribution 正态分布 normal equation 正规方程 null hypothesis 原假设O observational error 观测误差 * observed frequency 观测频率 observed value 观测值 OC(operating characteristic)curve 作用特性曲线 odds 奇 odds ratio 奇数比 one-sided 单侧 1-way layout 1 元布局法 open-ended question 可扩充解答法 optimum allocation 最佳分配法 ordered classification 顺序化 * ordinal scale 序数尺度 orthogonal polynomial 正交多项式 outlier 边际值output 输出、结果P paired comparison 成对比较法 panel survey 固定样本调查 parameter 系数partial confounding 部分混杂(法) * partial correlation coefficient 偏相关系数 Pearson's product moment correlation coefficient皮尔逊矩相关系数percentile 百分数 periodic 周期的 periodogram 周期图 phi coefficient φ系数 pie chart 饼状图 plot 点图 * point estimation 点估计 * Poisson distribution 泊松分布 pooled variance estimate 联合方差估计 * population 总体 population correlation coefficient 总体相关系数 * population mean 总体平均值 * population variance 总体方差 posterior probability(distribution)后验概率(分布) power(function)幂(函数) pre-coding 预编码 predicted value 预测值 * prediction 预测 predictive 预测(的) presentation 表示、表现(法) primary sampling unit 第 1 次抽样的单位 principal component, -- analysis 主成分(分析) prior probability(distribution)先验概率(分布) * probability 概率 * probability distribution 概率分布 probability proportionate sampling 概率比例抽样 probit analysis 概率单位分析 process 过程 producer's risk 生产者风险 projection pursuit 投影寻踪 proportion 比例 proportional hazard model 比例风险模型 prospective study 远景调查Q quartile 四分位(数) quartile deviation 四分位偏差 * quality 质qualitative定性的qualitative data定性的数据* quantity量quantitative 定量的、计量的 quota system 定额系统R * radar chart 雷达图 * random 随机的 random-effect model 随机效应模型randomization 概率化、随机化 * randomness 随机性 random number 随机数random sampling 随机抽样 random walk 随机游动 * range 范围(区域) * rank 秩 * rank correlation coefficients 等级相关系数 ranking method 秩评定法 * rank-size rule 秩规模规则 rank test 秩检验 rating method 比率法 * ratio scale 比率尺度 * regression 回归 * regression coefficient 回归系数regression diagnosis 回归诊断 * regression equation(line)回归方程(直线)* rejection region 拒绝区域 * relative frequency 相对频率 relative risk 相对风险 reliability(coefficient)信赖性(系数) * residual 残差 response curve(surface)相应曲线(曲面) retrospective study 追溯调查 risk 风险 risk factor 风险因素 robust, -ness 稳健的(性) * run 取遍S * sample 样本 * sample mean 样本均值 * sample size 样本量(大小) * sample variance样本方差* sampling抽样sampling error抽样误差sampling interval 抽样间隔 sampling unit 抽样单位 * scales 尺度 * scattergram, scatter plot(diagram)点状图 Scheffe's test Scheffe检验 score 得分 seasonality 季节性 secondary sampling unit 第 2 次单位抽样 serial correlation 序列相关 self-adminstration 自管理 semi-log 半对数 sigmoid 拟 S 型、S 状 signal to noise ratio SN(信噪)比 signed rank test 带符号的秩检验 * significance, significant 显著(的) * significance probability 显著概率 simple random sampling 简单随机抽样 * simple regression 简单回归single replication 1 次重复size proportionate allocation比例布局法skewed斜的* skewness失真slope斜率spectral window谱窗spectrogram 谱图 spectrum 谱 * Spearman's rank correlation coefficients 斯皮尔曼等级相关系数 * spurious correlation 伪相关 square 平方 * standard deviation, S.D. 标准方差 * standard error 标准误差 * standard score 标准得分 start number 起始编号 * stationary 平稳的 * statistic(for inference)统计量(统计推论的) statistical 统计的 statistically significant 统计显著的 stem-and-leaf presentation 茎叶表现 stereotype 陈腔滥调 stochastic process 随机过程 * stratification 分层 stratified sampling 分层抽样 * stratum([pl.] strata)层 Student('s) 学生(的) studentized range 学生化范围study研究sub-sampling二次抽样sufficiency充分性sufficient statistic 充分统计量 supervisor 管理者 survival analysis 生存时间分析 survey 调查 systematic sampling 系统抽样T taxonomy 分类(学) tail 尾 * test 检验 * test of goodness of fit 拟合良好性检定 * test of independence 无关性检验 3-way layout 3 元布局法threshold 阈值 tie 结 tie correction 结修正 *time series 时间序列total variation 全变差 treatment 处理 * trend 趋势 trend analysis 趋势分析 trial 尝试 * t-statistic, -test, -ratio t 统计量(t 检验、t 比)two-sided 双边的 * 2-sample t-test 2 样本 t 检验 2-stage sampling 2 阶段抽样法 two-by-two contingency table 2×2列联表 2-way layout 2 元布局法* 2-way table 2 重表 two-stage sampling 2 阶段抽样法U unbiased estimator 无偏估计量 unbiased variance 无偏方差 uncorrelated 不相关(的) uniform distribution 均匀分布 uniform random numbers 均匀随机数 uniqueness 唯一性 updating 更新 * upward trend 向上趋向V validity 有效性 variate 变量 * variance 方差 variance ratio 方差比varimax rotation varimax旋度 varimax solution varimax解 variation 变差variability 变异性W weighted sampling 加权抽样 Welch's test Welch检验 within (级)间 with probability 1(w.p.1)以概率 1 wording 措辞X Y Yates' correction Yates修正Z * Zipf's law Zipf法則 * z transformation z 变换。
logisticregression 三分类

逻辑回归的三分类问题在机器学习中,三分类问题是一个常见的问题类型,其中目标变量有三个可能的类别。
逻辑回归是一种广泛用于此类问题的算法。
在三分类逻辑回归中,我们使用逻辑函数将线性回归的输出转换为概率,以便为每个类别分配一个概率值。
1.工作原理逻辑回归基于一个前提,即数据中的因变量(也称为响应变量)是二元的或可转换为二元的。
在三分类问题中,我们需要稍作调整。
首先,我们需要使用一对多(One-Versus-All, OVA)或三分类策略将三分类问题转换为几个二元分类问题。
对于三分类问题,我们可以将其分解为以下三个二元分类问题:•类别1 vs. 类别2 vs. 类别3•类别2 vs. 类别3•类别3 vs. 其他(类别1和类别2)对于每个二元分类问题,我们可以训练一个逻辑回归模型。
然后,我们可以使用这些模型来预测新数据点的类别。
1.实现步骤以下是使用Python和scikit-learn库实现三分类逻辑回归的步骤:•数据准备:加载数据集并分割为训练集和测试集。
确保数据已经过预处理,并且因变量编码为适当的格式(通常是独热编码)。
•一对多转换:将三分类问题转换为多个二元分类问题。
这可以通过创建一个新的数据集来完成,其中包含原始特征和一个二元因变量,该因变量表示要预测的类别与其他类别的比较。
•训练逻辑回归模型:对于每个二元分类问题,使用训练数据来训练一个逻辑回归模型。
这可以通过调用scikit-learn的LogisticRegression类来完成,并设置multi_class参数为'ovr'(代表一对多)。
•预测:对于测试集中的每个数据点,使用所有三个逻辑回归模型进行预测。
根据每个模型的预测结果,可以确定数据点所属的类别。
通常,选择具有最高概率的类别作为预测结果。
•评估:使用适当的度量标准(如准确率、混淆矩阵等)评估模型的性能。
比较三分类逻辑回归与其他分类算法的结果,以确定哪种方法在您的特定问题上表现最佳。
逻辑回归(LogisticRegression)详解,公式推导及代码实现

逻辑回归(LogisticRegression)详解,公式推导及代码实现逻辑回归(Logistic Regression)什么是逻辑回归: 逻辑回归(Logistic Regression)是⼀种基于概率的模式识别算法,虽然名字中带"回归",但实际上是⼀种分类⽅法,在实际应⽤中,逻辑回归可以说是应⽤最⼴泛的机器学习算法之⼀回归问题怎么解决分类问题? 将样本的特征和样本发⽣的概率联系起来,⽽概率是⼀个数.换句话说,我预测的是这个样本发⽣的概率是多少,所以可以管它叫做回归问题在许多机器学习算法中,我们都是在追求这样的⼀个函数例如我们希望预测⼀个学⽣的成绩y,将现有数据x输⼊模型 f(x) 中,便可以得到⼀个预测成绩y但是在逻辑回归中,我们得到的y的值本质是⼀个概率值p在得到概率值p之后根据概率值来进⾏分类当然了这个1和0在不同情况下可能有不同的含义,⽐如0可能代表恶性肿瘤患者,1代表良性肿瘤患者逻辑回归既可以看做是回归算法,也可以看做是分类算法,通常作为分类算法⽤,只可以解决⼆分类问题,不过我们可以使⽤⼀些其他的技巧(OvO,OvR),使其⽀持解决多分类问题下⾯我们来看⼀下逻辑回归使⽤什么样的⽅法来得到⼀个事件发⽣的概率的值在线性回归中,我们使⽤来计算,要注意,因为Θ0的存在,所以x⽤⼩的X b来表⽰,就是每来⼀个样本,前⾯还还要再加⼀个1,这个1和Θ0相乘得到的是截距,但是不管怎样,这种情况下,y的值域是(-infinity, +infinity)⽽对于概率来讲,它有⼀个限定,其值域为[0,1]所以我们如果直接使⽤线性回归的⽅式,去看能不能找到⼀组Θ来与特征x相乘之后得到的y值就来表达这个事件发⽣的概率呢?其实单单从应⽤的⾓度来说,可以这么做,但是这么做不够好,就是因为概率有值域的限制,⽽使⽤线性回归得到的结果则没有这个限制为此,我们有⼀个很简单的解决⽅案:我们将线性回归得到的结果再作为⼀个特征值传⼊⼀个新的函数,经过转换,将其转换成⼀个值域在[0,1]之间的值Sigmoid函数:将函数绘制出来:其最左端趋近于0,最右端趋近于1,其值域在(0,1),这正是我们所需要的性质当传⼊的参数 t > 0 时, p > 0.5, t < 0 时, p < 0.5,分界点是 t = 0使⽤Sigmoid函数后:现在的问题就是,给定了⼀组样本数据集X和它对应的分类结果y,我们如何找到参数Θ,使得⽤这样的⽅式可以最⼤程度的获得这个样本数据集X对应的分类输出y这就是我们在训练的过程中要做的主要任务,也就是拟合我们的训练样本,⽽拟合过程,就会涉及到逻辑回归的损失函数逻辑回归的损失函数:我们定义了⼀个这样的损失函数:画出图像:让我们看⼀下这个函数有什么样的性质,据图像我们很容易发现: 当y=1时,p趋近于零的时候,在这个时候可以看此时-log(p)趋近于正⽆穷,这是因为当p趋近于0的时候,按照我们之前的这个分类的⽅式,我们就会把这个样本分类成0这⼀类,但是这个样本实际是1这⼀类,显然我们分错了,那么此时我们对它进⾏惩罚,这个惩罚是正⽆穷的,随着p逐渐的增⾼,可以看我们的损失越来越⼩,当我们的p到达1的时候,也就是根据我们的分类标准,我们会将这个样本x分类成1,此时,它和这个样本真实的y等于1是⼀致的,那么此时损失函数取0也就是没有任何损失,当y=0时同理现在这个损失函数还是太过复杂,需要判定y的值,我们对其进⾏简化:这个函数与上⾯的是等价的这样,根据我们求出的p,就可以得出这次估计的损失是多少最后,再把损失相加求平均值,其公式为:将两个式⼦整合:下⾯我们要做的事情,就是找到⼀组Θ,使得J(Θ)最⼩对于这个式⼦,我们很难像线性回归那样推得⼀个正规⽅程解,实际上这个式⼦是没有数学解的,也就是⽆法把X和直接套进公式获得Θ不过,我们可以使⽤梯度下降法求得它的解,⽽且,这个损失函数是⼀个凸函数,不⽤担⼼局部最优解的,只存在全局最优解现在,我们的任务就是求出J(Θ)的梯度,使⽤梯度下降法来进⾏计算⾸先,求J(Θ)的梯度的公式:⾸先,我们对Sigmoid函数求导:得到其导数,再对logσ(t)求导,求导步骤:由此可知, 前半部分的导数: 其中y(i)是常数再求后半部分:这其中将结果代⼊,化简得:就得到后半部分的求导结果:将前后部分相加:即:就可以得到:此时我们回忆⼀下线性回归的向量化过程参考这个,可以得到:这就是我们要求的梯度,再使⽤梯度下降法,就可以求得结果决策边界:这⾥引⼊⼀个概念,叫做判定边界,可以理解为是⽤以对不同类别的数据分割的边界,边界的两旁应该是不同类别的数据从⼆维直⾓坐标系中,举⼏个例⼦,⼤概是如下这个样⼦:使⽤OvR和OvO⽅法解决多分类:原本的逻辑回归只能解决双分类问题,但我们可以通过⼀些⽅法,让它⽀持多分类问题,⽐如OvR和OvO⽅法OvR: n 种类型的样本进⾏分类时,分别取⼀种样本作为⼀类,将剩余的所有类型的样本看做另⼀类,这样就形成了 n 个⼆分类问题,使⽤逻辑回归算法对 n 个数据集训练出 n 个模型,将待预测的样本传⼊这 n 个模型中,所得概率最⾼的那个模型对应的样本类型即认为是该预测样本的类型 n个类别就进⾏n次分类,选择分类得分最⾼的OvO: n 类样本中,每次挑出 2 种类型,两两结合,⼀共有 C n2种⼆分类情况,使⽤ C n2种模型预测样本类型,有 C n2个预测结果,种类最多的那种样本类型,就认为是该样本最终的预测类型这两种⽅法中,OvO的分类结果更加精确,因为每⼀次⼆分类时都⽤真实的类型进⾏⽐较,没有混淆其它的类别,但时间复杂度较⾼代码实现 :1import numpy as np2from .metrics import accuracy_score345class LogisticRegression:67def__init__(self):8"""初始化Linear Regression模型"""9 self.coef_ = None10 self.intercept_ = None11 self._theta = None1213def _sigmoid(self, t):14return 1. / (1. + np.exp(-t))1516def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):17"""根据训练数据集X_train, y_train, 使⽤梯度下降法训练Logistic Regression模型"""18assert X_train.shape[0] == y_train.shape[0], \19"the size of X_train must be equal to the size of y_train"2021def J(theta, X_b, y):22 y_hat = self._sigmoid(X_b.dot(theta))23try:24return - np.sum(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) / len(y)25except:26return float('inf')2728def dJ(theta, X_b, y):29return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(X_b)3031def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8): 3233 theta = initial_theta34 cur_iter = 03536while cur_iter < n_iters:37 gradient = dJ(theta, X_b, y)38 last_theta = theta39 theta = theta - eta * gradient40if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):41break4243 cur_iter += 14445return theta4647 X_b = np.hstack([np.ones((len(X_train), 1)), X_train])48 initial_theta = np.zeros(X_b.shape[1])49 self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)5051 self.intercept_ = self._theta[0]52 self.coef_ = self._theta[1:]5354return self55565758def predict_proba(self, X_predict):59"""给定待预测数据集X_predict,返回表⽰X_predict的结果概率向量"""60assert self.intercept_ is not None and self.coef_ is not None, \ 61"must fit before predict!"62assert X_predict.shape[1] == len(self.coef_), \63"the feature number of X_predict must be equal to X_train"6465 X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])66return self._sigmoid(X_b.dot(self._theta))6768def predict(self, X_predict):69"""给定待预测数据集X_predict,返回表⽰X_predict的结果向量"""70assert self.intercept_ is not None and self.coef_ is not None, \ 71"must fit before predict!"72assert X_predict.shape[1] == len(self.coef_), \73"the feature number of X_predict must be equal to X_train"7475 proba = self.predict_proba(X_predict)76return np.array(proba >= 0.5, dtype='int')7778def score(self, X_test, y_test):79"""根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""8081 y_predict = self.predict(X_test)82return accuracy_score(y_test, y_predict)8384def__repr__(self):85return"LogisticRegression()"。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 投影寻踪回归我们先介绍一下Peter Hall 提出的投影寻踪回归(Projection Pursuit Regression)的思想,它一点也不神秘。
我们手中的资料是k n k k k x Y x ,},{1=是p 元,Y k 是一元。
非参数回归模型是n k x G Y k k k ≤≤+=1 ,)(ε(10.1.0)我们的任务是估计p 元函数G ,当然}|{)(x x Y E x G k k ==。
G 是将p 元变量映像成一元变量,那么何不先将p 元变量投影成一元变量,即取k x u θ'=,再将这个一元实数u 送进一元函数G 作映像呢?由于要选择投影方向),,(1p θθθ =,使估计误差平方和最小,就是要寻踪了。
所以取名为投影寻踪回归。
具体操作如何选方向θ,如何定函数G ,如何证明收敛性,下面将逐步讲述。
需要指出的是,投影寻踪回归与单指针半参数回归模型的思想基本上一样,基本算法也差不多,差别大的方面是收敛结果及证明。
若论出现时间,投影寻踪回归较早,在1989年,单指针模型较晚,在1993年。
一、投影寻踪回归算法假设解释变量集合}1,{n k x k ≤≤是来自密度函数为f 的p 元随机样本,对每一个p 元样本x k ,有一元观察Y k 与之对应,并且)()|(x G x x Y E k k ==(10.1.1)这里G 是回归函数,也是目标函数。
令Ω为所有p 维单位向量的集合,θ,θ1,θ2,…是Ω中的元素。
如果H 是一个p 元函数,比如f 或G ,则H 沿方向θ的方向导数记作u x H u x H x H n /)}()({lim )(0)(-+=→θθ(10.1.2)假如这个极限存在的话。
高阶导数则记作)()()(2121)(θθθθH H =⋅,等等。
x ∈R p 的第i 个分量记作x (i ),点积)()(i i yx y x ∑=⋅,模长21)(x x x ⋅=。
符号A 表示R p 的子集,通常是指凸集。
I (·∈A)表示A 的示性函数,I (x ∈A )=1,0)(=∈A x I 。
u 一般代表实数。
我们的任务是从观察1},{1==n k k k y x 作出p 元函数G (x )的估计,遇到的问题是p 太大,维数太高,解决的办法是作投影寻踪回归。
作沿着θ方向的一元函数Ω∈=⋅=θθθ },|)({)(u X x G E u g(10.1.3)在区域pR A ⊂内对G 的第一次投影逼近是函数)()(111x g x G ⋅=θθ(10.1.4)这里θ1是极小化下式)}()]()({[)(2A X I X g x G E S ∈⋅-=θθθ(10.1.5)的结果。
当然这里G 是未知的,所以我们要作出S (θ)与g θ(u )的估计,才能得到G 1(x )的估计。
下面构造它们的估计。
设θ·x 的密度为f θ,称作沿方向θ的X 的边沿密度,利用样本x j 但不包括x k 构造f θ的核估计为⎪⎪⎭⎫⎝⎛⋅-∑-=≠h x u K h n u f j k j k θθ)1(1)(ˆ)( (10.1.6)这里K 是核函数,h 是窗宽。
排除x k 在外的g θ的估计为)(ˆ/)1(1)(ˆ)()(u f h x u K Y h n u g k jj k j k θθθ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⋅-∑-=≠ (10.1.7)借助于交叉核实的思想,作下式)()](ˆ[1)(ˆ2)(1A x I x gY n S k k k k nk ∈⋅-∑==θθθ (10.1.8)的极小化,其解1ˆθ就作为θ的估计。
于是)ˆ(ˆ)(ˆ1)(ˆ)(11x g x G k k ⋅=θθ (10.1.9)就可以作为回归函数G 在区域A 的第一次投影逼近。
将估计限制在区域A 的理由在于,用来估计G 1的统计量在分母中有密度的核估计。
这个核估计在f 的边界取值接近于0,再作分母就有问题了。
所以我们要对分母接近于0的区域加以限制。
刚才构造统计量时将x k 排除在外的目的是为了使交叉核实统计量获得的参数估计1ˆθ不致有额外偏差。
一旦1ˆθ确定下来,就可以在统计量中将x k 放回去,不再排除在外:)(1)(ˆ1h x u K nh u f j nj ⋅-∑==θθ(10.1.10))(ˆ/1)(ˆ1u f h x u K Y nh u g jj n j θθθ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⋅-∑== (10.1.11))(ˆ/ˆ1)(ˆ1ˆ111u f h x u KY nh u G j j n j θθ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⋅-∑== (10.1.12)我们称)(ˆ1u G 才真正是在区域A 内与f 有关的G 的第一次投影逼近。
要证明11ˆ,ˆG θ分别是θ1与G 的一致估计还是比较容易的。
我们还可以证明它们一致收敛的收敛速度。
下面我们给出核函数K 与窗宽h 的构造选择细节。
我们使用的核函数是一元的,满足f 与G 的一维投影的平滑条件。
假定f (x )与G (x )沿一切方向的前r 阶方向导数存在,定义},:{εε≤-∈∈=y x A y R x A p 对于(10.1.13)为了j gˆ不为0,进一步假定 f (x )在一个闭集外为0,而在A ε上不为0(10.1.14)为了保证集合}:{A x x ∈⋅θ是合适的区间,对于每一θ∈Ω,我们假定A 非空,是一p 维开凸集。
对于固定的θ,估计量如θθθf g f k k ˆ,ˆ,ˆ)()(和θg ˆ是经典的一元核估计,使用的是一元样本{θ·x k ,1≤k ≤n },为了得到较高的收敛速度,可以使用r 阶正交核函数K ,它满足⎩⎨⎧-≤≤==⎰∞+∞-11001)(r j j du u K u j(10.1.15)并且K 是lder o H连续的。
所谓lder o H 连续,即存在ε>0,c >0,对一切实数u ,ν,有 ε|||)()(|v u c v K u K -≤-(10.1.16)现在我们确定窗宽。
考虑模型n k x G Y k k k ≤≤+=1 ,)(ε(10.1.17)这里n k k ,,1, =ε是独立同分布的,其均值为0,方差为σ2,与n k x k ,,1, =相互独立。
假定h =h (n )→0,且nh →∞。
对于固定的θ∈Ω,假定f θ(u )>0,且2122]}|))()({([1)()(ˆσθθθθ+=⋅-+=u X u g X G E nhu g u g)(0),()()()}({21221r r h u c h u Z dx K u f +⋅+⋅⎰-θθ(10.1.18) 这里Z (u )是渐近服从正态N (0,1),当取121~+-r nh 收敛于)(ˆu gθ的收敛速度是)()12/(+-r r p n O 。
c (u ,θ)表示一个常数,它依赖于u ,θ取值,但不随n , r 改变。
二、投影寻踪回归收敛性质设θ1,θ0∈Ω,θ0固定而θ收敛于θ0。
为了引进S (θ)的Taylor 展开,令θ00是与θ、θ0在同一平面上两个单位向量之一,且与θ0垂直。
假定θ与θ0、θ00的关系如下000212)1(ηθθηθ+-=(10.1.19)这里-1≤η≤1。
这个式子对于变换:(η,θ00)(-η,-θ00)是相等的,并且当θ→θ时η=θ·θ00→0。
在合适的规则条件下,S (θ)有合适的Taylor 展式,当θ→θ0时:)(0),(21),()()(20002200010ηθθηθθηθθ+++=S S S S(10.1.20)下面的定理表述得更清楚一些:定理10.1.1 假定f 与G 在各个方向上的一阶方向导数都存在且在R p 上一致连续,A 是一非空p 维开凸集,其边界有两个方向,函数f 在一个闭集外为0,而在A ε上不为0。
令θ0与00θ为两个平行单位向量,定义000212000)1(),(ηθθηθθθθ+-==。
在上述条件下,则存在θ0与θ00的与η无关的一致连续函数S 1与S 2,当η→0时,(10.1.20)一致成立。
这个定理的结果可从如下Radon 变换的随机展开获得。
令T 为中心在原点半径为t 的p 维球,选择t 充分大使T 包含f 的支撑。
给定θ∈Ω,u ∈R ,定义Γθ=Γθ(u ),它是点集{x ∈T :θ·x =u }所形成的(p -1)维表面。
令)(x d θγ是位于x ∈Γθ的(p -1)维的微元,其法线平行于θ。
定义Radon 变换为)()(),(x d x u A θγαθθΓ⎰=(10.1.21)则对此随机变换有如下定理:定理10.1.2 假定在x ∈T 上沿各个方向都存在一致连续的两个一阶方向导数,令θ0,00θ是两个平行单位向量,按(10.1.19)定义θ=θ(θ0,θ00),则存在一致有界的连续函数A 1,A 2,使当η→0时,)(0|)},,(21),,(),({),(|sup 20002200010ηθθηθθηθθ=++-u A u A u A u A (10.1.22)这里上界对u ≥0所取,θ0,θ00∈Ω,并且θo ⊥θ00。
我们看到这个定理是上一定理的具体化。
这里的A (u,θ),A 1(u ,θ0,θ00),A 2 (u ,θ0,θ00)对应于上一定理的S (θ),S 1(θ0,θ00),S 2(θ0,θ00)。
我们再进一步把A 、A 1、A 2的表达式写具体。
在Radon 变换中,取α(x )=fG ,结果记为A ;取α(x )=f ,结果记为B ,再记A 1、B 1为)()}())(()())({(),,(0)(00)(000010000x d x fG x x fG x u A γθθθθθθθθ⋅-⋅⎰=Γ (10.1.23))()}()()(){(),,(00000)(00)(00001x d x f x x f x u B θθθγθθθθθ⋅-⋅⎰=Γ(10.1.24))/()/()()(),,(21100000010B AB B A x g x x g -+⋅'⋅=θθθθθ(10.1.25)这里A 1表示A 1(u ,θ0,θ00)在u =θ0·x 处取值,B 1亦然。
注意g θ(u )=A (u ,θ)/B (u ,θ),以及(10.1.5)关于S (θ)的定义,我们可以推出(10.1.20)中S 1(θ0,θ00)的表达式dx x f x g x G x g S A )(),,()}()({2),(0001000010θθθθθθ-⋅⎰=(10.1.26)类似还可推出S 2(θ0,θ00)的表达式,不过太复杂。
