运筹学黄皮版第二章习题答案
运筹学习题参考答案
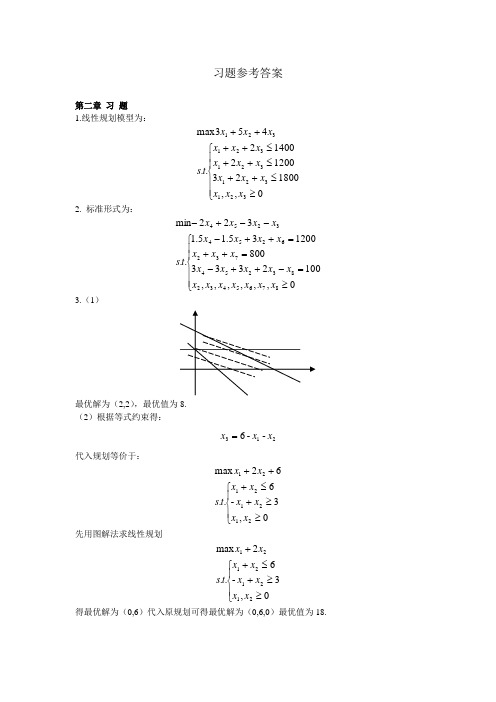
习题参考答案第二章 习 题1.线性规划模型为:⎪⎪⎩⎪⎪⎨⎧≥≤++≤++≤++++0,,1800231200214002..453max 321321321321321x x x x x x x x x x x x t s x x x 2. 标准形式为:⎪⎪⎩⎪⎪⎨⎧≥=-++-=++=++---+-0,,,,,,1002333800120035.15.1..322min 87654328325473262543254x x x x x x x x x x x x x x x x x x x t s x x x x 3.(1)最优解为(2,2),最优值为8.(2)根据等式约束得:213--6x x x =代入规划等价于:⎪⎩⎪⎨⎧≥≥+≤+++0,3-6..62max 21212121x x x x x x t s x x 先用图解法求线性规划⎪⎩⎪⎨⎧≥≥+≤++0,3-6..2max 21212121x x x x x x t s x x 得最优解为(0,6)代入原规划可得最优解为(0,6,0)最优值为18.4.(1)以21,x x 为基变量可得基可行解(3,1,0),对应的基阵为:⎪⎪⎭⎫⎝⎛1101 以31,x x 为基变量可得基可行解(2,0,1),对应的基阵为:⎪⎪⎭⎫ ⎝⎛2111 (2)规划转化为标准形式:⎪⎩⎪⎨⎧≥=++=++--0,,,55623..34min 432142132121x x x x x x x x x x t s x x 以32,x x 为基变量可得基可行解(0,1,4,0),对应的基阵为:⎪⎪⎭⎫⎝⎛0512 5. 以432,,x x x 为基变量可得基可行解(0,2,3,9),对应的典式为:32192231412=+=+=x x x x x 非基变量1x 的检验数为21-。
6. (1) a=0,b=3,c=1,d=0;(2) 基可行解为(0,0,1,6,2) (3)最优值为3.7.(1)最优解为(1.6,0,1.2),最优值为-4.4;(2)令11-=x y ,则0≥y ,11+=y x ,在规划中用1+y 替代1x ,并化标准形式。
运筹学第二章课后题
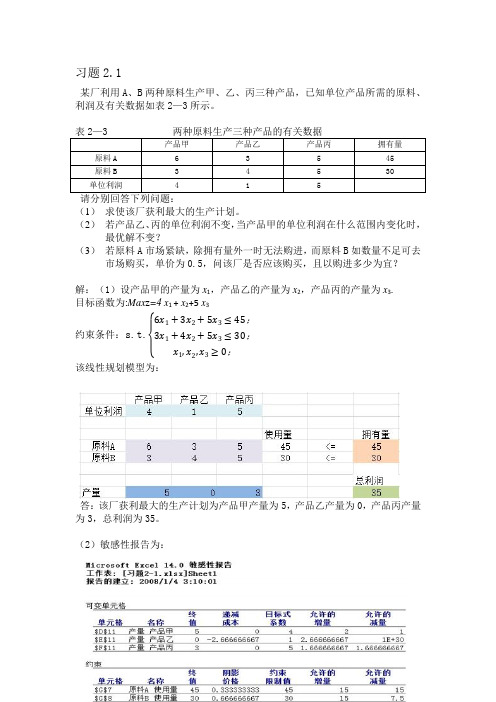
习题2.1某厂利用A 、B 两种原料生产甲、乙、丙三种产品,已知单位产品所需的原料、利润及有关数据如表2—3所示。
表2—3 两种原料生产三种产品的有关数据产品甲 产品乙 产品丙 拥有量 原料A 6 3 5 45 原料B 3 4 5 30 单位利润 4 1 5 请分别回答下列问题:(1) 求使该厂获利最大的生产计划。
(2) 若产品乙、丙的单位利润不变,当产品甲的单位利润在什么范围内变化时,最优解不变?(3) 若原料A 市场紧缺,除拥有量外一时无法购进,而原料B 如数量不足可去市场购买,单价为0.5,问该厂是否应该购买,且以购进多少为宜?解:(1)设产品甲的产量为x 1,产品乙的产量为x 2,产品丙的产量为x 3. 目标函数为:Max z =4 x 1 + x 2+5 x 3约束条件:s.t.{ 6x 1+3x 2+5x 3≤45;3x 1+4x 2+5x 3≤30;x 1,x 2,x 3≥0;该线性规划模型为:答:该厂获利最大的生产计划为产品甲产量为5,产品乙产量为0,产品丙产量为3,总利润为35。
(2)敏感性报告为:答:如数据显示,产品甲的单位利润变化范围为:[3,6]。
(3)敏感性报告为:由敏感性报告显示原料B允许的增量为15,其影子价格为0.667,又因为市场上原料B单价为0.5,此时,总利润为37.5。
答:该厂可购买15。
习题2.3已知某工厂计划生产三种产品,各产品需要在设备A、B、C上加工,有关数据如表2—5所示。
表2—5 生产三种产品的有关数据产品A产品B产品C每月设备有效台时设备A8210300设备B1058400设备C21310420单位利润(千元)32 2.9请分别回答下列问题:(1)如何充分发挥设备能力,才能使生产盈利最大?(2)为了增加产量,可借用其他工厂的设备B,若每月可借用60台时,租金为1.8万元,问借用设备B是否合算?(3)若另有两种新产品(产品4和产品5),其中生产每件新产品4需用设备A、B、C各12、5、10台时,单位赢利2.1千元;生产每件新产品5需用设备A、B、C各4、4、12台时,单位赢利1.87千元。
运筹学习题答案(第二章)

0
-5/4
(j)
第二章习题解答
2.4 给出线性规划问题 写出其对偶问题;(2)用图解法求解对偶问题;(3)利用(2)的结果及根据对偶问题性质写出原问题最优解。
最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。
01
由于 y1=-8/5,y2=1/5都不等于零,原问题中的约束取等号。又上面第4个约束不等号成立,故x4=0,令x3=0就可以得到最优解: x1=8/5,x2=1/5。
3
2
5
0
0
0
CB
基
b
X1
X2
X3
X4
X5
X6
2
X2
15-7/4
1/4
1
0
0
0
1/4
5
X3
30+
3/2
0
1
0
1/2
0
0
X4
3 /2-5
-1
0
0
1
-1/2
-1/2
Cj-Zj
-7
0
0
-1
-2
0
第二章习题解答
第二章习题解答
2.14 某厂生产A,B,C三种产品,其所需劳动力、材料等有关数据见下表:
第二章习题解答
已知原问题最优解为X*=(2,2,4,0),代入原问题,第4个约束不等式成立,故y4=0。有由于x1,x2,x3大于0,上面对偶问题前3个约束取等号,故得到最优解: y1=4/5, y2,=3/5, y3=1, y4=0
第二章习题解答
2.8 已知线性规划问题A和B如下:
01
01
02
2.6 已知线性规划问题
运筹学习题集(第二章)

运筹学习题集(第二章)判断题判断正误,如果错误请更正第二章线形规划的对偶理论1.原问题第i个约束是<=约束,则对偶变量yi>=0.2.互为对偶问题,或则同时都有最优解,或则同时都无最优解.3.原问题有多重解,对偶问题也有多重解.4.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解.5.原问题无最优解,则对偶问题无可行解.6.设X,Y分别为{minZ=CX|AX>=b,X>=0}和{maxw=Yb|YA<=C,Y>=0}的可行解,则有(1)CX<=Yb;(2)CX是w的上界;(3)当X,Y为最优解,CX=Yb;(4)当CX=Yb 时,有YXs+YsX=0;(5)X为最优解且B是最优基时,则Y=C B B-1是最优解;(6)松弛变量Ys的检验数是λs,则X=-λs是基本解,若Ys是最优解, 则X=-λs是最优解.7.原问题与对偶问题都可行,则都有最优解.8.原问题具有无界解,则对偶问题可行.9.若X,Y是原问题与对偶问题的最优解.则X=Y.10.若某种资源影子价格为0,则该资源一定有剩余.11影子价格就是资源的价格.12.原问题可行对偶问题不可行,可用对偶单纯形法计算.13.对偶单纯形法比值失效说明原问题具有无界解.14.对偶单纯形法是直接解对偶问题的一种解法.15.减少一个约束,目标值不会比原来变差.16.增加一个约束,目标值不会比原来变好.17增加一个变量, 目标值不会比原来变差.18.减少一个非基变量, 目标值不变.19.当Cj(j=1,2,3,……,n)在允许的最大范围内同时变化时,最优解不变。
选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。
第二章线性规划的对偶理论1.如果决策变量数列相等的两个线规划的最优解相同,则两个线性规划A约束条件相同B目标函数相同C最优目标函数值相同D以上结论都不对2.对偶单纯形法的最小比值规则是为了保证A使原问题保持可行B 使对偶问题保持可行C逐步消除原问题不可行性D逐步消除对偶问题不可行性3.互为对偶的两个线性规划问题的解存在关系A若最优解存在,则最优解相同B原问题无可行解,则对偶问题也无可行解C对偶问题无可行解,原问题可能无可行解D一个问题无界,则另一个问题无可行解E一个问题无可行解,则另一个问题具有无界解4.已知规范形式原问题(max)的最优表中的检验数为(λ1,λ2,……λn),松弛变量的检验数为(λn+1,λn+2,……λn+m),则对偶问题的最优解为A—(λ1,λ2,……λn)B (λ1,λ2,……λn)C —(λn+1,λn+2,……λn+m)D (λn+1,λn+2,……λn+m)5.原问题与对偶问题都有可行解,则A原问题有最优解,对偶问题可能没有最优解B原问题与对偶问题可能都没有最优解C可能一个问题有最优解,另一个问题具有无界解D原问题与对偶问题都有最优解计算题线性规划问题和对偶问题2.1 对于如下的线性规划问题min z = 3x1 + 2x2 +x3s.t. x1 + x2+ x3 ≤ 15 (1)2x1 - x2+ x3≥ 9 (2)-x1 + 2x2+2x3≤ 8 (3)x1 x2x3 ≥ 01、写出题目中线性规划问题的对偶问题;2、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解答:1、写出题目中线性规划问题的对偶问题;解:max w = 15y1 + 9y2 + 8y3s.t. y1 + 2y- y3 ≤ 3 (1)y1 - y2+ 2y3≤ 2 (2)y1 + y2+ 2y3≤ 1 (3)y1≤0、y2 ≥0、y3 ≤02、分别求出原始问题和对偶问题的最优解(求解的次序和方法不限);解:先将原问题化成以下形式,则有mi n z = 3x1 + 2x2 + x3s.t. x1 + x2+ x3+ x4= 15 (1)-2x1 + x23+ x5= -9 (2)-x1 + 2x2+2x3+x6= 8 (3)原始问题的最优解为(X 1 X 2 X 3 X 4 X 5 X 6)=(2,0,5,8,0,0),minz=11 对偶问题的最优解为(y 1 y 2 y 3 y 4 y 5 y 6)=(0,7/5,-1/5,0,19/5,0),maxw=112.2 对于以下线性规划问题max z = -x 1 - 2x 2s.t. -2x 1 + 3x 2 ≤ 12 (1) -3x 1 + x 2 ≤ 6 (2) x 1 + 3x 2 ≥ 3 (3) x 1 ≤ 0,x 2 ≥ 01、写出标准化的线性规划问题;2、用单纯形表求出这个线性规划问题的最优解和最优的目标函数值;3、写出这个(极大化)线性规划问题的对偶问题;4、求出对偶问题的最优解和最优解的目标函数值;5、第(2)个约束右端常数b 2=6在什么范围内变化,最优解保持不变。
运筹学第二章答案.
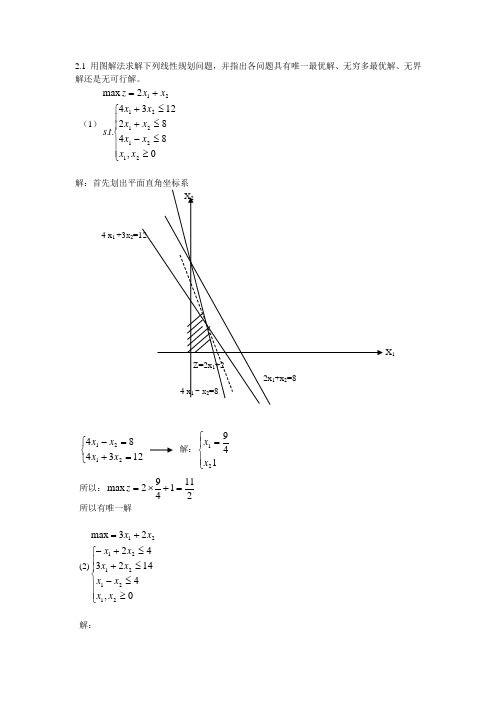
2.1 用图解法求解下列线性规划问题,并指出各问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤++=0,84821234..2max 2121212121x x x x x x x x t s x x z解:首先划出平面直角坐标系4 x 1 +3x 2X 1⎩⎨⎧=+=-1234842121x x x x 解:⎪⎩⎪⎨⎧=14921x x 所以:2111492max =+⨯=z 所以有唯一解(2)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤+-+=0,414234223max 2121212121x x x x x x x x x x 解:2=41⎩⎨⎧=+=+-1423422121x x x x 解得:⎪⎪⎩⎪⎪⎨⎧==4132521x x 所以:144132253max =⨯+⨯=z 因为直线02321=+x x 与直线142321=+x x 平行, 所以有无穷多最优解,max z=14(3) ⎪⎩⎪⎨⎧≥≤+-≤-+=0,432..32max 21212121x x x x x x t s x x z 解:(4)⎪⎩⎪⎨⎧≥-≤-≥-+=0,330..max 21212121x x x x x x t s x x z解:2.2将下列线性规划问题化为标准形式(1) s.t.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624322min x x x x x x x x x x x x z (2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束, 解:(1)令011≥-=x x )0'','('''33333≥-=x x x x x则上述形式可化为:)'''(32'2m ax 3321x x x x z --+=⎪⎩⎪⎨⎧≥=+--+=-++0,'',',,'6)'''('24)'''('..43321433213321x x x x x x x x x x x x x x t s(2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束, 解:令33'x x -= )0','','(322≥x x x 则上述形式可化为:')'''(23m ax 3221x x x x z ----=⎪⎪⎩⎪⎪⎨⎧≥=---=+--=+---0,,','',',2')'''(321')'''(3')'''(2..543221322153224322x x x x x x x x x x x x x x x x x x t s 2.3. 在下列线性规划问题中,找出所有基解,指出哪些是基可行解并分别代入目标函数,比较找出最优解。
运筹学第二章习题答案

School of Management
运பைடு நூலகம்学教程
第二章习题解答
min c x Z ij ij
i j 1 1 m n
n , , ) ij i (i 1m x a jn1 (3 ) st ij bj ( j 1n , , ) . x 1 i x , , , , , ) ij 0 (i 1m j 1n
0 X4 1 0 0 0 ┆
0 X5 0 1 0 0 ┆
0 X6 0 0 1 0 ┆
基 X1 X2 X3 Cj-Zj ┆ X4 X2 Cj-Zj
┆ ┆ 0 1 0 0 0 0 1 (k)
(l) -1/4 -1/4 0 0 0 3/4 (i)
X1 25/4 5/2
(h) 1/2 -5/4 of Management School (j)
page 14 November 1, 2010
School of Management
运筹学教程
第二章习题解答
min 21 2 y W y y 23 y y y 1 1 2 3 y 2 3 () 1 对偶问题: 2 1 y y st 1 y y 1 y 2 3 1 ,y y 无约束 ,y 3 0 02
(2) 最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。 (3)由于 y1=-8/5,y2=1/5都不等于零,原问题中的约 束取等号。又上面第4个约束不等号成立,故x4=0,令 x3=0就可以得到最优解: x1=8/5,x2=1/5。
page 13 November 1, 2010
School of Management
3在互为对偶的一对原问题与对偶问题中不管原问题是求极大或极小原问题可行解的目标函数值一定不超过其对偶问题可行解的目标函数值
《运筹学》(第二版)课后习题参考答案

生产工序
所需时间(小时)
每道工序可用时间(小时)
1
2
3
4
5
成型
3
4
6
2
3
3600
打磨
4
3
5
6
4
3950
上漆
2
3
3
4
3
2800
利润(百元)
2.7
3
4.5
2.5
3
解:设 表示第i种规格的家具的生产量(i=1,2,…,5),则
s.t.
通过LINGO软件计算得: .
11.某厂生产甲、乙、丙三种产品,分别经过A,B,C三种设备加工。已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表2—10所示。
-10/3
-2/3
0
故最优解为 ,又由于 取整数,故四舍五入可得最优解为 , .
(2)产品丙的利润 变化的单纯形法迭代表如下:
10
6
0
0
0
b
6
200/3
0
1
5/6
5/3
-1/6
0
10
100/3
1
0
1/6
-2/3
1/6
0
0
100
0
0
4
-2
0
1
0
0
-20/3
-10/3
-2/3
0
要使原最优计划保持不变,只要 ,即 .故当产品丙每件的利润增加到大于6.67时,才值得安排生产。
答:(1)唯一最优解:只有一个最优点;
(2)多重最优解:无穷多个最优解;
(3)无界解:可行域无界,目标值无限增大;
运筹学第二章课后题
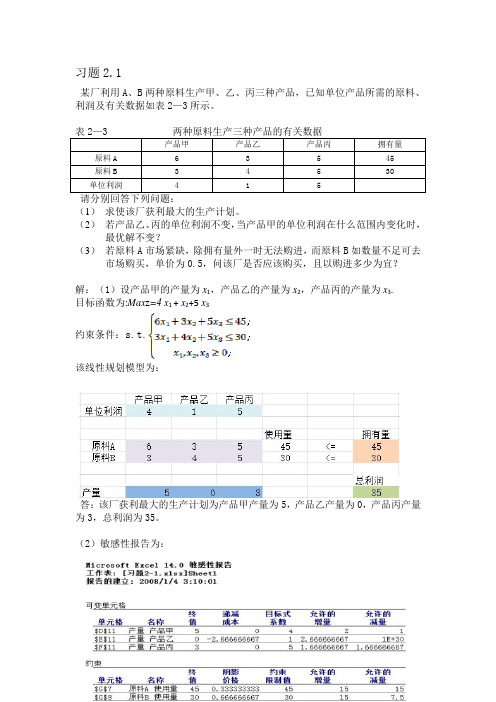
习题2.1某厂利用A、B两种原料生产甲、乙、丙三种产品,已知单位产品所需的原料、利润及有关数据如表2—3所示。
产品甲产品乙产品丙拥有量原料A63545原料B34530单位利润415(1)求使该厂获利最大的生产计划。
(2)若产品乙、丙的单位利润不变,当产品甲的单位利润在什么范围内变化时,最优解不变?(3)若原料A市场紧缺,除拥有量外一时无法购进,而原料B如数量不足可去市场购买,单价为0.5,问该厂是否应该购买,且以购进多少为宜?解:(1)设产品甲的产量为x1,产品乙的产量为x2,产品丙的产量为x3.目标函数为:Max z=4 x1 + x2+5 x3约束条件:s.t.该线性规划模型为:答:该厂获利最大的生产计划为产品甲产量为5,产品乙产量为0,产品丙产量为3,总利润为35。
(2)敏感性报告为:答:如数据显示,产品甲的单位利润变化范围为:。
(3)敏感性报告为:由敏感性报告显示原料B允许的增量为15,其影子价格为0.667,又因为市场上原料B单价为0.5,此时,总利润为37.5。
答:该厂可购买15。
习题2.3已知某工厂计划生产三种产品,各产品需要在设备A、B、C上加工,有关数据如表2—5所示。
产品A产品B产品C每月设备有效台时设备A8210300设备B1058400设备C21310420单位利润(千元)32 2.9请分别回答下列问题:(1)如何充分发挥设备能力,才能使生产盈利最大?(2)为了增加产量,可借用其他工厂的设备B,若每月可借用60台时,租金为1.8万元,问借用设备B是否合算?(3)若另有两种新产品(产品4和产品5),其中生产每件新产品4需用设备A、B、C各12、5、10台时,单位赢利2.1千元;生产每件新产品5需用设备A、B、C各4、4、12台时,单位赢利1.87千元。
如果设备A、B、C台时不增加,分别回答这两种新产品的投资在经济上是否合算?(4)对产品工艺重新进行设计,改进构造。
改进后生产每件产品1,需用设备A、B、C各9、12、4台时,单位赢利4.5千元,问这对原生产计划有何影响?解:(1)设每月产品A的产量为x1,产品B的产量为x2,产品C的产量为x3。
运筹学第二章作业的参考答案要点

第二章作业的参考答案73P 4、将下面的线性规划问题化成标准形式⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤-≤≤≤-+≥+-+-613032632..2max 21321321321x x x x x x x x t s x x x解:将max 化为 min ,3x 用54x x -代替,则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤≤-≤≤≤--+≥-+---+-0,61303)(26)(32..)(2min 5421542154215421x x x x x x x x x x x x t s x x x x令122+='x x ,则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤'≤≤≤≤---'+≥-+-'----'+-0,70303)()1(26)(3)1(2..)(21min 5421542154215421x x x x x x x x x x x x t s x x x x将线性不等式化成线性等式,则可得原问题的标准形式⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥'=+'=+=++-'+=--+'--+-'+-0,,,,,,,73424332..122min 98765421928175421654215421x x x x x x x x x x x x x x x x x x x x x x t s x x x x73P 5、用图解法求解下列线性规划问题:(1)⎪⎪⎩⎪⎪⎨⎧≥≤≤≥++212620..3min212121x x x x t s x x解:图2.1的阴影部分为此问题的可行区域。
将目标函数的等值线c x x =+213(c 为常数)沿它的负法线方向T),(31--移动到可行区域的边界上。
于是交点T),(812就是该问题的最优解,其最优值为36。
74P 12、对于下面的线性规划问题,以),,(632A A A B =为基写出对应的典式。
⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=+++-=++-=++-+-6,,1,010 83412 427 23..2min 63215214321321 j x x x x x x x x x x x x t s x x x j 解:先将方程组中基变量632,,x x x 的系数向量化成单位向量⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧=≥-=+---=++-=++++-6,,1,039 47 4 2253 41 21581 21 45..2min 65415215431321 j x x x x x x x x x x x x t s x x x j 利用线性方程组的典式,把32,x x 用541,,x x x 表示,再带入目标函数,则可得原问题相应于基),,(632A A A B =的典式⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥-=+---=++-=++++---6,,1,039 47 4 2253 41 21581 21 45..8321451min 65415215431541 j x x x x x x x x x x x x t s x x x j75P 16、用单纯形法求解下列线性规划问题:(1)⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤-+≤+-≤+++--=3,2,1,020102603..2min 321321321321j x x x x x x x x x x t s x x x z j解:将此问题化成标准形式⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=+-+=++-=++++--=6,5,4,3,2,1,020102603..2min 632153214321321j x x x x x x x x x x x x x t s x x x z j以654,,x x x 为基变量,可得第一张单纯形表为以1x 为以2x 为进基变量,6x 为离基变量旋转得 解为Tx )0,5,15(*=,最所以最优优值为-35。
运筹学第二章答案
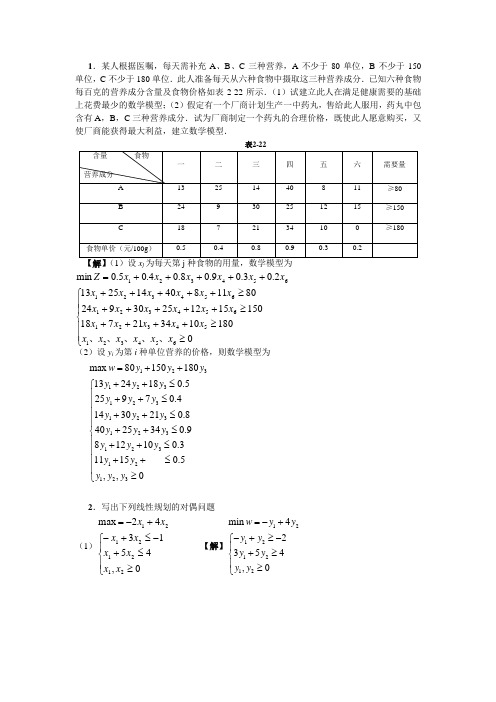
1.某人根据医嘱,每天需补充A 、B 、C 三种营养,A 不少于80单位,B 不少于150单位,C 不少于180单位.此人准备每天从六种食物中摄取这三种营养成分.已知六种食物每百克的营养成分含量及食物价格如表2-22所示.(1)试建立此人在满足健康需要的基础上花费最少的数学模型;(2)假定有一个厂商计划生产一中药丸,售给此人服用,药丸中包含有A ,B ,C 三种营养成分.试为厂商制定一个药丸的合理价格,既使此人愿意购买,又使厂商能获得最大利益,建立数学模型.表2-22【解】(1)设x j 为每天第j 种食物的用量,数学模型为 ⎪⎪⎩⎪⎪⎨⎧≥≥++++≥+++++≥++++++++++=01801034217181501512253092480118401425132.03.09.08.04.05.0min 65432154321654321654321654321x x x x x x x x x x x x x x x x x x x x x x x x x x x x x Z 、、、、、(2)设y i 为第i 种单位营养的价格,则数学模型为12312312312312312312123m ax 801501801324180.525970.41430210.84025340.9812100.311150.5,,0w y y y y y y y y y y y y y y y y y y y y y y y =++++≤⎧⎪++≤⎪⎪++≤⎪++≤⎨⎪++≤⎪⎪++≤⎪≥⎩2.写出下列线性规划的对偶问题 (1)⎪⎩⎪⎨⎧≥≤+-≤+-+-=0,451342max 21212121x x x x x x x x 【解】12121212m in 42354,0w y y y y y y y y =-+-+≥-⎧⎪+≥⎨⎪≥⎩(2)⎪⎩⎪⎨⎧≥≥+--=++-=0,8310232min 32132121321x x x x x x x x x x x Z 无约束, 【解】121212212m ax 108223130w y y y y y y y y y =+-=⎧⎪-=-⎪⎨≤⎪⎪≥⎩无约束;(3)⎪⎪⎩⎪⎪⎨⎧≤≥≤++-≥--+=--+-++=无约束43214321432143214321,0,0,66841052678410342max x x x x x x x x x x x x x x x x x x x x Z 【解】123123123123123123m in 8106107416822644530,0w y y y y y y y y y y y y y y y y y y =++++≥⎧⎪+-≥⎪⎪--+≤⎨⎪--+=-⎪≤≥⎪⎩无约束; (4)12341234134123411234m ax 236732696562225100,,,Z x x x x x x x x x x x x x x x x x x x x =-++--+-=⎧⎪+-≥⎪⎪-+-+≤-⎨⎪≤≤⎪≥⎪⎩无约束【解】123412341341234111234m ax 236732696562225100,,,Z x x x x x x x x x x x x x x x x x x x x x =-++--+-=⎧⎪+-≥⎪⎪-+-+≤-⎪⎨≥⎪⎪≤⎪≥⎪⎩无约束对偶问题为: 12345123451212312312345m in 962+510362223566270,000w y y y y y y y y y y y y y y y y y y y y y y x =--+--+-≥-⎧⎪-+=⎪⎪--=⎨⎪-++=-⎪≤≥≤≥⎪⎩无约束;,,, 3.考虑线性规划⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥++=0,73225442012min 2121212121x x x x x x x x x x Z(1)说明原问题与对偶问题都有最优解;(2)通过解对偶问题由最优表中观察出原问题的最优解; (3)利用公式C B B -1求原问题的最优解; (4)利用互补松弛条件求原问题的最优解. 【解】(1)原问题的对偶问题为123123123m ax 427212453200,1,2,3jw y y y y y y y y y y j =++⎧++≤⎪++≤⎨⎪≥=⎩容易看出原问题和对偶问题都有可行解,如X =(2,1)、Y =(1,0,1),由定理2.4知都有最优解。
《运筹学教程》第二章习题答案-推荐下载

1、(1)解:引入松弛变量 x4≥0,x5≥0,化不等式为等式为:
minz=2X1 +3X2+4X3
s.t.
X1+3X2+2X3+X4=7
4X1+2X2+X5=9
X1,X2,X4,X5≥0 化自由变量为非负,令 X3=X3′-X3〞,X3′,X3〞≥0 :
minz=2X1 +3X2+4X3′-4X3〞
x(10) (14 , 0, 2 , 0, 0)T 。 33
其中基础可行解为: x(1) (0, 0, 0, 6, 4)T , x(3) (0, 0, 3, 0, 7)T , x(5) (0,1, 0, 5, 0)T ,
。
将上解逐一带入原目标函数,得
Z1
其中
=0,
Z10
Z3
=
=-3,
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656min 52,22,233344,510ij ijij i jijZ c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij 数学模型为:,1213122324251323343524344546253545564656min 100,00110,(,)ij iji jij Z c x x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
《运筹学教程》第二章习题答案

《运筹学教程》第二章习题答案1、(1)解:引入松弛变量x4≥0,x5≥0,化不等式为等式为:minz=2X1 +3X2+4X3s.t. X1+3X2+2X3+X4=74X1+2X2+X5=9X1,X2,X4,X5≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :minz=2X1 +3X2+4X3′-4X3〞s.t. X1+3X2+2 X3′-2 X3〞+X4=74X1+2X2+X5=9X1,X2, X3′,X3〞,X4,X5 ≥0(2)解:引入松弛变量x5≥0,剩余变量X6≥0,化不等式为等式为:maxz=X1 -5X2+4X3- X4s.t. X1+2X3+X5=7X2-2X4-X6=9X1,X2,X4,X5 ,X6≥0化自由变量为非负,令X3=X3′-X3〞,X3′,X3〞≥0 :maxz=X1 -5X2+4X3′-4X3〞- X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥0化极大的目标函数为极小的目标函数:minz=-X1+5X2-4X3′+4X3〞+X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′,X3〞,X4,X5 , X6≥02、(1)是不等式表示下图阴影区域,过阴影部分任意两点的直线仍在该区域内。
(2)不是不等式表示下图阴影区域,过阴影部分且通过曲线上部的直线上的点不完全在该区域内。
(3)不是 不等式表示下图阴影区域,过阴影部分且通过圆内部的直线上的点不完全在该区域内。
3、在以下问题中,指出一组基础变量,求出所有基础可行解以及最优解。
(1)123123123123m ax 2..2644,,0z x x x s t x x x x x x x x x =+-⎫⎪++≤⎪⎬+-≤⎪⎪≥⎭解:将上式化成标准形式,如下:1231234123512345m in 2..2644,,,,0p x x x s t x x x x x x x x x x x x x =--+⎫⎪+++=⎪⎬+-+=⎪⎪≥⎭从上式中可以得出系数矩阵为[]12345112101411A P P P P P ⎡⎤==⎢⎥-⎣⎦, 取基础变量为45,x x ,令非基变量123,,x x x =0,解方程组123412352644x x x x x x x x +++=+-+=得基础可行解(1)(0,0,0,6,4)T x =同理得基础解:(2)(0,6,0,0,20)T x =-,(3)(0,0,3,0,7)T x =,(4)(0,0,4,24,0)T x =-,(5)(0,1,0,5,0)Tx =,(6)1420(0,,,0,0)99Tx =,(7)(6,0,0,0,2)T x =-,(8)(4,0,0,2,0)Tx=,(9)202(,,0,0,0)33Tx =-,(10)142(,0,,0,0)33Tx =。
运筹学第2章答案

即令 C1 ' = 3 + λ
σ 1 = −λ <= 0
1
σ2
=
λ 3
<=
0
σ3 =0
11 σ 1 = − 3 λ − 5 <= 0
13
σ5
=
λ 3
−
5
<=
0
P5=1/3X-3/5<=0
Cj
3
1
4
0
0
Cb
xb
b
x1
x2
x3
x4
x5
0
x4
15
3
-1
0
4
x3
6
3/5
4/5
1
σi
3/5
-11/5
0
x1 入基,min{15/3,3/(3/5)}=5,所以 x4 出基
Cj
3
1
4
Cb
xb
b
x1
x2
x3
3
x1
5
13
-1/3
0
4
x3
3
0
1
1
σi
0
-2
0
因为所有的σ i <=0,所以得到最优解 X=(5,0,3,0,0)T,
32/5
0
0
1
-1/5
8/5
2
x2
3/5
0
1
0
1/5
-3/5
3
18/5
1
0
01/52Fra bibliotek5x1
运筹学_第2章_对偶理论习题

第二章线性规划的对偶理论2.1 写出下列线性规划问题的对偶问题max z=2x1+2x2-4x3x1 + 3x2 + 3x3 ≤304x1 + 2x2 + 4x3≤80x1、x2,x3≥0解:其对偶问题为min w=30y1+ 80y2y1+ 4y2≥23y1 + 2y2 ≥23y1 + 4y2≥-4y1、y2≥02.2 写出下列线性规划问题的对偶问题min z=2x1+8x2-4x3x1 + 3x2-3x3 ≥30-x1 + 5x2 + 4x3 = 804x1 + 2x2-4x3≤50x1≤0、x2≥0,x3无限制解:其对偶问题为max w=30y1+80 y2+50 y3y1-y2 + 4 y3≥23y1+5y2 + 2y3≤8-3y1 + 4y2-4y3 =-4y1≥0,y2无限制,y3≤02.3已知线性规划问题max z=x1+2x2+3x3+4x4x1 + 2x2 + 2x3 +3x4≤202x1 + x2 + 3x3 +2x4≤20x1、x2,x3,x4≥0其对偶问题的最优解为y1*=6/5,y2*=1/5。
试用互补松弛定理求该线性规划问题的最优解。
解:其对偶问题为min w=20y1+ 20y2y1 + 2y2≥1 (1)2y1 + y2 ≥2 (2)2y1 +3y2≥3 (3)3y1 +2y2≥4 (4)y1、y2≥0将y1*=6/5,y2*=1/5代入上述约束条件,得(1)、(2)为严格不等式;由互补松弛定理可以推得x1*=0,x2*=0。
又因y1*>0,y2*>0,故原问题的两个约束条件应取等式,所以2x3*+3x4* = 203x3* +2x4* = 20解得x3* = x4* = 4。
故原问题的最优解为X*=(0,0,4,4)T2.4用对偶单纯形法求解下列线性规划min z=4x1+2x2+6x32x1 +4x2 +8x3 ≥244x1 + x2 + 4x3≥8x1、x2,x3≥0解将问题改写成如下形式max(-z)=-4x1-2x2-6x3-2x1-4x2 -8x3 + x4=-24-4x1-x2-4x3+x5 =-8x1、x2,x3,x4,x5≥0显然,p4、p5可以构成现成的单位基,此时,非基变量在目标函数中的系数全为负数,因此p4、p5构成的就是初始正侧基。
运筹学课后习题答案
s1 = 2, s2 = 0
5 、解: 标准形式: min f = 11x1 + 8x2 + 0s1 + 0s2 + 0s3
10x1 + 2x2 − s1 = 20 3x1 + 3x2 − s2 = 18 4x1 + 9x2 − s3 = 36 x1, x2 , s1, s2 , s3 ≥ 0
s1 = 0, s2 = 0, s3 = 13 6 、解:
3 车间每增加 1 工时,总利润增加 200 元 2、4 车间每增加 1 工时,总利润不增加。 d 3 车间,因为增加的利润最大 e 在 400 到正无穷的范围内变化,最优产品的组合不变
f 不变 因为在 [0,500]的范围内
g 所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条
件 1 的右边值在 [200,440]变化,对偶价格仍为 50(同理解释其他约束条件)
2、解:从上午 11 时到下午 10 时分成 11 个班次,设 xi 表示第 i 班次安排的临时 工的人数,则可列出下面的数学模型: min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11) s.t. x1+1 ≥ 9 x1+x2+1 ≥ 9 x1+x2+x3+2 ≥ 9 x1+x2+x3+x4+2 ≥ 3
x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0, x10=0,x11=0 最优值为 320。
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
2-9章运筹学课后题及答案

第二章决策分析2.1 某公司面对五种自然状态、四种行动方案的收益情况如下表:假定不知道各种自然状态出现的概率,分别用以下五种方法选择最优行动方案:1、最大最小准则2、最大最大准则3、等可能性准则4、乐观系数准则(分别取α=0.6、0.7、0.8、0.9)5、后悔值准则解:1、用最大最小准则决策S4为最优方案;2、用最大最大准则决策S2为最优方案;3、用等可能性准则决策S4为最优方案;4、乐观系数准则决策(1) α=0.6,S1为最优方案;(2) α=0.7,S1为最优方案;(3) α=0.8,S1为最优方案;(4) α=0.9,S2为最优方案;可见,随着乐观系数的改变,其决策的最优方案也会随时改变。
5、用后悔值准则决策S4为最优方案。
2.2 在习题1中,若各种自然状态发生的概率分别为P(N1)=0.1、P(N2)=0.3、P(N3)=0.4、P(N4)=0.2、P(N5)=0.1。
请用期望值准则进行决策。
解:期望值准则决策S1为最优方案。
3.3 市场上销售一种打印有生产日期的保鲜鸡蛋,由于确保鸡蛋是新鲜的,所以要比一般鸡蛋贵些。
商场以35元一箱买进,以50元一箱卖出,按规定要求印有日期的鸡蛋在一周内必须售出,若一周内没有售出就按每箱10元处理给指定的奶牛场。
商场与养鸡场的协议是只要商场能售出多少,养鸡场就供应多少,但只有11箱、12箱、15箱、18箱和20箱五种可执行的计划,每周一进货。
1、编制商场保鲜鸡蛋进货问题的收益表。
2、分别用最大最小准则、最大最大准则、等可能性准则、乐观系数准则(α=0.8)和后悔值准则进行决策。
3、根据商场多年销售这种鸡蛋的报表统计,得到平均每周销售完11箱、12箱、15箱、18箱和20箱这种鸡蛋的概率分别为:0.1、0.2、0.3、0.3、0.1。
请用期望值准则进行决策。
1、收益表2、用各准则模型求解(1)最大最小准则得S5为最优方案;(2)最大最大准则得S1为最优方案;(3)等可能性准则得S4为最优方案;(4)乐观系数( =0.8)准则得S1为最优方案;(5)后悔值准则得S3为最优方案。
运筹学(第二版)课后答案

( 2)
x1 6 x 4 12 x 2 3
T , Z 2 18 。 (6,0,2,12,0)
1 0 0 ( 3) T 。 (P3,P4,P5) (0,0,4,12,18) 0 1 0 ,得基本可行解 x 0 0 1
附录四习题参考答案
附录四:习题参考答案 第一章 线性规划及单纯形法
1.1 (1)解: 第一,求可行解集合。令两个约束条件为等式,得到两条直线,在第一 象限划出满足两个不等式的区域,其交集就是可行集或称为可行域,如图 1-1 所示,交集为(1/2, 0) 。 第二,绘制目标函数图形。将目标函数的系数组成一个坐标点(6,4) , 过原点 O 作一条矢量指向点(6,4) ,矢量的长度不限,矢量的斜率保持 4 比 6,再作一条与矢量垂直的直线,这条直线就是目标函数图形,目标函 数图形的位置任意,如果通过原点则目标函数值 Z=0,如图 1-2 所示。 第三,求最优解。图 1-2 的矢量方向是目标函数增加的方向或称梯度方 向, 在求最小值时将目标函数图形沿梯度方向的反方向平行移动, (在求最 大值时将目标函数图形沿梯度方向平行移动)直到可行域的边界,停止移 动,其交点对应的坐标就是最优解,如图 1-3 所示。最优解 x=(1/2, 0), 目标函数的最小值 Z=3。 X2 X2
CB 0 0 σj 0 10 σj 5 11
10 X1 3 5 10 0 1 0 1 0 0
5 X2 4 2 5 14/5 2/5 1 1 0 0
(表一)
T *
0 X3 1 0 0 1 0 0 5/14 -1/7 -5/14
0 X4 0 1 0 -3/5 1/5 -2 -3/14 2/7 -25/14
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
School of Management
运筹学教程
第二章习题解答
min W 2 y1 3 y 2
(1) 对偶问题:
y1 2 y 2 2
st
.
2 3
y1 y1
y2 y2
3 5
y1
3 y2
6
y1 0, y 2 0
(2) 最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。
运筹学黄皮版第二章习题答案
电话:5108157(H),5107443(O) E-mail:
运筹学教程(第二版) 习题解答
安徽大学管理学院 洪文
运筹学教程
第二章习题解答
2.1 写出下列线性规划问题的对偶问题。
min Z 2 x1 2 x2 4 x3
x1 3 x2 4 x3 2
(1)
st
(3)由于 y1=-8/5,y2=1/5都不等于零,原问题中的约束取等号。又上面第4个约束不等 号成立,故x4=0,令x3=0就可以得到最优解: x1=8/5,x2=1/5。
page 13 November 1, 2010
School of Management
运筹学教程
第二章习题解答
2.5 给出线性规划问题
page 8 November 1, 2010
School of Management
运筹学教程
第二章习题解答
(3)在互为对偶的一对原问题与对偶问题中,不管原问题是求极大或极小,原问题可 行解的目标函数值一定不超过其对偶问题可行解的目标函数值;
答:不对!如果原问题是求极小,结论相反。 (4)任何线性规划问题具有惟一的对偶问题。 答:结论正确!
School of Management
运筹学教程
第二章习题解答
m
maxZ cjxj
j1
n
aijxj bi
(i 1,,m1 m)
(4)
j1 st n aijxj bi
(i m1 1,m1 2,,m)
j1
xj 0 ( j 1,,n1, n),xj无约束( j n1 1,,n)
page 6 November 1, 2010
School of Management
运筹学教程
第二章习题解答
max Z 5x1 6x2 3x3
x1 2x2 2x3 5
(2)
st
4 xx1175xx22
3x3 3x3
3 8
x1无约束, x2 , 0, x3 0
maxW 5y1 3y2 8y3
y1 y2 4y3 5
对偶
问题: st22yy11
d=1/4, g=-3/4, i=-1/4, j=-1/4
page 10 November 1, 2010
School of Management
运筹学教程
Cj→
3
2
2
0
0
0
CB
基
b
X1
X2
X3
X4
X5
X6
0
X1
(b)
1
1
1
1
0
0
0
X2
15 (a) 1
2
0
1
0
0
X3
20
2 (c)
1
0
0
1
Cj-Zj
5y2 3y2
7y3 3y3
6 3
y1无约束, y2 0, y3 0
page 4 November 1, 2010
School of Management
运筹学教程
第二章习题解答
mn
min Z
cij xij
i1 j 1
n
xij ai
(i 1, , m )
(3)
j1
st
n
xij b j
max Z x1 2 x2 x3
x1 x2 x3 2
st
x1 2 x1
x
2
x
2
x
3
x
1 3
2
.
x1 0, x2 0, x3无约束
(1)写出其对偶问题;(2)利用对偶问题性质证明原问题目标函数值z≤1。
2 x1 x1 4
x x
2 2
3x3 3x3
3 5
x1 , x2 , 0, x3无约束
maxW 2y1 3y2 5y3
y1 2y2 y3 2
对偶问题: st34yy11
y2 4y3 2 3y2 3y3 4
y1 0, y2 0, y3无限制
page 3 November 1, 2010
( j 1, , n )
.
i1 xij 0
(i 1, , m , j 1, , n )
m
n
maW x aiyi bjyjm
对偶问 s.t 题 yyii无 y: ji 限 m 1 c制 ii j 1j(,, i1,1n, m ,m,j1, ,n)
page 5 November 1, 2010
page 9 November 1, 2010
School of Management
运筹学教程
第二章习题解答
2.3 已知某求极大化线性规划问题用单纯形法求解时的初始单纯形表及最终 单纯形表如下表所示,求表中各括弧内未知数的值。
解:
l=1, k=0 , h=-1/2, a=2,
c=3, b=10, e=5/4, f=-1/2,
3
2
2
0
0
0
┆┆
┆
┆┆
┆
┆
┆
┆
0
X4
5/4
0
0
(d) (l) -1/4 -1/4
3
X1
25/4
1
0
(e)
0
3/4 (i)
2
X2
5/2
page 11 November 1, 2010
Cj-Zj
0
1
(f)
0 (k) (g)
0
(h) 1/2
0 -5/4 (j) School of Management
运筹学教程
School of Management
运筹学教程
第二章习题解答
2.2 判断下列说法是否正确,为什么? (1)如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解; 答:不对!如原问题是无界解,对偶问题无可行解。 (2)如果线性规划的对偶问题无可行解,则原问题也一定无可行解; 答:不对!道理同上。
School of Management
运筹学教程
第二章习题解答
min j 1,2,,n1)
对偶问题: stim1 aijyi cj
( j n1 1,n1 2,,n)
i1 yi 0
(i 1,,m1)
yi无约束( j m1 1,,m)
page 7 November 1, 2010
第二章习题解答
2.4 给出线性规划问题
minZ 2x1 3x2 5x3 6x4
st.x21x1 2xx22
3x3 x4 x3 3x4
2 3
xj 0,( j 1,,4)
(1)写出其对偶问题;(2)用图解法求解对偶问题;(3)利用(2)的结果及根据对偶问题性 质写出原问题最优解。
page 12 November 1, 2010
