专题二:平行四边形常用辅助线的作法(精排版)
数学初三平行四边形中常做的辅助线

数学初三平行四边形中常做的辅助线一、平行四边形的对角线平行四边形有两条对角线,我们可以通过引入对角线来研究平行四边形的性质。
首先,我们可以证明平行四边形的对角线互相平分。
具体证明如下:设平行四边形ABCD的对角线AC和BD相交于点O,连接OA、OB、OC 和OD。
由于平行四边形的两对边分别平行且相等,所以可以得到AO=CO,BO=DO。
又由于AO=CO,BO=DO,所以AOBO和CODA都是菱形。
因为菱形的对角线互相平分,所以AC和BD互相平分。
利用对角线平分的性质,我们可以得到平行四边形中很多有用的结论。
例如,当平行四边形的两对角线相等时,它是一个矩形;当平行四边形的两对角线垂直且相等时,它是一个正方形。
二、平行四边形的中位线平行四边形的中位线是连接相邻两边中点的线段。
通过引入中位线,我们可以研究平行四边形的对应边的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的中位线互相平行且相等;2. 平行四边形的中位线平分平行四边形的面积;3. 平行四边形的中位线长度等于对应边长度的平均值。
三、平行四边形的高线平行四边形的高线是从一个顶点到与对立边垂直相交的线段。
通过引入高线,我们可以研究平行四边形的高度和底边的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的高线互相平行;2. 平行四边形的高线长度相等;3. 平行四边形的高线长度等于底边长度乘以对应高度的比值。
四、平行四边形的角平分线平行四边形的角平分线是从一个内角的顶点到对立边上的一点并且与对立边相交的线段。
通过引入角平分线,我们可以研究平行四边形的内角之间的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的角平分线互相平行;2. 平行四边形的角平分线平分对立角,即对立内角的两个角平分线相交于对立边上的一点。
五、平行四边形的中心连线平行四边形的中心连线是连接两对对边中点的线段。
通过引入中心连线,我们可以研究平行四边形的对角线之间的关系。
四边形辅助线常用做法

四边形常用的辅助线做法作辅助线的方法一:中点、中位线,延线,平行线。
如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以到达应用某个定理或造成全等的目的。
二:垂线、分角线,翻转全等连。
如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生。
其对称轴往往是垂线或角的平分线。
三:边边假设相等,旋转做实验。
如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生。
其对称中心,因题而异,有时没有中心。
故可分“有心”和“无心”旋转两种。
四:造角、平、相似,和、差、积、商见。
如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关。
在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移。
故作歌诀:“造角、平、相似,和差积商见。
”五:面积找底高,多边变三边。
如遇求面积,〔在条件和结论中出现线段的平方、乘积,仍可视为求面积〕,往往作底或高为辅助线,而两三角形的等底或等高是思考的关键。
如遇多边形,想法割补成三角形;反之,亦成立。
四边形平行四边形出现,对称中心等分点。
梯形问题巧转换,变为△和□。
平移腰,移对角,两腰延长作出高。
如果出现腰中点,细心连上中位线。
上述方法不奏效,过腰中点全等造。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
添加辅助线解特殊四边形题特殊四边形主要包括平行四边形、矩形、菱形、正方形和梯形.在解决一些和四边形有关的问题时往往需要添加辅助线.下面介绍一些辅助线的添加方法.和平行四边形有关的辅助线作法平行四边形是最常见的特殊四边形之一,它有许多可以利用性质,为了利用这些性质往往需要添加辅助线构造平行四边形.平行四边形中常用辅助线的添法平行四边形〔包括矩形、正方形、菱形〕的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有以下几种,举例简解如下:〔1〕连对角线或平移对角线:〔2〕过顶点作对边的垂线构造直角三角形〔3〕连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线〔4〕连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
专题二:平行四边形常用辅助线的作法(精排版)

平行四边形几何辅助线的作法补充中位线定理、三角形相似的性质及判定第一类:连结对角线,把平行四边形转化成两个全等三角形。
例1如左下图1,在平行四边形ABCD 中,点F E ,在对角线AC 上,且CF AE =,请你以F 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可) ⑴连结BF ⑵DE BF = ⑶证明:连结DF DB ,,设AC DB ,交于点O∵四边形ABCD 为平行四边形 ∴OB DO OC AO ==,∵FC AE = ∴FC OC AE AO -=- 即OF OE = ∴四边形EBFD 为平行四边形 ∴DE BF =图2图1OOECCDDEF练习1:如图1,E 是平行四边形ABCD 中AD 延长线上一点,ED 交BC 于F ,求证:。
简证:连BD ,由图易得(同底等高),(同底等高)所以,所以,即。
第二类:平移对角线,把平行四边形转化为梯形。
例2 如图2,平行四边形ABCD 中,对角线AC 、BD 交于O ,AC=a+b ,BD=a+c (),AB=m ,求m 的取值范围。
简解:要求AB 的值,需把AC 、BD 、AB 集中在一个三角形中,过C 作CE ∥DB 交AB 的延长线于E ,由图易得DBEC 是平行四边形,所以,,即,在△ACE 中,,即。
练习2:如右图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC ,10=BD ,m AB =,那么m 的取值范围是( )A 111<<mB 222<<mC 1210<<mD 65<<m 解:将线段DB 沿DC 方向平移,使得CE DB =,BE DC =,则有四边形CDBE 为平行四边形,∵在ACE ∆中,12=AC ,10==BD CE ,m AB AE 22==∴101221012+<<-m ,即2222<<m 解得111<<m 故选A第三类:过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
初二数学专题 四边形辅助线

初二数学专题:四边形辅助线做法总结(一)辅助线类型1.平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种:(1)连对角线或平移对角线:(2)过顶点作对边的垂线构造直角三角形(3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线(4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
(5)过顶点作对角线的垂线,构成线段平行或三角形全等.2.和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线,借助菱形的判定定理或性质定理解决问题:(1)作菱形的高;(2)连接菱形的对角线3.与矩形有关的辅助线的作法:(1)计算题型,一般通过作辅助线构造直角三角形借助勾股定理、锐角三角函数或相似解决问题(2)证明或探索问题,一般连接矩形的对角线,借助于对角线相等且平分这一性质解决问题4.与正方形有关辅助线的作法正方形是一种完美的几何图形,它既是轴对称图形,又是中心对称图形,有关正方形的试题较多.解决正方形的问题有时需要作辅助线,作正方形对角线或过对角线上的点向边作垂线、平行线是解决正方形问题的常用辅助线.(二)例题分析1.如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.(1)求证:FG=BE;(2)探索点F是否在∠DCG的平分线上,并说明你的理由.2. 已知□ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF.(1)如图,若PE=3,EO=1,求∠EPF的度数;(2)若点P是AD的中点,点F是DO的中点,BF =BC+32-4,求BC的长.3. 如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;(2)求证:NM=NP;(3)当△NPC为等腰三角形时,求∠B的度数.4.(2015年辽宁葫芦岛)在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连接BE,点G是BE的中点,连接AG、DG.(1)如图①,当∠BAC=∠DCF=90°时,直接写出AG与DG的位置和数量关系;(2)如图②,当∠BAC=∠DCF=60°时,试探究AG与DG的位置和数量关系,(3)当∠BAC=∠DCF=α时,直接写出AG与DG的数量关系.5.如图,点O是平行四边形ABCD的对角线AC与BD的交点,四边形OCDE是平行四边形.求证:OE与AD互相平分.6. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.(1)证明:四边形ADCE是菱形;(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)7 如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.(1)依题意补全图,并证明四边形EFCD是菱形;(2)若AB=3,BC=3,求平行线DE与AC间的距离.8. 如图,在▱ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,(1)求证:四边形ABCD为矩形;(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.9. 如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,PN⊥BE于点N,PM⊥AD于点M.(1)求证:BE=DE;(2)试判断AB和PM,PN的数量关系并说明理由.10. 如图,点F在▱ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.(1)求证:四边形ABEF是菱形;(2)若BE=5,AD=8,sin∠CBE=,求AC的长.11. (2015年广西玉林)如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.(1)当△CDQ≌△CPQ时,求AQ的长;(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.。
平行四边形题型和辅助线(完美打印版)

平行四边形题型和辅助线(完美打印版)平行四边形是一种特殊的四边形,具有以下性质:两组对边分别平行,两组对边分别相等,两组对角分别相等,对角线互相平分,邻角互补。
在判定平行四边形时,可以选择不同的方法。
常见的考点包括利用平行四边形的性质求解角度、线段长和周长,求解某边的取值范围,以及综合计算问题。
另外,还可以利用平行四边形的性质证明角相等、线段相等和直线平行,或利用判定定理证明四边形是平行四边形。
在解决平行四边形问题时,常用的辅助线方法包括:连对角线或平移对角线,过顶点作对边的垂线构造直角三角形,连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线,连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形,以及过顶点作对角线的垂线,构成线段平行或三角形全等。
平行四边形包括矩形、正方形和菱形,它们的两组对边、对角和对角线都具有相同的性质。
因此,在处理平行四边形问题时,可以将其转化为常见的三角形、正方形等问题处理,以达到更好的解决效果。
例如,在证明平行四边形的性质时,可以连对角线或平移对角线,或通过构造直角三角形和线段平行或中位线等方法,将问题简化为常见的三角形或线段问题。
这样可以更加方便地解决问题,提高解题效率。
四、构造相似或等积三角形例7:在正方形ABCD中,E、F分别为CD、DA的中点,BE、CF交于P,证明AP=AB。
证明:连接AP、BP,由于BE=EF,CF=DF,所以三角形BEP和CFP相似,即EP/FP=BE/CF=1,所以EP=FP,又因为EP=AB/2,所以AP=AB。
例8:在平行四边形ABCD中,E、F分别是DC、DA上一点,AE=CF,AE与CF交于P,证明PB平分∠APC。
证明:连接AP、BP、CP,由于AE=CF,所以△AEP和△CFP全等,即∠APE=∠CPF,又因为AB∥CD,所以∠APE=∠BPC,所以∠XXX∠XXX,即PB平分∠APC。
平行四边形辅助线

平行四边形中常用辅助线的添法平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下:(1)连对角线或平移对角线:(2)过顶点作对边的垂线构造直角三角形(3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线(4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
(5)过顶点作对角线的垂线,构成线段平行或三角形全等.第一类:连结对角线,把平行四边形转化成两个全等三角形。
例1如左下图1,在平行四边形ABCD 中,点F E ,在对角线AC 上,且CF AE =,请你以F 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可)⑴连结BF ⑵DE BF =⑶证明:连结DF DB ,,设AC DB ,交于点O∵四边形ABCD 为平行四边形 ∴OB DO OC AO ==,∵FC AE = ∴FC OC AE AO -=- 即OF OE =∴四边形EBFD 为平行四边形 ∴DE BF =图2图1E CAAB第二类:平移对角线,把平行四边形转化为梯形。
例2如右图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC , 10=BD ,m AB =,那么m 的取值范围是( )A 111<<mB 222<<mC 1210<<mD 65<<m解:将线段DB 沿DC 方向平移,使得CE DB =,BE DC =,则有四边形CDBE 为平行四边形,∵在ACE ∆中, 12=AC ,10==BD CE ,m AB AE 22==∴101221012+<<-m ,即2222<<m 解得111<<m 故选A第三类:过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
平行四边形辅助线总结
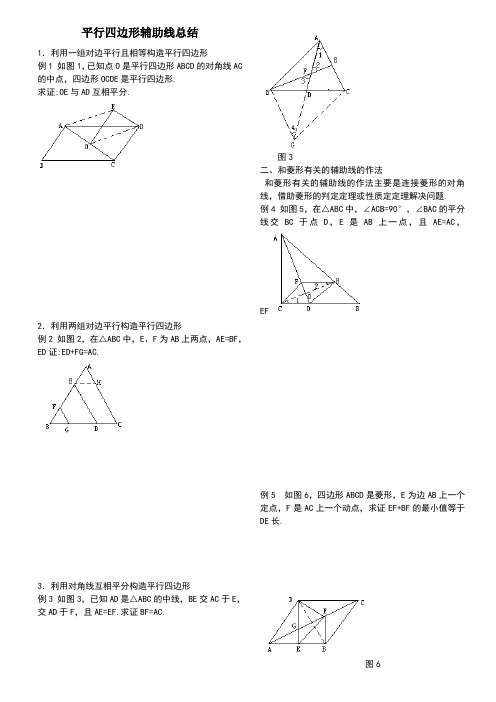
平行四边形辅助线总结1.利用一组对边平行且相等构造平行四边形例1 如图1,已知点O是平行四边形ABCD的对角线AC 的中点,四边形OCDE是平行四边形.求证:OE与AD互相平分.2.利用两组对边平行构造平行四边形例2 如图2,在△ABC中,E、F为AB上两点,AE=BF,ED证:ED+FG=AC.3.利用对角线互相平分构造平行四边形例3 如图3,已知AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证BF=AC.图3二、和菱形有关的辅助线的作法和菱形有关的辅助线的作法主要是连接菱形的对角线,借助菱形的判定定理或性质定定理解决问题.例4 如图5,在△ABC中,∠ACB=90°,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF例5 如图6,四边形ABCD是菱形,E为边AB上一个定点,F是AC上一个动点,求证EF+BF的最小值等于DE长.图6说明:菱形是一种特殊的平行四边形,和菱形的有关证明题或计算题作辅助线的不是很多,常见的几种辅助线的方法有:(1)作菱形的高;(2)连结菱形的对角线.与矩形有辅助线作法和矩形有关的题型一般有两种:(1)计算型题,一般通过作辅助线构造直角三角形借助勾股定理解决问题;(2)证明或探索题,一般连结矩形的对角线借助对角线相等这一性质解决问题.和矩形有关的试题的辅助线的作法较少.例6 如图7,已知矩形ABCD内一点,PA=3,PB=4,PC=5.求 PD的长.分析:要利用已知条件,因为矩形ABCD,可过P分别作两组对边的平行线,构造直角三角形借助勾股定理解决问题.图7四、与正方形有关辅助线的作法正方形是一种完美的几何图形,它既是轴对称图形,又是中心对称图形,有关正方形的试题较多.解决正方形的问题有时需要作辅助线,作正方形对角线是解决正方形问题的常用辅助线.例7如图8,过正方形ABCD的顶点B作BE证:∠BCF=21∠AEB.。
四边形中常见的辅助线

四边形中常见的辅助线特殊四边形主要包括平行四边形、矩形、菱形和正方形.在解决一些和四边形有关的问题时往往需要添加辅助线.下面介绍一些辅助线的添加方法.平行四边形是最常见的特殊四边形之一,它有许多性质。
为了利用这些性质往往需要添加辅助线构造平行四边形.平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种:(1)连对角线或平移对角线:(2)过顶点作对边的垂线构造直角三角形(3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线(4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
(5)过顶点作对角线的垂线,构成线段平行或三角形全等.一、与平行四边形有关的辅助线的作法:1.利用一组对边平行且相等构造平行四边形例题:如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形.求证:OE与AD 互相平分分析:因为四边形OCDE是平行四边形,所以OC//ED,OC=DE,又由O是AC的中点,得出AO//ED,AO=ED,则四边形AODE是平行四边形,问题得证.证明:连结AE、OD,因为是四边形OCDE是平行四边形,所以OC//DE,OC=DE,因为0是AC的中点,所以A0//ED,AO=ED,所以四边形AODE是平行四边形,所以AD与OE互相平分.说明:当已知条件中涉及到平行,且要求证的结论中和平行四边形的性质有关,可试通过添加辅助线构造平行四边形.2.利用两组对边平行构造平行四边形例题:如图,在△ABC中,E、F为AB上两点,AE=BF,ED//AC,FG//AC交BC分别为D,G.求证:ED+FG=AC. 分析:要证明ED+FG=AC,因为DE//AC,可以经过点E作EH//CD交AC于H得平行四边形,得ED=HC,然后根据三角形全等,证明FG=AH.证明:过点E作EH//BC,交AC于H,因为ED//AC,所以四边形CDEH是平行四边形,所以ED=HC,又FG//AC,EH//BC,所以∠AEH=∠B,∠A=∠BFG,又AE=BF,所以△AEH≌△FBG,所以AH=FG,所以FG+DE=AH+HC=AC.说明:当图形中涉及到一组对边平行时,可通过作平行线构造另一组对边平行,得到平行四边形解决问题.3.利用对角线互相平分构造平行四边形例题:如图,已知AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.,求证BF=AC.分析:要证明BF=AC,一种方法是将BF和AC变换到同一个三角形中,利用等边对等角;另一种方法是通过等量代换,寻找和BF、AC相等的相段代换.寻找相等的线段的方法一般是构造平行四边形.证明:延长AD到G,使DG=AD,连结BG,CG,因为BD=CD,所以四边形ABGC是平行四边形,所以AC=BG,AC//BG,所以∠1=∠4,因为AE=EF,所以∠1=∠2,又∠2=∠3,所以∠1=∠4,所以BF=BG=AC.说明:本题通过利用对角线互相平分构造平行四边形,实际上是采用了平移法构造平行四边形.当已知中点或中线应思考这种方法.4.连对角线构造三角形例题:如图,AB=3,BC=4,CD=13,AD=12,∠B=900,求四边形ABCD的面积分析:由∠B=900,AB=3,BC=4,联想到连结AC,利用勾股定理解得AC=5,又AD=12,CD=13,由勾股定理的逆定理有∠DAC为直角,从而S四边形ABCD=S△ABC+ S△ACD解:连接AC,在Rt△ABC中,AC2=AB2+BC2=32+42=25,∵CD=13,AD=12,∴AD2+AC2=CD2,∴△ACD是直角三角形,∠DAC=900,∴S四边形ABCD=S△ABC+ S△ACD=0.5AB·BC+0.5AD·AC=0.5×3×4+0.5×12×5=365.延长对边构造三角形例题:如图,在四边形ABCD中,∠A=600,∠B=∠D=900,BC=2,CD=3,则AB等于多少?6.延长一边中点与顶点连线,把平行四边形转化为三角形例题:如图,正方形ABCD中,E、F分别是CD、DA的中点,BE与CF交于P点。
平行四边形辅助线的常见添法

平行四边形辅助线的常见添法平行四边形是一种特殊的四边形,其对边平行且相等。
在平面几何中,我们常常需要绘制平行四边形,而平行四边形的绘制又离不开辅助线。
本文将介绍平行四边形的常见添法及其应用。
一、基础概念1. 平行四边形:对边分别平行且相等的四边形。
2. 辅助线:在图形中引入的额外直线,以便更容易地进行计算或绘制。
二、常见添法1. 中点法中点法是最简单也是最基础的添法之一。
它的原理是在两条对角线上各取一个中点,然后连接这两个中点即可得到平行四边形。
步骤如下:(1)画出任意一个四边形ABCD;(2)连接AC和BD两条对角线;(3)在AC和BD上各取一个中点E和F;(4)连接EF即可得到平行四边形。
2. 三角形法三角形法也是一种简单易懂的添法。
它的原理是在原来图形上构造一个与之相似但比例不同的三角形,然后通过旋转或移动这个三角形,使其与原来的图形组成平行四边形。
步骤如下:(1)在原来的四边形ABCD上选择一个顶点A;(2)连接AC和AD两条边;(3)以A为顶点,做一个与△ACD相似但比例不同的三角形AEF;(4)将三角形AEF沿着AD旋转或移动到AB上,得到平行四边形ABFE。
3. 重心法重心法是一种比较常用的添法。
它的原理是在四边形的对角线交点处作一条平行于其中一条边的直线,然后将这条直线延长至四边形另一侧,再将这两条直线分别延长至与四边形相交即可得到平行四边形。
步骤如下:(1)画出任意一个四边形ABCD;(2)连接AC和BD两条对角线,并求出它们的交点O;(3)在O点处作一条平行于CD的直线EF,并延长至BC上;(4)将EF和BD分别延长至与AC相交,即可得到平行四边形ABFE。
4. 中垂线法中垂线法也是一种比较实用的添法。
它的原理是在任意一侧边上取一点,然后分别连接这个点与对角线的中点,再将这两条线段延长至另一侧边上即可得到平行四边形。
步骤如下:(1)画出任意一个四边形ABCD;(2)在AB上取一点E,并连接EC和AD的中点F;(3)在BC上取一点G,并连接AG和BD的中点H;(4)将EF和GH分别延长至CD上,即可得到平行四边形EFGH。
与平行四边形有关的常用辅助线作法归类解析

平行四边形常用辅助线第一类:连结对角线,把平行四边形转化成两个全等三角形。
例1如左下图1,在平行四边形ABCD 中,点F E ,在对角线AC 上,且CF AE =,请你以F 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可)⑴连结BF ⑵DE BF =⑶证明:连结DF DB ,,设AC DB ,交于点O∵四边形ABCD 为平行四边形 ∴OB DO OC AO ==, ∵FC AE = ∴FC OC AE AO -=- 即OF OE =∴四边形EBFD 为平行四边形 ∴DE BF =图2图1E CAAB第二类:平移对角线,把平行四边形转化为梯形。
例2如右图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC , 10=BD ,m AB =,那么m 的取值范围是( )A 111<<mB 222<<mC 1210<<mD 65<<m解:将线段DB 沿DC 方向平移,使得CE DB =,BE DC =,则有四边形CDBE 为平行四边形,∵在ACE ∆中, 12=AC ,10==BD CE ,m AB AE 22==∴101221012+<<-m ,即2222<<m 解得111<<m 故选A第三类:过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
例3已知:如左下图3,四边形ABCD 为平行四边形求证:222222DA CD BC AB BD AC +++=+证明:过D A ,分别作BC AE ⊥于点E ,BC DF ⊥的延长线于点F∴BC BE BC AB BE BC BE AB CE AE AC ⋅-+=-+-=+=2)(22222222 CF BC BC CD CF BC CF CD BF DF BD ⋅++=++-=+=2)()(22222222 则BE BC CF BC DA CD BC AB BD AC ⋅-⋅++++=+22222222∵四边形ABCD 为平行四边形 ∴AB ∥CD 且CD AB =,BC AD = ∴DCF ABC ∠=∠ ∵090=∠=∠DFC AEB∴DCF ABE ∆≅∆ ∴CF BE =∴222222DA CD BC AB BD AC +++=+图4图3KD C F B B第四类:延长一边中点与顶点连线,把平行四边形转化为三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题讲义平行四边形+几何辅助线的作法、知识点1 •四边形的内角和与外角和定理:(1) 四边形的内角和等于360°; (2) 四边形的外角和等于360° . 2. 多边形的内角和与外角和定理:(1) n 边形的内角和等于(n-2)180 ° (2) 任意多边形的外角和等于 360° 3. 平行四边形的性质:4、平行四边形判定方法的选择..”■ 已知条件 选择的狎定方法i 边1. 一鲫边幘 L .... 讹⑵沁⑶ 一组对边平行 定文{方法1),方送⑶一纽对命相等方法《5〉方搓⑷5、和平行四边形有关的辅助线作法(1)利用一组对边平行且相等构造平行四边形例1、如图,已知点O 是平行四边形ABCD 勺对角线AC 的中点,四边形OCD 是平行四边形• 求证:OE 与AD 互相平分.说明:当已知条件中涉及到平行,且要求 证的结论中和平行四边形的性质有关, 可 试通过添加辅助线构造平行四边形—:性质四边形ABCD 是平行四边形判定(1) 两组对边分别平行;(2) 两组对边分别相等; (3) 两组对角分别相等;(4) 对角线互相平分; (5) 邻角互补.B CC(2)利用两组对边平行构造平行四边形例2、如图,在△ ABC中,E、F为AB上两点,AE=BF ED//AC, FG//AC交BC分别为D, G.说明:当图形中涉及到一组对边平行时,可通过作平行线构造另一组对边平行,得到平行四边形解决问(3)利用对角线互相平分构造平行四边形例3、如图,已知AD S^ ABC的中线,BE交AC于E,交AD于F,且AE=EF求证BF=AC.说明:本题通过利用对角线互相平分构造平行四边形,实际上是采用了平移法构造平行四边形.当已知中点或中线应思考这种方法•(4)连结对角线,把平行四边形转化成两个全等三角形。
例4、如图,在平行四边形ABCD中,点E,F在对角线AC上,且AE CF ,请你以F为一个端点,和图中已标明字母的某一点连成一条新线段, 猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可)C CA(5)平移对角线,把平行四边形转化为梯形例5、如右图2,在平行四边形ABCD中,对角线AC和BD相交于点0,如果AC 12,BD 10,AB m,那么m的取值范围是(11 B 、2 m 22C、10 m 12(6)过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
例6、已知:如图,四边形ABCD为平行四边形求证:AC2 BD2 AB2 BC2 CD2 DA2F(7)延长一边中点与顶点连线,把平行四边形转化为三角形 例7、已知:如右上图4,在正方形ABCD 中, 于P 点,求证:AP AB、课堂练习:1、如图,E 是平行四边形ABCD 的边AB 的中点,AC 与DE 相交于点F ,若平行四边形ABCD的面积为S ,则图中面积为Is 的三角形有(2A. 1个 B . 2个2、顺次连接一个任意四边形四边的中点,得到一个 _______________ 四边形.3、如图,AD ,BC 垂直相交于点 O , AB // CD , 贝U AB+CD 的长= _________ 。
4、已知等边三角形 ABC 的边长为a ,P 是厶ABC 内一点,PD// AB PE// BC ,PF // AC,点D E 、F 分别在 BC 、AC AB 上,猜想:PM PE+PF= ______ 猜想.5、平行四边形ABCD 中, E,G,F,H 分别是四条边上的点,且 AE CF ,BC DH ,BC=8,并证明你的K试说明:EF与GH相互平分.6如图,平行四边形ABCD勺对角线AC和BD 交于O, E、F分别为OB 0D的中点,过0 任作一直线分别交AB CD于G、H.试说明:GF// EH7、如图,已知AB AC , B是AD的中点,试说明:CD 2CE8、如图,E是梯形ABCD要DC的中点.试说明: S ABE 1 S梯形2 ABCD DE9、已知六边形ABCDEF勺6 个内角均为120°, CD= 2cm, BC= 8cm, AB= 8cm, AF=5cm 试求此六边形的周长.D_10、已知ABC是等腰三角形,AB=AC D是BC边上的任一点,且DE ABDF AC,CH AB,垂足分别为E、F、H,求证:DE DF CH11、已知:在Rt ABC中,AB BC ;在Rt ADE中,AD DE ;连结EC,取EC的中点M,连结DM和BM .(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,求证:BM DM 且BM DM ;(2)如果将图8-①中的ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.图①图-②答案:例4、⑴ 连结BF⑵BF DE⑶证明:连结DB,DF ,设DB,AC 交于点0•••四边形ABCD 为平行四边形 ••• A0 OC, DO OB ••• AE FC••• A0 AE OC FC 即 OE OF•••四边形EBFD 为平行四边形 ••• BFDE例5、解:将线段DB 沿DC 方向平移,使得DB CE, DC BE,则有四边形CDBE 为平行四边形,■••在ACE中, AC 12,CE BD 10,AE 2AB 2m- • 12 10 2m12 10,即 22m 22 解得1 m 11故选A例6、证明:过代D 分别作AEBC 于点 E , DFBC 的延长线于点F••• AC 2 AE 2 CE 2 AB 2BE 2 (BCBE)2 AB 2 BC 2 2BEBC BD 22 2DF 2BF 2(CD 2 22 CF 2) (BCCF) 2CD 2 BC 2 2BCCF边形具有对边平行的性质可得 GF // EH .贝U AC 2 BD 2 AB 2 BC 2 CD 2 DA 2 2BC CF 2BC BE四边形ABCD 为平行四边形 ••• AB // CD 且 AB CD , AD BCABC DCF I AEBDFC 900ABEDCF•• BE CFAC 22 2 2 2BD AB BC CDDA 2例7、证明:延长CF 交BA 的延长线于点K•••四边形ABCD 为正方形••• AB // CD 且 AB CD, CD )AD , BAD BCD D 900••• 1K又,D DAK 90°, DF AF ••• CDF 也 KAF••• AK CDAB--1 CE -CD DF2 ,1AD2••• CE DFT BCD D 900••• BCE 也 CDF••• 1 2T 13 90023 900• •• CPB900,则 KPB900••• AP AB二、课堂练习1、C2 平行 3、10 4 、a5、分析:观察图形,EF 与 HG 为四边形HEGF 的对角线,若能说明四边形 HEGF 是平行四边形,根据平行四边形的对角线互相平分这一性质即可得到6分析:观察图形,GF 与EH 为四边形GEHF 的对边,若能说明四边形 EHFG 是平行 四边形,平行四EF 与GH 相AH7、分析:延长CE 至F ,使EF = CE ,连结AF 、BF ,得四边形AFBC 是平行四边形,利 用平行四边形••• DF = CG的性质证明△ DBCFBC 即可8、分析:过点E 作MN // AB ,交BC 于N ,交AD 的延长线于M ,则四边形ABNM 是平 行四边形,△ ABE 与四边形ABNM 等底等高,所以S MBE =2S 梯形ABCD = S 平行四边形ABNM 即可。
9、■:, 1=120% /..|u 打監 -4=_7=_S=(.^T 椎导出 ACBH 都是正三pa-GA=FA=5R -O 他片 CD-DH-CH^2r ^H=60°. 丁 B+ AEH^GA, , G+ F=lfiO D J AC ;F/rRH阂此’平和回勉龙.GB=GA+AB=5-H=13, BH=BC-H?H=«+2=10. 四边JfeCBHE 的冏氏円心+讥沁="10、 证明:过D 点作DG 丄CH 于G又DE 丄AB 于E ,CH 丄AB 于H •••四边形DGHE 为矩形•••/ B = / GDC 又 AB = AC •••/ GDC = / ACB又/ DGC = / DFC = 90°••• DE = GHEH // DG•••/ B = / ACBCD = DC (公共边)D平行四边形ABNM,接下来说明又CH = CG + GH•••CH = DF + DG (等量代换)11、-:■..;■ : 一一八-一-_二占】二—亠一一—I. 1 I ■1- I ■・,冒" ■* LT !>・… I r 厂# r - '•・1 1晁魅瘵,更聊?湍讥瑕片7;臨 E^d=- E爲.*.:班彷磁1 ,;鸞W^J4C I;•■: jifBME 的外痈;仁疋日曙细◎上if®畫纠已同理^0ME-./WC+^H(D=2ZMCL>■:漬谢聡血迦必区癖询对就P)老總I;密r絶“跳谕嘛也訶備i讷⑵如图-廷长DM到阳使NN-LH逹结BJh BN,OtEI^CK , ZEM1J=ZC HK , IrfrUll<\AEMDW.^CMH/KCM=^ECM+ZECN 2 a-EH=AiD ,衽 A ABC 4 “ ;创AB十ZTEEAWF.'.^ACEl ^CAD+ZCED^.D,TETAD坯尸-2BAI 2DEM- ZNCH- ZECM+ ZBCWr-ZCED…2AUEt4t)* —ZBA£rb上兮LU十ZECNzya''又_ZACKtZBCM=4r、二4驚-ZEADt 4孙十匹ECN亨『■\2B AD=ZECU x-又辰足,皿CN /-^ABD^iCBN -■-ED-BN ZABD^2ZB®.■- ZEBC+ZCBN= ZDfi匚+£A3D=g(T $ 丈:RI>=EN. LM=W.';mMHDM 且EM丄114:平行四边形中常用辅助线的添法平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下:(1)连对角线或平移对角线:(2 )过顶点作对边的垂线构造直角三角形(3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线(4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
