(完整版)工程力学习题答案范钦珊蔡新着工程静力学与材料力学第二版
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第1章 静力学基础

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第1章)范钦珊 唐静静2006-12-18(a) (b) 习题1-1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影,比较两种情形下所得的分力与投影。
解:图(a ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b ): 分力:22)tan sin cos (i F ϕααF F x −= , 22sin sin j F ϕαF y =投影:αcos 2F F x = , )cos(2αϕ−=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图,并加以比较。
比较:解a 图与解b 图,两种情形下受力不同,二者的F R D 值大小也不同。
DR习题1-2b 解图DR习题1-2a 解2图C习题1-2a 解1图(a) (b)习题1-2图1一3 试画出图示各构件的受力图。
习题1-3图B F 习题1-3a 解2图 B习题1-3a 解1图习题1-3b 解1图F Ay Ax 习题1-3c 解图 A习题1-3b 解2图习题1-3d 解1图习题1-3e 解1图习题1-3e 解2图1-4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重,BD 杆自重为W ,作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1习题1-3f 解1图F习题1-3e 解3图'A习题1-3f 解2图1O 习题1-3f 解3图F F'F 1习题1-4d 解2图F y B 21习题1-4c 解1图 AA B 1B FDx y2B 习题1-4b 解2图 1习题1-4b 解3图 F y B 2习题1-4c 解2图 F A B1B FAxF'习题1-5b 解3图E D(a-3)E B F习题1-5b 解2图习题1-5b 解1图'AxFF B习题1-5c 解图1一5 试画出图示结构中各杆的受力图。
工程力学(工程静力学与材料力学)第二版答案(完整资料).doc

(a) (b)习题1-1图 【最新整理,下载后即可编辑】1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a ),图(c ):11 sin cos j i F ααF F +=分力:11 cos i F αF x = , 11 sin j F αF y = 投影:αcos 1F F x = , αsin 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b ),图(d ):1y F x xF 1y Fα1xF y F(c )2F2y F2y2x 2x F2y FF(d )(a) (b)习题1-2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力:22)tan sin cos (i F ϕααF F x -= ,22sin sin j FϕαF y =投影:αcos 2F F x = , )cos(2αϕ-=F F y 讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 、b 两情形下各物体的受力图,并进行比较。
比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
1-3 试画出图示各物体的受力图。
习题1-3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1-4图1-4 图a所示为三角架结构。
力F1作用在B铰上。
杆AB 不计自重,杆BD杆自重为W。
试画出图b、c、d所示的隔离体的受力图,并加以讨论。
范钦珊《工程力学》习题解答
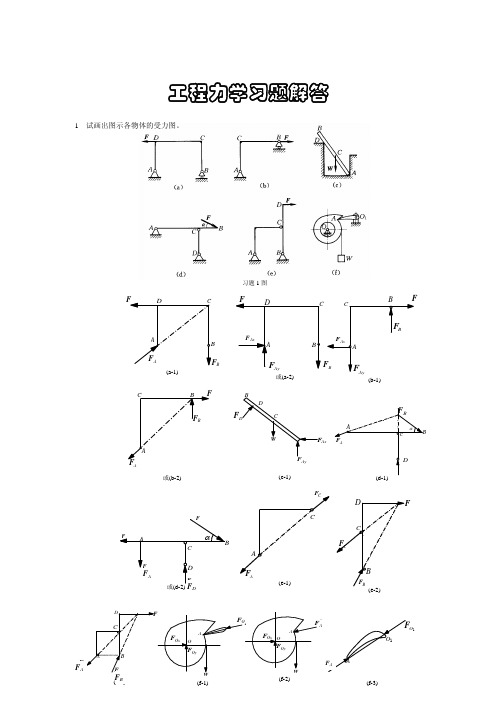
2F ⋅
(2) (3)
1 3 tan θ = sin θ = F cos θ 3 , θ = 30° 2 ,
代入(3) ,得
F1 = F2 = F3 =
W 2
8 如图所示,试求 F 对点 A 的力矩。 解: M A ( F ) = r AB × F
M2 d 由(1) 、 (2) ,得 M1 = M2
′ = FD
(2)
' FD
习题 14 图
A
D
B
M1
M
2
FA
FD
(a) (b)
15 试求图示两外伸梁的约束反力 FRA、FRB,其中(a)M = 60kN·m,FP = 20 kN; (b)FP = 10 kN,FP1 = 20 kN,q = 20kN/m,d = 0.8m。 解:图(a-1) ∑ Fx = 0 ,F = 0
F − FRA ⋅
(c)
FRC
FR D
2 2 − FRE ⋅ =0 2 2
(1) (2)
2 2 ∑ Fy = 0 , FRE ⋅ 2 − FRA ⋅ 2 = 0 由(2) FRE = FRA
代入(1) ,得
FRE =
2 F 2 ; 2 F 2
(3)
3.由图(b) : ∑ Fx = 0 ,
′E = FRA = FR
10 图示电动机固定在支架上,它受到自重 160N、轴上的力 120N 以及力偶矩为 25N·m 的力偶的作 用。试求此力系向点 A 简化的结果。
z
75
z
F1
工程力学(工程静力学和材料力学)第二版答案
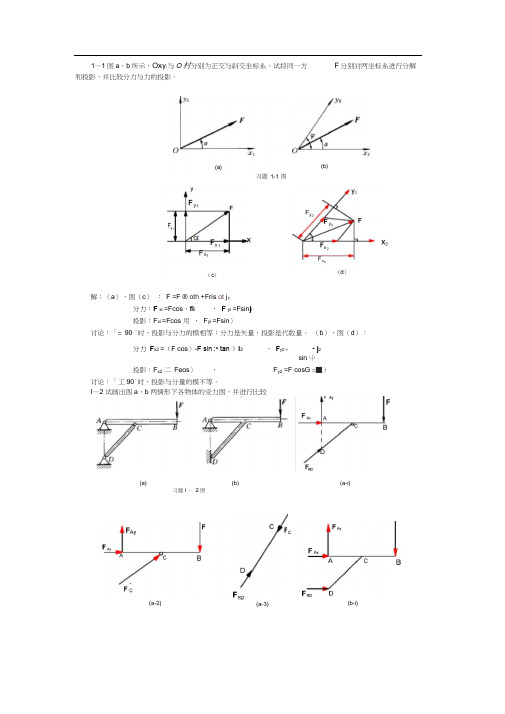
1—1图a、b所示,Ox i y i与O村分别为正交与斜交坐标系。
试将同一方F分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a),图(c): F =F ® oth +Fris ot j1分力:F xi =Fcos、fi i , F yi =Fsin j i投影:F xi =Fcos 用,F yi =Fsin〉讨论:「= 90 °时,投影与分力的模相等;分力是矢量,投影是代数量。
(b),图(d):分力F x2 =(F cos〉-F sin :• tan )i2 ,F y2 = - j2sin屮投影:F x2二Feos〉,F y2 =F cosG =■)讨论:「工90°时,投影与分量的模不等。
I—2试画出图a、b两情形下各物体的受力图,并进行比较(a) (b) (a-i)习题i —2图(a-2)(a-3)(b-i)(b)a-1 )与图(b-1 )不同,因两者之F R D值大小也不同试画出图示各物体的受力图。
AA Wi 丄A A 加习题1-3图F比较:图1-31-4图a所示为三角架结构。
力F i作用在B铰上。
杆AB不计自重,杆BD杆自重为W。
试画出图b、c、d所示的隔离体的受力图,并加以讨论。
(b)A B A B/p/ /D(c)(d)(d-1)B F B1------ A习题1-4图(b-1)i(b-3)F AFB1F'FF' B2yBBF' B2y(d-2)F1 1-5(s)W习题1-5图(C)1— 6图示刚性构件F 沿其作用线移至点 D 或点 E (如图示),是否会改变销钉 解:由受力图1— 6a , 1- 6b 和1— 6c 分析可知,F 从C移至E , A 端受力不变,这是因为力 F 在自身 刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为 HGC F CX! F Cy(b-3)在构件的点C 作用有一水平力F 。
范钦珊《工程力学》习题解答

rAB
9 齿轮箱有三个轴,其中 A 轴水平,B 和 C 轴位于 yz 铅垂平面内,轴上作用的力偶如图所示。试求合力 偶。 解:MA =(1, 0, 0)MA =3.6(1, 0, 0)kN·m MB =(0, sin40°,cos40°)MB =6(0, sin40°,cos40°)kN·m MC =(0, sin40°,-cos40°)MC =6(0, sin40°,-cos40°)kN·m ∴ M = ΣMi = MA+ MB + MC =(3.6, 12sin40°, 0)kN·m
即 ∴
2 FR·MO = − FO (l3 + l1 + l2)= 0 l1 + l2 + l3 = 0
12 齿轮箱两个外伸轴上作用的力偶如图所示。为保持齿轮箱平衡,试求螺栓 A、B 处所提供的约束 力的铅垂分力。
FBy
FAy
解:ΣMi = 0, −500 + 125 + FAy × 0.5 = 0 FAy = 750N(↓) FBy = 750N(↑) (本题中 FAx ,FBx 等值反向,对力偶系合成结果无贡献。 ) 13 试求图示结构中杆 1、2、3 所受的力。 解:3 杆为二力杆 图(a) :ΣM = 0, F3 ⋅ d − M = 0
10 图示电动机固定在支架上,它受到自重 160N、轴上的力 120N 以及力偶矩为 25N·m 的力偶的作 用。试求此力系向点 A 简化的结果。
z
75
z
F1
A
r
75 25 200 75
y
x
F2
习题 10 图
M
(a)
解:由已知 F1 =160N,F2 =120N,F3 =25N·m F1 =(0, 0, -160)N F2 =(-120, 0, 0)N M =(25, 0, 0)N·m r =(0.075, 0.2, 0.025)m 向 A 点简化,得 FR = F1 + F2 =(-120, 0, -160)N M A = M + r × F1 + r × F2
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题

角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解:1.查型钢表得
习题 11-12 图
No.16aI:Iz = 1130cm4,Wz = 141cm3 2No. 63×63×5: A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用,欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以,轴不安全。
11-11 图示正方形桁架结构,由五根圆截面钢杆组成,
连接处均为铰链,各杆直径均为 d=40 mm,a=1 m。材料 均为 Q235 钢,E=200 GPa,[n]st=1.8。试;
网
ww w
.k hd 案
μ =1
co
界力。
m
11-5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论,试判断哪一种是正确 的。 (A)FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d); (B)FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d); (C)FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c);
案
对于 A3 钢, λ P = 102,
λs = 61.6 。因此,第一杆为大柔度杆,第二杆为中柔度杆,
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度

课
后 答
案
网
解:由挠度表查得:
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m,取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状,并说明需要分几段 建立微分方程,积分常数有几个,确定积分常数的条件是什么?(不要求详细解答)
习题 8-3 图
后 答
案
网
习题 8-4 图
课
习题 8-4a 解图
解: (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
(静力学与材料力学)
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
(教师用书)
−3 9 4
(
.k hd
解:由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8-9 图
8
aw .
)
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .
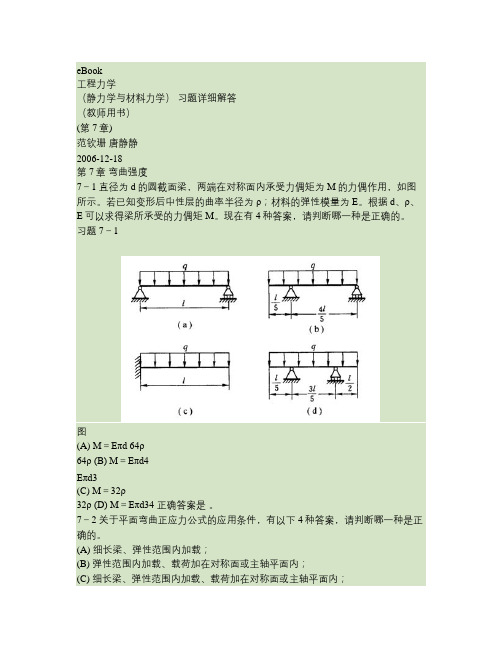
eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

解:1. 受力分析:由图(a)有
5 FP 3 4 4 ∑ Fx = 0 , F1 = − F3 = − FP 5 3
由图(b)由
2. 强度计算:
3m
F1
F3
F4
C
θ
B
F2
FP
F3
习题 5-7 图
(a)
(b)
∑ F y = 0 , F3 =
4 4 F3 = FP 5 3 5 ∑ F y = 0 , F2 = − F3 = − FP 3
5-4 螺旋压紧装置如图所示。现已知工件所受的压紧力为 F=4 kN。装置中旋紧螺栓 螺纹的内径 d1=13.8 mm;固定螺栓内径 d2=17.3 mm。两根螺栓材料相同,其许用应力 [σ ] =53.0 MPa。试校核各螺栓的强度是否安全。 解: ∑ M B = 0 ,FA = 2kN
∑ F y = 0 ,FB = 6kN
uB = 60 × 10 3 × 1.2 × 10 3 70 × 10 3 × 1.10 × 10 −3 × 10 6 = 0.935 mm
钢杆 C 端的位移为
FPlBC 60 ×103 × 2.1×103 uC = uB + = 0.935 + = 4.50mm π Es As 200 ×103 × ×152 4
解:当小车开到 A 点时,AB 杆的受力最大,此时轴力为 FNAB 。 (1) 受力分析,确定 AB 杆的轴力 FNAB ,受力图如图 5-12 解图所示, 由平衡方程
∑F
解得轴力大小为:
y
= 0,
0.8
FNAB sin α − FP = 0
sin α =
0.82 + 1.9 2
FNAB = 38.7kN
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第3章_静力学平衡问题

第3章 静力学平衡问题3-1 图a 、b 、c 所示结构中的折杆AB 以3种不同的方式支承。
假设3种情形下,作用在折杆AB 上的力偶的位置和方向都相同,力偶矩数值均为M 。
试求3种情形下支承处的约束力。
解:由习题3-1a 解图lM F F B A 2== 由习题3-1b 解图lM F F B A == 将习题3-1c 解1图改画成习题3-1c 解2图,则lM F F BD A ==习题3-1c 解2图)B习题3-1c 解1图B习题3-1b 解图习题3-1图B习题3-1a 解图'B A习题3-2解2图∴ l M F F BD B ==, lMF F BD D 22==3-2 图示的结构中,各构件的自重都略去不计。
在构件AB 上作用一力偶,其力偶矩数值M =800 N·m 。
试求支承A 和C 处的约束力。
解:BC 为二力构件,其受力图如习题3-2解1图所示。
考虑AB 平衡,由习题3-2解图,A 、B 二处的形成力偶与外加力偶平衡。
800269.4N 1.81.2A B M F F BD ′====3-3 图示的提升机构中,物体放在小台车C 上,小台车上装有A 、B 轮,可沿垂导轨ED 上下运动。
已知物体重2 kN 。
试求导轨对A 、B 轮的约束力。
解: W = 2kN ,T = W ΣF x = 0, F A = F BΣM i = 0, 0800300=×−×A F W ,kN 75.083==W FA ,FB = 0.75 kN ,方向如图示。
习题3-2图习题3-3图BF C习题3-2解1图 A F BF习题3-3解图MA习题3-4解1图3-4 结构的受力和尺寸如图所示,求:结构中杆1、2、3杆所受的力。
解:1、2、3杆均为为二力杆 由习题3-4解1图ΣM i = 0,03=−⋅M d F ,dMF =3, F = F 3(压) 由习题3-4解2图ΣF x = 0,F 2 = 0, ΣF y = 0,dMF F ==1(拉)3-5 为了测定飞机螺旋桨所受的空气阻力偶,可将飞机水平放置,其一轮搁置在地秤上。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 .

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第7章)范钦珊唐静静2006-12-18第7章弯曲强度7-1 直径为d的圆截面梁,两端在对称面内承受力偶矩为M的力偶作用,如图所示。
若已知变形后中性层的曲率半径为ρ;材料的弹性模量为E。
根据d、ρ、E可以求得梁所承受的力偶矩M。
现在有4种答案,请判断哪一种是正确的。
习题7-1图(A) M=Eπd 64ρ64ρ (B) M=Eπd4Eπd3(C) M=32ρ32ρ (D) M=Eπd34 正确答案是。
7-2 关于平面弯曲正应力公式的应用条件,有以下4种答案,请判断哪一种是正确的。
(A) 细长梁、弹性范围内加载;(B) 弹性范围内加载、载荷加在对称面或主轴平面内;(C) 细长梁、弹性范围内加载、载荷加在对称面或主轴平面内;(D) 细长梁、载荷加在对称面或主轴平面内。
正确答案是 C _。
7-3 长度相同、承受同样的均布载荷q作用的梁,有图中所示的4种支承方式,如果从梁的强度考虑,请判断哪一种支承方式最合理。
l 5习题7-3图正确答案是7-4 悬臂梁受力及截面尺寸如图所示。
图中的尺寸单位为mm。
求:梁的1-1截面上A、 2B两点的正应力。
习题7-4图解:1. 计算梁的1-1截面上的弯矩:M=−⎜1×10N×1m+600N/m×1m×2. 确定梁的1-1截面上A、B两点的正应力:A点:⎛⎝31m⎞=−1300N⋅m 2⎟⎠⎛150×10−3m⎞−20×10−3m⎟1300N⋅m×⎜2My⎝⎠×106Pa=2.54MPa(拉应力)σA=z=3Iz100×10-3m×150×10-3m()12B点:⎛0.150m⎞1300N⋅m×⎜−0.04m⎟My⎝2⎠=1.62×106Pa=1.62MPa(压应力)σB=z=3Iz0.1m×0.15m127-5 简支梁如图所示。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第4章_基本概念
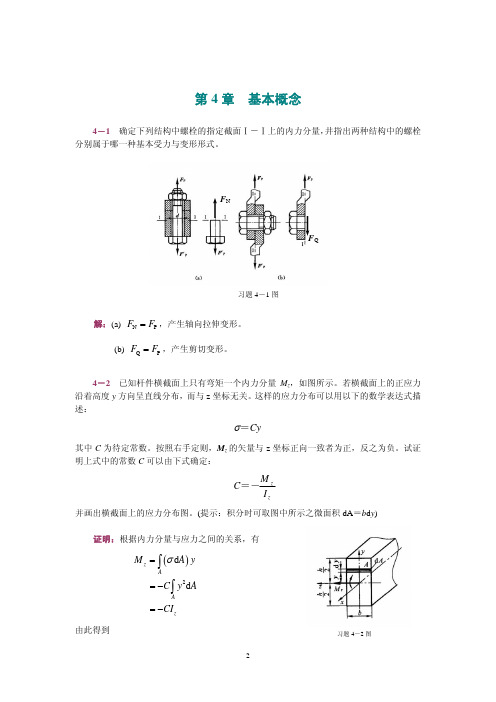
2习题4-2图第4章 基本概念4-1 确定下列结构中螺栓的指定截面Ⅰ-Ⅰ上的内力分量,井指出两种结构中的螺栓分别属于哪一种基本受力与变形形式。
解:(a) N P F F =,产生轴向拉伸变形。
(b) Q P F F =,产生剪切变形。
4-2 已知杆件横截面上只有弯矩一个内力分量M z ,如图所示。
若横截面上的正应力沿着高度y 方向呈直线分布,而与z 坐标无关。
这样的应力分布可以用以下的数学表达式描述:Cy =σ其中C 为待定常数。
按照右手定则,M z 的矢量与z 坐标正向一致者为正,反之为负。
试证明上式中的常数C 可以由下式确定:zzI M C =-并画出横截面上的应力分布图。
(提示:积分时可取图中所示之微面积dA =b d y )证明:根据内力分量与应力之间的关系,有()2d d z AAzM A yC y A CI σ==−=−∫∫由此得到习题4-1图F NF Q3习题4一3图zzI M C =-。
于是,横截面上的正应力表达式为:z zM yI σ−= 据此,可以画出横截面上的正应力分布图:4-3 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有4种答案,如图所示。
请根据弹性体横截面连续分布内力的合力必须与外力平衡这一特点,分析图示的4种答案中哪一种比较合理。
正确答案是 C 。
解:首先,从平衡的要求加以分析,横截面上的分布内力只能组成一个力偶与外加力偶矩M 平衡。
二答案(A )和(B )中的分布内力将合成一合力,而不是一力偶,所以是不正确的。
直杆在外力偶M 作用下将产生上面受拉、下面受压的变形。
根据变形协调要求,由拉伸变形到压缩变形,必须是连续变化的,因而,受拉与受压的材料之间必有一层材料不变形,这一层材料不受力。
因此,答案(D )也是不正确的。
正确的答案是(C )。
上一章 返回总目录 下一章。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第9章 应力状态与强度理论

τ max =
σ1 −σ 3
2
=
380 1 2 + 100 2 + 4τ xy < 160 4 4
解得 | τ xy | <120MPa
所以,取 | τ xy | <120MPa。 9- 6 图示外径为 300mm 的钢管由厚度为 8mm 的钢带沿 20°角的螺旋线卷曲焊接而
成。试求下列情形下,焊缝上沿焊缝方向的剪应力和垂直于焊缝方向的正应力。 1.只承受轴向载荷 FP = 250 kN; 2.只承受内压 p = 5.0MPa(两端封闭) *3.同时承受轴向载荷 FP = 250kN 和内压 p = 5.0MPa(两端封闭)
εt =
2 π ( r + Δ r ) − 2 πr Δ r = 2 πr r 1 Δr = ε t ⋅ r = [σ t −νσ m ] E 1 = (118.72 − 0.33 × 59.36 ) × 254 = 0.336mm 75 ×103
9- 8
构件中危险点的应力状态如图所示。 试选择合适的准则对以下两种情形作强度校
9- 7
承受内压的铝合金制的圆筒形薄壁容器如图所示。 已知内压 p = 3.5MPa, 材料
的 E = 75GPa, ν = 0.33。试求圆筒的半径改变量。
5
习题 9-7 图
解:
σm =
3.5 × (254 × 2 + 7.6) = 59.36 MPa 4 × 7.6 3.5 × (254 × 2 + 7.6) = 118.72 MPa σt = 2 × 7.6
σ r4 =
1 (100 2 + 20 2 + 120 2 ) = 111.4 MPa 2
2. σ =
工程力学课后习题答案_范钦珊(合订版)

C
BF
FB
FAx A
FAy
习题 1-3b 解 1 图
A FA
FB
α C
B
D
FD 习题 1-3d 解 1 图
D
F
C
F'c
B
FB
习题 1-3e 解 2 图
3
D
F
C
A
B
FA
FB
习题 1-3e 解 3 图
FO1 FOx O A
FOy
W
习题 1-3f 解 1 图
FA' FOx O A
FOy
W
习题 1-3f 解 2 图
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
图所示。对于给定的θ 角,试求平衡时的 β 角。
9
O
A
lθ
3
βG
2l
FRA
3
B G
θ
FRB
习题 1-13 图
习题 1-13 解图
解:AB 为三力汇交平衡,如图(a)所示ΔAOG 中:
AO = l sin β
∠AOG = 90° − θ ∠OAG = 90° − β
∠AGO = θ + β
l
由正弦定理: l sin β =
3
sin(θ + β ) sin(90° − θ )
= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sinϕ1
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转

该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6-5 图
解:1. τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2. M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3. τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
16 M x
3 π d1
=
16 M x
3 π D2 (1 − α 4 )
即
d1 = (1 − α 4 ) 3 D2
1
(a)
二者重量之比
W1 A1 d2 = = 2 1 2 W2 A2 D2 (1 − α )
(b)
式(a)代入式(b) ,得
W1 (1 − α 4 ) = W2 1−α2
2 3
所以,正确答案是
16 M x 3 16 × 10.53 × 10 6 = = 96.3 π [τ ] π × 60
(3)按刚度条件求轴的直径
θ=
Mx ≤ [θ ] GI P
[θ ] = 1D / 2m =
π
180 × 2 × 10 3
rad/mm
6
D≥4
32M x 32 × 10.53 × 10 6 =4 = 110.6mm Gπ [θ ] 82 × 10 3 π [θ ]
工程力学 第2版课后习题答案_范钦珊主编_第1章_静力学基础

工程力学第2版课后习题答案_范钦珊主编_第1章_静力学基础
1.静力学研究的对象是()
A、物体
B、流体
C、物质
D、刚体
2.两个大小为3N、4N的力合成一个力时,此合力最大值为()
A、5N
B、7N
C、12N
D、1N
3.在研究拉伸与压缩应力应变时,我们把杆件单位长度的绝对变形称为()
A、应力
B、线应变
C、变形
D、正应力
4.质点动力学基本方程为(D)
A、W=FS
B、P=MV
C、I=FT
D、F=ma
5.以下关于截面上内力的大小的结论哪一个是正确的?()
A、与截面的尺寸和形状无关
B、与截面的尺寸有关,但与截面的形状无关
C、与截面的尺寸和形状有关
D、与截面的形状有关,但与截面的尺寸无关
6.当作用在质点系上外力系的主矢在某坐标轴上的投影为零时,则质点系质心的()
A.速度一定为零
B.速度在该轴上的投影保持不变
C.加速度在该轴上的投影一定不为零
D.加速度在该轴上的投影保持不变
7.一空间力系中各力的作用线均平行于某一固定平面,而且该力系又为平衡力系,则可列独立平衡方程的个数是()
A.6个
B.5个
C.4个
D.3个
8.已知点的运动方程为x=2t3+4,y=3t3-3,则其轨迹方程为()
A.3x+4y-36=0
B.3x-2y-18=0
C.2x-2y-24=0
D.2x-4y-36=0。
工程力学(静力学与材料力学)范钦珊唐静静课后习题答案解析

= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sinϕ1
B 平衡: ∑ Fy = 0 , TB = 2 ⋅ sin ϕ 2
∵ TA = TB
10
(1)
(2) (3)
∴ sin ϕ1 = 2 sin ϕ 2 sin ϕ1 = 2 sin(114°35′ − ϕ1) ϕ1 = 84°44′
d =3
(2)
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2-2 解图
∴ F 点的坐标为(-3, 0) 合力方向如图所示,作用线过 B、F 点;
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
M A = FR × AG = FR × 4.8
FR
=
20 4.8
Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向,杆与水平面的夹角为 30°,碾子重量为 250 N。试比较这两种情形 下,碾子越过台阶所需力 F 的大小。
习题 1-10 图
(1) 油缸的受力图; (2) 活塞铆枪的受力图; (3) 铆钳的受力图。
6
习题 1-8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1-8 解图
1—9 安置塔器的竖起过程如图所示,下端搁在基础上,C 处系以钢绳,并用绞盘拉住; 上端在 B 处系以钢缆,通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW,试画出塔器 的受力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比较:图(a-1)与图(b-1)不同,因两者之1 - 3试画出图示各物体的受力图。
1 - 1图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方 F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
解:(a),图(c ):分力: 投影:=90 ° 时, (d ): F cos i 1 FX 1F y1 F sin F y1 F sinj l讨论:(b ),图F X 1 F cos投影与分力的模相等;分力是矢量, X 2投影是代数量。
F sinsin分力: j2BD(b)D(b-1)(a-3)投影: 工90°时, F X 2 F cos , 投影与分量的模不等。
讨论:1 -2试画出图a 、b 两情形下各物体的受力图,并进行比较。
F y2 F cos(F X 2 (F cos F sin tan )i 2 F y2(a)l F AyF A X1F RD 值大小也不同。
a5A■dFBFF CABB(a-1)(b-1)BC DBCBCWDAy或(b-2)(c-1)(d-1)DCABCDFt D或(d-2)(e-2)(e-1)CO iOyBFA(f-3)(e-3)IV2[fW(f-1)(c)习题1—3图F BF BF AxF AF DB FF cW(f-2)AOAF A力 F i 作用在,并加以讨论。
----------------- :B 铰上。
杆AB 不计自重,杆BD 杆自重为 W 。
试画出图1 —4图a 所示为三角架结构 b 、c 、d 所示的隔离体的受力图 A zz ” X Xzr 'i/A1rC[------------DF AxAB虾F 或(a_2)1 — 6图示刚性构件 ABC 由销钉A 和拉杆GH 支撑,在构件的点C 作用有一水平力F 。
试问如果将力 F 沿其作用线移至点 D 或点E (如图示),是否会改变销钉 A 的受力状况。
解:由受力图1 — 6a ,1 — 6b 和1 — 6c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力 F 在自身 刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为 HG 与ABC 为不同的刚体。
B F£1 - 5试画出图示结构中各杆的受力图。
习题1-5图EDA(a-1)CEtF(b-3)F AyF AX _FJ、/F E(a-2)(b-2)(a-3)(c)BAT161 -8图示压路碾子可以在推力或拉力作用下滚过 100mm 高的台阶。
假定力F 都是沿着连杆AB 的方向,与水平面成30°的夹角,碾子重为 250N 。
试比较这两种情形下所需力 F 的大小。
1 -9两种正方形结构所受力 F 均已知。
试分别求其中杆 1、2、3所受的力 解:图(a ): 2F 3COS45 F 01 -7试画出图示连续梁中的 AC 和CD 梁的受力图—HB-- +F AyFJ解:图(a ): 4arcsin5F XF sin(60 ) WsinF 1672 N图(b ): 53.13F X 0F cos( 30 ) Wsin F 217N(a)习题1 -8图2 亠 F3 — F (拉)2F 1 = F 3 (拉)F 2 2 F 3 cos45F 2 = F图(b ): F 3 F 30 F 1 = 0F 2 = F习题1 -7图cy(a)F AX AC F C X500(受压) (受拉)1 — 10图示为一绳索拔桩装置。
绳索的 E 、C 两点拴在架子上,点 B 与拴在桩A 上的绳索AB 连接, 在点D加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知 =O.lrad ,力F = 800N 。
试求绳ABA:F A =F B = M/22— 3bF A =F B = M /I 2-3CF A =F BD = M /l2-5中产生的拔桩力 (当 很小时, tan 〜 )。
解:F y 0, F ED sin FF ED FsinF x 0, F ED cosF DBF DB ----------10F2-3由图(a )计算结果。
可推出图(b )中 F AB = 10F DB = 100F = 80 kN* F DBF DB -a -n/(b)tanF EDBF ABF CBW = 2kN, T = W工Fx :=0,F A = F B工M i=0,W X300 --F A X800 = 0 , F A =3/8W=0.75 kN,F B = 0.75 kN. 2-6F3 ? d - M = 0 ,F 3 = M/d, F = F3 (压)工 F x ― 0, F2 ― 0,工 Fy = 0 ,F = F1= M/d (拉)2-7解:W/2=4.6 kNA F = 6.4-4.6 = 1.8 kN工 M i = 0, -M + A F?I = 0M= A F?I = 1.8 X 2.5 = 4.5 kN • m2-8M -2M2 dd 2对于图(b )中的结构,AB 为二力杆,CD 受力如习题3- 6b 解1图所示,根据力偶系 平衡的要求,由F RC FD M / dF RA F D ' M /d解:对于图(a )中的结构,CD 为二力杆,ADB 受力如图所示,根据力偶系平衡的要求, 由F RC解:BC 为二力构件,其受力图如图所示。
考虑 AB 平衡,A 、 偶平衡。
2-10M 2= M 12-9 1200 i I 缈BB 二处的形成力偶与外加力M BD800 1.2 、2 1.8/ 2269.4NF D FAM 1 dM 2 d2-11F By = F Ay = 0F Bx =M/dF RB = M /d (J)由对称性知F RA = M/ d (T )3-12M A =0, - M-F P X4+F RBX 3.5=0,-60-20M+F RB X 3.5=0,F RB =40kN (f) 牙y =0, F Ay +F RB -F P =0, F Ay =-20kN (J) 对于图b 中的梁,F艺F x =O , F =OM F p dM 0-Jqdg F p d F BR.2d F p1.3d 012qd F p 2F BR3F p10F BR21Fy O,F RA 15KN3-2解艺F x= 0, F Ax = 02F v = 0, F Ay = 0(f)2M A = 0, M A + M - Fd = 0 , M A = Fd - M3-3解:2M A (F) = 0 , -W X1.4 - F S X1+ F NB X 2.8 = 0 , F NB =13.6 kN2F y = 0, F NA = 6.4 kN3-4工 M B =0 , - F RA ?4h+T c Cosa?2h+Tc'sin a ?4h=0,F R A =(1/2+tan a )W (f)工 F y =0,F By=(1/2-ta n a)W (f)3-92F y = 0, F By =W +W i = 13.5 kN习M B = 0, 5F A - 1W -3W i = 0 , F A = 6.7 kN k)工 F x = 0, F Bx = 6.7 kN3-7图(a ),S F y = 0, 以整体为平衡对象:图(b ),S F x =0,T C =W / cos a (1)F BX =T C 'sin a =Wtan a解:以重物为平衡对象:解:以整体为平衡对象,有 工 M A = 0F RB 沦 X2.4COS 75° - 600 X1.8cos 75° -W(1.2 + 3.6) cos 75° = 0, F RB = 375 N工 F y = 0, F RA = 525 N 以BC 为平衡对象,有-T EF X1.8sin 75° -150X 1.2 cos75° + F RB X2.4 cos75° = 0T EF = 107 N3-11:以托架CFB 为平衡对象,有 工 F y = 0 , F By = F W2 ( 1 ) 以杠杆AOB 为平衡对象,有 工 M O = 0, F w ?|-F By ?a=0F w 〃F w2=a/l4-2图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合 理。
正确答案是_D_。
T EF Y5-1F/kN)丹(kN)■2C BA1AJ 「站ICI i°j习题4-2图1020£><kw>(d>解:(a)A截面:F Q =b/(a +b)F p, M=0C截面:F Q = b/(a +b) F P, M=ab/(a +b) F PD截面:F Q =- a/(a +b) F P, M=ab/(a +b) F PB截面:F Q =- a/(a +b) F P, M=0(b)WkN)5-4AJ.let If)A截面:F Q = M0/( a+b), M=0C截面:F Q=M0/(a+b),M=a/(a+b)M0D截面:F Q =- M o/( a+b), M=b/(a +b) M oB截面:F Q =- M o/( a+b), M=0(c)A截面:F Q =5/3 qa, M=0C截面:F Q =5/3 qa, M=7/6qa2B截面:F Q =-1/3 qa, M=0(d)A截面:F Q=1/2 ql , M=-3/8 qa2C截面:F Q=1/2 ql , M=-1/8 qa2□截面:F Q=1/2 ql , M=-1/8 qa2B截面:F Q =0, M=0(e)A截面:F Q =-2 F P, M=FPC截面:F Q =-2 F P, M=0B截面:F Q =FP,M=0(f)A截面:F Q =0, M= F P l/2C截面:F Q =0, M= F P 1/2□截面:F Q =- F P, M= F P l/2B截面:F Q =- FP,M=05-5(a)F Q ( x )=-M/2 l, M( x) =-M/2 l x ( 0 < x< l)F Q ( x ) =-M/2 l,M( x) =-Mx/2 l + M ( l< x < 2 l)F Q ( x )=-M/2 l,M( x)= -Mx/2 l + 3M(2 l < x < 3 l) F Q ( x )=-M2 l,M( x)= -Mx/2 l + 2M(3 l < x < 4 l)( b)F Q ( x ) = -(1/4)ql-qx , M( x) = ql2-(1/4)ql x -1/2)qx2( 0 < x < l)F Q ( x ) = -(1/4)ql, M( x) =(1/4)ql(2l- x) ( l < x < 2 l)(c)F Q ( x ) = ql-qx , M( x) = ql x + ql 2-(1/2)qx 2 F Q ( x ) = 0 , M( x) = ql 2 ( 2 l < x < 3 l)(d)F Q ( x) = (5/4) ql-qx, M( x) = (5/4) qlx-(1/2)qx 2 (0<x <2l)F Q ( x) =-ql + q(3 l-x) , M( x) = ql(3l-x) -1/2)q( 3l-x)2 (2 l <x < 3 l)(e)F Q ( x) = qx , M( x) =(1/2)qx 2(0 < x < l)F Q ( x) = ql-q( x-l) , M( x) = ql(x -1/2)-(1/2)q( x-l)2 ( l < x < 2 l)(f)F Q ( x) = -ql/2+ qx , M( x) = -(1/2)qlx +(1/2)qx 2( 0 < x < l)F Q ( x) =-ql/2+ q(2l-x) , M( x) = (ql/2)(2 l-x)-(1/2)q(2l-x)2( l < x < 2l)5-6画出5-5图示各梁的剪力图和弯矩图,并 确定〔F Q l max 、Mmax 。
