2012走美杯四年级真题
四年级走美杯大杂烩1

走美杯四年级大杂烩1计算 (1)计数 (1)数论 (2)几何 (2)应用题 (3)数字谜 (4)行程 (4)逻辑推理与杂题 (5)计算1. (第五届走美四年级初赛第1题)11353715____⨯-⨯=【解析】1135371511353735113511155(113111)10=⨯-⨯=⨯-⨯⨯=⨯-⨯=⨯-=原式2. (第六届走美四年级初赛第2题)(123200720082007321)2008+++⋯++++⋯+++÷=( )【解析】观察原式可知,1、2、3…2007分别可与2007、2006、2005…1组成2008,于是括号中有2008个2008,故原式结果为2008。
计数3. (第六届走美四年级初赛第8题/五年级初赛第12题)如右图所示,每个小正三角形边长为1,小虫每步走过1,从A 出发,恰走4步回到A 的路有( )条.(途中不再回A)解析:因为第一、三步到的点一定是以A为中心的六边形的六个顶点,根据一定的规则进行计数:(1)第一步与第三步是同一个点的情况有:6×5=30(种)(2)第一步与第三步不是同一个点的情况有:4×6=24(种)所以共有30+24=54(种)数论4.(第五届走美四年级初赛第6题)把100分拆成三个质数(只能被1和它本身整除且大于1的自然数叫做质数)的和,共有_____种方法。
解析:100是个偶数,拆成3个质数之和,而质数中除2以外,其他的都是奇数,3个奇数之和为奇数,所以其中必有2,现在知两个质数之和为98,则可拆成61+37、57+41、67+31、19+79。
所以共有4种方法。
5.(第六届走美四年级初赛第11题)10个各不相同的正整数排成一排.如果任何三个相邻的数和都大于20,这 10个正整数的和最小是 _______ .解析:任何三个相邻的数和都大于20可知:这10个各不相同正整数的最小和大于66,由构造法得这10个数是:1、5、15、2、6、13、3、7、11、4。
小学奥数杯赛真题1312

1.小泉做一道除数是一位数的除法时,误把除数9看成6,结果算出的商是7,余数是3。
你知道正确的结果是(2012世奥(中国区)选拔赛三年级A卷)2.杨阳是班里有名的小马虎,这次在做(200×9-□)÷25+13时,又没看到题里的括号,算的结果是1788,正确的结果应该是 (2012世奥数浙江赛区四年级)。
3.袋子里有若干个球,每次拿出其中的一半又一个球,这样共操作了4次,袋中还有5个球。
袋中原有____个球(2012年第十届走美杯三年级)。
4.盒子里有若干个球。
小明每次拿出盒中的一半再放回一个球。
这样共操作了7次,袋中还有3个球。
袋中原有个球(2010年走美杯三年级)。
5.抽屉里有若干个玻璃球, 小军每次操作都取出抽屉中球数的一半再放回一个球。
如此操作了2012次后, 抽屉里还剩有2个球。
那么原来抽屉里有个球(第十七届华杯赛小中组复赛)。
6.黑板上写有一个数,男同学从黑板前走过时,把他乘以3再减去14,擦去原数,换上答案,女同学从黑板前走过时,把他乘以2再减去7,擦去原数,换上答案。
全班25名男同学和15名女同学都走过后,老师把最后的数乘以5,减去5,结果是30。
那么,黑板上最初的数字是(湖北第七届创新杯)。
7.豆豆和苗苗各有一盒玻璃球,共108粒,豆豆给了苗苗10粒,豆豆剩下的玻璃比苗苗还多8粒。
原来苗苗有粒玻璃球(2010年第八届走美杯三年级)。
8.甲、乙、丙三人的平均年龄为42岁,若将甲的岁数增加7岁,乙的岁数扩大2倍,丙的岁数缩小2倍,则三人岁数相等。
丙的年龄为________岁(第四届迎春杯)。
9.甲、乙、丙、丁四人一共做了370个零件,如果把甲做的个数加上10个,乙做的个数减去20个,丙做的个数乘以2,丁做的个数除以2,四人做的零件数就正好相等。
那么乙实际做了_____ 个零件(第二届迎春杯)。
10.甲、乙、丙三所小学的学生人数的总和为1999。
已知甲校学生人数的2倍和乙校学生人数减去3人与丙校学生人数加上4人都相等。
走美杯孩子考试情况分析和试题分析

2012年走美杯孩子考试情况分析和试题分析2012年3月18日举行了2012年走美杯比赛,考试时间90分钟,试卷满分150分。
试题分布:1~5题各8分,6~10题各10分,11~15题各12分。
15道题目,孩子做了13道空了2道。
答案正确的: 3道(前五题)+3道(中间五题)+4道(后五题)=10道,得分102分。
答案错误的和没有作答的:2道(前五题)+2道(中间五题)+1道(后五题)=5道,这5道题目的题号是:3(空)、4(错)、6(错)、7(错)、12(空)。
做了13道对了10道,仅从正确率来看,孩子本次考试还是不错的。
错的题目中也有简单题目,例如数字迷那道题不是很难,做错了,但是同时也有不是难题孩子做出来了,例如年龄问题的第8题,五个数的数论问题的第10题都做对了,而且12分的5道题目做了4道都对了,有1道12题不会做。
从整体表现来看,孩子是值得表扬和肯定的。
从大家的反映情况来看,似乎比去年的题目要难,而且比前一天举行的华杯赛初赛和上周举行的希望杯初赛更要难上很多,从这个角度来看,孩子对于越难的题目得分越好,越简单的题目分数越不理想。
前一天参加的华杯赛初赛,10道题目满分100分(6道选择题4道填空题,每题10分),挺简单的,但是孩子只得了60分,选择题错了2个(第5、6题),填空题错了1个空着1个(第8题不会做),很多孩子满分或者八九十分。
前一周参加的希望杯初赛,20道题目满分120分(20道题全部是填空题,每题6分),更简单,但是孩子只得了83分,全对11道,部分对5道,全错4道(第18题已经算到最后一步56÷4了,计算错误得个16,这种错误多冤枉呀,不是不会而是不仔细呀),很多孩子超过了100分。
希望杯虽然进了复赛,但是也反映出来孩子的问题,希望孩子以后对于所有题目不管简单与否都能认真一些。
以下详细分析各道试题。
第1题,计算,等差数列,分组,难度级别:☆☆☆☆☆2012+2011+2010+……+1007-1006-1005-1004-……-1=________。
2012年走美决赛试卷(四年级)

第十届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛决赛注意事项:1.考生要按要求在密封线内填好考生的有关信息.总分2.不允许使用计算器.小学四年级试卷一、填空题Ⅰ(每题8分,共32分)1.算式2012×125×25×5×8的结果未尾有个零。
2.有50个苹果分别给甲、乙、丙三人,甲分的个数是乙的2倍,丙最少,但也不少于10个,丙分到个苹果。
3.去掉20.12中的小数点,得到的整数比原来的数增加了倍.4.小刚去买牛奶,发现牛奶本周特价,每袋0.9元,买二送一.小刚有5.4元,最多可以买袋奶.二、填空题Ⅱ(每题10分,共40分)5.写有1、2、3、4、5、6、7、8的八张卡片为一组。
每人从一组中抽2张,至少人抽过,才能保证有人抽的2张卡片上的数互质。
6.王伟的语文、数学的平均分是95分,英语、数学的平均分也是95分,他这3门课的平均分95分。
(填:大于、小于、等于或不一定)7.8.自然数N的所有数字互不相同,这些数字的乘积等于240。
N的最大值是9.如图,一个长方形,长增加2厘米,宽增加3厘米后,面积增加了44平方厘米,这时恰好成为一个正方形,原长方形的面积是平方厘米。
三、填空题Ⅲ(每题12分,共48分)10.汽车和自行车分别从A、B两地同时出发相向而行,汽车每小时行60千米,自行车每小时行12千米。
两车相遇后,各自仍沿原方向行驶,汽车到达B地后立即返回追上自行车源-于-网-络-收-集时距A地还有45千米。
A、B两地间的距离是千米。
11.两个长方形如图叠放,图上已标出一些线段的长。
EF= .12.下图的六条线分别连接着九个○,其中一个○里的数是7。
请选出九个连续自然数(包括7在内)填入○内,使每条线上各数之和都是23。
13.将下图中的正方形分割成形状和大小一样的四块,并且每一块恰好都有四种不同的图案。
在图中用不同的色笔把它们区分开。
源-于-网-络-收-集。
走美杯四年级试题及答案

第三届“走美杯”四年级初赛共12道题,每题10分。
1、33×34+34×35+35×36+36×37= 。
2、李东到商店买练习本,每本3角,共买9本,服务员问:“你有零钱吗?”李东说:“我带的全是5角一张的。
”服务员说:“真不巧,您没有2角一张的,我的零钱全是2角一张的,这怎么办?”你帮李东想一想,他至少应该给服务员张5角币。
3、幼儿园的老师给班里的小朋友送来40个橘子,200块饼干,120块奶糖,平均分发完毕,还剩4只橘子,20块饼干,12粒奶糖,这班里共有位小朋友。
4、有一家三口,爸爸比妈妈大3岁,他们全家今年的年龄加起来正好是58岁,而5年前他们全家人年龄加起来刚好是45岁,小孩子今年岁。
5、两个长方形如下图摆放,阴影三角形面积= 。
6、北京有一家餐馆,店号“天然居”里面有一副著名对联:客上天然居,居然天上客。
巧的很,这幅对联恰好能构成一个乘法算式(见右上图)相同的汉字代表相同的数字,不同的汉字代表不同的数字。
“天然居”表示成三位数是。
7、一个四位数给它加上小数点后比原来小2346.3,那么原四位数是。
8、用同样大小的木块堆成了如图所示的形状,这里共用了个木块。
9、下面图中有9个围棋子围成一圈,现将同色的相邻两子之间放入一个白子,在不同色的相邻两子间放入一个黑子,然后将原来的9个棋子拿掉,剩下新放入的9个棋子如右图,这算一次操作,如果继续这样操作下去,在一圈的9个子中最多有个是黑子。
10、在1999后面写一串数字,从第5个数字开始,每个数字都是它前面两个数字乘积的个位数字,这样得到1 9 8 9 2 8 6 8 4 2……,那么,这串数字中,前2005个数字的和是。
11、在下图的5×5方格表的空白处填入1~5中的数,使得每行、每列、每条对角线上的数各不相同。
2512、甲、乙二人轮流在右上图的10个方格中,甲画“○”,乙画“×”。
甲胜的情况是:最后一行有4个“○”或者其他的直线上有3个“○”;乙胜的情况是:最后一行有4个“ד或者其他的直线上有3个“×”,甲先画,他要取胜,第一步应填在标号为的方格中(至少写出2种)第四届“走美杯”四年级初赛共12题,每题10分1.计算:110+111+112+…+126=。
“走美”四年级选拔赛(二)
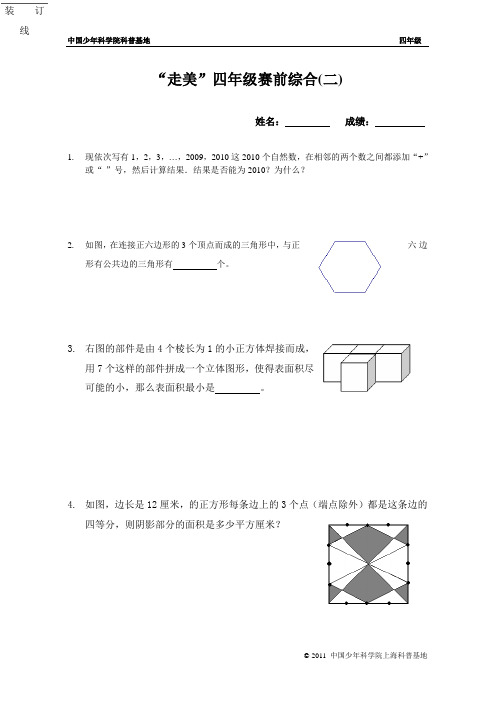
中国少年科学院科普基地 四年级“走美”四年级赛前综合(二)姓名: 成绩:1. 现依次写有1,2,3,…,2009,2010这2010个自然数,在相邻的两个数之间都添加“+”或“-”号,然后计算结果.结果是否能为2010?为什么?2. 如图,在连接正六边形的3个顶点而成的三角形中,与正六边形有公共边的三角形有 个。
3. 右图的部件是由4个棱长为1的小正方体焊接而成,用7个这样的部件拼成一个立体图形,使得表面积尽可能的小,那么表面积最小是 。
4. 如图,边长是12厘米,的正方形每条边上的3个点(端点除外)都是这条边的四等分,则阴影部分的面积是多少平方厘米?装订线5.如图,直角三角形ABC由红、绿两个直角三角形和一个黄色的长方形拼成,AE=25cm,BF=20cm。
问:黄色长方形的面积是多少平方厘米?6.若今天是星期六,从今天起102000天后的那一天是星期几?7.有四个互不相同的自然数,最大的数与最小的数之差是4,最大数与最小数之积是奇数,而这四个数的和是最小的两位奇数,则这四个数的乘积是。
8.22221012222-+++- =--561+4100329.2010×0.25-210÷4=________10.22010+32010的个位数字是几?11.如图,在右图的每个方框中填入一个1~6的数字,使算式成立。
12.六位数2003□□能被99整除,它的最后两位数是______________ 。
13.设五位数2X36Y能被315整除,其中X与Y分别是千位与个位上的数字,则该五位数是多少?14.ab是一个两位数。
若这个两位数的平方,其值的尾后两个数字仍是ab,问这个两位数最大是多少?15.某个三位数ABC与它的反序数CBA相乘,得到的积是2002的倍数,请将答案填入()中。
ABC×CBA=2002×()16.包含0,1,2,…,9十个数字的十位数称为“十全数”。
年第七届走美杯四年级初赛试题及答案

第七届“走进美妙的数学花园”初赛四年级试题解答一、填空题(每题8分,共40分)1、37×37+2×63×37+63×63=_10000_____2、下边的一排方格中,除9、8外,每个方格中的字都表示一个数(不同的字可以表示相同的数字),已22,则“走”+“进”+“数”+“学”+“花”+“园”=_40_3、“走美”商场有下列几种瓶装蜂蜜出售:甲,净重3kg,售价33.99元;乙,净重2kg,售价22.99元;丙,净重500g,售价5.99元,那么,_丙____种蜂蜜最贵, __甲___种蜂蜜最便宜。
4.一个数学玩具的包装盒是正方体,其表面展开图如下。
现在每方格内都填上相应的数字。
已知将这个表面展开图沿虚线折成正方体后,相对面的两数之和为“3”,则填在A、B、C内的三个数字依次是_3,1,2___。
5、某品牌乒乓球拍在北京奥运会后推出一款球拍的促销计划:该球拍每只售价为人民币60元,同时购买者可获赠1张奖券,积累3张奖券可兑换1只球拍。
由此可见,1张奖券价值为__15__元。
二、填空题(第题10分,共50分)6、(09年走美三、四、五年级都考)A,B都是整数,A大于B,且A×B=2009,那么A-B的最大值为_2008___,最小值为__8___。
7、(09年走美三、四、五年级都考)一天,红太狼和灰太狼同时从“野猪林”出发,到“天堂镇”。
红太狼一半路程溜达,一半路程奔跑。
灰太狼一半时间溜达,一半时间奔跑。
如果它们溜达的速度相同,奔跑的速度也相同,则先到“天堂镇”是_灰太狼______。
8、柯南家2008年一年用电10200千瓦时,上半年的月平均用电比下半年的月平均用电少100千瓦时。
柯南家下半年月平均用电为__900_____千瓦时。
9、某校A、B、C三名同学参加“走进美妙的数学花园”,其指导教师赛前预测“A获金牌,B不会获金牌,C不会获铜牌”。
结果出来后,三人之中,一人获金牌,一人获银牌,一人获铜牌,指导教师的预测只有一个人与结果相符。
四年级走美自测题 教师版

四年级走美杯自测卷填空题Ⅰ(每题8分,共40分)1、2000年后为三个连续自然数乘积的第一个年份是 。
【解析】:11×12×13=1716,12×13×14=2184。
2、将正整数1,2,3,4,5,6,…,10000排成一行。
若一个数不能表示成两个合数的和,则将此数划去。
例如要划去1,但是因为8=4+4,8就不能划去。
根据上面规定划掉所有能划掉的数之后,将剩下的由小到达排列,这时从左数第2016个数是 。
【解析】:从8开始往后的偶数可以拆成两个偶合数的和;从13开始的奇数可以拆成9+2n 的形式(n 大于等于2),而1、2、3、4、5、6、7、9、11要划去,所以剩下的数列为8、10、12、13、14、15……,第2016项即为2025。
3、图中共有 个三角形。
【解析】:①由1个小三角形构成的三角形有24个;②由2个小三角形构成的三角形有20个;③由3个小三角形构成的三角形有8个;④由4个小三角形构成的三角形有8个;⑤由5个小三角形构成的三角形有4个;⑥由6个小三角形构成的三角形有4个;⑦由7个小三角形构成的三角形有4个;所以图中共有三角形24+20+8+8+4+4+4=72个。
4、四位数abcd 与cdab 的和为3636,差为396,那么四位数abcd 为 。
【解析】:100abcd ab cd =+,100cdab cd ab =+。
当ab cd >时: ()1001003636100100396ab cd cd ab ab cd cd ab ⎧+++=⎪⎨+-+=⎪⎩ 整理得36ab cd +=,4ab cd -=,所以20ab =,16cd =,2016abcd =。
同理,ab cd <时,1620abcd =。
5、A、B、C、D四个箱子中分别装有一些小球,现将A箱中的部分小球按如下要求转移到其他三个箱子中:该箱中原有几个小球,就再放入几个小球,此后,按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中,此时,四个箱子都各有16个小球,那么开始时装有小球最多的是______箱,其中装有______小球个。
2024年走美杯数学竞赛详细解析-四年级卷

2024“走进美妙的数学花园”π数学趣味闯关活动注意事项:1.请在密封线内填好有关信息.2.不允许使用手机、计算器等电子设备.小学四年级填空题Ⅰ(每题8分,共32分)1.计算:1−(25+0.5)=.解:25=2/5=0.4,原式=1-(0.4+0.5)=1-0.9=0.12.有4个自然数(允许有相等的),从其中任意选取3个数求和,可以而且只能得到23,24,25.那么,原来的4解:由于23,24,25是等差数列,可以得到24/3=8,所以4个自然数中必有8且也是一个等差数列,最终可得7,8,8,9。
验算:7+8+8=23,8+8+9=25,7+8+9=243.能够被1到12的所有自然数整除的最小自然数为解:最小公倍数问题。
1-12之间,质数2,3,5,7,11没有公因数,4,8,12是2的倍数,6,9,12是3的倍数,10是5的倍数,所以最小公倍数为2x 3x 5x 7x 11x 2x 2x 3=277204.满足被6除余2,被9除余5,并且小于100解:分别求符合2个条件的数,找相同数被6除余2:8,14,20,26,32,38,44,50,56,62,68,74,80,86,92被9除余5:14,23,32,41,50,59,68,77,86,95填空题Ⅱ(每题10分,共40分)5.用宽为210毫米,长为297毫米规格的地砖,按照长与宽的方向保持一致的方总分式铺成一块正方形地面,这样铺成的正方形中,面积最小的正方形的边长为.解:求两数最小公倍数,如图210*2976.两本书的正文页码用从1开始的连续自然数标记,共用了(数码),如果第一本书正文比第二本书多5..解:数码问题。
1-9页所用数码总数:1*9=910-99页所用数码总数:90*2=180100-999页所用数码总数:3*901=2703180<705<2703,所以两本书都<999页,多出的5页每页是3位数第二本书总共页码数:(705-5*3)/2=345第二本的3位页码数:(345-180-9)/3=52第二本书总页数:99+52=151页7.用5个边长为单位长度的小正方形(单位正方形)可以构成如下图所示的5-联方(在中国又称为伤脑筋十二块).在西方国家,人们用形象的拉丁字母来标记每一个5-联方.请将具有中心对称性质的5-联方找出来,并将对应的拉丁字解:中心对称是指把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称。
2012年下期四年级美术期末试卷

2012年下期四年级美术期末试卷
班级姓名
1、书籍的封面一般是由、和出版社名称等
组成。
2、、、一起被称为“染缬”工艺,
是我国传统的民间工艺。
3、在没有发明钟表以前,人们是依靠日晷和来记录时间的。
4、依靠蔬菜、瓜果的、色泽、纹理和可以给
我们带来丰富的联想,创作出生动的蔬果作品。
5、剪纸是我国民间传统装饰艺术,它的制作工艺主要有有
和两种形式。
6、泥板造型的方法有、、、挖、粘等。
7、中国画中所用的红色是源自一种叫的矿石。
8、请设计并绘画一门你喜欢的课程标志,记得画上漂亮的颜色哦!。
第三届四年级走美杯的答案与解析

源-于-网-络-收-集第三届走进美妙的数学花园 四年级共12道题,每题10分。
1. 33×34+34×35+35×36+36×37= 4904 。
分析:33×43可以看成33×35-33,36×37可以看成35×37+37,所以整个式子可以看成33×35-33+34×35+35×36+35×37+37,利用乘法交换律和结合律,可以将式子再改写成35×(33+34+36+37)-33+37=35×140+4=35×2×70+4=70×70+4=4900+4=4904解答:33×34+34×35+35×36+36×37=33×35-33+34×35+35×36+35×37+37=35×(33+34+36+37)-33+37=35×140+4=35×2×70+4=70×70+4=4900+4=49042.李东到商店买练习本,每本3角,共买9本,服务员问:“你有零钱吗?”李东说:“我带的全是5角一张的。
”服务员说:“真不巧,您没有2角一张的,我的零钱全是2角一张的,这怎么办?”你帮李东想一想,他至少应该给服务员 7 张5角币。
分析:李华要付的钱为27加上服务员找回的钱,李东一共买了9本单价为3角的练习本,所以应付的钱为9×3角,即27角;服务员找的钱是有2角一张的纸币构成,所以找的钱为偶数,而奇数加偶数的和为奇数,所以李华要付的钱为奇数,比27大且最靠近27并能被5整除的奇数,是35,35÷5=7,所以李华要给服务员7张5角币。
解答:35÷5=7(张)答:给服务员7张5角币。
3.幼儿园的老师给班里的小朋友送来40个橘子,200块饼干,120块奶糖,平均分发完毕,还剩4只橘子,20块饼干,12粒奶糖,这班里共有 36 位小朋友。
走美杯四年级试题及答案

走美杯四年级试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正确的?A. 地球是平的B. 太阳是宇宙的中心C. 地球围绕太阳转D. 月亮是地球的卫星答案:C2. 哪个国家被称为“千岛之国”?A. 中国B. 日本C. 印度尼西亚D. 印度答案:C3. 下列哪个选项是数学中的“奇数”?A. 2B. 4C. 5D. 8答案:C4. 以下哪种动物是哺乳动物?A. 蛇B. 鳄鱼C. 鲸鱼D. 乌龟答案:C5. 世界上最高的山峰是?A. 珠穆朗玛峰B. 乞力马扎罗山C. 富士山D. 阿尔卑斯山答案:A二、填空题(每题2分,共10分)1. 一年有______个季节。
答案:四2. 地球上最大的陆地动物是______。
答案:非洲象3. 光年是长度单位,表示光在一年内通过的距离,大约是______公里。
答案:9.46万亿4. 人体最大的器官是______。
答案:皮肤5. 世界上最大的海洋是______。
答案:太平洋三、简答题(每题5分,共20分)1. 简述地球的自转和公转。
答案:地球的自转是指地球围绕自己的轴线旋转,周期约为24小时,导致了昼夜交替。
地球的公转是指地球围绕太阳的轨道运动,周期约为365.25天,导致了季节更替。
2. 请解释什么是生态系统。
答案:生态系统是由生物群落和其所在的非生物环境相互作用而形成的一个统一整体,包括了生产者、消费者和分解者等生物组成部分以及水、土壤、空气等非生物组成部分。
3. 请列举三种常见的哺乳动物。
答案:猫、狗、牛4. 描述一下水循环的过程。
答案:水循环是指地球上水分子在大气、陆地和海洋之间不断循环的过程,包括蒸发、凝结、降水和径流等环节。
四、计算题(每题10分,共20分)1. 如果一个长方形的长是8米,宽是5米,求其面积。
答案:面积 = 长× 宽 = 8米× 5米 = 40平方米2. 一个班级有40名学生,如果每名学生需要2本练习册,那么总共需要多少本练习册?答案:总练习册数 = 学生数× 每人练习册数= 40 × 2 = 80本五、阅读理解题(每题5分,共10分)阅读以下短文,回答后面的问题。
走美杯试题汇总及答案

走美杯试题汇总及答案一、选择题1. 甲、乙、丙三人分别从A、B、C三个地方同时出发,向同一个目的地D出发,他们的速度比为3:2:1。
如果甲到达D地后立即返回,在距离D地4千米的地方遇到乙,那么A、B两地之间的距离是多少千米?A. 24B. 28C. 36D. 40答案:C解析:设A、B两地之间的距离为x千米,甲、乙、丙的速度分别为3v、2v、v。
甲到达D地后返回,与乙相遇时,甲乙两人共行了2x+4千米。
根据速度比,甲乙相遇时,甲行了3/2 * (2x+4)千米,乙行了2/2 * (2x+4)千米。
由于甲乙速度比为3:2,所以有3/2 * (2x+4) = 3x,解得x=36。
2. 一个自然数N,如果它加上101后是一个完全平方数,那么N的最大值是多少?A. 990B. 999C. 1009D. 9801答案:B解析:设N+101=a^2,其中a为自然数。
要使N最大,a应尽可能大。
由于a^2-101=N,所以a^2应尽可能接近101的下一个完全平方数,即121。
因此,a=11,N=121-101=20。
但题目要求N的最大值,所以应取a=10,此时N=10^2-101=99。
但99不是选项,因此应取a=9,此时N=9^2-101=80,也不是选项。
最后取a=8,此时N=8^2-101=-3,显然不符合题意。
因此,应取a=10,此时N=999,是选项中的最大值。
3. 一个长方体的长、宽、高分别为a、b、c,且a、b、c均为正整数。
如果长方体的体积是2010,那么a+b+c的最小值是多少?A. 14B. 15C. 16D. 17答案:B解析:2010=2×3×5×67,要使a+b+c最小,应尽量使a、b、c的值接近。
因此,可取a=2×3=6,b=5,c=67,此时a+b+c=6+5+67=78。
但题目要求a+b+c的最小值,因此应取a=2,b=3×5=15,c=67,此时a+b+c=2+15+67=84。
全国小学生英语竞赛(四年级组)2012年决赛试题及详解【圣才出品】

全国小学生英语竞赛(四年级组)2012年决赛试题及详解听力部分(共四大题,计30分)I.听辨单词(Words)(共5小题,计5分)听音,选出你所听到的单词。
每个单词读两遍。
B.putC.but【答案】B【解析】三个选项中单词的发音分别为:us[ʌs](我们),put[pʊt](放),but[bət](但是),录音中出现的单词为put,因此答案选B。
【录音原文】put2.A.moreB.doorC.bore【答案】A【解析】三个选项中单词的发音分别为:more[mɔ:(r)](更多的),door[dɔ:(r)](门),bore[bɔ:(r)](使烦扰),录音中出现的单词为more,因此答案选A。
【录音原文】more3.A.boardB.horseC.about【答案】C【解析】三个选项中单词的发音分别为:board[bɔːd](木板;董事会),horse[hɔːs](马),about[ə’baʊt](关于;大约),录音中出现的单词为about,因此答案选C。
【录音原文】about4.A.backB.blackC.band【答案】B【解析】三个选项中单词的发音分别为:back[bæk](后面;背部),black[blæk](黑色),band[bænd](带子;乐队),录音中出现的单词为black,因此答案选B。
【录音原文】black5.A.knowB.boxC.nose【答案】C【解析】三个选项中单词的发音分别为:know[nəʊ](了解,熟悉),box[bɒks](盒子),nose[nəʊz](鼻子),录音中出现的单词为nose,因此答案选C。
【录音原文】noseII.句子理解(Sentences)(共10小题,计10分)A)听音,选出与你所听句子内容相符的图片。
每个句子读两遍。
6.A.B.C.【答案】B【解析】录音中问到,你是否能告诉我去银行(bank)怎么走,结合所给图片,可知答案是B项。
05年第三届至13年第十一届走美杯试题答案 (1)

目录第三届“走美杯”答案 (2)第四届“走美杯”答案 (3)第五届“走美杯”答案 (4)第六届走美杯三年级初赛试题参考答案 (6)第六届走美杯三年级决赛试题参考答案 (9)第七届走美杯三年级初赛试题参考答案 (10)第八届走美杯三年级初赛试题参考答案 (11)第九届走美杯三年级A卷初赛试题参考答案 (13)第十届走美杯三年级B卷试题及答案详解 (14)第三届走美杯四年级试题参考答案 (18)第四届走美杯四年级试题参考答案 (19)第六届走美杯四年级初赛试题参考答案 (20)第六届走美杯四年级决赛试题参考答案 (24)第七届走美杯四年级初赛试题参考答案 (24)第八届走美杯四年级初赛试题参考答案 (25)第九届走美杯四年级A卷初赛参考答案 (27)第九届走美杯四年级B卷初赛参考答案 (28)第三届走美杯五年级试题参考答案 (33)第四届走美杯五年级试题参考答案 (34)第五届走美杯五年级初赛试题参考答案 (35)第六届走美杯五年级初赛试题参考答案 (39)第六届走美杯五年级决赛试题参考答案 (42)第七届走美杯五年级初赛试题参考答案 (43)第八届走美杯五年级初赛试题参考答案 (46)第九届走美杯五年级初赛试题参考答案 (48)第九届走美杯五年级B卷初赛试题参考答案 (52)第三届走美杯六年级试题参考答案 (52)第四届走美杯六年级试题参考答案 (53)第五届走美杯六年级试题参考答案 (54)第六届走美杯六年级决赛试题参考答案 (58)第七届走美杯六年级初赛试题参考答案 (59)第八届走美杯六年级初赛试题参考答案 (62)第九届走美杯六年级A卷初赛试题参考答案 (65)第十届2012走美杯六年级试题及答案详 (66)第六届走美杯三年级初赛试题参考答案1.22222.861;574;5733.604.155.4;36.90÷15=34-28=67.10;28.169.22210.3711.略12.361.【答案】100012.【答案】100003.【答案】404.【答案】11705.【答案】MT79366.【答案】2008;87.【答案】38.【答案】49.【答案】灰太狼10.【答案】711.【答案】105 ;312.【答案】7; 213.【答案】55;540 14.【答案】4或315.【答案】1、2 、4 、8 .第八届走美杯三年级初赛试题参考答案第九届走美杯三年级A卷初赛试题参考答案第十届走美杯三年级B卷试题及答案详解1、49042、73、364、35、46、9787、2607或23708、509、810、1203111、12、5,2,6 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2第六届走美杯四年级初赛试题参考答案1.20082.64;15625(64×15625)3.2或54.155.906.200000077.168.1;2;2;39.5610.3011.147张,15块12.2100第七届走美杯四年级初赛试题参考答案1. 100002. 403. 丙;甲4. 3 、1 、25. 156. 2008;87. 灰太狼8. 9009. C.10. 1011. 55;54012. 413. 2614.55 ;259平方厘米15.21、555502、1043、254、445、19;5176、97、388、79、100010、126311、6412、328213、814、415、1176答案:1、2010012 2、19 3、0。
小学美术奥林匹克竞赛试题及答案(四年级)

小学美术奥林匹克竞赛试题及答案(四年
级)
试题一
题目描述:
请你绘制一幅你最喜欢的动物的画,并用颜色给它上色。
答案:
以下是一种可能的回答:

试题二
题目描述:
请你用线条勾勒出一个水果篮子,并根据你的想象给它上色。
答案:
以下是一种可能的回答:

试题三
题目描述:
请你用不同的形状拼出一个家的图案,并用彩色填充。
答案:
以下是一种可能的回答:

试题四
题目描述:
请你选择一个喜欢的名人或角色,用线条画出他/她的形象,并尽量用色彩丰富的颜料给他/她上色。
答案:
以下是一种可能的回答:

试题五
题目描述:
请你根据给出的植物图片,尝试用几种不同的颜色绘制出它的样子。
答案:
以下是一种可能的回答:

以上是小学美术奥林匹克竞赛四年级的试题及答案。
希望你能够享受绘画的过程,展示你的创意和想象力!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题Ⅰ(每题8分,共40分)
1.2012+2011+2010+……+1007-1006-1005-1004-……-1=__________。
2.某年7月恰有4个星期一和四个星期四,这月的15号是星期________。
3.从正整数1~N中去掉一个数,剩下的N~1个数的平均值是16.3;去掉的数是_______。
4.葛大财主请园艺师为其整修花园,要求一个月完成,3月1日开始31日结束,每天的工钱为一钱黄金。
葛大财主是出了名的守财奴,园艺师要求每天结束时结算工钱,葛大财主恰有一块31钱的金条。
聪明绝顶的葛大财主只做了______次(填最少次数)切割,就解决了这个问题。
5.在台球“斯诺克”比赛中,有红球15个,黄、绿、棕、蓝、粉、黑球各一个,其中红球落袋积1分,黄、绿、棕、蓝、粉、黑球落袋分别积2、3、4、5、6、7分。
比赛中,第一阶段先要将15个红球全击落袋,而每击落1个红球后必须再击落1个其他颜色的球,红球落袋不拿回,而其它颜色球在此阶段被击落袋后再放回台面;第二阶段要按黄、绿、棕、蓝、粉、黑的顺序依次将这些球击落袋。
那么,“斯诺克”比赛中最高能得______分。
二、填空题Ⅱ(每题10分,共50分)
6.小华需要构造一个3×3的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x等于______。
7.十进制下的三位数TWO和四位数FOUR满足:TWO+TWO=FOUR,其中不同的字母代表不同的数字,FOUR的最小可能的值是______。
8.今年,丹丹和父亲、母亲和弟弟的年龄和是120岁。
当父亲的年龄是丹丹年龄的3倍时,母亲的年龄恰好也是弟弟年龄的3倍,当时弟弟12岁。
那么丹丹今年______岁。
二、填空题Ⅱ(每题10分,共50分)
9.玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种。
单筒玉米炮每次发射1根玉米,可以消灭20个僵尸;双筒玉米炮每次发射2根玉米,每根玉米消灭17个僵尸,三筒玉米炮每次发射3根玉米,每根消灭16个僵尸。
玉米炮一共开炮10次,发射23根玉米,消灭______个僵尸。
10.有五个互不相等的非零自然数。
如果其中一个减少45,另外四个数都变成原先的2倍,那么得到的
仍然是这五个数。
这五个数的总和是______。
11.如图,大正六边形的面积是24平方厘米,其中放了三个一样的小正六边形。
阴影面积是_____平方厘米。
12.甲、乙、丙三人同时同向骑车,各自的速度都保持不变,乙在甲、丙的正中间。
甲20分钟追上乙,又过10分钟追上丙。
再过______分钟乙追上丙。
三、填空题Ⅲ(每题12分,共60分)
13.六位数2□012□个为上填_______时,万位上无论填入0~9中哪一个数,都不能被11整除。
14.1个4×4的棋盘,在每个小方格上染上黑白两色之一,染法与国际象棋盘的染法相同。
允许任意选择一个矩形(矩形的边都在格子上),被选中的矩形中的内个小正方格改变颜色(黑变白,白变黑)。
至少需要______次上述操作,才能使棋盘上的格子都同色。
15.将一个5×5×5的正方体分割成若干个3×3×3,2×2×2和1×1×1的小正方体。
1×1×1的小正方体最少有________个。
