(完整版)两倍角与半角公式与万能公式.doc
两倍角与半角公式与万能公式

两倍角与半角公式与万能公式
两倍角公式:
1. 正弦函数的两倍角公式:sin(2θ) = 2sinθcosθ
2. 余弦函数的两倍角公式:cos(2θ) = cos^2θ - sin^2θ =
2cos^2θ - 1 = 1 - 2sin^2θ
3. 正切函数的两倍角公式:tan(2θ) = 2tanθ / (1 - tan^2θ)半角公式:
1. 正弦函数的半角公式:sin(θ/2) = ±√((1 - cosθ)/2)
2. 余弦函数的半角公式:cos(θ/2) = ±√((1 + cosθ)/2)
3. 正切函数的半角公式:tan(θ/2) = ±√((1 - cosθ) / (1 + cosθ))
万能公式(辅助角公式):
1. sin(A ± B) = sinAcosB ± cosAsinB
2. cos(A ± B) = cosAcosB ∓ sinAsinB
3. tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)
这些公式在解决三角函数问题时非常有用,可以帮助化简表达式、求解特殊角度的值、结合其他角度等。
使用这些公式时,需要注意角度的范围、符号以及对应的关系,可以灵活运用来简化计算过程。
同时,需要注意避免混淆正负号以及其他基本运算的错误。
倍角公式和半角公式口诀

倍角公式和半角公式口诀倍角公式口诀:正弦二倍,正负取决;余弦二倍,正负不同;正切二倍,正负相同;余切二倍,正负取决。
半角公式口诀:正弦半角,加减号;余弦半角,加减号;正切半角,加减号;余切半角,加减号。
正文:在三角函数中,倍角公式和半角公式是非常重要的公式之一。
它们可以帮助我们简化复杂的三角函数表达式,从而更方便地进行计算和推导。
下面我们将分别介绍倍角公式和半角公式的口诀,并举例说明其应用。
倍角公式口诀是一种简单易记的口诀,可以帮助我们快速记忆倍角公式的变化规律。
首先我们来看倍角公式口诀:正弦二倍,正负取决;余弦二倍,正负不同;正切二倍,正负相同;余切二倍,正负取决。
这个口诀告诉我们,在倍角公式中,正弦和余切的正负取决于原角的正负,而余弦和正切的正负则与原角的正负相反。
这个口诀的记忆方式非常简单直观,让人很容易就能记住倍角公式的正负变化规律。
接下来我们通过一个具体的例子来说明倍角公式的应用。
假设我们需要计算sin(2x)的值,其中x是一个已知的角度。
根据倍角公式sin(2x) = 2sin(x)cos(x),我们可以利用已知角度x的正弦值和余弦值来求得sin(2x)的值,而无需直接求解sin(2x)的正弦值。
这样一来,我们可以大大简化计算的复杂度,提高计算效率。
接下来我们来看半角公式口诀:正弦半角,加减号;余弦半角,加减号;正切半角,加减号;余切半角,加减号。
这个口诀告诉我们,在半角公式中,正弦、余弦、正切和余切的正负变化规律。
根据这个口诀,我们可以很容易地记住半角公式的正负变化规律,从而在实际计算中更加得心应手。
接下来我们通过一个具体的例子来说明半角公式的应用。
假设我们需要计算sin(x/2)的值,其中x是一个已知的角度。
根据半角公式sin(x/2) = ±√[(1-cos(x))/2],我们可以利用已知角度x的余弦值来求得sin(x/2)的值,而无需直接求解sin(x/2)的正弦值。
高中必背数学公式有哪些

高中必背数学公式有哪些高中必背的数学公式(一)两角和公式1、sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA2、cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB3、tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)4、ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)(二)倍角公式1、cos2A=cos2A-sin2A=2cos2A-1=1-2sin2A2、tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgA(三)半角公式1、sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)2、cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)3、tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))4、ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))(四)和差化积1、2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2、2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)3、sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)4、tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB5、ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB(五)几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)高中必背的圆的公式(一)圆的公式1、圆体积=4/3(pi)(r^3)2、面积=(pi)(r^2)3、周长=2(pi)r4、圆的标准方程(x-a)2+(y-b)2=r2【(a,b)是圆心坐标】5、圆的一般方程x2+y2+dx+ey+f=0【d2+e2-4f0】(二)椭圆公式1、椭圆周长公式:l=2πb+4(a-b)2、椭圆周长定理:椭圆的周长等于该椭圆短半轴,长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差3、椭圆面积公式:s=πab4、椭圆面积定理:椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积高考数学答题的技巧是什么1、首先是精选题目,做到少而精。
三角函数的半角与二倍角公式

三角函数的半角与二倍角公式三角函数是数学中常见的一类函数,包括正弦函数、余弦函数和正切函数等。
在求解三角函数值时,我们常常会遇到半角和二倍角的情况。
为了简化计算,在三角学中引入了半角与二倍角公式,能够帮助我们快速求解。
一、正弦函数的半角与二倍角公式1. 正弦函数的半角公式正弦函数的半角公式可以用来计算一个角的一半的正弦值。
假设原角为α,则其一半的角为α/2。
正弦函数的半角公式如下:sin(α/2) = ±√[(1 - cosα)/2]其中,α/2为角的半角,cosα为原角的余弦值。
公式中的±表示结果的正负与角度所在象限相关。
2. 正弦函数的二倍角公式正弦函数的二倍角公式可以用来计算一个角的两倍的正弦值。
假设原角为α,则其两倍的角为2α。
正弦函数的二倍角公式如下:sin2α = 2sinαcosα其中,2α为角的两倍,sinα和cosα分别为原角的正弦值和余弦值。
二、余弦函数的半角与二倍角公式1. 余弦函数的半角公式角为α,则其一半的角为α/2。
余弦函数的半角公式如下:cos(α/2) = ±√[(1 + cosα)/2]其中,α/2为角的半角,cosα为原角的余弦值。
公式中的±表示结果的正负与角度所在象限相关。
2. 余弦函数的二倍角公式余弦函数的二倍角公式可以用来计算一个角的两倍的余弦值。
假设原角为α,则其两倍的角为2α。
余弦函数的二倍角公式如下:cos2α = cos²α - sin²α其中,2α为角的两倍,cos²α和sin²α分别为原角的余弦值的平方和正弦值的平方。
三、正切函数的半角与二倍角公式1. 正切函数的半角公式正切函数的半角公式可以用来计算一个角的一半的正切值。
假设原角为α,则其一半的角为α/2。
正切函数的半角公式如下:tan(α/2) = ±√[(1 - cosα)/(1 + cosα)]其中,α/2为角的半角,cosα为原角的余弦值。
二倍角公式和半角公式

二倍角公式和半角公式二倍角公式和半角公式是解决三角函数中角度加倍和减半的重要工具。
在三角函数中,角度常常是以弧度或度数表示的,通过二倍角公式和半角公式,我们可以方便地将角度进行转化和计算。
二倍角公式是指将一个角的度数加倍所得到的新角的三角函数值与原角的三角函数值之间的关系。
对于任意角θ,二倍角公式可以用来计算sin2θ、cos2θ和tan2θ的值。
其中,sin2θ = 2sinθcosθ,cos2θ = cos^2θ - sin^2θ,tan2θ = 2tanθ / (1 - tan^2θ)。
举个例子,假设θ = 30°,根据二倍角公式可以得出sin60° = 2sin30°cos30° = 2 * 0.5 * √3/2 = √3/2。
同样地,我们可以利用二倍角公式计算cos2θ和tan2θ的值。
半角公式是指将一个角的度数减半所得到的新角的三角函数值与原角的三角函数值之间的关系。
对于任意角θ,半角公式可以用来计算sin(θ/2)、cos(θ/2)和tan(θ/2)的值。
其中,sin(θ/2) = ±√((1 - cosθ)/2),cos(θ/2) = ±√((1 + cosθ)/2),tan(θ/2) = ±√((1 - cosθ)/(1 + cosθ))。
需要注意的是,半角公式中的正负号取决于角度的象限,可以根据具体问题进行判断。
举个例子,假设θ = 60°,根据半角公式可以得出sin30° = ±√((1 - cos60°)/2) = ±√((1 - 0.5)/2) = ±√(0.5/2) = ±√(1/8) = ±1/2√2。
同样地,我们可以利用半角公式计算cos(θ/2)和tan(θ/2)的值。
二倍角公式和半角公式在解决三角函数问题时非常有用。
倍角及半角公式

倍角及半角公式在三角函数中,倍角及半角公式是求解特定角的重要工具。
它们可以将一个角的角度加倍或减半,从而简化计算,提高效率。
本文将介绍倍角公式和半角公式的定义、推导以及应用。
一、倍角公式倍角公式是将一个角的角度加倍得到另一个角的角度的公式。
常用的倍角公式包括正弦倍角公式、余弦倍角公式和正切倍角公式。
1. 正弦倍角公式正弦倍角公式可以表达为:sin(2θ) = 2sinθcosθ其中,θ为原角的角度。
这个公式可以通过将正弦函数展开为欧拉公式的形式,然后利用三角恒等式和倍角公式进行推导得到。
2. 余弦倍角公式余弦倍角公式可以表达为:cos(2θ) = cos²θ - sin²θ该公式也可以通过将余弦函数展开为欧拉公式的形式,然后利用三角恒等式和倍角公式进行推导得到。
3. 正切倍角公式tan(2θ) = (2tanθ)/(1 - tan²θ)这个公式可以通过将正切函数展开为正弦和余弦的比值形式,然后利用倍角公式进行推导得到。
二、半角公式半角公式是将一个角的角度减半得到另一个角的角度的公式。
常用的半角公式包括正弦半角公式、余弦半角公式和正切半角公式。
1. 正弦半角公式正弦半角公式可以表达为:sin(θ/2) = ±√[(1 - cosθ)/2]其中,θ为原角的角度。
根据正弦半角公式,我们可以通过已知一个角的正弦值来求解该角对应的半角。
2. 余弦半角公式余弦半角公式可以表达为:cos(θ/2) = ±√[(1 + cosθ)/2]该公式可以通过将余弦函数展开为欧拉公式的形式,然后利用半角公式进行推导得到。
3. 正切半角公式tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]根据正切半角公式,我们可以通过已知一个角的正切值来求解该角对应的半角。
三、应用举例倍角及半角公式在实际问题中有广泛的应用。
例如,在三角函数的求值中,通过利用倍角公式可以将一个角的角度加倍,从而可以快速计算出正弦、余弦和正切值。
三角函数中的倍角公式与半角公式

三角函数中的倍角公式与半角公式三角函数是数学中的重要概念,在几何和物理学中有着广泛的应用。
在三角函数中,倍角公式和半角公式是其中两个重要的公式。
本文将详细介绍三角函数中的倍角公式和半角公式,以及它们的应用。
一、倍角公式倍角公式是指将一个角的两倍表示成该角的三角函数的形式。
三角函数的倍角公式主要包括正弦函数、余弦函数和正切函数。
1. 正弦函数的倍角公式:sin(2θ) = 2sinθcosθ正弦函数的倍角公式可以通过三角函数的和差公式推导得出。
根据和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ令α = β = θ,可以得到:sin(θ + θ) = sinθcosθ + cosθsinθ化简后得到正弦函数的倍角公式。
2. 余弦函数的倍角公式:cos(2θ) = cos²θ - sin²θ余弦函数的倍角公式也可以通过三角函数的和差公式推导得出。
根据和差公式:cos(α ± β) = cosαcosβ - sinαsinβ令α = β = θ,可以得到:cos(θ + θ) = cosθcosθ - sinθsinθ化简后得到余弦函数的倍角公式。
3. 正切函数的倍角公式:tan(2θ) = 2tanθ / (1 - tan²θ)正切函数的倍角公式可以通过正弦函数和余弦函数的倍角公式推导得出。
将正弦函数和余弦函数的倍角公式代入正切函数的定义式,经过简化和化简可以得到正切函数的倍角公式。
二、半角公式半角公式是指将一个角的一半表示成该角的三角函数的形式。
与倍角公式类似,三角函数的半角公式也包括正弦函数、余弦函数和正切函数。
1. 正弦函数的半角公式:sin(θ/2) = √[(1 - cosθ) / 2]正弦函数的半角公式可以通过正弦函数和余弦函数的和差公式推导得出。
根据和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ令α = θ/2,β = θ/2,可以得到:sin(θ/2 + θ/2) = sin(θ/2)cos(θ/2) + cos(θ/2)sin(θ/2)化简后得到正弦函数的半角公式。
三角函数中万能公式总结

三角函数中万能公式总结集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)两角和与差的三角函数三角函数基本公式总结1.和、差角公式βαβαβαsin cos cos sin )sin(±=±;βαβαβαsin sin cos cos )cos( =±; βαβαβαtg tg tg tg tg 1)(±=±. 2.二倍角公式αααcos sin 22sin =;ααααα2222sin 211cos 2sin cos 2cos -=-=-=; ααα2122tg tg tg -=. 3.降幂公式ααα2sin 21cos sin =;22cos 1sin 2αα-=;22cos 1cos 2αα+=. 4.半角公式2cos 12sin αα-±=;2cos 12cos αα+±=;αααααααsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg . 5.万能公式2122sin 2αααtg tg+=;2121cos 22αααtg tg +-=;21222αααtg tg tg -=. 6.积化和差公式)]sin()[sin(21cos sin βαβαβα-++=;)]sin()[sin(21sin cos βαβαβα--+=;)]cos()[cos(21cos cos βαβαβα-++=;)]cos()[cos(21sin sin βαβαβα--+-=. 7.和差化积公式2cos 2sin 2sin sin βαβαβα-+=+;2sin 2cos 2sin sin βαβαβα-+=-;2cos 2cos 2cos cos βαβαβα-+=+;2sin 2sin 2cos cos βαβαβα-+-=-. 倍角、半角的三角函数二倍角公式是两角和公式的特殊情况,即:由此可继续导出三倍角公式.观察角之间的联系应该是解决三角变换的一个关键.二倍角公式中余弦公式有三种形式,采用哪种形式应根据题目具体而定.倍角和半角相对而言,两倍角余弦公式的变形可引出半角公式.推导过程中可得到一组降次公式,即, 进一步得到半角公式:降次公式在三角变换中应用得十分广泛,“降次”可以作为三角变换中的一个原则.半角公式在运用时一定要注意正、负号的选取,而是正是负取决于所在的象限.而半角的正切可用α的正弦、余弦表示,即:.这个公式可由二倍角公式得出,这个公式不存在符号问题,因此经常采用.反之用tan也可表示sinα, cosα, tanα,即:,,这组公式叫做“万能”公式.教材中只要求记忆两倍角公式,其它公式并没有给出,需要时可根据二倍角公式及同角三角函数公式推出.。
倍角公式和半角公式

0 , ,
2
2
[f ()]2 2 4si…n2… …2… 0…. ……………………12分
4
1.(2011·大纲版全国卷)已知α∈( ,π),sinα= 5,则
2
5
tan2α=________.
【解析】由α∈( ,π),sinα= ,得c5osα=-
2
5
tan
sin cos
1 2
sin
1 cos
2 1 cos
sin
1、左 右 2、左二次降到右一次
3、公式本2质用角的余弦表示角 的点击三进角入相函应数模块
2
(3)用
sinα,cosα
表示
α tan2.
tanα2=__1_+_s_in_c_oα_s_α_=__1_-_s_inc_oα_s_α_.
3.升、降幂公式主要用于化简、求值和证明.
(只含 cos )
(只含 sin )
点击进入相应模块
复习回顾:
二倍角的正弦、余弦、正切公式
sin 2 2sin cos
cos 2 cos2 sin2
2cos2 1
1 2sin2
tan
2
2 tan 1 tan2
R,
k
,
k
+
点击进入相应模块
(k Z)
2
24
降幂扩角公式:
cos2 1 cos 2
4
4
4
…………………………………………………………………3分
∴f(x)的最小正周期T=2π,f(x)的最小值为-2.
…………………………………………………………………5分
(2)由已知得 coscos sinsin 4 ,
最新倍角公式和半角公式一资料

最新倍角公式和半角公式一资料倍角公式和半角公式是解析几何中常用的一组公式,用于求解两个角的倍角和半角。
它们在三角函数、平面几何和立体几何等应用领域都有广泛的应用。
下面将详细介绍最新的倍角公式和半角公式,并给出相关的例题和解析。
一、倍角公式倍角公式是指将一个角的角度加倍后的角的正弦、余弦、正切等三角函数与原来的角度的三角函数之间的关系。
1.正弦的倍角公式sin2θ = 2sinθcosθ通过这个公式,我们可以将一个角的正弦值表示为这个角的余弦值和正弦值的乘积的二倍。
例题1:已知角A的正弦值为1/2,求角2A的正弦值。
解析:根据倍角公式,sin2A = 2sinAcosA代入sinA = 1/2,得到sin2A = 2 × 1/2 × √3/2 = √3/2所以角2A的正弦值为√3/22.余弦的倍角公式cos2θ = cos^2θ - sin^2θ通过这个公式,我们可以将一个角的余弦值表示为这个角的余弦值和正弦值的差的平方。
解析:根据倍角公式,cos2B = cos^2B - sin^2B代入cosB = 3/5,sinB = √1 - cos^2B = √1 - 9/25 = 4/5,得到cos2B = (3/5)^2 - (4/5)^2 = 9/25 - 16/25 = -7/25所以角2B的余弦值为-7/253.正切的倍角公式tan2θ = (2tanθ)/(1 - tan^2θ)通过这个公式,我们可以将一个角的正切值表示为这个角的正切值的两倍除以1减去这个角的正切值的平方。
例题3:已知角C的正切值为2,求角2C的正切值。
解析:根据倍角公式,tan2C = (2tanC)/(1 - tan^2C)代入tanC = 2,得到tan2C = (2 × 2)/(1 - 2^2) = -8/3所以角2C的正切值为-8/3二、半角公式半角公式是指将一个角的角度减半后的角的正弦、余弦、正切等三角函数与原来的角度的三角函数之间的关系。
三角函数余切,正割,余割和差角,半角,二倍角等公式

三角函数余切,正割,余割和差角,半角,二倍角等公式三角函数,也叫三角形函数,是一类函数,可以表示和描述二维空间中三角形的属性、性质等,是非常重要的数学概念。
本文将主要介绍其中一些关于三角形的函数,如余切、正割、余割和差角、半角、二倍角等。
一、余切对于任一定模式三角形,我们可以把它分成三角形的各边和角,且每个角都有自己的度数,记作α,β,γ。
现在,我们把α的正切函数的反函数,就是α的余切函数,它的标记为tg(α)的倒函数,记作cotg(α),它可以用来表示三角形角α的余切。
公式表示为:cotg=tan (90°-α)二、正割对于任一定模式三角形,我们可以把它分成三角形的各边和角,即α、β、γ,α的正割函数的反函数就是α的正割,它的标记为ctg(α),它的定义为:把α的正弦函数的倒函数,即sin(α)的倒函数定义为α的正割函数。
公式表示为:ctg=cos (90°-α)三、余割余割与正割的定义类似,余割的定义为α的余弦函数的倒函数,它的标记为cosec(α),它的定义为:把α的余弦函数的倒函数,即cos(α)的倒函数定义为α的余割函数。
公式表示为:cosec =sin (90°-α)四、差角差角就是把两个角之间的夹角表达出来,该夹角就是所谓的差角。
差角可由以下公式表示:差角=α+β-γ其中,α、β、γ分别是三角形的三个角。
五、半角半角指的是三角形中某一角的一半,即α的一半。
其定义为:α的一半,可由以下公式表示:半角/2=α/2六、二倍角二倍角指的是三角形中某一角的两倍,即α的两倍。
该角度可表示为:二倍角 2α=2α以上就是关于三角函数的余切、正割、余割和差角、半角、二倍角等公式的介绍。
三角函数有着非常重要的概念和应用,熟悉三角函数,不但能帮助我们掌握一般函数的概念,而且可以帮助我们解决数学问题,提高学习效率,拓宽我们的知识面。
(完整版)两倍角与半角公式与万能公式

(完整版)两倍角与半角公式与万能公式两倍角公式、半角公式、万能公式①;sin cos cos sin )sin(βαβαβα+=+②;sin sin cos cos )cos(βαβαβα-=+③βαβαβαtan tan 1tan tan )tan(-+=+ αβ=令二倍角公式:①αααcos sin 22sin =;②ααααα2222sin 211cos 2sin cos 2cos -=-=-=;③ααα2tan 1tan 22tan -=两倍角公式中αααcos sin 22sin =是两个函数之积,可在2)cos (sin αα±中产生。
两倍角是“相对的”,应该广义地理解。
如ααααα2sin 2112cos 22sin 2cos 4cos 2222-=-=-= 2tan12tan2)tan(2βαβαβα+-+=+等等见到平方就见到1+并项公式sin 2α=±cos2α=±tg 2α=±ααcos 1cos 1+-=ααcos 1sin +=ααsin cos 1-. 半角公式中的正负号如何选取?依照左边2α的函数值而定。
如果给你象限角,如I ∈α,2α的终边在第几象限?公式前的±号如何选取?如果给你区间角,如()ππα4,3∈,2α的终边在第几象限?公式前的±号如何选取?如果给你三角比值,如0cos tan 0cos sin αααα,2α的终边在第几象限?公式前的±号如何选取?半角的正切公式中的后两个tg 2α=ααcos 1sin +=ααsin co s 1- 前面没有正负号,万能公式:(并非万能,仅是用2tan α可将αsin 、αcos 、αtan 都表示出来的含义)sin α=2tan 12tan22αα+,cos α=2tan 12tan 122αα+-,tan α=2tan 12tan22αα-题型一、求值问题补充问题已知91)2cos(=-βα,32)2sin(=-βα,且24παπ<<,44πβπ<<- 求)cos(βα+的值解:考虑目标角和已知角的关系:(2βα-)—(βα-2)=2βα+再运用两倍角公式求值题型二、化简问题。
三角函数的半角公式与二倍角公式

三角函数的半角公式与二倍角公式三角函数是数学中重要的概念之一,它们在解析几何、三角学、物理学等领域中都有广泛的应用。
在三角函数中,半角公式和二倍角公式是常用的公式之一,它们可以简化计算,增加易用性。
本文将介绍三角函数的半角公式和二倍角公式,并详细讨论其推导和应用。
一、半角公式在三角函数中,半角公式是一种将角的半角与原角之间的关系表示出来的公式。
半角公式可用于将一个角度的三角函数值表示成一个角度的三角函数值。
下面,我们将分别介绍三角函数中的半角公式。
1. 正弦函数的半角公式正弦函数的半角公式表达为:sin(θ/2) = ±√[(1 - cosθ) / 2]其中,θ代表原角的角度。
推导:设θ/2的正弦值为x,则有:sin(θ/2) = x根据正弦和余弦的关系,可以得到:cos(θ/2) = ±√(1 - x²)由于θ/2的正弦函数值为x,可以得到:sin²(θ/2) = x²再利用sin²(θ/2) + cos²(θ/2) = 1的三角恒等式,可得:x² + cos²(θ/2) = 1将cos(θ/2) = ±√(1 - x²)代入上式,可以得到:x² + (1 - x²) = 1化简后,可得:2x² - 1 = 0解方程可得:x = ±√(1/2)因此,sin(θ/2) = ±√[(1 - cosθ) / 2]。
2. 余弦函数的半角公式余弦函数的半角公式表达为:cos(θ/2) = ±√[(1 + cosθ) / 2]其中,θ代表原角的角度。
推导:设θ/2的余弦值为x,则有:cos(θ/2) = x根据正弦和余弦的关系,可以得到:sin(θ/2) = ±√(1 - x²)由于θ/2的余弦函数值为x,可以得到:cos²(θ/2) = x²再利用sin²(θ/2) + cos²(θ/2) = 1的三角恒等式,可得:sin²(θ/2) + x² = 1将sin(θ/2) = ±√(1 - x²)代入上式,可以得到:(1 - x²) + x² = 1化简后,可得:1 = 1因此,cos(θ/2) = ±√[(1 + cosθ) / 2]。
必修四3.2 二倍角公式及半角万能公式

半角公式:22cos 1sin 2αα-=,22cos 1cos 2αα+=,2sin 2cos 12αα=-,2cos 2cos 12αα=+sin2α=cos 2α=sin 1cos tan 21cos sin ααααα-===+ 积化和差公式:()()[]βαβαβ-++=sin sin 21cos sin a , ()()[]βαβαβ--+=sin sin 21sin cos a ()()[]βαβαβ-++=cos cos 21cos cos a , ()()[]βαβαβ--+-=cos cos 21sin sin a 和差化积公式:sin sin 2sincos22αβαβαβ+-+=, sin sin 2cossin22αβαβαβ+--=cos cos 2coscos22αβαβαβ+-+=, cos cos 2sinsin22αβαβαβ+--=-万能公式例1.已知1352sin =α,24παπ<<,求α4sin ,α4cos ,α4tan 的值例2的值求,x x x x x tan 1cos 22sin ,471217534cos 2-+<<=⎪⎭⎫ ⎝⎛+πππ。
例3.化简:)4(sin )4tan(21cos 222απαπα+⋅--例4.在△ABC 中,角A 、B 、C 满足4sin 22CA +-cos2B=27,求角B 的度数. 例5 求值:140cos 40cos 2)40cos 21(40sin 2-︒+︒︒+︒ 例6.)12sin12(cosππ-(cos12π+sin12π)的值。
例7.已知sin 2 2α+sin 2α cos α-cos2α=1,α∈(0,2π),求sin α、tan α的值.练习:1.若(0,)απ∈,且1cos sin 3αα+=-,则cos 2α=( ) A .917 B. C. D .3172.000016cos 46cos 46sin 16sin +=( )A.23 B.22 C.21 D.13.=⋅+ααααcos2cos cos212sin22( ) A. αtan B. αtan2 C. 1 D. 21 4.已知x 为第三象限角,化简=-x 2cos 1( ) A.x sin 2 B. x sin 2- C. x cos 2 D. x cos 2-5. 求=115cos 114cos 113cos 112cos11cosπππππ( )A. 521B. 421 C. 1 D. 06.已知(,0)2x π∈-,4cos 5x =,则=x 2tan ( )A .247 B .247- C .724 D .724-7.求值:0000tan 20tan 4020tan 40+=_____________。
万能公式

高考数学答题万能公式及解题技巧:公式篇1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(π2-a)=cos(a)cos(π2-a)=sin(a)sin(π2+a)=cos(a)cos(π2+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=tan(a)+tan(b)1-tan(a)tan(b)tan(a-b)=tan(a)-tan(b)1+tan(a)tan(b)3.和差化积公式sin(a)+sin(b)=2sin(a+b2)cos(a-b2)sin(a)−sin(b)=2cos(a+b2)sin(a-b2)cos(a)+cos(b)=2cos(a+b2)cos(a-b2)cos(a)-cos(b)=-2sin(a+b2)sin(a-b2)4.二倍角公式sin(2a)=2sin(a)cos(b)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a)5.半角公式sin2(a2)=1-cos(a)2cos2(a2)=1+cos(a)2tan(a2)=1-cos(a)sin(a)=sina1+cos(a)6.万能公式sin(a)=2tan(a2)1+tan2(a2)cos(a)=1-tan2(a2)1+tan2(a2)tan(a)=2tan(a2)1-tan2(a2)7.其它公式(推导出来的 )a⋅sin(a)+b⋅cos(a)=a2+b2sin(a+c) 其中 tan(c)=ba一生受用的数学公式若两直线的斜率分别为m与n,则它们的夹角θ满足于tanθ=m–n/1+mn半径为r、圆心在(a, b)的圆,以(x–a) 2+(y–b) 2=r2表示。
高数—二倍角与半角的余弦、正弦和正切教师版
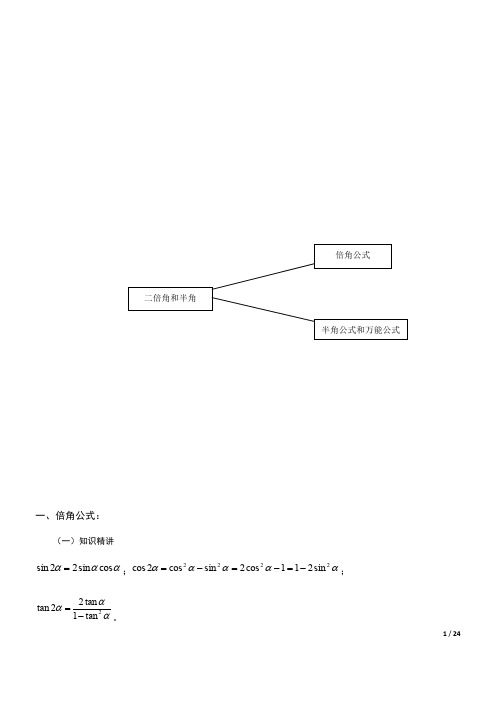
【答案】 证明:由 3sin2 1 2sin2 得 3sin2 cos 2 ……①
由 3sin 2 2sin 2 得 3sin cos sin 2 ……② , 都是锐角
①②得 sin cos 2 cos cos 2 sin sin 2 0 cos sin 2
22
2
二、半角公式和万能公式
(一)知识精讲
sin 1 cos ; cos 1 cos ; tan 1 cos
2
2
2
2
2 1 cos
( tan sin 1 cos ) 2 1 cos sin
2 tan
1 tan2
2 tan
13
5
【难度】★★
【答案】∵ 0 π ,∴ cos 1 sin2 5 .
2
13
又∵ 0 π , 0 π ,∴ 0 .若 0 π ,
2
2
2
∵ sin( ) sin ,∴ 不可能.故 π .∴ cos( ) 3 .
3 / 24
【难度】★★
【答案】 a b 1 ab
【例 8】(1)已知 sin 5 , ( , ) ,求 sin 2 , cos 2 , tan 2 的值;
13
2
(2) tan 1 , 则cos 2
;
2
(3)若 cos 48 a , 则sin 2004 的值是
0,
2
,则
sin
.
7 / 24
【难度】★★
【答案】 sin 4 2 . 9
三角函数倍角半角公式大全

三角函数倍角半角公式大全三角函数是数学中的一个重要分支,它在几何、物理、工程等领域都有着广泛的应用。
其中,倍角公式和半角公式是三角函数中常见的一类公式,它们可以帮助我们简化复杂的三角函数表达式,从而方便求解问题。
在本文中,我们将详细介绍三角函数的倍角公式和半角公式,帮助读者更好地理解和应用这些重要的数学工具。
1.倍角公式的概念和推导在三角函数中,倍角指的是角度的两倍。
而倍角公式则是用来表示一个角的两倍的三角函数值与该角的三角函数值之间的关系。
常见的倍角公式包括正弦函数的倍角公式、余弦函数的倍角公式和正切函数的倍角公式。
1.1正弦函数的倍角公式正弦函数的倍角公式可以表示为:sin(2θ) = 2sinθcosθ其中,θ表示原角的大小。
这个公式可以通过利用三角形的性质和勾股定理来进行推导。
假设在单位圆上,一个角的终边与x轴的交点为P(x, y),那么P点的坐标可以表示为(cosθ, sinθ)。
因此,角2θ的终边与x轴的交点可以表示为(cos2θ, sin2θ)。
通过单位圆的性质,我们可以得到:cos2θ = cos^2θ - sin^2θsin2θ = 2sinθcosθ将sin2θ的表达式带入上述公式中,即可得到正弦函数的倍角公式。
1.2余弦函数的倍角公式余弦函数的倍角公式可以表示为:cos(2θ) = cos^2θ - sin^2θcos(2θ) = 2cos^2θ - 1cos(2θ) = 1 - 2sin^2θ这个公式可以通过正弦函数的倍角公式推导得到。
首先,根据正弦函数的倍角公式,我们可以将cos2θ表示为cos2θ = 1 -2sin^2θ。
然后,利用三角恒等式sin^2θ + cos^2θ = 1,可以将cos2θ用sinθ表示出来。
1.3正切函数的倍角公式正切函数的倍角公式可以表示为:tan(2θ) = (2tanθ)/(1 - tan^2θ)这个公式可以通过利用sin2θ和cos2θ的表达式,以及tanθ = sinθ/cosθ的表达式,将sin2θ和cos2θ用tanθ表示出来,并进行简化得到。
三角函数的倍角公式与半角公式

三角函数的倍角公式与半角公式三角函数是数学中重要的概念,广泛应用于各个领域。
在三角函数的研究中,倍角公式与半角公式是常见且重要的公式。
本文将详细介绍三角函数的倍角公式与半角公式,并探讨它们在实际问题中的应用。
一、倍角公式倍角公式是指将一个角的度数加倍所得到的三角函数的关系式。
常见的三角函数有正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。
1. 正弦函数的倍角公式:sin(2θ) = 2sinθcosθ正弦函数的倍角公式表明,某个角的两倍角的正弦等于原角的正弦乘以余弦。
2. 余弦函数的倍角公式:cos(2θ) = cos²θ - sin²θ余弦函数的倍角公式是著名的二次三角函数公式,它表示某个角的两倍角的余弦等于该角的余弦的平方减去正弦的平方。
3. 正切函数的倍角公式:tan(2θ) = (2tanθ) / (1 - tan²θ)正切函数的倍角公式可以用于计算某个角的两倍角的正切值。
倍角公式在解决三角函数相关问题时起到了重要的作用,简化了计算过程。
二、半角公式半角公式是指将一个角的度数减半所得到的三角函数的关系式。
与倍角公式类似,半角公式同样适用于正弦函数、余弦函数和正切函数。
1. 正弦函数的半角公式:sin(θ/2) = ±√[(1-cosθ)/2]正弦函数的半角公式可以用于计算某个角的一半角的正弦值。
需要注意的是,计算结果可能有两个值,取决于具体角度的范围。
2. 余弦函数的半角公式:cos(θ/2) = ±√[(1+cosθ)/2]余弦函数的半角公式可以用于计算某个角的一半角的余弦值。
同样地,计算结果可能有两个值。
3. 正切函数的半角公式:tan(θ/2) = ±√[(1-cosθ) / (1+cosθ)]正切函数的半角公式可以用于计算某个角的一半角的正切值。
同样地,计算结果需要考虑正负两个值。
三、应用举例倍角公式与半角公式在解决实际问题时起到了重要的作用。
三角函数中万能公式总结

两角和与差的三角函数三角函数基本公式总结1.和、差角公式βαβαβαsin cos cos sin )sin(±=±;βαβαβαsin sin cos cos )cos(μ=±; βαβαβαtg tg tg tg tg μ1)(±=±. 2.二倍角公式αααcos sin 22sin =;ααααα2222sin 211cos 2sin cos 2cos -=-=-=; ααα2122tg tg tg -=. 3.降幂公式ααα2sin 21cos sin =;22cos 1sin 2αα-=;22cos 1cos 2αα+=. 4.半角公式2cos 12sin αα-±=;2cos 12cos αα+±=;αααααααsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg . 5.万能公式2122sin 2αααtg tg+=;2121cos 22αααtg tg +-=;21222αααtg tg tg -=. 6.积化和差公式)]sin()[sin(21cos sin βαβαβα-++=;)]sin()[sin(21sin cos βαβαβα--+=; )]cos()[cos(21cos cos βαβαβα-++=;)]cos()[cos(21sin sin βαβαβα--+-=. 7.和差化积公式2cos 2sin 2sin sin βαβαβα-+=+;2sin 2cos 2sin sin βαβαβα-+=-;2cos 2cos 2cos cos βαβαβα-+=+;2sin 2sin 2cos cos βαβαβα-+-=-. 倍角、半角的三角函数二倍角公式是两角和公式的特殊情况,即:由此可继续导出三倍角公式.观察角之间的联系应该是解决三角变换的一个关键.二倍角公式中余弦公式有三种形式,采用哪种形式应根据题目具体而定.倍角和半角相对而言,两倍角余弦公式的变形可引出半角公式.推导过程中可得到一组降次公式,即, 进一步得到半角公式: 降次公式在三角变换中应用得十分广泛,“降次”可以作为三角变换中的一个原则.半角公式在运用时一定要注意正、负号的选取,而是正是负取决于所在的象限.而半角的正切可用α的正弦、余弦表示,即:.这个公式可由二倍角公式得出,这个公式不存在符号问题,因此经常采用.反之用tan 也可表示sinα, cosα, tanα,即:,,这组公式叫做“万能”公式.教材中只要求记忆两倍角公式,其它公式并没有给出,需要时可根据二倍角公式及同角三角函数公式推出.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两倍角公式、半角公式、万能公式
① sin( ) sin cos cos sin ;
② cos( ) cos cos sin sin ;
③ tan( )
tan tan 令1 tan tan
二倍角公式:
① sin 2 2sin cos ;
② cos2 cos2 sin 2 2 cos2 1 1 2sin 2 ;
③ tan 2
2 tan 1 tan 2
两倍角公式中 sin 2 2 sin cos 是两个函数之积,可在(sincos ) 2 中产生。
两倍角是“相对的” ,应该广义地理解。
如 cos4 cos2 2 sin 2 2 2 cos2 2 1 1 2 sin 2 2
tan( )
2tan
2
等等tan 2
1
2
升次公式: sin2 1 cos2 、 cos2 1 cos2 ;
2 2
见到平方就降次,降次角加倍
降次公式: 1 cos 2 cos2
2 1 cos 2 sin 2
2
见到 1 cos 、 1 cos 就升次,升次角减半并项公式 : 1 sin 2 = (sin cos ) 2
半角公式:
sin =±1 cos
,
2 2
cos =±1 cos
,
2 2
1
tg =± 1 cos = sin = 1
cos .
2 1 cos 1 cos sin
半角公式中的正负号如何选取?依照左边的函数值而定。
2
如果给你象限角,如I ,的终边在第几象限?公式前的号如何选取?
2
如果给你区间角,如 3 ,4 ,的终边在第几象限?公式前的号如何选取?
2
如果给你三角比值,如sin cos 0
的终边在第几象限?公式前的号如何选取?tan cos
,
0 2
半角的正切公式中的后两个tg = sin =1
cos 前面没有正负号,
2 1 cos sin
万能公式:(并非万能,仅是用tan 可将 sin 、 cos 、 tan 都表示出来的含义)
2
sin α = 2 tan
2 ,
1 tan2
2
1 tan
2 cos α = 2 ,
1 tan2
2
2 tan
tan α = 2
1 tan2
2
题型一、求值问题
补充问题
已知 cos( ) 1 , sin( ) 2
,且
4 2
,
4
2 9 2
3
4 求 cos( ) 的值
解:考虑目标角和已知角的关系:()—()=
22 2
再运用两倍角公式求值
题型二、化简问题
2。
