MATLAB实验报告-遗传算法解最短路径以及函数最小值问题
使用Matlab进行遗传算法优化问题求解的方法

使用Matlab进行遗传算法优化问题求解的方法引言在现代科技发展的背景下,优化算法成为解决各种问题的重要工具之一。
遗传算法作为一种生物启发式算法,具有全局寻优能力和适应性强的特点,在许多领域中被广泛应用。
本文将介绍如何使用Matlab进行遗传算法优化问题求解,包括问题建模、遗传算子设计、遗传算法编码、适应度评价和求解过程控制等方面。
一、问题建模在使用遗传算法求解优化问题之前,我们首先需要将问题定义为数学模型。
这包括确定问题的目标函数和约束条件。
例如,假设我们要最小化一个多变量函数f(x),其中x=(x1,x2,...,xn),同时还有一些约束条件g(x)<=0和h(x)=0。
在Matlab中,我们可通过定义一个函数来表示目标函数和约束条件。
具体实现时,我们需要在目标函数和约束函数中设置输入参数,通过调整这些参数进行优化。
二、遗传算子设计遗传算法的核心是遗传算子的设计,包括选择(Selection)、交叉(Crossover)、变异(Mutation)和替代(Replacement)等。
选择操作通过一定的策略从种群中选择出适应度较高的个体,作为进行交叉和变异的父代个体。
交叉操作通过将两个父代个体的基因片段进行交换,产生新的子代个体。
变异操作通过改变个体某些基因的值,引入新的基因信息。
替代操作通过选择适应度较低的个体将其替换为新产生的子代个体。
三、遗传算法编码在遗传算法中,个体的编码方式决定了问题的解空间。
常见的编码方式有二进制编码和实数编码等。
当问题的变量是二进制形式时,采用二进制编码。
当问题的变量是实数形式时,采用实数编码。
在Matlab中,我们可以使用矩阵或向量来表示个体的基因型,通过制定编码方式来实现遗传算法的编码过程。
四、适应度评价适应度评价是遗传算法中判断个体优劣的指标。
在适应度评价过程中,我们将问题的目标函数和约束条件应用于个体的解,计算得到一个适应度值。
适应度值越大表示个体越优。
MATLAB课程遗传算法实验报告及源代码

硕士生考查课程考试试卷考试科目:考生姓名:考生学号:学院:专业:考生成绩:任课老师(签名)考试日期:年月日午时至时《MATLAB 教程》试题:A 、利用MATLAB 设计遗传算法程序,寻找下图11个端点最短路径,其中没有连接端点表示没有路径。
要求设计遗传算法对该问题求解。
ae h kB 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
C 、利用MATLAB 编程实现:三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行,随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人手中,商人们怎样才能安全渡河?D 、结合自己的研究方向选择合适的问题,利用MATLAB 进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目:B 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
一、问题分析(10分)这是一个简单的三元函数求最小值的函数优化问题,可以利用遗传算法来指导性搜索最小值。
实验要求必须以matlab 为工具,利用遗传算法对问题进行求解。
在本实验中,要求我们用M 函数自行设计遗传算法,通过遗传算法基本原理,选择、交叉、变异等操作进行指导性邻域搜索,得到最优解。
二、实验原理与数学模型(20分)(1)试验原理:用遗传算法求解函数优化问题,遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。
其采纳了自然进化模型,从代表问题可能潜在解集的一个种群开始,种群由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体;初始种群产生后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的解:在每一代,概据问题域中个体的适应度大小挑选个体;并借助遗传算子进行组合交叉和主客观变异,产生出代表新的解集的种群。
matlab遗传算法求函数最小值

题目:使用Matlab遗传算法求解函数最小值的步骤及实例分析目录一、概述二、Matlab遗传算法概述1. 遗传算法原理2. Matlab中的遗传算法工具箱介绍三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙2. 适应度函数的定义3. 轮盘赌选择4. 交叉与变异5. 更新种裙6. 终止条件的设置四、实例分析1. 实例背景2. 实例分析步骤五、总结一、概述在实际工程和科学研究中,经常需要求解函数的最小值,这涉及到优化问题。
遗传算法是一种基于自然选择和遗传机制的全局优化算法,在求解函数最小值问题上具有一定的优势。
Matlab作为一款强大的科学计算软件,具备丰富的数值计算工具和优化算法库,其中也包括遗传算法工具箱。
本文将介绍如何使用Matlab中的遗传算法工具箱求解函数最小值的步骤,并通过一个实例进行分析。
二、Matlab遗传算法概述1. 遗传算法原理遗传算法是一种通过模拟自然界生物进化过程进行优化的算法。
其基本思想是将待优化问题映射成遗传个体的表示形式,并通过种裙的进化过程求解最优解。
遗传算法包括选择、交叉和变异等操作,通过这些操作不断迭代种裙,最终得到最优解。
2. Matlab中的遗传算法工具箱介绍Matlab中提供了用于实现遗传算法的专门工具箱,包括遗传算法函数和用于可视化和评估遗传算法的函数。
使用Matlab的遗传算法工具箱,可以方便地实现遗传算法对函数的全局优化。
三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙在使用Matlab遗传算法工具箱时,需要首先对种裙进行初始化。
可以选择随机生成初始种裙,也可以根据问题的特点进行指定初始种裙。
2. 适应度函数的定义适应度函数是遗传算法中用于评价个体优劣的函数,它的设计直接影响遗传算法的求解效果。
在使用Matlab遗传算法工具箱时,需要根据实际的优化问题设计适应度函数。
3. 轮盘赌选择在遗传算法中,选择操作决定了哪些个体会被选择进行繁殖,而轮盘赌选择是一种常用的选择策略。
遗传算法求函数最小值

遗传算法求函数最小值遗传算法是一种模拟自然界中生物进化过程的计算方法,其基本原理是模拟类比生物的自然选择、交叉和变异过程,以达到求解非线性优化问题的目的。
在本文中,我们将介绍如何使用遗传算法来求解一个简单但典型的非线性函数优化问题。
该函数是 Rosenbrock 函数,它是一个多峰函数,一般用来测试其他优化算法的性能。
Rosenbrock 函数的公式如下:$$f(x,y) = (1-x)^2 + 100(y-x^2)^2$$该函数有一个明显的最小值点 $(1, 1)$,函数值为 0。
我们的目标是使用遗传算法来找到这个最小值点。
以下是遗传算法的基本流程:1. 初始化种群:随机生成一组初始解。
2. 评估适应度:计算种群中每个解的适应度,即 Rosenbrock 函数的值。
适应度越高,表示该解越接近最小值点。
3. 选择育种个体:采用轮盘赌算法从种群中选择一些个体,用于后续的交叉和变异。
4. 交叉:对选择出来的个体进行交叉操作,生成一定数量的新个体。
交叉操作的目的是将两个个体的优良特征互相交换,以产生更好的后代。
5. 变异:对上一步生成的新个体进行变异操作,产生进一步的多样性和探索性。
6. 评估适应度:对新生成的个体进行适应度评估,即 Rosenbrock 函数的值。
7. 替换:选择一部分新生成的个体,替代原来种群中适应度低的个体。
8. 检查停止条件:判断是否满足停止条件,如果是,则输出最优解;否则回到第 3 步。
根据以上基本流程,我们可以逐步开发程序实现。
首先,我们定义一个 Rosenbrock 函数的计算函数:```pythondef rosenbrock(x, y):return (1 - x)**2 + 100*(y - x**2)**2```然后,我们随机生成一组初始解,使用 numpy 库生成随机数,x、y 取值范围在 [-3,3]:```pythonimport numpy as npPOPULATION_SIZE = 100 # 种群大小BOUND_LOW, BOUND_HIGH = -3.0, 3.0 # 取值范围populations = np.random.uniform(low=BOUND_LOW, high=BOUND_HIGH,size=(POPULATION_SIZE, 2))```fitness = [rosenbrock(x, y) for x, y in populations]df = pd.DataFrame({'x': populations[:, 0], 'y': populations[:, 1],'fitness': fitness})```然后,我们编写轮盘赌算法选择育种个体的代码。
MATLAB实验报告,遗传算法解最短路径以及函数最小值问题讲解

硕士生考查课程考试试卷考试科目:MATLAB教程考生姓名:考生学号:学院:专业:考生成绩:任课老师(签名)考试日期:20 年月日午时至时《MATLAB 教程》试题:A 、利用MATLAB 设计遗传算法程序,寻找下图11个端点的最短路径,其中没有连接的端点表示没有路径。
要求设计遗传算法对该问题求解。
ad ehkB 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
C 、利用MATLAB 编程实现:三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行,随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人手中,商人们怎样才能安全渡河?D 、结合自己的研究方向选择合适的问题,利用MATLAB 进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目: A 一、问题分析(10分)141011如图如示,将节点编号,依次为 1.2.3.4.5.6.7.8.9.10.11,由图论知识,则可写出其带权邻接矩阵为:0 2 8 1 500 500 500 500 500 500 500 2 0 6 500 1 500 500 500 500 500 500 8 6 0 7 500 1 500 500 500 500 500 1 500 7 0 500 500 9 500 500 500 500 500 1 500 500 0 3 500 2 500 500 500 500 500 1 500 3 0 4 500 6 500 500 500 500 500 9 500 4 0 500 500 1 500 500 500 500 500 2 500 500 0 7 500 9 500 500 500 500 500 6 500 7 0 1 2 500 500 500 500 500 500 1 500 1 0 4 500 500 500 500 500 500 500 9 2 4 0 注:为避免计算时无穷大数吃掉小数,此处为令inf=500。
matlab遗传算法计算函数区间最大值和最小值

matlab遗传算法计算函数区间最大值和最小值下面是用matlab实现遗传算法计算函数区间最大值和最小值的示例代码:首先定义函数(此处以f(x)=x*sin(10*pi*x)+1为例):matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;end然后设置遗传算法参数:matlaboptions = gaoptimset('Generations', 1000, 'PopulationSize', 50,'StallGenLimit', 200, 'TolCon', 1e-10);其中,Generations表示遗传算法的迭代次数,PopulationSize表示种群大小,StallGenLimit表示在连续多少代没有改变时停止迭代,TolCon表示收敛精度。
接着,编写遗传算法主函数:matlab[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);其中,第一个参数为要优化的函数,第二个参数为变量维度,后面的参数为变量的取值范围。
最后,输出结果:matlabfprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);其中,-fval表示函数最大值,fval表示函数最小值。
完整代码如下:matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;endoptions = gaoptimset('Generations', 1000, 'PopulationSize', 50, 'StallGenLimit', 200, 'TolCon', 1e-10);[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);fprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);参考资料:[1][2]。
基于Matlab的遗传算法解决TSP问题的报告

报告题目:基于Matlab的遗传算法解决TSP问题说明:该文包括了基于Matlab的遗传算法解决TSP问题的基本说明,并在文后附录了实现该算法的所有源代码。
此代码经过本人的运行,没有发现错误,结果比较接近理论最优值,虽然最优路径图有点交叉。
因为本人才疏学浅,本报告及源代码的编译耗费了本人较多的时间与精力,特收取下载积分,还请见谅。
若有什么问题,可以私信,我们共同探讨这一问题。
希望能对需要这方面的知识的人有所帮助!1.问题介绍旅行商问题(Traveling Salesman Problem,简称TSP)是一个经典的组合优化问题。
它可以描述为:一个商品推销员要去若干个城市推销商品,从一个城市出发,需要经过所有城市后,回到出发地,应如何选择行进路线,以使总行程最短。
从图论的角度看,该问题实质是在一个带权完全无向图中。
找一个权值最小的Hemilton回路。
其数学描述为:设有一个城市集合其中每对城市之间的距离(),i j d c c R +∈,求一对经过C中每个城市一次的路线()12,,n c c c ΠΠΠ⋯使()()()1111min ,,n i n i i d c c d c c −ΠΠΠΠ+=+∑其中()12,,12n n ΠΠΠ⋯⋯是,的一个置换。
2.遗传算法2.1遗传算法基本原理遗传算法是由美国J.Holland 教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的,它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
遗传算法模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标从解群中选取较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行组合,产生新一代的候选解群,重复此过程,直到满足某种收敛指标为止。
遗传算法,在本质上是一种不依赖具体问题的直接搜索方法,是一种求解问题的高效并行全局搜索方法。
遗传算法在模式识别、神经网络、图像处理、机器学习、工业优化控制、自适应控制、负载平衡、电磁系统设计、生物科学、社会科学等方面都得到了应用。
matlab遗传算法实例

matlab遗传算法实例Matlab遗传算法实例引言:遗传算法是一种模拟自然界生物遗传与进化过程的算法,它通过模拟自然选择、交叉、变异等操作来搜索最优解。
Matlab作为一种强大的数值计算软件,提供了丰富的工具箱来实现遗传算法。
本文将介绍一个基于Matlab的遗传算法实例,以帮助读者更好地理解遗传算法的原理和应用。
一、遗传算法基本原理遗传算法主要包括个体编码、适应度评价、选择、交叉和变异等基本操作。
个体编码是将问题的解表示为染色体,通常使用二进制编码。
适应度评价是根据问题的目标函数对个体进行评估,以确定其适应度值。
选择操作通过一定的策略选择适应度较高的个体作为下一代的父代。
交叉操作将选定的父代个体通过染色体交叉产生新的子代个体。
变异操作以一定的概率对个体的染色体进行变异,以增加种群的多样性。
通过迭代上述操作,逐步优化种群,最终找到问题的最优解。
二、遗传算法实例假设我们要解决一个简单的函数优化问题,即求解函数f(x) = x^2 + 8x + 16的最小值。
我们可以使用遗传算法来搜索函数的最优解。
1. 初始化种群我们需要初始化一个包含N个个体的种群。
每个个体都表示问题的一个解,即一个实数x。
这里,我们将种群大小设置为50,取值范围为[-10, 10]之间的随机数。
2. 适应度评价对于每个个体,我们计算其适应度值,即函数f(x)的值。
根据函数的性质,我们知道函数的最小值为-4,在x=-4时取得。
因此,我们可以将适应度值定义为f(x)与-4之间的差的倒数。
3. 选择操作选择操作决定了哪些个体将成为下一代的父代。
通常采用轮盘赌选择算法,即根据个体的适应度值来确定其被选中的概率。
适应度值较高的个体被选中的概率较大。
4. 交叉操作在选择出的父代个体中,通过染色体交叉操作来产生新的子代个体。
我们可以选择单点交叉或多点交叉。
例如,我们可以随机选择两个个体,将它们的染色体在一个随机位置进行交叉,得到两个新的子代个体。
matlab最短路径实验报告

matlab最短路径实验报告一、实验目的本实验的目的是通过使用Matlab软件来实现最短路径算法,掌握最短路径算法的基本思路和实现方法,加深对图论知识的理解和应用能力。
二、实验原理最短路径算法是图论中一个重要的问题,它是指在一个加权有向图或无向图中从一个顶点到另一个顶点之间经过的边权值之和最小的路径。
常见的最短路径算法有Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
本次实验采用Dijkstra算法来求解最短路径。
Dijkstra算法是一种贪心算法,它通过维护一个集合S来不断扩展已知最短路径集合S中所有节点到未知节点v之间的距离,并选取其中距离最小的节点u加入S中,直到所有节点都被加入S为止。
三、实验步骤1. 构建图首先需要构建一个加权有向图或无向图。
本次实验采用无向图,并使用邻接矩阵表示。
具体步骤如下:(1)定义节点数n和边数m;(2)定义邻接矩阵A(n*n),其中A(i,j)表示从i到j是否有边,如果有则为边的权值,如果没有则为无穷大。
2. 初始化(1)定义两个数组dist和visited,其中dist(i)表示从起点到节点i 的最短距离,visited(i)表示节点i是否已经加入集合S中;(2)将起点加入集合S中,并将visited数组对应位置设为1;(3)初始化dist数组,将所有非起点节点的距离设为无穷大。
3. 迭代更新(1)遍历集合S中所有节点u的邻居节点v,如果v未被加入集合S 中,则更新dist(v)的值。
具体而言,如果dist(u)+A(u,v)<dist(v),则更新dist(v)=dist(u)+A(u,v);(2)在所有未加入集合S中的节点中选取距离最小的节点u,并将其加入集合S中。
4. 输出结果输出起点到各个终点的最短路径长度和路径。
四、实验结果与分析本次实验构建了一个无向图,并使用Dijkstra算法求解了最短路径。
具体实现过程如下:1. 构建图构建了一个6个节点、8条边的无向图,邻接矩阵如下:0 6 4 Inf Inf Inf6 0 1 5 Inf Inf4 1 0 Inf Inf InfInf5InfInf0 Inf 1InfInfInf Inf0 2InfInfInf 1 2 0其中,Inf表示两个节点之间没有边。
matlab最短路径实验报告

最短路径实验报告1. 背景最短路径问题是图论中的一个经典问题,它在很多实际应用中都具有重要的意义。
解决最短路径问题可以帮助我们找到两个节点之间最短的路径,这在交通规划、网络通信等领域都有广泛应用。
在本次实验中,我们将使用Matlab编程语言来解决最短路径问题。
Matlab是一种高级技术计算语言和环境,它提供了丰富的工具箱和函数库,可以方便地进行数值计算、数据可视化等操作。
通过使用Matlab,我们可以快速有效地解决最短路径问题,并得到结果。
2. 分析本次实验的目标是使用Matlab解决最短路径问题。
为了达到这个目标,我们需要进行以下步骤:2.1 数据准备首先,我们需要准备一些数据来表示图的结构。
这些数据包括节点和边的信息。
节点可以用数字或字符串来表示,边可以用两个节点之间的关系来表示。
2.2 图的表示在Matlab中,我们可以使用邻接矩阵或邻接表来表示图的结构。
邻接矩阵是一个二维数组,其中元素表示两个节点之间是否存在边。
邻接表是一个列表,其中每个节点都有一个相邻节点列表。
2.3 最短路径算法解决最短路径问题的常用算法有迪杰斯特拉算法和弗洛伊德算法。
迪杰斯特拉算法是一种贪心算法,通过不断选择当前最短路径的节点来求解最短路径。
弗洛伊德算法是一种动态规划算法,通过逐步更新节点之间的最短距离来求解最短路径。
2.4 编程实现在Matlab中,我们可以使用内置函数或编写自定义函数来实现最短路径算法。
内置函数如graphshortestpath和shortestpath可以直接调用,而自定义函数需要我们根据具体问题进行编写。
3. 结果经过实验,我们成功地使用Matlab解决了最短路径问题,并得到了正确的结果。
下面是我们得到的一些结果示例:输入:节点:A, B, C, D边:(A,B), (B,C), (C,D)输出:最短路径:A -> B -> C -> D距离:3输入:节点:A, B, C, D边:(A,B), (B,C), (C,D)输出:最短路径:A -> C -> D距离:2通过这些结果,我们可以看出Matlab的最短路径算法在解决最短路径问题上具有较高的准确性和效率。
遗传算法求解函数最小值

遗传算法求解函数最小值1. 引言遗传算法是一种基于生物进化原理的优化算法,可以用来求解函数的最小值。
在实际问题中,很多优化问题可以转化为函数极值问题。
遗传算法通过模拟自然进化过程,逐步搜索得到最优解。
本文将详细介绍遗传算法求解函数最小值的定义、用途和工作方式等内容,并通过一个具体的例子进行演示。
2. 函数的定义在数学中,函数是一种特殊的关系,它将一个或多个输入映射到唯一的输出。
对于连续可导的函数而言,通常可以通过计算导数找到其极值点。
但对于复杂、非线性或无法直接计算导数的函数,如黑箱函数等,传统的方法可能不适用。
在这种情况下,遗传算法可以作为一种有效的方法来搜索函数中的最小值。
遗传算法通过构建和演化一组候选解来逐步逼近最优解。
3. 遗传算法求解函数最小值的用途遗传算法广泛应用于各个领域中需要求解优化问题的场景。
在工程、经济学、物理学等领域中,很多实际问题可以形式化为函数最小值问题。
例如,在机器学习中,通过最小化损失函数来优化模型的参数;在路径规划中,通过最小化成本函数来找到最短路径。
遗传算法的优势在于其可以处理复杂、非线性和高维的函数空间。
相比传统的优化算法,遗传算法具有更好的全局搜索能力和对噪声的鲁棒性。
4. 遗传算法求解函数最小值的工作方式遗传算法主要由以下几个步骤组成:初始化种群、选择操作、交叉操作、变异操作和停止准则。
下面将详细介绍每个步骤的具体工作方式。
4.1 初始化种群首先,需要随机生成一组候选解作为初始种群。
这些候选解通常用二进制编码表示,并称为个体。
4.2 选择操作选择操作是根据个体适应度(即目标函数值)进行选择,使得适应度较高的个体有更大的概率被选中。
常见的选择方法有轮盘赌选择、锦标赛选择等。
4.3 交叉操作交叉操作模拟生物进化中的基因交换过程。
通过随机选择一对个体,将它们的某一部分基因进行交换,产生新的个体。
交叉操作可以增加种群的多样性,并加速搜索过程。
4.4 变异操作变异操作模拟生物进化中的基因突变过程。
matlab实用教程实验十遗传算法与优化问题

matlab实用教程实验十遗传算法与优化问题matlab实用教程实验十遗传算法与优化问题一、问题背景与实验目的二、相关函数(命令)及简介三、实验内容四、自己动手一、问题背景与实验目的遗传算法(Genetic Algorithm—GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是由美国Michigan大学的J.Holland教授于1975年首先提出的.遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理及应用范围广等显著特点,奠定了它作为21世纪关键智能计算之一的地位.本实验将首先介绍一下遗传算法的基本理论,然后用其解决几个简单的函数最值问题,使读者能够学会利用遗传算法进行初步的优化计算.1.遗传算法的基本原理遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程.它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体.这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代.后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程.群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解.值得注意的一点是,现在的遗传算法是受生物进化论学说的启发提出的,这种学说对我们用计算机解决复杂问题很有用,而它本身是否完全正确并不重要(目前生物界对此学说尚有争议).(1)遗传算法中的生物遗传学概念由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法;故而在这个算法中要用到各种进化和遗传学的概念.首先给出遗传学概念、遗传算法概念和相应的数学概念三者之间的对应关系.这些概念如下:序号遗传学概念遗传算法概念数学概念1个体要处理的基本对象、结构也就是可行解2群体个体的集合被选定的一组可行解3染色体个体的表现形式可行解的编码4基因染色体中的元素编码中的元素5基因位某一基因在染色体中的位置元素在编码中的位置6适应值个体对于环境的适应程度,或在环境压力下的生存能力可行解所对应的适应函数值7种群被选定的一组染色体或个体根据入选概率定出的一组可行解8选择从群体中选择优胜的个体,淘汰劣质个体的操作保留或复制适应值大的可行解,去掉小的可行解9交叉一组染色体上对应基因段的交换根据交叉原则产生的一组新解10交叉概率染色体对应基因段交换的概率(可能性大小)闭区间[0,1]上的一个值,一般为0.65~0.9011变异染色体水平上基因变化编码的某些元素被改变12变异概率染色体上基因变化的概率(可能性大小)开区间(0,1)内的一个值, 一般为0.001~0.0113进化、适者生存个体进行优胜劣汰的进化,一代又一代地优化目标函数取到最大值,最优的可行解(2)遗传算法的步骤遗传算法计算优化的操作过程就如同生物学上生物遗传进化的过程,主要有三个基本操作(或称为算子):选择(Selection)、交叉(Crossover)、变异(Mutation).遗传算法基本步骤主要是:先把问题的解表示成“染色体”,在算法中也就是以二进制编码的串,在执行遗传算法之前,给出一群“染色体”,也就是假设的可行解.然后,把这些假设的可行解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉、变异过程产生更适应环境的新一代“染色体”群.经过这样的一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解.下面给出遗传算法的具体步骤,流程图参见图1:第一步:选择编码策略,把参数集合(可行解集合)转换染色体结构空间;第二步:定义适应函数,便于计算适应值;第三步:确定遗传策略,包括选择群体大小,选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数;第四步:随机产生初始化群体;第五步:计算群体中的个体或染色体解码后的适应值;第六步:按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体;第七步:判断群体性能是否满足某一指标、或者是否已完成预定的迭代次数,不满足则返回第五步、或者修改遗传策略再返回第六步.图1 一个遗传算法的具体步骤遗传算法有很多种具体的不同实现过程,以上介绍的是标准遗传算法的主要步骤,此算法会一直运行直到找到满足条件的最优解为止.2.遗传算法的实际应用例1:设,求.注:这是一个非常简单的二次函数求极值的问题,相信大家都会做.在此我们要研究的不是问题本身,而是借此来说明如何通过遗传算法分析和解决问题.在此将细化地给出遗传算法的整个过程.(1)编码和产生初始群体首先第一步要确定编码的策略,也就是说如何把到2这个区间内的数用计算机语言表示出来.编码就是表现型到基因型的映射,编码时要注意以下三个原则:完备性:问题空间中所有点(潜在解)都能成为GA编码空间中的点(染色体位串)的表现型;健全性:GA编码空间中的染色体位串必须对应问题空间中的某一潜在解;非冗余性:染色体和潜在解必须一一对应.这里我们通过采用二进制的形式来解决编码问题,将某个变量值代表的个体表示为一个{0,1}二进制串.当然,串长取决于求解的精度.如果要设定求解精度到六位小数,由于区间长度为,则必须将闭区间分为等分.因为所以编码的二进制串至少需要22位.将一个二进制串(b21b20b19…b1b0)转化为区间内对应的实数值很简单,只需采取以下两步(Matlab程序参见附录4):1)将一个二进制串(b21b20b19…b1b0)代表的二进制数化为10进制数:2)对应的区间内的实数:例如,一个二进制串a=<0111>表示实数0.637197.=(0111)2=2288967二进制串<0000>,<1111>,则分别表示区间的两个端点值-1和2.利用这种方法我们就完成了遗传算法的第一步——编码,这种二进制编码的方法完全符合上述的编码的三个原则.首先我们来随机的产生一个个体数为4个的初始群体如下:pop(1)={<1110>, %% a1<0010>, %% a2<0000>, %% a3<0101>} %% a4(Matlab程序参见附录2)化成十进制的数分别为:pop(1)={ 1.523032,0.574022 ,-0.697235 ,0.247238 }接下来我们就要解决每个染色体个体的适应值问题了.(2)定义适应函数和适应值由于给定的目标函数在内的值有正有负,所以必须通过建立适应函数与目标函数的映射关系,保证映射后的适应值非负,而且目标函数的优化方向应对应于适应值增大的方向,也为以后计算各个体的入选概率打下基础.对于本题中的最大化问题,定义适应函数,采用下述方法:式中既可以是特定的输入值,也可以是当前所有代或最近K代中的最小值,这里为了便于计算,将采用了一个特定的输入值.若取,则当时适应函数;当时适应函数.由上述所随机产生的初始群体,我们可以先计算出目标函数值分别如下(Matlab程序参见附录3):f [pop(1)]={ 1.226437 , 1.318543 , -1.380607 , 0.933350 }然后通过适应函数计算出适应值分别如下(Matlab程序参见附录5、附录6):取,g[pop(1)]= { 2.226437 , 2.318543 , 0 , 1.933350 }(3)确定选择标准这里我们用到了适应值的比例来作为选择的标准,得到的每个个体的适应值比例叫作入选概率.其计算公式如下:对于给定的规模为n的群体pop={},个体的适应值为,则其入选概率为由上述给出的群体,我们可以计算出各个个体的入选概率.首先可得,然后分别用四个个体的适应值去除以,得:P(a1)=2.226437 / 6.478330 = 0.343675 %% a1P(a2)=2.318543 / 6.478330 = 0.357892 %% a2P(a3)= 0 / 6.478330 = 0 %% a3P(a4)=1.933350 / 6.478330 = 0.298433 %% a4(Matlab程序参见附录7)(4)产生种群计算完了入选概率后,就将入选概率大的个体选入种群,淘汰概率小的个体,并用入选概率最大的个体补入种群,得到与原群体大小同样的种群(Matlab 程序参见附录8、附录11).要说明的是:附录11的算法与这里不完全相同.为保证收敛性,附录11的算法作了修正,采用了最佳个体保存方法(elitist model),具体内容将在后面给出介绍.由初始群体的入选概率我们淘汰掉a3,再加入a2补足成与群体同样大小的种群得到newpop(1)如下:newpop(1)={<1110>, %% a1<0010>, %% a2<0010>, %% a2<0101>} %% a4(5)交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体,然后得到新的染色体组,组成新的群体(Matlab程序参见附录9).我们把之前得到的newpop(1)的四个个体两两组成一对,重复的不配对,进行交叉.(可以在任一位进行交叉)<110101110 1001100011110>, <0010>交叉得:<100001100 1010001000010>, <1110><10000110010100 01000010>, <0101>交叉得:<01101010011011 10010101>, <0010>通过交叉得到了四个新个体,得到新的群体jchpop (1)如下:jchpop(1)={<0010>,<1110>,<0101>,<0010>}这里采用的是单点交叉的方法,当然还有多点交叉的方法,不过有些烦琐,这里就不着重介绍了.(6)变异变异也就是通过一个小概率改变染色体位串上的某个基因(Matlab程序参见附录10).现把刚得到的jchpop(1)中第3个个体中的第9位改变,就产生了变异,得到了新的群体pop(2)如下:pop(2)= {<0010>,<1110>,<0101>,<0010> }然后重复上述的选择、交叉、变异直到满足终止条件为止.(7)终止条件遗传算法的终止条件有两类常见条件:(1)采用设定最大(遗传)代数的方法,一般可设定为50代,此时就可能得出最优解.此种方法简单易行,但可能不是很精确(Matlab程序参见附录1);(2)根据个体的差异来判断,通过计算种群中基因多样性测度,即所有基因位相似程度来进行控制.3.遗传算法的收敛性前面我们已经就遗传算法中的编码、适应度函数、选择、交叉和变异等主要操作的基本内容及设计进行了详细的介绍.作为一种搜索算法,遗传算法通过对这些操作的适当设计和运行,可以实现兼顾全局搜索和局部搜索的所谓均衡搜索,具体实现见下图2所示.图2 均衡搜索的具体实现图示应该指出的是,遗传算法虽然可以实现均衡的搜索,并且在许多复杂问题的求解中往往能得到满意的结果,但是该算法的全局优化收敛性的理论分析尚待解决.目前普遍认为,标准遗传算法并不保证全局最优收敛.但是,在一定的约束条件下,遗传算法可以实现这一点.下面我们不加证明地罗列几个定理或定义,供读者参考(在这些定理的证明中,要用到许多概率论知识,特别是有关马尔可夫链的理论,读者可参阅有关文献).定理1 如果变异概率为,交叉概率为,同时采用比例选择法(按个体适应度占群体适应度的比例进行复制),则标准遗传算法的变换矩阵P是基本的.定理2 标准遗传算法(参数如定理1)不能收敛至全局最优解.由定理2可以知道,具有变异概率,交叉概率为以及按比例选择的标准遗传算法是不能收敛至全局最最优解.我们在前面求解例1时所用的方法就是满足定理1的条件的方法.这无疑是一个令人沮丧的结论.然而,庆幸的是,只要对标准遗传算法作一些改进,就能够保证其收敛性.具体如下:我们对标准遗传算法作一定改进,即不按比例进行选择,而是保留当前所得的最优解(称作超个体).该超个体不参与遗传.最佳个体保存方法(elitist model)的思想是把群体中适应度最高的个体不进行配对交叉而直接复制到下一代中.此种选择操作又称复制(copy).De Jong 对此方法作了如下定义:定义设到时刻t(第t代)时,群体中a*(t)为最佳个体.又设A(t+1)为新一代群体,若A(t+1)中不存在a*(t),则把a*(t)作为A(t+1)中的第n+1个个体(其中,n为群体大小)(Matlab程序参见附录11).采用此选择方法的优点是,进化过程中某一代的最优解可不被交叉和变异操作所破坏.但是,这也隐含了一种危机,即局部最优个体的遗传基因会急速增加而使进化有可能限于局部解.也就是说,该方法的全局搜索能力差,它更适合单峰性质的搜索空间搜索,而不是多峰性质的空间搜索.所以此方法一般都与其他选择方法结合使用.定理3 具有定理1所示参数,且在选择后保留当前最优值的遗传算法最终能收敛到全局最优解.当然,在选择算子作用后保留当前最优解是一项比较复杂的工作,因为该解在选择算子作用后可能丢失.但是定理3至少表明了这种改进的遗传算法能够收敛至全局最优解.有意思的是,实际上只要在选择前保留当前最优解,就可以保证收敛,定理4描述了这种情况.定理4 具有定理1参数的,且在选择前保留当前最优解的遗传算法可收敛于全局最优解.例2:设,求,编码长度为5,采用上述定理4所述的“在选择前保留当前最优解的遗传算法”进行二、相关函数(命令)及简介本实验的程序中用到如下一些基本的Matlab函数:ones, zeros, sum, size, length, subs, double 等,以及 for, while 等基本程序结构语句,读者可参考前面专门关于Matlab的介绍,也可参考其他数学实验章节中的“相关函数(命令)及简介”内容,此略.三、实验内容上述例1的求解过程为:群体中包含六个染色体,每个染色体用22位0—1码,变异概率为0.01,变量区间为,取Fmin=,遗传代数为50代,则运用第一种终止条件(指定遗传代数)的Matlab程序为:[Count,Result,BestMember]=Genetic1(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,50)执行结果为:Count =50Result =1.0316 1.0316 1.0316 1.0316 1.0316 1.03161.4990 1.4990 1.4990 1.4990 1.4990 1.4990BestMember =1.03161.4990图2 例1的计算结果(注:上图为遗传进化过程中每一代的个体最大适应度;而下图为目前为止的个体最大适应度——单调递增)我们通过Matlab软件实现了遗传算法,得到了这题在第一种终止条件下的最优解:当取1.0316时,.当然这个解和实际情况还有一点出入(应该是取1时,),但对于一个计算机算法来说已经很不错了.我们也可以编制Matlab程序求在第二种终止条件下的最优解.此略,留作练习.实践表明,此时的遗传算法只要经过10代左右就可完成收敛,得到另一个“最优解”,与前面的最优解相差无几.四、自己动手1.用Matlab编制另一个主程序Genetic2.m,求例1的在第二种终止条件下的最优解.提示:一个可能的函数调用形式以及相应的结果为:[Count,Result,BestMember]=Genetic2(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,0.00001)Count =13Result =1.0392 1.0392 1.0392 1.0392 1.0392 1.03921.4985 1.4985 1.4985 1.4985 1.4985 1.4985BestMember =1.03921.4985可以看到:两组解都已经很接近实际结果,对于两种方法所产生的最优解差异很小.可见这两种终止算法都是可行的,而且可以知道对于例1的问题,遗传算法只要经过10代左右就可以完成收敛,达到一个最优解.2.按照例2的具体要求,用遗传算法求上述例2的最优解.3.附录9子程序 Crossing.m中的第3行到第7行为注解语句.若去掉前面的%号,则程序的算法思想有什么变化?4.附录9子程序 Crossing.m中的第8行至第13行的程序表明,当Dim(1)>=3时,将交换数组Population的最后两行,即交换最后面的两个个体.其目的是什么?5.仿照附录10子程序Mutation.m,修改附录9子程序 Crossing.m,使得交叉过程也有一个概率值(一般取0.65~0.90);同时适当修改主程序Genetic1.m 或主程序Genetic2.m,以便代入交叉概率.6.设,求,要设定求解精度到15位小数.。
遗传算法的Matlab实现讲解

Matlab函数调用实现GA
• Matlab的GA函数
[x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[], options);
fitnessfcn — Fitness function nvars — Number of variables for the problem Aineq — Matrix for inequality constraints Bineq — Vector for inequality constraints Aeq — Matrix for equality constraints Beq — Vector for equality constraints LB — Lower bound on x UB — Upper bound on x nonlcon — Nonlinear constraint Function options — Options structure
global Cmin;
Cmin=-10^6; popsize=50; %群体大小 Gene=20; chromlength=20; %字符串长 度(个体长度) pc=0.8; %交叉概率 pm=0.01; %变异概率 Xmax=10; Xmin=0;
[bestindividual,bestfit]=best(pop,fitvalue); %求出群体中适应值最大的 个体及其适应值
Matlab函数调用实现GA
• GA函数调用步骤
第一步:编写适应度函数; 第二步:对GA参数进行设置; options = gaoptimset(‘参数名’, 参数值, …, ‘参数名’, 参数值) 例:options = gaoptimset('PopulationSize', 100) 第三步:调用GA函数; [x fval] = ga(@fitnessfun, nvars) [x fval exitflag output population scores] = ga(@fitnessfcn, nvars) [x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[],options);
matlab遗传算法求函数最小值

matlab遗传算法求函数最小值function obj=yichuan(lb,ub,px,pm)%lb,ub为自变量的下界与上界,px为杂交概率,pm为变异概率popsize=40; %设定种群大小为40maxgen=500; %设定最大遗传代数为500代dim=20; %定义变量的维数为20bits=20; %设定变量的二进制位数为20duan=20;trace=zeros(maxgen,2); %遗传算法性能跟踪chrom=crt(popsize,dim*bits); %创建初始种群gen=0; %代计数器x=bs(chrom,lb,ub,dim,bits);obj=fun(x);figure(1)plot(obj,'-xr');grid;title('初始种群中个体的分布图')xlabel('个体');ylabel('目标函数值');Nesl=popsize; %轮盘选择个数,设定为与种群大小相等gen=0; %遗传代数计数器,设定初始值为0obj=fun(x);fitv=fel(x);%基于适应度的轮盘选择chrom=exrws(chrom,fitv,Nesl);while gen<maxgen%单点交叉后得到大小为popsize子代新种群,与原来的父代种群合并为大小为2*popsize的新种群newchrom=[chrom;exxov(chrom,px)];%最优个体保护策略(先提出种群中的最优个体,然后用轮盘选择出Nesl-1个个体%构建成新的种群,再将最优个体插入新种群的第一行)x=bs(newchrom,lb,ub,dim,bits);fitv=fel(x);[Y,I]=max(fitv);newchrom=[newchrom(I,:);exrws(newchrom,fitv,Nesl-1)];%变异概率为pm的基本位变异,假设有N个染色体发生了变异,将这N个染色体插入原来的种群中,得到大小为popsize+N的新种群chrom=[newchrom;exmut(newchrom,pm)];%最优个体保护策略(先提出种群中的最优个体,然后用轮盘选择出Nesl-1个个体%构建成新的种群,再将最优个体插入新种群的第一行)x=bs(chrom,lb,ub,dim,bits);fitv=fel(x);[Y,I]=max(fitv);chrom=[chrom(I,:);exrws(chrom,fitv,Nesl-1)];%计算新种群的目标函数值x=bs(chrom,lb,ub,dim,bits);obj=fun(x);fitv=fel(x);if gen==20figure(2)plot(obj,'-xr');grid;title('经过20次遗传迭代后种群中个体的分布图')xlabel('个体');ylabel('目标函数值');endif gen==100figure(3)plot(obj,'-xr');grid;title('经过100次遗传迭代后种群中个体的分布图') xlabel('个体');ylabel('目标函数值');endif gen==250figure(4)plot(obj,'-xr');grid;title('经过250次遗传迭代后种群中个体的分布图') xlabel('个体');ylabel('目标函数值');endgen=gen+1;trace(gen,1)=min(obj);trace(gen,2)=sum(obj)/length(obj);aver=zeros(length(fitv),1);aver(:,1)=sum(fitv)/length(fitv);aver=(fitv-aver)</maxgen.^2;trace(gen,3)=sum(aver)/length(fitv);%trace(gen,4)=shang(fitv);% trace(gen,5)=cshang(chrom,duan);endfigure(5)plot(obj,'-xr');grid;title('经过500次遗传迭代后种群中个体的分布图') xlabel('个体');ylabel('目标函数值');obj=min(obj);figure(5)plot(trace(:,1));title('经过500次遗传迭代后种群最优解的变化') xlabel('迭代次数');ylabel('目标函数值');figure(7)plot(trace(:,2));title('经过500次遗传迭代后种群平均值的变化') xlabel('迭代次数');ylabel('目标函数值');figure(8)plot(trace(:,3));xlabel('迭代次数');ylabel('种群的方差');title('500次迭代过程中种群方差的变化');%十进制转换function phen=bs(chrom,lb,ub,dim,bits) [m,n]=size(chrom);li=[1:bits:n-bits+1];lf=[bits:bits:n];phen=zeros(m,dim);for i=1:dimexchrom=chrom(:,li(i):lf(i));for j=1:bitsphen(:,i)=exchrom(:,j).*2^(bits-j)+phen(:,i);endendphen=lb+phen.*(ub-lb)/(2^bits-1);%创建种群function [chrom]=crt(popsize,bits)chrom=zeros(popsize,bits);for i=1:popsizepop=round(rand(1,bits));chrom(i,:)=pop;endfunction mutchrom=exmut(chrom,pm)[m,n]=size(chrom);s=rand(m,n)<=pm;domut=find(sum(s')>0);mutchrom=zeros(length(domut),n);j=1:n;mutchrom=(~chrom(domut,j)).*s(domut,j)+chrom(domut,j). *(~s(domut,j));%基于适应度的轮盘选择function newchrom=exrws(chrom,fitv,Nsel);[Nind,ans]=size(fitv);cumfit=cumsum(fitv);decumfit=[0;cumfit(1:Nind-1)];for i=1:Nselch=rand(1)*cumfit(Nind);for j=1:Nindif (ch<=cumfit(j))&(ch>decumfit(j)),newcode(i)=j;endendendnewchrom=chrom(newcode,:);%单点交叉操作function newchrom=exxov(chrom,px)[nind,lind]=size(chrom);docross=rand(nind,1)<px;temp=chrom(find(docross),:);[m,n]=size(temp);xops=floor(m/2);odd=1:2:m-1;even=2:2:m;for i=1:xopsdot=ceil(rand(1).*lind);mask=[zeros(1,dot) ones(1,lind-dot)];newtemp(odd(i),:)=(temp(odd(i),:).*mask)+(temp(even(i),:).*(~mask));newtemp(even(i),:)=(temp(even(i),:).*mask)+(temp(odd(i),:).* (~mask));endif rem(m,2),newtemp(m,:)=temp(m,:);endnewchrom(find(docross),:)=newtemp;newchrom(find(~docross),:)=chrom(find(~docross),:);%适应度计算function fitv=fel(x)ob=512^2*20-fun(x);fitv=ob/sum(ob);%目标函数function y=fun(x)[nind,lind]=size(x);y=zeros(nind,1);for i=1:lindy=x(:,i).^2+y;end%基本位变异操作function newchrom=mut(chrom,pm)[m,n]=size(chrom);s=rand(m,n)<=pm;i=1:m;j=1:n;newchrom(i,j)=(~chrom(i,j)).*s(i,j)+chrom(i,j).*(~s(i,j)); </px;。
基于遗传算法的最短路径问题及其MATLAB实现(1)
·与@相连且不在当前路径上的节 点有⑥和⑨,其中节点⑨的权较大,为 8.将节点⑨加入到当前路径中,当前 路径变为①一③一⑤一@一⑨。
至此.我们根据染色体找到了一 条路径①一③一⑤一⑥一⑨.这条路径 的长度为12。但是.需要注意的是,并 不是根据优先权编码的染色体都对应一 条路.例如表2染色体。
即将问题的解表示成一个编码串 (染色体).每一染色体对应问题的一 个解。 遗传过程
对染色体进行操作,以产生新的 染色体,通常有不同染色体之间的交叉
操作以及一条染色体的变异操作。 评价与选择
对每条染色体计算其适应值.用 以评价染色体的优劣,从而从父代和子 过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③.其中节点②的权较大,为 6,将节点②加入当前路径.当前路径 变为:①一②; 重复此过程.我们会找到路径 ①一②一④一@一⑤一③.已经没有与 ③相连且不在当前路径的节点,从而找 不到从①到⑨的一条路。当出现这种情 况时.我们抛弃这条染色体.用一条合 法染色体去取代它。 染色体的适应值 染色体的适应值是我们选择较优 染色体的依据。这里染色体的适应值即 为我们得到的路径长度。由于我们得到 的路径为①一③一⑤一⑨一⑨,因此该 染色体的适应值即为此路径的长度:
104
万方数据
节点号
1
2
3
4
5
6
7
8
9
·变异算子:采用交换变异操作. 随机选择染色体上两个位置,将他们的 优先权进行交换,如图4所示。
·选择:根据每条染色体的适应 值,从父代和子代中选择路径最短的 n条染色体.作为父代,进入下一代繁 殖,其中n为种群规模。
最短路径问题matlab求解详尽版

MATLAB 求最短路径利用graphshortestpath 可以求最短路径,具体用法参考MATLAB帮助Examples:S=[1 1 2 2 3 3 4 4 4 4 5 6 6 7 8]; %起始节点向量E=[2 3 5 4 4 6 5 7 8 6 7 8 9 9 9]; %终止节点向量W=[1 2 12 6 3 4 4 15 7 2 7 7 15 3 10]; %边权值向量,有向图,G(9,9)=0; 9个节点G=sparse(S,E,W); %关联矩阵的稀疏矩阵表示G(9,9)=0;P=biograph(G,[],'ShowWeights','on');%建立有向图对象PH=view(P);%显示各个路径权值[Dist,Path]=graphshortestpath(G,1,9,'Method','Dijkstra') %求节点1到节点9的最短路径set(H.Nodes(Path),'Color',[1 0.4 0.4]);%以下三条语句用红色修饰最短路径edges=getedgesbynodeid(H,get(H.Nodes(Path),'ID'));set(edges,'LineColor',[1 0 0]);set(edges,'LineWidth',2.0);%以下是运行结果,节点1到节点9的最短路径为19Dist =19Path =1 3 4 5 7 9利用graphallshortestpaths可以求出所有最短路径Dists=graphallshortestpaths(G) %求所有最短路径Dists =0 1 2 5 9 6 16 12 19 Inf 0 Inf 6 10 8 17 13 20 Inf Inf 0 3 7 4 14 10 17 Inf Inf Inf 0 4 2 11 7 14Inf Inf Inf Inf 0 Inf 7 Inf 10Inf Inf Inf Inf Inf 0 Inf 7 15Inf Inf Inf Inf Inf Inf 0 Inf 3Inf Inf Inf Inf Inf Inf Inf 0 10Inf Inf Inf Inf Inf Inf Inf Inf 0。
基于遗传算法的最短路径问题及其MATLAB实现(1)

子代l 父代2
父代l
子代2 父代2
田3
父代
子代
圈4
结论
将以上算法用maUab实现(程序见 附录).我们找到对应于我们算例的最 短路为:①一③一④一⑦一⑨.路径总 长度为6。
此外.不难发现,使用遗传算法 来进行全局寻优.基本上不需要关于问 题本身的信息.这使得遗传算法的应用 可以扩展到模拟技术.非线性规划问题 等领域,具有广阔的前景。6
其作为问题可行解的集合。初始 种群中染色体个数称为种群规模。
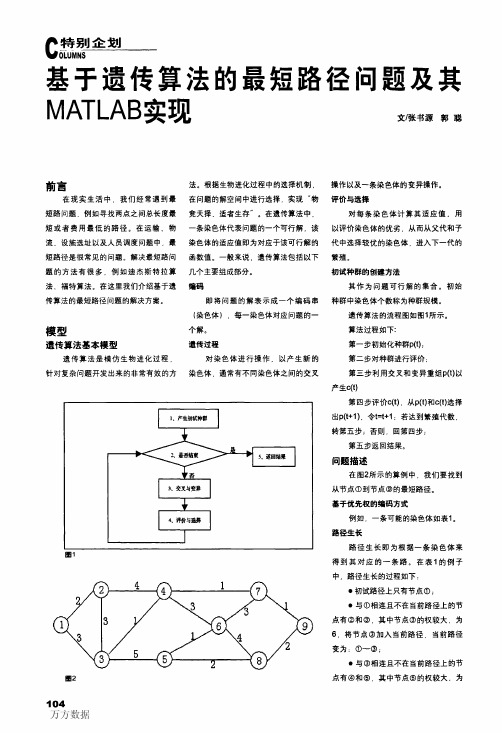
遗传算法的流程图如图1所示。 算法过程如下: 第一步初始化种群p(t); 第二步对种群进行评价; 第三步利用交叉和变异重组p(t)以 产生c(t) 第四步评价c(t).从p(t)和c(t)选择 出p(t+1),令t=t+l:若达到繁殖代数, 转第五步;否则,回第四步: 第五步返回结果。 问题描述 在图2所示的算例中.我们要找到 从节点①到节点⑨的最短路径。 基于优先权的编码方式 例如.一条可能的染色体如表1。 路径生长 路径生长即为根据一条染色体来 得到其对应的一条路。在表1的例子 中,路径生长的过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③,其中节点③的权较大.为 6.将节点③加入当前路径,当前路径 变为:①~③; ·与③相连且不在当前路径上的节 点有④和⑤.其中节点⑤的权较大.为
路径生长过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③.其中节点②的权较大,为 6,将节点②加入当前路径.当前路径 变为:①一②; 重复此过程.我们会找到路径 ①一②一④一@一⑤一③.已经没有与 ③相连且不在当前路径的节点,从而找 不到从①到⑨的一条路。当出现这种情 况时.我们抛弃这条染色体.用一条合 法染色体去取代它。 染色体的适应值 染色体的适应值是我们选择较优 染色体的依据。这里染色体的适应值即 为我们得到的路径长度。由于我们得到 的路径为①一③一⑤一⑨一⑨,因此该 染色体的适应值即为此路径的长度:
遗传算法求解最短路径问题

遗传算法求解最短路径问题最短路径问题的图论描述 在中,与V 中的有序偶(Vi ,Vj )对应的边e ,称为图的有向边,同时与V 中的顶点的无序偶Vi*Vj 相对应的边e ,称为图的无向边,并且如果在中,与V 中的顶点的无序偶Vi*Vj 相对应的边e ,全部都是无向边的话,这个图就叫做无向图,与V 中的有序偶(Vi ,Vj )对应的边e ,都是有向边的话,这个图就叫做有向图。
为了方便实验,与进行仿真分析,本文所有实验的算法都选用的是无向图。
染色体编码具体在进行染色体编码的时候,我么对于各顶点号是进行按自然编排的,然后按照编排的顺序将每个待选的顶点作为一个染色体的基因,基因编排的顺序也就是一条路径之中出现的先后顺序,所以可以看出来,具体的染色体的总长度应该和顶点的个数保持持平。
适应函数对于前面假设的性能函数在此处可以进行一些稍微的改进,因为是求距离,所以此处我们将前面误差的平方和,看成是各个顶点之间距离的平方和,具体如下面公式(3-6)以及公式(3-7)所示:()()()()21x x =v x v x N Ti i f v ==∑ (3-6) ()()1,i i v x d v v += (3-7) 具体就是对于求出来多个xi ,计算出对应的fi,求出其中最小的()min f x 对应的就是最优解。
(,,)G V E =ψ(,,)G V E =ψmin x选择操作从上一次迭代过程之中的染色体,选择二个染色体作为双亲,而这里具体的染色体选择的是交叉的节点,这个是根据前面的适应函数选取的,原理就是选择操作更容易选择距离较短的二个顶点。
交叉与变异操作1、交叉操作:将被选中要进行操作的染色体在进行交叉操作的具体步骤是,先在染色体上产生一个随机数,然后弄清楚这个随机基因的具体位置,从而确定与这个随机基因交叉点的位置,一般来说是同一个位置,然后将与这个随机基因在交叉点交叉的基因进行互换。
具体交叉操作的示意图如图3-1所示:图3-1交叉操作2、变异操作将被选中要进行操作的染色体在进行变异操作的具体步骤是,先在染色体上产生一个随机数,然后弄清楚这个随机基因的具体位置,然后将这个位置之上的基因从0变成1,或者从1变成0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
染色体编码为从1到11的无重复编码,所以不能采用一般的生成一个随机 数替代的办法。此处采用交换变异法。 即随机产生两个数, 交换两个节点的顺序。
例:p[1,2,3,4,5,6,7,8,9,10,11],K1 3, K2 8则新染色体编码为:
p[1,2,8,4,5,6,7,3,9,10,11]
%************Step 3 :
temppath2=path;
for i=1:2:row
[l m]=find(path(i+1,:)~=0);
v2=path(i+1,m);%取出i+1行的非零元素,成一向量path(i,:)=[v1(1:temPm4-1) temp2 v1(temPm4-1+size(temp1):end)];
0 50
0 1
500
500
500
500
500
2
500
500
0
7 500
9
500
500
500
500
500
6
500
7
0 1
2
500
500
500
500
500
500
1
500
1 0
4
500
500
500
500
500
500
500
9
2 4
0
注:为避免计算时无穷大数吃掉小数,此处为令inf=500。
问题要求求出任意两点间的最短路径,Floyd算法采用的是在两点间尝试插 入顶点,比较距离长短的方法。 我思考后认为, 用遗传算法很难找到一个可以统 一表示最短路径的函数, 但是可以对每一对点分别计算, 然后加入for循环,可 将相互之间的所有情况解出。 观察本题可发现, 所有节点都是可双向行走, 则可 只计算i到j的路径与距离,然后将矩阵按主对角线翻折即可得到全部数据。
硕士生考查课程考试试卷
考试科目:
MATLAB教程
考生姓名:
考生学号:
学 院: 专 业:
考 生 成 绩:
任课老师(签名)
考试日期:20年 月 日 午 时至 时
MATLAB教程》试题:
A、利用MATLAB设计遗传算法程序,寻找下图11个端点的最短路径,其中没有 连接的端点表示没有路径。要求设计遗传算法对该问题求解。
ei(Pi1,Pi2)且eiE,若(Pi1,Pi2) (Pi2,Pi1),则G为一个有向图;又设ei的值为
ai,A{a1,a2...am},故G可表示为一个三元组G {P,E,A}
则求最短路径的数学模型可以描述为:
n
min Ai* Ei
i1
s.t. AiA EiE
实验具体: 第一:编码与初始化 因采用自然编码,且产生的编码不能重复,于是我采用了randperm函数产 生不重复的随机自然数。 因解题方法是使用的是计算每一对点, 则我们编码时将 第一个节点单独放入,合并成完整编码。
(1)在表示路径的染色体Tx和Ty中,随机选取两个基因座(不能为起点 基因座)i和j,即将i个基因座和第j个基因座之间的各个基因座定义为交叉 域,并将交叉的内容分别记忆为temp1和temp2。
(2)根据交叉区域中的映射关系, 在个体Tx中找出所有与temp2相同的元 素,在个体Ty中找出所有与temp1相同的元素,全部置为0。
因为节点有11个,可采用一个1行11列的矩阵储存数据, 同时,由于编号 为数字,可直接使用数字编码表示路径的染色体。具体如下:
采用等长可变染色体的方式, 例如由2到9的路径,染色体编码可能为 (2,5,1,8,4,6,9,3,10,7,11),超过9之后的编码,用来进行算子的运算, 不具备实际意义。
500
2
0
6 50
0 1
500
500
500
500
500
500
8
6
0 7
500
1
500
500
500
500 5
00
15Leabharlann 070 500 50
0 9
500
500
500
500
500
1
500
500
0
3 50
0 2
500
500
500
500
500
1
500
3
0 4
500
6
500 5
00
500
500
500
9
500
4
0 50
path(i+1,:)=[v2(1:temPm4-1) temp1 v2(temPm4-1+size(temp2):end)];%基因交叉end
end
path(Popsize,:)=BestS;
for i=1:Popsize
tempPm=rand(1);
if(tempPm<Pm)
temPm6=fix((rand(1)+0.2)*10);
二、实验原理与数学模型(20分)
实现原理为遗传算法原理: 按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选, 使得适应度高的个体被保留下来, 组成新的群体, 新的群体既继承了上一代的信 息,又优于上一代。这样周而复始,群体中个体适应度不断提高,直到满足一定 的条件。
数学模型如下:
设图G由非空点集合V {V1,V2...Vn}和边集合E {e1,e2...em}组成,其中
D、结合自己的研究方向选择合适的问题,利用MATLAB进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目:A
一、问题分析(10分)
如图如示,将节点编号,依次为1.2.3.4.5.6.7.8.9.10.11,由图论知识, 则可写出其带权邻接矩阵为:
0
2
8 1
500
500
500
500
500
500
(3)将个体Tx、Ty进行循环左移,遇到0就删除,直到编码串中交叉区域 的左端不再有0:然后将所有空位集中到交叉区域,而将交叉区域内原有的基因 依次向后移动。因0元素可能较多,在程序实现时,我是将非零元素提出,后面 再合成。
(4)将temp2插入到Tx的交叉区域,temp1插入到Ty的交叉区域。形成 新的染色体[1]。
temppath=path;
roulette=cumsum(Fitness);
for i=1:Popsize
tempP=rand(1);
for j=1:length(roulette)
if tempP<roulette(j)
break;
end
end
path(i,:)=temppath(j,:);
end
B、设计遗传算法求解f(x)极小值,具体表达式如下:
3
f (x1, x2,x3)xi2
i1
5.12xi5.12,i 1,2,3
要求必须使用m函数方式设计程序。
C、利用MATLAB编程实现:三名商人各带一个随从乘船渡河, 一只小船只能容纳 二人,由他们自己划行, 随从们密约,在河的任一岸, 一旦随从的人数比商人多, 就杀人越货, 但是如何乘船渡河的大权掌握在商人手中, 商人们怎样才能安全渡 河?
第二:计算适应度,因取最短路径值,即最小值,常用方法为C-F(x)或C/F(x)(C为一常数),此处采用前一种方式。于是,可进一步计算相对适应度。
第三:选择与复制
采用轮盘赌算法, 产生一个随机值, 比较它与累计相对适应度的关系, 从而 选择出优良个体进入下一代。
第四:交叉。
因编码是不重复的数字, 所以采用传统的交叉方法, 即上一行与下一行对位 交叉,会产生无效路径,于是,采用了不同的交叉方法,具体如下:
三、实验过程记录(含基本步骤、 程序代码 及异常情况记录等) (60分) 首先,写程序,修复Bug。
然后,调试种群数量,遗传代数,交叉概率,变异概率等,不断运行程序, 以达到较理想的状态。
有一次异常情况:算出来的最短距离均为
Matlab
clc;clear;
%初始化参数
%******Step 2 :选择与复制操作******
