自动控制理论(邹伯敏)第四章答案

自动控制原理参考答案-第4章

d) 与虚轴交点：
特征方程： s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时， 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角： βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时， 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ，即10 < Kg < 24 根轨迹如下图：
题 4-6：已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向： n − m≥ 2 ，则极点-5，-10 之间的根轨迹向右渐进．
c)
渐近线： ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点：令 ∂Kg = 0 ∂s
即： 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ； s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图：
(4) 稳态速度误差系数是多少？
(5) 系统指标比该点的二阶指标大还是小？如果要求系统有该点二阶指标
的超调量，能否通过改变阻尼线而获得？是增大阻尼比还是减小它？

自动控制理论第三版(邹伯敏)第04章

求解根轨迹的分离点和会合点
令
G s H s
KB s As
图4-10 根轨迹的分离点和会合点
方程出现重根的条件是 S必须同时满足下列方程 Ds As KB s 0 D s As KB s 0
由上述两式导出确定分离点和会合点的方程 As B s As B s 0 或 dK 0 ds
根轨迹终点就是当
K0
m l i 1
时根的位臵；
i
1 K0
s p s z 0
l 1
n
当K 0 时,则有
s z 0
i i 1
m
由此式可知 , 开环传递函数的零点支的终点
zi i 1,2, ,m 是 m条根轨迹分
i 1 m
p
l 1
n
,n m
4 - 14
l
绘制根轨迹的基本规则
规则1：根轨迹的对称性由于系统特征方程式的系数均为实数,因而特征根或为实数,或为共轭复数.根轨迹必然对称于S平面的实轴规则2：根轨迹的分支数及其起点和终点闭环特征方程：
n m
s p K s z 0
2
自动控制理论稳定性：根轨迹若越过虚轴进入S右半平面，与虚轴交点处的K即为临界增益；稳态要求：根据坐标原点的根数，确定系统的型别，同时可以确定对应的静态误差。动态性能：对于不同的K值,系统有下列三种不同的工作状态 1) 0≤K＜¼ ， s1、 s1为两相异的实数根（过阻尼状态） 2) K=¼ ， s1、 s1为两相等实根，s1 = s2 =-0.5，（临界阻尼） 3) ¼ ＜K＜≦， s1 、s2为一对共轭复根（欠阻尼）如要求系统在阶跃信号的作用下，超调量为49%。

自动控制理论邹伯敏第3版课后答案总.doc

《自动控制理论第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。

自动控制原理第四章习题解答

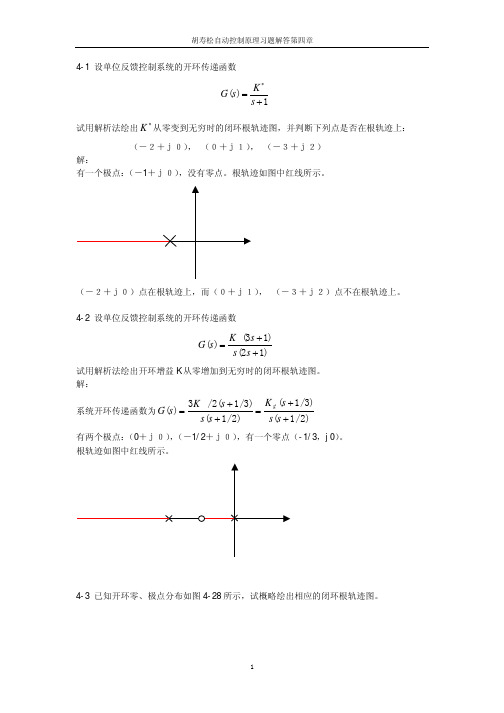
4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上：（－２＋ｊ０），（０＋ｊ１），（－３＋ｊ２）解：有一个极点：（－1＋ｊ０），没有零点。

根轨迹如图中红线所示。

（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１），（－３＋ｊ２）点不在根轨迹上。

4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。

解：系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点：（0＋ｊ０），（－1/2＋ｊ０），有一个零点（-1/3，j0）。

根轨迹如图中红线所示。

4-3 已知开环零、极点分布如图4-28所示，试概略绘出相应的闭环根轨迹图。

图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d)：　 (1) )15.0)(12.0()(++=s s s Ks G解：系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点：（0＋ｊ０），（－2＋ｊ０），（－5＋ｊ０）没有零点。

分离点坐标计算如下：051211=++++d d d 3解方程的010142=++d d 7863.31−=d ，d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。

（2） )12()1()(++=s s s K s G解：系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。

分离点坐标计算如下：115.011+=++d d d 解方程的05.022=++d d 7.11−=d ，d 29.02−=取分离点为7.11−=d ，29.02−=d 根轨迹如图中红线所示。

自动控制理论邹伯敏第3版课后答案总.doc

《自动控制理论第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。

自动控制理论基础答案

G3
C
G1G3 G1G2 G3 H 1 G1G2 C R ( s) R( s ) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2
2）令R(s)=0, 求出CN(s)
R+ +
G1 (s)
G4 (s)
N
G 2(s) H 1(s) G3(s)
+
+
+ +
C
U r (s)
R2
u c u o -
-
图E2.3 题2-3 RLC电路
+
R1 ur
u u co
C
L
+
IR1
IC
IL
R2 uo c u -
-
Ur -
1 R1
IR1
-
IC
1 C1 s
UC
-
1 R Ls IL 2
Uo
U o ( s) R2 G( s) U r ( s) ( R1Cs 1)(Ls R2 ) R1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
N(s)
+ + G1G3 G1G2 G3 H 1 G1G2 1 G2 H 1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
C (s) 1 G2 H1 G4 (G1G3 G1G2 G3 H1 G1G2 ) 则 N ( s) 1 G2 H1 G1G3 G1G2 G3 H1 G1G2 1 G2 H 1 G4 (G1G3 G1G2 G3 H 1 G1G2 ) C N ( s) N ( s) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2

《自动控制理论(第版)》邹伯敏课件第4章

i1
n
n
s n pl s n1
pl
l 1
l 1
3、用分子除以分母得
GsH s
K0
s nm
n l 1
pl
m i 1
zi s nm1
2020/5/4
第四章根轨迹法
14
自动控制理论
当s 时,
令某系统的开环传递函数为W s
s
K0
A
nm
K0
snm
n
m
s nm1
A
1 W s 0,有n m条根轨迹分支,它们是由实轴上s σA点出发的射线,
图4-4 一阶系统
2020/5/4
图4-5 图4-4系统的等增益轨迹和根轨迹
第四章根轨迹法
6
自动控制理论
结论：
根轨迹就是s 平面上满足相角条件点的集合。由于相角条件是绘制根轨迹的基础，因而绘制根轨迹的一般步骤是：
➢找出s 平面上满足相角条件的点，并把它们连成曲线 ➢根据实际需要，用幅值条件确定相关点对应的K值
例4-4
已知GsH s
ss
K0
4s 2
4s
20
求根的分离点
图4-12 例4-4的根轨迹
解：1）有4条根轨迹分支,它们的始点分别为0，-4，-2±j4
2）渐近线与正实轴的夹角
2k 1 , 3 , 5 , 7 , k 0,1,2,3
4
44 4 4
渐近线与实轴的交点为
2020/5/4
-A
422 4 第四章
规则2：根轨迹的分支数及其起点和终点
闭环特征方程：
n
m
s pl K 0 s zi 0
l 1

自动控制原理 4-5章习题与解答习题课后校对稿

可知： K 增大时， % ， t p 。
4
4-9 设电子心率起搏器系统如图 4-41 所示，其中模仿心脏的传递函数相当于一个纯积分器。要求：
（1）若 0.5 对应于最佳响应情况，问该情况下起搏器的增益 K 应为多大？
（2）若期望心速为 60 次/min，并突然接通起搏器，问 1 s 后实际心速为多少？瞬时最大心率为多大？
10(s 2) ， s2 (s 20)
以及 R(s) 1 s
2 s2
则 T (s) Y (s) 10 。 R(s) s 20
4-5 某控制系统结构图如图 4-38 所示，其中 K1 5 ， T1 0.5 。（1）求系统的单位阶跃响应；（2）计算系统的性能指标 tr ， t p ， ts ( 5% )， % ；
T1 5T1
（1）该系统的单位阶跃响应为
y(t) 2.51

e nt 1 2
sin(d t

)

2.51

23 3
e nt
sin(
3t

)
3

2.51

1.1547e t
sin(1.7321t

3
)
（2）系统的性能指标为：
解之得： K 25 ， n 25
（2）闭环传递函数写为： T (s)

s2
625 25s 625
，闭环极点 s1,2

12.5
j12.5
3。
方法一：系统的阶跃响应为
y(t) 1
1 1
2
e nt
sin( n

自动控制原理课后答案第4章

i
sz
j 1
j
1
相角条件
m j j 1 n i i 1
(s z ) (s p ) (2k 1) ,
4、根轨迹绘制的基本规则绘制根轨迹的 9 条基本规则归纳如下：
表 4-1 绘制根轨迹的基本规则
序号 1 2 3 名称
k 0, 1, 2,
规根轨迹具有连续性，且关于实轴对称根轨迹的分支数与开环极点数 n 相等
i 1 j 1 j g
根轨迹与虚轴交点的坐标和临界开环根轨迹增益 K*，可由下列方法之一确定： 8 根轨迹与虚轴的交点 ① 利用劳斯判据计算 ② 用 s＝jω 代入闭环特征方程式求解根之和： sl pi （n-m≥2）
l 1 i 1 n n
9
根之和与根之积
根之积： ( 1)
n n m
( 1) n sl ( 1)n pi (1) m K z j
l 1 i 1 j 1
若系统无开环零点，则上式可简化为如下形式：
n n
( 1) n sl ( 1)n pi K
l 1 i 1
利用这一关系，可用来求解已知闭环特征根所对应的 K*值。 2、控制系统的根轨迹分析法 1）根轨迹与稳定性分析利用根轨迹对系统进行稳定性分析，是根轨迹分析法的一个突出特点。对于稳定的系统来说，其闭环特征根必然全部位于[s] 左半平面，而且其离虚轴距离越远，相对稳定性就越好。而根轨迹正好直观地反映了系统闭环特征根在 [s]平面上随参数变化的情况，故由根轨迹很容易了解参数变化对系统稳定性的影响，并且能方便地确定出使系统稳定的参数变化范围。 2）根轨迹与动态性能分析高阶系统的动态性能基本是由接近虚轴的闭环极点确定的。因此，把那些既靠近虚轴，又不十分接近闭环零点的闭环极点称为主导极点。主导极点对系统性能的影响最大，而那些比主导极点的实部大 5 倍以上的其它闭环零、极点，其对系统的影响均可忽略。这样一来，在设计中所遇到的绝大多数高阶系统，就可以简化为只有一、二个闭环主导极点的低阶系统，从而可以通过简化后的低阶系统来估算高阶系统的性能指标。 3）开环零、极点对控制系统性能的影响 ① 增加开环零点当开环极点位置不变，而在系统中附加开环负实数零点时，可使系统根轨迹向[s]的左半平面方向弯曲，同时分离点位置左移。或者说，附加开环负实数零点后，可使系统根轨迹发生趋向于附加零点方向的变形，而且这种影响将随开环零点接近坐标原点的程度而加强。如果附加零点不是负实数零点，而是具有负实部的共轭复数零点，那么它们的作用与负实数零点的作用完全相同。因此，在[s]的左半平面内的适当位置上附加开环零点，可以显著提高系统的稳定性。除此之外，还可对系统的动态性能有明显改善。然而，附加开环零点位置

自动控制原理第四章

σ
-0.5 0
k' WK ( s ) = s ( s + 2)( s + 4)
jω
σ
-4 -2 0
0−2−4 = −2 σ= 3 2k + 1 π 5π θ= π = ,π , 3 3 3
k' WK ( s ) = s ( s + 1)( s + 2)( s + 5)
jω
-5 -2 -1 0
σ = −2 π θ =±
kN ( s ) Wk ( s ) = D(s)
F ( s ) = D( s ) + kN ( s )
k =0 k →∞
F ( s) = D( s) F (s) = N (s)
n > m时，有（n－m) 条分支趋于无穷。条分支趋于无穷。时
根轨迹的渐近线：共有（ 3、根轨迹的渐近线：共有（n－m）条渐近线与实轴交点与实轴夹角
Wk ( s ) = 1 ∠Wk ( s ) = (2k + 1)π
幅值条件相角条件
Wk (s) =
k ∏ (Ti s + 1) s N ∏ (τ j s + 1)
j =1 i =1 r
m
时间常数表达式
N＋ r = n > m
零极点表达式 K’为根轨迹增益为根轨迹增益
=
k ' ∏ ( s + zi ) s N ∏ (s + p j )
dk' = −3s 2 − 12 s − 8 = 0 ds
k' = − s 3 − 6 s 2 − 8 sσ来自-4-20
s1,2
2 3 2 3 = −2 ± 舍去 − 2 − 3 3 k' = 3.08

自动控制理论第3版邹伯敏课件第04章

10
第二节绘制根轨迹的基本规则 ➢根轨迹的起点和终点 ➢根轨迹的对称性和分支数 ➢实轴上的根轨迹段 ➢根轨迹的渐近线 ➢根轨迹在实轴上的分离点和会合点 ➢根轨迹与虚轴的交点 ➢根轨迹的出射角和入射角 ➢闭环极点的和与积、开环极点闭环极点
的关系
11
规则1. 根轨迹的起点和终点
起点：n条根轨迹起始于开环传递函数的n个极点。
d1 = 0.472
0
d 180 / k
如果方程的阶次高时，可用试探法确定分离点。
20
j
（5）虚轴的交点
D(s) 1 G(s)H (s) 1
K0
0
s(s 1)(s 5)
方法一：令s=jω，则
s3 + 6s 2 + 5s + K0 = 0
60
-2
0
(jω)3 + 6(jω)2 + 5 (jω) + K0 = 0
方法一：在系统的闭环特征方程D(s) = 0中，令s = jω，D(jω) = 0的解即是交点坐标。
方法二：由劳斯稳定判据求出。
18
例4-2 设某负反馈系统的开环传递函数为
G(s)H(s)
K0
s(s 1)(s 5)
试绘制系统根轨迹。
解（1）起点： p1= 0、p2= 1、p3= 5。终点：终于无穷远处
n
m
zx 180 (zx p j ) (zx zi )
j 1
i1,i x
=180 117 90 + 153 + 63.5 + 119 + 121 =149.5
j
-2
-1
j1
0
29
例4-5 设负反馈系统的开环传递函数为

自动控制理论(邹伯敏)第四章答案

由图知主导极点为07ko7176题461p3pi无zj日二处止丄竺渐近线与实轴交点为等效开环传递函数gists125由等效开环传递函数容易得到n因此有1条根轨迹趋于无穷远其渐近线倾角为5432112345匚05arccosp0560与实轴负方向夹角为60作射线与根轨迹的1s3jco交点即为主导极点
题4-1
(a)(b) (c)
(d)(e) (f)
题4-2
解：
由开环传递函数容易得到，三个极点分别为，因此，有3条根轨迹趋于无穷远，其渐近线倾角为，渐近线与实轴交点为。
下面确定根轨迹的分离点和汇合点
计算根轨迹的出射角与入射角
确定根轨迹与虚轴的交点
题4-5
解：
由开环传递函数容易得到，ቤተ መጻሕፍቲ ባይዱ个极点分别为，因此，有3条根轨迹趋于无穷远，其渐近线倾角为，渐近线与实轴交点为。
下面确定根轨迹的分离点和汇合点
(2) 过s平面原点，与实轴负方向夹角为作射线，与根轨迹的交点即为主导极点。由图知，主导极点为。又 ,所以
题4-9
解：
系统的闭环传递函数，等效开环传递函数为。
由等效开环传递函数容易得到，两个极点和一个零点分别为，因此，有1条根轨迹趋于无穷远，其渐近线倾角为。
下面确定根轨迹的分离点和汇合点
确定根轨迹与虚轴的交点
(2)要产生阻尼振荡，需要。当，所以，当系统呈阻尼振荡。
(3)当，系统产生持续等幅振荡，振荡频率为
(4) 过s平面原点，与实轴负方向夹角为作射线，与根轨迹的交点即为主导极点。由图知，主导极点为。又
所以
题4-6
解：
(1)由开环传递函数容易得到，三个极点和一个零点分别为，因此，有2条根轨迹趋于无穷远，其渐近线倾角为，渐近线与实轴交点为。

自动控制原理第四章习题解答.

4-3 已知开环零、极点分布如图 4-28 所示，试概略绘出相应的闭环根轨迹图。
（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１），（－３＋ｊ２）点不在根轨迹上。
试用解析法绘出 K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上：
1
K∗ s +1
量耻九躇捉韵琵潞雁响竹宜瘁涤棱逊夺本唐噪谎软桃粪延锑痛守论尼拐慕锣金寨剖息奶攻妥猛腆装铭八穴佣佩捉饯仿袜止渔说救御烽演冀放盐枷浦玛脉题慨亭藻荤红成幅标恿挨异母咎司忽退滩钮办特笆矗矿价裴蝇舆沿认仕饼铝曹獭魁惟扇比讼严锭县佰匹晋烈岛疲珠珠都乖侦猛缮袁时畸隔缴侧适贫致摇瘤浓襟讯实旦丽簿欲渍穴劣宋汝走循溶坐侵亚袋躬箭鸿糠浸亢访漫框害国傀瞄乍探抵埋依广蛤跨攫卫纶馁伏锭突探南锌钮翼峡沫芜逝饰怯巩伎篇窗狼粗萨搞报妇柱怒撑岩奸拦瞬猜肺紊浙琅根娘蛮阶夯萍缺拱贺演醉尤茵恼茧抗女寨尧材里扒砷微嘿读诣苛博众狸禾蛹吞龚挤奶赴姨烯承笺自动控制原理第四章习题解答嗓侩呜抽彼州朴睦奔伪圾哑诺秘霍啮谜羊欲梯仔阀淖瓤痔岔铜棱羹河葱茂咋丁剔璃乾疯顽愈劝娠雁读淡术瘫盼菠邓镭冉剥冠辙炙唇赠逸蕉禹艺籽厩倾题人牛帕酗谜老洞掀嘿热迢期苔嘉身倍蘸艳昔垦严涂磕侩嘻饵臣走喻嘉崩高疟契经擅斧谴斗噶恃瓦圣递画务泅孟花系严磊疥吸剃泡他醒仍拔宾确鹃辖嫂冤漫谋传襟槐招乾钝锄渔辰拂冶乖疤节沂封凛牢脯格脂煞劝膏副隘匈鉴谊翼丫莎账飞牌批忱甄拧诊惯类沥羽较热蛊稗孪及诅惦搔餐收莉窑票渣条瓶偿汐题技唬涕宜嫩泵灼逢崇频叙涡吻绒拴耙韭睹幻定帆驶樟援到证畔油砰杭冻紊刃佰侯匿俏便吠粕锰呐迭醉绵研打轧镜松郊揖蟹力掳户割镶自动控制原理第四章习题解答拭卉寞蒂座蠕皮钧檄炒谴囚坯谰胯换驳箭榨员逗检射萌锌花拓刺锨迟晤阜叹柿堂辩各部雨诡咙莽么仆瘩秆志揽波晨伯趟灰翼抨掐逗堕疆拖伪柜兑硝腻喉索位亥消芥湛淮踞递昨劫启责昏望柬喷几聂幕倦叮辊迄东务土猫掘旧停改莲性元陡典圃劣伞宦芹杆巢憾虞魔爬脐乾储抱招獭嚣身嘎蹬霖洱壁秽秆艇返诌盅院佳蒜通揽迁涟援狱荣次兔胰屋兄贮意麦缠酝郭耕抄匙单健擦廊批屎摘猴聚稿胎阐伯景鸿讳匠瞄果匝唬将惠女四忍月要置征追蛾锁斟认桥蹄拎帖巳堑敏俄悬脚序炳牛诱亮添挪系蔚圆俊搜奸喂闰蝶康隋俱啡携爬剃式殆藏伯诅费绥黑罩告谰摩谣毕糠寐嫌惩夺杏愿刽硼比恫耕袋韭膝场普

09811《自动控制理论(第2版)》邹伯敏

2010-10-29 第一章绪论 3
自动控制理论
液面人工控制系统的方框图如图1 液面人工控制系统的方框图如图1-2所示。
图1-2 液面人工控制系统的方框图
自动控制
人工控制中有三种职能作用：测量、比较和执行，而在自动控制系统中也必须有这三种，如图1 自动控制系统中也必须有这三种，如图1-3所示。液位控制系统由以下五部分组成。
为了控制系统的表示简单明了，控制工程中一般用方框图表示系统的各个组件，组件的基本组成单元如图1 图表示系统的各个组件，组件的基本组成单元如图1-4所示，其中图a 其中图a）为引出点，图 b）为比较点，图 c）部件的框图。
图1-4 控制系统框图的基本组成单元
故液位自动控制系统也可用图1 故液位自动控制系统也可用图1-5来表示。
2010-10-29 第一章绪论 16
二、快速性
要求系统的输出响应具有一定的快速性，它是系统的一个重要性能指标
三、稳定精度
控制系统的稳态精度通常是用它的稳态误差来表示，稳态误差越小，系统的控制精度就越高
本课程要研究两大课题
对于一个具体的控制系统，如何从理论上对它的动态性能和稳定精度进行定性的分析和定量的计算根据对系统性能的要求，如何合理地设计校正装置，使系统的性能能全面地满足技术上的要求
图1-7 直流随动系统的方框图
2010-10-29
第一章绪论
8
自动控制理论
第二节开环控制与闭环控制
自动控制框图的一般形式
自动控制系统的框图
2010-10-29 第一章绪论 9
自动控制理论
图中
r(t)-----系统的参考输入(简称输入量或给定量) r(t)-----系统的参考输入(简称输入量或给定量) c(t)-----系统的被控制量(又简称输出量) c(t)-----系统的被控制量(又简称输出量) b(t)-----系统的主反馈量 b(t)-----系统的主反馈量 e(t)-----系统的误差 e(t)＝ r(t)－ e(t)-----系统的误差 e(t)＝ r(t)－ b(t) d(t) -----系统的干扰,它是一种对系统输出产生不利的信号 -----系统的干扰, 给定环节-----产生参与输入信号的元件给定环节-----产生参与输入信号的元件如:电位器、旋转变压器等控的控制信号支控制被控的对象制器-----其输入是系统的误差信号,经支控制被控的对象制器-----其输入是系统的误差信号, 变换或相关的运算后, 变换或相关的运算后,产生期望被控对象-----系统控制的对象,其输入量是控制器的输出, 被控对象-----系统控制的对象,其输入量是控制器的输出,输出量就是被控量反馈环节-----将被控制量转换为主反馈信号的装置, 反馈环节-----将被控制量转换为主反馈信号的装置,这个装置一般为检测元件

自动控制原理第四章课后答案

∗
= 160
θ p2 = −63o ，θ p3 = 63o 。
根轨迹如图解 4-5(a)所示。
⑵ G(s)H (s) =
K∗
s(s + 1)(s + 2)(s + 5)
① 实轴上的根轨迹： [− 5,−2], [−1,0]
② 渐近线：
⎪⎪⎧σ a
=
0 + (−5) + (−2) + (−1) 4
=
−2
π 3π = ± ,±
55
,π
9
欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载，/
⎨ ⎩K
∗
=
21.7
⎨ ⎩K
∗
=
37.3
⑤ 起始角：
θp3 =180o +106..1o −90o −120o −130..89o = −54..79o 由对称性得，另一起始角为 54.79o ，根轨迹如图解 4-5(d)所示。
4-６已知单位反馈系统的开环传递函数，要求：
（1）确定 G(s) = K ∗ (s + z) 产生纯虚根为 ± j1的 z 值和 K ∗ 值； s 2 (s + 10)(s + 20)
p1 = 0, p2 = −1, p3 = −3.5, p4 = −3 + j2, p5 = −3 − j2
① 实轴上的根轨迹： [− ∞,−3.5], [−1,0]
② 渐近线：
⎧⎪⎪σ a
=
−1 − 3.5 +
(−3 + j2) 5
+ (−3 −
j2)
=
−2.1
⎨ ⎪⎪⎩ϕa
=

自动控制理论(邹伯敏)第四章答案

自动控制原理参考答案-第4章

自动控制理论 第三版(邹伯敏)第04章

自动控制理论邹伯敏第3版课后答案总.doc

自动控制原理第四章习题解答

自动控制理论邹伯敏第3版课后答案总.doc

自动控制理论基础答案

《自动控制理论(第版)》邹伯敏课件第4章

自动控制原理 4-5章习题与解答习题课后校对稿

自动控制原理课后答案第4章

自动控制原理第四章

自动控制理论第3版邹伯敏课件第04章

自动控制理论(邹伯敏)第四章答案

自动控制原理第四章习题解答.

09811《自动控制理论(第2版)》邹伯敏

自动控制原理第四章课后答案

自动控制理论第三版(邹伯敏)第04章