一个小波变换实例及Matlab实现

合集下载

MATLAB小波变换指令及其功能介绍(超级有用)解读

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能：一维离散小波变换格式：[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT说明：[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname' 对信号X 进行分解，cA、cD 分别为近似分量和细节分量；[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。

(2) idwt 函数功能：一维离散小波反变换格式：X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明：X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。

'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。

X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。

2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换-----------------------------------------------------------(1) wcodemat 函数功能：对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式：Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明：Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ；NB 伪编码的最大值，即编码范围为 0～NB，缺省值 NB＝16；OPT 指定了编码的方式（缺省值为 'mat'），即：别可以实现一维、二维和 N 维 DFTOPT＝'row' ，按行编码OPT＝'col' ，按列编码OPT＝'mat' ，按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数（缺省值为 '1'），即：ABSOL＝0 时，返回编码矩阵ABSOL＝1 时，返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能：二维离散小波变换格式：[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明：[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻；cA，cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量；[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。

小波变换-图像融合matlab代码

%对图像进行放大算子的运算
PIC3 = conv2(conv2(Y, 2*fw, 'valid'),2*fw','valid');
%第i1级图像重构；
PIC1 = PIC3 + L{i};
%选取图像范围
PIC1 = PIC1(1:k1(i),1:k2(i));
% %end;
% %end;
% %%
% %for k=1:256,
% % p1(k)=p1(k)/(d);
% % p2(k)=p2(k)/(d);
% %end;
%
% %for i=1:256
% % for j=1:256
% % p3(i,j) =p3(i,j)/(d);
%图像隔行隔列插值扩展恢复到原尺寸图像
[c d] = size(Y4);
Y6 = zeros(2*c, 2*d);
Y6(1:2:2*c,1:2:2*d) = Y4;
Y7 = zeros(2*c, 2*d);
%PIC2 = X2;
X1 = PIC1;
X2 = PIC2;
%定义滤波窗口；
fw = 1/16.*[1 4 6 4 1];
z =3;
L = cell(1,z);
L1 = cell(1,z);
for i = 1:z % N1
G3 = conv2(conv2(Y3, fw, 'valid'),fw', 'valid');
%将图像进行隔行隔列减半
[a b] = size(G2);
Y4 = G2(1:2:a, 1:2:b);

第5章小波变换的matlab实现

19
A3=wrcoef('a',C,L,'db1',3); D1=wrcoef('d',C,L,'db1',1); D2=wrcoef('d',C,L,'db1',2); D3=wrcoef('d',C,L,'db1',3);
Approximation A3 600
Detail D1 40
20 400
2000 1500 1000
500 0 0
50
Approximation cA3
200
400
600
Detail cD2
40 20
0 -20 -40
0
50
Detail cD1
500 1000 1500 2000 Detail cD3
0 0
-50
-50 0
-100
500
1000
0
200
400
600
18
重构系数命令：wrcoef 格式：
50 100 150 200 250
50 100 150 200 250
Horizontal Detail H1
50 100 150 200 250
50 100 150 200 250
Diagonal Detail D1
50 100 150 200 250
50 100 150 200 250
32
二维逆变换命令：idwt2 格式：
title('Vertical Detail V1')subplot(2,2,4);
image(wcodemat(D1,192));title('Diagonal Detail

matlab中图像小波变换的应用实例

matlab中图像小波变换的应用实例如下：1 一维小波变换的Matlab 实现(1) dwt 函数功能：一维离散小波变换格式：[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)说明：[cA,cD]=dwt(X,'wname') 使用指定的小波基函数'wname' 对信号X 进行分解，cA、cD分别为近似分量和细节分量；[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组Lo_D、Hi_D 对信号进行分解。

(2) idwt 函数功能：一维离散小波反变换格式：X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)X=idwt(cA,cD,Lo_R,Hi_R,L)说明：X=idwt(cA,cD,'wname') 由近似分量cA 和细节分量cD 经小波反变换重构原始信号X 。

'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器Lo_R 和Hi_R 经小波反变换重构原始信号X 。

X=idwt(cA,cD,'wname',L) 和X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号X 中心附近的L 个点。

2 二维小波变换的Matlab 实现二维小波变换的函数-------------------------------------------------函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换-------------------------------------------------------------(1) wcodemat 函数功能：对数据矩阵进行伪彩色编码格式：Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明：Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵X 的编码矩阵Y ；NB 伪编码的最大值，即编码范围为0～NB，缺省值NB＝16；OPT 指定了编码的方式（缺省值为'mat'），即：OPT＝'row' ，按行编码OPT＝'col' ，按列编码OPT＝'mat' ，按整个矩阵编码ABSOL 是函数的控制参数（缺省值为'1'），即：ABSOL＝0 时，返回编码矩阵ABSOL＝1 时，返回数据矩阵的绝对值ABS(X)(2) dwt2 函数功能：二维离散小波变换格式：[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明：[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号X 进行二维离散小波变幻；cA，cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量；[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器Lo_D 和Hi_D 分解信号X 。

小波变换matlab

小波变换是一种在信号和图像处理中广泛应用的工具。

在Matlab 中，你可以使用内置的函数来进行小波变换。

以下是一个基本的示例，显示了如何在Matlab中使用小波变换：
```matlab
首先，我们需要导入图像或者信号
I = imread('lena.bmp'); 导入图像
转换为灰度图像
I = rgb2gray(I);
使用'sym4'小波基进行小波分解
[C, S] = wavedec2(I, 1, 'sym4');
显示小波分解的结果
figure, wave2gray(C, S, -6);
```
在这个例子中，我们首先导入了图像，然后将其转换为灰度图像。

接着，我们使用`wavedec2`函数和`'sym4'`小波基进行小波分解。

最后，我们使用`wave2gray`函数显示小波分解的结果。

这只是使用Matlab进行小波变换的一个基本示例。

实际上，你
可以根据你的需求来选择不同的小波基（例如'haar'、'Daubechies'、'Symlet'、'Coiflet'等）以及进行不同级别的小波分解。

同时，Matlab也提供了其他的小波变换函数，例如`wavelet`和`wfilters`等，可以满足不同的需求。

小波变换(内附奇异值分析matlab程序)

2、算法及其应用实例
小波在信号的奇异性检测中的应用举例信号的突变点和奇异点等不规则部分通常包含重要信息，一般信号的奇异性分为两种情况：（1）信号在某一时刻其幅值发生突变，引起信号的非连续，这种类型的突变称为第一类型的间断点；（2）信号在外观上很光滑，幅值没有发生突变，但是信号的一阶微分有突变发生且一阶微分不连续，这种类型的突变称为第二类型的间断点。应用小波分析可以检测出信号中的突变点的位置、类型以及变化的幅度。
程序代码
load nearbrk; x=nearbrk; %使用db4对信号进行2层分解 [c,l]=wavedec(x,2,‘db4’); subplot(411); subplot(4,1,i+2); plot(x); plot(d); ylabel('x'); ylabel(['d',num2str(3-i)]); %对分解的第六层低频系数进行重构 end a=wrcoef('a',c,l,'db4',2); subplot(412); plot(a); ylabel('a2'); for i=1:2 %对分解的第2层到第1层的高频系数进行重构 a=wrcoef('a',c,l,'db4',3-i);
3、小波分析的优缺点
小波变换与Fourier变换相比，是一个时间和频域的局域变换因而能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析（Multiscale Analysis），解决了Fourier变换不能解决的许多困难问题。小波变换存在以下几个优点：小波变换存在以下几个优点： (1)小波分解可以覆盖整个频域(提供了一个数学上完备的描述) (2)小波变换通过选取合适的滤波器，可以极大的减小或去除所提取得不同特征之间的相关性 (3)小波变换具有“变焦”特性，在低频段可用高频率分辨率和低时间分辨率(宽分析窗口)，在高频段，可用低频率分辨率和高时间分辨率(窄分析窗口) 。 (4)小波变换实现上有快速算法(Mallat小波分解算法)。

小波变换原理matlab

小波变换原理及在MATLAB中的应用小波变换是一种有效的信号分析方法，可以将时间序列信号按照不同频率分解为时频域上的小波系数。

其原理是利用小波基函数对信号进行多尺度分析，从而揭示信号中的局部特征和潜在信息。

在MATLAB中，小波变换得到了广泛的应用，可以用于信号处理、图像处理、数据压缩等领域。

小波变换原理小波变换的基本原理是将原始信号通过小波基函数的卷积运算，得到不同频率和时域范围的小波系数。

小波基函数是由母小波函数通过平移和尺度变换得到的。

小波基函数具有局部化特性，可以更精准地描述信号的局部特征。

小波变换可以通过连续小波变换（CWT）和离散小波变换（DWT）来实现。

CWT将小波基函数连续地与信号进行卷积，得到连续尺度的小波系数。

而DWT则通过对信号进行多级离散尺度下采样和滤波，从而得到离散的小波系数。

小波系数表示了信号在不同频率和时域范围上的能量分布，可以用于分析信号的频谱特性、辨识信号中的脉冲或噪声等。

小波变换能够同时提供时间和频率信息，比传统的傅里叶变换更符合实际问题的需求。

MATLAB中的小波变换MATLAB提供了丰富的小波变换函数和工具箱，方便用户进行小波分析和处理。

以下是一些常用的小波变换函数及其功能：wavefun函数该函数用于生成不同类型的小波基函数，供小波变换使用。

可以选择不同的小波类型（如“haar”、“db”、“sym”等）和小波尺度，生成对应的小波基函数。

cwt函数该函数实现了连续小波变换（CWT），可以对信号进行连续尺度的小波分解。

可以选择不同尺度和小波基函数进行分析，并可设置阈值进行信号去噪。

dwt函数该函数实现了离散小波变换（DWT），可以对信号进行多级离散尺度的小波分解。

可以选择不同小波基函数和分解层数，得到对应的离散小波系数。

idwt函数该函数实现了离散小波变换的逆变换，可以根据离散小波系数进行重构。

可以选择相同的小波基函数和分解层数，得到原始信号的重构。

wdenoise函数该函数基于小波变换提供了信号去噪的功能。

matlab morlet小波变换

在MATLAB中，Morlet小波变换可以通过使用内置的cwt函数来实现。

cwt函数用于执行连续小波变换，它支持多种小波类型，包括Morlet小波。

以下是一个示例代码，演示如何在MATLAB中执行Morlet小波变换：
matlab复制代码
% 创建一个信号
x = sin(2 * pi * 10 * (0:0.01:1)) + randn(size(0:0.01:1));
% 定义Morlet小波的参数
scales = logspace(-1, 2, 128); % 尺度范围
waveletName = 'morl'; % 小波名称
% 执行Morlet小波变换
[cwtmatr, freqs] = cwt(x, scales, waveletName);
% 绘制结果
imagesc(freqs, 1:length(x), abs(cwtmatr));
colormap(jet);
xlabel('Frequency (Hz)');
ylabel('Time (s)');
title('Morlet Wavelet Transform');
在上述示例中，首先创建了一个包含噪声的正弦波信号。

然后，定义了Morlet小波的参数，包括尺度范围和小波名称。

接下来，使用cwt函数执行Morlet小波变换，并将结果存储在cwtmatr和freqs变量中。

最后，使用imagesc函数绘制了变换结果的图像。

请注意，cwt函数的参数可以根据需要进行调整，例如可以更改尺度范围、小波类型等。

第5章小波变换的matlab实现

1.Matlab中小波种类
15种经典类小波：Harr小波、Morlet小波、Mexican
hat小波、Gaussian小波
正交小波：db小波、对称小波、Coiflets小波、
Meyer小波
双正交小波查看命令
wavemngr('read',1)
1
小波分析示例
一维连续小波
1. coefs = cwt(s,scale,’wname’)
46 43 40 37 34 31 28 25 22 19 16 13 10
7 4 1
100 200 300 400 500 600 700 800 900 1000 time (or space) b
2
scales a
C=cwt(noissin,2:2:128,’db4’,’plot’)
Absolute Values of Ca,b Coefficients for a = 2 4 6 8 10 ...
1.X=waverec(C,L,’wname’) 2.X=waverec(C,L,Lo_R,Hi_R) 例子： A0=waverec(C,L,’db1’); 重构最大误差： Err=max(abs(s-A0))
20
original Level 3 Approximation Original Approximation
低频系数 150 100 0 800
500 1000 1500 2000 2500 3000 3500 4000 30
原始信号高频系数
700
20
600 10
500 0
400
-10 300
-20 200
100 0
200 400 600 800 1000 1200 1400 1600 1800 2000

MATLABwavelate小波变换

MA TLAB语言实现小波变换使用上面的误差分析方法,我们选择比较好的、适合地震数据处理的小波基函数,运用MA TLAB语言编制小波程序来实现小波分析。

3.1 小波变换程序的实现function For-cwt(Filein, Fileout, traces, samples, scale, wavelet)% For-cwt(Filein, Fileout, traces, samples, scale, wavelet)连续小波变换%输入Filein: 原始的地震剖面文件(*.sgy)% Fileout:小波分解剖面文件(*.sgy)% traces: 整个剖面文件的总道数% samples:每一道地震记录的采样点数% scale: 小波变换尺度值% wavlelet:小波类型:′morl′, Morlet小波;′gaus′, Gaussian小波;′mexh′,墨西哥帽子小波%输出生成由输入所指定的小波分解剖面文件Infile=char(Filein)Outfile=char(Fileout)Type=char(wavelet)fp1=fopen(Infile,′r′); %打开一原始的输入文件fp2=fopen(Outfile,′w′); %要写入的小波分解剖面文件cc=fread(fp1,1800,′integer*2′); %读取sgy文件的文件头信息fwrite(fp2,cc,′integer*2′);for k=1:traces %循环处理bb=fread(fp1,120,′integer*2′); %读取sgy文件的道头信息fwrite(fp2,bb,′integer*2′);s=fread(fp1, samples,′integer*2′); %读出一道数据w=cwt(s, scale, wavelet); %小波变换后该道的变换系数数据fwrite(fp2, w,′integer*2′); %将该道的小波变换数据写入到文件中endfclose(fp1);fclose(fp2);function For-dwt(Filein, traces, samples, wavelet)%function For-dwt(Filein, traces, samples, wavelet)离散小波变换%输入Filein: 原始的地震剖面文件(*.sgy)% traces: 整个剖面文件的总道数% samples:每一道地震记录的采样点数% wavelet:小波类型;可供选择的有Daubechies小波、Coiflets小波、Symlets小波等%输出生成不同分层结构的小波分解剖面文件% 本程序以3层分解为例。

小波分析MATLAB实例

小波分析MATLAB实例小波分析是一种信号处理方法，可以用于信号的时频分析和多尺度分析。

在MATLAB中，可以使用Wavelet Toolbox实现小波分析。

这个工具箱提供了丰富的函数和工具，可以方便地进行小波分析的计算和可视化。

小波分析的核心是小波变换，它将信号分解成一组不同尺度和频率的小波基函数。

在MATLAB中，可以使用`cwt`函数进行连续小波变换。

以下是一个小波分析的MATLAB实例，用于分析一个心电图信号的时频特性。

首先，导入心电图信号数据。

假设心电图数据保存在一个名为`ecg_signal.mat`的文件中，包含一个名为`ecg`的变量。

可以使用`load`函数加载这个数据。

```MATLABload('ecg_signal.mat');```接下来，设置小波变换的参数。

选择一个小波基函数和一组尺度。

这里选择Morlet小波作为小波基函数，选择一组从1到64的尺度。

可以使用`wavelet`函数创建一个小波对象，并使用`scal2frq`函数将尺度转换为频率。

```MATLABwavelet_name = 'morl'; % 选择Morlet小波作为小波基函数scales = 1:64; % 选择1到64的尺度wavelet_obj = wavelet(wavelet_name);scales_freq = scal2frq(scales, wavelet_name, 1);```然后，使用`cwt`函数进行小波变换，得到信号在不同尺度和频率下的小波系数。

将小波系数的幅度平方得到信号的能量谱密度。

```MATLAB[wt, f] = cwt(ecg, scales, wavelet_name);energy = abs(wt).^2;``````MATLABimagesc(1:length(ecg), scales_freq, energy);colormap('jet');xlabel('时间（样本）');ylabel('频率（Hz）');```运行整个脚本之后，就可以得到心电图信号的时频图。

小波变换的Matlab例子

小波变换
1.“小波”公认的起源于地质信号的研究。

2.小波变换极大地克服了傅里叶和加窗傅里叶变换的不足，可以分析时变信号
的局部特征。

原则上讲，能用傅里叶变换分析的问题，都可以用小波变换来代替。

3.MATAB可以直接进行快速的小波变换。

4.一个例子：
sin(^Z) , Os 5 / < 41s
sin(0・25?H), 41s < t < 825'
y(t)二sm(Kt) + sin((J.25^)?
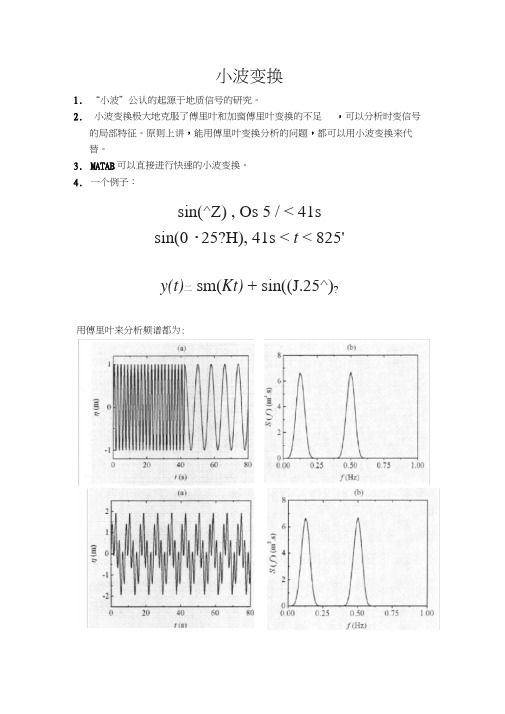
用傅里叶来分析频谱都为:
脣
呈
OT
利用小波变换分析“人工透射边界”得出的时域结果，是不是可以解决入射波与反射波分离。

入射波的能量过滤过程。

小波变换还应用于拟合多维设计反应谱的地震波。

利用离散的快速小波变换，是不是可以有助于解决M(w)与M(t)之间的变换。

(完整版)小波变换图像去噪MATLAB实现

基于小波图像去噪的MATLAB 实现一、论文背景数字图像处理(Digital Image Processing ，DIP)是指用计算机辅助技术对图像信号进行处理的过程。

数字图像处理最早出现于 20世纪50年代，随着过去几十年来计算机、网络技术和通信的快速发展，为信号处理这个学科领域的发展奠定了基础，使得DIP 技术成为信息技术中最重要的学科分支之一。

在现实生活中，DIP 应用十分广泛，医疗、艺术、军事、航天等图像处理影响着人类生活和工作的各个方面。

然而，在图像的采集、获取、编码和传输的过程中，都存在不同程度被各种噪声所“污染”的现象。

如果图像被污染得比较严重，噪声会变成可见的颗粒形状，导致图像质量的严重下降。

根据研究表明，当一张图像信噪比(SNR)低于14.2dB 时，图像分割的误检率就高于0.5%，而参数估计的误差高于0.6%。

通过一些卓有成效的噪声处理技术后，尽可能地去除图像噪声，我们在从图像中获取信息时就更容易，有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。

小波变换处理应用于图像去噪外，在其他图像处理领域都有着十分广泛的应用。

本论文以小波变换作为分析工具处理图像噪声，研究数字图像的滤波去噪问题，以提高图像质量。

二、课题原理1.小波基本原理在数学上，小波定义为对给定函数局部化的新领域，小波可由一个定义在有限区域的函数()x ψ来构造，()x ψ称为母小波，（mother wavelet ）或者叫做基本小波。

一组小波基函数，()}{,x b a ψ，可以通过缩放和平移基本小波来生成：())(1,ab x a x b a -ψ=ψ （1）其中，a 为进行缩放的缩放参数，反映特定基函数的宽度，b 为进行平移的平移参数，指定沿x 轴平移的位置。

当a=2j 和b=ia 的情况下，一维小波基函数序列定义为：()()1222,-ψ=ψ--x x j j j i （2）其中，i 为平移参数，j 为缩放因子，函数f （x ）以小波()x ψ为基的连续小波变换定义为函数f （x ）和()x b a ,ψ的内积：()dx ab x a x f f x W b a b a )(1)(,,,-ψ=ψ=⎰+∞∞- （3）与时域函数对应，在频域上则有： ())(,ωωa e a x j b a ψ=ψ- （4）可以看出，当|a|减小时，时域宽度减小，而频域宽度增大，而且()x b a ,ψ的窗口中心向|ω|增大方向移动。

小波变换matlab程序

小波变换matlab程序小波变换是一种信号处理技术，它可以将信号分解成不同频率的成分，并且可以在不同时间尺度上进行分析。

在Matlab中，可以使用内置的小波变换函数来实现这一技术。

下面是一个简单的小波变换Matlab程序示例：matlab.% 生成一个示例信号。

t = 0:0.001:1; % 时间范围。

f1 = 10; % 信号频率。

f2 = 50; % 信号频率。

y = sin(2pif1t) + sin(2pif2t); % 信号。

% 进行小波变换。

[c, l] = wavedec(y, 3, 'db1'); % 进行3层小波分解，使用db1小波基函数。

% 重构信号。

yrec = waverec(c, l, 'db1'); % 使用小波系数和长度进行信号重构。

% 绘制原始信号和重构信号。

subplot(2,1,1);plot(t, y);title('原始信号');subplot(2,1,2);plot(t, yrec);title('重构信号');这个程序首先生成了一个包含两个频率成分的示例信号，然后使用`wavedec`函数对信号进行小波分解，得到小波系数和长度。

接着使用`waverec`函数对小波系数和长度进行信号重构，最后绘制了原始信号和重构信号的对比图。

小波变换在信号处理、图像处理等领域有着广泛的应用，可以用于信号去噪、特征提取、压缩等方面。

通过Matlab中的小波变换函数，我们可以方便地进行小波分析和处理，从而更好地理解和利用信号的特性。

matlab中对复信号矩阵小波变换

matlab中对复信号矩阵小波变换在MATLAB中，对复信号矩阵进行小波变换，可以使用Wavelet Toolbox提供的函数。

以下是一个简单的示例，展示如何对复信号矩阵进行小波变换：1. 首先，确保已经安装了Wavelet Toolbox。

2. 创建一个复信号矩阵。

例如，我们可以创建一个2x3的复数矩阵：```MATLABA = [1+1i, 2+2i, 3+3i;4+4i, 5+5i, 6+6i];```3. 使用`wavedec`函数对复信号矩阵A进行小波分解。

`wavedec`函数需要两个输入参数：信号矩阵A和所需的分解层数。

例如，我们可以选择进行3层分解：```MATLABnlevels = 3;[C, L] = wavedec(A, nlevels);```在这里，`C`是分解后的系数矩阵，`L`是分解层数。

4. 显示原始信号矩阵A和小波分解后的系数矩阵C：```MATLABoriginal_A = A;disp('原始信号矩阵A：');disp(original_A);disp('小波分解后的系数矩阵C：');disp(C);```5. 若要显示小波分解的结果，可以使用`waverec`函数重建信号：```MATLABrecon_A = waverec(C, L);disp('重建后的信号矩阵recon_A：');disp(recon_A);```通过以上步骤，您已经成功地对一个复信号矩阵进行了小波变换。

需要注意的是，这里的示例仅适用于简单的复信号矩阵。

对于更复杂的情况，您可能需要根据实际需求调整参数或使用其他小波变换方法。

小波变换去噪matlab源码

小波变换去噪matlab源码小波变换是一种广泛应用于信号处理和图像处理的技术。

它通过将信号分解成不同频率的子信号，从而提供了一种有效的降噪方法。

要在MATLAB中进行小波变换去噪，您可以使用MATLAB的信号处理工具箱中提供的函数。

下面是一个示例的MATLAB源代码，用于实现小波变换去噪：```MATLAB% 加载待处理的信号signal = load('input_signal.mat');% 设置小波函数和分解层数wavelet = 'db4'; % 使用 Daubechies 4 小波函数level = 5; % 设置分解层数% 执行小波变换[coefficients, levels] = wavedec(signal, level, wavelet);% 通过阈值处理降噪threshold = wthrmngr('dw2ddenoLVL', coefficients, levels);cleaned_coefficients = wthresh(coefficients, 'h', threshold);denoised_signal = waverec(cleaned_coefficients, levels, wavelet);% 显示和保存降噪后的信号plot(denoised_signal);save('denoised_signal.mat', 'denoised_signal');```这段代码首先加载了待处理的信号，然后定义了所使用的小波函数和分解层数。

接下来，它执行了小波变换，并通过阈值处理来降噪信号。

最后，代码显示了降噪后的信号，并将其保存到文件中。

值得注意的是，该示例中使用了默认的阈值选取方式（dw2ddenoLVL），您可以根据具体的应用场景选择适合的阈值选取方法。

以上是关于在MATLAB中使用小波变换进行信号去噪的简单示例代码。

小波变换(内附奇异值分析matlab程序)

a6
0 0 0
100 100 100
200 200 200
300 300 300
400 400 400
500 500 500
600 600 600
700 700 700
800 800 800
900 900 900
1000 1000 1000
0.5 0 -0.5 0.5 0 -0.5 2 0 -2
d4
4、应用及与以后研究的结合
（1）小波的应用
小波分析作为一个新的数学分支，它是泛函分析、Fourier分析、样调分析、数值分析的完美结晶。被广泛用于数学领域的许多学科；信号分析、图象处理；量子力学、理论物理；军事电子对抗与武器的智能化；计算机分类与识别；音乐与语言的人工合成；医学成像与诊断；地震勘探数据处理；大型机械的故障诊断等方面；比如用在故障诊断中的应用小波分析在故障诊断中的应用已取得了极大的成功，小波分析不仅可以在低信噪比的信号中检测到故障信号，而且可以滤去噪声恢复原信号，它可以用于边界的处理与滤波、时域分析、信噪分离与提取弱信号、求分形指数、信号的识别与诊断以及多尺度边缘检测等。
程序代码
load nearbrk; x=nearbrk; %使用db4对信号进行2层分解 [c,l]=wavedec(x,2,‘db4’); subplot(411); subplot(4,1,i+2); plot(x); plot(d); ylabel('x'); ylabel(['d',num2str(3-i)]); %对分解的第六层低频系数进行重构 end a=wrcoef('a',c,l,'db4',2); subplot(412); plot(a); ylabel('a2'); for i=1:2 %对分解的第2层到第1层的高频系数进行重构 a=wrcoef('a',c,l,'db4',3-i);

一个小波变换实例及Matlab实现

1、选择()t ϕ或ˆ()ϕω，使{}()k Zt k ϕ∈-为一组正交归一基；之勘阻及广创作2、求n h 。

或ˆˆ()(2)/()H ωϕωϕω= 3、由n h 求n g 。

或()()i G e H t ωωωπ-= 4、由n g ，()t ϕ构成正交小波基函数()t φ或ˆˆ()(/2)(/2)G φωωϕω= Haar 小波的构造1）、选择尺度函数。

易知(n)t ϕ-关于n 为一正交归一基。

2）、求n h其中当n=0时，当n=1时，故，当n=0，n=1时当n=0时，当n=1时，故3）、求n g 。

4）、求()t φ。

=0-1,011,1()()g t g t ϕϕ-+(2)(21)t t-=11021112tt⎧≤≤⎪⎪⎪- ≤≤⎨⎪⎪⎪⎩其他其图形如下：1、Haar尺度函数Haar尺度函数空间：}{,(22),(21),(2),(21),(21),j j j j jx x x x xϕϕϕϕϕ++--j为非负的整数，该空间又称为j级阶梯函数空间j V。

则随j的增加，分辨更为精细。

2、性质函数集}{/22(2):j j x k k Zϕ-∈是j V的一个尺度正交基。

()f x V∈当且仅当(2)j jf x V∈。

3、Haar小波函数函数满足两点：（1）φ是1V的成员；（2）φ与0V正交。

性质：()0x dxφ+∞-∞=⎰()xφ是对称的、局部支撑的函数；小波函数空间:(2),j j k k k Z W a x k a R φ∈-∈∑ jW 是j V 的正交互补，即1j j j V V W +=⊕ 函数集}{/22(2):j j x k k Z φ-∈是j W 的一个尺度正交基 4、 Haar 小波分解与重建对Haar 小波，有11(2)((2)(2))j j j x x x φφϕ--=+/211(21)((2)(2))/2j j j x x x φφϕ---=-Haar 小波分解定理：设：()(2),()j j k j jk Z f x a x k f x V φ∈=-∈∑则它可以有如下分解：把函数f 分解成一个小波空间与一个尺度空间的分量解：依照分解定理，此j=2,；k=0,1,2,3对应的系数是2,2,1，-1；代入公式，得出分解后尺度函数空间元素的系数是2222+=，1102-=；分解后小波函数空间元素的系数是2202-=，1(1)12--=；从而Matlab程序image1=imread('512.jpg');image1=rgb2gray(image1);subplot(2,2,1);imshow(image1);title('original image');image1=double(image1);imagew=imread('shuiyin.bmp'); imagew=rgb2gray (imagew);subplot(2,2,2);imshow(imagew);title('original watermark'); [ca,ch,cv,cd]=dwt2(image1,'db1');[cas,chs,cvs,cds]=dwt2(ca1,'db1');M=512;N=64;for i=1:Nfor j=1:NCa(i,j)=cas(i,j)+0.01*imagew(i,j);end;end;IM=idwt2(Ca,chs,cvs,cds,'db1');IM1=idwt2(IM,ch1,cv1,cd1,'db1');markedimage=double(idwt2(IM1,ch,cv,cd,'db1'));subplot(2,2,3);colormap(gray(256));image(markedimage);title('marked image');imwrite(markedimage,gray(256),'watermarked.bmp','bmp'); image1=imread('512.jpg');image1=rgb2gray(image1);image1=double(image1);imaged=imread('watermarked.bmp');[ca,ch,cv,cd]=dwt2(image1,'db1');[cas,chs,cvs,cds]=dwt2(ca1,'db1');[caa,chh,cvv,cdd]=dwt2(imaged,'db1');[caa1,chh1,cvv1,cdd1]=dwt2(caa,'db1'); [caas,chhs,cvvs,cdds]=dwt2(caa1,'db1');for p=1:Nfor q=1:NW(p,q)=100*(caas(p,q)-cas(p,q));end;subplot(2,2,4);colormap(gray(256));image(W);title('从含水印图像中提取的水印');imwrite(W,gray(256),'watermark.bmp','bmp');。

一个小波变换实例及Matlab实现

MATLAB小波变换指令及其功能介绍(超级有用)解读

小波变换-图像融合matlab代码

第5章 小波变换的matlab实现

matlab中图像小波变换的应用实例

小波变换matlab

小波变换(内附奇异值分析matlab程序)

小波变换原理matlab

matlab morlet小波变换

第5章小波变换的matlab实现

MATLABwavelate小波变换

小波分析MATLAB实例

小波变换的Matlab例子

(完整版)小波变换图像去噪MATLAB实现

小波变换matlab程序

matlab中对复信号矩阵小波变换

小波变换去噪matlab源码

小波变换(内附奇异值分析matlab程序)

一个小波变换实例及Matlab实现

第5章小波变换的matlab实现