第三章 红外吸收光谱
波谱分析 第三章 03红外谱图解析

C= C : 16பைடு நூலகம்0~1450 cm-1区域吸收峰的强弱及个数与分子结 构有关,是判断苯环存在的主要依据。 有2-4个峰,峰数取决于取代基对苯环对称性破坏的程度
苯 甲苯 取代基与苯环共轭时 烷基存在时 1600 cm-1 无吸收 1500 、 1600 cm-1 有吸收 1580 cm-1 处出现强吸收 1450 cm-1 有吸收
烷烃
表3-4, (CH2)n结构 中亚甲基面内摇 摆振动
CH3 –CH – CH2 –CH – CH3 CH3
1168 1386 1468 1367
CH3
2,4 - 二甲基戊烷
78
2.烯烃
基团 = CH中C-H C=C骨架
3080 2975 1680~1620
1000~800 (面外摇摆)
(1) = CH >3000 cm-1为不饱和碳上质子振动吸收,是与饱 和碳上质子的重要区别。 (2) C=C的 位置及强度 与烯碳的取代情况及分子对称性 密切相关。 末端烯烃 C=C吸收最强,双键移向碳链中心时结构对称 性增强, C=C带减弱。顺式较反式强。 共轭双键中由于双键的相互作用出现两个 C=C (1650、1600 cm-1 )。 46
饱和环醚: 在 1260~780 cm-1 范围出现两条或两条以上的吸收带。 环张力增加as波数降低, s波数升高。 O 1071 913 O 983 1028
(3) CH(面外)最有用。 特点是: 不同类型的烯烃,有其独特的波数,且比较固定,不受 取代基的变化而发生很大的变化。 吸收强度特别强。 根据烯氢被取代的个数、取代位置及顺反异构的不同, 出峰的个数、位置及强度不同。
烯烃类型 R1CH=CH2 R1R2CH=CH2 R1CH=CHR2 (顺) R1CH=CHR2 (反) R1R2CH=CHR3 面外弯曲振动位置/cm-1 995 ~985, 910 ~905 895 ~ 885 730 ~ 650 980 ~ 965 840 ~ 790
第三章 红外吸收光谱分析-1

波长和波数
红外区光谱用波长和波数( 红外区光谱用波长和波数(wave number) 波长和波数 ) 来表征 ; 波长多用m做单位; 做单位; 波长多用 做单位 波数: 表示, 波数:以σ表示,定义为波长的倒数,单位 表示 定义为波长的倒数, cm-1,其物理意义是每厘米长光波中波的数 目. σ=1/λ(cm)=104/λ(m)=υ/c 用波数表示频率的好处是比用频率要方便, 用波数表示频率的好处是比用频率要方便,且 数值小. 数值小. 一般用透光率 波数曲线或透光度-波长曲线 透光率-波数曲线 波长曲线来 一般用透光率 波数曲线或透光度 波长曲线来 描述红外吸收光谱. 描述红外吸收光谱.
第三章 红外吸收光谱分析
3.2 基本原理 3.2.1 产生红外吸收的条件
产生红外吸收的条件
1) 辐射光子具有的能量与发生振动 跃迁所需的跃迁能量相等. 跃迁所需的跃迁能量相等. 2)辐射与物质之间有耦合作用. )辐射与物质之间有耦合作用.
条件一: 条件一:辐射光子的能量应与振动跃 迁所需能量相等
红外光谱的特点-1 红外光谱的特点
紫外,可见吸收光谱常用于研究不饱和 紫外,可见吸收光谱常用于研究不饱和 有机物, 有机物,特别是具有共轭体系的有机化 合物; 红外光谱法主要研究在振动中 合物;而红外光谱法主要研究在振动中 伴随有偶极矩变化的化合物. 伴随有偶极矩变化的化合物. 因此,除了单原子和同核分子如Ne, , 因此,除了单原子和同核分子如 ,He, O2,H2等之外,几乎所有的有机化合物 等之外, 在红外光谱区均有吸收. 在红外光谱区均有吸收. 一般只要结构上不同, 一般只要结构上不同,就会有不同的红 外光谱图. 外光谱图.
红外光谱的特点-2 红外光谱的特点
红外谱图吸收带的位置与吸收谱带的强 红外谱图吸收带的位置与吸收谱带的强 度反映了分子结构上的特点, 度反映了分子结构上的特点,可以用来 定基团,定结构; 定基团,定结构; 谱带的强度与分子组成以及含量有关 与分子组成以及含量有关, 谱带的强度与分子组成以及含量有关, 可以用来进行定量分析及纯度的检查; 可以用来进行定量分析及纯度的检查; 红外光谱分析特征性强,气体, 红外光谱分析特征性强,气体,液体和 固体样品均可以测定,并且具有用量少, 固体样品均可以测定,并且具有用量少, 分析速度快和不破坏样品等特点. 分析速度快和不破坏样品等特点.
第三章红外光谱IR
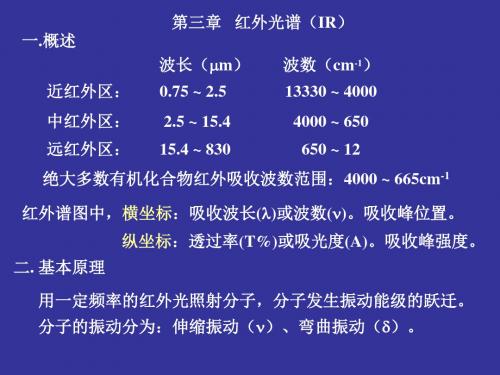
烷烃吸收峰
正己烷的红外光谱图
2,2,4-三甲基戊烷的红外光谱图
2、不饱和烃
• 烯烃 • 炔烃 • 芳香烃
2、1 烯烃 烯烃双键的特征吸收
影响双键碳碳伸缩振动吸收的因素
• 对称性:对称性越高,吸收强度越低。 • 与吸电子基团相连,振动波数下降,吸
收强度增加。 • 取代基的质量效应:双键上的氢被氘取
代后,波数下降10-20厘米-1。质量效应 • 共轭效应:使波数下降约30厘米-1 。
1-己烯的红外光谱图
~3060cm-1: 烯烃C—H伸缩振动;~1820:910cm-1倍频; ~1650cm-1: C=C伸缩振动;~995,905cm-1: C=CH2 非平面摇摆振动
顺式和反式2,2,5,5-四甲基己烯红外光谱 a 顺式 b 反式
v~
=
1
——
K
2C M
M = m1 m2 m1 + m2
双原子分子红外吸收的频率决定于折合质量和键力常数。
C-H C-C C-O C-Cl C-Br C-I
-1 cm
3000
1200 1100
800
550
500
v cm-1
力常数/g.s-2
CC 2200~2100
12~18105
C=C 1680~1620
C-H面外弯曲振动吸收峰位置(cm-1) 670
770-730,710-690 770-735
810-750,710-690 833-810
780-760,745-705 885-870,825-805 865-810,730-675
810-800 850-840 870-855
870
各类取代苯的倍频吸收和面外弯曲振动吸收
有机波谱解析-第三章_红外光谱

由于红外光谱吸收强度受狭缝宽度、温度和溶剂等因素影 响,故不易精确测定,在实际分析中,只是通过与羰基等强吸 收峰对比来定性研究。
谱带强度与振动时偶极矩变化有关,偶极矩变化愈 基团极性 大,谱带强度愈大;偶极矩不发生变化,谱带强度为0, 即为红外非活性。 电子效应
红外吸收强度 偶极距变化幅度 振动偶合
伸缩振动(
as
)两种形式。
弯曲振动:原子垂直于化学键方向的运动。又可以分
它们还可以细分为摇摆、卷曲等振动形式。
为面内弯曲振动()和面外弯曲振动( )两种形式,
+和-表示垂直于纸面方向的前后振动。
亚甲基的振动形式
三、分子振动与红外吸收峰的关系
理论上具有特定频率的每一种振动都能吸收相应 频率的红外光,在光谱图对应位臵上出现一个吸收 峰。实际上,因种种原因分子振动的数目与谱图中
纵坐标为: 百分透过率(%) 横坐标为: 波长(µ m)或波 数(cm-1)。
环戊烷
也可用文字形式表示为:2955cm-1(s)为CH2的反对称伸缩振动 (υasCH2),2870cm-1(m)为CH2的对称伸缩振动(υsCH2) 1458cm-1(m) 为CH2的面内弯曲振动(δ面内CH2),895cm-1(m)为CH2的面外弯曲振动 (面外CH2)
诱导效应大于共轭效应, C=O 蓝移至 1735 cm-1
三、空间效应
(1)空间位阻 破坏共轭体系的共平面性,使共
轭效应减弱,双键的振动频率蓝移(增大)。
CH(CH3)2 O O O
CH3 CH3
CH3 CH(CH3)2
CH3
1663cm-1
1686cm-1
1693cm-1
(2)环的张力:环的大小影响环上有关基 团的频率。
第三章 红外吸收光谱法

红外吸收光谱法
01 基础知识
02 光栅型红外分光光度计
目录
CONTENTS
03 傅里叶变换红外光谱仪 04 样品的制备
05 实训五 乙酰苯胺的红外光谱测定
06 实训六 苯乙酮的红外光谱测定
案例 导入
药检中经常会遇到硫酸小诺霉素注射液与硫酸庆 大霉素注射液,虽然两者临床药理作用和毒副反应 相差甚多,但从它们的显色反应、薄层斑点位置等 化学鉴定方法来看,两者是难以进行区分的,由于 硫酸小诺霉素注射液在市场上的出售价格要比硫酸 庆大霉素注射液高出许多倍,这样就导致一些不法 分子利用这可乘之机,来进行假药的制作与销售。 因此,必须严把药品质量关,解决这一问题。用什 么方法可以高度准确地将问题彻底解决呢?
04 典型光谱
1 . 芳烃类 取代苯的主要特征峰有: νΦ—H3100~3030cm-1(m);νC=C(骨架振动)~1600cm-1(m或s)及~ 1500cm-1(m或s);γΦ—H910~665cm-1(s);泛频峰2000~1667cm-1(w,vw)。现 以甲苯为例说明取代苯的红外吸收特征,如图3-1所示。
04 典型光谱
2 . 醇、酚、羧酸类 (3)νC=O
νC=O是此三类化合物中羧酸独有的重要特征吸收峰,峰位为1740~1650cm-1的高 强吸收峰,干扰较少。可据此区别羧酸与醇和酚。
04 典型光谱
3 . 醛、酮类 (1)醛类
主要特征峰:νC=O1725cm-1(s)及醛基氢νO=C—H~2820与2720cm-1两个吸收 峰。若羰基与双键或芳环共轭,将使νC=O峰向低波数方向移动至1710~1685cm-1。
2 . 醇、酚、羧酸类
图 3-4 正辛醇、丙酸、苯酚的红外吸收光谱图
第三章 红外光谱法--本科生

1. 红外辐射光的频率与分子振动的频率相 当,才能满足分子振动能级跃迁所需的能 量,而产生吸收光谱。 2. 必须是能引起分子偶极矩变化的振动才能 产生红外吸收光谱。
4 吸收谱带的强度
红外光谱的吸收带强度即可用于定量分析,也是 化合物定性分析的重要依据。 基态分子中的很小一部分,吸收某种频率的红外 光,产生振动的能级跃迁而处于激发态。激发态分子 通过与周围基态分子的碰撞等原因,损失能量而回到 基态,它们之间形成动态平衡。跃迁过程中激发态分 子占总分子的百分数,称为跃迁几率,谱带的强度即 跃迁几率的量度。跃迁几率与振动过程中偶极矩的变 化(△μ)有关,△μ越大,跃迁几率越大,谱带强度 越强。
特征区(官能团区)分为三个区域:
(2)2500~1900 为叁键和累积双键区。 主要包括-CC、 -CN等等叁键的伸缩振动,以及-C =C=C、C=C=O等累积双键的不对称性伸缩振动。 对于炔烃类化合物,可以分成R-CCH和R-C C-R两种类型, RCCH的伸缩振动出现在2100~2140 cm-1附近; R-C C-R出现在 2190~2260 cm-1附近;-C N基的 伸缩振动在非共轭的情况下出现在 2240~2260 cm-1附近。当与不饱和键或芳香核共轭时,该峰位移到 2220~2230 cm-1附近。
k /N.cm
7.7 6.4
折合质量μ :μ ↓,(v)↑,红外吸收信号将出现在 高波数区。
v
振 σ
1 k 2 c
吸收峰的峰位:化学键的力常数k越大,原子的折 合质量越小,振动频率越大,吸收峰将出现在高波数 区(短波长区);反之,出现在低波数区(高波长区)
v
v
ቤተ መጻሕፍቲ ባይዱ
结论:
产生红外光谱的必要条件是:
第三章-红外吸收光谱分析

第三章红外吸收光谱分析3.1概述3.1.1红外吸收光谱的基本原理红外吸收光谱法又称为分子振动转动光谱,属于分子光谱的范畴,是有机物结构分析的重要方法之一。
当一定频率的红外光照射分子时,若分子中某个基团的振动频率和红外辐射的频率一致,两者产生共振,光的能量通过分子偶极矩的变化传递给分子,该基团就吸收了这个频率的红外光,产生振动能级跃迁;如果红外辐射的频率和分子中各基团的振动能级不一致,该频率的红外光将不被吸收。
如果用频率连续变化的红外光照射某试样,分子将吸收某些频率的辐射,引起对应区域辐射强度的减弱,用仪器以吸收曲线的形式记录下来,就得到该试样的红外吸收光谱,稀溶液谱带的吸光度遵守Lambert-Beer定律。
图3-1为正辛烷的红外吸收光谱。
红外谱图中的纵坐标为吸收强度,通常用透过率或吸光度表示,横坐标以波数或波长表示,两者互为倒数。
图中的各个吸收谱带表示相应基团的振动频率。
各种化合物分子结构不同,分子中各个基团的振动频率不同。
其红外吸收光谱也不同,利用这一特性,可进行有机化合物的结构分析、定性鉴定和定量分析。
图3-1 正辛烷的红外光谱图几乎所有的有机和无机化合物在红外光谱区均有吸收。
除光学异构体,某些高分子量的高聚物以及一些同系物外,结构不同的两个化合物,它们的红外光谱一定不会相同。
吸收谱带出现的频率位置是由分子振动能级决定,可以用经典力学(牛顿力学)的简正振动理论来说明。
吸收谱带的强度则主要取决于振动过程中偶极矩的变化和能级跃迁的概率。
也就是说,红外光谱中,吸收谱带的位置、形状和强度反映了分子结构的特点,而吸收谱带的吸收强度和分子组成或官能团的含量有关。
因此,红外吸收光谱在化学领域中的应用,大体上可分为两个方面,即分子结构的基础研究和用于化学组成的分析。
首先,红外光谱可以研究分子的结构和化学键。
利用红外光谱法测定分子的键长和键角,以此推断出分子的立体构型;利用红外光谱法测定分子的力常数和分子对称性等,根据所得的力常数就可以知道化学键的强弱;由简正频率来计算热力学函数等等。
材料分析方法第三章_红外光谱剖析

烯烃类型对=C-H的面外弯曲振动的影响
对判断烯烃类 型非常有用
烯烃类型
R1CH=CH2 R1R2C=CH2 R1CH=CHR2(顺) R1CH=CHR2(反) R1R2C=CHR3
(4)分析时间短。一般红外光谱做一个样可在10~30分钟 内完成。如果采用傅里叶变换红外光谱仪在一秒钟以内 就可完成扫描。为快速分析的动力学研究提供了十分有 用的工具。
(5)所需样品用量少,且可以回收。红外光谱分析一次 用样量约1~5mg,有时甚至可以只用几十微克。
IR光谱表示法: 横坐标为吸收波长(m),或吸收频率(波数
1947年第一台实用的双光束自动记录的红外分光光度计 问世。这是一台以棱镜作为色散元件的第一代红外分光光 度计。
到了六十年代,用光栅代替棱镜作分光器 的第二 代红外光谱仪投入了使用。这种计算机化的光栅为分光 部件的第二代红外分光光度计仍在应用。
七十年代后期,干涉型傅里叶变换红外光谱仪(FTIR)投入了使用,这就是第三代红外分光光度计。
断烯烃的存在 , 苯环 C-H 大于3000
初步判断烯烃结构 的存在
影响碳碳双键伸缩振动吸收的因素
对称性:对称性越高,吸收强度越低。 取代基:与吸电子基团相连,振动波数下
降。 取代基的质量效应:双键上的氢被氘取代
后,波数下降10-20 厘米-1。 共轭效应:使波数下降约30厘米-1 。
1-己烯的红外光谱图
吸收池和检测器
由于玻璃,石英等常规透明材料不能透过红外线, 因此红外吸收池必须采用特殊的透红外材料制作 如:NaCl,KBr,CsI,KRS-5等作为窗口。由于 该类材料均属于无机盐,很容易吸收水汽发生潮 解。固体粉体样品可以直接与KBr混合压片,直 接进行测定。
第三章红外吸收光谱

CH3, CH2
酯C=O CH2,CH3 CH3 酯得特征 酯得特征
3)官能团
CH2
CH3
4)可能得结构
C=O
C-O
νas(C-O-C)
1180cm-1
5)确定结构
O
1240cm-1
O C CH3
1160cm-1
例3、某化合物分子式C8H8,试根据如下红外光 谱图,推测其结构。
例3解:
1)不饱和度 分子式: C8H8,
(CH2)n
gC-H(oop)
1-己烯和1-己炔
g=CH2 (面外) (CH2)n
例2:烷烃(另一种形式得IR谱)
例3:烯烃
例4:炔烃
例5:苯环上得取代
例6:芳香族化合物
例7:醇类化合物
例8:酚类化合物
例9:醚类化合物
例10:羰基化合物-醛类
例11:羰基化合物-酮类
例12:羧酸类化合物
结构验证 其不饱和度与计算结果相符;并与标准谱图对照证明结构正确。
例5、化合物C4H8O,根据如下IR谱图确定结构, 并说明依据。
O
CCC
例5解:
1)不饱和度 分子式: C4H8O,
2)峰归属
U=1-8/2+4=1
波数(cm-1 )
归属
结构信息
3336 3078 2919,2866 1622 1450 1036
例13:酯类化合物
例14:酸酐类化合物
例15:酰卤类化合物
例16:酰胺类化合物
H 3 C C
例17:胺类化合物
例18:腈类化合物
O
O
O
H C O CH2CH2CH 3 H3C C O C H2CH3 H3CH 2C C O C H3
红外吸收光谱法31概述分子中基团的振动和转动能级跃迁
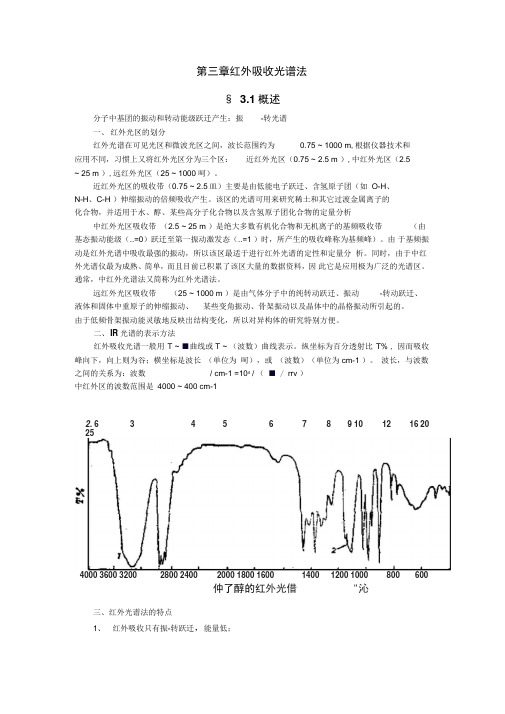
第三章红外吸收光谱法§ 3.1概述分子中基团的振动和转动能级跃迁产生:振-转光谱一、红外光区的划分红外光谱在可见光区和微波光区之间,波长范围约为0.75 ~ 1000 m,根据仪器技术和应用不同,习惯上又将红外光区分为三个区:近红外光区(0.75 ~ 2.5 m ),中红外光区(2.5~ 25 m ),远红外光区(25 ~ 1000 呵)。
近红外光区的吸收带(0.75 ~ 2.5皿)主要是由低能电子跃迁、含氢原子团(如O-H、N-H、C-H )伸缩振动的倍频吸收产生。
该区的光谱可用来研究稀土和其它过渡金属离子的化合物,并适用于水、醇、某些高分子化合物以及含氢原子团化合物的定量分析中红外光区吸收带(2.5 ~ 25 m )是绝大多数有机化合物和无机离子的基频吸收带(由基态振动能级(..=0)跃迁至第一振动激发态(..=1 )时,所产生的吸收峰称为基频峰)。
由于基频振动是红外光谱中吸收最强的振动,所以该区最适于进行红外光谱的定性和定量分析。
同时,由于中红外光谱仪最为成熟、简单,而且目前已积累了该区大量的数据资料,因此它是应用极为广泛的光谱区。
通常,中红外光谱法又简称为红外光谱法。
远红外光区吸收带(25 ~ 1000 m )是由气体分子中的纯转动跃迁、振动-转动跃迁、液体和固体中重原子的伸缩振动、某些变角振动、骨架振动以及晶体中的晶格振动所引起的。
由于低频骨架振动能灵敏地反映出结构变化,所以对异构体的研究特别方便。
二、IR光谱的表示方法红外吸收光谱一般用T ~ ■曲线或T ~ (波数)曲线表示。
纵坐标为百分透射比T% , 因而吸收峰向下,向上则为谷;横坐标是波长(单位为呵),或(波数)(单位为cm-1 )。
波长,与波数之间的关系为:波数/ cm-1 =104/ (■ / rrv )中红外区的波数范围是4000 ~ 400 cm-12. 6 3 4 5 6 7 8 9 10 12 16 20254000 3600 3200 2800 2400 2000 1800 1600 1400 1200 1000 800 600仲了醇的红外光借"沁三、红外光谱法的特点1、红外吸收只有振-转跃迁,能量低;2、应用范围广,除单原子分子及单核分子外,几乎所有的有机物均有红外吸收;3、分子结构更为精细的表征:通过波谱的波数位置、波峰数目及强度确定分子基团和分子结构;4、气体、液体、固体样品都可测定;5、具有用量少;分析速度快;不破坏样品。
第三章-红外吸收光谱分析-1

由于分子非谐振性质,各倍频峰并非正好是基频峰的 整数倍,而是略小一些。
HCl的基频峰和倍频峰
基频峰(V0→1) 二倍频峰( V0→2 ) 三倍频峰( V0→3 ) 四倍频峰( V0→4 ) 五倍频峰( 0→5 )
折合质量μ的影响
对于相同化学键的基团,波数与折合 质量μ平方根成反比。例如C-C、C-O、 C-N键的力常数相近,但折合质量不同。
μ : C-C < C-N < C-O 1430 cm-1 1330 cm-1 1280 cm-1
第三章 红外吸收光谱分析
3.2 基本原理 3.2.3 多原子分子振动
在红外吸收光谱上除基频峰外,还有振动能级由基 态( V =0)跃迁至第二激发态( V =2)、第三激 发态( V =3),所产生的吸收峰称为倍频峰。
除此之外,还有合频峰(1+2,21+2,),差 频峰( 1-2,21-2, )等,这些峰多数很弱, 一般不容易辨认。
倍频峰、合频峰和差频峰统称为泛频峰。
通过试样后的红外光在一些波数范围减弱,在 另一些波数范围内仍然较强,用仪器记录该试 样的红外吸收光谱,进行样品的定性和定量分 析。
第三章 红外吸收光谱分析
3.2 基本原理 3.2.2 双原子分子的振动
红外光谱是由于分子振动能级的跃迁(同时伴有转动能级跃迁) 而产生,即分子中的原子以平衡位置为中心作周期性振动,其振 幅非常小。这种分子的振动通常想象为一根弹簧联接的两个小球 体系,称为谐振子模型。这是最简单的双原子分子情况,如下图 所示。
EL=hL 产生红外吸收光谱的第一条件为:
EL =△Ev hL = △Vh 即 L= △V
第三章红外

第三章 红外吸收光谱法一、 选择题0 ll x1. 化合物中只有一个羰基,却在 1773cm ,和1736 cm -1处出现 两个吸收峰,这是因为(1)诱导效应 (2)共轭效应 (3)费米共振 (4)空间位阻 2. 一种能作为色散型红外光谱仪的色散元件材料为(1)玻璃 (2)石英 (3)红宝石 (4)卤化物晶体二、 解答及解析题1.羰基化合物I 、U 、M 、W 中,C=O 伸缩振动出现最低者为0 0 I 、R[一 CH 》—[―CHj- ; 口、0 IID川、冃—:■- .. 「 卜】0 G— C — U1 化合物中只有一个羰基,别在1773cm -1和1736 cm -1,这是因为:A.诱导效应B.共轭效应C.空间效应D.偶合效应E.费米共振F.氢键效应3. 下列5组数据中,哪一种数据所涉及的红外光谱区域能包括-一「|,_「一的吸收带:111(1) 3000〜2700 cm 1675〜1500 cm 1475〜1300 cm ;1 1 1 (2) 3000〜2700 cm -12400〜2100 cm 1000〜650 cm ;R 】-CH -CH -C -GH 厂旳 0C-CH^CH-R却有两个 C=O 的吸收带,分W 、-1_1 _1(3) 3300〜3010 cm 1675〜1500 cm(4) 3300〜3010 cm -1 1900〜1650 cm1475〜1300 cm -1;-1-1 -1(5) 3000〜2700 cm 1900〜1650 cm 1475〜1300 cm ;4. 试用红外光谱区别下列异构体:(3)和 O=□5. 一种能作为色散型红外光谱仪的色散元件材料为:(1)玻璃;(2)石英;(3)红宝石;(4)卤化物晶体6•写出用下列分子式表示的羧酸的两种异构体,并预测它们的红外光谱。
(1)C 4H 8O 2(2)C 5H 8O 47. 乙醇的红外光谱中,羟基的吸收峰在 3333 cm -1,而乙醇的1%CCb 溶液的红外光谱中羟基却在 3650 cm -1和3333 cm -1两处有吸收峰, 试解释之。
第3章红外光谱法

Rayleigh散射:
激发虚态
弹性碰撞;无能
E1 + h0
h(0 - )
量交换,仅改变方向
Raman散射:
h0
非弹性碰撞;方
向改变且有能量交换 E1
E0 + h0
h0 h0 V=1
h0 +
E0
V=0
Rayleigh散射
Raman散射
h
E0基态, E1振动激发态; E0 + h0 , E1 + h0 激发虚态;
发生振动能级跃迁需要能量的大小取决于键两端原子 的折合质量和键的力常数,即取决于分子的结构特征。
14.06.2019
分析化学研究所
第8页
分子中基团的基本振动形式
1.两类基本振动形式
伸缩振动
弯曲振动
亚甲基
14.06.2019
亚甲基
分析化学研究所
第9页
伸缩振动
甲基的振动形式
弯曲振动
对称 υ s(CH3) 2870 ㎝-1
频峰
14.06.2019
分析化学研究所
第13页
官能团区和指纹区
• 官能团区 4000~1300cm-1是基团伸缩振动出现的区域,对鉴定 基团很有价值
• 指纹区 1300~600cm-1是单键振动和因变形振动产生的复杂光 谱区,当分子结构稍有不同时,该区的吸收就有细微 的差异,对于区别结构类似的化合物很有帮助。
共轭效应:使共轭体系中的电子云密度平均化,使双键略有伸 长,因此,双键的吸收频率向低波数方向位移。
中介效应:当含有孤对电子的原子(如:O, N, S等)与具有多 重键的原子相连时,也可起类似的共轭作用,使吸收频率向低 波数方向位移。
第三章 红外吸收光谱完整版本ppt课件

解析完后,进行验证,不饱和度与计 算值是否相符,性质与文献值是否一致, 与标准图谱进行验证
谱图对照应注意:所用的仪器在分辨 率和精确度一致;测定的条件一致;杂质 引进的吸收带应仅可能避免。
.
三、红外光谱解析实例C8H16
例一:未知物分子式为C8H16,其红外图谱如 下图所示,试推其结构。
.
解:由其分子式可计算出该化合物不饱和度为1, 即该化合物具有一个烯基或一个环。
C C 2100
H 763 ,694(双峰)
CO 1638 C(C 芳环)1597 ,1495 ,1445
.
➢
解:
U
2
29
1
7
7
可能含有苯环
2
1638cm1强吸收 为 CO 3270cm1有吸收 NH 1132353123003300ccccmmmm( ( 1111吸强 强收) ) C N含 含NHCCCH 13023608ccmm11 为CH H 1597 ,1495 和 1445cm(1 三峰) 为 C(C 芳环) 763 和 694cm(1 双峰) 为 H(单取代)
❖ 3387、3366 cm-1 :NH2的伸缩振动; ❖ 1624 cm-1 : NH2弯曲振动; ❖ 1274 cm-1 :C-N伸缩振动;
❖综合上述信息及分子式,可知该化合物为:
邻苯二胺
.
图谱解析实例 例1 某化合物,测得分子式为C8H8O,其红外
光谱如下图所示,试推测其结构式。
C8H8O红外光谱图
1查找基团时先否定以逐步缩小范围2在解析特征吸收峰时要注意其它基团吸收峰的干扰3350和1640cm1处出现的吸收峰可能为样品中水的吸收3吸收峰往往不可能全部解析特别是指纹区4掌握主要基团的特征吸收
【2024版】第三章-红外吸收光谱分析-4

附图A1 固载氯烷基硅氧烷原料硅胶在常温时测 定的IR谱图
附图A2 固载氯烷基硅氧烷的硅胶中间体在常温 时测定的IR谱图
附图A3 氯烷基硅氧烷做偶联剂研制的杀菌剂产 品在常温时测定的IR谱图
附图A4 固载氯烷基硅氧烷原料硅胶在200℃时测 定的IR谱图
附图A6 固载氯烷基硅氧烷的硅胶中间体在 200℃时测定的IR谱图
MeO
MeO Si O SiCH 2CH2CH2Cl + MeOH
MeO
以硅胶为载体通过γ-氯丙基三甲氧基硅烷固载 季铵盐制备水不溶性杀菌剂
CH 3
Si
CH2Cl + N CnH2n+1
Si
CH 2
CH 3
叔胺可以是 N,N-二甲基-n 烷基胺,n 为 12-18。
CH 3 N + CnH2n+1Cl-
入封闭液体池中,液层厚度一般为 0.01~1mm。
液体和溶液试样
液体和溶液试样
(2)液膜法 ➢ 沸点较高的试样,直接滴在两片盐片之间,形成液膜。 ➢ 一些固体也可以溶液的形式进行测定。 ➢ 常用的红外光谱溶剂应在所测光谱区内本身没有强烈的
吸收,不侵蚀盐窗,对试样没有强烈的溶剂化效应等。 如CS2(1350-600cm-1)和CCl4(4000-1350 cm-1) 等。
(3)试样的浓度和测试厚度应选择适当,以使光谱图中 的大多数吸收峰的透射比处于20%~80%范围内。
制样的方法
1 .气体样品 气态样品可在玻璃气槽内进行测定,它
的两端粘有红外透光的NaCl或KBr窗片。先 将气槽抽真空,再将试样注入。
气体样品
液体和溶液试样
(1)液体池法 沸点较低,挥发性较大的试样,可注
分析化学-第三章 红外光谱分析

与一定结构单元相联系的、在一定范围内出现的化学键振动 频率——基团特征频率(特征峰)
例: 2800 3000 cm-1 —CH3 特征峰; 1600 1850 cm-1 — C=O 特征峰
11/8/2013
环境分析化学(2013-2014学年)
18
环境科学与工程系
1、基团特征频率分组
Environmental Analytical Chemistry
环境科学与工程系
Environmental Analytical Chemistry
一、概述 -----1、红外吸收光谱的概念
红外光谱是当分子受到红外区域的电磁辐射后,吸收一部分红外光,使分子中原 子的振动能级与转动能级跃迁所产生的分子吸收光谱。因此,红外光谱也称红外 吸收光谱或分子振动-转动光谱
环境分析化学(2013-2014学年)
19
环境科学与工程系
Environmental Analytical Chemistry
2. 氰基 R-C N (s C N) 非共轭 2240 2260 cm-1 共轭 2220 2230 cm-1
仅含C、H、N时:峰较强、尖锐;有O原子存在时; O越靠近C N,峰越弱;
=C-H 伸缩振动
( C-H)
C-H 伸缩振动
( C-H)
(2) 2500 1900 cm-1 三键,累积双键伸缩振动区
1. 炔基 R-C C-H C C 2140 2100 cm-1 (m)
R-C C-R ´ C C 2260 2190 cm-1 (w)
R-C C-R
无吸收带
11/8/2013
第二节 红外吸收光谱与分子结构
Infrared spectroscopy and molecular structure
红外吸收光谱分析

吸收峰位置σ(cm-1) 1429 1667 2222
2920
§4 分子振动的形式
多原子中基团的振动形式极为复杂,振动形式的总 数可如下计算
非直线型分形 子式 的 3原 = 总子 振 6数 动 直线型分子式 的3= 总 原振 子 5动 数形
非直线型分子以水分子为例
直线型分子以CO2为例
二、多原子分子的振动
合物
位置
1715 1805
1735 ~1740
1740 ~1770
~1680
1775
~1700
1710
1750
1750~ 1800
羧酸、酰卤、酸酐、 酰亚胺
羧酸与羧酸盐: 2700~3300、双峰 (1550~ 1620)+(1330~1420)
酰卤:
向高频移动
RCOF:1850 RCOCl:1795
900~600cm-1
应用:
1 (CH2)n:n≥4,722;n减小,吸收峰红移; 2 烯烃
RCH=CH2 890(较强)
RHC=CHR
顺式
反式
690(弱)
970(强)
CH3
3 C C H 3 :(1370~1380)+(1380~1385)双峰
4 苯环取代情况 苯环:1600、1580、1500cm-1处、两 到三个峰
当C=C与C=O共轭时,吸收强度较低; 苯环取代情况主要看700~900(强)和
1660~2000cm-1(弱) 单取代:~710和~750双强峰 四个相邻氢:770~735强峰 三个相邻氢:810~750强峰 两个相邻氢:860~800强峰 单独的氢 :900~800弱峰
C=N:1630~1690,强度不定 硝基化合物:~1350 与 ~1560 两强峰 C-O键(1070~1150,强)判断醚、醇、
第三章 红外吸收光谱分析-3

外部因素
外部因素主要指测定时物质的状态以及溶剂效应等因
素。 同一物质的不同状态,由于分子间相互作用力不同, 所得到光谱往往不同。 分子在气态时,其相互作用力很弱,此时可以观察到 伴随振动光谱的转动精细结构。 液态和固态分子间作用力较强,在有极性基团存在时, 可能发生分子间的缔合或形成氢键,导致特征吸收带 频率、强度和形状有较大的改变。 例如,丙酮在气态时的C-H为1742 cm-1 ,而在液态时 为1718 cm-1 。
C=O :→降低
注意:有时在化合物中,I效应与M效应同时存在,如果二者方 向不一致,这时应考虑哪个效应起主导作用。例如,饱和酯的 C=O为1735cm-1,比酮(1715cm-1)高,就是由于I效应大于M效应, 二者的净效应使得电子云密度由氧移向双键中间,使键力常数增 加的缘故。
当含有孤对电子的原子(O、S、N等)与具有多重键
游离羧酸的co键频率出现在1760cm1左右在固体或液体中由于羧酸形成二聚体co键频率出现在1700cm1当两个振动频率相同或相近的基团相邻具有一公共原子时由于一个键的振动通过公共原子使另一个键的长度发生改变产生一个微扰从而形成了强烈的振动相互作用
第三章 红外吸收光谱分析
3.3 基团频率和特征吸收峰
利用指纹区中苯环的C-H面外变形振动吸收峰 和2000~ 1667cm-1区域苯的倍频或组合频吸收 峰,可以共同配合确定苯环的取代类型。下图为不 同的苯环取代类型在2000~ 1667cm-1和 900~600cm-1区域的光谱。
指纹区
变形振动- 亚甲基
指纹区
变形振动 - 甲基
对称δ s(CH3)1380㎝-1
共轭效应- C效应
共轭效应使共轭体系中的电子云密度平 均化。 双键略有伸长,单键略有缩短,即双键 电子云密度降低,化学键力常数变小, 伸缩振动频率向低频方向移动。 共轭效应常引起C=O双键的双键性降低, 伸缩振动频率向低波数位移。
第三章红外光谱分析法(波普分析)

第三章红外光谱分析法紫外-可见吸收光谱常用于研究具有共轭体系的有机化合物,而红外吸收谱则主要研究在振动中伴随偶极矩变化的化合物。
通常红外吸收带的波长位置与吸收谱带的强度,反映了分子结构上的特点,可用以鉴定未知物结构组成或确定其化学基团。
由于红外光谱分析特征性强,对气体、液体、固体均可分析,是鉴定有机化合物的最常用的方法之一。
常用的范围是400 - 4000cm-1。
一、红外吸收光谱的基本原理红外吸收光谱产生应满足两个条件:(1)辐射应具有能满足物质产生振动跃迁所需的能量;(2)辐射与物质间有相互偶合作用。
分子在振动过程中必须有瞬间偶极矩的改变。
对称分子:没有偶极矩,辐射不能引起共振,无红外活性。
如:N2、O2、Cl2 等。
非对称分子:有偶极矩,红外活性。
分子的振动可近似看为一些用弹簧连接的小球的运动。
分子的振动能级(量子化): E振=(V+1/2)hnV:化学键的振动频率;n:振动量子数。
任意两个相邻的能级间的能量差为:K化学键的力常数,与键能和键长有关, m为双原子的折合质量 m =m1m2/(m1+m2)发生振动能级跃迁需要能量的大小取决于键两端原子的折合质量和键的力常数,即取决于分子的结构特征。
多原子分子的振动多原子分子的振动较双原子分子振动复杂得多。
其振动的基本类型有伸缩振动(ν)和弯曲振动(δ)两大类。
伸缩振动是指原子沿键轴方向伸缩,使键长发生周期性变化的振动。
由于振动偶合作用,3个原子以上的基团还可分为对称伸缩振动和不对称伸缩振动,表示为ν对称和ν不对称。
弯曲振动又叫变形或变角振动,指基团键角发生周期性变化的振动。
弯曲振动的力常数较小,因此常出现在低频区。
红外吸收峰的强度主要取决于吸收过程中偶极矩的变化。
变化越大,吸收越强。
通常两个原子的电负性相差越大,吸收越强。
如C=O吸收峰是大多数红外谱图中吸收最强的峰。
二、基团频率与特征吸收峰组成分子的各个基团均有其特定的红外吸收区域。
根据化学健的性质,可将其分为四个区:4000 - 2500 cm-1 氢键区;2500 - 2000 cm-1 参键区;2000 - 1500 cm-1 双键区;1500 - 1000 cm-1 单键区。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
C O
H
O
O
注意:能级的跃迁有一定的选律,当振动量子数变化(△V ) 为±1时,跃迁几率最大。 振动能级是量子化的,可能存在的能级要满足下式: E=(V+1/2)hv 式中h为普朗克常数, v为振动频率,V为振动量子数(0、1、 2· · · · · · · ), E是与振动量子数相应的体系能量。 当有红外辐射照射到分子时,若红外辐射的光子所具有的 能量恰好等于分子振动能级的能量差(△E)时,则分子将吸 收红外辐射而跃迁至激发态,导致振幅增大。
第三章 红外吸收光谱
目
第一节 概述
录
第二节 红外吸收光谱的基本原理 第三节 红外光谱与分子结构的关系 第四节 各类化合物的红外光谱特征 第五节 谱图解析
美国MAGNA550型 (尼高力)
第一节 概述
1、 红外吸收光谱与紫外吸收光谱一样是一种分子吸收光谱。
红外光的能量(△E=0.05-1.0ev)较紫外光(△E=1-20ev)低,
H H
C
C
对称伸缩振动
不对称伸缩振动
(2)弯曲振动(bending or deforming) 指原子垂直于化学键方向的运动。可分为面内和面外两种。 面内弯曲振动又分为剪式振动( )和平面内的摇摆( ); 面外弯曲振动也可分为非平面摇摆( )和扭曲振动( )。
H H
H H
H H
H H
例如:苯的三个基频为:1485cm-1,1585cm-1和3070cm-1, 前两个基频的组合频为(1485 cm-1 + 1585 cm-1)3070 cm-1,于 是基频(3070 cm-1)和组合频发生费米共振,在3019 cm-1和 3045 cm-1两处观测到两个强度差不多的吸收带。 又如醛基在2850 和2750 cm-1产生两个特征吸收峰,这是由 于C-H(2800 cm-1)和C-H(1390 cm-1)的倍频峰(2780cm-1) 费米共振引起的。
5、红外光谱表示方法:
(1)红外光谱图 红外光谱图以透光率T%为纵坐标,表示吸收强度,以波长 (mm)或波数 v(cm-1)为横坐标,表示吸收峰的位置,现主要以波 数作横坐标。波数是频率的一种表示方法(表示每厘米长的光波 中波的数目)。通过吸收峰的位置、相对强度及峰的形状提供化 合物结构信息,其中以吸收峰的位置最为重要。
当红外光照射分子时不足以引起分子中价电子能级的跃迁,而 能引起分子振动能级和转动能级的跃迁,故红外吸收光谱又称 为分子振动光谱或振转光谱。
2、红外光谱的特点:特征性强、适用范围广。 红外光谱对化合物的鉴定和有机物的结构分析具有鲜明的 特征性,构成化合物的原子质量不同、化学键的性质不同、原
子的连接次序和空间位置不同都会造成红外光谱的差别。
势 能
V=2 V=1 V=0 r/A0 双 原 子 分 子 势 能 曲 线
振动能级不止一种激发态。常温下分子处于最低振动能级,此 时叫基态,V=0。
从基态V0跃迁到第一激发态V=1,V0V1产生的吸收带较强, 叫基频或基峰。
也有从基态跃迁到第二激发态甚至第三激发态,V0V2或V0V3 的跃迁产生的吸收带依次减弱,叫倍频吸收,用2v1、 2v2等表示。
各种振动形式能量高低顺序:
不对称伸缩振动 对称伸缩振动 面内弯曲振动 面外弯曲振动
高 频
低 频
下面以 -CH2- 为例,表示出各种振动形式: 1) 伸缩振动:
对称伸缩
不对称伸缩
2)弯曲振动:
面内弯曲
剪式振动
平面摇摆
+
面外弯曲++ Nhomakorabea-
非平面摇摆
扭曲振动
二、红外光谱中几种常见的振动吸收频率峰
1、基频(峰) 当分子从基态(V=0)跃迁到第一激发态(V=1)时,产生 的吸收频率称为基频。在红外光谱上产生一条谱带,称为基频 带(峰)。基频峰强度大——红外主要吸收峰 一般不对称伸缩振动比对称伸缩振动的频率要高,弯曲 振动的频率比伸缩振动要低得多。 在红外光谱中,除了基频吸收峰之外,还有倍频、组合频、 振动偶合、费米共振等吸收频率。
剪 式 振 动
C
平 面 内 的 摇 摆
C
C
非 平 面 摇 摆
C
扭 曲 振 动
面内弯曲振动
面外弯曲振动
注:箭头表示纸面上的振动,+和-表示向纸面前和后的振动。 以上六种振动形式都有其特定的振动频率。一般前三种形式的振动(两 种伸缩及剪式振动)的频率较高,具有较高的能量,形成的谱带在较短 的波长(高波数)范围,其它几种振动形式,能量较低,吸收谱带在长 波范围(低波数) 。
红外光谱对样品的适用性相当广泛,无论固态、液态或气 态都可进行测定。
3、红外光谱波长覆盖区域:0.76 mm ~ 1000mm
红外光按其波长的不同又划分为三个区段。 (1)近红外:波长在0.76-2.5mm之间(波数12820-4000cm-1) (2) 中红外:波长在2.5-25mm(在4000-400 cm-1) 通常所用的红外光谱是在这一段的(2.5-15mm,即 4000-660
二、分子的振动光谱方程式(分子基团吸收频率的确定)
最简单的分子是双原子分子,如在理论上搞清楚双原子分子的振动 光谱,就可把多原子分子看成是双原子的集合而加以讨论。
为了便于讨论,暂忽略分子的转动,并把双原子分子看成是一个谐振 子,即把两个原子看成质量为mA与 mB的两个质点,其间的化学键看成无 质量的弹簧,当分子吸收红外光时,两个原子将在连接的轴线上作振动, 就如谐振子所作的简谐振动。
2、倍频(峰): 分子吸收红外光后,从基态(V=0)跃迁到第二、第三激发态 (V=2,3,4---)等所对应的吸收频率称为第一倍频,第二倍频, 第三倍频----,统称为倍频。倍频带强度很弱,一般只考虑第一 倍频。由于相邻振动能级间的间距近似相等,所以第一倍频的 频率近似为基频的一倍。 例如:酯类化合物的 C=O 伸缩振动的基频在1740 cm-1附近, 在3450cm-1附近可观察到其第一倍频吸收带。
苯甲酰氯的红外光谱
苯甲酰氯C-Cl的伸缩振动在874cm-1,其倍频峰在1730cm-1左右,正好落在 C=O的伸缩振动吸收峰位置附近,发生费米共振从而倍频峰吸收强度增加。
6. IR光谱在化学领域中的应用:
分子结构基础研究:应用IR测定分子的键长、键角,以 此推断出分子的立体构型; 根据所得的力常数可以知道化学键的强弱,由简正频率 来计算热力学函数等。 化学组成分析:根据光谱中吸收峰的位置和形状来推断未 知物结构,依照特征吸收峰的强度来测定混合物中各组分 的含量。
第二节 红外吸收光谱的基本原理
双原子分子只有一种振动形式—伸缩振动
由虎克定律来计算振动频率近似值
1 振 2
k
m
1
1
k
2 c m
1307
k
m
式中:k — 化学键的力常数,单位为N.cm-1
m1.m2 m m1 m2
力常数k:与键长、键能有关:键能↑(大),键长↓(短),k↑。
化学 键 C― C C= C C≡ C 键长 (nm) 0.154 0.134 0.116 键能 (KJ mol-1) 347.3 610.9 836.8 力常数 k(N.cm-1) 4.5 9.6 15.6 波数范围 (cm-1) 700~1200 1620~1680 2100~2600
例如,酸酐羰基有两个吸收峰是两个羰基振动耦合的结果:
O CH3 CH3 C O C O CH3 CH3 O C O C O
-1 1750 cm
-1 1828 cm
又如:
s
as
-CH3中的C-H伸缩振动偶合:2870 cm-1,2960 cm-1 -CH2中的C-H伸缩振动偶合:2850 cm-1,2930 cm-1 -CH中无振动偶合:2890 cm-1
表3-1 化学键的力常数
键 H-F 分子 HF k(×105dyn/cm) 9.7 4.8 4.1 键 H-C H-C C-C 分子 CH≡CH k(×105dyn/cm) 5.9 4.5-5.6 CH2=CH2 5.1
H-Cl HCl H-Br HBr
H-I
H-O H-O H-S H-N H-C
一、红外吸收光谱产生的条件
1. 电磁波的能量与分子某能级差相等 E红外光 = △E分子振动 2. 红外光与分子之间有偶合作用,分子振动时其偶极矩(m) 必须发生变化,即△m≠0 。 即并非所有的振动都会产生红外吸收,只有发生偶极矩 变化(△m≠0 )的振动才能引起可观测的红外吸收带,这种 振动称为红外活性的,反之( △m=0)则为红外非活性的。 如单原子和同核分子象Ne、He、O2、H2等,CO2的对称伸 缩振动也为红外非活性。
1、分子的振动类型:
能引起偶极矩变化的分子振动形式可以分为两大类:即伸缩振 动(用表示 )和弯曲振动(用表示 )。 (1)伸缩振动(stretching) 指原子沿键轴方向往复运动,振动过程只改变键的长度, 不发生键角的变化。可分为对称伸缩振动(用S表示)和不 对称伸缩振动(用as表示),
H H
3、组合频(峰):
组合频是一种频率的红外光同时被两个振动所吸收,即光的 能量用于两种振动能级的跃迁。 倍频、组合频统称为泛频。因为不符合跃迁选律,发 生的几率很小,显示为弱峰。
4、振动偶合 (Vibrational Coupling) 当两个基团相邻,并且振动基频相同或相近时,它们之间发生 较强的相互作用,引起了吸收频率偏离单个振动基频,一个向高频 方向移动,一个向低频方向移动,此现象称为振动偶合。
HI
H2 O 游离 H2 S NH3
3.2
7.8 7.12 4.3 6.5
C=C
C≡C C-O C=O C-Cl C≡N CH3Cl
