自控-二阶系统Matlab仿真
自动控制原理MATLAB仿真实验报告

实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性; 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为:)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ; ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =(二) 分析系统稳定性 有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果: p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
自动控制原理MATLAB仿真实验(于海春)

自动控制原理MATLAB仿真实验(于海春)实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入imulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个imulink仿真环境常规模板。
图1-1SIMULINK仿真界面图1-2系统方框图3.在imulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击imulink下的“Continuou”,再将右边窗口中“TranferFen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在imulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的imulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击imulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
自控-二阶系统Matlab仿真

自动控制原理二阶系统性能分析Matlab 仿真大作业附题目+ 完整报告内容设二阶控制系统如图1所示,其中开环传递函数)1(10)2()(2+=+=s s s s s G n n ξωω图1图2图3要求:1、分别用如图2和图3所示的测速反馈控制和比例微分控制两种方式改善系统的性能,如果要求改善后系统的阻尼比ξ ,则t K 和d T 分别取多少? 解:由)1(10)2()(2+=+=s s s s s G n n ξωω得1021,10,102===ξωωn 22nn ()s s ωξω+R (s )C (s )-对于测速反馈控制,其开环传递函数为:)2()s (22n t n nK s s G ωξωω++=; 闭环传递函数为:222)21(2)(nn n t ns K s s ωωωξωφ+++=;所以当n t K ωξ21+时,347.02)707.0(t =÷⨯-=n K ωξ;对于比例微分控制,其开环传递函数为:)2()1()(2n nd s s s T s G ξωω++=;闭环传递函数为:))21(2)1()(222n n n d nd s T s s T s ωωωξωφ++++=;所以当n d T ωξ21+=0.707时,347.02)707.0(=÷⨯-=n d T ωξ;2、请用MATLAB 分别画出第1小题中的3个系统对单位阶跃输入的响应图; 解:①图一的闭环传递函数为:2222)(n n n s s s ωξωωφ++=,1021,10n ==ξω Matlab 代码如下:clc clear wn=sqrt(10); zeta=1/(2*sqrt(10)); t=0:0.1:12;Gs=tf(wn^2,[1,2*zeta*wn,wn^2]); step(Gs,t)title('图一单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');响应图如下:②图二的闭环传递函数为:222)21(2)(nn n t ns K s s ωωωξωφ+++=,707.0,10n ==t ξωMatlab 代码如下:clc clear wn=sqrt(10); zeta=0.707; t=0:0.1:12;Gs=tf(wn^2,[1,2*zeta*wn,wn^2]);step(Gs,t)title('图二单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');响应图如下:③图三的闭环传递函数为:222)21(2)1()(nn n d nd s T s s T s ωωωξωφ++++=,707.0,10n ==d ξωMatlab 代码如下:clc clear wn=sqrt(10); zeta=0.707; t=0:0.1:12;Gs=tf([0.347*wn^2,wn^2],[1,2*zeta*wn,wn^2]); step(Gs,t)title('图三单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');响应图如下:3、分别求出在单位斜坡输入下,3个系统的稳态误差; 解:①当t t =)(r 时,图一的开环传递函数为:)1(10)2()(2+=+=s s s s s G n n ξωω是I 型系统 100020lim lim lim lim )()(,1)()(11)()(11e -→→→→====⋅+⋅=v s s v vs s ss s Ks H s sG K K s H s sG ss H s G s 其中K=10,所以101e =ss②当t t =)(r 时,图二的开环传递函数为:)1224.0(237.2)47.31(10)2()s (22+=++=++=s s s s K s s G n t n n ωξωω是I 型系统 100020lim lim lim lim )()(,1)()(11)()(11e -→→→→====⋅+⋅=v s s v vs s ss s Ks H s sG K K s H s sG ss H s G s 其中,所以447.0237.21e ==ss ③当t t =)(r 时,图三的开环传递函数为:)1()1s 374.0(10)2()1()(2++=++=s s s s s T s G n n d ξωω是I 型系统 100020lim lim lim lim )()(,1)()(11)()(11e -→→→→====⋅+⋅=v s s v vs s ss s Ks H s sG K K s H s sG ss H s G s 其中K=10,所以101e =ss4、列表比较3个系统的动态性能和稳态性能,并比较分析测速反馈控制和比例微分控制对改善系统性能的不同之处; 解:可以利用Matlab 求峰值时间、超调量、上升时间、调节时间,代码以系统一为例:clc clear wn=sqrt(10); zeta=1/(2*sqrt(10)); t=0:0.1:12;G=tf(wn^2,[1,2*zeta*wn,wn^2]); C=dcgain(G); [y,t]=step(G);plot(t,y);[Y,k]=max(y);timetopeak=t(k) percentovershoot=100*(Y-C)/C n=1;while y(n)<Cn=n+1;endrisetime=t(n)i=length(t)while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettingtime=t(i)得到结果如下:动态性能比较峰值时间(s) 超调量(﹪)上升时间(s)调节时间(s)系统一系统二5、试用绘制图3对应的系统中参数d T 变化时的根轨迹图,分析d T 变化对系统性能的影响;用MATLAB 画出d T 分别为0,时的系统单位阶跃响应图,比较其动态性能。
基于MATLAB语言环境的二阶惯性系统PID控制仿真

基于MATLAB语言环境的二阶惯性系统PID控制仿真目录一、课程设计要求 (3)二、PID控制简述 (3)三、系统性能分析 (5)四、参数整定 (6)五、PID三参数变化对系统的影响 (7)六、人机交互界面设计 (9)七、心得体会 (15)一、课程设计要求1.在MATLAB语言环境下,给定参数下的二阶惯性系统,要求分析在单位阶跃函数作用下,系统的动态响应性能;2.在系统的前向通道加入比例、积分、微分控制器,调整系统控制器的比例、积分、微分参数,需求系统的最佳输出性能;3.利用所学知识分析三参数增大或减小时,对系统动静态性能的影响,并用仿真实验验证其正确性。
4.设计人机交互界面,可通过对界面输入参数,实现参数修改于曲线显示。
注:二阶系统前向通道传递函数为2()()/()0,1,100,4,80 G s as b cs ds ea b c d e=+++=====。
二、PID控制简述PID控制器由比例单元(P)、积分单元(I)和微分单元(D)组成。
其输入e(t)与输出u(t)的关系为:u(t)=kp[e(t)+1/TI∫e(t)dt+TD*de(t)/dt]式中积分的上下限分别是0和t。
因此它的传递函数为:G(s)=U(s)/E(s)=kp[1+1/(TI*s)+TD*s]。
其中kp为比例系数;TI为积分时间常数;TD为微分时间常数。
比例(P)控制比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差(ady-state error)。
积分(I)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统,如果在进入稳态后存在稳态误差,则这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。
为了消除稳态误差,在控制器中必须引入项”。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
二阶系统瞬态响应分析Matlab仿真.doc

二阶系统瞬态响应分析Matlab仿真.doc本文介绍了使用Matlab软件进行二阶系统瞬态响应分析的方法。
首先,介绍了二阶系统的数学模型和瞬态响应的定义。
然后,通过Matlab编写了程序并进行仿真,分析了不同的输入信号对系统响应的影响。
二阶系统是指由两个一阶系统级联组成的系统。
它可以用以下的微分方程表示:$$\frac{d^2y(t)}{dt^2}+2\zeta\omega_n\frac{dy(t)}{dt}+\omega_n^2y(t)=f(t)$$其中,$y(t)$是系统输出,$f(t)$是系统输入,$\omega_n$是固有频率,$\zeta$是阻尼系数。
对于二阶系统,其瞬态响应指的是系统在输入信号发生变化时,从初始状态到达新的稳态的过程。
瞬态响应包括过渡过程和稳态响应两部分。
为了进行仿真,首先需要确定系统的参数。
在本文的仿真中,我们取$\omega_n=1$,$\zeta=0.2$,并将输入信号设置为单位阶跃信号。
Matlab代码如下:```% 设置系统参数omega_n = 1;zeta = 0.2;% 设计系统sys=tf([omega_n^2],[1, 2*zeta*omega_n, omega_n^2]);step(sys);```运行程序,可以得到如下图所示的系统响应曲线:从图中可以看出,系统的响应可以分为两个阶段:过渡过程和稳态响应。
在过渡过程中,系统响应从初始值开始逐渐趋近于稳态响应。
稳态响应是系统响应达到稳定状态后的响应值。
接下来,我们尝试分析不同的输入信号对系统响应的影响。
我们将输入信号分别设置为正弦波、方波和三角波,并绘制出对应的系统响应曲线。
Matlab代码如下:正弦波:```% 生成正弦波输入信号t=0:0.01:6*pi;f=sin(2*pi*0.5*t);u=[t' f'];从图中可以看出,在正弦波输入下,系统响应呈现周期性变化的特点。
线性二阶系统性能的MATLAB仿真
0
0
2
4
6
8
10 12
14 16
18 20
时间(s)
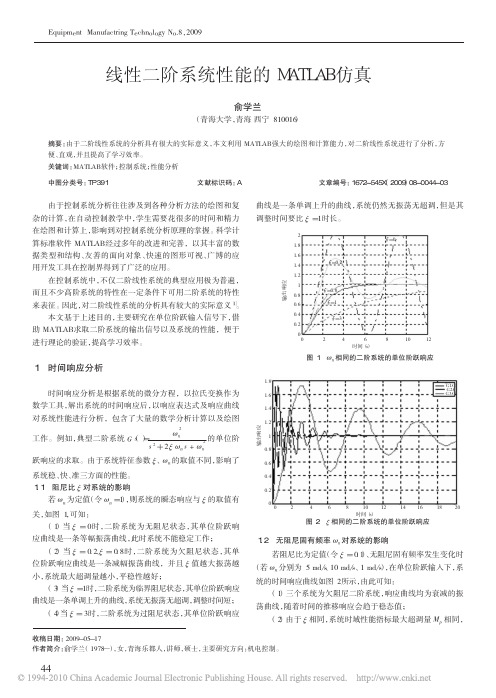
图 2 ξ 相同的二阶系统的单位阶跃响应
1.2 无阻尼固有频率 ωn 对系统的影响 若阻尼比为定值(令 ξ = 0.1)、无阻尼固有频率发生变化时
(若 ωn 分别为 5 rad/s、10 rad/s 、1 rad/s),在单位阶跃输入下,系 统的时间响应曲线如图 2 所示,由此可知:
x
0.89
0.81
0.68
0.5
0.3
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
实轴
图 3 二阶系统零极点分布图
45
Equipment Manufactring Technology No.8,2009
3 二阶系统的分子对系统的影响
在线性系统传递函数的特点中,已知传递函数的分母反
映的是系统本身的固有特性,输入变化不会影响系统传递函
《装备制造技术》2009 年第 8 期
的简化以及求出系统传递函数。 (3)方法 3—— —根据零极点图判断系统的稳定性,即二阶
系统的闭环传递函数的极点严格位于左半 s 平面上,则此系统 稳定。pzmap 函数可以实现零、极点的求取及分布图的绘制。
(4)方法 4—— —系统的相对稳定性的判定。利用 MATLAB 提供的 margin 函数可以求出系统的幅值裕度、相位裕度、幅值 穿越频率、相位穿越频率,用于判定系统的相对稳定性。
本文以第三种方式直观表述二阶系统的稳定性。 2.2 系统型阶的区分
二阶系统特征方程形如 F(s) = a2 s2+ a1 s+ a0 ,根据特征方 程系数的取值不同可以将系统分为以下几种:
自动控制原理MATLAB仿真实验报告

实验一 典型环节的MATLAB 仿真 一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验内容① 比例环节1)(1=s G 和2)(1=s G ;Simulink 图形实现:示波器显示结果:② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现:示波器显示结果:③ 积分环节s s G 1)(1Simulink 图形实现:示波器显示结果:④ 微分环节s s G )(1Simulink 图形实现:波器显示结果:⑤ 比例+微分环节(PD )2)(1+=s s G 和1)(2+=s s G1)、G1(s )=s+2Simulink 图形实现:示波器显示结果:2)、G2(s)=s+1 Simulink图形实现:示波器显示结果:⑥ 比例+积分环节(PI )s s G 11)(1+=和s s G 211)(2+=1)、G1(1)=1+1/sSimulink 图形实现:示波器显示结果:2)G2(s)=1+1/2s Simulink图形实现:示波器显示结果:三、心得体会通过这次实验我学到了很多,对课本内容加深了理解,熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法,加深对各典型环节响应曲线的理解,这为对课程的学习打下了一定基础。
实验二线性系统时域响应分析一、实验目的1.熟练掌握step( )函数和impulse( )函数的使用方法,研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2.通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。
3.熟练掌握系统的稳定性的判断方法。
二、实验内容1.观察函数step( )的调用格式,假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线?2.对典型二阶系统222()2n n n G s s s ωζωω=++1)分别绘出2(/)n rad s ω=,ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线,分析参数ζ对系统的影响,并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。
自控原理实验二阶系统的阶跃响应

二阶系统的阶跃响应一、实验目的1. 通过实验了解参数ζ(阻尼比)、n ω(阻尼自然频率)的变化对二阶系统动态性能的影响;2. 掌握二阶系统动态性能的测试方法。
二、实验内容1. 观测二阶系统的阻尼比分别在0<ζ<1,ζ=1和ζ>1三种情况下的单位阶跃响应曲线;2. 调节二阶系统的开环增益K ,使系统的阻尼比21=ζ,测量此时系统的超调量p δ、调节时间t s (Δ= ±0.05);3. ζ为一定时,观测系统在不同n ω时的响应曲线。
三、实验原理1. 二阶系统的瞬态响应用二阶常微分方程描述的系统,称为二阶系统,其标准形式的闭环传递函数为2222)()(nn n S S S R S C ωζωω++= (2-1)闭环特征方程:0222=++n n S ωζω其解 122,1-±-=ζωζωn n S ,针对不同的ζ值,特征根会出现下列三种情况: 1)0<ζ<1(欠阻尼),22,11ζωζω-±-=n n j S此时,系统的单位阶跃响应呈振荡衰减形式,其曲线如图2-1的(a)所示。
它的数学表达式为:)(111)(2βωζζω+--=-t Sin e t C d t n式中21ζωω-=n d ,ζζβ211-=-tg。
2)1=ζ(临界阻尼)n S ω-=2,1此时,系统的单位阶跃响应是一条单调上升的指数曲线,如图2-1中的(b)所示。
3)1>ζ(过阻尼),122,1-±-=ζωζωn n S此时系统有二个相异实根,它的单位阶跃响应曲线如图2-1的(c)所示。
(a) 欠阻尼(0<ζ<1) (b)临界阻尼(1=ζ) (c)过阻尼(1>ζ)图2-1 二阶系统的动态响应曲线虽然当ζ=1或ζ>1时,系统的阶跃响应无超调产生,但这种响应的动态过程太缓慢,故控制工程上常采用欠阻尼的二阶系统,一般取ζ=0.6~0.7,此时系统的动态响应过程不仅快速,而且超调量也小。
自控实验—二、三阶系统动态分析

实验二.二、三阶系统动态分析一.实验目的:1.学习二、三阶系统的电模拟方法及参数测试方法;2.观察二、三阶系统的阶跃响应曲线,了解参数变化对动态特性的影响; 3.学习虚拟仪器(超抵频示波器)的使用方法; 4.使用MATLAB 仿真软件进行时域法分析; 5.了解虚拟实验的使用方法。
二.实验设备及仪器1.模拟实验箱; 2.低频信号发生器;3.虚拟仪器(低频示波器); 4.计算机;5.MATLABL 仿真软件。
三.实验原理及内容实验原理:1、二阶系统的数学模型系统开环传递函数为系统闭环传递函数为2、 二阶系统暂态性能(a) 延迟时间t d : 系统响应从 0 上升到稳态值的 50% 所需的时间。
)2s (s n 2nςω+ω为阻尼比(,为无阻尼自然振荡频率其中:ςωω+ςω+ω==n 2nn 22ns 2s )s (G )s (R )s (C(b) 上升时间t r : 对于欠阻尼系统是指 , 系统响应从 0 上升到稳态值所需的时间 ; 对于过阻尼系统则指 , 响应从稳态值的 10% 上升到 90% 所需的时间。
(c) 峰值时间t p : 系统响应到达第一个峰值所需的时间。
(d) 最大超调量σp ( 简称超调量 ) : 系统在暂态过程中输出响应超过稳态值的最大偏离量。
通常以单位阶跃响应稳态值的百分数来表示 , 即%100e e esin 1e)t sin(1e1)y(t )y()y()y(t σ22pn pn pn 11t 2t p d 2t p p p ⨯===-=+--=-=∞∞-=-------ζπζζπζζωζωζωϕζϕωζ超调量)t sin(1e 1)t (y d 2tn ϕωζζω+--=- 2n d p d 1ωπωπt 0)t sin()t (y ζω-==∴= 峰值时间求导可得对dr t t ωπt 1y(t)rϕ-=== 可令2n21n πϕωξ-=-t ≈n2d n d 2.06.01t 7.01ως+ς+ως+≈或n2d n d2.06.01t 7.01t ως+ς+≈ως+≈或(e) 调节时间t s : 系统响应到达并不再越出稳态值的容许误差带±Δ所需的最短时间 , 即通常取Δ为稳态值的 5% 或 2% 。
如何用matlab仿真自控系统框图

谢谢观看
方法/步骤
检查系统框图无误后点击运行按钮 (如下图箭头所指),大概几秒后仿 真结束:
方法/步骤
双击图中的示波器就可以查看系统仿 真输出,如下图所示:
参考资料:MATLAB控制系统仿真与实例详解
《MATLAB控制系统仿真与实例详解》是2008年人民邮电出版社出版的图书,作者是夏玮、常春 藤。
参考资料:自动控制系统及其MATLAB仿真
参考资料:基于MATLAB的控制系统仿真及应用(第2版)
《基于MATLAB的控制系统仿真及应用(第2版)》是2018年8月电子工业出版社出版的图书,作 者是张聚。
参考资料:MATLAB/Simulink与控制系统仿真(第4版)
《MATLAB/Simulink与控制系统仿真(第4版)》是2017年5月电子工业出版社出版的图书,作者 是王正林。
方法/步骤
首先打开matlab软件,点击Simulink 按钮打开Simulink仿真环境(需要一 点时间),如下图所示:
方法/步骤
打开Simulink后,主界面如下所示:
方法/步骤
点击Simulink界面中的 File/New/Model,如下图所示建立并 保存模型文件:
方法/步骤
在Simulink的左侧资源栏拖拽控件到 model文件内并设置连线,完成后如 下图所示:
参考资料:MATLABR2008控制系统动态仿真实例教程
《MATLABR2008控制系统动态仿真实例教程》由谢仕宏所著,本书结合MATLAB的最新版本R2008, 介绍了MATLAB应用的基本知识、控制系统计算机辅助分析与设计、动态系统的Simulink建模与 仿真,以及模糊控制系统仿真设计等内容。
《自动控制系统及其MATLAB仿真》是一本2020年出版的图书,由化学工业出版社出版
典型二阶系统的控制仿真实验

图1
3.在取 1 的某一固定值时,T 取大于 0 的三个不同值,输入参数如下: 取 Kosai1=0.5,T1=0.如图 2:
图2 4.在 MATLAB—Simulink 仿真环境下绘制曲线: 在固定时间常数情况下:
图3 其中黄线、紫线、蓝线的参数分别为: Kosai1=0.5,T1=2;Kosai2=1,T2=2; Kosai=1.8,T3=2
其总体布置图为:
图4 其中每个图形如下:
图 5Kosai1=0.5,T1=2
图 6 Kosai2=1,T2=2
图 8Kosai=1.8,T3=2 在固定阻尼情况下:Kosai1=0.5,T1=0.5;Kosai2=0.5,T2=1; Kosai=0.5,T3=2
实验一 典型二阶系统的控制仿真实验
一、 实验目的
1. 了解 MATLAB 语言的简单程序设计。 2. 了解 MATLAB Simulink 仿真环境,并能简单建立二阶系统模型。 3. 分别在计算环境和 Simulink 环境下, 通过调整系统参数, 观察系统输出, 加深理解典型二阶系统各参数的意义。
四、 实验结果
1.编制 MATLAB 程序如下: clear all %清除当前窗口中所有的变量 Kosai1=input('Input Kosai1:'); %输入阻尼比ξ1 T1=input('Input T1:'); %输入时间常数 T1 M1=[0 0 1]; %输入传递函数的分子数组 D1=[T1^2 2*Kosai1*T1 1]; %输入传递函数的分母数组 step(M1,D1); %输入阶跃命令 grid on %打开坐标网格 title('二阶系统单位阶跃响应曲线'); %输入图形标题 hold on %保留当前图形窗口 %· · · · · · · · ·重复输入参数、绘制输出响应曲线· · · · · · · · · · · · · · · · Kosai2=input('Input Kosai2:'); T2=input('Input T2:'); M2=[0 0 1]; D2=[T2^2 2*Kosai2*T2 1]; step(M2,D2); hold on Kosai3=input('Input Kosai3:'); T3=input('Input T3:'); M3=[0 0 1]; D3=[T3^2 2*Kosai3*T3 1]; step(M3,D3); hold on 2.在固定时间常数的情况下,输入参数分别为: Kosai1=0.5,T1=2;Kosai2=1,T2=2; Kosai=1.8,T3=2 输出图形如下截图:
二阶控制系统的Multisim建模与仿真

运城 学 院 “ 自动控 制原 理 ” 课程 实验 采用 Ma t l a b
闭环 特征方 程 为 :
S + 2 S + 0 。 ( 2 )
望
《 f
面
E
o
t i m e( s )
R 4 = l 0 K -j 丑 阻尼骱跃响应
£
里
《I
面
E
o
T i m e( s )
图 3 二 阶 系统 的 阶跃 响 应
从 图 3中可 知 : S 1 A断 开 , 系 统处 于无 阻尼 状 态, 阶跃 响应 为 等 幅 正 弦振 荡 曲线 。S 1 A闭合 , R 4
电
图1 二 阶 系统 动 态 结 构 图
闭环传 递 函数 为 :
c
一
尺 鼽
: S + S + : ’ 。
图 2 二 阶 系统 Mu l t i s i m 建模 图
当开关 S 1 A闭合 , u : 、 c 、 、 R 构成惯性环节 ,
( 4 )
T i m e( s )
R 4 = 2 5 K ・ 过 阻尼阶跃 响应
经计算得 : 当开关 S 1 A闭合 , R , = 5 0 K时, = l ;
当0 < P u < 5 0 K时 , > 1 ; 当I  ̄ > 5 0 K , 0 < < 1 。当开
£
3 二 阶系统 时域仿真分析
线性控制系统的时域分析具有直观 、 准确的优 点, 可以提供系统时间响应 的全部信息 。时域分析 中常用到 的输人信号有 阶跃 、 斜坡 、 加速度及脉 冲 信号 。如图 2 中, 输入采用直流电源 V l 和开关 J l 模拟单位阶跃输入信号 , 电源 V 1 参数值为 1 V , 开 关J 1 的T O N时间设为0 . 1 s 『 5 ] , 输出采用示波器来观 测, 仿真结果如图 3 所示 。
实验二 二阶系统matlab仿真(dg)

利用simulink进行仿真的步骤:1.打开Matlab软件;2.在Command Window命令行>>后输入simulink并回车或点击窗口上部图标直接进入simulink界面;3.点击File-New-Modle就可以在新的界面上建立系统的仿真模型了;4.在左面的器件模型库中找到所需模型,用鼠标将器件模型拖到建立的界面上,然后用鼠标将它们用连线连起来,系统的仿真模型就建立起来了;5.点击界面上部的图标‘’进行仿真,双击示波器就可以看到仿真结果。
实验要用到的元件模型的图标及解释如下:阶跃信号:在simulink-source中可以找到,双击可以设定阶跃时间。
sum:在simulink-math operations中可以找到,双击可以改变器属性以实现信号相加还是相减;比例环节:在simulink-math operations中可以找到,双击可以改变器属性以改变比例系数;积分环节:在simulink-continues中可以找到;传函的一般数学模型表达形式:在simulink-continues中可以找到,双击可以对传递函数进行更改(通过设定系数)。
示波器:在simulink-sinks中可以找到。
实验二二阶系统的Matlab仿真一、实验目的1、研究二阶系统的特征参数―阻尼比ζ和无阻尼自然频率ωn对系统动态性能的影响。
2、利用simulink工具和MATLAB语句实现二阶系统的仿真。
3、熟悉MATLAB语句对二阶系统传函的表达形式以及阶跃响应的表达形式。
二、实验内容1、simulink仿真(标准二阶系统ωn=1,ζ=0.5)2、用Matlab语句实现二阶系统仿真(1)对于标准二阶系统,当ωn=4,改变ζ值对性能的影响-1<ζ<0(负阻尼)>> step(tf(4^2,[1,2*(-0.5)*4,4^2]))ζ<-1(负阻尼)>> step(tf(4^2,[1,2*(-1.5)*4,4^2]))ζ=0(零阻尼)>> step(tf(4^2,[1,2*0*4,4^2]))0<ζ<1(欠阻尼)>> figure>> step(tf(4^2,[1,2*0.1*4,4^2]))>>hold on>> step(tf(4^2,[1,2*0.2*4,4^2]))>> step(tf(4^2,[1,2*0.3*4,4^2]))>> step(tf(4^2,[1,2*0.4*4,4^2]))>> step(tf(4^2,[1,2*0.5*4,4^2]))>> step(tf(4^2,[1,2*0.6*4,4^2]))>> step(tf(4^2,[1,2*0.7*4,4^2]))>> step(tf(4^2,[1,2*0.8*4,4^2]))>> step(tf(4^2,[1,2*0.9*4,4^2]))ζ=1(临界阻尼)>> figure>> step(tf(4^2,[1,2*1*4,4^2]))ζ>1(过阻尼)>> hold on>> step(tf(4^2,[1,2*2.0*4,4^2]))>> step(tf(4^2,[1,2*4.0*4,4^2]))>> step(tf(4^2,[1,2*8.0*4,4^2]))(2)对于标准二阶系统,当ζ=0.5,改变ωn时的情况:>> figure>> step(tf(1^2,[1,2*0.5*1,1^2])) (ωn=1)>> hold on>> step(tf(2^2,[1,2*0.5*2,2^2])) (ωn=2)>> step(tf(4^2,[1,2*0.5*4,4^2])) (ωn=4)>> step(tf(8^2,[1,2*0.5*8,8^2])) (ωn=8)三、实验报告要求:1、记录由matlab仿真所得到的阶跃响应曲线。
经典-二阶系统的MATLAB仿真设计

《二阶系统单位阶跃响应MATLAB 仿真设计》设计的题目:控制系统开环传递函数为()()1100.51K G s s s =+,要求5/v K s =0.5,ζ=2s t s ≥。
设计目的:1.学会使用MATLAB 语言及Simulink 动态仿真工具进行系统仿真与调试。
学会使用硬件仿真软件对系统进行模拟仿真。
2.掌握自动控制原理的时域分析法,根轨迹法,频域分析法,以及各种补偿(校正)装置的作用及用法,能够利用不同的分析法对给定系统进行性能分析,能根据不同的系统性能指标要求进行合理的系统设计,并调试满足系统的指标。
设计要求:1、未校正系统的分析,利用MATLAB 绘画未校正系统的开环和闭环零极点图,绘画根轨迹,分析未校正系统随着根轨迹增益变化的性能(稳定性、快速性);编写M 文件作出单位阶跃输入下的系统响应,分析系统单位阶跃响应的性能指标。
绘出系统开环传函的bode 图,利用频域分析方法分析系统的频域性能指标(相角裕度和幅值裕度,开环振幅)。
2、利用频域分析方法,根据题目要求选择校正方案,要求有理论分析和计算。
并与Matlab 计算值比较。
选定合适的校正方案(串联滞后/串联超前/串联滞后-超前),理论分析并计算校正环节的参数,并确定何种装置实现。
3、绘画已校正系统的bode 图,与未校正系统的bode 图比较,判断校正装置是否符合性能指标要求,分析出现大误差的原因4、根据选用的装置,使用multisim 电路设计仿真软件(或其他硬件电路仿真软件)绘画模拟电路。
求此系统的阶跃响应曲线。
分析采用的校正装置的效果。
目录1.未校正系统分析 (4)1.1未校正系统的开环和闭环零极点图 (4)1.1.1校正前开环零极点图 (4)1.1.2 校正前系统的闭环零极点 (5)1.2 未校正系统的根轨迹及性能分析 (5)1.3单位阶跃输入下的系统响应及系统性能分析 (6)1.4开环传递函数的bode图及系统的频域性能分析 (7)2.校正方案的计算与选择 (8)3.已校正系统Bode图及性能分析 (9)4.电路设计仿真 (12)5.总结与心得 (14)5.1设计总结 (14)5.2设计心得 (15)6.参考文献 (16)1.未校正系统的分析:由静态速度误差5/v K s ,可以取K=0.51.1利用MATLAB 绘画未校正系统的开环和闭环零极点图 1.1.1开环零极点图 程序如下: >> num=[5];>>den=conv([1 0],[0.5 1]); >>pzmap(num,den)得如下未校正系统的开环零极点:从图象中看出,未校正的开环传递函数的没有零点,极点有2个,分别为:s=0,s=-2。
二阶系统性能改善的Matlab仿真分析

二阶系统性能改善的Matlab仿真分析刘洋;杨薇;张付杰【摘要】It is very important for the systems' analysis and designs to grasp the variation regularity of system performance with parameters. In the second-order systems, the proportion-differential control and tachometer feedback control are used to improve its property generally. The system before and after correction is simulated with Matlab. The result of a second-order system performance improved separately by two methods is analyzed. Through the calculation with an instance, both control methods of proportion-differential control and tachometer feedback control can improve the rapidity and stability of the system. The simulation result indicates that both of the two methods can observably improve the performance of second-order systems.%掌握系统性能随参数变化的规律性,对于分析和设计系统是十分重要的.在二阶系统中,一般采用比例-微分控制和测速反馈控制改善其性能.这里利用Matlab对校正前后的系统进行仿真,分析两种方法对二阶系统性能改善的效果.同时通过实例计算,得出比例-微分控制和测速反馈控制均可使系统快速性和稳定性提高.仿真结果表明,两种方法均可显著改善二阶系统的性能.【期刊名称】《现代电子技术》【年(卷),期】2012(035)012【总页数】3页(P98-100)【关键词】二阶系统;比例-微分控制;测速反馈控制;Matlab【作者】刘洋;杨薇;张付杰【作者单位】昆明理工大学现代农业工程学院,云南昆明 650500;昆明理工大学现代农业工程学院,云南昆明 650500;昆明理工大学现代农业工程学院,云南昆明650500【正文语种】中文【中图分类】TN911-340 引言由于计算机技术的迅速发展和进步,自动控制技术已广泛应用于制造业、农业、交通以及航空航天等领域,从而提高了社会劳动生产率,改善了人类的生产环境,促进了人类的进步。
控制系统的MATLAB计算及仿真

控制系统的MATLAB计算及仿真控制系统是一种用来实现对物理系统或工程系统进行控制的方法和工具。
MATLAB是一种强大的计算机软件包,能够方便地进行控制系统的计算和仿真。
本文将介绍MATLAB在控制系统中的应用,并以一个简单的例子来说明如何用MATLAB进行控制系统的计算和仿真。
首先,我们需要打开MATLAB软件并创建一个新的脚本文件。
在脚本文件中,我们可以使用MATLAB提供的函数来定义控制系统的传递函数和状态空间模型。
例如,我们可以使用tf函数来定义一个传递函数模型。
传递函数是描述系统输入与输出之间关系的一种数学模型。
以下是一个例子:```MATLABs = tf('s');G=1/(s^2+2*s+1);```这个传递函数模型表示一个具有二阶惯性的系统。
我们可以使用step函数来绘制系统的阶跃响应曲线:```MATLABstep(G);```通过运行脚本文件,我们可以得到系统的阶跃响应曲线。
此外,MATLAB还提供了许多其他的函数和命令来计算和仿真控制系统。
另外,我们还可以使用stateSpace函数来定义一个状态空间模型。
状态空间模型是控制系统中另一种常用的数学模型。
以下是一个例子:```MATLABA=[01;-1-1];B=[0;1];C=[10];D=0;sys = ss(A, B, C, D);```这个状态空间模型描述了一个二阶系统的状态方程和输出方程。
我们可以使用step函数来绘制系统的阶跃响应曲线:```MATLABstep(sys);```通过运行脚本文件,我们可以得到系统的阶跃响应曲线。
除了step函数外,MATLAB还提供了许多其他的函数和命令来计算和仿真状态空间模型。
在控制系统中,还常常需要对系统进行参数调节和性能优化。
MATLAB提供了一系列的控制系统工具箱,用于进行控制系统的分析和设计。
例如,Control System Toolbox提供了用于线性系统分析和设计的工具。
matlab二阶系统数值仿真程序

《Matlab二阶系统数值仿真程序:深度与广度的探索》一、引言在工程学和科学研究中,对于控制系统和信号处理系统的分析和设计是非常重要的。
而二阶系统作为控制系统中常见的一种类型,其数值仿真程序的编写和应用更是至关重要。
在本文中,我们将深入探讨Matlab中二阶系统的数值仿真程序,帮助读者全面理解并灵活运用这一主题。
二、Matlab中二阶系统数值仿真程序的基本原理在Matlab中,我们可以使用一系列内置函数来构建二阶系统的数值仿真程序。
我们需要定义二阶系统的参数,包括阻尼比、自然频率和初始条件等。
我们可以利用Matlab中的控制系统工具箱来建立系统的传递函数或状态空间模型。
通过调用相关的数值仿真函数,如step()和impulse()等,可以对二阶系统进行时域响应和频域分析,从而深入理解其特性和行为。
三、深入探讨二阶系统数值仿真程序的应用1. 时域响应分析:利用Matlab中的step()函数,我们可以得到二阶系统的阶跃响应曲线。
通过观察阶跃响应曲线的波形和参数,我们可以了解系统的过渡过程、稳态性能以及动态特性。
2. 频域分析:利用Matlab中的bode()函数,我们可以绘制二阶系统的频率响应曲线。
通过分析频率响应曲线的幅频特性和相频特性,我们可以了解系统的频率选择性、共振特性以及稳定性边界。
3. 参数变化分析:利用Matlab中的sensitivity()函数,我们可以对二阶系统的参数进行变化分析。
通过观察不同参数对系统特性的影响,我们可以进行灵活的系统设计和优化。
四、对二阶系统数值仿真的个人观点和理解在我看来,Matlab中二阶系统的数值仿真程序是非常实用和强大的工具。
通过深入探索和灵活应用,我们可以更好地理解和分析控制系统的性能和特性。
我也认为在实际工程和科学项目中,对于二阶系统数值仿真的深度和广度探索,能够为我们带来更多有价值的思考和经验。
五、总结与回顾在本文中,我们深入探讨了Matlab中二阶系统数值仿真程序的基本原理和应用。
基于MATLAB的二阶线性系统分析与仿真

第26卷第5期 河池学院学报 Vol .26No .52006年10月 JOURNAL OF HECH IUN I V ERSI TY Oct .2006基于MAT LAB 的二阶线性系统分析与仿真才娟,肖洪祥,邵彭飞(桂林工学院 电子与计算机系,广西 桂林 541004)[摘 要] 二阶线性系统应用非常广泛,MAT LAB 语言是功能十分强大的工程计算及数值分析软件,它提供了高效的信号处理工具箱。
介绍利用MAT LAB 语言对二阶线性系统进行分析与仿真的方法,尤其对系统稳定性的分析,并给出相关的例子、程序和相应的仿真结果。
[关键词] MAT LAB 语言;二阶线性系统;稳定性;仿真[中图分类号] TP391.9 [文献标识码] A [文章编号] 1672-9021(2006)05-0085-03[作者简介] 才娟(1979-),女(满族),辽宁义县人,桂林工学院电子与计算机系硕士研究生,主要研究方向为检测技术与自动化装置;肖洪祥(1965-),男,湖北武汉人,桂林工学院电子与计算机系高级工程师,主要研究方向为检测技术与自动化装置。
在控制工程中,不仅二阶线性系统的典型应用极为普遍,而且不少高阶系统的特性在一定条件下可用二阶系统的特性来表征。
因此,对二阶线性系统的分析具有较大的实际意义[1]。
MAT LAB 已经成为国际上最流行的科学与工程计算的软件工具,现在的MAT LAB 已经不仅仅是一个“矩阵实验室”了,它已经成为了一种具有广泛应用前景的、全新的计算机高级编程语言,有人称它为“第四代”计算机语言,MAT LAB 语言的功能越来越强大。
它在国内外高校和研究部门正扮演着重要的角色,在科学运算、信号处理、自动控制与科学绘图等许多领域得到了广泛的应用。
本文探讨MAT LAB 语言在线性系统分析中的应用,主要研究在给定典型输入信号下求取系统的输出信号以及系统的稳定性。
t 图1 不同阻尼比ξ下系统的单位阶跃响应1 二阶线性系统阶跃响应的分析二阶线性系统的闭环传递函数为Φ(s )=ω2n s 2+2ξωn s +ω2n,当输入不同时,对其单位阶跃响应进行比较和仿真。
自动控制原理MATLAB仿真实验指导书(4个实验)

自动控制原理MATLAB仿真实验实验指导书电子信息工程教研室实验一典型环节的MA TLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MA TLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink仿真环境常规模板。
图1-1 SIMULINK仿真界面图1-2 系统方框图3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理
二阶系统性能分析Matlab 仿真大作业附题目+ 完整报告内容
设二阶控制系统如图
1所示,其中开环传递函数
)
1(10
)2()(2+=+=s s s s s G n n ξωω
图1
图2
图3
要求:
1、分别用如图2和图3所示的测速反馈控制和比例微分控制两种方式改善系统的性能,如果要求改善后系统的阻尼比ξ =0.707,则t K 和
d T 分别取多少?
解:
由)1(10
)2()(2
+=
+=s s s s s G n n ξωω得10
21,10,102===ξωωn 22n
n ()
s s ωξω+R (s )C (s )
-
对于测速反馈控制,其开环传递函数为:)
2()s (2
2n t n n
K s s G ωξωω++=; 闭环传递函数为:2
2
2)2
1(2)(n
n n t n
s K s s ωωωξωφ+++=
;
所以当n t K ωξ2
1+=0.707时,347.02)707.0(t =÷⨯-=n K ωξ;
对于比例微分控制,其开环传递函数为:)2()1()(2
n n
d s s s T s G ξωω++=;
闭环传递函数为:)
)2
1(2)1()(2
22
n n n d n
d s T s s T s ωωωξωφ++++=;
所以当n d T ωξ2
1
+=0.707时,347.02)707.0(=÷⨯-=n d T ωξ;
2、请用MATLAB 分别画出第1小题中的3个系统对单位阶跃输入的响应图; 解:
①图一的闭环传递函数为:
2
22
2)(n n n s s s ωξωωφ++=,10
21
,10n ==ξω Matlab 代码如下:
clc clear wn=sqrt(10); zeta=1/(2*sqrt(10)); t=0:0.1:12;
Gs=tf(wn^2,[1,2*zeta*wn,wn^2]); step(Gs,t)
title('图一单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');
响应图如下:
②图二的闭环传递函数为:
2
22)2
1(2)(n
n n t n
s K s s ωωωξωφ+++=
,707.0,10n ==t ξω
Matlab 代码如下:
clc clear wn=sqrt(10); zeta=0.707; t=0:0.1:12;
Gs=tf(wn^2,[1,2*zeta*wn,wn^2]);
step(Gs,t)
title('图二单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');
响应图如下:
③图三的闭环传递函数为:
2
22
)2
1(2)1()(n
n n d n
d s T s s T s ωωωξωφ++++=,707.0,10n ==d ξω
Matlab 代码如下:
clc clear wn=sqrt(10); zeta=0.707; t=0:0.1:12;
Gs=tf([0.347*wn^2,wn^2],[1,2*zeta*wn,wn^2]); step(Gs,t)
title('图三单位阶跃响应曲线'); xlabel('t/s');ylabel('c(t)');
响应图如下:
3、分别求出在单位斜坡输入下,3个系统的稳态误差; 解:
①当t t =)(r 时,图一的开环传递函数为:
)
1(10
)2()(2+=
+=s s s s s G n n ξωω是I 型系统 1
00020lim lim lim lim )()(,1)()(11
)()(11e -→→→→====
⋅+⋅
=v s s v v
s s ss s K
s H s sG K K s H s sG s
s H s G s 其中K=10,所以10
1
e =
ss
②当t t =)(r 时,图二的开环传递函数为:
)
1224.0(237
.2)47.31(10)2()s (2
2+=++=++=s s s s K s s G n t n n ωξωω是I 型系统 1
00020lim lim lim lim )()(,1)()(11
)()(11e -→→→→====
⋅+⋅
=v s s v v
s s ss s K
s H s sG K K s H s sG s
s H s G s 其中K=2.237,所以447.0237
.21
e ==
ss ③当t t =)(r 时,图三的开环传递函数为:
)
1()
1s 374.0(10)2()1()(2
++=
++=s s s s s T s G n n d ξωω是I 型系统 1
00020lim lim lim lim )()(,1)()(11
)()(11e -→→→→====
⋅+⋅
=v s s v v
s s ss s K
s H s sG K K s H s sG s
s H s G s 其中K=10,所以10
1
e =ss
4、列表比较3个系统的动态性能和稳态性能,并比较分析测速反馈控制和比例微分控制对改善系统性能的不同之处; 解:
可以利用Matlab 求峰值时间、超调量、上升时间、调节时间,代码以系统一为例:
clc clear wn=sqrt(10); zeta=1/(2*sqrt(10)); t=0:0.1:12;
G=tf(wn^2,[1,2*zeta*wn,wn^2]); C=dcgain(G); [y,t]=step(G);
plot(t,y);
[Y,k]=max(y);
timetopeak=t(k)
percentovershoot=100*(Y-C)/C
n=1;
while y(n)<C
n=n+1;
end
risetime=t(n)
i=length(t)
while(y(i)>0.98*C)&(y(i)<1.02*C)
i=i-1;
end
settingtime=t(i)
得到结果如下:
动态性能比较峰值时间
(s)
超调量
(﹪)
上升时间
(s)
调节时间
(s) 系统一 1.0154 60.4417 0.5712 7.2985 系统二 1.4077 4.3253 1.0619 1.8769
5、试用绘制图3对应的系统中参数d T 变化时的根轨迹图,分析d T 变化对系统性能的影响;用MATLAB 画出d T 分别为0,0.1,0.2,0.5和1时的系统单位阶跃响应图,比较其动态性能。
解:
①)
1(10
s 10)2()1()(d 2
++=
++=s s T s s s T s G n n d ξωω,由特征方程0)(1=+s G 得: 010102=+++s T s s d ,010
1012=+++
s s s
T d 此时可利用Matlab 编程得到根轨
迹
Matlab 代码如下:
clc clear num=[10 0]; den=[1 1 10]; G=tf(num,den); rlocus(G);
title('Td 变化的参数根轨迹'); xlabel('实轴');ylabel('虚轴');
根轨迹图如下:
②图三的闭环传递函数为:
222
)2
1(2)1()(n n n d n d s T s s T s ωωωξωφ++++=,1021
,10n ==ξω,在Td 分别取0,0.1,
0.2,0.5和1时,可以用for 语句实现 Matlab 代码如下:
clc clear wn=3.1623; zeta=0.1581; t=0:0.1:12; Td=[0,0.1,0.2,0.5,1];
__________________________________________________
hold on;
for i=1:length(Td)
Gs=tf([Td(i)*wn^2,wn^2],[1,2*(zeta+0.5*Td(i)*wn)*wn,wn^2])
step(Gs,t)
end
hold on;
title('图三Td变化单位阶跃响应曲线');
xlabel('t/s');ylabel('c(t)');
响应图如下:
随着Td的增大,系统的峰值时间、上升时间、延迟时间、调节时间减小;超调量、振荡次数减小,系统的平稳性提高,快速性也提高了。
__________________________________________________。
