九年级数学下册 1.2 有关三角函数的计算课件 浙教版
合集下载
新浙教版九年级数学下册第一章《有关三角函数的计算(第2课时)》公开课课件.ppt
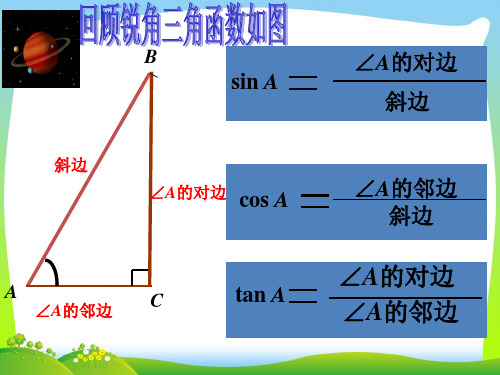
2ndf
按键的顺序 sin 0 · 2
9 7 4 2ndf
DMS
显示结果
17°18′5.43″
即∠α =17°18′5.43″
w例如,根据下面的条件,求锐角β的大小(精确 到1″ w(1)sinβ=0.4511;(2)cosβ=0.7857;
w(3) tanβ=1.4036 w按键盘顺序如下:
按键的顺序
B
∠A的对边
sin A
斜边
斜边
∠A的对边 cos A
A
∠A的邻边
C
tan A
∠A的邻边 斜边
∠A的对边 ∠A的邻边
sinA=cosB= a, cosA=sinB= b,
c
c
a
tan A=
b
tan A = sin A . cos A
w互余两角之间的三角函数关系: wsin A=cos B,tan A·tan B=1. A
解 : tanA C D =A D =100.5208, C D19.2
∴∠ACD≈27.5° .
∴∠ACB=2∠ACD≈2×27.5°=55°.
∴V型角的大小约55°.
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/142021/1/14Thursday, January 14, 2021
锐角三角函数(复习)
☆ 应用练习
1.已知角,求值 2.已知值,求角 3. 确定值的范围 4. 确定角的范围
确定角的范围
3. 当∠A为锐角,且tan A的
值大于 3 时,∠A( B )
3
(A)小于30° (B)大于30° (C) 小于60° (D)大于60°
有关三角函数的计算课件(浙教版)

3
(A)小于30°
(B)大于30°
(C) 小于60° (D)大于60°
5、当∠A为锐角,且tanA的值小于 3 时,∠A为( C )
(A)小于30°
(B)大于30°
(C) 小于60° (D)大于60°
课外拓展
6、当∠A为锐角,且cosA= 1 ,那么( D )
5
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
动,如果木桩向上运动了1cm,楔子沿水平方向前进5
cm(如箭头所示),那么楔子的倾斜角为多少度?
F
F
P
A
P
A
B
C
BNC
解:由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,
木桩上升的距离为PN,即PN=1cm.
在Rt△PBN中, tanB= =
∠B=?
探求新知
已知三角函数值求角度,要用到sin,cos,tan的 第二功能健“sin-1 cos-1,tan-1”健例如:已知 sinα=0.2974,求锐角α.按健顺序为:
按键的顺序
显示结果
SHIFT sin 0 . 4 5 1 1
= °′″
2ndf 1
sin 0 . 4 5 1
2ndf
DMS
26048’51” 26048’51”
即∠β=26048’51”
(2)cos α=0.7857
shift cos 0 . 7 8 5 7 = 0'''
(3)tan α=1.4036 shift tan 1 . 4 0 3 6 = 0'''
B
在Rt△AOC中,
sin∠AOC=
AC OA
(A)小于30°
(B)大于30°
(C) 小于60° (D)大于60°
5、当∠A为锐角,且tanA的值小于 3 时,∠A为( C )
(A)小于30°
(B)大于30°
(C) 小于60° (D)大于60°
课外拓展
6、当∠A为锐角,且cosA= 1 ,那么( D )
5
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
动,如果木桩向上运动了1cm,楔子沿水平方向前进5
cm(如箭头所示),那么楔子的倾斜角为多少度?
F
F
P
A
P
A
B
C
BNC
解:由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,
木桩上升的距离为PN,即PN=1cm.
在Rt△PBN中, tanB= =
∠B=?
探求新知
已知三角函数值求角度,要用到sin,cos,tan的 第二功能健“sin-1 cos-1,tan-1”健例如:已知 sinα=0.2974,求锐角α.按健顺序为:
按键的顺序
显示结果
SHIFT sin 0 . 4 5 1 1
= °′″
2ndf 1
sin 0 . 4 5 1
2ndf
DMS
26048’51” 26048’51”
即∠β=26048’51”
(2)cos α=0.7857
shift cos 0 . 7 8 5 7 = 0'''
(3)tan α=1.4036 shift tan 1 . 4 0 3 6 = 0'''
B
在Rt△AOC中,
sin∠AOC=
AC OA
新浙教版九年级数学下册第一章《直角三角函数的计算2》公开课课件.ppt
(2)AC=4,BC=5.
A
C
B
2.如图,测得一商场自动扶梯的长L为
8米,该自动扶梯到达的高度h是5米. 问自动扶梯与地面所成的角θ是多少度
(精确到 1 )?
L
h
θ
例题赏析
例1 如图,在△ ABC中,AD是BC边上的高, A
若tanB=cos∠DAC,
Байду номын сангаас
(1)AC与BD相等吗?说明理由;
B
(2)若sinC=
)
5,A已,知相在等Rt△BA,BC中互,余∠C=C9,0°互,补sinDA,= 12不,确则定co。sB=( A )
A1 2
B,√22
C,√23
D,√3
当例堂题训赏练析二
(1)计算: sin60°·tan60°+cos ² 45°= 2
(2)如果tanA·tan30°=1,∠A=___6_0_°____。
弦值和余弦值( A )
A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。
2,在△ABC中,若 sinA=√22 , 3, 在Rt△ABC中∠, C=90°, AC=
tanB=√3,则∠C=
√3,
AB=2,tan
B 2
75° √3
3
4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( B )
(3)已知cosα<0.5,那么锐角α的取值范围( A )
A、60°<α<90° B、 0°< α <60° C、30°< α <90° D、 0°< α <30°
(4)如果√cosA – —12
那么△ABC是( D
A
C
B
2.如图,测得一商场自动扶梯的长L为
8米,该自动扶梯到达的高度h是5米. 问自动扶梯与地面所成的角θ是多少度
(精确到 1 )?
L
h
θ
例题赏析
例1 如图,在△ ABC中,AD是BC边上的高, A
若tanB=cos∠DAC,
Байду номын сангаас
(1)AC与BD相等吗?说明理由;
B
(2)若sinC=
)
5,A已,知相在等Rt△BA,BC中互,余∠C=C9,0°互,补sinDA,= 12不,确则定co。sB=( A )
A1 2
B,√22
C,√23
D,√3
当例堂题训赏练析二
(1)计算: sin60°·tan60°+cos ² 45°= 2
(2)如果tanA·tan30°=1,∠A=___6_0_°____。
弦值和余弦值( A )
A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。
2,在△ABC中,若 sinA=√22 , 3, 在Rt△ABC中∠, C=90°, AC=
tanB=√3,则∠C=
√3,
AB=2,tan
B 2
75° √3
3
4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( B )
(3)已知cosα<0.5,那么锐角α的取值范围( A )
A、60°<α<90° B、 0°< α <60° C、30°< α <90° D、 0°< α <30°
(4)如果√cosA – —12
那么△ABC是( D
浙教版九年级下《有关三角函数的计算》课件

数、邻边长,求对边,需要较强的空间想象能力和分析 问题的能力,是本节教学的难点。
课后反思
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐,提高生活质量。2022/3/22022/3/22022/3/22022/3/2
怎样用科学计算器求锐角的三角函数值呢?
用科学计算器求锐角的三角函数值, 要用到三个键: sin cos tan
例如,求 sin160,cos420, tan850 和sin720 38′25″的按键 盘顺序如下:
例如,求sin160,cos420, tan850 和sin720 38′25″的按键盘顺序如 下:
•1.2.有关三角函数的
•
计算(1)
•
•
锐角三角函数
sinAcoBsa, c
coAs sinBb, c
B
tanA= a
b
互余两角之间的三角函数关系:
A
sinA=cosB,tanA.tanB=1.
c
a
┌
b
C
同角之间的三角函数关系: sin2A+cos2A=1.tanA sinA.
cosA
特殊角300,450,600角的三角函数值.
课后反思
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐,提高生活质量。2022/3/22022/3/22022/3/22022/3/2
怎样用科学计算器求锐角的三角函数值呢?
用科学计算器求锐角的三角函数值, 要用到三个键: sin cos tan
例如,求 sin160,cos420, tan850 和sin720 38′25″的按键 盘顺序如下:
例如,求sin160,cos420, tan850 和sin720 38′25″的按键盘顺序如 下:
•1.2.有关三角函数的
•
计算(1)
•
•
锐角三角函数
sinAcoBsa, c
coAs sinBb, c
B
tanA= a
b
互余两角之间的三角函数关系:
A
sinA=cosB,tanA.tanB=1.
c
a
┌
b
C
同角之间的三角函数关系: sin2A+cos2A=1.tanA sinA.
cosA
特殊角300,450,600角的三角函数值.
浙教版初中数学九年级下册1.2《有关三角函数的计算》(17页)课件

A
△ABC其余各边的长,各角的
a
度数和△ABC的面积.
α
B
β
C
咋办
?
w7 如图,根据图中已知 数据,求AD.
w老师期望: w你能得到作为“模型”的它给你带 来的成功.
w 2模型:
A α β┌ Ba C D
某居民小区有一朝向为正南方向的居民楼,该居民楼的一 楼是高6米的小区超市,超市以上是居民住房.在该楼的前面 要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为 25°时.问:若要使超市采光不受影响,两楼应相距多少米?
A
怎样 做?
w5 如图,根据图中已 4cm 知数据,求△ABC其 B 45° 余各边的长,各角的 度数和△ABC的面积
30°
C
A
. w老师期望:
30° 45°┌
w体会这两个图形的“模B 4cm C D
型”作用.将会助你登上
希望的峰顶.
真知在实践中诞生
驶向胜利 的彼岸
w6 如图,根据图中已知数据,求
1.2有关三角函数的计算课件
1 . 2
直角三角的边角关系
驶向胜利 的彼岸
w直角三角形三边的关系:勾股定理 a2+b2=c2. w直角三角形两锐角的关系:两锐角互余 ∠A+∠B=90o. w直角三角形边与角之间的关系:锐角三角函数
w互余两角之间的三角函数关系:
wsin A=cos B
w同角之间的三角函数关系:
∠ A=35 °,求△ABC 的周长和面积(周长精确到 0.1cm,面积保留3个是效数字).
模型: △ABC 的面积=1/2AC・AB ・sin ∠ A
随堂练习
行家看“门道”
w1 用计算器求下列各式的值: w(1)sin56°,(2) sin15°49′,(3)cos20°,(4)tan29°, w(5)tan44°59′59″,(6)sin15°+cos61°+tan76°.
新浙教版九年级数学下册第一章《有关三角函数的计算(第2课时)》优质课课件
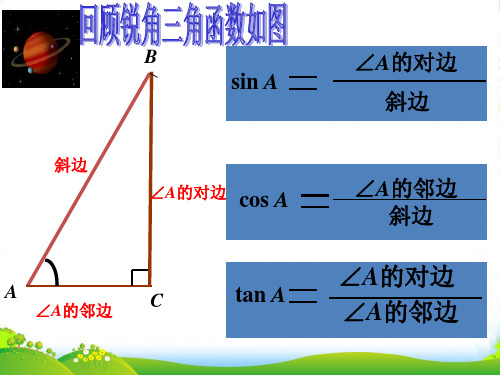
(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°
锐角三角函数(复习)
☆ 应用练习
1.已知角,求值 2.已知值,求角 3. 确定值的范围 4. 确定角的范围
确定角的范围
5.当∠A为锐角,且cos A= 1
5
那么( D ) (A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
显示结果
SHIFT =
2ndf 1
sin 0 . 4 5 1 1 °′″
sin 0 . 4 5 1
2ndf
DMS
26°48′51″ 26°48′51″
即∠β=26°48′51″
w例 如图,工件上有一V型槽,测得它 的上口宽20mm,深19.2mm.求V型角 (∠ACB)的大小(结果精确到1° ).
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
1
6. 当∠A为锐角,且sin A= 3 那么( A )
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
已知三角函数值求角度,要用到sin,cos,tan的第二 功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974, 求锐角α.按健顺序为:
B
∠A的对边
sin A
斜边
斜边
∠A的对边 cos A
A
∠A的邻边
C
tan A
∠A的邻边 斜边
∠A的对边 ∠A的邻边
sinA=cosB= a, cosA=sinB= b,
c
c
a
tan A=
b
tan A = sin A . cos A
(C) 小于60° (D)大于60°
锐角三角函数(复习)
☆ 应用练习
1.已知角,求值 2.已知值,求角 3. 确定值的范围 4. 确定角的范围
确定角的范围
5.当∠A为锐角,且cos A= 1
5
那么( D ) (A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
显示结果
SHIFT =
2ndf 1
sin 0 . 4 5 1 1 °′″
sin 0 . 4 5 1
2ndf
DMS
26°48′51″ 26°48′51″
即∠β=26°48′51″
w例 如图,工件上有一V型槽,测得它 的上口宽20mm,深19.2mm.求V型角 (∠ACB)的大小(结果精确到1° ).
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
1
6. 当∠A为锐角,且sin A= 3 那么( A )
(A)0°<∠A≤ 30 ° (B) 30°<∠A≤45°
(C)45°<∠A≤ 60 ° (D) 60°<∠A≤ 90 °
已知三角函数值求角度,要用到sin,cos,tan的第二 功能健“sin-1 Cos-1,tan-1”健例如:已知sinα=0.2974, 求锐角α.按健顺序为:
B
∠A的对边
sin A
斜边
斜边
∠A的对边 cos A
A
∠A的邻边
C
tan A
∠A的邻边 斜边
∠A的对边 ∠A的邻边
sinA=cosB= a, cosA=sinB= b,
c
c
a
tan A=
b
tan A = sin A . cos A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊角300,450,600角的三角函数值.
如图,当登山缆车的吊箱经过点A到达 点B时,它走过了200m.已知缆车行驶的 路线与水平面的夹角为∠α=160,那么 缆车垂直上升的距离是多少?
如图,在Rt△ABC中,∠C=90°,BC=ABsin16° .
你知道sin160等于多少吗?
对于不是30,45,60这些特殊角的三角函数值, 可以利用计算器来求
例1。如图1——13,在Rt△ABC中, ∠C =90 ° 。 已知AB=12cm, ∠ A=35 ° ,求的周长和面积 (周长精确到0。1cm,面积保留3个是效数字).
C
A
A
B
随堂练习
1 用计算器求下列各式的值: (1)sin560,(2) sin15049′, (3)cos200,(4)tan290, (5)tan44059′59″, (6)sin150+cos610+tan760.
△ABC的面积.
Bα
β
C
A
9 如图,根据图中
已知数据,求AD.
α β┌ Ba C D
回味无穷
• 直角三角形中的边角关系
1填表(一式多变,适当选用):
已知两边求角 已知一边一角 已知一边一角
及其三角函数 求另一边
求另一边
sin A a , c
acsin A. c a . sin A
B
ca ┌
A bC
对于本节一开始提出的问题,利用 科学计算器可以求得: BC=ABsin160 ≈200×0.2756≈55.12.
当缆车继续从点B到达点D时,它又走 过了200m.缆车由点B到点D的行驶路线 与水平面的夹角为∠β=420,由此你能 计算什么?
老师提示:用计算器求三角函数值时, 结果一般有10个数位.本书约定,如无 特别声明,计算结果一般精确到万分位.
450
300
C
A
300 450┌
B 4cmC
D
数和△ABC的面积.
随堂练习
6 如图,根据图中已知 数据,求△ABC其余各边 A
20
的长,各角的度数和 B 550 △ABC的面积.
250
C
A
7 如图,根据图中已 知数据,求AD.
250 550┌
B 20 C
D
随堂练习
8 如图,根据图中已知
数据,求△ABC其余各边 A 的长,各角的度数和 a
怎样用科学计算器求锐角的三角函数值呢?
用科学计算器求锐角的三角函数值, 要用到三个键: sin cos tan
例如,求 sin160,cos420, tan850 和sin720 38′25″的按键 盘顺序如下:
例如,求sin160,cos420, tan850 和sin720 38′25″的按键盘顺序如 下:
Sin160 Cos420 tan850
sin720 38′25″
按键的顺序 sin 1 6 °′″ = cos 4 2 °′″ = tan 8 5 °′″ = sin 7 2 °′″ 3 8 °′″ 2 5 °′″ =
显示结果 0.275635355 0.743144825 11.4300523
0.954450312
cos A b , c
bccoA.s c b . cos A
A
tan A a , b
abtaA n. b a . tan A
α β┌
2模型: A D ta9n00 ata9n00 . B a C
D
P16 习题1.4 1,2题
1.用计算器求下列各式的值: (1)tan320;(2)sin24.530; (3)sin62011′;(4)tan39039′39″.
1.2三角函数的有关计算(1) 由角求三角函数值
锐角三角函数
sinAcoBsa, c
coAs sinBb, c
B
tanA= a
b
互余两角之间的三角函数关系: A sinA=cosB,tanA.tanB=1.
c
a
┌
b
C
同角之间的三角函数关系: sin2A+cos2A=1.tanA sinA.
cosA
2.如图,物华大厦离小伟家60m,小伟 从自家的窗中眺望大厦,并测得大厦顶 部仰角是450,而大厦底部的俯角是370, 求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水 平线所成的锐角称为仰角.当从高处观察低处的目 标时.视线与水平线所成的锐角称为俯角.
随堂练习
2 一个人由山底爬到山顶,需 先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确 到0.01m).
3.求图中避雷 针的长度(结果 精确到0.01m).
Hale Waihona Puke 随堂练习4 如图,根据图中已知数据,求
△ABC其余各边的长,各角的度数
和△ABC的面积.
A
4cm
5 如图,根据图中已 B 知数据,求△ABC其余 各边的长,各角的度
如图,当登山缆车的吊箱经过点A到达 点B时,它走过了200m.已知缆车行驶的 路线与水平面的夹角为∠α=160,那么 缆车垂直上升的距离是多少?
如图,在Rt△ABC中,∠C=90°,BC=ABsin16° .
你知道sin160等于多少吗?
对于不是30,45,60这些特殊角的三角函数值, 可以利用计算器来求
例1。如图1——13,在Rt△ABC中, ∠C =90 ° 。 已知AB=12cm, ∠ A=35 ° ,求的周长和面积 (周长精确到0。1cm,面积保留3个是效数字).
C
A
A
B
随堂练习
1 用计算器求下列各式的值: (1)sin560,(2) sin15049′, (3)cos200,(4)tan290, (5)tan44059′59″, (6)sin150+cos610+tan760.
△ABC的面积.
Bα
β
C
A
9 如图,根据图中
已知数据,求AD.
α β┌ Ba C D
回味无穷
• 直角三角形中的边角关系
1填表(一式多变,适当选用):
已知两边求角 已知一边一角 已知一边一角
及其三角函数 求另一边
求另一边
sin A a , c
acsin A. c a . sin A
B
ca ┌
A bC
对于本节一开始提出的问题,利用 科学计算器可以求得: BC=ABsin160 ≈200×0.2756≈55.12.
当缆车继续从点B到达点D时,它又走 过了200m.缆车由点B到点D的行驶路线 与水平面的夹角为∠β=420,由此你能 计算什么?
老师提示:用计算器求三角函数值时, 结果一般有10个数位.本书约定,如无 特别声明,计算结果一般精确到万分位.
450
300
C
A
300 450┌
B 4cmC
D
数和△ABC的面积.
随堂练习
6 如图,根据图中已知 数据,求△ABC其余各边 A
20
的长,各角的度数和 B 550 △ABC的面积.
250
C
A
7 如图,根据图中已 知数据,求AD.
250 550┌
B 20 C
D
随堂练习
8 如图,根据图中已知
数据,求△ABC其余各边 A 的长,各角的度数和 a
怎样用科学计算器求锐角的三角函数值呢?
用科学计算器求锐角的三角函数值, 要用到三个键: sin cos tan
例如,求 sin160,cos420, tan850 和sin720 38′25″的按键 盘顺序如下:
例如,求sin160,cos420, tan850 和sin720 38′25″的按键盘顺序如 下:
Sin160 Cos420 tan850
sin720 38′25″
按键的顺序 sin 1 6 °′″ = cos 4 2 °′″ = tan 8 5 °′″ = sin 7 2 °′″ 3 8 °′″ 2 5 °′″ =
显示结果 0.275635355 0.743144825 11.4300523
0.954450312
cos A b , c
bccoA.s c b . cos A
A
tan A a , b
abtaA n. b a . tan A
α β┌
2模型: A D ta9n00 ata9n00 . B a C
D
P16 习题1.4 1,2题
1.用计算器求下列各式的值: (1)tan320;(2)sin24.530; (3)sin62011′;(4)tan39039′39″.
1.2三角函数的有关计算(1) 由角求三角函数值
锐角三角函数
sinAcoBsa, c
coAs sinBb, c
B
tanA= a
b
互余两角之间的三角函数关系: A sinA=cosB,tanA.tanB=1.
c
a
┌
b
C
同角之间的三角函数关系: sin2A+cos2A=1.tanA sinA.
cosA
2.如图,物华大厦离小伟家60m,小伟 从自家的窗中眺望大厦,并测得大厦顶 部仰角是450,而大厦底部的俯角是370, 求该大厦的的高度 (结果精确到0.1m).
老师提示:当从低处观察高处的目标时.视线与水 平线所成的锐角称为仰角.当从高处观察低处的目 标时.视线与水平线所成的锐角称为俯角.
随堂练习
2 一个人由山底爬到山顶,需 先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确 到0.01m).
3.求图中避雷 针的长度(结果 精确到0.01m).
Hale Waihona Puke 随堂练习4 如图,根据图中已知数据,求
△ABC其余各边的长,各角的度数
和△ABC的面积.
A
4cm
5 如图,根据图中已 B 知数据,求△ABC其余 各边的长,各角的度
