双曲线的几何性质(一)

合集下载

双曲线的几何性质(1)

5、离心率：e>1
双曲线的焦距与实轴长的比
e

c a
叫做
双
曲线的
离
心率。
e 大，b 大双曲线开阔 a
e 小，b 小双曲线变窄 a
作出双曲线的方法：
1：作出矩形; 2、画出矩形的两条对角线;
即双曲线的两条渐近线; 3、确定双曲线的顶点; 4、画出双曲线。
x2 y2 1 8 18
y2 x2 1 18 8
重要结论：
与x a
y b
0共渐近线的
双曲线方程可设为
x2 a2

y2 b2
(
0)
等轴双曲线: 实轴和虚轴等长的双曲线
在方程 x2 a2

y2 b2
1中，如果a

b
方程即为x 2 y 2 a 2
双曲线的几何性质
双曲线的标准方程：
1
x2 a2

y2 b2
1(焦点在x轴上)
a>0，b>0
2
y2 a2

x2 b2
1(焦点在y轴上)
双曲线的几何性质
1、范围： x a或x a
2、对称轴：
坐标轴是双曲线的对称轴，
双曲原线点的是对双称曲中线心的叫对做称双中曲心线，的中心。
3、顶点：双曲线和它的对称轴的两个交点叫做双曲线的顶点。
； https:///ruhechaogu/ 怎样炒股；
几按.随即说道：“桂天澜已给清宫卫士害伤啦.图图禅师曾将著名的武林人物和著名的宝箭讲给我听.”两人谈起别后情况.作为要挟.在云雾封琐之中.在伤未好之前.竟把佛橡的手臂切了下来.他禁不住又几次

双曲线的几何性质(一)

B2 A1 A2 B1
线段B1B2叫做双曲线的虚轴
其中B1(0,－b)、 B2(0, b)
4.渐近线
y N M B2 A1
Q
N
M
O B1
A2
X
2 y x b 两条直线 y a x 叫做双曲线 2 2 1 的 a b 2
渐近线.
5.离心率 c 双曲线的焦距与实轴长的比 e 叫做双曲线的离心率.
B1
a
o
A1 F2
b
B2
X
4、轴：实轴 A1A2 ; 虚轴 B1B2
y x 5、渐近线方程： 2 2 0 a b
2 2
c e 6、离心率： a
例题: 1.双曲线 9y2－16x2 = 144 的实半
轴长是
4
, 虚半轴长
(0, －5) 、(0, 5)
3
,
焦点坐标是
,
5 离心率为 4 ,渐近线方程 4 y x . 是 3
a
双曲线的离心率的取值范围是 (1, +∞).
焦点在y轴上的双曲线的几何性质
双曲线性质：
y2 x2 双曲线标准方程： 2 2 1(a 0, b 0) a b y
F2 A2
1、范围： y≥a，或y≤－a
2、对称性：关于x轴，y轴，原点对称。
3、顶点 A1（0，－a）,A2（0，a）
1. 范围双曲线在不等式 x≤－a与 x≥a所表示的区域内.
X=－a X=a
2. 对称性双曲线关于坐标轴和原点都是对称的，坐标轴是双曲线的对称轴, 原点是双曲线的对称中心. 双曲线的对称中心叫做双曲线的中心.
3.顶点
双曲线和它的对称轴有两个交点, 它们叫做双曲线的顶点. 顶点坐标 A1 (－a, 0), A2 (a,0) 线段A1A2叫做双曲线的实轴

双曲线的几何性质(一)

1、范围
x 2 2 2 1,即x a a x a, x a
2、对称性
2
y
(-x,y)
-a
(x,y)
o a
x
(-x,-y)
(x,-y)
关于x轴、y轴和原点都是对称。 x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心。
3、顶点
（1）双曲线与对称轴的交点，叫做双曲线的顶点
x2 y 2 25 设双曲线方程为 2 2 1(b 0, ), 点C (13, y ). B/ 12 b 132 y 2 25 2 ( y 55) 2 则点B(25, y 55), 2 1或 2 1. 2 2 12 b 12 b
B
5b 联立方程组解得, y (负值舍去) 12
3 思考:一个双曲线的渐近线的方程为: y x ,它的 4
离心率为
.
例3 双曲线型自然通风塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m, 高55m,选择适当的坐标系,求出双曲线方程. y 13 建立如图直角坐标系,使小圆直径AA'在x 轴 C/ 解: C '，上,圆心与原点重合,这时上、下口的直径CC 12 BB'平行于x轴。 A/ O A x 且 | CC'| 13 2(m), | BB'| 25 2(m).
MF ( x c ) y ,
2 2
MF c ∴ , 依题意 d a
( x c )2 y 2 a2 x c
c ①, a
x y 令 c a b ,方程②化为 2 2 1 这就是所求的轨迹方程. a b
2 2 2

双曲线的简单几何性质课件

1(λ≠0，－b2<λ<a2).
x2 y2
x2 y2
(4) 与双曲线 a2 － b2 ＝ 1 具有相同渐近线的双曲线方程可设为 a2 － b2 ＝
λ(λ≠0).
(5)渐近线为 ax±by＝0 的双曲线方程可设为 a2x2－b2y2＝λ(λ≠0).
求满足下列条件的双曲线的标准方程． (1)以直线 2x±3y＝0 为渐近线，过点(1，2)；
b
b
b2
程求解，另一种方法是消去 c 转化成含a 的方程，求出a 后利用 e＝ 1＋a2 求
离心率．
2．求离心率的范围技巧 (1)根据条件建立 a，b，c 的不等式． (2)通过解不等式得ca 或ba 的范围，求得离心率的范围．
(2)双曲线离心率对曲线形状有何影响？ x2 y2
提示：以双曲线a2 －b2 ＝1(a＞0，b＞0)为例．
c
a2＋b2
b2
b
b
e＝a ＝ a ＝ 1＋a2 ，故当a 的值越大，渐近线 y＝a x 的斜率越大，双
曲线的开口越大，e 也越大，所以 e 反映了双曲线开口的大小，即双曲线的离心
率越大，它的开口就越大．
巧设双曲线方程的方法与技巧
x2 y2 (1)焦点在 x 轴上的双曲线的标准方程可设为a2 －b2 ＝1(a>0，b>0).
y2 x2 (2)焦点在 y 轴上的双曲线的标准方程可设为a2 －b2 ＝1(a>0，b>0).
x2
y2
x2
y2
(3) 与双曲线 a2 － b2 ＝ 1 共焦点的双曲线方程可设为 a2－λ － b2＋λ ＝
B．y＝±34 x

双曲线的简单几何性质(经典)

双曲线的简单几何性质【知识点1】双曲线22a x -22b y ＝1的简单几何性质(1)范围：｜x ｜≥a,y∈R.(2)对称性：双曲线的对称性与椭圆完全相同，关于x 轴、y 轴及原点中心对称.(3)顶点：两个顶点：A 1(-a,0),A 2(a,0)，两顶点间的线段为实轴长为2a ，虚轴长为2b ，且(4)＝1中的1(5)(6)e ＝2(7)注意：且λ（2）与椭圆2a +2b ＝1(a ＞b ＞0)共焦点的曲线系方程可表示为λ-2a -λ-2b ＝1(λ＜a 2,其中b 2-λ＞0时为椭圆，b 2＜λ＜a 2时为双曲线)（3）双曲线的第二定义：平面内到定点F(c,0)的距离和到定直线l :x ＝c a 2的距离之比等于常数e ＝a c(c ＞a ＞0)的点的轨迹是双曲线，定点是双曲线的焦点，定直线是双曲线的准线，焦准距(焦参数)p ＝c b 2，与椭圆相同.1、写出双曲线方程1254922-=-y x 的实轴长、虚轴的长，顶点坐标，离心率和渐近线方程2、已知双曲线的渐近线方程为x y 43±=，求双曲线的离心率3、求以032=±y x 为渐近线，且过点p （1,2）的双曲线标准方程4、已知双曲线的中心在原点，焦点在y 轴上，焦距为16，离心率为43，求双曲线的标准方程。

5、求与双曲线221169x y -=共渐近线，且经过()23,3A -点的双曲线的标准方及离心率．【知识点2】弦长与中点弦问题（1）．直线和圆锥曲线相交时的一般弦长问题：一般地，若斜率为k 的直线被圆锥曲线所截得的弦为AB ，A 、B 两点分别为A(x 1，y 1)、B(x 2，y 2)，则弦长]4))[(1(1212212122x x x x k x x k AB -++=-⋅+=]4)[()11(11212212122y y y y ky y k -+⋅+=-⋅+=,这里体现了解析几何“设而不求”的（2）设A(x 1；对于y 2【变1变4】7、过双曲线2212y x -=的右焦点F 作直线l 交双曲线于A,B 两点,若|AB|=4,这样的直线有几条？【题型2】双曲线离心率的求法一、根据离心率的范围，估算e ：即利用圆锥的离心率的范围来解题，有时可用椭圆的离心率e ∈()01，，双曲线的离心率e >1，抛物线的离心率e =1来解决。

双曲线的简单几何性质(一)导学案

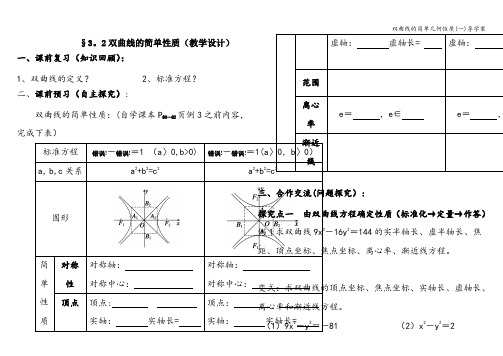
1标准方程错误!－错误!＝1 （a 〉0,b>0) 错误!－错误!＝1(a 〉0，b 〉0） a ，b,c 关系 a 2+b 2=c 2 a 2+b 2=c 2
渐近
线
探究点二由性质求标准方程(定型→设方程→定量→作答)
例2 求满足下列条件的双曲线的标准方程:
(1)双曲线的焦点为（2，0)，右顶点为(错误!，0)； (2)实半轴长为8，离心率为错误!；
变式:求满足下列条件的双曲线方程
(1）双曲线C的焦点为（0,5)，虚轴长为4; （2）实轴长为2,离心率为2；
四、巩固提高（链接高考）：
1、（2013陕西卷）双曲线x2
16
－错误!＝1的离心率为______，两条渐近线的方程为_____．
2、(2011年高考安徽卷）双曲线2x2－y2＝8的实轴长是
3、（2011年高考江西卷）若双曲线错误!-错误!=1的离心率e=2，则m=__ __.
4、思考：若a=b，则渐近线的方程为_____，离心率e＝
五、小结(方法总结）：
（1）双曲线的简单性质（2）应用：①方程→性质②性质→方程
六、作业：1、P835 2、补充:求适合下列条件的双曲线的标准方程：
（1）焦点分别为F1（－3,0），F2（3,0)，离心率e＝ 3
（2)虚轴长为12,离心率为4
5
；。

双曲线的简单几何性质 (一) - 浙江省桐乡

双曲线的简单几何性质（一）高二数学方蕾教学目标：1．使学生掌握双曲线的范围、对称性、顶点、渐近线、离心率等几何性质.2．用双曲线的方程去研究其几何性质，进一步反应了解析几何的特点，并用图像帮助理解双曲线的几何性质，解决一些相关问题.2．通过类比椭圆的简单几何性质的方法来研究双曲线的简单几何性质，在老师引导下让学生积极讨论、归纳，培养学生的观察、研究能力，增强他们的自信心. 教学重点：双曲线的简单几何性质教学难点：渐近线的求法及理解授课类型：新授课课时安排：1课时教具：多媒体、三角板内容分析：本节知识是讲完了双曲线及其标准方程之后，反过来利用双曲线的方程研究双曲线的几何性质. 它是教学大纲中要求学生必须掌握的内容，也是高考的一个考点用坐标法研究几何问题，是数学中一个很大的课题，这里主要是对双曲线的几何性质的讨论以及利用性质解决相关数学问题.本节内容类似于“椭圆的简单的几何性质”，教学中也可以与其类比讲解，主要应指出它们的联系与区别.教学流程： (一)复习引入1. 双曲线的定义及其标准方程平面内到两定点21,F F 的距离的差的绝对值为常数（大于0且小于21F F ）的动点的轨迹叫双曲线。

即a MF MF 221=-（0<2a <21F F ）焦点在x 轴上时：()0,012222>>=-b a b y a x 焦点在y 轴上时：()0,012222>>=-b a b x a y(注：双曲线是根据项的正负来判断焦点所在的位置)c b a ,,的关系：222b a c +=0>>a c ,c 最大，b a ,可以a =2.椭圆的简单几何性质以()012222>>=+b a bya x为例⑴范围： b y b a x a ≤≤-≤≤- ,⑵对称性：以坐标轴为对称轴，原点为对称中心⑶顶点坐标：()()()(),b ,B ,-b , B a,,A a,A 00002121-长轴：线段21A A 长为2a ，a 短轴：线段21B B 长为2b ，b ⑷离心率：()1,0 ,∈=e ac e探究：类比椭圆几何性质的研究，你认为应研究双曲线的哪些性质？应如何研究这些性质？（二）新课讲解利用双曲线的方程研究双曲线的几何性质以焦点坐标在x 轴上的标准方程为例，()0,012222>>=-b a by ax1．范围由标准方程12222=-b y a x 可得112222≥+=b y a x ，即22a x ≥，当a x ≥时，y 才有实数值，这说明双曲线在不等式a x -≤与a x ≥所表示的区域内；对于y 的任何值，x 都有实数值这说明从横的方向来看，直线a x a x =-=和之间没有图象，从纵的方向来看，随着x的增大，y 的绝对值也无限增大，所以曲线在纵方向上可无限伸展，不像椭圆那样是封闭曲线2.对称性：类比研究椭圆对称性的研究方法，容易得到，双曲线关于x 轴、y 轴和原点都是对称的，这时，坐标轴是双曲线的对称轴，原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心. 2．顶点在双曲线方程12222=-b y a x 中，令讲解：结合图形，讲解顶点和轴的概念，0=y 得a x ±=，故它与x 轴有两个交点),0,(1a A()0,2a A -，且x 轴为双曲线12222=-b y a x 的对称轴，所以()0,),0,(21a A a A -为其对称轴的交点，称为双曲线的顶点(一般而言，曲线的顶点均指与其对称轴的交做双曲线12222=-by ax 的实轴，它点)，而对称轴上位于两顶点间的线段21A A 叫的长是2a .在方程12222=-by a x 中令0=x 得22b y -=，这个方程没有实数根，说明双曲线和y 轴没有交点。

2020高中数学 2.2.2 双曲线的简单几何性质(1)(含解析)

课时作业16 双曲线的简单几何性质（1)知识点一由双曲线的标准方程研究几何性质1。

若直线x＝a与双曲线错误!－y2＝1有两个交点,则a的值可以是( )A。

4 B.2C。

1 D.－2答案A解析∵双曲线错误!－y2＝1中，x≥2或x≤－2,∴若x＝a与双曲线有两个交点，则a>2或a<－2，故只有A选项符合题意．2．双曲线错误!－错误!＝1的焦点到渐近线的距离为( )A.2错误!B.2C.错误!D。

1答案A解析不妨取焦点（4,0)和渐近线y＝3x，则所求距离d＝错误!＝2错误!。

故选A.3．求双曲线4x2－y2＝4的顶点坐标、焦点坐标、实半轴长、虚半轴长、离心率和渐近线方程．解把方程化为标准形式为错误!－错误!＝1，由此可知,实半轴长a＝1,虚半轴长b＝2。

顶点坐标是（－1,0),（1，0）．c＝错误!＝错误!＝错误!,∴焦点坐标是（－5，0)，（错误!,0)．离心率e＝错误!＝错误!，渐近线方程为错误!±错误!＝0，即y＝±2x。

知识点二求双曲线的离心率4。

下列方程表示的曲线中离心率为错误!的是（）A.错误!－错误!＝1 B.错误!－错误!＝1C.错误!－错误!＝1 D。

错误!－错误!＝1答案B解析∵e＝ca，c2＝a2＋b2，∴e2＝错误!＝错误!＝1＋错误!＝错误!2＝错误!。

故错误!＝错误!，观察各曲线方程得B项系数符合,应选B。

5．已知F1，F2是双曲线错误!－错误!＝1(a>0，b>0)的两个焦点，PQ 是经过F1且垂直于x轴的双曲线的弦，如果∠PF2Q＝90°，求双曲线的离心率．解设F1（c,0），将x＝c代入双曲线的方程得错误!－错误!＝1，∴y ＝±错误!。

由｜PF2|＝｜QF2|，∠PF2Q＝90°，知|PF1|＝｜F1F2|，∴b2a＝2c.∴b2＝2ac.∴c2－2ac－a2＝0.∴错误!2－2·错误!－1＝0.即e2－2e－1＝0。

双曲线的简单几何性质(1)b

B2 A1
O
A2
x
B1
应用举例:
求双曲线9y 例1.求双曲线 2 – 16x2 =144的实半轴与虚半轴求双曲线的实半轴与虚半轴焦点坐标,离心率及渐进线方程长,焦点坐标离心率及渐进线方程焦点坐标离心率及渐进线方程.
y 2 x2 解：原方程可化为 : 2 − 2 = 1 4 3
∴ 实半轴长 a = 4 ，虚半轴长 b = 3 .
2
y2 − 2 =1 b
y
B2 A1
O
2、对称性：关于轴，y轴，原点对称. 、对称性：关于x轴轴），A ，），，） 3、顶点：A1（-a，0）， 2（a，0）、顶点：线段A 线段B 线段 1A2叫实轴 . 线段 1B2叫虚轴 . 实轴长|A 实轴长 1A2|=2a
，虚轴
A2
x
B1
A2
x
B1
y 先取双曲线在第一象限内的部分进行证明。先取双曲线在第一象限内的部分进行证明。
x − y = 1 得 y = b x 2 − a 2 ( x > a) ，由 2 2 a a b
2
2
Q M
B2 A1
O
设M(x，y) 是双曲线上的点，则，是双曲线上的点，它到渐近线 bx − ay = 0 的距离为：的距离为：
A2
x
B1
| bx − b x 2 − a 2 | | MQ | = = 2 2 c a +b = b | x − x2 − a2 | c
| bx − ay |
| ( x − x 2 − a 2 )( x + x 2 − a 2 ) | ba 2 1 = ⋅ = b⋅ c x + x2 − a2 c x + x2 − a2

双曲线的简单几何性质课件

A1（- a，0），A2（a，0）
e c (e 1) a
y b x a
例3：
x2 y2 1 16 9
1、双曲线 9x2-16y2=144的实半轴长
等于 4 虚半轴长等于 3 顶点坐
标是 4,0 渐近线方是y
3 4
x (或 x
4
y
.3
0)
5
离心率e= 4 。
2、离充心要率e=条件2 是。双（曲用线“为充等分轴条双件曲”线“的必要条件”“充要条件”填空。）
双曲线定义的简单几何性质
定义
图象
方程范围对称性顶点离心率渐近线
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
y
M
M
F2
F1
o
F2
x
x
F1
x2 a2
y2 b2
1
x≤－a或x≥a
y2 a2
x2 b2
1
y≤－a或y≥a
关于坐标轴、原点对称（实轴、虚轴、中心）
(－a, 0) (a, 0)
法二由双曲线的渐近线方程为 y＝±12x，可设双曲线方程为x222－y2＝λ(λ≠0)， ∵A(2，－3)在双曲线上， ∴2222－(－3)2＝λ，即 λ＝－8. ∴所求双曲线的标准方程为y82－3x22 ＝1.
5 离心率
与椭圆类似,双曲线的焦距与实轴长的比 c , a
叫做双曲线的离心率.因为c a 0,所以双
2 2
y2 b2
1
渐进线方程
k
b a
B2
b
k
y
(a,b)
b a
yb x a
可由双曲线

双曲线的几何性质(第一课时)

c 5 , c 10 a 4
又 e
b 2 c 2 a 2 10 2 82 36
x2 y 2 双曲线的方程为 1 64 36 3 渐近线方程为y x 4
焦点F1 (10,0), F2 (10,0)
如果我是双曲线，你就是那渐近线如果我是反比例函数，你就是那坐标轴虽然我们有缘，能够生在同一个平面然而我们又无缘，漫漫长路无交点为何看不见，等式成立要条件难到正如书上说的，无限接近不能达到为何看不见，明月也有阴晴圆缺此事古难全，但愿千里共婵娟
y x 双曲线 2 2 1(a 0, b 0)的简单几何性质 y a b
a
-b o b x
2 2
（1）范围: y a, y a
（2）对称性: 关于x轴、y轴、原点都对称
（3）顶点: (0,-a)、(0,a) （4）渐近线: y a x
b
-a
c （5）离心率: e a
e
4 渐近线方程: y x 3
c 5 a 4
新课探究：双曲线的几何性质 5 例2: 已知双曲线顶点间的距离是16，离心率e= 4 ，
焦点在x轴上，中心在原点，写出双曲线的方
x y 解：依题意可设双曲线的方程为 2 2 1 a b
程，并且求出它的渐近线和焦点坐标. 2 2
2a 16，即a 8
2.3.2 双曲线简单的几何性质
第一课时
学习目标 1、类比椭圆，能够推出双曲线的几何性质； 2、会根据条件求双曲线的方程
复习回顾
定义 | |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
M
M F2
y
图象

双曲线的几何性质1

2.3.3双曲线的几何性质(一)一、教学目标知识与技能：了解双曲线的性质，能运用双曲线的标准方程讨论他的几何性质。

过程与方法：进一步掌握利用方程研究曲线的基本方法，通过与椭圆几何性质的对比，提高类比分析的能力。

理解并掌握代数知识在解析几何运算中的作用。

情感态度价值观：提高分析问题解决问题的能力，培养学生形结合思想、方程思想及等价转化思想。

二、学习重难点重点：双曲线的几何性质难点：双曲线的离心率，渐近线的问题三、学法指导：教师平等地参与学生的自主探究活动，引导学生全员参与，全过程参与。

通过启发、调整、激励来体现自己的主导作用，保证学生的认知水平和情感体验分层次向前推进。

四、知识链接【A 】练习：在一个坐标系中，画出下列双曲线的图形1、（1）1242522=-y x （2）1202522=-y x2、（1）1252422=-y x （2）1252022=-y x （3）1162522=-y x （4）192522=-y x （3）1251622=-y x （4）125922=-y x问题2、离心率可以刻画椭圆的圆扁程度，双曲线的离心率刻画双曲线的什么？【A 】例1、求双曲线14416922=-x y 的半实轴长和半虚轴长、焦点坐标、离心率、渐近线方程。

【A 】练习：1、求下列双曲线的实轴长和虚轴长、顶点和焦点坐标、离心率、渐近线方程。

（1）32822=-y x （2）81922=-y xOy xO y x【B 】2、求适合下列条件的双曲线的标准方程。

（1）顶点在x 轴上，两顶点间的距离是8，45=e （2）焦点在y 轴上，焦距是16，34=e六、达标训练【A 】1、求下列双曲线的实轴长和虚轴长、顶点和焦点坐标、离心率、渐近线方程。

（1）422-=-y x （2）1254922-=-y x（3）14491622=-y x （4）14491622-=-y x【B 】2、求适合下列条件的双曲线的标准方程。

高中数学选择性必修一课件：双曲线的简单几何性质(第1课时)

y52＝1.
题型四双曲线的离心率
例 4 (1)如果双曲线的渐近线方程是 y＝±34x，求离心率．【解析】方法一：若双曲线焦点在 x 轴上，设双曲线方程为ax22－by22＝1(a>0， b>0)．由题意知ba＝34，又∵c2＝a2＋b2， ∴e2＝ac22＝1＋ba22＝1＋342＝542，∴e＝54. 若双曲线的焦点在 y 轴上，设双曲线方程为 ay22－bx22＝1(a>0，b>0)．由题意知ab＝34，
3.2.2 双曲线的简单几何性质(第1课时)
要点 1 双曲线的几何性质
标准方程
ax22－by22＝1(a>0，b>0)
ay22－bx22＝1(a>0，b>0)
图形
焦点焦距范围对称性性质顶点轴长
离心率
渐近线
(－c，0)，(c，0)
(0，－c)，(0，c)
2c
|x|≥a，y∈R
|y|≥a，x∈R
题型二求渐近线方程
例 2 (1)求双曲线x42－y82＝1 的渐近线方程．【解析】方法一：∵a＝2，b＝2 2，且焦点在 x 轴上， ∴双曲线x42－y82＝1 的渐近线方程为 y＝± 2x. 方法二：令x42－y82＝0，得2x±2 y 2＝0， ∴双曲线x42－y82＝1 的渐近线方程为 y＝± 2x.
(4)易知所求双曲线的焦点在 x 轴上，可设双曲线方程为6x42 －1y62 ＝λ(λ>0)，
将点(2，0)的坐标代入方程得 λ＝116，故所求双曲线的标准方程为x42－y2＝1.
探究 3 巧设双曲线方程的方法： (1)当双曲线的焦点不明确时，方程可能有两种形式，此时应注意分类讨论，为了避免讨论，也可设双曲线的方程为 mx2－ny2＝1(mn>0)． (2)常见双曲线方程的设法． ①渐近线为 y＝±mn x 的双曲线方程可设为mx22－ny22＝λ(λ≠0，m>0，n>0)；如果两条渐近线的方程为 Ax±By＝0，那么双曲线的方程可设为 A2x2－B2y2＝m(m≠0， A>0，B>0)．

双曲线的简单几何性质(一) 精品教案

1、复习
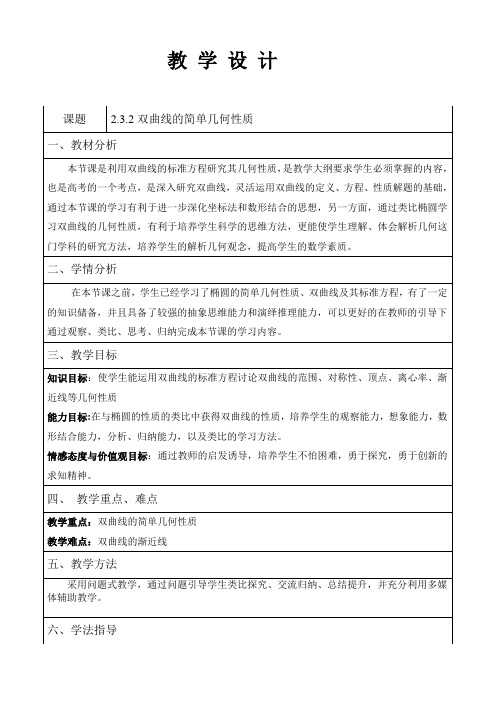
（1）双曲线的定义和标准方程？
（2）椭圆有哪些简单几何性质？（填表）
2、引入
类比椭圆的简单几何性质，猜想双曲线有哪些简单几何性质？
（三）类比探究，研究性质
以方程为例研究双曲线的简单几何性质
1、范围：
提问：类比椭圆如何研究其范围？
（幻灯片）
2、对称性：
提问：看图可知其有怎样的对称性？
（幻灯片）对称性：双曲线关于x轴、y轴和原点都是对称的.
七、教学过程：
(一)欣赏美图，引出课题
提问：在以上图片中，有没有我们所熟悉的数学图形？
要想运用双曲线的知识做出精美的物品或建造如此宏伟的建筑物，光掌握双曲线的定义和标准方程是远远不够的，我们还有了解更多双曲线的知识，这节课我们就一起来学习《双曲线的简单几何性质》。（引导学生类比探究、交流归纳、总结提升，并充分利用多媒体辅助教学。
六、学法指导
在教师的组织引导下，从学生已有的知识和生活经验出发，让学生经历知识的形成过程。使学生真正成为学习的主体。通过阅读教材，以恰当的问题为纽带，给学生创设自主探究、合作交流的空间，让学生在参与中获得知识，发展思维，感悟数学。
（2）椭圆的离心率刻画了椭圆图形的什么几何特性，双曲线的离心率刻画了双曲线的什么几何特性？《几何画板》演示
5、渐近线：
从学生曾经学习过的反比例函数入手，它的图像是双曲线，当双曲线伸向远处时，它与x、y轴无限接近，此时x、y轴是的渐近线。
提问：双曲线有没有渐近线？渐近线方程是什么？《几何画板》演示
二、学情分析
在本节课之前，学生已经学习了椭圆的简单几何性质、双曲线及其标准方程，有了一定的知识储备，并且具备了较强的抽象思维能力和演绎推理能力，可以更好的在教师的引导下通过观察、类比、思考、归纳完成本节课的学习内容。

双曲线的几何性质(一).

§2.2.2双曲线的简单几何性质学习目标（1）理解双曲线的范围、对称性及对称轴，对称中心、离心率、顶点、渐近线的概念；（2）掌握双曲线的标准方程。

学习重点：双曲线的几何性质学习难点：双曲线的渐近学习过程：一、课前预习1、双曲线k y x 222=-的焦距是6，求k 。

二、探究互动双曲线的简单几何性质：①范围：由双曲线的标准方程得，222210y x b a=-≥，进一步得：．这说明双曲线在不等式所表示的区域；②对称性：双曲线是以轴和轴为对称轴，为称中心；③顶点：双曲线有个顶点，由于双曲线的对称轴有实虚之分，焦点所在的对称轴叫做，焦点不在的对称轴叫做。

④渐近线：直线叫做双曲线22221x y a b-=的渐近线；图形标准方程范围顶点轴长实轴长虚轴长焦点焦距 |对称性对称轴对称中心离心率 e= 渐近线一、典型例题例 1：求双曲线22916144y x -=的实半轴长和虚半轴长、焦点的坐标、离心率、渐近线方程．练习1：求双曲线），（0n 0m m n m y nx 22=-的实半轴长和虚半轴长、焦点的坐标、离心率、渐近线方程．练习2：求适合下列条件的双曲线的标准方程（1）虚轴长为12，离心率为54（2）求与双曲线2y 2x 22=-有公共渐近线，且过点M(2,-2)的双曲线方程.例2：如图，设(),M x y 与定点()5,0F 的距离和它到直线l ：165x =的距离的比是常数54，求点M 的轨迹方程．三．巩固提升1.双曲线与椭圆164y 16x 22=+有相同的焦点，它的一条渐近线为y=x ，则双曲线方程为（A ）96y x 22=- （B ）160x y 22=- （C ）80y x 22=- （D ）24x y 22=- 2.双曲线的渐近线为x 43y ±=，则双曲线的离心率是（）（A ）54 （B ）2 （C ）54或35（D ）25或3153.已知双曲线的离心率为2，焦点是（-4，0），（4，0），则双曲线的方程为（A ）112y -4x 22=（B ）14y -12x 22=（C ）16y -10x 22=（D ）110y -6x 22= 4.若双曲线1m y -4x 22=的渐近线方程为x 23y ±=，则双曲线的焦点是 5.已知双曲线13x -ay 222=的离心率为2，求双曲线的渐近线方程。