砍脚法速解鸡兔同笼问题

小学数学“鸡兔同笼”例题13种讲解方法，考试常考，家长快为孩子收藏！

小学数学“鸡兔同笼”例题13种讲解方法，考试常考，家长快为孩子收藏！题目：现有一笼子，里面有鸡和兔子若干只，数一数，共有头14个，腿38条，球鸡和兔子各有多少只？（请用尽量多的方法解答）『方法一：人见人爱的列表法』如果二年级小朋友做这道题，可以用列表法！直观、易理解，还不容易出错~好啦，我们来看一下！鸡9 ...0 3 5 7兔14 11 9 7 5 ...腿56 50 46 42 38 ...根据上面的表格，我们可以看出，鸡为9只，兔子为5只。

我们在列表的时候不要按顺序列，否则做题的速度会很慢，比如说列完鸡为0只，兔子为14只，发现腿的数量56条，和实际38条相差较大，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些哦！『方法二：最快乐的画图法』画图可以让数学变得形象化，而且经常画图还有助于创造力的培养！假设14只全部是鸡，先把鸡给画好。

14×2=28条，差38-28=10条，而每一只鸡补2条腿就变成兔子，需要把5只鸡每只补2条腿，所以有5只兔子，14-5=9只鸡。

『方法三：最酷的金鸡独立法』分析：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只。

『方法四：最逗的吹哨法』分析：假设鸡和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有38-14=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有24-14=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有14-5=9只。

（惊现跑男中包贝尔的抬脚法有木有！）『方法五：最常用的假设法』分析：假设全部是鸡，则有14×2=28条腿，比实际少38-28=10只，一只鸡变成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡变成兔子，即兔子为5只，鸡为14-5=9只。

鸡兔同笼问题专题解析

鸡兔同笼【专题解析】：基本概念：鸡兔同笼问题又称为置换问题、假设问题，就是把假设错的那部分置换出来。

基本公式：（1）已知总头数和总脚数，求鸡、兔各多少：①把所有鸡假设成兔子：鸡数=(兔脚数×总头数-总脚数)÷(兔脚数一鸡脚数)总头数一鸡数=兔数。

②把所有兔子假设成鸡：兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)总头数一兔数=鸡数。

关键问题：找出总量的差与单位量的差。

形象解释：砍足法：假设砍去每个鸡和兔的两条腿，则此时鸡就没有腿了，兔子还剩下两条腿，这时剩下的总腿数就是兔子的头数的两倍，把剩下的腿数除以2就是兔子的头数了。

（2）已知总头数和鸡兔脚数的差数，当鸡的总脚数比兔的总脚数多时，可用公式①（每只鸡脚数×总头数-脚数之差）÷（每只鸡的脚数+每只兔的脚数）=兔数；总头数-兔数=鸡数②（每只兔脚数×总头数+鸡兔脚数之差）÷（每只鸡的脚数+每只免的脚数）=鸡数；总头数-鸡数=兔数。

（3）已知总头数与鸡兔脚数的差数，当兔的总脚数比鸡的总脚数多时，可用公式：①（每只鸡脚数×总头数+鸡兔脚数之差）÷（每只鸡脚数+每只兔的脚数）=兔数；总头数-兔数=鸡数。

②（每只兔的脚数×总头数-鸡兔脚数之差）÷（每只鸡的脚数+每只兔的脚数）=鸡数；总头数-鸡数=兔数。

（4）得失问题（鸡兔问题的推广题）的解法，可以用下面的公式：①（1只合格品得分数×产品总数-实得总分数）÷（每只合格品得分数+每只不合格品扣分数）=不合格品数。

②总产品数-（每只不合格品扣分数×总产品数+实得总分数）÷（每只合格品得分数+每只不合格品扣分数）=不合格品数。

（5）鸡兔互换问题（已知总脚数及鸡兔互换后总脚数，求鸡兔各多少的问题），可用下面的公式：①〔（两次总脚数之和）÷（每只鸡兔脚数和）+（两次总脚数之差）÷（每只鸡兔脚数之差）〕÷2=鸡数；②〔（两次总脚数之和）÷（每只鸡兔脚数之和）-（两次总脚数之差）÷（每只鸡兔脚数之差）〕÷2=兔数。

鸡兔同笼解题方法公式口诀经典例题

鸡兔同笼解题方法公式口诀经典例题鸡兔同笼问题是数学中的经典例题，解题方法有假设法、公式法、排除法、金鸡独立法、吹哨法、特异功能法和砍足法等多种。

其中，假设法是最常用的一种方法。

假设全是鸡，则兔的只数为：（总头数×2-总脚数）÷2；假设全是兔，则鸡的只数为：（总头数×4-总脚数）÷2.总只数减去鸡只数即为兔只数。

基本原理是，若总头数×2等于总脚数，则全是鸡；若总头数×4等于总脚数，则全是兔。

若总头数×2小于总脚数，则有兔存在，每少2只脚就有1只兔；若总头数×4大于总脚数，则有鸡存在，每多2只脚就有1只鸡。

公式法也是解题的一种常用方法。

总脚数÷2减去总头数即为兔只数，总只数减去兔只数即为鸡只数。

基本原理是，原来的头总量是鸡头和兔头的总量，脚总量也是鸡脚和兔脚的总量。

用脚总数÷2是按全是鸡来计算的，如果商等于总头数，则全是鸡；如果商大于总头数，则有兔存在，每多1个头就是1只兔。

因为1只兔有4只脚，前面÷的是2，1只兔就变成2个头，也就多了1个头，所以总脚数÷2减去总头数的差是多少就有多少只兔。

排除法也是解题的一种方法。

先让每只鸡兔各抬起2只脚，这时鸡无剩下的脚，排除鸡后剩下的脚都是兔的。

前面抬起2只脚，现在每只兔还剩下2只脚。

所以用总脚数减去总头数×2的差再÷2就是兔的只数。

金鸡独立法是一种比较酷的解题方法。

让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从总脚数减去头数就是兔的脚数，再用兔的脚数÷2就是兔的只数，鸡的只数则是总头数减去兔的只数。

吹哨法是一种比较逗的解题方法。

假设鸡和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有剩余的腿在站着。

再吹一声哨，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

鸡兔同笼的13种解法(教育材料)

根据上面的表格，我们可以看出，鸡为9只，兔子为5只。

我们在列表的时候不要按顺序列，否则做题的速度会很慢，比如说列完鸡为0只，兔子为14只，发现腿的数量56条，和实际38条相差较大，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些！（方法二：最快乐的方法“画图法”）分析：画图法也是低年级小朋友很好接受的一个方法，呵呵，画图还可以让数学变得形象化，而且经常画图还有助于创造力的培养！假设14只全部是鸡，先把鸡给画好。

这样就有14×2=28条，差38-28=10条，而每一只鸡补2条腿就变成兔子，需要把5只鸡每只补2条腿，所以有5只兔子，14-5=9只鸡。

（方法三：最酷的方法“金鸡独立法”）分析：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只。

（方法四：最逗的方法“吹哨法”）分析：假设及和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有38-14=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有24-14=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有14-5=9只。

（方法五：最常用的方法“假设法”）分析：假设全部是鸡，则有14×2=28条腿，比实际少38-28=10只，一只鸡变成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡变成兔子，即兔子为5只，鸡为14-5=9只。

（方法六：最常用的方法“假设法”）分析：假设全部是兔子，则有14×4=56条腿，比实际多56-38=18只，一只兔子变成一只鸡腿减少2条，18÷2=9只，所以需要9只鸡9兔子变成鸡，即鸡为9只，兔子为14-9=5只。

“砍足法”解“鸡兔同笼”

掌数掌点通
这一思路新颖而奇特叫做 “ 砍足法” ，这种思维方法叫化归法，化归法就是在解决问题时。先不对问题采取直接的分析，而是将题中
的条件或问题进行变形，使之转化，直到最终把它归成某个已经解决
的问题。
一
个笼子里，从上面数，有３个头；从下面数，有９只脚。求笼中各５４
有几只鸡和兔你会解答这个问题吗≥ 想知道《子算经》中是如何解答这个问你孙
题的吗
解答思路是这样的：假如砍去每只鸡、每只兔一半的脚，则每只鸡就变成了 “ 独脚鸡” ，每只兔就变成了“双脚免” 。这样： ‘
（）鸡和兔的脚的总数就由９只变成了４只：１４７
（２）如果笼子里有一只兔子，则脚的总数就比头的总数多１。因此，脚的总只数４与总头数３的差，就是兔子的只数，ｇ４ — ７５Ｆ７
３＝１（。显然，鸡的只数就是３ — ２２（了。５２Ｒ）５１＝３Ｒ）
同学们不妨试练一下：
小红数她家的鸡与兔，数头有２个，数脚有５只。问：小红家的０６鸡与兔各有多少只答案鸡１只兔子８（２只）
鬼＾工件的珐，走定觜每一分钟。— — 连象又
名题欣赏
同学们。你以前听说过 “பைடு நூலகம்鸡兔同笼” 问题吗？这个问题，是我国古
代著名趣题之一。大约在１０年前，《子算经》中就记载了这个有５０孙

人教版四年级数学下第十四讲鸡兔同笼精讲精练基础版

人教版四年级数学下第14讲鸡兔同笼基础篇知识点一：“鸡兔同笼”问题的特点：鸡兔同笼是已知鸡、兔的总头数和总脚数，求其中鸡和兔务有多少只的问题。

知识点二：“鸡兔同笼”问题的解题方法1、砍足法（抬腿法）解答思路：假如砍去每只鸡、每只兔一半的脚，则每只鸡就变成了“独脚鸡”，每只兔就变成了“双脚兔”．这样，鸡和兔的脚的总数就由94只变成了47只；如果笼子里有一只兔子，则脚的总数就比头的总数多1．因此，脚的总只数47与总头数35的差，就是兔子的只数，即473512-=-=（只）．显然，鸡的只数就是351223（只）了．2、假设法（经典）鸡兔同笼问题的基本关系式是：如果假设全是兔，那么则有：鸡数=（每只兔子脚数×鸡兔总数-实际脚数）÷（每只兔子脚数-每只鸡的脚数）兔数=鸡兔总数-鸡数如果假设全是鸡，那么就有：兔数=（实际脚数-每只鸡脚数×鸡兔总数）÷（每只兔子脚数-每只鸡的脚数）鸡数=鸡兔总数-兔数3、方程法: 根据鸡兔的脚之和列方程解答。

考点1：图解法和列表法【典例1】（2020春•雄县期末）鸡兔10只关在一个笼子里，共有32条腿，请你算算鸡有只．考点2：假设法【典例1】（2020春•桐梓县期末）一个饲养组养的鸡和兔一共13只，共有36只脚，这个饲养组养兔（）只．A．3B．4C．5【典例2】（2020春•诸城市期末）小花有10张5元和2元的人民币，面值一共是32元．5元的有张，2元的有张．【典例3】（2019•湖南模拟）有一首民谣：“一队猎手一队狗，两队并成一队走，数头一共三百六，数脚一共八百九，问有多少猎手多少狗．”你能算出来吗？考点3：方程法【典例1】（2020春•英山县期末）钢笔每支12元，圆珠笔每支7元．小明共买了6支笔，用了62元，钢笔买了（）支．A．5B．4C．3【典例2】（2020•岳麓区）某班订来50张游园票，其中一部分是1元5角的票价，另一部分是2元的票价，总共的票价是88元，两种票各买了多少张？综合练习一．选择题1．（2020•河口县）李华参加知识抢答竞赛，答对一题加10分，答错一题倒扣6分，他共抢答了10题，最后得分36分，他答错了（）题．A．3B．4C．5D．62．（2020春•衡水期末）某单位买了台灯和电扇共10台，总价750元．台灯买了（）台．A．3B．4C．5D．6 3．（2019•成都）鸡和兔同笼，共有30个头，88只脚，笼中鸡有（）只．A．14B．12C．164．（2020春•桃江县期末）停车场有自行车和小汽车共20辆，一共有64个车轮，符合题意的答案是（）A．自行车8辆，小汽车12辆B．自行车12辆，小汽车8辆C．自行车10辆，小汽车10辆5．（2019秋•任丘市期末）红星商店托运50箱饮料，合同规定每箱的运费是20元，若损坏一箱，除不给运费外，还要赔偿损失100元，运后结算时共付运费760元，求损坏了几箱饮料，下面列式正确的是（）A．（20×50﹣760）÷（100﹣20）B．（100×50+760）÷（100+20）C．（20×50﹣760）÷（100+20）二．填空题6．（2020春•麦积区期末）两轮摩托车和四轮汽车有16辆，共46个车轮，汽车有辆，摩托车有辆．7．（2020春•北川县期末）“今有鸡兔共居一笼，从上面数，有10个头，从下面数，有26只脚．鸡和兔各有几只？”假设笼子里全是鸡，就有只脚，比题目里的26只少了只脚；那么需要用兔来换鸡，一只兔比比一只鸡多2只脚，所以有只兔．8．（2020春•太原期末）体育课上，四（2）班38人都在场上打乒乓球，有的是两人单打，有的是4人双打，一共用了12张乒乓球台．正在进行单打的乒乓球台有张．9．（2020春•中原区期末）童车厂五月份生产三轮车和四轮车共16辆，使用轮子60个．童车厂五月份生产三轮车辆，四轮车辆．①14②12③410．（2020春•西华县期末）有龟和鹤共38只，腿共有102条．龟有只，鹤有只．三．判断题11．（2020•雄县）丽丽的压岁钱里有面值20元和50元的人民币共计30张，总金额是1200元．丽丽20元的人民币一共有10张．（判断对错）12．（2015春•南部县期末）解决鸡兔同笼问题常用假设法．．（判断对错）13．（2015春•古浪县期末）鸡和狗共8个头，22只脚，则鸡和狗的只数一样多．．（判断对错）五．应用题14．（2020春•湖滨区期末）为了促进消费，乐华商场举行购物大抽奖活动：一等奖和二等奖各有多少个？15．（2020春•通许县期末）四年级有40名同学参加植树活动．男生每人种3棵，女生每人种2棵，他们一共种了98棵树．这个班男生、女生各有多少人？16．（2020春•太原期末）“迎七一”要挂彩色气球，四（1）班有13人参加吹气球小组．男生每人吹8个，女生每人吹7个，一共吹了100个气球．男生、女生各有多少人？17．（2020春•陇县期末）鸡兔同笼，共有头14个，脚34只，鸡、兔各有多少只？六．解答题18．（2020秋•肇源县期末）一个停车场共有自行车和小轿车共有24辆车，一共有56个轮子，这个停车场有自行车和小轿车各多少辆？18．（2020•石阡县）六（1）班48名同学去划船，一共乘坐10只船，大船每只坐6人，小船每只坐4人，需要大船、小船各几只？19．（2020春•永昌县期末）六年级同学分组参加课外兴趣小组，每人只能参加一个小组．科技类每5人一组，艺术类每3人一组，共有37名学生报名，正好分成9个组．参加科技类和艺术类的学生各有多少人？第14讲鸡兔同笼知识点一：“鸡兔同笼”问题的特点：鸡兔同笼是已知鸡、兔的总头数和总脚数，求其中鸡和兔务有多少只的问题。

鸡兔同笼9种解题方法(完整版)

鸡兔同笼9种解题方法鸡兔同笼问题是我国古代著名趣题之一，同时也是是小学阶段一个重要的奥数问题。

让我们看看这道大约在1500年前就存在的有趣的问题都有哪些方法可以解决吧！题目：现有一笼子，里面有鸡和兔子若干，数一数，共有头14个，腿38条，求鸡和兔子各有多少只？[方法一：列表法]列表法直观、易理解、不易出错，一起来看一下①鸡有2只脚，比兔子少2只脚。

但是鸡有2只翅膀，兔子没有。

假设鸡有特异功能，把2只翅膀变成2条腿，那么鸡也有4只脚。

此时脚的总数是14×4=56只，但实际上只有38只，为什么呢？因为我们把鸡的翅膀当做脚来算，所以鸡的翅膀有56-38=18只，鸡有18÷2=9只，兔子就是14-9=5只。

②假设每只鸡都具有“特异功能”，鸡飞起来，兔立起来，这时立在地上的脚全是兔子的，它的脚数就是38-14×2=10只，因此兔的只数有10÷2=5只，鸡有14-5=9只。

③假如每只兔子又长出一个头来，然后魔术师说“劈开”，变成“一头两脚”的两只“半兔”，半兔与鸡都是两只脚，因而共有28÷2=19只鸡兔，19-14=5只，这就是兔子的数目。

鸡就有14-5=9只。

[方法七：砍足法]假如把每只鸡砍掉一只脚，每只兔子砍掉一只脚，则每只鸡就变成了“独脚鸡”，每只兔子就变成了“双脚兔”。

这样，鸡和兔的脚的总数就由38变成了19；如果笼子里有一只兔子，则脚的总数就比头的总数多1.因此，脚的总数19与总头数14的差，就是兔子的只数，即19-14=5（只）。

所以，鸡的只数就是14-5=9（只）了。

[方法八：耍兔法]假如训兔师喊口令：“兔子，站起来！”此时兔子们都把两只前脚高高抬起来，两只后脚着地。

此时鸡兔都是两只脚着地的。

在地上脚的总数是14×2=28只，而原来有38只脚，多出38-28=10只脚。

为什么会多出来呢？因为兔子们把他们的2只前脚抬了起来，所以兔的只数是10÷2=5只，则鸡是14-5=9只。

用“砍腿法”解鸡兔同笼问题

用“砍腿法”解鸡兔同笼问题鸡兔同笼问题是我国古代著名趣题之一。

大约在1500年前，《孙子算经》中就记载了这个有趣的问题。

书中是这样叙述的：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”上世纪初，人们就把鸡兔同笼问题编入到小学数学教材中，作为典型应用题用以培养学生分析、解决问题的水平。

不过，鸡兔同笼问题曾在课程改革中几进几出，是什么原因？作者不敢妄加猜测，但解决鸡兔同笼问题的方法一直是教师在教学中的一个难点问题，即绝大部分学生不能很好的掌握用“假设法”解题，其主要原因是学生对“假设法”中的数量关系难以理解。

这个轮课程改革，北师大版教材把鸡兔同笼问题编入到五年级上册教材中，教材是通过假设举例与列表的方法(列表枚举方法)，寻找解决问题的结果。

编者的意图是：教材选鸡兔同笼这个题材，主要不是为了解决鸡兔同笼问题本身，而是要借助鸡兔同笼这个载体让学生经历列表、尝试和持续调整的过程，从中体会出解决问题的一般策略——列表。

但学生并不这么认为，他们觉得既然要解答鸡兔同笼问题应该用最简便的方法，而不应该选用如此笨拙、麻烦、低效益的解题策略，说得直白一点，就是学生对“列表枚举方法”不感兴趣，甚至有抵触情绪，他们希望用其他方法来解答。

教师也认为“列表枚举方法”太“原始”太“朴素”，缺乏思维的空间，没有挑战性，不太适合五年级学生的思维特点，也不利于提升学生解决问题的水平，且有局限性(适合数量小的鸡兔同笼问题)。

作者通过对鸡兔同笼问题的研究和实践，觉得用“砍腿法”解鸡兔同笼问题，更符合小学生的思维特点，下面就以举例的方式介绍“砍腿法”的解题思路。

例1 鸡兔同笼，有20个头，54条腿，鸡、兔各有多少只？解题思路：先砍掉每只鸡、每只兔的两条腿，这样，每只鸡就没有腿了，每只兔也就变成了两条腿的兔，腿的总数从54条变成(54-2×20=)14条。

因为这14条腿是砍掉两条腿后的兔的腿，所以，兔的只数就是(14÷2=)7只，鸡的只数就是(20-7=)13只。

小学奥数鸡兔同笼问题(三) 精选练习例题含答案解析(附知识点拨及考点)

1. 熟悉鸡兔同笼的“砍足法”和“假设法”.2. 利用鸡兔同笼的方法解决一些实际问题，需要把多个对象进行恰当组合以转化成两个对象．一、鸡兔同笼这个问题，是我国古代著名趣题之一．大约在1500年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚．求笼中各有几只鸡和兔？你会解答这个问题吗？你想知道《孙子算经》中是如何解答这个问题的吗？二、解鸡兔同笼的基本步骤解答思路是这样的：假如砍去每只鸡、每只兔一半的脚，则每只鸡就变成了“独脚鸡”，每只兔就变成了“双脚兔”．这样，鸡和兔的脚的总数就由94只变成了47只；如果笼子里有一只兔子，则脚的总数就比头的总数多1．因此，脚的总只数47与总头数35的差，就是兔子的只数，即473512-=（只）．显然，鸡的只数就是351223-=（只）了。

这一思路新颖而奇特，其“砍足法”也令古今中外数学家赞叹不已．除此之外，“鸡兔同笼”问题的经典思路“假设法”．假设法顺口溜：鸡兔同笼很奥妙，用假设法能做到，假设里面全是鸡，算出共有几只脚，和脚总数做比较，做差除二兔找到．解鸡兔同笼问题的基本关系式是：如果假设全是兔，那么则有：鸡数=（每只兔子脚数×鸡兔总数-实际脚数）÷（每只兔子脚数-每只鸡的脚数）兔数=鸡兔总数-鸡数如果假设全是鸡，那么就有：兔数=（实际脚数-每只鸡脚数×鸡兔总数）÷（每只兔子脚数-每只鸡的脚数）鸡数=鸡兔总数-兔数当头数一样时，脚的关系：兔子是鸡的2倍当脚数一样时，头的关系：鸡是兔子的2倍在学习的过程中，注重假设法的运用，渗透假设法的重要性，在以后的专题中，如工程，行程，方程等专题中也都会接触到假设法模块一、多个量的“鸡兔同笼”——鸡兔同笼问题【例 1】有蜘蛛、蜻蜓、蝉三种动物共18只，共有腿118条，翅膀20对(蜘蛛8条腿；蜻蜓6条腿，两对翅膀；蝉6条腿，一对翅膀)，求蜻蜓有多少只？【考点】鸡兔同笼问题【难度】4星【题型】解答【关键词】假设思想方法【解析】这是在鸡兔同笼基础上发展变化的问题.观察数字特点，蜻蜓、蝉都是6条腿，只有蜘蛛8条腿.因此，可先从腿数入手，求出蜘蛛的只数.我们假设三种动物都是6条腿，则总腿数为618108⨯=(条)，所例题精讲知识精讲教学目标6-1-9.鸡兔同笼问题（三）差11810810-=(条)，必然是由于少算了蜘蛛的腿数而造成的.所以，应有(118108)(86)5-÷-=(只)蜘蛛.这样剩下的18513-=(只)便是蜻蜓和蝉的只数.再从翅膀数入手，假设13只都是蝉，则总翅膀数11313-=(对)，这是由于蜻蜓有两对翅膀，而我们只按一对翅膀计⨯=(对)，比实际数少20137算所差，这样蜻蜓只数可求7(21)7÷-=(只).【答案】7只【巩固】希望小学的生物标本室里有蜻蜓，蝉，蜘蛛共11只，它们共有74条腿，10对翅膀，由图7知该标本室里有只蜘蛛。

鸡兔同笼问题的13种解法

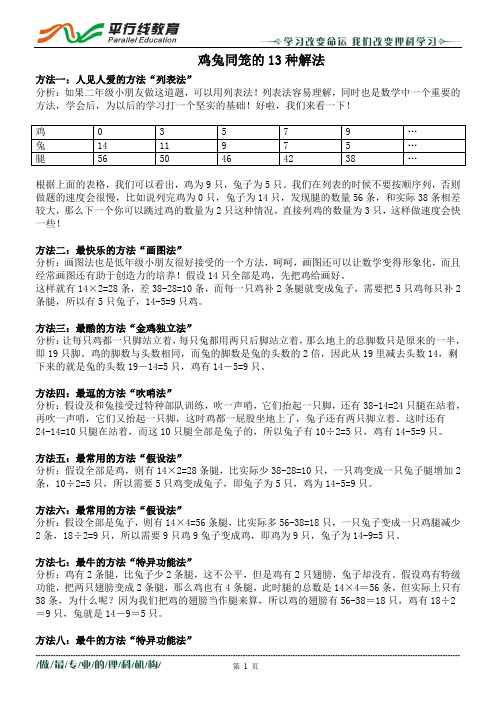
鸡兔同笼的13种解法方法一：人见人爱的方法“列表法”分析：如果二年级小朋友做这道题，可以用列表法！列表法容易理解，同时也是数学中一个重要的方法，学会后，为以后的学习打一个坚实的基础！好啦，我们来看一下！鸡0 3 5 7 9 …兔14 11 9 7 5 …腿56 50 46 42 38 …根据上面的表格，我们可以看出，鸡为9只，兔子为5只。

我们在列表的时候不要按顺序列，否则做题的速度会很慢，比如说列完鸡为0只，兔子为14只，发现腿的数量56条，和实际38条相差较大，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些！方法二：最快乐的方法“画图法”分析：画图法也是低年级小朋友很好接受的一个方法，呵呵，画图还可以让数学变得形象化，而且经常画图还有助于创造力的培养！假设14只全部是鸡，先把鸡给画好。

这样就有14×2=28条，差38-28=10条，而每一只鸡补2条腿就变成兔子，需要把5只鸡每只补2条腿，所以有5只兔子，14-5=9只鸡。

方法三：最酷的方法“金鸡独立法”分析：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只。

方法四：最逗的方法“吹哨法”分析：假设及和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有38-14=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有24-14=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有14-5=9只。

方法五：最常用的方法“假设法”分析：假设全部是鸡，则有14×2=28条腿，比实际少38-28=10只，一只鸡变成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡变成兔子，即兔子为5只，鸡为14-5=9只。

鸡兔同笼砍足法原理

鸡兔同笼砍足法原理
鸡兔同笼砍足法是一种古老的数学问题，其原理是通过解方程组来确定鸡和兔的数量。

问题中给出了总头数和总脚数，求解出鸡和兔的数量。

具体步骤是：
1. 设鸡的数量为x，兔的数量为y。

2. 根据题意列出方程组：x+y=总头数，2x+4y=总脚数。

3. 通过消元法或代入法解出x和y的值。

4. 检查解是否符合题意，如符合则得出鸡和兔的数量。

此问题的思维难度较高，需要运用代数知识和逻辑推理能力。

同时，此问题也可以引申出更多有趣的数学问题，是培养学生数学思维的好方法。

- 1 -。

鸡兔同笼问题的几种解法

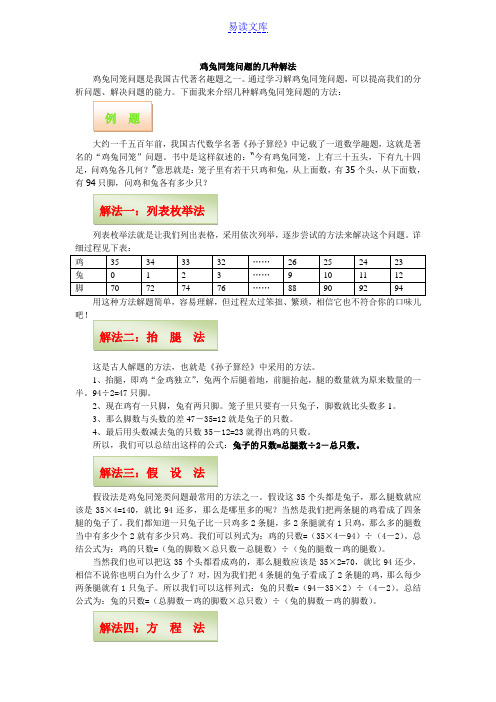
鸡兔同笼问题的几种解法鸡兔同笼问题是我国古代著名趣题之一。

通过学习解鸡兔同笼问题，可以提高我们的分析问题、解决问题的能力。

下面我来介绍几种解鸡兔同笼问题的方法：大约一千五百年前，我国古代数学名著《孙子算经》中记载了一道数学趣题，这就是著名的“鸡兔同笼”问题。

书中是这样叙述的：“今有鸡兔同笼，上有三十五头，下有九十四从上面数，有35个头，从下面数，有采用依次列举，逐步尝试的方法来解决这个问题。

详半。

94÷2=47只脚。

2、现在鸡有一只脚，兔有两只脚。

笼子里只要有一只兔子，脚数就比头数多1。

3、那么脚数与头数的差47－35=12就是兔子的只数。

12=23就得出鸡的只数。

兔子的只数=总腿数÷2－总只数。

35个头都是兔子，那么腿数就应腿的兔子了。

我们都知道一只兔子比一只鸡多2条腿，多2条腿就有1只鸡，那么多的腿数当中有多少个2就有多少只鸡。

我们可以列式为：鸡的只数=（35×4－94）÷（4－2）。

总结公式为：鸡的只数=（兔的脚数×总只数－总腿数）÷（兔的腿数－鸡的腿数）。

当然我们也可以把这35个头都看成鸡的，那么腿数应该是35×2=70，就比94还少，相信不说你也明白为什么少了？对，因为我们把4条腿的兔子看成了2条腿的鸡，那么每少=（94－35×2）÷（4－2）。

总结。

下面我就用这种方法来这样每只鸡就没有腿了，每只兔子就剩下了两条腿，腿的总数也就变成了94－35×2=24（条），那么这24条腿都是砍掉两条腿后的兔子的腿，所以兔子的只数就是24÷2=12（只），鸡的只数就是35－12=23（只）。

我们仔细观察会发现它的计算过程和假设法中先把所有的都看成鸡的做法是一样的。

只不过这种说法，我们理解起来更容易而已。

看完了上面的5种解法，不知你有何感想？你一定会觉得学习数学真是一件很有趣的事情，数学中充满了无穷的奥妙。

砍脚法速解鸡兔同笼问题

“砍脚法”巧解鸡兔共笼问题原理：同时砍掉兔子和鸡的两只脚，这样笼子里的脚就减少了总头数×2只，由于鸡只有2只脚，所以笼子里只剩下两只脚的“兔子”了，再÷2就是兔子数。

例题1：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？题：总共35只。

脚94只。

解：先全数砍掉两只脚：35*2=70.在地上就刹时少了70只脚。

剩下的24只脚就全数是兔子的了，此刻每只“兔子”都是两只脚的。

兔子数就是此刻的脚数24除以2了，即12只。

那么鸡为35-12=23只。

例2 红铅笔每支0.19元，蓝铅笔每支0.11元，两种铅笔共买了16支，花了2.80元。

问红，蓝铅笔各买几支？这题相当于红铅笔有0.19只脚，蓝铅笔有0.11只脚。

先全砍0.11只脚16*0.11=1.76.还剩2.80-1.76=1.04只脚。

剩下的都是红笔的脚了，红笔此刻只有0.19-0.11=0.08只脚。

那么红笔的个数为1.04/0.08=13只。

那么蓝笔为3只。

升级版：例6 某次数学考试考五道题，全班52人参加，共做对181道题，已知每人至少做对1道题，做对1道的有7人，5道全对的有6人，做对2道和3道的人数一样多，那么做对4道的人数有多少人？先把这题简化为：对2道，3道，4道题的人共有52-7-6=39（人）.他们共做对181-1×7-5×6=144（道）.由于对2道和3道题的人数一样多，咱们就可以够把他们看做是对2.5道题的人（(2+3)÷2=2.5).即题目变成：转化为了简单的鸡兔同笼问题，鸡兔共有39只，脚144只，其中每只鸡2.5只脚，每只兔4只脚。

求鸡兔数。

通过砍脚得出兔为（144-2.5*39）/4-2.5=34只。

答对4道题的为34人！。

鸡兔同笼-教师版

鸡兔同笼第一部分：知识介绍鸡兔同笼这个问题，是我国古代著名趣题之一．大约在1500年前，《孙子算经》中就记载了这个有趣的问题。

书中是这样叙述的：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚．求笼中各有几只鸡和兔？你会解答这个问题吗？你想知道《孙子算经》中是如何解答这个问题的吗？解鸡兔同笼的基本步骤1.砍足法（金鸡独立）：解答思路是这样的：假如砍去每只鸡、每只兔一半的脚，则每只鸡就变成了“独脚鸡”，每只兔就变成了“双脚兔”。

这样，鸡和兔的脚的总数就由94只变成了47只；如果笼子里有一只兔子，则脚的总数就比头的总数多1。

因此，脚的总只数47与总头数35的差，就是兔子的只数，即473512-=（只）了。

-=（只）．显然，鸡的只数就是351223这一思路新颖而奇特，其“砍足法”也令古今中外数学家赞叹不已。

除此之外，还有“鸡兔同笼”问题的经典思路“假设法”。

2.假设法：假设法顺口溜：鸡兔同笼很奥妙，用假设法能做到，假设里面全是鸡，算出共有几只脚，和脚总数做比较，做差除二兔找到。

解鸡兔同笼问题的基本关系式是：如果假设全是兔，那么则有：鸡数=（每只兔子脚数×鸡兔总数-实际脚数）÷（每只兔子脚数-每只鸡的脚数）兔数=鸡兔总数-鸡数如果假设全是鸡，那么就有：兔数=（实际脚数-每只鸡脚数×鸡兔总数）÷（每只兔子脚数-每只鸡的脚数）鸡数=鸡兔总数-兔数3.鸡兔关系：当头数一样时，脚的关系：兔是鸡的2倍；当脚数一样时，头的关系：鸡是兔的2倍。

在学习的过程中，注重假设法的运用，渗透假设法的重要性，在以后的专题中，如工程、行程、方程等专题中也都会接触到假设法。

第二部分：例题精讲【例 1】鸡兔同笼，头共46，足共128，鸡兔各几只？【考点】鸡兔同笼【解析】假设46只都是兔，一共应有446184⨯=（只）脚，这和已知的128只脚相比多了18412856-=（只）脚，这是因为我们把鸡当成了兔子，如果把1只鸡当成1只兔，就要比实际多422-=（只）脚，那么56只脚是我们把56228÷=（只）鸡当成了兔子，所以鸡的只数就是28，兔的只数是462818-=（只）。

鸡兔同笼趣味解答：砍腿法

鸡兔同笼趣味解答：砍腿法
鸡兔同笼，有17个头，42条腿，鸡兔各有多少只？
分析与解：
解法1：把兔腿砍去一半，那么鸡腿和兔腿一样多，都有2条，17个头就一共有腿2×17=34（条），其实一共有腿42条，由此可以知道一共砍去了42—34 =8（条）腿，每一只兔被砍去了4－2=2（条）腿，所以，兔一共有8÷2=4（只），鸡有17－4= 13（只）。

综合算式为：
兔的只数：（42－2×17）÷（4－2）= 4（只）
鸡的只数：17－4=13（只）
解法2：把鸡腿全部砍去，那么只有兔有腿，17个头全按兔腿算，一共有腿4×17=68（条），其实一共只有42条腿，多算了68－42=26（条）腿，每砍一只鸡就会多算4－2=2（条）腿，所以一共有鸡26÷2=13（只），有兔17－13=4（只）。

综合算式为：
鸡的只数：（4×17－42）÷（4－2）=13（只）
兔的只数：17－13=4（只）
解法3：把每只鸡和每只兔一半的腿砍去，那么每只鸡就变成了“独腿鸡”，每只兔就变成了“双腿兔”，这样，“独腿鸡”和“双腿兔”的腿就有42÷2=21（条）。

这时的每只“鸡”有1头1腿，头和腿一样多；每只“兔”有1头2腿，腿的数量比头的数量多1，所以“独腿鸡”和“双腿兔”的腿的数量与它们的头的数量之差，就是兔的只数，是21－17=4（只），鸡的只数是17－4=13（只）。

综合算式为：
兔的只数：42÷2－17 = 4（只）
鸡的只数：17－4 =13（只）。

鸡兔同笼的3种解法

鸡兔同笼的13种解法欧阳歌谷（2021.02.01）例、现有一笼子，里面有鸡和兔子若干只，数一数，共有头14个，根据上面的表格，我们可以看出，鸡为9只，兔子为5只。

我们在列表的时候不要按顺序列，不然做题的速度会很慢，比方说列完鸡为0只，兔子为14只，发明腿的数量56条，和实际38条相差较年夜，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些！（办法二：最快乐的办法“画图法”）欧阳歌谷创编2021年2月阐发：画图法也是低年级小朋友很好接受的一个办法，呵呵，画图还可以让数学变得形象化，并且经常画图还有助于创作创造力的培养！假设14只全部是鸡，先把鸡给画好。

这样就有14×2=28条，差3828=10条，而每一只鸡补2条腿就酿成兔子，需要把5只鸡每只补2条腿，所以有5只兔子，145=9只鸡。

（办法三：最酷的办法“金鸡自力法”）阐发：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只。

（办法四：最逗的办法“吹哨法”）阐发：假设及和兔接受过特种军队训练，吹一声哨，它们抬起一只脚，还有3814=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有2414=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有145=9只。

（办法五：最经常使用的办法“假设法”）阐发：假设全部是鸡，则有14×2=28条腿，比实际少3828=10只，一只鸡酿成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡酿成兔子，即兔子为5只，鸡为145=9只。

欧阳歌谷创编2021年2月（办法六：最经常使用的办法“假设法”）阐发：假设全部是兔子，则有14×4=56条腿，比实际多5638=18只，一只兔子酿成一只鸡腿减少2条，18÷2=9只，所以需要9只鸡9兔子酿成鸡，即鸡为9只，兔子为149=5只。

鸡兔同笼的3种解法之欧阳术创编

例、现有一笼子，里面有鸡和兔子若干只，数一数，共有头14根据上面的表格，我们可以看出，鸡为9只，兔子为5只。

我们在列表的时候不要按顺序列，不然做题的速度会很慢，比方说列完鸡为0只，兔子为14只，发明腿的数量56条，和实际38条相差较年夜，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些！（办法二：最快乐的办法“画图法”）阐发：画图法也是低年级小朋友很好接受的一个办法，呵呵，画图还可以让数学变得形象化，并且经常画图还有助于创作创造力的培养！假设14只全部是鸡，先把鸡给画好。

这样就有14×2=28条，差3828=10条，而每一只鸡补2条腿就酿成兔子，需要把5只鸡每只补2条腿，所以有5只兔子，145=9只鸡。

（办法三：最酷的办法“金鸡自力法”）阐发：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚。

鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只。

（办法四：最逗的办法“吹哨法”）阐发：假设及和兔接受过特种军队训练，吹一声哨，它们抬起一只脚，还有3814=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着。

这时还有2414=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有145=9只。

（办法五：最经常使用的办法“假设法”）阐发：假设全部是鸡，则有14×2=28条腿，比实际少3828=10只，一只鸡酿成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡酿成兔子，即兔子为5只，鸡为145=9只。

（办法六：最经常使用的办法“假设法”）阐发：假设全部是兔子，则有14×4=56条腿，比实际多5638=18只，一只兔子酿成一只鸡腿减少2条，18÷2=9只，所以需要9只鸡9兔子酿成鸡，即鸡为9只，兔子为149=5只。

解决鸡兔同笼问题的几种方式简单介绍

鸡兔同笼教学内容：人教版四年级数学下册数学广角《鸡兔同笼》鸡兔同笼问题是我国古代闻名趣题之一。

通过学习解鸡兔同笼问题，能够提高咱们的分析问题、解决问题的能力。

例题：大约一千五百年前，我国古代数学名著《孙子算经》中记载了一道数学趣题，这确实是闻名的“鸡兔同笼”问题。

书中是如此叙述的：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”意思确实是：笼子里有若干只鸡和兔，从上面数，有35个头，从下面数，有94只脚，问鸡和兔各有多少只？方式一：列表列举法列表列举法确实是让咱们列出表格，采纳依次列举，慢慢尝试的方式来解决那个问题。

详细进程见下表：用这种方式解题简单，容易明白得，但进程太过笨拙、繁琐。

方式二：抬腿法这是前人解题的方式，也就是《孙子算经》中采纳的方式。

一、抬腿，即鸡“金鸡独立”，兔两个后腿着地，前腿抬起，腿的数量就为原先数量的一半。

94÷2=47只脚。

二、此刻鸡有一只脚，兔有两只脚。

笼子里只要有一只兔子，脚数就比头数多1。

3、那么脚数与头数的差47－35=12确实是兔子的只数。

4、最后用头数减去兔的只数35－12=23就得出鸡的只数。

因此，咱们能够总结出如此的公式：兔子的只数=总腿数÷2－总只数。

方式三：假设法假设法是鸡兔同笼类问题最经常使用的方式之一。

假设这35个头都是兔子，那么腿数就应该是35×4=140，就比94还多，那么是哪里多的呢？固然是咱们把两条腿的鸡看成了四条腿的兔子了。

咱们都明白一只兔子比一只鸡多2条腿，多2条腿就有1只鸡，那么多的腿数当中有多少个2就有多少只鸡。

咱们能够列式为：鸡的只数=（35×4－94）÷（4－2）。

总结公式为：鸡的只数=（兔的脚数×总只数－总腿数）÷（兔的腿数－鸡的腿数）。

固然咱们也能够把这35个头都看成鸡的，那么腿数应该是35×2=70，就比94还少，相信不说你也明白什么缘故少了？对，因为咱们把4条腿的兔子看成了2条腿的鸡，那么每少两条腿就有1只兔子。

砍脚法速解鸡兔同笼问题

小学数学“鸡兔同笼”例题13种讲解方法，考试常考，家长快为孩子收藏！

鸡兔同笼问题专题解析

鸡兔同笼解题方法公式口诀 经典例题

鸡兔同笼的13种解法(教育材料)

“砍足法”解“鸡兔同笼”

人教版四年级数学下 第十四讲 鸡兔同笼 精讲精练 基础版

鸡兔同笼9种解题方法(完整版)

用“砍腿法”解鸡兔同笼问题

小学奥数 鸡兔同笼问题(三) 精选练习例题 含答案解析(附知识点拨及考点)

鸡兔同笼问题的13种解法

鸡兔同笼砍足法原理

鸡兔同笼问题的几种解法

砍脚法速解鸡兔同笼问题

鸡兔同笼-教师版

鸡兔同笼趣味解答：砍腿法

鸡兔同笼的3种解法

鸡兔同笼的3种解法之欧阳术创编

解决鸡兔同笼问题的几种方式简单介绍

鸡兔同笼解题方法公式口诀经典例题

人教版四年级数学下第十四讲鸡兔同笼精讲精练基础版

小学奥数鸡兔同笼问题(三) 精选练习例题含答案解析(附知识点拨及考点)