运筹学-线性规划-第一次

合集下载

运筹学1

解：设 x1和x2分别表示产品甲和乙的产量，这样可以建立如下的数学模型。目标函数：Max 20x1 +30 x2 约束条件：s.t. 3 x1 + 7 x2 ≤ 240（劳动力限制） 2 x1 + 4 x2 ≤ 150（原材料限制） 4 x1 + 3 x2 ≤ 250（设备限制） x1，x2≥ 0（非负约束）
16/10
若将目标函数变为max Z = 2x1 + 4x2 ，则表示目标函数的等值线与约束条件x1 + 2x2 ≤8的边界线x1 + 2x2 = 8平行。当Z值由小变大时，与线段Q 2Q3重合，如图1.3所示，线段Q2Q3上任意一点都使Z取得相同的最大值，即这个线性规划问题有无穷多最优解。
17/10
运筹学第一次作业指导
储宜旭
이 문서는 나눔글꼴로 작성되었습니다. 설치하 기
运筹学
2/10
3/10
4/10
5/10
实际问题线性规划模型的基本步骤： (1) 确定决策变量。这是很关键的一步，决策变量选取得当，不仅会使线性规划的数学模型建得容易，而且求解比较方便。 (2) 找出所有限制条件，并用决策变量的线性等式或不等式来表示，从而得到约束条件。一般可用表格形式列出所有的限制数据，然后根据所列出的数据写出相应的约束条件，以避免遗漏或重复所规定的限制要求。 (3) 把实际问题所要达到的目标用决策变量的线性函数来表示，得到目标函数，并确定是求最大值还是最小值。
10/10
11/10
12/10
线性规划问题的图解法
为了给后面的线性问题的基本理论提供较直观的几何说明，先介绍线性规划问题的图解法。我们把满足约束条件和非负条件的一组解叫做可行解，所有可行解组成的集合称为可行域。图解法的一般步骤如下。 (1) 建立平面直角坐标系。 (2) 根据线性规划问题的约束条件和非负条件画出可行域。 (3) 作出目标函数等值线Z = c(c 为常数)，然后根据目标函数平移等值线至可行域边界，这时目标函数与可行域的交点即最优解。

第一章运筹学绪论和线性规划

The srandard Form of the Model：
max(min) s.t. z =c1x1 + c2x2 +…+ cnxn (1.1) a11x1 + a12x2 +…+ a1nxn ( = , ) b1 a21x1 + a22x2 +…+ a2nxn ( = , ) b2 … … (1.2) am1x1 + am2x2 +…+ amnxn ( = , ) bm x1，x2，…，xn 0 (1.3)
(3)An very effective method of finding the optimal distribution under the scarcity, to obtain the maximum profit or minimum cost
1.1The simplification of Prototype Example: The WYNDOR GLASS CO. produces a high-quality glass products and wants to launch two new products. It has 3 plants and product 1 need plants 1 and 3, while products 2 needs plants 2 and 3.All the products (1 and 2) can be sold and table 3.1 on page 27 summarizes the data gathered by the OR team. The goal of the company is to get the maximum profit from the sold products 1 and 2.

运筹学基础-线性规划(方法)

问题描述
线性规划问题通常由三个基本部分组成，即决策变量、约束条件和目标函数。决策变量是问题中需要求解的未知数，约束条件是限制决策变量取值的条件，目标函数是要求最大或最小的函数。
线性规划的应用领域
01
02
03
04
生产计划
在制造业中，线性规划可以用于制定最优的生产计划，以最大化利润或最小化成本。
02
线性规划的基本概念
线性方程组
线性方程组是由多个线性方程组成的数学模型，描述了多个变量之间的线性关系。
线性方程组可以用矩阵和向量表示，通过矩阵运算和代数方法求解。
线性方程组有多种解法，如高斯消元法、LU分解、迭代法等。
约束条件与目标函数
02
01
03
约束条件是限制变量取值的条件，通常表示为变量的上界、下界或等式约束。
目标函数是描述问题目标的数学表达式，通常是最小化或最大化的线性或非线性函数。
约束条件和目标函数共同构成了线性规划问题的数学模型。
线性规划的解
线性规划的解是指满足所有约束条件并使目标函数取得最优值的变量取值。
线性规划问题可能有多个解，也可能无解或无界解。
最优解的性质包括最优性、可行性和唯一性。
最优解可以通过求解线性方程组或使用专门的优化软件获得。
03
线性规划的求解方法
单纯形法
01
基本概念
单纯形法是一种求解线性规划问题的迭代算法，通过不断迭代寻找最优解。
02 1. 初始化选择一个初始可行解，并确定初始基可行解。
03
2. 迭代
根据目标函数系数和约束条件系数，计算出单纯形表格，然后进行迭代更新。
运筹学基础-线性规划(方法)

《运筹学》课件第一章线性规划

10
解：令
xi=
1， Si被选中
min z= ci xi i 1 10
0， Si没被选中
xi 5
i 1
x1 x8 1 x7 x8 1
称为技术系数
b= (b1,b2, …, bm) 称为资源系数
2、非标准型
标准型
（1）Min Z = CX
Max Z' = -CX
（2）约束条件
• “≤”型约束，加松弛变量；
松弛变量
例如： 9 x1 +4x2≤360
9 x1 +4x2+ x3=360
• “≥”型约束，减松弛变量；
例、将如下问题化为标准型
数据模型与决策 (运筹学）
课程教材：
吴育华,杜纲. 《管理科学基础》，天津大学出版社。
绪论
一、运筹学的产生与发展
运筹学（Operational Research) 直译为“运作研究”。
• 产生于二战时期 • 60年代，在工业、农业、社会等各领域得到广泛应用 • 在我国，50年代中期由钱学森等引入
Min z x1 2x2 3x3
x1 x2 x3 7
s.t
.
x1 x2 x3 3x1 x2 2
x3
2
5
x1, x2 , x3 0
解：令 Min z Max z' (z' z) ，第一个约束加松弛变量x5，
第二个约束减松弛变量x6，得标准型：
Max z' x1 2x2 +3x3
x1 x2 x3 x4 7
s.t .
x1 x2 3x1
x3 x2
x5 2 2x3 5
x1 , , x5 0

运筹学第1章-线性规划

凸集的数学定义:设K为n维欧氏空间的一个点集，若K中任意两个点X1和X2连线上的所有点都属于K，即“X =αX1+(1-α) X2 ∈ K(0≤a ≤ 1)”，则称K为凸集。设X(x1，x2，…，xn)，X1(u1， u2，...，un)，X2(v1，v2，…，vn)，如图1一5所示，“X =αX1+(1α) X2 ∈ K(0≤a ≤ 1)”的证明思路如下:
下一页返回
图解法步骤：
（1）建立坐标系；（2）将约束条件在图上表示；（3）确立满足约束条件的解的范围；（4）绘制出目标函数的图形（5）确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。生产计划问题是典型的已知资源求利润最大化的问题，对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产过程的损失忽略不计;③市场需求无限制，即假设生产的产品全部卖出。
下一页返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容器，应如何裁剪，使做成的窗口的容积为最大？
解：设 x1, x2分别表示从A,B两处采购的原油量（单
位：吨），则所有的采购方案的最优方案为：
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式，其中模型(1-7)较为常用。

《运筹学》课件

cj→
CB
XB
31
x1
0
x4
0
x5
-z
b
30 280 120 -930
31 22 0 0 0
ห้องสมุดไป่ตู้
x1
x2
x3
x4
x5
1 1/3 1/6 0 0
约束条件：≥,=,≤
∑aijxj ≤(=, ≥) bi (i=1,2, …n)
变量符号：≥0,unr,≤0 xj ≥0
(j=1,2, …n)
线性规划的标准形式目标函数：max 约束条件：= 变量符号：≥0
max z=∑cjxj ∑aijxj = bi (i=1,2, …n) xj ≥0 (j=1,2, …n)
x2
50
当z的值增加时，目
标函数与约束条件：
40
4x1+3x2 120
30
重合，Q1与Q2之间都
是最优解。
20
Q2（15，20）
可行域
10
Q1（25，0）
10
20
30
40
x1
解的讨论：
无界解：
例：max z=x1+x2 s.t. -2x1+x2 40 x1-x2 20 x1,x2 0
取目标函数最大正系数对应的非基变量为入基变量；取最小比值所对应方程的基变量为出基变量。本例中，取 x1为入基变量， x3为出基变量。
x1+ 1/3x2 +1/6x3 26/3x2 -2/3x3 +x4 4x2 -1/2x3 +x5
= 30 =280 =120
令非基变量 x2=x3=0,z(1)=930, 相应的基可行解为 x(1)=(30,0,0,280,120)T

运筹学-1、线性规划

则：
x1 x2 100
x1 ( x3 ) x4 x2 2
设x3为第二年新的投资； x4为第二年的保留资金；
则：
18
•设x5为第三年新的投资；x6为第三年的保留资金；
则：
x3 ( x5 ) x6 x4 2 x1 2
•设x7为第四年新的投资；第四年的保留资金为x8；
max Z 2 x7 x9 x1 x2 100 x 2x 2x 2x 0 2 3 4 1 4 x1 x3 2 x4 2 x5 2 x6 0 s.t 4 x3 x5 2 x6 2 x7 2 x8 0 4 x5 x7 2 x 8 2 x9 0 x 0, j 1, 2, , 9 j
13
例3：（运输问题）设有两个砖厂A1 、A2 ，产量分别为23万块、27万块，现将其产品联合供应三个施工现场B1 、 B2 、 B3 ，其需要量分别为17万块、18万块、15万块。各产地到各施工现场的单位运价如下表：现场砖厂 B1 B2 B3
A1 A2
5 6
14 18
7 9
问如何调运才能使总运费最省？
20
例5：（下料问题）某一机床需要用甲、乙、丙三种规格的钢轴各一根，这些轴的规格分别是 2.9,2.1, 1.5(m),这些钢轴需要用同一种圆钢来做，圆钢长度为7.4m。现在要制造100台机床，最少要用多少根圆钢来生产这些钢轴？
解：第一步：设一根圆钢切割成甲、乙、丙三种钢轴的根数分别为y1,y2,y3，则切割方式可用不等式2.9y1+2.1y2+1.5y3≤7.4 表示，求这个不等式的有实际意义的非负整数解共有8组，也就是有8种不同的下料方式，如下表所示：

运筹学第1章：线性规划问题及单纯型解法

原料甲原料乙最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为最优解? 最优解?
是
求最优解的目标函数值
否确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8

运筹学：第1章线性规划第3节对偶问题与灵敏度分析

s.t.
4x1 3x1
5x2 200 10x2 300
x1, x2 0
9x1 4x2 360
s.t.
34xx11
5x2 10 x
200 2 300
3x1 10x2 300
x1, x2 0
则D为
min z 360y1 200y2 300y3 300y4
9 y1 4 y2 3y3 3y4 7 s.t.4 y1 5y2 10 y3 10 y4 12
amn xn bm ym xn 0
机会成本 a1 j y1 a2 j y2 aij yi amj ym
表示减少一件产品所节省的可以增加的利润
（3）对偶松弛变量的经济解释——产品的差额成本
机会成本
利润
min w b1 y1 b2 y2 bm ym
a11 y1
st
a12
y1
a1n y1
max z CX
（P）
AX b
s
.t
.
X
0
（D）
min w Yb
s.t.
YA C Y 0
• （2）然后按照（D）、（P）式写出其对偶
例：写出下面线性规划的对偶规划模型：
max z 2x1 3x2
min w 3 y1 5y2 1y3
x1 2x2 3 y1 0
s.t.
2xx11
例如，在前面的练习中已知
max z 2.5x1 x2 的终表为
3x1 5x2 15 s.t.5x1 2x2 10
x1, x2 0
0 x3 9 2.5 x1 2
0 19 1 - 3
5
5
1
2
0
1
5

运筹学实验一

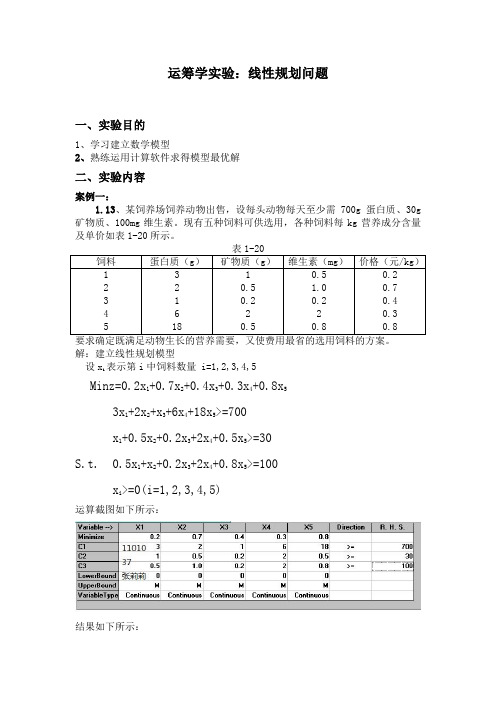
运筹学实验：线性规划问题一、实验目的1、学习建立数学模型2、熟练运用计算软件求得模型最优解二、实验内容案例一：1.13、某饲养场饲养动物出售，设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。

现有五种饲料可供选用，各种饲料每kg 营养成分含量及单价如表1-20所示。

表1-20饲料蛋白质（g ）矿物质（g ）维生素（mg ）价格（元/kg ） 1 2 3 4 5 3 2 1 6 18 1 0.5 0.2 2 0.5 0.5 1.0 0.2 2 0.8 0.2 0.7 0.4 0.30.8 要求确定既满足动物生长的营养需要，又使费用最省的选用饲料的方案。

解：建立线性规划模型设x i 表示第i 中饲料数量 i=1,2,3,4,5Minz=0.2x 1+0.7x 2+0.4x 3+0.3x 4+0.8x 53x 1+2x 2+x 3+6x 4+18x 5>=700x 1+0.5x 2+0.2x 3+2x 4+0.5x 5>=30S.t. 0.5x 1+x 2+0.2x 3+2x 4+0.8x 5>=100x i >=0(i=1,2,3,4,5)运算截图如下所示：结果如下所示：案例二：1.18、宏银公司承诺为某建设项目从2003年起的4年中每年初分别提供以下数额贷款：2003年——100万元，2004年——150万元，2005年——120万元，2006年——110万元。

以上贷款资金均需于2002年底前筹集齐。

但为了充分发挥这笔资金的作用，在满足每年贷款额情况下，可将多余资金分别用于下列投资项目：（1）、于2003年初购买A种债券，期限3年，到期后本息合计为投资额的140%，但限购60万元；（2）、于2003年初购买B种债券，期限2年，到期后本息合计为投资额的125%，且限购90万元；（3）、于2004年初购买C种债券，期限2年，到期后本息合计为投资额的130%，但限购50万元；（4）、于每年年初将任意数额的资金存放于银行，年息4%，于每年年底取出。

解答-运筹学-第一章-线性规划及其单纯形法习题

项目 X1 X2 X3 X4
X5
X4 6 (b) (c) (d) 1 0
X5 1 -1
3 (e) 0 1
Cj-ZJ
(a) -1 2
00
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj-ZJ
0
-7A (j) (k) (l)
25
首先由于x1、x5为基变量，故g=1, h=0, l = 0
检验数j
14M 4M-2 6M-3 2M-1 -M -M
A
0
0
18
Cj
-2 -3 -1 0 0 -M -M 比
CB XB
b x1 x2 x3 x4 x5 x6 x7 值
-M x6 8 1 4 2 -1 0 1 0 2
-M x7 6 3 2 0 0 -1 0 1 3
检验数j 14M 4M-2 6M-3 2M-1 -M -M 0 0
5 x2 15
s
t
.
6
x1 x1
2 x2 x2
24 5
x 1 , x 2 0
A
10
Cj
10 5 0 0 比
CB XB
b
x1
x2
x3
x4
值
0 x3
9
3
4
1
0 9/3=3
0 x4
8
5
20
1
8/5
检验数j 0 10 5 0 0
0 x3 21/5 0 14/5 1 -3/5 3/2
10 x1 8/5 1 2/5 0 1/5
4
x
2
12
x 1, x 2 0 无可行解
m ax Z x1 x2

运筹学课后习题答案

第一章线性规划1、由图可得：最优解为2、用图解法求解线性规划：Min z=2x1+x2解：由图可得：最优解x=1.6,y=6.43用图解法求解线性规划：Max z=5x1+6x2解：由图可得：最优解Max z=5x1+6x2, Max z= +4用图解法求解线性规划：Maxz = 2x 1 +x 2 由图可得：最大值⎪⎩⎪⎨⎧==+35121x x x ，所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.6将线性规划模型化成标准形式：Min z=x 1-2x 2+3x 3 解：令Z ’=-Z,引进松弛变量x 4≥0，引入剩余变量x 5≥0，并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’7将线性规划模型化为标准形式Min Z =x1+2x2+3x3解：令Z’ = -z，引进松弛变量x4≥0,引进剩余变量x5≥0,得到一下等价的标准形式。

x2’=-x2 x3=x3’-x3’’Z’ = -min Z = -x1-2x2-3x39用单纯形法求解线性规划问题：Max Z =70x1+120x2解： Max Z =70x1+120x2单纯形表如下Max Z =3908.11.解：（1）引入松弛变量X4，X5，X6，将原问题标准化，得max Z=10X1+6X2+4X3X1+X2+X3+X4=10010 X1+4X2+5X3+X5=6002 X1+2X2+6X3+X6=300X1,X2,X3,X4,X5,X6≥0得到初始单纯形表：（2）其中ρ1 =C1-Z1=10-（0×1+0×10+0×2）=10，同理求得其他根据ρmax =max{10,6,4}=10,对应的X1为换入变量，计算θ得到，θmin =min{100/1,600/10,300/2}=60,X5为换出变量，进行旋转运算。

（3）重复（2）过程得到如下迭代过程ρj≤0，迭代已得到最优解，X*=（100/3，200/3，0，0，0，100）T，Z* =10×100/3+6×200/3+4×0 =2200/3。

运筹学第01章线性规划问题

线性规划建模步骤
设定决策变量明确约束条件并用决策变量的线性等式或不等式表示用变量的线性函数表示要达到的目标，并确定是求极小还是求极大根据变量的物理性质确定变量是否具有非负性注：其中最关键是设定决策变量这一步
生产计划问题(1)
某工厂用三种原料生产三种产品，已知的条件如下表所示，试制订总利润最大的日生产计划
线性规划问题解的有关概念(2)
基本解：令模型中所有非基变量的值等于零后，由模型的约束方程组得到的一组解。基本可行解：满足非负条件的基本解称为基本可行解。可行基：对应于基本可行解的基称为可行基。退化解：基本可行解的非零分量个数小于m时，称为退化解。最优基：若对应于基B的基本可行解X是线性规划的最优解，则称B为线性规划的最优基
人员安排问题(1)
医院护士24小时值班，不同时段需要的护士人数不等（见下表）。每个护士每天连续值班8小时，在各时段开始时上班。问最少需要多少护士？
序号 1 2 3 4 时段 06—10 10—14 14—18 18—22 最少人数 60 70 60 50
5 6
22—02 02—06
20 30
人员安排问题(2)
设xj为第j时段开始值班的护士人数
目标函数为：使人数最少，则有
min f ( X ) x1 x2 x3 x4 x5 x6 x6 x1 60 x x 70 1 2 x2 x3 60 s.t. x3 x4 50 x x 20 5 4 x5 x6 30 x1 , x2 , x3 , x4 , x5 , x6 0且为整数
运筹学
第一章线性规划问题
本章重点
线性规划建模线性规划的图解法线性规划的标准形式单纯形法两阶段法大M法

运筹学_第1章_线性规划习题

第一章线性规划习题1.1（生产计划问题）某企业利用A、B、C三种资源，在计划期内生产甲、乙两种产品，已知生产单位产品资源的消耗、单位产品利润等数据如下表，问如何安排生产计划使企业利润最大？解：设x1、x2分别代表甲、乙两种产品的生产数量（件），z表示公司总利润。

依题意，问题可转换成求变量x1、x2的值，使总利润最大，即ma x z=50x1+100x2且称z=50x1+100x2为目标函数。

同时满足甲、乙两种产品所消耗的A、B、C三种资源的数量不能超过它们的限量，即可分别表示为x1 + x2≤3002x1 + x2≤400x2≤250且称上述三式为约束条件。

此外，一般实际问题都要满足非负条件，即x1≥0、x2≥0。

这样有ma x z=50x1+100x2x1 + x2≤3002x1 + x2≤400x2≤250x1、x2≥0习题1.2 靠近某河流有两个化工厂，流经第一化工厂的河流流量为每天500万m 3，在两个工厂之间有一条流量为200万m 3的支流。

两化工厂每天排放某种有害物质的工业污水分别为2万m 3和1.4万m 3。

从第一化工厂排出的工业污水流到第二化工厂以前，有20%可以自然净化。

环保要求河流中工业污水含量不能大于0.2%。

两化工厂处理工业污水的成本分别为1000元/万m 3和800元/万m 3。

现在要问在满足环保要求的条件下，每厂各应处理多少工业污水，使这两个工厂处理工业污水的总费用最小。

解：设x 1、x 2分别代表工厂1和工厂2处理污水的数量(万m 3)。

则问题的目标可描述为min z =1000x 1+800x 2 约束条件有第一段河流（工厂1——工厂2之间）环保要求 (2－x 1)/500 ≤0.2% 第二段河流（工厂2以下河段）环保要求 [0.8(2－x 1) +(1.4－x 2)]/700≤0.2% 此外有x 1≤2； x 2≤1.4 化简得到min z =1000x 1+800x 2 x 1 ≥1 0.8x 1 + x 2 ≥1.6 x 1 ≤2 x 2≤1.4 x 1、x 2≥0习题1.3ma x z =50x 1+100x 2x 1 + x 2≤300 2x 1 + x 2≤400x 2≤250图1—1 x 2x1、x2≥0用图解法求解。

运筹学1至6章习题参考答案

C(j)-Z(j)
0
2
11/8
0
-3/4
0
9
X4
0
0
0
9/8
1
7/16
-1/4
27/4
6
X1
3
1
0
-1/2
0
1/4
0
3
M
X2
2
0
1
[11/16]
0
-3/32
1/8
1/8
0.181818
C(j)-Z(j)
0
0
0
0
-9/16
-1/4
37/4
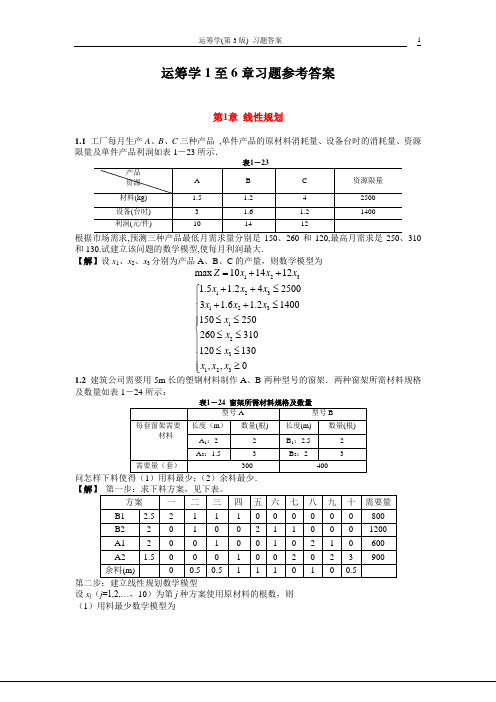
X3进基、X2出基，得到另一个基本最优解。
C(j)
3
2
-0.125
6重油
7残油
辛烷值
80
115
105
蒸汽压：公斤／平方厘米
1.0
1.5
0.6
0.05
每天供应数量(桶)
2000
1000
1500
1200
1000
1000
800
问炼油厂每天生产多少桶成品油利润最大，建立数学模型。
解设xij为第i（i＝1,2,3,4）种成品油配第j(j=1,2,…,7)种半成品油的数量（桶）。
10
-5
1
0
0
0
* Big M
5
3
1
0
0
0
X1
10
1
3/5
1/5
0
1/5
2
X4
0
0
4
-9
1
1
25
C(j)-Z(j)
0
-11
-1

运筹学第一章 1.5 线性规划的应用

例、营养问题
要求制定一个既经济又合乎健康标准的食谱
一个简单的例子：一个简单的例子：现准备采购甲、乙两种食品，表中给现准备采购甲、乙两种食品，出了已知价格及相关的营养成分。出了已知价格及相关的营养成分。最右栏给出了按营养学标准每人每天的最低需要量。问应如何采购食品才能在保证营养要求的前提下花费最省？求的前提下花费最省？
(二) 合理下料问题
在加工业中，经常遇到这类问题。在加工业中，经常遇到这类问题。问题的一般提法是：问题的一般提法是：已知某种尺寸的棒料或板材，料或板材，需要将其切割成一定数量既定规格的几种零件毛坯，定规格的几种零件毛坯，问应如何选取合理的下料方法，合理的下料方法，使得既满足对截出毛坯的数量要求，坯的数量要求，又使所用的原材料最少或废料最少）？（或废料最少）？
产品计划问题有关信息表
单位产品所需资源资源产品
A1
A2
L
An
可供应资源
B1 B2 M Bm
a11 a21 L am1
a12 a21 L am2
L L L L
a1n a2n L amn
b1 b2 M bm
单位产品所得利润
c1
c2
L
cn
设出产品的计划数，可列出这类问设出产品的计划数，题的数学模型如下：题的数学模型如下：
注意——Z是非线性表达式！是非线性表达式！注意是非线性表达式
Y ① 引入一个新变量，
处理
令 Y=
8 x + 10 x + 16 x + + 21x32 11 21 31 6 x12 15 x 22 min , 2 3

运筹学第1章线性规划及单纯形法复习题

max (min)
Z = CX
AX ≤ ( = , ≥ ) b X ≥ 0
3、线性规划的标准形式、
ma0
4、线性规划问题的解、（一）求解方法
一般有两种方法图解法单纯形法两个变量、两个变量、直角坐标三个变量、三个变量、立体坐标
适用于任意多个变量、适用于任意多个变量、但需将一般形式变成标准形式
（二）线性规划问题的解
1、解的概念可行解：满足约束条件② 的解为可行解。 ⑴ 可行解：满足约束条件②、③的解为可行解。所有解的集合为可行解的集或可行域。所有解的集合为可行解的集或可行域。最优解：达到最大值的可行解。 ⑵ 最优解：使目标函数①达到最大值的可行解。 ⑶ 基：B是矩阵A中m×m阶非奇异子矩阵是矩阵A ≠0），），则是一个基。（∣B∣≠0），则B是一个基。
§2 图解法
例一、例一、 max
Z = 2 x 2 x 2 x 4 x
2 2 1
+ 3 x
2
2 x1 + x + 1 4 x1 x1 ≥
≤ 12 ≤ 8 ≤ 16 ≤ 12
2
⑴ ⑵ ⑶ ⑷
2
0, x
≥ 0
max
Z = 2 x1 + 3 x 2 x 2 x
2 2
当xj=0时, 必有 j=zj=0, 因此时必有y
∑P x = ∑P y = ∑P z
j =1
r
r
r
r
j
j
j =1
j
j
j =1
j
j
=b
∑(y
j =1
j
− z j ) Pj = 0