习题参考解答(图论部分)
图论第一章课后习题解答

bi 个 (i = 1,2,…,s),则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分,称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ,E H E G , 重数,则称 H 是 G 的子图,记为 H G 。有时又称 G 是 H 的母图。 当 H G ,但 H G 时,则记为 H G ,且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集,以两端点均在 V 中的边的全体为边集 所组成的子图,称为 G 的由 V 导出的子图,记为 G[ V ];简称为 G 的导出子图,导出子图 G[V\ V ]记为 G V ; 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集,以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图,记为 G E ;简称为 G 的边导出子图,边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ,则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图(包括 G 和空图)的个数是 2m 个。 定义 2 设 G1,G2 是 G 的子图。若 G1 和 G2 无公共顶点,则称它们是不相交的;若 G1 和 G2 无公共边,则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图,其顶点 集为 V(G1)∪V(G2),其边集为 E(G1)∪E(G2);如果 G1 和 G2 是不相交的,有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2,但此时 G1 和 G2 至少要有一个公共顶点。
图论习题答案

习题一1. 一个工厂为一结点;若两个工厂之间有业务联系,则此两点之间用边相联;这样就得到一个无向图。
若每点的度数为3,则总度数为27,与图的总度数总是偶数的性质矛盾。
若仅有四个点的度数为偶数,则其余五个点度数均为奇数,从而总度数为奇数,仍与图的总度数总是偶数的性质矛盾。
2. 若存在孤立点,则m 不超过K n-1的边数, 故 m <= (n-1)(n-2)/2, 与题设矛盾。
3.4. 用向量(a 1,a 2,a 3)表示三个量杯中水的量, 其中a i 为第i 杯中水的量, i = 1,2,3.以满足a 1+a 2+a 3 = 8 (a 1,a 2,a 3为非负整数)的所有向量作为各结点, 如果(a 1,a 2,a 3)中某杯的水倒满另一杯得到 ( a ’1, a ’2, a ’3 ) , 则由结点到结点画一条有向边。
这样可得一个有向图。
本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路,以下即是这样的一条:5. 可以。
7. 同构。
同构的双射如下:8. 记e 1= (v 1,v 2), e 2= ( v 1,v 4), e 3= (v 3,v 1), e 4= (v 2,v 5), e 5= (v 6,v 3), e 6= (v 6,v 4), e 7= (v 5,v 3), e 8= (v 3,v 4), e 9 = (v 6,v 1), 则邻接矩阵为: 关联矩阵为:∑∑∑∑∑∑∑==+====-=++=-==---=--=ni i n i i n i n i n i ni i i n i i n i i i i a a n n a a a n n n a n a v v 1111121212/)1()1(2)1(])1[(。
, 所以 因为 ,+ 的负度数,则为结点的正度数,为结点记-----22 222 i i C a a ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------100110000001001000010100010011010100000001001100000111, 001101000100000000001001010000001010⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡( 8, 0, 0 ) ( 5, 3, 0 ) ( 5, 0, 3 ) ( 2, 3, 3 ) ( 2, 5, 1 )(7, 0, 1 ) ( 7, 1, 0 ) ( 4, 4, 0 )( 4, 1, 3 )边列表为:A= (1,1,3,2,6,6,5,3,6), B= (2,4,1,5,3,4,3,4,1). 正向表为:A= (1,3,4,6,6,7,10), B= (2,4,5,1,4,3,3,4,1).习题二1. 用数学归纳法。
图论习题答案

图论习题答案
《图论习题答案》
图论作为数学中的一个重要分支,研究的是图的性质和图之间的关系。
在学习
图论的过程中,我们常常会遇到各种各样的习题,通过解答这些习题可以帮助
我们更好地理解图论的知识。
下面就让我们来看一些图论习题的答案吧。
1. 问:一个图中有多少条边?
答:一个图中的边数可以通过计算每个顶点的度数之和再除以2来得到。
2. 问:一个图中有多少个连通分量?
答:一个图中的连通分量可以通过使用深度优先搜索或广度优先搜索来求得。
3. 问:一个图中是否存在欧拉回路?
答:一个图中存在欧拉回路的充分必要条件是每个顶点的度数都是偶数。
4. 问:一个图中是否存在哈密顿回路?
答:一个图中存在哈密顿回路的判定是一个NP难题,目前还没有有效的多项式时间算法。
5. 问:一个图中的最小生成树有多少条边?
答:一个图中的最小生成树的边数恰好等于顶点数减一。
通过解答这些图论习题,我们可以更好地掌握图论的基本概念和算法。
图论不
仅在数学领域有着重要的应用,而且在计算机科学、电信网络等领域也有着广
泛的应用。
因此,熟练掌握图论知识对我们的学习和工作都有着重要的意义。
希望通过本文的分享,能够帮助大家更好地理解图论知识,提高解决问题的能力。
同时也希望大家在学习图论的过程中能够多多练习,勇于挑战各种各样的
图论习题,不断提升自己的图论水平。
祝大家在图论的学习道路上取得更大的
进步!。
图论1-3藏习题解答

学号:0441 姓名:张倩 习题14.证明图1-28中的两图是同构的证明:将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )?u i (1? i ? 10)容易证明,对?v i v j ?E((a)),有f(v i v j )?u i u j ?E((b)) (1? i ? 10, 1?j? 10 ) 由图的同构定义知,图1-27的两个图是同构的。
5.证明:四个顶点的非同构简单图有11个。
证明:设四个顶点中边的个数为m ,则有: m=0:m=1 :(a)v 2 v 3u 4u (b)m=2:m=3:m=4:m=5:m=6:因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。
11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。
证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列;(6,6,5,4,3,3,1)是图序列()11123121,1,,1,,,=d d n d d d d d π++---L L 是图序列(5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。
12.证明:若δ≥2,则G 包含圈。
证明 只就连通图证明即可。
设V(G)={v1,v2,…,vn},对于G 中的路v1v2…vk,若vk 与v1邻接,则构成一个圈。
若vi1vi2…vin 是一条路,由于?? 2,因此,对vin ,存在点vik 与之邻接,则vik?vinvik 构成一个圈 。
17.证明:若G 不连通,则G 连通。
证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支,显然u 与v 在_G 中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,则u 与w ,v 与w 分别在_G 中连通,因此,u 与v 在_G 中连通。
离散数学习题解答第6部分(图论)
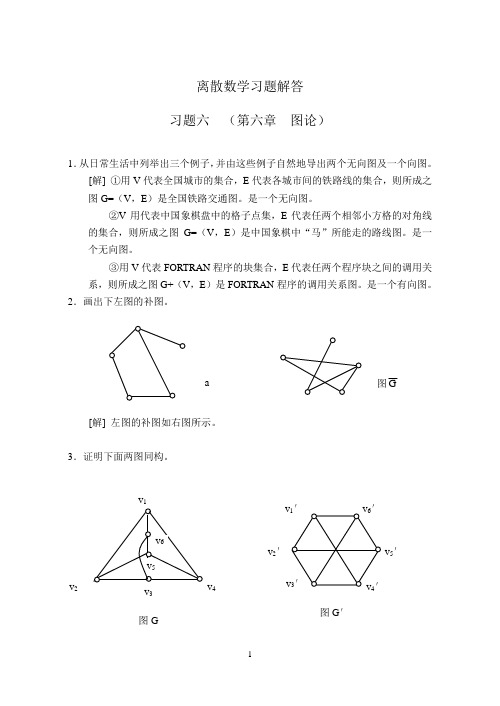
离散数学习题解答 习题六 (第六章 图论)1.从日常生活中列举出三个例子,并由这些例子自然地导出两个无向图及一个向图。
[解] ①用V 代表全国城市的集合,E 代表各城市间的铁路线的集合,则所成之图G=(V ,E )是全国铁路交通图。
是一个无向图。
②V 用代表中国象棋盘中的格子点集,E 代表任两个相邻小方格的对角线的集合,则所成之图G=(V ,E )是中国象棋中“马”所能走的路线图。
是一个无向图。
③用V 代表FORTRAN 程序的块集合,E 代表任两个程序块之间的调用关系,则所成之图G+(V ,E )是FORTRAN 程序的调用关系图。
是一个有向图。
2.画出下左图的补图。
[解] 左图的补图如右图所示。
3.证明下面两图同构。
a v 2 v 3 v 4图G图G ′[证] 存在双射函数ϕ:V →V ′及双射函数ψ : E →E ′ϕ (v 1)=v 1′ ϕ (v 1,v 2)=(v 1′,v 2′) ϕ (v 2)=v 2′ ϕ (v 2,v 3)=(v 2′,v 3′) ϕ (v 3)=v 3′ ϕ (v 3,v 4)=(v 3′,v 4′) ϕ (v 4)=v 4′ ϕ (v 4,v 5)=(v 4′,v 5) ϕ (v 5)=v 5′ ϕ (v 5,v 6)=(v 5′,v 6′) ϕ (v 6)=v 6′ϕ (v 6,v 1)=(v 6′,v 1′) ϕ (v 1,v 4)=(v 1′,v 4′) ϕ (v 2,v 5)=(v 2′,v 5′) ϕ (v 3,v 6)=(v 3′,v 6′)显然使下式成立:ψ (v i ,v j )=(v i ,v j ′)⇒ ϕ (v i )=v i ′∧ϕ (v j )=v j ′ (1≤i ·j ≤6) 于是图G 与图G ′同构。
4.证明(a ),(b )中的两个图都是不同构的。
图G 中有一个长度为4的圈v 1v 2v 6v 5v 1,其各顶点的度均为3点,而在图G ′中却没有这样的圈,因为它中的四个度为3的顶点v 1',v 5',v 7',v 3'不成长度的4的圈。
图论习题答案2

图论习题课(二)
第二次作业
一(40) . 证明 : G是单图, k , 则G有长k的轨。 证:若P为G的一条最长轨,它的长度l<k,设P为v1v2 v3 ...vl 1 , 而d v1 k l , 从而P外恒存在一点v0与v1邻接, 于是v0 v1v2 v3 ...vl 1是G中长于P的一条轨,这与P是最长轨矛盾,故l k . 故G中有长k的轨。
第四次作业
三(11).设是平面图G的连通片个数,则 (G ) (G ) (G ) 1 证:对于每个连通片G i, 1 i ,运用欧拉定理:
(Gi ) (Gi ) (Gi ) 2
[ (G ) (G ) (G )] 2
第二次作业
• 二(5).证明:树有一个中心或者两个中心,但有两 个中心时,此二中心是邻顶。 • 证明:结论对于树K1,K2显然成立。对于任何一 个其它的树T,与除去T的所有度为1的顶点得到 的树T' 有同样的中心。因为T有限,经过有限步 后,得到树K1或K2。且K1,K2的中心即为T的中心。 得证。
第四次作业
• 四(2).树上是否可能有两个不同的完备匹配? • 解:不可能,理由如下: • 设M1和M2为两个不同的完备匹配,则M1ΘM2≠Ø, 且T(M1ΘM2)中所有点的度都为2,所以T(M1ΘM2) 中有圈,不为树,与题意矛盾,假设不成立。
第四次作业
• 四(11).矩阵的行或列成为矩阵的”线“,证明:0-1 矩阵中含所有1的线集合的最小阶数(集合元素个 数)等于没有两个在同一线上的1的个数。 • 证明:设X为行集合,Y为列集合 • 若某行与某列交点为1,则将这两点之间连线,构 成二分图G。 • 含所有1的线集合的最小阶数为最小覆盖|M|。 • 没有两个在同一线上的1的个数为最大匹配β(G)。 • 由konig定理,|M|=β(G),得证。
图论习题参考答案

二、应用题题0:(1996年全国数学联赛)有n(n≥6)个人聚会,已知每个人至少认识其中的[n/2]个人,而对任意的[n/2]个人,或者其中有两个人相互认识,或者余下的n-[n/2]个人中有两个人相互认识。
证明这n个人中必有3个人互相认识。
注:[n/2]表示不超过n/2的最大整数。
证明将n个人用n个顶点表示,如其中的两个人互相认识,就在相应的两个顶点之间连一条边,得图G。
由条件可知,G是具有n个顶点的简单图,并且有(1)对每个顶点x,)N G≥[n/2];(x(2)对V的任一个子集S,只要S=[n/2],S中有两个顶点相邻或V-S中有两个顶点相邻。
需要证明G中有三个顶点两两相邻。
反证,若G中不存在三个两两相邻的顶点。
在G中取两个相邻的顶点x1和y1,记N G(x1)={y1,y2,……,y t}和N G(y1)={x1,x2,……,x k},则N G(x1)和N G(y1)不相交,并且N G(x1)(N G(y1))中没有相邻的顶点对。
情况一;n=2r:此时[n/2]=r,由(1)和上述假设,t=k=r且N G(y1)=V-N G(x1),但N G(x1)中没有相邻的顶点对,由(2),N G(y1)中有相邻的顶点对,矛盾。
情况二;n=2r+1: 此时[n/2]=r,由于N G(x1)和N G(y1)不相交,t≥r,k≥r,所以r+1≥t,r+1≥k。
若t=r+1,则k=r,即N G(y1)=r,N G(x1)=V-N G(y1),由(2),N G(x1)或N G(y1)中有相邻的顶点对,矛盾。
故k≠r+1,同理t≠r+1。
所以t=r,k=r。
记w∈V- N G(x1) ∪N G(y1),由(2),w分别与N G(x1)和N G(y1)中一个顶点相邻,设wx i0∈E, wy j0∈E。
若x i0y j0∈E,则w,x i0, y j0两两相邻,矛盾。
若x i0y j0∉E,则与x i0相邻的顶点只能是(N G(x1)-{y j0})∪{w},与y j0相邻的顶点只能是(N G(y1)-{x j0})∪{w}。
图论(张先迪-李正良)课后习题答案(第一章)

习题一作者---寒江独钓1.证明:在n 阶连通图中(1) 至少有n-1条边;(2) 如果边数大于n-1,则至少有一条闭迹;(3) 如果恰有n-1条边,则至少有一个奇度点。
证明: (1) 若G 中没有1度顶点,由握手定理:()2()21v V G m d v n m n m n ∈=≥⇒≥⇒>-∑若G 中有1度顶点u ,对G 的顶点数作数学归纳。
当n=2时,结论显然;设结论对n=k 时成立。
当n=k+1时,考虑G-u,它仍然为连通图,所以,边数≥k-1.于是G 的边数≥k.(2) 考虑G 中途径:121:n n W v v v v -→→→→L若W 是路,则长为n-1;但由于G 的边数大于n-1,因此,存在v i 与v j ,它们相异,但邻接。
于是:1i i j i v v v v +→→→→L 为G 中一闭途径,于是也就存在闭迹。
(3) 若不然,G 中顶点度数至少为2,于是由握手定理:()2()21v V G m d v n m n m n ∈=≥⇒≥⇒>-∑这与G 中恰有n-1条边矛盾! 2.(1)2n −12n 2−12n −1 (2)2n−2−1(3) 2n−2。
证明:u 1的两个邻接点与v 1的两个邻接点状况不同。
所以,两图不同构。
4.证明下面两图同构。
u 1 v 1证明:作映射f : v i ↔ u i (i=1,2….10)容易证明,对∀v i v j ∈E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b))(1≤ i ≤ 10, 1≤j ≤ 10 )由图的同构定义知,图(a)与(b)是同构的。
5.指出4个顶点的非同构的所有简单图。
分析:四个顶点的简单图最少边数为0,最多边数为6,所以可按边数进行枚举。
(a)v 2 v 3u 4u(b)6.证明:1)充分性:当G 是完全图时,每个顶点的度数都是n −1,共有n 个顶点,总的度数为n(n −1),因此总的边数是n(n−1)2=(n 2). 2)必要性:因为G 是简单图,所以当G 是完全图的时候每个顶点的度数才达到最大:n −1.若G 不是完全图,则至少有一个顶点的度数小于n −1,这样的话,总的度数就要小于n (n −1),因此总的边数小于(n 2),矛盾。
(图论)离散数学习题参考答案2
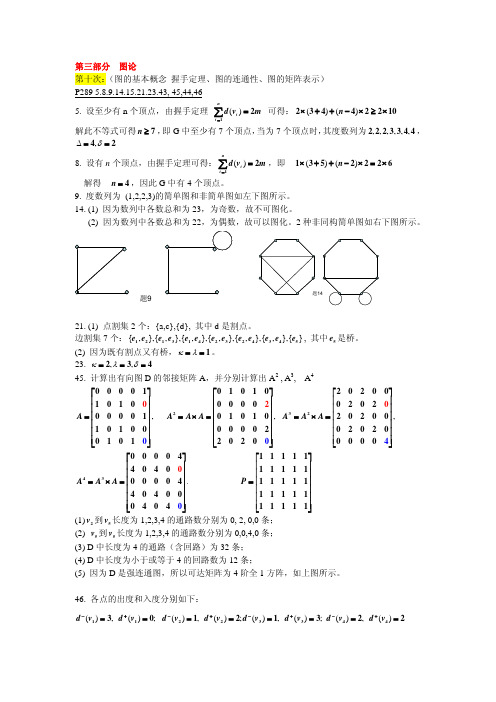
解此不等式可得 n ≥ 7 , 即 G 中至少有 7 个顶点, 当为 7 个顶点时, 其度数列为 2, 2, 2, 3, 3, 4, 4 , Δ = 4, δ = 2 8. 设有 n 个顶点,由握手定理可得: ∑ d (vi ) = 2m ,即
i =1 n
1 × (3 + 5) + (n − 2) × 2 = 2 × 6
d − (v1 ) = 3, d + (v1 ) = 0; d − (v2 ) = 1, d + (v2 ) = 2; d − (v3 ) = 1, d + (v3 ) = 3; d − (v4 ) = 2, d + (v4 ) = 2
第十一次: (欧拉图与哈密顿图)P305 1.2.11.21 (无向树及其性质)P318 2.24(a), 25(b) 1. (a),(c) 是欧拉图,因为它们均连通且都无奇度顶点; (b),(d)都不是欧拉图;因为(b) 不连通,(d) 既不连通又有奇度顶点;要使(b),(d)变为欧拉图 均至少加两条边,使其连通并且无奇度顶点。如下图所示。
(1) v2 到 v5 长度为 1,2,3,4 的通路数分别为 0, 2, 0,0 条; (2) v5 到 v5 长度为 1,2,3,4 的通路数分别为 0,0,4,0 条; (3) D 中长度为 4 的通路(含回路)为 32 条; (4) D 中长度为小于或等于 4 的回路数为 12 条; (5) 因为 D 是强连通图,所以可达矩阵为 4 阶全 1 方阵,如上图所示。 46. 各点的出度和入度分别如下:
(v2,12)** (v5, 7)*
根据上表的最后一行,从 v1 到其余各点的最短路径和距离如下: v1v2, d(v1,v2)=6 v1v2v6, d(v1,v6)=12 v1v3, d(v1,v3)=3 v1v3v4v5v7, d(v1,v7)=7 v1v3v4, d(v1,v4)=5 v1v3v4v5v7v8, d(v1,v8)=10 v1v3v4v5, d(v1,v5)=6
张清华 图论课后题答案

第1章 图论预备知识1.1解:(1) p={φ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}(2) p={,{a},{{b,c}},{a,{b,c}}} (3) p={,{}}(4) p={,{},{{}},{,{}}}(5)p={,{{a,b}},{{a,a,b}},{{a,b,a,b}},{{a,b},{a,a,b}},{{a,b},{a,b,a,b}},{{a,b},{a,a,b},{a,b,a,b}}} 1.2 解:(1) 真 (2) 假 (3)假 (4)假 1.3 解:(1) 不成立,A={1} B={1,2} C={2} (2) 不成立,A={1} B={1,2} C={1,3}1.4 证明:设(x,y)∈(A ∩B)X(C ∩D) 说明x ∈A ∩B,y ∈C ∩D 由于 x ∈A,y ∈C 所以 (x,y) ∈A X C 由于x ∈B,y ∈D 所以 (x,y) ∈B X D 所以 (x,y) ∈(A X C )∩(B X D ) 反过来,如果(x,y )∈(A X C) ∩(B X D ) 由于 (x,y) ∈(A X C )所以 x ∈A,y ∈C 由于 (x,y) ∈(B X D )所以x ∈B,y ∈D 所以x ∈(A ∩B) y ∈(C ∩D) 所以 (x,y) ∈(A ∩B)X(C ∩D)所以(A ∩B)X(C ∩D)= (A X C) ∩(B X D ) 1.5 解:Hasse 图φφφφφφφφφ极大元{9,24,10,7} 极小元{3,2,5,7} 最大元{24} 最小元{2}1.6 解(2)关系图为:(3)不存在最大元,最小元为{2}1.7 解:(1)R={<1,1>,<2,2>,<3,3>,<4,4>,<1,2>,<2,1>,<2,3>,<3,2>} (2)略(3)I A ⊆R 故R 是自反的。
图论习题及答案

图论习题及答案(总24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业解答练习题2 利用matlab编程FFD算法完成下题:设有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。
解答一:function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD(降序首次适应)算法求解:先将物体按长度从大到小排序, %然后按FF算法对物体装箱%输入参数w为物品体积,capacity为箱子容量%输出参数num为所用箱子个数,s为元胞数组,表示装箱方案,s{i}为第i个箱子所装%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:nfor j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endendends = s(1:num);解答二:clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) endoutput:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三:function box_count=FFD(x)%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:nj=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;endendif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入:>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, i122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w= {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32,i22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。
离散数学及其应用图论部分课后习题答案
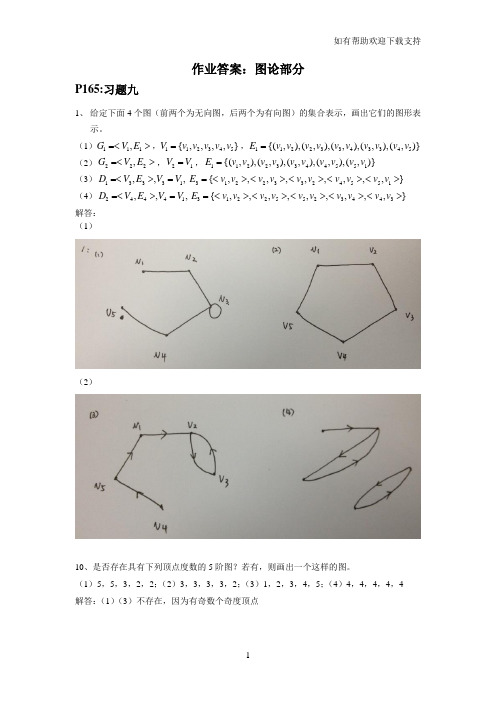
(2)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(3)构成了初级通路,因为点不重复;
(4)不构成通路,因为边 不存在;
(5)构成通路,但是不为简单通路和初级通路,因为有重复的边
(6)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(7)构成了初级通路;
(8)简单通路,但是不为初级通路,有重复边。
23、用Dijkstra标号法求图9.22中各图从顶点 到其余各点的最短路径和距离。
解答
步骤
1
2
3
4
5
6
7பைடு நூலகம்
到 最短路为 ,路长为6;
到 最短路为 ,路长为3;
到 最短路为 ,路长为5;
到 最短路为 ,路长为6;
到 最短路为 ,路长为12;
到 最短路为 ,路长为7;
那么对于n阶m条边的无向图G是 棵树组成的森林,在任意两棵树中分别找一点进行连一条边,那么得到的图则为n阶m+1条边的无向图G是 棵树组成的森林,
那么 ,所以 。
方法二:设 棵树中,分别有 个顶点和 条边, ,则有
, , ,即可得证。
19、求图10.17中两个带权图的最小生成树。
解答:
P204:习题十一
16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
解答:
(1)三条边一共提供6度;所以点度序列可能是
①3,3,0,0,0,0;②3,2,1,0,0,0;③3,1,1,1,0,0;④2,2,2,0,0,0;⑤2,2,1,1,0,0;⑥2,1,1,1,1,0;⑦1,1,1,1,1,1;
由于是简单图,①②两种情形不可能
图论习题参考答案

二、应用题题0:(1996年全国数学联赛)有n (n ≥6)个人聚会,已知每个人至少认识其中的[n /2]个人,而对任意的[n /2]个人,或者其中有两个人相互认识,或者余下的n -[n /2]个人中有两个人相互认识。
证明这n 个人中必有3个人互相认识。
注:[n /2]表示不超过n /2的最大整数。
证明 将n 个人用n 个顶点表示,如其中的两个人互相认识,就在相应的两个顶点之间连一条边,得图G 。
由条件可知,G 是具有n 个顶点的简单图,并且有(1)对每个顶点x ,)(x N G ≥[n /2];(2)对V 的任一个子集S ,只要S =[n /2],S 中有两个顶点相邻或V-S 中有两个顶点相邻。
需要证明G 中有三个顶点两两相邻。
反证,若G 中不存在三个两两相邻的顶点。
在G 中取两个相邻的顶点x 1和y 1,记N G (x 1)={y 1,y 2,……,y t }和N G (y 1)={x 1,x 2,……,x k },则N G (x 1)和N G (y 1)不相交,并且N G (x 1)(N G (y 1))中没有相邻的顶点对。
情况一;n=2r :此时[n /2]=r ,由(1)和上述假设,t=k=r 且N G (y 1)=V-N G (x 1),但N G (x 1)中没有相邻的顶点对,由(2),N G (y 1)中有相邻的顶点对,矛盾。
情况二;n=2r+1: 此时[n /2]=r ,由于N G (x 1)和N G (y 1)不相交,t ≥r,k ≥r,所以r+1≥t,r+1≥k 。
若t=r+1,则k=r ,即N G (y 1)=r ,N G (x 1)=V-N G (y 1),由(2),N G (x 1)或N G (y 1)中有相邻的顶点对,矛盾。
故k ≠r+1,同理t ≠r+1。
所以t=r,k=r 。
记w ∈V- N G (x 1) ∪N G (y 1),由(2),w 分别与N G (x 1)和N G (y 1)中一个顶点相邻,设wx i0∈E, wy j0∈E 。
图论习题参考答案

二、应用题题0 : (1996年全国数学联赛)有n (n_6)个人聚会,已知每个人至少认识其中的[n/2]个人,而对任意的[n/2]个人,或者其中有两个人相互认识,或者余下的n-[n/2]个人中有两个人相互认识。
证明这n个人中必有3个人互相认识。
注:[n/2]表示不超过n/2的最大整数。
证明将n个人用n个顶点表示,如其中的两个人互相认识,就在相应的两个顶点之间连一条边,得图G。
由条件可知,G是具有n个顶点的简单图,并且有(1)对每个顶点x, N G(X)工[n/2];(2)对V的任一个子集S,只要S = [n/2], S中有两个顶点相邻或V-S中有两个顶点相邻。
需要证明G中有三个顶点两两相邻。
反证,若G中不存在三个两两相邻的顶点。
在G中取两个相邻的顶点X i和y i,记N G(X I)={y i,y2, ,y t}和N G(y i)={x i,X2, ,X k},贝U N G(X I)和N G(y i)不相交,并且N G(X I) (N G(y i)) 中没有相邻的顶点对。
情况一;n=2r:此时[n/2]=「,由(i)和上述假设,t=k=r 且N G(y i) = V-N G(X I),但N G(X I)中没有相邻的顶点对,由(2), N G(y i)中有相邻的顶点对,矛盾。
情况二;n=2r+i:此时[n/2]= r,由于N G(X I)和N G(y i)不相交,t亠r,k ",所以r+i 亠t,r+i 丄k。
若t=r+i,则k=r,即N G(y i)=r, N G(X I)= V-N G(y i),由(2), N G(X I)或N G(y i)中有相邻的顶点对,矛盾。
故k z r+i,同理r+i。
所以t=r,k=r。
记w^V- N G(X I) U N G(y i),由(2), w 分别与N G(X I)和N G(y i)中一个顶点相邻,设wx io,E, wy jo,E。
若X io y jo・E,则w , X io, y jo两两相邻,矛盾。
第四部分图论练习题答案

《离散数学》第四部分---图论练习题答案一、选择或填空1、设G是一个哈密尔顿图,则G一定是( )。
(1) 欧拉图(2) 树(3) 平面图(4) 连通图答:(4)2、下面给出的集合中,哪一个是前缀码?( )(1) {0,10,110,101111} (2) {01,001,000,1}(3) {b,c,aa,ab,aba} (4) {1,11,101,001,0011}答:(2)3、一个图的哈密尔顿路是一条通过图中( )的路。
答:所有结点一次且恰好一次4、在有向图中,结点v的出度deg+(v)表示( ),入度deg-(v)表示( )。
答:以v为起点的边的条数,以v为终点的边的条数5、设G是一棵树,则G 的生成树有( )棵。
(1) 0 (2) 1 (3) 2 (4) 不能确定答:16、n阶无向完全图K n 的边数是( ),每个结点的度数是( )。
答:2)1(nn, n-17、一棵无向树的顶点数n与边数m关系是( )。
8、一个图的欧拉回路是一条通过图中( )的回路。
答:所有边一次且恰好一次9、有n个结点的树,其结点度数之和是( )。
答:2n-210、下面给出的集合中,哪一个不是前缀码( )。
(1) {a,ab,110,a1b11} (2) {01,001,000,1}(3) {1,2,00,01,0210} (4) {12,11,101,002,0011}答:(1)11、n个结点的有向完全图边数是( ),每个结点的度数是( )。
答:n(n-1),2n-212、一个无向图有生成树的充分必要条件是( )。
答:它是连通图13、设G是一棵树,n,m分别表示顶点数和边数,则(1) n=m (2) m=n+1 (3) n=m+1 (4) 不能确定。
答:(3)14、设T=〈V,E〉是一棵树,若|V|>1,则T中至少存在( )片树叶。
答:215、任何连通无向图G至少有( )棵生成树,当且仅当G 是( ),G的生成树只有一棵。
图论习题及答案

作业解答练习题2 利用matlab编程FFD算法完成下题:设有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。
解答一:function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD(降序首次适应)算法求解:先将物体按长度从大到小排序,%然后按FF算法对物体装箱%输入参数w为物品体积,capacity为箱子容量%输出参数num为所用箱子个数,s为元胞数组,表示装箱方案,s{i}为第i个箱子所装%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:nfor j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endendends = s(1:num);解答二:clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) endoutput:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三:function box_count=FFD(x)%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:nj=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;endendif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入:>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v i= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, 122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w i = {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32, 22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)
(2)子图略
长度为三的回路:Ae1Ae1Ae1A,Ae1Ae3De2A,Ae4Be7Ce5A,Ae4Be8Ce5A
长度为四的回路:AAAAA,AAADA,AABe7CA,AABe8CA,ABe7CDA,ABe8CDA
16. 证明:G是二部图当且仅当G的回路都是偶长回路。
证明:设二部图G,顶点分为两个集合V1 ,V2
充分性:
先证明在二部图中,奇长路的道路的两个端节点一定分别在两个顶点集合中,对道路长度使用归纳法,
(1)当道路长度为1是,根据二部图的定义,每条边的两个顶点分别在两个点集合中,结论成立
(2)假设道路长度为2n-1 ( n≥2)时结论成立
(3)=〉(4)
对任意两条边e1,e2其端点分别为u1,u2,v1,v2。根据(3)存在回路C1 = u1…v1v2…u1,C2=u2…v1v2…u2。那么可以形成新的闭道路P=u1…v1v2…u2…v1v2…u1,在其中将重复边剔出到,得到新的回路C3,其中包含e2和u1,u2结点,可以将回路中u1…u2用u1u2=e1替换,就得到新的新的回路,包含e1,e2,满足要求.
(3)(4,4,2,2,4); (4)(7,6,8,3,9,5)
解:除序列(1)不是图序列外,其余的都是图序列。因为在(1)中,总和为奇数,不满足图总度数为偶数的握手定理。
可以按如下方法构造满足要求的图:序列中每个数字ai对应一个点,如果序列数字是偶数,那么就在对应的点上画ai/2个环,如果序列是奇数,那么在对应的点上画(ai-1)/2个环。最后,将奇数序列对应的点两两一组,添加连线即可。下面以(2)为例说明:
习题十
1. 设G是一个(n,m)简单图。证明:,等号成立当且仅当G是完全图。
证明:(1)先证结论:
因为G是简单图,所以G的结点度上限 max(d(v))≤n-1, G图的总点度上限为 max(Σ(d(v))≤n﹒max(d(v))≤n(n-1) 。根据握手定理,G图边的上限为 max(m)≤n(n-1)/2,所以。
(6 , 3, 3, 2, 2 ) 对应图G的点集合V= { v1,v2,v3,v4,v5}
每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)
将奇数3,3 对应的结点v2,v3一组,画一条连线
其他序列可以类式作图,当然大家也可以画图其它不同的图形。■
必要性:(仅对连通分支证明)
在图中任意取一点着色为白色,将和此点最短距离为奇数的点着色为黑点,为偶数的着色为白点,那么将结点分为白色和黑色连个点集,任何同色点之间没有边相连。否则将形成奇数长度的回路,例如同色结点v1,v2 相邻,那么从初始着色点v开始通过最短路径可以形成如下回路v…v1v2…v,因为v…v1,v2…v长度和为偶数,那么回路v…v1v2…v长度为奇数,与题设矛盾。所以是二部图
hong(1).2.
20. 证明:图中距离满足欧几里德距离的三条公理。
证明:(1)d(u,v)≥0,即任何两个结点之间的最短路长度大于等于0
显然,结点u与自己之间的距离为0,而和其他结点之间的最短距离不为0。
(2)d(u,v)=d(v,u),两个结点之间的最短距离相等
显然,如果长度为k的最短道路p=u…v ,即使u到v的最短道路,也是v到u的最短道路。
(2)=〉(3)
因为G中任意两个结点都位于同一回路中,所以任意结点u,和任意边e的两个端点v1,v2都分别在两个回路C1,C2中,如果C1=C2=u…v1…v2…u,那么将回路中v1…v2,用v1v2=e替换,就得到新的新的回路,并满足要求。如果C1≠C2,C1=u…v1…u,C2=u…v2…u,那么构成新的道路P=u…v1…u…v2…u,在其中将重复边剔出掉,得到新的回路C3,其中包含v1,v2结点,可以将回路中v1…v2用v1v2=e替换,就得到新的新的回路,并满足要求.
m=m`(2)
(1),(2)联立求解得:m=n(n-1)/4, 及一个图为自补图,最低条件为结点数为4的倍数或为4的倍数加1。
图示略■
10.判断图10.29中的两个图是否同构,并说明理由。
解:题中两个图不同构,因为左边图的唯一3度点有2个1度点为其邻接点,而右图唯一的3度点只有1个1度点为其邻接点。因此这两个图不可能同构■
(3)当道路长度为2n+1时,设P=v1v2…v2n-1v2nv2n+1,在此路径上删除最后两个结点,那么道路P将变为长度为2n-1的奇长道路,根据假设,v1,v2n-1分别在两个顶点集合中,那么v2n和v1在同一顶点集合中,而v2n+1和v1在不同顶点集合,结论成立
因为G中的任何回路,写成道路的形式,起点和终点时一个结点,当然在同一个顶点集合中,因此长度必为偶数;
引论2:引论1中G’’(V’,E’’)的任意点诱导子图,也是G图的点诱导子图。
证明:略,请读者证明。
设有完全图Kn( n≥1),现根据其p阶点诱导子图作归纳证明。
Kn的1阶点诱导子图,显然是完全图,且都是K1图。当n≥2,Kn的2阶点诱导子图,显然是完全图,且都是K2图
假设Kn的p(n>p>2)阶点诱导子图,为Kp图,那么对任意的p+1阶点诱导子图G,根据引理2结论,G的任意p阶点诱导子图G’为Kn的p阶点诱导子图,且为Kp图。因此,G必为Kp+1图。
(4)=>(1)
因为任意两条边都在同一回路中,所以不存在割边。假设边e是割边,那么删除此边,图不连通,分支中的任何一对不在同一分支中的边,不能构成回路,与条件矛盾。所以,G中无割边■
19. 设G=(V,E)是点度均为偶数的连通图。证明:对任何。
证明:G-v最多产生d(v)个奇数度点,又因为每个连通分支中奇数度点的个数是偶数,即G-v的连通分支最少有两条边和v相连,所以总连通分支数小于等于d(v)/2■
长度为五的回路:AAAAAA,AAAADA,AAABe7CA,AAABe8CA,AABe7CDA,AABe8CDA, AADADA,AAAe4Be7Ce5A,AAAe4Be8Ce5A, ADAe4Be7Ce5A,ADAe4Be8Ce5A■
14.试证明在任意6个人的组里,存在3个人相互认识,或者存在3个人相互不认识。
17.设(n, m)简单图G满足,证明G必是连通图。构造一个的非连通简单图。
证明:假设G不连通,分支G1,G2..Gk,那么他们的边数的最大值max(m)=Σ(ni-1)ni/2≤Σ(ni-1)(n-1)/2=(n-1)/2Σ(ni-1)=(n-1)(n-k)/2,所以,只有当k=1时,才能满足题设要求,G是连通图。如果将顶点集合分成两个点集,|V1|=1,|V2|=n-1,构成如下的有两个分支的非连通简单图,G1=(1,0),G2=Kn-1,满足题设条件■
11.证明: 图10.30中的两个图是同构的。
解:略■
12.求具有4个结点完全图K4的所有非同构的生成子图。
解:我们可以把生成子图按总度数不同进行分类,不同总度数的子图类决不同构。总度数相同的子图类中,再去找出不同购的子图。因此求解如下:
Σd(v) = 0: (0,0,0,0)
=2: (1,1,0,0)
证明:设A为6人中的任一人,那么A要么至少与3人认识,要么至少与3人不认识,二者必居其一。
假设A与B,C,D三人认识,如果B,C,D三人互不认识,结论成立
如果B,C,D三人中,至少有两人相互认识,则它们和A一起,构成相互认识的3人,结论成立。
同理,A至少与3人不认识,结论也成立。因此,题设结论成立■
(3)d(u,v)+d(v,w)≥d(u,w)
假设d(u,v)+d(v,w)≤d(u,w),那么最短道路P=u…w ,就不是最短道路,因为另一条道路p’=u…v…w其长度小于P,与最短道路相矛盾,因此原结论存立■
21. 证明:在非平凡连通图G中,e为割边的充要条件是它不包含于G的任何圈中。
=4: (2,1,1,0) (1,1,1,1)
=6: (3,1,1,1) (2,2,1,1)(2,2,2,0)
=8: (2,2,2,2) (3,2,2,1)
=10: (3,3,2,2)
=12: (3,3,3,3)
总共10个不同构生成子图■
13.设有向图D=<V,E>如下图10.31所示。
(1) 在图中找出所有长度分别为1,2,3,4的圈 (至少用一种表示法写出它们,并以子图形式画出它们)。
证明:反证法,假设,则G的总点度上限为max(Σ(d(u))≤2 n,根据握手定理,图边的上限为max(m)≤2n/2=n。与题设m = n+1,矛盾。因此,G中存在顶点u,d(u)≥3。■
3.确定下面的序列中哪些是图的序列,若是图的序列,画出一个对应的图来:
(1)(3,2,0,1,5); (2)(6,3,3,2,2)
4.证明:在(n,m)图中。
证明:图的点度数是一组非负整数{d(v1),d(v2)…d(vn)},那么这组数的算术平均值一定大于等于其中的最小值,同时小于等于其中的最大值。对应到图的术语及为:最大值为,最小值为δ,平均值 = (d(v1)+d(v2)…+d(vn))/n = 2m/n,所以。■
5.证明定理10.2。
15. 若u和v是图G中仅有的两个奇数度结点,证明u和v必是连通的。
证明:反证法,假设u和v不连通,那么他们必然分布于此图的两个连通分支中。那么它们将分别是各连通分支中唯一的奇数度结点。根据握手定理,一个图中奇度点的个数为偶数。而两个连通分支中,奇度点的个数为奇数。矛盾。矛盾的产生,是由于假设不连通导致的,因此,题设结论成立■
【定理10.2】对于任何(n,m)有向图G =(V,E),
证明:有向图中,每条有向边为图贡献一度出度,同时贡献一度出度,所以总出度和总入度相等,并和边数相等。因此,上述关系等式成立。■
