2020_2021学年高中数学第2章平面向量阶段综合提升第3课平面向量阶段训练含解析新人教A版必修4
高中数学第二章平面向量第2节平面向量的线性运算(第3课时)向量数乘运算及其几何性质课下能力提升(十

2018-2019学年高中数学第二章平面向量第2节平面向量的线性运算(第3课时)向量数乘运算及其几何性质课下能力提升(十六)(含解析)新人教A 版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第二章平面向量第2节平面向量的线性运算(第3课时)向量数乘运算及其几何性质课下能力提升(十六)(含解析)新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第二章平面向量第2节平面向量的线性运算(第3课时)向量数乘运算及其几何性质课下能力提升(十六)(含解析)新人教A版必修4的全部内容。
课下能力提升(十六)[学业水平达标练]题组1 向量的线性运算1。
错误!错误!等于( )A.2a-b B.2b-aC.b-a D.a-b解析:选B 原式=16(2a+8b)-错误!(4a-2b)=错误!a+错误!b-错误!a+错误!b=-a+2b=2b-a。
2.已知m,n是实数,a,b是向量,则下列命题中正确的为()①m(a-b)=m a-m b;②(m-n)a=m a-n a;③若m a=m b,则a=b;④若m a=n a,则m=n。
A.①④ B.①②C.①③ D.③④解析:选B ①和②属于数乘对向量与实数的分配律,正确;③中,若m=0,则不能推出a=b,错误;④中,若a=0,则m,n没有关系,错误.题组2 用已知向量表示未知向量3.在△ABC中,AB=c,AC=b,若点D满足BD=2DC,则AD等于()A。
错误!b+错误!c B.错误!c-错误!bC.错误!b-错误!c D。
高中数学:第2章 平面向量 素养提升——平面向量的线性运算

答案:-23
9.(2018·上海徐汇二模)如图,在△ABC 中,M 为边 BC 上 不同于 B,C 的任意一点,点 N 满足A→N=2N→M.若A→N=xA→B+yA→C, 求 x2+9y2 的最小值.
又 e1 与 e2 不共线, 所以32= =-λ3-λ2kk, +1, 解得 k=-94. [答案] (1)A (2)-94
方法活用——平面向量共线定理的 3 个应用 证明向 对于非零向量 a,b,若存在实数 λ,使 量共线 a=λb,则 a 与 b 共线 证明三 若存在实数 λ,使A→B=λA→C,A→B与A→C有 点共线 公共点 A,则 A,B,C 三点共线 求参数 利用向量共线定理及向量相等的条件 的值 列方程(组)求参数的值
【例 1】 (2019·湖北咸宁联考)如图,在△ABC 中,点 M 为 AC 的中点,点 N 在 AB 上,A→N=3N→B,点 P 在 MN 上,M→P =2P→N,那么A→P=( )
A.23A→B-16A→C C.31A→B-16A→C
B.13A→B-12A→C D.12A→B+61A→C
[解析] A→P=A→M+M→P=A→M+23M→N=A→M+23(A→N-A→M)=13 A→M+23A→N=16A→C+21A→B.故选 D.
(2)证明三点共线问题,可用向量共线来解决,但应注意向 量共线与三点共线的区别与联系,当两向量共线且有公共点时, 才能得到三点共线.
(3)直线的向量式参数方程:A,P,B 三点共线⇔O→P=(1- t)·O→A+tO→B(O 为平面内任一点,t∈R).
2020-2021高中数学人教版第二册学案:6.3.1平面向量基本定理含解析

新教材2020-2021学年高中数学人教A版必修第二册学案:6.3.1平面向量基本定理含解析6.3平面向量基本定理及坐标表示6.3.1平面向量基本定理[目标]1.了解平面向量基本定理产生的过程和基底的含义,理解平面向量基本定理;2.掌握平面向量基本定理并能熟练应用.[重点] 平面向量基本定理.[难点] 平面向量基本定理的应用.要点整合夯基础知识点平面向量基本定理[填一填](1)定理:如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.(2)若e1,e2不共线,我们把{e1,e2}叫做表示这一平面内所有向量的一个基底.[答一答]1.基底有什么特点?平面内基底唯一吗?提示:基底中的两向量e1,e2不共线,这是基底的最大特点.平面内的基底并不是唯一的,任意不共线的两个向量都可以作为基底.2.如图,设OA、OB、OC为三条共端点的射线,P为OC上一点,能否在OA 、OB 上分别找一点M 、N ,使OP →=错误!+错误!?提示:能。
过点P 作OA 、OB 的平行线,分别与OB 、OA 相交,交点即为N 、M .3.若向量a ,b 不共线,且c =2a -b ,d =3a -2b ,试判断c ,d 能否作为基底.提示:设存在实数λ使得c =λd ,则2a -b =λ(3a -2b ),即(2-3λ)a +(2λ-1)b =0.由于a ,b 不共线,从而2-3λ=2λ-1=0,这样的λ是不存在的,从而c ,d 不共线,故c ,d 能作为基底。
典例讲练破题型类型一 基底的概念[例1] 下面说法中,正确的是( )①一个平面内只有一对不共线向量可作为表示该平面内所有向量的基底;②一个平面内有无数多对不共线向量可作为表示该平面内所有向量的基底;③零向量不可作为基底中的向量;④对于平面内的任一向量a 和一组基底e 1,e 2,使a =λe 1+μe 2成立的实数对一定是唯一的.A .②④B .②③④C .①③D .①③④[解析] 因为不共线的任意两个向量均可作为平面的一组基底,故②③正确,①不正确;由平面向量基本定理知④正确.综上可得②③④正确.[答案]B根据平面向量基底的定义知,判断能否作为基底问题可转化为判断两个向量是否共线的问题,若不共线,则它们可以作为一组基底;若共线,则它们不能作为一组基底。
2020-2021学年人教A版数学必修4:第2章阶段综合提升第3课平面向量
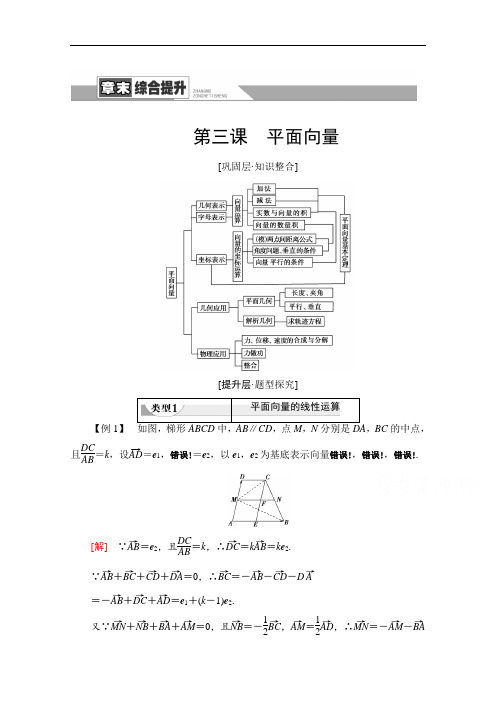
第三课 平面向量[巩固层·知识整合][提升层·题型探究]平面向量的线性运算【例1】 ,BC 的中点,且DC AB =k ,设AD →=e 1,错误!=e 2,以e 1,e 2为基底表示向量错误!,错误!,错误!.[解] ∵AB →=e 2,且DC AB =k ,∴DC →=kAB →=k e 2.∵AB →+BC →+CD →+DA →=0,∴BC →=-AB →-CD →-D A → =-AB →+DC →+AD →=e 1+(k -1)e 2. 又∵MN→+NB →+BA →+AM →=0,且NB →=-12BC →,AM →=12AD →,∴MN →=-AM →-BA →-NB →=-12AD →+AB →+12BC →=k +12e 2.向量线性运算的基本原则和求解策略 (1)基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量.因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.(2)求解策略:①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.②字符表示下线性运算的常用技巧: 首尾相接用加法的三角形法则,如共起点两个向量作差用减法的几何意义,如[跟进训练]1.如图所示,在△ABC 中,AN→=13NC →,P 是BN 上的一点,若AP →=mAB →+211AC→,则实数m 的值为________.311[设BP →=λBN →, 则BP→=BA →+AP →=-AB →+mAB →+211AC →=(m -1)AB →+211AC →. BN→=BA →+AN →=-AB →+14AC →.∵BP →与BN →共线,∴14(m -1)+211=0,∴m =311.]平面向量数量积的运算【例2】 (1)已知点A (-1,1),B (1,2),C (-2,-1),D (3,4),则向量AB →在CD →方向上的投影为( )A.322 B.3152 C .-322D .-3152(2)如图,在梯形ABCD 中,AB ∥CD ,AB =4,AD =3,CD =2,AM →=2MD →.若AC →·BM →=-3,则AB →·AD→=________.(1)A (2)32 [(1)AB→=(2,1),CD →=(5,5),向量AB →=(2,1)在CD →=(5,5)上的投影为|AB →|cos 〈AB →,CD →〉=|AB →|·AB →·CD →|AB →||CD →|=AB →·CD →|CD →|=1552=322.(2)因为AC →·BM →=⎝ ⎛⎭⎪⎫AD →+12AB →·⎝ ⎛⎭⎪⎫-AB →+23AD →=-2-23AB →·AD →=-3,所以AB →·AD→=32.]向量数量积的求解策略(1)利用数量积的定义、运算律求解.,在数量积运算律中,有两个形似实数的完全平方公式在解题中的应用较为广泛,即(a +b )2=a 2+2a·b +b 2,(a -b )2=a 2-2a·b +b 2,上述两公式以及(a +b )·(a -b )=a 2-b 2这一类似于实数平方差的公式在解题过程中可以直接应用.(2)借助零向量.即借助“围成一个封闭图形且首尾相接的向量的和为零向量”,再合理地进行向量的移项以及平方等变形,求解数量积.(3)借助平行向量与垂直向量.,即借助向量的拆分,将待求的数量积转化为有垂直向量关系或平行向量关系的向量数量积,借助a ⊥b ,则a·b =0等解决问题.(4)建立坐标系,利用坐标运算求解数量积.[跟进训练]2.(2018·全国卷Ⅱ)已知向量a ,b 满足|a |=1,a·b =-1,则a ·(2a -b )=( ) A .4 B .3 C .2 D .0B [a ·(2a -b )=2a 2-a·b =2-(-1)=3,故选B.]3.已知正方形ABCD 的面积为2,点P 在边AB 上,则PD →·PC →的最大值为( ) A.62 B.32C .2 D. 2 C [如图建立平面直角坐标系,由题意得,D (2,2),C (2,0),设P (0,t )(0≤t ≤2),∴PD →=(2,2-t ),PC →=(2,-t ),∴PD →·PC→=t 2-2t +2=⎝⎛⎭⎪⎫t -222+32,∴当t =0或2时,(PD →·PC →)max=2,故选C.]平面向量的坐标运算【例3】 a ⊥(m a -b ),则m =________.(2)设a =(2,0),b =(1,3). ①若(λa -b )⊥b ,求λ的值;②若m =λa +μb ,且|m |=23,〈m ,b 〉=π6,求λ,μ的值. 思路点拨:(1)用坐标表示出m a -b ,再利用垂直关系列出方程求解. (2)将向量坐标表示后列方程或方程组求解. (1)-1 [∵a =(1,0),b =(-1,m ), ∴m a -b =(m,0)-(-1,m )=(m +1,-m ), 由a ⊥(m a -b )得:a ·(m a -b )=0,∴a ·(m a -b )=m +1=0, 即m =-1.](2)[解] ①因为a =(2,0),b =(1,3),所以λa -b =(2λ,0)-(1,3)=(2λ-1,-3). 又(λa -b )⊥b ,所以(λa -b )·b =0,即(2λ-1,-3)·(1,3)=0, 所以2λ-1-3=0.所以λ=2.②因为a =(2,0),b =(1,3),m =λa +μb =λ(2,0)+μ(1,3)=(2λ+μ,3μ). 因为|m |=23,〈m ,b 〉=π6,所以⎩⎨⎧(2λ+μ)2+(3μ)2=(23)2,cos π6=(2λ+μ,3μ)·(1,3)23×2,即⎩⎨⎧ λ2+λμ+μ2=3,λ+2μ=3.解得⎩⎨⎧ λ=1μ=1或⎩⎨⎧λ=-1μ=2, 所以λ=1,μ=1或λ=-1,μ=2.向量的坐标运算若a =(a 1,a 2),b =(b 1,b 2),则 ①a +b =(a 1+b 1,a 2+b 2); ②a -b =(a 1-b 1,a 2-b 2); ③λa =(λa 1,λa 2); ④a ·b =a 1b 1+a 2b 2;⑤a ∥b ⇔a 1=λb 1,a 2=λb 2(λ∈R ),或(b 1≠0,b 2≠0);⑥a ⊥b ⇔a 1b 1+a 2b 2=0;⑧若θ为a 与b 的夹角,则[跟进训练]4.已知A (-1,-1),B (sin θ,cos θ),C (2,5)三点共线,且θ≠k π2(k ∈Z ).求tan θ.[解] 由题意得AB→=(sin θ+1,cos θ+1),AC →=(3,6).因为A ,B ,C 三点共线,所以AB →与AC →共线,所以3(cos θ+1)-6(sin θ+1)=0, 即cos θ-2sin θ=1.两边平方得cos 2θ-4sin θcos θ+4sin 2θ=sin 2θ+cos 2θ. 即3sin 2θ=4sin θcos θ.因为θ≠k π2,k ∈Z , 所以cos θ≠0,所以tan θ=43.平面向量的平行与垂直问题【例4-n ),则λ=( )A .-4B .-3C .-2D .-1(2)设A ,B ,C ,D 为平面内的四点,且A (1,3),B (2,-2),C (4,1). ①若AB→=CD →,求D 点的坐标. ②设向量a =AB→,b =BC →,若k a -b 与a +3b 平行,求实数k 的值.(1)B [因为m +n =(2λ+3,3), m -n =(-1,-1), 且(m +n )⊥(m -n ),所以(m +n )·(m -n )=-2λ-3-3=0, 解得λ=-3.](2)[解] ①设D (x ,y ).因为AB →=CD →,所以(2,-2)-(1,3)=(x ,y )-(4,1), 化为(1,-5)=(x -4,y -1), 所以⎩⎨⎧x -4=1,y -1=-5,解得⎩⎨⎧x =5,y =-4,所以D (5,-4).②因为a =AB→=(2,-2)-(1,3)=(1,-5),b =BC →=(4,1)-(2,-2)=(2,3),所以k a -b =k (1,-5)-(2,3)=(k -2,-5k -3),a +3b =(1,-5)+3(2,3)=(7,4).因为k a -b 与a +3b 平行, 所以7(-5k -3)-4(k -2)=0, 解得k =-13.1.将本例(2)②中的“BC →”改为“AC →”,“平行”改为“垂直”,求实数k的值.[解] 因为a =AB→=(1,-5),b =AC →=(3,-2),所以k a -b =(k -3,-5k +2), a +3b =(10,-11), 因为(k a -b )⊥(a +3b ),所以(k a -b )·(a +3b )=10(k -3)-11(-5k +2) =65k -52=0, 解得k =5265.2.在本例(2)中若A ,B ,D 三点共线,且AC ⊥CD ,求点D 的坐标. [解] 设点D 的坐标为(x ,y ),则 AB→=(1,-5),AD →=(x -1,y -3),AC →=(3,-2),CD →=(x -4,y -1), 由题意得AB→∥AD →,AC →⊥CD →,所以⎩⎨⎧ -5(x -1)-(y -3)=0,3(x -4)-2(y -1)=0,整理得⎩⎨⎧5x +y =8,3x -2y =10,解得x =2,y =-2, 所以点D 的坐标为(2,-2).1.证明共线问题常用的方法(1)向量a ,b (a ≠0)共线⇔存在唯一实数λ,使b =λa . (2)向量a =(x 1,y 1),b =(x 2,y 2)共线⇔x 1y 2-x 2y 1=0. (3)向量a 与b 共线⇔|a ·b |=|a ||b |.(4)向量a 与b 共线⇔存在不全为零的实数λ1,λ2,使λ1a +λ2b =0. 2.证明平面向量垂直问题的常用方法 a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0, 其中a =(x 1,y 1),b =(x 2,y 2).平面向量的模、夹角问题【例5】 已知向量e 1,e 2,且|e 1|=|e 2|=1,e 1与e 2的夹角为π3.m =λe 1+e 2,n =3e 1-2e 2.(1)求证(2e 1-e 2)⊥e 2; (2)若|m |=|n |,求λ的值; (3)若m ⊥n ,求λ的值;(4)若m 与n 的夹角为π3,求λ的值.思路点拨:利用两向量垂直则数量积为零,关于向量模的问题,先对其平方,以及合理使用夹角公式.[解] (1)证明:因为|e 1|=|e 2|=1,e 1与e 2的夹角为π3,所以(2e1-e2)·e2=2e1·e2-e22=2|e1||e2|cos π3-|e2|2=2×1×1×12-12=0,所以(2e1-e2)⊥e2.(2)由|m|=|n|得(λe1+e2)2=(3e1-2e2)2,即(λ2-9)e21+(2λ+12)e1·e2-3e22=0.因为|e1|=|e2|=1,〈e1,e2〉=π3,所以e21=e22=1,e1·e2=1×1×cos π3=1 2,所以(λ2-9)×1+(2λ+12)×12-3×1=0,即λ2+λ-6=0.所以λ=2或λ=-3.(3)由m⊥n知m·n=0,即(λe1+e2)·(3e1-2e2)=0,即3λe21+(3-2λ)e1·e2-2e22=0.因为|e1|=|e2|=1,〈e1,e2〉=π3,所以e21=e22=1,e1·e2=1×1×cos π3=1 2,所以3λ+(3-2λ)×12-2=0.所以λ=14.(4)由前面解答知e21=e22=1,e1·e2=12,|n|=7.而|m|2=(λe1+e2)2=λ2e21+2λe1·e2+e22=λ2+λ+1,所以|m|=λ2+λ+1.m·n=(λe1+e2)·(3e1-2e2)=3λe21+(3-2λ)e1·e2-2e22=3λ+(3-2λ)×12-2=2λ-12.因为〈m,n〉=π3,由m·n=|m||n|cos〈m,n〉得2λ-12=λ2+λ+1·7×12,化简得3λ2-5λ-2=0,所以λ=2或λ=-13.经检验知λ=-13不成立,故λ=2.1.解决向量模的问题常用的策略(1)应用公式:|a|=x2+y2(其中a=(x,y)).(2)应用三角形或平行四边形法则.(3)应用向量不等式||a|-|b||≤|a±b|≤|a|+|b|.(4)研究模的平方|a±b|2=(a±b)2.2.求向量的夹角设非零向量a=(x1,y1),b=(x2,y2),两向量夹角θ(0≤θ≤π)的余弦cos θ=a·b|a||b|=x1x2+y1y2x21+y21x22+y22.[跟进训练]5.已知c=m a+n b,c=(-23,2),a⊥c,b与c的夹角为2π3,b·c=-4,|a|=22,求实数m,n的值及a与b的夹角θ.[解]∵c=(-23,2),∴|c|=4.∵a⊥c,∴a·c=0.∵b·c=|b||c|cos 2π3=|b|×4×⎝⎛⎭⎪⎫-12=-4,∴|b|=2.∵c=m a+n b,∴c2=m a·c+n b·c,∴16=n×(-4),∴n=-4.在c=m a+n b两边同乘以a,得0=8m-4a·b. ①在c=m a+n b两边同乘以b,得m a·b=12. ②由①②,得m=±6,∴a·b=±26,∴cos θ=±2622×2=±32,∴θ=π6或5π6.]平面向量在平面几何和物理中的应用【例6】 (1)用两条成120°角的等长的绳子悬挂一个物体,如图所示,已知物体的重力大小为10 N ,则每根绳子的拉力大小是________.(2)如图所示,在正方形ABCD 中,P 为对角线AC 上任一点,PE ⊥AB ,PF ⊥BC ,垂足分别为E ,F ,连接DP ,EF ,求证:DP ⊥EF .(1)10 N [因绳子等长,所以每根绳子上的拉力和合力所成的角都相等,且等于60°,故每根绳子的拉力大小都是10 N .](2)证明:法一:(基向量法)设正方形ABCD 的边长为1,AE =a (0<a <1),则EP =AE =a ,PF =EB =1-a ,AP =2a ,∴DP →·EF →=(DA →+AP →)·(EP →+PF →)=DA →·EP →+DA →·PF →+AP →·EP →+AP →·PF→ =1×a ×cos 180°+1×(1-a )×cos 90°+2a ×a ×cos 45°+2a ×(1-a )×cos 45°=-a +a 2+a (1-a )=0,∴DP→⊥EF →,即DP ⊥EF . 法二:(坐标法)设正方形边长为1,建立如图所示的平面直角坐标系,设P (x ,x ),则D (0,1),E (x,0),F (1,x ),所以DP→=(x ,x -1),EF →=(1-x ,x ),由DP →·EF→=x (1-x )+x (x -1)=0, 所以DP→⊥EF →,即DP ⊥EF .平面向量两个方面的应用(1)平面几何应用向量几何问题 共线向量点共线问题、直线与直线平行 数乘向量求线段长度之比 数量积 线段的长度、直线与直线的夹角(2)[跟进训练]6.已知点O ,N ,P 在△ABC 所在平面内,且|OA→|=|OB →|=|OC →|,NA →+NB →+NC →=0,P A →·PB →=PB →·PC →=PC →·P A →,则点O ,N ,P 依次是△ABC 的( )A .重心、外心、垂心B .重心、外心、内心C .外心、重心、垂心D .外心、重心、内心C [因为点O 到△ABC 的三个顶点距离相等,所以点O 是△ABC 的外心.因为NA→+NB →+NC →=0,所以NA →+NB →=-NC →, 设线段AB 的中点为M ,则2NM→=-NC →. 由此可知N 为AB 边中线的三等分点(靠近中点M )所以N 是△ABC 的重心.因为P A →·PB →=PB →·PC →,所以PB →·(P A →-PC→)=0, 即PB →·CA→=0,所以PB →⊥CA →. 同理由PB →·PC →=PC →·P A →可证PC→⊥AB →, 所以P 是△ABC 的垂心.]莘莘学子,最重要的就是不要去看远方模糊的,而要做手边清楚的事。
2021年高考数学二轮复习 专题2 第3讲 平面向量素能训练(文、理)

2021年高考数学二轮复习专题2 第3讲平面向量素能训练(文、理)一、选择题1.(xx·新课标Ⅱ理,3)设向量a、b满足|a+b|=10,|a-b|=6,则a·b=( )A.1 B.2C.3 D.5[答案] A[解析] 本题考查平面向量的模,平面向量的数量积.∵|a+b|=10,|a-b|=6,∴a2+b2+2ab=10,a2+b2-2ab=6.联立方程解得ab=1,故选A.2.设x∈R,向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|=( )A. 5B.10C.2 5 D.10[答案] B[解析] 本题考查向量的模及垂直问题.∵a⊥b,∴a·b=0,∴x-2=0,∴x=2,∴a+b=(3,-1),|a+b|=10.3.(xx·福建理,8)在下列向量组中,可以把向量a=(3,2)表示出来的是( ) A.e1=(0,0),e2=(1,2)B.e1=(-1,2),e2=(5,-2)C.e1=(3,5),e2=(6,10)D.e1=(2,-3),e2=(-2,3)[答案] B[解析] 一个平面内任意不共线的两个向量都可以作为平面的基底,它能表示出平面内的其它向量.A中,e1=0,且e2与a不共线;C、D中的两个向量都是共线向量且不与a 共线,故表示不出a.B中的两个向量不共线,可以作为平面的一组基底,故可表示出a,4.(文)如果不共线向量a 、b 满足2|a |=|b |,那么向量2a +b 与2a -b 的夹角为( ) A.π6 B.π3 C.π2D.2π3[答案] C[解析] ∵(2a +b )·(2a -b )=4|a |2-|b |2=0, ∴(2a +b )⊥(2a -b ),∴选C.(理)若两个非零向量a 、b 满足|a +b |=|a -b |=2|a |,则向量a +b 与a -b 的夹角是( )A.π6B.π3C.2π3D.5π6[答案] C[解析] 解法1:由条件可知,a ·b =0,|b |=3|a |,则cos θ=-2a 24a 2=-12⇒θ=2π3.解法2:由向量运算的几何意义,作图可求得a +b 与a -b 的夹角为2π3.5.(xx·新课标Ⅰ文,6)设D ,E ,F 分别为△ABC 的三边BC 、CA 、AB 的中点,则EB →+FC →=( )A.AD →B.12AD →C.BC →D.12BC → [答案] A [解析] 如图,EB →+FC →=-12(BA →+BC →)-12(CB →+CA →)=-12(BA →+CA →)=12(AB →+AC →)=AD →. 选A.6.若a 、b 、c 均为单位向量,且a ·b =0,(a -c )·(b -c )≤0,则|a +b -c |的最大值为( )A.2-1 B .1 C. 2 D .2[答案] B[解析] |a +b -c |2=|a |2+|b |2+|c |2+2a ·b -2a ·c -2b ·c =3-2(a ·c +b ·c ) (a -c )·(b -c )=a ·b -a ·c -b ·c +|c |2=1-(a ·c +b ·c )≤0,∴|a +b -c |2≤1,∴|a +b -c |max =1. 二、填空题7.(文)(xx·湖北文,12)若向量OA →=(1,-3),|OA →|=|OB →|,OA →·OB →=0,则|AB →|=________.[答案] 2 5[解析] |OA →|=|OB →|,OA →·OB →=0⇒△AOB 是直角边为|OA →|=10的等腰直角三角形,AB 是斜边,所以|AB →|=2 5.解向量试题有代数和几何两种思路,若能利用向量的几何意义,则可以避免复杂的代数运算.(理)(xx·江西理,14)已知单位向量e 1与e 2的夹角为α,且cos α=13,向量a =3e 1-2e 2与b =3e 1-e 2的夹角为β,则cos β=________.[答案]223[解析] 本题考查平面向量数量积的性质及运算.依题意e 1·e 2=|e 1||e 2|cos α=13,∴|a |2=9e 21-12e 1·e 2+4e 22=9,∴|a |=3,|b |2=9e 21-6e 1·e 2+e 22=8,a ·b =9e 21-9e 1·e 2+2e 22=8,∴|b |=22, cos β=a ·b |a |·|b |=83×22=223.8.(xx·重庆文,14)若OA 为边,OB 为对角线的矩形中,OA →=(-3,1),OB →=(-2,k ),则实数k =________.[答案] 4[解析] 本题考查向量的数量积及坐标运算.∵OA →=(-3,1),OB →=(-2,k ),∴AB →=OB →-OA →=(1,k -1). 由题意知OA →⊥AB →,∴OA →·AB →=0即(-3,1)·(1,k -1)=0. ∴-3+k -1=0,∴k =4.9.已知向量a =(1,0),b =(1,1),则(1)与2a +b 同向的单位向量的坐标表示为________; (2)向量b -3a 与向量a 夹角的余弦值为________. [答案] (1)(31010,1010) (2)-255[解析] 本题主要考查了向量的坐标运算,单位向量及夹角的求法.(1)2a +b =2(1,0)+(1,1)=(3,1),其单位向量为(31010,1010),(2)∵b -3a =(-2,1),|a |=1,|b -3a |=5,a ·(b -3a )=-2,∴cos 〈a ,b -3a 〉=a ·b -3a |a |·|b -3a |=-255. 10.如图所示,A 、B 、C 是圆O 上的三点,线段CO 的延长线与线段BA 的延长线交于圆O 外的点D ,若OC →=mOA →+nOB →,则m +n 的取值范围是________.[答案] (-1,0)[解析] 根据题意知,线段CO 的延长线与线段BA 的延长线的交点为D ,则OD →=tOC →. ∵D 在圆外,∴t <-1,又D 、A 、B 共线,∴存在λ、μ,使得OD →=λOA →+μOB →,且λ+μ=1,又由已知,OC →=mOA →+nOB →,∴tmOA →+tnOB →=λOA →+μOB →, ∴m +n =1t,故m +n ∈(-1,0).一、选择题11.设向量a ,b 满足|a |=2,a ·b =32,|a +b |=22,则|b |等于( )A.12 B .1 C.32 D .2[答案] B[解析] ∵|a +b |2=|a |2+2a ·b +|b |2=4+3+|b |2=8,∴|b |=1.12.(文)已知平面上不共线的四点O ,A ,B ,C .若OA →+2OC →=3OB →,则|BC →||AB →|的值为( )A.12B.13C.14D.16[答案] A[解析] 如图,设OD →=2OC →,作▱OAED ,则OE →=3OB →,∴|AB →|=|DF →|=2|BC →|,∴|BC →||AB →|=12.(理)(xx·新课标Ⅰ理,10)已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP →=4FQ →,则|QF |=( )A.72B.52 C .3 D .2[答案] C[解析] 抛物线的焦点坐标是F (2,0),过点Q 作抛物线的准线的垂线,垂足是A ,则|QA |=|QF |,抛物线的准线与x 轴的交点为G ,因为FP →=4FQ →,∴|PQ →||PF →|=34,由于三角形QAP与三角形FGP 相似,所以可得|QA ||FG |=|PQ →||PF →|=34,所以|QA |=3,所以|QF |=3.13.(文)(xx·中原名校第二次联考)在三角形ABC 中,∠A =60°,∠A 的平分线交BC于D ,AB =4,AD →=14AC →+λAB →(λ∈R ),则AD 的长为( )A .1 B. 3 C .3 D .3 3[答案] D[解析] 在AC 上取E 点,在AB 上取F 点,使AE →=14AC →,AF →=λAB →,∵AD →=14AC →+λAB →=AE →+AF →,∴DE ∥AB ,DF ∥AC ,∴AF BF =CD BD =CEAE=3,∵AF +BF =AB =4,∴BF =1,AF =3,在△ADF 中,AF =3,DF =3,∠DFA =120°,∴AD =3 3.(理)(xx·湖南文,10)在平面直角坐标系中,O 为原点,A (-1,0),B (0,3),C (3,0),动点D 满足|CD →|=1,则|OA →+OB →+OD →|的取值范围是( )A .[4,6]B .[19-1,19+1]C .[23,27]D .[7-1,7+1][答案] D[解析] 考查了向量的坐标运算,圆的有关知识. 设D (x ,y ),则由|CD →|=1,得(x -3)2+y 2=1, 而|OA →+OB →+OD →|=x -12+y +32表示点D (x ,y )到点(1,-3)的距离,(x-3)2+y 2=1表示以(3,0)为圆心,1为半径的圆,点(1,-3)与点(3,0)的距离为7,∴|CA →+OB →+OD →|的取值范围为[7-1,7+1].14.(xx·浙江理,8)记max{x ,y }=⎩⎪⎨⎪⎧x ,x ≥yy ,x <y ,min{x ,y }=⎩⎪⎨⎪⎧y ,x ≥yx ,x <y ,设a ,b为平面向量,则( )A .min{|a +b |,|a -b |}≤min{|a |,|b |}B .min{|a +b |,|a -b |}≥min{|a |,|b |}C .max{|a +b |2,|a -b |2}≤|a |2+|b |2D .max{|a +b |2,|a -b |2}≥|a |2+|b |2[答案] D[解析] 由新定义知,max{x ,y }是x 与y 中的较大值,min{x ,y }是x ,y 中的较小值,据此可知A 、B 是比较|a +b |与|a -b |中的较小值与|a |与|b |中的较小值的大小,由平行四边形法则知其大小与〈a ,b 〉有关,故A 、B 错;当〈a ,b 〉为锐角时,|a +b |>|a -b |,此时|a +b |2>|a |2+|b |2. 当〈a ,b 〉为钝角时,|a +b |<|a -b |,此时|a +b |2<|a |2+|b |2<|a -b |2. 当〈a ,b 〉=90°时,|a +b |=|a -b |,此时|a +b |2=|a |2+|b |2. 故选D. 二、填空题15.(xx·山东理,12)在△ABC 中,已知AB →·AC →=tan A ,当A =π6时,△ABC 的面积为________.[答案]16[解析] AB →·AC →=|AB →||AC →|cos π6=tan π6∴|AB →||AC →|=23S △ABC =12|AB →||AC →|sin π6=12×23×12=16.16.(文)(xx·苏北四市一调)如图,在四边形ABCD 中,AC 和BD 相交于点O ,设AD →=a ,AB →=b ,若AB →=2DC →,则AO →=________(用向量a 和b 表示).[答案]23a +13b [解析] 据题意可得AC →=AD →+DC →=AD →+12AB →=a +12b ,又由AB →=2DC →,可得AO →=23AC →=23(a+12b )=23a +13b (理)(xx·南昌高三调研)已知O 为坐标原点,点M (3,2),若N (x ,y )满足不等式组⎩⎪⎨⎪⎧x ≥1,y ≥0,x +y ≤4.则OM →·ON →的最大值为________.[答案] 12[解析] 据不等式组得可行域如图所示:由于z =OM →·ON →=3x +2y ,结合图形进行平移可得点A (4,0)为目标函数取得最大值的最优解.即z max =3×4+2×0=12.三、解答题17.已知向量a =(cos θ,sin θ),θ∈[0,π],向量b =(3,-1). (1)若a ⊥b ,求θ的值;(2)若|2a -b |<m 恒成立,求实数m 的取值范围. [解析] (1)∵a ⊥b ,∴3cos θ-sin θ=0,得tan θ= 3. 又θ∈[0,π],∴θ=π3.(2)∵2a -b =(2cos θ-3,2sin θ+1), ∴|2a -b |2=(2cos θ-3)2+(2sin θ+1)2=8+8(12sin θ-32cos θ)=8+8sin(θ-π3).又θ∈[0,π],∴θ-π3∈[-π3,2π3],∴sin(θ-π3)∈[-32,1], ∴|2a -b |2的最大值为16,∴|2a -b |的最大值为4. 又|2a -b |<m 恒成立,∴m >4.18.在△ABC 中,角A 、B 、C 所对的对边长分别为a 、b 、c .(1)设向量x =(sin B ,sin C ),向量y =(cos B ,cos C ),向量z =(cos B ,-cos C ),若z ∥(x +y ),求tan B +tan C 的值;(2)若sin A cos C +3cos A sin C =0,证明:a 2-c 2=2b 2. [解析] (1)x +y =(sin B +cos B ,sin C +cos C ), ∵z ∥(x +y ),∴cos B (sin C +cos C )+cos C (sin B +cos B )=0, 整理得tan C +tan B +2=0, ∴tan C +tan B =-2.(2)证明:∵sin A cos C +3cos A sin C =0,∴由正、余弦定理得:a ·a 2+b 2-c 22ab +3×b 2+c 2-a 22bc×c =0,∴a 2-c 2=2b 2.) 4223443 5B93 宓{29694 73FE 現26930 6932 椲21657 5499 咙 `l y。
高中数学第二章平面向量章末复习提升课课件b必修4b高一必修4数学课件

(2)若 A(x1,y1),B(x2,y2),则
|A→B|= (x2-x1)2+(y2-y1)2.
(3)若 a=(x1,y1),b=(x2,y2),θ 为 a 与 b 的夹角,
则 cos θ=|aa|·|bb|=
x1x2+y1y2 x21+y12 x22+y22
.
12/10/2021
第五页,共三十一页。
12/10/2021
第二十八页,共三十一页。
本部分 内容讲解结 (bù fen) 束
按ESC键退出(tuìchū)全屏播放
12/10/2021
第二十九页,共三十一页。
12/10/2021
第三十页,共三十一页。
内容(nèiróng)总结
第二章 平面(píngmiàn)向量
No Image
12/10/2021
12/10/2021
第十四页,共三十一页。
当点 D 的坐标为(2,1)时, 设A→C=pA→B+qA→D, 则(-2,1)=p(1,2)+q(3,1), 所以- 1=2= 2p+p+q.3q,所以pq= =- 1,1.所以A→C=A→B-A→D. 所以,当点 D 的坐标为(-2,3)时,A→C=-A→B+A→D; 当点 D 的坐标为(2,1)时,A→C=A→B-A→D.
12/10/2021
第十七页,共三十一页。
同理可得:|d|= 3.而 c·d=(2a-b)·(b-a)=3a·b-2a2-b2
=-92,设 θ 为 c 与 d 的夹角,
则 cos θ=|cc|·|dd|
= 2
-9 7×
3
=-3
21 14 .
12/10/2021
第十八页,共三十一页。
【点评】 对于非零向量 a=(a1,a2),b=(b1,b2),则 a⊥b⇔a·b
2020-2021学年人教A版必修4第二章平面向量综合测试卷(A)含答案(共3套)

必修4 第二章 向量(一)一、选择题:1.下列各量中不是向量的是 ( )A .浮力B .风速C .位移D .密度2.下列命题正确的是( )A .向量AB 与BA 是两平行向量B .若a 、b 都是单位向量,则a =bC .若AB =DC ,则A 、B 、C 、D 四点构成平行四边形 D .两向量相等的充要条件是它们的始点、终点相同3.在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 MC MB MA -+等于( )A .OB .MD 4C .MF 4D .ME 44.已知向量b a 与反向,下列等式中成立的是 ( )A .||||||b a b a -=-B .||||b a b a -=+C .||||||b a b a -=+D .||||||b a b a +=+5.在△ABC 中,AB =AC ,D 、E 分别是AB 、AC 的中点,则( )A .AB 与AC 共线 B .DE 与CB 共线 C .与相等D .与相等6.已知向量e 1、e 2不共线,实数x 、y 满足(3x -4y )e 1+(2x -3y )e 2=6e 1+3e 2,则x -y 的值等于( ) A .3 B .-3 C .0 D .2 7. 设P (3,-6),Q (-5,2),R 的纵坐标为-9,且P 、Q 、R 三点共线,则R 点的横坐标为 ( ) A .-9 B .-6 C .9 D .6 8. 已知a 3=,b 23=,a ⋅b =-3,则a 与b 的夹角是( )A .150︒B .120︒C .60︒D .30︒9.下列命题中,不正确的是( )A .a =2aB .λ(a ⋅b )=a ⋅(λb )C .(a -b )c =a ⋅c -b ⋅cD .a 与b 共线⇔a ⋅b =a b10.下列命题正确的个数是( ) ①=+0 ②0=⋅0③=-④(a ⋅b )c =a (b ⋅c )A .1B .2C .3D .411.已知P 1(2,3),P 2(-1,4),且12P P 2PP =,点P 在线段P 1P 2的延长线上,则P 点的坐标为( )A .(34,-35) B .(-34,35) C .(4,-5)D .(-4,5) 12.已知a 3=,b 4=,且(a +k b )⊥(a -k b ),则k 等于( )A .34±B .43±C .53±D .54±二、填空题13.已知点A(-1,5)和向量a ={2,3},若AB =3a ,则点B 的坐标为 . 14.若3=OA 1e ,3=OB 2e ,且P 、Q 是AB 的两个三等分点,则=OP ,=OQ . 15.若向量a =(2,-x )与b =(x, -8)共线且方向相反,则x= . 16.已知e 为一单位向量,a 与e 之间的夹角是120O ,而a 在e 方向上的投影为-2,则a = .三、解答题17.已知菱形ABCD 的边长为2,求向量AB -CB +CD 的模的长.18.设OA 、OB 不共线,P 点在AB 上.求证: OP =λOA +μOB 且λ+μ=1,λ、μ∈R .19.已知向量,,32,32212121e e e e e e 与其中+=-=不共线向量,9221e e -=,问是否存在这样的实数,,μλ使向量c b a d 与μλ+=共线20.i、j是两个不共线的向量,已知AB=3i+2j,CB=i+λj, CD=-2i+j,若A、B、D三点共线,试求实数λ的值.必修4 第二章 向量(一)必修4第三章向量(一)参考答案 一、选择题1.D 2.A 3.C 4.C 5.B 6. A 7. D 8.C 9.B 10.A 11.D 12.C 二、填空题 13.3 14.12e 2e +122e e + 15.4- 16.4三、解答题17.解析: ∵AB -CB +CD =AB +(CD -CB )=AB +BD =AD又|AD |=2 ∴|AB -CB +CD |=|AD |=218.证明: ∵P 点在AB 上,∴AP 与AB 共线.∴AP =t AB (t ∈R )∴OP =OA +AP =OA +t AB =OA +t (OB -OA )=OA (1-t )+ OB令λ=1-t ,μ=t ∴λ+μ=1∴OP =λOA +μOB 且λ+μ=1,λ、μ∈R19.解析:222,2,,.2339,k R k λμλμλμλμλμ+=⎧=-∈=-⎨-+=-⎩解之故存在只要即可.20.解析: ∵BD =CD -CB =(-2i +j )-(i +λj )=-3i +(1-λ)j∵A 、B 、D 三点共线,∴向量AB 与BD 共线,因此存在实数μ,使得AB =μBD , 即3i +2j =μ[-3i +(1-λ)j ]=-3μi +μ(1-λ)j ∵i 与j 是两不共线向量,由基本定理得:⎩⎨⎧=-=∴⎩⎨⎧=-=-312)1(33λμλμμ 故当A 、B 、D 三点共线时,λ=3.第二章平面向量(A 卷)(测试时间:120分钟 满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知向量a 与b 的夹角是120︒,且5a =, 4b =,则 a b ⋅=( ). A. 20 B. 10 C. 10- D. 20- 【答案】C【解析】向量a 与b 的夹角是120︒,且5a =, 4b =,则a b a b ⋅=⨯ 1cos12054102⎛⎫︒=⨯⨯-=- ⎪⎝⎭.故选:C .2.【2017届北京房山高三上期末】已知向量31,2BA ⎛⎫= ⎪ ⎪⎝⎭, ()0,1BC =,则向量BA 与BC 夹角的大小为( ) A.π6 B. π4 C. π3 D. 2π3【答案】C3.【2018届四川省成都市郫都区高三上期中】已知向量()11a =-,, ()12b =-,,则()2a b a +⋅=( ) A. 1- B. 0 C. 1 D. 2 【答案】C【解析】()()()21,01,11a b a +⋅=-=,故选:C. 4.已知向量,若,则实数m 的值为 ( ) A. 0 B. 2 C. D. 2或【答案】C 【解析】∵向量,且∴, ∴.选C.5.如上图,向量1e , 2e , a 的起点与终点均在正方形网格的格点上,则向量a 用基底1e , 2e 表示为( )A. 1e +2eB. 21e -2eC. -21e +2eD. 21e +2e 【答案】C6.若三点()1,2A --、()0,1B -、()5,C a 共线,则a 的值为( ) A. 4 B. 4- C. 2 D. 2- 【答案】A 【解析】()1,2A --, ()()0,1,5B C a -,三点共线ABACλ∴→=→即()()1162a λ=+,,()16{ 12a λλ==+ 16λ∴=, 4a = 故答案选A .7.【2018届全国名校大联考高三第二次联考】已知平面向量,a b 的夹角为60°,()1,3a =, 1b =,则a b +=( )A. 2B. 23C. 7D. 4 【答案】C8.已知向量a 与b 的夹角是120︒,且5a =, 4b =,则 a b ⋅=( ). A. 20 B. 10 C. 10- D. 20- 【答案】C【解析】向量a 与b 的夹角是120︒,且5a =, 4b =,则a b a b ⋅=⨯ 1cos12054102⎛⎫︒=⨯⨯-=- ⎪⎝⎭.故选:C .9.【2018届福建省福安市一中上学期高三期中】已知向量()()()3,1,0,1,,3a b c k ==-=,若(2a b -)与c 互相垂直,则k 的值为 A. 1 B. 1- C. 3 D. 3- 【答案】D 【解析】()23,3a b -=,因为(2a b -)与c 互相垂直,则()233303a b c k k -⋅=+=⇒=-,选D.10.【2018届河南省中原名校高三第三次考评】已知点()0,1A , ()1,2B , ()2,1C --, ()3,4D ,则向量AB 在CD 方向上的投影为( )A.322 B. 2 C. 322- D. 3152- 【答案】B【解析】()()1,1.5,5AB CD ==则向量AB 在CD 方向上的投影为10cos ,252AB CD AB AB CD AB AB CD⋅=⋅== 故选B.11.【2018届黑龙江省齐齐哈尔地区八校高三期中联考】在矩形ABCD 中, 3AB =, 3BC =,2BE EC =,点F 在边CD 上,若•3AB AF =,则•AE BF 的值为( )A. 0B. 833C. 4-D. 4 【答案】C【解析】12.【2018届河南省漯河市高级中学高三上期中】已知ABC ∆是边长为4的等边三角形, P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值为 ( ) A. 3- B. 6- C. 2- D. 83- 【答案】B【解析】如图建立坐标系, (()()0,23,2,0,2,0A B C -,设(),P x y ,则()()(),23,2,,2,PA x y PB x y PC x y =--=---=--,()()()22,232,22243PA PB PC x y x y x y ∴⋅+=-⋅--=+-()222366x y ⎡⎤=+--≥-⎢⎥⎣⎦, ∴最小值为6-,故选B.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设a 与b 是两个不共线向量,且向量a b λ+与2a b -共线,则λ=__________. 【答案】12-【解析】由题意得()11:2:12λλ=-∴=-. 14.【2018届河北省邢台市高三上学期第二次月考】已知单位向量a , b 满足()1•232a a b -=,则向量a 与b 的夹角为__________. 【答案】60°(或3π) 【解析】因为()1232a a b ⋅-=,化简得: 2123232a a b a b -⋅=-⋅=,即12a b ⋅=,所以1cos ,2a b a b a b⋅==⋅,又0,a b π≤≤,所以,3a b π=,故填3π. 15.【2018届福建省三明市第一中学高三上学期期中】在平行四边形ABCD 中, AC 与BD 交于点 O ,E 是线段OD 的中点, AE 的延长线与CD 交于点F . 若AC a =, BD b =,则AF 等于_______【答案】2133a b +【解析】∵AC a =, BD b =,∴11112222AD AC BD a b =+=+. ∵E 是OD 的中点,∴=,∴DF =AB .∴111111332266DF AB AC BD a b ⎛⎫==-=- ⎪⎝⎭, ∴111121226633AF AD DF a b a b a b =+=++-=+. 16.已知正方形ABCD 的边长为1,点E 在线段AB 边上运动(包含线段端点),则DE CB ⋅的值为__________; DE DB ⋅的取值范围为__________. 【答案】 1 []1,2【解析】如图,以D 为坐标原点,以DC , DA 分别为x , y 轴,建立平面直角坐标系, ()0,0D , ()0,1DE x , ()1,1B , ()0,1CB ,()1,0C , ()1,1DB , ()0,1E x , []00,1x ∈,∴1DE CB ⋅=, 01DE DB x ⋅=+,∵001x ≤≤,0112x ≤+≤,∴DE DB ⋅的取值范围为[]1,2,故答案为1, []1,2.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题10分)已知四点A (-3,1),B (-1,-2),C (2,0),D (23,4m m +) (1)求证: AB BC ⊥;【答案】(1)见解析(2) 12-或1 【解析】试题分析:(1)分别根据向量的坐标运算得出AB BC ,算出AB BC ⋅(2)由向量的平行进行坐标运算即可. 试题解析:(1)依题意得, ()()2,3,3,2AB BC =-= 所以()23320AB BC ⋅=⨯+-⨯= 所以AB BC ⊥.18.(本小题12分)已知向量()1,2a =,()3,4b =-. (1)求a b +与a b -的夹角; (2)若()a ab λ⊥+,求实数λ的值. 【答案】(1)34π;(2)1-. 【解析】(1)因为()1,2a =,()3,4b =-,所以()2,6a b +=-,()4,2a b -=- 所以2,64,22cos ,240204020a b a b -⋅-+-===-⨯⨯,由[],0,a b a b π+-∈,则3,4a b a b π+-=; (2)当()a ab λ⊥+时,()0a a b λ⋅+=,又()13,24a b λλλ+=-+,所以13480λλ-++=,解λ=-.得:119.(本小题12分)已知是夹角为的两个单位向量,,.(1)求;(2)求与的夹角.【答案】(1) ;(2) 与的夹角为.【解析】试题分析:(1)向量点积的运算规律可得到再展开根据向量点积公式得最终结果;(2)同第一问,由向量点积公式展开=0.∵是夹角为的两个单位向量,∴,(1)(2) ,,∴,∴与的夹角为.20.(本小题12分)如图,在平行四边形中,,是上一点,且. (1)求实数的值;(2)记,,试用表示向量,,.【答案】(1);(2),,.【解析】试题分析:(1)根据平面向量共线定理得到,由系数和等于1,得到即。
2021_2022学年新教材高中数学第2章平面向量及其应用章末综合提升学案含解析北师大版必修第二册

第2章 平面向量及其应用类型1 向量的线性运算及应用1.要熟练掌握向量的有关概念,平行向量定理,平面向量基本定理,用基表示向量,三角形法则,平行四边形法则,这是向量线性运算的基础.2.向量是一个有“形”的几何量,因此在研究向量的有关问题时,一定要结合图形进行分析判断求解,这是研究平面向量的重要方法和技巧.【例1】 (1)已知O 是△ABC 的重心,点P 满足OP →=13⎝ ⎛⎭⎪⎫12OA →+12OB →+2OC →,则点P 一定是△ABC 的( )A .重心B .AB 边的中点C .AB 边中线的中点D .AB 边中线的非重心的三等点(2)若向量a =(1,1),b =(-1,1),c =(4,2),则c =( ) A .3a +b B .3a -b C .-a +3bD .a +3b(1)D (2)B [(1)取AB 中点M ,连接CM , 因为M 是AB 的中点,所以OM →=12()OA →+OB →,所以OP →=13⎝ ⎛⎭⎪⎫12OA →+12OB →+2OC →=13(OM →+2OC →),即13()OP →-OM→=23()OC →-OP→,即MP →=2PC →,由此可得,C ,P ,M 三点共线,且|MP →|=2|PC →|, 所以点P 是△ABC 的AB 边中线的非重心的三等点. (2)设c =x a +y b ,则⎩⎪⎨⎪⎧x -y =4,x +y =2,∴⎩⎪⎨⎪⎧x =3,y =-1.∴c =3a -b .] [跟进训练]1.(1)已知O 为直线AB 外任意一点,且OP →=λOA →+μOB →(λ,μ∈R ),若点P 在直线AB 上,则λ+μ=________.(2)已知向量OA →=(3,-4),OB →=(6,-3),OC →=(5-m ,-3-m ),若点A 、B 、C 能构成三角形,则实数m 满足的条件是________.(1)1 (2)m ≠12 [(1)∵点P 在直线AB 上,∴AP →∥AB →,设AP →=xAB →,∵AP →=OP →-OA →,AB →=OB →-OA →, ∴OP →-OA →=x (OB →-OA →), ∴OP →=(1-x )OA →+xOB →. 又OP →=λOA →+μOB →, ∴λ=1-x ,μ=x , ∴λ+μ=1.(2)因为OA →=(3,-4),OB →=(6,-3),OC →=(5-m ,-3-m ), 所以AB →=(3,1),BC →=(-m -1,-m ).由于点A 、B 、C 能构成三角形,所以AB →与BC →不共线, 而当AB →与BC →共线时,有3-m -1=1-m ,解得m =12,故当点A 、B 、C 能构成三角形时,实数m 满足的条件是m ≠12.]类型2 向量的数量积运算及应用 求两个向量数量积的方法1.如果无法寻找到计算数量积的要素(模与夹角),那么可考虑用一组基将a ,b 两个向量表示出来,再进行运算.这是在几何图形中处理向量数量积的一个重要方法.2.若几何图形易于建系,则考虑将向量坐标化,用数量积的坐标表示来计算数量积. 3.根据数量积的几何意义求数量积,通常适用于处理几何图形中的向量问题.(1)图形中出现与所求数量积相关的垂直条件,例如:直角三角形,菱形对角线,三角形的外心等,可考虑用投影法计算数量积.(2)在求数量积的范围中,如果所求数量积中的向量中有一个模是定值,则可以考虑利用投影,从而将问题转化为寻找投影数量最大与最小的问题.【例2】 已知正方形ABCD 的边长为1,点E 是AB 边上的动点,求DE →·CB →的值与DE →·DC →的最大值.[解] 法一:以D 为坐标原点,建立平面直角坐标系如图所示. 则D (0,0),A (1,0),B (1,1),C (0,1), 设E (1,a )(0≤a ≤1).所以DE →·CB →=(1,a )·(1,0)=1,DE →·DC →=(1,a )·(0,1)=a ≤1, 故DE →·DC →的最大值为1.法二:由图知,无论E 点在哪个位置, DE →在CB →方向上的投影数量都是CB =1, ∴DE →·CB →=|CB →|·1=1,当E 运动到B 点时,DE →在DC →方向上的投影数量最大即为DC =1, ∴(DE →·DC →)max =|DC →|·1=1. [跟进训练]2.(1)如图所示,在平面四边形ABCD 中,若AC =3,BD =2,则(AB →+DC →)·(AC →+BD →)=________;(2)已知直角梯形ABCD 中,AD ∥BC ,∠ADC =90°,AD =2,BC =1,P 是腰DC 上的动点,则|PA →+3PB →|的最小值为________.(1)5 (2)5 [(1)因为AB →=AC →+CB →,DC →=DB →+BC →,所以AB →+DC →=AC →+CB →+DB →+BC →=AC →-BD →.所以(AB →+DC →)·(AC →+BD →)=(AC →-BD →)·(AC →+BD →)=|AC →|2-|BD →|2=9-4=5.(2)以D 为原点,分别以DA 、DC 所在直线为x 、y 轴建立如图所示的平面直角坐标系,设DC =a ,DP =x .∴D (0,0),A (2,0),C (0,a ),B (1,a ),P (0,x ),PA →=(2,-x ), PB →=(1,a -x ),∴PA →+3PB →=(5,3a -4x ),|PA →+3PB →|2=25+(3a -4x )2≥25,∴|PA →+3PB →|的最小值为5.]类型3 平面向量与三角形的“四心”在平面向量的应用中,用平面向量解决平面几何问题时,首先将几何问题中的几何元素和几何关系用向量表示,然后选择适当的基,先将相关向量表示为基向量的线性组合,再把问题转化为基向量的运算问题,最后将运算的结果再还原为几何关系.【例3】 (1)已知A ,B ,C 是平面上不共线的三点,O 为坐标原点,动点P 满足OP →=13[(1-λ)OA →+(1-λ)OB →+(1+2λ)·OC →],λ∈R ,则点P 的轨迹一定经过( )A .△ABC 的内心B .△ABC 的垂心 C .△ABC 的重心D .AB 边的中点(2)已知在△ABC 中,AB =1,BC =6,AC =2,点O 为△ABC 的外心,若AO →=xAB →+yAC →,则x =________,y =________.(1)C (2)45 35[(1)取AB 的中点D ,则2OD →=OA →+OB →,∵OP →=13[(1-λ)OA →+(1-λ)OB →+(1+2λ)OC →],∴OP →=13[2(1-λ)OD →+(1+2λ)OC →]=2(1-λ)3OD →+1+2λ3OC →,而2(1-λ)3+1+2λ3=1,∴P ,C ,D 三点共线, ∴点P 的轨迹一定经过△ABC 的重心.(2)取AB 的中点M 和AC 的中点N ,连接OM ,ON (图略),则OM →⊥AB →,ON →⊥AC →, OM →=AM →-AO →=12AB →-(xAB →+yAC →)=⎝ ⎛⎭⎪⎫12-x AB →-yAC →,ON →=AN →-AO →=12AC →-(xAB →+yAC →)=⎝ ⎛⎭⎪⎫12-y AC→-xAB →. 由OM →⊥AB →,得⎝ ⎛⎭⎪⎫12-x AB →2-yAC →·AB →=0,① 由ON →⊥AC →,得⎝ ⎛⎭⎪⎫12-y AC →2-xAC →·AB →=0,②又因为BC →2=(AC →-AB →)2=AC →2-2AC →·AB →+AB →2, 所以AC →·AB →=AC →2+AB →2-BC →22=-12,③把③代入①、②得⎩⎪⎨⎪⎧1-2x +y =0,4+x -8y =0,解得x =45,y =35.][跟进训练]3.(1)已知O 是平面上的一个定点,A ,B ,C 是平面上不共线的三个点,动点P 满足AP →=λ⎝ ⎛AB→|AB →|cos B+⎭⎪⎪⎫AC→|AC →|cos C ,λ∈(0,+∞),则动点P 的轨迹一定通过△ABC 的( )A .重心B .垂心C .外心D .内心(2)已知△ABC 的角A ,B ,C 所对的边分别是a ,b ,c ,且aOA →+bOB →+cOC →=0. 求证:O 为△ABC 的内心.(1)B [因为AP →=λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|cos B +AC →|AC →|cos C , 所以BC →·AP →=BC →·λ⎝ ⎛⎭⎪⎪⎫AB→|AB →|cos B +AC→|AC →|cos C =λ(-|BC →|+|BC →|)=0,所以BC →⊥AP →,所以点P 在BC 的高线上,即动点P 的轨迹一定通过△ABC 的垂心.](2)[证明] OB →=OA →+AB →,OC →=OA →+AC →,则由题意得()a +b +c OA →+bAB →+cAC →=0. 又因为bAB →+cAC →=bc ⎝ ⎛⎭⎪⎫AB →c +AC →b ,所以AO →=bc a +b +c ⎝ ⎛⎭⎪⎫AB →c +AC →b , 因为AB →c 与AC→b分别是AB →与AC →方向上的单位向量,所以AO →是∠BAC 平分线的方向向量,即AO 平分∠BAC , 同理BO 平分∠ABC ,CO 平分∠ACB , 所以O 为△ABC 的内心.类型4 余、正弦定理与向量的综合应用 1.余弦定理及其变形a 2=b 2+c 2-2bc cos A ;cos A =b 2+c 2-a 22bc;b 2+c 2-a 2=2bc cos A ;2.正弦定理及其变形a =2R sin A ;sin A =a2R;a sin B =b sin A .【例4】 在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若AB →·AC →=BA →·BC →=1. (1)求证:A =B ; (2)求边长c 的值;(3)若|AB →+AC →|=6,求△ABC 的面积. [解] (1)证明:∵AB →·AC →=BA →·BC →,∴bc cos A =ac cos B ,即b cos A =a cos B .由余弦定理得b ·b 2+c 2-a 22bc =a ·a 2+c 2-b 22ac,整理得a 2=b 2, ∴a =b .∴A =B .(2)∵AB →·AC →=1,∴bc cos A =1.由余弦定理得bc ·b 2+c 2-a 22bc=1,即b 2+c 2-a 2=2.∵由(1)得a =b ,∴c 2=2,∴c = 2. (3)∵|AB →+AC →|=6,∴|AB →|2+|AC →|2+2AB →·AC →=6.即c 2+b 2+2=6, ∴c 2+b 2=4.∵c 2=2,∴b 2=2,b = 2. ∴△ABC 为正三角形, ∴S △ABC =34×(2)2=32. [跟进训练]4.在△ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 的面积是△ADC 面积的2倍. (1)求sin Bsin C ;(2)若AD =1,DC =22,求BD ,AC 的长. [解] (1)S △ABD =12AB ·AD ·sin ∠BAD ;S △ADC =12AC ·AD ·sin ∠CAD ,∵S △ABD =2S △ADC ,∠BAD =∠CAD , ∴S △ABD S △ADC =ABAC=2,∴sin B sin C =AC AB =12. (2)S △ABD S △ADC =BDDC=2, ∴BD =2DC = 2.在△ABD ,△ADC 中,由余弦定理可得:⎩⎪⎨⎪⎧AB 2=AD 2+BD 2-2AD ·BD cos ∠ADB AC 2=AD 2+CD 2-2AD ·CD cos ∠ADC ∴AB 2+2AC 2=3AD 2+BD 2+2DC 2=6, 再由AB =2AC 可解得AC =1.1.(2020·全国Ⅲ卷)已知向量a ,b 满足|a|=5,|b|=6,a ·b =-6,则cos 〈a ,a +b 〉=( )A .-3135B .-1935C .1735D .1935D [由题意,得a ·(a +b )=a 2+a ·b =25-6=19,|a +b |=a 2+2a ·b +b 2=25-12+36=7,所以cos 〈a ,a +b 〉=a ·(a +b )|a ||a +b |=195×7=1935,故选D.]2.(2020·新高考全国Ⅰ卷)已知P 是边长为2的正六边形ABCDEF 内的一点,则AP →·AB →的取值范围是( )A .(-2,6)B .(-6,2)C .(-2,4)D .(-4,6)A [AP →·AB →=|AP →|·|AB →|·cos ∠PAB =2|AP →|cos ∠PAB ,又|AP →|cos ∠PAB 表示AP →在AB →方向上的投影,所以结合图形可知,当P 与C 重合时投影最大,当P 与F 重合时投影最小.又AC →·AB →=23×2×cos 30°=6,AF →·AB →=2×2×cos 120°=-2,故当点P 在正六边形ABCDEF 内部运动时,AP →·AB →∈(-2,6),故选A.]3.(2020·全国Ⅰ卷)设a ,b 为单位向量,且|a +b |=1,则|a -b |=________. 3 [∵a ,b 为单位向量,且|a +b |=1,∴(a +b )2=1,∴1+1+2a ·b =1,∴a ·b =-12,∴|a -b |2=a 2+b 2-2a ·b =1+1-2×⎝ ⎛⎭⎪⎫-12=3,∴|a -b |= 3.] 4.(2020·全国Ⅱ卷)已知单位向量a ,b 的夹角为45°,k a -b 与a 垂直,则k =________.22 [由题意,得a ·b =|a|·|b|cos 45°=22.因为向量k a -b 与a 垂直,所以(k a -b )·a =k a 2-a ·b =k -22=0,解得k =22.] 5.(2020·北京卷)已知正方形ABCD 的边长为2,点P 满足AP →=12(AB →+AC →),则|PD →|=________;PB →·PD →=________.5 -1 [法一:如图,由题意及平面向量的平行四边形法则可知,点P 为BC 的中点,在三角形PCD 中,|PD →|= 5.cos ∠DPB =-cos ∠DPC =-15,∴PB →·PD →=|PB →|·|PD →|cos ∠DPB =1×5×⎝⎛⎭⎪⎫-15=-1.法二:以A 为坐标原点,AB ,AD 所在直线分别为x 轴,y 轴,建立如图所示的平面直角坐标系,则A (0,0),B (2,0),C (2,2),D (0,2),∴AP →=12(AB →+AC →)=(2,1),P (2,1),∴PD →=(-2,1),PB →=(0,-1),∴|PD →|=5,PB →·PD →=(0,-1)·(-2,1)=-1.]。
(全国通用版)2020高中数学 第二章 平面向量 2.2 平面向量的线性运算 2.2.2 向量减法运算及其几何意义课

『规律总结』 解此类问题要根据图形的几何性质,运用向量的平行四边 形法则和三角形法则解题.要特别注意向量的方向以及运算式中向量之间的关 系.
〔跟踪练习 2〕 如图所示,解答下列各题: (1)用 a、d、e 表示D→B; (2)用 b、c 表示D→B; (3)用 a、b、e 表示E→C; (4)用 c、d 表示E→C.
『规律总结』 掌握向量加、减法的定义及向量加法的交换律、结合律等基 础知识,可以将杂乱的向量运算有序化处理,进行向量的加减运算时,常用的变 形如下:
(1)运用A→B=-B→A化减为加; (2)运用A→B+B→A=0 或A→B+B→C=A→C化繁为简; (3)运用A→B=O→B-O→A转化为共起点的两个向量的差.
〔跟踪练习 4〕如图所示,已知 O 为平行四边形 ABCD 内一点,O→A=a,O→B =b,O→C=c,求O→D.
[解析] B→C=O→C-O→B=c-b,又A→D=B→C,∴A→D=c-b, ∴O→D=O→A+A→D=a+c-b.
1.下列等式:①0-a=-a;②-(-a)=a;
③a+(-a)=0;④a+0=a;⑤a-b=a+(-b);
[解析] (1)D→B=D→E+E→A+A→B =d+e+a=a+d+e. (2)D→B=C→B-C→D=-B→C-C→D=-b-c. (3)E→C=E→A+A→B+B→C=a+b+e. (4)E→C=-C→E=-(C→D+D→E)=-c-d.
向量加减法的综合运用
典例 3 已知 O 为四边形 ABCD 所在平面外的一点,且向量O→A,O→B,O→C, O→D满足O→A+O→C=O→B+O→D,则四边形 ABCD 的形状为___平__行__四__边__形___.
命题方向2 ⇨利用已知向量表示其他向量
2020_2021学年高中数学第二章平面向量2.3.1平面向量基本定理训练含解析新人教A版必修4

第二章 平面向量2.3 平面向量的基本定理及坐标表示2.3.1 平面向量基本定理 [A 组 学业达标]1.若k 1a +k 2b =0,则k 1=k 2=0,那么下面关于向量a ,b 的判断正确的是( )A .a 与b 一定共线B .a 与b 一定不共线C .a 与b 垂直D .a 与b 中至少有一个为0解析:由平面向量基本定理可知,当a ,b 不共线时,k 1=k 2=0. 答案:B2.如图所示,平面内的两条相交直线OP 1和OP 2将该平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包括边界).若OP →=aOP 1→+bOP 2→,且点P 落在第Ⅲ部分,则实数a ,b 满足 ( )A .a >0,b >0B .a >0,b <0C .a <0,b >0D .a <0,b <0解析:取第Ⅲ部分内一点画图易得a >0,b <0. 答案:B3.如果e 1,e 2是平面α内两个不共线的向量,那么在下列各命题中不正确的有( )①λe 1+μe 2(λ,μ∈R )可以表示平面α内的所有向量;②对于平面α内的任一向量a ,使a =λe 1+μe 2的实数λ,μ有无数多对;③若向量λ1e 1+μ1e 2与λ2e 1+μ2e 2共线,则有且只有一个实数λ,使λ1e 1+μ1e 2=λ(λ2e 1+μ2e 2);④若实数λ,μ使λe 1+μe 2=0,则λ=μ=0. A .①② B .②③ C .③④D .②解析:由平面向量基本定理可知,①④是正确的;对于②,由平面向量基本定理可知,一旦一个平面的基底确定,那么任意一个向量在此基底下的实数对是唯一的;对于③,当两向量的系数均为零,即λ1=λ2=μ1=μ2 =0时,这样的λ有无数个.故选B. 答案:B4.在△ABC 中,点D 在BC 边上,且BD →=2DC →,设AB →=a ,AC →=b ,则AD →可用基底a ,b 表示为 ( )A.12(a +b ) B.23a +13b C.13a +23b D.13(a +b ) 解析:∵BD →=2DC →,∴BD →=23BC →.∴AD →=AB →+BD →=AB →+23BC →=AB →+23(AC →-AB →)=13AB →+23AC →=13a +23b .答案:C5.设向量m =2a -3b ,n =4a -2b ,p =3a +2b ,试用m ,n 表示p ,p =________.解析:设p =x m +y n ,则3a +2b =x (2a -3b )+y (4a -2b )=(2x +4y )a +(-3x -2y )b ,得⎩⎪⎨⎪⎧2x +4y =3,-3x -2y =2,解得⎩⎨⎧x =-74,y =138.所以p =-74m +138n .答案:-74m +138n6.已知向量e 1,e 2不共线,实数x ,y 满足(3x -4y )e 1+(2x -3y )e 2=6e 1+3e 2,则x -y =________.解析:∵e 1,e 2不共线,∴⎩⎪⎨⎪⎧3x -4y =6,2x -3y =3,解得⎩⎪⎨⎪⎧x =6,y =3,∴x -y =3.答案:37.设D ,E 分别是△ABC 的边AB ,BC 上的点,AD =12AB ,BE =23BC .若DE →=λ1AB →+λ2AC →(λ1,λ2为实数),则λ1+λ2=________.解析:易知DE →=12AB →+23BC →=12AB →+23(AC →-AB →)=-16AB →+23AC →,所以λ1+λ2=12.答案:128.在梯形ABCD 中,AB ∥CD ,M ,N 分别是DA ,BC 的中点,且DC AB=k (k ≠1).设AD →=e 1,AB →=e 2,选择基底{e 1,e 2},试写出下列向量在此基底下的分解式:DC →,BC →,MN →. 解析:如图,∵AB →=e 2,且DC AB=k ,∴DC →=kAB →=k e 2.又∵AB →+BC →+CD →+DA →=0,∴BC →=-AB →-CD →-DA →=-AB →+DC →+AD →=-e 2+k e 2+e 1=e 1+(k -1)e 2. ∵MN →+NB →+BA →+AM →=0,∴MN →=-NB →-BA →-AM →=BN →+AB →-AM →=12BC →+e 2-12AD →=12[e 1+(k -1)e 2]+e 2-12e 1=k +12e 2. 9.在△ABC 中,点M 是BC 的中点,点N 在AC 上且AN →=2NC →,AM 交BN 于P 点,求AP与AM 的比值.解析:设BM →=a ,CN →=b ,则AM →=AC →+CM →=-a -3b ,BN →=2a +b . ∵A ,P ,M 和B ,P ,N 分别共线, ∴存在实数λ,μ使AP →=λAM →=-λa -3λb , BP →=μBN →=2μa +μb .∴BA →=BP →-AP →=(λ+2μ)a +(3λ+μ)b . 又∵BA →=BC →+CA →=2a +3b ,由平面向量基本定理得⎩⎪⎨⎪⎧λ+2μ=2,3λ+μ=3,解得⎩⎨⎧λ=45,μ=35,则AP →=45AM →.∴AP 与AM 的比值为45.[B 组 能力提升]10.若OP 1→=a ,OP 2→=b ,P 1P →=λPP 2→(λ≠-1),则OP →=( )A .a +λbB .λa +bC .λa +(1+λ)bD.a +λb 1+λ解析:∵P 1P →=λPP 2→,∴OP →-OP 1→=λ(OP 2→-OP →),(1+λ)OP →=λOP 2→+OP 1→,∴OP →=a +λb1+λ.答案:D11.如图,在△ABC 中,D ,E 分别为AB ,AC 的中点,CD 与BE 交于点F ,设AB →=a ,AC →=b ,AF →=m a +n b ,则m +n =( )A .1 B.43 C.23D.56解析:AF →=mAB →+nAC →=mAB →+2nAE →, 由B ,F ,E 三点共线,得m +2n =1,① AF →=mAB →+nAC →=2mAD →+nAC →, 由C ,F ,D 三点共线,得2m +n =1,② ①+②得3(m +n )=2,m +n =23.答案:C12.设G 为△ABC 的重心,O 为坐标原点,OA →=a ,OB →=b ,OC →=c ,试用a ,b ,c 表示OG →,则OG →=________.解析:OG →=OC →+CG →=OC →+13(CA →+CB →)=OC →+13(OA →-OC →+OB →-OC →)=13(a +b +c ).答案:13(a +b +c )13.在平行四边形ABCD 中,AB →=e 1,AC →=e 2,NC →=14AC →,BM →=12MC →,则MN →=________.(用e 1,e 2表示)解析:如图,MN →=CN →-CM →=CN →+2BM →=CN →+23BC →=-14AC →+23(AC →-AB →)=-14e 2+23(e 2-e 1)=-23e 1+512e 2.答案:-23e 1+512e 214.已知△ABC 内一点P 满足AP →=λAB →+μAC →,若△P AB 的面积与△ABC 的面积之比为1∶3,△P AC 的面积与△ABC 的面积之比为1∶4,求实数λ,μ的值.解析:如图,过点P 作PM ∥AC ,PN ∥AB ,则AP →=AM →+AN →,所以AM →=λAB →,AN →=μAC →.作PG ⊥AC 于点G ,BH ⊥AC 于点H . 因为S △P AC S △ABC =14,所以PG BH =14.又因为△PNG ∽△BAH ,所以PG BH =PN AB =14,即AM AB =14,所以λ=14,同理μ=13. 15.如图,已知三点O ,A ,B 不共线,且OC →=2OA →,OD →=3OB →,设OA →=a ,OB →=b .(1)试用a ,b 表示向量OE →;(2)设线段AB ,OE ,CD 的中点分别为L ,M ,N ,试证明:L ,M ,N 三点共线.解析:(1)∵B ,E ,C 三点共线, ∴OE →=xOC →+(1-x )OB →=2x a +(1-x )b .①同理,∵A ,E ,D 三点共线,∴OE →=y a +3(1-y )b .②比较①②,得⎩⎪⎨⎪⎧2x =y ,1-x =3(1-y ),解得x =25,y =45,∴OE →=45a +35b .(2)证明:∵OL →=a +b 2,OM →=12OE →=4a +3b 10,ON →=12(OC →+OD →)=2a +3b 2,∴MN →=ON →-OM→=6a +12b 10,ML →=OL →-OM →=a +2b10, ∴MN →=6ML →,又MN →与ML →有公共点M , ∴L ,M ,N 三点共线.。
2020-2021学年数学4教师用书:第2章 §3 3.2平面向量基本定理含解析

2020-2021学年北师大版数学必修4教师用书:第2章§3 3.2平面向量基本定理含解析3。
2平面向量基本定理学习目标核心素养1.了解平面向量基本定理及其意义.(重点)2。
能应用平面向量基本定理解决一些实际问题.(难点)1。
通过学习平面向量基本定理,提升数学抽象素养.2。
通过平面向量基本定理解决实际问题,培养直观想象素养.平面向量基本定理如果e1,e2(如图①所示)是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,存在唯一一对实数λ1,λ2,使a=λ1e1+λ2e2(如图②所示),其中不共线的向量e1,e2叫作表示这一平面内所有向量的一组基底.思考:若存在λ1,λ2∈R,μ1,μ2∈R,且a=λ1e1+λ2e2,a=μ1e1+μ2e2,那么λ1,μ1,λ2,μ2有何关系?[提示]由已知得λ1e1+λ2e2=μ1e1+μ2e2,即(λ1-μ1)e1=(μ2-λ2)e2.∵e1与e2不共线,∴λ1-μ1=0,μ2-λ2=0,∴λ1=μ1,λ2=μ2.1.设e1,e2是同一平面内两个不共线的向量,以下各组向量中不能作为基底的是()A.e1,e2B.e1+e2,3e1+3e2C.e1,5e2D.e1,e1+e2[答案]B2.设O为平行四边形ABCD的对称中心,错误!=4e1,错误!=6e2,则2e1-3e2等于()A.错误!B.错误!C.错误!D.错误!B[如图,错误!=错误!错误!=错误!(错误!-错误!)=2e1-3e2。
]3.已知向量a与b是一组基底,实数x,y满足(3x-4y)a +(2x-3y)b=6a+3b,则x-y=________.3[由原式可得错误!解得错误!所以x-y=3.]4.已知向量a与b不共线,且错误!=a+4b,错误!=-a+9b,错误!=3a-b,则共线的三点为________.A,B,D[错误!=错误!+错误!=-a+9b+3a-b=2a+8b,因为错误!=a+4b,所以错误!=错误!错误!,所以A,B,D三点共线.]对向量基底的理解【例1】设O是平行四边形ABCD两对角线的交点,给出下列向量组:①错误!与错误!;②错误!与错误!;③错误!与错误!;④错误!与错误!,其中可作为这个平行四边形所在平面的一组基底的是() A.①②B.①③C.①④D.③④B[①错误!与错误!不共线;②错误!=-错误!,则错误!与错误!共线;③错误!与错误!不共线;④错误!=-错误!,则错误!与错误!共线.由平面向量基底的概念知,只有不共线的两个向量才能构成一组基底,故①③满足题意.]考查两个向量是否能构成基底,主要看两向量是否非零且不共线.此外,一个平面的基底一旦确定,那么平面上任意一个向量都可以由这个基底唯一线性表示出来.1.设e1,e2是平面内一组基向量,且a=e1+2e2,b=-e1+e2,则向量e1+e2可以表示为另一组基向量a,b的线性组合,即e1+e2=________a+________b。
高中数学 第二章 平面向量章末归纳提升课件 新人教版

如图所示,M、N 分别是平行四边形 ABCD 的对边 AD、 BC 的中点,且 AD=2AB.求证:四边形 PMQN 为矩形.
图 2-2
【证明】 设B→A=a,B→N=b, 由 M、N 分别是平行四边形 ABCD 的对边 AD、BC 的中 点,且 AD=2AB,得|a|=|b|,N→A=a-b,C→M=a-b, 故N→A=C→M,所以 NA∥CM. 又B→M=a+b,N→D=a+b, 所以B→M=N→D,所以 BM∥ND. 从而四边形 PMQN 是平行四边形. 又由B→M·N→A=(a+b)·(a-b)=a2-b2=0, 故B→M⊥N→A,即 BM⊥NA. 所以四边形 PMQN 为矩形.
已知 P 是边长为 2 的正三角形 ABC 的边 BC 上的动点,
则A→P·(A→B+A→C)( )
A.最大值为 8
B.是定值 6
C.最小值为 2
D.与 P 的位置有关
【解析】 如图,∵A→B+A→C= A→D=2A→O,△ABC 为正三角形, ∴四边形 ABDC 为菱形, BC⊥AO, ∴A→P在向量A→D上的射影为A→O,又|A→O|= 3, ∴A→P·(A→B+A→C)=|A→O|·|A→D|=6,故选 B. 【答案】 B
(2)由已知得P→B=(3,1)-(2,y)=(1,1-y), B→D=(-4,-3)-(3,1)=(-7,-4). 又P→B=λB→D, ∴(1,1-y)=λ(-7,-4), 则11=--y=7-λ,4λ,
∴λy==-37. 17,
设 a=( 3,-1),b=(12, 23),若存在不同时为零的实 数 k 和 t,使 x=a+(t-3)b,y=-ka+tb,且 x⊥y.
1.向量的加法、减法和数乘向量的综合运算通常叫作向 量的线性运算.
2020-2021学年北师大版数学必修4课件:阶段提升课 第三课 平面向量

则点O是△ABC的( )
A.外心
B.内心
C.垂心
D.重心
【方法技巧】 利用向量解决几何问题的常用思路 把已知问题转化为向量的形式,再通过相应的向量运算去完成,同时,引入平面 向量的坐标可以使向量的运算代数化,让平面向量的坐标成为数与形的载体.
阶段提升课 第三课 平 面 向 量
思维导图·构建网络
考点整合·素养提升
题组训练一 平面向量数量积的运算
1.△ABC的外接圆半径为1,圆心为O,且 3OA 4OB 5OC =0,则 OC Aห้องสมุดไป่ตู้ 的值为
()
A. 1
B. 1
C. 6
D. 6
5
5
5
5
【解析】选A.由已知得 4OB 3OA 5OC ⇒ 4OB 2 ( 3OA 5OC)2,
即16=34+3O0A OC,解得 OA=OC
3 ;同理3OA 4OB 5OC,解得OB OC 4 ,
5
5
因此 OC AB OC(OB OA) OC OB OC OA 1 .
5
2.已知|a|=1,|b|= 2 . (1)若a∥b,求a·b. (2)若a,b的夹角为60 °,求|a+b|. (3)若(2a-b)⊥b,求a与b的夹角.
3.已知向量a=(1,2),b=(1,0),c=(3,4).若λ为实数,(a+λb)∥c,则λ= ( )
A. 1 B. 1 C.1 D.2
4
2
【解析】选B.因为向量a=(1,2),b=(1,0),可得a+λb=(1+λ,2),由(a+λb)∥c
得(1+λ)×4-3×2=0,所以λ= 1.
2
【方法技巧】 1.证明共线问题常用的方法 (1)向量a,b(a≠0)共线⇔存在唯一实数λ使b=λa. (2)向量a=(x1,y1),b=(x2,y2)共线⇔x1y2-x2y1=0. (3)向量a与b共线⇔|a·b|=|a||b|. (4)向量a与b共线⇔存在不全为零的实数λ1,λ2,使λ1a+λ2b=0. 2.证明平面向量垂直问题的常用方法 a⊥b⇔a·b=0⇔x1x2+y1y2=0,其中a=(x1,y1),b=(x2,y2).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阶段强化训练(三)一、选择题1.如图所示,若向量AB →=a ,AC →=b ,CD →=c ,则向量BD →可以表示为( )A .a +b -cB .a -b +cC .b -a +cD .b +a -cC [BD →=AD →-AB →=AC →+CD →-AB →=b +c -a =b -a +c .] 2.若a =(1,2),b =(-3,0),(2a +b )⊥(a -m b ),则m =( ) A .-73B.73 C .2D .-2B [因为a =(1,2),b =(-3,0),所以2a +b =(-1,4),a -m b =(1+3m,2), 由2a +b 与a -m b 垂直, 得-1-3m +8=0,解得m =73.]3.已知平面向量a ,b 夹角为π3,且|a |=1,|b |=12,则|a -2b |=( )A .1 B. 3 C .2D.32A [根据条件:a ·b =1×12×12=14,∴(a -2b )2=a 2-4a ·b +4b 2=1-4×14+4×14=1,∴|a -2b |=1.]4.已知向量a 与b 不共线,AB →=a +m b ,AC →=n a +b (m ,n ∈R ),则AB →与AC →共线的条件是( )A .m +n =0B .m -n =0C .mn +1=0D .mn -1=0D [由AB →=a +m b ,AC →=n a +b ,(m ,n ∈R )共线得a +m b =λ(n a +b ),即mn -1=0.故选D.]5.若向量a =(1,1),b =(1,-1),c =(-1,2),则c =( ) A .-12a +32bB.12a -32b C.32a -12b D .-32a +12bB [设c =x a +y b ,则 (-1,2)=x (1,1)+y (1,-1) =(x +y ,x -y ),∴⎩⎪⎨⎪⎧x +y =-1,x -y =2,解得⎩⎪⎨⎪⎧x =12,y =-32,∴c =12a -32b .]二、填空题6.如图所示,在边长为3的正方形ABCD 中,AC 与BD 交于F ,AE =13AD ,则EF →·BD→=________.-3 [建立平面直角坐标系如图所示,则A (0,0),B (3,0),C (3,3),D (0,3),E (0,1),F ⎝ ⎛⎭⎪⎫32,32,则EF →·BD →=⎝ ⎛⎭⎪⎫32,12·(-3,3)=32×(-3)+12×3=-3.]7.已知a =(1,-2),b =(4,2),设2a 与a -b 的夹角为θ,则cos θ=________. 55[2a =2(1,-2)=(2,-4), a -b =(1,-2)-(4,2)=(-3,-4),cos θ=2a ·a -b |2a ||a -b |=-6+1620×5=55.]8.设向量m =2a -3b ,n =4a -2b ,p =3a +2b ,且a 与b 不共线,若用m ,n 表示p ,则p =________.-74m +138n [设p =x m +y n ,则p =x (2a -3b )+y (4a -2b )=(2x +4y )a +(-3x -2y )b =3a +2b ,又∵a 与b 不共线,∴⎩⎪⎨⎪⎧2x +4y =3,-3x -2y =2,解得⎩⎪⎨⎪⎧x =-74,y =138,故p =-74m +138n .]三、解答题9.如图,▱ABCD 的两条对角线交于M .且AC →=a ,BD →=b .(1)用a ,b 表示AB →与AD →;(2)对于平面上任一点O ,若OA →+OB →+OC →+OD →=kOM →,求k 的值. [解] (1)在▱ABCD 中,AB →+AD →=AC →=a .① AD →-AB →=BD →=b .②①+②得2AD →=a +b , ①-②得2AB →=a -b , 所以AD →=12(a +b )=12a +12b ,AB →=12(a -b )=12a -12b .(2)因为OA →+OB →+OC →+OD →=kOM →,所以kOM →=OM →+MA →+OM →+MB →+OM →+MC →+OM →+MD →=4OM →+(MA →+MC →)+(MB →+MD →).由于平行四边形的对角线互相平分,所以MA →+MC →=0,MB →+MD →=0,所以kOM →=4OM →,所以k =4.10.平面内有向量OA →=(1,7),OB →=(5,1),OP →=(2,1),点X 为直线OP 上的一个动点. (1)当XA →·XB →取最小值时,求OX →的坐标;(2)当点X 满足(1)的条件和结论时,求cos ∠AXB 的值. [解] (1)设OX →=(x ,y ),因为点X 在直线OP 上, 所以向量OX →与OP →共线.又OP →=(2, 1), 所以x ×1-y ×2=0,即x =2y , 所以OX →=(2y ,y ).又XA →=OA →-OX →=(1-2y,7-y ),XB →=OB →-OX →=(5-2y,1-y ),于是XA →·XB →=(1-2y )(5-2y )+(7-y )(1-y )=5y 2-20y +12=5(y -2)2-8. 可知当y =2时,XA →·XB →取最小值-8,此时OX →=(4,2).(2)当OX →=(4,2)即y =2时,有XA →=(-3,5),XB →=(1,-1),XA →·XB →=(-3)×1+5×(-1)=-8,所以cos ∠AXB =XA →·XB→|XA →||XB →|=-834·2=-41717.1.如图所示,矩形ABCD 中,AB =4,点E 为AB 的中点,若DE →⊥AC →,则|DE →|等于( )A.52 B .23 C .3D .22B [建立平面直角坐标系如图所示,设|AD |=t ,则A (0,0),C (4,t ),D (0,t ),E (2,0),则DE →=(2,-t ),AC →=(4,t ), 由DE →⊥AC →得DE →·AC →=8-t 2=0, 解得t =22,所以DE →=(2,-22),|DE →|=22+-222=23.]2.已知向量a =(1,0),b =(cos θ,sin θ),θ∈⎣⎢⎡⎦⎥⎤-π2,π2,则|a +b |的取值范围是( )A .[0,2]B .(1,2]C .[1,2]D .[2,2]D [∵a +b =(1,0)+(cos θ,sin θ) =(1+cos θ,sin θ),∴|a +b |2=(1+cos θ)2+sin 2θ=2+2cos θ.又θ∈⎣⎢⎡⎦⎥⎤-π2,π2,∴cos θ∈[0,1],∴|a +b |2∈[2,4]. ∴|a +b |的取值范围是[2,2].]3.已知锐角△ABC 三个内角为A ,B ,C ,向量p =(2-2sin A ,cos A +sin A )与向量q =(sin A -cos A,1+sin A )是共线向量,则角A =________.π3[∵p ∥q , ∴(2-2sin A )(1+sin A )-(sin A -cos A )(cos A +sin A )=0, ∴2-2sin 2A =sin 2A -cos 2A , ∴sin 2A =34.又A 为锐角,∴sin A =32,∴A =π3.]4.已知平面内的三个单位向量a ,b ,c ,a ·b =0,则|a +b -c |的取值范围为________. [2-1,2+1] [三个向量a ,b ,c 在同一平面内,且均为单位向量,a ·b =0,可设a =(1,0),b =(0,1),c =(x ,y ),则a +b -c =(1-x,1-y ),|c |=x 2+y 2=1,∴|a +b -c |=x -12+y -12,它表示单位圆上的点到定点P (1,1)的距离,其最大值是|OP |+r =1+2,最小值是|OP |-r =2-1,∴|a +b -c |的取值范围是[2-1,2+1].]5.已知OA →=(4,0),OB →=(2,23),OC →=(1-λ)OA →+λOB →(λ2≠λ).(1)求OA →·OB →,OA →在OB →上的投影;(2)证明:A ,B ,C 三点共线,并在AB →=BC →时,求λ的值; (3)求|OC →|的最小值.[解] (1)OA →·OB →=8,设OA →与OB →的夹角为θ, 则cos θ=OA →·OB→|OA →||OB →|=84×4=12,∴OA →在OB →上投影为|OA →|cos θ=4×12=2.(2)AB →=OB →-OA →=(-2,23),BC →=OC →-OB →=(1-λ)OA →-(1-λ)OB →=(λ-1)AB →,∴A ,B ,C 三点共线.当AB →=BC →时,λ-1=1,所以λ=2.(3)|OC →|2=(1-λ)2OA 2→+2λ(1-λ)OA →·OB →+λ2OB 2→=16λ2-16λ+16=16⎝ ⎛⎭⎪⎫λ-122+12,∴当λ=12时,|OC →|min =23.。
