最新光的干涉计算题及答案
光的干涉试题及答案

光的干涉试题及答案一、选择题1. 光的干涉现象是指:A. 光波的叠加B. 光波的衍射C. 光波的反射D. 光波的折射答案:A2. 以下哪个条件是产生光的干涉的必要条件?A. 光波的频率相同B. 光波的振幅相同C. 光波的传播方向相同D. 光波的相位差恒定答案:D3. 杨氏双缝干涉实验中,干涉条纹的间距与以下哪个因素无关?A. 双缝间的距离B. 光的波长C. 屏幕与双缝的距离D. 观察者与屏幕的距离答案:D二、填空题1. 在光的干涉中,当两列波的相位差为0时,光强增强,这种现象称为________。
答案:相长干涉2. 光的干涉条纹的间距可以通过公式________计算得出。
答案:Δx = (λL) / d三、简答题1. 请简述光的干涉现象是如何产生的?答案:光的干涉现象是由两列或多列光波在空间某点相遇时,由于光波的相位差,导致光强在某些区域增强,在另一些区域减弱,从而形成明暗相间的干涉条纹。
2. 光的干涉实验中,如何改变干涉条纹的间距?答案:可以通过改变光源的波长、改变双缝间的距离或者改变屏幕与双缝之间的距离来改变干涉条纹的间距。
四、计算题1. 已知杨氏双缝干涉实验中,双缝间的距离d=0.5mm,屏幕与双缝之间的距离L=1.5m,光的波长λ=600nm,求干涉条纹的间距。
答案:Δx = (λL) / d = (600×10^-9 m × 1.5m) / (0.5×10^-3 m) = 1.8×10^-4 m2. 如果在上述实验中,将双缝间的距离增加到1.0mm,求新的干涉条纹间距。
答案:Δx = (λL) / d = (600×10^-9 m × 1.5m) / (1.0×10^-3 m) = 9.0×10^-4 m。
光的干涉(答案)

光的干涉(参考答案)一、选择题1. 【答案】AB【解析】A .肥皂膜因为自重会上面薄而下面厚,因表面张力的原因其截面应是一个圆滑的曲面而不是梯形,A 正确;B .薄膜干涉是等厚干涉,其原因为肥皂膜上的条纹是前后表面反射光形成的干涉条纹,B 正确;C .形成条纹的原因是前后表面的反射光叠加出现了振动加强点和振动减弱点,形成到破裂的过程上面越来越薄,下面越来越厚,因此出现加强点和减弱点的位置发生了变化,条纹宽度和间距发生变化,C 错误;D .将肥皂膜外金属环左侧的把柄向上转动90︒,由于重力,表面张力和粘滞力等的作用,肥皂膜的形状和厚度会重新分布,因此并不会跟着旋转90°;D 错误。
2. 【答案】D【解析】从薄膜的上下表面分别反射的两列光是相干光,其光程差为△x =2d ,即光程差为薄膜厚度的2倍,当光程差△x =nλ时此处表现为亮条纹,故相邻亮条纹之间的薄膜的厚度差为12λ,在图中相邻亮条纹(或暗条纹)之间的距离变大,则薄膜层的厚度之间变小,因条纹宽度逐渐变宽,则厚度不是均匀变小。
选项D 正确。
3. 【答案】D【解析】【分析】本题考查折射定律以及双缝干涉实验。
【详解】由双缝干涉条纹间距的公式Lx d λ∆=可知,当两种色光通过同一双缝干涉装置时,波长越长条纹间距越宽,由屏上亮条纹的位置可知12λλ>反射光经过三棱镜后分成两束色光,由图可知M 光的折射角大,又由折射定律可知,入射角相同时,折射率越大的色光折射角越大,由于12λλ>则12n n <所以N 是波长为λ1的光出射位置,故D 正确,ABC 错误。
故选D 。
4. 【答案】C【解析】解:因为路程差即(膜的厚度的两倍)是半波长的偶数倍,振动加强,为亮条纹,路程差是半波长的奇数倍,振动减弱,为暗条纹。
所以人从同侧看,可看到亮条纹时,同一高度膜的厚度相同,则彩色条纹水平排列,因竖直放置的肥皂薄膜受到重力的作用,下面厚,上面簿,形状视如凹透镜,因此,在薄膜上不同的地方,来自前后两个面的反射光所走的路程差不同,导致上疏下密,故C 正确,ABD 错误。
光的干涉习题答案

学号 班级 姓名 成绩第十六章 光的干涉(一)一、选择题1、波长mm 4108.4-⨯=λ的单色平行光垂直照射在相距mm a 4.02=的双缝上,缝后m D 1=的幕上出现干涉条纹。
则幕上相邻明纹间距离是[ B ]。
A .0.6mm ;B .1.2 mm ;C .1.8 mm ;D . 2.4 mm 。
2、在杨氏双缝实验中,若用一片透明云母片将双缝装置中上面一条缝挡住,干涉条纹发生的变化是[ C ]。
A .条纹的间距变大;B .明纹宽度减小;C .整个条纹向上移动;D .整个条纹向下移动。
3、双缝干涉实验中,入射光波长为λ,用玻璃薄片遮住其中一条缝,已知薄片中光程比相同厚度的空气大2.5λ,则屏上原0级明纹处[ B ]。
A .仍为明条纹;B .变为暗条纹;C .形成彩色条纹;D .无法确定。
4、在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是[ B ]。
A .使屏靠近双缝; B .使两缝的间距变小; C .把两个缝的宽度稍微调窄; D .改用波长较小的单色光源。
5、在双缝干涉实验中,单色光源S 到两缝S 1、S 2距离相等,则中央明纹位于图中O 处,现将光源S 向下移动到S ’的位置,则[ B ]。
A .中央明纹向下移动,条纹间距不变;B .中央明纹向上移动,条纹间距不变;C .中央明纹向下移动,条纹间距增大;D .中央明纹向上移动,条纹间距增大。
二、填空题1、某种波长为λ的单色光在折射率为n 的媒质中由A 点传到B 点,相位改变为π,问光程改变了2λ , 光从A 点到B 点的几何路程是 2nλ 。
2、从两相干光源s 1和s 2发出的相干光,在与s 1和s 2等距离d 的P 点相遇。
若s 2位于真空中,s 1位于折射率为n 的介质中,P 点位于界面上,计算s 1和s 2到P 点的光程差 d-nd 。
3、光强均为I 0的两束相干光相遇而发生干涉时,在相遇区域内有可能出现的最大光强是04I ;最小光强是 0 。
光的干涉参考答案

光的干涉参考解答一 选择题1.如图示,折射率为n 2厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3,已知n 1<n 2<n 3,若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束之间的光程差是 (A )2n 2e (B )2n 2e -2λ (C )2n 2e -λ (D )2n 2e -22n λ[A ][参考解]:两束光都是在从光疏介质到光密介质的分界面上反射,都有半波损失存在,其光程差应为δ=(2n 2e +2λ)-2λ= 2n 2e 。
2.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2,路径S 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过一块厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径光的光程差等于 (A )(r 2+ n 2t 2)-(r 1+ n 1t 1)(B )[r 2+ (n 2-1)t 2] -[r 1+ (n 1-1)t 1] (C )(r 2-n 2t 2)-(r 1-n 1t 1) (D )n 2t 2-n 1t 1[ B ]3.如图,用单色光垂直照射在观察牛顿环的装置上,当平凸透镜垂直向上缓缓平移而离开平面玻璃板时,可以观察到环状干涉条纹 (A )向右移动 (B )向中心收缩 (C )向外扩张 (D )静止不动[ B ][参考解]:由牛顿环的干涉条件(k 级明纹)λλk ne k =+22 ⇒ nk e k 2)21(λ-= 可知。
4.在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传到B ,若A 、B 两点的相位差是3π,则此路径AB 的光程差是 (A )1.5λ (B )1.5n λ (C )3λ (D )1.5λ/n[ A ][参考解]:由相位差和光程差的关系λδπϕ2=∆可得。
3S 1PS 空气二 填空题1.如图所示,波长为λ的平行单色光斜入射到距离为d 的双缝上,入射角为θ,在图中的屏中央O 处(S 1O=S 2O ),两束相干光的相位差为λθπsin 2d 。
高三物理光的干涉试题答案及解析

高三物理光的干涉试题答案及解析1.把双缝干涉实验装置放在折射率为n的水中,两缝间距离为d,双缝到屏的距离为 D(D>>d),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹间的距离为_________【答案】λD/(nd)【解析】光在水中的波长为:,根据条纹间距的表达式:【考点】双缝干涉;光的折射定律。
2.用绿光做双缝干涉实验,在光屏上呈现出绿、暗相间的条纹,相邻两条绿条纹间的距离为。
下列说法中正确的有A.如果增大单缝到双缝间的距离,将增大B.如果增大双缝之间的距离,将增大C.如果增大双缝到光屏之间的距离,将增大D.如果减小双缝的每条缝的宽度,而不改变双缝间的距离,将增大【答案】C【解析】公式中表���双缝到屏的距离,d表示双缝之间的距离。
因此与单缝到双缝间的距离无关,于缝本身的宽度也无关。
本题选C。
3.平行光通过小孔得到的衍射图样和泊松亮斑比较,下列说法中正确的有A.在衍射图样的中心都是亮斑B.泊松亮斑中心亮点周围的暗环较宽C.小孔衍射的衍射图样的中心是暗斑,泊松亮斑图样的中心是亮斑D.小孔衍射的衍射图样中亮、暗条纹间的间距是均匀的,泊松亮斑图样中亮、暗条纹间的间距是不均匀的【答案】AB【解析】从课本上的图片可以看出:A、B选项是正确的,C、D选项是错误的。
衍射图样的中心都是亮斑,衍射图样的亮暗条纹间距是非均匀的。
4.(1)用双缝干涉测光的波长。
实验装置如下图a所示,已知单缝与双缝的距离L1=60mm,双缝与屏的距离L2=700mm,单缝宽d1=0.10mm,双缝间距d2=0.25mm。
用测量头来测量光屏上干涉亮条纹中心的距离。
测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻度对准屏上亮纹的中心,(如下图b所示),记下此时手轮的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的刻度。
①分划板的中心刻线分别对准第1条和第4条亮纹的中心时,手轮上的读数如下图c所示,则对准第1条时读数x1=-----________mm,对准第4条时读数x2=-----________mm,相邻两条亮纹间的距离Δx=________mm。
光的干涉习题(附答案)

π
S1
S2
3λ 4
4. 用波长为 λ 的单色光垂直照射牛顿环装置,观察牛顿环,如图所示。若使凸 透镜慢慢向上垂直移动距离 d, 移过视场中某固定观察点的条纹数等于 2d/λ 。
5. 空气中两块玻璃形成的空气劈形膜, 一端厚度为零, 另一端厚度为 0.005 cm, 玻璃折射率为 1.5,空气折射率近似为 1。如图所示,现用波长为 600 nm 的 单色平行光, 沿入射角为 30°角的方向射到玻璃板的上表面, 则在劈形膜上形 成的干涉条纹数目为 144 。
6. 维纳光驻波实验装置示意如图。MM 为金属反射镜,NN 为涂有极薄感光层 的玻璃板。MM 与 NN 之间夹角 φ=3.0×10-4 rad,波长为 λ 的平面单色光通过 NN 板垂直入射到 MM 金属反射镜上,则反射光与入射光在相遇区域形成光 驻波, NN 板的感光层上形成对应于波腹波节的条纹。 实验测得两个相邻的驻 波波腹感光垫 A、B 的间距 1.0 mm,则入射光的波长为 6.0×10-4 mm 。
8. 如图所示,折射率为 n2,厚度为 e 的透明介质薄膜的上、下方透明介质的折 射率分别为 n1 和 n3,且 n1<n2<n3,若用波长为 λ 的单色平行光垂直入射到该 薄膜上,则从薄膜上下两表面反射的光束之间的光程差为 2长为 λ 的单色平行光垂直照射两个劈尖上,两劈尖角分别为 θ1 和 θ2,折射 率分别为 n1 和 n2, 若两者分别形成的干涉条纹的明条纹间距相等, 则 θ1, θ2, n1,n2 之间的关系为 n1θ1= n2θ2 。
2h c arcsin 0.1 5.7 o arcsin 2hf
11. 油船失事,把大量石油(n=1.2)泄漏在海面上,形成一个很大的油膜。试求: (1)如果你从飞机上竖直地向下看油膜厚度为 460nm 的区域,哪些波长的 可见光反射最强? (2 ) 如果你戴了水下呼吸器从水下竖直的向上看这油膜同 一区域,哪些波长的可见光透射最强?(水的折射率为 1.33) 答:因为在油膜上下表面反射光都有半波损失, (1)反射光干涉加强:2nd=k
(完整版)光的干涉练习题及答案

(完整版)光的⼲涉练习题及答案⼀、选择题1、严格地讲,空⽓折射率⼤于1,因此在⽜顿环实验中,若将玻璃夹层中的空⽓逐渐抽去⽽成为真空时,⼲涉环将:()A.变⼤;B.缩⼩;C.不变;D.消失。
【答案】:A2、在迈克⽿逊⼲涉仪的⼀条光路中,放⼊⼀折射率n ,厚度为h 的透明介质板,放⼊后,两光束的光程差改变量为:()A.h n )1(2-;B.nh 2;C.nh ;D.h n )1(-。
【答案】:A3、⽤劈尖⼲涉检测⼯件(下板)的表⾯,当波长为λ的单⾊光垂直⼊射时,观察到⼲涉条纹如图。
图中每⼀条纹弯曲部分的顶点恰与左边相邻的直线部分的连线相切。
由图可见⼯件表⾯:()A.⼀凹陷的槽,深为λ/4;B.有⼀凹陷的槽,深为λ/2;C.有⼀凸起的埂,深为λ/4;D.有⼀凸起的埂,深为λ。
【答案】:B4、⽜顿环实验装置是⽤⼀平凸透镜放在⼀平板玻璃上,接触点为C ,中间夹层是空⽓,⽤平⾏单⾊光从上向下照射,并从下向上观察,看到许多明暗相间的同⼼圆环,这些圆环的特点是:()A.C 是明的,圆环是等距离的;B.C 是明的,圆环是不等距离的;C.C 是暗的,圆环是等距离的;D.C 是暗的,圆环是不等距离的。
【答案】:B5、若将⽜顿环玻璃夹层中的空⽓换成⽔时,⼲涉环将:()A .变⼤;B .缩⼩;C .不变;D .消失。
【答案】:B6、若把⽜顿环装置(都是⽤折射率为1.52的玻璃制成的)由空⽓搬⼊折射率为1.33的⽔中,则⼲涉条纹()A .中⼼暗斑变成亮斑;B .变疏;C .变密;D .间距不变。
【答案】:C7、两个不同的光源发出的两个⽩光光束,在空间相遇是不会产⽣⼲涉图样的,这是由于()A.⽩光是由许多不同波长的光组成;B.两个光束的光强不⼀样;C.两个光源是独⽴的不相⼲光源;D.两个不同光源所发出的光,频率不会恰好相等。
【答案】:C8、在双缝⼲涉实验中,若单⾊光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于O 处。
第11章 光的干涉

(D)2500 二、填空题 11.7 在杨氏双缝实验中,如果用厚度为L,折射率分别为n1和n2 ( n1<n2)的薄玻璃片分别盖住S1、S2光源,这时从S1和S2到达原来中央 亮纹P0点的光程差△= 。 11.8 光产生干涉现象的必要条件 是_____________;_____________;_______________。 11.9 杨氏双缝实验中,已知d=0.3mm,D=1.2m,测得两个第五级暗条 纹的间隔为22.78mm,求入射单色光的波长_______nm.
题图
11.22 在空气牛顿环中,用波长为 的单色光垂直入射,测得第k个暗 环半径为5.63mm,第k+5个暗环半径为7.96mm。求曲率半径R。 11.23 一玻璃劈尖,折射率n=1.52。波长的钠光垂直入射,测得相邻 条纹的间距L=5mm,求劈尖角。
11.24 迈克耳孙干涉仪可用来测量单色光的波长,当某次测得可动反射 镜移动距离时,测得某单色光的干涉条纹移过条,试求该单色光的波 长。 11.25 使一束水平的氦氖激光器发出的激光()垂直照射到一双缝 上,在缝后2m处的墙上观察到中央明条纹和第一级明纹的间隔为14cm, 求:1)两缝的间隔; 2)在中央条纹上还能看到几条明纹?
第十一章光的干涉习题答案
一、选择题 11.1 B 11.2 B 11.3 D 11.4 11.6 C 二、填空题 11.7、(n2 - n1)L 11.8、频率相同、相位差恒定、振动方向相同。 11.9、632.8 nm 11.10、4600 nm D 11.5 C
11.11、6.4 三、计算题 11.12 解:(1)根据明纹坐标 , 所以有: 。 (2)当时,相邻明纹间距为 11.13 解:暗条纹中心位置为: 解得单色光的波长 .14 解:加上透明簿膜后的光程差为 因为第四级明条纹是原零级明纹的位置: , 得到: 11.15 解:(1)根据题中给的已知条件 λ=632.8×10-9m,d=0.022×10-2m,r0=180×10-2m, 代入公式 (2)已知d=0.45cm, r0=120cm, 11.16 解:(1)同侧的第一级明纹中心到第四级明纹中心为三个暗纹 宽度,根据公式和已知条件可得: =3 (2)当则条纹宽度: m 11.17 解:由题 n1=1<n2=1.38<n3=1.52,则光程差为: 由干涉相消的条件: 得到: 所以膜的最小厚度 因此当薄膜厚度为的奇数倍时,反射光相消,透射光增强。 11.18 解:空气劈尖两相邻明纹空气间距为: 相邻明纹间距与其空气间距存在关系: 11.19 解:(1)玻璃劈的光程差为 , 当时,厚度为处出现明条纹 相邻明纹之间的空气间距为 Δy=0.015cm
光的干涉计算题及答案

《光的干涉》计算题1.在双缝干涉实验中,用波长λ=546.1nm (1 nm=10-9m)的单色光照射,双缝与屏的距离D =300 mm.测得中央明条纹两侧的两个第五级明条纹的间距为12.2 mm,求双缝间的距离.解:由题给数据可得相邻明条纹之间的距离为∆x=12.2 / (2×5)mm=1.22 mm 2分由公式∆x=Dλ / d,得d=Dλ / ∆x=0.134 mm 3分2. 在图示的双缝干涉实验中,若用薄玻璃片(折射率n1=1.4)覆盖缝S1,用同样厚度的玻璃片(但折射率n2=1.7)覆盖缝S2,将使原来未放玻璃时屏上的中央明条纹处O变为第五级明纹.设单色光波长λ=480 nm(1nm=109m),求玻璃片的厚度d(可认为光线垂直穿过玻璃片).解:原来,δ = r2-r1= 0 2分覆盖玻璃后,δ=( r2 + n2d–d)-(r1 + n1d-d)=5λ3分∴(n2-n1)d=5λ125nnd-=λ2分= 8.0×10-6 m 1分3. 薄钢片上有两条紧靠的平行细缝,用波长λ=546.1 nm (1 nm=10-9 m)的平面光波正入射到钢片上.屏幕距双缝的距离为D=2.00 m,测得中央明条纹两侧的第五级明条纹间的距离为∆x=12.0 mm.(1) 求两缝间的距离.(2) 从任一明条纹(记作0)向一边数到第20条明条纹,共经过多大距离?(3) 如果使光波斜入射到钢片上,条纹间距将如何改变?解:(1) x=2kDλ / dd = 2kDλ /∆x2分此处k=5∴d=10 Dλ / ∆x=0.910 mm 2分(2) 共经过20个条纹间距,即经过的距离l=20 Dλ / d=24 mm 2分(3) 不变2分4. 在双缝干涉实验中,单色光源S0到两缝S1和S2的距离分别为l1和l2,并且l1-l2=3λ,λ为入射光的波长,双缝之间的距离为d,双缝到屏幕的距离为D(D>>d),如图.求:(1) 零级明纹到屏幕中央O点的距离.(2) 相邻明条纹间的距离.屏解:(1) 如图,设P 0为零级明纹中心则 D O P d r r /012≈- 3分(l 2 +r 2) - (l 1 +r 1) = 0∴ r 2 – r 1 = l 1 – l 2 = 3λ ∴()d D d r r D O P /3/120λ=-= 3分 (2) 在屏上距O 点为x 处, 光程差 λδ3)/(-≈D dx 2分 明纹条件 λδk ±= (k =1,2,....) ()d D k x k /3λλ+±=在此处令k =0,即为(1)的结果.相邻明条纹间距d D x x x k k /1λ=-=+∆ 2分5. 在双缝干涉实验中,用波长λ=500 nm 的单色光垂直入射到双缝上,屏与双缝的距离D =200 cm ,测得中央明纹两侧的两条第十级明纹中心之间距离为Δx =2.20 cm ,求两缝之间的距离d .(1nm=109m)解:相邻明纹间距 ∆x 0 = D λ / d 2分两条缝之间的距离 d = D λ / ∆x 0 =D λ / (∆x / 20) =20 D λ/∆x= 9.09×10-2 cm 3分6. 双缝干涉实验装置如图所示,双缝与屏之间的距离D =120 cm ,两缝之间的距离d =0.50 mm ,用波长λ=500 nm (1 nm=10-9 m)的单色光垂直照射双缝. (1) 求原点O (零级明条纹所在处)上方的第五级明条纹的坐标x . (2) 如果用厚度l =1.0×10-2 mm , 折射率n =1.58的透明薄膜复盖在图中的S 1缝后面,求上述第五级明条纹的坐标x '.解:(1) ∵ dx / D ≈ k λx ≈Dk λ / d = (1200×5×500×10-6 / 0.50)mm= 6.0 mm 4分(2) 从几何关系,近似有r 2-r 1≈ D x /d '有透明薄膜时,两相干光线的光程差 δ = r 2 – ( r 1 –l +nl ) = r 2 – r 1 –(n -1)l ()l n D x 1/d --'=对零级明条纹上方的第k 级明纹有 λδk = 零级上方的第五级明条纹坐标()[]d k l n D x /1λ+-=' 3分=1200[(1.58-1)×0.01±5×5×10-4] / 0.50mm=19.9 mm 3分P d λ x '7. 在如图所示的瑞利干涉仪中,T 1、T 2是两个长度都是l 的气室,波长为λ的单色光的缝光源S 放在透镜L 1的前焦面上,在双缝S 1和S 2处形成两个同相位的相干光源,用目镜E 观察透镜L 2焦平面C 上的干涉条纹.当两气室均为真空时,观察到一组干涉条纹.在向气室T 2中充入一定量的某种气体的过程中,观察到干涉条纹移动了M 条.试求出该气体的折射率n (用已知量M ,λ和l 表示出来).解:当T 1和T 2都是真空时,从S 1和S 2来的两束相干光在O 点的光程差为零.当T 1中充入一定量的某种气体后,从S 1和S 2来的两束相干光在O 点的光程差为(n – 1)l . 1分 在T 2充入气体的过程中,观察到M 条干涉条纹移过O 点,即两光束在O 点的光程差改变了M λ.故有(n -1)l -0 = M λ 3分 n =1+M λ / l . 1分8.用波长λ=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少?解: 明纹, 2ne +λ21=k λ (k =1,2,…)3分 第五条,k =5, ne 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分9. 在Si 的平表面上氧化了一层厚度均匀的SiO 2薄膜.为了测量薄膜厚度,将它的一部分磨成劈形(示意图中的AB 段).现用波长为600 nm 的平行光垂直照射,观察反射光形成的等厚干涉条纹.在图中AB 段共有8条暗纹,且B 处恰好是一条暗纹,求薄膜的厚度.(Si 折射率为3.42,SiO 2折射率为1.50)解:上下表面反射都有相位突变π,计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹,2ne =21( 2k +1 )λ, (k =0,1,2,…) 2分 A 处为明纹,B 处第8个暗纹对应上式k =7 1分 ()nk e 412λ+==1.5×10-3 mm 2分A ,膜10. 图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .(1) 求入射光的波长.(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.解:(1) 明环半径 ()2/12λ⋅-=R k r 2分()Rk r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ)对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分 故在OA 范围内可观察到的明环数目为50个. 1分11. 波长为λ的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹.(1) 从形膜顶部O 开始向右数起,第五条暗纹中心所对应的薄膜厚度e 5是多少?(2) 相邻的二明纹所对应的薄膜厚度之差是多少?解:∵ n 1<n 2<n 3,二反射光之间没有附加相位差π,光程差为δ = 2n 2 e第五条暗纹中心对应的薄膜厚度为e 5,2n 2 e 5 = (2k - 1)λ / 2 k = 5()2254/94/152n n e λλ=-⨯= 3分 明纹的条件是 2n 2 e k = k λ相邻二明纹所对应的膜厚度之差∆e = e k+1-e k = λ / (2n 2) 2分3。
最新大学物理第12章光的干涉测试题(附答案及知识点总结)

大学物理第12章光的干涉测试题(附答案及知识点总结)第12章 习题精选试题中相关常数:m 10μm 16-=,m 10nm 19-=,可见光范围(400nm~760nm ) 1、在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为π3,则此路径AB 的光程为:(A )λ5.1. (B )n /5.1λ. (C )λn 5.1. (D )λ3.[ ]2、在相同的时间内,一束波长为λ的单色光在空气中与在玻璃中: (A )传播路程相等,走过光程相等. (B )传播路程相等,走过光程不相等.(C )传播路程不相等,走过光程相等.(D )传播路程不相等,走过光程不相等.[ ]3、如图所示,折射率为2n 、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为1n 和3n ,已知321n n n <<.若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束①与②的光程差是:(A )e n 22. (B )2/22λ+e n .(C )λ+e n 22. (D ))2/(222n e n λ-.[ ]4、在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是:(A )使屏靠近双缝. (B )使两缝的间距变小.(C )把两个缝的宽度稍微调窄. (D )改用波长较小的单色光源.[ ]35、在双缝干涉实验中,入射光的波长为λ,用玻璃纸遮住双缝中的一个缝,若玻璃纸中光程比相同厚度的空气的光程大λ5.2,则屏上原来的明纹处:(A )仍为明条纹. (B )变为暗条纹.(C )既非明纹也非暗纹. (D )无法确定是明纹,还是暗纹.[ ]6、如图,用单色光垂直照射在观察牛顿环的装置上.当平凸透镜垂直向上缓慢平移而远离平面玻璃时,可以观察到这些环状干涉条纹:(A )向右平移. (B )向中心收缩. (C )向外扩张. (D )向左平移.[ ]7、在牛顿环实验装置中,曲率半径为R 的平凸透镜与平玻璃板在中心恰好接触,它们之间充满折射率为n 的透明介质,垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ,则反射光形成的干涉条纹中暗环半径k r 的表达式为:(A )R k r λ=k . (B )n R k r /k λ=. (C )R kn r λ=k . (D ))/(k nR k r λ=.[ ]8、用波长为λ的单色光垂直照射置于空气中的厚度为e折射率为1.5的透明薄膜,两束反射光的光程差=δ_______________.9、单色平行光垂直入射到双缝上.观察屏上P 点到两缝的距离分别为1r 和2r .设双缝和屏之间充满折射率为n 的介质,则P 点处光线的光程差为___________.S S 110、用一定波长的单色光进行双缝干涉实验时,欲使屏上的干涉条纹间距变大,可采用的方法是:(1)________________________________________. (2)________________________________________.11、在双缝干涉实验中,若使两缝之间的距离增大,则屏幕上干涉条纹间距_________;若使单色光波长减小,则干涉条纹间距_____________.12、在双缝干涉实验中,若两缝的间距为所用光波波长的N 倍,观察屏到双缝的距离为D ,则屏上相邻明纹的间距为_______________.13、用波长为λ的单色光垂直照射如图所示的牛顿环装置,观察从空气膜上下表面反射的光形成的牛顿环.若使平凸透镜慢慢地垂直向上移动,从透镜顶点与平面玻璃接触至移动到两者距离为d 的过程中,移过视场中某固定观察点的条纹数目等于_______________.14、图a 为一块光学平板玻璃与一个加工过的平面一端接触,构成的空气劈尖,用波长为λ的单色光垂直照射.看到反射光干涉条纹(实线为暗条纹)如图b 所示.则干涉条纹上A 点处所对应的空气薄膜厚度为=e _________________.15、用波长为λ的单色光垂直照射如图示的劈形膜(321n n n >>),观察反射光干涉.从劈形膜尖顶开始算起,第2条明条纹中心所对应的膜厚度=e _______________________.图b图an 1n 2 n 316、波长为λ的平行单色光垂直照射到劈形膜上,若劈尖角为θ以弧度计),劈形膜的折射率为n ,则反射光形成的干涉条纹中,相邻明条纹的间距为__________________.17、波长为λ的平行单色光垂直照射到折射率为n 的劈形膜上,相邻的两明纹所对应的薄膜厚度之差是____________________.18、在双缝干涉实验中,双缝与屏间的距离m 2.1=D ,双缝间距m m 45.0=d ,若测得屏上干涉条纹相邻明条纹间距为1.5mm ,求光源发出的单色光的波长λ.19、在杨氏双缝干涉实验中,用波长nm 1.546=λ的单色光照射,双缝与屏的距离m m 300=D .测得中央明条纹两侧的两个第5级明条纹的间距为12.2mm ,求双缝间的距离.20、在双缝干涉实验中,波长nm 550=λ的单色平行光垂直入射到缝间距m 1024-⨯=a 的双缝上,屏到双缝的距离m 2=D .求:(1)中央明纹两侧的两条第10级明纹中心的间距;(2)用一厚度为m 106.65-⨯=e 、折射率为58.1=n 的玻璃片覆盖一缝后,零级明纹将移到原来的第几级明纹处?21、用白光垂直照射置于空气中的厚度为μm 50.0的玻璃片.玻璃片的折射率为50.1=n .在可见光范围内哪些波长的反射光有最大限度的增强?22、波长nm 650=λ的红光垂直照射到劈形液膜上,膜的折射率33.1=n ,液面两侧是同一种介质.观察反射光的干涉条纹.(1)离开劈形膜棱边的第一条明条纹中心所对应的膜厚度是多少? (2)若相邻的明条纹间距m m 6=l ,上述第1条明纹中心到劈形膜棱边距离x 是多少?23、用波长为nm 600=λ的光垂直照射由两块平玻璃板构成的空气劈形膜,劈尖角rad 1024-⨯=θ.改变劈尖角,相邻两明条纹间距缩小了mm 0.1=∆l ,求劈尖角的改变量θ∆.24、曲率半径为R 的平凸透镜和平板玻璃之间形成空气薄层,如图所示.波长为λ的平行单色光垂直入射,观察反射光形成的牛顿环.设平凸透镜与平板玻璃在中心O 点恰好接触.求:(1)从中心向外数第k 个明环所对应的空气薄膜的厚度k e .(2)第k 个明环的半径用k r (用R 、波长λ和正整数k 表示,R 远大于上一问的k e .)25、图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的R OλO 1曲率半径是cm 400=R .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30cm .(1)求入射光的波长.(2)设图中cm 00.1=OA ,求半径为OA 范围内可观察到的明环数目.26、用波长nm 500=λ的单色光作牛顿环实验,测得第k 个暗环半径m m4k =r ,第10+k 个暗环半径m m 610k =+r ,求平凸透镜的凸面的曲率半径R .总体要求:理解产生相干光的三个条件和获得相干光的两种方法.了解分波阵面法和分振幅法干涉的典型实验;掌握光程的概念以及光程差和相位差的关系;掌握杨氏双缝干涉条纹及薄膜干涉条纹(尤其是劈尖和牛顿环)的分布规律,利用相关公式计算条纹分布.第12章 参考答案1、A2、C3、A4、B5、B6、B7、B8、23λ+e 或23λ-e 9、)(12r r n -10、(1)使两缝间距变小;(2)使屏与双缝之间的距离变大. 11、变小;变小 12、N D / 13、λ/2d 14、λ23 15、22n λ 16、θλn 2 17、n2λ18、解:nm 5.562/=∆=D x d λ. 19、解:m m 268.0/=∆==x D d λλ. 20、解:(1)m 11.0/20==∆a D x λ (2)零级明纹移到原第7级明纹处.21、解:nm 600=λ和nm 6.428=λ. 22、解:(1)λλk ne k =+2/2(明纹中心)现1=k ,1e e k=,则膜厚度m m1022.1)4/(41-⨯==n e λ.(2)m m 32/==l x23、解:rad 100.442-⨯=-=∆θθθ.24、解:(1)第k 个明环,λλk e k =+212 4/)12(λ-=k e k .(2)λλk R r k =+21)2/(22,2/)12(λR k r k -= ,...2,1=k .25、解:(1)()cm 10512252×Rk r -=-=λ (或500 nm ).(2)λR r k 2212=-,对于cm 00.1=r ,5.505.02=+=λR r k .故在OA 范围内可观察到的明环数目为50个.26、解:()()m 410/2210=-=+λk k r r R .第12章 光的干涉一、基本内容1.单色光单色光是指具有单一频率的光波,单色光不是单种颜色的光.可见光的波长是(380~760)nm .虽然绝对单一频率的单色光不易得到,但可以通过各种方法获取谱线宽度很小的单色光.例如激光就可看作谱线宽度很小的单色光.2.相干光只有两列光波的振动频率相同、振动相位差恒定、振动方向相同时才会发生干涉加强或减弱的现象,满足上述三个条件的两束光称为相干光,相应的光源称为相干光源.3.半波损失光由光疏介质(即折射率相对小的介质)射到光密介质发生反射时,反射光的相位较入射光的相位发生π的突变,这一变化导致了反射光的光程在反射过程中增加了半个波长,通常称为“半波损失”.4.光程和光程差 (1)光程光波的频率v 是单色光的本质属性,与在何种介质中传播没有关系,而传播速度则与介质有关.在折射率为n 的介质中光速是真空中光速的n /1,由光速v u n n λ=可知,在折射率为n 的介质中,光波的波长n λ也是真空中波长的n /1.这样光在不同介质中经历同样的波数,但经历的几何路程却不同.所以有必要把光在折射率n 的介质中通过的几何路程折算到真空中所能传播的长度,只有这样才便于比较两束经过不同介质的光相位的变化.所以把光在折射率为n 的介质中通过的几何的路程r 乘以折射率n 折算成真空中所能传播的长度nr ,称nr 为光程.(2)光程差当采用了光程概念以后就可以把由相位差决定的干涉加强、减弱等情况用光程差来表示,为计算带来方便.即相位差π2λδϕ=∆(λ为真空中波长,δ为光程差),亦即λδϕπ2=∆.二、基本规律光程差(含半波损失)是半波长偶数倍时干涉加强,干涉相长,明条纹中心;是半波长奇数倍时,干涉相消,暗条纹中心.1.杨氏双缝干涉结果(分波阵面干涉),只讨论同一介质中传播:等间隔明暗相间条纹.光程差:Dx d=δ dD kx λ±=k ),2,1,0( =k 明条纹位置(k x —k 级干涉条纹位置,D —屏距,d —缝距)2)12(k λd D k x -±= ),2,1( =k 暗条纹位置 条纹中心间距:λdD x =∆ 2.薄膜干涉结果(分振幅干涉)薄膜干涉基础公式相同,考虑从1n 入射到2n (21n n <),i 为入射角,d —薄膜厚度,此时要考虑“半波损失”,故反射加强(上表面亮纹位置)为λλδk i n n d =+-=2sin 222122 ),2,1( =k反射减弱(上表面暗纹位置)为(注意此处k 可以取0,厚度为0处是暗纹)2)12(2sin 222122λλδ+=+-=k i n n d ),2,1,0( =k注意,一定要先分析反射光是否存在“半波损失”的情况,不能死搬硬套,一般介质折射率中间大两边小或中间小两边大都有半波损失,而三种介质折射率大小顺序排列无半波损失.薄膜干涉光程差是入射角和厚度的函数.等倾干涉:对于上两式,如果薄膜厚度不变,而光线倾角(入射角i )变化,入射角i 相同的位置光线光程差相同,条纹花样相同,叫做等倾干涉.如有侵权请联系网站删除,仅供学习交流仅供学习交流 等厚干涉:对于上两式,所有光线以同一入射角i 入射,而薄膜厚度变化,则厚度相同的位置光线光程差相同,条纹干涉花样相同,叫做等厚干涉.对空气劈尖(上玻璃板下表面和下玻璃板上表面两束光反射)两侧介质相同,由于存在“半波损失”,所以上两式适用于在空气劈尖的上表面干涉.一般取垂直入射,0=i ,则在劈尖上表面干涉,光程差满足λλδk nd =+=22 ),2,1( =k 明条纹2)12(22λλδ+=+=k nd ),2,1,0( =k 暗条纹n 代表劈尖内介质折射率.劈尖端点处是暗纹,相邻明纹(或暗纹)厚度差n d 2λ=∆,条纹线间距:θλn l 2=∆. 如果两侧介质不同,且满足折射率递增或递减顺序,则无半波损失,光程差满足λδk nd ==2 ),2,1,0( =k 明条纹2)12(2λδ-==k nd ),2,1( =k 暗条纹劈尖劈尖端点处是暗纹,相邻明纹(或暗纹)厚度差和条纹线间距与有半波损失时相同.利用劈尖原理检测零件平整度,上表面放标准板,顶角在左侧,下板凹陷条纹向左弯,凸起向右弯.牛顿环的上表面干涉也是空气劈尖干涉,两侧介质相同,有半波损失,只不过牛顿环的空气厚度测量常转换成距透镜中心距离r 与透镜的曲率半径R 来表示牛顿环的明暗纹.2)12(k λR k r -= ),2,1( =k (明环) λkR r =k ),2,1,0( =k (暗环)。
第14章光的干涉习题答案

7.法布里-珀罗标准具的两个反射面平行并严格保持距离 1cm,标准具两侧各有一个直径为1cm的单色光源,波长 λ=0.49μm,设仪器严格共轴。求第二个透镜后焦点上干 涉条纹的级次以及后焦面上有多少条明条纹,其最大直径 为多少? A B
解:相当于在AB间形成1cm空气薄膜, 等倾入射,焦面上一点 对于薄膜来说, 对应于同一入射角 i
11.两光相干除了满足干涉的三个必要条件,即频率相同、 振动方向相同、相位相等或相位差恒定之外,还必须满足 两个附加条件 两相干光的振幅不可相差太大 , 两相干光的光程差不能太大 。
三、计算题
1.波长为λ的两束相干的单色平行光分别以图所示的入射 角θ、φ入射在屏幕面MN上。求屏幕上干涉条纹的间隔。 解:考虑相邻两明条纹,条纹 中心为A、B,级次分别为k、 k+1,并设AB两点间距为x。
2e n2 n1 sin i k
2
2
2
A
B
n2 1
n1 1(??) e 1 10
2
4.9 10
7
2e cos i k
f 2焦点上 i 0 kmax
f f
2
2e
40816
i最大时,对应如图过 f 1中心的光线 cos i r2 15 15 2 0.5 2
5.用劈尖干涉检测工件的表面,当波长为的单色光垂直 入射时,观察到干涉条纹如图。图中每一条纹弯曲部分 的顶点恰与左边相邻的直线部分的连线相切。由图中可 见工件表面:( ) A.有一凹陷的槽,深入 / 4 B. 有一凹陷的槽,深入 / 2 C.有一凸起的埂,深入 / 4 D. 有一凸起的埂,深入
3.波长为 的平行单色光垂直地照射到劈尖薄膜上, 劈尖薄膜的折射率为n,第二级明纹与第五条明纹所对 应的薄膜厚度之差 3λ/2n 。
第一章光的干涉习题与答案解析

第一章光的干涉• 1.波长为50011111的绿光投射在间距d 为0.022cm 的双缝上,在距离180cm 处的光屏上形成干涉条纹,求两个亮条纹之间的距离•若改用波长为700nm 的红 光投射到此双缝上,两个亮条纹之间的距离又为多少算出这两种光第2级亮纹位 置的距离.=0.573cmy“ = =2x0.409 = 0.818cm""dy 22 =厶 # = 2x0.573 = 1.146cm△)k = y 22 一 y 2i = 1.146-0.818 = 0.328cm•2.在杨氏实验装置中.光源波长为640nm,两狭缝间距为0.4mm.光屏离狭缝的距离为50cm.试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若p 点离中央亮条纹 为0.1111111,问两束光在P 点的相位差是多少(3)求P 点的光强度和中央点的强度之比.解:⑴由公式:r50Av = 42 ——x6.4xl0'5 =8.0xl0"2cmd = 0.4(2)由课本第20页图1-2的几何关系可知八一人 dsinOdxanO = d — = 0.04^^ = 0.8xl0"5cm/o 50解:由条纹间距公式">,y+1~ ?得:x500x107 =0.409cm1800.022/ = &' + 疋 + 2AA. cosg= 44; 由公式4A ; cos 2 — cos 2- ————=—=cos^ 4心肘塑COS_0° 82•3.把折射率为的玻璃片插入杨氏实验的一束光路中•光屏上原来第5级亮条纹所在 的位置为中央亮条纹,试求插入的玻璃片的厚度•已知光波长为6XW 7m.△0 _ Ar解:未加玻璃片时,'、二到P 点的光程差,由公式2兀 几可知为r^-r= — x 5 x 2龙=5兄 A r = ~ 2龙现在亠发岀的光束途中插入玻璃片时,P 点的光程差为E - [0; _/?)+〃/?] =亍△© =于%0=o所以玻璃片的厚度为h =上—-=—=102 = 6 xl0~4cm n-1 0.54.波长为500nm 的单色平行光射在间距为的双狭缝上.通过其中一个缝的能 量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样•求干涉条纹间距和条 纹的可见度.Ay = ^.2 = —X 500X W 6 = 1.25 解: d 0.2 mmA = 人=2 人 = 2A ; A>V = 2(人 仏)、=空=0.9427 « 0.941 + (4"J 1 + 2I P A P1+COS —_____ =25•波长为700nm的光源与菲涅耳双镜的相交棱之间距离为20cm,棱到光屏间的距离L 为180cm,若所得干涉条纹中相邻亮条纹的间隔为1mm,求双镜平面之间的夹角6。
光的干涉练习题及答案

光的干涉练习题及答案三、分析题1、在双缝干涉实验中,在下列情况下,干涉条纹将如何变化?试说明理由。
(1) 入射光由红光换为紫光;(2) 屏与双缝的间距D 不断增大;(3) 在下面一条缝后放一块云母片。
【答案】:双缝干涉条纹相邻明条纹(或暗条纹)的间距为 λdD x =∆ (2分) (1) 红光变紫光波长λ减小,其他条件不变时,条纹变窄(或密或向屏中央集中)(3分)(2) D 不断增大时,x ∆增大,条纹变稀(或变宽)(3分)(3) 在下面一条缝后放一块云母片,通过它的光线的光程增大(2分),干涉条纹向下平移(2分)。
2、杨氏双缝干涉实验条件作如下变化,干涉条纹将如何变化?试说明理由。
(1)加大双缝间距d ;(2)把整套装置浸入水中;(3)在两缝后分别放红色和绿色的滤光片。
【答案】:根据:条纹宽度λdD x =∆(2分) (1)d 变大,其他条件不变,则x ∆变小,所以条纹变窄(或密或向屏中央集中)(2分)。
d 增大到一定程度,条纹过于细密而无法分辨,拥挤在一起成为一条明亮带。
(2分)(2)装置没入水中后的条纹宽度为λdD n x 1=∆,因为1>n (2分) 所以x ∆变小,条纹变窄(或密或向屏中央集中)。
(2分)(3)使通过两缝的光频率不同,不满足相干条件(2分),干涉条纹消失(2分)。
3、如图所示,A ,B 两块平板玻璃构成空气劈尖,分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移[见图(a)];(2) A 绕棱边逆时针转动[见图(b)]。
【答案】:相邻明纹或暗纹介质膜厚度差n d 2λ=∆(2分),相邻明纹或暗纹间距θλn l 2=(2分)。
(1)上表面A 向上平移时,棱边明暗交替变化,相同厚度的空气薄模向棱边处移动,条纹间距不变。
(4分)(2) A 绕棱边逆时针转动时,棱边明暗不变,各级条纹向棱边方向移动,条纹变密。
(4分)4、在玻璃(5.1=n )上镀上25.1=n 的介质薄膜,波长 nm 500=λ的光从空气中垂直照射到此薄膜上,要使其为高反膜和增透膜求膜的厚度。
关于光的干涉的习题与答案

关于光的干涉的习题与答案
光的干涉习题与答案
光的干涉是光学中非常重要的一个现象,它揭示了光波的波动性质。
在干涉现象中,光波会相互叠加,形成明暗条纹,从而产生干涉图样。
下面我们来看一些关于光的干涉的习题与答案。
习题一:两束相干光波在空气中相遇,它们的波长分别为600nm和450nm,求它们的相位差。
解答:相位差可以用公式Δφ=2πΔx/λ来计算,其中Δx为两束光波的光程差,λ为光波的波长。
由于光程差Δx=0,所以相位差Δφ=0。
习题二:在双缝干涉实验中,两个狭缝间距为0.2mm,波长为500nm的光波垂直入射到狭缝上,求干涉条纹的间距。
解答:干涉条纹的间距可以用公式dλ/D来计算,其中d为狭缝间距,λ为光波的波长,D为观察屏到狭缝的距离。
代入数据可得,间距为0.1mm。
习题三:在双缝干涉实验中,两个狭缝间距为0.1mm,波长为600nm的光波垂直入射到狭缝上,观察屏到狭缝的距离为2m,求干涉条纹的间距。
解答:代入数据可得,间距为0.3mm。
通过以上习题与答案,我们可以看到光的干涉现象在实际问题中的应用。
对于学习光学的同学来说,掌握光的干涉原理和计算方法是非常重要的。
希望大家能够通过练习,加深对光的干涉现象的理解,提高解决实际问题的能力。
(完整版)6光的干涉习题详解
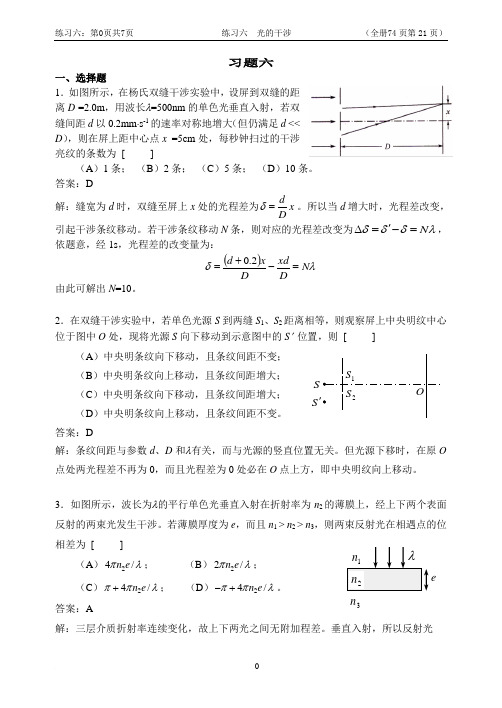
练习六:第0页共7页 练习六 光的干涉 (全册74页第21页)习题六一、选择题1.如图所示,在杨氏双缝干涉实验中,设屏到双缝的距离D =2.0m ,用波长λ=500nm 的单色光垂直入射,若双缝间距d 以0.2mm ⋅s -1的速率对称地增大(但仍满足d << D ),则在屏上距中心点x =5cm 处,每秒钟扫过的干涉亮纹的条数为 [ ] (A )1条; (B )2条; (C )5条; (D )10条。
答案:D解:缝宽为d 时,双缝至屏上x 处的光程差为dx Dδ=。
所以当d 增大时,光程差改变,引起干涉条纹移动。
若干涉条纹移动N 条,则对应的光程差改变为N δδδλ'∆=-=,依题意,经1s ,光程差的改变量为:()λδN Dxd D x d =-+=2.0 由此可解出N =10。
2.在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明纹中心位于图中O 处,现将光源S 向下移动到示意图中的S ' 位置,则 [ ](A )中央明条纹向下移动,且条纹间距不变; (B )中央明条纹向上移动,且条纹间距增大; (C )中央明条纹向下移动,且条纹间距增大; (D )中央明条纹向上移动,且条纹间距不变。
答案:D解:条纹间距与参数d 、D 和λ有关,而与光源的竖直位置无关。
但光源下移时,在原O 点处两光程差不再为0,而且光程差为0处必在O 点上方,即中央明纹向上移动。
3.如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉。
若薄膜厚度为e ,而且n 1 > n 2 > n 3,则两束反射光在相遇点的位相差为 [ ](A )24/n e πλ; (B )22/n e πλ; (C )24/n e ππλ+; (D )24/n e ππλ-+。
答案:A解:三层介质折射率连续变化,故上下两光之间无附加程差。
光的干涉计算题及答案

《光的干涉》计算题1.在双缝干涉实验中,用波长=546.1nm (1 nm=10-9 m)的单色光照射,双缝与屏的距离D=300 mm .测得中央明条纹两侧的两个第五级明条纹的间距为12.2 mm ,求双缝间的距离.解:由题给数据可得相邻明条纹之间的距离为 ∆x =12.2 / (2×5)mm =1.22 mm 2分 由公式 ∆x =D / d ,得d =D / ∆x =0.134 mm 3分2. 在图示的双缝干涉实验中,若用薄玻璃片(折射率n 1=1.4)覆盖缝S 1,用同样厚度的玻璃片(但折射率n 2=1.7)覆盖缝S 2,将使原来未放玻璃时屏上的中央明条纹处O 变为第五级明纹.设单色光波长=480 nm(1nm=109m),求玻璃片的厚度d (可认为光线垂直穿过玻璃片).解:原来, = r 2-r 1= 02分 覆盖玻璃后, =( r 2 + n 2d – d )-(r 1 + n 1d -d )=5 3分 ∴ (n 2-n 1)d =5 125n n d -=λ 2分 = 8.0×10-6 m 1分3. 薄钢片上有两条紧靠的平行细缝,用波长=546.1 nm (1 nm=10-9 m)的平面光波正入射到钢片上.屏幕距双缝的距离为D =2.00 m ,测得中央明条纹两侧的第五级明条纹间的距离为x =12.0 mm .(1) 求两缝间的距离. (2) 从任一明条纹(记作0)向一边数到第20条明条纹,共经过多大距离? (3) 如果使光波斜入射到钢片上,条纹间距将如何改变?解:(1) x = 2kD / dd = 2kD /x 2分 此处 k =5∴ d =10 D / x =0.910 mm 2分(2) 共经过20个条纹间距,即经过的距离l =20 D / d =24 mm 2分(3) 不变 2分4. 在双缝干涉实验中,单色光源S 0到两缝S 1和S 2的距离分别为l 1和l 2,并且l 1-l 2=3,为入射光的波长,双缝之间的距离为d ,双缝到屏幕的距离为D (D >>d ),如图.求: (1) 零级明纹到屏幕中央O 点的距离. (2) 相邻明条纹间的距离.S 1 S 2 n 2 n 1 r 1 r 2 d 屏 d S 2S 1 l 1 S 0 l 2 D解:(1) 如图,设P 0为零级明纹中心则 D O P d r r /012≈- 3分(l 2 +r 2) (l 1 +r 1) = 0∴ r 2 – r 1 = l 1 – l 2 = 3 ∴ ()d D d r r D O P /3/120λ=-= 3分 (2) 在屏上距O 点为x 处, 光程差 λδ3)/(-≈D dx 2分 明纹条件 λδk ±= (k =1,2,....) ()d D k x k /3λλ+±=在此处令k =0,即为(1)的结果.相邻明条纹间距d D x x x k k /1λ=-=+∆ 2分5. 在双缝干涉实验中,用波长=500 nm 的单色光垂直入射到双缝上,屏与双缝的距离D =200 cm ,测得中央明纹两侧的两条第十级明纹中心之间距离为Δx =2.20 cm ,求两缝之间的距离d .(1nm=109m)解:相邻明纹间距 x 0 = D / d 2分两条缝之间的距离 d = D / x 0 =D / (x / 20) =20 D /x= 9.09×10-2 cm 3分6. 双缝干涉实验装置如图所示,双缝与屏之间的距离D =120cm ,两缝之间的距离d =0.50 mm ,用波长=500 nm (1 nm=10-9 m)的单色光垂直照射双缝. (1) 求原点O (零级明条纹所在处)上方的第五级明条纹的坐标x . (2) 如果用厚度l =1.0×10-2 mm , 折射率n =1.58的透明薄膜复盖在图中的S 1缝后面,求上述第五级明条纹的坐标x .解:(1) ∵ dx / D ≈ kx ≈Dk / d = (1200×5×500×10-6 / 0.50)mm= 6.0 mm 4分(2) 从几何关系,近似有r 2-r 1≈ D x /d '有透明薄膜时,两相干光线的光程差 = r 2 – ( r 1 –l +nl ) = r 2 – r 1 –(n -1)l ()l n D x 1/d --'= 对零级明条纹上方的第k 级明纹有 λδk = 零级上方的第五级明条纹坐标()[]d k l n D x /1λ+-=' 3分=1200[(1.58-1)×0.01±5×5×10-4] / 0.50mm=19.9 mm 3分O 0 r 1 r 2 Dl 2 s 1 s 2 d l1 0x x λ S 1S 2 d DP r 1r 2 d λ s 1 s 2d n l x 'D7. 在如图所示的瑞利干涉仪中,T 1、T 2是两个长度都是l 的气室,波长为的单色光的缝光源S 放在透镜L 1的前焦面上,在双缝S 1和S 2处形成两个同相位的相干光源,用目镜E 观察透镜L 2焦平面C 上的干涉条纹.当两气室均为真空时,观察到一组干涉条纹.在向气室T 2中充入一定量的某种气体的过程中,观察到干涉条纹移动了M 条.试求出该气体的折射率n (用已知量M ,和l 表示出来).解:当T 1和T 2都是真空时,从S 1和S 2来的两束相干光在O 点的光程差为零.当T 1中充入一定量的某种气体后,从S 1和S 2来的两束相干光在O 点的光程差为(n – 1)l . 1分 在T 2充入气体的过程中,观察到M 条干涉条纹移过O 点,即两光束在O 点的光程差改变了M .故有(n -1)l -0 = M 3分 n =1+M / l . 1分8.用波长=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少?解: 明纹, 2ne +λ21=k (k =1,2,…)3分 第五条,k =5, ne 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分9. 在Si 的平表面上氧化了一层厚度均匀的SiO 2薄膜.为了测量薄膜厚度,将它的一部分磨成劈形(示意图中的AB 段).现用波长为600 nm 的平行光垂直照射,观察反射光形成的等厚干涉条纹.在图中AB 段共有8条暗纹,且B 处恰好是一条暗纹,求薄膜的厚度.(Si 折射率为3.42,SiO 2折射率为1.50)解:上下表面反射都有相位突变,计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹,2ne =21( 2k +1 ), (k =0,1,2,…) 2分 A 处为明纹,B 处第8个暗纹对应上式k =7 1分()n k e 412λ+==1.5×10-3 mm 2分E OC L 2L 1T 1T 2l S 1S 2λS Si A B SiO ,膜10. 图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .(1) 求入射光的波长.(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.解:(1) 明环半径 ()2/12λ⋅-=R k r 2分()R k r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R )对于r =1.00 cm , k =r 2 / (R )+0.5=50.5 3分故在OA 范围内可观察到的明环数目为50个. 1分11. 波长为的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹.(1) 从形膜顶部O 开始向右数起,第五条暗纹中心所对应的薄膜厚度e 5是多少?(2) 相邻的二明纹所对应的薄膜厚度之差是多少?解:∵ n 1<n 2<n 3,二反射光之间没有附加相位差,光程差为= 2n 2 e 第五条暗纹中心对应的薄膜厚度为e 5, 2n 2 e 5 = (2k - 1)/ 2 k = 5()2254/94/152n n e λλ=-⨯= 3分 明纹的条件是 2n 2 e k = k相邻二明纹所对应的膜厚度之差e = e k+1-e k = / (2n 2) 2分O A n 2n 13O λ。
第 9 章 光的干涉.习题答案

第9章 光的干涉 习题9.1 在杨氏实验中,若对实验装置做如下调节,干涉条纹将如何变化?(1)入射光的波长变大;(2)用一折射率为n 、厚度为t 的透明介质片覆盖其中一条狭缝(n >1);(3)双缝之间的距离逐渐变大;(4)将整个装置置于折射率为n >1的透明介质中。
解 杨氏实验的干涉条纹有如下特点:对一定波长的单色光来说,相邻明条纹(或暗条纹)的间距相等,均为/y l d λΔ=,式中l 为双缝到屏幕的距离,d 为双缝的间距,因此有(1)入射光的波长变大,相邻条纹间距变大。
(2)用一个折射率为n 、厚度为t 的透明介质片覆盖其中一条狭缝(n >1),由该狭缝发出的光的光程将增加(-1)n t ,中央明纹中心的位置将向覆盖介质片的方向移动,移动条数为(-1)/n t λ,因为相邻条纹明对应的光程差之差为λ。
原来中央明纹中心的位置将变成(-1)/n t λ级明纹的中心。
(3)双缝之间的距离逐渐变大,相邻条纹间距变小。
(4)将整个装置置于折射率为n >1的透明介质中,因由双缝S 1、S 2发出的光到达任意点P 处的光程差为 21()n r r δ=−=lyd n =λk ± (1) 式(1)中y 为点P 相对点O 的坐标,k 级明条纹中心的位置是,0,1,2,l y k k ndλ=±=" (2) 因而相邻明条纹(或暗条纹)的间距相等,所以均为 nd l y λ=Δ 可以看出,将整个装置置于折射率为n >1的透明介质中,条纹间距会变小。
9.2 由汞弧灯发出的光,通过一个绿色滤光片后,照射到相距为0.50mm 的双缝上,在距双缝 2.5m 的屏幕上观测其干涉条纹。
若测得相邻两明条纹中心的距离为 2.72mm ,求入射光的波长。
解 因对一定波长的单色光来说,相邻明条纹(或暗条纹)的间距相等为2.72mm y Δ=。
已知双缝到屏幕的距离l=2.5m ,双缝d=0.50mm ,根据双缝干涉条纹间距公式可得入射光的波长为42.720.5 5.4410(mm)544nm 2500y d l λ−Δ⋅×===×=9.3 两列相干光束的振幅比分别为E 01/E 02=1,1/3,3,6,1/6。
第一章--光的干涉--习题及答案

λdr y 0=∆第一章 光的干涉●1.波长为nm 500的绿光投射在间距d 为cm 022.0的双缝上,在距离cm 180处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为nm 700的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离.解:由条纹间距公式λd r y y y j j 01=-=∆+得:●2.在杨氏实验装置中,光源波长为nm 640,两狭缝间距为mm 4.0,光屏离狭缝的距离为cm 50.试求:<1>光屏上第1亮条纹和中央亮条纹之间的距离;〔2〕若p 点离中央亮条纹为mm 1.0,问两束光在p 点的相位差是多少?〔3〕求p 点的光强度和中央点的强度之比.解:〔1〕由公式: 得λd r y 0=∆=cm100.8104.64.05025--⨯=⨯⨯〔2〕由课本第20页图1-2的几何关系可知(3)由公式2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆=得●3. 把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m .解:未加玻璃片时,1S 、2S 到P 点的光程差,由公式2rϕπλ∆∆=可知为 Δr =215252r r λπλπ-=⨯⨯=现在1S 发出的光束途中插入玻璃片时,P 点的光程差为所以玻璃片的厚度为4. 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解:6050050010 1.250.2r y d λ-∆==⨯⨯=mm5. 波长为700nm 的光源与菲涅耳双镜的相交棱之间距离为20cm ,棱到光屏间的距离L为180cm ,若所得干涉条纹中相邻亮条纹的间隔为1mm ,求双镜平面之间的夹角θ.解:64()(2001800)70010sin 3510222001r L r y λθθ--++⨯⨯====⨯∆⨯⨯弧度12'≈6. 在题1.6图所示的劳埃德镜实验中,光源S 到观察屏的距离为1.5m ,到劳埃德镜面的垂直距离为2mm .劳埃德镜长40cm ,置于光源和屏之间的中央.<1>若光波波长λ=500nm ,问条纹间距是多少?<2>确定屏上可以看见条纹的区域大小,此区域内共有几条条纹?<提示::产生干涉的区域P 1P 2可由图中的几何关系求得.>解:〔1P 点位置为1y ()01212d r r ⨯'-〔3〕劳埃镜干涉存在半波损失现象 N ∴暗yy =∆N 亮=N 暗1- 2.311121110.1875y y =-=-=-=∆条亮纹●7. 试求能产生红光<λ=700nm>的二级反射干涉条纹的肥皂膜厚度.已知肥皂膜折射率为1.33,且平行光与法向成30°角入射.解:根据题意●8. 透镜表面通常镀一层如MgF 2〔n=1.38〕一类的透明物质薄膜,目的是利用干涉来降低玻璃表面的反射.为了使透镜在可见光谱的中心波长〔550nm 〕处产生极小的反射,则镀层必须有多厚?解:可以认为光是沿垂直方向入射的.即︒==021i i由于上下表面的反射都由光密介质反射到光疏介质,所以无额外光程差.因此光程差nh i nh 2cos 22==δ2mmP 2P 1 P 0题1.6图如果光程差等于半波长的奇数倍即公式2)12(λ+=∆j r ,则满足反射相消的条件因此有2)12(2λ+=j nh所以),1,20(4)12( =+=j n j h λ当0=j 时厚度最小cm10nm 64.9938.1455045-min ≈=⨯==nh λ●9. 在两块玻璃片之间一边放一条厚纸,另一边相互压紧.玻璃片l 长10cm,纸厚为0.05mm,从60°的反射角进行观察,问在玻璃片单位长度内看到的干涉条纹数目是多少?设单色光源波长为500nm.解:由课本49页公式〔1-35〕可知斜面上每一条纹的宽度所对应的空气尖劈的厚度的变化量为1221221sin 2i n n h h h j j -=-=∆+λ如果认为玻璃片的厚度可以忽略不记的情况下,则上式中︒===60,1122i n n .而厚度h 所对应的斜面上包含的条纹数为故玻璃片上单位长度的条纹数为1010100==='l N N 条/厘米●10. 在上题装置中,沿垂直于玻璃片表面的方向看去,看到相邻两条暗纹间距为1.4mm.—已知玻璃片长17.9cm,纸厚0.036mm,求光波的波长.解:依题意,相对于空气劈的入射角220,cos 1.sin i i θ==L d==θtan 0.12=n 11. 波长为400760nm 的可见光正射在一块厚度为1.2×10-6m,折射率为1.5玻璃片上,试问从玻璃片反射的光中哪些波长的光最强.解:依题意,反射光最强即为增反膜的相长干涉,则有:故1242+=j d n λ当0=j 时,nm 7200102.15.14432=⨯⨯⨯==-d n λ 当1=j 时,nm24003102.15.143=⨯⨯⨯=-λ 当2=j 时,nm14405102.15.143=⨯⨯⨯=-λ当3=j 时,nm10707102.15.143=⨯⨯⨯=-λ当4=j 时,nm8009102.15.143=⨯⨯⨯=-λ 当5=j 时,nm5.65411102.15.143=⨯⨯⨯=-λ 当6=j 时,nm8.55313102.15.143=⨯⨯⨯=-λ 当7=j 时,nm48015102.15.143=⨯⨯⨯=-λ 当8=j 时,nm5.42317102.15.143=⨯⨯⨯=-λ 当9=j 时,nm37819102.15.143=⨯⨯⨯=-λ所以,在nm 760~390的可见光中,从玻璃片上反射最强的光波波长为12. 迈克耳孙干涉仪的反射镜M 2移动0.25mm 时,看到条纹移过的数目为909个,设光为垂直入射,求所用光源的波长.解:根据课本59页公式可知,迈克耳孙干涉仪移动每一条条纹相当h 的变化为:现因 02=i , 故2λ=∆h909=N 所对应的h 为故13. 迈克耳孙干涉仪平面镜的面积为4×4cm 2,观察到该镜上有20个条纹.当入射光的波长为589nm 时,两镜面之间的夹角为多大?解: 因为2cm 44⨯=S所以40mm cm 4==L所以mm 22040===∆N L L又因为θλ2=∆L所以()73.301025.1471022589266''=⨯=⨯⨯=∆=-rad Lλθ14. 调节一台迈克耳孙干涉仪,使其用波长为500nm 的扩展光源照明时会出现同心圆环条纹.若要使圆环中心处相继出现1000条圆环条纹,则必须将移动一臂多远的距离?若中心是亮的,试计算第一暗环的角半径.〔提示:圆环是等倾干涉图样.计算第一暗环角半径是可利用θ≈sin θ与cos θ≈1-θ2/2的关系.〕解:〔1〕因为光程差δ每改变一个波长λ的距离,就有一亮条A 纹移过.所以λδN =∆又因为对于迈克耳孙干涉仪光程差的改变量d ∆=∆2δ〔Δd 为反射镜移动的距离〕所以d N ∆==∆2λδ所以0.25mm nm 10255002100024=⨯=⨯==∆λN d〔2〕因为迈克耳孙干涉仪无附加光程差并且021==i i 0.121==n n它形成等倾干涉圆环条纹,假设反射面的相位不予考虑 所以光程差12222cos 2l l d i d -===δ即两臂长度差的2倍若中心是亮的,对中央亮纹有: λj d =2〔1〕对第一暗纹有:()212cos 22λ-=j i d 〔2〕〔2〕-〔1〕得:()2cos 122λ=-i d所以︒====1.8rad 032.01000122di λ这就是等倾干涉条纹的第一暗环的角半径,可见2i 是相当小的.15. 用单色光观察牛顿环,测得某一亮环的直径为3mm,在它外边第5个亮环的直径为4.6mm,所用平凸透镜的凸面曲率半径为1.03m,求此单色光的波长.解:对于亮环,有Rj r j 2)12(λ+=〔 ,3,2,1,0=j 〕所以λR j r j )21(2+=λR j r j )215(25++=+所以590.3nm mm 10903.51030540.36.4545422225225=⨯=⨯⨯-=⨯⨯-=-=-++R d d Rr r jj j j λ16. 在反射光中观察某单色光所形成的牛顿环.其第2级亮环与第3级亮环间距为1mm,求第19和20级亮环之间的距离.解:对于亮环,有Rj r j 2)12(λ+=〔 ,3,2,1,0=j 〕所以R r λ)211(1+=Rr λ)212(2+=又根据题意可知两边平方得所以1541-=R λ故RR r r λλ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=-211921201920 17 牛顿环可有两个曲率半径很大的平凸透镜之间的空气产生〔图〕.平凸透镜A 和B 的曲率半径分别为AR 和BR ,在波长为600nm 的单射光垂直照射下观察到第10个暗环半径4ABrmm=.若另有曲率半径为CR 的平凸透镜C 〔图中未画出〕,并且B 、C 组合和A 、C组合产生的第10个暗环半径分别为4.5BC r mm=和5AC r mm=,试计算AR 、BR 和CR .解:22r h R =22211()22211,()211()2AB AB AB ABA B A B A BBC BC B CAC AC A Cr r r h h h R R R R r h R R r h R R ∴=+=+=+=+=+同理又对于暗环:2(21)22h j λλδ=-=+即2h jλ=∴21110()ABA Br R R λ=+ <1>21110()BC B Cr R R λ=+ <2>21110()AC A B r R R λ=+ <3>18 菲涅尔双棱镜实验装置尺寸如下:缝到棱镜的距离为5cm ,棱镜到屏的距离为95cm ,棱镜角为'17932α=构成棱镜玻璃材料的折射率'1.5n =,采用的是单色光.当厚度均匀的肥皂膜横过双冷静的一半部分放置,该系统中心部分附近的条纹相对原先有0.8mm 的位移.若肥皂膜的折射率为 1.35n =, 试计算肥皂膜厚度的最小值为多少? 解:如图所示:光源和双棱镜系统的性质相当于相干光源1s 和2s ,它们是虚光源.由近似条件'(1)n Aθ≈-和1()2d lθ≈得'22(1)d l l n Aθ==- <1>按双棱镜的几何关系得2A απ+=所以'142A πα-== <2>肥皂膜插入前,相长干涉的条件为0dy j r λ= <3>由于肥皂膜的插入,相长干涉的条件为'(1)d y n t j r λ+-= <4>由<3>和 <4>得'''00()2(1)()(1)(1)d y y l n A y y t r n r n ---==--代入数据得74.9410t m -=⨯19 将焦距为50cm 的会聚透镜中央部分C 切去〔见题图〕,余下的A 、B 两部分仍旧粘起来,C 的宽度为1cm .在对称轴线上距透镜25cm 处置一点光源,发出波长为692nm 的红宝石激光,在对称轴线上透镜的另一侧50cm 处置一光屏,平面垂直于轴线.试求:S S<a><b>题1.18图<1>干涉条纹的间距是多少?<2>光屏上呈现的干涉图样是怎样的?解:<1>透镜由A、B两部分粘合而成,这两部分的主轴都不在该光学系统的中心轴线上,A部分的主轴在中心线上0.5cm处,B部分的主轴在中心线下0.5cm处,由于单色点光源P经凸透镜A和B所成的像是对称的,故仅需考虑P经B的成像位置即可.由111''s s f-=得'50s cm=-由因为''y sy sβ==所以''1s yy cms==即所成的虚像在B的主轴下方1cm处,也就是在光学系统对称轴下方0.5cm处,同理,单色光源经A所成的虚像在光学系统对称轴上方0.5cm处,两虚像构成相干光源,它们之间的距离为1cm,所以36.9210y r cmdλ-∆==⨯<2>光屏上呈现的干涉条纹是一簇双曲线.20将焦距为5cm的薄透镜L沿直线方向剖开〔见题图〕分成两部分A和B,并将A部分沿主轴右移至2.5cm处,这种类型的装置称为梅斯林对切透镜.若将波长为632.8nm的点光源P置于主轴上离透镜L B距离为10cm处,试分析:<1> 成像情况如何?<2>若在L B右边10.5cm处置一光屏,则在光屏上观察到的干涉图样如何?解:〔1〕如图〔b〕所示,该情况可以看作由两个挡掉一半的透镜L A和L B构成,其对称轴为PO,但是主轴和光心却发生了平移.对于透镜L A,其光心移到O A处,而主轴上移0.01cm到O A F A;对于透镜L B,其光心移到O B处,而主轴下移0.01cm到O B F B.点光源P恰恰在透镜的对称轴上二倍焦距处.由于物距和透镜L A、L B的焦距都不变,故通过L A 、L B成像的像距也不变.根据物像公式将p=-10cm和'f=5cm代入上式,得'p=5cm'yyβ=='pp=-1故'y=-0.01 cm由于P点位于透镜L A的光轴下方0.01 cm,按透镜的成像规律可知,实像P A应在透镜L A 主轴上方0.01 cm处;同理,P点位于透镜L B主轴上方0.01 cm处, 实像P B应在主轴下方0.01 cm处.两像点的距离为上方0.01 cm处.P A P B=d=2|'y|+hC题1.19图=0.04cm<2>由于实像P A 和P B 构成了一对相干光源,而且相干光束在观察屏的区域上是相互交叠的,故两束光叠加后将发生光的干涉现象,屏上呈现干涉花样.按杨氏干涉规律,两相邻亮条纹的间距公式为将数据代入得y ∆=1.582mm21 如图所示,A 为平凸透镜,B 为平玻璃板,C 为金属柱,D 为框架,A 、B 间有空隙,图中绘出的是接触的情况,而A 固结在框架的边缘上.温度变化时,C 发生伸缩,而假设A 、B 、D 都不发生伸缩.以波长632.8nm 的激光垂直照射.试问: <1>在反射光中观察时,看到牛顿环条纹移向中央,这表示金属柱C 的长度在增加还是减小?<2>若观察到有10个亮条纹移向中央而消失,试问C 的长度变化了对少毫米?解:〔1〕因为:在反射光中观察牛顿环的亮条纹,与干涉级j 随着厚度h 的增加而增大,即随着薄膜厚度的增加,任意一个指定的j 级条纹将缩小其半径,所以各条纹逐渐收缩而在中心处消失, 膜厚h 增加就相当于金属的长度在缩短.所以,看到牛顿环条纹移向中央时,表明C 的长度在减少.〔2〕由2/)(2/λλj N h ∆==∆ 得3164h nm ∆=.D题 1.21。
(完整版)光的干涉练习题及答案

(完整版)光的干涉练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题1、严格地讲,空气折射率大于1,因此在牛顿环实验中,若将玻璃夹层中的空气逐渐抽去而成为真空时,干涉环将:( )A.变大;B.缩小;C.不变;D.消失。
【答案】:A2、在迈克耳逊干涉仪的一条光路中,放入一折射率n ,厚度为h 的透明介质板,放入后,两光束的光程差改变量为:( )A.h n )1(2-;B.nh 2;C.nh ;D.h n )1(-。
【答案】:A3、用劈尖干涉检测工件(下板)的表面,当波长为λ的单色光垂直入射时,观察到干涉条纹如图。
图中每一条纹弯曲部分的顶点恰与左边相邻的直线部分的连线相切。
由图可见工件表面: ( )A.一凹陷的槽,深为λ/4;B.有一凹陷的槽,深为λ/2;C.有一凸起的埂,深为λ/4;D.有一凸起的埂,深为λ。
【答案】:B4、牛顿环实验装置是用一平凸透镜放在一平板玻璃上,接触点为C ,中间夹层是空气,用平行单色光从上向下照射,并从下向上观察,看到许多明暗相间的同心圆环,这些圆环的特点是:( )是明的,圆环是等距离的; 是明的,圆环是不等距离的;是暗的,圆环是等距离的; 是暗的,圆环是不等距离的。
【答案】:B5、若将牛顿环玻璃夹层中的空气换成水时,干涉环将: ( )A .变大;B .缩小;C .不变;D .消失。
【答案】:B6、若把牛顿环装置(都是用折射率为的玻璃制成的)由空气搬入折射率为的水中,则干涉条纹 ( )A .中心暗斑变成亮斑;B .变疏;C .变密;D .间距不变。
【答案】:C7、两个不同的光源发出的两个白光光束,在空间相遇是不会产生干涉图样的,这是由于( )A.白光是由许多不同波长的光组成;B.两个光束的光强不一样;C.两个光源是独立的不相干光源;D.两个不同光源所发出的光,频率不会恰好相等。
【答案】:C8、在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于O处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《光的干涉》计算题
1.在双缝干涉实验中,用波长λ=546.1nm (1 nm=10-9 m)的单色光照射,双缝与屏的距离D
=300 mm .测得中央明条纹两侧的两个第五级明条纹的间距为12.2 mm ,求双缝间的距离.
解:由题给数据可得相邻明条纹之间的距离为
∆x =12.2 / (2×5)mm =1.22 mm 2分
由公式 ∆x =D λ / d ,得d =D λ / ∆x =0.134 mm 3分
2. 在图示的双缝干涉实验中,若用薄玻璃片(折射率n 1=1.4)覆盖缝S 1,用同样厚度的玻璃片(但折射率n 2=1.7)覆盖缝S 2,将使原来未放玻璃时屏上的中央明条纹处O 变为第五级明纹.设
单色光波长λ=480 nm(1nm=109m ),求玻璃片的厚度d (可认为光线垂直穿过玻璃片).
解:原来, δ = r 2-r 1= 0
2分
覆盖玻璃后, δ=( r 2 + n 2d – d )-(r 1 + n 1d -d )=5λ 3分
∴ (n 2-n 1)d =5λ 1
25n n d -=λ 2分 = 8.0×10-6 m 1分
3. 薄钢片上有两条紧靠的平行细缝,用波长λ=546.1 nm (1 nm=10-9 m)的平面光波正入射到
钢片上.屏幕距双缝的距离为D =2.00 m ,测得中央明条纹两侧的第五级明条纹间的距离为∆x =12.0 mm .
(1) 求两缝间的距离.
(2) 从任一明条纹(记作0)向一边数到第20条明条纹,共经过多大距离?
(3) 如果使光波斜入射到钢片上,条纹间距将如何改变?
解:(1) x = 2kD λ / d
d = 2kD λ /∆x 2分
此处 k =5
∴ d =10 D λ / ∆x =0.910 mm 2分
(2) 共经过20个条纹间距,即经过的距离
l =20 D λ / d =24 mm 2分
(3) 不变 2分
4. 在双缝干涉实验中,单色光源S 0到两缝S 1和S 2的距离分别为l 1和l 2,并且l 1-l 2=3λ,λ为入射光的波长,双缝之间的距离为d ,双缝到屏幕的距离为D (D >>d ),如图.求: (1) 零级明纹到屏幕中央O 点的距离. (2) 相邻明条纹间的距离.
S 1 S 2 n 2 n 1 r 1 r 2 d 屏 d S 2
S 1 l 1 S 0 l 2 D
解:(1) 如图,设P 0为零级明纹中心
则 D O P d r r /012≈- 3分
(l 2 +r 2) - (l 1 +r 1) = 0
∴ r 2 – r 1 = l 1 – l 2 = 3λ ∴ ()d D d r r D O P /3/120λ=-= 3分 (2) 在屏上距O 点为x 处, 光程差 λδ3)/(-≈D dx 2分 明纹条件 λδk ±= (k =1,2,....) ()d D k x k /3λλ+±=
在此处令k =0,即为(1)的结果.相邻明条纹间距
d D x x x k k /1λ=-=+∆ 2分
5. 在双缝干涉实验中,用波长λ=500 nm 的单色光垂直入射到双缝上,屏与双缝的距离D =200 cm ,测得中央明纹两侧的两条第十级明纹中心之间距离为Δx =2.20 cm ,求两缝之间的距离d .(1nm=109m)
解:相邻明纹间距 ∆x 0 = D λ / d 2分
两条缝之间的距离 d = D λ / ∆x 0 =D λ / (∆x / 20) =20 D λ/∆x
= 9.09×10-2 cm 3分
6. 双缝干涉实验装置如图所示,双缝与屏之间的距离D =120 cm ,两缝之间的距离d =0.50 mm ,用波长λ=500 nm (1 nm=10-9 m)的单色光垂直照射双缝. (1) 求原点O (零级明条纹所在处)上方的第五级明条纹的坐标x . (2) 如果用厚度l =1.0×10-2 mm , 折射率n =1.58的透明薄膜复盖在图中的S 1缝后面,求上述第五级明条纹的坐标x '.
解:(1) ∵ dx / D ≈ k λ
x ≈Dk λ / d = (1200×5×500×10-6 / 0.50)mm= 6.0 mm 4分
(2) 从几何关系,近似有
r 2-r 1≈ D x /d '
有透明薄膜时,两相干光线的光程差 δ = r 2 – ( r 1 –l +nl ) = r 2 – r 1 –(n -1)l ()l n D x 1/d --'= 对零级明条纹上方的第k 级明纹有 λδk = 零级上方的第五级明条纹坐标()[]d k l n D x /1λ+-='
3分
=1200[(1.58-1)×0.01±5×5×10-4] / 0.50mm
=19.9 mm 3分
O 0 r 1 r 2 D l 2 s 1 s 2 d
l 1 0
x
x
λ S 1
S 2 d D
P r 1
r 2 d λ s 1 s 2
d n l
x '
D
7. 在如图所示的瑞利干涉仪中,T 1、T 2是两个长度
都是l 的气室,波长为λ的单色光的缝光源S 放在透镜L 1的前焦面上,在双缝S 1和S 2处形成两个同相
位的相干光源,用目镜E 观察透镜L 2焦平面C 上的干涉条纹.当两气室均为真空时,观察到一组干涉条纹.在向气室T 2中充入一定量的某种气体的过程中,观察到干涉条纹移动了M 条.试求出该气体的
折射率n (用已知量M ,λ和l 表示出来).
解:当T 1和T 2都是真空时,从S 1和S 2来的两束相干光在O 点的光程差为零.
当T 1中充入一定量的某种气体后,从S 1和S 2来的两束相干光在O 点的光程
差为(n – 1)l . 1分
在T 2充入气体的过程中,观察到M 条干涉条纹移过O 点,即两光束在O 点的光程差改变了M λ.故有
(n -1)l -0 = M λ 3分
n =1+M λ / l . 1分
8.用波长λ=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少?
解: 明纹, 2ne +
λ21=k λ (k =1,2,…)
3分 第五条,k =5, n
e 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分
9. 在Si 的平表面上氧化了一层厚度均匀的SiO 2薄膜.为了测量薄膜厚度,将它的一部分磨成劈形(示意图中的AB 段).现用波长为600 nm 的平行光垂直照射,观察反射光形成的等厚干涉条
纹.在图中AB 段共有8条暗纹,且B 处恰好是一条暗纹,求薄
膜的厚度.(Si 折射率为3.42,SiO 2折射率为1.50)
解:上下表面反射都有相位突变π,计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹,
2ne =2
1( 2k +1 )λ, (k =0,1,2,…) 2分 A 处为明纹,B 处第8个暗纹对应上式k =7 1分 ()n
k e 412λ+=
=1.5×10-3 mm 2分
A ,膜
10. 图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜
凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察
反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .
(1) 求入射光的波长.
(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的
明环数目.
解:(1) 明环半径 ()2/12λ⋅-=R k r 2分 ()R
k r 1222
-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ)
对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分 故在OA 范围内可观察到的明环数目为50个. 1分
11. 波长为λ的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹.
(1) 从形膜顶部O 开始向右数起,第五条暗纹中心所对应的薄膜厚度e 5是多少?
(2) 相邻的二明纹所对应的薄膜厚度之差是多少?
解:∵ n 1<n 2<n 3,
二反射光之间没有附加相位差π,光程差为
δ = 2n 2 e
第五条暗纹中心对应的薄膜厚度为e 5,
2n 2 e 5 = (2k - 1)λ / 2 k = 5
()2254/94/152n n e λλ=-⨯= 3分 明纹的条件是 2n 2 e k = k λ
相邻二明纹所对应的膜厚度之差
∆e = e k+1-e k = λ / (2n 2) 2分
酒精领用流程
为了加强医院危险物品的管理,坚决杜绝火灾、爆炸等潜在事故的发生,根据本院的实际情况,制定以下科室领用酒精流程:
一、科室每年一次申请领用审批备案,根据备案数量每次领取。
O A n 2n 13O λ
对科室洒精领用的管理实行领用审批备案管理,科室在酒精领用中,需提前做好领用审批备案工作。
科室提交领用申请表(附件1:科室领用酒精审批表),经审批后方可到药库请领;备案申请期限原则上每年备案一次。
二、科室填写请领单,请领数量加上剩余实物库存数量不得大于备案最大库存量。
科室填写好请领单(附件2:科室请领酒精单),经科护长签名确认,药剂科审核后交药品会计出库。
三、药品会计凭经审核后的请领单打印出库单;
四、药库仓管员凭出库单出库发放酒精。
