BP神经网络的基本原理很清楚
BP神经网络算法原理

隐藏层节点数
合理选择隐藏层节点数 可以提高像识别、语音识别、自然语言处理等领域有广泛应用,并且不断发展和完善。
隐含层
通过多层神经元的计算和传 递信息,提取输入数据的特 征。
输出层
输出神经元将经过计算后的 结果作为最终预测或分类的 结果。
前向传播算法
前向传播是从输入层到输出层的信息流传递过程,各层神经元依次计算并传 递信息,最终得到预测结果。
反向传播算法
反向传播是通过计算输出误差对权值和偏置进行更新,以最小化输出与实际值之间的误差。
权值更新与训练过程
1
初始化权值
随机初始化权值和偏置,开始训练过程。
2
前向传播计算
通过前向传播算法计算输出结果。
3
反向传播更新
根据误差计算反向传播梯度并更新权值和偏置。
优化技巧与常见问题
学习率
学习率的选择会影响算 法的收敛速度和稳定性。
过拟合
过拟合问题可能导致训 练集表现良好但测试集 表现不佳,需要采取正 则化等方法进行处理。
BP神经网络算法原理
BP神经网络算法是一种基于误差反向传播原理的机器学习算法,用于解决复 杂的非线性问题。
BP神经网络算法的基本思想
BP神经网络通过输入层、隐含层和输出层构成,利用前向传播和反向传播的 机制不断调整权值以减小输出与真实值之间的误差。
BP神经网络的结构
输入层
负责接收外部输入数据的层 级。
bp网络原理

bp网络原理BP网络,即反向传播神经网络(Backpropagation Neural Network),是一种基于梯度下降算法的前馈神经网络。
它是一种常用的人工神经网络模型,被广泛应用于模式识别、预测和分类等任务中。
BP网络的基本原理是建立一个多层的神经网络结构,包括输入层、隐藏层和输出层。
每个神经元都与下一层的所有神经元连接,并通过权重连接进行信息传递。
输入信号从输入层经过权重连接传递到隐藏层,再经过隐藏层的激活函数作用后传递到输出层。
BP网络的训练过程主要分为前向传播和反向传播两个阶段。
在前向传播阶段,输入样本经过网络的各层神经元,得到输出结果。
每个神经元将输入信号与权重相乘并累加,然后经过激活函数进行非线性转换,得到该神经元的输出。
在反向传播阶段,通过计算输出层和期望输出之间的误差,按照梯度下降的方法不断调整每个神经元的权重,以最小化误差。
误差通过链式法则从输出层回传到隐藏层和输入层,根据权重的梯度进行更新。
反复迭代上述的前向传播和反向传播过程,直到网络的输出误差满足要求或训练次数达到指定值为止。
BP网络具有较好的非线性拟合能力和学习能力。
它的优点在于能够通过训练样本自动调整权重,从而对输入样本进行分类和预测。
然而,BP网络也存在一些问题,如容易陷入局部最小值、训练速度慢等。
为了克服BP网络的局限性,研究者们提出了一些改进方法,如改进的激活函数、正则化技术、自适应学习率等。
这些方法在提高网络性能和加速训练过程方面起到了积极的作用。
总结起来,BP网络是一种基于梯度下降算法的前馈神经网络,通过前向传播和反向传播的方式不断调整神经元的权重,以实现输入样本的分类和预测。
虽然存在一些问题,但通过改进方法可以提高其性能和训练速度。
bp神经网络的原理

bp神经网络的原理BP神经网络(也称为反向传播神经网络)是一种基于多层前馈网络的强大机器学习模型。
它可以用于分类、回归和其他许多任务。
BP神经网络的原理基于反向传播算法,通过反向传播误差来调整神经网络的权重和偏差,从而使网络能够学习和适应输入数据。
BP神经网络的基本结构包括输入层、隐藏层和输出层。
每个层都由神经元组成,每个神经元都与上一层的所有神经元连接,并具有一个权重值。
神经元的输入是上一层的输出,通过加权和和激活函数后得到输出。
通过网络中的连接和权重,每层的输出被传递到下一层,最终得到输出层的结果。
BP神经网络的训练包括两个关键步骤:前向传播和反向传播。
前向传播是指通过网络将输入数据从输入层传递到输出层,计算网络的输出结果。
反向传播是基于网络输出结果与真实标签的误差,从输出层向输入层逆向传播误差,并根据误差调整权重和偏差。
在反向传播过程中,通过计算每个神经元的误差梯度,我们可以使用梯度下降算法更新网络中的权重和偏差。
误差梯度是指误差对权重和偏差的偏导数,衡量了误差对于权重和偏差的影响程度。
利用误差梯度,我们可以将误差从输出层反向传播到隐藏层和输入层,同时更新每层的权重和偏差,从而不断优化网络的性能。
通过多次迭代训练,BP神经网络可以逐渐减少误差,并提高对输入数据的泛化能力。
然而,BP神经网络也存在一些问题,如容易陷入局部最优解、过拟合等。
为了克服这些问题,可以采用一些技巧,如正则化、随机初始权重、早停等方法。
总结而言,BP神经网络的原理是通过前向传播和反向传播算法来训练网络,实现对输入数据的学习和预测。
通过调整权重和偏差,网络可以逐渐减少误差,提高准确性。
BP人工神经网络的基本原理模型与实例

BP人工神经网络的基本原理模型与实例BP(Back Propagation)人工神经网络是一种常见的人工神经网络模型,其基本原理是模拟人脑神经元之间的连接和信息传递过程,通过学习和调整权重,来实现输入和输出之间的映射关系。
BP神经网络模型基本上由三层神经元组成:输入层、隐藏层和输出层。
每个神经元都与下一层的所有神经元连接,并通过带有权重的连接传递信息。
BP神经网络的训练基于误差的反向传播,即首先通过前向传播计算输出值,然后通过计算输出误差来更新连接权重,最后通过反向传播调整隐藏层和输入层的权重。
具体来说,BP神经网络的训练过程包括以下步骤:1.初始化连接权重:随机初始化输入层与隐藏层、隐藏层与输出层之间的连接权重。
2.前向传播:将输入向量喂给输入层,通过带有权重的连接传递到隐藏层和输出层,计算得到输出值。
3.计算输出误差:将期望输出值与实际输出值进行比较,计算得到输出误差。
4.反向传播:从输出层开始,将输出误差逆向传播到隐藏层和输入层,根据误差的贡献程度,调整连接权重。
5.更新权重:根据反向传播得到的误差梯度,使用梯度下降法或其他优化算法更新连接权重。
6.重复步骤2-5直到达到停止条件,如达到最大迭代次数或误差小于一些阈值。
BP神经网络的训练过程是一个迭代的过程,通过不断调整连接权重,逐渐减小输出误差,使网络能够更好地拟合输入与输出之间的映射关系。
下面以一个简单的实例来说明BP神经网络的应用:假设我们要建立一个三层BP神经网络来预测房价,输入为房屋面积和房间数,输出为价格。
我们训练集中包含一些房屋信息和对应的价格。
1.初始化连接权重:随机初始化输入层与隐藏层、隐藏层与输出层之间的连接权重。
2.前向传播:将输入的房屋面积和房间数喂给输入层,通过带有权重的连接传递到隐藏层和输出层,计算得到价格的预测值。
3.计算输出误差:将预测的价格与实际价格进行比较,计算得到输出误差。
4.反向传播:从输出层开始,将输出误差逆向传播到隐藏层和输入层,根据误差的贡献程度,调整连接权重。
BP神经网络的基本原理_一看就懂

BP神经网络的基本原理_一看就懂BP神经网络(Back Propagation Neural Network)是一种常用的人工神经网络模型,用于解决分类、回归和模式识别问题。
它的基本原理是通过反向传播算法来训练和调整网络中的权重和偏置,以使网络能够逐渐逼近目标输出。
1.前向传播:在训练之前,需要对网络进行初始化,包括随机初始化权重和偏置。
输入数据通过输入层传递到隐藏层,在隐藏层中进行线性加权和非线性激活运算,然后传递给输出层。
线性加权运算指的是将输入数据与对应的权重相乘,然后将结果进行求和。
非线性激活指的是对线性加权和的结果应用一个激活函数,常见的激活函数有sigmoid函数、ReLU函数等。
激活函数的作用是将线性运算的结果映射到一个非线性的范围内,增加模型的非线性表达能力。
2.计算损失:将网络输出的结果与真实值进行比较,计算损失函数。
常用的损失函数有均方误差(Mean Squared Error)和交叉熵(Cross Entropy)等,用于衡量模型的输出与真实值之间的差异程度。
3.反向传播:通过反向传播算法,将损失函数的梯度从输出层传播回隐藏层和输入层,以便调整网络的权重和偏置。
反向传播算法的核心思想是使用链式法则。
首先计算输出层的梯度,即损失函数对输出层输出的导数。
然后将该梯度传递回隐藏层,更新隐藏层的权重和偏置。
接着继续向输入层传播,直到更新输入层的权重和偏置。
在传播过程中,需要选择一个优化算法来更新网络参数,常用的优化算法有梯度下降(Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)等。
4.权重和偏置更新:根据反向传播计算得到的梯度,使用优化算法更新网络中的权重和偏置,逐步减小损失函数的值。
权重的更新通常按照以下公式进行:新权重=旧权重-学习率×梯度其中,学习率是一个超参数,控制更新的步长大小。
梯度是损失函数对权重的导数,表示了损失函数关于权重的变化率。
BP神经网络的基本原理_一看就懂

5.4 BP神经网络的基本原理BP(Back Propagation)网络是1986年由Rinehart和McClelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)(如图5.2所示)。
5.4.1 BP神经元图5.3给出了第j个基本BP神经元(节点),它只模仿了生物神经元所具有的三个最基本也是最重要的功能:加权、求和与转移。
其中x1、x2…xi…xn分别代表来自神经元1、2…i…n的输入;wj1、wj2…wji…wjn则分别表示神经元1、2…i…n与第j个神经元的连接强度,即权值;bj 为阈值;f(·)为传递函数;yj为第j个神经元的输出。
第j个神经元的净输入值为:(5.12)其中:若视,,即令及包括及,则于是节点j的净输入可表示为:(5.13)净输入通过传递函数(Transfer Function)f (·)后,便得到第j个神经元的输出:(5.14)式中f(·)是单调上升函数,而且必须是有界函数,因为细胞传递的信号不可能无限增加,必有一最大值。
5.4.2 BP网络BP算法由数据流的前向计算(正向传播)和误差信号的反向传播两个过程构成。
正向传播时,传播方向为输入层→隐层→输出层,每层神经元的状态只影响下一层神经元。
若在输出层得不到期望的输出,则转向误差信号的反向传播流程。
通过这两个过程的交替进行,在权向量空间执行误差函数梯度下降策略,动态迭代搜索一组权向量,使网络误差函数达到最小值,从而完成信息提取和记忆过程。
5.4.2.1 正向传播设 BP网络的输入层有n个节点,隐层有q个节点,输出层有m个节点,输入层与隐层之间(·),的权值为,隐层与输出层之间的权值为,如图5.4所示。
bp神经网络原理

bp神经网络原理
BP神经网络,全称为反向传播神经网络,是一种常用的前馈
神经网络,通过反向传播算法来训练网络模型,实现对输入数据的分类、回归等任务。
BP神经网络主要由输入层、隐藏层
和输出层构成。
在BP神经网络中,每个神经元都有自己的权重和偏置值。
数
据从输入层进入神经网络,经过隐藏层的计算后传递到输出层。
神经网络会根据当前的权重和偏置值计算输出值,并与真实值进行比较,得到一个误差值。
然后,误差值会反向传播到隐藏层和输入层,通过调整权重和偏置值来最小化误差值。
这一过程需要多次迭代,直到网络输出与真实值的误差达到可接受的范围。
具体而言,BP神经网络通过梯度下降算法来调整权重和偏置值。
首先,计算输出层神经元的误差值,然后根据链式求导法则,将误差值分配到隐藏层的神经元。
最后,根据误差值和激活函数的导数,更新每个神经元的权重和偏置值。
这个过程反复进行,直到达到停止条件。
BP神经网络的优点是可以处理非线性问题,并且具有较强的
自适应能力。
同时,BP神经网络还可以通过增加隐藏层和神
经元的数量来提高网络的学习能力。
然而,BP神经网络也存
在一些问题,如容易陷入局部最优解,训练速度较慢等。
总结来说,BP神经网络是一种基于反向传播算法的前馈神经
网络,通过多次迭代调整权重和偏置值来实现模型的训练。
它
可以应用于分类、回归等任务,并具有较强的自适应能力。
但同时也有一些问题需要注意。
BP网络的原理与应用

BP网络的原理与应用1. 简介BP神经网络,即反向传播神经网络(Back Propagation Neural Network),是一种常见的人工神经网络模型,广泛应用于模式识别、分类、预测等领域。
它通过训练数据进行反向传播的方式来调整神经网络的权重和偏置,从而实现对输入数据的学习和预测。
2. 原理BP神经网络由输入层、隐藏层和输出层构成,每层由多个神经元组成。
其中,输入层接收外界输入的数据,隐藏层进行信号的处理和转换,最终输出层给出模型的预测结果。
BP网络的训练过程主要由两个阶段组成:前向传播和反向传播。
2.1 前向传播在前向传播阶段,输入数据经过一次性的计算和传递,从输入层逐层向前,最终记录到输出层的神经元中。
具体步骤如下: 1. 将输入数据传递给输入层神经元,每个神经元计算输入数据与其对应权重和偏置的乘积之和。
2. 将计算结果经过激活函数(如Sigmoid函数)进行处理,得到隐藏层神经元的输出。
3. 重复以上步骤,将隐藏层的输出作为下一层的输入,直到传递到输出层。
2.2 反向传播在反向传播阶段,根据训练数据与实际输出之间的差距,计算输出误差,并根据误差大小调整权重和偏置,以达到提高网络性能的目的。
具体步骤如下: 1. 计算输出层的误差,即实际输出与训练数据的差值。
2. 通过链式法则逐层计算隐藏层的误差,以及权重和偏置的调整值。
3. 更新每个神经元的权重和偏置,通过选择合适的优化算法(如梯度下降法)进行调整。
4. 重复以上步骤,通过多次迭代,不断减小预测误差和损失函数,提高网络的精确度和泛化能力。
3. 应用BP神经网络广泛应用于许多领域,如图像识别、语音识别、文本分类、金融预测等。
下面列举一些常见的应用场景:•图像识别:通过训练大量图像数据,可以实现对不同物体、人脸等的自动识别和分类。
•语音识别:通过训练大量语音数据,可以实现对语音信号的识别和转换,用于语音助手、智能家居等。
•文本分类:通过训练大量文本数据,可以实现对文本内容的分类和情感分析,用于垃圾邮件过滤、情感识别等。
BP神经网络模型的基本原理

BP神经网络模型的基本原理
1. 神经网络的定义简介:
神经网络是由多个神经元组成的广泛互连的神经网络, 能够模拟生物神经系统真实世界及物体之间所做出的交互反应. 人工神经网络处理信息是通过信息样本对神经网络的训练, 使其具有人的大脑的记忆, 辨识能力, 完成名种信息处理功能. 它不需要任何先验公式, 就能从已有数据中自动地归纳规则, 获得这些数据的内在规律, 具有良好的自学习, 自适应, 联想记忆, 并行处理和非线性形转换的能力, 特别适合于因果关系复杂的非确定性推理, 判断, 识别和分类等问题. 对于任意一组随机的, 正态的数据, 都可以利用人工神经网络算法进行统计分析, 做出拟合和预测. 基于误差反向传播(Back propagation)算法的多层前馈网络(Multiple-layer feedforward network, 简记为BP网络), 是目前应用最成功和广泛的人工神经网络.
2. BP模型的基本原理:
学习过程中由信号的正向传播与误差的逆向传播两个过程组成. 正向传播时, 模式作用于输入层, 经隐层处理后, 传入误差的逆向传播阶段, 将输出误差按某种子形式, 通过隐层向输入层逐层返回, 并“分摊”给各层的所有单元, 从而获得各层单元的参考误差或称误差信号, 以作为修改各单元权值的依据. 权值不断修改的过程, 也就是网络学习过程. 此过程一直进行到网络输出的误差准逐渐减少到可接受的程度或达到设定的学习次数为止. BP网络模型包括其输入输出模型, 作用函数模型, 误差计算模型和自学习模型. BP网络由输入层, 输出层以及一个或多个隐层节点互连而成的一种多层网, 这种结构使多层前馈网络可在输入和输出间建立合适的线性或非线性关系, 又不致使网络输出限制在-1和1之间.。
bp神经网络算法原理

bp神经网络算法原理BP神经网络算法(Backpropagation algorithm)是一种监督学习的神经网络算法,其目的是通过调整神经网络的权重和偏置来实现误差的最小化。
BP神经网络算法基于梯度下降和链式法则,在网络的前向传播和反向传播过程中进行参数的更新。
在前向传播过程中,输入样本通过网络的各个神经元计算,直到达到输出层。
每个神经元都会对上一层的输入进行加权求和,并经过一个非线性激活函数得到输出。
前向传播的结果即为网络的输出。
在反向传播过程中,首先需要计算网络的输出误差。
误差是实际输出与期望输出的差异。
然后,从输出层开始,沿着网络的反方向,通过链式法则计算每个神经元的误差贡献,并将误差从输出层反向传播到输入层。
每个神经元根据自身的误差贡献,对权重和偏置进行调整。
这一过程可以看作是通过梯度下降来调整网络参数,以最小化误差。
具体而言,对于每个样本,BP神经网络算法通过以下步骤来更新网络的参数:1. 前向传播:将输入样本通过网络,计算得到网络的输出。
2. 计算误差:将网络的输出与期望输出进行比较,计算得到输出误差。
3. 反向传播:从输出层开始,根据链式法则计算每个神经元的误差贡献,并将误差沿着网络反向传播到输入层。
4. 参数更新:根据每个神经元的误差贡献,使用梯度下降方法更新神经元的权重和偏置。
5. 重复以上步骤,直到达到预设的训练停止条件,例如达到最大迭代次数或误差小于某个阈值。
总的来说,BP神经网络算法通过计算输出误差和通过反向传播调整网络参数的方式,实现对神经网络的训练。
通过不断迭代优化网络的权重和偏置,使得网络能够更准确地进行分类、回归等任务。
BP神经网络原理及应用

BP神经网络原理及应用BP神经网络,即反向传播神经网络(Backpropagation Neural Network),是一种基于梯度下降算法的多层前馈神经网络,常用于分类与回归等问题的解决。
BP神经网络通过反向传播算法,将误差从输出层往回传播,更新网络权值,直至达到误差最小化的目标,从而实现对输入模式的分类和预测。
BP神经网络的结构包括输入层、隐藏层和输出层。
输入层接收外部输入的特征向量,隐藏层负责将输入特征映射到合适的高维空间,输出层负责输出网络的预测结果。
每个神经元与其前后的神经元相连,每个连接都有一个权值,用于调整输入信号的重要性。
BP神经网络利用激活函数(如sigmoid函数)对神经元的输出进行非线性变换,增加网络的非线性表达能力。
1.前向传播:将输入信号传递给网络,逐层计算每个神经元的输出,直至得到网络的输出结果。
2.计算误差:将网络输出与期望输出比较,计算误差。
常用的误差函数包括平方误差和交叉熵误差等。
3.反向传播:根据误差,逆向计算每个神经元的误差贡献,从输出层往回传播到隐藏层和输入层。
根据误差贡献,调整网络的权值和阈值。
4.更新权值和阈值:根据调整规则(如梯度下降法),根据误差贡献的梯度方向,更新网络的权值和阈值。
1.模式识别与分类:BP神经网络可以通过训练学习不同模式的特征,从而实现模式的自动分类与识别。
例如,人脸识别、文本分类等。
2.预测与回归:BP神经网络可以通过历史数据的训练,学习到输入与输出之间的映射关系,从而实现对未知数据的预测与回归分析。
例如,股票价格预测、天气预测等。
3.控制系统:BP神经网络可以用于建模和控制非线性系统,实现自适应、自学习的控制策略。
例如,机器人控制、工业过程优化等。
4.信号处理与图像处理:BP神经网络可以通过学习复杂的非线性映射关系,实现信号的去噪、压缩和图像的识别、处理等。
例如,语音识别、图像分割等。
5.数据挖掘与决策支持:BP神经网络可以根据历史数据学习到数据之间的相关关系,从而帮助决策者进行数据挖掘和决策支持。
bp神经网络3篇

bp神经网络第一篇:BP神经网络的基本原理BP神经网络是一种最为经典的人工神经网络之一,它在模拟神经元之间的信息传输和处理过程上有很高的效率,可以被应用于多种领域,如图像处理、模式识别、预测分析等。
BP神经网络的核心思想是通过将神经元之间的权值调整来达到优化网络结构的目的,从而提高网络的准确率和泛化能力。
BP神经网络包含三个基本部分:输入层、隐层和输出层。
其中,输入层用于接收原始数据,隐层是神经元之间信号处理的地方,而输出层则用于输出最终的结果。
与其他的神经网络不同,BP神经网络使用了反向传播算法来调整神经元之间的权值。
这个算法是一种基于梯度下降的优化方法,通过最小化目标函数来优化权值,从而获得最小的误差。
具体来说,反向传播算法分为两个步骤:前向传播和反向传播。
前向传播是指从输入层开始,将数据经过神经元的传递和处理,一直到输出层,在这个过程中会计算每一层的输出值。
这一步完成后,就会得到预测值和实际值之间的误差。
接着,反向传播将会计算每个神经元的误差,并将误差通过链式法则向后传播,以更新每个神经元的权值。
这一步也被称为误差反向传播,它通过计算每个神经元对误差的贡献来更新神经元之间的权值。
总的来说,BP神经网络的优点在于其具有灵活性和较高的准确率。
但同时也存在着过拟合和运算时间过长等问题,因此在实际应用中需要根据实际情况加以取舍。
第二篇:BP神经网络的应用BP神经网络作为一种人工智能算法,其应用范围非常广泛。
以下是BP神经网络在不同领域的应用案例。
1. 图像处理BP神经网络在图像处理方面的应用主要有两个方面:图像分类和图像增强。
在图像分类方面,BP神经网络可以通过对不同特征之间的关系进行学习,从而对图像进行分类。
在图像增强方面,BP神经网络可以根据图像的特征进行修复和增强,从而提高图像的质量。
2. 股票预测BP神经网络可以通过对历史数据的学习来预测未来股市趋势和股票价格变化,对投资者提供参考依据。
3. 语音识别BP神经网络可以对人声进行测量和分析,从而识别出人说的话,实现语音识别的功能。
机器学习-BP(back propagation)神经网络介绍
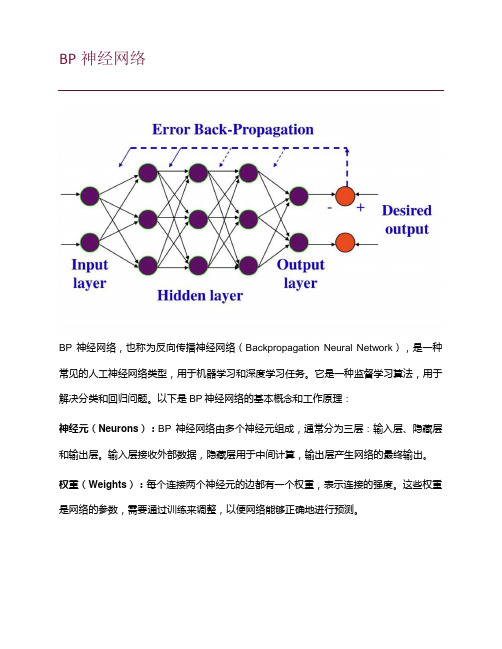
BP神经网络BP神经网络,也称为反向传播神经网络(Backpropagation Neural Network),是一种常见的人工神经网络类型,用于机器学习和深度学习任务。
它是一种监督学习算法,用于解决分类和回归问题。
以下是BP神经网络的基本概念和工作原理:神经元(Neurons):BP神经网络由多个神经元组成,通常分为三层:输入层、隐藏层和输出层。
输入层接收外部数据,隐藏层用于中间计算,输出层产生网络的最终输出。
权重(Weights):每个连接两个神经元的边都有一个权重,表示连接的强度。
这些权重是网络的参数,需要通过训练来调整,以便网络能够正确地进行预测。
激活函数(Activation Function):每个神经元都有一个激活函数,用于计算神经元的输出。
常见的激活函数包括Sigmoid、ReLU(Rectified Linear Unit)和tanh(双曲正切)等。
前向传播(Forward Propagation):在训练过程中,输入数据从输入层传递到输出层的过程称为前向传播。
数据经过一系列线性和非线性变换,最终产生网络的预测输出。
反向传播(Backpropagation):反向传播是BP神经网络的核心。
它用于计算网络预测的误差,并根据误差调整网络中的权重。
这个过程分为以下几个步骤:1.计算预测输出与实际标签之间的误差。
2.将误差反向传播回隐藏层和输入层,计算它们的误差贡献。
3.根据误差贡献来更新权重,通常使用梯度下降法或其变种来进行权重更新。
训练(Training):训练是通过多次迭代前向传播和反向传播来完成的过程。
目标是通过调整权重来减小网络的误差,使其能够正确地进行预测。
超参数(Hyperparameters):BP神经网络中有一些需要人工设置的参数,如学习率、隐藏层的数量和神经元数量等。
这些参数的选择对网络的性能和训练速度具有重要影响。
BP神经网络在各种应用中都得到了广泛的使用,包括图像分类、语音识别、自然语言处理等领域。
BP算法的基本原理

BP算法的基本原理BP算法(反向传播算法)是一种神经网络训练算法,用于更新神经网络的权重和偏置,以使之能够适应所需任务的输入输出关系。
BP算法基于梯度下降优化方法,通过求解损失函数关于权重和偏置的偏导数来进行参数更新。
其基本原理涉及到神经网络的前向传播和反向传播两个过程。
以下将详细介绍BP算法的基本原理。
1.前向传播:在神经网络的前向传播过程中,输入数据通过网络的各个层,通过各个神经元的激活函数,最终得到网络的输出。
在前向传播过程中,每个神经元接收到上一层的信号,并通过权重和偏置进行加权求和,然后经过激活函数处理后输出。
具体而言,假设神经网络有L层,第l层的神经元为h(l),输入为x,激活函数为f(l),权重为w(l),偏置为b(l)。
其中,输入层为第1层,隐藏层和输出层分别为第2层到第L层。
对于第l层的神经元h(l),其输入信号为:z(l)=w(l)*h(l-1)+b(l)其中,h(l-1)表示第(l-1)层的神经元的输出。
然后,通过激活函数f(l)处理输入信号z(l)得到第l层的输出信号:h(l)=f(l)(z(l))。
依次类推,通过前向传播过程,神经网络可以将输入信号转化为输出信号。
2.反向传播:在神经网络的反向传播过程中,根据网络的输出和真实值之间的差异,通过链式法则来计算损失函数对于各层权重和偏置的偏导数,然后根据梯度下降法则对权重和偏置进行更新。
具体而言,假设网络的输出为y,损失函数为L,权重和偏置为w和b,求解L对w和b的偏导数的过程为反向传播。
首先,计算L对于网络输出y的偏导数:δ(L)/δy = dL(y)/dy。
然后,根据链式法则,计算L对于第L层的输入信号z(L)的偏导数:δ(L)/δz(L)=δ(L)/δy*δy/δz(L)。
接着,计算L对于第(L-1)层的输入信号z(L-1)的偏导数:δ(L)/δz(L-1) = δ(L)/δz(L) * dz(L)/dz(L-1)。
依次类推,通过链式法则得到L对于各层输入信号z(l)的偏导数。
阐述bp神经网络的原理

阐述bp神经网络的原理
BP神经网络全称为反向传播神经网络,是一种常用的人工神经网络模型。
其原理基于两个基本思想:前向传播和反向误差传播。
前向传播:BP神经网络是一个多层感知器,由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层负责处理输入,并传递给输出层,输出层根据处理结果生成输出。
隐藏层和输出层的每个神经元都有一个权重向量,用于对输入数据进行线性组合。
然后,通过激活函数对线性组合结果进行非线性变换,得到该神经元的输出。
隐藏层和输出层的每个神经元的输出都会作为下一层神经元的输入。
反向误差传播:当神经网络的输出与期望输出之间存在差异时,需要通过反向传播算法来调整权重,以减小这个误差。
算法的基本思想是将误差从输出层向隐藏层逐层传递,通过调整每个神经元的权重,最终使得网络的输出与期望输出尽可能接近。
具体实现时,首先计算输出层的误差,然后根据误差调整输出层的权重。
接下来,将误差反向传播到隐藏层,再根据误差调整隐藏层的权重。
这个过程会不断迭代,直到网络的输出与期望输出的误差足够小。
通过反向误差传播算法,BP神经网络可以学习到输入-输出的映射关系,从而能
够对未知输入进行预测或分类。
然而,BP神经网络也存在一些问题,例如容易陷入局部极小值、对初始权重较敏感等,因此在实际应用中需要进行一定的调优和训练策略。
bp神经网络的基本原理

bp神经网络的基本原理
BP神经网络是一种常用的人工神经网络模型,用于解决分类和回归问题。
它的基本原理是通过反向传播算法来调整网络的权重和偏置,从而使网络能够学习和逼近输入输出之间的非线性关系。
BP神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层是网络中间的处理层,输出层给出最终的结果。
每个神经元都与前一层的神经元以及后一层的神经元相连接,每个连接都有一个权重值。
BP神经网络的学习过程首先需要给定一个训练数据集,并设置好网络的结构和参数。
然后,通过前向传播将输入数据从输入层传递到隐藏层和输出层,计算网络的输出结果。
接着,根据输出结果与实际输出之间的差异,使用误差函数来评估网络的性能。
在反向传播阶段,根据误差函数的值,利用链式法则计算每个连接的权重和偏置的梯度。
然后,根据梯度下降法更新连接的权重和偏置,使误差不断减小。
这个过程反复进行,直到网络输出的误差达到了可接受的范围或者训练次数达到了预设的最大值。
通过不断地调整权重和偏置,BP神经网络可以逐渐学习到输入输出之间的映射关系,从而在面对新的输入数据时能够给出合理的输出。
同时,BP神经网络还具有一定的容错性和鲁棒性,可以处理一些噪声和不完整的数据。
总的来说,BP神经网络的基本原理是通过反向传播算法来训练网络,将输入数据从输入层传递到输出层,并且根据实际输出与期望输出之间的差异来优化网络的权重和偏置,以达到学习和逼近输入输出之间关系的目的。
bp网络的基本原理

bp网络的基本原理bp网络是一种常用的人工神经网络模型,用于模拟和解决复杂问题。
它是一种前馈型神经网络,通过前向传播和反向传播的过程来实现信息的传递和参数的更新。
在bp网络中,首先需要定义输入层、隐藏层和输出层的神经元。
输入层接收外部输入的数据,隐藏层用于处理和提取数据的特征,输出层用于输出最终的结果。
每个神经元都有一个对应的权重和偏置,用于调节输入信号的强弱和偏移。
前向传播是bp网络中的第一步,它从输入层开始,将输入的数据通过每个神经元的加权和激活函数的运算,逐层传递到输出层。
加权和的计算公式为:S = Σ(w * x) + b其中,w是权重,x是输入,b是偏置。
激活函数则负责将加权和的结果转换为神经元的输出。
常用的激活函数有sigmoid 函数、ReLU函数等。
反向传播是bp网络的第二步,它通过比较输出层的输出与实际值之间的误差,反向计算每个神经元的误差,并根据误差调整权重和偏置。
反向传播的目标是不断减小误差,使神经网络的输出与实际值更加接近。
具体的反向传播算法是通过梯度下降法实现的,它通过计算每个神经元的误差梯度,按照梯度的方向更新权重和偏置。
误差梯度表示误差对权重和偏置的变化率,通过链式法则可以计算得到。
在更新权重和偏置时,一般使用学习率来调节更新的步长,避免权重和偏置的变化过大。
通过多次迭代的前向传播和反向传播过程,bp网络不断优化和调整参数,最终使得输出与实际值的误差达到最小。
这样的训练过程可以使bp网络逐渐学习到输入数据之间的关联性和规律性,从而达到对问题进行分类、回归等任务的目的。
总结起来,bp网络的基本原理是通过前向传播将输入的数据逐层传递并计算每个神经元的输出,然后通过反向传播根据实际输出与目标输出之间的误差来调整权重和偏置,最终达到训练和优化神经网络的目标。
BP神经网络的基本原理_一看就懂

BP神经网络的基本原理_一看就懂BP神经网络(Back propagation neural network)是一种常用的人工神经网络模型,也是一种有监督的学习算法。
它基于错误的反向传播来调整网络权重,以逐渐减小输出误差,从而实现对模型的训练和优化。
1.初始化网络参数首先,需要设置网络的结构和连接权重。
BP神经网络通常由输入层、隐藏层和输出层组成。
每个神经元与上下层之间的节点通过连接权重相互连接。
2.传递信号3.计算误差实际输出值与期望输出值之间存在误差。
BP神经网络通过计算误差来评估模型的性能。
常用的误差计算方法是均方误差(Mean Squared Error,MSE),即将输出误差的平方求和后取平均。
4.反向传播误差通过误差反向传播算法,将误差从输出层向隐藏层传播,并根据误差调整连接权重。
具体来说,根据误差对权重的偏导数进行计算,然后通过梯度下降法来更新权重值。
5.权重更新在反向传播过程中,通过梯度下降法来更新权重值,以最小化误差。
梯度下降法的基本思想是沿着误差曲面的负梯度方向逐步调整权重值,使误差不断减小。
6.迭代训练重复上述步骤,反复迭代更新权重值,直到达到一定的停止条件,如达到预设的训练轮数、误差小于一些阈值等。
迭代训练的目的是不断优化模型,使其能够更好地拟合训练数据。
7.模型应用经过训练后的BP神经网络可以应用于新数据的预测和分类。
将新的输入数据经过前向传播,可以得到相应的输出结果。
需要注意的是,BP神经网络对于大规模、复杂的问题,容易陷入局部最优解,并且容易出现过拟合的情况。
针对这些问题,可以采用各种改进的方法,如加入正则化项、使用更复杂的网络结构等。
综上所述,BP神经网络通过前向传播和反向传播的方式,不断调整权重值来最小化误差,实现对模型的训练和优化。
它是一种灵活、强大的机器学习算法,具有广泛的应用领域,包括图像识别、语音识别、自然语言处理等。
BP人工神经网络的基本原理、模型与实例
BP人工神经网络的实例
BP人工神经网络可以应用于多个领域,如图像识别、语音处理、预测分析等,为解决复杂问题提供了有效的神经网络的输入是具体问题的相关数据,比如图像数据、声音数据等。 输出是经过神经网络计算后得出的结果。
神经元和连接权重
神经元是BP人工神经网络的基本单元,通过调整连接权重来不断优化神经网 络的表现和学习能力。
前向传播和反向传播
前向传播是指输入数据从输入层经过隐藏层到达输出层的过程。反向传播是指根据误差计算,通过调整连接权 重来优化神经网络的过程。
训练和优化算法
BP人工神经网络的训练过程是通过不断调整连接权重使得神经网络的输出结 果接近于期望结果的过程。优化算法如梯度下降算法等可以加速训练的过程。
BP人工神经网络的基本 原理、模型与实例
人工神经网络(Artificial Neural Network)以人类大脑神经网络的的运作方式 为模型,用于模拟智能行为和解决复杂问题。
BP人工神经网络的基本原理
BP人工神经网络通过多层神经元和连接权重的组合,实现输入数据到输出结 果的计算和转换过程。
BP人工神经网络的模型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若视,— 〔,即令三及—'包括"及:",则其中:BP 神经网络的基本原理BP (Back Propagatio n )网络是 1986 年由 Rin ehart 和 McClelland 为首的科学家小组提出,是一种按误差逆传播算 法训练的多层前馈网络,是目前应用最广泛的神经网络模型 之一。
BP 网络能学习和存贮大量的输入-输出模式映射关系, 而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值 和阈值,使网络的误差平方和最小。
BP 神经网络模型拓扑结 构包括输入层(in put )、隐层(hide layer)和输出层(output layer)(如图所示)。
BP 神经元图给出了第j 个基本BP 神经元(节点),它只模仿了生物神经元所具有的三个最基本也是 最重要的功能:加权、求和与转移。
其中 X 1、X 2…X i …X n 分别代表来自神经元1、2…i …n 的输入;W 1、W …W i …W n 则分别表示神经元1、2…i …n 与第j 个神经元的连接强度,即权 值;b 为阈值;f( •)为传递函数;力为第j 个神经元的输出。
第j 个神经元的净输入值〔为:()输出层5.2 BP 神经阴塔结枸示意图图5.3 BP 神经无于是节点j的净输入--可表示为:()净输入-通过传递函数(Transfer Function ) f ( •)后,便得到第j个神经元的输出」」:丹=血卜f(Z松小做X)()式中f(•)是单调上升函数,而且必须是有界函数,因为细胞传递的信号不可能无限增加,必有一最大值。
BP网络BP算法由数据流的前向计算(正向传播)和误差信号的反向传播两个过程构成。
正向传播时,传播方向为输入层f隐层f输出层,每层神经元的状态只影响下一层神经元。
若在输出层得不到期望的输出,则转向误差信号的反向传播流程。
通过这两个过程的交替进行,在权向量空间执行误差函数梯度下降策略,动态迭代搜索一组权向量,使网络误差函数达到最小值,从而完成信息提取和记忆过程。
正向传播n q m图5.4三层神经网络曲拓扑结构设BP网络的输入层有n个节点,隐层有q个节点,输出层有m个节点,输入层与隐层之间的权值为% ,隐层与输出层之间的权值为'■,如图所示。
隐层的传递函数为「( •),输出层的传递函数为f2(•),贝临层节点的输出为(将阈值写入求和项中):k=1,2, ....... q()输出层节点的输出为:片二也工叫Q—j=1,2, ......... m()至此B-P网络就完成了n维空间向量对m维空间的近似映射。
反向传播1) 定义误差函数输入P个学习样本,用来表示。
第个样本输入到网络后得到输出'(j=i,2,…m。
采用平方型误差函数,于是得到第P个样本的误差&:S () 式中:「为期望输出。
对于「个样本,全局误差为:1 p w p() 2) 输出层权值的变化采用累计误差BP算法调整使全局误差己变小,即W 一 dSj _ 豁知卸血J是输出层传递函数的偏微分 于是:4亠£殍-旳从心)E由链定理得:于是输出层各神经元的权值调整公式为:△% =22^(^-刃)上(为)瓯曲冋3)隐层权值的变化6 p』()式中::一学习率 定义误差信号为:其中第一项:121=-z (^旳()第二项:()()()()()二亍I 亍另谢-刃尸八另©-疗)器 爼 E £ >1 Z-1 %號叫%3 3是隐层传递函数的偏微分。
于是:Mr r务严迟©-刃)力咼)叫』(必);-1由链定理得:込 dE… as*.*tt~ = ~~= s = -2LQ% J m从而得到隐层各神经元的权值调整公式为:定义误差信号为: 其中第一项:遞 d fpBE#皿…瓦…瓦字歼2/訂()()依链定理有:第二项:()()2>1 ()()()3厂£ (球-用M 込)叫小傀用a /-1BP 算法的改进BP 算法理论具有依据可靠、推导过程严谨好等优点,但标准BP 算法存在以下缺点:收敛速度缓慢;容易陷入局部极小值;难以确定隐层数和隐层节点个数。
在实际应用中,BP 算法很难胜任,因此出现了很多改进算法。
1) 利用动量法改进BP 算法标准BP 算法实质上是一种简单的最速下降静态寻优方法,在修正W(K)时,只按照第K 步的负梯度方向进行修正,而没有考虑到以前积累的经验,即以前时刻的梯度方向,从而常常 使学习过程发生振荡,收敛缓慢。
动量法权值调整算法的具体做法是:将上一次权值调整 量的一部分迭加到按本次误差计算所得的权值调整量上,作为本次的实际权值调整量,即:其中:a 为动量系数,通常O VaV ;n —学习率,范围在〜10之间。
这种方法所加的动 量因子实际上相当于阻尼项,它减小了学习过程中的振荡趋势,从而改善了收敛性。
动量 法降低了网络对于误差曲面局部细节的敏感性,有效的抑制了网络陷入局部极小。
2) 自适应调整学习速率标准BP 算法收敛速度缓慢的一个重要原因是学习率选择不当,学习率选得太小,收敛太慢;学习率选得太大,则有可能修正过头,导致振荡甚至发散。
可采用图所示的自适应方法调 整学习率。
调整的基本指导思想是:在学习收敛的情况下,增大n,以缩短学习时间;当n 偏大致使不能收敛时,要及时减小n, 直到收敛为止。
3) 动量-自适应学习速率调整算法采用动量法时,BP 算法可以找到更优的解;采用自适应学习速率法时, BP 算法可以缩短训练时间。
将以上两种方法结合起来,就得到动量 -自适应学习速率调整算法。
()精度较高、通用性较图55自适应学习4) L-M学习规则L-M (Levenberg-Marquardt )算法比前述几种使用梯度下降法的BP算法要快得多,但对于复杂问题,这种方法需要相当大的存储空间。
L-M(Levenberg-Marquardt)优化方法的权值调整率选为:()其中:e—误差向量;J—网络误差对权值导数的雅可比(Jacobian )矩阵;卩一标量,当卩很大时上式接近于梯度法,当卩很小时上式变成了Gauss-Newton法,在这种方法中,卩也是自适应调整的。
综合考虑,拟采用L-M学习规则和动量法分别作为神经网络的训练函数和学习函数。
BP神经网络的训练策略及结果本文借助于MATLAB申经网络工具箱来实现多层前馈BP网络(Multi-layer feed-forward backpropagation network )的颜色空间转换,免去了许多编写计算机程序的烦恼。
神经网络的实际输出值与输入值以及各权值和阈值有关,为了使实际输出值与网络期望输出值相吻合,可用含有一定数量学习样本的样本集和相应期望输出值的集合来训练网络。
训练时仍然使用本章节中所述的实测样本数据。
另外,目前尚未找到较好的网络构造方法。
确定神经网络的结构和权系数来描述给定的映射或逼近一个未知的映射,只能通过学习方式得到满足要求的网络模型。
神经网络的学习可以理解为:对确定的网络结构,寻找一组满足要求的权系数,使给定的误差函数最小。
设计多层前馈网络时,主要侧重试验、探讨多种模型方案,在实验中改进,直到选取一个满意方案为止,可按下列步骤进行:对任何实际问题先都只选用一个隐层;使用很少的隐层节点数;不断增加隐层节点数,直到获得满意性能为止;否则再采用两个隐层重复上述过程。
训练过程实际上是根据目标值与网络输出值之间误差的大小反复调整权值和阈值,直到此误差达到预定值为止。
确定BP网络的结构BP网络。
确定了网络层数、每层节点数、传递函数、初始权系数、学习算法等也就确定了确定这些选项时有一定的指导原则,但更多的是靠经验和试凑。
1) 隐层数的确定: 1998年Robert Hecht-Nielson证明了对任何在闭区间内的连续函数,都可以用一个隐层的BP网络来逼近,因而一个三层的BP网络可以完成任意的n维到m维的映照。
因此我们从含有一个隐层的网络开始进行训练。
2) BP网络常用传递函数:團北BP刚缮常用的越逛函数BP网络的传递函数有多种。
Log-sigmoid型函数的输入值可取任意值,输出值在0和1之间;ta n-sigmod型传递函数tan sig的输入值可取任意值,输出值在-1到+1之间;线性传递函数purelin的输入与输出值可取任意值。
BP网络通常有一个或多个隐层,该层中的神经元均采用sigmoid型传递函数,输出层的神经元则采用线性传递函数,整个网络的输出可以取任意值。
各种传递函数如图所示。
只改变传递函数而其余参数均固定,用本章节所述的样本集训练BP网络时发现,传递函数使用tan sig函数时要比logsig函数的误差小。
于是在以后的训练中隐层传递函数改用tan sig函数,输出层传递函数仍选用purelin函数。
3) 每层节点数的确定:使用神经网络的目的是实现摄像机输出RGB颜色空间与CIE-XYZ色空间转换,因此BP网络的输入层和输出层的节点个数分别为3。
下面主要介绍隐层节点数量的确定。
对于多层前馈网络来说,隐层节点数的确定是成败的关键。
若数量太少,则网络所能获取的用以解决问题的信息太少;若数量太多,不仅增加训练时间,更重要的是隐层节点过多还可能出现所谓“过渡吻合”(Ovefitti ng )问题,即测试误差增大导致泛化能力下降,因此合理选择隐层节点数非常重要。
关于隐层数及其节点数的选择比较复杂,一般原则是: 在能正确反映输入输出关系的基础上,应选用较少的隐层节点数,以使网络结构尽量简单。
本论文中采用网络结构增长型方法,即先设置较少的节点数,对网络进行训练,并测试学习误差,然后逐渐增加节点数,直到学习误差不再有明显减少为止。
误差的选取在神经网络训练过程中选择均方误差MSE较为合理,原因如下:①标准BP算法中,误差定义为:1甜s ()每个样本作用时,都对权矩阵进行了一次修改。
由于每次权矩阵的修改都没有考虑权值修改后其它样本作用的输出误差是否也减小,因此将导致迭代次数增加。
②累计误差BP算法的全局误差定义为:()这种算法是为了减小整个训练集的全局误差,而不针对某一特定样本,因此如果作某种修改能使全局误差减小,并不等于说每一个特定样本的误差也都能同时减小。
它不能用来比较P和m不同的网络性能。
因为对于同一网络来说,P越大,E也越大;P值相同,m越大E也越大。
③均方误差MSE()其中:咗一输出节点的个数,"一训练样本数目,二网络期望输出值,「-—网络实际输出值。
均方误差克服了上述两种算法的缺点,所以选用均方误差算法较合理。
训练结果训练一个单隐层的三层BP网络,根据如下经验公式选择隐层节点数[125]:()式中:n为输入节点个数,m为输出节点个数,a为1到10之间的常数。
