沪教版(上海)数学高三上册-14.3 直线与平面的位置关系(1) 课件 优质课件PPT
合集下载
沪教版(上海)数学高三上册-14.3 直线和平面所成角 课件 优质课件PPT

图示直:线l与其在平面上的射影OM所成的锐角叫l 做直线l和平面所成角。
A
范围:
M
O
设直线l与平面斜交于点M,
直线和平面 所
过l上任意一点A,作平面的垂线,垂足为O,我们把点O叫做点A在
成 的
定平义面:上的射影,
角
把直线OM叫做直线l在平面上的射影。
图示直:线l与其在平面上的射影OM所成的锐角叫l 做直线l和平面所成角。
小。 A
B
A’
练习:在正方体ABCD-A’B’C’D’ , 求:直线DB’和平面ABCD所成角的大小。
D A
C B
D’ A’
C’ B’
思考:在正方体ABCD—A1B1C1D1中,E是A1D1的中点,求:(1)EB
和平面ABCD所成角的大小。
D F A
C B
E
D1
D1
A1
C1 B1
思考:在正方体ABCD—A1B1C1D1中,E是A1D1的中点,求:( 2)
过l上任意一点A,作平面的垂线,垂足为O,我们把点O叫做点A在
成 的
定平义面:上的射影,
角
把直线OM叫做直线l在平面上的射影。
图示直:线l与其在平面上的射影OM所成的锐角叫l 做直线l和平面所成角。
A
范围:
M
O
设直线l与平面斜交于点M,
直线和平面 所
过l上任意一点A,作平面的垂线,垂足为O,我们把点O叫做点A在
直线与平面所成角
直线与平面相交且不垂直时,
叫直线与平面斜交,直线叫作平面的斜线
14.3 直线与平面位置关系
观察直思线考l与平面 斜交于点M,
讨论:如何定义直线与平面所成的角?
沪教版高中数学高三上册第十四章空间直线与平面的位置关系课件

D1
C1
A1
B1
G
O
用举例:
例 1、正方体 ABCD A1B1C1D1 的棱长为 a 。
(5)求直线 C1B 与平面 ACD1 所成角的大小;
D1
C1
A1
B1
D A
C B
二、应用举例:
例 1、正方体 ABCD A1B1C1D1 的棱长为 a 。
(6)求直线 C1B1 与平面 ACD1 所成角的大小。
第十四章 空间直线与平面
90
,所以 BC
AB2 AC 2 2 6 a ,
3
14.
D BC 为 第十四章 空间直线与平面 中点,所以 DC
6a ,在 RtACD 中, AD
CD2 CA2 a ,
14.
3
PA 又因为 第十四章 空间直线与平面 平面ABC ,所以 PD 在平面 ABC 上射影为 AD ,
所以 MC 就是直线 B1C 在平面 A1BCD1 上的射影,
所以 MCB1 为直线 B1C 与平面 A1BCD1 所成角,
易求 MCB1 30 , 所以直线 B1C 与平面 A1BCD1 所成角的大小为 30 ;
二、应用举例:
例 1、正方体 ABCD A1B1C1D1 的棱长为 a 。
(4)求直线 A1C 与平面 ABC1D1 所成角的大小;
14.
PDA 就是 3 空间直线与平面的位置关系(2)
第十四章 空间直线与平面
PD
与平面
ABC
所成角,PA
AD
a
,所以
PDA
45
,
PD 14. 所以 与平面
第十四章 空间直线与平面
ABC
所成角的大小为
沪教版(上海)数学高三上册-14.3 空间直线与平面的位置关系(2) 课件 教学课件

A1
可证 BC 平面A1ABB1,
所以 BC B1M ,可证得: B1M 平面A1BCD1 ,
M
所以 MC 就是直线 B1C 在平面 A1BCD1 上的射影,
D
A
所以 MCB1 为直线 B1C 与平面 A1BCD1 所成角,
易求 MCB1 30 ,
所以直线 B1C 与平面 A1BCD1 所成角的大小为 30 ;
l A
α
M
O
一、新课讲授:
2、直线和平面所成角:
(1)平面的斜线与它在平面内的射影所成的锐角,叫这条直线与这个
平面所成的角。
由定义可知:斜线与平面所成角的范围为
0,
2
;
(2)直线与平面垂直时,它们的所成角为 ;
2
(3)直线与平面平行(或直线在平面内)时,它们的所成角为 0。
结论:直线与平面所成角的范围为
脚踏实地过好每一天,最简单的恰恰是最难的。拿梦想去拼,我怎么能输。只要学不死,就往死里学。我会努力站在万人中央成为别人的光。行为决定性格, 性格决定命运。不曾扬帆,何以至远方。人生充满苦痛,我们有幸来过。如果骄傲没有被现实的大海冷冷拍下,又怎么会明白要多努力才能走到远方。所有的 豪言都收起来,所有的呐喊都咽下去。十年后所有难过都是下酒菜。人生如逆旅,我亦是行人。驾驭命运的舵是奋斗,不抱有一丝幻想,不放弃一点机会,不 停止一日努力。失败时郁郁寡欢,这是懦夫的表现。所有偷过的懒都会变成打脸的巴掌。越努力,越幸运。每一个不起舞的早晨,都是对生命的辜负。死鱼随 波逐流,活鱼逆流而上。墙高万丈,挡的只是不来的人,要来,千军万马也是挡不住的既然选择远方,就注定风雨兼程。漫漫长路,荆棘丛生,待我用双手踏 平。不要忘记最初那颗不倒的心。胸有凌云志,无高不可攀。人的才华就如海绵的水,没有外力的挤压,它是绝对流不出来的。流出来后,海绵才能吸收新的 源泉。感恩生命,感谢她给予我们一个聪明的大脑。思考疑难的问题,生命的意义;赞颂真善美,批判假恶丑。记住精彩的瞬间,激动的时刻,温馨的情景, 甜蜜的镜头。感恩生命赋予我们特有的灵性。善待自己,幸福无比,善待别人,快乐无比,善待生命,健康无比。一切伟大的行动和思想,都有一个微不足道 的开始。在你发怒的时候,要紧闭你的嘴,免得增加你的怒气。获致幸福的不二法门是珍视你所拥有的、遗忘你所没有的。骄傲是胜利下的蛋,孵出来的却是 失败。没有一个朋友比得上健康,没有一个敌人比得上病魔,与其为病痛暗自流泪,不如运动健身为生命添彩。有什么别有病,没什么别没钱,缺什么也别缺 健康,健康不是一切,但是没有健康就没有一切。什么都可以不好,心情不能不好;什么都可以缺乏,自信不能缺乏;什么都可以不要,快乐不能不要;什么 都可以忘掉,健身不能忘掉。选对事业可以成就一生,选对朋友可以智能一生,选对环境可以快乐一生,选对伴侣可以幸福一生,选对生活方式可以健康一生。 含泪播种的人一定能含笑收获一个有信念者所开发出的力量,大于个只有兴趣者。忍耐力较诸脑力,尤胜一筹。影响我们人生的绝不仅仅是环境,其实是心态 在控制个人的行动和思想。同时,心态也决定了一个人的视野、事业和成就,甚至一生。每一发奋努力的背后,必有加倍的赏赐。懒惰像生锈一样,比操劳更 消耗身体。所有的胜利,与征服自己的胜利比起来,都是微不足道。所有的失败,与失去自己的失败比起来,更是微不足道挫折其实就是迈向成功所应缴的学 费。在这个尘世上,虽然有不少寒冷,不少黑暗,但只要人与人之间多些信任,多些关爱,那么,就会增加许多阳光。一个能从别人的观念来看事情,能了解 别人心灵活动的人,永远不必为自己的前途担心。当一个人先从自己的内心开始奋斗,他就是个有价值的人。没有人富有得可以不要别人的帮助,也没有人穷 得不能在某方面给他人帮助。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵,昨天的太阳,晒不干今天的衣裳。今天做别人不 愿做的事,明天就能做别人做不到的事。到了一定年龄,便要学会寡言,每一句话都要有用,有重量。喜怒不形于色,大事淡然,有自己的底线。趁着年轻, 不怕多吃一些苦。这些逆境与磨练,才会让你真正学会谦恭。不然,你那自以为是的聪明和藐视一切的优越感,迟早会毁了你。无论现在的你处于什么状态, 是时候对自己说:不为模糊不清的未来担忧,只为清清楚楚的现在努力。世界上那些最容易的事情中,拖延时间最不费力。崇高的理想就像生长在高山上的鲜 花。如果要搞下它,勤奋才能是攀登的绳索。行动是治愈恐惧的良药,而犹豫、拖延将不断滋养恐惧。海浪的品格,就是无数次被礁石击碎又无数闪地扑向礁 石。人都是矛盾的,渴望被理解,又害怕被看穿。经过大海的一番磨砺,卵石才变得更加美丽光滑。生活可以是甜的,也可以是苦的,但不能是没味的。你可
高中数学沪教版高三第一学期第14章14.3 平面及其 基本性质 课件

1、判定两个平面相交。方法是:若两个平 面有一个公共点,则这两个平面相交。
2、判定点在直线上。方法是:点若是两个 平面的公共点,则该点就在这两个平面的 交线上。
例1.将下列符号语言转化为图形语言:
(1)A , B , A l , B l
(2)a , b , c ,
a // c , b c p
求证
:
直线l
,
l1
,
l
在同一平面上
2
l1 // l2 l1, l2唯一确定平面
l l1
A l2
B
A l1, B l2 A, B
A, B l l
直线l, l1, l2共面
高中数学沪教版高三第一学期第14章1 4.3 平面及其 基本性质 课件【精品】
练习:已知直线 l1, l2 , l3 , l4是两两相交且不共点的 四条
2、平面竖直放置
3、一个平面的部分被另一个平面遮住 M
N M
N
相交平面画法:
β β
α
α
β
α
画两个平面相交时,当一个平面的一部分被 另一个平面遮住时,应把被遮住的部分画成 虚线或不画
点、线、面的基本位置关系
1、符号表示:
点P,直线a(是点的集合),平面 (也是点的集合) 2、集合关系:
(1)点线关系:
几个平面
3个
例、
(1)两个平面的公共点的个数可能有......( D )
(A)0 (B)1Βιβλιοθήκη (C)2(D)0或无数
(2)三个平面两两相交,则它们交线的条数……( B )
(A)最多4条最少3条 (B)最多3条最少1条
(C)最多3条最少2条 (D)最多2条最少1条
高中数学沪教版(上海)高三第一学期第14章14.3 空间直线与平面 课件 _2

(2).直线a与平面α没有公共点,直线a在平面β上; (注意:平面α与β有两种不同的位置关系)
(3).平面α与平面β相交于AB,直线CD与平面α相交与 点C,与平面β相交与点D,且直线CD与直线AB没有公 共点;
2.用几何语言叙述下列集合符号表示的图形关系,并 画出相应的图形. (1).P∈l,l α,所以P∈α; (2).l∩α=O,AO α,因此l∩AO=O; (3).l∩α=φ,P∈l,因此P∉α ; (4).α∩β=l,P∈l,所以P∈α,P∈β; (5).α∩β=l,P∈l,CP α,DP β,所以CP∩DP=P.
注意:三角形ABC所在的平面可以写成平面ABC。 特别地,在一些复杂的图形中,这样的写法更确切、 具体。
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
例3、用下列符号表示的点、直线和平面的位置关 系画出图形:
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
(作法简述) (1).可先作出不同的两个垂直放置的平面的直观图.
(2).注意画出相交直线和用虚线表示被遮部分直线.
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
新课讲解
重点难点
四.空间点,线,平面之间的相应位置关系的 集合语言 表
示法:
点--- 组成集合的基本元素;
说明 线--- 由基本元素点组成的集合.
面---由基本元素点组成的集合.
①点与直线的位置关系:
(3).平面α与平面β相交于AB,直线CD与平面α相交与 点C,与平面β相交与点D,且直线CD与直线AB没有公 共点;
2.用几何语言叙述下列集合符号表示的图形关系,并 画出相应的图形. (1).P∈l,l α,所以P∈α; (2).l∩α=O,AO α,因此l∩AO=O; (3).l∩α=φ,P∈l,因此P∉α ; (4).α∩β=l,P∈l,所以P∈α,P∈β; (5).α∩β=l,P∈l,CP α,DP β,所以CP∩DP=P.
注意:三角形ABC所在的平面可以写成平面ABC。 特别地,在一些复杂的图形中,这样的写法更确切、 具体。
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
例3、用下列符号表示的点、直线和平面的位置关 系画出图形:
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
(作法简述) (1).可先作出不同的两个垂直放置的平面的直观图.
(2).注意画出相交直线和用虚线表示被遮部分直线.
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
高中数学沪教版(上海)高三第一学 期第14 章14.3 空间直线与平面 课件 _2
新课讲解
重点难点
四.空间点,线,平面之间的相应位置关系的 集合语言 表
示法:
点--- 组成集合的基本元素;
说明 线--- 由基本元素点组成的集合.
面---由基本元素点组成的集合.
①点与直线的位置关系:
高中数学沪教版《14.3 空间直线与平面的位置关系》省级名师优质课教案比赛获奖教案示范课教案公开课教案

高中数学沪教版高三上册第14章《14.3 空间直线与平面的位置关系》省级名师优质课教案比赛获奖教案示范课教案公开课教案
【省级名师教案】
1教学目标
(一) 知识与技能目标
理解直线与平面垂直的定义,掌握直线与平面垂直的判定定理及其应用。
(二) 过程与方法目标
通过直观感知、操作,归纳概括出直线与平面垂直的判定定理。
(三) 情感与态度目标
通过该内容的学习,培养学生的空间想象能力及合情推理能力,并从中体会“转化”的数学思想。
2学情分析
同学们在学习本节课之前,学生已经学习了掌握了平面及其基本性质以及空间直线与直线的位置关系的知识,学生在日常生活中接触到线面垂直的模型,因此学生对于线面垂直知识的学习有一定的认知基础。
但同学们对于理解线面垂直的定义中的“任何直线”有一定的困难,误认为由一直线垂直于一平面内某一直线就能得出线面垂直;同时,线面垂直判定定理的发现具有一定的隐蔽性,学生不易想到。
3重点难点
教学重点:直线与平面垂直的判定定理的理解。
教学难点:直线与平面垂直的判定定理的归纳。
4教学过程
4.1第一学时
教学活动
1【导入】一、复习引入
教师提问:空间直线和平面的位置关系有哪些?。
沪教版(上海)数学高三上册-1直线与平面平行的性质课件

达标检测
4.如图所 示 ,四 边形 ABCD是梯 形, AB∥CD,且 AB∥平面α,AD,BC与平面α分别交于点M,N,且 点M是AD的中点,AB=4,CD=6,则MN=_5___. 解析 因为AB∥平面α,AB⊂平面ABCD,平面ABCD∩平面α=MN, 所以AB∥MN,又点M是AD的中点, 所以MN是梯形ABCD的中位线,故MN=5.
12345
解析 答案
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
达标检测
3.如图所示,在空间四边形ABCD中,点E,F分别为 边AB,AD上的点,且AE∶EB=AF∶FD=1∶4, 又点H,G分别为BC,CD的中点,则 A.BD∥平面EFGH,且四边形EFGH是矩形
A
B
设该平面为β.则α∩β=CD. AB AB//平面α
C
D
AB//CD
AC//BD
四边形ABCD是平行四边形
AC=BD
直线和平面平行的性质的应用:
跟踪训练1.如图,用平行于四面体ABCD的一组对棱AB,CD 的平面截此四面体,求证:截面MNPQ是平行四边形.
直线和平面平行的性质的应用: 例2.如图所示,在四棱锥P-ABCD中,底面ABCD是平行
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
12345
解析 答案
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
达标检测
5.如图所示,过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面CDD1C1 于EE1,求证:BB1∥EE1.
4.如图所 示 ,四 边形 ABCD是梯 形, AB∥CD,且 AB∥平面α,AD,BC与平面α分别交于点M,N,且 点M是AD的中点,AB=4,CD=6,则MN=_5___. 解析 因为AB∥平面α,AB⊂平面ABCD,平面ABCD∩平面α=MN, 所以AB∥MN,又点M是AD的中点, 所以MN是梯形ABCD的中位线,故MN=5.
12345
解析 答案
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
达标检测
3.如图所示,在空间四边形ABCD中,点E,F分别为 边AB,AD上的点,且AE∶EB=AF∶FD=1∶4, 又点H,G分别为BC,CD的中点,则 A.BD∥平面EFGH,且四边形EFGH是矩形
A
B
设该平面为β.则α∩β=CD. AB AB//平面α
C
D
AB//CD
AC//BD
四边形ABCD是平行四边形
AC=BD
直线和平面平行的性质的应用:
跟踪训练1.如图,用平行于四面体ABCD的一组对棱AB,CD 的平面截此四面体,求证:截面MNPQ是平行四边形.
直线和平面平行的性质的应用: 例2.如图所示,在四棱锥P-ABCD中,底面ABCD是平行
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
12345
解析 答案
沪 教 版 ( 上 海)数 学高三 上册-1 直 线与 平面平 行的性 质 课 件
达标检测
5.如图所示,过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面CDD1C1 于EE1,求证:BB1∥EE1.
沪教版数学高三上册-14.3 直线和平面所成的角 课件
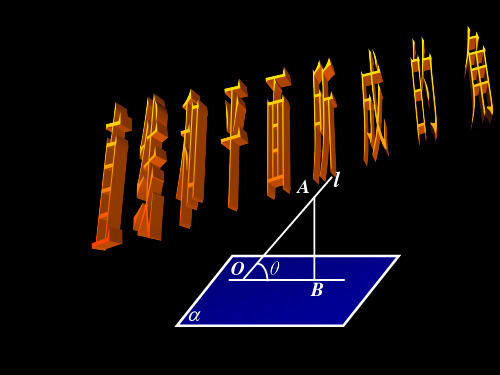
一条直线和平面平行,或在平面内,它们 所成的角是0 的角。
直线和平面所成角的范围是[0,90]。
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
最小角原理
A
l
l是平面 的斜线,A是l
上任意一点,AB是平面
的垂线,B是垂足,
N到平面β的距离是4,求MN与平面β所成角的
余弦值。
N ∠MOM'就是MN
与平面β所成的角 N
M O M' β
移出图 N'
M6
4
1
O
N'
M'
解:当M,N在平面同则时有
OM 1
sin MOM '
OM 6 4
OM=2
cos MOM '
1 2 3
.
2
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
D C
AD1O 300.
A
B
求直线(或斜线)与平面所成的角关键 是确定斜线在平面的射影
其步骤是:一找,二证,三求。
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
小结 1. 平面的一条斜线和它在平面上的射影所成 的锐角,叫做这条直线和这个平面所成的角。
Al
O B
沪教版数学高三上册-14.3 直线和平面所成的角 课件【精品】
复习回顾
1、点在平面上的射影是一个点,斜线在平面 上的射影是一条直线;直线在平面上的射影是 一个点或一条直线
2、从平面外同一点分别作该平面的垂线段和斜 线段: (1)射影相等的两条斜线段相等,射影较长的斜 线段也较长; (2)相等的斜线段的射影相等,较长的斜线段的 射影也较长;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使自己失去动力。如果你的主要目标不能激发你的想象力,目标的实现就会遥遥无期。因此,真正能激励你奋发向上的是确立一个既宏伟又具体的远大目标。实
是呈现出一条波浪线,有起也有落,但你可以安排自己的休整点。事先看看你的时间表,框出你放松、调整、恢复元气的时间。即使你现在感觉不错,也要做好
自己的事业波峰时,要给自己安排休整点。安排出一大段时间让自己隐退一下,即使是离开自己挚爱的工作也要如此。只有这样,在你重新投入工作时才能更富
变: 点A到面BDD1B1的距离
变 式 : 在 长 方 体ABCD A1B1C1D1中,
已 知AB 4,AD 5,AA1 3
(1) 求 点A和 点C1的 距 离
(2) 求 点A和 棱B1C1的 距 离
(3) 求 棱AB和 平 面A1B1C1D1的 距 离
D
C
AH
D1
B
变式:
点A1到面DAB1C1 C1 的距离
A1
B1
4.如 图 , 已 知 正 三 角 形ABC的 边 长 为6cm, 点O到ABC各 顶 点 距 离 都 是4cm, 求 点O到 这 个 三 角 形 所 在 平 面的 距 离.
解:设H为点O在平面ABC内的射影,
OA OB OC ,
O
HA HB HC ,
即H是△ABC的外心。在Rt △OBH中,
中重要的组成部分,主要表现在对于在压力或者困境中,个体自我安慰、自我积极暗示、自我调节的能力,在个体克服困难、顶住压力、勇对挑战等情况下,都
激励能力的人,富有弹性,经常表现出反败为胜、后来居上、东山再起的倾向,而缺乏这种能力的人,在逆境中的表现就大打折扣,表现为过分依赖外界的鼓励
院练习棒球。在挥动球棒前,对自己大喊:“我是世界上最棒的棒球手!”然后扔出棒球,挥动……但是没有击中。接着,他又对自己喊:“我是世界上最棒的
a
b
证明:过直线a与平面的交点P
作两条相交直线m和n
a
m
,
n
b
a
m
m,a
a //
n
b
mP
bn
m n P
b
n
m ,n
解决四个距离的计算
1.点到平面的距离:
2.直线到平面的距离: 前提:线面平行 实质:转化为点到面的距离 3.两个平行平面间的距离: 前提:面面平行 实质:转化为点到面的距离
证明:
PA
l l
P
同理PPBA
l l
PA PB P
PA 平面PAB
B
PB 平面PAB
Q
A
l 平面PAB PQ 平面APB
l
PQ
l 平面APB,l PQ
例3.
已知:M是菱形ABCD所在平面外一点,且MA=MC
求证:AC 平面MBD 证明:连接BD,交AC于点O
连接MOBiblioteka BM O四边形ABCD为菱形 AC BD
A
MA MC O为AC中点
AC
MO
MO BD O
MO 平 面MBD
C
D
BD 平 面MBD
AC 平面MBD
直线和平面垂直的第二判定定理
如果两条平行直线中的一条垂直于一个平面,那么
另一条也垂直于这个平面.
集合语言:若 a ,a / /b, 则b
记作a A
直线与平面平行
记作a //
直线在平面外
直线和平面垂直的定义
如果一条直线和平面内的任意一条直线都垂直,
那么这条直线和这个平面垂直。
直线l叫做平面的垂线,平面叫做直线l的垂面;
它们唯一的公共点,即垂线和平面的交点叫做垂足。
p O
自一点向平面 引垂线,垂足叫 做这点在这个平 面上的射影;
这个点与垂足间的线段叫做这点 到这个平面的垂线段。
判断
(1)如果一条直线和一个平面内的一条直线垂 直,那么这条直线就和这个平面垂直( )
(2)如果一条直线和一个平面内的无数条直 线垂直,那么这条直线就和这个平面垂直( )
直线和平面垂直的判定定理:
如果一条直线和一个平面相交,并且和这个平
面内的两条相交直线都垂直,那么这条直线就垂直
A
A
A
A
A
A
4.异面直线的距离
在正方体中,棱AA’和BC所在直线是异面直线, 哪直条线直AB线和和它它们们都都垂垂直直相相交交。?
和两条异面直线都垂直 相交的直线叫做两条异
面直线的公垂线。
直线AB就是两异面直 线AA’和BC的公垂 线 垂足A,B间的距离叫做两条异面直线的距离。
例5.在棱长为a的正方体中求: (1)点A到面BCC1B1的距离; a (2)B1D1到面ABCD的距离 。 a (3)平面ADD1A1到面BCB1C1的距离 。
BH 2 3
OH
OB2 BH 2
42 (2
3 )2
2 (cm)
A
,
C H
B
即点O到这个三角形所在平面的距离为2 cm.
练习
3.已知: PA 平面ABC, AB是圆O的直径, C是 圆O上 任 意 一 点
求证: PC BC
E
•
我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。
,不过是一场场艰辛的比赛。真正的运动者总是盼望比赛。如果把困难看作对自己的诅咒,就很难在生活中找到动力,如果学会了把握困难带来的机遇,你自然
没有击中。男孩子停下来,检查了球棒和球,然后用更大的力气对自己喊:“我是世界上最棒的棒球手!”可是接下来的结果,并未如愿。男孩子似乎有些气馁
,一定是个很棒的挥球手。接着男孩子又对自己喊:“我是世界上最棒的挥球手!”其实,大多数情况下,很多人做不到这看似荒谬的自我鼓励,可是,这故事
励下的执著,而这执著是很多人并不具备的……而许多奇迹往往是执著者造成的。许多人惊奇地发现,他们之所以达不到自己孜孜以求的目标,是因为他们的主
于这个平面.
l
m
n
m n A l m
lm
A
n
A
ln
(线线垂直
线面垂直)
例1.正方体ABCD ABCD中, 求证:(1)AA 平面ABCD (2)AC BB (3)AC 平面BBDD
例2.已知:PA α,PB β,A,B为垂足,α β l
l 平面PAB Q
求证:(1)l 平面PAB; (2)l PQ
直线和平面的位置关系
一条直线和一个平面的位置关系有且只有以下三种:
(1)直线在平面内——有无数个公共点. (2)直线和平面相交——有且只有一个公共点. (3)直线和平面平行——无公共点.
直线和平面相交或平行的情况统称为直线在平面外.
直线和平面的三种位置关系的画法
直线在平面内
记作a
直线与平面相交
