用姓名测试姻缘,80%准确率
供配电常用公式(验算)

供配电案例常用的公式1.负荷计算:设备功率、需要功率和平均功率补前的功率因数:cosφ1={1/[1+(βQ/αP)]2}1/2,补后的功率因数:cosφ={1/[1+[(Qc-Q)/Pc]2]}1/2。
Qc=Pc(tgφ1-tgφ2),设备功率:Pe=2P rεr1/2.Pe= P rεr1/2.Pe= S rεr1/2cosφ. 负荷持续率。
二项式法:Pjs=cPn+bPs,Pn表示n个最大功率设备功率和,Ps表示全部运转设备的功率和(除去备用设备)。
线负荷转为三相负荷:Pd=1.73P UV+1.27P WV=1.73P UV。
相负荷中最大和第二大的功率。
相负荷计算P U=p*P UV+q*P WU。
Q U=p*Q UV+q*Q WU。
单相功率转为三相功率是最大相负荷的三倍。
需要系数法:需要系数和同时系数,利用系数法:利用系数和最大系数。
计算负荷:设备组:Pc=KxPe,Qc=Petgφ,Sc=[P2+Q2]1/2,Ic=Sc/(1.732Ur)变电所:Pc=K∑p∑(KxPe),Qc=K∑q ∑(KxPetgφ)。
同时系数K∑p、K∑q(两个不计入,一个择大者即备用设备和消防设备不计入,季节性计入最大者)利用系数:设备组平均负荷:P av=K l*Pe,Qav=Pav*tgφ。
计算负荷:Pc=K m∑P av;Qc=K m ∑Q av。
节能传动钢铁设计手册找,以配电手册为主,如它没有及时翻到钢铁手册对应部分。
2.电源质量:n次谐波电压含有率:HRU n=1.732U N*h*I h/10S k。
谐波电流的计算:I1=I n*n,I h=I1/h=I n*n/h。
详见工业与民用配电设计手册P282。
全部用户允许注入公共连接点的谐波电流短路容量不同时:I n=S k1/S k2*I(n)p, 不同用户注入公共接点的允许值I n=I h(Sj/St)1/α。
两个用户(变压器)注入同一公共接点的谐波电流:I n=(I n12+I n22+KI n1I n2)1/2。
C M Y K色值

C M Y K色值印刷肤色参考、常用印刷色值非洲人肤色:C35 M45 Y50 K30以上亚洲人肤色:C15 M43 Y53 K0白种人肤色:C15-18 M45 Y30 K0天空的颜色:天蓝:C60 M23 Y0 K0偏暖:C60 M45 Y0 K0偏冷:C60 M15 Y0 K0 深紫色:C100 M68 Y10 K45 深紫红:C85 M95 Y10 K0 海水蓝:C60 M20-28 柠檬黄:C5 M18 Y75 桔红:C5 M100 Y100 K5 橙色:C5 M50 Y100 K0 粉红色:C5 M40 Y5 K0 假金色(四色模拟而非专色):C5 M15 Y65 K0 假银色(四色模拟而非专色):C20 M15 Y14 K0 掌握了这些基本规律,再调图时就能把握主次了,知道改减什么色,加深什么色了。
人物肤色的调图规律: M、Y的量差不多,C是M的1/3至1/5人脸数值规律:C8 M36 Y35头发数值:C71 M82 Y73 K22苹果:C7 M99 Y71香蕉:C4 M54 Y93橙子:M55 Y78红色系列M10淡粉红色M20 Y10玉红色M30粉红色M30 Y10淡桃红色M20 K10浅红色C10 M30浅曙红色M50樱红色C20 M50玫红色M70洋红色M40 Y20 K10暗桃色M60 Y20浅桃红色C10 M30 Y30 K10水红色M50 Y30 K10绯红色C10 M70 Y20桃红色M80猩红色M70 Y50胭脂红色M100品红色M60 Y40 K10橘红色M80 Y20淡艳红色M70 Y4-0珊瑚红色C30 M100玫瑰红色M100 Y60艳红色C20 M70 Y40 K10锈红色M90 Y85朱红色C20 M80 Y40 K10朱砂色M100 Y100大红色C50 M100紫红色C20 M100 Y30 K10绛红色C40 M70 Y60 K10土红色C10 M100 K30曙红色C20 M90 Y70 K20枣红色C20 M100 Y100 K10石榴红色C20 M80 Y60 K30酒红色M90 Y50 K50深艳红色M90 Y70 K50棕红色C50 M100 Y90 K20酱红色M100 Y100 K50深红色M100 K80暗红色C80 M100 Y30 K80深玫红色橙(棕)色系列M10 Y10蛋壳色M20 Y20肤色M30 Y30藕色C10 M30 Y40木色M50 Y50橙色M30 Y30 K10奶咖色M40 Y80杏色M60 Y90橘色C10 M20 Y40 K30浅褐色M80 Y60红橘色C20 M40 Y40 K20浅棕色C40 M50 Y60茶色M80 Y90赤橙色M50 Y80 K20土棕色M70 Y90 K10黄棕色C10 M80 Y90铁锈色C50 M60 Y50 K30褐色C40 M60 Y80 K30棕色C10 M30 Y70 K80深褐色C60 M80 Y70 K30紫陶色C20 M70 Y100 K60棕褐色C10 M50 Y100 K80古铜色C70 M90 Y100 K30深棕色黄色系列Y10乳白色Y30月黄色M10 Y30米黄色Y50淡黄色Y70菊黄色C5 M10 Y40米黄色Y80黄色M20 Y50奶黄色Y100黄色C20 Y70韭黄色M20 Y80金黄色M30 Y70蛋黄色C10 M20 Y70中米色M20 Y100菜花黄色M20 Y70 K10土黄色C20 M30 Y50 K10暗黄色M20 Y100 K30深黄色M50 Y100 K10橙黄色M20 Y70 K10灰黄色绿色系列C10 Y10淡青色C10 Y20豆绿色C20 Y20 K10淡湖色C20 M10 Y50新茶色C50 Y50嫩绿色C40 M10 Y60黄绿色C40 Y100嫩草色C80 Y50青绿色C90 Y100苹绿色C100 Y50 K10湖绿色C90 Y40 K20蓝绿色C60 M20 Y50 K10秋香绿色C100 Y100绿色C70 M40 Y80 K10橄榄色Y90 K70咸菜色C90 M50 Y60 K10山青色C100 M40 Y70 K10深绿色C90 M40 Y90 K10翡翠色C80 Y70 K50中绿色C90 M30 Y30 K50黛青色C70 Y60 K70灰绿色C100 M70 Y100 K20墨绿色C100 M10 Y70 K80暗绿色C80 M30 Y80 K80深墨绿色蓝色系列C10粉蓝色C30淡蓝色C20 M10鸭蛋色C30 Y10玻璃色C50 Y20薄荷青色C60浅蓝色C50 M10 Y15浅湖蓝色C60 M20蔚蓝色C70 Y30湖蓝色C85天蓝色C30 K30浅蓝灰色C85 Y20瓦蓝色C100蓝色C80 M40浅海色C100 M40海蓝色C80 M60钴蓝色C60 K50灰蓝色C100 M60普蓝色C100 M10 Y20 K20孔雀蓝色C100 Y20 K30宝蓝色C90 M60 K20藏青色C100 M60 Y40 K20青蓝色C100 M60 Y10 K50深海蓝色C100 M10 K80深蓝色紫色系列C10 M10鱼白色C20 M20浅紫色C50 M50淡紫色C30 M70浅红紫色C30 M80 K10海棠红色C60 M70 Y15绛紫色C40 M40 K30灰紫色C60 M90玫紫色C70 M80明紫色C80 M70 Y20青紫色C70 M80 Y20紫罗兰色C60 M100 K20红紫色C100 M100紫色C80 M80 Y20 K20茄色C60 M100 Y10 K30深玫瑰色C50 M80 K50暗紫色C100 M80 Y10 K30蓝紫色C80 M100 Y40 K30深紫色C90 M70 K80黑紫色灰(黑)色系列Y20 K10豆灰色C30 M20 Y20浅灰色C10 M10 Y10 K20淡灰色C20 M10 K30浅蓝灰色C50 M30 Y50 K20绿灰色C40 M30 Y80 K20黄灰色C80 M50 K40蓝灰色C60 M60 Y70棕灰色K80纯黑灰色M50 K60红灰色C50 M50 Y50 K30深灰色K100纯黑色C60 M40 Y10 K50铁灰色C80 M100 M80 K10黑红色C70 M80 Y80 K30褐灰色Y100 K100纯黄黑色C100 M100 Y100混黑色C90 M70 Y100 K30绿黑色C90 M100 Y70 K30紫黑色C80 M100 Y100 K30黑棕色C100 K100纯蓝黑色M100 K100纯红黑色C80 M80 Y100 K50土黑色C100 M90 Y60 K50蓝黑色*名片成品:90*54mm,加2个毫米出血为:92*56mm。
3-04 K80-115塔吊安装施工工法
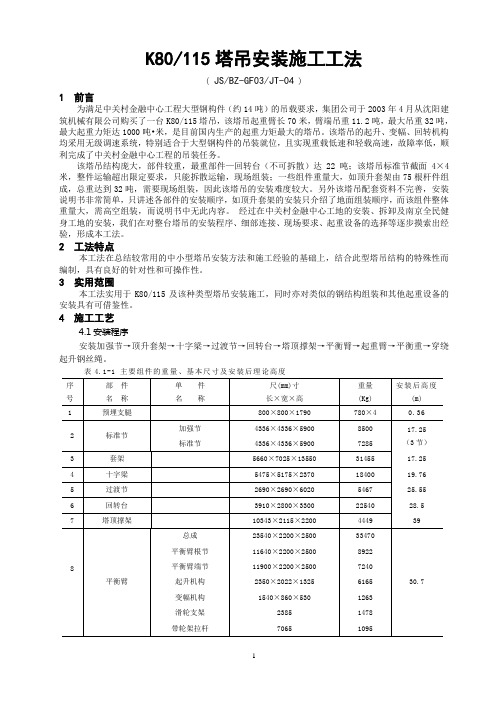
K80/115塔吊安装施工工法( JS/BZ-GF03/JT-04 )1前言为满足中关村金融中心工程大型钢构件(约14吨)的吊载要求,集团公司于2003年4月从沈阳建筑机械有限公司购买了一台K80/115塔吊,该塔吊起重臂长70米,臂端吊重11.2吨,最大吊重32吨,最大起重力矩达1000吨•米,是目前国内生产的起重力矩最大的塔吊。
该塔吊的起升、变幅、回转机构均采用无级调速系统,特别适合于大型钢构件的吊装就位,且实现重载低速和轻载高速,故障率低,顺利完成了中关村金融中心工程的吊装任务。
该塔吊结构庞大,部件较重,最重部件—回转台(不可拆散)达22吨;该塔吊标准节截面4×4米,整件运输超出限定要求,只能拆散运输,现场组装;一些组件重量大,如顶升套架由75根杆件组成,总重达到32吨,需要现场组装,因此该塔吊的安装难度较大。
另外该塔吊配套资料不完善,安装说明书非常简单,只讲述各部件的安装顺序,如顶升套架的安装只介绍了地面组装顺序,而该组件整体重量大,需高空组装,而说明书中无此内容。
经过在中关村金融中心工地的安装、拆卸及南京全民健身工地的安装,我们在对整台塔吊的安装程序、细部连接、现场要求、起重设备的选择等逐步摸索出经验,形成本工法。
2工法特点本工法在总结较常用的中小型塔吊安装方法和施工经验的基础上,结合此型塔吊结构的特殊性而编制,具有良好的针对性和可操作性。
3实用范围本工法实用于K80/115及该种类型塔吊安装施工,同时亦对类似的钢结构组装和其他起重设备的安装具有可借鉴性。
4施工工艺4.1安装程序安装加强节→顶升套架→十字梁→过渡节→回转台→塔顶撑架→平衡臂→起重臂→平衡重→穿绕起升钢丝绳。
表4.1-1 主要组件的重量、基本尺寸及安装后理论高度4.2.1安装加强节(8500kg/节)本塔吊共有4节加强节,首次安装至少需要安装3节,高度17.25米。
A在地面组装好三节加强节;B依次将加强节安装在已经埋设好的预埋支腿上。
《寿险精算学(第3版)》 PPT-ch2

例2.5
• 假设某人群每10万个新生婴儿, 能活到40 岁的人数为 97369, 能活到85 岁的人数为33851, 而在85~86 岁这一年 死亡的人数为3758。
• 在新生婴儿时期寿命的密度函数有一个递减趋势。 这是 因为新生婴儿是脆弱的,各种先天不足都会在刚出生时暴 露, 所以新生婴儿阶段死亡概率是偏高的。 经过医学治疗 和自然淘汰, 婴儿死亡率迅速下降。
• 青少年时期是人一生中死亡率最低的一段时期。 这段时 期是人类的健康黄金期。
• 从40 岁左右开始, 随着年龄的增长, 人的器官逐渐老化, 开 始罹患各种疾病,身体进入失效期, 死亡率开始递增。 60 岁前后进入加速失效期, 80 岁前后达到死亡率的顶峰。
f0 (t)
d dt
F0 (t)
lim
dt 0
F0 (t
dt) dt
F0 (t)
• 生存函数与分布函数具有补函数关系, 所以寿命的密度函 数也可以表达为生存函数导函数的负数
f0 (t)
d dt
S0 (t)
lim
dt 0
S0 (t)
S0 (t+dt) dt
人类寿命密度函数示意图
密度函数曲线展示的人类生存规律
• 寿险业务关心的是被保险人购买了寿险产品之后的未来生存状 况。 所以, 寿险研究的主要变量是被保险人的未来寿命。
• 从统计分析的角度而言, 对寿命变量和未来寿命变量的分析是不 一样的
• 寿命分布和未来寿命分布最主要的差别
高低压电动机保护定值整定

低压电动机保护定值整定U無定原则1.K短略保护山机粗路时〃电流为110倍额定电流I鉄定値推荐取8倍1总庞时0.2s f 如果在启劝过程屮跳IW,可取9侪1恥1. 2>堵转保护电机堵转时,电流为4飞倍额定电流1“定值5倍I刊延时1头1.3.定时限保护定吋限保护件为堵转后备保护*可取询g延时5肌1.4.反时眼保护启动电流设置为l.lle t忖间常教设置为2齐电机aS1.2Ie运行时, 保护将在4加左Q跳阿2倍h电购运行时「保护将在5倍h 电流运行吋,保护將在3秒左右跳闸L 5*欠載保护也机运行在空sm况下■也流论期处于小电流运行惰况下,久载保护可用干报警口如果运行条件允许,可作用于跳闸「切除空毂运行也机,省久载电流可取0, 2U,延时1伽.L 6.不半衡保护当电机内WWffife路或缺相时.使电机运行不呼衡状态,如果段期运行” 则会烧毁ill机.不平衡百分比设置为™h延忖肚1 7.漏血保护需配置专门湎11互感XLO,潞毗电流収0.4A,延Iff 5s,用于跳叭1.8.过压探护山圧氏期过示运行,将影响电机的绝緣,甚至造成短路。
过斥值収1・lUe (Ue为220v),延时5s・1.9、欠圧保护山斥过低将引起电机转速降低,电流増人。
.欠圧值取0. 95Ue(Ue为220v), 延时5s«1. 10. TE吋间保护用于增安型吐机的过鐵保护。
TE时间取2s°1. Ll> I】艺联锁保护用于外部跳闸(DCS跳闸)> 延时0.5s1. 12.晃电再起对于ie:»u机,在系统晃电造成停机,恢复供电后要求电机重启口晃电电用80U4 恢复电圧0.95U。
,晃电时间可设置为3s,再起延时设置为Is (用于分批启动.根据实际情况设置)1. 13.电机启动时间在“参数设置”屮,根据电机启动过程时间设置,默认为6s°1. 14.额定电流在“参数设置”中,根据由机实际情况设置,110B狀札额定电流为207A,互感器选择SCT300,参数中额定电流设置为3・5A・1.15、CT 变比根堀选择的互感器设置,SCI300时,设置为60°2、定值整定说明:例fl: llOkw lU-^J 机,额定电流le=207A,选样SCT300, CT 变比60短路保护81沪1656A 折算到二次1656/60=27. 6A,在短路保护内,设置短路电流设置为27. 6A,保护延时0・2s堵转探护5Lo=1035A 折算到-)^1035 ;6(} 17. 25A.在堵转保护内,设置堵转电流为17,3A,保护延时g (注:堵转保护在壯动机E动过腥中关讯启动后打开,因此在胆动过程屮不会造成堵转觇护动作〉定时般探护二621A 折算到二次621/2 W. 35A r在定时限保护内,设置定时限H1流为10. 4九保护延Iff 5s,反时眼过流启劝电流1- lIe = 227.7A 折算到一•次227- 7/&0=3. 795A.在应忖限过流内』设置甘动也说为;J.SM.时间常ft2s=其它保护依次根据整定原则计算,讨算出次定值氐根据CT变比计算山—次定值.作为保护定值输入乜电动机的主要保护及计算、速断保护1•速断高值:动作电流高定值Isdg计算。
nk80 钢 成分

nk80 钢成分摘要:1.NK80 钢的简介2.NK80 钢的主要成分3.NK80 钢的性能特点4.NK80 钢的应用领域正文:K80 钢是一种高强度、高韧性的合金结构钢,是我国钢铁行业在20 世纪80 年代研发的一种新型钢材。
这种钢材主要由铁、碳、锰、硅、铬、钼、镍、硼等元素组成,其中,镍、硼等元素的含量对NK80 钢的性能影响较大。
K80 钢的主要成分如下:碳(C)0.10-0.25%,硅(Si)0.15-0.35%,锰(Mn)0.30-0.70%,铬(Cr)0.30-0.70%,钼(Mo)0.10-0.30%,镍(Ni)1.70-2.30%,硼(B)0.005-0.015%。
这些元素的合理配比使得NK80 钢具有优良的力学性能、焊接性能和耐腐蚀性能。
K80 钢的性能特点主要表现在以下几个方面:1.高强度:NK80 钢的强度高于一般的碳结构钢,可以满足各种工程机械、船舶等高强度部件的需求。
2.高韧性:NK80 钢具有良好的韧性和塑性,可以抵御较大的冲击和振动,适用于承受动载荷的部件。
3.良好的焊接性能:NK80 钢的焊接性能较好,可以采用各种焊接方法进行焊接,焊缝质量较高。
4.良好的耐腐蚀性能:NK80 钢含有一定量的铬、钼等合金元素,具有良好的耐腐蚀性能,可在恶劣环境下使用。
K80 钢广泛应用于以下领域:1.工程机械:如挖掘机、装载机、起重机等关键部件。
2.船舶制造:如船舶甲板、船舱等结构件。
3.石油化工:如炼油厂、化工厂的管道、阀门等设备。
4.桥梁建筑:如大型桥梁的梁、柱等承重结构。
5.压力容器:如锅炉、压力罐等设备制造。
人教版八年级数学上册 第十四章《整式乘法与因式分解》单元测试卷(含解析)

第十四章《整式乘法与因式分解》单元测试卷一、单选题(本大题共10小题,每小题3分,共30分)二、填空题(本大题共8小题,每小题4分,共32分)三、解答题(本大题共6小题,共58分)19.(8分)计算:20.(8分)分解因式:21.(10分)(1)若,求的值;(2)已知,求的值.22.(10分)观察下列等式:…(1)根据以上等式写出______;(2)直接写出的结果(n 为正整数)______;2225,()9m n m n -=+=m n -()()2121y y y m +-+=224424y my m y m -+-+()()2111x x x -÷-=+()()32111xx x x -÷-=++()()432111xx x x x -÷-=+++()()511x x -÷-=()()11nx x -÷-(3)计算:.23.(10分)材料:把多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.例如:.(1)分解因式:(2)若a ,都是正整数且满足,求的值;(3)若a ,b为实数且满足 , ,求S 的最小值.24.(12分)我们学习了完全平方公式,把它适当变形,可解决很多数学问题.2342023122222+++++⋅⋅⋅+()()()()()()am an bm bn am an bm bn a m n b m n a b m n +++=+++=+++=++1ab a b +++()b a b >40ab a b ---=a b +50ab a b ---=22235S a ab b a b =+++-()()22222222a b a ab b a b a ab b +=++-=-+,例如:若,求的值.解∶又根据上面的解题思路与方法,解决下列问题:(1)若,求的值;(2)①若,则___________;②若,则________________;(3)如图点C 是线段上的一点,以为边向线段的两侧作正方形,已知,两正方形的面积和20,求图中阴影部分的面积.42a b ab +==,²²a b +4a b += 2()16a b ∴+=22216a ab b ∴++=2ab = 2216216412a b ab ∴+=-=-=22626x y x y +=+=,xy 231m n mn +==,2m n -=()()456m m --=()()2245m m -+-=AB AC BC 、AB 5AB =12S S +=答案解析:一、单选题1.B【分析】先利用多项式与多项式乘法法则,展开后合并同类项,再令含x 、y 的一次项的系数均为零,列方程组求解即可得到答案.【详解】解:==展开后多项式不含x 、y 的一次项,,,,故选B .2.A【分析】本题考查了整式的运算问题,分别利用同底数幂的乘法法则、幂的乘方、积的乘方法则、多项式的除法、乘法法则计算各式进行判断即可.【详解】(1)若,,则; 小明计算正确;(2);小明计算正确;(3);小明计算错误;(4);小明计算错误;(5).小明计算错误;故正确的有2个故答案为:A .3.D【分析】利用面积公式以及面积的和差将阴影面积表示出来即可.【详解】解:∵由图知阴影部分边长分别为(x -1),(x -2),()()2342x y x ay b +-++22422633844x axy bx xy ay by x ay b +++++---224(26)(28)(34)34x a xy b x b a y ay b+++-+-+- 280340b b a -=⎧∴⎨-=⎩34a b =⎧∴⎨=⎩1a b ∴-=-3m a =7n a =3721m n m n a a a +==⨯= ()()2020202020210.12580.125888-⨯=-⨯⨯=()222221a b ab ab a b ab ab ab a -÷=÷-÷=-()3328a a -=-()()22321263253x x x x x x x -+=+--=--连接,则阴影部分的面积,BD ()()1122a a b b a b =+++()212a b =+10=(2)由题意得,故答案为:;(3)由题意得,23.(1);(2)由得,,,,,,,,,解得,,;(3)由得,,,()121(1)1,n n n x x x x x ---÷-=++++ 121n n x x x --++++ ()2342023202412222221++++++=-÷ 2024(21)2 1.-=-1ab a b +++1()()ab a b =+++(1)(1)a b b =+++11()()a b =++40ab a b ---=15ab a b --+=115()()a b b ---=(1)(1)5a b --=a b > 11a b ∴->-551=⨯ 15a ∴-=11b -=6a =2b =8a b ∴+=50ab a b ---=5ab a b =++22235S a ab b a b∴=+++-()222355a a b b a b=+++++-22233155a a b b a b=+++++-2228215a b a b =++++22288216a ab b =++++++()()222216a b =++++,,,当,时,,∴S 的最小值为6.24.(1)解:;(2)①,,,,;②(3)设,则,所以,()2220a +≥ ()210b +≥6S ∴≥2a =-1b =-6S =6x y += 222()236x y x y xy ∴+=++=2226x y += 210xy ∴=5xy ∴=231m n mn +== ,()2222449m n m mn n ∴+=++=2245m n ∴+=()2222441m n m n mn -=+-= 21m n ∴-=±4,5,m a m b -=-= 4(5)45a b m m m ∴-=---=--1m +=-(4)(5)6,m m --= 6,ab ∴=2222(4)(5)m m a b ∴-+-=+2()2a b ab=-+2(1)26=-+⨯112=+13,=,AC m BC n ==2212,S m S n ==221220S S m n +=+=。
莫扎特(Mozart)弦乐四重奏

莫扎特(Mozart)弦乐四重奏莫扎特共作有23⾸弦乐四重奏,创作时间⾃1770-1790年,20年间中间中断了约10年。
这23⾸四重奏包括两个阶段的创作:前13⾸为早期作品,为1770-1773年在旅⾏时期所作,其创作先是意⼤利风格后转向海顿风格,明显受他⼈影响。
这13⾸中第⼀号因在⽶兰近郊罗迪所作,称为《罗迪》。
第⼆⾄第七号因在⽶兰所作,称为《⽶兰四重奏》。
第⼋⾄第⼗三号因在维也纳所作,称为《维也纳四重奏》。
⾃到萨尔茨堡后,包括旅⾏曼海茵、巴黎期间,莫扎特未曾作过⼀⾸弦乐四重奏,此段时间,海顿也停⽌了弦乐四重奏的创作。
直⾄移居维也纳的第⼆年,也就是1782年末,可以说是受海顿创作OP.33的启⽰,莫扎特在1个⽉内作成6⾸第⼗四⾄第⼗九号的《海顿四重奏》献给海顿。
这是莫扎特23⾸弦乐四重奏中的精华。
在这6⾸《海顿四重奏》之后,1786年8⽉,在完成《费加罗的婚礼》之后,他创作了为出版界好友霍夫曼斯特⽽作的单⾸第⼆⼗号《霍夫曼斯特四重奏》。
之后,莫扎特的注意⼒移⾄弦乐五重奏,直⾄1788年访问柏林后,才计划创作6⾸⼀组弦乐四重奏呈献给当时的普鲁⼠王腓德烈·威廉⼆世,可惜只完成了第⼆⼗⼀⾄第⼆⼗三的3⾸。
这3⾸《普鲁⼠四重奏》是他晚年清澄风格的杰作。
莫扎特的弦乐四重奏全集的版本可选:1.意⼤利四重奏团演奏版,Philips,CD编号422 512-2,莫扎特全集第⼗⼋集,8张,《企鹅》评介三星。
2.阿玛德乌斯四重奏团演奏版,DG,CD编号423 300-2(6张)。
莫扎特:第⼀号弦乐四重奏MOZART: String Quartet No.1 这⾸《第⼀号弦乐四重奏》,G⼤调,K80/73f,作于1770年3⽉15⽇,时正是莫扎特第⼀次意⼤利旅⾏,作于⽶兰前往波隆纳途中的罗迪,所以有《罗迪》标题。
共4个乐章:1.慢板,G⼤调,奏鸣曲式,⼆段体。
整体上呈现三重奏奏鸣曲⼿法,风格接近于当时洛可可教会奏鸣曲的第⼀乐章,第⼀、第⼆主题都是在中提琴和⼤提琴的数字低⾳型进⾏上,由双⼩提琴⾳域交错呈⽰。
图纸公差符号全解

x .G (V 4z 7R v :P &` / 。间之 线直等平两的 40.0 值 差公为离距�内面平 向轴于位须必内度长 001 意任在线素一任 上面表柱圆 )� _ 1e 1w -f 0R *u 1M 8。间之线 直等平两的 20.0 值差 公为离距�内面平向 轴于位须必线素一任 上面表柱圆 )� c &O -\ 5U 5W ,S :g *�例图
` !w 1X -] 6O "q $] 8k 。域区的间之面平行平两的 t 值差公为离距是带差公——义定带差公 L 0c *N *} (c :度 面 平 .2
时小 915 间时线在 8-9-1102 录登后最 021 限权读阅 点 8318 券纪世 BK 6021211 量流 9159 分积 0 享分 2211 题主 9315 子帖 38 友好 主版
由理 起收
分评人 1 有已
。线实细是线 的外头箭的号符动跳但� �宽线实粗为 b�b�2/b 为度宽型线的号符差公位形�注
解详差公位形用常间车工加
` 3` -A 'w (H ,D 2 。域区的间之圆 心同两的 t 值差公为差径半上面截正一同在是带差公——义定带差公 r ,r 'G !l )t *Z 5T :W #度 圆 .3 h &n +? !V 1z %z -S ! l "w 5@ 0v #m 。内面平行平两的 1.0 值差 :n -| " 。内面平行平两的 L 1S (W K \ 1j 7@ 5J 2Y ,S 9T )C 3u ( 公 为 离 距 于 位 须 必 6X ;R $W "m -1.0 值差公为 �围范的 001×001 意任上面表 �例图 离距于正修须必面表上�例图
i +r 5\ &A 5G )z 。 - 内面柱 圆的 50.0 值差公为径 直于位须必线轴的件 零个整 )� K /b 9D 7E /U 0d %Z ;U * 。内 面柱圆的 40.0 值差公 为径直于位须必线轴 的体柱圆 dφ )� v 6C 3v "C 0? 9g "L 2�例图
LED照明灯具全参数对比表_图文(精)

选票公示栏:所有投票单位名称选票公示:组委会对所有适合要求的提名选票进展实名公示,评选过程承受业界监视。
(在线填写提名选票公示时间:2012年 11月 15-30日。
注:12月 1-4日为选票审核和统计阶段, 5日公布最终票数与入围评选咨询:谢先生 26981898-845 :sy.xiegg-led.选票编号 T8811253投票单位某某光世界科技某某投票结果查看选票编号T8811252投票单位某某雷创电子投票结果查看选票编号 T8811251投票单位艾丽信照明投票结果查看选票编号 T8811250投票单位某某光为科技某某投票结果查看查看更多项选择票材料与配套类提名选票统计:衬底(点击查看更多企业名称四联光电 (查看投票者票数 94企业名称京晶光电 (查看投票者票数 68企业名称皓天光电 (查看投票者票数 63企业名称康蓝光电 (查看投票者票数 59企业名称 Rubicon (查看投票者票数 37荧光粉(点击查看更多企业名称英特美 (查看投票者票数 186企业名称根本化学 /弘大 (查看投票者票数 139企业名称有研稀土 (查看投票者票数 107企业名称中村宇极(查看投票者票数 51企业名称新力光源 (查看投票者票数 42封装硅胶(点击查看更多企业名称道康宁 (查看投票者票数 189企业名称恒大新材料 (查看投票者票数 121企业名称信越化学 (查看投票者票数 105支架(点击查看更多企业名称一诠支架 (查看投票者票数 138企业名称佳乐电子 (查看投票者票数 131企业名称亿润电子 (查看投票者票数 129选票编号 T8811249投票单位某某市古镇铭煌照明电器某某投票结果查看选票编号 T8811248投票单位某某市英豪灯饰厂投票结果查看选票编号T8811247投票单位某某市盛彩大地照明科技某某投票结果查看选票编号T8811246投票单位某某市富嘉灯饰厂投票结果查看选票编号 T8811245投票单位某某市森本光电科技某某投票结果查看选票编号 T8811244投票单位某某市鸿海亚克力灯饰厂投票结果查看选票统计注:评选投票通道关闭, 12月 1~4日为选票审核和统计阶段, 5日公布最终入围。
NMOS_K80E08K3

1
2011-08-09 Rev.1.0
TK80E06K3A
5. Thermal Characteristics
Characteristics Channel-to-case thermal resistance Channel-to-ambient thermal resistance Symbol Rth(ch-c) Rth(ch-a) Max 1.00 83.3 Unit /W
Note 1: Ensure that the channel temperature does not exceed 150. Note 2: VDD = 25 V, Tch = 25 (initial), L = 16.3 µH, RG = 1.2 Ω, IAR = 80 A
Note:
This transistor is sensitive to electrostatic discharge and should be handled with care.
Note:
Using continuously under heavy loads (e.g. the application of high temperature/current/voltage and the significant change in temperature, etc.) may cause this product to decrease in the reliability significantly even if the operating conditions (i.e. operating temperature/current/voltage, etc.) are within the absolute maximum ratings. Please design the appropriate reliability upon reviewing the Toshiba Semiconductor Reliability Handbook ("Handling Precautions"/"Derating Concept and Methods") and individual reliability data (i.e. reliability test report and estimated failure rate, etc).
60分钟KDJ指标怎么使用

60分钟KDJ指标怎么运用kdj指标超短线实战须要充分利用kdj随机指标的快速波动特性,并运用分时指标来实施超短线操作。
那么今口在这里给大家整理一下kdj指标相关学问,我们一起看看吧!60分钟KDJ指标运用技巧1、K80,说明短线市场和个股进入强势区域;K20,说明短线市场和个股进入底部区域,J103为短线超买,指数或股价有回荡要求;J-IO为短线超卖,指数或股价有剧烈回升要求。
2、线K在20以下向上突破线D,并且线K有效突破20,且指数或股价突破8小时均线为买进信号;线K在80以上向下跌破线D.并且线K有效跌破80时,为标准的短线卖出信号。
3、线K与线D的交叉发生在80以下,20以上,则可以作为杂波过滤掉,不具备参考意义。
最终,还要说明一点,60分钟KDJ的运用仍有不足和缺陷,应用于个股的短线操作时,肯定要记得操作原则,即使不幸被套也要等到线K突破80而后再破80后出局,那样或许不至于把股票割在地板上。
怎样看kdj指标投资者在运用KDJ指标作为技术分析时,可以从KDJ指标的K值范围、D值范围、J值范围以及KDJ指标所构成的金叉、死叉动身进行分析。
KDJ指标由黄、绿、紫三种颜色的线条构成,黄色的是K、绿色的是D、紫色的是J,它们的取值范围为0—100。
就敏感性而言,J最敏感,K次之,D最差;就平安性而言,J值最差、K次之、D最平安。
KDJ的取值范围在不同区域,所发出的信号不同,当K、D,J三值在20以下,则是超卖区,发出的信号为买入;K、D、J三值在80以上,则是超买区,发出的信号为卖出;K、DU三值范围在20-80之间,则为徘徊区,发出的信号为观望。
当K、D、J三种在50旁边时,则表明多空双方力气处于平衡状态。
KDJ指标应用在股票市场中,投资者可以通过布林线和KDJ技术指标的形态相互进行参考运用,来提高技术指标形态的有效率。
在KDJ技术指标中,J线(紫线〉处于20数值左右和K线(白线)处于20数值旁边上穿D线(黄线),J线(紫线)和K线(白线)持续在D线(黄线)上方运行。
圆柱式墩柱模板垂直度控制方法

圆柱式墩柱模板垂直度控制方法摘要:本文从测量专业角度出发,对传统的圆柱式墩柱模板垂直度控制方法优缺点进行分析,并以长福高速A3项目龙江特大桥工程为例,提出“三点圆”理论控制圆柱式墩柱模板垂直度的新方法。
关键词:圆柱式墩柱;垂直度控制;三点圆1.引言随着现代化经济建设的不断发展,道路桥梁成为一个国家经济发展的大动脉,圆柱式墩柱是现代化桥梁建设普遍采用的形式之一。
本文从测量的角度出发,以长福高速A3项目龙江特大桥工程为例,分析传统的圆柱式墩柱模板垂直度精度控制方法的优缺点,在传统方法的基础上提出了“三点圆”理论控制垂直度的新方法,进一步提高了施工效率与工程质量。
本合同段位于福建省东部沿海福州辖区的福清市龙山街道、海口镇境内。
起点K74+400与A2合同段相接,位于福清市阳下街道北山隧道中,路线由北向南,穿越北山隧道进入龙山街道,建柏渡大桥,经塘头、先强,于龙山互通接清荣大道(X177),经柏渡,建龙江特大桥跨过福清市东部新区、龙江,经海口镇桐屿,终于东峤村龙江特大桥83#墩(桩号K80+485.5),全线包括柏渡大桥等龙江特大桥共计4.5座。
其中龙江特大桥全长2869米,圆柱式墩柱共计336根,墩柱高度最高在15m左右。
根据设计要求,桥墩墩身倾斜度必须满足《公路桥涵施技术规范》(JTG/TF50-2011)中相关内容的规定,即墩柱倾斜度应小于3%H(H为墩柱高度),且垂直度最大允许偏差不大于20mm。
如果施工过程中测量控制不到位,很容易超出规范要求,留下质量隐患,因此对墩柱模板垂直度的测量控制显得十分重要。
2.传统圆柱体墩柱模板垂直度控制方法2.1吊垂球法准确测量放样设计桩位中心坐标,拼装墩柱模板,在墩柱模板上口边缘四周吊垂球,用直钢尺反复丈量垂球垂线距离模板上端和下端距离,再不断调整缆风绳,直至模板各个方向的上下端与垂球垂线距离误差在允许范围内即可。
这种方法操作简单,效率高,但精度较低,只能粗略的判断墩柱的垂直度,在刮风的天气情況下,垂球受风的影响会来回摆动,这种方法就不能使用了。
最新北师大版四年级数学上册第6单元除法教案

最新北师大版四年级数学上册第6单元除法教案第1节买文具(这是边文,请据需要手工删加)教材第66~68页的内容。
1.结合实际情境,理解和掌握整十、整百数除以整十数的口算方法,能正确地口算,并在交流中体会算法的多样化。
2.探索除数是两位数(整十数)除法的计算过程,发现并归纳判断商是几位数的方法,理解计算的道理,能正确地计算。
3.在提出问题、解决问题的过程中,逐步养成独立思考、认真倾听、清楚表达的良好习惯。
重点:掌握除数是整十数除法的算法,并能正确地计算。
难点:掌握除数是整十数除法的算理。
教材中的情境图制成的课件及实物投影仪。
出示教材情境图。
1.今天我们逛一逛文具店,一边买文具,一边学习新知识。
(板书课题:买文具)2.你发现了哪些数学信息?学生可能提出的问题:①书包的单价是文具盒的几倍?②80元可以买多少个书包?③160元可以买多少个计算器?1.老师也有个问题给大家。
(师手中拿着一叠十元钱,有8张)猜猜老师手中有多少钱?现在老师想用这些钱买书包,可以买多少个?(将问题卡片贴在黑板上)(1)谁能列出算式?板书:80÷20=(2)你能用哪些方法计算出它的结果?(学生独立思考)可以在练习本写一写。
(3)小组讨论:写完的同学,可以小组交流一下。
(4)全班汇总。
①减法:理解除法的含义;②乘法:为后面的试商做准备;③人民币:帮助学生理解除数是整十数的除法的算理。
④列竖式:师黑板演示。
思考问题:“4”为什么写在个位上?(补全板书)(这是边文,请据需要手工删加)设计意图:把主动权交给学生,让他们自己去选择。
尊重差异,交流互动。
如在讨论80÷20为什么等于4时,因为学生个体不同,解决问题的策略和方法也就不同,这样的差异为数学提供了资源,充分尊重学生的选择,对不同方法的交流使教师和学生、学生和学生之间在思维上发生碰撞,促使参与数学活动的每个人都有所思。
2.80元可以买4个书包,160元能买几个计算器?还剩多少元?(1)估计一下,比刚才买的书包多还是少?够不够买10个?(2)谁能列出算式?板书:160÷30=(3)独立计算:下面用你喜欢的方法算一算,160里面有几个30(4)全班汇总:竖式方法由学生板演。
长郡中学2024-2025学年高一上学期综合能力检测(入学分班考试)数学试卷(解析版)

长郡中学2024级高一综合能力检测试卷数学时量:90分钟 满分100分一、选择题:本题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一个选项是符题目要求的.1.《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿日兆.”说明了大数之间的关系:1亿1=万1万,1兆1=万1×万1×亿.若1兆10m=,则m 的值为( ) A.4 B.8C.12D.16【答案】D 【解析】【分析】由指数幂的运算性质即可求解. 【详解】1万=410,所以1亿=810, 所以1兆=8816101010×=, 所以16m =. 故选:D2.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨),夏季(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒大寒),若从二十四个节气中随机抽取一个节气,则抽到的节气在夏季的概率为( )A.12B.112C.16D.14【答案】D 【解析】【分析】根据概率的计算公式即可求解.【详解】从二十四个节气中随机抽取一个节气,则抽到的节气在夏季的概率为61244=, 故选:D3.如图,矩形ABCD 中,3AB =,1AD =,AB 在数轴上,若以点A 为圆心,对角线AC 的长为半径作弧交数轴的正半轴于M ,则点M 所表示的数为( )A. 2B.1−C.D.1【答案】B 【解析】【分析】利用勾股定理和数轴的知识求得正确答案.【详解】由于AC =,所以点M所表示的数为)231+−=−.故选:B4. 若关于x 的不等式组()532223x x x x a + ≥−+<+恰好只有四个整数解,则a 的取值范围是( )A. 53a <−B. 5433a −≤<− C. 523a −<−≤D. 523a −<<−【答案】C 【解析】【分析】化简不等式组,由条件列不等式求a 的取值范围. 【详解】解不等式532x x +≥−,得11x ≤, 解不等式()223x x a +<+,得23x a >−, 由已知可得7238a ≤−<, 所以523a −<−≤.故选:C.5. 在ABC ,3AC =,4BC =,5AB =,点P 在ABC 内,分别以A ,B ,P 为圆心画圆,圆A 的半径为1,圆B 的半径为2,圆P 的半径为3,圆A 与圆P 内切,圆P 与圆B 的关系是( ) A. 内含 B. 相交 C. 外切 D. 相离【答案】B 【解析】【分析】由题意条件分析两圆圆心距与两半径和差的大小关系即可得. 【详解】由圆A 与圆P 内切,则312PA =−=,5AB =, 又点P 在ABC 内,则PA PB AB +>,且PB AB <, 所以523PB AB PA >−=−=,且5PB <, 则3232PB −<<+,由圆B 的半径为2,圆P 的半径为3, 所以圆P 与圆B 相交. 故选:B.6. 对于正整数k 定义一种运算:1()[][]44k k f k +=−,例:313(3)[][]44f +=−,[]x 表示不超过x 的最大整数,例:[3.9]3=,[ 1.8]2−=−.则下列结论错误的是( ) A. ()10f =B. ()0f k =或1C. ()()4f k f k +=D. ()()1f k f k +≥【答案】D 【解析】【分析】根据给定的定义,逐项计算判断即可.【详解】对于A ,11(1)[][]00024f =−=−=,A 正确; 对于B ,取4,1,2,3,4k n i i =+=,n 为自然数, 当4i =时,1()[1][1][1]044f k n n ++−+,当3i =时,33()[1][]1([])144f k n n n n =+−+=+−+=,当1,2i =时,11()[][][]([])04444i i i if k n n n n ++=+−+=+−+=,B 正确; 对于C ,11(4)[1][1]1[](1[])()4444k k k kf k f k +++=+−+=+−+=,C 正确; 对于D ,414313(31)[][]0,(3)[][]14444f f +++=−==−=,即(31)(3)f f +<,D 错误.故选:D7. 如图,点A 为反比例函数()10y x x=−<图象上的一点,连接AO ,过点O 作OA 的垂线与反比例函数()40yx x=>的图象交于点B ,则AO BO 的值( )A.12B.14C.D.13【答案】A 【解析】【分析】设121214,,,A x B x x x −,由,A B 两点分别做x 轴的垂线,垂足分别为,E F ,由AO BO ⊥,得∽∠ AOE OBF ,由==AEEO AO OFBF BO,可得答案. 【详解】设AA �xx 1,−1xx 1�,BB �xx 2,4xx 2�(xx <0,xx 2>0),由,A B 两点分别做x 轴的垂线,垂足分别为,E F , 且()()12,0,,0E x F x ,因为AO BO ⊥,所以,∠=∠∠=∠AOE OBF OAE BOF , 所以∽∠ AOE OBF ,所以AE EO OF BF =,可得112214−−=x x x x ,即22124x x =,所以122x x =−, 所以12121211==−==−=A Ex x x OA BO OFx.故选:A.8. 若二次函数的解析式为()()()2215y x m x m =−−≤≤,且函数图象过点(),p q 和点()4,p q +,则q 的取值范围是( ) A. 124q −≤≤ B. 50q −≤≤C. 54q −≤≤D. 123q −≤≤【答案】A 【解析】【分析】由二次函数解析式可求得对称轴为1x m =+,进而可得412p p m ++=+,由函数图象过点(),p q ,可得2(1)4q m =−−+,可求q 的取值范围.【详解】因为二次函数解析式为()()()2215y x m x m =−−≤≤, 所以二次函数的对称轴为1x m =+,函数图象过点(),p q 和点()4,p q +,故点(),p q 和点()4,p q +关于直线1x m =+对称, 所以412p p m ++=+,所以1[0,4]p m −∈, 又()()()()2222121223(1)4q p m p m m m m m m =−−=−−−−=−++=−−+, 当1m =,max 4q =,当5m =,min 12q =−,所以124q −≤≤. 故选:A.二、填空题:本题共4小题,每小题4分,共16分.9. 分解因式:432449a a a −+−=______. 【答案】2(23)(1)(3)a a a a −++− 【解析】【分析】根据给定条件,利用公式法及十字相乘法分解因式即可得解.【详解】43222222449(2)9(23)(23)(23)(1)(3)a a a a a a a a a a a a a −+−=−−=−+−−=−++−. 故答案为:2(23)(1)(3)a a a a −++−的10. 直线1:1l y x =−与x 轴交于点A ,将直线1l 绕点A 逆时针旋转15°,得到直线2l ,则直线2l 对应的函数表达式是______.【答案】y =【解析】【分析】先求得2l 的倾斜角,进而求得直线2l 对应的函数表达式. 【详解】直线1:1l y x =−与x 轴交于点 1,0A , 直线1:1l y x =−的斜率为1,倾斜角为45°,所以2l 的倾斜角为60°所以直线2l 对应的函数表达式是)1y x =−=.故答案为:y=−11. 若关于x 的分式方程22411x a x ax x −−+−=−+的解为整数,则整数a =______. 【答案】1± 【解析】【分析】由分式方程有意义可知1x ≠且1x ≠−,再化简方程求解2x a=,由,a x 均为整数可求.【详解】则方程241x a x −−−1x ≠且1x ≠−. 方程可化为222211x a x ax x −−+−=+−+,即2211a a x x −+=−+, 解得2x a=,由1x ≠且1x ≠−,所以2a ≠且2a ≠−.由a 为整数,且x 为整数,则当1a =−,2x =−,或当1a =,2x =时满足题意. 所以1a =±. 故答案为:1±.12. 如图,已知两条平行线1l ,2l ,点A 是1l 上的定点,2AB l ⊥于点B ,点C ,D 分别是1l ,2l 上的动点,且满足AC BD =,连接CD 交线段AB 于点E ,BH CD ⊥于点H ,则当BAH ∠最大时,sin BAH ∠的值为______.【答案】13【解析】【分析】因为BH CD ⊥于点H ,所以点 H 在以BE 为直径的圆上运动, 当 AH 与圆 O 相切时, BAH ∠ 最大,据此在OHA 求解即可. 【详解】12//,//,AC BD l l∴ 四边形 ACBD 是平行四边形 12AE BE AB ∴==A 为定点, 且 2//AB l AE ∴ 为定值,BH CD ⊥ 90BHE ∠∴=, 如图,取BE 的中点O ,则点 H 在以BE 为直径的圆上运动,此时 1123OE BE OA ==, 当 AH 与圆 O 相切时, BAH ∠ 最大1sin 3OH BAH OA ∠∴==故答案为:13.三、解答题:本题共4小题,共52分.应写出文字说明、证明过程或演算步骤.13. 某学校举办的“青春飞扬”主题演讲比赛分为初赛和决赛两个阶段.(1)初赛由10名教师评委和45名学生评委给每位选手打分(百分制),对评委给某位选手的打分进行整理、描述和分析下面给出了部分信息.a .教师评委打分:86 88 90 91 91 91 91 92 92 98b .学生评委打分的频数分布直方图如下(数据分6组:第1组8285x ≤<,第2组8588x ≤<,第3组8891x ≤<,第4组9194x ≤<,第5组9497x ≤<,第6组97100x ≤≤);平均数中位数众数教师评委 91 91 m 学生评委90.8n93c .评委打分的平均数、中位数、众数如上: 根据以上信息,回答下列问题:①m 的值为______,n 的值位于学生评委打分数据分组的第______组;②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为x ,则x ______91(填“>”“=”或“<”);(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计算5名专业评委给其打分的平均数和方差.平均数较大的选手排序靠前,若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决赛的甲、乙、丙三位选手的打分如下:评1评委2评委3评委4评委5甲 93 90 92 93 92 乙9192929292丙 90 94 90 94 k若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前的是______,表中k (k 为整数)的值为______.【答案】(1)①91;4;②< (2)甲;92 【解析】【分析】(1)①根据众数以及中位数的定义解答即可;②根据算术平均数的定义求出8名教师评委打分的平均数,即可得出答案; (2)根据方差的定义和平均数的意义求解即可. 【小问1详解】①由题意得,教师评委打分中91出现次数最多,故众数91m =;45名学生评委打分数据的中位数是第23个数,故n 的值位于学生评委打分数据分组的第4组; ②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分的平均数为x , 则1(8890919191919292)90.758x =×+++++++=,91x ∴<.【小问2详解】甲选手的平均数为1(9390929392)925×+++=, 乙选手的平均数为1(9192929292)91.85×++++=, 因为丙在甲、乙、丙三位选手中的排序居中,所以三位选手中排序最靠前的是甲,且丙的平均数大于或等于乙的平均数, 因为5名专业评委给乙选手的打分为91,92,92,92,92, 乙选手的方差2221[4(9291.8)(9191.8)]0.165S =××−+−=乙, 5名专业评委给丙选手的打分为90,94,90,94,k , 所以乙选手的方差小于丙选手的方差,所以丙选手的平均数大于乙选手的平均数,小于或等于甲选手的平均数,∴9390929392909490949192929292k ++++≥++++>++++,9291k ∴≥>, k 为整数,的k ∴的值为92.14. 根据以下素材,探索完成任务——如何设计摇椅的椅背和坐垫长度?素材一:某公司设计制作一款摇椅,图1为效果图,图2为其侧面设计图,其中FC 为椅背,EC 为坐垫,C ,D 为焊接点,且CD 与AB 平行,支架AC ,BD 所在直线交于圆弧形底座所在圆的圆心O .设计方案中,要求A ,B 两点离地面高度均为5厘米,A ,B 两点之间距离为70厘米;素材二:经研究,53OCF ∠=°时,舒适感最佳.现用来制作椅背FC 和坐垫EC 的材料总长度为160厘米,设计时有以下要求: (1)椅背长度小于坐垫长度;(2)为安全起见,摇椅后摇至底座与地面相切于点A 时(如图3),F 点比E 点在竖直方向上至少高出12厘米.(sin530.8°≈,cos530.6°≈,tan53 1.3°≈)任务:(1)根据素材求底座半径OA ; (2)计算图3中点B 距离地面的高度;(3)①求椅背FC 的长度范围;(结果精确到0.1m ) ②设计一种符合要求的方案. 【答案】(1)125厘米;(2)19.6厘米 (3)①64.580FC ≤<;②70cm ,90cm (答案不唯一). 【解析】【分析】(1)根据四边形AHNB 为矩形,35AG BG ==厘米,5AH GM ==厘米,设底座半径OA r =厘米,则OM OA r ==厘米,由勾股定理求出r 即可得出答案;(2)由四边形ANBK 为矩形,进而得AK BN h ==,()125cm,125cm OK h OB =−=,然后在直角三角形中由勾股定理列出关于h 的方程,解方程求出h 即可得出答案;(3)①过F 作FP OA ⊥于P ,过点E 作EQ OA ⊥于Q ,先求出cos cos 0.28QCD OAB ∠=∠=,设椅背FC x =厘米,则坐垫(160)EC x =−,即可得0.60.28(160)12x x −−≥,由此解得64.5x ≥,据此可得椅背FC 的长度范围;②在①中椅背FC 的长度范围任取一个FC 的值,再计算出EC 的值即可,例如取70FC =厘米,则1607090EC =−=(厘米);(答案不唯一,只要在FC 的长度范围内即可). 【小问1详解】过点A 作AH 垂直地面于H ,过点O 作OG AB ⊥于G ,OG 的延长线于地面交于点M ,如图所示:AB 平行于地面,∴四边形AHNB 为矩形,1352AG BG AB ===厘米, 5AH GM ==厘米,设底座半径OA r =厘米,则OM OA r ==厘米,(5)OG OM GM r ∴=−=−厘米,在Rt OAG ∆中,OA r =厘米,35AG =厘米,(5)OGr =−厘米, 由勾股定理得:222OA OG AG =+,即:222(5)35r r =−+, 解得:125r =,∴底座半径OA 的长度为125厘米;【小问2详解】过点B 作BN 垂直地面于N ,BK OA ⊥于K ,如图所示:设BN h =,底座与地面相切于点A ,OA ∴垂直地面于点A ,∴四边形ANBK 为矩形,AK BN h ∴==,由任务一可知:125cm,125OA OB OK OA AK h ==∴==--, 在Rt ABK △中,cm,=70cm AK h AB =, 由勾股定理得:2222270BK AB AK h =−=−,在Rt OBK 中,()125cm,125cm OK h OB =−=, 由勾股定理得:22222125(125)BK OB OK h =−=−−,222270125(125)h h ∴−=−−,解得:19.6h =,∴点B 距离地面的高度为19.6厘米;【小问3详解】①过F 作FP OA ⊥于P ,过点E 作EQ OA ⊥于Q ,如图所示://CD AB ,QCD OAB ∴∠=∠,由任务②可知:19.6AK h ==厘米,70AB =厘米, 在Rt ABK △中,19.6cos 0.2870AK OAB AB ∠===, cos cos 0.28QCD OAB ∴∠=∠=,椅背FC 和坐垫EC 的材料总长度为160厘米, ∴设椅背FC x =厘米,则坐垫(160)EC x =−, 椅背长度小于坐垫长度,160x x ∴<−,解得:80x <,在Rt CQE △中,cos 0.28CQQCD CE∠==, 0.280.28(160)CQ CE x ∴==−厘米,在Rt CFP △中,cos CPOCF CF∠=, cos cos530.6CP CF OCF x x ∴=⋅∠=⋅°≈(厘米), F 点比E 点在竖直方向上至少高出12厘米,12AP AN ∴−≥,即:()12AC CP AC CQ +−+≥,12CP CQ ∴−≥,0.60.28(160)12x x ∴−−≥,解得:64.5x ≥, 又80x < ,64.580x ∴≤≤,即:64.580FC ≤≤,∴椅背FC 的长度范围是:64.580FC ≤<;②由于64.580FC ≤<,故取70cm FC =,则1607090cm EC ==-.15. 定义:在平面直角坐标系中,直线x m =与某函数图象交点记为点P ,作该函数图象中点P 及点P 右侧部分关于直线x m =的轴对称图形,与原函数图象上的点P 及点P 右侧部分共同构成一个新函数的图象,称这个新函数为原函数关于直线x m =的“迭代函数”.例如:图1是函数1y x =+的图象,则它关于直线0x =的“迭代函数”的图象如图2所示,可以得出它的“迭代函数”的解析式为()()10,10.x x y x x +≥ =−+<(1)函数1y x =+关于直线1x =的“迭代函数”的解析式为______.(2)若函数243y x x =−++关于直线x m =的“迭代函数”图象经过()1,0−,则m =______.(3)已知正方形ABCD 的顶点分别为:(),A a a ,(),B a a −,(),C a a −−,(),D a a −,其中0a >.①若函数6y x=关于直线2x =−的“迭代函数”的图象与正方形ABCD 的边有3个公共点,求a 的值; ②若6a =,函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,求n 的取值范围.【答案】(1)1,13,1x x y x x +≥ =−+<(2)m =m =,(3)①3;②()5,1,12−∞−∪−. 【解析】【分析】(1)取点()2,3M ,()3,4N ,求两点关于1x =的对称点,利用待定系数法求左侧图象的解析式,由此可得结论;(2)判断点()1,0−与函数243y x x =−++的图象的关系,再求()1,0−关于直线x m =的对称点,由条件列方程求m 即可;(3)①求函数6y x=关于直线2x =−的“迭代函数”的解析式,作函数图象,观察图象确定a 的值; ②分别在0n >,0n =,0n <时求函数6y x=关于直线x n =的“迭代函数”解析式,讨论n ,由条件确定n 的范围.小问1详解】在函数1y x =+的图象上位于1x =右侧的部分上取点()2,3M ,()3,4N , 点()2,3M 关于直线1x =对称点为(0,3), 点()3,4N 关于直线1x =的对称点为()1,4−,设函数1y x =+,1x >的图象关于1x =对称的图象的解析式为,1y kx b x =+<, 则34b k b = −+=,解得13k b =− = ,所以函数1y x =+关于直线1x =的“迭代函数”的解析式为1,13,1x x y x x +≥ =−+<;【的【小问2详解】取1x =−可得,2431432y x x =−++=−−+=−, 故函数243y x x =−++的图象不过点()1,0−, 又点()1,0−关于直线x m =的对称点为()21,0m +, 由已知可得()()20214213m m =−++++,1m >−,所以m =或m =,【小问3详解】①当0x >或20x −≤<时,函数6y x =关于直线2x =−的“迭代函数”的图象的解析式为6y x =, 当2x <−时,设点EE (xx ,yy )在函数6y x=关于直线2x =−的“迭代函数”的图象上,则点()4,x y −−在函数6y x=的图象上,所以64y x=−−, 所以函数6y x =关于直线2x =−的“迭代函数”的解析式为[)()()6,2,00,6,,24x xy x x∞∞ ∈−∪+ =∈−− −− , 作函数6y x=关于直线2x =−的“迭代函数”的图象如下:观察图象可得3a =时,函数6y x=关于直线2x =−的“迭代函数”的图象与正方形ABCD 的边有3个公共点,②若0n >,当x n ≥时,函数6y x =关于直线x n =的“迭代函数”的图象的解析式为6y x=, 当0x <或0x n <<时,设点EE (xx ,yy )在函数6y x=关于直线x n =的“迭代函数”的图象上,则点()2,n x y −在函数6y x=的图象上,所以62y n x=−, 所以函数6y x =关于直线x n =“迭代函数”的解析式为()()()6,,6,,00,2x n xy x n n x∞∞ ∈+ =∈−∪ − , 当6n >时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有2个公共点,的当6n =时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有2个公共点,当16n <<时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有2个公共点,当1n =时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有3个公共点,当01n <<时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,当0n =时,函数6y x =关于直线xx =0的“迭代函数”的解析式为6,06,0x xy x x> =−< , 作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,若0n <,当0n x ≤<或0x >时,函数6y x =关于直线x n =的“迭代函数”的图象的解析式为6y x=, 当x n <时,设点EE (xx ,yy )在函数6y x=关于直线x n =的“迭代函数”的图象上, 则点()2,n x y −在函数6y x=的图象上, 所以62y n x=−,所以函数6y x =关于直线x n =的“迭代函数”的解析式为[)()()6,,00,6,,2x n xy x n n x ∞∞ ∈∪+ = ∈− −,当10n −<<时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,当1n =−时,作函数6y x=关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有5个公共点,当512n−<<−时,作函数6yx=关于直线x n=的“迭代函数”的图象可得,函数6yx=关于直线x n=的“迭代函数”的图象与正方形ABCD有6个公共点,当52n=−时,作函数6yx=关于直线x n=的“迭代函数”的图象可得,函数6yx=关于直线x n=的“迭代函数”的图象与正方形ABCD有5个公共点,当7522n−<<−时,作函数6yx=关于直线x n=的“迭代函数”的图象可得,函数6yx=关于直线x n=的“迭代函数”的图象与正方形ABCD有4个公共点,当72n=−时,作函数6yx=关于直线x n=的“迭代函数”的图象可得,函数6yx=关于直线x n=的“迭代函数”的图象与正方形ABCD有4个公共点,当762n −<<−时,作函数6y x =关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,当6n =−时,作函数6y x =关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,当6n <−时,作函数6y x =关于直线x n =的“迭代函数”的图象可得, 函数6y x=关于直线x n =的“迭代函数”的图象与正方形ABCD 有4个公共点,综上,n 的取值范围为()51,12∞−−∪−,. 【点睛】方法点睛:“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.16. 已知抛物线2y x bx c =−++与x 轴交于点()1,0A −,()3,0B .(1)如图1,抛物线与y 轴交于点C ,点P 为线段OC 上一点(不与端点重合),直线PA ,PB 分别交抛物线于点E ,D ,设PAD △面积为1S ,PBE △面积为2S ,求12S S 的值; (2)如图2,点K 是抛物线的对称轴与x 轴的交点,过点K 的直线(不与对称轴重合)与抛物线交于点M ,N ,过抛物线顶点G 作直线//l x 轴,点Q 是直线l 上一动点求QM QN +的最小值.【答案】(1)19(2)【解析】【分析】(1)把点()1,0A −,()3,0B 代入抛物线方程,解出抛物线的解析式,设(0,)P p ,求出直线AP 解析式为y px p =+,联立方程223y px p y x x =+ =−++, 可得2(3,4)E p p p −−+,同理可得234(,)393p p p D −−+,即可得1S ,2S ,化简可得结果; (2)作点N 关于直线l 的对称点N ′,连接MN ′,过M 点作MF NN ′⊥于F ,求出(1,0)K ,设直线MN解析式为y kx d =+,把点K 坐标代入即可知直线MN 的解析式y kx k =−,设2(,23)M m m m −++,2(,23)N n n n −++,求出2(,25)N n n n ′−+,可得QM QN QM QN MN ′′+=+≥,结合2(,23)F n m m −++,可得222421780MN MF N F k k =+=++′′,从而得到QM QN +的最小值. 【小问1详解】把点()1,0A −,()3,0B 代入抛物线方程2y x bx c =−++得:10930b c b c −−+= −++=, 解得:23b c = =, 所以抛物线方程为:223y x x =−++, 设(0,)P p ,直线AP 解析式为11y k x b =+, 把点()1,0A −,(0,)P p 代入得:1110k b b p −+= = , 所以线AP 解析式为y px p =+,联立223y px p y x x =+ =−++ ,解得:10x y =−=或234x p y p p =− =−+ , 所以2(3,4)E p p p −−+,设直线BP 解析式为22y k x b =+ 把点()3,0B ,(0,)P p 代入得:22230k b b p+= = , 直线BP 解析式为3py x p =−+ 联立2323p y x p y x x =−+ =−++ ,解得:30x y = = 或233493p x p p y − = =−+可得234(,)393p p p D −−+, 所以221142()2(3)2939ABD ABP D P p p S S S AB y y p p p =−=⋅−=−+−=− , ()2221()242(3)2ABE ABP E P S S S AB y y p p p p p =−=⋅−=−+−=− , 所以2122192(3)92(3)S p p S p p −=−= 【小问2详解】作点N 关于直线l 的对称点N ′,连接MN ′,过M 点作MF NN ′⊥于F ,如图:因为2223(1)4y x x x =−++=−−+,所以抛物线223y x x =−++的对称轴为1x =, 所以(1,0)K ,设直线MN 解析式为y kx d =+, 把点(1,0)K 代入得:=0k d +,所以=d k −,所以直线MN 的解析式为y kx k =− 设2(,23)M m m m −++,2(,23)N n n n −++,联立223y x x y kx k =−++ =−,可得2(2)30x k x k +−−−= 则2m n k +=−,3mn k =−−,因为N ,N ′关于直线l :4y =对称,所以2(,25)N n n n ′−+,则QM QN QM QN MN ′′+=+≥,又2(,23)F n m m −++, 所以222()2N F m n m n +−++′,FM m n =−, 在Rt MFN ′ 中,2222222()2()2MN MF N F m n m n m n =+=−++−++ ′ ′,222()4()22()2m n mn m n mn m n =+−++−−++222(2)4(3)(2)2(3)2(2)2k k k k k =−−−−+−−−−−−+ 421780k k =++所以当0k =时,2MN ′最小为80,此时MN ′=所以QM QN +≥,即QM QN +的最小值为。
筛分过滤实验报告

筛分实验一、实验目的(1)测定天然河砂的颗粒级配。
(2)绘制筛分级配曲线,求d0、d80、K80。
(3)按设计要求对上述河砂进行再筛选。
二、实验原理滤料级配是指将不同大小粒径的滤料按一定比例加以组合,以取得良好的过滤效果。
滤料是带棱角的颗粒,其粒径是指把滤料颗粒包围在内的球体直径(这是一个假想直径)。
在生产中简单的筛分方法是用一套不同孔径的筛子筛分滤料试样,选取合适的粒径级配。
我国现行规范是以筛孔孔径0.5 mm及1.2mm两种规格的筛子过筛,取其中段。
这虽然简便易行但不能反映滤料孔径的均匀程度,因此还应该考虑级配情况。
能反映级配状况的指标是通过筛分级配曲线求得的有效粒径的d10以及d80和不均匀系数K80。
d10是表示通过滤料质量10%的筛孔孔径,它反映滤料中细颗粒尺寸,即产生水头损失的“有效”部分尺寸;d80系指通过滤料质量80%的筛孔孔径,它反映粗颗粒尺寸;K80为d80与d10之比,即K80=d80/d10。
K80越大表示粗细颗粒尺寸相差越大,滤料粒径越不均匀,这样的滤料对过滤及反冲均不利。
尤其是反冲时,为了满足滤料粗颗粒的膨胀要求就会使细颗粒固过大的反冲强度而被冲走:反之,若为满足细颗粒个被冲走的要求而减小反冲强度,粗颗粒可能因冲不起来而得不到充分清洗。
故滤料需经过筛分级配。
三、实验内容3.1 实验设备与试剂(1)圆孔筛一套,直径0.15-0.9mm,筛孔尺寸如表4-1所示。
(2)托盘天平,称量300g,感量0.1g。
(3)烘箱。
(4)带拍摇筛机,如无,则人工手摇。
(5)浅盘和刷(软、硬)。
(6)1000mL量筒。
3.2 实验步骤(1)取样。
取天然河砂300g,取样时要先将取样部位的表层铲去,然后取样。
将取样器中的砂样洗净后放在栈盘中,将浅盘置于105℃恒温箱中烘干,冷至室温备用。
(2)称取砂样200g,选用一组筛子过筛。
筛子按筛孔大小顺序排列,砂样放在最上面的一只筛(1.68mm 筛)中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你们的差距很大,你们的结合完全打破了门当户对的传说。但是不管别人怎么看,你们就是这么恩爱。白天鹅怎么会爱上丑小鸭,只有他们自己清楚。
十八画:单恋一枝花
你的爱情也是从暗恋开始的,不过你会让他(她)上你。或许很曲折,会受伤,但你一直执着。朋友劝你天涯处处有芳草,你却单恋一枝花。
十九画:悠悠岁月,爱情长跑
你们爱情的战线拉得很长,或许三五年,或许十几年。但是结果是令人满意的,爱与被爱的人最后都会死心塌地。
二十画:顺其自然,水到渠成
如果问你们是谁先追的谁,是谁主动,你们回答不出来,因为你们的爱情在不知不觉中就来了,你们只不过是顺其自然地携起手。
二十一画:爱是永恒,平淡是真
九画:你喜欢他(她),他(她)爱别人
在爱情的舞会上,你来晚了一步,你的心上人已经有了自己的NO.1,两人亲密无间,你已无缝插针。因此注定了你这段感情要深埋在心里,注定你是暗恋了小倒霉蛋。所以赶快清理一下心绪,去属于自己的爱情里做主角吧。
十画:浓情蜜意,情手难牵
你们真的很合适,总能从对方的一个眼神洞悉心上人心中的一切。但是你们却走不到一起,并不是你们的原因,而是其他的因素,所以你们这段无疾而终的恋情令所有知情者扼腕。
十五画:水深火热,水火相容
谁水火不相容的,你们就相处得不错。你们一个似水,平和,内殓。一个如火,热情,洒脱。两个性情迥异的人一样可以找到共同点,一样可以谱写爱曲。
十六画:一本好书,只看一半
你们都是很有内秀的人,也都能看穿人的内心。你们的感情甜美却不持久,当对方不能吸引你时,你会决然地放手。他(她)就像一本小说,你打开了,却没能读完。
五画:风雨之后,亮丽彩虹
你们都是性情中人,你们都受过感情的伤,你们都一样脆弱而敏感同。同样的经历,同样的伤痛,让你更容易靠近。你们的感情在相互疗伤中一点一点加深,你们的心痊愈了,你们的爱情也圆满了。
六画:日久生情,顺理成章
你们很可能是在一起工作的同事,你们发展的是办公室爱情。朝九晚五的生活使你们互相产生好感,上下班路上的闲谈增进你们相互了解。你们的手牵在一起是顺理成章的事,在办公室里偷看一眼心上人也是你们最大的乐趣。
你和你心仪的他(她)姓名笔画之差就是你们破译你们缘分的密码,赶快测一下吧,很谁的哦!(注意:第一要用大名,小名、乳名和昵称不算数的,第二要一定用规范的汉字来测。)
零画:天生一对,佳偶天成
你们是如此的匹配,如此和谐,往往是你刚想说“可惜”他已经开始叹惜。你们性格相合,有共同的爱好,品味一致。就是这么默契,令人们羡慕得不得了。没办法,谁叫你们连姓名的笔画也一样呢。
三画:欢喜冤家,分分合合
你们前世是冤家,今生做情侣,所以就难免有一些不和谐的音符出现来折磨你们的爱情。你们的感情大起大落,分分合合,不过你们最终会修成正果,恩爱到老的。
四画:有缘无分,两两相忘
你们的感情一般是从学生时代开始的,那青涩的恋爱留给你们酸酸甜甜的味道遗忘对方,开始自己新的生活,但心中那最温柔的角落一直被初恋占据。
你们可能是经人介绍的,你们可能没有经过热就结婚。但是你们感情却很真实,与其你们的爱情平淡,不如说你们是大爱无声。
二十二画:一眼万年,相思连连
你们可能是被现实分开的情侣,你们可能是在有归宿后相见。你们相爱,却不能在一起,只能遥远地思念。
七画:知心朋友,心灵相通
你们可以无话不谈,你们可以心有灵犀,但是你们却很难成为情侣。因为你们太熟悉彼此,太了解对方了,所以很难擦出火花。其实你们不用遗憾,人生得一知己足矣,就这样一直做朋友也很不错。
八画:青梅竹马,两小无猜
你们的父母就很好的朋友,你们从穿开裆裤时就在一起。一起进幼儿园,一起上小学,一起过家家,一起闯祸后对家长撒谎。你们是长辈默认的娃娃亲,你们是邻居眼中的金童玉女,走到一起是天经地义的事。
十三画:同床异梦,貌合神离
在外人的眼中你们或许是一对模范夫妻,只有你自己心里明白根本不是那么一回事。你们根本就不了解对方,也不想去了解,各自有各自的圈子,交集很少。长痛不如短痛,还是选择放手吧。
十四画:缘分天定,破镜重圆
你们真是一对打不散的鸳鸯,情投意合,相互吸引。但是或话由于你们都太花心,都想有更多的选择,所以你们的罗曼史都很丰富。但是经历过后都会回头看到彼此,做出最正确的选择。
十一画:牛郎织女,聚少离多
你们的爱情基础非常深厚,牢不可破,然而却因为求学或工作的原因,使得你们分隔两地,聚少离多。也许是因为相聚短暂而益显珍贵,而e信来往,电话传情给你们平添一份情调。
十二画:相约黄昏,共赏夕阳
你们或许因为年少轻狂,或许月老作弄,你们错过了年轻时激扬的热情。当你们的缘分到来的时候,你们已经经历了大半辈子的沧桑。好不容易结合的你们会更加珍惜、享受这迟来的爱。
用姓名测试姻缘,80%准确率
他—她的姓名=他们的爱情
存在即有理,没有用的东西也是不会存在的,天以适者生存。姓名作为人与事物的接触外延,在人生中起着一个支柱桥梁的作用。名字就像是一个人的影子,这个影子的好坏将会直接影响到整个事物本身,因为如影随形。
雁过留声,人过留名。大家都知道中国人的姓名是由中国的汉字组成,没有汉字根本就不存在中国的姓名学,这是姓名学当中一个最根本、最直接的道理。我们的名字离不开阴阳五行和八卦,读音和意境联系着我们的命运,每一笔一画都暗藏玄机,你和你心目中的他(她)是不是天生的一对,能不能够白头偕老,你们之间到底有怎样的姻缘,都能在你们的姓名中找到答案。
一画:一见钟情,两情相悦
你们在看到对方的第一眼就深深地被吸引,并立刻爱上对方,接着就是干柴烈火般的热。海誓山盟的爱情宣言是你们奉行的金科玉律。她崇拜他,同样她也令他着迷,他们就像磁石与铁一样相互吸引。
二画:执子之手,与子携老
你们是众人眼中的神仙眷侣,站在一起怎么看怎么般配,很有传说中的夫妻相。你们之间或许没有惊天地泣鬼神的爱情神话,或许没有刻骨铭心的激情,但是你的之间的温情和默契却能让你们的心越走越近,一起慢慢变老。
