有理数的除法 课件 .ppt
合集下载
有理数的除法课件
4
(4) 4 7
(5)0.2 (6)-0.5
• 问:请同学们回忆一下小学所学过 的除法法则是什么? 例如:8÷0.2=?
引入负数以 后,以前学 的除法运算 是否成立?
• 问:你能说出有理数除法法则吗?
有理数除法法则: 除以一个数等于乘以这个数的倒数.
注意:0不能作除数.
为什么零不 能作除数?
想一想
1 7
)
(2) (-1) ÷(-1.5)
(3)
(-3)
÷(
2 5
)
÷(
1 4
)
(4)
(-3)
÷[(
2 5
)
÷(
1 4
)]
把下图中第一个圈内的每个数分别
2
咳 除以 5 ,将结果写在第二个圈内相应的位置 2
,4
你 15
行 吗
7 30
8
÷( 5)
2 3
7
12
4
? 45
9
3 50
3 20
•课本第38页3、4、5、6、7 •课本第40页13、14、15
探索题:设a,b,c为非零有 理数,求下列式子的值。
abc abc
有本领,你就勇敢 地上吧!
例3 计算:
(4)(1 3
3) 4
(112)注意视察
(5) (24 6) (6)寻求最佳方法 7
(6)
(
2) 3
(
4) 5
(12) 5
(7)
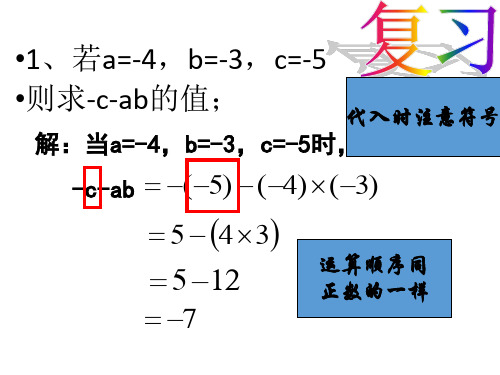
•1、若a=-4,b=-3,c=-5
•则求-c-ab的值;
代入时注意符号
解:当a=-4,b=-3,c=-5时,
-c-ab (5) (4) (3)
5 43
(4) 4 7
(5)0.2 (6)-0.5
• 问:请同学们回忆一下小学所学过 的除法法则是什么? 例如:8÷0.2=?
引入负数以 后,以前学 的除法运算 是否成立?
• 问:你能说出有理数除法法则吗?
有理数除法法则: 除以一个数等于乘以这个数的倒数.
注意:0不能作除数.
为什么零不 能作除数?
想一想
1 7
)
(2) (-1) ÷(-1.5)
(3)
(-3)
÷(
2 5
)
÷(
1 4
)
(4)
(-3)
÷[(
2 5
)
÷(
1 4
)]
把下图中第一个圈内的每个数分别
2
咳 除以 5 ,将结果写在第二个圈内相应的位置 2
,4
你 15
行 吗
7 30
8
÷( 5)
2 3
7
12
4
? 45
9
3 50
3 20
•课本第38页3、4、5、6、7 •课本第40页13、14、15
探索题:设a,b,c为非零有 理数,求下列式子的值。
abc abc
有本领,你就勇敢 地上吧!
例3 计算:
(4)(1 3
3) 4
(112)注意视察
(5) (24 6) (6)寻求最佳方法 7
(6)
(
2) 3
(
4) 5
(12) 5
(7)
•1、若a=-4,b=-3,c=-5
•则求-c-ab的值;
代入时注意符号
解:当a=-4,b=-3,c=-5时,
-c-ab (5) (4) (3)
5 43
有理数的除法ppt课件

=- .
故原式=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
利用有理数的运算律进行巧算
11. [新考法·逆用运算律法]计算:
(1)
−
1
× +
2
3
4
−
5
6
× +
7
8
−
9
10
11
12
÷5+76 ÷5;
13
【解】原式=
−
−
× +
−
× +
× +76 ×
=[ −
+ −
+(-196 )+76 ]×
6
7
=(-20-120)×
=-140×
=-28.
1
2
3
4
5
8
9
10
11
12
13
(2)(-3.85)×(-13)+(-13)×(-6.15)+0.79×
×0.79.
【解】原式=(-13)×[(-3.85)+(-6.15)]+
如何抽取?最大值是多少?
【解】抽取写有-7和-5的卡片,
最大值是-7×(-5)=35.
1
2
3
4
5
《有理数的除法》有理数PPT课件全

D. –4×(2÷8)和 –4×2÷8
课堂检测
基 础 巩 固 题
2.计算:
(1)23×(–5)–(–3)÷
13
(2)–7×(–3)×(–0.5)+(–12)×(–2.6)
20.7
课堂检测
基 础 巩 固 题
3.计算: (1)2×(–3÷
)–4×(–3)+15;
(2)–8+(–3)×[–4÷(–
3
12
解 : (1)
(2)
12
(12) 3 4
3
45
15
(45) (12) 45 12
4
12
巩固练习
2. 化简:
72
(1) 9 = (–72)
30
(2) 45
0
75
(3)
÷ 9 = –8 .
=(–30)÷(–45)
0
= _____.
= 30÷45
4
2
4
1
3 3 4
解:原式= - = – 2
4 2 9
(2) (3) [(
2
1
) ( )]
5
4
2
5
15
解:原式= (3) ( 4) 3
8
8
5
巩固练习
连 接 中 考
1.(苏州中考)(–21)÷7的结果是( B )
A.3
B.–3
1
3
D. –
C.
2.(大连中考)计算:(–12)÷3= –4
有理数乘法的运算律简化运算.
定积的符号,最后求出结果(乘除混合运算按
从左到右的顺序进行计算).
课堂检测
基 础 巩 固 题
2.计算:
(1)23×(–5)–(–3)÷
13
(2)–7×(–3)×(–0.5)+(–12)×(–2.6)
20.7
课堂检测
基 础 巩 固 题
3.计算: (1)2×(–3÷
)–4×(–3)+15;
(2)–8+(–3)×[–4÷(–
3
12
解 : (1)
(2)
12
(12) 3 4
3
45
15
(45) (12) 45 12
4
12
巩固练习
2. 化简:
72
(1) 9 = (–72)
30
(2) 45
0
75
(3)
÷ 9 = –8 .
=(–30)÷(–45)
0
= _____.
= 30÷45
4
2
4
1
3 3 4
解:原式= - = – 2
4 2 9
(2) (3) [(
2
1
) ( )]
5
4
2
5
15
解:原式= (3) ( 4) 3
8
8
5
巩固练习
连 接 中 考
1.(苏州中考)(–21)÷7的结果是( B )
A.3
B.–3
1
3
D. –
C.
2.(大连中考)计算:(–12)÷3= –4
有理数乘法的运算律简化运算.
定积的符号,最后求出结果(乘除混合运算按
从左到右的顺序进行计算).
《有理数除法》有理数PPT课件 (共10张PPT)

1 1 1 (3)能否用上述方法解决: 12 ( ) 6 2 3
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
挫折的名言 1、 我觉得坦途在前,人又何必因为一点小障碍而不走路呢?——鲁迅 2、 “不耻最后”。即使慢,弛而不息,纵会落后,纵会失败,但一定可以达到他所向的目标。——鲁迅 3、 故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为,所以动心忍性,曾益其所不能。 战胜挫折的名言 1、卓越的人一大优点是:在不利与艰难的遭遇里百折不饶。——贝多芬 2、每一种挫折或不利的突变,是带着同样或较大的有利的种子。——爱默生 3、我以为挫折、磨难是锻炼意志、增强能力的好机会。——邹韬奋 4、斗争是掌握本领的学校,挫折是通向真理的桥梁。——歌德 激励自己的座右铭 1、 请记得,好朋友的定义是:你混的好,她打心眼里为你开心;你混的不好,她由衷的为你着急。 2、 要有梦想,即使遥远。 3、 努力爱一个人。付出,不一定会有收获;不付出,却一定不会有收获,不要奢望出现奇迹。 4、 承诺是一件美好的事情,但美好的东西往往不会变为现实。 工作座右铭 1、 不积跬步,无以至千里;不积小流,无以成江海。——《荀子劝学》 2、 反省不是去后悔,是为前进铺路。 3、 哭着流泪是怯懦的宣泄,笑着流泪是勇敢的宣言。 4、 路漫漫其修远兮,吾将上下而求索。——屈原《离骚》 5、 每一个成功者都有一个开始。勇于开始,才能找到成功的路。 国学经典名句 1、知我者,谓我心忧,不知我者,谓我何求。(诗经王风黍离) 2、人而无仪,不死何为。 (诗经风相鼠) 3、言者无罪,闻者足戒。 (诗经大序) 4、他山之石,可以攻玉。 (诗经小雅鹤鸣) 5、投我以桃,报之以李。 (诗经大雅抑) 6、天作孽,犹可违,自作孽,不可活。(尚书) 7、满招损,谦受益。 (尚书大禹谟) 青春座右铭 1、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 2、把手握紧,什么也没有;把手伸开,你就拥有了一切。 3、不在打击面前退缩,不在困难面前屈服,不在挫折面前低头,不在失败面前却步。勇敢前进! 4、当你能飞的时候就不要放弃飞。 5、当你能梦的时候就不要放弃梦。 激励向上人生格言 1、实现自己既定的目标,必须能耐得住寂寞单干。 2、世界会向那些有目标和远见的人让路。 3、为了不让生活留下遗憾和后悔,我们应该尽可能抓住一切改变生活的机会。 4、无论你觉得自己多么的不幸,永远有人比你更加不幸。 5、无论你觉得自己多么的了不起,也永远有人比你更强。 6、打击与挫败是成功的踏脚石,而不是绊脚石。 激励自己的名言 1、忍别人所不能忍的痛,吃别人所别人所不能吃的苦,是为了收获得不到的收获。 2、销售是从被别人拒绝开始的。 3、好咖啡要和朋友一起品尝,好机会也要和朋友一起分享。 4、生命之灯因热情而点燃,生命之舟因拼搏而前行。 5、拥有梦想只是一种智力,实现梦想才是一种能力。 6、有识有胆,有胆有识,知识与胆量是互相促进的。 7、体育锻炼可以(有时可以迅速)使人乐观(科学实验证明)。 8、勤奋,机会,乐观是成功的三要素。(注意:传统观念认为勤奋和机会是成功的要素,但是经过统计学和成功人士的分析得出,乐观是成功的第三要素) 9、自信是人格的核心。 10、获得的成功越大,就越令人高兴。
2.2.2 有理数的除法 第1课时 课件 2024--2025学年人教版七年级数学上册

表达式为:
除号变乘号
a÷b
=a
×
1 b
(b
≠
0)
除数变倒数作因数
72÷9 =_7_2__19__=__8__,
同号两÷(- 1 ) =_(_-__1_2_)_×__(-__4_)_=__4_8_, 相乘,结果得正
4
(-
6 5
)÷2
=_(__65_)__12__=__53__,
1 4
)
.
8÷(-4)= 8×(- 1 ) .
4
一个数除以 -4,等于乘 -4 的倒数 - 1 . 4
换其他数的除法进行类似讨论,是否仍有除以 a(a ≠ 0) 可以转化为乘 1 ?
a
12÷(-6) = -2
12×(-
1 6
)=
-2
有理数除法法则1: 除以一个不等于 0 的数,等于乘这个数的倒数.
除法能否转化为乘法?商的符号如何确定? 商的绝对值如何确定?
思考
怎样计算 8÷(-4)?
根据除法是乘法的逆运算,计算 8÷(-4),就是
要求一个数,使它与 -4 相乘得 8.
因为
(-2)×(-4)= 8,
所以
8÷(-4)= -2 .
另一方面,我们有
8×(-
1 4
)=
-2
.
于是有
8÷(-4)=
8×(-
72÷9 =__8___,
(-4)×3 =_-__1_2_,
(-12)÷3 =_-__4__,
2×(-3) =__-__6_,
(-6)÷2 =_-__3__,
(-4)×(-3) =__1_2__, 12÷(-4) =_-__3__,
0×(-6) =___0__,
2.2.2有理数的除法法则(第1课时)(课件)七年级数学上册(人教版2024)

a b c
a b c
故 的值为
1或 3.
的值为±1或±3.
故
a b c
例8
一天, 果果与维维利用温差测量山峰的高度,果果在山顶测得温度是-
1℃,维维此时在山脚测得温度是5℃.已知该地区高度每增加100米,气温
大约降低0.8℃, 这个山峰的高度为多少? (山脚海拔0米)
解: 依题意得
( 36 ) 9
解:原式=
= (36 9)
= 4
12 3
(2)
25 5
12 3
解:原式=
25 5
12 5
=
25 3
4
=
5
例2
(1) (-15) ÷ (-3) ;
(3) (-0.75) ÷0.25;
到右的顺序进行计算).
例5
2 1 1
计算
计算:
50 ( )
3 4 6
2
1
1
3
48 48 = 48 48 4 48 6 = 408;
3
4
6
2
8
3 2
3
(方法二)原式 = 48 ( ) = 48 = 192;
(法二)原式=
12 12 12
B.和为负
4.如果a÷b=0,那么(
A.a=0,b=0
B
D.无法确定
C
)
C.积为正
)
B.a=0,b≠0
C. a≠ 0,b=0
D.a=0
D.异号
5.计算(-12)÷4 的结果等于(
A.-3
B.3
6.下列运算错误的是(
a b c
故 的值为
1或 3.
的值为±1或±3.
故
a b c
例8
一天, 果果与维维利用温差测量山峰的高度,果果在山顶测得温度是-
1℃,维维此时在山脚测得温度是5℃.已知该地区高度每增加100米,气温
大约降低0.8℃, 这个山峰的高度为多少? (山脚海拔0米)
解: 依题意得
( 36 ) 9
解:原式=
= (36 9)
= 4
12 3
(2)
25 5
12 3
解:原式=
25 5
12 5
=
25 3
4
=
5
例2
(1) (-15) ÷ (-3) ;
(3) (-0.75) ÷0.25;
到右的顺序进行计算).
例5
2 1 1
计算
计算:
50 ( )
3 4 6
2
1
1
3
48 48 = 48 48 4 48 6 = 408;
3
4
6
2
8
3 2
3
(方法二)原式 = 48 ( ) = 48 = 192;
(法二)原式=
12 12 12
B.和为负
4.如果a÷b=0,那么(
A.a=0,b=0
B
D.无法确定
C
)
C.积为正
)
B.a=0,b≠0
C. a≠ 0,b=0
D.a=0
D.异号
5.计算(-12)÷4 的结果等于(
A.-3
B.3
6.下列运算错误的是(
有理数的除法 课件(共21张PPT) 2024-2025学年数学沪科版(2024)七年级上册

理
法则二
数
a b a 1 (b 0) b
除
法
注意
0除以任何一个不等于0的数,都得0.
应用
2 2 0 0 2
2 2 0 0 2
a b ab
习题4
a,b,c为非零有理数,求
ab bc ac abc ab bc ac abc
的值.
解:当a<0,b>0,c>0时,
原式= ab bc ac abc =−1+1+(−1)+(−1)=−2; ab bc ac abc
当a<0,b<0,c>0时,
原式= ab bc ac abc =1+(−1)+(−1)+1=0; ab bc ac abc
1.5.2 有理数的除法
2 2 0 0 2
学习目标
1. 认识有理数的除法,经历除法的运算过程; (重点) 2. 理解除法法则,体验除法与乘法的转化关系.(难点)
2 2 0 0 2
复习导入
问题1 小学中你学过的除法运算法则是什么?
除法是已知两个因数的积与其中一个因数,求另一个因数的运算.除 法是乘法的逆运算.
−2
3
= (−8) × (−3 ) =12; 2
(2)
(− 370)÷10
=
(−
30 7
)×
110=−
3 7
.
(3)(−4)
÷
(−
2)
5
×
(−5)
=
(−4)
×
(−
5)
2
×
(−5)
=
−(4
×
5 2
×
5)
=
−5
2 2 0 0 2
1.10 有理数的除法(课件)七年级数学上册(华东师大版2024)

【详解】∵ + + = 0,
∴ + = −, + = −, + = −,
∴原式=
−
+
−
+
−
=
+
+
��
,
∵ + + = 0和 ≠ 0,
∴在、、中必为两正一负或两负一正,
∴当为两正一负时,原式= 1 + 1 − 1 = 1,
当为两负一正时,原式= −1 − 1 + 1 = −1,
【注意事项】
(1)倒数是指两个数的关系,0没有倒数.
(2)正数的倒数是正数,负数的倒数是负数,倒数等于本身的有±1.
典例分析
例1:请你指出下列各数的倒数
1
6
−1,4, ,− .
5
25
1
25
解:-1, ,5,− .
4
6
课堂小结
求一个数的倒数的方法:
1)一个不为0的整数的倒数,是用这个整数作分母,1作分子的分数;
(2)原式= −
1
5
×
(3)原式= 72 ×
1
10
2
3
× 25 × 10 = −5;
×
3
5
×
15
8
9
8
= 48 × = 54.
课堂测试
5.(23-24七年级上·广东惠州·期中)若 = 4, = 2,且 > 0,则 − 的值是( )
A.−2
B.−6
C.6或−6
D.2或−2
【详解】∵ = 4, = 2,∴ = ±4, = ±2;
有理数的除法(共20张PPT)

除以一个有理数等于乘以它的倒数
总结词
当一个数除以一个有理数时,结果等于这个数乘以这个有理数的倒数。
详细描述
这是有理数除法的基本运算规则。例如,如果要将10除以2,可以将其转化为 10乘以2的倒数(即1/2),结果仍然是10/2。
有理数除法运算的顺序
总结词
在进行多个有理数的除法运算时,应遵循从左到右的顺序进 行计算。
详细描述
在进行多个有理数的除法运算时,应按照从左到右的顺序进行 计算,以避免混淆和错误。例如,在计算表达式"a/b/c"时,应 先计算a除以b,然后再将结果除以c。
04
有理数除法的运算技巧
利用乘法分配律简化运算
总结词
乘法分配律是有理数除法中常用的简 化运算技巧,通过将除法转化为乘法 ,可以简化计算过程。
例子
如 $10 div 3 = 3frac{1}{3}$,表示 $10$ 除以 $3$ 的结果是 $3$ 余 $frac{1}{3}$。
有理数除法的性质
性质1
除法的结合律。即 $(a div b) div c = a div (b times c)$。
性质2
除法的倒数。如果 $a div b = c$,那么 $b = a div c$。
Байду номын сангаас
综合练习题
总结词
综合运用除法解决实际问题
详细描述
综合练习题着重于培养学生运用除法解决实 际问题的能力。题目设计更加贴近生活,涉 及各种实际情境中的除法问题,如购物计算 、时间计算等。通过解决这些实际问题,学 生能够更好地理解和掌握除法的实际应用,
提高解决实际问题的能力。
THANK YOU
感谢聆听
理解有理数除法在实际问题中的应用,提高解决实际 问题的能力。 通过练习和实例,加深对有理数除法的理解和掌握。
数学人教版(2024)版七年级初一上册 2.2.2 有理数的除法 教学课件03

RJ(2024)·七年级数学上册
第二章 有理数的运算
2.2.2 有理数的除法
1.认识有理数的除法,经历除法的运算过程 2.理解除法法则,体验除法,每分钟走70米,共走了20分钟,
问小明家离学校有多远?
70×20=1400(米)
放学后,小明仍然以每分钟70米的速度回家,应该
走多少分钟才会到家?
1400÷70=20(分)
怎样计算-8÷4呢?
因为 -_2__×4=-8 所以 -8÷4=_-_2_ 即:
活动1:能独立计算8÷(-4) 吗?因为 __-2_×(-4)=8
所以 8÷(-4)=___-2
即:
商的符号怎样确定的?
异号得负
活动2:仿照前面的方法,你会计算-8÷(-4)吗?
因为 ___×(-4)=-8 所以 -8÷(-4=)___ 即:
计算:0÷(-4)= ? 0÷(-8)= ?
商的符号怎样确定的?
同号得正
0除以一个不为零的数都得 0
有理数除法法则
1:两数相除,同号得正,异号得负,并把绝对值相除. 2:0除以任何一个不等于0的数,都得0.
-8÷4=?
因为 __-2_×4=-8 所以 -8÷4=__-2_ 即:
例2.化简下列各式:
解:
例2.化简下列各式:
解:
一、有理数除法法则: 法则一:两数相除,同号得正,异号得负,并把绝对值相除. 0除以任何一个不等于0的数,都得0.
法则二:除以一个不等于0的数,等于乘这个数的倒数.
RJ(2024)·七年级数学上册
感谢聆听
还可以怎么计算?
因为 -8×( )=-2 所以
③式表明,一个数除以4可以转化为乘 来进行,即一个数除以4, 等于乘4的倒数 .
第二章 有理数的运算
2.2.2 有理数的除法
1.认识有理数的除法,经历除法的运算过程 2.理解除法法则,体验除法,每分钟走70米,共走了20分钟,
问小明家离学校有多远?
70×20=1400(米)
放学后,小明仍然以每分钟70米的速度回家,应该
走多少分钟才会到家?
1400÷70=20(分)
怎样计算-8÷4呢?
因为 -_2__×4=-8 所以 -8÷4=_-_2_ 即:
活动1:能独立计算8÷(-4) 吗?因为 __-2_×(-4)=8
所以 8÷(-4)=___-2
即:
商的符号怎样确定的?
异号得负
活动2:仿照前面的方法,你会计算-8÷(-4)吗?
因为 ___×(-4)=-8 所以 -8÷(-4=)___ 即:
计算:0÷(-4)= ? 0÷(-8)= ?
商的符号怎样确定的?
同号得正
0除以一个不为零的数都得 0
有理数除法法则
1:两数相除,同号得正,异号得负,并把绝对值相除. 2:0除以任何一个不等于0的数,都得0.
-8÷4=?
因为 __-2_×4=-8 所以 -8÷4=__-2_ 即:
例2.化简下列各式:
解:
例2.化简下列各式:
解:
一、有理数除法法则: 法则一:两数相除,同号得正,异号得负,并把绝对值相除. 0除以任何一个不等于0的数,都得0.
法则二:除以一个不等于0的数,等于乘这个数的倒数.
RJ(2024)·七年级数学上册
感谢聆听
还可以怎么计算?
因为 -8×( )=-2 所以
③式表明,一个数除以4可以转化为乘 来进行,即一个数除以4, 等于乘4的倒数 .
人教版初中七年级上册数学《有理数的除法》精品课件

强化练习 计算: ①(-18)÷6
-3 ④0÷(-8)
0
②(-63)÷(-7) 9
⑤(-6.5)÷0.13 -50
③1÷(-9)
1 9
⑥
6 5
2 5
3
随堂演练
1.已知(-2)×(-3)=6,则6÷(-2)= -3 , 6÷(-3)= -2 .
2.下列运算结果等于1的是( D )
A.(-3)+(-3)
推进新课
知识点1 有理数除法法则
知识回顾
你能很快地说出下列各数的倒数吗?
9
原数
-5
8
7
0
-1
1 2 3
倒数
1 5
8 9
1 7
-1
3 5
正数除以负数 负数除以负数 零除以负数
8÷(-4) =-2 (-8)÷(-4) =2 0÷(-4) =0
8 ( 1 ) =-2 4
(8) ( 1 ) =2
0
(
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
下课了!
B.(-3)-(-3)
C.(-3)×(-3)
D.(-3)÷(-3)
3.计算题.
(1) 91 13
7
(3) 0.25 3 8
2 3
(2)48 16
3
(4) 1
3
2
3
3
11
4.用“>”“<”或“=”填空. (1)如果a<0,b>0,那么ab < 0,a < 0; (2)如果a>0,b<0,那么ab < 0,ab < 0;
b (3)如果a<0,b<0,那么ab > 0,a > 0;
有理数的除法(第1课时有理数除法法则)课件(共39张PPT) 七年级数学上册(人教版2024)

这两个法则分别在什么情况下使用?
如果两数相除,能够整除的就选择法则2,不能够整除的就选择用法则1.
总结归纳
思考:
到现在为止我们有了两个除法法则,那么两
个法则是不是都可以用于解决两数相除呢?
要点归纳:
1.两个法则都可以用来求两个有理数相除.
2.如果两数相除,能够整除的就选择法则二,
不能够整除的就选择用法则一.
(3)原式=1 8÷(-54)=- ;(4)原式=-[(-9)÷3 6 ]=-(- )= .
练一练
4.化简:
-
(1)
; 解:原式=-9;
-
(2)
;
-
56 7
原式=48=6;
-
(3)
; 原式=-30=-2;
45
3
-
(4) ;
.
原式=-30.
总结归纳
一般地,根据有理数的除法,形如 (p,q 是整数, q ≠0)的数都是
4/5
(-12/25)×(-5/3)=___
-8
-72×(1/9)=___
问题:上面各组数计算结果有什么关系?由此你能
得到有理数的除法法则吗?
观察下列两组式子,你能找到它们的共同点吗?
“÷”变“×”
(1)(+6)÷(+2)= +3
6
1
=
2
+3
互为倒数
“÷”变“×”
(2)(+6)÷(-2)= -3
分层练习-巩固
11. 下列四名同学的说法中,正确的是(
A
)
A. 墨墨:0除以任何一个不等于0的数都得0
人教版2024年新版七年级数学上册课件:2.2.2 第1课时 有理数的除法法则

= (−72) ÷9=−( 72÷9) =−8;
9
−30
2
(2)
= (−30) ÷(−45)= 30÷45 = ;
−45
3
0
(3)
= 0;
−75
27
9
(4)
= −27 ÷6=− .
−6
2
27
(4) .
−6
随堂练习
1. 如果两个有理数的商等于0,则 ( C )
A.这两个数中有一个数为0
B.两数都为0
回忆在小学中你学过的除法运算.
除法是已知两个因数的积与其中一个因数,求另一个
因数的运算.
除法是乘法的逆运算.
思 有理数的除法呢??
新知探究
思考
怎样计算8÷(−4)?
根据除法是乘法的逆运算,计算8÷(−4) ,就是要求
一个数,使它与−4相乘得8.
因为
(−2)×(−4)=____.
8
所以
8÷(−4)=−2.
0除以任何一个不等于0的数,都得
1
a÷b=a· (b≠0)
b
0
.
典型例题
例1 计算:
(1) (-36) ÷9;
(2)
−
÷
−
.
解: (1) (-36)÷9=-(36÷9)=-4.
变倒数
(2)
−
÷
− = − × −
=
.
当除数是分数时,一般选择方法:
把除法转化为乘法进行计算.
2
69÷(−23)=−(69÷23)=−3
随堂练习
3. 下列运算结果等于1的是(
9
−30
2
(2)
= (−30) ÷(−45)= 30÷45 = ;
−45
3
0
(3)
= 0;
−75
27
9
(4)
= −27 ÷6=− .
−6
2
27
(4) .
−6
随堂练习
1. 如果两个有理数的商等于0,则 ( C )
A.这两个数中有一个数为0
B.两数都为0
回忆在小学中你学过的除法运算.
除法是已知两个因数的积与其中一个因数,求另一个
因数的运算.
除法是乘法的逆运算.
思 有理数的除法呢??
新知探究
思考
怎样计算8÷(−4)?
根据除法是乘法的逆运算,计算8÷(−4) ,就是要求
一个数,使它与−4相乘得8.
因为
(−2)×(−4)=____.
8
所以
8÷(−4)=−2.
0除以任何一个不等于0的数,都得
1
a÷b=a· (b≠0)
b
0
.
典型例题
例1 计算:
(1) (-36) ÷9;
(2)
−
÷
−
.
解: (1) (-36)÷9=-(36÷9)=-4.
变倒数
(2)
−
÷
− = − × −
=
.
当除数是分数时,一般选择方法:
把除法转化为乘法进行计算.
2
69÷(−23)=−(69÷23)=−3
随堂练习
3. 下列运算结果等于1的是(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) (2) 3 5
计算: (1) 3 7 ( 7 )
2
5
(2) (3.5) (11) 5
67
(3) ( 3) (11) 8 4
4
3
(4)
1 12
5 3
(0.25)
(5)
(
3 4
)
1
1 2
(2
1 4
)
计算:
若a, b互为相反数, c, d互为 倒数, m的倒数是2, 求 a b cd 的值
计算:
8×9=__7_2_, 72÷9=__8__,
(-4)×2 =_-__8_, (-8)÷(-4)=__2__, 2×(-3)=_-__6_, (-6) ÷2=_-__3_,
(-4)×(-3)=_1_2__, 12÷(-4)=_-__3_, 0×(-6)=__0__, 0÷(-6)=__0__,
a b ab
我国古代有一道名题:”一百馒头一百僧,大僧 三个便无争;小僧三人分一个,大小和尚各几丁?
=2
(3)原式
6 5
5 7
6
7
=-40
(1) (-8)÷(-4) (2) (-3.2)÷0.08
(3) 11 1.4
5
求解中的第一步是 ___选__择___法___则____; 第二步是___求__出__结__果_____;
计算:
(1) (21) 3
计算: (2) (36) (9)
商的符号如何确定? 商的绝对值如何确定?
两个有理数相除, 同号得___正_, 异号得__负___,并把绝对值__相__除___.
0除以任何非0数都得__0___.
0不能作为除数
(1) (-8)÷(-4) (2) (-3.2)÷0.08
(3) 11 1.4
5
解: (1)原式 =+(8÷4) (2)原式 =- (3.2÷0.08)
m
一天, 小红与小莉利用温差测量山峰的 高度, 小红在山顶测得温度是-1℃, 小 莉此时在山脚测得温度是5℃. 已知该地 区高度每增加100米,气温大约降低0.8℃, 这个山峰的高度为多少? (山脚海拔0米)
解: 依题意得
5 (1) 0.8 100
=6÷0.8×100 =750(米)
答: 这个山峰的高度为750米.
观察右侧算式, 两个有理数相除时: 商的符号如何确定? 商的绝对值如何确定?
72÷9=__)÷(-4)=__2__, , 并把绝对值相除
(-6) ÷2=_-__3_, 12÷(-4)=_-__3_,
异号两数相除得负 , 并把绝对值相除
0÷(-6)=__0__, 零除以任何非零数得零
提供一个能用 900 9 2 表示的
实际问题的情景,并说明负数表示的
意义.
1.除法法则:
两个有理数相除, 同号得正, 异号得负,并把绝对值相除; 0除以任何非0数都得0.
2.除法和乘法之间的关系: 除以一个数, 等于乘以这个数的倒数
设a,b,c为非零有理数,求 下列式子的值
abc abc
若ab 0, 则 a b ab ______ .
计算: (3) (1.6) 0.4
计算: (4) 0 ( 7 )
83
计算:
(5) 1 ( 2) 5
比较大小: (1) 1 (
2)
与
1 ( 5)
5
2
(2)
(
1 4
)
(
1 6
)
与
(
1) 4
(6)
除以一个数, 等于__乘__以__这_个__数__的__倒__数__.
计算:
(1) ( 3 ) ( 3) 10 5
计算: (1) 3 7 ( 7 )
2
5
(2) (3.5) (11) 5
67
(3) ( 3) (11) 8 4
4
3
(4)
1 12
5 3
(0.25)
(5)
(
3 4
)
1
1 2
(2
1 4
)
计算:
若a, b互为相反数, c, d互为 倒数, m的倒数是2, 求 a b cd 的值
计算:
8×9=__7_2_, 72÷9=__8__,
(-4)×2 =_-__8_, (-8)÷(-4)=__2__, 2×(-3)=_-__6_, (-6) ÷2=_-__3_,
(-4)×(-3)=_1_2__, 12÷(-4)=_-__3_, 0×(-6)=__0__, 0÷(-6)=__0__,
a b ab
我国古代有一道名题:”一百馒头一百僧,大僧 三个便无争;小僧三人分一个,大小和尚各几丁?
=2
(3)原式
6 5
5 7
6
7
=-40
(1) (-8)÷(-4) (2) (-3.2)÷0.08
(3) 11 1.4
5
求解中的第一步是 ___选__择___法___则____; 第二步是___求__出__结__果_____;
计算:
(1) (21) 3
计算: (2) (36) (9)
商的符号如何确定? 商的绝对值如何确定?
两个有理数相除, 同号得___正_, 异号得__负___,并把绝对值__相__除___.
0除以任何非0数都得__0___.
0不能作为除数
(1) (-8)÷(-4) (2) (-3.2)÷0.08
(3) 11 1.4
5
解: (1)原式 =+(8÷4) (2)原式 =- (3.2÷0.08)
m
一天, 小红与小莉利用温差测量山峰的 高度, 小红在山顶测得温度是-1℃, 小 莉此时在山脚测得温度是5℃. 已知该地 区高度每增加100米,气温大约降低0.8℃, 这个山峰的高度为多少? (山脚海拔0米)
解: 依题意得
5 (1) 0.8 100
=6÷0.8×100 =750(米)
答: 这个山峰的高度为750米.
观察右侧算式, 两个有理数相除时: 商的符号如何确定? 商的绝对值如何确定?
72÷9=__)÷(-4)=__2__, , 并把绝对值相除
(-6) ÷2=_-__3_, 12÷(-4)=_-__3_,
异号两数相除得负 , 并把绝对值相除
0÷(-6)=__0__, 零除以任何非零数得零
提供一个能用 900 9 2 表示的
实际问题的情景,并说明负数表示的
意义.
1.除法法则:
两个有理数相除, 同号得正, 异号得负,并把绝对值相除; 0除以任何非0数都得0.
2.除法和乘法之间的关系: 除以一个数, 等于乘以这个数的倒数
设a,b,c为非零有理数,求 下列式子的值
abc abc
若ab 0, 则 a b ab ______ .
计算: (3) (1.6) 0.4
计算: (4) 0 ( 7 )
83
计算:
(5) 1 ( 2) 5
比较大小: (1) 1 (
2)
与
1 ( 5)
5
2
(2)
(
1 4
)
(
1 6
)
与
(
1) 4
(6)
除以一个数, 等于__乘__以__这_个__数__的__倒__数__.
计算:
(1) ( 3 ) ( 3) 10 5
