计算例题
工程量计算例题
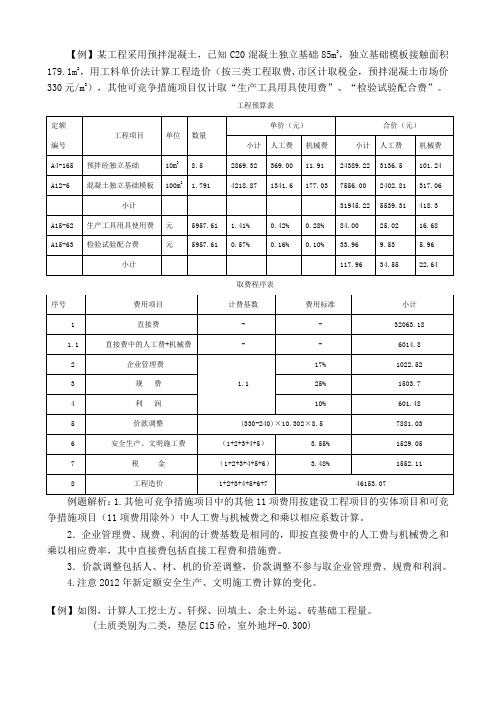
【例】某工程采用预拌混凝土,已知C20混凝土独立基础85m3,独立基础模板接触面积179.1m2,用工料单价法计算工程造价(按三类工程取费,市区计取税金,预拌混凝土市场价330元/m3),其他可竞争措施项目仅计取“生产工具用具使用费”、“检验试验配合费”。
工程预算表取费程序表例题解析:1.其他可竞争措施项目中的其他11项费用按建设工程项目的实体项目和可竞争措施项目(11项费用除外)中人工费与机械费之和乘以相应系数计算。
2.企业管理费、规费、利润的计费基数是相同的,即按直接费中的人工费与机械费之和乘以相应费率,其中直接费包括直接工程费和措施费。
3.价款调整包括人、材、机的价差调整,价款调整不参与取企业管理费、规费和利润。
4.注意2012年新定额安全生产、文明施工费计算的变化。
【例】如图,计算人工挖土方、钎探、回填土、余土外运、砖基础工程量。
(土质类别为二类,垫层C15砼,室外地坪-0.300)【例】如下图所示尺寸,求混凝土带型基础模板和混凝土的工程造价。
备注:按三类工程取费,企业管理费费率为17%,利润费率为10%,规费费率为25%,税金税率为3.48%,安全生产、文明施工费为4.25%。
解:(1)带型基础外侧模板 S1=[(4.5×2+0.5×2)×2+(4.8+0.5×2)×2]×0.3=9.48 m2(2) 带型基础内侧模板 S2=[(4.5-0.5×2)×2+(4.8-0.5×2)×2]×0.3×2=8.76 m2带型基础模板工程量 S= S1+ S2=18.24 m2(模板工程量3分)(3)带形基础混凝土外墙 V=1×0.3×(4.5+4.5+4.8)×2=8.28 m3 (混凝土工程量2分)内墙 V=1×0.3×(4.8-1)=1.14 m3 (混凝土工程量2分)合计:9.42 m3预算表取费:1. 直接费 3329.7元2.其中人+机 1021.36元3.企业管理费 1021.36×17%=173.63元4.规费 1021.36×25%=255.34元5.利润 1021.36×10%=102.14元6安全生产、文明施工费 3860.81×4.25%=164.08元7.税金 4024.89×3.48%=140.07元【例】如图所示内外墙毛石基础、砖基础平面图和剖面图,毛石基础每级高度为350mm,试计算砌体基础工程量。
房贷例题计算题

1、张先生购买了一套总价100万元的房子,首付比例30%,剩余部分申请商业贷款,贷款年限为30年,年利率为5%,采用等额本息还款法。
张先生每月需还款的金额大约为?A. 3,685元B. 4,368元C. 5,036元D. 5,630元(答案:A)2、李女士贷款80万元购房,贷款期限为20年,年利率为4.5%,使用等额本金还款法。
首月还款金额约为?A. 6,000元B. 5,450元C. 4,900元D. 4,350元(答案:B)3、王先生以4.9%的年利率贷款90万元,贷款期限15年,选择等额本息方式还款。
他每年大约需要偿还的总金额是?A. 90,000元B. 78,000元C. 63,000元D. 108,000元(答案:D,按每月还款额乘以12计算)4、赵小姐购房贷款60万元,贷款期10年,年利率3.8%,采用等额本金还款。
最后一个月的还款额比第一个月少多少?A. 1,900元B. 1,520元C. 1,140元D. 760元(答案:C,考虑本金逐月递减的影响)5、刘先生贷款70万元买房,贷款期25年,年利率4.2%,等额本息还款。
若5年后提前还清剩余贷款,需一次性支付约?A. 580,000元B. 620,000元C. 660,000元D. 700,000元(答案:B,根据剩余本金计算)6、陈女士购房贷款50万元,贷款期限10年,年利率为4%,等额本金还款。
第二年的总还款额比第一年少多少?A. 2,000元B. 1,600元C. 1,200元D. 800元(答案:C,因本金减少导致利息减少)7、孙先生贷款120万元购房,贷款期限30年,年利率为3.5%,等额本息还款。
前五年他总共支付的利息约为?A. 105,000元B. 126,000元C. 147,000元D. 168,000元(答案:C,按年计算累计利息)8、周小姐贷款80万元,贷款期限20年,年利率4%,等额本金还款。
第10年的年还款总额约为?A. 72,000元B. 64,000元C. 56,000元D. 48,000元(答案:C,考虑本金递减)9、吴先生贷款90万元,贷款期限10年,年利率为5%,采用等额本息还款法。
潮流计算 例题

例题:如图1所示的简单电力网中,已知变压器的参数为S N =31.5MV A ,0S S 031kW,190kW,%=10.5,%=0.7P P U I ∆=∆=;线路单位长度的参数为61110.21/km,0.416/km, 2.7410S/km r x b -=Ω=Ω=⨯。
如图所示的简单电力网中,当线路首端电压U A =120kV 时,试求:(1)线路和变压器的电压损耗;(2)变压器运行在额定变比时的低压侧电压及电压偏移。
说明:以上计算忽略电压降落的横分量。
图1解:如题画等值电路图如下:线路参数为:0.21408.40.4164016.64l l l l R rl X x l ==⨯=Ω==⨯=Ω变压器参数为Ω=⨯⨯⨯=⨯∆=317.210)105.31(110190103232322N N S T S U P R Ω=⨯⨯⨯⨯⨯=33.4010105.311001105.1010100%33232N N S T S U U X (1) 变压器的功率损耗和励磁功率为222T S 02N 2515()19031193.760.1937631.5S P P P kW MW S +∆=∆+∆=⨯+==222S 0N T N %%10.5(2515)0.731.5 3.0538var 10010010031.5100U S I S Q M S ⨯+⨯∆=+=+=⨯1点处线路的充电功率var 66308.01104074.22121222M lU b Q N l B =⨯⨯⨯==计算L S 2 为:MVAj j Q Q Q j P P S B T LD T LD L 39.1719.25)66308.00538.315(19376.025)(22+=-+++=-∆++∆+=线路阻抗中的功率损耗为:MW R U Q P P l L L l 65044.0104021.011017390251901032223222222=⨯⨯⨯+=⨯+=∆-- v a r 2885.11040416.011017390251901032223222222M X U Q P Q l L L l =⨯⨯⨯+=⨯+=∆-- 计算功率1S 为 M V Aj j Q Q j P P S l L l I 68.1884.25)2885.139.17(65044.019.25)(221+=+++=∆++∆+=线路电压损耗(忽略电压降落的横分量) 1125.848.418.6816.64 4.40120=l l l A PR Q X U kV U +⨯+⨯∆== 1点电压为:1120 4.40115.60-A l U U U kV =∆=-=计算功率TS 2 为 M V Aj j Q Q j P P S T LD T LD T 833.17163.25)833.215(163.025)(2+=+++='∆++'∆+= 变压器电压损耗 22125.163 2.3217.83340.33 6.73115.60=T T T T T P R Q X U kV U +⨯+⨯∆== (2) 变压器低压侧折算到高压侧的电压为21115.60 6.73108.87=-T U U U kV '∆=-= 变压器低压侧的实际电压 22108.8710.8910=U U kV k '== 电压偏移为2210.8910%100%8.9%10N N U U m U --=⨯==。
计算题典型例题汇总

计算题典型例题汇总:1 消费者均衡条件。
1. 已知张先生每月收入收入1600元,全部花费于X 和Y 两种产品,他的效用函数为U XY =,X 的价格是10元,Y 的价格20元。
求:为获得最大效用,他购买的X 和Y 各为多少?2 APL MPL 的极大值的计算。
假定某厂商只有一种可变要素劳动L ,产出一种产品Q ,固定成本为既定,短期生产函数L L L Q 1261.023++-=,求解:(1)劳动的平均产量L AP 为极大时雇佣的劳动人数。
(2)劳动的边际产量L MP 为极大时雇佣的劳动人数3 成本一定,产量最大化;产量一定,成本最小化条件。
3588=Q L K 已知某厂商的生产函数为,劳动价格为3美元,资本价格为5美元,求产量为10时的最低成本,求总成本为160美元时的产量。
4 完全竞争厂商长期生产中利润最大化条件。
322+1510Q Q -+完全竞争厂商的短期成本函数为STC=0.1Q ,试求厂商的短期供给函数。
5 完全垄断厂商短期均衡。
2=32Q ++已知某垄断厂商的成本函数为TC 0.6Q ,反需求函数为P=8-0.4Q.求厂商实现利润最大化时的产量、价格、收益和利润。
6 GDP 核算假定某国某年发生了一下活动:(a )一银矿公司支付7.5万美元给矿工开采了50千克银卖给一银器制造商,售价10万美元;(b )银器制造商支付5万美元工资给工人造了一批项链卖给消费者,售价40万美元。
(1)用最终产品生产法计算GDP(2)每个生产阶段生产多少价值?用增值法计算GDP(3)在生产活动中赚得的工资和利润各为多少?7均衡收入的决定。
假定某经济社会的消费函数为C =100+0.8YD (YD 为可支配收入),投资支出为I=50, 政府购买为G =200,政府转移支付为TR=62.5,税收为T =250 求:(1)均衡的国民收入(2)投资乘数,政府购买乘数,税收乘数,转移支付乘数。
8 IS —LM 模型产品市场货币市场同时均衡时的利率和收入。
算术题大全

算术题大全1. 加法1.1 两位数相加例题:计算以下两位数相加的结果:34 + 58 = ?答案:921.2 三位数相加例题:计算以下三位数相加的结果:247 + 359 = ?答案:6061.3 带进位的相加例题:计算以下带进位的相加的结果:35 + 68 = ?答案:1032. 减法2.1 两位数相减例题:计算以下两位数相减的结果:75 - 23 = ?答案:522.2 三位数相减例题:计算以下三位数相减的结果:387 - 125 = ?答案:2622.3 减法中的借位例题:计算以下减法中的借位后的结果:54 - 78 = ?答案:-243. 乘法3.1 乘数为个位数例题:计算以下乘数为个位数的乘法结果:7 × 6 = ?答案:423.2 乘数为两位数例题:计算以下乘数为两位数的乘法结果:15 × 24 = ?答案:3603.3 乘法竖式计算例题:计算以下乘法竖式的结果:23× 14-----答案:3224. 除法4.1 除数为个位数例题:计算以下除数为个位数的除法结果:12 ÷ 3 = ?答案:44.2 除数为两位数例题:计算以下除数为两位数的除法结果:120 ÷ 8 = ?答案:154.3 除法中的余数例题:计算以下除法中的余数:24 ÷ 7 = ?答案:35. 混合运算5.1 加法与减法混合例题:计算以下加法与减法混合运算的结果:27 + 10 - 8 = ?答案:295.2 加法、减法与乘法混合例题:计算以下加法、减法与乘法混合运算的结果:12 + 3 × 5 = ?答案:275.3 多项式运算例题:计算以下多项式运算的结果:(8 + 3) × (5 - 2) = ?答案:33以上是一些常见的算术题,通过练习可以提升计算能力。
希望这些例题能对您有所帮助!。
安全库存计算方法例题

安全库存计算方法例题例题1某产品的平均日需求量为50 个,需求的标准差为10,提前期为 5 天。
服务水平要求为95%,对应的Z 值为 1.645。
求安全库存。
解析:安全库存= Z 值×需求的标准差×提前期的平方根安全库存= 1.645×10×√5 ≈ 36.74。
例题2产品平均日需求为80 个,需求标准差为15,提前期为 4 天,服务水平为90%,对应Z 值为1.28。
求安全库存。
解析:安全库存= 1.28×15×√4 = 1.28×15×2 = 38.4。
例题3平均日需求60 个,标准差12,提前期 6 天,服务水平92%,对应Z 值为1.41。
求安全库存。
解析:安全库存= 1.41×12×√6 ≈ 36.44。
例题4某商品平均日需求为75 个,需求标准差为18,提前期为 3 天,服务水平96%,对应Z 值为1.75。
求安全库存。
安全库存= 1.75×18×√3 ≈ 55.32。
例题5平均日需求40 个,标准差8,提前期7 天,服务水平94%,对应Z 值为1.56。
求安全库存。
解析:安全库存= 1.56×8×√7 ≈ 31.88。
例题6产品平均日需求为90 个,需求标准差为20,提前期为8 天,服务水平为93%,对应Z 值为1.50。
求安全库存。
解析:安全库存= 1.50×20×√8 ≈ 60。
例题7平均日需求30 个,标准差6,提前期 5 天,服务水平91%,对应Z 值为1.34。
求安全库存。
解析:安全库存= 1.34×6×√5 ≈ 18.27。
例题8某物品平均日需求为65 个,需求标准差为16,提前期为 4 天,服务水平95%,对应Z 值为1.645。
求安全库存。
安全库存= 1.645×16×√4 = 1.645×16×2 = 52.64。
六种折扣计算的例题

六种折扣计算的例题折扣是消费者在购买商品时可以享受到的一种优惠方式,通过降低商品价格来吸引消费者。
在日常生活中,我们经常会遇到各种不同形式的折扣计算问题。
本文将介绍六种常见的折扣计算例题,帮助读者更好地理解和应用折扣计算。
1. 固定折扣计算例题:某商店正在举行清仓活动,一款原价为100元的衣服打6折,求该衣服的最终价格。
解答:打6折表示打九折,即打1-0.4=0.6折。
最终价格 = 原价 ×折扣 = 100元 × 0.6 = 60元。
2. 百分数折扣计算例题:一本书原价是80元,半价出售,请问这本书的折扣是多少?解答:折扣 = (原价 - 出售价格)/ 原价 × 100% = (80元 - 40元)/ 80元 × 100% = 50%。
3. 多项折扣计算例题:某品牌手机原价为5000元,商场正在进行活动,先打8折,然后再打95折,最终价格是多少?解答:先打8折,最终价格 = 原价 ×折扣1 = 5000元 × 0.8 = 4000元;再打95折,最终价格 = 上一步的价格 ×折扣2 = 4000元 × 0.95 = 3800元。
4. 连续折扣计算例题:某品牌服装店举行促销活动,一件原价200元的外套先打6折,然后再打8折,最终价格是多少?解答:先打6折,最终价格 = 原价 ×折扣1 = 200元 × 0.6 = 120元;再打8折,最终价格 = 上一步的价格 ×折扣2 = 120元 × 0.8 = 96元。
5. 满额减免折扣计算例题:某超市举行满300元减50元的活动,小明购买了价值400元的商品,他需要支付多少钱?解答:满300元减50元,小明购买了400元的商品,根据减免规则,需要支付的金额 = 购买总额 - 减免金额 = 400元 - 50元 = 350元。
6. 满额赠品折扣计算例题:某化妆品品牌进行满100元赠送礼品的活动,小红购买了该品牌的商品,共计120元,她将获得什么样的礼品?解答:满100元赠送礼品,小红购买了120元的商品,根据满赠规则,小红将获得对应的礼品,具体礼品可以根据活动具体规定而定。
劳动定额的计算例题

劳动定额的计算涉及到多个方面,以下是一个简化的例子:
假设有一名砌墙工人,他的时间定额是1个工日,产量定额是2m³的砖墙。
1. 时间定额:是指工人在单位时间内完成合格产品的数量。
在这里,1个工日意味着工人在1天内完成的工作量。
2. 产量定额:是指工人在单位时间内完成的合格产品数量。
在这里,2m³的砖墙意味着工人可以在1天内完成2m³的砖墙。
接下来,我们可以通过以下公式计算劳动定额:
劳动定额 = 时间定额× 产量定额
将时间定额和产量定额代入公式,我们得到:
劳动定额 = 1个工日× 2m³的砖墙 = 2m³的砖墙/天
这个计算结果表明,砌墙工人每天可以完成2m³的砖墙。
以上例子仅供理解劳动定额的计算方法,实际情况中,劳动定额的确定需要考虑多种因素,如工人的技能水平、工作条件、生产设备的状况等。
物质的量经典例题计算过程

物质的量经典例题计算过程物质的量是描述物质数量的物理量,用单位摩尔(mol)表示。
计算物质的量需要知道物质的质量和相应物质的摩尔质量。
一般来说,计算物质的量的公式为:物质的量(mol)= 质量(g)/ 摩尔质量(g/mol)以下是几个经典的例题,包括计算物质的量、质量和摩尔质量的过程和方法。
例题1:计算铁(Fe)的物质的量。
已知质量为10g,求物质的量。
解答:首先,我们需要知道铁的摩尔质量。
根据元素周期表,铁的摩尔质量约为55.845g/mol。
将已知的质量和铁的摩尔质量代入公式:物质的量(mol)= 质量(g)/ 摩尔质量(g/mol)物质的量= 10g / 55.845g/mol ≈ 0.1788 mol所以,铁的物质的量约为0.1788 mol。
例题2:计算硫酸铜(CuSO4)含有的铜(Cu)的质量。
已知硫酸铜的物质的量为0.1 mol,求铜的质量。
解答:首先,我们需要知道硫酸铜和铜的摩尔质量。
硫酸铜(CuSO4)的摩尔质量可通过元素周期表得知:63.546g/mol (Cu) + 32.07g/mol (S) + 4 * 16.00g/mol (O) ≈ 159.60g/mol 铜(Cu)的摩尔质量可直接从元素周期表得知:63.546g/mol将已知的物质的量和硫酸铜的摩尔质量代入公式:质量(g)= 物质的量(mol)* 摩尔质量(g/mol)质量= 0.1 mol * 159.60g/mol ≈ 15.96g所以,硫酸铜含有的铜的质量约为15.96g。
例题3:计算氯化钠(NaCl)溶液中的氯离子(Cl-)的物质的量。
已知氯化钠的物质的量为0.5 mol,求氯离子的物质的量。
解答:首先,我们需要知道氯化钠和氯离子的摩尔质量。
氯化钠(NaCl)的摩尔质量可通过元素周期表得知:22.99g/mol (Na) + 35.45g/mol (Cl) ≈ 58.44g/mol氯离子(Cl-)的摩尔质量可直接从元素周期表得知:35.45g/mol由于氯化钠中的氯离子与钠离子的物质的量相等,所以氯离子的物质的量也为0.5 mol。
主要计算题例题

基本预备费、涨价预备费的计算 基本预备费= (设备及工器具购置费+建筑安装工程费+工程建设其他费) *基本预备费率P163 涨价预备费, 例 4:某建设工程项目在建设期初的建筑安装工程费、设备及工器具购置费为 45000 万元。
按本项目实施进度计划,项目建设期 3 年,投资分年使用比例为:第一年 25%,第二年 55%, 第三年 20%,建设期内预计年平均价格总水平上涨率为 5%。
建设期贷款利息为 1395 万元,建设工程项目其他费用 为 3860 万元,基本预备费率为 10% 。
试估算项目的建设投资。
解:计算涨价预备费:第 1 年: 45000×25% × [ (1+0.05) 1-1 ]=562.5第 2 年: 45000×55%× [ (1+0.05)2-1 ]=2536.88第 3 年: 45000×20% × [ (1+0.05)3-1 ]=1418.631. 涨价预备费=562.5+2536.88+1418.63=4518.01 万元项目的建设投资:建设投资=静态投资+动态投资=建筑安装工程费+设备及工器具购置费+建设工程项目其他费用+基本预备费+涨价预备费+建设期利息 = (建筑安装工程费+设备及工器具购置费+建设工程项目其他费用)×( 1+基本预备费率) +涨价预备费+建 设期利息= (45000+3860)×(1+10%) +4518.01+1395=59659.01 万元75.建设期利息的计算-P163例 5: 某新建项目,建设期 3 年,共向银行贷款 1300 万,贷款时间为:第 1 年 300 万,第 2 年 600 万,第 3 年 400 万,年利率 6%,计算建设期利息。
第 1 年应计利息: 1 300 6% = 9万元 2第 2 年应计利息: (300 + 9 + 1 600) 6% = 36.54万元 2第 1 年应计利息: (300 + 9 + 600 + 36.54 + 1 400) 6% = 68.73万元 2存货的总成本由 (订货成本、储存成本、缺货成本)构成-P150——存货经济采购批量的计算- P1512KD Q * = K :订货变动成本; D :存货年需要量; K 2 :单位成本 2P151 例 3:某施工企业生产所需 A 材料,年采购总量为 1000 吨,材料单价为 5000 元/吨,一次订货成本 为 2000 元,每吨材料的年平均储备成本为 100 元,则 A 材料的经济采购指为:2KD 2 2000 1000 K 100 2 Q * = = = 200吨 K。
移动加权平均法计算公式例题

10 道移动加权平均法计算公式例题例题一:某企业月初库存材料100 千克,单价10 元。
5 日购入200 千克,单价12 元。
求5 日的移动加权平均单价。
解析:总库存成本= 月初库存成本+ 5 日购入成本= 100×10 + 200×12 = 1000 + 2400 = 3400 元。
总库存数量= 月初库存数量+ 5 日购入数量= 100 + 200 = 300 千克。
移动加权平均单价= 总库存成本÷总库存数量= 3400÷300 ≈ 11.33 元/千克。
例题二:月初有货物50 件,单价8 元。
10 日购入30 件,单价10 元。
求10 日的移动加权平均单价。
解析:总库存成本= 50×8 + 30×10 = 400 + 300 = 700 元。
总库存数量= 50 + 30 = 80 件。
移动加权平均单价= 700÷80 = 8.75 元/件。
例题三:月初库存商品80 个,单价15 元。
15 日购入40 个,单价18 元。
求15 日的移动加权平均单价。
解析:总库存成本= 80×15 + 40×18 = 1200 + 720 = 1920 元。
总库存数量= 80 + 40 = 120 个。
移动加权平均单价= 1920÷120 = 16 元/个。
例题四:月初存货60 吨,单价1200 元。
8 日购入40 吨,单价1300 元。
求8 日的移动加权平均单价。
解析:总库存成本= 60×1200 + 40×1300 = 72000 + 52000 = 124000 元。
总库存数量= 60 + 40 = 100 吨。
移动加权平均单价= 124000÷100 = 1240 元/吨。
例题五:月初库存材料120 千克,单价20 元。
12 日购入80 千克,单价22 元。
求12 日的移动加权平均单价。
有关溶解度的计算典型例题

有关溶解度的计算典型例题[例1]已知15℃时碘化钾的溶解度为140g,计算在该温度下250g水中最多能溶解多少克碘化钾?[分析]:15℃时碘化钾的溶解度为140g,这表明在该温度下100g水最多能溶解140g碘化钾。
那么,250g水最多能溶解多少克碘化钾,可通过关系式法列比例求得,亦可用基本公式法求解。
解法1:关系式法设:15℃时,250g水里最多能溶解x克碘化钾。
关系式:m质+m剂=m液15℃时 140g 100g? x250g[解答]:15℃时,250g水最多能溶解350g碘化钾。
解法2:基本公式法已知: s=140g m剂=250g求: m质=?[解答]:解之,得:m质=350g[例2] 把20℃的282g硝酸钾饱和溶液加热,升温到60℃,需要加入多少克硝酸钾才能使溶液重新达到饱和?(已知20℃时硝酸钾的溶解度为31.6g,60℃时为110g)。
分析:溶剂量不变,当饱和溶液的温度升高时,由于溶解度的增大,使溶液由饱和变为不饱和。
如果要在高温时使溶液重新达到饱和,则需加入一定量的溶质。
所加溶质的量可用质量关系式通过比例进行计算,也可用公式法求得。
解答1 关系式法设:所需加的硝酸钾为x克。
关系式: m质+m剂=m液20℃→60℃添加量20℃ 31.6g 100g 131.6g 110g-31.6g=78.4g282gx每有131.6g硝酸钾饱和溶液从20℃升到60℃时,需要加入78.4g硝酸钾才能使溶液在60℃时亦达饱和,那么282g20℃的硝酸钾饱和溶液升温到60℃,应加入多少克硝酸钾才能使溶液重新达到饱和,可通过比例求得。
答:应加入168g硝酸钾。
解答2:公式法根据上述的比例式,可导出如下的计算公式。
设:应添加硝酸钾晶体为x克。
答:(略)[例3]已知30℃时硝酸钾的溶解度为45.8g。
100道简便运算带答案例题

100道简便运算带答案例题1.计算题结果:6×1/12+6×1/15+6×1/4=5+4+15=24.2.计算题结果:(5/12-3/8)×72=5/12×72-3/8×72=3-27=3.3.计算题结果:32×125×25=4×8×125×25=(4×25)×(8×125)=1×1=1948÷26=(26+2 6+26+1248)÷26=26÷26+26÷26+26÷26+1248÷26=1+1+1+48=48.4.计算题结果:2881÷43=(129+1591)÷43=129÷43+1591÷43=3+37=40.5.计算题结果:1.8+18÷1.5-.5×.3=1.8+12-.15=13.8-.15=13.65.6.计算题结果:6.5×8+3.5×8-47=52+28-47=33.7.计算题结果:8×7分之4÷[1÷(3.2-2.95)]=8×4/7÷[1÷.25]=8×4/7÷4=8/7.8.计算题结果:27×(56-499)÷9=27×7÷9=189÷9=21.9.计算题结果:33.2-(148.4-9.85)÷2.5=33.2-57.55÷2.5=33.2-23.2=10.11.计算题结果:(1÷1-1)÷5.1=0÷5.1=0.12.计算题结果:4+3.2+5+6.825×(8×.4)×1.257又4/15-(2又4/15-1/23)=4+5+(3.2+6.8)=25×.4×(8×1.25)=7又4/15-2又4/15+1/23=9+1=10.13、根据四则运算法则,先计算括号内的加法,得到11/12+7/18+5/24=23/24,然后将23/24乘以7293.5,再除以3又1/2,最后除以2/716和2.5,得到最终结果19 32/5.14、根据四则运算法则,先计算括号内的乘法和除法,得到87+87+87=261,然后依次计算加减法,得到最终结果111.15、将125拆分为100+25,然后根据乘法分配律,分别计算100×8.81+25×8.81、100×1.3+25×1.3、4.25+3.7+3.75、17.15-3.5+2.85,最后依次计算加减法,得到最终结果16.5.16、根据乘法交换律,将5×41转化为25×4+25×1,然后依次计算加法,得到最终结果125.17、根据乘法交换律,将39×11转化为39×1+39×1,然后依次计算加法,得到最终结果429.18、根据加法结合律,将56和24先相加,得到80,然后再加上31,得到最终结果111.19、将7拆分为1×7,然后根据乘法结合律和交换律,将式子转化为1×7×8×125,最后计算得到最终结果4900.。
计算题例题及公式.doc

计算题1.>某板坯连铸机拉坯速度为2.0m/min,出结晶器的安全坯壳厚度为12mm,结晶器冷凝系数为20mm/,求该铸机的结晶器长度。
答案:解:l=V([δ]/K)2+100=(15/20)2×2000+100=820mm答:该铸机的结晶器长度为820mm。
2.>已知铸坯断面尺寸是250mm×1500mm,拉速是1.3m/min,比水量是11/kg,取凝固系数k=28,计算液芯深度?(结果保留二位小数)答案:解:根据公式:L=(D/K)2×V=(125/28)2×1.3=25.91m答:液芯深度为25.91m。
3.>一台断面200mm×1250mm单流铸机,平均拉速为0.9m/min,铸坯理论比重7.8t/m3,铸机平均作业率为85%,求该铸机的年产量多少?(保留一位小数)答案:解:G=0.2×1.25×0.9×60×24×85%×7.8×365=784063.8t答:该铸机的年产量为784063.8t。
4.>已知铸坯的断面为150mm×150mm,拉速为1.4m/min,二冷却水的耗水量为270L/min,求该铸机二冷区的冷却强度。
(已知铸坯的比重为7.6t/m3)答案:解:G=Q/(FVγ)=270/(0.15×0.15×1.4×7.6×103)=1.13kg/t5.>已知铸坯的名义宽度为1000mm,结晶器下口宽度为1005mm,上口宽度为1015mm,求宽度方向的锥度值是多少?(计算结果保留三位小数点)答案:解:锥度值=(上口宽度-下口宽度)/下口宽度×100%=0.995% 6.>某厂二月份产坯20418t,浇钢98次,中间包浇注时间累计为496小时45分钟,若每次浇注的生产准备时间平均为:开浇前,中间包在中间包车就位装定径水口、吊包盖,中间包在线对中,共计30分钟,最后一流浇毕,至最后一根铸坯离线计15分钟,求该机二月份的作业率。
浮力计算题典型例题

浮力计算题的典型例题
1.一个体积为2000立方米的热气球在空中静止,此时它受到的浮力为多少牛?(空气的密度为1.29千克/立方米)
答案:热气球受到的浮力为F=ρgV=1.29千克/立方米×9.8牛/千克×2000立方米=25284牛。
2.一个重为10牛的物体,浸没在水中时受到的浮力为4牛,问当它漂浮在水面上时受到的浮力为多少牛?(水的密度为1.0×10³千克/立方米)
答案:因为F=G排=m排g=ρ液gV排,所以V排=F/ρ液g=4牛/(1.0×10³千克/立方米×9.8牛/千克)=4×10^-4立方米,所以当物体漂浮在水面上时F=G=mg=ρgV=1.0×10³千克/立方米×9.8牛/千克×4×10^-4立方米=3.92牛。
3.一个重为58.8牛、体积为20立方分米的物体,将它放入水中静止时受到的浮力为多少?(水的密度为1.0×10³千克/立方米)
答案:物体的密度ρ=m/V=G/gV=58.8牛/(9.8牛/千克×20立方分
米)=0.3×10³千克/立方米<1.0×10³千克/立方米,所以物体将漂浮在水面上,受到的浮力F=G=58.8牛。
以上是浮力计算题的典型例题,通过这些例题的练习,可以帮助我们更好地掌握浮力的计算方法。
六种利息计算的例题

六种利息计算的例题利息计算是金融领域中非常重要的一部分。
在实际的贷款、投资和存款场景中,了解利息的计算方法能够帮助我们做出更加明智的决策。
本文将介绍六种常见的利息计算方法,并通过例题加深理解。
一、简单利息计算简单利息是指根据本金、利率和时间计算出的利息,利息没有复利效应。
简单利息计算公式为:利息 = 本金 ×利率 ×时间。
下面是一个例题:例题1:小明借了1000元,年利率为4%,借款期限为3年,求应还的本息总额。
解答:利息 = 1000 × 0.04 × 3 = 120元。
应还的本息总额为:1000 + 120 = 1120元。
二、复利计算复利是指在每个计息周期结束时,将利息和本金再次计算利息的一种计算方法。
复利计算公式为:复利 = 本总 ×(1 + 年利率)^ 年数 -本金。
下面是一个例题:例题2:小红投资了5000元,年利率为3%,存款期限为5年,求到期后的本息总额。
解答:复利 = 5000 ×(1 + 0.03)^ 5 - 5000 = 5503.03元。
到期后的本息总额为5503.03元。
三、按月付息、到期还本按月付息、到期还本是贷款中一种常见的方式。
这种方式下,每个月支付利息,到期时一次性还清本金。
下面是一个例题:例题3:小王借了5000元,贷款年利率为5%,贷款期限为2年,按月付息,到期还本,求每个月的利息和到期时应还的本息总额。
解答:每个月的利息 = 贷款额 ×月利率 = 5000 ×(0.05 ÷ 12) = 20.83元。
到期时应还的本息总额 = (每个月的利息 ×贷款期限)+ 贷款额 = (20.83 × 24)+ 5000 = 5097.92元。
四、等额本息还款法等额本息还款法是贷款中的一种常见方式。
按照该方式,每月支付的还款额固定,由本金和利息共同决定。
下面是一个例题:例题4:小丽贷款30000元,年利率为6%,贷款期限为3年,按等额本息还款方式,求每个月应付的还款额。
2024年个人所得税计算题例题

根据2024年的个人所得税法,居民个人的综合所得,以每一纳税年度的收入额减除费用标准后的余额,为应纳税所得额。
2024年的费用标准是多少?A. 5000元/月(正确答案)B. 6000元/月C. 7000元/月D. 8000元/月张某2024年3月取得工资收入8000元,假设无其他扣除项,其应缴纳的个人所得税是多少?A. 30元B. 90元(正确答案)C. 150元D. 210元李某2024年将一套自有住房出租,月租金为4000元。
若不考虑其他税费和扣除项,李某每月应缴纳的个人所得税是多少?A. 80元B. 120元C. 240元D. 400元(正确答案)王某2024年取得稿酬收入30000元,若不考虑其他扣除项,其应缴纳的个人所得税是多少?A. 3360元(正确答案)B. 4200元C. 4800元D. 5600元根据2024年的个人所得税法,居民个人取得全年一次性奖金,应如何计算个人所得税?A. 与综合所得合并计算B. 单独计算,但税率固定为20%C. 单独计算,可选择并入综合所得或单独计税(正确答案)D. 免征个人所得税赵某2024年从上市公司取得股息红利5000元,其应缴纳的个人所得税是多少?A. 0元(正确答案)B. 500元D. 1500元根据2024年的个人所得税法,个人将其所得对教育、扶贫、济困等公益慈善事业进行捐赠,捐赠额未超过纳税人申报的应纳税所得额的部分,可以从其应纳税所得额中扣除。
扣除的比例是多少?A. 10%B. 20%C. 30%(正确答案)D. 50%刘某2024年取得特许权使用费收入20000元,若不考虑其他扣除项,其应缴纳的个人所得税是多少?A. 2000元B. 2800元(正确答案)C. 3200元D. 3600元根据2024年的个人所得税法,非居民个人的工资、薪金所得,以每月收入额减除费用标准后的余额为应纳税所得额。
2024年的费用标准是多少?A. 4800元/月(正确答案)B. 5000元/月C. 5200元/月D. 6000元/月。
挣值法计算及例题

【挣值法案例】1 .背景某装饰工程公司承接一项酒店装修改造工程,前5 个月各月完成费用情况如表2A320075 一1 所示。
合同总价1500 万元,总工期6 个月。
2 .问题( 1 )计算各月的已完工程预算费用BCWP 及5 个月的BCWP 。
( 2 )计算5 个月累计的计划完成预算费用BCWS 、实际完成预算费用ACWP 。
( 3 )计算5 个月的费用偏差CV 、进度偏差SV ,并分析成本和进度状况。
( 4 )计算5 个月的费用绩效指数CPI 、进度绩效指数SPI ,并分析成本和进度状况。
【答案】( 1 )各月的BCWP 计算结果见表2A320075 一2 。
其中:已完工作预算费用BCWP =计划完成预算费用BCWS×已经完成工作量的百分比5 个月的已完工作预算费用BCWP 合计为1250 万元。
( 2 )从表2A320075 一2 中可见,5 个月的累计的计划完成预算费用BCWS 为1220 万元,实际完成预算费用ACWP 为 1 225 万元。
( 3 ) 5 个月的费用偏差CV :CV = BCWP —ACWP = 1250 一1225 = 25 万元,由于CV 为正,说明费用节约。
5 个月的进度偏差SV :SV = BCWP —BCWS = 1 250 一1220 = 30 万元,由于SV 为正,说明进度提前。
( 4 )费用绩效指数CPI = BCWP / ACWP = 1250 / 1225 = 1 . 0204 ,由于CPI 大于1 ,说明费用节约。
进度绩效指数SPI = BCWP / BCWS = 1 250 / 1220 = 1 . 0246 ,由于SPI 大于1 ,说明进度提前。
.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算例题Delta 系数例子1. 对于投资者来说,Delta 的意义主要在于以下两个方面:( 1)通过参照Delta 值,投资者可以用适量的权证来代替正股。
例如,认购证之前价格为 1 元,Delta 值为0.5 ,对应正股价格为10 元。
假设现在正股价格涨至11 元,则认购证涨至 1.5 元。
若投资者之前买入了一份正股,则所花费的资金为10 元,收益为11-10=1 元;若投资者之前买入了1/0.5=2 份认购证,则其所用资金仅为 2 元,而收益同样为2X( 1.5-1 ) =1元,可见,两种情况下投资者所用的资金不同,所得的收益却相同。
( 2 )权证投资具有杠杆效用,会放大投资的收益和亏损。
上周五收盘时,武钢CWB收盘价是6.306 元,正股武钢股份(5.75,0.18,3.23%, 吧)收盘价是15.59元,这样武钢CWB的名义杠杆是2.47,而武钢CWB的Delta是0.927,所以有效杠杆是2.29 (0.927 X 2.47)。
这就意味着,武钢股份的价格每变动1%理论上,武钢CWB应变动2.29%2. 衡量持仓部位风险如看涨期权的delta 为0.4 ,意味着期货价格每变动一元,期权的价格则变动0.4元。
Delta 具有可加性,如果投资者持有以下投资组合:持仓部位Delta数量(张)买入小麦期货11买入看涨期权0.472 买入看跌期权-0.533所有部位的Delta 值相加:1+2 x 0.47-3 x0.53=0.35 。
可见,该交易者的总体持仓的Delta 值为0.35 ,也就是说这是一个偏多的部位,相当于0.35 手期货多头。
3. Delta 中性套期保值。
如果投资者希望对冲期权或期货部位的风险,Delta 就是套期保值比率。
只要使部位的整体Delta 值保持为0. 就建立了一个中性的套期策略。
例如,某黄金投资组合当前价值117000 美元,当黄金价格从每盎司800 变为800.10 美元时,投资组合价格变为116900 美元,损失100 美兀。
即△ = —100/ 0.1 =—1000交易员可以买入1000 盎司黄金来消除风险,使得△= 0。
1000盎司黄金投资,当黄金价格从每盎司800 变为800.10 美兀时,投资组合盈利1000* 0.1 = 100 美元。
即△= 100/0.1 = 1000Gamma寸冲的示例:假设一个Delta中性的资产组合,GammO值为r, 一个期权的Gamm值为r c,如果将x份期权加入到这个组合中,则组合的Gamm值为x r c +『。
所以,要想使该组合的Gamm值为零,x = —r/r c。
但是,Gamm为零,Delta 又不为零了,因此还需要改变目标资产的数假设某个Delta中性的资产组合Gamm值为-5000,该组合中资产的某个看涨期权多头的Delta和Gamma分别为0.8和2。
为保持组合Gamm和Delta中性,该组合应购买多少份期权,同时卖出多少份资产?为保持Gammah性而购入的看涨期权数量=5000/2=2500。
购入2500 份期权后,新组合的Delta 值由0 增加到2500*0.8=2000.因此,应出售2000 份标的资产久期计算1. 利率计算假定利率计量方法为一年计复利一次,银行报告中注明的10%利率指100 美元的投资在年终会变成,100*( 1 + 10% )= 100* 1.1 = 110(美元)当利率计量方法为一年计复利两次,银行报告中注明的10%利率指100 美元的投资在 6 个月会有5%的利息收入,假设利息被用于再投资,则100 美元的投资年终会变成,100* 1.05 *1.05=110.25(美元)当利率计量方法为一年计复利 4 次,银行报告中注明的10%利率指100 美元的投资在 3 个月会有2.5 %的利息收入,假设利息被用于再投资,则100 美元的投资年终会变成,100* 1.025* 1.025 衣 1.025 衣 1.025 = 110.38 (美元)当利率计量方法为连续复利计算,银行报告中注明的10%利率,假设利息被用于再投资,则100美元的投资年终会变成,(A= 100, R =0.1,n = 1 )=10(k01 =110.522.零息利率和远期利率的计算3.持续期计算某面值为100美元,券息利率为10%的3 年期债券,该债券连续复利的年收益率为12%,即y =0.12,每6个月付息一次,息值为5美元,现值汽,权重等于现值除以债券价格计算得到该债券持续期为2.653年期限(:年)现金流现值权重时间*权重0554,7090,050025 154,4350.04700471.55 4.1760.0440.06625 3.9330,0420,0832.553.7040,0390,098 310573.2560.7782333总计13094213(债券价格)1.002.653(持续期)由上面计算得道,债券价格为94.213,持续期为2.653 ;根据公式△ P=—PD A y=- 94.213*2.653 △ y =-249.95 A y假设收益率增加10个基点(0.1 %),即A y =0.001则A P= —249.95 卞 0.001 = —0.250则债券价格通过持续期公式预计会下降到94.213 —0.25 = 93.963同样,可用上面表格计算债券价格,第三列5严m + 5严m +5严m + 5严山+4. 持续期法衡量债券资产价值的利率风险(选取组合加权平均法(PWAD法)计算)2003年末民生银行所持主要政府债券债券+ 105^-O'. 121 *1.0=93_963组合的持续期为7.124 ,说明如果收益率平均上升100 个基点,民生银行该债券组合的价值将下降约7.124%,即减少达115327.45 万元;2003 年12 月30 日银行间债市平均到期收益率为 3.06%,到2004 年7 月2 日的平均到期收益率为3.99%,上升了93 个基点,民生银行因此受损达到107254.533 万元。
5. 持续期缺口管理模型运用假如一家商业银行,其拥有的资产和负债(均以市场价值入账,单位为百万美元,利息按年支付)如下:资产包括现金100,年收益率为14%、偿还期为3 年的商业贷款900,年收益率为10%、偿还期为10 年的国债。
负债包括年利率为7%、一年期的一般定期存款500,年利率为8%、偿还期为4 年的可转让大额存单600。
股本为100。
各类资产和负债的利息按年计算。
(1)表 1 说明了银行资产负债情况和每项资产负债的持续期。
资产, [AA.J(X)持续期 (年)負债和[匝万臭凡1利爭 (%) 持续期 (年〉现金100一般定 期存款5007 1 商业 贷款夕0012 2.69 可转让 大额存单 60083.58K)债200 10676蕙负債1100100总计1200平均3J41200平均241⑵假设所有资产和负债的利率上升 2%(3)为了使银行股本净值不受利率变动的影响, 特别是利率上升的影响,该银行可以采取免疫的 策略,使得持续期缺口为零。
银行可以通过缩减 资产的加权平均持续期或者增加负债的加权平 均持续期来实现。
假设银行减少一般性的一年期 存款224,而增加利率为8%勺6年期以复利计算 的定期存款224。
产全贷債」计资殊业国总100一股吃再存款491935814 可鹤让大魏存单562 1017712总负债 1053股本3211351135市场价僵 利率(X)员債和股本 市场价橙 利牟(%)费产(S)底本1审吊价値 【石石畫Q利率(4 )现金 1002767 1 茴业覧牧90012269224 3 620010$0033 58HOC100总计1200平沟3 141200平均343(4)同上面,当利率上升2%寸,银行的资产的 市场价值是1135,但负债的市场价值有所不同。
谨产 市场備值刹率“)竟債辛股本市炀价僅和率")VaR 计算 1•例子(1) 当T =5,a =95%寸,VaR 对应于投资 组合在5天后收益分布的5%分位数的负值,也 对应于投资组合在5天后损失分布的95%分位 数。
N -1(0.95)=1.65(2) 假定一个交易组合在6个月时的收益 服从正态分布,分布的均值为 2 (单位:百万美 元),标准差为10。
由正态分布的性质可知,收O 8 0 5 7〜腔疋扇再款271 9 冬年期笔颠存款 201 10 可转讣大茹存单562 10 i恵负債1034 「 101113514 12益分布的1 %分位数为2-2.33 X 10,即-21.3。
因此,对于6个月的时间期限,在99%置信度下的VaR为21.3 (百万美元)。
(3)假定一个1年期项目的最终结果介于5000万美元损失和5000万美元收益之间,中间的任意结果具有均等的可能性。
项目的最终结果服从由-5000万美元到+5000万美元的均匀分布,损失大于4900万美元的可能性为1%。
因此,在1年后,基于99%置信度的VaR为4900 万美元。
(4)一个1年期项目,有98%的概率收益200万美元,1.5 %的概率损失400万美元,0.5 % 的概率损失1000万美元。
试求99.5 %置信度下的VaR咧CumulitlvtProbtbiH^D.^75ft 97D965.0 960.^55 -0 950 14在这样的累积分布下,对应于99%累积概率的损失为400万美元。
VaR= 400万美元可以这样描述:我们有99%的把握认为在未来1 年后该项目损失不会超过400 万美元。
上图显示,介于400 万美元和1000 万美元中的任何损失值出现的可能性都不超过99.5 %。
VaR在这一情形下不具备唯一性。
合理选择:将VaR 设定为这一区间的中间值,即99.5%置信度下的VaR为700万美元。
2. 方差- 协方差法计算VaR 票资产组合一个由两种股票(微软和埃克森)构成的资产组合,微软公司股票为100 亿,埃克森公司股票为200 亿,每股股票价格变动百分比分别为/ X1和/X2,则资产组合的每天价值变动为:/ P= 100/X1+ 200/X2;假设,两只股票每天价格变动的标准差分别为b 1 = 0.03 , (T 2 = 0.01,两者得相关系数为p 1,2 = 0.6,则/P的方差为:b 2p = 1002*2 2 20.03 2+ 2002*0.01 2+2*100*200*0.03*0.01*0.6 = 20.2 。
因此此投资组合每天价值变动得标准差b p = 4.494。
则投资组合每10 天价值变动标准差10b p= 4.494* V10 = 14.213若假设99%置信区间,Z值为2.33 ,则VaR 值为33.116 亿(VaR= 14.213*2.33 = 33.116)。
