14节点系统图
IEEE_14-bus母线标准试验系统数据[1]
![IEEE_14-bus母线标准试验系统数据[1]](https://img.taocdn.com/s3/m/3dc6af677e21af45b307a894.png)
IEEE14母线标准试验系统数据大连理工大学电气工程学院应用PSASP 对IEEE14节点系统进行潮流计算IEEE14节点系统图1413126111095478321母线电压上下限为1.1~0.97倍的基准电压支路号首末端母线号支路电阻支路电抗1/2充电电容电纳支路数据(标幺值,S B=100MV A)11-20.019380.059170.0264022-30.046990.019790.0219032-40.058110.176320.0187041-50.054030.223040.0246052-50.056950173880.0170063-40.067010.171030.0173074-50.013350.042110.0064087-80.00000.176150.0000097-90.00000.110010.00000109-100.031810.084500.00000116-110.094980.198900.00000126-120.122910.155810.00000136-130.066150.130270.00000149-140.127110.270380.000001510-110.082050.192070.000001612-130.220920.199880.000001713-140.170930.348020.00000185-60.00000.252020.00000194-70.00000.209120.00000204-90.00000.556180.00000变压器数据(标幺值)备注变压器序号首末端母线号非标准变比(标幺值)185-60.932非标准变比在首端194-70.978204-90.969并联电容数据(标幺值)母线号电纳90.19负荷数据(有名值)母线号有功无功221.712.7394.219.0447.8-3.9057.6 1.6611.27.5929.516.6109 5.811 3.5 1.812 6.1 1.61313.5 5.81414.9 5.0发电数据(有名值)母线号电压相角有功无功1 1.06?230?2 1.045?40?无功可调母线数据母线号电压幅值(标幺值)无功极限值(Mvar)下限上限2 1.045-40503 1.01040 6 1.07-624 8 1.09-624计算结果母线号母线电压发电机输出功率幅值p.u.相角(°)有功(MW)无功(Mvar)1 1.060232.38-16.892 1.045-4.98084042.43 1.01-12.717623.394 1.0186-10.32415 1.0203-8.78256 1.07-14.222312.247 1.062-13.36808 1.09-13.368017.369 1.0563-14.946210 1.0513-15.103911 1.0571-14.794912 1.0569-15.077113 1.0504-15.158614 1.0358-16.0386。
EA14种图像以及连线

EA 14种图像以及连线关系一、结构建模1.1 类图类图展示了面向对象系统的构造模块。
描绘了模型或部分模型的静态视图,显示它包含的属性和行为,而不是详细描述操作的功能或完善方法。
类图最常用来表达多个类和接口之间的关系。
泛化(Generalizations),聚合(aggregations)和关联(associations)分别是类之间继承,复合或应用,及连接的表现。
下面的图显示了类之间的聚合关系。
弱聚合(浅色箭头)表现在类 "Account" 使用 "AddressBook",但是不必要包含它的一个实例。
强聚合(图中的黑色箭头)表示了目标类包含源类,例如,"Contact" 和"ContactGroup"值被包含在 "AddressBook"中。
类(Classes)类是定义对象所具有的属性和行为的元素。
行为用类能理解的合适消息和适合每条消息的操作来描述。
类中也可能定义约束,标记值,构造型。
类的标柱(Class Notation)类用矩形表示。
除类的名称外,还可以选择性地显示属性和操作。
分栏分别用来显示类的名称,属性和操作。
在下面图中,类的类名显示在最上面的分栏,它下面的分栏显示详细属性,如:"center" 属性显示初始化的值。
最后面的分栏显示操作,如: setWidth,setLength 和 setPosition 以及他们的参数。
属性和操作名前的标注表示了该属性或操作的可见性: 如果使用 "+"号,这个属性或操作是公共的 ; "-" 号则代表这个属性或操作是私有的。
"#"号是这个属性或操作被定义为保护的," ~" 号代表包的可见性。
接口(Interfaces)接口是实施者同意满足的行为规范,是一种约定。
UML科普文,一篇文章掌握14种UML图

UML科普⽂,⼀篇⽂章掌握14种UML图前⾔上⼀篇⽂章写了⼀篇建造者模式,其中有⼏个UML类图,有的读者反馈看不懂了,我们今天就来解决⼀哈。
什么是UML?UML是Unified Model Language的缩写,中⽂是统⼀建模语⾔,是由⼀整套图表组成的标准化建模语⾔。
为什么要⽤UML?通过使⽤UML使得在软件开发之前,对整个软件设计有更好的可读性,可理解性,从⽽降低开发风险。
同时,也能⽅便各个开发⼈员之间的交流。
UML提供了极富表达能⼒的建模语⾔,可以让软件开发过程中的不同⼈员分别得到⾃⼰感兴趣的信息。
Page-Jones 在《Fundamental Object-Oriented Design in UML》⼀书中总结了UML的主要⽬的,如下:1. 为⽤户提供现成的、有表现⼒的可视化建模语⾔,以便他们开发和交换有意义的模型。
2. 为核⼼概念提供可扩展性 (Extensibility) 和特殊化 (Specialization) 机制。
3. 独⽴于特定的编程语⾔和开发过程。
4. 为了解建模语⾔提供⼀个正式的基础。
5. ⿎励⾯向对象⼯具市场的发展。
6. ⽀持更⾼层次的开发概念,如协作,框架,模式和组件。
7. 整合最佳的⼯作⽅法 (Best Practices)。
UML图有哪些?UML图分为结构图和⾏为图。
结构图分为类图、轮廓图、组件图、组合结构图、对象图、部署图、包图。
⾏为图⼜分活动图、⽤例图、状态机图和交互图。
交互图⼜分为序列图、时序图、通讯图、交互概览图。
UML图概览什么是类图?【概念】类图是⼀切⾯向对象⽅法的核⼼建模⼯具。
类图描述了系统中对象的类型以及它们之间存在的各种静态关系。
【⽬的】⽤来表⽰类、接⼝以及它们之间的静态结构和关系。
在类图中,常见的有以下⼏种关系。
泛化(Generalization)【泛化关系】是⼀种继承关系,表⽰⼦类继承⽗类的所有特征和⾏为。
【箭头指向】带三⾓箭头的实线,箭头指向⽗类。
Tekla节点示例(已全).

Tekla最全节点示例200号节点,契型梁接契型梁(梁梁节点)14号节点,节点板(梁梁对接节点)144号节点,端板(梁柱节点)上部:1002号节点,端板细部下部:1003号节点,加劲肋1014号节点,加劲肋底板146号节点,单剪板,(用于抗风柱节点)2号节点,冷弯卷边套管,(用于檩托板)抗风支撑(1)节点,用于水平支撑节点契型柱S44节点,用于门式钢架中的T型柱2号节点,冷弯卷边套管,(用于檩托板,角隅撑)105号节点,连接支撑,(用于系杆节点)常用系统节点图例1 粱柱节点a梁接柱腹板常用186 188 其他133 128例:186 133B梁接柱翼缘常用186 188 其他181 190 144 141 例:186 1442 粱梁节点常用146 184 其他13 44 梁梁对接US77 41例:184 77特殊的全深度 1853 支撑节点常用11 57 60 其他110 51 19 10例:11 57 604 屋面檩拖+隅撑节点5 墙皮檩拖常用 1 常用86 支座节点7 底板节点常用71 其他55 95 301031常用1047其他1014 1053 1016 1066 1052其他8 端板常用10029 缀板常用104610 组件契形梁S45 S98 契形柱S44 S99带节点板钢管S47 双截面角钢S50箱形梁S13 相交截面S32 S3311 建模工具阵列2912开孔节点常用打孔32梁开孔1033 柱开孔103213加劲板100314 梁柱节点用144 梁梁对接用200 支撑节点53 105 S47可以用来做系杆节点1046 11可以做柱间支撑节点15 水平加劲肋1017 柱加劲肋103016 端板节点144多重加劲肋1064Tekla常用节点分类汇总类别代号名称类别代号名称柱底节点71 美国底板节点/带角钢支撑加劲肋1003 加劲肋1014 加劲肋底板1017 水平加劲肋1016 腹板带加劲肋底板1030 翼板处加劲肋1042 底板1034 加劲肋1047 美国底板1041 加劲肋1048 美国支座细部1058 穿透膜板1052 圆形底板1059 内膜板1066 箱形柱底板1060 腹板加劲板1068 楔形柱底板1064 多重加劲。
基于内点法最优潮流计算

1.1246e-001
4
-1.2326e-002
-1.8264e-001
1.9823e-001
-2.0804e-002
-1.9440e-002
5.0985e-002
5
-3.8403e-004
-7.6535e-002
7.7332e-002
-5.7025e-002
-2.2982e-003
5.3726e-002
基于内点法最优潮流计算
1
主要内容
1、 课题研究旳意义和现状 2、 最优潮流旳原对偶内点算法 3、 最优潮流旳预测校正内点算法 4、 结论
2
一、课题研究旳意义和现状
概念:
最优潮流问题(OPF)就是在系统构造参数及负荷 给定旳情况下,经过优选控制变量,拟定能满足全 部旳指定约束条件,并使系统旳某个性能指标到达 最优时旳潮流分布。
5 0.7754 0.9323
11 0.9995 0.9995
6 0.9716 0.9838
12 0.9995 0.9995
18
收敛特征分析
下表为计算过程中5节点系统旳迭代步长:
迭代次
数
1
2
3
4
5
6
7
8
ap
0.5222 0.0016 0.4027 0.3444 0.0016 0.9365 0.3377 0.6978
三个系统旳迭代次数分别为16、11、12次,迭代次数较少,计算时
间短,收敛特征好。
系统规模扩大时,迭代次数不会明显增长,阐明算法对系统规模不
敏感。
初始点为非内点时,算法也能够收敛至最优解,阐明算法对初始点
不敏感。
17
收敛特征分析
以IEEE14、30、39节点为例应用计算机形成关联矩阵教材

2、IEEE30节点
1
2
5
7
8
3
4
6
13
11 9
12
14
16 15
17 10
28
29 27
18 15
21
22
19
20
24
IEEE30节点系统图
30 25 26
30个节点,41条支路
2、IEEE30节点系统各线路数据
将各线路数据输入到excel表格中, 便于程序的调用
高等电力网络分析
题目
以IEEE14、30、39节点为例应用计算机形成关联 矩阵,用matlab编程,结果存到excel中
电力系统中IEEE节点:是为了验证某一个计算方法行不行 而设立的节点
1、IEEE14节点
14个节点,20条支路
IEEE14节点系统图
1、IEEE14节点程序设 计
对于含有变压器的支路, 节点电流的正负规则不变, 以支路首端为参考,则末 端为负的变比。
设计思路:将IEEE14节点系统的数据存入到data中,定义14*20的零矩阵,以 支路号为循环变量并作为A的列元素,取出data中该支路号对应的首端节点数 并作为A的行元素,令节点数并作为A的行元素,令A矩阵对应的位置为-1。遵循节点电流流出 为正,流入为负的规则。
含有变压器的支路中变压器的变比
2、IEEE30节点程序设计
编程思路与IEEE14节点系统类似。 区别之处在于:调用的excel数据库不同;定义的关联矩阵A 维数不同。
2、IEEE30节点A矩阵结果
剩下的结果略
3、IEEE39节点系统图
未查到相关数据,思路与前面的一样
电力系统中的潮流计算与分析

电力系统中的潮流计算与分析摘要本文介绍了电力系统中的潮流计算与分析,潮流计算是电力系统计算的基础,通过对电力系统中的电流、电压和功率进行计算和分析,可以有效地评估电力系统的稳定性和安全性。
在本文中,我们讨论了潮流计算的原理和方法,并介绍了一种基于改进的高斯-赛德尔迭代算法的潮流计算方法。
同时,我们还介绍了一种基于Python语言的潮流计算程序的设计和实现,该程序可以对电力系统进行潮流计算和分析,并生成相关的报告和图表。
最后,我们利用该程序对IEEE 14节点测试系统进行了潮流计算和分析,并分析了系统的稳定性和安全性。
关键词:电力系统;潮流计算;高斯-赛德尔迭代算法;Python语言AbstractThis paper introduces the load flow calculation and analysis in power system. Load flow calculation is the basis of power system calculation. By calculating and analyzing the current, voltage and power in the power system, the stability and safety of the power system can be effectively evaluated. In this paper, we discuss the principles and methods of load flow calculation, and introduce an improved Gauss-Seidel iterative algorithm based load flow calculation method. At the same time, we also introduce the design and implementation of a load flow calculation program based on the Python language. The program can perform load flow calculation and analysis on the power system, and generate relevant reports and charts. Finally, we use the program to perform load flow calculation and analysis on the IEEE 14-bus test system, and analyze the stability and safety of the system.Keywords: power system; load flow calculation; Gauss-Seidel iterative algorithm; Python language一、引言电力系统是现代工业和生活的基础设施之一,它承担着输送和分配电能的重要任务。
潮流计算 课程设计

课程设计(论文)题目名称潮流计算课程名称电力系统稳态分析学生姓名学号系、专业电气工程系、09级电力一班指导教师2012年1月7 日**课程设计(论文)任务书注:1.此表由指导教师填写,经系、教研室审批,指导教师、学生签字后生效;2.此表1式3份,学生、指导教师、教研室各1份。
指导教师(签字):学生(签字):**课程设计(论文)评阅表学生姓名学号系电气工程及其自动化专业班级题目名称潮流计算课程设计课程名称电力系统分析一、学生自我总结二、指导教师评定注:1、本表是学生课程设计(论文)成绩评定的依据,装订在设计说明书(或论文)的“任务书”页后面;2、表中的“评分项目”及“权重”根据各系的考核细则和评分标准确定。
目录摘要 (Ⅰ)第1章潮流计算概述及课题 (1)1.1 潮流计算概述 (1)1.2 潮流计算课题 (1)1.3 分析课题及求解思路 (2)第2章 PSCAD软件的应用及仿真结果 (3)2.1 PSCAD简介 (4)2.2 PSCAD的应用 (4)2.3 PSCAD仿真结果 (5)总结 (8)参考文献 (9)摘要从数学上说,朝流计算是要求解一组有潮流方程描述的非线性方程组。
电力系统潮流计算是电力系统分析中最重要最基本的计算,是电力运行、规划以及安全性、可靠性分析和优化的基础,也是各种电磁暂态和机电暂态分析的基础和出发点。
随着现代化的调度中心的建立,为了对电力系统进行实时安全监控,需要根据实时数据库所提供的信息。
PSCAD代表电力系统计算机辅助设计,PSCAD的开发成功,使得用户能更方便地使用EMTDC进行电力系统分析,使电力系统复杂部分可视化成为可能,而且软件可以作为实时数字仿真器的前置端。
可模拟任意大小的交直流系统。
关键词:潮流计算;PSCAD1潮流计算概述及题目1.1 潮流计算概述在电力系统运行和规划中,都需要研究电力系统稳定运行情况,确定电力系统的稳态运行状态。
给定电力系统的网络结构、参数和决定电力系统运行状况的边界条件,,确定电力系统运行的方法之一是朝流计算。
电气工程PSASP仿真软件实践

东南大学研究生课程《电气工程仿真软件实践》课程报告院(系、所)电气工程学院学科(专业)电气工程研究生姓名郝攀学科门类与学位级别工学硕士导师姓名张金旺入学年月 2015年8月31日结题报告日期 2016年5月26日东南大学电气工程学院1实验目的掌握电力系统稳态运行的基本要求;培养应用电力系统仿真计算软件PSASP进行潮流调整、电压调整、网损分析的实践能力;培养运用所学知识分析和解决问题的能力。
2PSASP简介2.1PSASP综述《电力系统分析综合程序》(Power System Analysis Software Package, PSASP)是由中国电力科学研究院研发的电力系统分析程序。
主要用于电力系统规划设计人员确定经济合理、技术可行的规划设计方案;运行调度人员确定系统运行方式、分析系统事故、寻求反事故措施;科研人员研究新设备、新元件投入系统等新问题以及高等院校用于教学和研究。
2.2PSASP特点PSASP具有基于公用数据和模型的三层体系结构, 如图1所示。
第一层是公用数据和模型的资源库;第二层是基于资源库的应用程序包;第三层是计算结果库和分析工具,极大地资源共享,高度集成和开放。
PSASP 有着友好、方便的人机界面,如基于图形的数据输入和图上操作,自定义模型图以及图形、曲线、报表等各种形式输入。
PSASP 与Excel、AutoCAD、Matlab 等通用的软件分析工具有着方便的接口,可充分利用这些软件的资源。
PSASP 应用程序的共同特点是:●可计算大规模(可达3000 个母线或更多)的交直流混合电力系统;●有公用的数据库做支持,不必为每一种计算准备其基础数据。
●有固定模型库和用户自定义模型库作支持。
●不但有通常的文本方式计算,而且还有单线图上的操(修改数据、操作开关、增加故障等)计算,其计算结果直接标注在图上,具有仿真的效果。
●具有多种形式(图形、图示、报表、曲线等)的结果分析的输出。
提供了与 Excel、AutoCAD、Matlab等常用软件工具的接口。
IEEE14节点系统图与数据整理

I E E E14节点系统图与数据整理-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1 3 0.0 0.0 232.4 -16.9 0.0 1.060 0.02 2 21.7 12.7 40.0 0.0 0.0 1.045 0.03 2 94.2 19.0 0.0 0.0 0.0 1.010 0.04 0 47.8 -3.9 0.0 0.0 0.0 1 0.05 0 7.6 1.6 0.0 0.0 0.0 1 0.06 2 11.2 7.5 0.0 0.0 0.0 1.070 0.07 0 0.0 0.0 0.0 0.0 0.0 1 0.08 2 0.0 0.0 0.0 0.0 0.0 1.090 0.09 0 29.5 16.6 0.0 0.0 0.0 1 0.1910 0 9.0 5.8 0.0 0.0 0.0 1 0.011 0 3.5 1.8 0.0 0.0 0.0 1 0.012 0 6.1 1.6 0.0 0.0 0.0 1 0.013 0 13.5 5.8 0.0 0.0 0.0 1 0.014 0 14.9 5.0 0.0 0.0 0.0 1 0.0矩阵列依次为:节点序号,节点分类编号(3表示平衡节点,2表示PV节点,0表示PQ节点),节点负荷有功,节点负荷无功%发电机有功功率,发电机无功功率,节点电压初始值,节点所接并联电容器的电纳1 2 0.01938 0.05917 0.0528 0.01 5 0.05403 0.22304 0.0492 0.02 3 0.04699 0.19797 0.0438 0.02 4 0.05811 0.17632 0.0374 0.02 5 0.05695 0.17388 0.0340 0.03 4 0.06701 0.17103 0.0346 0.04 5 0.01335 0.04211 0.0 0.04 7 0.0 0.20912 0.0 0.9784 9 0.0 0.55618 0.0 0.9695 6 0.0 0.25202 0.0 0.9326 11 0.09498 0.19890 0.0 0.06 12 0.12291 0.25581 0.0 0.06 13 0.06615 0.13027 0.0 0.07 8 0.0 0.17615 0.0 0.07 9 0.0 0.11001 0.0 0.09 10 0.03181 0.08450 0.0 0.09 14 0.12711 0.27038 0.0 0.010 11 0.08205 0.19207 0.0 0.012 13 0.22092 0.19988 0.0 0.013 14 0.17093 0.34802 0.0 0.0矩阵列依次为:支路首端节点i,节点末端j(i<j),支路电阻,支路电抗,支路对地容抗,变压器变比(无变压器为0)输入原始数据形成节点导纳阵给定电压幅值和相位的初值计算功率误差判断精度计算雅克比矩阵求解修正方程,得修正量修正电压的幅值和相角计算电压分布和功率分布。
含双馈型风力发电机的电力系统潮流计算

含双馈型风力发电机的电力系统潮流计算齐晓光;安佳坤;胡君慧【摘要】以双馈型风力发电机为主的风电场接入电网后,由于不同于同步发电机的异构电源形态,造成传统电力系统潮流算法在计算时会产生较大误差.针对这一问题,对双馈型风力发电机的电磁特性和控制策略进行了研究,进而描述风电场的输出特性,并在此基础上采用改进的电力系统潮流计算方法进行计算.结果表明,所采用的改进潮流计算方法效果良好.【期刊名称】《上海电气技术》【年(卷),期】2018(011)004【总页数】6页(P4-9)【关键词】风力发电机;电力系统;潮流;计算【作者】齐晓光;安佳坤;胡君慧【作者单位】国家电网河北省电力公司经济技术研究院石家庄 050000;国家电网河北省电力公司经济技术研究院石家庄 050000;国家电网北京经济技术研究院北京 102209【正文语种】中文【中图分类】TM744;TM6141 研究背景近些年,随着风电的快速发展,电力能源中风力发电的占比逐步增大。
在几种主要风力发电机中,双馈型风力发电机是当前风力发电的主要装备[1-2]。
双馈型风力发电机具有不同于同步发电机的异构电源形态,其大规模接入将对电网节点电压、网损、线路功率和传输方向产生较大影响。
同时,双馈型风力发电机具有不同于同步发电机的结构特征,相应的潮流计算方法与传统方法也有所不同。
可见,研究大规模双馈型风力发电机接入后的电网潮流计算方法具有重要的工程实践意义。
针对含风、光、储等多类型新能源的电力系统潮流计算,文献[3]将多类型新电源直接处理为PQ节点,并用牛顿-拉弗森法求解潮流。
文献[4]将各类型新能源处理为PV节点,并采用牛顿-拉弗森法进行计算。
文献[3]和文献[4]并未充分考虑各类型新能源的电磁特征和控制策略,只是将不同类型的新能源处理成PV或PQ节点,电网潮流计算存在误差。
文献[5]对风、光等类型的新能源进行建模,根据电源并网点的电压或电流,计算参与迭代的节点功率。
考虑关键节点和重要线路的电力系统PMU_优化配置

第 42 卷第 4 期2023年 7 月Vol.42 No.4Jul. 2023中南民族大学学报(自然科学版)Journal of South-Central Minzu University(Natural Science Edition)考虑关键节点和重要线路的电力系统PMU优化配置徐光辉1,2,肖克1,2,柯善焜1,2,王淑青1,2,汪繁荣1,2(1 湖北工业大学电气与电子工程学院,武汉430068;2 湖北工业大学产业研究院,襄阳441000)摘要相量测量单元(PMU)是一种测量电压和电流的设备,随着电力系统的规模和结构越来越复杂,PMU的数量也大幅增加.利用改进蝠鲼觅食优化算法(IMRFO)对PMU进行了配置,使电力系统在正常运行、考虑关键节点和考虑重要线路时都能完全可观测,同时使PMU配置数最少.在蝠鲼觅食算法的基础上增加了混沌映射以提升算法的收敛速度,增加了跳跃因子以提高算法的勘测能力,从而避免算法陷入局部最优. 通过度、特征向量和接近度三种指标,利用TOPSIS综合评价寻找系统的关键节点,利用线的中间中心度判断系统的重要线路.对IEEE-14和IEEE-69节点系统进行了实验仿真,结果表明:IMFRO算法与未改进时相对比,在配置时所需的PMU数和迭代次数均有一定的减少,验证了所提方法对解决PMU优化配置问题的有效性和优越性.关键词电力系统;相量测量单元;关键节点;重要线路;蝠鲼觅食算法中图分类号TP242;TM711 文献标志码 A 文章编号1672-4321(2023)04-0535-06doi:10.20056/ki.ZNMDZK.20230415Optimization of PMU for power system considering key nodesand important linesXU Guanghui1,2,XIAO Ke1,2,KE Shankun1,2,WANG Shuqing1,2,WANG Fanrong1,2(1 School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China;2 Industrial Institute, Hubei University of Technology, Xiangyang 441000, China)Abstract Phasor measuring unit (PMU) is a device for measuring voltage and current. As the scale and structure of power system become more complex,the number of PMUs increases greatly. The improved manta ray foraging optimization algorithm (IMRFO)is used to configure PMUs,so that the power system can be fully observable during normal operation, considering critical nodes and important lines, and at the same time, the number of configured PMUs is minimized. On the basis of the manta ray foraging algorithm, chaotic mapping is added to improve the convergence speed of the algorithm, and a jump factor is added to improve the exploration ability of the algorithm, so as to avoid the algorithm falling into local optimal. The key nodes of the system are found by TOPSIS comprehensive evaluation through three indexes of degree, feature vector and proximity. The central degree of the line is used to judge the important line of the system. Experimental simulations of the IEEE-14 and IEEE-69 node systems are performed. The results show that compared with IMFRO algorithm without improvement, the number of PMU and iteration times are reduced to a certain extent,which verifies the effectiveness and superiority of the proposed method to solve the problem of optimal PMU configuration.Keywords power system; phasor measuring unit; key node; important line; manta ray foraging algorithm随着电网规模越来越大,一些关键的节点发生故障可能引起级联效应而导致整个电网崩溃;一些重要的输电线路因自然因素等原因而造成运行故障[1],为了保障电网的安全性和稳定性,需要实时对电网的各相数据进行监测,同步相量测量单元(Phase Measurement Unit,PMU)的出现能解决这一收稿日期2023-02-24作者简介徐光辉(1986-),男,副教授,博士,研究方向:复杂网络群集控制和优化,E-mail:************.cn 基金项目国家自然科学基金资助项目(61603127)第 42 卷中南民族大学学报(自然科学版)问题.PMU能实时测量节点电压、电流相量等信号,在配电网状态估计[2]、检测线路故障[3]等方面上取得了不错的效果,为电力系统部门及时掌握系统运行状态,出现异常情况采取必要的控制措施.由于PMU具有高采样率,若电网中所有的节点都配置PMU,会产生冗余的数据并且是不经济的,在此背景下,PMU最优配置(Optimal PMU Placement, OPP)这一问题具有重要的意义.目前,解决OPP问题的算法主要为数值算法和启发式算法[4].数值算法发展较成熟,对小型的电力系统,具有计算速度快、收敛能力强等特点,但在大型系统中,存在着全局搜索能力弱、普适性差等问题.闰玲玲等[5]提出了基于0‐1整数规划算法的PMU配置方法,在配置小型电力系统节点上有很好的实用性,但在大型电力系统节点上所需时间较长.郑明忠等[6]利用了整数规划算法,能解决考虑故障情况下的OPP问题,但同样存在收敛过慢等不足.启发式优化方法具有全局搜索能力强、运行速度快等特点,在求解多目标、高维度模型上有一定的优势,由于OPP问题一般是多约束和高维度的,所以在OPP问题上,启发式优化方法使用得较多,如遗传算法[7]、模拟退火算法[8].MAJI T K等[9]提出了一种改进二进制粒子群算法,通过非线性惯性权重系数来提高搜索能力,通过改进阈值函数来提高收敛速度,但没有考虑关键节点等问题.PAL A等[10]提到了关键节点,但配置时只对关键节点优先考虑且没有保证系统的完全可观测性.ALMASABI S等[11]提出了用脆弱性指数来评判线路的重要性,将脆弱性指数集成到可观察性中,作为目标函数的一个指标使总安装成本最小化.虽然上述部分文献提到了关键节点和重要线路,但没有针对考虑关键节点和重要线路时的PMU配置情况,基于此,本文的主要贡献如下:本文提出改进蝠鲼觅食(Improved Manta Ray Foraging Optimization,IMRFO)算法来实现OPP问题,通过混沌映射增加算法初始化的多样性,通过跳跃因子使算法易于跳出局部解.实验表明:改进后的算法能有效地跳出局部最优;使用图论的3种指标来判断电力系统的关键节点,利用线的中间中心度判断电力系统的重要线路,在保证系统完全可观测和PMU配置数目最小的情况下,分别对正常运行、考虑关键节点和考虑重要线路的PMU配置情况加以分析.通过仿真分析验证所提出的方法的正确性和优越性.1 PMU最优配置规则和模型1.1 PMU配置规则当一个电力系统的所有节点电压相量能被PMU 直接或间接观测时,称这个系统是全网可观测的.电力系统节点的可观测性由以下规则来判断[12]:规则1:若节点i安装了PMU,其节点的电压相量能被直接测量,则节点i是直接可观测的;规则2:若节点i安装了PMU,通过欧姆定律能计算其所有邻接节点的电压相量,则与节点i所有的邻接节点是间接可观测的.在原有的基础上本文通过新增加两条规则来对关键节点和重要线路加以说明.规则3:为了确保在关键节点上测量数据的有效性,所以在关键节点处至少能被两个PMU所观测;规则4:由于一些客观的因素(如线路老化)影响线路中的参数,为了尽可能使PMU测量线路电流和电压的准确性,所以在重要线路的两端,至少有一端能被PMU直接观测.1.2 PMU的配置模型要使配置PMU数量最小并且使整个电力系统节点完全可观测,则电力系统n个节点PMU配置模型的目标函数如下:min f(x)=∑i=1n x i,(1)其中:f(x)表示n个节点所安装PMU的最小数量;x i 是一个二进制数,若节点i安装了PMU,则为1,否则为0.根据以上条件,就可以写出PMU配置的约束条件:AX≥b,(2)Aij=ìíî1,i=j或i、j相连,0,其他,(3)其中:X=(x1,x2,...,x n)T表示相应节点PMU配置的情况;式中b在正常情况下为[1,1,…,1]的n维列向量;矩阵A表示节点的连接情况,如果节点i连接到节点j或节点i和j是同一节点,则A ij=1,否则A ij=0. 2 改进蝠鲼觅食算法原理2.1 蝠鲼觅食算法蝠鲼觅食算法(Manta Ray Foraging Optimization,536第 4 期徐光辉,等:考虑关键节点和重要线路的电力系统PMU 优化配置MRFO )是一种群智能优化算法,虽然蝠鲼的食物并不是均匀分布或集中在某些地区,但是蝠鲼在群体觅食中总能精准找到食物,这是因为它们进化出了一套智能觅食策略,将这种智能策略转换为数学模型就可得到MRFO 算法[13].2.2 基于改进蝠鲼觅食算法的最优配置问题虽然MRFO 算法具有较好的性能,但还是存在容易陷入局部最优解和收敛性过慢等问题,因此需要通过对MRFO 算法进行改进使性能得以提升,并更加适用于OPP 问题的求解.种群初始化的位置能在一定程度影响算法性能.与随机搜索相比,混沌映射在搜索空间上遍历性更好,可使算法在一定程度上跳出局部最优.在配置PMU 时,只有两种情况,即“1”为配置PMU ,“0”为不配置PMU.在算法的初始化过程中,种群有较大的概率在0和1附近,能增加算法的收敛速度和准确性.Sine 映射倾向于在0‐1之间的两端[14],因此在种群初始化时用Sine 映射,其数学模型如下:z k +1=a4sin (πz k ),(4)其中:z k 是迭代序列值,z 0∈(0,1),a ∈(0,4];一般情况下,z 0取0.152,a 取4.在算法迭代前期,权重因子β值过大有利于提高算法的勘察能力;在迭代后期时,β值过小有利于提高算法的开发能力.在迭代过程中,用较大概率的短步来提高开发能力,用较小概率的长步来提高探索能力,使算法有机会跳出局部解.为了增加种群搜索的多样性,提出了跳跃因子来增加种群的搜索能力,如式(5)所示:βnew =ìíîïïβ+2(rand 1-0.5)(h -t T ),rand 2≤0.2,β,rand 2>0.2,(5)其中:h 为跳跃因子,一般设置为15;t 和T 分别表示当前迭代和最大迭代次数;rand 1和rand 2均为[0,1]是随机数.为了验证改进的有效性,采用单峰、多峰和固定维测试函数,测试函数如表1[15].为了保证公平的比较,所有算法都采用相同的维数,相关参数均未改变.最大迭代次数和种群数量相同,所有测试函数运行30次.表2为GWO 、PSO 、MRFO 和IMRFO 的收敛结果的比较.可以看出,在MRFO 在改进后性能有一定的提升.IMRFO 算法求解OPP 问题的流程图如图1所示.3 关键节点和重要线路的判断3.1 关键节点的判断本文利用TOPSIS 综合图论中的度、特征向量和接近度三种指标,评价关键节点的位置.节点的度说明自身和周围节点的连接程度,本文认为节点的度越大,说明该节点越重要.节点i 的度计算公式为:De(i )=∑j =1L A ij ,(6)其中,L 为支路总数.表1 测试函数Tab.1 Test function函数f 1f 2f 3函数名QuarticRastrigin Hartmann 3D搜索范围[‒1.28, 1.28][‒5.12, 5.12][0,1]最优值00‒3.86表2 测试函数的仿真数据Tab.2 Simulation data of test function 函数f 1f 2f 3指标平均数标准差平均数标准差平均数标准差GWO4.21×10‒52.42×10‒55.86×10‒134.73×10‒11‒3.862.07×10‒3PSO7.86×10‒22.63×10‒26.45×1011.67×101‒3.863.10×10‒15MRFO5.92×10‒65.96×10-61.07×10‒62.26×10‒7‒3.860IMRFO4.92×10‒64.61×10‒600‒3.86图1 基于IMRFO 算法的OPP 流程图Fig.1 Flowchart of OPP based on IMRFO algorithm537第 42 卷中南民族大学学报(自然科学版)在评估节点的重要性时不仅考虑节点的连接情况,而且还考虑了节点的连接关系.在电力系统中有N个节点,λ1,...,λn为邻接矩阵B的N个特征值,e=[e1,e2,...e n]T为最大特征值λ对应的最大特征向量,则邻接矩阵的最大特征值的特征向量为:T(i)=λ-1∑j=1N B ij e j,(7)其中:T(i)中各分值大小代表着相应节点的重要程度,分值越大表明对应的节点越重要.接近度反映了节点通过网络到达其他节点的容易程度[16].节点i的接近度为该节点到达网络中其他节点的最短距离之和的倒数,节点i的接近度为:D i=éëêê∑j=1N d ijùûúú-1,(8)其中:d ij为节点i到节点j的最短距离,N为系统中总节点数.3.2 重要线路的判断在电力系统输电线中,每条线路发生故障的概率与环境条件、输电等级和线路所处的位置等因素有关.由于环境条件因素辨别困难,本文只考虑在相同条件下线路所处的位置造成的影响.线的中间中心度测量的是一条线出现在一条最短路径上的次数,需要考虑系统中所有经过该线路两点之间的最短路径,计算该线路在全部最短路径中所占的比例,它能反映线路的重要程度[17].4 算例分析4.1 IEEE-14节点分析图2所示为输电网IEEE-14节点系统.表3为IEEE-14节点系统的度、特征向量和接近度三种指标的计算结果.利用TOPSIS综合评价得出得分权重矩阵S=[0.06 0.13 0.07 0.16 0.13 0.08 0.08 0 0.10 0.03 0.03 0.03 0.05 0.04].关键节点占总节点数的10%左右[10],因此本文取3个权重大的节点为关键节点,所以节点2、4、5为关键节点.根据规则3,节点2、4、5至少能被两个PMU所观测.TOPSIS 处理的步骤如下.步骤1:将3种判断结果写成矩阵Z n×m,其中n为电力系统中节点的个数,m为判断关键节点的种类,即在IEEE-14节点系统中,n为14,m为3;步骤2:正向化和标准化.正向化是得出的结果越大则该节点越重要;标准化是消除量纲的影响;步骤3:找出每列中的最大值矩阵D+和最小值矩阵D-,并计算出各个节点与D+和D-的欧式距离,并将m种指标赋予相同的权重;步骤4:计算出所有节点的得分矩阵S,再进行归一化处理.通过计算得出线的中间中心度矩阵M,M为对称矩阵,“0”表示节点之间不相连或为自身节点,数值的大小代表输电线路的重要程度.由式(9)可知线路5-6、4-5、4-9和9-14相比于其他线路为重要线路.根据规则4,这两条线路至少有一端能被PMU直接观测.表3 三类关键节点判断结果Tab.3 Judgment results of three types of critical nodesIEEE-14 节点节点1节点2节点3节点4节点5节点6节点7节点8节点9节点10节点11节点12节点13节点14度35365542533343特征向量0.2470.4210.2710.4910.4110.2240.2560.0760.2940.1180.1020.1070.1360.128接近度0.0290.0360.0290.0420.0400.0370.0340.0240.0400.0310.0300.0280.0310.032图2 IEEE-14节点系统Fig.2 IEEE-14 node system538第 4 期徐光辉,等:考虑关键节点和重要线路的电力系统PMU 优化配置M =éëêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêùûúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúú050040089087016000002300001300000000013000015001100000000001300000011000900000090000000000090000040015110 .(9)表4为IEEE -14和IEEE -69节点系统三种情况下的OPP 配置情况.由表4可知,在IEEE -14节点正常情况下需要配置4个PMU ,而在关键节点和考虑关键线路情况下,需要配置5个PMU.考虑关键节点和重要线路是在正常情况的基础上分别增加了规则3和规则4,故这两种情况配置的PMU 数都大于或等于正常情况下的配置数目.本文所提出的IMRFO 和MRFO 算法分别对IEEE -14节点进行了仿真,对比结果如图3所示.对比MRFO 算法和文献[18]采用的改进整数规划法,本文方法迭代次数相对较少,说明本文算法有较快的收敛速度.4.2 IEEE -69节点分析图4所示为配电网IEEE -69节点系统.利用TOPSIS 综合评价得出IEEE -69节点系统的关键节点为节点3、4、8、11和12.利用线的中间中心度得出重要线路为线路3-4、3-26、4-5、8-9、9-53、9-10、12-13和11-12.配置的结果和仿真图分别为表4和图5.由图5可知,IMRFO 与MRFO 算法相比,表4 IEEE -14和IEEE -69节点的配置情况Tab.4 Configuration of IEEE -14 node and IEEE -69 node3种情况下PMU 配置情况正常情况下考虑关键节点考虑关键线路IEEE -14 节点2,6,7,93,5,6,8,94,5,6,8,9IEEE -69 节点2,4,7,9,14,17,20,23,26,28,31,34,37,40,43,45,49,51,55,58,61,64,66,682,5,7,9,12,15,18,21,24,26,28,31,34,37,40,43,45,47,49,51,55,58,61,64,66,682,4,7,9,12,15,18,21,24,26,29,32,34,36,39,42,45,49,51,55,58,61,64,66,68迭代次数44.24.44.64.855.25.45.65.86配置P M U 数图3 正常情况下IEEE -14节点系统仿真图Fig.3 Simulation diagram of IEEE -14 node system under normal conditions图4 IEEE -69节点系统Fig.4 IEEE -69 node system539第 42 卷中南民族大学学报(自然科学版)IMRFO5 结语针对MRFO 算法易陷入局部最优和收敛速度慢等问题,本文提出了一种增加混沌映射和跳跃因子的IMRFO 算法,利用图论的3种指标和线的中间中心度寻找电力系统的关键节点和重要线路.为了保证电力系统完全可观测,利用IMRFO 算法分别在3种情况下进行了PMU 配置仿真,结果表明了IMRFO 算法对求解OPP 问题的有效性和优越性.在今后的研究中,应根据实际情况判断关键节点和重要线路,并进一步开发MRFO 算法的性能.参 考 文 献[1] 王沛. 基于大数据技术的输电线路运行故障诊断关键技术[J ]. 电测与仪表,2021,58(5):182-189.[2] 曹鹏. 面向状态估计的配电网量测系统优化配置研究[D ]. 贵阳:贵州大学,2022.[3] AHSACE M G , SADEH J. A novel fault -locationalgorithm for long transmission lines compensated by series FACTS devices [J ]. IEEE Transactions on Power Delivery , 2011, 26(4):2299-2308.[4] CHAKRABARTI S , KYRIAKIDES E. Optimal placementof phasor measurement units for power system observability[J ]. IEEE Transactions on Power System , 2008, 23(3):1433-1440.[5] 闰玲玲,刘中印,艾永乐,等. 基于0-1整数规划算法的PMU 量测点优化配置新方法[J ]. 电力系统保护与控制,2017,45(12):101-106.[6] 郑明忠,张道农,张小易,等. 基于节点集合的PMU 优化配置方法[J ]. 电力系统保护与控制,2017,45(13):138-142.[7] 徐岩,郅静. 基于改进自适应遗传算法的PMU 优化配置[J ]. 电力系统保护与控制,2015,43(2):55-62.[8] 袁澎,艾芊,赵媛媛. 基于改进的遗传-模拟退火算法和误差度分析原理的PMU 多目标优化配置[J ]. 中国电机工程学报,2014,34(13):2178-2187.[9] MAJI T K , ACHARJEE P. Multiple solutions of optimalPMU placement using exponential binary PSO algorithm for smart grid applications [J ]. IEEE Transactions onIndustry Applications , 2017,53(3):2500-2559.[10] PAL A , SANCHEZ -AYALA G A , CENTENO V A , et al.A PMU placement scheme ensuring real -time monitoring of critical buses of the network [J ]. IEEE Transactions on Power Delivery ,2014,29(2):510-517.[11] ALMASABI S , MITRA J. A fault -tolerance based approachto optimal PMU placement [J ]. IEEE Transactions onSmart Grid , 2019, 10(6):6070-6079.[12] 孔祥玉,王玉婷,袁枭枭,等. 基于定制遗传算法考虑配电网多种拓扑可观性的PMU 优化配置[J ]. 电力自动化设备,2020,40(1):66-72.[13] GHOSH K K , GUHA R , BERA S K , et al. S -shapedversus V -shaped transfer functions for binary manta ray foraging optimization in feature selection problem [J ]. Neural Computing and Applications ,2021,33(17):11027-11041.[14] YU Y , GAO S , CHENG S , et al. CBSO : A memeticbrain storm optimization with chaotic local search [J ].Memetic Computing , 2018, 10:353-367.[15] 张晓萌,张艳珠,刘禄,等. 融合多策略的改进麻雀搜索算法[J ]. 计算机应用研究,2022,39(4):1086-1091,1117.[16] 张岐山,文闯. 基于均衡接近度灰关联的增强二部图推荐算法[J ]. 计算机应用研究,2020,37(9):2620-2624.[17] CRUZ M A R S , ROCHA H R O , PAIVA M H M , et al.An algorithm for cost optimization of PMU and communication infrastructure in WAMS [J ]. International Journal of Electrical Power & Energy Systems , 2019,106:96-104.[18] 曹鹏,刘敏. 基于改进的整数规划法结合零注入节点的PMU 优化配置方法[J ]. 电力系统保护与控制,2021,49(16):143-150.(责编 曹东,校对 刘钊)迭代次数242628303234363840配置P M U 数图5 正常情况下IEEE -69节点系统仿真图Fig.5 Simulation diagram of IEEE -69 node system under normal conditions540。
2009-新息图法电力系统不良数据检测与辨识

新息图法电力系统不良数据检测与辨识张永超,黄彦全,宋廷珍,穆亚东(西南交通大学电气工程学院,四川成都 610031)摘 要:不良数据检测和辨识是电力系统状态估计的重要组成部分;所采用的新息图方法,结合动态和静态两方面理论,将具有具体物理意义的数据(新息向量),转化为虚拟假设条件下的等价表示,并利用基本的电路理论,达到检测和辨识坏数据以及拓扑错误的目的。
该方法具有模型简单、快速准确等优点。
以I EEE-14节点系统算例,初步验证了所提方法的有效性。
关键词:不良数据检测与辨识;新息图;拓扑错误Abstract:Detecti on and identificati on of bad data is one of the most i m portant parts of power syste m state esti m ati on.The in2 novati on graph technique based on dynam ic and static theory is p resented,which translates the material date(innovati on vec2 t or)int o an equivalent variable of another abstract domain f or detecting and identifying t opol ogy err or and bad data using the basic theory of circuit.This method is of si m p le model,s peediness and nicety,whose efficiency is verified by the examp le ofI EEE14.Key words:bad data detecti on and identificati on;innovati on graph;t opol ogy err or中图分类号:T M744 文献标识码:A 文章编号:1003-6954(2009)03-0014-02 在电力系统状态估计过程中,检测和辨识出不良数据,并消除其影响,从而为实时电力系统提供一个可靠的数据库,是状态估计器的一项非常重要的任务。
IEEE14节点电力网络分析

IEEE14节点电力网络分析《高等电力网络分析》—— IEEE14节点电力网络分析专业班级: 电力工程1403班姓名:学号: Z14050394同组成员:导师: 刘润华二〇一四年十二月第1章 IEEE14简介 ..................................................1 第2章汇报内容总结 (3)2.1 用支路追加法建立节点阻抗矩阵 (3)2.2 补偿法求网络方程的修正解(前补偿、中补偿、后补偿) (9)2.3 统一的网络分块解法 (14)第3章调节变比使中枢点电压控制在给定值 (21)第4章连续潮流法在静态电压稳定性分析和计算中的应用 (23)4.1连续潮流算法 (23)4.2连续潮流计算方法在静态电压稳定性的分析和计算中的应用 (24)4.3正确认识连续潮流及其对静态稳定分析的作用 (26)第5章课程总结....................................................27第1章 IEEE简介第1章 IEEE14简介本文选用14节点系统作为分析对象,绘制IEEE14节点标准试验系统图如图1.1所示:1651224111371038914图1.1 IEEE14系统图母线系统数据如下表格:表1.1 母线数据表节点号节点类型有功功率无功功率电压幅值电压相角并联电容 1 3 0 0 1.0600 0 0 2 2 21.7000 12.7000 1.0450 -4.9800 0 3 2 94.2000 19.00001.0100 -12.7200 0 4 1 47.8000 -3.9000 1.0190 -10.3300 0 5 1 7.60001.6000 1.0200 -8.7800 0 6 2 11.2000 7.5000 1.0700 -14.2200 0 7 1 0 01.0620 -13.3700 0 8 2 0 0 1.0900 -13.3600 0 9 1 29.5000 16.6000 1.0560 -14.9400 0.19 10 1 9 5.8000 1.0510 -15.1000 0 11 1 3.5000 1.8000 1.0570 -14.7900 0 12 1 6.1000 1.6000 1.0550 -15.0700 0 13 1 13.5000 5.80001.0500 -15.1600 0 14 1 14.9000 5 1.0360 -16.0400 01第1章 IEEE简介表1.2 支路数据表支路号发点收点电阻电抗电纳变比 1 1 2 0.01938 0.05917 0.0264 0 2 1 5 0.05403 0.22304 0.0246 0 3 2 3 0.04699 0.19797 0.0219 0 4 2 40.05811 0.17632 0.0187 0 5 2 5 0.05695 0.17388 0.0170 0 6 3 4 0.06701 0.17103 0.0173 0 7 4 5 0.01335 0.04211 0.0064 0 8 4 7 0 0.20912 0 0.97809 4 9 0 0.55618 0 0.9690 10 5 6 0 0.25202 0 0.9320 11 6 11 0.094980.19890 0 0 12 6 12 0.12291 0.25581 0 0 13 6 13 0.06615 0.13027 0 0 14 7 8 0 0.17615 0 0 15 7 9 0 0.11001 0 0 16 9 10 0.03181 0.08450 0 0 17 9 14 0.12711 0.27038 0 0 18 10 11 0.08205 0.19207 0 0 19 12 13 0.220920.19988 0 0 20 13 14 0.17093 0.34802 0 02第2章汇报内容总结第2章汇报内容总结2.1 用支路追加法建立节点阻抗矩阵1、部分网络部分网络是指所要分析的电网的一个连通子网络。
基于网络结构重要度和安全隐患脆弱度的配电网脆弱线路辨识

基于网络结构重要度和安全隐患脆弱度的配电网脆弱线路辨识孙顺祥;李晓明;张繁碧;史文超;郝超超【摘要】为了辨识配电网中的脆弱线路,提出一种基于网络结构重要度和安全隐患脆弱度的线路综合脆弱性评估模型.该模型一方面以复杂网络理论基本参数结合配电网的特点定义了线路的网络结构重要度指标,另一方面以负荷冲击和故障断线两种情况对系统安全运行造成的影响定义了线路的安全隐患脆弱度指标.通过层次分析法(Analytic Hierarchy Process,AHP)计算各指标的权重系数,从而综合反映线路的脆弱性.以IEEE33节点配电系统进行计算分析,验证了该线路综合脆弱度评估模型具有合理性和有效性.【期刊名称】《电力系统保护与控制》【年(卷),期】2018(046)014【总页数】7页(P107-113)【关键词】有功度数;改进介数;负荷冲击脆弱度;故障断线脆弱度;层次分析法【作者】孙顺祥;李晓明;张繁碧;史文超;郝超超【作者单位】武汉大学电气工程学院,湖北武汉 430072;武汉大学电气工程学院,湖北武汉 430072;广东电网公司惠州惠阳供电局,广东惠州 516211;武汉大学电气工程学院,湖北武汉 430072;武汉大学电气工程学院,湖北武汉 430072【正文语种】中文近年来,国内外频发的大停电事故引起了人们的广泛关注,以2003年美加大停电和2006年西欧大停电为例的诸多停电事故的发生严重影响到人们的正常生活,造成了巨大的经济损失[1-4]。
事故分析表明,大规模停电往往是由个别元件的相继故障开始,在事故的传播扩大阶段与电力系统中的脆弱环节有着密切的联系[5-8]。
因此,准确地辨识电力系统中的脆弱环节并采取相应的控制策略对提高电力系统的安全性、降低故障发生概率具有重要的意义。
文献[9-11]将复杂网络理论引入电力系统的脆弱线路辨识中,结合电力系统的实际特点对复杂网络理论的拓扑参数进行改进,从而分析识别出电网中的脆弱线路。
IEEE14节点潮流计算
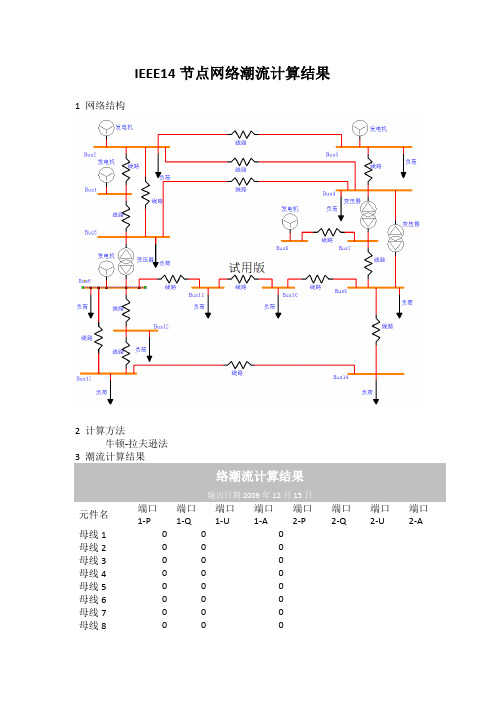
IEEE14节点网络潮流计算结果1 网络结构2 计算方法牛顿-拉夫逊法3 潮流计算结果络潮流计算结果输出日期:2009年12月15日元件名端口1-P端口1-Q端口1-U端口1-A端口2-P端口2-Q端口2-U端口2-A母线1000母线2000母线3000母线4000母线5000母线6000母线7000母线8000母线9000母线10000母线11000母线12000母线13000母线14000发电机10发电机20发电机3发电机40发电机50负荷100负荷200负荷300负荷400负荷500负荷600负荷700负荷800负荷900负荷1000负荷1100线路1线路2线路3线路4线路5线路60线路70线路8线路9线路10线路11线路12线路13-2E-16线路14线路15线路16线路17双卷变压器1双卷变压器2双卷变压器3FACTS技术的研究现状综述汪洋1012 电力系统及其自动化1柔性交流输电技术的时代背景众所周知,电力网络的输电可控性和发电、配电相比较差,网络中功率潮流的自然分布会随着负荷变化而变化,可能造成过大的电能损失或危及安全运行而被迫降低输送功率,从而造成已有输线的负担日益加重,输送能力不足的矛盾日益突出。
一般说来,电力网络的输电能力受到静态稳定、动态稳定、暂态稳定、电压稳定和热稳定极限的限制,其中前四种因素是限制电网输送能力的主要因素。
同时,由于一系列的社会、环境与经济方面的原因,限制了新的发电厂和输电网络的建设,这就使得电力系统在二十一世纪面临的主要问题之一就是:如何最大限度地提高电力设备的利用率、如何最大限度地提高输电网络的传输能力。
随着电力电子技术、计算机技术、控制技术的不断发展,电力工业技术也取得了许多新的进步,其中一个重大的成就就是柔性交流输电系统(FlexibleACTransmissionsystem,简称FACTS)的提出和应用。
柔性交流输电系统技术是目前电力系统新技术中最引人注目的方向之一,它为解决电力系统中存在的经济运行和安全稳定问题提供了有效的手段。
IEEE标准测试系统数据
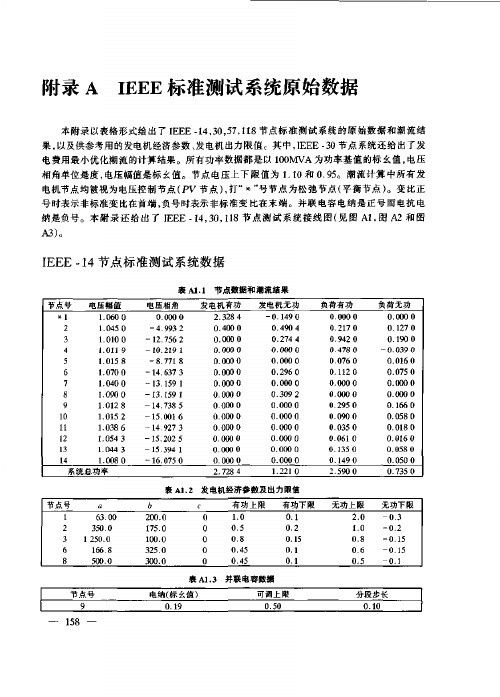
对地电纳 12
。但640
额定电流
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
1-2 2-3 2-4 1-5 2-5 3-4 4-5 7-8 7-9 9-10 6-11 6-12 6-13 9-14 10-11 12-13 l3-14
0.01938 0.046 99 0.058 11 0.05403 0.05695 0.06701 Q. 013 35
。 000
0.0320 0.0950 0.022 0 0.1750
。例lO O
。+刷70
。 .1120
0.000 0 0.000 0 0.000 0
0
。"翩。
。 .0160
。.()(胁。
O. 倒胁。
0.991 5 1. 017 1
1 凶69
28
29 30
0.997 2 0.985 6
系统总功率
-10.0866 -9.3952 -5.8249 -10. 剧03 -1 1. 5344
并联电容搬据
0.1 0.2 0.15 0.1 0.1
2.0 1. 0 0.8 0.6 。 .1
爱 A1. 3 咆纳(标么值)
可调上限
分段步长
9
一 158 一
0.19
0.50
0.10
裴 A1. 4 直路号首末瑞节点号 电阻
。。 。。 。。
lI:Bi器直路戴蟹
变比 变比上限 变比下限
电抗
额定电流
2 3
4-7 4-9 5-6
Q.209 12 0.556 18
。 .25202
0.978 0.%9 0.932
线路'监据
(完整word)IEEE-30节点系统数据

IEEE—30节点系统数据资料
图1 IEEE-30节点系统接线图IEEE-30节点系统节点数据和潮流结果
初始潮流状态下系统有功网损709(MW)
P=.
Loss
IEEE-30节点系统各线路数据
在潮流计算中,为了使修正方程式中的系数矩阵B’、B’'形成更加方便,更加符合C语言编程的特点,我们对系统中的30个节点重新进行编号。
编号从0开始,PQ节点最前,PV节点居中,平衡节点的编号最后。
重新编号对系统的潮流计算并没有影响,同时还可以简化计算程序。
重新编号后的系统数据资料
重新编号后各线路数据
(标记部分为4条变压器支路)
初始潮流状态下系统有功网损709(MW)
P=.
Loss。
