第四章仿射坐标与仿射平面

合集下载

仿射变换理论及其在几何中的应用

例2 试证明梅内劳斯(Menelaus)定理[3]:在的三边或其延长线上分别取三点则共线的充要条件是
(1.14)
证以为原点为坐标向量建立仿射坐标系如图五
若令则根据定比分点公式,有关点的坐标为
,
共线的充要条件是 ,而
所以的充要条件是
化简得 ,(1.14)式成立.
古希腊亚历山大里亚的数学家、天文学家梅内劳斯(公元98年左右),在其幸运的保留下来的三卷≤球面几何≥( )[4]中提出了着个定理.
1平面上的仿射坐标系与仿射变换
我们引进仿射坐标系：在平面上任取一点及两个不共线的向量
(不一定是单位向量，且不一定垂直的)这样我们就建立了仿射坐标系
如图1
对于平面上任一点，则向量可唯一地表示为
数组称为关于仿射坐标系的仿射坐标.
定理1.0 在仿射坐标系下，直线方程一定是关于仿射坐标系的一次方程
故
推论1 两个平行四边形面积之比是仿射不变量.
推论2 两个封闭图形面积之比是仿射不变量.
例1 求椭圆的面积(图4).
方法一:解在直线坐标系下,
椭圆
经仿射变换 (1.13)
变为圆
如图4,椭圆内经(1.13)对应为 ,其中 , , , 从而
即
于是,椭圆的面积为
方法二[2]:解化椭圆为参数方程
求得椭圆所围面积为
,
即共线.
定义1.1在平面上点之间的一个线性变换
（1.05）
叫做仿射变换，其中分别是的仿射坐标.
从仿射变换的代数表示可知平面内不共线的三对对应点（原像不共线，像也不共线）唯一决定一个仿射变换，称为仿射几何的基本定理.
例1 有公式所确定的变换表示分别沿轴与轴两个压缩变换的乘积，显然是一个仿射变换.

仿射坐标系

命题 1.2.2
设Pi ( xi , yi , zi ), i = 1,2, 则分线段PP2成定比（λ ≠ -1)的分点 λ 1 P的坐标是 x1 + λ x2 y1 + λ y2 z1 + λ z2 x= ,y= ,z = . 1+ λ 1+ λ 1+ λ
推论 1.2.1 线段PP2的中点坐标为 1
e3
O
e3
O
e1
e2
右手系
e2
e1
左手系
定义1.2.2 如果 e 1 , e 2 , e 3是两两垂直的单位向定义量，则 {O; e1 , e 2 , e3 } 称为直角标架或直角坐标系直角标架或直角坐标系. 直角标架或直角坐标系直角标架是特殊的仿射标架。点（或向量）在直角标架中的坐标称为它的直角坐标，在仿射标架中的坐标称为它的仿射坐标。注：如果 e , e , e 仅是两两垂直的向量，则 1 2 3
一标架、向量和点的坐标标架、
u ur ur r 空间中任一三个有次序的不共面的向量组e1 , e2 , e3 称为空间的一个基.根据定理11 2，对于空间中任 .. r 一向量a, 存在唯一的数组（x, y, z），使得 r u r ur ur a = xe1 + ye2 + ze3 , r u ur ur r 我们把有序的三元实数组（x, y, z）称为a在基e1 , e2 , e3 r 下的坐标，记为a = x, y, z）. （在空间中任意取定一点O，则任意一点M 与向量 uuuu r uuuu r OM 一一对应，我们把向量OM 称为点M的位置向量（或径矢）.
{O; e1, e2 , e3} 称为为笛卡儿标架。
例

保距变换和仿射变换

sin
cos

y

a
sin

b
cos

: px, y p"
x", y"

p'
x', y'
则στ的公式为：由
x' 1

y'

0
cos sin
0 x" a 1
1
y"

τσ:P(x,y)

P″(x″,y″)

P'(x',y'),则τσ的公式为：，
x' cos sin x cos sin x a

y'

sin
cos

y

sin
cos

y

b
cos sin x a cos bsin
(1)恒等1变换GI,∈ 2G; G, 1 2 G;
(2)若
，则 1 G.
(3)若σ∈G,则它的逆变换
。
则称G为S的一个变换群。
保距变换在§1中我们介绍了平面上的三种点变换:平移、旋转和反
射。它们有一个共同的特点:保持点之间的距离不变。定义1.３平面上的一个点变换,如果保持点之间的距离不变,

b
A1 , A2 , A3
由于
不共线,所以行列式
x1 y1 1
x2 y2 1 0,
x3 y3 1
因此,以上两个方程组有唯一解 a11 , a12 , a和a21 , a22 , b.

仿射变换原理解析

详细描述
平移仿射变换涉及将图形在二维平面内沿某一方向进行移动，而不改变图形之间的相对位置和形状。这种变换通常由一个平移矩阵表示，其中包含平移向量和单位矩阵。平移向量决定了图形移动的距离和方向。
旋转仿射变换
总结词
旋转仿射变换是围绕某一点旋转图形，同时保持图形之间的相对位置和形状不变。
详细描述
旋转仿射变换涉及将图形围绕某一点进行旋转，同时保持图形之间的相对位置和形状不变。这种变换通常由一个旋转矩阵表示，其中包含旋转角度和旋转中心点坐标。旋转角度决定了图形旋转的角度，而旋转中心点坐标决定了旋转的基准点。
缩放仿射变换
总结词
缩放仿射变换是改变图形的大小，同时保持图形之间的相对位置和形状不变。
详细描述
缩放仿射变换涉及将图形的大小进行缩放，同时保持图形之间的相对位置和形状不变。这种变换通常由一个缩放矩阵表示，其中包含缩放因子和缩放中心点坐标。缩放因子决定了图形缩放的程度，而缩放中心点坐标决定了缩放的基准点。
03
图像校正
通过仿射变换，可以将倾斜的图像进行校正，使其恢复水平或垂直状态。
图像拼接
在图像拼接过程中，可以使用仿射变换将多张图像进行对齐，实现无缝拼接。
特征点匹配
通过仿射变换，可以将不同视角下的图像进行对齐，便于特征点匹配和计算。
计算机图形学中的仿射变换
3D模型渲染
在3D模型渲染过程中，可以使用仿射变换对模型进行旋转、缩放和平移等操作，以实现各种视觉
THANKS.
仿射变换的基本性质
仿射变换不改变图形间的相对位置和大小关系，即保持平行性和等比例性。
仿射变换可以分解为一系列基本变换的组合，如平移、旋转、缩放等。
仿射变换可以保持直线的性质，如直线的平行性和垂直性。

仿射变换

§3 仿射对应
1. 仿射对应图形表示
ÖÐÎ çÑô¹ ß âÏ
代数表示
ÔçÉÏ Ñô¹ ß âÏ
B0 A0
0
C0 B
1
1 1
2
C B' C' A'
µØÃæ
2 11
A

Ç½ ±Ú
仿射对应：有限个平行投影的积称为仿射对应。仿射变换：从平面到自身的仿射对应称为仿射变换。
2 31 4 ( ABC ) 。 2 ( 1) 3 2 1 3
D A C E B
4. 仿射变换的代数表示如图, OP OO OP , 另一方面, OP xe1 ye2 , 所以 xe1 ye2 OO OP 。 OO x 0 e1 y0 e 2 又
。
例2 试确定仿射变换, 使 y 轴, x 轴的象分别为直线 x + y + 1 = 0,
x – y – 1 = 0，且点 (1, 1) 的象为原点。
解：设
hx x y 1, ky x y 1
将 (1, 1) 变为 (0, 0) 得 h = 1 , k = –1，所以
x a x c 1 ( 1) 2 , x b x c 2 ( 1) 3
( ABC )
ya yc 2 0 2 ， yb yc 3 0 3
2 。 3
所以A、B、C三点共线，所以
例2 已知A(1, 1), B(–1, 2), 直线AB交直线2x + 3y – 1 = 0于C，求 (ABC) 。解：
仔细观察下列各图:
A A0 A' B'
B B0 C'

仿射变换.

换的定义有
| AB | | BC || AC | | A' B ' | | B 'C ' || A'C ' | .
即A', B', C'仍然为共线三点且B'在A', C'之间. 若A, B, C不共线, 则必有
| AB | | BC || AC | | AB | | BC || AC |
即A', B', C'仍然为不共线三点.
x y
' '
a11x a21x
a12 a22
y y
a13 a23
或
x' y'
a1
a13 a23
.
(1.1)
其中(x, y)与(x', y')为的任一对对应点P, P'的坐标, 矩阵
A
a11 a21
a12
a22
称为的矩阵, 满足AAT=ATA=E, 为二阶正交矩阵.
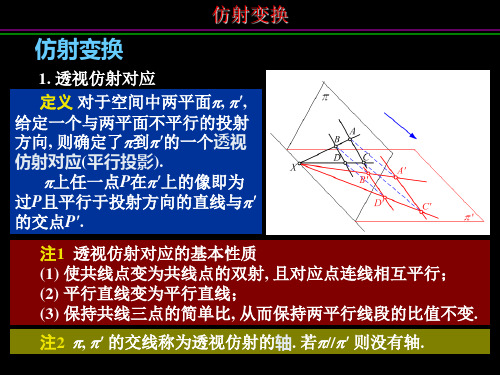
注. 仿射变换的基本性质 (1) 使共线点变为共线点的双射； (2) 平行直线变为平行直线； (3) 保持共线三点的简单比, 从而保持两平行线段的比值不变.
仿射变换
定义设为平面上的一个点变换, 满足 (1) 为一个使共线点变为共线点的双射； (2) 使得共线三点的简单比等于其对应共线三点的简单比； (3) 使得相互平行的直线变为相互平行的直线, 则称为上的一个仿射变换.
注对于正交变换的矩阵A, 显然有A1=AT, 且|A|=1.
x
OPx OEx
( Px ExO)
y
OPy OEy
(PyEyO)
uuur OP xex yey.

仿射坐标系

• 向量的线性相关和线性无关--几何理论引发的代数革命
• 观察：几何中向量的几种关系 • 代数学的革命也因为这些熟悉的向量关系就此展开。
空间几何向量引发的思考
• 在空间几何中，从原点出发的几个向量会出现以下几种情况。 1，两个向量 , 共线 2，两个向量 , 不共线
3，三个向量 , , 共面 4，三个向量 , , 不共面 • 当是否共线的几何现象通过解析几何出现在代数学中时，引出了代数学最重要的概念：相关和无关
向量的线性相关和线性无关
引言
• 自从笛卡尔发明了坐标系以后，几何中的点和向量被一组有顺序的数（x，y）表示了出来，几何图形也可以用代数形式来表示，经典的几何问题瞬时变成了代数方程问题，几何学与代数学从此架起了一座桥梁—解析几何，使几何学与代数学合为一家人。
• 但几何思想与代数思想的融合并没有就此结束，古典几何思想沿着解析几何这座桥梁，不断的向代数学输送着给养，学科之间的交点意外的为代数学带来了革命性的改变。
代数中的不共线和不共面
• 反之： 2，两个向量 , 不共线，则不存在不全为零的 k1 , k2 使得 k1 k2 0 我们说如果有 k1 k2 0 则 k1 k2 0
4，三个向量 , , 不共面，则不存在不全为零的 k1 , k2 , k3 使得 k1 k2 k3 0 我们说如果有 k1 k2 k3 0 则 k1 k2 k3 0
则 1, 2 , 3 , 4 线性相关。容易看出： 1, k2 , k2 , k3 于是有 1 2 3 4 0 而又因为系数不全为零，则1, 2 , 3 , 4 ，线性相关。 • 例三：观察空间4向量的相关性由于红色向量能被三条蓝色向量表示出则 k11 k2 2 k33 1, k2 , k2 , k3 于是根据之前的例子，存在不全为零，于是他们线性相关

保距变换和仿射变换

第四章保距变换和仿射变换本章教学目的：通过本章的学习，使学生掌握保距变换和仿射变换这两类重要的几何变换，从而深化几何学的研究，并掌握解决几何问题的一个有效方法。

本章教学重点：（1）保距变换和仿射变换的定义和性质；（2）仿射变换的基本定理；（3）保距变换和仿射变换的变换公式；（4）图形的仿射分类与仿射性质。

本章教学难点：仿射变换的性质和基本定理；仿射变换的变换公式的求法。

本章教学内容：§1 平面的仿射变换与保距变换1.1 ――对应与可逆变换集合X 到集合Y 的一个映射f:X →Y 是把X 中的点对应到Y 中的点的一个法则，即∀x ∈X ，都决定Y 中的一个元素f(x)，称为点x 在f 下的像。

对X 的一个子集A,记f(A)={f(a)|a ∈A} ，它是Y 的一个子集，称为A 在f 下的像。

对Y 的一个子集B ，记 f -1(B)={x ∈X|f(x)∈B},称为B 在F 下的完全原像，它是X 的子集。

如果f 是X 到Y 的映射，g 上Y 到Z 的映射，则它们的复合上X 到Z 的映射，记作 g f: X →Z ，规定为g f(x)=g(f(x)), ∀x ∈X.对A ⊂X ，g f(A)=g(f(A));对C ⊂Z,(g f)-1(C)=f -1(g -1(C)).映射的复合无交换律，但有结合律。

映射f: X →X 称为X 上的一个变换，id X : X →X ，∀x ∈X ，id X （x ）=x ，称为X 的恒同变换。

对映射f: X →Y ，如果有映射g: Y →X,使得g f= id X ：X →X ，f g=id Y ：Y →Y ，则说f 是可逆映射，称g 是f 的逆映射。

如果在映射f: X →Y 下X 的不同点的像一定不同，则称f 是单射。

如果f(X)=Y ，则称f 是满射。

如果映射f: X →Y 既是单射，又是是满射，则称f 为——对应。

此时∀f -1 f=id X,, f f -1= id Y ,于是f 是可逆映射，并且f 的逆映射是f -1。

高观点下的中学数学第四章仿射变换在初等几何证明中的作用

一、必做作业1．用仿射几何与初等几何两种方式证明以下各题：1）过的极点任作一条直线，与边及中线别离交于点及，求证．证明1(初等几何)：过点B作CF∥BH,并延长AD交HB于点G.因为CD=DB,易患四边形CFBH为平行四边形，从而取得ED=DG;由平行线分线段成比例，那么AE:EG=AF:FB,又EG=2ED,因此AE:2ED=AF:FB,即AE:ED=2AF:FB.证明2（仿射变换）成立仿射坐标系：A(0，0),B(b，0)，C(0，c)那么D(b/2,c/2),下面设CF:y=kx+c,别离求E和F的坐标。

因为AB:y=0，从而取得F(-c/k,0),AD:cx-by=0.与CF联立，得E(bc/(c-kb),c2/(c-kb))AF:FB=-c/k:((b+c/k)=-c/(kb+c),AE:ED= bc/(c-kb):[ b/2-bc/(c-kb)]=-2c/(kb+c)因此AE:ED=2AF:FB.2）（梅耐劳斯定理）设别离在的边及（或延长线）上，求证：三点共线的充要条件是证明：如图，成立仿射坐标系：以BC为x轴，以BA为y轴，B(0，0),C(a,0),A(0，b)，M(x0,0),L(0,y0)，那么直线AC的方程为：1x ya b+=，直线ML的方程为：001x yx y+=，联立上述方程，可求得N点坐标为（00000000()(),ax b y by b ybx ay bx ay----）。

000000000000000000000000()(),,()()()==1()ax b yab y x bx ay y x aAL BM CNax b yLB y MC x a NA x b ybx ayb y x y x aAL BM CNLB MC NA y x a x b y-----====------⋅⋅--所以，故本题结论得证3）已知中，是边上的中点，是上的任一点，连结并延长交于，连并延长交于，求证//．证明：如图，延长AD至K使得DG=DK,由于BD=DC,因此四边形BKCG为平行四边形，因此进一步取得FG∥BK,KC∥GE,在△ABK和△AKC中，依照平行线分线段成比例知：=,,=AF AG AE AG AF AEFB GK EC GK FB EC=从而，所以FE∥BC2．利用“圆的仿射变换像是椭圆”这一结论，试将与圆有关的一些结论移植到椭圆上去，并给出证明．。

高等几何仿射坐标与仿射变换

a 11
原象点： A,B,C,D…… 直线a上的点
映象点：A, B,C, D…… 直线上 a 的点平行射影的方向：直线 l
记透视仿射对应T： T A A,T B B ………
透视仿射对应与方向有关，方向变了，则得到另外的透视仿射
对应
D
a
C
l
A
B
O A B C D
a
点 O 为自对应点( 同一平面上两相交直线的公共点 ) 12
CB
10
二.两直线间透视仿射对应、仿射对应与仿射变换
1..两直线间的透视仿射对应
≠ ≠
点若A直,B线,C,aD,…a… a，,l过点A,B,且C,Dl…作a直线, ll的平行a线交, a于
A, B,C, D……，则可得直线 a 到直线 a的一个映射。
称为透视仿射对应，记为 T D
a
l AB C
A B C D
1.透视仿射对应：如图
点A,B,C共线a，则 A, B,C 共线 a
T A A T B B T C C g
C a l
B A
T a a
A B
两相交平面的交线为自对应点的集合即对应轴 C
a
15
第一章、仿射坐标与仿射变换如图
16
2仿射对应：平面到平面的仿射对应是有限次透视仿射对应的积组成的，是透视仿射对应链。
2.两直线间的仿射对应
T Tn T 1 n2
T2T1
仿射对应是透视仿射对应链或平行射影链
T1,T2, Tn2 ,Tn1 表示透视仿射链，T表示仿射对应（如图）
A1
B1
C1
A2
B2
C2
l2
A3 B3
C3

仿射坐标系在中学几何中的应用

仿射坐标系在中学几何中的应用1.建立仿射坐标系来解决初等几何问题对于仿射性质的几何命题，建立直角坐标系不易求解，可考虑建立直角坐标系，由于仿射坐标系两坐标轴的夹角及单位点的选取，都比直角坐标有较大的任意性，因此在仿射坐标系下常常可以非常便利，可避免一些繁琐的三角运算，起到柳暗花明的功效.建立仿射坐标系的一般方法如下：1、坐标轴的选取要尽量利用图中已有的直线和已知的点.2、单位点的选取可以在x 轴上取一已知点坐标设为（1,0），y 轴上取一已知点坐标设为（0,1）.3、x 轴上及y 轴上其它的已知点可设为（a,0）和(0,b).4、直线Ax+By+c=0上的点的坐标设定要满足此直线方程.5、过两已知点A 、B 直线上的点的坐标也可设为A B λ+.6、x 轴上的两线段（或平行x 轴的线段）之比值可用端点x 坐标的差之比表示，y 轴上的两线段（或平行y 轴的线段）之比值可用端点y 坐标差之比表示.1.1 线段间的比例问题例1．证明三角形中位线定理图4证明如图4所示AOB ∆中，123,,E E E 分别为OA,OB,AB 的中点，建立仿射坐标系12O e e -，使1122,e OE e OE ==，则A ，B 的坐标分别为（2,0），（0,2）.因为3E 坐标为02021,122x y ++====，既3E （1,1）.由直线23E E 与直线OA 的斜率相等为21210y yx x -=-,知23E E ||OA.又23212311,202,2E E x x OA E E OA =-==-==可知. 例2．在ABC ∆中,E 在AC 上，D 为BC 中点.E 、D 交AB 于F ，则AE AFCE BF=.图5证明：以AB 为x 轴，AC 为y 轴，A 为原点，建立仿射坐标系（图5）.设坐标B （1,0），E （0,1），C （0，b ）.则BC 中点D 坐标为（0.5,0.5b ），得出直线ED 的方程为y=（b-2）x+1，和x 轴联立得交点F 坐标为（1,02b-），可推出：110112,111102AE AF b EC b b BF b b ---====----- 可见用仿射坐标系来解此题多么方便.1.2 关于图形面积问题若已知三角形三顶点坐标1122(,),(,),(,A x yB xy C x y .则112233x y 11=x y 12x y 1ABC ∆的面积的绝对值例3．在ABC ∆的三边AB ，BC ，CA 上各取AZ ，BY,CZ 各等于该边的23，求证面积13S XYZ S ABC ∆∆=.图6证明：如图6,取B 为原点，BC 为x 轴，BA 为y 轴建立仿射坐标系，设A （0,3）.C(3,0).从而知Y （2,0）.Z(0,1).据定比分点公式Z （1,2）.所以0311900122301S ABC ∆==.0111320122121S XYZ ∆== 所以 13S XYZ S ABC ∆∆=1.3 关于点共线和直线共点的问题要证三点112233(,),(,),(,)A x y B x y C x y 共线，可证1122331101x y x y x y =，也可证AB BC λ=.要证三直线0i i i A x B y C ++=（i=1,2,3）共点.可证1112223330A B C A B C A B C =.若123i 123,,0i i M M M x B y C SM SM SM ++===分别是三直线A 上的点，也可以证明.（点S 一般可以是原点，也可以是其它的点）.（4）如图7.设在ABC ∆的三边各取一点L 、M 、N,则L 、M 、N 共线的充要条件是:1AN BL CMNB LC MA⨯⨯=-图7证明：建立仿射坐标系{;,}B BC BA ，则B(0,0),A(0,1),C （1,0），设L 、M 、N 分有向线段BC 、CA 、AB 的比分别为v λμ、、.则1(,0)M(,))11+1L λμλμμν++1、、N(0,1+ 所以111(,),(,)11111LN LM λλλνμλμ=-=-+++++.故L 、M 、N 三点共线的充要条件是LM LN 与共线.即111()011111λλλμνμλ-⨯-⨯-=+++++ 化简得AN CM-1,= -1NB MABL LC λμν=⨯⨯也就是例4．证明对于任意梯形两底的中点、两对角线的交点及两腰的交点4点共线.图8证明：设ABCD 为任意梯形，其中AB//CD ，P 为两腰交点，M,N 分别为两底的中点，如图8建立仿射坐标系，则下列各点的坐标分别为A(0,0)，B （1,0），C （c,1），D （0,1），M （0.5,0），N （0.5c ，1），直线AP ，BP,AC,BD 的方程分别为：AP ：x=0 BP ：x+（1-c ）y=1 AC ：x-cy=0 BD ：x+y=1于是AP ，BP 的交点P 坐标为10,1c ⎛⎫ ⎪-⎝⎭;AC 与BD 的交点Q 的坐标为1,11cc c ⎛⎫ ⎪++⎝⎭.直线MN 的方程为： 2x+（1-c ）y=1 （1）而点P,Q 的坐标满足方程（1），故M,N,P,Q ，4点共线例5．用坐标法证明四面体对棱中点的连线交于一点.证明：设四面体ABCD(图9)的棱AB ，AC ，AD ，BC ，CD ，DB 的中点分别为''',,,,,B C D E F G .取仿射标架{;,,}A AB AC AD ，则各点的坐标分别为图9 A （0,0,0），B （1,0,0），C （0,1,0），D （0,0,1）'''111,0,0,0,,0,0,0,,222B C D ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111111,,0,0,,,,0,.222222E F G ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭假设'D'E B F 与交于P(x,y,z)，设'',,B P kPF D P lPE ==则P 的坐标为111000222,,111k k k x y z k k k+⋅+⋅+⋅===+++ 111000222,,111l l l x y z l l l+⋅+⋅+⋅===+++ 解得k=l=1，从而交点P 存在，且P 的坐标为111,,.444⎛⎫⎪⎝⎭设'',B F C G '与交于P 同理可得'111,,,444P ⎛⎫⎪⎝⎭所以P 与'P 重合，即''',,B F D E C G 交于一点.1.4 关于向量的线性关系问题若已知()()111111A ,,,,x y z x y z 和B 两点.而在AB 直线上的点M 分有向线段AB 为两部分AM MB 、，使它们的值的比等于某数()1,λλ≠即,AMMBλ=可求出分点坐标121212,,.111x x y y z z M λλλλλλ+++⎛⎫ ⎪+++⎝⎭当M 为中点时，M 的坐标为121212,,.222x x y y z z +++⎛⎫ ⎪⎝⎭例10．在ABC ∆中，,OA a OB b ==.点M 、点N 分别在AB 、OA 上，且AM ：MB=2:1，ON ：NA=3:1，OM 与BN 交于点P ，用b a 、表示OP .解：建立如图10所示仿射坐标系.则A （1,0），B(0,1).图10由AM ：MB=2:1.ON:NA=3:1,及定比分点坐标公式.可得123(,),(,0)234M N .则直线OM 、BN 的方程分别为：20,4330x y x y -=+-= 设P(x,y).联立方程组，得33.105x y ==故33105OP a b =+ 例7. 如图11所示平行四边形ABCD 中，M 为DC 中点.N 为BC 中点.设AN ;AB b AD d AM m n ====、、、（1）以b d 、为基底，表示MN ；（2）A 以n m 、为基底表示AB图11解（1）建立仿射坐标系{;,}A b d.则A（0,0），D（0,1）,B(1,0),C(1,1),由中点坐标公式.得1111(,1),(1,).MN=-2222M N所以（，）即得11MN=b-d22（2）由（1）得11(,1),(1,).22 AM AN==即12m AB AD=+12AB AD=+n反解得4233 AB n m =-2.建立仿射坐标系在数学解题中的几点注意事项建立仿射坐标系不是所有题目都能用此方法解题而是要在解题过程中对题目进行合理有效的分析。

仿射变换仿射平面与投影变换平面

仿射平面与投影平面第一章仿射几何学本章内容的安排在于揭示一种思想方法，从观察到概念形成到不变量系统再到代数系统，这种安排思想也充分反映了历史上射影几何建立过程中综合方法与解析方法各有所长交替作用互相影响的发展历程。

本节研究的内容来自于生活、自然与生产建设实践，如正交变换是从研究我们生活空间中物体位置改变的最简单的情形移动、转动和镜面反射开始的，仿射变换则是从太阳光的照射开始的。

因此在本章的学习中应注重于培养观察能力。

《数学发现的艺术》中是这样描述“观察”与“归纳”的：“观察是有意知觉的高级形式，它与有意注意结合在一起，与思维相联系。

怎样进行观察？需要注意三点：一是有意识、有目标，处处留心，总想‘找岔儿’，从中发现点什么，否则就会熟视无睹，看等于不看；二是要有基础，有必要的相关知识，否则难以看出‘门道儿’，而只能是‘外行看热闹’；三是要有方法，否则就看不到‘点子’上，抓不住要领。

在观察中，要特别注意从个别想到一般，从平常中发现异常”；而“归纳是由个别事例向关于这一类事物的一般性的过渡，是一种对经验、以实验观察结果进行去粗取精、去伪存真的综合处理方法。

人们用归纳法清理事实，概括经验，处理资料，从而形成概念，发现规律”。

通过本章学习，首先对观察、归纳应该有一个较为深刻的认识，为在以后的学习中能熟练应用观察而打下良好的基础，其次对数学研究的目标之一——对象的结构——有一个初步的了解。

1213§1 正交变换本单元分两个部分介绍正交变换，其一是解析几何中坐标变换的复习，主要通过讨论刚体运动中的特例——平移、旋转和反射，揭示其中最基本的不变量——距离，进而提炼出正交变换的概念。

其二是利用不变量系统建立相应的坐标系，从而引入解析法，用代数方法解决正交变换的结构问题。

一、基本概念实例 (a) 平移是沿一定的方向推移物体的过程，建立适当的坐标系，就有平移0X l ： îíì+=¢+=¢00y y y x x x ，即 0X X X +=¢； (b) 旋转是物体绕着固定点转动的过程，建立适当的坐标系，就有旋转q r ： îíì+=¢-=¢qq q q cos sin sin cos y x y y x x ，即 X X ÷÷øöççèæ-=¢q q q q cos sin sin cos ；(c) 反射是关于一条固定直线的对称，建立适当的坐标系，就有反射x r ： îíì-=¢=¢y y x x ，即 X X ÷÷øöççèæ-=¢1001。

高等几何讲义第一章欧氏平面及仿射平面上的变换仿射坐标及仿射坐标变换

§1 变换与变换群
• 4．变换群
• 若集合 S 上的某些变换构成的集合 G 满足条件： 1. G 中任二变换的乘积仍属于 G ； 2. G 中每一变换 T 的逆 T 1也属于 G ，则称 G 为集合 S 上的一个变换群．
• 由定义知：任何变换群一定包含恒等变换．
• 可以证明：平面上绕定点 O 的旋转变换的集合 G 是一个变换群，称为旋转群．记为 G1 ．
|OM/| |OM|，MOM/
的点变换称为以 O 为中心的旋转变换，简称
旋转，记为R ．其表达式为：y M/
R
：
x/ y/
xcos ysin xsin ycos
(1.3)
j
oi
M x
§1 变换与变换群
• 例4．镜射变换对平面上的定直线，使原象点 M与象点M/之间的线段被垂直平分的点变换称为以为轴的镜射变换，简称镜射．建立如图坐
主要内容
欧氏几何仿射几何射影几何
第一章：欧氏平面及仿射平面上的变换，仿
射坐标及仿射坐标变换
本
重点讨论共点性与共线性
教材基
射影几
第二章：射影平面的定义，射影坐标，交比，调和共轭，对偶原理第三章：射影变换，包括透视、一维射
本框架
何
影变换、直射、对射、配极第四章：配极与二次曲线、一维射影变换与二次曲线、二次曲线的射影分类
标系，则其表达式为： y
Mox： xy//
x
y
(1.4)
M
j
Oi
x
M/
§1 变换与变换群
• 例5．平行射影二平面
、 / 交于直线，向量
M
与二平面都不平行．对

仿射变换原理解析ppt课件

若位似中心的坐标为C(c1, c2), 则(1.8)可化为 y x '' k k y x a a 1 2 3 3 或 x y '' k 0k 0 x y a a 1 2 3 3
( 1 .9 )
一个一般的位似变换是一个以原点为中心的位似与一个平移的积, 若k1则为平移, 故平移是特殊的位似.
仿射变换仿射变换仿射坐标系定义设在平面上取定一点o和以o为起点的两个线性无关向量则由此构成平面上一个仿射坐标系或仿射坐标架记作o平面上任一点p的仿射坐标xy由下式唯一确定opxeye反之对任意给定的有序实数偶x112式可唯一确定仿射平面上的一个点具有坐标x建立了仿射坐标系的平面称为仿射平面为单位正交向量则oepeooeoppeooe仿射变换仿射变换点变换为上的一个仿射变换有表达式111213131112212223232122的坐标矩阵11122122满足a0称为仿射变换的矩阵
.
几种特殊的仿射变换
2. 相似变换
定义设为上的一个点变换, P, Q为上任意相异二点, (P)P', (Q)Q'. 满足
P 'Q ' k (0 k R 为常数 ) (1 .1 0 ) P Q 则称为上的一个以k为相似比的相似变换.
注. 相似变换的基本性质 (1) 保持共线三点的简单比不变. (2) 使得任意图形变成其相似图形; 使平行直线变为平行直线. (3) 保持任意两条线段的比值不变. 从而保持两直线夹角不变. (4) 正交变换、位似变换都是其特例.
其中(x, y)与(x', y')为任一对对应点P, P' 的坐标, 矩阵
A
a11 a21
a12
a22
满足|A|0, 称为仿射变换的矩阵.

第四章仿射坐标系剖析

由上的定义可知，仿射对应是由有限次透视仿射对应组成
的，所以仿射对应是透视仿射对应链，透视仿射对应是最简单的仿射对应。而一个仿射对应是否是透视仿射对应，只需看两对对应点的连线是否平行。
由于仿射对应(变换)可以理解成为一个透视仿射对应链，所以不难证明仿射对应(变换)的下列性质：
(1) 保持同素性和结合性；
，则系数
叫做三点 P1，P2，P
1
的简单比(简称单比)，记为
2
(P1P2 P) ，其中点 P1，P2 叫做基点，点 P 叫做分点。
由定义可知，若 P1P，P2P是有向线段，则单比
显然，当点
(P1P2 P)
P1P。 P2 P
在P点 P1，P之2 间时，单比 (P1P2 P) ；0 否则
当点与P点 P重1 合时，单比 (P1P2 P) 0
于点A’,B‘,C’, ... ，这样便得到
了一个平面上的点到另一个平面上
的点之间的一个一一对应，叫做两
个平面间的平行射影或透视仿射对
应，如左图所示，这个平行射影记
为
，则有
( A)
A'，(B)
B '，
显然，如果两个平面交于直线 n，则直线 n 上的每一个点都是平行射影下的自对应点，我们把直线 n 叫做自对应直线，也叫做透视轴，简称轴。
平行射影(透视仿射对应)的推广
这个对应叫做直线 a1 到直线 an 的仿射对应，记为，于是有 n1n221 。
特别地，当直线 a1与 an 重合时，则把 a1到 an 的仿射对应叫做直线 a1 到自身的仿射变换。
特别地，当平面与1
到1 自身的仿射变换。
n重合时，则把到1 的n 仿射对应叫做平面

第四章仿射几何学2013.2.20

第四章仿射几何学本章用射影观点介绍平面仿射几何学的基础知识。

§1仿射几何的内容仿射群1·1 仿射平面第一章所讲的欧几里得观点,认为平面上有一条与众不同的特殊直线,叫做无穷远直线。

而射影观点则对平面上所有直线都同等看待,不存在什么特殊直线。

这是两种截然不同的观点。

现在我们采用同这两个极端的观点相区别的折衷观点来研究平面,这时的对象不是欧氏平面,也不是射影平面,而是仿射平面。

仿射平面的定义是：定义在射影平面上指定一条直线ζ,称为无穷远直线。

除无穷远直线ζ上的点以外,所有射影点的集合称为仿射平面。

记作ωa 。

对于这个定义有两种解释：1、在射影平面上任意画一条直线ζ,作为无穷远直线,但ζ上的点都不属于仿射平面。

2、在射影平面上任意画一条直线ζ,作为无穷远直线,然后把直线ζ挖掉,或者说沿着直线ζ把射影平面切开。

在仿射平面上可以建立平行的概念。

在第一种解释下,平行线是相交于ζ上的直线,在第二种解释下,则是永远不相交的直线。

直线ξ通常总取它作为δ3,即x 3=0,用第一种解释,ωa 上每一个点都与x 3=0上的点不同,而x 3=0上的点的第三个坐标都是0,其它点都没有这个性质,所以仿射平面ωa 上每个点的第三个坐标都不是0,因而可以用(x 1,x 2,1)来表示。

数x 1和x 2称为点的仿射坐标。

因此,(x 1,x 2)就表示一个仿射点,它的意思就是射影点(x 1,x 2,1)。

对应于仿射平面的两种解释,仿射坐标系就有两种形式,如图4·1所示图4·1(a)中,把δζ3~(x 3＝O)画成虚线,表示这条直线上的点不算是仿射平面上的点。

沿直线x 3=0把射影平面切开,就得到图4·1(b)的形式。

这两种形式,在研究问题时都可图4.1（a ）图4.1（b ）采用,视其方便而定。

但是,通常说的仿射坐标系,都是指第二种形式而言的。

它与笛卡尔斜坐标系很有点象,实际上两者是大不相同的,在仿射坐标系里,点的仿射坐标是纯粹的数,与角度和长度无关,而笛卡尔坐标系则是以线段的长(或者结合角度)为依据的。

第四章仿射坐标与仿射平面

仿射变换理论及其在几何中的应用

仿射坐标系

保距变换和仿射变换

仿射变换原理解析

仿射变换

仿射变换.

仿射坐标系

保距变换和仿射变换

高观点下的中学数学第四章仿射变换在初等几何证明中的作用

高等几何仿射坐标与仿射变换

仿射坐标系在中学几何中的应用

仿射变换仿射平面与投影变换平面

高等几何讲义第一章欧氏平面及仿射平面上的变换仿射坐标及仿射坐标变换

仿射变换原理解析ppt课件

第四章 仿射坐标系剖析

第四章 仿射几何学2013.2.20

第四章仿射坐标系剖析

第四章仿射几何学2013.2.20