高中数学-三角函数图像及性质与值域及最值
三角函数的图像与性质

抓住1个考点
突破3个考向
揭秘3年高考
求较为复杂的三角函数的单调区间时,首先化简 成y=Asin(ωx+φ)形式,再求y=Asin(ωx+φ)的单调区间,只
需把ωx+φ看作一个整体代入y=sin x的相应单调区间内即
抓住1个考点
突破3个考向
揭秘3年高考
两种方法 求三角函数值域(最值)的两种方法
(1)将所给函数化为y=Asin(ωx+φ)的形式,通过分析ωx+φ
的范围,结合图象写出函数的值域; (2)换元法:把sin x(cos x)看作一个整体,化为二次函数来解 决.
抓住1个考点
突破3个考向
揭秘3年高考
考点自测 1.函数
).
抓住1个考点
突破3个考向
揭秘3年高考
1 1-cos 2x 1 1 解析 f(x)=sin x-2= -2=-2cos 2x, 故函数 2 的最小正周期为 T=π,且为偶函数.
2
答案 D
抓住1个考点
突破3个考向
揭秘3年高考
3.(2013· 安顺模拟)已知函数
π f(x)=sinωx+3(ω>0)的最小正
抓住1个考点
突破3个考向
揭秘3年高考
π 5π 在[0,2π]内,满足 sin x=cos x 的 x 为4, 4 ,再结合正弦、余 弦函数的周期是 2π,所以原函数的定义域为
π 5π x2kπ+ ≤x≤2kπ+ 4 4 ,k∈Z.
法二
利用三角函数线,如图,MN 为正弦线,OM 为余弦
解.
(2)求解三角函数的值域(最值)常见到以下几种类型的题目: ①形如y=asin x+bcos x+c的三角函数化为y=Asin(ωx+φ)+ k的形式,再求最值(值域); ②形如y=asin2x+bsin x+c的三角函数,可先设sin x=t,化
正弦函数和余弦函数的图像与性质

例2.求下列函数的最大值与最小值,及取到最值 时的自变量 x 的值. (2) y 3sin x cos x (1) y sin(2 x )
4 解:(1)视为 y sin u , u 2 x 4
8 3 当 u 2k ,即 x k , k Z 时, 2 8 ymin 1 2
二、正弦函数与余弦函数的周期
对于任意 x R 都有
sin( x 2k ) sin x, k Z cos( x 2k ) cos x, k Z
正弦函数是周期函数, k , k Z , k 0 都是它的 2
周期,最小正周期是 2 余弦函数是周期函数, k , k Z , k 0 都是它的 2 周期,最小正周期是 2
注:一般三角函数的周期都是指最小正周期
1 (1) f ( x) cos 2 x (2) f ( x) sin( x ) 2 6 解: (1)设 f ( x)的周期为 T f ( x T ) f ( x)
即 cos[2( x T )] cos 2 x 即 cos(2 x 2T ) cos 2 x 即 对任意 u 都成立:cos(u 2T ) cos u 因此 2T 2 ,从而 T 解毕
第六章 三角函数
5.6.4 正弦定理、余弦定理和解斜三角形
6.1.1 正弦函数和余弦函数的图像与性质
一、正弦函数和余弦函数的概念 实数集与角的集合可以建立一一对应的关系, 每一个确定的角都对应唯一的正弦(余弦)值. 因此,任意给定一个实数 x ,有唯一确定的值
sin x(cos x) 与之对应.
函数 y sin x 叫做正弦函数 函数 y cos x 叫做余弦函数 正弦函数和余弦函数的定义域是 R 正弦函数和余弦函数的值域是[1,1]
三角函数及反三角函数图像性质、知识点总结

千里之行,始于足下。
三角函数及反三角函数图像性质、知识点总结三角函数及反三角函数是高中数学中重要的内容之一,它们的图像性质是我们学习和理解这些函数的基础。
下面是关于三角函数及反三角函数图像性质的知识点总结。
一、正弦函数的图像性质:1. 定义域:正弦函数的定义域为全体实数。
2. 值域:正弦函数的值域为闭区间[-1,1]。
3. 周期性:正弦函数的周期是2π,即在一个周期内,正弦函数的图像重复出现。
4. 奇偶性:正弦函数是奇函数,即sin(-x)=-sin(x)。
5. 对称轴:正弦函数的对称轴是y轴。
6. 最值点:正弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的整数倍。
二、余弦函数的图像性质:1. 定义域:余弦函数的定义域为全体实数。
2. 值域:余弦函数的值域为闭区间[-1,1]。
3. 周期性:余弦函数的周期是2π,即在一个周期内,余弦函数的图像重复出现。
4. 奇偶性:余弦函数是偶函数,即cos(-x)=cos(x)。
5. 对称轴:余弦函数的对称轴是x轴。
6. 最值点:余弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的半整数倍。
三、正切函数的图像性质:1. 定义域:正切函数的定义域为全体实数,除了临界点kπ(k为整数)。
第1页/共3页锲而不舍,金石可镂。
2. 值域:正切函数的值域为全体实数。
3. 周期性:正切函数的周期是π,即在一个周期内,正切函数的图像重复出现。
4. 奇偶性:正切函数是奇函数,即tan(-x)=-tan(x)。
5. 渐近线:正切函数有两条渐近线,分别是x=kπ+π/2(k为整数)和x=kπ(k为整数)。
6. 最值点:正切函数没有最值点。
四、反正弦函数的图像性质:1. 定义域:反正弦函数的定义域为闭区间[-1,1]。
2. 值域:反正弦函数的值域为闭区间[-π/2,π/2]。
3. 奇偶性:反正弦函数是奇函数,即arcsin(-x)=-arcsin(x)。
4. 递增性:反正弦函数在定义域内是递增的。
高中数学 第三章 三角函数 3.3 三角函数的图像与性质 3.3.1 正弦函数、余弦函数的图象与性质

3.3.1 正弦函数、余弦函数的图象与性质(二)[学习目标] 1.掌握y =sin x 与y =cos x 的定义域,值域,最值、单调性、奇偶性等性质,并能解决相关问题.2.掌握y =sin x ,y =cos x 的单调性,并能利用单调性比较大小.3.会求函数y =A sin(ωx +φ)及y =A cos(ωx +φ)的单调区间.[知识链接]1.观察正弦曲线和余弦曲线的对称性,你有什么发现?答 正弦函数y =sin x 的图象关于原点对称,余弦函数y =cos x 的图象关于y 轴对称. 2.上述对称性反映出正弦、余弦函数分别具有什么性质?如何从理论上加以验证? 答 正弦函数是R 上的奇函数,余弦函数是R 上的偶函数.根据诱导公式得,sin(-x )=-sin x ,cos(-x )=cos x 均对一切x ∈R 恒成立.3.观察正弦曲线和余弦曲线,正弦、余弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?答 正弦、余弦函数存在最大值和最小值,分别是1和-1. [预习导引]正弦函数、余弦函数的性质(下表中k ∈Z ): 函数 y =sin x y =cos x图象定义域 R R 值域 [-1,1][-1,1]对称轴x =k π+π2x =k π对称中心 (k π,0) ⎝ ⎛⎭⎪⎫k π+π2,0 奇偶性 奇函数偶函数单调递增⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π[]-π+2k π,2k π 单调递减⎣⎢⎡⎦⎥⎤π2+2k π,3π2+2k π []2k π,π+2k π最值在x =π2+2k π时,y max =1;在x =-π2在x =2k π时,y max =1;在x =π+2k π要点一 求正弦、余弦函数的单调区间例1 求函数y =2sin ⎝ ⎛⎭⎪⎫π4-x 的单调递增区间. 解 y =2sin ⎝ ⎛⎭⎪⎫π4-x =-2sin ⎝⎛⎭⎪⎫x -π4,令z =x -π4,则y =-2sin z .因为z 是x 的一次函数,所以要求y =-2sin z 的递增区间, 即求sin z 的递减区间,即2k π+π2≤z ≤2k π+3π2(k ∈Z ).∴2k π+π2≤x -π4≤2k π+3π2(k ∈Z ),2k π+3π4≤x ≤2k π+7π4(k ∈Z ),∴函数y =2sin ⎝⎛⎭⎪⎫π4-x 的递增区间为⎣⎢⎡⎦⎥⎤2k π+3π4,2k π+7π4(k ∈Z ).规律方法 用整体替换法求函数y =A sin(ωx +φ)或y =A cos(ωx +φ)的单调区间时,如果式子中x 的系数为负数,先利用诱导公式将x 的系数变为正数再求其单调区间.再将最终结果写成区间形式.跟踪演练1 求下列函数的单调递增区间:(1)y =1+2sin ⎝ ⎛⎭⎪⎫π6-x ;(2)y =log 12cos x .解 (1)y =1+2sin ⎝ ⎛⎭⎪⎫π6-x =1-2sin ⎝⎛⎭⎪⎫x -π6.令u =x -π6,则根据复合函数的单调性知,所给函数的单调递增区间就是y =sin u 的单调递减区间,即2k π+π2≤u ≤2k π+32π(k ∈Z ),亦即2k π+π2≤x -π6≤2k π+3π2(k ∈Z ).亦即2k π+23π≤x ≤2k π+53π(k ∈Z ),故函数y =1+2sin ⎝ ⎛⎭⎪⎫π6-x 的单调递增区间是⎣⎢⎡⎦⎥⎤2k π+23π,2k π+53π(k ∈Z ).(2)由cos x >0,得2k π-π2<x <2k π+π2,k ∈Z .∵0<12<1,∴函数y =log 12cos x 的单调递增区间即为u =cos x ,x ∈⎝⎛⎭⎪⎫2k π-π2,2k π+π2(k ∈Z )的递减区间,∴2k π≤x <2k π+π2,k ∈Z .故函数y =log 12cos x 的单调递增区间为⎣⎢⎡⎭⎪⎫2k π,2k π+π2(k ∈Z ). 要点二 正弦、余弦函数的单调性的应用例2 利用三角函数的单调性,比较下列各组数的大小.(1)sin ⎝ ⎛⎭⎪⎫-π18与sin ⎝ ⎛⎭⎪⎫-π10;(2)sin196°与cos156°;(3)cos ⎝ ⎛⎭⎪⎫-235π与cos ⎝ ⎛⎭⎪⎫-174π. 解 (1)∵-π2<-π10<-π18<π2,∴sin ⎝ ⎛⎭⎪⎫-π18>sin ⎝ ⎛⎭⎪⎫-π10.(2)sin196°=sin(180°+16°)=-sin16°, cos156°=cos(180°-24°)=-cos24°=-sin66°, ∵0°<16°<66°<90°,∴sin16°<sin66°; 从而-sin16°>-sin66°,即sin196°>cos156°.(3)cos ⎝ ⎛⎭⎪⎫-235π=cos 235π=cos(4π+35π)=cos 35π, cos ⎝ ⎛⎭⎪⎫-174π=cos 174π=cos ⎝ ⎛⎭⎪⎫4π+π4=cos π4.∵0<π4<35π<π,且y =cos x 在[0,π]上是减函数,∴cos 35π<co s π4,即cos ⎝ ⎛⎭⎪⎫-235π<cos ⎝ ⎛⎭⎪⎫-174π. 规律方法 用正弦函数或余弦函数的单调性比较大小时,应先将异名化同名,把不在同一单调区间内的角用诱导公式转化到同一单调区间,再利用单调性来比较大小. 跟踪演练2 比较下列各组数的大小.(1)sin ⎝ ⎛⎭⎪⎫-376π与sin ⎝ ⎛⎭⎪⎫493π; (2)cos870°与sin980°.解 (1)sin ⎝ ⎛⎭⎪⎫-376π=sin ⎝ ⎛⎭⎪⎫-6π-π6=sin ⎝ ⎛⎭⎪⎫-π6,sin ⎝ ⎛⎭⎪⎫493π=sin ⎝⎛⎭⎪⎫16π+π3=sin π3,∵y =sin x 在⎣⎢⎡⎦⎥⎤-π2,π2上是增函数,∴sin ⎝ ⎛⎭⎪⎫-π6<sin π3,即sin ⎝ ⎛⎭⎪⎫-376π<sin 493π. (2)cos870°=cos(720°+150°)=cos150°,sin980°=sin(720°+260°)=sin260°=sin(90°+170°)=cos170°, ∵0°<150°<170°<180°,∴cos150°>cos170°,即cos870°>sin980°. 要点三 求正弦、余弦函数的最值(值域)例3 (1)求函数y =3-2sin x 取得最大值、最小值时的自变量x 的集合,并分别写出最大值、最小值;(2)求函数f (x )=2sin 2x +2sin x -12,x ∈⎣⎢⎡⎦⎥⎤π6,5π6的值域.解 (1)∵-1≤sin x ≤1,∴当sin x =-1,即x =2k π+3π2,k ∈Z 时,y 取得最大值5,相应的自变量x 的集合为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x =2k π+3π2,k ∈Z .当sin x =1,即x =2k π+π2,k ∈Z 时,y 取得最小值1,相应的自变量x 的集合为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x =2k π+π2,k ∈Z .(2)令t =sin x ,y =f (t ),∵x ∈⎣⎢⎡⎦⎥⎤π6,5π6,∴12≤sin x ≤1,即12≤t ≤1. ∴y =2t 2+2t -12=2⎝ ⎛⎭⎪⎫t +122-1,∴1≤y ≤72,∴函数f (x )的值域为⎣⎢⎡⎦⎥⎤1,72.规律方法 (1)形如y =a sin x +b (或y =a cos x +b )的函数的最值或值域问题,利用正弦、余弦函数的有界性(-1≤sin x ,cos x ≤1)求解.求三角函数取最值时相应自变量x 的集合时,要注意考虑三角函数的周期性.(2)求解形如y =a sin 2x +b sin x +c (或y =a cos 2x +b cos x +c ),x ∈D 的函数的值域或最值时,通过换元,令t =sin x (或cos x ),将原函数转化为关于t 的二次函数,利用配方法求值域或最值即可.求解过程中要注意t =sin x (或cos x )的有界性.跟踪演练3 已知0≤x ≤π2,求函数y =cos 2x -2a cos x 的最大值M (a )与最小值m (a ).解 设cos x =t , ∵0≤x ≤π2,∴0≤t ≤1.∵y =t 2-2at =(t -a )2-a 2,∴当a <0时,M (a )=1-2a ,m (a )=0; 当0≤a ≤12时,M (a )=1-2a ,m (a )=-a 2;当12<a <1时,M (a )=0,m (a )=-a 2; 当a ≥1时,M (a )=0,m (a )=1-2a . 综上,M (a )=⎩⎪⎨⎪⎧1-2a , a ≤12,0,a >12,m (a )=⎩⎪⎨⎪⎧0, a <0,-a 2,0≤a <1,1-2a ,a ≥1.要点四 三角函数的奇偶性 例4 判断下列函数的奇偶性:(1)f (x )=sin ⎝ ⎛⎭⎪⎫-12x +π2;(2)f (x )=lg(1-sin x )-lg(1+sin x ); (3)f (x )=1+sin x -cos 2x1+sin x .解 (1)显然x ∈R ,f (x )=cos 12x ,f (-x )=cos ⎝ ⎛⎭⎪⎫-12x =cos 12x =f (x ),∴f (x )是偶函数.(2)由⎩⎪⎨⎪⎧1-sin x >0,1+sin x >0,得-1<sin x <1.解得定义域为⎩⎨⎧⎭⎬⎫x |x ∈R 且x ≠k π+π2,k ∈Z .∴f (x )的定义域关于原点对称. 又∵f (x )=lg(1-sin x )-lg(1+sin x ) ∴f (-x )=lg[1-sin(-x )]-lg[1+sin(-x )] =lg(1+sin x )-lg(1-sin x )=-f (x ). ∴f (x )为奇函数.(3)∵1+sin x ≠0,∴sin x ≠-1, ∴x ∈R 且x ≠2k π-π2,k ∈Z .∵定义域不关于原点对称,∴该函数是非奇非偶函数.规律方法 判断函数奇偶性,要先判断函数的定义域是否关于原点对称,定义域关于原点对称是函数为奇函数或偶函数的前提条件,然后再判断f (-x )与f (x )之间的关系. 跟踪演练4 判断下列函数的奇偶性:(1)f (x )=cos ⎝ ⎛⎭⎪⎫32π+2x +x 2·sin x ;(2)f (x )=1-2cos x +2cos x -1. 解 (1)f (x )=sin2x +x 2sin x ,又∵x ∈R ,f (-x )=sin(-2x )+(-x )2sin(-x )= -sin2x -x 2sin x =-f (x ),∴f (x )是奇函数.(2)由⎩⎪⎨⎪⎧1-2cos x ≥0,2cos x -1≥0,得cos x =12.∴f (x )=0,x =2k π±π3,k ∈Z .∴f (x )既是奇函数又是偶函数.1.函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π6的一个递减区间是( )A.⎣⎢⎡⎦⎥⎤-π2,π2B .[-π,0]C.⎣⎢⎡⎦⎥⎤-23π,23πD.⎣⎢⎡⎦⎥⎤π2,23π答案 D解析 由π2≤x +π6≤32π解得π3≤x ≤43π.故选D.2.下列不等式中成立的是( )A .sin ⎝ ⎛⎭⎪⎫-π8>sin ⎝ ⎛⎭⎪⎫-π10 B .sin3>sin2 C .sin 75π>sin ⎝ ⎛⎭⎪⎫-25π D .sin2>cos1 答案 D解析 ∵sin2=cos ⎝ ⎛⎭⎪⎫π2-2=cos ⎝ ⎛⎭⎪⎫2-π2,且0<2-π2<1<π,∴cos ⎝ ⎛⎭⎪⎫2-π2>cos1,即sin2>cos1.故选D.3.函数y =cos ⎝ ⎛⎭⎪⎫x +π6,x ∈⎣⎢⎡⎦⎥⎤0,π2的值域是( )A.⎣⎢⎡⎦⎥⎤-32,12B.⎣⎢⎡⎦⎥⎤-12,32 C.⎣⎢⎡⎦⎥⎤32,1 D.⎣⎢⎡⎦⎥⎤12,1答案 B解析 ∵0≤x ≤π2,∴π6≤x +π6≤23π.∴cos 23π≤cos ⎝ ⎛⎭⎪⎫x +π6≤cos π6,∴-12≤y ≤32.故选B. 4.设a =sin33°,b =cos55°,c =tan35°,则( ) A .a >b >c B .b >c >a C .c >b >a D .c >a >b 答案 C解析 ∵a =sin33°,b =cos55°=sin35°,c =tan35°=sin35°cos35°,又0<cos35°<1,∴c >b >a .1.求函数y =A sin(ωx +φ)(A >0,ω>0)单调区间的方法是:把ωx +φ看成一个整体,由2k π-π2≤ωx +φ≤2k π+π2 (k ∈Z )解出x 的范围,所得区间即为增区间,由2k π+π2≤ωx +φ≤2k π+32π (k ∈Z )解出x 的范围,所得区间即为减区间.若ω<0,先利用诱导公式把ω转化为正数后,再利用上述整体思想求出相应的单调区间.2.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断. 3.求三角函数值域或最值的常用求法:将y 表示成以sin x (或cos x )为元的复合函数再利用换元或配方或利用函数的单调性等来确定y 的范围.一、基础达标1.若y =sin x 是减函数,y =cos x 是增函数,那么角x 在( ) A .第一象限B .第二象限C .第三象限D .第四象限答案 C2.若α,β都是第一象限的角,且α<β,那么( ) A .sin α>sin β B .sin β>sin αC .sin α≥sin βD .sin α与sin β的大小不定答案 D3.函数y =2sin 2x +2cos x -3的最大值是( ) A .-1B .1 C .-12D .-5答案 C解析 由题意,得y =2sin 2x +2cos x -3=2(1-cos 2x )+2cos x -3=-2⎝ ⎛⎭⎪⎫cos x -122-12.∵-1≤cos x ≤1,∴当cos x =12时,函数有最大值-12.4.对于下列四个命题:①sin ⎝ ⎛⎭⎪⎫-π18>sin ⎝ ⎛⎭⎪⎫-π10; ②cos ⎝ ⎛⎭⎪⎫-25π4>cos ⎝ ⎛⎭⎪⎫-17π4; ③sin138°<sin143°;④tan40°>sin40°. 其中正确命题的序号是( ) A .①③B.①④ C .②③D .②④答案 B5.关于x 的函数f (x )=sin(x +φ)有以下命题:①对任意的φ,f (x )都是非奇非偶函数;②不存在φ,使f (x )既是奇函数,又是偶函数;③存在φ,使f (x )是奇函数;④对任意的φ,f (x )都不是偶函数.其中正确命题的序号是________. 答案 ②③解析 易知②③成立,令φ=π2,f (x )=cos x 是偶函数,①④都不成立.6.若|x |≤π4,则函数f (x )=cos 2x +sin x 的最小值是________.答案 12-22解析 由cos 2x =1-sin 2x ,故f (x )=1-sin 2x +sin x ,令sin x =t ,由|x |≤π4,由图象知t ∈[-22,22],故函数化为y =-t 2+t +1=-(t -12)2+54,当t =-22时,y min =12-22. 7.求下列函数的单调增区间. (1)y =1-sin x2;(2)y =log 12cos ⎝ ⎛⎭⎪⎫π3-x 2.解 (1)由2k π+π2≤x 2≤2k π+32π,k ∈Z ,得4k π+π≤x ≤4k π+3π,k ∈Z .∴y =1-sin x2的增区间为[4k π+π,4k π+3π] (k ∈Z ). (2)y =log 12cos ⎝ ⎛⎭⎪⎫π3-x 2=log 12cos ⎝ ⎛⎭⎪⎫x 2-π3.要求原函数的增区间,即求函数y =cos ⎝ ⎛⎭⎪⎫x 2-π3的减区间,且cos ⎝ ⎛⎭⎪⎫x 2-π3>0.∴2k π≤x 2-π3<2k π+π2(k ∈Z ).整理得4k π+23π≤x <4k π+53π(k ∈Z ).所以函数y =log 12cos ⎝ ⎛⎭⎪⎫π3-x 2的单调递增区间是⎣⎢⎡⎭⎪⎫4k π+23π,4k π+53π(k ∈Z ).二、能力提升 8.函数y =2sin x的单调增区间是( )A .[2k π-π2,2k π+π2](k ∈Z )B .[2k π+π2,2k π+3π2](k ∈Z ) C .[2k π-π,2k π](k ∈Z )D .[2k π,2k π+π](k ∈Z )答案 A解析 函数y =2x 为增函数,因此求函数y =2sin x 的单调增区间即求函数y =sin x 的单调增区间9.M ,N 是曲线y =πsin x 与曲线y =πcos x 的两个不同的交点,则|MN |的最小值为( )A .πB.2πC.3πD .2π 答案 C解析 在同一坐标系中画出函数y =πsin x 与y =πcos x 的图象,如图所示,则|MN |的最小值为|PQ |.又P (π4,2π2),Q (5π4,-2π2), 故|PQ |=π4-5π42+2π2+2π22=3π.10.sin1,sin2,sin3按从小到大排列的顺序为__________________.答案 sin3<sin1<sin2解析 ∵1<π2<2<3<π, sin(π-2)=sin2,sin(π-3)=sin3.y =sin x 在⎝⎛⎭⎪⎫0,π2上递增,且0<π-3<1<π-2<π2, ∴sin(π-3)<sin1<sin(π-2),即sin3<sin1<sin2.11.已知ω是正数,函数f (x )=2sin ωx 在区间[-π3,π4]上是增函数,求ω的取值范围.解 由-π2+2k π≤ωx ≤π2+2k π(k ∈Z ), 得-π2ω+2k πω≤x ≤π2ω+2k πω. ∴f (x )的单调递增区间是[-π2ω+2k πω,π2ω+2k πω],k ∈Z . 根据题意,得[-π3,π4]⊆[-π2ω+2k πω,π2ω+2k πω]. 从而有⎩⎪⎨⎪⎧ -2π2ω≤-π3,π2ω≥π4,ω>0,解得0<ω≤32. 故ω的取值范围是(0,32]. 12.判断下列函数的奇偶性:(1)f (x )=2sin ⎝⎛⎭⎪⎫2x +52π;(2)f (x )=2sin x -1;(3)f (x )=lg(sin x +1+sin 2x ). 解 (1)函数定义域为R ,且f (x )=2sin ⎝ ⎛⎭⎪⎫2x +52π=2sin ⎝⎛⎭⎪⎫2x +π2=2cos2x ,显然有f (-x )=f (x )恒成立.∴函数f (x )=2sin ⎝⎛⎭⎪⎫2x +52π为偶函数. (2)由2sin x -1>0,即sin x >12,得函数定义域为⎝⎛⎭⎪⎫2k π+π6,2k π+56π(k ∈Z ),此定义域在x 轴上表示的区间不关于原点对称.∴该函数不具有奇偶性,为非奇非偶函数.(3)函数定义域为R . f (-x )=lg(-sin x +1+sin 2x )=lg 1sin x +1+sin 2x=-lg ()sin x +1+sin 2x =-f (x ),∴函数f (x )=lg(sin x +1+sin 2x )为奇函数.三、探究与创新 13.设函数y =-2cos ⎝ ⎛⎭⎪⎫12x +π3,x ∈⎣⎢⎡⎦⎥⎤28π5,a ,若该函数是单调函数,求实数a 的最大值. 解 由2k π≤12x +π3≤2k π+π(k ∈Z )得4k π-23π≤x ≤4k π+43π(k ∈Z ). ∴函数的单调递增区间是⎣⎢⎡⎦⎥⎤4k π-23π,4k π+43π(k ∈Z ), 同理函数的单调递减区间是⎣⎢⎡⎦⎥⎤4k π+43π,4k π+103π(k ∈Z ). 令285π∈⎣⎢⎡⎦⎥⎤4k π-23π,4k π+43π, 即1615≤k ≤4730,又k ∈Z ,∴k 不存在. 令285π∈⎣⎢⎡⎦⎥⎤4k π+43π,4k π+103π,得k =1. ∴285π∈⎣⎢⎡⎦⎥⎤4k π+43π,4k π+103π, 这表明y =-2cos ⎝ ⎛⎭⎪⎫12x +π3在⎣⎢⎡⎦⎥⎤28π5,22π3上是减函数,∴a 的最大值是22π3.。
专题五+5.3三角函数的图像与性质课件——2023届高三数学一轮复习

标):ωx+φ=π+2kπ.(以上k∈Z)
例1
(2022重庆十一中月考,5)函数f(x)=Asin(ωx+φ)
A
0,
ω
0,
0
φ
2
的部分图象如图所示,将其向右平移 3 个单位长度后得到图象对应的函
数解析式为 ( )
A.y= 2 sin 2x
B.y=
2
sin
2x
3
C.y=
2
sin
2x
3
D.y=
5 3
, 13 6
⫋
3 2
, 5 2
,易知函数y=sin
x在
3 2
,
5 2
上单调递增,则函数f(x)=sin
2
x
3
在区间
,
5 4
上单调递增,故
D正确.故选BD.
答案 BD
考法三 三角函数的最值 求三角函数最值常见的函数形式
1.y=asin x+bcos x= a2 b2 sin(x+φ),其中cos φ= a ,sin φ= b .
2
,
0
,(π,-1),
3 2
,
0
,(2π,1).
2.用“五点法”画y=Asin(ωx+φ)(A,ω≠0)在一个周期内的简图 用五点法画y=Asin(ωx+φ)(A,ω≠0)在一个周期内的简图时,一般先列表,后 描点,连线,其中所列表如下:
ωx+φ
x
y=A· sin(ωx+φ)
0
π
2
-
π - + 2
左平移 个单位长度,得到曲线C2
12
高中数学三角函数及反三角函数图像性质、知识点总结

高中数学三角函数及反三角函数图像性质、知识点总结高中数学中,三角函数及反三角函数是重要的内容之一。
在学习这一部分知识时,需要掌握其图像性质以及相关的知识点。
下面将对这些内容进行总结。
一、三角函数的图像性质1. 正弦函数(sin)的图像性质:- 周期性:sin函数的周期为2π,即在每个周期内,函数的图像重复出现;- 奇函数性质:sin函数关于原点对称;- 取值范围:sin函数的取值范围为[-1,1],即函数的值始终在该区间内波动。
2. 余弦函数(cos)的图像性质:- 周期性:cos函数的周期为2π;- 偶函数性质:cos函数关于y轴对称;- 取值范围:cos函数的取值范围也为[-1,1]。
3. 正切函数(tan)的图像性质:- 周期性:tan函数的周期为π;- 奇函数性质:tan函数关于原点对称;- 无界性:tan函数的值域为实数集,即函数在某些点无界。
二、三角函数的知识点1. 基本正弦函数的性质:- 特殊角的正弦值:0°、90°、180°、270°和360°对应的正弦值分别为0、1、0、-1和0;- 正弦函数的增减性:在0°到180°的区间上,sin函数是单调递增的;- 正弦函数的奇偶性:sin(-x)=-sin(x),即sin函数关于原点对称。
2. 基本余弦函数的性质:- 特殊角的余弦值:0°、90°、180°、270°和360°对应的余弦值分别为1、0、-1、0和1;- 余弦函数的增减性:在0°到180°的区间上,cos函数是单调递减的;- 余弦函数的奇偶性:cos(-x)=cos(x),即cos函数关于y轴对称。
3. 基本正切函数的性质:- 特殊角的正切值:0°、90°、180°和270°对应的正切值分别为0、无穷大、0和无穷大;- 正切函数的周期性:tan(x+π)=tan(x),即tan函数的周期是π。
(完整版)最全三角函数的图像与性质知识点总结
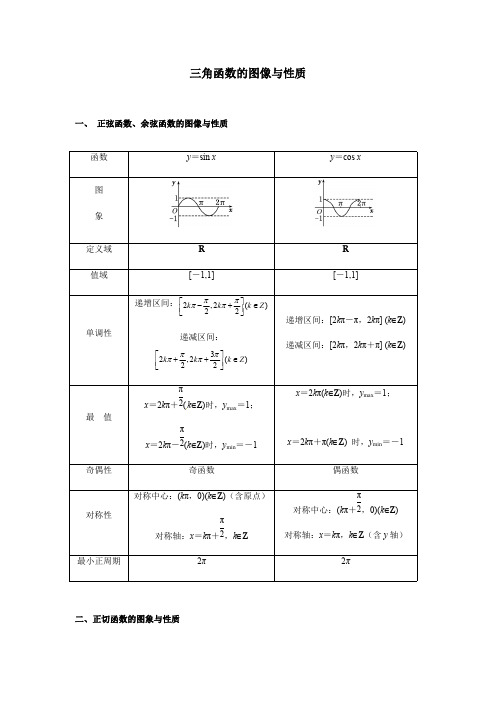
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y =sin x y =cos x图象定义域RR 值域[-1,1][-1,1]单调性递增区间:2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间:32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间:[2k π-π,2k π] (k ∈Z )递减区间:[2k π,2k π+π] (k ∈Z )最 值x =2k π+(k ∈Z )时,y max =1;π2x =2k π-(k ∈Z )时,y min =-1π2x =2k π(k ∈Z )时,y max =1;x =2k π+π(k ∈Z ) 时,y min =-1奇偶性奇函数偶函数对称性对称中心:(k π,0)(k ∈Z )(含原点)对称轴:x =k π+,k ∈Zπ2对称中心:(k π+,0)(k ∈Z )π2对称轴:x =k π,k ∈Z (含y 轴)最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心:(含原点)(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一:先平移后伸缩方法二:先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意:平移变换或伸缩变换都是针对自变量x 而言的,因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
原创三角函数的概念图像及性质.ppt

① asin□与bcos□之间是“+”连接
② a,b分别是sin□与cos□的系数 注3.辅助角φ的确定方法:
(a,b)
方法甚多凭爱好 坐标定义是基础
φ
数形结合两限制 注释说明一般角
O
X
(2) a sin □ bcos□ a2 b2 cos(□ )
(其中 tan a,Φ与点(b,a)同象限)
cos A b2 c2 a2 2bc
cos B a2 c2 b2 2ac
cos C a2 b2 c2 2ab
三角式运算公式总述
1.公式:
①同角关系 ②异角关系
2.作用:
一角二名三结构……
世上本无路三角走运的算人公多式了关便联有图了路
半角
作用
商数 平方 关系 关系
倒数
关系
同角
基本
1、同角基本关系式
(1)公式:
①平方关系 sin 2 cos2 1
②商数关系 sin tan cos③倒数关系 tan Fra bibliotekot 1 sinx
注:记忆图
①平方关系:阴影三角形…
tanx
②商数关系:边上左右邻居…
③倒数关系:对角线……
secx
cosx
1
cotx
cscx
1、同角基本关系式
(1).公式:……
(2).作用: 变名变结构
注:经典题型:同角两弦的和差商积可互化.即“知一有n”
桥梁: (sin x cos x)2 1 2sin x cos x 1 sin 2x
sin x n1 sin x cos x n3 sin x cos x n5 sin 2 x cos2 x n7
五点做图象 “代
三角函数的图像及其性质

三角函数的图像及其性质1、三角函数的图像及性质sin y xsin y A x k图像值域周期对称轴2x k2x k对称中心(零点)令x k 代入求y令x k 代入,求出x 和y 单调增区间2,222x k k2,222x k k单调减区间32,222x k k32,222x k kcos y xcos y A x k图像值域周期对称轴x kx k 对称中心(零点)2x k代入,求y 2x k求出x 和y 单调增区间 2,2x k k 2,2x k k 单调减区间2,2x k k2,2x k k tan y x图像定义域值域周期单调性与对称性性质【考点分类】考点一:图像变换:1.把函数y =sin x 的图象向右平移个单位得到y =g (x )的图象,再把y =g (x )图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为()A.B.C.D.2.将函数f (x )=sin x 图象上所有点的横坐标变为原来的(ω>0),纵坐标不变,得到函数g (x )的图象,若g (x )的最小正周期为6π,则ω=()A.B.6C.D.33.将函数y =2sin2x 图象上的所有点向右平移个单位,然后把图象上所有点的横坐标缩短为原来的倍,(纵坐标不变)得到y =f (x )的图象,则f (x )等于()A.2sin(x ﹣)B.2sin(x ﹣)C.2sin(4x ﹣)D.2sin(4x ﹣)4.已知曲线C 1:y =cos x ,C 2:y =sin(2x +),则下面结论正确的是()A.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向右平移个单位长度,得到曲线C 2B.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向左平移个单位长度,得到曲线C 2C.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向右平移个单位长度,得到曲线C 2D.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度,得到曲线C 25.把函数y =cos(3x +4)的图象适当变动就可以得到y =sin(-3x )的图象,这种变动可以是()A 向右平移4 B 向左平移4 C 向右平移12 D 向左平移126..函数32sin( x y 的图象是由2sin xy 的图象沿x 轴()得到的。
三角函数的图像和性质知识点讲解+例题讲解(含解析)

三角函数的图像与性质一、知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫3π2,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )π3.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期. (2)正切曲线相邻两对称中心之间的距离是半个周期.(3).对于y =tan x 不能认为其在定义域上为增函数,而是在每个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内为增函数.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)余弦函数y =cos x 的对称轴是y 轴.( ) (2)正切函数y =tan x 在定义域内是增函数.( ) (3)已知y =k sin x +1,x ∈R ,则y 的最大值为k +1.( ) (4)y =sin|x |是偶函数.( )解析 (1)余弦函数y =cos x 的对称轴有无穷多条,y 轴只是其中的一条. (2)正切函数y =tan x 在每一个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上都是增函数,但在定义域内不是单调函数,故不是增函数.(3)当k >0时,y max =k +1;当k <0时,y max =-k +1. 答案 (1)× (2)× (3)× (4)√2.若函数y =2sin 2x -1的最小正周期为T ,最大值为A ,则( ) A.T =π,A =1 B.T =2π,A =1 C.T =π,A =2D.T =2π,A =2解析 最小正周期T =2π2=π,最大值A =2-1=1.故选A. 答案 A3.函数y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为________.解析 由-π2+k π<2x -3π4<π2+k π(k ∈Z ), 得π8+k π2<x <5π8+k π2(k ∈Z ),所以y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z ). 答案 ⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z )4.(2017·全国Ⅱ卷)函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的最小正周期为( )A.4πB.2πC.πD.π2解析 由题意T =2π2=π. 答案 C5.(2017·全国Ⅲ卷)函数f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6的最大值为( )A.65B.1C.35D.15解析 cos ⎝ ⎛⎭⎪⎫x -π6=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫x +π3=sin ⎝ ⎛⎭⎪⎫x +π3,则f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+sin ⎝ ⎛⎭⎪⎫x +π3=65sin ⎝ ⎛⎭⎪⎫x +π3,函数的最大值为65. 答案 A6.(2018·江苏卷)已知函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2 的图象关于直线x =π3对称,则φ的值是________.解析 由函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2的图象关于直线x =π3对称,得sin ⎝ ⎛⎭⎪⎫2π3+φ=±1.所以2π3+φ=π2+k π(k ∈Z ),所以φ=-π6+k π(k ∈Z ),又-π2<φ<π2,所以φ=-π6. 答案 -π6考点一 三角函数的定义域【例1】 (1)函数f (x )=-2tan ⎝ ⎛⎭⎪⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x |x ≠π6 B.⎩⎨⎧⎭⎬⎫x |x ≠-π12 C.⎩⎨⎧⎭⎬⎫x |x ≠k π+π6(k ∈Z ) D.⎩⎨⎧⎭⎬⎫x |x ≠k π2+π6(k ∈Z ) (2)不等式3+2cos x ≥0的解集是________.(3)函数f (x )=64-x 2+log 2(2sin x -1)的定义域是________. 解析 (1)由2x +π6≠k π+π2(k ∈Z ),得x ≠k π2+π6(k ∈Z ).(2)由3+2cos x ≥0,得cos x ≥-32,由余弦函数的图象,得在一个周期[-π,π]上,不等式cos x ≥-32的解集为⎩⎨⎧⎭⎬⎫x |-5π6≤x ≤56π,故原不等式的解集为⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z .(3)由题意,得⎩⎨⎧64-x 2≥0,①2sin x -1>0,②由①得-8≤x ≤8,由②得sin x >12,由正弦曲线得π6+2k π<x <56 π+2k π(k ∈Z ).所以不等式组的解集为⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8. 答案 (1)D (2)⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z (3)⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8【训练1】 (1)函数y =sin x -cos x 的定义域为________. (2)函数y =lg(sin x )+cos x -12的定义域为______.解析 (1)要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]上,满足sin x =cos x 的x 为π4,5π4再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z .(2)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0,cos x -12≥0, 即⎩⎪⎨⎪⎧sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π(k ∈Z ),所以2k π<x ≤π3+2k π(k ∈Z ),所以函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z .答案(1)⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z (2)⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z考点二 三角函数的值域与最值【例2】 (1)y =3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域是________.(2)(2017·全国Ⅱ卷)函数f (x )=sin 2x +3cos x -34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0,π2的最大值是________. (3)函数y =sin x -cos x +sin x cos x 的值域为________.解析 (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1,故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即y =3sin ⎝ ⎛⎭⎪⎫2x -π6的值域为⎣⎢⎡⎦⎥⎤-32,3. (2)由题意可得f (x )=-cos 2x +3cos x +14=-(cos x -32)2+1.∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴cos x ∈[0,1].∴当cos x =32,即x =π6时,f (x )max =1. (3)设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x cos x ,sin x cos x =1-t22,且-2≤t ≤2,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2 .所以函数的值域为⎣⎢⎡⎦⎥⎤-12-2,1. 答案 (1)⎣⎢⎡⎦⎥⎤-32,3 (2)1 (3)⎣⎢⎡⎦⎥⎤-12-2,1【训练2】 (1)函数f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x 的最大值为( )A.4B.5C.6D.7(2)(2019·临沂模拟)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π3,a ,若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,则实数a 的取值范围是________. 解析 (1)由f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x =1-2sin 2x +6sin x =-2⎝ ⎛⎭⎪⎫sin x -322+112,又sin x ∈[-1,1],所以当sin x =1时函数的最大值为5.(2)由x ∈⎣⎢⎡⎦⎥⎤-π3,a ,知x +π6∈⎣⎢⎡⎦⎥⎤-π6,a +π6.因为x +π6∈⎣⎢⎡⎦⎥⎤-π6,π2时,f (x )的值域为⎣⎢⎡⎦⎥⎤-12,1,所以由函数的图象知π2≤a +π6≤7π6,所以π3≤a ≤π. 答案 (1)B(2)⎣⎢⎡⎦⎥⎤π3,π考点三 三角函数的单调性 角度1 求三角函数的单调区间【例3-1】 (1)函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间是( ) A.⎣⎢⎡⎦⎥⎤k π12-π12,k π2+5π12(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π12-π12,k π2+5π12(k ∈Z )C.⎝ ⎛⎭⎪⎫k π+π6,k π+2π3(k ∈Z )D.⎝ ⎛⎭⎪⎫k π-π12,k π+5π12(k ∈Z ) (2)函数y =sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为________. 解析 (1)由k π-π2<2x -π3<k π+π2(k ∈Z ),得k π2-π12<x <k π2+5π12(k ∈Z ),所以函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2-π12,k π2+5π12(k ∈Z ).(2)y =-sin ⎝ ⎛⎭⎪⎫2x -π3,它的减区间是y =sin ⎝ ⎛⎭⎪⎫2x -π3的增区间.令2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故其单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z . 答案 (1)B (2)⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z角度2 利用单调性比较大小【例3-2】 已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6,设a =f ⎝ ⎛⎭⎪⎫π7,b =f ⎝ ⎛⎭⎪⎫π6,c =f ⎝ ⎛⎭⎪⎫π4,则a ,b ,c 的大小关系是( ) A.a >b >c B.a >c >b C.c >a >bD.b >a >c解析 令2k π≤x +π6≤2k π+π,k ∈Z ,解得2k π-π6≤x ≤2k π+5π6,k ∈Z ,∴函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6在⎣⎢⎡⎦⎥⎤-π6,5π6上是减函数,∵-π6<π7<π6<π4<5π6, ∴f ⎝ ⎛⎭⎪⎫π7>f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4. 答案 A角度3 利用单调性求参数【例3-3】 (2018·全国Ⅱ卷)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( ) A.π4B.π2C.3π4D.π解析 f (x )=cos x -sin x =2cos ⎝ ⎛⎭⎪⎫x +π4,由题意得a >0,故-a +π4<π4,因为f (x )=2cos ⎝ ⎛⎭⎪⎫x +π4在[-a ,a ]是减函数,所以⎩⎪⎨⎪⎧-a +π4≥0,a +π4≤π,a >0,解得0<a ≤π4,所以a 的最大值是π4.答案 A【训练3】 (1)设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎣⎢⎡⎦⎥⎤-π2,π,则以下结论正确的是( )A.函数f (x )在⎣⎢⎡⎦⎥⎤-π2,0上单调递减B.函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增 C.函数f (x )在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减 D.函数f (x )在⎣⎢⎡⎦⎥⎤5π6,π上单调递增(2)cos 23°,sin 68°,cos 97°的大小关系是________.(3)若函数f (x )=sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=________.解析 (1)由x ∈⎣⎢⎡⎦⎥⎤-π2,0,得2x -π3∈⎣⎢⎡⎦⎥⎤-4π3,-π3,此时函数f (x )先减后增;由x ∈⎣⎢⎡⎦⎥⎤0,π2,得2x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,此时函数f (x )先增后减;由x ∈⎣⎢⎡⎦⎥⎤π2,5π6,得2x -π3∈⎣⎢⎡⎦⎥⎤2π3,4π3,此时函数f (x )单调递减;由x ∈⎣⎢⎡⎦⎥⎤5π6,π,得2x -π3∈⎣⎢⎡⎦⎥⎤4π3,5π3,此时函数f (x )先减后增.(2)sin 68°=cos 22°,又y =cos x 在[0°,180°]上是减函数,∴sin 68°>cos 23°>cos 97°.(3)法一 由于函数f (x )=sin ωx (ω>0)的图象经过坐标原点,由已知并结合正弦函数的图象可知,π3为函数f (x )的14周期,故2πω=4π3,解得ω=32.法二 由题意,得f (x )max =f ⎝ ⎛⎭⎪⎫π3=sin π3ω=1.由已知并结合正弦函数图象可知,π3ω=π2+2k π(k ∈Z ),解得ω=32+6k (k ∈Z ),所以当k =0时,ω=32.答案 (1)C (2)sin 68°>cos 23°>cos 97° (3)32考点四 三角函数的周期性、奇偶性、对称性 角度1 三角函数奇偶性、周期性【例4-1】 (1)(2018·全国Ⅰ卷)已知函数f (x )=2cos 2x -sin 2x +2,则( ) A.f (x )的最小正周期为π,最大值为3 B.f (x )的最小正周期为π,最大值为4 C.f (x )的最小正周期为2π,最大值为3 D.f (x )的最小正周期为2π,最大值为4(2)(2019·杭州调研)设函数f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ⎝ ⎛⎭⎪⎫|θ|<π2的图象关于y 轴对称,则θ=( ) A.-π6 B.π6 C.-π3 D.π3解析 (1)易知f (x )=2cos 2x -sin 2x +2=3cos 2x +1=3cos 2x +12+1=32cos 2x +52,则f (x )的最小正周期为π,当2x =2k π,即x =k π(k ∈Z )时,f (x )取得最大值,最大值为4.(2)f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ=2sin ⎝ ⎛⎭⎪⎫12x +θ-π3, 由题意可得f (0)=2sin ⎝ ⎛⎭⎪⎫θ-π3=±2,即sin ⎝ ⎛⎭⎪⎫θ-π3=±1,∴θ-π3=π2+k π(k ∈Z ),∴θ=5π6+k π(k ∈Z ). ∵|θ|<π2,∴k =-1时,θ=-π6. 答案 (1)B (2)A角度2 三角函数图象的对称性【例4-2】 (1)已知函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,则函数g (x )=sin x +a cos x 的图象( )A.关于点⎝ ⎛⎭⎪⎫π3,0对称B.关于点⎝ ⎛⎭⎪⎫2π3,0对称 C.关于直线x =π3对称 D.关于直线x =π6对称解析 (1)因为函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,所以f (0)=f ⎝ ⎛⎭⎪⎫π3,所以1=32a +12,a =33,所以g (x )=sin x +33cos x =233sin ⎝ ⎛⎭⎪⎫x +π6,函数g (x )的对称轴方程为x +π6=k π+π2(k ∈Z ),即x =k π+π3(k ∈Z ),当k =0时,对称轴为直线x =π3,所以g (x )=sin x +a cos x 的图象关于直线x =π3对称. 规律方法 1.对于可化为f (x )=A sin(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可;如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z ),求x 即可.2.对于可化为f (x )=A cos(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=k π(k ∈Z ),求x ;如果求f (x )的对称中心的横坐标,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可.【训练4】 (1)(2018·全国Ⅲ卷)函数f (x )=tan x1+tan 2x的最小正周期为( )A.π4B.π2C.πD.2π(2)设函数f (x )=cos ⎝ ⎛⎭⎪⎫x +π3,则下列结论错误的是( )A.f (x )的一个周期为-2πB.y =f (x )的图象关于直线x =8π3对称 C.f (x +π)的一个零点为x =π6 D.f (x )在⎝ ⎛⎭⎪⎫π2,π单调递减解析 (1)f (x )的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π+π2,k ∈Z .f (x )=sin x cos x 1+⎝ ⎛⎭⎪⎫sin x cos x 2=sin x ·cos x =12sin 2x ,∴f (x )的最小正周期T =2π2=π.(2)A 项,因为f (x )的周期为2k π(k ∈Z 且k ≠0),所以f (x )的一个周期为-2π,A 项正确.B 项,因为f (x )图象的对称轴为直线x =k π-π3(k ∈Z ),当k =3时,直线x =8π3是其对称轴,B 项正确.C 项,f (x +π)=cos ⎝ ⎛⎭⎪⎫x +4π3,将x =π6代入得到f ⎝ ⎛⎭⎪⎫7π6=cos 3π2=0,所以x =π6是f (x+π)的一个零点,C 项正确.D 项,因为f (x )=cos ⎝ ⎛⎭⎪⎫x +π3的递减区间为⎣⎢⎡⎦⎥⎤2k π-π3,2k π+2π3 (k ∈Z ),递增区间为⎣⎢⎡⎦⎥⎤2k π+2π3,2k π+5π3 (k ∈Z ),所以⎝ ⎛⎭⎪⎫π2,2π3是减区间,⎣⎢⎡⎭⎪⎫2π3,π是增区间,D 项错误.答案 (1)C (2)D三、课后练习1.若对于任意x ∈R 都有f (x )+2f (-x )=3cos x -sin x ,则函数f (2x )图象的对称中心为( )A.⎝ ⎛⎭⎪⎫k π-π4,0(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π-π8,0(k ∈Z ) C.⎝ ⎛⎭⎪⎫k π2-π4,0(k ∈Z ) D.⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ) 解析 因为f (x )+2f (-x )=3cos x -sin x ,所以f (-x )+2f (x )=3cos x +sin x .解得f (x )=cos x +sin x =2sin ⎝ ⎛⎭⎪⎫x +π4,所以f (2x )=2sin ⎝ ⎛⎭⎪⎫2x +π4. 令2x +π4=k π(k ∈Z ),得x =k π2-π8(k ∈Z ).所以f (2x )图象的对称中心为⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ). 答案 D2.(2017·天津卷)设函数f (x )=2sin(ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π,则( ) A.ω=23,φ=π12 B.ω=23,φ=-11π12C.ω=13,φ=-11π24D.ω=13,φ=7π24解析 ∵f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π, ∴f (x )的最小正周期为4⎝ ⎛⎭⎪⎫11π8-5π8=3π, ∴ω=2π3π=23,∴f (x )=2sin ⎝ ⎛⎭⎪⎫23x +φ. ∴2sin ⎝ ⎛⎭⎪⎫23×5π8+φ=2,得φ=2k π+π12(k ∈Z ), 又|φ|<π,∴取k =0,得φ=π12.答案 A3.已知x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,则f (x )的单调递减区间是________.解析 因为x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,所以sin ⎝ ⎛⎭⎪⎫2×π3+φ=1,解得φ=2k π-π6(k ∈Z ). 不妨取φ=-π6,此时f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6, 令2k π+π2≤2x -π6≤2k π+3π2(k ∈Z ),得f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z ). 答案 ⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z )4.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫π2-x sin x -3cos 2x +32. (1)求f (x )的最大值及取得最大值时x 的值;(2)若方程f (x )=23在(0,π)上的解为x 1,x 2,求cos(x 1-x 2)的值.解 (1)f (x )=cos x sin x -32(2cos 2x -1) =12sin 2x -32cos 2x =sin ⎝ ⎛⎭⎪⎫2x -π3. 当2x -π3=π2+2k π(k ∈Z ),即x =512π+k π(k ∈Z )时,函数f (x )取最大值,且最大值为1.(2)由(1)知,函数f (x )图象的对称轴为x =512π+k π(k ∈Z ),∴当x ∈(0,π)时,对称轴为x =512π.又方程f (x )=23在(0,π)上的解为x 1,x 2.∴x 1+x 2=56π,则x 1=56π-x 2,∴cos(x 1-x 2)=cos ⎝ ⎛⎭⎪⎫56π-2x 2=sin ⎝ ⎛⎭⎪⎫2x 2-π3, 又f (x 2)=sin ⎝ ⎛⎭⎪⎫2x 2-π3=23, 故cos(x 1-x 2)=23.5.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x -π6,若对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,则实数m 的最小值是________.解析 因为α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,所以α-π6∈⎣⎢⎡⎦⎥⎤-π,-2π3,则f (α)=sin ⎝ ⎛⎭⎪⎫α-π6∈⎣⎢⎡⎦⎥⎤-32,0,因为对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,所以f (β)在[0,m ]上单调,且f (β)∈⎣⎢⎡⎦⎥⎤0,32,则sin ⎝ ⎛⎭⎪⎫β-π6∈⎣⎢⎡⎦⎥⎤0,32,则β-π6∈⎣⎢⎡⎦⎥⎤0,π3,所以β∈⎣⎢⎡⎦⎥⎤π6,π2,即实数m 的最小值是π2. 答案 π26.(2017·山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( )A.π2B.2π3C.πD.2π解析 ∵y =2⎝ ⎛⎭⎪⎫32sin 2x +12cos 2x =2sin ⎝ ⎛⎭⎪⎫2x +π6, ∴T =2π2=π.答案 C7.(2019·石家庄检测)若⎝ ⎛⎭⎪⎫π8,0是函数f (x )=sin ωx +cos ωx 图象的一个对称中心,则ω的一个取值是( )A.2B.4C.6D.8解析 因为f (x )=sin ωx +cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx +π4,由题意,知f ⎝ ⎛⎭⎪⎫π8=2sin ⎝ ⎛⎭⎪⎫ωπ8+π4=0,所以ωπ8+π4=k π(k ∈Z ),即ω=8k -2(k ∈Z ),当k =1时,ω=6.答案 C8.已知函数f (x )=2sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤-π3,π4上的最小值是-2,则ω的最小值等于( ) A.23 B.32 C.2 D.3解析 ∵ω>0,-π3≤x ≤π4,∴-ωπ3≤ωx ≤ωπ4.由已知条件知-ωπ3≤-π2,∴ω≥32.答案 B9.(2019·湖南十四校联考)已知函数f (x )=2sin ωx -cos ωx (ω>0),若f (x )的两个零点x 1,x 2满足|x 1-x 2|min =2,则f (1)的值为( ) A.102 B.-102 C.2 D.-2解析 依题意可得函数的最小正周期为2πω=2|x 1-x 2|min =2×2=4,即ω=π2,所以f (1)=2sin π2-cos π2=2.答案 C10.(2018·北京卷)设函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx -π6(ω>0).若f (x )≤f ⎝ ⎛⎭⎪⎫π4对任意的实数x 都成立,则ω的最小值为________.解析 由于对任意的实数都有f (x )≤f ⎝ ⎛⎭⎪⎫π4成立,故当x =π4时,函数f (x )有最大值,故f ⎝ ⎛⎭⎪⎫π4=1,πω4-π6=2k π(k ∈Z ),∴ω=8k +23(k ∈Z ).又ω>0,∴ωmin =23. 答案 2311.(2019·北京通州区质检)已知函数f (x )=sin ωx -cos ωx (ω>0)的最小正周期为π.(1)求函数y =f (x )图象的对称轴方程;(2)讨论函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调性. 解 (1)∵f (x )=sin ωx -cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx -π4,且T =π, ∴ω=2,于是f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π4. 令2x -π4=k π+π2(k ∈Z ),得x =k π2+3π8(k ∈Z ).即函数f (x )图象的对称轴方程为x =k π2+3π8(k ∈Z ).(2)令2k π-π2≤2x -π4≤2k π+π2(k ∈Z ),得函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π8,k π+3π8(k ∈Z ). 注意到x ∈⎣⎢⎡⎦⎥⎤0,π2,所以令k =0,得函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调递增区间为⎣⎢⎡⎦⎥⎤0,3π8; 同理,其单调递减区间为⎣⎢⎡⎦⎥⎤3π8,π2.。
三角函数的图像及性质

正弦函数的图象和性质正弦函数的图象和性质要点一:正弦函数性质类型一:正弦函数定义域与值域 例1.求函数lg(2sin 1)y x =-的定义域 【解析】依题意得2sin x -1>0,即1sin 2x >,∴52266k x k ππππ+<<+(k ∈Z ),∴函数的定义域为522,66x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭.例2.求下列函数的值域: (1)y=3―2sin x(2)2sin 23y x π⎛⎫=+ ⎪⎝⎭,,66x ππ⎡⎤∈-⎢⎥⎣⎦;【解析】 (1)∵-1≤sin x ≤1,∴-2≤2sin x ≤2,∴-2≤-2sin x ≤2,∴1≤3-2sin x ≤5,∴函数的值域为[1,5].(2)∵66x ππ-≤≤,∴20233x ππ≤+≤. ∴0sin 213x π⎛⎫≤+≤ ⎪⎝⎭.∴02sin 223x π⎛⎫≤+≤ ⎪⎝⎭,∴0≤y ≤2.∴函数的值域为[0,2]. 举一反三:【变式】 求y=cos 2x+4sin x ―2的值域. 【解析】y=cos 2x+4sin x ―2=―sin 2x+4sin x ―1 =―(sin x ―2)2+3. ∵-1≤sin x ≤1,∴当sin x=―1时,y min =―6;当sin x=1时,y max =2. ∴函数的值域为[-6,2]. 类型二:正弦函数单调性例3.求2sin 4y x π⎛⎫=- ⎪⎝⎭的单调区间.【解析】∵2sin 2sin 44y x x ππ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭,∴函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递增区间就是函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递减区间.∴322242k x k πππππ+≤-≤+(k ∈Z ),得372244k x k ππππ+≤≤+(k ∈Z ).∴函数2sin 4y x π⎛⎫=- ⎪⎝⎭的递增区间为372,244k k ππππ⎡⎤++⎢⎥⎣⎦(k ∈Z ).举一反三:【变式】求函数sin 23y x π⎛⎫=- ⎪⎝⎭的递减区间.【解析】已知函数sin 2sin 233y x x ππ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭.欲求该函数的单调递减区间,只需求sin 23y x π⎛⎫=- ⎪⎝⎭的单调递增区间.由222232k x k πππππ-≤-≤+(k ∈Z ),解得51212k x k ππππ-≤≤+(k ∈Z ). 所以原函数的单调递减区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z ).类型三:正弦函数的奇偶性 例4.判断下列函数的奇偶性:5())2f x x π=+;【解析】函数定义域为R ,且5()2s i n 2c o s 222f x x x x ππ⎛⎫⎛⎫=+=+=⎪⎪⎝⎭⎝⎭,显然有()()f x f x -=恒成立.∴函数5()22f x x π⎛⎫=+ ⎪⎝⎭为偶函数.举一反三:【变式1】()f x =; 【解析】由2sin x -1>0,即1s i n 2x >,得函数定义域为52,266k k ππππ⎛⎫++ ⎪⎝⎭(k ∈Z ),此定义域在x 轴上表示的区间不关于原点对称.∴该函数不具有奇偶性,为非奇非偶函数. 类型四:三角函数图象的综合应用例5.(1)方程lg sin x x =的解的个数为( ) A .0 B .1 C .2 D .3 (2)若02x π<<,则2x 与3sin x 的大小关系为( )A .23sin x x >B .23sin x x <C .23sin x x =D .与x 的取值有关【解析】(1) 作出lg y x =与sin y x =的图象,当52x π=时,5lg 12y π=<,5sin 12y π==,当92x π=时,9lg 12y π=>,lg y x =与sin y x =再无交点。
三角函数图像与性质
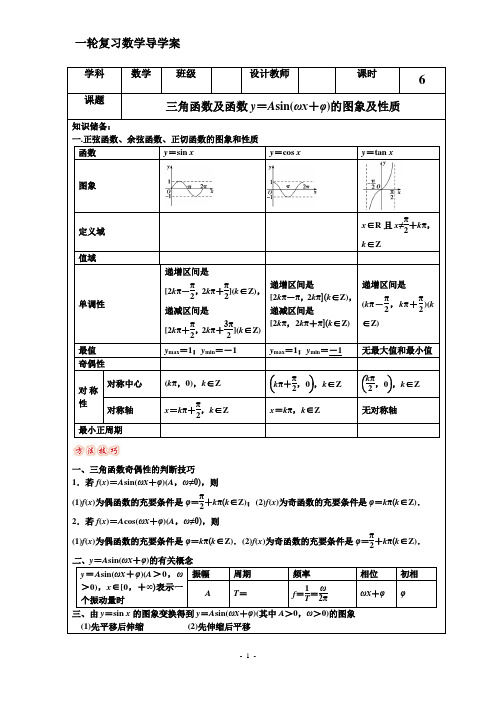
图3-4-2 A.2,- B.2,- C.4,- D.4,
自测后你觉得哪类题做起来困难呢?那我们一起来解决吧!
典例:
题型一三角函数的定义域和值域
(1)函数y= 的定义域为________.
A.向右平移 个单位B.向右平移 个单位C.向左平移 个单位D.向左平移 个单位
3.[2014·福建卷]将函数y=sinx的图像向左平移 个单位,得到函数y=f(x)的图像,则下列说法正确的是()
A.y=f(x)是奇函数B.y=f(x)的周期为π
C.y=f(x)的图像关于直线x= 对称D.y=f(x)的图像关于点 对称
导疑:由解析式求函数定义域应考虑________.
导学:由tanx-1 0得tanx 1所以x ________.
所以所求定义域为________.
(2)求下列函数的值域①y=2cos2x+2cosx②y=3cosx- sinx,x∈[0,π];
导疑:二次函数给定区间如何求值域?形如y=Asin(ωx+φ)函数的值域?
A. B.
C. D.
2.函数f(x)=2cos 是()
A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数
C.最小正周期为2π的非奇非偶函数D.最小正周期为π的偶函数
3.函数f(x)=sin 的图象的一条对称轴是()
A.x= B.x= C.x=- D.x=-
4.比较大小:sin ________sin .
A.A=3,T= ,φ=- B.A=1,T= ,φ=
C.A=1,T= ,φ=- D.A=1,T= ,φ=-
图3-4-3图3-4-4
高中数学必修一-三角函数图像性质总结(精华版)

(2) /(航+如型三角函数的奇偶性(i ) g (x ) = /沏(颜+如(x€ R)(x)为偶函数匕鼠U 力(而+ 出=j4sin (-<at + 炉)(x W 氏)0 sin 曲匚*0=。
(工 W R )7Tcos 卯=。
=上7T+一1左 e Z )由此得 2 ,同理,式夫4皿皈+双相的 为奇函数 =顺@=0/3=上网海2)(ii )飙# =+劭SwR]妖N = .Aa 式题+钠为偶函数见双t");就= 式以+如为奇函数7T=中=无产+ — (k e Z)3、周期性(1)基本公式(ii) 〃皈+⑺+氏型三角函数的周期竺y =+ G + 5 =加+中出 的周期为何;(一)三角函数的性质1、定义域与值域2、奇偶性(1)基本函数的奇偶性奇函数:y = sinx y= tanx ; 偶函数:y=cosx.(i )基本三角函数的周期的周期为;丁.y=sinx , y=cosx 的周期为 之并 ;y = tanx , y = cotx4-212yy=cotxy=tanx 3-32X 03 27 3,y=cosx-5-4 .7223 2322 5 2“如血的+朗+9=心服如+沟+用的周期为何.(2)认知⑴A =1/W +创型函数的周期y = |月劭(枷+或)| j = A 匚。
5(西+励|(ii )若函数为,(收斗劭 型两位函数之和,则探求周期适于“最小公倍数法”. (iii )探求其它“杂”三角函数的周期,基本策略是试验一一猜想一一证明.(3)特殊情形研究JT(i ) y = tanx — cotx 的最小正周期为27T(ii ) y=卜由H+|M 幻的最小正周期为,;7T(iii ) y = sin 4x + cos 4x 的最小正周期为,. _由此领悟“最小公倍数法”的适用类型,以防施错对象 .4、单调性(1)基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”:①选周期:在原点附近选取那个包含全部锐角,单调区间完整,并且最好关于原点对称的 一个周期;②写特解:在所选周期内写出函数的增区问(或减区问);③获通解:在②中所得特解区间两端加上有关函数的最小正周期的整数倍,即得这一函数 的增区间族(或减区间族)循着上述三部曲,便可得出课本中规范的三角函数的单调区间族 .揭示:上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域(2) y=/(而+初 型三角函数的单调区问的周期为y = (助+切1_r= |达匚祖(姗+阖| 的周期为 7T(ii) > = 1/(耽+如+同3=0)的周期1y 二|金£血(为工卜8]妣+3)+甘¥ = |例如(而+5+上] J = |总二加侬大+的+. 的周期为祠;,7T的周期为:. 均同它们不加绝对值时的周期相同,即对 数的周期不变.注意这一点与(i )的区别.y=八加+◎+上的解析式施加绝对值后,该函此类三角函数单调区间的寻求“三部曲”为 ①换元、分解:令u =z 中,将所给函数分解为内、外两层:y = f (u) , u =®x+卯;②套用公式:根据对复合函数单调性的认知,确定出 f (u)的单调性,而后利用(1)中公 式写出关于u 的不等式;③还原、结论:将u =^+W 代入②中u 的不等式,解出x 的取值范围,并用集合或区间 形成结论.正弦、余弦、正切、余切函数的图象的性质:/y sinx y cosxy tanxy cotxy Asin x(A 、 >0)定义域 R R x | x R 且 x k 1 ,k Zx| x R 且x k ,k ZR值域 [1, 1][1, 1]R RA, A周期性 2 22奇偶性奇函数 偶函数奇函数 奇函数当 0,非奇非偶 当0,奇函数单调性[2 2k , —2k ] 2上为增函 数; [2 2k ,3——2k ] 2上为减函 数(k Z )[2k 1 , 2k ]上为增函 数[2k , 2k 1 ]上为减函数(k Z )一k ,一 k 2 2 上为增函数(k Z )k , k 1上为减函数(k Z )2k2(A),2k -2( A)上为增函数;2k 一------ 2— (A), 2k------ 2——(A)上为减函数(k Z )注意:①y sinx 与y sinx 的单调性正好相反;y cosx 与y cosx 的单调性也同样相反.一般 地,若y f(x)在[a,b ]上递增(减),则y f (x)在[a,b ]上递减(增)y忖n x 与y cosx 的周期是.-(k Z),对称中心(k ,0); y cos( x )的对称轴方); y tan( x )的对称中心(工,0).,02③ y sin( x )或 y cos( x )0)的周期T 2y tan x 的周期为2 2 (T _ T 2,如图,翻折无效)④y sin( x )的对称轴方程是x k 程是x k (k Z ),对称中心(ky cos2x 原点对称 y cos( 2x) cos2x⑤ 当 tan tan 1, k ,(k Z) ; tan tan 1, k ,(k Z).⑥y cosx 与y s in x _ 2k是同一函数,而y ( x )是偶函数,则2 1 、,、y ( x ) sin( x k ) cos( x).2⑦函数y tanx 在R 上为增函数.(耳[只能在某个单调区间单调递增 .若在整个定义域,y tanx 为增函数,同样也是错误的].⑧定义域关于原点对称是f (x)具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域 关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数:f( x) f(x),奇函数:f( x) f(x)) 奇偶性的单调性:奇同偶反.例如:y tanx 是奇函数,y tan(x 1)是非奇非偶.(定义域不 3 关于原点对称)奇函数特有性质:若0 x 的定义域,则f(x)一定有f(0) 0. (0 x 的定义域,则无此性质)⑨y sinx 不是周期函数;y sinx 为周期函数(T ); y cosx 是周期函数(如图);y cosx 为周期函数(T );y cos2x1的周期为(如图),并非所有周期函数都有最小正周期,2y f (x) 5 f (x k),k R . ⑩ y a cos bsinVa 2 b 2sin( ) cos b 有 Va 2 b 2 y .、形如y Asin( x )的函数:11、几个物理量:A 一振幅;f 1—频率(周期的倒数);x 一相包; 一初相;2、函数y Asin( x )表达式的确定:A 由最值确定; 由周期确定; 由图象上的特殊点确定,如 f(x) Asin( x )(A 0,0, | 3.函数 y Asin( x ) B (其中 A 0,0)最大值是A B,最小值是B A,周期是T —,最小正周期T 六频率是f「相位是x,初相是;其图象的对称轴是直线x k 7k Z),凡| "^0的图象如图所小,则f (x)(答:f(x)152sin(-2x -));y=| cos2x+1/2|图象是该图象与直线y B 的交点都是该图象的对称中心4、研究函数y Asin( x )性质的方法:类比于研究y sin x 的性质,只需将y Asin( x ) 中的x 看成y sinx 中的x,但在求y Asin( x )的单调区间时,要特别注意 A 和 的 符号,通过诱导公式先将 化正。
高中数学第五章三角函数正弦函数余弦函数的图象与性质第3课时正弦函数余弦函数的单调性与最值学生用书湘教

第3课时 正弦函数、余弦函数的单调性与最值教材要点要点 正、余弦函数的图象与性质正弦函数余弦函数图象值域________________单调性在________________(k ∈Z )上递增,在________________(k ∈Z )上递减在________________(k ∈Z )上递增,在________________(k ∈Z )上递减最值x =________(k ∈Z )时,y max =1;x =________(k ∈Z )时,y min =-1x =________(k ∈Z )时,y max =1;x =________(k ∈Z )时,y min =-1状元随笔 (1)正、余弦函数的单调性:①求解或判断正弦函数、余弦函数的单调区间(或单调性)是求与之相关的复合函数值域(最值)关键的一步;②单调区间要在定义域内求解;③确定含有正弦函数或余弦函数的复合函数的单调性时,要注意用复合函数法来判断.(2)正、余弦函数的最值①明确正、余弦函数的有界性,即|sin x|≤1, |cos x|≤1;②对有些函数,其最值不一定就是1或-1,要依赖函数的定义域来决定;③形如y =A sin (ωx +φ)(A >0,ω>0)的函数求最值时,通常利用“整体代换”,即令ωx +φ=z ,将函数转化为y =A sin z 的形式求最值.基础自测1.思考辨析(正确的画“√”,错误的画“×”)(1)在区间[0,3π]上,函数y =cos x 仅在x =0时取得最大值1.( )(2)正弦函数在第一象限是增函数.( )(3)存在实数x,使得cos x=√2.( )(4)余弦函数y=cos x在[0,π]上是减函数.( )2.下列函数中,既为偶函数又在(0,π)上单调递增的是( ) A.y=cos|x| B.y=cos|-x|C.y=sin (x-π2) D.y=-sinx23.函数y=1-2cos π2x的最小值,最大值分别是( )A.-1,3B.-1,1 C.0,3D.0,14.比较大小:sin 3π5________cosπ5.题型1 正弦、余弦函数的单调性例1 求函数y=√2sin (π4−2x)的单调区间.方法归纳求与正、余弦函数有关的单调区间的策略(1)结合正、余弦函数的图象,熟记它们的单调区间.(2)在求形如y=A sin (ωx+φ)(A>0,ω>0)的函数的单调区间时,应采用“换元法”整体代换,将“ωx+φ”看作一个整体“z”,即通过求y=A sin z的单调区间而求出原函数的单调区间.求形如y=A cos (ωx+φ)(A>0,ω>0)的函数的单调区间同上.(3)①ω<0时,一般用诱导公式转化为-ω>0后求解;②若A<0,则单调性相反.跟踪训练1 (1)函数f(x)=2sin (x-〖(π)/(3)〗),x∈[-π,0]的单调递增区间是( )A.B.C.D.(2)函数y=cosπx的单调减区间为________.题型2 单调性在三角函数中的应用角度1 比较大小例2 比较下列各组数的大小.(1)sin 21π5与sin42π5.(2)cos 17π8与cos37π9方法归纳比较三角函数值大小的方法(1)利用诱导公式转化为求锐角三角函数值.(2)不同名的函数化为同名函数.(3)自变量不在同一单调区间化至同一单调区间.角度2 利用正弦、余弦函数的单调性求参数例3 已知ω>0,函数f(x)=sin (ωx+π4)在(π2,π)上单调递减,则ω的取值范围是( )A.B.C.D.(0,2)方法归纳对于已知形如y=A sin (ωx+φ)或y=A cos (ωx+φ)(A>0,ω>0)的函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子区间;其次,要确定已知函数的单调区间,从而利用它们之间的关系求解.跟踪训练2 (1)sin1,sin2,sin3的大小关系是( )A.sin1<sin2<sin3B.sin3<sin2<sin1C.sin2<sin3<sin1D.sin3<sin1<sin2(2)若函数f(x)=cos2ωx(ω>0)在区间上为减函数,在区间上为增函数,则ω等于( )A.3B.2C.32D.23 三角函数的值域(或最值)问题角度1 正弦、余弦函数的值域(或最值)问题例4 求函数y=2sin (2x−π3),x∈[π3,3π4]的值域方法归纳形如y=A sin (ωx+φ)或y=A cos (ωx+φ)的三角函数值域(或最值)问题,要注意x的取值范围.一般情况下先利用x的取值范围,求出ωx+φ的范围,再求三角函数的值域(或最值).角度2 形如y=A sin2x+B sin x+C或y=A cos2x+B cos x+C型的最值(或值域)问题例5 求函数y=cos2x-sin x,x∈[−π3,π6]的最大值和最小值及相应的x值.方法归纳求形如y=A sin2x+B sin x+C,A≠0,x∈R的函数的值域或最值时,可以通过换元,令t=sin x,将原函数转化为关于t的二次函数,利用配方法求值域或最值,求解过程中要注意正弦函数的有界性(有时也用t来替换cos x).跟踪训练3 (1)函数y=2cos(2x+π6)-1的最小值是________,此时x=________.(2)函数y=y=2sin2x+2sin x-12,x∈[π6,5π6]的值域是________.易错辨析 忽视参数的分类致误例6 已知函数y=2a sin (2x−π3)+b的定义域为[0,π2],函数的最大值为1,最小值为-5,求a和b的值.解析:∵0≤x≤π2,∴-π3≤2x-π3≤2π3.∴-√32≤sin(2x−π3)≤1.若a>0,则{2a+b=1,−√3a+b=−5,解得{a=12−6√3,b=−23+12√3.若a<0,则{2a+b=−5,−√3a+b=1,解得{a=−12+6√3,b=19−12√3.易错警示易错原因纠错心得只考虑a>0的情况,漏掉了a<0的情况,导致丢解.形如y=A sin (ωx+φ)+B或y=A cos (ωx +φ)+B的函数,其最值与参数A的正负有关,因此在解决这类问题时,要注意对A分A>0和A<0两种情况进行分类讨论.课堂十分钟1.下列不等式中成立的是( ) A.sin (−π8)>sin (−π10)B.sin 3>sin 2C.sin 75π>sin (−25π)D.sin 2>cos 12.函数y=sin (−2x+π3)在区间[0,π]上的单调递增区间为( ) A.[5π12,11π12]B.[0,5π12]C.[π6,2π3]D.[2π3,π]3.已知函数f(x)=2sin (2x+π6)-1(x∈R),则f(x)在区间[0,π2]上的最大值与最小值分别是( )A.1,-2B.2,-1C.1,-1D.2,-24.已知函数f(x)=sinωx(ω>0),若f(x)在[0,π2]上单调递增,则实数ω的取值范围是________.5.求函数y=cos2x-4cos x+1,x∈[π3,2π3]的值域.第3课时 正弦函数、余弦函数的单调性与最值新知初探·课前预习要点[-1,1] [-1,1] [2kπ−π2,2kπ+π2][2kπ+π2,2kπ+3π2] [2kπ-π,2kπ] [2kπ,2kπ+π] 2kπ+π2 2kπ-π2 2kπ 2kπ+π[基础自测]1.答案:(1)× (2)× (3)× (4)√2.解析:y=cos |x|在(0,π2)上是减函数,排除A;y=cos |-x|=cos |x|,排除B;y=sin (x−π2)=-sin (π2−x)=-cos x是偶函数,且在(0,π)上单调递增,符合题意;y=-sin x2在(0,π)上是单调递减的,排除D.故选C.答案:C3.解析:∵-1≤cos π2x≤1,∴-1≤y≤3.故选A.答案:A 4.解析:sin 3π5=sin (π2+π10)=cos π10.∵0<π10<π5<π,y =cos x 在[0,π]上递减,∴cosπ10>cos π5,即sin 3π5>cos π5.答案:>题型探究·课堂解透例1 解析:∵y =√2sin (π4−2x )=-√2sin (2x−π4),∴由π2+2k π≤2x -π4≤3π2+2k π(k ∈Z ),得3π8+k π≤x ≤7π8+k π,k ∈Z .所以函数y =√2sin (π4−2x )的单调增区间为[kπ+3π8,kπ+7π8](k ∈Z ),由2k π-π2≤2x -π4≤π2+2k π,(k ∈Z ),得k π-π8≤x ≤k π+3π8(k ∈Z ).所以函数y =√2sin(π4−2x )的单调减区间为[kπ−π8,kπ+3π8](k ∈Z ).跟踪训练1 解析:(1)令2k π-π2≤x -π3≤2k π+π2,k ∈Z ,解得2k π-π6≤x ≤2k π+5π6,k ∈Z ,又∵-π≤x ≤0,∴-π6≤x ≤0.故选D.(2)由2k π≤πx ≤π+2k π,k ∈Z 得2k ≤x ≤1+2k ,k ∈Z ,即函数y =cos πx 的单调减区间为[2k ,2k +1](k ∈Z ).答案:(1)D (2)[2k ,2k +1](k ∈Z )例2 解析:(1)∵sin 21π5=sin (4π+π5)=sin π5,sin42π5=sin (8π+2π5)=sin 2π5,又∵y =sin x 在[0,π2]上单调递增,且0<π5<2π5<π2,∴sin π5<sin2π5,∴sin 21π5<sin 42π5.(2)∵cos 17π8=cos (2π+π8)=cos π8,cos37π9=cos (4π+π9)=cos π9.又∵y =cos x 在[0,π]上单调递减,∴cos π9>cos π8,∴cos37π9>cos 17π8.例3 解析:方法一 由π2<x <π,ω>0,得ωπ2+π4<ωx +π4<ωπ+π4.又因为y =sin x 在(π2,3π2)上单调递减,所以{ωπ2+π4≥π2,ωπ+π4≤3π2.解得12≤ω≤54,故选A.方法二 由π2+2k π≤ωx +π4≤3π2+2k π,k ∈Z ,ω>0,得π4ω+2kπω≤x ≤5π4ω+2kπω,k ∈Z .因此函数f (x )的单调递减区间为[π4ω+2kπω,5π4ω+2kπω],k ∈Z .由题意知(π2,π) [π4ω,5π4ω],所以{π2≥π4ω,π≤5π4ω.解得12≤ω≤54,故选A.答案:A跟踪训练2 解析:(1)sin 2=sin (π-2),sin 3=sin (π-3).∵0<π-3<1<π-2<π2,y=sin x在[0,π2]上为增函数,∴sin (π-3)<sin 1<sin (π-2),故sin 3<sin1<sin 2.故选D.(2)因为y=cos x在[0,π]上为减函数,在[π,2π]上为增函数,所以当0≤2ωx≤π,即0≤x≤π2ω时,f(x)=cos 2ωx(ω>0)为减函数,当π≤2ωx≤2π,即π2ω≤x≤πω时,f(x)=cos 2ωx(ω>0)为增函数,由题意知π2ω=π3,∴ω=32.故选C.答案:(1)D (2)C例4 解析:∵x∈[π3,3π4],∴2x∈[2π3,3π2],∴(2x−π3)∈[π3,7π6],∴sin (2x−π3)∈[−12,1].∴2sin (2x−π3)∈[-1,2],故f(x)=2sin (2x−π3)在[π3,3π4]上的值域为[-1,2].例5 解析:y=cos2x-sin x=1-sin2x-sin x=-sin2x-sin x+1,令sin x=t,∵x∈[−π3,π6],∴t∈[−√32,12],∴y =-t 2-t +1=-(t +12)2+54,∴当t =-12,即x =-π6时,f (x )有最大值,f (x )max =54;当t =12,即x =π6时,f (x )有最小值,f (x )min =14.跟踪训练3 解析:(1)当2x +π6=π+2k π,k ∈Z ,x =5π12+k π,k ∈Z ,y min =-2-1=-3.(2)令t =sin x ,∵x ∈[π6,5π6],∴t ∈[12,1],∴y =2t 2+2t -12=2(t +12)2-1,∴y ∈[1,72],故函数f (x )的值域为[1,72].答案:(1)-3 5π12+k π,k ∈Z (2)[1,72][课堂十分钟]1.解析:因为sin 2=cos (π2−2)=cos (2−π2),且0<2-π2<1<π,所以cos (2−π2)>cos 1,即sin 2>cos 1.故选D.答案:D2.解析:y =sin (−2x +π3)=-sin (2x−π3),当2k π+π2≤2x -π3≤2k π+3π2,即k π+5π12≤x ≤k π+11π12时,k ∈Z ,函数单调递增,∴函数在区间[0,π]上的单调递增区间为[5π12,11π12].故选A.答案:A3.解析:∵0≤x≤π2,∴π6≤2x+π6≤7π6,∴当2x+π6=π2时,即sin (2x+π6)=1时,函数取得最大值为2-1=1,当2x+π6=7π6时,即sin (2x+π6)=-12时,函数取得最小值为(−12)×2-1=-2.故选A.答案:A4.解析:由题意知:ω×π2≤π2,即0<ω≤1.答案:(0,1]5.解析:∵x∈[π3,2π3],∴-12≤cos x≤12.∵y=cos2x-4cos x+1=(cos x-2)2-3,∴当cos x=-12时,y max=134;当cos x=12时,y min=-34,∴y=cos2x-4cos x+1的值域为[−34,134].。
(完整版)三角函数公式和图像大全(最新整理)

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα反三角函数的图形设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
高中数学-三角函数图像及性质与值域及最值

高中数学总复习- 三角函数第5课 三角函数的图像和性质(一) 【考点导读】1.能画出正弦函数,余弦函数,正切函数的图像,借助图像理解正弦函数,余弦函数在[0,2]π,正切函数在(,)22ππ-上的性质; 2.了解函数sin()y A x ωϕ=+的实际意义,能画出sin()y A x ωϕ=+的图像; 3.了解函数的周期性,体会三角函数是描述周期变化现象的重要函数模型. 【基础练习】1. 已知简谐运动()2sin()()32f x x ππϕϕ=+<的图象经过点(0,1),则该简谐运动的最小正周期T =_____6____;初相ϕ=______6π____.2. 三角方程2sin(2π-x )=1的解集为_______________________. 3. 函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达为_)48sin(4π+π-=x y _.4. 要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象向右平移______π6____个单位.【范例解析】例1.已知函数()2sin (sin cos )f x x x x =+.(Ⅰ)用五点法画出函数在区间,22ππ⎡⎤-⎢⎥⎣⎦上的图象,长度为一个周期;(Ⅱ)说明()2sin (sin cos )f x x x x =+的图像可由sin y x =的图像经过怎样变换而得到.{2,}3x x k k Z ππ=±∈分析:化为sin()A x ωϕ+形式.解:(I )由x x x x x x f 2sin 2cos 1cos sin 2sin 2)(2+-=+=)42sin(21)4sin 2cos 4cos 2(sin 21πππ-+=-⋅+=x x x .列表,取点,描图:x 83π- 8π-8π 83π 85π y121-121+1故函数)(x f y =在区间]2,2[-上的图象是:(Ⅱ)解法一:把sin y x =图像上所有点向右平移4π个单位,得到sin()4y x π=-的图像,再把sin()4y x π=-的图像上所有点的横坐标缩短为原来的12(纵坐标不变),得到sin(2)4y x π=-的图像,然后把sin(2)4y x π=-的图像上所有点纵坐标伸长到原来的2倍(横坐标不变),得到2sin(2)4y x π=-的图像,再将2sin(2)4y x π=-的图像上所有点向上平移1个单位,即得到12sin(2)4y x π=+-的图像.解法二:把sin y x =图像上所有点的横坐标缩短为原来的12(纵坐标不变),得到sin 2y x =的图像,再把sin 2y x =图像上所有点向右平移8π个单位,得到sin(2)4y x π=-的图像,然后把sin(2)4y x π=-的图像上所有点纵坐标伸长到原来,得到)4y x π=-的图像,再将)4y x π=-的图像上所有点向上平移1个单位,即得到1)4y x π=+-的图像.例2.已知正弦函数sin()y A x ωϕ=+(0,0)A ω>>的图像如右图所示. (1)求此函数的解析式1()f x ;(2)求与1()f x 图像关于直线8x =对称的曲线的解析式2()f x ; (3)作出函数12()()y f x f x =+的图像的简图.分析:识别图像,抓住关键点.解:(1)由图知,A =22(62)16πω=⨯+=Q ,8πω∴=,即sin()8y x πϕ=+. 将2x =,y =代入,得sin()4πϕ+=,解得4πϕ=,即1()sin()84f x x ππ=+.(2)设函数2()f x 图像上任一点为(,)M x y ,与它关于直线8x =对称的对称点为(,)M x y ''',得8,2.x x y y '+⎧=⎪⎨⎪'=⎩解得16,.x x y y '=-⎧⎨'=⎩代入1()sin()84f x x ππ''=+中,得2()sin()84f x x ππ=-.(3)12()()sin()sin()2cosy f x f x x x x πππππ=+=+--=,简图如图所示.点评:由图像求解析式,A 比较容易求解,困难的是待定系数求ω和ϕ,通常利用周期确定ω,代入最高点或最低点求ϕ.【反馈演练】1.为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数2sin y x =,x R ∈的图像上所有的点 ①向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变); ②向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变); ③向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变); ④向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变).其中,正确的序号有_____③______.2.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向右平移__3π__个单位长度.3.若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)3f =,则ω=__2____;ϕ=__________.4.在()π2,0内,使x x cos sin >成立的x 取值范围为____________________. 5.下列函数:①sin 6y x π⎛⎫=+ ⎪⎝⎭; ②sin 26y x π⎛⎫=- ⎪⎝⎭;③cos 43y x π⎛⎫=- ⎪⎝⎭; ④cos 26y x π⎛⎫=- ⎪⎝⎭.其中函数图象的一部分如右图所示的序号有_____④_____.6.如图,某地一天从6时至14时的温度变化曲线近似满足函数b x A y ++=)sin(ϕω(1)求这段时间的最大温差; (2)写出这段时间的函数解析式.解:(1)由图示,这段时间的最大温差是201030=-℃(2)图中从6时到14时的图象是函数b x A y ++=)sin(ϕω的半个周期∴614221-=⋅ωπ,解得8πω=由图示,10)1030(21=-=A 20)3010(21=+=b这时,20)8sin(10++=ϕπx y将10,6==y x 代入上式,可取43πϕ= 综上,所求的解析式为20)438sin(10++=ππx y (]14,6[∈x )7.如图,函数π2cos()(00)2y x x >ωθωθ=+∈R ,,≤≤的图象与y 轴相交于点(03),,且该函数的最小正周期为π. (1)求θ和ω的值;(2)已知点π02A ⎛⎫⎪⎝⎭,,点P 是该函数图象上一点,点00()Q x y ,是的中点,第6题 3π 5,44ππ⎛⎫ ⎪⎝⎭第5题y x 3O PA第7题当0y =0ππ2x ⎡⎤∈⎢⎥⎣⎦,时,求0x 的值.解:(1)将0x =,y =2cos()y x ωθ=+得cos θ=因为02θπ≤≤,所以6θπ=.又因为该函数的最小正周期为π,所以2ω=,因此2cos 26y x π⎛⎫=+ ⎪⎝⎭.(2)因为点02A π⎛⎫⎪⎝⎭,,00()Q x y ,是PA 的中点,02y =,所以点P 的坐标为022x π⎛- ⎝.又因为点P 在2cos 26y x π⎛⎫=+ ⎪⎝⎭的图象上,所以05cos 46x π⎛⎫-= ⎪⎝⎭因为02x ππ≤≤,所以075194666x πππ-≤≤,从而得0511466x ππ-=或0513466x ππ-=. 即023x π=或034x π=.第6课 三角函数的图像和性质(二) 【考点导读】1.理解三角函数sin y x =,cos y x =,tan y x =的性质,进一步学会研究形如函数sin()y A x ωϕ=+的性质;2.在解题中体现化归的数学思想方法,利用三角恒等变形转化为一个角的三角函数来研究. 【基础练习】1.写出下列函数的定义域: (1)y =______________________________; (2)sin 2cos x y x=的定义域是____________________. 2.函数f (x ) = | sin x +cos x |的最小正周期是____________.3.函数 22sin sin 44f x x x ππ=+--()()()的最小正周期是_______. 4. 函数y =sin(2x +3π)的图象关于点_______________对称. 5. 已知函数tan y x ω= 在(-2π,2π)内是减函数,则ω的取值范围是______________. 【范例解析】例1.求下列函数的定义域: (1)sin tan xy x =+(2)y = 解:(1),2tan 0,2sin 10.x k x x ππ⎧≠+⎪⎪≠⎨⎪+≥⎪⎩即,2,722.66x k x k k x k πππππππ⎧≠+⎪⎪≠⎨⎪⎪-≤≤+⎩,故函数的定义域为7{2266x k x k ππππ-≤≤+且,x k π≠,}2x k k Z ππ≠+∈ {663,}x k x k k Z πππ≤≤+∈ {,}2x x k k Z ππ≠+∈ π π (3π,0) 10ω-≤<(2)122log 0,tan 0.x x +≥⎧⎪⎨⎪≥⎩即04,.2x k x k πππ<≤⎧⎪⎨≤<+⎪⎩故函数的定义域为(0,)[,4]2ππ⋃. 点评:由几个函数的和构成的函数,其定义域是每一个函数定义域的交集;第(2)问可用数轴取交集.例2.求下列函数的单调减区间:(1)sin(2)3y x π=-; (2)2cos sin()42x y x π=-;解:(1)因为222232k x k πππππ-≤-≤+,故原函数的单调减区间为5[,]()1212k k k Z ππππ-+∈. (2)由sin()042x π-≠,得{2,}2x x k k Z ππ≠+∈,又2cos 4sin()24sin()42x x y x ππ==+-, 所以该函数递减区间为3222242x k k πππππ+<+<+,即5(4,4)()22k k k Z ππππ++∈. 点评:利用复合函数求单调区间应注意定义域的限制. 例3.求下列函数的最小正周期:(1)5tan(21)y x =+;(2)sin sin 32y x x ππ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭ .解:(1)由函数5tan(21)y x =+的最小正周期为π2,得5tan(21)y x =+的周期2T π=. (2)sin()sin()(sin cos cos sin )cos 3233y x x x x x ππππ=++=+2111cos 2sin cos cos sin 222422x x x x x +=+=+1sin(2)23x π=++ T π∴=. 点评:求三角函数的周期一般有两种:(1)化为sin()A x ωϕ+的形式特征,利用公式求解;(2)利用函数图像特征求解.【反馈演练】1.函数x x y 24cos sin +=的最小正周期为_____________.2.设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ,则()f x 在[0,2]π上的单调递减区间为___________________.3.函数()sin ([,0])f x x x x π=∈-的单调递增区间是________________.4.设函数()sin 3|sin 3|f x x x =+,则()f x 的最小正周期为_______________. 5.函数22()cos 2cos 2xf x x =-在[0,]π上的单调递增区间是_______________. 6.已知函数π124()πsin 2x f x x ⎛⎫- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭. (Ⅰ)求()f x 的定义域; (Ⅱ)若角α在第一象限且3cos 5α=,求()f α. 解:(Ⅰ) 由πsin 02x ⎛⎫+≠ ⎪⎝⎭得ππ2x k ≠-+,即ππ2x k ≠-()k ∈Z .故()f x 的定义域为π|π2x x k k ⎧⎫∈≠-∈⎨⎬⎩⎭R Z ,.(Ⅱ)由已知条件得4sin 5α===.从而π124()πsin 2f ααα⎛⎫- ⎪⎝⎭=⎛⎫+ ⎪⎝⎭ 2π[,0]6π-32π [,]3ππ 2[,]63ππ,75[,]63ππππ1cos2cos sin2sin44cosααα⎫++⎪⎝⎭=21cos2sin22cos2sin coscos cosααααααα+++==142(cos sin)5αα=+=.7.设函数)(),()2sin()(xfyxxf=<<-+=ϕπϕ图像的一条对称轴是直线8π=x.(Ⅰ)求ϕ;(Ⅱ)求函数)(xfy=的单调增区间;(Ⅲ)画出函数)(xfy=在区间],0[π上的图像解:(Ⅰ))(8xfyx==是函数πΘ的图像的对称轴,,1)82sin(±=+⨯∴ϕπ,.42k k Zππϕπ∴+=+∈.43,0πϕϕπ-=<<-Θ(Ⅱ)由(Ⅰ)知).432sin(,43ππϕ-=-=xy因此由题意得.,2243222Zkkxk∈+≤-≤-πππππ所以函数.],85,8[)432sin(Zkkkxy∈++-=πππππ的单调增区间为(Ⅲ)由知)32sin(π-=xy故函数上图像是在区间],0[)(πxfy=第7课 三角函数的值域与最值 【考点导读】1.掌握三角函数的值域与最值的求法,能运用三角函数最值解决实际问题;2.求三角函数值域与最值的常用方法:(1)化为一个角的同名三角函数形式,利用函数的有界性或单调性求解;(2)化为一个角的同名三角函数形式的一元二次式,利用配方法或图像法求解;(3)借助直线的斜率的关系用数形结合求解;(4)换元法. 【基础练习】1.函数x x y cos 3sin +=在区间[0,]2π上的最小值为 1 .2.函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于 .3.函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是___________________. 4.当20π<<x 时,函数x xx x f 2sin sin 82cos 1)(2++=的最小值为 4 .【范例解析】例1.(1)已知1sin sin 3x y +=,求2sin cos y x -的最大值与最小值.(2)求函数sin cos sin cos y x x x x =⋅++的最大值. 分析:可化为二次函数求最值问题.解:(1)由已知得:1sin sin 3y x =-,sin [1,1]y ∈-Q ,则2sin [,1]3x ∈-.22111sin cos (sin )212y x x ∴-=--,当1sin 2x =时,2sin cos y x -有最小值1112-;当2sin 3x =-时,2sin cos y x -有最小值49.(2)设sin cos x x t +=(t ≤≤,则21sin cos 2t x x -⋅=,则21122y t t =+-,当t =时,y有最大值为12点评:第(1)小题利用消元法,第(2)小题利用换元法最终都转化为二次函数求最值问题;但要注意变量的取值范围.43(,1][1,)-∞-⋃+∞例2.求函数2cos (0)sin xy x xπ-=<<的最小值. 分析:利用函数的有界性求解.解法一:原式可化为sin cos 2(0)y x x x π+=<<,得)2x ϕ+=,即sin()x ϕ+=1≤,解得y ≥y ≤,所以y 解法二:2cos (0)sin xy x xπ-=<<表示的是点(0,2)A 与(sin ,cos )B x x -连线的斜率,其中点B 在左半圆221(0)a b a +=<上,由图像知,当AB 与半圆相切时,y 最小,此时AB k =y点评:解法一利用三角函数的有界性求解;解法二从结构出发利用斜率公式,结合图像求解.例3.已知函数2π()2sin 24f x x x ⎛⎫=+- ⎪⎝⎭,ππ42x ⎡⎤∈⎢⎥⎣⎦,.(I )求()f x 的最大值和最小值;(II )若不等式()2f x m -<在ππ42x ⎡⎤∈⎢⎥⎣⎦,上恒成立,求实数m 的取值范围.分析:观察角,单角二次型,降次整理为sin cos a x b x +形式.解:(Ⅰ)π()1cos 221sin 222f x x x x x ⎡⎤⎛⎫=-+=+ ⎪⎢⎥⎝⎭⎣⎦∵π12sin 23x ⎛⎫=+- ⎪⎝⎭.又ππ42x ⎡⎤∈⎢⎥⎣⎦,∵,ππ2π2633x -∴≤≤,即π212sin 233x ⎛⎫+- ⎪⎝⎭≤≤,max min ()3()2f x f x ==,∴.(Ⅱ)()2()2()2f x m f x m f x -<⇔-<<+∵,ππ42x ⎡⎤∈⎢⎥⎣⎦,,max ()2m f x >-∴且min ()2m f x <+,14m <<∴,即m 的取值范围是(14),. 点评:第(Ⅱ)问属于恒成立问题,可以先去绝对值,利用参数分离转化为求最值问题.本小题主要考查三角函数和不等式的基本知识,以及运用三角公式、三角函数的图象和性质解题的能力. 【反馈演练】1.函数))(6cos()3sin(2R x x x y ∈+--=ππ的最小值等于____-1_______.2.当04x π<<时,函数22cos ()sin sin xf x x xx =-的最小值是______4 _______.3.函数sin cos 2xy x =+4.函数cos tan y x x =⋅的值域为 .5.已知函数()2sin (0)f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,则ω的最小值等于_________.6.已知函数()2cos (sin cos )1f x x x x x =-+∈R ,. (Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值.解:(Ⅰ)π()2cos (sin cos )1sin 2cos 224f x x x x x x x ⎛⎫=-+=-=- ⎪⎝⎭.因此,函数()f x 的最小正周期为π.(Ⅱ)因为π()24f x x ⎛⎫=- ⎪⎝⎭在区间π3π88⎡⎤⎢⎥⎣⎦,上为增函数,在区间3π3π84⎡⎤⎢⎥⎣⎦,上为减函数,又π08f ⎛⎫= ⎪⎝⎭,3π8f⎛⎫= ⎪⎝⎭3π3πππ14244f ⎛⎫⎛⎫=-==- ⎪ ⎪⎝⎭⎝⎭, 32(1,1)-故函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,,最小值为1-.。
§4.3 三角函数的图象与性质

于点( x0 ,0) 中心对称.
( ) 设 f( x) =
4cos
ωx-
π 6
sin ωx - cos ( 2ωx + π) , 其 中 ω
>0.
(1)求函数 y = f(x)的值域;
[ ] (2)若 f(x)在区间
- 32π,
π 2
上为增函数,求 ω 的最大值.
( ) 解析 (1)f(x)= 4
.
(2) (2019 成都七中 1 月月考,14) 如图为一弹簧振子作简 谐运动的图象,横轴表示振动的时间,纵轴表示振动的位移,则 这个振子振动的一个函数解析式是 .
解析
( 1) 由
T 4
=
11 12
π-
2 3
π=
π 4
,得
T
=
π,
∵
T=
2π ,∴
ω
ω = 2,∴
f( x) =
对称性
对称轴:x = kπ+
π 2
( k∈Z) ;
对称中心:( kπ,0) ( k∈Z)
周期
2π
单调性
单调增区间:
[ ] 2kπ-
π 2
,2kπ+
π 2
( k∈Z) ;
单调减区间:
[ ] 2kπ+
π 2
,2kπ+
3π 2
( k∈Z)
奇偶性
奇函数
[ -1,1]
对称轴:x = kπ( k∈Z) ;
( ) 对称中心:
换,设
z
=
ωx+φ,由
z
取
0,
π 2
3π ,π, ,2π
2
来求出相
应的
x,通过列
表、计算得出五点坐标,描点连线后得出图象.
第四章 第5讲 三角函数的图象与性质-2025年高考数学备考

第四章三角函数第5讲三角函数的图象与性质课标要求命题点五年考情命题分析预测1.借助单位圆能画出三角函数(正弦、余弦、正切)的图象,了解三角函数的周期性、单调性、奇偶性、最大(小)值.2.借助图象理解正弦函数、余弦函数在[0,2π]上,正切函数在(-π2,π2)上的性质.三角函数的定义域本讲每年必考,主要考查三角函数的定义域、值域(最值)、周期性、单调性、对称性和奇偶性,有时与函数零点和极值点综合命题,题型以选择题和填空题为主,难度中等.预计2025年高考命题趋势变化不大,备考时要注意区分正弦函数和余弦函数的图象与性质,不要混淆,另应关注新角度、新综合问题.三角函数的值域(最值)2021全国卷乙T4三角函数的性质及应用2023新高考卷ⅠT15;2023全国卷乙T6;2023天津T5;2022新高考卷ⅠT6;2022全国卷乙T15;2022全国卷甲T11;2022北京T5;2021新高考卷ⅠT4;2020全国卷ⅢT16;2019全国卷ⅠT11;2019全国卷ⅡT9学生用书P0801.用“五点法”作正弦函数和余弦函数的简图在正弦函数y =sin x ,x ∈[0,2π]的图象上,起关键作用的五个点是(0,0),(π2,1),①(π,0),(3π2,-1),②(2π,0).在余弦函数y =cos x ,x ∈[0,2π]的图象上,起关键作用的五个点是(0,1),(π2,0),③(π,-1),(3π2,0),④(2π,1).五点法作图有三步:列表、描点、连线(注意光滑).2.正弦、余弦、正切函数的图象与性质三角y =sin xy =cos xy =tan x函数图象定义域R R ⑤{x |x ≠k π+2,k ∈Z}值域⑥[-1,1]⑦[-1,1]R周期性周期是2k π(k ∈Z 且k ≠0),最小正周期是⑧2π.周期是2k π(k ∈Z 且k ≠0),最小正周期是⑨2π.周期是k π(k ∈Z 且k ≠0),最小正周期是⑩π.对称性对称轴方程是⑪x =k π+2(k ∈Z ),对称中心是⑫(k π,0)(k ∈Z ).对称轴方程是⑬x =k π(k ∈Z ),对称中心是⑭(k π+2,0)(k ∈Z ).无对称轴,对称中心是⑮(2,0)(k ∈Z ).奇偶性⑯奇函数⑰偶函数⑱奇函数单调性在⑲[-2+2k π,2+2k π](k ∈Z )上单调递增,在⑳[2+2k π,32+2k π](k ∈Z )上单调递减.在㉑[2k π-π,2k π](k ∈Z )上单调递增,在㉒[2k π,2k π+π](k ∈Z )上单调递减.在㉓(-2+k π,2+k π)(k ∈Z )上单调递增.注意y =tan x 在其定义域内不单调.常用结论1.三角函数的对称性与周期T 的关系(1)相邻的两条对称轴(或两个对称中心)之间的距离为2;(2)相邻的对称中心与对称轴之间的距离为4;(3)相邻的两个最低点(或最高点)之间的距离为T .2.与三角函数奇偶性有关的结论(1)若函数y =A sin (ωx +φ)(x ∈R )是奇函数,则φ=k π(k ∈Z );若为偶函数,则φ=k π+π2(k ∈Z ).(2)若函数y =A cos (ωx +φ)(x ∈R )是奇函数,则φ=k π+π2(k ∈Z );若为偶函数,则φ=k π(k ∈Z ).(3)若y=A tan(ωx+φ)为奇函数,则φ=kπ(k∈Z).1.设A是△ABC最小的内角,则sin A+cos A的取值范围是(D)A.(-2,2)B.[-2,2]C.(1,2)D.(1,2]解析∵A是△ABC最小的内角,∴0<A≤π3,∴π4<A+π4≤7π12,sin(A+π4)≤1,则sin A+cos A=2sin(A+π4)∈(1,2],故选D.2.函数f(x)=tan(-4x+π6)的最小正周期为(A)A.π4B.π2C.πD.2π解析函数f(x)=tan(-4x+π6)的最小正周期T=π||=π|-4|=π4.3.[全国卷Ⅱ]若x1=π4,x2=3π4是函数f(x)=sinωx(ω>0)两个相邻的极值点,则ω=(A)A.2B.32C.1D.12解析依题意得函数f(x)的最小正周期T=2π=2×(3π4-π4)=π,解得ω=2,选A.4.函数f(x)=sin(x-π4)的图象的一条对称轴的方程是(C)A.x=π4B.x=π2C.x=-π4D.x=-π2解析函数y=sin x的图象的对称轴方程为x=kπ+π2(k∈Z),令x-π4=kπ+π2(k∈Z),得x=kπ+3π4(k∈Z),故函数f(x)=sin(x-π4)的图象的对称轴方程为x=kπ+3π4(k∈Z).令k=-1,得x=-π4.故选C.5.[易错题]函数y=2sin(-x+π3)(x∈[-π,0])的单调递增区间是(A)A.[-π,-π6]B.[-5π6,-π6]C.[-π3,0]D.[-π6,0]解析令π2+2kπ≤-x+π3≤3π2+2kπ,k∈Z,则-7π6-2kπ≤x≤-π6-2kπ,k∈Z.又x∈[-π,0],所以所求单调递增区间为[-π,-π6].6.函数f(x)=tan(3x+π6)的图象的对称中心为(χ6-π18,0)(k∈Z).解析令3x +π6=χ2,k ∈Z ,解得x =χ6-π18,k ∈Z ,所以f (x )的图象的对称中心为(χ6-π18,0),k ∈Z.学生用书P082命题点1三角函数的定义域例1函数y =lg (sin x 的定义域为{x |2k π<x ≤π3+2k π,k ∈Z}.解析要使函数有意义,则sin >0,Hs -12≥0,解得2χ<<π+2χ(Ap,-π3+2χ≤≤π3+2χ(Ap,所以2k π<x ≤π3+2k π(k ∈Z ),所以函数的定义域为{x |2k π<x ≤π3+2k π,k ∈Z}.方法技巧求三角函数的定义域实质上是解不等式或不等式组,常借助于三角函数的图象解决.训练1函数f (x )=tanbtan2tan2-tan 的定义域为{x |x ≠χ4,k ∈Z}.解析tan 2x ,tan x 有意义,则≠π2+χ,2≠π2+χ,k ∈Z ,又tan 2x -tan x ≠0,即2tan1-tan 2-tan x ≠0,则tan x ≠0,即x ≠k π,k ∈Z ,综上可得,x ≠χ4,k ∈Z ,则函数f (x )的定义域为{x |x ≠χ4,k ∈Z}.命题点2三角函数的值域(最值)例2(1)[2021全国卷乙]函数f (x )=sin3+cos3的最小正周期和最大值分别是(C)A.3π和2B.3π和2C.6π和2D.6π和2解析因为函数f (x )=sin3+cos 3=2(sin 3cos π4+cos3sin π4)=2sin (3+π4),所以函数f (x )的最小正周期T =2π13=6π,最大值为2.故选C.(2)已知函数f (x )=cos (2x +π3)+2的定义域为[α,π],值域为[52,3],则α的取值范围是(C )A.[2π3,π]B.[0,2π3]C.[2π3,5π6]D.[π2,5π6]解析由题意知,2x+π3∈[2α+π3,7π3],且y=cos(2x+π3)在[α,π]上的值域为[12,1],∴2α+π3≥5π3,且2α+π3≤2π,解得2π3≤α≤5π6,∴α的取值范围是[2π3,5π6],故选C.方法技巧三角函数值域的不同求法1.把所给的三角函数式变换成y=A sin(ωx+φ)+b的形式求值域.2.把sin x或cos x看作一个整体,转换成二次函数求值域.3.利用sin x±cos x和sin x cos x的关系转换成二次函数求值域.训练2(1)[2023四川省模拟]已知函数f(x)=cos2x+sin x-14的定义域为[0,m],值域为[34,1],则实数m的最大值为(A)A.πB.7π6C.4π3D.3π2解析由已知,得f(x)=cos2x+sin x-14=1-sin2x+sin x-14=-sin2x+sin x+34,令t=sin x,函数f(x)可转换为y=-t2+t+34=-(t-12)2+1,因为y∈[34,1],所以根据二次函数的图象与性质可得t∈[0,1],即sin x∈[0,1],又x∈[0,m],所以根据三角函数的图象与性质可得m∈[π2,π],所以实数m的最大值为π,故选A.(2)函数y=sin x-cos x+sin x cos x12解析令sin x-cos x=t,则t=2sin(x-π4),t∈[-2,2],t2=sin2x+cos2x-2sin x cos x,故sin x cos x=1-22,所以y=t+1-22=-12(t-1)2+1,所以当t=1时,函数有最大值1;当t=-2时,函数有最小值-2-12,即值域为[-2-12,1].命题点3三角函数的性质及应用角度1三角函数的周期性例3(1)[2023天津高考]已知函数f(x)图象的一条对称轴为直线x=2,f(x)的一个周期为4,则f(x)的解析式可能为(B)A.f(x)=sin(π2x)B.f(x)=cos(π2x)C.f(x)=sin(π4x)D.f(x)=cos(π4x)解析对于A,f(x)=sin(π2x),其最小正周期为2ππ2=4,因为f(2)=sinπ=0,所以函数f(x)=sin(π2x)的图象不关于直线x=2对称,故排除A;对于B,f(x)=cos(π2x),其最小正周期为2ππ2=4,因为f(2)=cosπ=-1,所以函数f(x)=cos(π2x)的图象关于直线x=2对称,故选项B符合题意;对于C,D,函数y=sin(π4x)和y=cos(π4x)的最小正周期均为2ππ4=8,均不符合题意,故排除C,D.综上,选B.(2)[全国卷Ⅲ]函数f(x)=tG1+B2的最小正周期为(C)A.π4B.π2C.πD.2π解析f(x)=tan1+tan2=sin cos1+sin2cos2=sinvoscos2+sin2=sin x cos x=12sin2x,所以f(x)的最小正周期T=2π2=π.故选C.方法技巧1.求三角函数周期的基本方法(1)定义法.(2)公式法:函数y=A sin(ωx+φ)(或y=A cos(ωx+φ))的最小正周期T=2π||,函数y=A tan(ωx+φ)的最小正周期T=π||.(3)图象法:求含有绝对值符号的三角函数的周期时可画出函数的图象,通过观察图象得出周期.2.有关周期的2个结论(1)函数y=|A sin(ωx+φ)|,y=|A cos(ωx+φ)|,y=|A tan(ωx+φ)|的最小正周期T均为π||.(2)函数y=|A sin(ωx+φ)+b|(b≠0),y=|A cos(ωx+φ)+b|(b≠0)的最小正周期T均为2π||.角度2三角函数的单调性例4(1)[2022北京高考]已知函数f(x)=cos2x-sin2x,则(C)A.f(x)在(-π2,-π6)上单调递减B.f(x)在(-π4,π12)上单调递增C.f(x)在(0,π3)上单调递减D.f(x)在(π4,7π12)上单调递增解析依题意可知f(x)=cos2x-sin2x=cos2x,对于A,因为x∈(-π2,-π6),所以2x∈(-π,-π3),函数f(x)=cos2x在(-π2,-π6)上单调递增,所以A不正确;对于B,因为x∈(-π4,π12),所以2x∈(-π2,π6),函数f(x)=cos2x在(-π4,π12)上不单调,所以B不正确;对于C,因为x∈(0,π3),所以2x∈(0,2π3),函数f(x)=cos2x在(0,π3)上单调递减,所以C正确;对于D,因为x∈(π4,7π12),所以2x∈(π2,7π6),函数f(x)=cos2x在(π4,7π12)上不单调,所以D不正确.故选C.(2)[全国卷Ⅱ]若f(x)=cos x-sin x在[-a,a]上是减函数,则a的最大值是(A)A.π4B.π2C.3π4D.π解析f(x)=cos x-sin x=2cos(x+π4),因为函数y=cos x在区间[0,π]上单调递减,则由0≤x+π4≤π,得-π4≤x≤3π4.因为f(x)在[-a,a]上是减函数,|-π4|<3π4,所以-a≥-π4,解得a≤π4.又区间[-a,a]有意义时,a>0,所以0<a≤π4,所以a的最大值是π4.方法技巧三角函数单调性问题的常见类型及求解策略常见类型求解策略已知三角函数解析式求单调区间(1)将函数化简为“一角一函数”的形式,如y=A sin(ωx+φ)+b(A>0,ω>0);(2)利用整体思想,视“ωx+φ”为一个整体,根据y=sin x的单调区间列不等式求解.对于y=A cos(ωx+φ),y=A tan(ωx+φ),可以利用类似方法求解.注意求函数y=A sin(ωx+φ)+b的单调区间时要先看A和ω的符号,尽量化成ω>0的形式,避免出现增减区间的混淆.已知三角函数的单调性求参数(1)求出原函数的相应单调区间,由已知区间是求出的单调区间的子集,列不等式(组)求解.(2)由所给区间求出“ωx+φ”的范围,由该范围是某相应正、余弦函数的某个单调区间的子集,列不等式(组)求解.角度3三角函数的奇偶性与对称性例5(1)[2022全国卷甲]将函数f(x)=sin(ωx+π3)(ω>0)的图象向左平移π2个单位长度后得到曲线C,若C关于y轴对称,则ω的最小值是(C)A.16B.14C.13D.12解析记曲线C的函数解析式为g(x),则g(x)=sin[ω(x+π2)+π3]=sin[ωx+(π2ω+π3)].因为函数g(x)的图象关于y轴对称,所以π2ω+π3=kπ+π2(k∈Z),得ω=2k+13(k∈Z).因为ω>0,所以ωmin=13.故选C.(2)[2022新高考卷Ⅰ]记函数f(x)=sin(ωx+π4)+b(ω>0)的最小正周期为T.若2π3<T <π,且y=f(x)的图象关于点(3π2,2)中心对称,则f(π2)=(A)A.1B.32C.52D.3解析因为2π3<T<π,所以2π3<2π<π,解得2<ω<3.因为y=f(x)的图象关于点(3π2,2)中心对称,所以b=2,且sin(3π2ω+π4)+b=2,即sin(3π2ω+π4)=0,所以3π2ω+π4=kπ(k∈Z),又2<ω<3,所以13π4<3π2ω+π4<19π4,所以3π2ω+π4=4π,解得ω=52,所以f(x)=sin(52x+π4)+2,所以f(π2)=sin(52×π2+π4)+2=sin3π2+2=1.故选A.方法技巧1.三角函数图象的对称轴和对称中心的求解方法:对于函数f(x)=A sin(ωx+φ)(ω≠0),令ωx+φ=kπ+π2,k∈Z,求出对称轴方程;令ωx+φ=kπ,k∈Z,求出对称中心的横坐标(纵坐标为0).对于y=A cos(ωx+φ),y=A tan(ωx+φ),可以利用类似方法求解(注意y=A tan(ωx+φ)的图象无对称轴).说明选择题可以通过验证f(x0)的值进行判断,即f(x0)=±A⇔x=x0是函数f(x)图象的对称轴方程;f(x0)=0⇔点(x0,0)是函数f(x)图象的对称中心.2.三角函数中奇函数一般可化为y=A sinωx或y=A tanωx的形式,而偶函数一般可化为y =A cosωx+b的形式.训练3(1)[2023全国卷乙]已知函数f(x)=sin(ωx+φ)在区间(π6,2π3)单调递增,直线x=π6和x=2π3为函数y=f(x)的图象的两条相邻对称轴,则f(-5π12)=(D)A. B.-12 C.12解析由题意得12×2π||=2π3-π6=π2,解得|ω|=2,易知x=π6是f(x)的最小值点.若ω=2,则π6×2+φ=-π2+2kπ(k∈Z),得φ=-5π6+2kπ(k∈Z),于是f(x)=sin(2x-6π5+2kπ)=sin(2x-5π6),f(-5π12)=sin(-5π12×2-5π6)=sin(-5π3)=sinπ3=ω=-2,则π6×(-2)+φ=-π2+2kπ(k∈Z),得φ=-π6+2kπ(k∈Z),于是f(x)=sin(-2x-π6+2kπ)=sin(-2x-π6)=sin(2x-56π),所以f(-5π12)故选D.(2)在函数①y=cos|2x|,②y=|cos x|,③y=cos(2x+π6),④y=tan(2x-π4)中,最小正周期为π的所有函数为(A)A.①②③B.①③④C.②④D.①③解析对于①,y=cos|2x|=cos2x,其最小正周期为2π2=π;对于②,y=|cos x|的最小正周期为π;对于③,y=cos(2x+π6)的最小正周期为2π2=π;对于④,y=tan(2x-π4)的最小正周期为π2.所以最小正周期为π的所有函数为①②③.(3)函数f(x)=3sin(2x-π3+φ)+1,φ∈(0,π),且f(x)为偶函数,则φ=5π6,f(x)图象的对称中心为(π4+χ2,1),k∈Z.解析∵f(x)=3sin(2x-π3+φ)+1为偶函数,∴-π3+φ=kπ+π2,k∈Z,即φ=5π6+kπ,k∈Z.又φ∈(0,π),∴φ=5π6,∴f(x)=3sin(2x+π2)+1=3cos2x+1.由2x=π2+kπ,k∈Z,得x=π4+χ2,k∈Z,∴f(x)图象的对称中心为(π4+χ2,1),k∈Z.1.[命题点2/2023福建模拟]若对任意x∈R都有f(sin x)=-cos2x+cos2x+2sin x-3,则f(x)的值域为[-4,0].解析易知f(sin x)=2sin2x-1+1-sin2x+2sin x-3=sin2x+2sin x-3,所以f(x)=x2+2x-3(-1≤x≤1),曲线y=x2+2x-3的对称轴为直线x=-1,所以函数f(x)在区间[-1,1]上单调递增,所以f(-1)≤f(x)≤f(1),即-4≤f(x)≤0,所以f(x)的值域为[-4,0].2.[命题点2/2023潍坊市高三统考]已知函数f(x)=3sin x+4cos x,且f(x)≤f(θ)对任意x∈R恒成立,若角θ的终边经过点P(4,m),则m=3.解析因为f(x)=3sin x+4cos x=5sin(x+φ),其中cosφ=35,sinφ=45,则sin(θ+φ)=1,所以θ+φ=π2+2kπ(k∈Z),所以θ=π2-φ+2kπ(k∈Z),所以sinθ=sin(π2-φ)=cosφ=35,同理cosθ=45,所以tanθ=4=sin cos=34,所以m=3.3.[命题点3角度1/多选/2023福建省福州市联考]如图所示,一个质点在半径为2的圆O上以点P为起始点,沿逆时针方向运动,每3s转一圈.该质点到x轴的距离关于时间t的函数记为f(t).下列说法正确的是(AC)A.f(t)=|2sin(2π3t-π4)|B.f(t)=2sin(2π3t-π4)C.f(t)的最小正周期为32D.f(t)的最小正周期为3解析由题可知,质点的角速度为2π3rad/s,因为点P为起始点,沿逆时针方向运动,设经过t s之后所成角为φ,则φ=2π3-π4,根据任意角的三角函数定义有y P=2sin(2π3-π4),所以该质点到x轴的距离为f(t)=|2sin(2π3t-π4)|,故A正确,B错误;因为f(t)=|2sin(2π3t-π4)|,所以f(t)的最小正周期为π2π3=32,故C正确,D错误.故选AC.4.[命题点3/多选/2023河北名校联考]已知函数f(x)=2sin(ωx+π4)+b(ω>0)的最小正周期T满足π2<T<3π2,且P(-π8,1)是f(x)图象的一个对称中心,则(AC)A.ω=2B.f(x)的值域是[-2,2]C.直线x=π8是f(x)图象的一条对称轴D.f(x+π4)是偶函数解析对于A,因为P(-π8,1)是函数f(x)图象的一个对称中心,所以-π8ω+π4=kπ(k∈Z),且b=1,得ω=2-8k(k∈Z).又π2<T<3π2,且ω>0,即π2<2π<3π2,所以43<ω<4,所以ω=2,故A正确.对于B,由对A的分析得f(x)=2sin(2x+π4)+1,因为-1≤sin(2x+π4)≤1,所以f(x)∈[-1,3],故B不正确.对于C,解法一由2x+π4=kπ+π2(k∈Z),得x=χ2+π8(k∈Z),当k=0时,x=π8,所以直线x=π8是函数f(x)图象的一条对称轴,故C正确.解法二将x=π8代入f(x),可得f(π8)=3(f(x)的最大值),所以直线x=π8是f(x)图象的一条对称轴,故C正确.对于D,因为f(x+π4)=2sin[2(x+π4)+π4]+1=2sin(2x+π2+π4)+1=2cos(2x+π4)+1,显然该函数不是偶函数,故D不正确.综上所述,选AC.学生用书·练习帮P2961.函数f(x)=tan(2x+π4)的定义域为(C)A.{x|x≠kπ+π2,k∈Z}B.{x|x≠2kπ+π2,k∈Z}C.{x|x≠χ2+π8,k∈Z}D.{x|x≠kπ+π8,k∈Z}解析由2x+π4≠kπ+π2,k∈Z,得2x≠kπ+π4,k∈Z,∴x≠χ2+π8,k∈Z,∴函数y=tan(2x+π4)的定义域为{x|x≠χ2+π8,k∈Z}.2.[2023天津新华中学统练]下列函数中,最小正周期为π的奇函数是(D)A.y=sin(2x+π2)B.y=tan2xC.y=2sin(π-x)D.y=tan(x+π)解析对于函数y=sin(2x+π2)=cos2x,最小正周期为π,是偶函数,排除A;对于函数y=tan2x,最小正周期为π2,是奇函数,排除B;对于函数y=2sin(π-x)=2sin x,最小正周期为2π,是奇函数,排除C;对于函数y=tan(π+x)=tan x,最小正周期为π,是奇函数,故选D.3.下列函数中,以π2为周期且在区间(π4,π2)单调递增的是(A)A.f(x)=|cos2x|B.f(x)=|sin2x|C.f(x)=cos|x|D.f(x)=sin|x|解析A中,函数f(x)=|cos2x|的最小正周期为π2,当x∈(π4,π2)时,2x∈(π2,π),函数f(x)单调递增,故A正确;B中,函数f(x)=|sin2x|的最小正周期为π2,当x∈(π4,π2)时,2x∈(π2,π),函数f(x)单调递减,故B不正确;C中,函数f(x)=cos|x|=cos x的最小正周期为2π,故C不正确;D中,f(x)=sin|x|=sin,≥0,由正弦函数图象知,在x≥0和x<0时,f(x)均以2π为周期,但在整个-sin,<0,定义域上f(x)不是周期函数,故D不正确.故选A.4.已知函数f(x)=sin(ωx+θ)+3cos(ωx+θ)(θ∈[-π2,π2])是偶函数,则θ的值为(B)A.0B.π6C.π4D.π3解析由已知可得f(x)=2sin(ωx+θ+π3),若函数为偶函数,则必有θ+π3=kπ+π2(k∈Z),又由于θ∈[-π2,π2],故有θ+π3=π2,解得θ=π6,经代入检验符合题意.故选B.5.[2023江西月考]已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π2)的两个相邻的零点为-13,23,则f(x)的图象的一条对称轴方程是(B)A.x=-16B.x=-56C.x=13D.x=23解析设f(x)的最小正周期为T,则2=23-(-13)=1,得T=2π=2,所以ω=π,又因为-π3+φ=kπ(k∈Z),且0<φ<π2,所以φ=π3,则f(x)=sin(πx+π3),由πx+π3=kπ+π2(k∈Z),解得x=k+16(k∈Z),取k=-1,得一条对称轴方程为x=-56.6.已知函数f(x)=-2tan(2x+φ)(0<φ<π2)的图象的一个对称中心是点(π12,0),则该函数的一个单调递减区间是(D)A.(-5π6,π6)B.(-π6,π3)C.(-π3,π6)D.(-5π12,π12)解析因为函数f(x)=-2tan(2x+φ)的图象的一个对称中心是点(π12,0),所以2×π12+φ=χ2,k∈Z,解得φ=χ2-π6,k∈Z.又0<φ<π2,所以φ=π3,所以f(x)=-2tan(2x+π3).令-π2+kπ<2x+π3<π2+kπ,k∈Z,解得-5π12+χ2<x<π12+χ2,k∈Z,所以函数f(x)的单调递减区间为(-5π12+χ2,π12+χ2),k∈Z.当k=0时,得f(x)的一个单调递减区间为(-5π12,π12).7.[全国卷Ⅰ]设函数f(x)=cos(ωx+π6)在[-π,π]的图象大致如图,则f(x)的最小正周期为(C)A.10π9B.7π6C.4π3D.3π2解析解法一由题图知,f(-4π9)=0,∴-4π9ω+π6=π2+kπ(k∈Z),解得ω=-3+94(k∈Z).设f(x)的最小正周期为T,易知T<2π<2T,∴2π||<2π<4π||,∴1<|ω|<2,当且仅当k=-1时,符合题意,此时ω=32,∴T=2π=4π3.故选C.解法二由题图知,f(-4π9)=0且f(-π)<0,f(0)>0,∴-4π9ω+π6=-π2(ω>0),解得ω=32,经验证符合题意,∴f(x)的最小正周期T=2π=4π3.故选C.8.[2024安徽铜陵模拟]已知函数f(x)=a sin4x+cos4x的图象关于直线x=π12对称,则f(π24)=(A)A.3 C.-12 D.-1解析由题设f(x)=2+1sin(4x+φ)(a≠0)且tanφ=1,又函数图象关于直线x=π12对称,所以π3+φ=π2+kπ,k∈Z⇒φ=π6+kπ,k∈Z,则tanφ=tan(π6+kπ)=tanπ6=1⇒a=3,综上,f(x)=3sin4x+cos4x=2sin(4x+π6),故f(π24)=2sinπ3=3.故选A.9.[多选/2023江苏南京模拟]已知x1,x2是函数f(x)=2sin(ωx-π6)(ω>0)的两个不同零点,且|x1-x2|的最小值是π2,则下列说法正确的是(ABD)A.函数f(x)在[0,π3]上单调递增B.函数f(x)的图象关于直线x=-π6对称C.函数f(x)的图象关于点(π,0)中心对称D.当x∈[π2,π]时,函数f(x)的值域是[-2,1]解析由题意可知,最小正周期T=2π=π,所以ω=2,f(x)=2sin(2x-π6).对于选项A,当x∈[0,π3]时,2x-π6∈[-π6,π2],所以f(x)在[0,π3]上单调递增,故A正确;对于选项B,f(-π6)=2sin[2×(-π6)-π6]=2sin(-π2)=-2,所以f(x)的图象关于直线x =-π6对称,故B正确;对于选项C,f(π)=2sin(2π-π6)=-1≠0,所以f(x)的图象不关于点(π,0)中心对称,故C错误;对于选项D,当x∈[π2,π]时,2x-π6∈[5π6,11π6],sin(2x-π6)∈[-1,12],f(x)∈[-2,1],故D正确.故选ABD.10.定义运算a*b为:a*b=(≤p,(>p,例如,1*2=1,则函数f(x)=sin x*cos x的值域为[-1,22].解析f(x)=sin x*cos x,当x∈[π+2kπ,5π4+2kπ],k∈Z,这时sin x≥cos x,所以f(x)=cos x,这时函数的值域为[-1;当x∈[-3π4+2kπ,π4+2kπ],k∈Z,这时sin x≤cos x,所以f(x)=sin x,这时函数的值域为[-1综上,函数的值域为[-1 11.[2023上海松江二中模拟]若函数y=sin(πx-π6)在[0,m]上单调递增,则m的最大值为23.解析由x∈[0,m],知πx-π6∈[-π6,mπ-π6],因为函数在[0,m]上单调递增,所以-π6<mπ-π6≤π2,即0<m≤23,所以m的最大值为23.12.[2024安徽合肥一中模拟]已知函数f(x)=sin x cos x-3cos2x(1)求函数f(x)的最小正周期和单调递减区间;(2)求函数f(x)在区间[-π6,π4]上的值域.解析(1)因为f(x)=sin x cos x-3cos2x=12sin2x=12sin2x-2x=sin(2x-π3),所以函数f(x)的最小正周期为T=2π2=π.由2kπ+π2≤2x-π3≤2kπ+3π2(k∈Z)可得kπ+5π12≤x≤kπ+11π12(k∈Z),所以函数f(x)的单调递减区间为[kπ+5π12,kπ+11π12](k∈Z).(2)当-π6≤x≤π4时,-2π3≤2x-π3≤π6,则-1≤sin(2x-π3)≤12,因此,函数f(x)在区间[-π6,π4]上的值域为[-1,12].13.设函数f(x)=2cos(12x-π3),若对于任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为(C)A.π2B.πC.2πD.4π解析函数f(x)=2cos(12x-π3),若对于任意的x∈R,都有f(x1)≤f(x)≤f(x2),则f(x1)是函数的最小值,f(x2)是函数的最大值,|x1-x2|的最小值就是函数的半个周期,故2=12×2π12=2π,故选C.14.[2023湘潭模拟]若函数f(x)=cos2x+sin(2x+π6)在(0,α)上恰有2个零点,则α的取值范围为(B)A.[5π6,4π3)B.(5π6,4π3]C.[5π3,8π3)D.(5π3,8π3]解析由题意得,函数f(x)=cos2x+sin(2x+π6)=3sin(2x+π3),因为0<x<α,所以π3<2x+π3<2α+π3,又由f(x)在(0,α)上恰有2个零点,可得2π<2α+π3≤3π,解得5π6<α≤4π3,所以α的取值范围为(5π6,4π3].15.[2023福建龙岩模拟]已知函数f(x)=2|sin x|+cos x,则f(x)的最小值为(C)A.-5B.-2C.-1D.0解析解法一f(x)=2|sin x|+cos x,分别作出y=2|sin x|(图1)与y=cos x (图2)的部分图象,如图所示.图1图2从图中可以看出,当x=π时,两个函数同时取得最小值,此时f(π)=2|sinπ|+cosπ=-1最小.解法二因为f(-x)=2|sin(-x)|+cos(-x)=2|sin x|+cos x=f(x),所以f(x)=2|sin x|+cos x为偶函数,又f(x+2π)=2|sin(x+2π)|+cos(x+2π)=2|sin x|+cos x=f(x),所以f(x)的一个周期为2π.当x∈[0,π]时,f(x)=2sin x+cos x,f'(x)=2cos x-sin x,令f'(x)=0,则tan x=2,故存在x0∈(0,π2),使得f'(x0)=0,当x∈[0,x0)时,f'(x)>0,f(x)单调递增;当x∈(x0,π]时,f'(x)<0,f(x)单调递减,又f(0)=1,f(π)=-1,结合f(x)为偶函数,周期为2π,作出f(x)=2|sin x|+cos x的图象如图,由图可知,函数的最小值为-1.故选C.16.[多选/2022新高考卷Ⅱ]已知函数f(x)=sin(2x+φ)(0<φ<π)的图象关于点(2π3,0)中心对称,则(AD)A.f(x)在区间(0,5π12)单调递减B.f(x)在区间(-π12,11π12)有两个极值点C.直线x=7π是曲线y=f(x)的对称轴D.直线y x是曲线y=f(x)的切线解析因为函数f(x)的图象关于点(2π3,0)中心对称,所以sin(2×2π3+φ)=0,可得4π3+φ=kπ(k∈Z),结合0<φ<π,得φ=2π3,所以f(x)=sin(2x+2π3).对于A,解法一由2kπ+π2≤2x+2π3≤2kπ+3π2(k∈Z),得kπ-π12≤x≤kπ+5π12(k∈Z);当k =0时,-π12≤x≤5π12.因为(0,5π12)⊆(-π12,5π12),所以函数f(x)在区间(0,5π12)单调递减,故A正确.解法二当x∈(0,5π12)时,2x+2π3∈(2π3,3π2),所以函数f(x)在区间(0,5π12)单调递减,故A正确.对于B,解法一由2x+2π3=kπ+π2(k∈Z),得x=χ2-π12(k∈Z),当k=0时,x=-π12;当k=1时,x=5π12;当k=2时,x=11π12.所以函数f(x)在区间(-π12,11π12)只有一个极值点,故B不正确.解法二当x∈(-π12,11π12)时,2x+2π3∈(π2,5π2),所以函数f(x)在区间(-π12,11π12)只有一个极值点,故B不正确.对于C,解法一由选项B解法一的分析知,函数f(x)图象的对称轴方程为x=χ2-π12(k∈Z),而方程χ2-π12=7π6(k∈Z)无解,故C不正确.解法二因为f(7π6)=sin(2×7π6+2π3)=sin3π=0,所以x=7π6不是曲线y=f(x)的对称轴,故C不正确.对于D,因为f'(x)=2cos(2x+2π3),若直线y x为曲线y=f(x)的切线,则由2cos(2x+2π3)=-1,得2x+2π3=2kπ+2π3或2x+2π3=2kπ+4π(k∈Z),所以x=kπ或x=kπ+π3(k∈Z).当x=kπ(k∈Z)时,f(x)kπ(k∈Z),解得k=0;当x=kπ+π3(k∈Z)时,f(x)kπ-π3(k∈Z)无解.综上所述,直线y x为曲线y=f(x)的切线,故D正确.综上所述,选AD.17.[条件创新]已知函数f(x)=2sinωx(ω>0)在区间[-3π4,π4]上单调递增,且直线y=-2与函数f(x)的图象在[-2π,0]上有且仅有一个交点,则实数ω的取值范围是[14,23].解析易知f(x)的图象关于点(0,0)对称,则由函数f(x)在[-3π4,π4]上单调递增可得4≥3π4(T为f(x)的最小正周期),即2π4≥3π4,结合ω>0,解得0<ω≤23.因为直线y=-2与函数f(x)的图象在[-2π,0]×2π≤2π,×2π>2π,解得14≤ω<54.综上,ω∈[14,23].18.[2023湖北省部分重点中学联考]已知函数f(x)=4sin2(π4+2)sin x+(cos x+sin x)·(cos x-sin x)-1.(1)求f(x)的解析式及其图象的对称中心;(2)若函数g(x)=12[f(2x)+af(x)-af(π2-x)-a]-1在区间[-π4,π2]上的最大值为2,求实数a的值.解析(1)f(x)=2[1-cos(π2+x)]·sin x+cos2x-sin2x-1=sin x·(2+2sin x)+1-2sin2x-1=2sin x.对称中心为(kπ,0),k∈Z.(2)g(x)=sin2x+a sin x-a cos x-2-1,令sin x-cos x=t,则sin2x=1-t2,(小技巧:函数式中既含正余弦的和或差(sin x-cos x或sin x+cos x),又含二者的乘积(即sin x·cos x),可令sin x-cos x=t或sin x+cos x=t,然后转化为关于t的二次函数求最值)∴y=1-t2+at-2-1=-(t-2)2+2 4-2.∵t=sin x-cos x=2sin(x-π4),x∈[-π4,π2],∴x-π4∈[-π2,π4],∴-2≤t≤1.①当2<-2,即a <-22时,y max =-(-2-2)2+24-2=-2a -2-2.令-2a -2-2=2,解得a .②当-2≤2≤1,即-22≤a ≤2时,y max =24-2,令24-2=2,解得a =-2或a =4(舍去).③当2>1,即a >2时,y max =-(1-2)2+24-2=2-1,由2-1=2,得a =6.综上,a =-2或6.19.[条件创新/多选]已知函数f (x )=cos (2x +φ)(|φ|<π2),F (x )=f (x )+'(x )为奇函数,则下述四个结论正确的是(BC )A.tan φ=3B.若f (x )在[-a ,a ]上存在零点,则a 的最小值为π6C.F (x )在(π4,3π4)上单调递增D.f (x )在(0,π2)上有且仅有一个极大值点解析由f (x )=cos (2x +φ),得f '(x )=-2sin (2x +φ),则F (x )=f (x )+'(x )=cos (2x +φ)-3sin (2x +φ)=-2sin (2x +φ-π6).因为F (x )为奇函数,所以φ-π6=k π(k ∈Z ),所以φ=k π+π6(k ∈Z ).因为|φ|<π2,所以φ=π6.对于A ,由以上可得tan φA 错误;对于B ,令f (x )=cos (2x +π6)=0,得2x +π6=k π+π2(k ∈Z ),则x =χ2+π6(k ∈Z ),即函数f (x )的零点为x =χ2+π6(k ∈Z ),且该函数零点的绝对值的最小值为π6,所以a 的最小值为π6,故B 正确;对于C ,F (x )=-2sin 2x ,当x ∈(π4,3π4)时,2x ∈(π2,3π2),此时函数F (x )单调递增,故C 正确;对于D ,函数f (x )=cos (2x +π6),令2x +π6=2k π(k ∈Z ),得x =k π-π12(k ∈Z ),所以函数f (x )在(0,π2)上无极大值点,故D 错误.。
高中数学课件三角函数ppt课件完整版

高中数学课件三角函数ppt课件完整版目录•三角函数基本概念与性质•三角函数诱导公式与恒等式•三角函数的加减乘除运算•三角函数在解三角形中的应用•三角函数在数列和概率统计中的应用•总结回顾与拓展延伸PART01三角函数基本概念与性质三角函数的定义及性质三角函数的定义正弦、余弦、正切等函数在直角三角形中的定义及在各象限的性质。
特殊角的三角函数值0°、30°、45°、60°、90°等特殊角度下各三角函数的值。
诱导公式利用周期性、奇偶性等性质推导出的三角函数诱导公式。
正弦、余弦函数的图像及其特点,如振幅、周期、相位等。
三角函数图像周期性图像变换正弦、余弦函数的周期性及其性质,如最小正周期等。
通过平移、伸缩等变换得到其他三角函数的图像。
030201三角函数图像与周期性正弦、余弦函数的值域为[-1,1],正切函数的值域为R 。
值域在各象限内,正弦、余弦函数的单调性及其变化规律。
单调性利用三角函数的性质求最值,如振幅、周期等参数对最值的影响。
最值问题三角函数值域和单调性PART02三角函数诱导公式与恒等式诱导公式及其应用诱导公式的基本形式01通过角度的加减、倍角、半角等关系,将任意角的三角函数值转化为基本角度(如0°、30°、45°、60°、90°)的三角函数值。
诱导公式的推导02利用三角函数的周期性、对称性、奇偶性等性质,通过逻辑推理和数学归纳法等方法推导出诱导公式。
诱导公式的应用03在解三角函数的方程、求三角函数的值、证明三角恒等式等方面有广泛应用。
例如,利用诱导公式可以简化计算过程,提高解题效率。
恒等式及其证明方法恒等式的基本形式两个解析式之间的一种等价关系,即对于某个变量或一组变量的取值范围内,无论这些变量取何值,等式都成立。
恒等式的证明方法通常采用代数法、几何法或三角法等方法进行证明。
其中,代数法是通过代数运算和变换来证明恒等式;几何法是通过几何图形的性质和关系来证明恒等式;三角法是通过三角函数的性质和关系来证明恒等式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学总复习-三角函数第5课 三角函数的图像和性质(一)【考点导读】1. 能画出正弦函数,余弦函数,正切函数的图像,借助图像理解正弦函数,余弦 函数在[0,2 ],正切函数在(一,一)上的性质;2 22. 了解函数y Asin( x )的实际意义,能画出y A si n( x )的图像;3. 了解函数的周期性,体会三角函数是描述周期变化现象的重要函数模型. 【基础练习】动的最小正周期T _____L_;初相 —-2.三角方程2sin(_ - x)=1的解集为4. 要得到函数y sinx 的图象,只需将函数 y cos x______ - ____ 个单位. 【范例解析】例 1.已知函数 f (x) 2sin x(sin x cosx).(I)用五点法画出函数在区间 ——上的图象,长度为一个周期;2’ 2(H)说明f(x) 2s in x(si nx cosx)的图像可由y si nx 的图像经过怎样变换而1.已知简谐运动f(x) 2sin (3X )(2)的图象经过点(0,1),则该简谐运3.函数 y Asin( x )( 0,尹R)的部分图象如图所示,则函数表达为y4si n( x ) 8 4的图象向右平移分析:化为Asin( x )形式.得到•列表,取点,描图:x33588888y11逅1 1 V21故函数y f(x)在区间[-,2]上的图象是:(U)解法一:把y sinx图像上所有点向右平移—个单位,得到y sin(x )4 41的图像,再把y sin(x -)的图像上所有点的横坐标缩短为原来的丄(纵坐标不4 2变),得到y si n(2x —)的图像,然后把y sin(2x —)的图像上所有点纵坐标4 4伸长到原来的倍(横坐标不变),得到y 2 sin(2x -)的图像,再将4y . 2 sin(2x )的图像上所有点向上平移1个单位,即得到4y 1 - 2 sin(2x -)的图像.1解法二:把y sinx图像上所有点的横坐标缩短为原来的-(纵坐标不变),得2到y sin 2x的图像,再把y sin 2x图像上所有点向右平移—个单位,得到8解:(I)由f(x)2sin2x 2sin xcosx 1 cos2x sin 2x2(sin 2x cos —4cos2xs in )4 2sin(2x 4).分析:化为Asin( x )形式.x -)的图像上所有点纵坐标伸长到原来 的2倍(横坐标不变),得到y 、2sin(2x)的图像,再将y 二sin(2x) 44的图像上所有点向上平移1个单位,即得到y 1 ,2sin(2x -)的图像. 4例2.已知正弦函数y Asin( x ) (A 0, 0)的图像如右图所示.(1) 求此函数的解析式f 1(x);(2) 求与fdx)图像关于直线x 8对称的曲线的解析式f 2(x); (3) 作出函数y h(x) f 2(x)的图像的简图.£(x) 一 2sin(gx 4).(2)设函数f 2(x)图像上任一点为M(x,y),与它关于直线x 8对称的对称点为M (x,y),f 2(x)2sin (尹 4)y sin(2x —)的图像,然后把y sin(2 分析:识别图像,抓住关键点. 解:(1)由图知,A 伍,Q 2 将x 2, y 2代入,,即 y 2 sin( x ).88 、、2sin (— ).2,解得一,即(6 2) 16,8得 28,解得y y. 16 x,y.代入 f 1(x) 、2sin( x84-)中,得(3) y f i(x)示.点评:由图像求解析式,A比较容易求解,困难的是待定系数求和,通常利用周期确定,代入最高点或最低点求【反馈演练】1. 为了得到函数y 2sin(°),x R的图像,只需把函数y 2sin x,x R的图3 6像上所有的点①向左平移-个单位长度,再把所得各点的横坐标缩短到原来的-倍(纵坐6 3标不变);②向右平移-个单位长度,再把所得各点的横坐标缩短到原来的-倍(纵坐6 3标不变);③向左平移-个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐6标不变);④向右平移-个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐6标不变).其中,正确的序号有__③_ .62. 为了得到函数y sin(2x )的图象,可以将函数y cos2x的图象向右平移___ 个单位长度.—3 —65. 下列函数:其中函数图象的一部分如右图所示的序号有y Asin( x ) b(1)求这段时间的最大温差; (2)写出这段时间的函数解析式.n __7.如图,函数y 2cos( x )(x R , >0,0< <-)的图象与y 轴相交于点(0, 3),且该函数的最小正周期为(1)求和的值;(2)已知点A n ,0,点P 是该函数图象上一点,点23.若函数 f(x) 2sin( x ),x R (其中 0, 2)的最小正周期是, 且 f(0)、3,则3_2 ______ 4.在0,2 内,使sin x5 4盲cosx 成立的x 取值范围为 ________① y sin x —6② y sin 2x③ y cos 4x — 3④ y cos 2x6. 如图,某地一天从6时至14时的温度变化曲线近似满足函数解:(1)由图示,这段时间的最大温差是 30 10 20 °C(2)图中从6时到14时的图象是函数yAsin( x )b 的半个周期• •• 1 — 14 6,解得21由图示,A —(30 10)2101 b 2(1030) 2020这时,y 10sin(8x )将x 6,y10代入上式,可取3 4综上,所求的解析式为y 10si n( —x —) 8 420 ( x [6,14])第6题第7题当y 。
n时,求X 。
的值. 解:(1)将 x 0 , y ,3代入函数y 2cos( x )得 cos因为0 < W —,所以 -. 2 6 又因为该函数的最小正周期为,所以 2 , 因此 y 2cos 2x — 6(2)因为点A —,0 , 2 Q(x °,y °)是 PA 的中点,y ° 所以点P 的坐标为2x 0 又因为点P 在y 2cos 2x 的图象上,所以cos 6 4x 0 56因为一w x 0 <2 5 从而得4x 0 — 6 即x 0 — 或x3xo ,所以—<6 11 ——或4x 。
64 .4x o 5 19 5 = W ,13 6 .第6课三角函数的图像和性质(二)【考点导读】1. 理解三角函数y sinx , y cosx , y tan x的性质,进一步学会研究形如函数y Asin( x )的性质;2. 在解题中体现化归的数学思想方法,利用三角恒等变形转化为一个角的三角函数来研究.【基础练习】1.写出下列函数的定义域:(1)y Qsin £的定义域是{ x 6 k x 6k 3 , k Z } ;(2)y s^的定义域是x x k 孑,k Z} _cosx 22 .函数f (x) = | sinx+cosx|的最小正周期是_________________ .3. 函数f(x) sin(x ) sin2(x )的最小正周期是4 4f 一,0)4. 函数y=sin(2x+§)的图象关于点3 对称.5. 已知函数y tan x在(一一,一)内是减函数,贝U 的取值范围是2 2【范例解析】例1.求下列函数的定义域:(1) y . 2si nx 1 ; (2) y 2 log1x ta nx .tan x V 7x k一x k2,2解:f 1) ta n x0,即x k J2sin x10.2k2k7一x66故函数的疋义域为{x2k x2k7且x k , x k-,k Z}662224 222 log 1 x(2)2 tan x 0. 0, 0 即 kx 4,故函数的定义域为 (0,—) 2 点评:由几个函数的和构成的函数, 其定义域是每一个函数定义域的交集;第(2)问可用数轴取交集. 例2•求下列函数的单调减区间: (1)y sin(i 2x);(2)2cos x ; sin( x )4 2因为2k 2 3 2x 2k -,故原函数的单调减区间为[k —](k Z). 12(2) 由 sin(7 /,得{x2k-,k Z},2cosx2)4sin(;-),所以该函数递减区间为2k -3 2kQ ,即(4 k 5y )(k Z ).点评:2,4k 利用复合函数求单调区间应注意定义域的限制. 例3. 求下列函数的最小正周期: (1)5tan(2x 1) ; (2) y sin x — sin x —3 2解: (1)由函数y 5tan(2x 1)的最小正周期为-, 2 得y 5tan(2x 1)的周期(2) y sin(x評n(x)(sin xcoscosxs in )cosx 23 31 . sinxcosx .3 21 . c 3 1 cos2x cos xsin2x子 1sin(2x 3) T点评:求三角函数的周期一般有两种:(1)化为Asin( 公式求解;(2)利用函数图像特征求解.【反馈演练】1 ■.2 cos 2 从而f () --------------------------nsin1 .函数 y sin 4 x cos2 x 的最小正周期为22 .设函数f(x) sin x 一3(x R),则 f(x)在[0,2 丄—乙]厶乞]]上的单调递减区间为6 ' 33. 4. 函数f(x) sinx 亦cosx(x [ ,0])的单调递增区间是 __ 2 设函数f(x) sin 3x |si n3x|,贝U f (x)的最小正周期为__3 5. 函数f (x) cos 2 x 2cos 2 x在[0 ,]上的单调递增区间是[3,] 6. 1 、2 cos 2x —已知函数f (x) 4nx —2 sinI)求f(x)的定义域;(U)若角在第一象限且 cos3,求 f().5解:(I)由 sin x2 k n,即 xnk n2(k Z ).故f (x)的定义域为x R | x k n(U)由已知条件得 sin■■■ 1cos 2x )的形式特征,禾I 」用n ncos — sin 2 sin —4 4 cos21 cos2 sin 2 2cos 2sin coscoscos7.设函数 f(x) sin(2x )(0), y f (x)图像的一条对称轴是直线x8(I)求;(川)画出函数y f (x)在区间[0,]上的图像. 3(川)由y sin(2x——)知故函数y f(x)在区间[0,]上图像是2(cos sin )145(U)求函数yf(x)的单调增区间;sin(2- ) 1_k,k Z.0, 3 .424(U)由 (I )知3J,因此y 3 sin (2x).44由题意得 2k_ 2x 32k,k Z.24 2所以函数 y sin (2x3 4•)的单调增区 间为[k -,k8 Z.解:⑴x 8是函数y f(x)的图像的对称轴,第7课三角函数的值域与最值【考点导读】1•掌握三角函数的值域与最值的求法,能运用三角函数最值解决实际问题;2. 求三角函数值域与最值的常用方法:(1)化为一个角的同名三角函数形式,利用函数的有界性或单调性求解;(2)化为一个角的同名三角函数形式的一元二次式,利用配方法或图像法求解;(3)借助直线的斜率的关系用数形结合求解;(4)换元法.【基础练习】1. _______________________________________________ 函数y sinx 3cosx在区间[0,—]上的最小值为 _________________________________ 1 _____ .2 31 -2. ______________________________________________ 函数f (x) cosx cos2x (x R)的最大值等于_4 ______________________________ .23. 函数y tan(— x)(— x 一且x 0)的值域是(,1 ] [ 1 > ).2 4 4. 24. 当0 x —时,函数f(x)1 cOs2x 8sin x的最小值为 4 .2 sin 2x【范例解析】1例1. (1)已知sin x siny -,求sin y cos2 x的最大值与最小值.3(2)求函数y si nx cosx si nx cosx的最大值.分析:可化为二次函数求最值问题.1 2解:(1)由已知得:si ny si nx,Q si ny [ 1,1],则sin x [ ,1].3 3si ny cos2 x (s in x 丄)2 11,当si nx 丄时,si ny cos2 x 有最小值11;当2 12 2 12sin x2时, sin y cos2 x有最小值439(2) 设sinx cosx t ( ,2 t2)t2 1 1 1,贝U sin x cosx ,贝U y t t2 2 2当t、迈时, 1y有最大值为-22.点评: 第(1)小题利用消元法,第(2)小题利用换元法最终都转化为二次函数求最值问题;但要注意变量的取值范围.2 cosx例2•求函数y 2 COSX(0 x )的最小值.sin x分析:利用函数的有界性求解.解法一:原式可化为ysinx cosx 2(0 x ),得..1 y2sin(x ) 2,即2sin(x ) ^=2,J i y2故21,解得y 、、3或y .3 (舍),所以y的最小值为3 .1.1 y2解法二:y 2 COsx(0 x )表示的是点A(0, 2)与B( sinx,cosx)连线的斜率,si nx其中点B在左半圆a2 b2 1(a 0)上,由图像知,当AB与半圆相切时,y最小,此时k AB 3,所以y的最小值为,3 .点评:解法一利用三角函数的有界性求解;解法二从结构出发利用斜率公式,结合图像求解.例3.已知函数f (x) 2sin 2 n x V3COS2X,x n n4,.4(I)求f (x)的最大值和最小值;(II)若不等式f(x) m2在x4,-上恒成立求实数m的取值范围.分析:观察角,单角二次型,降次整理为asinx bcosx形式.解: (I)•- f(x) 1 cos2x23 cos2x 1 sin2x.3 cos2x12sinn2x —3又•xn n—,—,•冗< 2xn 2 n-< 一,即 2 < 1 2sin 2x冗<3,4 26 3 33f (x)max3, f (x)min 2.(n) v f (x) m 2 f (x) 2 m f (x) 2, x n ,n ,4 2• m f (x)max2 且 m f (x)min2,••• 1 m 4,即m 的取值范围是(1,4).点评:第(U)问属于恒成立问题,可以先去绝对值,利用参数分离转化为求最 值问题.本小题主要考查三角函数和不等式的基本知识, 以及运用三角公式、 角函数的图象和性质解题的能力. 【反馈演练】3n、2 sin 5、2 cos — 1,42 4 4解:(I) f(x) 2cos x(si nx cos x) 1sin2x cos2x 2 sin 2x n4因此,函数f(x)的最小正周期为冗・(n)因为 f(x)云in2x n在区间n 3 * * * * 8n 上为增函数,在区间丁, 3n 上 1 .函数cos(―6x)(x R)的最小值等于 ______ 二1 2.当0 3.函数 2cos上-的最小值是 cosxsin xsin x _的最大值为3 ,最小值为3—时,函数 4 sin x f(x)cosx 24.函数cosx tan x 的值域为(1,1).为减函数,又fn 0「3n• 2 ,f故函数f(X)在区间n3n上的最大值为J,最小值为1•。
