数学浙江省学业水平考试专题复习选修
浙江省高中数学学业水平考试知识条目精校版
第二章基本初等函数必修2 第一章空间几何体第三章圆的方程和第一章平面向量第二章三角恒等变换选修2-1 第一章常用逻辑用语第二章圆锥曲线与方程第一章空间向量与立体几何考试形式与试题结构一、考试形式数学学业水平考试采用闭卷、笔答形式。
考试时间为110分钟。
试卷满分为100分。
二、考试结构数学学业水平考试卷的结构如下:1.考试内容分布《教学指导意见》所规定必修课程内容。
2.考试要求分布了解:约占10%;理解:约占40%;掌握:约占40%;综合运用:约占10%3.试题类型分布选择题:约占60%;填空题:约占10%;解答题:约占30%4.试题难度分布容易题:约占70%稍难题:约占20%较难题:约占10%参考试卷一、选择题(共25小题,1-15每小题2分,16-25每小题3分,共60分。
) 1.已知集合{1,2,3,4}A =,{2,4,6}B =,则AB 的元素个数是(A)0个 (B)1个 (C)2个 (D)3个 2.22log 12log 3-=(A)2- (B)0 (C)12(D)2 3.若右图是一个几何体的三视图,则这个几何体是 (A)圆锥 (B)棱柱 (C)圆柱 (D)棱锥 4.函数R))(3π2sin()(∈+=x x x f 的最小正周期为 (A)2π(B) π (C) π2 (D) 4π 5.直线230x y ++=的斜率是 (A)12-(B)12(C)2- (D)2 6.若1x =满足不等式2210ax x ++<,则实数a 的取值范围是 (A)(3,)-+∞ (B)(,3)-∞- (C)(1,)+∞ (D)(,1)-∞ 7.函数3()log (2)f x x =-的定义域是(A)[2,)+∞ (B)(2,)+∞ (C)(,2]-∞ (D)(,2)-∞(第3题图)8.圆22(1)3x y -+=的圆心坐标和半径分别是(A)(1,0),3- (B)(1,0),3(C)(1,-(1,9.各项均为实数的等比数列{}n a 中,11a =,54a =,则3a = (A)2 (B)2-(D) 10.下列函数中,图象如右图的函数可能是(A)3y x = (B)2xy =(C)y =2log y x =11.已知a ∈R ,则“2a >”是“22a a >”的(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 12.如果222=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是(A) ()+∞,0 (B)()2,0 (C)()+∞,1 (D) ()1,013.设x 为实数,命题p :x ∀∈R ,20x ≥,则命题p 的否定是 14.若函数()(1)()f x x x a =+-是偶函数,则实数a 的值为(A)1 (B)0 (C)1- (D)1±15.在空间中,已知,a b 是直线,,αβ是平面,且,,//a b αβαβ⊂⊂,则,a b 的位置关系是 (A)平行 (B)相交 (C)异面 (D)平行或异面16.在△ABC 中,三边长分别为c b a ,,,且︒=30A ,︒=45B ,1=a ,则b 的值是(A)21(B) 22 (C) 2 (D) 2617.若平面向量,a b 的夹角为60,且|2|=|a b |,则(A)()⊥+a b a (B)()⊥-a b a (C)()⊥+b b a(D)()⊥-b b a18.如图,在正方体1111D C B A ABCD -中,E 为1BC 的中点,则DE 与面11B BCC 所成角的正切值为(A)23 (D)2(第10题图) A 1(第18题图)19.函数44sin cos y x x =-在]3π,12π[-的最小值是 (A)1-(B)2- (C)12(D)1 20.函数1()2xf x x=-的零点所在的区间可能是 (A)(1,)+∞ (B)1(,1)2 (C)11(,)32 (D)11(,)4321.已知数列{}n a 满足121a a ==,2111n n n na a a a +++-=,则65a a -的值为 (A)0 (B)18 (C)96 (D)60022.若双曲线22221x y a b-=的一条渐近线与直线310x y -+=平行,则此双曲线的离心率是(B)323.若将一个真命题...中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题...,则该命题称为“可换命题”.下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行; ③平行于同一直线的两直线平行; ④平行于同一平面的两直线平行. 其中是“可换命题”的是(A)①② (B)①④ (C)①③ (D)③④24.用餐时客人要求:将温度为10C 、质量为25.0 kg 的同规格的某种袋装饮料加热至C C ~︒︒4030.服务员将x 袋该种饮料同时放入温度为80C 、5.2 kg 质量为的热水中,5分钟后立即取出.设经过5分钟加热后的饮料与水的温度恰好相同,此时,1m kg 该饮料提高的温度1t C ∆与2m kg 水降低的温度2t C ∆满足关系式11220.8m t m t ⨯∆=⨯⨯∆,则符合客人要求的x 可以是 (A)4 (B)10 (C)16 (D)2225.若满足条件20,20,210x y x y kx y k -+≥⎧⎪+-≥⎨⎪--+≤⎩的点(,)P x y 构成三角形区域,则实数k 的取值范围是(A)(1,)+∞ (B)(0,1) (C)(1,1)- (D)(,1)(1,)-∞-+∞二、填空题(共5小题,每小题2分,共10分)26.已知一个球的表面积为4πcm 3,则它的半径等于 ▲ cm .27.已知平面向量(2,3)=a ,(1,)m =b ,且//a b ,则实数m 的值为 ▲ .28.已知椭圆中心在原点,一个焦点为F (-23,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 ▲ .29.数列{}n a 满足⎩⎨⎧≤≤≤≤=--,1911,2,101,2191n n a n n n 则该数列从第5项到第15项的和为 ▲ .30.若不存在...整数x 满足不等式2(4)(4)0kx k x ---<,则实数k 的取值范围是 ▲ . 三、解答题(共4小题,共30分)31.(本题7分) 已知,54sin ),π,2π(=∈θθ求θcos 及)3πsin(+θ的值.32.(本题7分,有A 、B 两题,任选其中一题完成,)(A ) 如图,在直三棱柱111ABC A B C -中, 3AC =, 4BC =, 5AB =点D 是AB 的中点.(1)求证:1AC BC ⊥; (2)求证:1AC ∥平面1CDB .(B )如图,在底面为直角梯形的四棱锥,//,BC AD ABCD P 中-,90︒=∠ABC平面⊥PA ABCD ,32,2,3===AB AD PA ,BC =6.(1)求证:;PAC BD 平面⊥ (2)求二面角A BD P --的大小.33.(本题8分) 如图,由半圆221(0)x y y +=≤和部分抛物线 2(1)y a x =-(0y ≥,0a >)合成的曲线C 且曲线C 经过点(2,3). (1)求a 的值;(2)设(1,0)A ,(1,0)B -,过A 且斜率为k 的直线 l 与“羽毛 球形线”相交于P ,A ,Q 三点,问是否存在实数k ,使得(第32题B 图)A B 1BC (第32题A 图)QBA PBA ∠=∠?若存在,求出k 的值;若不存在,请说明理由.34.(本题8分) 已知函数9()||f x x a a x=--+,[1,6]x ∈,a R ∈. (1)若1a =,试判断并证明函数()f x 的单调性;(2)当(1,6)a ∈时,求函数()f x 的最大值的表达式()M a .。
2023年7月浙江省普通高中学业水平考试数学试题含答案

2023年7月浙江省普通高中学业水平考试数学(答案在最后)本试题卷分选择题和非选择题两部分,共4页,满分100分,考试时间80分钟.考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效.3.非选择题的答案必须使用黑色字迹的签字笔或钢笔写在答题纸上相应区域内,作图时可先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑.选择题部分(共52分)一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)1.已知集合{}1,0,1,2A =-,{}|0B x x =>,则下列结论不正确的是()A.1A B ∈ B.A B∅⊆ C.{}2A B ⊆ D.{}|0x x A B>= 【答案】D 【解析】【分析】根据交集、并集的定义求出A B ⋂,A B ⋃,再根据元素与集合的关系、集合与集合的关系判断即可.【详解】因为{}1,0,1,2A =-,{}0B x x =,所以{}1,2⋂=A B ,{}{}|01A B x x ⋃=≥⋃-,所以1A B ∈ ,A B ∅⊆ ,{}2A B ⊆⋂,故A 、B 、C 正确,D 错误;故选:D 2.函数的定义域是()A.1-2⎛⎫∞ ⎪⎝⎭, B.1-2⎛⎤∞ ⎥⎝⎦,C.12⎛⎫+∞ ⎪⎝⎭,D.12⎡⎫+∞⎪⎢⎣⎭,【答案】C 【解析】【分析】根据偶次方根的被开方数为非负数、分式的分母不为零列不等式,由此求得函数的定义域.【详解】依题意210x ->,解得12x >,所以()f x 的定义域为12⎛⎫+∞ ⎪⎝⎭,.故选:C【点睛】本小题主要考查函数定义域的求法,属于基础题.3.复数()i 2i z =+在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B 【解析】【分析】根据复数乘法运算化简,即可求解.【详解】()1i i 22i z =-+=+,故对应的点为()1,2-,位于第二象限,故选:B4.已知平面向量()1,1a =- ,()2,b λ= ,若a b ⊥,则实数λ=()A.2B.2- C.1D.1-【答案】A 【解析】【分析】依题意可得0a b ⋅=,根据数量积坐标表示计算可得.【详解】因为()1,1a =- ,()2,b λ= 且a b ⊥,所以()1210a b λ⋅=⨯+-⨯=,解得2λ=.故选:A 5.已知πsin cos 6θθ⎛⎫+= ⎪⎝⎭,则tan2θ=()A.3B.C.3D.【答案】B【解析】【分析】利用给定条件得到tan 3θ=,再利用二倍角公式求解即可.【详解】若πsin cos 6θθ⎛⎫+= ⎪⎝⎭,可得1sin cos cos 22θθθ+=,化简得31sin cos 022θθ-=,解得3tan 3θ=,由二倍角公式得232322tan 33tan221tan 3θθθ⨯===-,故B 正确.故选:B6.上、下底面圆的半径分别为r 、2r ,高为3r 的圆台的体积为()A.37πrB.321πrC.(35πr+D.(35πr+【答案】A 【解析】【分析】根据圆台的体积公式计算可得.【详解】因为圆台的上、下底面圆的半径分别为r 、2r ,高为3r ,所以()23221π227π33V r r r r r ⎡⎤=++⨯=⎣⎦.故选:A7.从集合{}1,2,3,4,5中任取两个数,则这两个数的和不小于5的概率是()A.35B.710C.45 D.910【答案】C 【解析】【分析】列出所有可能结果,再由古典概型的概率公式计算可得.【详解】从集合{}1,2,3,4,5中任取两个数所有可能结果有()1,2、()1,3、()1,4、()1,5、()2,3、()2,4、()2,5、()3,4、()3,5、()4,5共10个,其中满足两个数的和不小于5的有()1,4、()1,5、()2,3、()2,4、()2,5、()3,4、()3,5、()4,5共8个,所以这两个数的和不小于5的概率84105P ==.故选:C8.大西洋鲑鱼每年都要逆游而上,游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v (单位:m /s )可以表示为3log 100Ov k =,其中O 表示鲑鱼的耗氧量的单位数.若一条鲑鱼游速为2m /s 时耗氧量的单位数为8100,则游速为1m /s 的鲑鱼耗氧量是静止状态下鲑鱼耗氧量的()A.3倍 B.6倍C.9倍D.12倍【答案】C 【解析】【分析】利用给定条件得到31log 2100O v =,再算出不同情况的消耗氧气的数量,再作比值求倍数即可.【详解】由题意得381002log 100k =,解得12k =,故31log 2100O v =,当1v =时,有311log 2100O=,解得900O =,当0v =时,有310log 2100O=,解得100O =,故得9009100=倍,故C 正确.故选:C9.不等式()()e e 10xx --<(其中e 为自然对数的底数)的解集是()A.{01}xx <<∣ B.{|0e}x x << C.{0x x <∣或1}x > D.{0xx <∣或e}x >【答案】B 【解析】【分析】写出不等式的等价不等式组,解得即可.【详解】不等式()()e e 10xx --<等价于e 0e 10x x -<⎧⎨->⎩或e 0e 10x x ->⎧⎨-<⎩,解得0e x <<或x ∈∅,所以不等式的解集为{|0e}x x <<.故选:B10.已知a 为实数,则“0x ∀>,12ax x+≥”是“1a ≥”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C 【解析】【分析】利用分离参数法求出a 的取值范围判断充分性,利用基本不等式反推必要性成立即可.【详解】若10,2,x ax x ∀>+≥则22121(1)1,a x x x≥-+=--+当1x =时,不等式的右边取得最大值1,故1,a ≥充分性成立;若1,a ≥则0x >时,12,ax x+≥≥当且仅当1x a ==时取等,即12ax x +≥恒成立,因此,由 1 a ≥可以推出0,x ">1 2ax x+≥,故必要性成立.综上所述,10,2x ax x∀>+≥是 1 a ≥的充要条件.故选:C.11.若函数()()πsin 06f x x ωω⎛⎫=+> ⎪⎝⎭在区间ππ,126⎡⎤-⎢⎥⎣⎦上单调递增,则ω的取值范围是()A.(]0,2 B.(]0,4 C.(]0,6 D.(]0,8【答案】A 【解析】【分析】利用给定的区间,求出π6x ω+的范围,然后写出正弦函数的单调递增区间,转化为子集问题处理即可.【详解】当ππ[,]126x ∈-时,πππππ[,+]661266x ωωω+∈-,若函数π()sin(0)6f x x ωω=+>在区间ππ[,]126-上单调递增,则πππ2π662πππ2π2612k k ωω⎧+≤+⎪⎪⎨⎪-+≤-⎪⎩,Z k ∈,解得212,824,Z k k k ωω≤+≤-∈,又0ω>,当0k =时,可得02ω<≤.故选:A.12.在正三棱台111ABC A B C -中,2AB =,11AB A B >,侧棱1AA 与底面ABC所成角的余弦值为3.若此三棱台存在内切球(球与棱台各面均相切),则此棱台的表面积是()A.2B.2C.4D.4【答案】A 【解析】【分析】取BC 和11B C 的中点分别为P ,Q ,上、下底面的中心分别为1O ,2O ,设11A B x =,内切球半径为r ,根据题意求出侧棱长以及2O P ,1O Q ,再根据切线的性质及等腰梯形11BB C C 和梯形1AA QP 的几何特点列方程组求出半径,再根据面积计算公式即可.【详解】如图,取BC 和11B C 的中点分别为P ,Q ,上、下底面的中心分别为1O ,2O ,设11A B x =,内切球半径为r ,因为123cos 3A AO ∠=,棱台的高为2r ,所以126sin 3A AO ∠=,111122sin 63r AA BB CC A AO =====∠,211333323O P AP AB ==⨯=,同理136O Q x =.因为内切球与平面11BCC B 相切,切点在PQ 上,所以()21326PQ O P O Q x =+=+①,在等腰梯形11BB C C中,)22222x PQ -⎛⎫=- ⎪⎝⎭②,由①②得()222226212x x r +-⎛⎫-=⎪⎝⎭.在梯形1AA QP 中,()22233236PQ r x ⎛⎫=+- ⎪ ⎪⎝⎭③,由②③得2x -=,代入得1x =,则棱台的高23h r ==,所以()2133262PQ O P O Q x =+=+=,所以1sin 2ABC S AB AC A =⋅=△111111111sin 24A B C S A B A C A =⋅= ,()1111124BCB C S BC B C PQ =+=正三棱台三个侧面都是面积相等的等腰梯形,故侧面积为4,所以此棱台的表面积是442S =++=.故选:A二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中,有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)13.下列不等式正确的是()A.4> B.4< C.24log 3log 5> D.24log 3log 5<【答案】BC 【解析】【分析】根据指数幂的运算及指数函数的性质判断A 、B ,根据对数的运算性质及对于函数的性质判断C 、D.【详解】414142222224⨯==⎭==⎛⎫< ⎪⎝A 错误,B 正确;2421log 5log 5log log 32==<,故C 正确,D 错误.故选:BC14.如图,在正方体1111ABCD A B C D -中,下列结论正确的是()A.11//BC A DB.1//BC 平面11A ADDC.111BC B D ⊥D.1BC ⊥平面11A B CD【答案】BD 【解析】【分析】连接1AD ,1A D ,11B D ,1AB ,1B C ,根据正方体的性质得到11//BC AD ,即可判断A 、B 、C ,证明11BC B C ⊥、1CD BC ⊥,即可判断D.【详解】连接1AD ,1A D ,11B D ,1AB ,1B C ,对于A :在正方体中11//AB D C 且11AB D C =,所以四边形11ABC D 为平行四边形,所以11//BC AD ,又11A D AD ⊥,所以11BC A D ⊥,所以A 错误;对于B ,因为11//BC AD ,1AD ⊂平面11A ADD ,1BC ⊄平面11A ADD ,所以1//BC 平面11A ADD ,所以B 正确;对于C :因为11AB D 为等边三角形,所以1160AD B ∠=︒,又11//BC AD ,所以11AD B ∠为异面直线1BC 与11B D 所成的角,即直线1BC 与11B D 所成的角为60︒,则1BC 与11B D 不垂直,所以C 错误;对于D :在正方体中,11BC B C ⊥,CD ⊥平面11BCC B ,1BC ⊂平面11BCC B ,所以1CD BC ⊥,又1CD B C C ⋂=,1,CD B C ⊂平面11A B CD ,所以1BC ⊥平面11A B CD ,所以D 正确.故选:BD .15.已知函数()2sin cos2f x x x =+,则()A.()f x 的最小值是3-B.()f x 5C.()f x 在区间π,06⎛⎫- ⎪⎝⎭内存在零点 D.()f x 在区间π,π2⎛⎫⎪⎝⎭内不存在零点【答案】ACD 【解析】【分析】利用三角恒等变换将函数化为二次函数,求解最值判断A ,B ,利用换元法求解零点,再判断范围求解C ,D 即可.【详解】易得2213()2sin cos 22sin 12sin 2(sin )22f x x x x x x =+=+-=--+,故函数()f x 在1sin 2x =时,取得的最大值为32,当sin 1x =-时,函数取得的最小值为3-,故A 正确,B 错误,令[]sin 1,1x t =∈-,故2()212f t t t =+-,令()0f t =,解得11322t =+或21322t =-,当113122t =+>时,排除,无法解出x ,当21322t =-时,可得13sin 22x =-,而sin y x =在π(,0)6-上单调递增,故当π(,0)6x ∈-,1sin ,02x ⎛⎫∈- ⎪⎝⎭,且1130222-<-<,则()f x 在区间π,06⎛⎫-⎪⎝⎭内存在零点,故C 正确,而当π,π2x ⎛⎫∈⎪⎝⎭时,sin 0y x =>,1022y =-<,显然sin y x =和122y =-无交点,则()f x 在区间π,π2⎛⎫⎪⎝⎭内不存在零点,故D 正确.故选:ACD.16.在ABC 中,3AB =,1AC =,π3BAC ∠=,点D ,M 分别满足3AB AD = ,2BC MC = ,AM 与CD 相交于点F ,则()A.1233CD AB AC=- B.12AF AM=C.132AM =D.13cos 13DFM ∠=【答案】BCD 【解析】【分析】根据平面向量线性运算法则判断A ,设AF AM λ=,用AD 、AC 表示AF ,根据共线定理的推论得到方程求出λ,即可判断B ,由1122AM AB AC =+及数量积的运算判断C ,求出cos ,CD AM ,即可判断D.【详解】对于A ,13CD AD AC AB AC =-=-,故A 错误;对于B ,设AF AM λ=,又1122AM AB AC =+ ,∴1132222AF AB AC AD AC λλλλ=+=+,又F ,D ,C 三点共线,∴3122λλ+=,12λ∴=,∴12AF AM = ,故B 正确;对于C ,1122AM AB AC =+,∴()()222211244AM AB ACAB AB AC AC =+=+⋅+111391231424⎛⎫=⨯++⨯⨯⨯= ⎪⎝⎭,2AM ∴= ,故C 正确;对于D , 111322CD AM AB AC AB AC ⎛⎫⎛⎫⋅=-⋅+ ⎪ ⎪⎝⎭⎝⎭222211111111331163263222AB AB AC AC =-⋅-=⨯-⨯⨯⨯-⨯= ,又222211212191311393932CD AB AC AB AB AC AC ⎛⎫=-=-⋅+=⨯+-⨯⨯⨯= ⎪⎝⎭,∴1CD =,又2AM =,12cos cos ,13132CD AM DFM CD AM CD AM⋅∴∠===⋅ ,故D 正确.故选:BCD.非选择题部分(共48分)三、填空题(本大题共4小题,每空3分,共15分)17.已知A ,B 是相互独立事件,()23P A =,()12P B =,则()P AB =_____________.【答案】13【解析】【分析】根据相互独立事件的概率公式计算即可.【详解】因为A ,B 是相互独立事件,所以()()()211323P AB P A P B ==⨯=.故答案为:1318.函数2()log f x x =的反函数为_______.【答案】2xy =【解析】【分析】设2log y x =,由指对数式的互化得到2y x =,再将,x y 位置互换即可得出答案.【详解】解:设2log y x =,则2y x =,所以函数2()log f x x =的反函数为2x y =.故答案为:2x y =.19.已知()f x 是定义域为R 的偶函数,且()()24f x f x +-=,则()2023f =_____________.【答案】2【解析】【分析】利用给定条件,得到函数的周期性,将所求函数值化为已知函数值,代入求解即可.【详解】由题意得()f x 是定义域为R 的偶函数,且()()24f x f x +-=,故()()()224f x f x f x -=-=-,可得()()442()f x f x f x -=--=,故得函数的周期4T =,而令1x =,可得()214f =,解得()12f =,则()()()()()2023450533211f f f f f =⨯+==-==.故答案为:220.已知,,a b c 是同一平面上的3个向量,满足3a =,b = ,6a b ⋅=- ,则向量a 与b 的夹角为_____________,若向量c a - 与c b - 的夹角为π4,则c r 的最大值为_____________.【答案】①.3π4##135︒②.【解析】【分析】由cos ,a b a b a b⋅=⋅ 求出向量a 与b 的夹角,设OA a = ,OB b = ,OC c = ,即可得到,,,O A B C 四点共圆,利用正弦定理求出AOB 外接圆的直径,即可求出c的最大值.【详解】因为3a =,b = ,6a b ⋅=- ,所以cos ,2a b a b a b ⋅===-⋅ ,又[],0,πa b ∈ ,所以3π,4a b = ,因为3a =,b = ,3π,4a b = ,如图,设OA a = ,OB b = ,OC c = ,则c a OC OA AC -=-= ,c b OC OB BC -=-= ,又向量c a - 与c b - 的夹角为π4,则π4ACB ∠=,又3π4AOB ∠=,所以,,,O A B C 四点共圆,又AB b a =- ,所以AB == 设AOB 外接圆的半径为R ,由正弦定理23πsin 42AB R ===c故答案为:3π4四、解答题(本大题共3小题,共33分)21.人工智能发展迅猛,在各个行业都有应用.某地图软件接入了大语言模型后,可以为用户提供更个性化的服务,某用户提出:“请统计我早上开车从家到公司的红灯等待时间,并形成统计表.”地图软件就将他最近100次从家到公司的导航过程中的红灯等待时间详细统计出来,将数据分成了[)55,65,[)65,75,[)75,85,[)85,95,[]95,105(单位:秒)这5组,并整理得到频率分布直方图,如图所示.(1)求图中a 的值并且估计该用户红灯等待时间的第60百分位数(结果精确到0.1);(2)根据以上数据,估计该用户在接下来的10次早上从家到公司的出行中,红灯等待时间低于85秒的次数.【答案】(1)0.035a =,估计该用户红灯等待时间的第60百分位数约为82.1(2)7次【解析】【分析】(1)根据频率之和为1以及直方图数据即可求解,先确认频率分布直方图中频率为0.6的位置,再结合百分位数定义求解即可.(2)根据频率分布直方图求出红灯等待时间低于85秒的频率即可求解.【小问1详解】因为各组频率之和为1,组距为10,所以()100.010.0250.020.011a ⨯++++=,解得0.035a =.因为()100.010.0250.350.6⨯+=<,()100.010.0250.0350.70.6⨯++=>,所以中位数位于第三组[)75,85中,设中位数为x ,则()0.10.250.035750.6x ++-=,解得0.257582.10.035x =+≈,所以该用户红灯等待时间的中位数的估计值为82.1.【小问2详解】由题红灯等待时间低于85秒的频率为0.10.250.350.7++=,故估计该用户在接下来的10次中红灯等待时间低于85秒的次数为100.77⨯=次.22.如图,在三棱锥-P ABC 中,PA ⊥平面ABC ,AC BC ⊥,1PA AC ==,BC =(1)求三棱锥-P ABC 的体积;(2)求证:平面PAC ⊥平面PBC ;(3)设点D 在棱PB 上,AD CD =,求二面角D AC B --的正弦值.【答案】(1)6(2)证明见解析(3)3【解析】【分析】(1)先求出底面积,再利用体积公式求解体积即可.(2)先利用线面垂直判定定理得到BC ⊥平面PAC ,再利用面面垂直定理判定面面垂直即可.(3)合理作图,找到二面角的平面角,利用三角函数的定义求解即可.【小问1详解】因为,1,AC BC AC BC ⊥==,所以111222ABC S AC BC =⋅=⨯= ,因为PA ⊥平面ABC ,所以三棱锥-P ABC 的体积11326V =⨯⨯=.【小问2详解】因为PA ⊥平面ABC ,BC ⊂平面PBC ,所以PA BC ⊥,又,,AC BC PA AC A ⊥⋂=,PA AC ⊂平面PAC ,所以BC ⊥平面PAC ,因为BC ⊂平面PBC ,所以平面PAC ⊥平面PBC .【小问3详解】过点D 作DE AB ⊥于E ,取AC 的中点F ,连接,EF 因为PA ⊥平面,ABC PA ⊂平面,PAB 所以平面PAB ⊥平面ABC ,又平面PAB ⋂平面,ABC AB DE =⊂平面,PAB 所以DE ⊥平面,ABC DE ∥PA ,因为,AD CD =且F 是AC 的中点,所以,,,DF AC AC DE DF DE D AC ⊥⊥⋂=⊥平面DEF ,,EF AC ⊥所以DFE ∠是二面角——D AC B 的平面角,因为,,EF AC AC BC F ⊥⊥是AC 的中点,所以E 是AB 的中点,又DE //PA ,所以D 是PB 的中点,在Rt DEF △中,32DF ===,所以12sin 332DE DFE DF ∠==即二面角——D AC B的正弦值为3.23.已知函数()2π2sin 2f x x x a x ⎛⎫=-- ⎪⎝⎭,R a ∈.(1)若1a =,求()f x 在区间[]0,1上的最大值;(2)若关于x 的方程()10f x a ++=有且只有三个实数根1x ,2x ,3x ,且123x x x <<.证明:(ⅰ)1322x x x +=;(ⅱ)()()311217818f x f x x +-+≤.【答案】(1)0(2)(ⅰ)证明见解析.(ⅱ)证明见解析【解析】【分析】(1)利用分析法得到函数的单调性,再求解最值即可.(2)(ⅰ)合理构造新函数,求出一个零点,再结合对称性求解即可.(ⅱ)将目标式合理表示为函数,利用不等式的性质证明即可.【小问1详解】由已知得1a =,则2π()(1)sin()12f x x x =---,易知2(1)y x =-,πsin()2y x =-在区间[0,1]上单调递减,所以()f x 在区间[0,1]上单调递减,所以max ()(0)0.f x f ==【小问2详解】(ⅰ)若2π()(1)sin()1,2f x x a x =---且()10,f x a ++=即2π(1)(sin()1)02x a x ---=有且只有三个实数根,所以0,a <令2π()(1)(sin()1),2g x x a x =---且(1)0g =,则()g x 的图象关于直线1x =对称,所以1322 2.x x x +==(ⅱ)由题意可知,令3πsin 2t x =,则有1()10,f x a ++=()310f x a ++=()()()()2311333217841cos π8271f x f x x x a x x a +-+=--+-++()()233342cos π1571x x a x a =--+++2233ππ4(sin 1)722(12sin )(242)1822a x a a a a x a t t =--++--=+++,因为0,a <所以2(242)1818a t t +++≤,即311(21)7()818f x f x x +-+≤得证.【点睛】关键点点睛:本题考查导数,解题关键是合理表示出目标式,然后结合不等式的性质,得到所要求的不等关系即可.。
浙江省高中数学学业水平考试知识条目精校版

必修1第一章集合与函数概念第二章基本初等函数第三章函数的应用必修2 第一章空间几何体第一章点、直线、平面之间的位置关系第二章直线与方程第三章圆的方程必修4三角函数和第一章平面向量第二章 三角恒等变换必修5解三角形第一章 数列第二章不等式选修2-1 第一章常用逻辑用语第二章圆锥曲线与方程第一章空间向量与立体几何考试形式与试题结构一、考试形式数学学业水平考试采用闭卷、笔答形式。
考试时间为110分钟。
试卷满分为100分。
二、考试结构数学学业水平考试卷的结构如下: 1.考试内容分布《教学指导意见》所规定必修课程内容。
2.考试要求分布了解:约占10%;理解:约占40%;掌握:约占40%;综合运用:约占10% 3.试题类型分布选择题:约占60%;填空题:约占10%;解答题:约占30% 4.试题难度分布容易题:约占70% 稍难题:约占20% 较难题:约占10%参考试卷一、选择题(共25小题,1-15每小题2分,16-25每小题3分,共60分。
) 1.已知集合{1,2,3,4}A =,{2,4,6}B =,则AB 的元素个数是(A)0个 (B)1个 (C)2个 (D)3个 2.22log 12log 3-=(A)2- (B)0 (C)12(D)2 3.若右图是一个几何体的三视图,则这个几何体是 (A)圆锥 (B)棱柱 (C)圆柱 (D)棱锥 4.函数R))(3π2sin()(∈+=x x x f 的最小正周期为(A)2π(B) π (C) π2 (D) 4π 5.直线230x y ++=的斜率是(第3题图)(A)12-(B)12 (C)2- (D)26.若1x =满足不等式2210ax x ++<,则实数a 的取值范围是 (A)(3,)-+∞ (B)(,3)-∞- (C)(1,)+∞ (D)(,1)-∞ 7.函数3()log (2)f x x =-的定义域是(A)[2,)+∞ (B)(2,)+∞ (C)(,2]-∞ (D)(,2)-∞ 8.圆22(1)3x y -+=的圆心坐标和半径分别是(A)(1,0),3- (B)(1,0),3(C)(1,-(1,9.各项均为实数的等比数列{}n a 中,11a =,54a =,则3a = (A)2 (B)2-(D) 10.下列函数中,图象如右图的函数可能是 (A)3y x = (B)2xy =(C)y =2log y x =11.已知a ∈R ,则“2a >”是“22a a >”的 (A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 12.如果222=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是(A) ()+∞,0 (B)()2,0 (C)()+∞,1 (D) ()1,013.设x 为实数,命题p :x ∀∈R ,20x ≥,则命题p 的否定是14.若函数()(1)()f x x x a =+-是偶函数,则实数a 的值为(A)1 (B)0 (C)1- (D)1±15.在空间中,已知,a b 是直线,,αβ是平面,且,,//a b αβαβ⊂⊂,则,a b 的位置关系是 (A)平行 (B)相交 (C)异面 (D)平行或异面16.在△ABC 中,三边长分别为c b a ,,,且︒=30A ,︒=45B ,1=a ,则b 的值是(A)21(B) 22 (C) 2 (D) 2617.若平面向量,a b 的夹角为60,且|2|=|a b |,则(A)()⊥+a b a (B)()⊥-a b a (C)()⊥+b b a (第10题图) A 1(第18题图)(D)()⊥-b b a18.如图,在正方体1111D C B A ABCD -中,E 为1BC 的中点,则DE 与面11B BCC 所成角的正切值为(A)23219.函数44sin cos y x x =-在]3π,12π[-的最小值是 (A)1-(B)2-12(D)1 20.函数1()2x f x x=-的零点所在的区间可能是 (A)(1,)+∞ (B)1(,1)2 (C)11(,)32 (D)11(,)4321.已知数列{}n a 满足121a a ==,2111n n n na a a a +++-=,则65a a -的值为 (A)0 (B)18 (C)96 (D)60022.若双曲线22221x y a b-=的一条渐近线与直线310x y -+=平行,则此双曲线的离心率是(C)323.若将一个真命题...中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题...,则该命题称为“可换命题”.下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行; ③平行于同一直线的两直线平行; ④平行于同一平面的两直线平行. 其中是“可换命题”的是(A)①② (B)①④ (C)①③ (D)③④24.用餐时客人要求:将温度为10C 、质量为25.0 kg 的同规格的某种袋装饮料加热至C C ~︒︒4030.服务员将x 袋该种饮料同时放入温度为80C 、5.2 kg 质量为的热水中,5分钟后立即取出.设经过5分钟加热后的饮料与水的温度恰好相同,此时,1m kg 该饮料提高的温度1t C ∆与2m kg 水降低的温度2t C ∆满足关系式11220.8m t m t ⨯∆=⨯⨯∆,则符合客人要求的x 可以是 (A)4 (B)10 (C)16 (D)2225.若满足条件20,20,210x y x y kx y k -+≥⎧⎪+-≥⎨⎪--+≤⎩的点(,)P x y 构成三角形区域,则实数k 的取值范围是(A)(1,)+∞ (B)(0,1) (C)(1,1)- (D)(,1)(1,)-∞-+∞二、填空题(共5小题,每小题2分,共10分)26.已知一个球的表面积为4πcm 3,则它的半径等于 ▲ cm .27.已知平面向量(2,3)=a ,(1,)m =b ,且//a b ,则实数m 的值为 ▲ .28.已知椭圆中心在原点,一个焦点为F (-23,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 ▲ .29.数列{}n a 满足⎩⎨⎧≤≤≤≤=--,1911,2,101,2191n n a n n n 则该数列从第5项到第15项的和为 ▲ .30.若不存在...整数x 满足不等式2(4)(4)0kx k x ---<,则实数k 的取值范围是 ▲ . 三、解答题(共4小题,共30分)31.(本题7分) 已知,54sin ),π,2π(=∈θθ求θcos 及)3πsin(+θ的值.32.(本题7分,有A 、B 两题,任选其中一题完成,)(A ) 如图,在直三棱柱111ABC A B C -中, 3AC =, 4BC =, 5AB =,点D 是AB 的中点.(1)求证:1AC BC ⊥; (2)求证:1AC ∥平面1CDB .(B )如图,在底面为直角梯形的四棱锥,//,BC AD ABCD P 中-,90︒=∠ABC平面⊥PA ABCD ,32,2,3===AB AD PA ,BC =6.(1)求证:;PAC BD 平面⊥ (2)求二面角A BD P --的大小.33.(本题8分) 如图,由半圆221(0)x y y +=≤ 2(1)y a x =-(0y ≥,0a >)合成的曲线C 且曲线C 经过点(2,3). (1)求a 的值;(2)设(1,0)A,(1,0)B -,过A 且斜率为k 的直线 l 球形线”相交于P ,A ,Q 三点,问是否存在实数k ,使得QBA PBA ∠=∠?若存在,求出k y(第33题图)A B 1BC (第32题A 图)34.(本题8分) 已知函数9()||f x x a a x=--+,[1,6]x ∈,a R ∈.(1)若1a =,试判断并证明函数()f x 的单调性;(2)当(1,6)a ∈时,求函数()f x 的最大值的表达式()M a .。
2022年7月浙江省普通高中学业水平考试数学试题(含详细答案)

2022年7月浙江省普通高中学业水平考试数学试题卷(时间80分钟,总分100分)选择题部分一、单项选择题(本大题共12小题,每小题3分,共36分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.已知集合{}0,1,2A =,{}1,2,3,4B =,则A B =()A.∅B.{}1 C.{}2 D.{}1,2【答案】D【解析】∵{}0,1,2A =,{}1,2,3,4B =,∴{}1,2A B = .2.复数2i -(i 为虚数单位)的实部是()A.1B.1-C.2D.2-【答案】C【解析】显然复数2i -的实部是2.3.函数()f x =的定义域是()A.(),1-∞ B.[)1,+∞ C.(),1-∞- D.[)1,-+∞【答案】D【解析】∵10x +≥,∴1x ≥-,即函数()f x =的定义域为[)1,-+∞.4.已知tan 1α=,ππ,22⎛⎫∈- ⎪⎝⎭α,则α=()A.4π B.π4-C.π3D.π3-【答案】A【解析】∵tan 1α=,∴ππ4k α=+,又ππ,22⎛⎫∈- ⎪⎝⎭α,∴π4α=.5.袋子中有5个大小质地完全相同的球,其中2个红球,3个黄球,从中随机摸出1个球,则摸到黄球的概率是()A.15B.25C.35D.45【答案】C【解析】5个大小质地完全相同的球,黄球有3个,则随机摸出1个球,有5种方法,摸到黄球有3种方法,所以摸到黄球的概率为35.6.已知平面向量()2,4a =r ,(),6b x = .若//a b r r,则实数x =()A.3-B.3C.12-D.12【答案】B【解析】由a b ∥,可得2640x ⨯-=,解得3x =.7.已知球的半径是2,则该球的表面积是()A.2π B.4π C.8π D.16π【答案】D【解析】224π4π216πS R ==⨯=,8.设0a >,下列选项中正确的是()A.313a a ⎛⎫= ⎪⎝⎭B.2233a a-= C.2332a a a= D.2332a a a÷=【答案】A【解析】对于A ,311333a a a ⨯⎛⎫== ⎪⎝⎭,故A 正确;对于B ,2223023331a aa a--===,故B 错误;对于C ,23213332362a a aa ==,故C 错误;对于D ,221133332a a a a a a-÷===,故D 错误.9.中国茶文化博大精深,茶水口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水的温度降至60℃时饮用,可以产生最佳口感.已知在25℃的室温下,函数()600.9227250ty t =⨯+≥近似刻画了茶水温度y (单位:℃)随时间t (单位:min )的变化规律.为达到最佳饮用口感,刚泡好的茶水大约需要放置(参考数据: 6.70.92270.5833≈,8.70.92270.4966≈)()A.5min B.7min C.9min D.11min 【答案】B【解析】由题可知,函数()600.9227250ty t =⨯+≥,当 6.7t =,59.998y ≈,已经接近60,又函数()600.9227250ty t =⨯+≥在()0,∞+上单调递减,则大约在7min 时口感最佳.故A ,C ,D 错误.10.设a ,b 是实数,则“a b >”是“a b >”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】对于a b >,比如3a ==-,显然13a b =<=,不能推出a b >;反之,如果a b >,则必有0,a a a b b >∴=>≥;所以“a b >”是“a b >”的必要不充分条件;11.在ABC 中,设2AD DB = ,2BE EC =,CF FA λ= ,其中R λ∈.若DEF 和ABC 的重心重合,则λ=()A.12B.1C.32D.2【答案】D【解析】设O 为DEF 和ABC 的重心,连接DO 延长交EF 与N ,连接AO 延长交BC 与M ,所以N 是EF 的中点,M 是BC 的中点,所以()2211133233AO AM AB AC AB AC==+=+,2111133333DO DA AO AB AB AC AB AC=+=-++=-+,()()22113323DO DN DE DF DB BE DA AF==+=+++()112211121333313331AB BC AB AC AB AC AB AC λλ=+-+=-+-+++11213331AB AC λ=-+++,可得21131λ=++,解得2λ=.12.如图,棱长均相等的三棱锥-P ABC 中,点D 是棱PC 上的动点(不含端点),设CD x =,锐二面角A BD C --的大小为θ.当x 增大时,()A.θ增大 B.θ先增大后减小 C.θ减小 D.θ先减小后增大【答案】C【解析】由题意,三棱锥-P ABC 是正四面体,以PBC 的重心为原点,BC 边的中线PG 为x 轴,OA 为z 轴,过O 点平行于BC 的直线为y 轴,建立空间直角坐标系如图:设三棱锥P -ABC的棱长为,则有:22221228OA AP PO =-=-=,()(()()1,,0,0,,1,,2,0,0B A C P --,3231,,022x D x ⎛⎫- ⎪ ⎪⎝⎭,(1,,1,,22x AB AD x ⎛-=--=-- ⎝ ,设(),,m t y z = 是平面ABD 的一个法向量,则有·0·0m AB m AD ⎧=⎪⎨=⎪⎩,即01022t x x t y ⎧--=⎪⎛⎫⎛⎫⎨--+-= ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎩,令y =,解得(,,,t x z m x =-=-=-,显然()0,0,1n =是平面PBC 的一个法向量,cos m nm n θ∴===;显然当x =x 的取值范围是0x <<),πcos 0,2θθ==最大,当x >或x <时,cos θ都变大,即θ变小;二、多项选择题(本大题共4小题,每小题4分,共16分.每小题列出的四个备选项中有多个是符合题目要求的,全部选对得4分,部分选对且没有错选得2分,不选、错选得0分)13.图象经过第三象限的函数是()A.2y x= B.3y x= C.23y x= D.1y x -=【答案】BD【解析】由幂函数的图象可知,A 中,2y x =过第一、二象限;B 中,3y x =过第一、三象限;C 中,320y x ==≥且定义域为R ,过第一、二象限;D 中,1y x -=过第一、三象限.14.下列命题正确的是()A.过平面外一点,有且只有一条直线与这个平面垂直B.过平面外一点,有且只有一条直线与这个平面平行C .过直线外一点,有且只有一个平面与这个直线垂直D.过直线外一点,有且只有一个平面与这个直线平行【答案】AC【解析】对于A ,根据线面垂直的定义,可得经过平面外一点作已知平面的垂线,有且仅有一条,故A 正确;对于B ,过平面外一点可以作一个平面与已知平面平行,在这个平行平面内的经过已知点作直线,它就和已经平面平行,故过平面外一点有无数条直线与这个平面平行,故B 不正确;对于C ,由直线与平面垂直的性质知:过直线外一点只能作一个平面与这条直线垂直,故C 正确;对于D ,过直线外一点,有无数个平面与这条直线平行,故D 不正确.15.在锐角ABC 中,有()A.sin sin sin A B C +> B.222sin sin sin A B C +>C.cos cos sin A B C +> D.222cos cos sin A B C +>【答案】ABC【解析】对于A ,根据正弦定理,因为a b c +>可得sin sin sin A B C +>,故A 正确;对于B ,因为222cos 02a b c C ab+-=>可得222a b c +>,再由正弦定理可得222sin sin sin A B C +>,故B 正确;对于C ,因为π0,2A B <<中,所以0sin ,sin 1A B <<,所以()cos cos cos sin cos sin sin sin A B A B B A A B C +>+=+=,故C 正确;对于D ,当222π13cos cos sin 324A B C A B C ===⇒+=<=,故D 错误16.已知a ∈R ,设()11,A x y ,()22,B x y 是函数()2y x a =-与1sin y x =-图象的两个公共点,记()12f a x x =-.则()A.函数()f a 是周期函数,最小正周期是πB.函数()f a 在区间π0,2⎛⎫⎪⎝⎭上单调递减C.函数()f a 的图象是轴对称图形D.函数()f a 的图象是中心对称图形【答案】BC【解析】分别作出()2y x a =-与1sin y x =-(周期为2π)的图象(如图).对于B ,由图可知,当3ππ,22a ⎛⎫∈-- ⎪⎝⎭时,()f a 单调递增;当ππ,22a ⎛⎫∈- ⎪⎝⎭时,()f a 单调递减,故B 正确;对于C 、D ,对于任意a ∈R ,此时作()2y x a =-关于2x π=-的对称函数()2πy x a =---⎡⎤⎣⎦,且1sin y x =-也关于2x π=-对称,故()()πf a f a --=,即()f a 关于2x π=-对称,即()f a 关于2x π=-对称,故C 正确,D 错误.错误.对于A ,由于当3ππ,22a ⎛⎫∈-- ⎪⎝⎭时,()f a 单调递增;当ππ,22a ⎛⎫∈- ⎪⎝⎭时,()f a 单调递减,()f a 关于π2x =-对称,由于1sin y x =-是最小正周期为2π的函数,其图象呈周期性变换,而()2y x a =-在平移过程中大小与形状不变,所以()12f a x x =-呈周期性变换,根据函数的对称性作出()f a 的大致图像(如图),可知其为周期函数,且最小正周期为2πT =,故A错误;非选择题部分三、填空题(本大题共4小题,每空分3分,共15分)17.已知函数()25,1,log ,1,x x f x x x +<⎧=⎨≥⎩则()1f -=______,()1f f -=⎡⎤⎣⎦______.【答案】①.4②.2【解析】()1154f -=-+=;()()214log 42f f f ⎡⎤-===⎣⎦.故答案为:4;2.18.某广场设置了一些石凳供大家休息,每个石凳都是由正方体截去八个一样的四面体得到的(如图,从棱的中点截).如果被截正方体的棱长是4(单位:dm ),那么一个石凳的体积是______(单位:3dm ).【答案】1603【解析】正方体的体积为3464=,正方体截去的八个四面体是全等的正三棱锥,截去的一个正三棱锥的体积为114222323⨯⨯⨯⨯=,则石凳的体积为416064833-⨯=.19.已知实数0x >,0y >,则2x yx y x++的最小值是______.【答案】1-【解析】211x y x y xx y x x y x ++=+-≥-++,当且仅当2x y xx y x+==+.20.已知平面向量a ,b 是非零向量.若a 在b上的投影向量的模为1,21a b -= ,则()4a b b -⋅ 的取值范围是______.【答案】[]3,4【解析】解:由题意,令(),0b b = ,()1,a y =±,则()()2221221a b b y -=⇒±-+= ,所以[]240,1y ∈,由21a b -= ,得22441a a b b -⋅+= ,所以()2441a b b a -⋅=- .()[]222411433,4y y ⎡⎤=±+-=+∈⎣⎦.四、解答题(本大题共3小题,共33分)21.在某市的一次数学测试中,为了解学生的测试情况,从中随机抽取100名学生的测试成绩,被抽取成绩全部介于40分到100分之间(满分100分),将统计结果按如下方式分成六组:第一组[)40,50,第二组[)50,60,L ,第六组[]90,100,画出频率分布直方图如图所示.(1)求第三组[)60,70的频率;(2)估计该市学生这次测试成绩的平均值(同一组中的数据用该组区间的中点值为代表)和第25百分位数.解:(1)由频率分布直方图知,第三组的频率为0.020100.2⨯=.(2)平均值450.00410550.01210650.02010750.03010850.02410x =⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯950.0101073.8+⨯⨯=,因为()0.0040.012100.16+⨯=,()0.0040.0120.020100.36++⨯=,所以第25百分位数为0.250.16601064.50.2-+⨯=.22.已知函数()222cos f x x x =+.(1)求π4f ⎛⎫⎪⎝⎭的值;(2)求函数()f x 的最小正周期;(3)当[],2x t t ∈([][],20,2πt t ⊆)时,()1f x ≤恒成立,求实数t 的最大值.解:(1)22πππππ22cos 2cos 144424f ⎛⎫⎛⎫=⨯+=+=⎪ ⎪⎝⎭⎝⎭.(2)()2π22cos 2cos 212sin 216f x x x x x x ⎛⎫=+=++=++ ⎪⎝⎭,所以函数()f x 的最小正周期2ππ2T ==.(3)当[],2x t t ∈,()1f x ≤恒成立,即π2sin 2116x ⎛⎫++≤ ⎪⎝⎭,所以π1sin 206x ⎛⎫-≤+≤ ⎪⎝⎭,因为[],2x t t ∈,[][],20,2πt t ⊆,所以πππ242π66t t ≤+<+≤,解得5π11π1224t ≤≤,即实数t 的最大值为11π24.综上,π14f ⎛⎫= ⎪⎝⎭,最小正周期为π,实数t 的最大值为11π24.23.已知函数()()20xa f x a x x x=+->,其中1a >.(1)若()24f ≤,求实数a 的取值范围;(2)证明:函数()f x 存在唯一零点;(3)设()00f x =,证明:()22021222a a f x a a -+<+<-+.解:(1)因为()()20xaf x a x x x=+->,由()2224f a a =+-≤,可得220a a --≤,所以()()210a a -+≤,即12a -≤≤,又1a >,所以12a <≤;(2)证明:因为函数()()20xaf x a x x x=->,其中1a >,所以()f x 在()0,∞+上单调递增,且()11210f a a a =+-=-<,()221722024f a a a ⎛⎫=+-=-+> ⎪⎝⎭,所以由零点存在定理,得()f x 在()1,2内有唯一零点,即函数()f x 存在唯一零点;(3)证明:若()00f x =,则()()001,212,3x x ∈⇒+∈,所以()()20221f a a f x =+-<+,又()000020xa f x a x x =+-=,0002x a a x x =-,所以()()()021000000022211111x a a af x ax ax x x x x ++=++-=-++-++()200002211a x a x x x ⎛⎫=-+++ ⎪+⎝⎭,令()()22000002222212211g a a a f x a x a x x x ⎛⎫⎛⎫=-+-+=-+-++- ⎪ ⎪+⎝⎭⎝⎭,又0220x ->,所以()g a 的图象开口向上,对称轴()()200020000000221104141222x x x x x x a x x x x ⎛⎫--+ ⎪++⎝⎭=-=-=--+⎛⎫⋅- ⎪⎝⎭,所以()g a 在()1,+∞上单调递增,所以()()20000002222121211111g a g x x x x x x ⎛⎫⎛⎫>=-⋅+-+⋅+-=-+ ⎪ ⎪++⎝⎭⎝⎭()()()()()()22000000000000002122120111x x x x x x x x x x x x x x +-+++-+-===>+++,即()201222f x a a +<-+,所以()22021222a a f x a a -+<+<-+.。
2019版数学浙江省学业水平考试专题复习选修2-1-§3

知识点一双曲线定义平面内与两个定点F i, F2的距离的差的绝对值等于非零常数(小于I F1F2I)的点的轨迹叫做双曲线•这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线______________集合P= {M|||MF i|—|MF2|| = 2a}, |F i F2|= 2C,其中a, c为常数且a>0 , c>0.(1) 当2a<|F i F2|时,P点的轨迹是双曲线;(2) 当2a= |F 1F2L时,P点的轨迹是两条射线;(3) 当2a>|F i F g|时,P点不存在.知识点二双曲线的标准方程和几何性质题型一双曲线的定义y已知双曲线x 2 — = 1的两个焦点为24F 1, F 2, P 为双曲线右支上的一点.知识点三有关双曲线的计算、证明 1 •待定系数法求双曲线方程的常用方法 x 2 y 2 与双曲线a ^ - b^=1共渐近线的可设为 X 2 a 2y 2 = K 5); b x 2 y 2 若渐近线方程为y = ±a x ,则可设为旷^=?(刊; x 2 y 2 若过两个已知点则设为 + — = 1( mn <0).m n 2 •等轴双曲线的离心率与渐近线关系 双曲线为等轴双曲线 ?双曲线的离心率 2?双曲线的两条渐近线互相垂直3 •双曲线的焦点到渐近线的距离等于半虚轴长 b .4 •渐近线与离心率 x 2 y 2 話—b^= 1(a >0 , b >0)的一条渐近线的斜率为 (位置关系).|PF2|,则△ F1PF2的面积为()A. 48B. 24C. 12D. 6答案B解析由双曲线的定义可得1|PF i|_ |PF2| = _|PF2| = 2a= 2,3解得|PF2| = 6,故|PF i|= 8,又|F i F2|= 10 ,由勾股定理可知厶PF1F2为直角三角形,1因此S VPF1F2 = — |PF11 XPF21 = 24.感悟与点拨利用双曲线的定义时,要特别注意条件“差的绝对值”,弄清研究对象是整条双曲线,还是双曲线的一支.跟踪训练1 (1)已知圆C1: (x+ 3)2+ y2= 1和圆C2:(x —3)2+ y2= 9,动圆M同时与圆G 及圆C2相外切,则动圆圆心M的轨迹方程为 __________________ .(2)设过双曲线x2—y2= 9左焦点F1的直线交双曲线的左支于点P, Q, F2为双曲线的右焦点•若|PQ| = 7,则A F2PQ的周长为__________y2答案(1)x2—= 1(x <—1) (2)26解析(1)如图所示,设动圆M与圆C1及圆C2分别外切于点A和B.根据两圆外切的条件,得|MC i|—|AC i|=|MA |,|MC2| —|BC2| = |MB |,•••|A |= |MB|,•••MC i|—|AC i| = |MC2| —|BC2|,即|MC2|—|MC i| = |BC2|—|AC i| = 2<6 ,•••点M到两定点C i, C2的距离的差是常数且小于|C i C2|.与C i的距离又根据双曲线的定义,得动点M的轨迹为双曲线的左支(点M与C2的距离大, 小),其中a= 1 , c = 3,贝U b2= 8.故点M的轨迹方程为x2——= 1(x<—1).8(2)如图,由双曲线的定义可得|PF2| —|PF i| = 2a,|QF2| —|QF i|= 2a,将两式相加得|PF2| + |QF2|—|PQ| = 4a, •••△2PQ的周长为|PF2|+|QF2|+|PQ|=4a + |PQ|+ |PQ|= 4 x 3 + 2 x 216.题型二 求双曲线的标准方程y 252= 1的离心率e =匚,且其右焦点为F 2(5,0),则双曲线C 的b 24标准万程为()x 2 B._ 9 y 2——=1 16x 2A.—- 4y 2=13 x2y 2x 2y 2c — ——=1 D._ ——=1 193 4X 2答案(1)C(2) — y 2 = 14解析 ⑴由焦点F 2(5,0)知c = 5 ,c 5又 e = _=_,得 a = 4, b 2= c 2— a 2 = 9,a 4x 2 y 2•••双曲线C 的标准方程为 一—=1.16 91(2) •••双曲线的渐近线方程为 y = ±;x , •可设双曲线的方程为 x 2— 4y 2= A( "0. •••双曲线过点(4,“ 3), •"= 16 — 4 XC 3)2 = 4 ,x 2•双曲线的标准方程为 —一 y 2= 1.4感悟与点拨 求双曲线的标准方程常用待定系数法.待定系数法的具体过程是先定形,再定 量,即先确定双曲线标准方程的形式,再根据a ,b ,c , e 及渐近线之间的关系,求出 a , b例2(1)已知双曲线 x 2C : a 2(2)已知双曲线过点(4,- 3),且渐近线方程为1 y=±尹则该双曲线的标准方程为的值•如果已知双曲线的渐近线方程,求双曲线的标准方程,可利用有公共渐近线的双曲线x 2 y 2方呈为a 2- b ^7小,再由条件求出入的值即可.x 2 y 2x 2 y 2跟踪训练2⑴已知双曲线-1(a >0,b >o )和椭圆16 + ; = 1有相同的焦点,且双曲 线的离心率是椭圆离心率的2倍,则双曲线的标准方程为 __________(2)与双曲线x 2— 2y 2= 2有公共渐近线,且过点M (2 , - 2)的双曲线的标准方程为 __________x 2 y 2 x 2 y 2由于双曲线a 2 -旷1与椭圆和+ 9=1有相同的焦点,.•.a 2 + b 2= 7.•••a = 2, b 2 = c 2— a 2= 3,x 2 y 2故双曲线的标准方程为--7 =「x 2(2)x 2 — 2y 2= 2化为标准方程得 ——y 2 = 1 ,x 2设与双曲线J -y 2=1有公共渐近线的双曲线方程为 x 22 — y 2 = k (k *0),22将点(2 , — 2)代入得 k = — — (— 2)2 = — 2.y 2 x 2•••双曲线的标准方程为 一一一=1.x 2 y 2答案⑴;■- 3 =1y 2 x 2 解析x 2 y 2⑴椭圆石+ 了 = 1的焦点为F i (— 7, 0) , F 2(“ 7, 0),离心率为又双曲线的离心率2 4题型三双曲线的几何性质x2 y2例3 (1)(2017年4月学考)过双曲线--2 = 1(a>0 , b>0)的左顶点A作倾斜角为45 °的a b直线l, l交y轴于点B,交双曲线的一条渐近线于点C,若AB = BC,则该双曲线的离心率为( )A. 5B.“ 5C. 3 D-^-x2 y2⑵设双曲线二一2 = 1(a>0 , b>0)的右焦点是F,左、右顶点分别是A i, A2,过F作A1A2a2 b2的垂线与双曲线交于B, C两点•若A1B丄A2C,则该双曲线的渐近线方程为___________ _答案(1)B (2)x ±y = 0解析(1)由题意可知,设双曲线的右顶点为D,连接CD,由题意可知,|OA|=|OB|=|OD|=a,OB是△ADC的中位线,贝U |CD| = 2a,则C(a,2a),将C代入双曲线的渐近线方程b y蔦x,整理得,b = 2a,则该双曲线的离心率•••双曲线的离心率为b2b2⑵由题设易知A i(—a,0), A2(a,0), Be, , C c,- ,a abj bja a因为A i B丄A2C,所以•—= —1,整理得a= b.e + a e—ab因此该双曲线的渐近线方程为y =±,x,即x±y = 0.a感悟与点拨双曲线的几何性质的常考题型为求双曲线的渐近线和离心率.(1)对于双曲线的渐近线问题,注意公式中双曲线的焦点所在的坐标轴,当焦点在b a渐近线方程为y = ±一x.当焦点在y轴上时,渐近线方程为y =±—x.a b解即可.跟踪训练3 (1)(2018 年4月学考)双曲线x2—匸=1的渐近线方程是()31A. y=±3xD. y=±3x—y2⑵设双曲线二一二=1(b> a>0)的焦距为2e,直线I过A(a,0), B(0, b)两点,已知原点到x轴上时,⑵对于双曲线的离心率问题,根据条件,建立关于a, b, e的齐次方程(或不等式),然后求x2a2 b2直线I的距离为e,则双曲线的离心率为4答案(1)C (2)2解析(2)过点0作AB的垂线,垂足为E,如图所示,在△ OAB中, g a, .OB, = b,叱二,4 |AB|= - a2+ b2= c.因为|AB| 0E| = |0A| 0B|,所以 c = ab,即(a2+ b2) = ab ,4 4寸3 b b 寸3两边同除以a2,得丁二-a=0,b 厂b解得=“ 3或=a Y a所以、选择题x2 y21 - (2018年6月学考)双曲线16- 了= 1的焦点坐标是()A • (- 5,0), (5,0) B. (0,- 5), (0,5)C • (-■, 7, 0), ( 7, 0)D • (0,—7) , (0 , 7)答案Ax22 •已知双曲线 --y2= 1的焦点坐标为(2,0),则此双曲线的渐近线方程是()aB. y =±答案 C解析由题意可知"a 2+ 1 = 2,.••a =±" 3, x 2 y 23 .若双曲线 一一—=1上点P 到点(5,0)的距离为15,则点P 到点(-5,0)的距离为()16 9•••双曲线的渐近线方程为1y =±—x =±ax .3答案 Dx 2 y 2解析 •••双曲线16—9= 1,I O vJ•••2a = 8 , (5,0) , (— 5,0)是双曲线的两个焦点, •••点 P 在双曲线上,•PF i ||— |PF 2||= 8,•••点P 到点(5,0)的距离为15 , •••点P 到点(一5,0)的距离是15 + 8 = 23或15 — 8= 7.x 2 y 24 .已知双曲线 ——=1(a >0)的实轴长、虚轴长、焦距长成等差数列,则双曲线的渐近线a 2 4方程为()4 B .y =±5x3 C.y=±4x答案 D解析 由题意可知实轴长为 2a ,虚轴长为4,焦距长为2 a 2+ 4 ,因为实轴长、虚轴长、焦距长成等差数列,x 2 y 2因此双曲线的方程为 一—=1,9 4 44则双曲线的渐近线方程为 y = ±;x .3x 2 y 25 .设双曲线—+:= 1的渐近线方程为3x±2y = 0,则a 的值为()a 9B . 23C . 5 或 25D . 7 或 235A. y =±4x4D . y =±3x一3+4=8,解得 a =2则 2a + 2A 4B 3C . 2D . 1 答案 A解析 因为方程表示双曲线,所以a <0 ,y 2 x 2标准方程为孑——;=1,3 所以渐近线方程为 y =±— x ,—3 3所以 —=一,解得a =— 4.—a 26 .若双曲线过点(m , n )(m > n >0)且渐近线方程为 y =±x ,则双曲线的焦点()A .在x 轴上 C .在x 轴或y 轴上 答案 A解析 因为m >n >0,所以点(m , n )在第一象限且在直线 y = x 的下方,故焦点在 x 轴上.x 2 y 27 . (2016年10月学考)设双曲线-—二=1(a >0 , b >0)的左、右焦点分别为 F i , F 2,以F i a 2 b 2 为圆心,|F 1F 2|为半径的圆与双曲线在第一、 二象限内依次交于 A , B 两点,若|F 1B |= 3|F 2A |,则该双曲线的离心率是( )5 4 3A. 一B.— CT D . 2 4 3 2答案C解析由题意知|F 1B |= |F 1A |= 2c , |AF 2| = 2C — 2a ,B .在y 轴上 D •无法判断已知|F i B| = 2c= 3|AF2|= 6c-6a,即即4c= 6a,x2 y28 .若双曲线—-2= 1(a>0 , b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离a2 b2心率为(b bc解析焦点(c,0)到渐近线y = -x的距离为 --------- =2a,解得b = 2a.答案Aa V a2+ b2又a2+ b2= c2,「.5a2= c2,c离心率e=_a9 .设直线l过双曲线C的一个焦点,且与C的一条对称轴垂直,I与C交于A, B两点,|AB|为C的实轴长的2倍,贝U C的离心率为()x2 y2解析设双曲线的标准方程为;一;=1(a>0 , b>0),a2 b2答案B由于直线I 过双曲线的焦点且与对称轴垂直,因此直线 I 的方程为x = c 或x = -c ,x 1 2 y 2代入旷b ^ = 1D._ 2 答案 Bc 2得 y 2=b 2 品-i b2a 2,b 2 2b 2•••y =±一,故 |AB| = a a2b 2依题意,得 =4a , ab 2c 2 - a 2•2 = 2,•丁=e 2-1 = 2,x 2 y 210 •已知F 1,F 2分别是双曲线a 2-站i (a >0,b >°)的左、右焦点,|1,12为双曲线的两条 渐近线,设过点 M (b,O)且平行于|1的直线交I 2于点P 若PF 1丄PF 2,则该双曲线的离心率为B.“ 5'14 + 2沖114 - 241 C.解析 根据题意可得 F i ( — c ,0), F 2(C ,0),b双曲线的渐近线方程12为y = 一x ,① ab直线PM 的方程为y =— ;(x — b ),②b联立①②,可得x =2,b b 2"P 2,2a••PF i 丄 PF 2,.・.—T ? —2P = 0,b • +c , b 2 b b 2c , = 0, 2a 2 2ab 2b 4 書—c 2+4^=0,又 a 2+ b 2 = c 2,「.b 2= 4a 2,「.c 2= 5a 2,B.二、填空题11 •已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为 6,则该双曲线的离心率为 ________答案 3 --- > ••• — P =bi2a , F 2P = ― c , 2a ,12 .设中心在原点的椭圆与双曲线2x 2— 2y 2= 1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程为 ______________ x 2答案 -+ y 2 = 1x 2 y 2设椭圆的标准方程为 二+ 2 = 1(a >b >0). a 2 b 2•••a = ” 2, b = a 2 — c 2 = 1 ,x 2•椭圆的方程为一 + y 2= 1. 2x 2 y 213 .已知双曲线旷恳=1(a >0,b >0),过其右焦点且垂直于实轴的直线与双曲线交于M , N 两点,0为坐标原点•若 0M 丄ON ,则双曲线的离心率为解析 设右焦点为F ,由条件可得b 2 1 ±认 |MF |=|OF |,即—=c ,则 c 2 — ac — a 2 = 0,即 e 2— e — 1 = 0 ,解得 e = J.由 e >1 可得 e a2 x 2 y 214 .已知双曲线 二一二=1(a >0 , b >0)的一条渐近线垂直于直线 I : x — 2y — 5 = 0,双曲线a 2b 2 的一个焦点在l 上,则双曲线的方程为 ___________________ .X 2解析 由题意知,双曲线y 27=1的焦点为F 1( -1,0), F 2(1,0),离心率 e = 2.x2 y2答案——=15 20b 解析 由题意得一一=—2,即b = 2 a , a 又焦点(c ,0)在x — 2y — 5 = 0上,所以c = 5, 双曲线中 a 2+ b 2= c 2,解得 a = ' 5, b = 2 i 5, x 2 y 2 所以双曲线的方程为 —一=1. 5 20n 2 直线PA , PB 的斜率记为 m , n ,贝U m 2 + 一的最小值为 ___________ 4 答案 4 解析 由PA + PB = 2PO 知点O 为线段AB 的中点, 设 A (x i , y i ), P (x 2, y 2), y 2 — y i y 2 + y i 则 B ( — x i , — y i ),所以 m = , n = — X 2 — x i X 2 + x i y 2 + y i y 2 — y i 故mn = X 2 + x i X 2 — x i 由于点A , B , P 在双曲线上, y 2 — y 2mn = = 4, i-y 2—y 24 n 2m 2 • = mn = 4(当且仅当n 2= 4m 2时等号成立),故最小值为4. 4三、解答题15 •已知A,B,P 为双曲线x 2 —厂=1 4 上不同的三点, 且满足PA + y 2 — y 2 x 2 — x 2' 所以 x i — W = i , 4x 2 —匕=i4代入上式中,有 n 2 所以m 2+ >2 4x2 y2i6 •已知F i, F2分别是双曲线C:二一二=i的左、右焦点,若F2关于渐近线的对称点恰a2 b2落在以F i为圆心,|OF i|为半径的圆上,求C的离心率.解设点F2关于渐近线的对称点为A , 可得|0A| = |OF2|, 根据题意有|F i O| = |F i A|,•••OA|= |0F2|= |OF i|= |F i A|,•••筮F i O是等边三角形,•••/AF i O= 60 °,AOF2= 120 ° .设AF2与渐近线交于点D,则/ DOF2 = 60-------- ca2+ b2= 2a,「.e = 一= 2.a。
2019版数学浙江省学业水平考试专题复习选修2-1-§5

2019版数学浙江省学业水平考试专题复习选修2-1-§5推论的表达式为AP→=xAB →+yAC →或对空间任意一点O ,有OP→=OA →+xAB →+yAC →或OP →=xOA →+yOB →+zOC→,其中x +y +z =1. 3.空间向量基本定理如果三个向量a ,b ,c 不共面,那么对空间任一向量p ,存在有序实数组{x ,y ,z },使得p =xa +yb +zc ,把{a ,b ,c }叫做空间的一个基底. 知识点三 空间向量的数量积及运算律1.数量积及相关概念(1)两向量的夹角已知两个非零向量a ,b ,在空间任取一点O ,作OA→=a ,OB →=b ,则∠AOB 叫做向量a 与b 的夹角,记作〈a ,b 〉,其范围是0≤〈a ,b 〉≤π.如果〈a ,b 〉=π2,那么向量a ,b 互相垂直,记作a ⊥b .(2)两向量的数量积已知两个非零向量a ,b ,则|a||b |cos 〈a ,b 〉叫做a,b的数量积,记作a·b.即a·b=|a||b|cos〈a,b〉.2.空间向量数量积的运算律(1)(λa)·b=λ(a·b);(2)交换律:a·b=b·a;(3)分配律:a·(b+c)=a·b+a·c.知识点四空间向量的坐标运算设a=(a1,a2,a3),b=(b1,b2,b3),则:(1)a+b=(a1+b1,a2+b2,a3+b3).(2)a-b=(a1-b1,a2-b2,a3-b3).(3)λa=(λa1,λa2,λa3).(4)a·b=a1b1+a2b2+a3b3.(5)若a,b为非零向量,则a⊥b⇔a·b=0⇔a1b1+a2b2+a3b3=0.(6)若b≠0,则a∥b⇔a=λb⇔a1=λb1,a2=λb2,a3=λb3.(7)|a|=a·a=a21+a22+a23.(8)cos 〈a ,b 〉=a ·b |a ||b |=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 23. (9)若A (a 1,a 2,a 3),B (b 1,b 2,b 3),则AB→=(b 1-a 1,b 2-a 2,b 3-a 3),d AB =|AB →|=(b 1-a 1)2+(b 2-a 2)2+(b 3-a 3)2.知识点五 立体几何中的向量方法1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:在直线上任取一非零向量即可作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎨⎧n ·a =0,n ·b =0. 2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量为v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数x,y,使v=xv1+yv2.(3)设直线l的方向向量为v,平面α的法向量为u,则l∥α或l⊂α⇔v⊥u.(4)设平面α和β的法向量分别为u1,u2,则α∥β⇔u1∥u2.3.用向量证明空间中的垂直关系(1)设直线l1和l2的方向向量分别为v1和v2,则l1⊥l2⇔v1⊥v2⇔v1·v2=0.(2)设直线l的方向向量为v,平面α的法向量为u,则l⊥α⇔v∥u.(3)设平面α和β的法向量分别为u1和u2,则α⊥β⇔u1⊥u2⇔u1·u2=0.4.空间向量与空间角的关系(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2所成的角θ满足cos θ=|cos〈m1,m2〉|.(2)设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α所成角θ满足sin θ=|cos〈m ,n 〉|.(3)求二面角的大小①如图①所示,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.②如图②③所示,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos 〈n 1,n 2〉或-cos 〈n 1,n 2〉.题型一 空间向量及其运算例1 已知空间中三点A (-2,0,2),B (-1,1,2),C (-3,0,4),设a =AB→,b =AC →. (1)求向量a 与向量b 的夹角的余弦值;(2)若ka +b 与ka -2b 互相垂直,求实数k 的值.解 (1)∵a =AB→=(1,1,0),b =AC →=(-1,0,2),∴a ·b =1×(-1)+1×0+0×2=-1.又|a |=12+12+02=2,|b |=(-1)2+02+22=5,∴cos 〈a ,b 〉=a ·b |a ||b |=-12·5=-1010, 即向量a 与向量b 的夹角的余弦值为-1010. (2)∵ka +b =(k -1,k,2),ka -2b =(k +2,k ,-4),∴(ka +b )·(ka -2b )=(k -1,k ,2)·(k +2,k ,-4) =(k -1)(k +2)+k 2-8=2k 2+k -10=0,∴k =-52或k =2. 感悟与点拨 (1)空间向量的运算法则及求解思想与平面向量相同,因此,可参照平面向量的运算法则和求解思想进行处理.(2)空间向量的问题可通过坐标运算和非坐标的线性运算两种途径来处理,另外,要抓住垂直与平行两种特殊位置关系.跟踪训练1 (1)(2018年4月学考)在三棱锥O -ABC 中,若D 为BC 的中点,则AD →等于( ) A.12OA →+12OC →-OB →B.12OA →+12OB →+OC →C.12OB →+12OC →-OA →D.12OB →+12OC →+OA → (2)(2016年4月学考)已知空间向量a =(2,-1,5),b =(-4,2,x )(x ∈R),若a ⊥b ,则x 等于( ) A .-10 B .-2 C .2 D .10(3)已知向量a =(1,2,3),b =(x ,x 2+y -2,y ),并且a ,b 同向,则x ,y 的值分别为________. 答案 (1)C (2)C (3)1,3 解析 (2)∵a ⊥b ,∴a ·b =2×(-4)+(-1)×2+5x =0,得x =2.(3)∵a ∥b ,∴x1=x 2+y -22=y 3,解得⎩⎨⎧ x =-2,y =-6或⎩⎨⎧x =1,y =3,当⎩⎨⎧x =-2,y =-6时,a =-12b ,不符合要求,舍去,当⎩⎨⎧ x =1,y =3时,a =b ,符合要求, ∴⎩⎨⎧x =1,y =3.题型二 利用空间向量证明平行与垂直 例2 如图所示,已知在直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D ,E ,F 分别为B 1A ,C 1C ,BC 的中点.求证:(1)DE ∥平面ABC ; (2)B 1F ⊥平面AEF .证明 (1)如图建立空间直角坐标系Axyz ,令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4). 设AB 的中点为N ,连接CN , 则N (2,0,0),C (0,4,0),D (2,0,2), ∴DE→=(-2,4,0),NC →=(-2,4,0), ∴DE→=NC →,∴DE ∥NC , 又∵NC ⊂平面ABC ,DE ⊄平面ABC , ∴DE ∥平面ABC .(2)∵B 1F —→=(-2,2,-4),EF →=(2,-2,-2), AF→=(2,2,0). ∴B 1F —→·EF→=(-2)×2+2×(-2)+(-4)×(-2)=0,B 1F —→·AF →=(-2)×2+2×2+(-4)×0=0. ∴B 1F —→⊥EF →,B 1F —→⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF , 又∵AF ∩FE =F ,AF ,FE ⊂平面AEF , ∴B 1F ⊥平面AEF .感悟与点拨 (1)用向量证明线面平行的方法: ①证明该直线的方向向量与平面的某一法向量垂直;②证明该直线的方向向量与平面内某直线的方向向量平行;③证明该直线的方向向量可以用平面内的两个不共线的向量线性表示. (2)用向量证明垂直的方法:①线线垂直:证明两直线所在的方向向量互相垂直,即证明它们的数量积为零;②线面垂直:证明直线的方向向量与平面的法向量共线,或将线面垂直的判定定理用向量表示;③面面垂直:证明两个平面的法向量垂直,或将面面垂直的判定定理用向量表示.跟踪训练2 在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点. (1)求证:EF ⊥CD ;(2)在平面PAD 内求一点G ,使GF ⊥平面PCB ,并证明你的结论.(1)证明 如图所示,以DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系Dxyz ,设AD =a ,则D (0,0,0),A (a ,0,0),B (a ,a ,0),C (0,a ,0),E ⎝⎛⎭⎪⎪⎫a ,a 2,0,P (0,0,a ),F ⎝⎛⎭⎪⎪⎫a 2,a 2,a 2,∴EF →=⎝⎛⎭⎪⎪⎫-a 2,0,a 2,DC →=(0,a ,0).∵EF →·DC →=-a 2×0+0×a +a 2×0=0, ∴EF→⊥DC →,即EF ⊥CD . (2)解 点G 为AD 的中点. 证明如下:设G (x ,0,z ),则FG →=⎝⎛⎭⎪⎪⎫x -a 2,-a 2,z -a 2. 若使GF ⊥平面PCB ,则由FG →·CB →=⎝⎛⎭⎪⎪⎫x -a 2,-a 2,z -a 2·(a ,0,0) =a ⎝⎛⎭⎪⎪⎫x -a 2=0,得x =a 2;由FG →·CP →=⎝⎛⎭⎪⎪⎫x -a 2,-a 2,z -a 2·(0,-a ,a ) =a 22+a ⎝ ⎛⎭⎪⎪⎫z -a 2=0,得z =0. ∴点G 的坐标为⎝⎛⎭⎪⎪⎫a 2,0,0,即点G 为AD 的中点. 题型三 利用空间向量求空间角例3 如图,在矩形ABCD 中,AB =22,AD =2,M 为DC 的中点,将△DAM 沿AM 折到△D′AM的位置,AD′⊥BM.(1)求证:平面D′AM⊥平面ABCM;(2)若E为D′B的中点,求二面角E-AM-D′的余弦值.(1)证明由题意知,在矩形ABCD中,∠AMD =∠BMC=45°,所以∠AMB=90°,即AM⊥BM.又D′A⊥BM,D′A∩AM=A,D′A,AM⊂平面AD′M,所以BM⊥平面D′AM,又BM⊂平面ABCM,所以平面ABCM⊥平面D′AM.(2)解由(1)知,在平面D′AM内过M作直线NM⊥MA,则NM⊥平面ABCM,故以M 为原点,MA→,MB →,MN →分别为x ,y ,z 轴的正方向建立空间直角坐标系, 则M (0,0,0),A (2,0,0), B (0,2,0),D ′(1,0,1), 于是E ⎝⎛⎭⎪⎪⎫12,1,12,MA →=(2,0,0),ME →=⎝⎛⎭⎪⎪⎫12,1,12, 设平面EAM 的法向量为m =(x ,y ,z ),则⎩⎨⎧2x =0,12x +y +12z =0,令y =1,得z =-2, 则平面EAM 的一个法向量m =(0,1,-2), 显然平面D ′AM 的一个法向量为n =(0,1,0), 故cos 〈m ,n 〉=15,由图知,二面角为锐角,即二面角E -AM -D ′的余弦值为55.感悟与点拨 (1)用向量方法求两条异面直线所成的角,是通过两条直线的方向向量的夹角来求解.(2)用向量法求线面角,是通过直线的方向向量和平面的法向量来求解.(3)求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角. 跟踪训练3 (1)如图,在四棱锥P -ABCD 中,四边形ABCD 为平行四边形,且BC ⊥平面PAB ,PA ⊥AB ,M 为PB 的中点,PA =AD =2.若AB =1,则二面角B -AC -M 的余弦值为( )A.66B.36C.26D.16答案 A解析 因为BC ⊥平面PAB ,AD ∥BC ,所以AD ⊥平面PAB ,PA ⊥AD ,又PA ⊥AB ,且AD ∩AB =A ,AD ,AB ⊂平面ABCD ,所以PA ⊥平面ABCD .以点A 为坐标原点,分别以AD ,AB ,AP 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz .则A (0,0,0),C (2,1,0),P (0,0,2),B (0,1,0),M ⎝⎛⎭⎪⎪⎫0,12,1,所以AC →=(2,1,0),AM →=⎝ ⎛⎭⎪⎪⎫0,12,1, 求得平面AMC 的一个法向量n =(1,-2,1), 又平面ABC 的一个法向量AP→=(0,0,2),所以cos 〈n ,AP →〉=n ·AP →|n ||AP→| =21+4+1·2=16=66. 所以二面角B -AC -M 的余弦值为66. (2)如图所示,在四面体ABCD 中,AB ,BC ,BD 两两垂直,AB =BC =BD =4,E ,F 分别为棱BC ,AD 的中点.求:①异面直线AB 与EF 所成角的余弦值; ②点E 到平面ACD 的距离;③EF 与平面ACD 所成角的正弦值.解 如图所示,分别以直线BC ,BD ,BA 为x ,y ,z 轴建立空间直角坐标系,则各相关点的坐标为A (0,0,4),B (0,0,0),C (4,0,0),D (0,4,0),E (2,0,0),F (0,2,2).①∵AB→=(0,0,-4), EF→=(-2,2,2), ∴|cos 〈AB →,EF →〉|=⎪⎪⎪⎪⎪⎪-84×23=33, ∴异面直线AB 与EF 所成角的余弦值为33. ②设平面ACD 的一个法向量为n =(x ,y ,1), ∵AC→=(4,0,-4),CD →=(-4,4,0), 则⎩⎪⎨⎪⎧ n ·AC →=0,n ·CD →=0,即⎩⎨⎧4x -4=0,-4x +4y =0, ∴x =y =1,∴n =(1,1,1).∵F ∈平面ACD ,EF→=(-2,2,2), ∴点E 到平面ACD 的距离为d =|n ·EF →||n |=23=233.③EF 与平面ACD 所成角的正弦值为|cos 〈n ,EF→〉|=23×23=13. 题型四 立体几何中的探索性问题例4 如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=1,底面ABCD 的周长为4.(1)当长方体ABCD -A 1B 1C 1D 1的体积最大时,求直线BA 1与平面A 1CD 所成的角;(2)线段A 1C 上是否存在一点P ,使得A 1C ⊥平面BPD ?若存在,求出P 点的位置,若不存在,请说明理由.解 (1)根据题意,令AB =t ,则长方体的体积为V =t (2-t )×1=t (2-t )≤⎝ ⎛⎭⎪⎫t +2-t 22=1, 当且仅当t =2-t ,即t =1时体积V 有最大值为1.所以当长方体ABCD-A1B1C1D1的体积最大时,底面四边形ABCD为正方形.又AA1=1.所以ABCD-A1B1C1D1为正方体.如图,连接B1C,取B1C的中点O,连接BO,A1O.由题意知,CD⊥平面C1B1BC,所以BO⊥CD,在等腰Rt△B1BC中,BO⊥B1C,又B1C∩CD=C,B1C,CD⊂平面A1B1CD,所以BO⊥平面A1B1CD,即∠BA1O就是直线BA1与平面A1CD所成的角.又BO=22,BA1=2,所以∠BA1O=30°.即长方体ABCD-A1B1C1D1的体积最大时,直线BA1与平面A1CD所成的角为30°.(2)根据题意可知,AA 1,AB ,AD 两两垂直,以AB 为x 轴,AD 为y 轴,AA 1为z 轴,建立如图所示的空间直角坐标系.根据题意及(1)可得B (t,0,0),C (t ,2-t ,0),D (0,2-t,0),若线段A 1C 上存在一点P 满足要求,不妨设A 1P _x001F_—→=λA 1C —→,可得P (λt ,λ(2-t ),1-λ). BP→=(λt -t ,λ(2-t ),1-λ),BD →=(-t,2-t,0), A 1C —→=(t,2-t ,-1),⎩⎪⎨⎪⎧BP →·A 1C —→=0,BD →·A 1C —→=0,即⎩⎨⎧ t (λt -t )+λ(2-t )2-(1-λ)=0,-t 2+(2-t )2=0,解得t =1,λ=23.即只有当底面四边形是正方形时才存在符合要求的点P,位置是线段A1C上A1P∶PC=2∶1处.感悟与点拨对于立体几何中的探索性问题,可以凸显坐标方法的优势,通常从假设存在入手,利用空间向量坐标建立方程,然后按部就班求解.跟踪训练4如图所示,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(1)求证:AA1⊥平面ABC;(2)求二面角A1-BC1-B1的余弦值;(3)在线段BC1上是否存在一点D,使得AD⊥A1B?若存在,求BDBC1的值;若不存在,请说明理由.(1)证明在正方形AA1C1C中,A1A⊥AC.又∵平面ABC⊥平面AA1C1C,且平面ABC∩平面AA1C1C=AC,AA1⊂平面AA1C1C,∴AA1⊥平面ABC .(2)解 在△ABC 中,AC =4,AB =3,BC =5, ∴BC 2=AC 2+AB 2,AB ⊥AC ,∴以A 为坐标原点,建立如图所示的空间直角坐标系Axyz .则A 1(0,0,4),B (0,3,0),C 1(4,0,4),B 1(0,3,4),A 1C 1—→=(4,0,0),A 1B —→=(0,3,-4),B 1C 1—→=(4,-3,0),BB 1—→=(0,0,4). 设平面A 1BC 1的法向量n 1=(x 1,y 1,z 1), 平面B 1BC 1的法向量n 2=(x 2,y 2,z 2). ∴⎩⎪⎨⎪⎧ A 1C 1—→·n 1=0,A 1B —→·n 1=0,即⎩⎨⎧4x 1=0,3y 1-4z 1=0, ∴可取向量n 1=(0,4,3),由⎩⎪⎨⎪⎧ B 1C 1—→·n 2=0,BB 1—→·n 2=0,即⎩⎨⎧4x 2-3y 2=0,4z 2=0. ∴可取向量n 2=(3,4,0),∴cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=165×5=1625. 由题意知二面角A 1-BC 1-B 1为锐角,∴二面角A 1-BC 1-B 1的余弦值为1625. (3)解 假设在线段BC 1上存在一点D ,使AD ⊥A 1B ,设D (x ,y ,z )是直线BC 1上一点,且BD→=λBC 1→. ∴(x ,y -3,z )=λ(4,-3,4),解得x =4λ,y =3-3λ,z =4λ.∴AD→=(4λ,3-3λ,4λ). 又∵AD ⊥A 1B ,∴0+3(3-3λ)-16λ=0,则λ=925,∴BD BC 1=925.一、选择题1.如图所示,在直三棱柱ABC -A 1B 1C 1中,若CA→=a ,CB →=b ,CC 1—→=c ,则A 1B —→等于( )A .a +b -cB .a -b +cC .-a +b +cD .-a +b -c答案 D解析 如图所示,连接A 1C ,则在△A 1CB 中,有A 1B —→=CB →-CA 1—→=CB →-(CC 1—→+CA→)=b -(a +c )=-a +b -c . 2.若向量a =(1,1,x ),b =(1,2,1),c =(1,1,1),满足条件(c -a )·2b =-2,则x 的值为( )A .-4B .-2C .4D .2 答案 D解析 ∵a =(1,1,x ),b =(1,2,1),c =(1,1,1), ∴c -a =(0,0,1-x ),2b =(2,4,2). ∴(c -a )·2b =2(1-x )=-2, ∴x =2.3.已知A (2,3,-1),B (2,6,2),C (1,4,-1),则向量AB→与AC →的夹角为( ) A .45° B .90° C .30° D .60° 答案 D解析 ∵A (2,3,-1),B (2,6,2),C (1,4,-1), ∴AB→=(0,3,3),AC →=(-1,1,0), ∴AB →·AC →=0×(-1)+3×1+3×0=3, 且|AB→|=32,|AC →|=2, ∴cos 〈AB →,AC →〉=AB →·AC →|AB →||AC →|=332×2=12,∴AB →与AC →的夹角为60°.4.已知a =(2,-1,3),b =(-4,2,x ),c =(1,-x ,2),若(a +b )⊥c ,则x 等于( ) A .4 B .-4 C.12 D .-6答案 B解析 ∵(a +b )⊥c , ∴(a +b )·c =0.又a +b =(-2,1,x +3),∴-2×1+1×(-x )+(x +3)×2=0,解得x =-4. 故选B.5.如图,在平行六面体ABCD -A 1B 1C 1D 1中,M 为A 1C 1与B 1D 1的交点.若AB →=a ,AD →=b ,AA 1—→=c ,则下列向量中与BM→相等的向量是( )A .-12a +12b +c B.12a +12b +cC .-12a -12b +c D.12a -12b +c答案 A解析 由题意,得BM →=BC →+CC 1—→+C 1M —→=BC →+CC 1—→+12C 1A 1—→=BC →+CC 1—→-12(AB →+BC →)=-12AB →+12BC →+CC 1—→=-12a +12b +c . 6.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则( ) A .l ∥α B .l ⊥αC .l ⊂αD .l 与α相交但不垂直答案 B解析 ∵a =(1,0,2),n =(-2,0,-4), ∴n =-2a ,∴a ∥n ,∴l ⊥α.7.如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点E ,F ,G 分别是DD 1,AB ,CC 1的中点,则异面直线A 1E 与GF 所成角的余弦值是( )A.155B.22C.105 D .0答案 D解析 以DA →,DC →,DD 1—→的方向为x ,y ,z 轴正方向,建立空间直角坐标系(图略),则可得A 1(1,0,2),E (0,0,1),G (0,2,1),F (1,1,0). ∴A 1E —→=(-1,0,-1),GF →=(1,-1,-1), 设异面直线A 1E 与GF 所成的角为θ, 则cos θ=|cos 〈A 1E —→,GF→〉|=0. 8.正方体ABCD -A 1B 1C 1D 1的棱长为a ,点M 在AC 1上且AM →=12MC 1—→,N 为B 1B 的中点,则|MN→|为( ) A.216aB.66aC.156aD.153a答案 A解析 以D 为原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Dxyz ,则A (a,0,0),C 1(0,a ,a ), N ⎝⎛⎭⎪⎪⎫a ,a ,a 2.设M (x ,y ,z ),因为点M 在AC 1上且AM →=12MC 1—→, 所以(x -a ,y ,z )=12(-x ,a -y ,a -z ),所以x =23a ,y =a 3,z =a3,所以M ⎝⎛⎭⎪⎪⎫2a 3,a 3,a 3,所以|MN →|= ⎝⎛⎭⎪⎪⎫a -2a 32+⎝ ⎛⎭⎪⎪⎫a -a 32+⎝ ⎛⎭⎪⎪⎫a 2-a 32=216a .9.在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 和CD 成60°角(如图),则B ,D 间的距离为( )A .1B .2 C. 2 D .2或 2 答案 D解析 因为∠ACD =90°,所以AC →·CD →=0. 同理BA →·AC→=0, 因为AB 和CD 成60°角,所以〈BA →,CD →〉=60°或120°.因为BD→=BA →+AC →+CD →, 所以|BD →|2=|BA →|2+|AC →|2+|CD →|2+2BA →·CD →+2BA →·AC →+2AC →·CD→=|BA →|2+|AC →|2+|CD →|2+2BA →·CD →=3+2×1×1×cos 〈BA →,CD →〉=3+2cos 60°或3+2cos 120°, 所以|BD→|=2或 2. 即B ,D 间的距离为2或2,故选D.10.如图,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,F ,G 分别是线段AE ,BC 的中点,则AD 与GF 所成角的余弦值为( )A.36 B .-36C.33 D .-33答案 A解析 如图,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,DC ⊥AC ,平面ACDE ∩平面ACB=AC ,DC ⊂平面ACDE ,所以DC ⊥平面ABC ,F ,G 分别是线段AE ,BC 的中点.以C 为原点建立空间直角坐标系如图所示,则 A (0,2,0),B (2,0,0),D (0,0,2),G (1,0,0),F (0,2,1). 所以AD→=(0,-2,2),GF →=(-1,2,1). 所以|AD →|=22,|GF →|=6,AD →·GF →=-2. 所以cos 〈AD →,GF →〉=AD →·GF →|AD →||GF →|=-36.则直线AD 与GF 所成角的余弦值为36.故选A.二、填空题11.已知O 为空间任一点,A ,B ,C ,D 四点满足任意三点不共线,但四点共面,且OA →=2xBO →+3yCO→+4zDO →,则2x +3y +4z 的值为________.答案 -1解析 由题意知A ,B ,C ,D 共面的充要条件是:对空间任意一点O ,存在实数x 1,y 1,z 1,使得OA →=x 1OB →+y 1OC →+z 1OD →且x 1+y 1+z 1=1,因此2x +3y +4z =-1.12.已知向量a =(2,-1,3),b =(-4,2,x ).若a ⊥b ,则x =________;若a ∥b ,则x =________. 答案 103-613.设O 为坐标原点,向量OA→=(1,2,3),OB →=(2,1,2),OP→=(1,1,2),点Q 在直线OP 上运动,则当QA →·QB →取得最小值时,点Q 的坐标为________. 答案 ⎝⎛⎭⎪⎪⎫43,43,83解析 设OQ →=λOP →=(λ,λ,2λ),故Q (λ,λ,2λ), 故QA →=(1-λ,2-λ,3-2λ),QB →=(2-λ,1-λ,2-2λ).则QA →·QB →=6λ2-16λ+10=6⎝⎛⎭⎪⎪⎫λ-432-23,当QA →·QB →取最小值时,λ=43, 此时Q 点的坐标为⎝⎛⎭⎪⎪⎫43,43,83.14.如图,PA ⊥平面ABC ,AC ⊥BC ,PA =AC =1,BC =2,则二面角A -PB -C 的余弦值为________.答案 33解析 如图所示,建立空间直角坐标系,则C (0,0,0),A (1,0,0),P (1,0,1),B (0,2,0), ∴AP →=(0,0,1),PB →=(-1,2,-1),CB →=(0,2,0).设平面ABP 的法向量为m =(x 1,y 1,z 1), 平面PBC 的法向量为n =(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧ m ·AP →=0,m ·PB →=0,即⎩⎨⎧z 1=0,-x 1+2y 1-z 1=0, ∴⎩⎨⎧ z 1=0,x 1=2y 1,令y 1=1,得m =(2,1,0). 由⎩⎪⎨⎪⎧ n ·PB →=0,n ·CB →=0,即⎩⎨⎧-x 2+2y 2-z 2=0,2y 2=0, ∴⎩⎨⎧x 2=-z 2,y 2=0,令z 2=1, 得n =(-1,0,1).∴|cos 〈m ,n 〉|=⎪⎪⎪⎪⎪⎪-22×3=33. 由题意可知,所求二面角的平面角是锐角,故二面角A -PB -C 的余弦值为33. 三、解答题15.如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =22AB .(1)证明:BC 1∥平面A 1CD ;(2)求二面角D -A 1C -E 的正弦值.(1)证明 连接AC 1交A 1C 于点F ,则F 为AC 1的中点.又D 是AB 的中点,连接DF ,则BC 1∥DF . 因为DF ⊂平面A 1CD ,BC 1⊄平面A 1CD ,所以BC 1∥平面A 1CD .(2)解 由AC =CB =22AB , 得AC ⊥BC .以C 为坐标原点,CA →的方向为x 轴正方向,CB→的方向为y 轴正方向,CC 1—→的方向为z 轴正方向,建立如图所示的空间直角坐标系Cxyz . 设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2), CD →=(1,1,0),CE →=(0,2,1),CA 1—→=(2,0,2). 设n =(x 1,y 1,z 1)是平面A 1CD 的法向量, 则⎩⎪⎨⎪⎧ n ·CD →=0,n ·CA 1→=0,即⎩⎨⎧x 1+y 1=0,2x 1+2z 1=0. 可取x 1=1,则n =(1,-1,-1). 同理,设m =(x 2,y 2,z 2)是平面A 1CE 的法向量, 则⎩⎪⎨⎪⎧ m ·CE →=0,m ·CA 1—→=0,即⎩⎨⎧2y 2+z 2=0,2x 2+2z 2=0, 可取y 2=1,则m =(2,1,-2).从而cos 〈n ,m 〉=n ·m |n ||m |=33,故sin 〈n ,m 〉=63. 即二面角D -A 1C -E 的正弦值为63.16.如图,在四棱锥S-ABCD中,AB∥CD,AB⊥AD,SA=AB=2CD=2,SB=2AD=22,平面SAB⊥平面ABCD,E为SB的中点..(1)求证:CE∥平面SAD;(2)求证:BD⊥平面SAC;(3)求直线CE与平面SAC所成角的余弦值.(1)证明∵SA=AB=2,SB=22,∴SA⊥AB,又平面SAB⊥平面ABCD,平面SAB∩平面ABCD=AB,SA⊂平面SAB,∴SA⊥平面ABCD,又AB⊥AD,∴建立如图所示的空间直角坐标系,则A(0,0,0),B(2,0,0),C(1,2,0),D(0,2,0),S(0,0,2),E(1,0,1),CE→=(0,-2,1),平面SAD 的法向量为AB →=(2,0,0),∴CE →·AB→=0,即CE →⊥AB →, 又CE ⊄平面SAD ,∴CE ∥平面SAD .(2)证明 设平面SAC 的法向量为n =(x ,y ,z ), AS→=(0,0,2),AC →=(1,2,0),BD →=(-2,2,0),∴⎩⎪⎨⎪⎧n ·AS →=2z =0,n ·AC →=x +2y =0,令y =1,得x =- 2. ∴n =(-2,1,0),∴n ∥BD→,∴BD ⊥平面SAC . (3)解 CE→=(0,-2,1), 平面SAC 的法向量n =(-2,1,0), 设直线CE 与平面SAC 所成的角为θ,则sin θ=|CE →·n ||CE→||n |=23,∴cos θ=73,∴直线CE与平面SAC所成角的余弦值为7 3.。
2019版数学浙江省学业水平考试专题复习选修211

知识点一命题的看法在数学中,把用语言、符号或式子表达的,能够判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.知识点二四种命题的关系知识点三四种命题的真假性关系原命题抗命题否命题逆否命题真真真真真假假真假真真假假假假假结论1:两个命题互为逆否命题,它们有相同的真假性.结论2:两个命题为互抗命题或互否命题,它们的真假性没有关系.知识点四充分条件与必要条件1.假设p?q,那么p是q的充分条件,q是p的必要条件.2.假设p?q,且q?p,那么p是q的充要条件.3.假设p?q,且q?p,那么p是q的充分不用要条件.4.假设p?q,且q?p,那么p是q的必要不充分条件.5.假设p?q,且q?p,那么p是q的既不充分也不用要条件.题型一命题及其关系例 1 (1) a,b,c∈R,命题“a+b+c=3,那么a2+b2+c2≥3〞的否命题是( )2+b2+c2<3A.假设a+b+c≠3,那么aB.假设a+b+c=3,那么a2+b2+c2<32+b2+c2≥3C.假设a+b+c≠3,那么aD.假设a2+b2+c2≥3,那么a+b+c=3(2)命题“假设x=3,那么x2-2x-3=0〞的逆否命题是( )2-2x-3≠0A.假设x≠3,那么xB.假设x=3,那么x2-2x-3≠0C.假设x2-2x-3≠0,那么x≠32-2x-3≠0,那么x=3D.假设x答案(1)A (2)C剖析(1) 依照四种命题的定义可得.感悟与点拨(1)熟悉四种命题的看法是正确书写或判断四种命题真假的要点;(2)依照“原命题与逆否命题同真同假,抗命题与否命题同真同假〞这一性质,当一个命题直接判断不易进行时,可转变成判断其等价命题的真假;(3)判断一个命题为假命题可举反例.追踪训练 1 (1)命题“假设α=π,那么cosα=312〞的抗命题是( )A.假设α=π,那么cosα≠312B.假设α≠π1 ,那么cosα≠3 2C.假设cos α=1π,那么α=2 3D.假设cos α≠12,那么α≠π3(2)以下命题:①“假设a≤b,那么a< b〞的否命题;②“假设a=1,那么ax2-x+3≥0 的解集为R〞的逆否命题;③“周长相同的圆面积相等〞的抗命题;④“假设2x 为有理数,那么x 为无理数〞的逆否命题.其中真命题的序号为( )A.②④B.①②③C.②③④D.①②③④答案(1)C (2)B剖析(2) 对于①,抗命题为真,故否命题为真;对于②,“假设a=1,那么ax2-x+3≥0 的解集为R〞,原命题为真,故逆否命题为真;对于③,“面积相等的圆周长相同〞为真;对于④,“假设2x 为有理数,那么x 为0 或无理数〞,故原命题为假,逆否命题为假.题型二充分条件、必要条件与充要条件的判断1 1例 2 (1)(2021 年4 月学考)设a 为实数,那么“a>〞是“a2> 〞的( )a2aA.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件(2)(2021 年10 月学考)非零向量a,b,那么“a∥b〞是“|a-b|=|a|-|b |〞的( ) A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案(1)A (2)B1剖析(1) 由a> 2,知a>0,a1∴a2>,a1 1〞是“a2>a2∴“a> 〞的充分条件,a12>由 a 不能够确定a>0 还是a<0,a1∴推不出a>2,a1 1∴“a>2〞不是“a2>〞的必要条件.a a(2)由“a∥b〞显然推不出|a-b|=|a |-|b |,比方:|a|<|b|时,显然不行立.∴“a∥b〞不是“|a-b |=|a |-|b |〞的充分条件.由|a-b |=|a |-|b |得,|a-b|2=(|a |-|b|)2,∴a·b=|a| ·b||,∴cos θ=1(θ为 a 与 b 的夹角),∴θ=0,即a∥b.感悟与点拨充要关系的几种判断方法:(1)定义法:直接判断假设p 那么q,假设q 那么p 的真假.(2)等价法:即利用A? B 与綈B? 綈A;B? A 与綈A? 綈B;A? B 与綈B? 綈A 的等价关系,对于条件或结论可否认形式的命题,一般运用等价法.(3)利用会集间的包含关系判断:设A={ x|p(x)} ,B={ x|q( x)} ,假设A? B,那么p 是q 的充分条件或q 是p 的必要条件;假设A=B,那么p 是q 的充要条件.1追踪训练 2 (1)设a>0,且a≠1,那么“a>1〞是“log a <1〞的( )2A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件(2)直线l ⊥平面α,直线m? 平面β,那么“α∥β〞是“l⊥m〞的( )A.充要条件B.必要不充分条件C.充分不用要条件D.既不充分也不用要条件(3)(2021 年4 月学考)设实数a,b 满足|a |>|b |,那么“a-b>0〞是“a+b>0〞的( )A.充分不用要条件B.必要不充分条件C.充要条件D.即不充分也不用要条件答案(1)A (2)C (3)C1a a=1,剖析(1) 当a>1 时,有log a2<log所以充分性建立;1 1当log a <1 时,即log a <1=log a a,2 211当a>1时,上式恒建立,当0<a<1时,解得0<a<,那么a的取值范围是a>1或0<a<,所以22必要性不行立.(2)由α∥β?l⊥β?l⊥m,∴“α∥β〞是“l⊥m〞的充分条件,由l⊥m可知,l⊥β或l不垂直于β,∴α∥β或α不平行β,必要性不行立.(3)由|a|>|b|得a2-b2>0,即(a-b)(a+b)>0,a-b>0,由得a+b>0.a-b a+b>0,a+b>0,又得a-b>0.a-b a+b>0,∴“a-b>0〞是“a+b>0〞的充要条件.题型三依照充要条件求参数范围例3(1)“|x-a|<1〞是“x2-6x<0〞的充分不用要条件,那么实数a的取值范围是________.答案[1,5]剖析∵|x-a|<1,∴a-1<x<a+1.∵x2-6x<0,∴0<x<6.又∵“|x-a|<1〞是“x2-6x<0〞的充分不用要条件,a-1≥0,a-1>0,∴或a+1<6a+1≤6,∴1≤a≤5.2- 3 (2)会集A=y y=x x+1,x∈234,2,B={x|x+m2≥1}.假设“x∈A〞是“x∈B〞的充分条件,求实数m的取值范围.32解y=x2-x+1=x-342+7,16因为x∈34,2,所以7≤y≤2,16所以A=y 7≤y≤2. 162≥1,得x≥1-m2,所以B={x|x≥1-m2}.由x+m因为“x∈A〞是“x∈B〞的充分条件,7所以A?B,所以1-m2≤16,解得m≥33或m≤-,44故实数m的取值范围是-∞,-34∪3,+∞.4感悟与点拨会集与充要条件综合问题,一般先化简会集,尔后依照充要条件建立等式也许不等式,进而求出参数的取值范围.追踪训练3p:|x-a|≤5;q:x2-6x+8≤0.假设x∈p是x∈q的必要不充分条件,求实数a的取值范围.解对于p,不等式|x-a|≤5的解集为-5+a≤x≤5+a;对于q,不等式x2-6x+8≤0的解集为2≤x≤4.∵x∈p是x∈q的必要不充分条件,∴{x|2≤x≤4}{x|-5+a≤x≤5+a},-5+a<2,-5+a≤2,即或可得-1≤a≤7,4≤5+a4<5+a,∴实数a的取值范围是[-1,7].一、选择题11.a,b∈R,命题“假设a+b=1,那么a2+b2≥〞的否命题是()21A.假设a2+b2<2,那么a+b≠11B.假设a+b=1,那么a2+b2<21C.假设a+b≠1,那么a2+b2<21D.假设a2+b2≥,那么a+b=12答案C11剖析“a+b=1〞,“a2+b2≥〞的否认分别是“a+b≠1〞,“a2+b2<22〞,1故否命题为“假设a+b≠1,那么a2+b2<〞.22+y2=0,那么x,y全为零〞的逆否命题是()2.“假设x,y∈R, xA.假设x,y∈R,x,y全不为零,那么x2+y2≠0B.假设x,y∈R,x,y不全为零,那么x2+y2=02+y2≠0C.假设x,y∈R,x,y不全为零,那么xD.假设x,y∈R,x,y全为零,那么x2+y2≠0答案C剖析依题意得,原命题的题设为“假设x2+y2=0〞,结论为“那么x,y全为零〞.逆否命题为“假设x,y不全为零,那么x2+y2≠0〞,应选 C.3.以下三个命题:①“假设xy=0,那么x=0 且y=0〞的逆否命题;②“正方形是菱形〞的否命题;③“假设m>2,那么不等式x2-2x+m>0 的解集为R〞.其中真命题的个数为( )A.0 B.1 C.2 D.3答案 B剖析对于①,原命题为假,所以逆否命题为假;对于②,抗命题为“菱形是正方形〞,是假命题,所以否命题为假命题;对于③,Δ=4-4m,当m>2 时,Δ<0,所以f(x)=x2-2x+m 张口向上且与x 轴无公共点,故x2-2x+m>0 的解集为R,③为真命题.应选 B.2-x<0,那么p 的一个必要不充分条件是( )4.p:xA.0<x<1 B.-1< x<11 2C.2<x<3 D. 12< x<2答案 B剖析p:0< x<1,0< x<1 ? -1<x<1,-1<x<1D //? 0<x<1.应选 B.5.a>0 且a≠1,那么“log a b>0〞是“( a-1)( b-1)>0〞的( )A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案 Ab>1,0< b<1,剖析因为log a b>0 等价于或0<a<1 a>1,b>1,b<1,而( a-1) ·b-(1)>0 等价于应选 A.或a<1 a>1,6.“m=2 018〞是“直线mx+(m-2 017) y-2=0 和直线x-my+5=0 垂直〞的( )A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案 A2+b2<1〞的( ) 7.(2021 年11 月学考)a,b 是实数,那么“|a|<1 且|b |<1〞是“aA.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案B8.(2021年6月学考)直线l,m和平面α,m?α,那么“l⊥m〞是“l⊥α〞的() A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案B9.“a=1〞是“函数f(x)=|x-a|在区间[1,+∞)上为增函数〞的()A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案Ax-1,x≥1,剖析①由“a=1〞得f(x)=1-x,x<1,所以“f(x)在[1,+∞)上为增函数〞.②由“f(x)在[1,+∞)上为增函数〞得a≤1.10.(2021年4月学考)设n∈N*,那么“数列{a n}为等比数列〞是“数列1a2n为等比数列〞的()A.充分不用要条件B.必要不充分条件C.充要条件D.既不充分也不用要条件答案A剖析{a n}是等比数列,设公比为q,a n+1那么=q,a n1a2n+ 12an由=1a2n+ 12an=a na n+12=1,,q2∴12an为等比数列,那么“数列{a n}为等比数列〞是“数列1a2n为等比数列〞的充分条件.-1,n=1,假设数列{a n}的通项公式为a n=1,n>1且n∈N*,数列{a n}不是等比数列,1而=1,故2an 12an是等比数列,∴“数列{a n}为等比数列〞是“数列12an为等比数列〞的不用要条件,∴“数列{a n}为等比数列〞是“数列1a2n为等比数列〞的充分不用要条件.二、填空题11.命题“假设ab=0,那么a,b中最少有一个为零〞的逆否命题是________________________.答案假设a,b都不为零,那么ab≠012.假设不等式|x-m|<1建立的充分不用要条件是11,那么实数m的取值范围是________.<x<32答案-14,23剖析设A=x 11<x<32,B={x|m-1<x<m+1},那么A是B的真子集.∴13m-1≤,12m+1≥(等号不相同时建立),解得-12≤m≤4.32-x-2<0},B={x|-2<x<a},那么“A∩B≠?〞的充要条件是________.13.假设会集A={x|x答案a>-1剖析A={x|-1<x<2},B={x|-2<x<a},由A∩B≠?得a>-1.14.以下四个结论中:①“λ=0〞是“λa=0〞的充分不用要条件;②在△ABC中,“AB2+AC2=BC2〞是“△ABC为直角三角形〞的充要条件;③假设a,b∈R,那么“a2+b2≠0〞是“a,b全不为零〞的充要条件;④假设a,b∈R,那么“a2+b2≠0〞是“a,b不全为零〞的充要条件.正确的选项是________.(填序号)答案①④剖析由λ=0能够推出λa=0,但是由λa=0不用然能推出λ=0建立,所以①正确.由AB2+AC2=BC2能够推出△ABC是直角三角形,但是由△ABC是直角三角形不能够确定哪个角是直角,所以②不正确.由a2+b2≠0能够推出a,b不全为零;反之,由a,b不全为零能够推出a2+b2≠0,所以③不正确,④正确.三、解答题15.会集A={x|x≥3或x≤-2},B={x|x>-a或x<2a}(a<0).设p:x∈A,q:x∈B,且綈p是綈q的必要不充分条件,求实数a的取值范围.解∵綈p是綈q的必要不充分条件,那么綈q?綈p,且綈p?綈q,由此可得p?q,且q?p,∴A B,-a<3,∴可得a>-1,-2<2a,又∵a<0,∴-1<a<0.16.会集A={x|x2-4x-5≤0,x∈R},B={x|x2-2x-m<0}.(1)当m=3时,求A∩(?R B);(2)假设m=a是A∩B={x|-1≤x<4}的充要条件,求实数a的值.解(1)当m=3时,A={x|-1≤x≤5},B={x|-1<x<3},那么?R B={x|x≤-1或x≥3},所以A∩(?R B)={x|3≤x≤5或x=-1}.(2)因为A={x|-1≤x≤5},A∩B={x|-1≤x<4},所以有42-2×4-a=0,解得a=8,此时B={x|-2<x<4},吻合题意,故实数a的值为8.。
学业水平考试数学浙江-知识清单与训练25椭圆
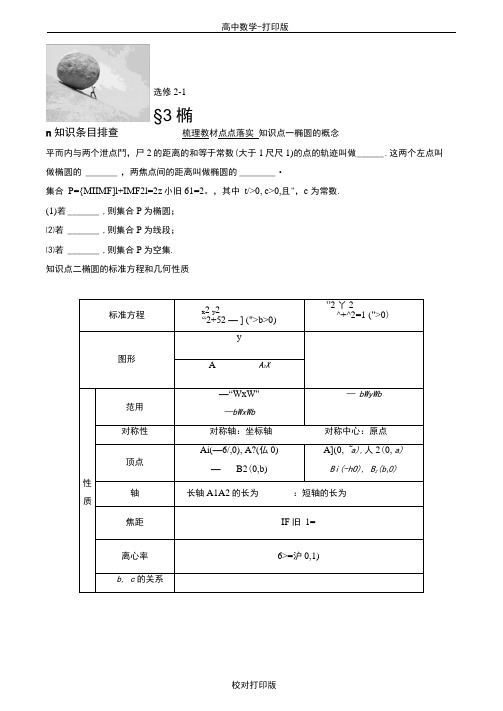
n 知识条目排查梳理教材点点落实 知识点一椭圆的概念平而内与两个泄点鬥,尸2的距离的和等于常数(大于1尺尺1)的点的轨迹叫做 ______ .这两个左点叫 做椭圆的 _______ ,两焦点间的距离叫做椭圆的 ________ •集合 P={MIIMF]l+IMF2l=2z 小旧61=2。
,其中 t/>0, c>0,且",c 为常数.(1)若 _______ ,则集合P 为椭圆;⑵若 _______ ,则集合P 为线段; ⑶若 _______ ,则集合P 为空集. 知识点二椭圆的标准方程和几何性质选修2-1§3椭知识点三 直线与椭圆的位置关系1. 直线与椭圆位置关系判断的步骤 (1) 联立直线方程与椭圆方程;(2) 消元得出关于x (或刃的一元二次方程:⑶当£>0时,直线与椭圆相交;当£=0时,直线与椭圆相切;当4<0时,直线与椭圆相离.2. 直线与椭圆相交时的常见问题的处理方法注意:弦长公式IP 1 用=J 1 +£1\/(X 】+恐)2 —4门兀2 =、y 1 + 右7©1+户尸 一 4yp2.例1 (1)已知圆(x+2)2+y 2=36的圆心为设A 为圆上任一点,且点M2.0),线段AN 的垂直平 分线交MA 于点P,则动点P 的轨迹是()A.圆B.椭圆C.双曲线D.抛物线⑵设P 是椭圆£+£=1上一点,鬥,5是椭圆的焦点,若ZF,PF 2=60°,则屮F2的面积为2 °例2已知椭圆卡+糸=1(“”>0)的右焦点为F (3,0),过点F 的直线交E 于儿B 两点.若AB 的 中点坐标为(1,一 1),则椭圆E 的方程为()X 2 V 2 A45 + 36=1 X 2 V 2 X 2 V 2 C-27+18= 1D.亟1例3已知椭圆经过点(誓,羽)和点(军,1),则椭圆的标准方程为 __________ 例4 (1)若椭圆长轴的长度、短轴的长度和焦距成等差数列,求该椭圆的离心率.(2)从椭圆亲+右=1("”>0)上一点P 向A -轴作垂线,垂足恰为左焦点Fi ,A 是椭圆与x 轴正半轴的交题型分类示例典例演练深层突破y- B-36+27=1点,B是椭圆与y轴正半轴的交点,且AB//OP(0是坐标原点),求该椭圆的离心率.例5已知点A(-LO), 直线AM.相交于点M,且加\・灯佃=一2・(1)求点M的轨迹C的方程;⑵过左点(0.1)作直线PQ与曲线C交于P, Q两点,且IPQI=牢,求直线PQ的方程.例6 (2016年10月学考)设Fi,尺为椭圆手+£= 1的左、右焦点,动点P的坐标为(T,加),过点鬥的直线与椭圆交于A,B两点.(1)求Fi, F2的坐标;(2)若直线PA, PF2. PB的斜率之和为0,求加的所有整数值. 例7 (2016年4月学考)已知椭圆才+尸=1,P是椭圆的上顶点,过P作斜率为心H0)的直线/交椭圆于另一点设点A关于原点的对称点为B.(1)求△PAB而积的最大值:(2)设线段的中垂线与y轴交于点N,若点N在椭圆内部,求斜率£的取值范羽.例8 (2015年10月学考)设尺,尺分别是椭圆C:,+尸=1的左,右焦点,过尺且斜率不为零的动宜线/与椭圆C交于A, B两点.(1)求AAFiFz的周长;(2)若存在直线/,使得直线FzA, AB, F出与直线^= 一*分别交于P, Q, /?三个不同的点,且满足P、Q, R到x轴的距离依次成等比数列,求该直线/的方程.一、选择题1. 到两左点鬥(一2,0)和F 2(2.0)的距离之和为4的点M 的轨迹是() A.椭圆 B.线段 C.圆D.以上都不对2. 如果方程牙+鸟 =1表示焦点在x 轴上的椭圆,则实数"的取值范用是() A. (3, +°°)B. (—8, —2)C. (3,+8)u (-8, -2) D ・(3, +8)U (-6, -2)3・若椭圆*+阳2=1的焦点在y 轴上,且长轴长是短轴长的两倍,则加的值为()4•如图所示,已知椭圆£+£= 1上的点M 到该椭圆一个焦点F 的距离为2, N 是MF 的中点,O 为坐标原点,那么线段ON 的长是(A. 2B. 4C. 8D.|35・焦点在x 轴上,短轴长为&离心率为§的椭圆的标准方程是(C-25+16=16. 椭圆亲+荒=1(“”>0)的左、右顶点分别是A 、B,左、右焦点分别是Fi 、F2,若lAFil, IF02I, IF1BI成等比数列,则此椭圆的离心率为()7. 椭圆“用+"护=1与直线y=lr 交于M, N 两点,过原点与线段MN 中点的直线的斜率为乎, 则号的值是()返 2^3 班n^3/>• ° D • 32 *-/• 27考点专项训练课后检测考点强化1-4AX 2 V 2D石+〒1 -4A1-2c遁52D&已知椭圆C:卡+$=l(">b>0)的左、右焦点为鬥、F1,离心率为零过尸2的直线/交椭圆C于A、B两点,若MF\B的周长为4萌,则椭圆C的方程为()A.y= 1B.令+护=1x1 2 v2C.迈+討1二、填空题9.与椭圆亍+£= 1具有相同的离心率,焦点在x轴上且过点(2, —回的椭圆的标准方程是____________ •10.已知P(m,椭圆^+f=l上的一个动点,则存+“2的取值范用是_______________ .11.椭圆「:吕+$=l(“>b>0)的左,右焦点分别为戸,E,焦距为2c.若直线y=*(x+c)与椭圆T的一个交点M满足ZMF02=2ZMF2F I,则该椭圆的离心率为____________ .三' 解答题12.已知椭圆的方程为/+号=1,直线/经过椭圆的焦点与椭圆交于A,B两点,若ZkAOB的而积为|,求直线/的方程.13.如图,己知/”>1,直线/:x—niy—^-=0,椭圆C:和+护=1, F】、分别为椭圆C的左、右焦答案精析知识条目排查知识点一椭圆焦点焦距1 当直线/过右焦点尸2时,求直线/的方程:2 设直线/与椭圆C交于A, B两点,AAFiFz. ABF1F2的重心分别为G, H.若原点0在以线段GH 为直径的圆内,求实数加的取值范用.(1 )a>c (2)a=c (3 )a<c知识点二加2b 2c*=“2题型分类示例例1 (1)B (2)乎解析(DY点P在线段AN的垂直平分线上,:.\PA\=\PN\.又AM是圆的半径,••• IPMI + \PN\=IPMI + IPAI=L4MI= 6>IMNI,由椭圆定义知,点P的轨迹是椭圆.75(2)由椭圆方程知,以=25,沪=亍,.? 25 . 5* /•c=2» 2c=5 ・在△PFlF2 中,IFi F2 卩=IPFi 卩+IPF2I2一2 IPFillPFilcos 60°,即25 = IPFiI2+IPF2I2 - IPFi I- IPFzI.® 由椭圆的定义得10=IPF】l + IPF2l,即1OO=IPF1I2+IPF212+2IPF1MPF2I.② 由②一①,得3IPF1MPF2I=75,AIPFihlPF2l=25,/.SAFiPF2=ylPFil lPF2l-sin 60°例2 D例3 "+春=1解析设椭圆的方程为mx2+ny2 = 1 (m>0, n>0. m^n)・因为点(晋,书)和点(晋,1)都在椭圆上,"(誓)2 + 小(萌)2= 1 , 加(斗^)2+”・ 2 = 1 ,所以所求的椭圆的标准方程为*+曽=1. 例4解(1)由題意得2b=“+c, :.4b 2=(a+c )2, 又•.•“2=夕+<?2,.・.4(“2_c2)=a2+2“c+c 2, 即 3a 2—2ac •—5c 2=O t巧-5・(护=0, 即 5・(£)2+2・£一3=0,a a• c 3• • £=一=三・a 5(2)由题意可设P (—c,)®)(c 为半焦距), kop=—严,k :\B= 一夕,由于 OP//AB, ■ • U _ •一7一一7 爪一丁把K _c,牛)代入椭圆方程得•」一」一=“■>•W+号=i (xH±i ).(2)当直线的斜率不存在,即P0是椭圆的长轴时,其长为2迈,显然不合题意,即直线P0的斜 率存在・所以例 5 解(1)设 M (x, y )设直线P0的方程是y=kx+\. P(x n yj), Q(X29力),则yi—yi=k(x\—X2)9V』=4后+4 伙2+2)=8 (Q +1)>0,• •MR•: \PQ\=t\l(X\ —A*2)2+G T1—J2)2 =7(\ +疋)[(*1 +也)2 —4XI X2]=° & L+ 1-272肿+2,3yf2厂Q +1A \PQ\= 2 =2返疋+2‘疋=2, k=±yf29•••直线P0的方程是y=±A/2.V+ 1.例6 解(1)尺(一1,0), F2(l,0).(2)①当直线AB的斜率不存在时,由对称性可知,皿=0.②当直线的斜率存在时,设直线的斜率为匕A(・m yi)> B(X29 ya).由题意得R H—1, X2H-1,直线AB的方程为y=kx-k.直线PF2的斜率为一给g—伙+加)A2 + 1化简整理得(4k—〃】)X]X2—3〃?(JVI+Q)—(4k+5皿)=0.(*) 将直线AB方程y=k(x-V)代入椭圆方程,化简整理得(4Q+3)*—8Q X+4Q— 12=0.联立消去y得(疋+2)卫+2恋一1 =0,由根与系数的关系得“+X2 =8Q4后+3‘4112X\+X2 =2k股+2' X\X2 =1Q+2'直线PA的斜率为十彳3—伙+加)Xi+ 1由题意得kx2-(k+m)Q+1代入(#)式并化简整理得16Q加+20£+加=0・"十20斤川W=_T6?+1-当k=0时,m=0;….20比1 .. 201 则5 当诊°时'|〃戶碍^簪P故加的所有整数值是一2, 一1,0丄2・例7解(1)由题意得椭圆的上顶点P(O,1).设点A为(xo, yo),因为B是A关于原点O的对称点,=2S 匕PAO = 2X*IPOIIx()l =I AO L因为一2WxoW2, 所以当xo=±2时,S有最大值为2.(2)由⑴知P(0.1), B(—xg一对血H0且內工一1), 所以直线PB的斜率为中,线段PB的中点为(一岁号巴于是PB的中垂线方程为由题意,Xo =Ek _\-4k1 2 一1+4心>,0=l+4F1-(-悬)2_(务郑-以 $N= ] _4p2(E 尹 1)_ 12股二—1+4T因为点N 在椭圆内部,12启所以 一 lv —yzp 莎<1,解得—%:普.又由已知EHO,所以斜率k 的取值范围是(一乎,0)U (0,咨). 例8解 ⑴因为椭圆的长轴长2“=2辺,焦距2c=2.又由椭圆的定义得L4Fil+IAF2l=2n,所以AAF,F 2的周长为IAFil+lAF2l+lFiF2l=2 迈+2.(2)由题意得/不垂直于两坐标轴,故设/的方程为y=k (x+l )(RHO ),1 L于是直线I 与直线x=—㊁交点Q 的纵坐标为yQ=j.设 Ag yi ), B (X2. yz )>显然 X2^ 1 ♦所以直线尸2人的方程为 >==(兀一1), X]"故直线恥与直线一技点P 的纵坐标为k 尹,因为P, Q 、R 到x 轴的距离依次成等比数列,所以1〉词・1艸1=切|2,整理得 9LV|X2 +(X1+X2)+ ll = LviX2 —(XJ-|-X2)+ 11.(*) 联立y=k (x+l )与椭圆方程,消去y 得 (1 +2Q )W+4Rr+2Q —2=0,同理, 点R 的纵坐标为艸= —3y2 2(也一1)' 一 3”1) _3力 Q 2(也一1)亍代入(*)并化简#18^-11=9.解得k=^,经检验,直线/的方程为>'=±^(1-4-1). 考点专项训练1. B2. D3・A4. B5. C6. B7. A8- A [•••△AFiB 的周长为4伍 •••滋=込戸,离心率为習,・・・c=l,・・・bfp 二?=逗,・•・椭圆C 的方程为¥+弓=1.]9舟解析由题意可设椭圆的方程为 兰+丘=14加十3/7将点(2, —护)代入椭圆方程,解得加=2,・•・椭圆的标准方程为扌+£=】•10. [1.2]解析 因为P (加,")是椭圆^+-|=1上的一个动点, 所以协2十与=1,即宀2—加2,所以 /rr+??2=2—/rr,又一所以 1W2—“FW2,所以 lW"*+“2£2.11 .y[3 — 1所以X\+X2 = -4k 2 1+2心 2k 2-2 X\X2 = 1+20解析由直线方程为y=V3(x+c),知ZMF]F2=60。
05高二数学浙江省学考选考高中数学复习资料重难点知识汇总三角恒等变换
4.两角和的正弦公式(简记 S(α+β)): sin sin cos cos sin . 5.两角差的正弦公式(简记 S(α-β)): sin sin cos cos sin .
(三)半角公式(这类公式不要求记忆)
半角的正弦(简记 S )、余弦(简记 C )、正切(简记 T )公式:
2
2
2
cos2
2
1 cos 2
,cos 2
1 cos , 2
sin50°
=sin-50°• 1 =-2. cos60° sin50°
(2)[2sin50°+sin10°(1+ 3tan10°)]• 2sin280°
cos10°+ 3sin10°
= 2sin50°+sin10°
cos10°
• 2cos210°
2sin50°+2sin10°·cos50°
=
cos10° • 2cos10°
2
解:(1)(tan10°- 3)•cos10° sin50°
=(tan10°-tan60°)•cos10° sin50°
=
sin10° - sin60° cos10° cos60°
•cos10°
sin50°
=sin10°·cos60°-cos10°·sin60°•cos10°
cos10°·cos60°
17 13
17 13
221
221
sin(α-β)=sinαcosβ-cosαsinβ=15×(- 5 )-(- 8 )×12= 21 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识点一 空间向量的有关概念名称 概念 表示 零向量 长度为0的向量 0 单位向量 模为1的向量 相等向量 方向相同且模相等的向量 a =b 相反向量 与向量a 长度相等而方向相反的向量-a 共线向量 表示空间向量的有向线段所在的直线互相平行或重合的向量a ∥b 共面向量 平行于同一个平面的向量知识点二 共线向量、共面向量定理和空间向量基本定理 1.共线向量定理对空间任意两个向量a ,b (b ≠0),a ∥b 的充要条件是存在实数λ,使a =λb .推论:如图所示,对空间任意一点O ,点P 在l 上的充要条件是存在实数t ,使OP →=OA →+t a ,①其中a 叫做直线l 的方向向量.在l 上取AB →=a ,则①可化为OP →=OA →+tAB →. 2.共面向量定理的向量表达式:p =x a +y b ,其中x ,y ∈R ,a ,b 为不共线向量,推论的表达式为AP →=xAB →+yAC →或对空间任意一点O ,有OP →=OA →+xAB →+yAC →或OP →=xOA →+yOB →+zOC →,其中x +y +z =1. 3.空间向量基本定理如果三个向量a ,b ,c 不共面,那么对空间任一向量p ,存在有序实数组{x ,y ,z },使得p =x a +y b +z c ,把{a ,b ,c }叫做空间的一个基底. 知识点三 空间向量的数量积及运算律 1.数量积及相关概念 (1)两向量的夹角已知两个非零向量a ,b ,在空间任取一点O ,作OA →=a ,OB →=b ,则∠AOB 叫做向量a 与b 的夹角,记作〈a ,b 〉,其范围是0≤〈a ,b 〉≤π.如果〈a ,b 〉=π2,那么向量a ,b 互相垂直,记作a ⊥b . (2)两向量的数量积已知两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做a ,b 的数量积,记作a·b .即a·b =|a ||b |cos 〈a ,b 〉.2.空间向量数量积的运算律 (1)(λa )·b =λ(a·b ); (2)交换律:a·b =b·a ; (3)分配律:a·(b +c )=a·b +a·c . 知识点四 空间向量的坐标运算设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),则: (1)a +b =(a 1+b 1,a 2+b 2,a 3+b 3). (2)a -b =(a 1-b 1,a 2-b 2,a 3-b 3). (3)λa =(λa 1,λa 2,λa 3). (4)a ·b =a 1b 1+a 2b 2+a 3b 3.(5)若a ,b 为非零向量,则a ⊥b ⇔a ·b =0⇔a 1b 1+a 2b 2+a 3b 3=0. (6)若b ≠0,则a ∥b ⇔a =λb ⇔a 1=λb 1,a 2=λb 2,a 3=λb 3.(7)|a |=a ·a =a 21+a 22+a 23. (8)cos 〈a ,b 〉=a ·b |a ||b |=a 1b 1+a 2b 2+a 3b 3a 21+a 22+a 23·b 21+b 22+b 23. (9)若A (a 1,a 2,a 3),B (b 1,b 2,b 3),则AB →=(b 1-a 1,b 2-a 2,b 3-a 3),d AB =|AB →|=(b 1-a 1)2+(b 2-a 2)2+(b 3-a 3)2. 知识点五 立体几何中的向量方法 1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:在直线上任取一非零向量即可作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎪⎨⎪⎧n ·a =0,n ·b =0.2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量为v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数x ,y ,使v =x v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u . (4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1∥u 2. 3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0. (2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u . (3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0. 4.空间向量与空间角的关系(1)设异面直线l 1,l 2的方向向量分别为m 1,m 2,则l 1与l 2所成的角θ满足cos θ=|cos 〈m 1,m 2〉|.(2)设直线l 的方向向量和平面α的法向量分别为m ,n ,则直线l 与平面α所成角θ满足sin θ=|cos 〈m ,n 〉|. (3)求二面角的大小①如图①所示,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.②如图②③所示,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos 〈n 1,n 2〉或-cos 〈n 1,n 2〉.题型一 空间向量及其运算例1 已知空间中三点A (-2,0,2),B (-1,1,2),C (-3,0,4),设a =AB →,b =AC →. (1)求向量a 与向量b 的夹角的余弦值;(2)若k a +b 与k a -2b 互相垂直,求实数k 的值. 解 (1)∵a =AB →=(1,1,0),b =AC →=(-1,0,2),又|a |=12+12+02=2, |b |=(-1)2+02+22=5,∴cos 〈a ,b 〉=a ·b |a ||b |=-12·5=-1010,即向量a 与向量b 的夹角的余弦值为-1010. (2)∵k a +b =(k -1,k,2),k a -2b =(k +2,k ,-4), ∴(k a +b )·(k a -2b )=(k -1,k ,2)·(k +2,k ,-4) =(k -1)(k +2)+k 2-8 =2k 2+k -10=0, ∴k =-52或k =2.感悟与点拨 (1)空间向量的运算法则及求解思想与平面向量相同,因此,可参照平面向量的运算法则和求解思想进行处理.(2)空间向量的问题可通过坐标运算和非坐标的线性运算两种途径来处理,另外,要抓住垂直与平行两种特殊位置关系.跟踪训练1 (1)(2018年4月学考)在三棱锥O -ABC 中,若D 为BC 的中点,则AD →等于( ) A.12OA →+12OC →-OB → B.12OA →+12OB →+OC → C.12OB →+12OC →-OA → D.12OB →+12OC →+OA → (2)(2016年4月学考)已知空间向量a =(2,-1,5),b =(-4,2,x )(x ∈R ),若a ⊥b ,则x 等于( )A .-10B .-2C .2D .10(3)已知向量a =(1,2,3),b =(x ,x 2+y -2,y ),并且a ,b 同向,则x ,y 的值分别为________. 答案 (1)C (2)C (3)1,3 解析 (2)∵a ⊥b ,得x =2.(3)∵a ∥b ,∴x 1=x 2+y -22=y3,解得⎩⎪⎨⎪⎧ x =-2,y =-6或⎩⎪⎨⎪⎧x =1,y =3,当⎩⎪⎨⎪⎧x =-2,y =-6时,a =-12b ,不符合要求,舍去,当⎩⎪⎨⎪⎧ x =1,y =3时,a =b ,符合要求, ∴⎩⎪⎨⎪⎧x =1,y =3.题型二 利用空间向量证明平行与垂直例2 如图所示,已知在直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D ,E ,F 分别为B 1A ,C 1C ,BC 的中点.求证:(1)DE ∥平面ABC ; (2)B 1F ⊥平面AEF .证明 (1)如图建立空间直角坐标系Axyz ,令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4). 设AB 的中点为N ,连接CN ,则N (2,0,0),C (0,4,0),D (2,0,2), ∴DE →=(-2,4,0),NC →=(-2,4,0), ∴DE →=NC →,∴DE ∥NC ,又∵NC ⊂平面ABC ,DE ⊄平面ABC , ∴DE ∥平面ABC .(2)∵B 1F —→=(-2,2,-4),EF →=(2,-2,-2), AF →=(2,2,0).∴B 1F —→·EF →=(-2)×2+2×(-2)+(-4)×(-2)=0, B 1F —→·AF →=(-2)×2+2×2+(-4)×0=0.∴B 1F —→⊥EF →,B 1F —→⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF , 又∵AF ∩FE =F ,AF ,FE ⊂平面AEF , ∴B 1F ⊥平面AEF .感悟与点拨 (1)用向量证明线面平行的方法: ①证明该直线的方向向量与平面的某一法向量垂直; ②证明该直线的方向向量与平面内某直线的方向向量平行;③证明该直线的方向向量可以用平面内的两个不共线的向量线性表示. (2)用向量证明垂直的方法:①线线垂直:证明两直线所在的方向向量互相垂直,即证明它们的数量积为零;②线面垂直:证明直线的方向向量与平面的法向量共线,或将线面垂直的判定定理用向量表示;③面面垂直:证明两个平面的法向量垂直,或将面面垂直的判定定理用向量表示.跟踪训练2 在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点. (1)求证:EF ⊥CD ;(2)在平面P AD 内求一点G ,使GF ⊥平面PCB ,并证明你的结论.(1)证明 如图所示,以DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系Dxyz ,设AD =a ,则D (0,0,0),A (a ,0,0), B (a ,a ,0),C (0,a ,0),E ⎝⎛⎭⎫a ,a2,0, P (0,0,a ),F ⎝⎛⎭⎫a 2,a 2,a 2,∴EF →=⎝⎛⎭⎫-a 2,0,a 2,DC →=(0,a ,0). ∵EF →·DC →=-a 2×0+0×a +a 2×0=0,∴EF →⊥DC →,即EF ⊥CD . (2)解 点G 为AD 的中点. 证明如下:设G (x ,0,z ), 则FG →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2. 若使GF ⊥平面PCB ,则由FG →·CB →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2·(a ,0,0) =a ⎝⎛⎭⎫x -a 2=0,得x =a2; 由FG →·CP →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2·(0,-a ,a ) =a 22+a ⎝⎛⎭⎫z -a 2=0,得z =0. ∴点G 的坐标为⎝⎛⎭⎫a2,0,0,即点G 为AD 的中点. 题型三 利用空间向量求空间角例3 如图,在矩形ABCD 中,AB =22,AD =2,M 为DC 的中点,将△DAM 沿AM 折到△D ′AM 的位置,AD ′⊥BM .(1)求证:平面D ′AM ⊥平面ABCM ;(2)若E 为D ′B 的中点,求二面角E -AM -D ′的余弦值. (1)证明 由题意知,在矩形ABCD 中,∠AMD =∠BMC =45°, 所以∠AMB =90°,即AM ⊥BM .又D ′A ⊥BM ,D ′A ∩AM =A ,D ′A ,AM ⊂平面AD ′M , 所以BM ⊥平面D ′AM , 又BM ⊂平面ABCM , 所以平面ABCM ⊥平面D ′AM .(2)解 由(1)知,在平面D ′AM 内过M 作直线NM ⊥MA , 则NM ⊥平面ABCM ,故以M 为原点,MA →,MB →,MN →分别为x ,y ,z 轴的正方向建立空间直角坐标系, 则M (0,0,0),A (2,0,0), B (0,2,0),D ′(1,0,1), 于是E ⎝⎛⎭⎫12,1,12, MA →=(2,0,0),ME →=⎝⎛⎭⎫12,1,12, 设平面EAM 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧2x =0,12x +y +12z =0,令y =1,得z =-2, 则平面EAM 的一个法向量m =(0,1,-2),故cos 〈m ,n 〉=15, 由图知,二面角为锐角, 即二面角E -AM -D ′的余弦值为55. 感悟与点拨 (1)用向量方法求两条异面直线所成的角,是通过两条直线的方向向量的夹角来求解.(2)用向量法求线面角,是通过直线的方向向量和平面的法向量来求解.(3)求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角. 跟踪训练3 (1)如图,在四棱锥P -ABCD 中,四边形ABCD 为平行四边形,且BC ⊥平面P AB ,P A ⊥AB ,M 为PB 的中点,P A =AD =2.若AB =1,则二面角B -AC -M 的余弦值为( )A.66 B.36 C.26 D.16答案 A解析 因为BC ⊥平面P AB ,AD ∥BC ,所以AD ⊥平面P AB ,P A ⊥AD , 又P A ⊥AB ,且AD ∩AB =A ,AD ,AB ⊂平面ABCD , 所以P A ⊥平面ABCD .以点A 为坐标原点,分别以AD ,AB ,AP 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz .则A (0,0,0),C (2,1,0),P (0,0,2),B (0,1,0),M ⎝⎛⎭⎫0,12,1,所以AC →=(2,1,0),AM →=⎝⎛⎭⎫0,12,1,又平面ABC 的一个法向量AP →=(0,0,2), 所以cos 〈n ,AP →〉=n ·AP →|n ||AP →|=21+4+1·2=16=66.所以二面角B -AC -M 的余弦值为66. (2)如图所示,在四面体ABCD 中,AB ,BC ,BD 两两垂直,AB =BC =BD =4,E ,F 分别为棱BC ,AD 的中点.求:①异面直线AB 与EF 所成角的余弦值; ②点E 到平面ACD 的距离; ③EF 与平面ACD 所成角的正弦值.解 如图所示,分别以直线BC ,BD ,BA 为x ,y ,z 轴建立空间直角坐标系,则各相关点的坐标为A (0,0,4),B (0,0,0),C (4,0,0),D (0,4,0),E (2,0,0),F (0,2,2). ①∵AB →=(0,0,-4), EF →=(-2,2,2),∴|cos 〈AB →,EF →〉|=⎪⎪⎪⎪⎪⎪-84×23=33, ∴异面直线AB 与EF 所成角的余弦值为33. ②设平面ACD 的一个法向量为n =(x ,y ,1),∵AC →=(4,0,-4),CD →=(-4,4,0), 则⎩⎪⎨⎪⎧n ·AC →=0,n ·CD →=0,即⎩⎪⎨⎪⎧4x -4=0,-4x +4y =0,∴x =y =1,∴n =(1,1,1). ∵F ∈平面ACD ,EF →=(-2,2,2),∴点E 到平面ACD 的距离为d =|n ·EF →||n |=23=233.③EF 与平面ACD 所成角的正弦值为|cos 〈n ,EF →〉|=23×23=13.题型四 立体几何中的探索性问题例4 如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=1,底面ABCD 的周长为4.(1)当长方体ABCD -A 1B 1C 1D 1的体积最大时,求直线BA 1与平面A 1CD 所成的角;(2)线段A 1C 上是否存在一点P ,使得A 1C ⊥平面BPD ?若存在,求出P 点的位置,若不存在,请说明理由.解 (1)根据题意,令AB =t ,则长方体的体积为 V =t (2-t )×1=t (2-t )≤⎝⎛⎭⎪⎫t +2-t 22=1,当且仅当t =2-t ,即t =1时体积V 有最大值为1.所以当长方体ABCD -A 1B 1C 1D 1的体积最大时,底面四边形ABCD 为正方形. 又AA 1=1.所以ABCD -A 1B 1C 1D 1为正方体.如图,连接B 1C ,取B 1C 的中点O ,连接BO ,A 1O .由题意知,CD ⊥平面C 1B 1BC , 所以BO ⊥CD ,在等腰Rt △B 1BC 中,BO ⊥B 1C ,又B 1C ∩CD =C ,B 1C ,CD ⊂平面A 1B 1CD , 所以BO ⊥平面A 1B 1CD ,即∠BA 1O 就是直线BA 1与平面A 1CD 所成的角. 又BO =22,BA 1=2,所以∠BA 1O =30°. 即长方体ABCD -A 1B 1C 1D 1的体积最大时,直线BA 1与平面A 1CD 所成的角为30°.(2)根据题意可知,AA 1,AB ,AD 两两垂直,以AB 为x 轴,AD 为y 轴,AA 1为z 轴,建立如图所示的空间直角坐标系.根据题意及(1)可得B (t,0,0),C (t ,2-t ,0),D (0,2-t,0),若线段A 1C 上存在一点P 满足要求,不妨设A 1P —→=λA 1C —→,可得P (λt ,λ(2-t ),1-λ). BP →=(λt -t ,λ(2-t ),1-λ),BD →=(-t,2-t,0), A 1C —→=(t,2-t ,-1), ⎩⎨⎧BP →·A 1C —→=0,BD →·A 1C —→=0,即⎩⎪⎨⎪⎧t (λt -t )+λ(2-t )2-(1-λ)=0,-t 2+(2-t )2=0,解得t =1,λ=23.即只有当底面四边形是正方形时才存在符合要求的点P ,位置是线段A 1C 上A 1P ∶PC =2∶1处.感悟与点拨 对于立体几何中的探索性问题,可以凸显坐标方法的优势,通常从假设存在入手,利用空间向量坐标建立方程,然后按部就班求解.跟踪训练4 如图所示,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形,平面ABC ⊥平面AA 1C 1C ,AB =3,BC =5.(1)求证:AA 1⊥平面ABC ;(2)求二面角A 1-BC 1-B 1的余弦值;(3)在线段BC 1上是否存在一点D ,使得AD ⊥A 1B ?若存在,求BD BC 1的值;若不存在,请说明理由.(1)证明 在正方形AA 1C 1C 中,A 1A ⊥AC .又∵平面ABC ⊥平面AA 1C 1C ,且平面ABC ∩平面AA 1C 1C =AC ,AA 1⊂平面AA 1C 1C ,∴AA 1⊥平面ABC .(2)解 在△ABC 中,AC =4,AB =3,BC =5, ∴BC 2=AC 2+AB 2,AB ⊥AC ,∴以A 为坐标原点,建立如图所示的空间直角坐标系Axyz .则A 1(0,0,4),B (0,3,0),C 1(4,0,4),B 1(0,3,4),A 1C 1—→=(4,0,0), A 1B —→=(0,3,-4),B 1C 1—→=(4,-3,0),BB 1—→=(0,0,4). 设平面A 1BC 1的法向量n 1=(x 1,y 1,z 1), 平面B 1BC 1的法向量n 2=(x 2,y 2,z 2).∴⎩⎨⎧ A 1C 1—→·n 1=0,A 1B —→·n 1=0,即⎩⎪⎨⎪⎧4x 1=0,3y 1-4z 1=0,∴可取向量n 1=(0,4,3), 由⎩⎨⎧B 1C 1—→·n 2=0,BB 1—→·n 2=0,即⎩⎪⎨⎪⎧4x 2-3y 2=0,4z 2=0.∴可取向量n 2=(3,4,0),∴cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=165×5=1625.由题意知二面角A 1-BC 1-B 1为锐角, ∴二面角A 1-BC 1-B 1的余弦值为1625.(3)解 假设在线段BC 1上存在一点D ,使AD ⊥A 1B , 设D (x ,y ,z )是直线BC 1上一点,且BD →=λBC 1→. ∴(x ,y -3,z )=λ(4,-3,4), 解得x =4λ,y =3-3λ,z =4λ. ∴AD →=(4λ,3-3λ,4λ). 又∵AD ⊥A 1B ,∴0+3(3-3λ)-16λ=0,则λ=925,∴BD BC 1=925.一、选择题1.如图所示,在直三棱柱ABC -A 1B 1C 1中,若CA →=a ,CB →=b ,CC 1—→=c ,则A 1B —→等于( )A .a +b -cB .a -b +cC .-a +b +cD .-a +b -c 答案 D解析 如图所示,连接A 1C ,则在△A 1CB 中,有A 1B —→=CB →-CA 1—→=CB →-(CC 1—→+CA →)=b -(a +c )=-a +b -c .2.若向量a =(1,1,x ),b =(1,2,1),c =(1,1,1),满足条件(c -a )·2b =-2,则x 的值为( ) A .-4 B .-2 C .4 D .2 答案 D解析 ∵a =(1,1,x ),b =(1,2,1),c =(1,1,1), ∴c -a =(0,0,1-x ),2b =(2,4,2). ∴(c -a )·2b =2(1-x )=-2, ∴x =2.3.已知A (2,3,-1),B (2,6,2),C (1,4,-1),则向量AB →与AC →的夹角为( ) A .45° B .90° C .30° D .60° 答案 D解析 ∵A (2,3,-1),B (2,6,2),C (1,4,-1), ∴AB →=(0,3,3),AC →=(-1,1,0), ∴AB →·AC →=0×(-1)+3×1+3×0=3, 且|AB →|=32,|AC →|=2,∴cos 〈AB →,AC →〉=AB →·AC →|AB →||AC →|=332×2=12,∴AB →与AC →的夹角为60°.4.已知a =(2,-1,3),b =(-4,2,x ),c =(1,-x ,2),若(a +b )⊥c ,则x 等于( ) A .4 B .-4 C.12 D .-6答案 B解析 ∵(a +b )⊥c , ∴(a +b )·c =0.又a +b =(-2,1,x +3),∴-2×1+1×(-x )+(x +3)×2=0,解得x =-4. 故选B.5.如图,在平行六面体ABCD -A 1B 1C 1D 1中,M 为A 1C 1与B 1D 1的交点.若AB →=a ,AD →=b ,AA 1—→=c ,则下列向量中与BM →相等的向量是( )A .-12a +12b +cB.12a +12b +c C .-12a -12b +cD.12a -12b +c 答案 A解析 由题意,得BM →=BC →+CC 1—→+C 1M —→=BC →+CC 1—→+12C 1A 1—→=BC →+CC 1—→-12(AB →+BC →)=-12AB→+12BC →+CC 1—→=-12a +12b +c . 6.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则( ) A .l ∥α B .l ⊥αC .l ⊂αD .l 与α相交但不垂直 答案 B解析 ∵a =(1,0,2),n =(-2,0,-4), ∴n =-2a ,∴a ∥n ,∴l ⊥α.7.如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2,AD =1,点E ,F ,G 分别是DD 1,AB ,CC 1的中点,则异面直线A 1E 与GF 所成角的余弦值是( )A.155B.22C.105D .0答案 D解析 以DA →,DC →,DD 1—→的方向为x ,y ,z 轴正方向,建立空间直角坐标系(图略), 则可得A 1(1,0,2),E (0,0,1),G (0,2,1),F (1,1,0). ∴A 1E —→=(-1,0,-1),GF →=(1,-1,-1), 设异面直线A 1E 与GF 所成的角为θ, 则cos θ=|cos 〈A 1E —→,GF →〉|=0.8.正方体ABCD -A 1B 1C 1D 1的棱长为a ,点M 在AC 1上且AM →=12MC 1—→,N 为B 1B 的中点,则|MN →|为( ) A.216a B.66a C.156a D.153a 答案 A解析 以D 为原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Dxyz ,则A (a,0,0),C 1(0,a ,a ), N ⎝⎛⎭⎫a ,a ,a 2. 设M (x ,y ,z ),因为点M 在AC 1上且AM →=12MC 1—→,所以(x -a ,y ,z )=12(-x ,a -y ,a -z ),所以x =23a ,y =a 3,z =a3,所以M ⎝⎛⎭⎫2a 3,a 3,a 3, 所以|MN →|=⎝⎛⎭⎫a -2a 32+⎝⎛⎭⎫a -a 32+⎝⎛⎭⎫a 2-a 32=216a .9.在平行四边形ABCD 中,AB =AC =1,∠ACD =90°,将它沿对角线AC 折起,使AB 和CD 成60°角(如图),则B ,D 间的距离为( )A .1B .2 C. 2 D .2或2 答案 D解析 因为∠ACD =90°,所以AC →·CD →=0. 同理BA →·AC →=0,因为AB 和CD 成60°角,所以〈BA →,CD →〉=60°或120°. 因为BD →=BA →+AC →+CD →,所以|BD →|2=|BA →|2+|AC →|2+|CD →|2+2BA →·CD →+2BA →·AC →+2AC →·CD →=|BA →|2+|AC →|2+|CD →|2+2BA →·CD →=3+2×1×1×cos 〈BA →,CD →〉=3+2cos 60°或3+2cos 120°, 所以|BD →|=2或 2.即B ,D 间的距离为2或2,故选D.10.如图,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,F ,G 分别是线段AE ,BC 的中点,则AD 与GF 所成角的余弦值为( )A.36 B .-36 C.33D .-33答案 A解析 如图,正方形ACDE 与等腰直角三角形ACB 所在的平面互相垂直,且AC =BC =2,∠ACB =90°,DC ⊥AC ,平面ACDE ∩平面ACB =AC ,DC ⊂平面ACDE ,所以DC ⊥平面ABC ,F ,G 分别是线段AE ,BC 的中点. 以C 为原点建立空间直角坐标系如图所示,则 A (0,2,0),B (2,0,0),D (0,0,2),G (1,0,0),F (0,2,1). 所以AD →=(0,-2,2),GF →=(-1,2,1). 所以|AD →|=22,|GF →|=6,AD →·GF →=-2. 所以cos 〈AD →,GF →〉=AD →·GF →|AD →||GF →|=-36.则直线AD 与GF 所成角的余弦值为36.故选A. 二、填空题11.已知O 为空间任一点,A ,B ,C ,D 四点满足任意三点不共线,但四点共面,且OA →=2xBO →+3yCO →+4zDO →,则2x +3y +4z 的值为________. 答案 -1解析 由题意知A ,B ,C ,D 共面的充要条件是:对空间任意一点O ,存在实数x 1,y 1,z 1,使得OA →=x 1OB →+y 1OC →+z 1OD →且x 1+y 1+z 1=1,因此2x +3y +4z =-1.12.已知向量a =(2,-1,3),b =(-4,2,x ).若a ⊥b ,则x =________;若a ∥b ,则x =________. 答案103-6 13.设O 为坐标原点,向量OA →=(1,2,3),OB →=(2,1,2),OP →=(1,1,2),点Q 在直线OP 上运动,则当QA →·QB →取得最小值时,点Q 的坐标为________. 答案 ⎝⎛⎭⎫43,43,83解析 设OQ →=λOP →=(λ,λ,2λ),故Q (λ,λ,2λ), 故QA →=(1-λ,2-λ,3-2λ),QB →=(2-λ,1-λ,2-2λ).则QA →·QB →=6λ2-16λ+10=6⎝⎛⎭⎫λ-432-23, 当QA →·QB →取最小值时,λ=43,此时Q 点的坐标为⎝⎛⎭⎫43,43,83.14.如图,P A ⊥平面ABC ,AC ⊥BC ,P A =AC =1,BC =2,则二面角A -PB -C 的余弦值为________.答案33解析 如图所示,建立空间直角坐标系,则C (0,0,0),A (1,0,0),P (1,0,1),B (0,2,0),∴AP →=(0,0,1),PB →=(-1,2,-1),CB →=(0,2,0). 设平面ABP 的法向量为m =(x 1,y 1,z 1), 平面PBC 的法向量为n =(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧m ·AP →=0,m ·PB →=0,即⎩⎪⎨⎪⎧z 1=0,-x 1+2y 1-z 1=0,∴⎩⎪⎨⎪⎧z 1=0,x 1=2y 1,令y 1=1,得m =(2,1,0). 由⎩⎪⎨⎪⎧n ·PB →=0,n ·CB →=0,即⎩⎪⎨⎪⎧-x 2+2y 2-z 2=0,2y 2=0,∴⎩⎪⎨⎪⎧ x 2=-z 2,y 2=0,令z 2=1, 得n =(-1,0,1).∴|cos 〈m ,n 〉|=⎪⎪⎪⎪⎪⎪-22×3=33. 由题意可知,所求二面角的平面角是锐角,故二面角A -PB -C 的余弦值为33. 三、解答题15.如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =22AB .(1)证明:BC 1∥平面A 1CD ;(2)求二面角D -A 1C -E 的正弦值.(1)证明 连接AC 1交A 1C 于点F ,则F 为AC 1的中点.又D 是AB 的中点,连接DF ,则BC 1∥DF .因为DF ⊂平面A 1CD ,BC 1⊄平面A 1CD ,所以BC 1∥平面A 1CD .(2)解 由AC =CB =22AB , 得AC ⊥BC .以C 为坐标原点,CA →的方向为x 轴正方向,CB →的方向为y 轴正方向,CC 1—→的方向为z 轴正方向,建立如图所示的空间直角坐标系Cxyz . 设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2),CD →=(1,1,0),CE →=(0,2,1),CA 1—→=(2,0,2).设n =(x 1,y 1,z 1)是平面A 1CD 的法向量,则⎩⎪⎨⎪⎧ n ·CD →=0,n ·CA 1→=0,即⎩⎪⎨⎪⎧x 1+y 1=0,2x 1+2z 1=0. 可取x 1=1,则n =(1,-1,-1).同理,设m =(x 2,y 2,z 2)是平面A 1CE 的法向量,则⎩⎪⎨⎪⎧ m ·CE →=0,m ·CA 1—→=0,即⎩⎪⎨⎪⎧2y 2+z 2=0,2x 2+2z 2=0, 可取y 2=1,则m =(2,1,-2).从而cos 〈n ,m 〉=n ·m |n ||m |=33,故sin 〈n ,m 〉=63. 即二面角D -A 1C -E 的正弦值为63. 16.如图,在四棱锥S -ABCD 中,AB ∥CD ,AB ⊥AD ,SA =AB =2CD =2,SB =2AD =22,平面SAB ⊥平面ABCD ,E 为SB 的中点..(1)求证:CE ∥平面SAD ;(2)求证:BD ⊥平面SAC ;(3)求直线CE 与平面SAC 所成角的余弦值.(1)证明 ∵SA =AB =2,SB =22,∴SA ⊥AB ,又平面SAB ⊥平面ABCD ,平面SAB ∩平面ABCD =AB ,SA ⊂平面SAB ,∴SA ⊥平面ABCD ,又AB ⊥AD ,∴建立如图所示的空间直角坐标系,则A (0,0,0),B (2,0,0),C (1,2,0),D (0,2,0),S (0,0,2),E (1,0,1),CE →=(0,-2,1),平面SAD 的法向量为AB →=(2,0,0),∴CE →·AB →=0,即CE →⊥AB →,又CE ⊄平面SAD ,∴CE ∥平面SAD .(2)证明 设平面SAC 的法向量为n =(x ,y ,z ), AS →=(0,0,2),AC →=(1,2,0),BD →=(-2,2,0),∴⎩⎪⎨⎪⎧ n ·AS →=2z =0,n ·AC →=x +2y =0,令y =1,得x =- 2. ∴n =(-2,1,0),∴n ∥BD →,∴BD ⊥平面SAC .(3)解 CE →=(0,-2,1),平面SAC 的法向量n =(-2,1,0),设直线CE 与平面SAC 所成的角为θ,则sin θ=|CE →·n ||CE →||n |=23,∴cos θ=73, ∴直线CE 与平面SAC 所成角的余弦值为73.。
