高考有方法三视图解题超级策略.doc
2018届高考复习小专题坐标法拿下三视图

3.求果.注意到△ACD 与△BCD 是有公共斜边且全等的直角三角形,故
3
取 CD 中点 M , 2, 0 , 则 MA MB MC MD 2
2
V 43 23 323 . ,故选 B.
,知所求外接球体积为:
4.(河北武邑中学高三下质检 1.11 题)
2.(湖南师大附中,3 月考)某几何体的三视图如图所示,则其体积为
A. 83 B.2
C. 43 D. 23
9
【解析】构造如图的正方体及相应的空间直角坐标系. 3 个视图形状大小完全一样,故可直接想象该直观图是一个正八面体.其 6 个
顶点分别是正方体各个表面正方形的中心.其坐标依次为(1,2,1),(2,1,1),(1,2,1),
第 2 步:定位.由于主视图的节点更 多,所以如解图 2,以主视图为基准,去 依次确定 A,B,C,D 的坐标.
在主视图中,点 A1 在左下方,可以定位为 (x,0,0);在左视图中,点 A2 在左后方,可以定位 为(0,y,o),令(x,0,0)=(0,y,o),得 x=y=0,于 是有 A(0,0,0);
11
N,连结 AMGN.显然四边形 AMGN 为平行四边形,但 MN<AG.故□AMGN 不可
能为矩形.即△AMG 不是直角三角形.据此,原直
观图中的直角三角形仅有 1 个,故选 A.
5.(青岛高三三月考.5 题)
某几何体的三视图如图所示,则该几何体的
体积为
A.
56 3
B. 56
8 3
C.
64 3
3 的正三角形,所以它界定了这个长方体的宽为 3
格为 4
3
32
,高为 3/2.故其直观图包容在规
三视图解题技巧

三视图解题技巧————————————————————————————————作者:————————————————————————————————日期:备课资讯16 空间几何体与三视图问题的解题思想作为新课程中的新增内容,几何体与三视图必将成为今后高考考查的热点.本文以高考题为据,重在揭示解决此类问题的基本思想.一、直观构造思想【例1】(2008·山东)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A.9π B.10πC.11π D.12π解析几何体为一个球与一个圆柱的组合体,S=4π·12+π·12·2+2π·1·3=12π.二、内部构造思想【例2】(2009·海南)一个棱锥的三视图如下图,则该棱锥的全面积(单位:cm2)为 ( )A.48+12 2 B.48+24 2C.36+12 2 D.36+24 2解析 该几何体是一个底面为直角三角形的三棱锥,如图,SE =5,SD =4,AC =6,AB =BC=6, ∴S 全=S △ABC +2S △SAB +S △ASC2.2124842621652126621+=⨯⨯+⨯⨯⨯+⨯⨯=【例3】 若某多面体的三视图(单位:cm)如下图所示,则此多面体的体积是________ cm 3.解析 通过对三视图的观察,三视图对应几何体为正四棱锥P —ABC D .在正四棱锥P —ABC D 中间构筑底面的垂面△PEF 为投影面,侧视图即为△PEF , 从而求出该几何体的高度PO = . 3.3343431=⨯⨯=-ABCD P V 故点评例2、例3在几何体内部构造投影面,通过该投影面观察几何体的侧视图,就将问题化繁为简.投影面的构造需要垂直于几何体的下底面和后投影面.三、外部补形思想【例4】 (2008·海南,12)某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为 ( )A .2 2B .2 3C .4D .2 5解析由题意可构造长方体如图,长方体的对角线A1C为题中要求的几何体的棱长,长方体的三个面分别作为三视图中的三个投影面.设长方体的三棱长分别为x,y,z,将平面D D1C1C作为正视图投影面,则x2+y2+z2=7,x2+z2=6,∴y2=1.侧视图中棱的投影长为a=z2+1,俯视图中棱的投影长为b=x2+1.∴a+b=x2+1+z2+1≤2x2+1+1+z22=4.∴a+b的最大值为4(当x=z时取等号).【例5】直三棱柱A1B1C1-ABC的三视图如下图所示,D,E分别是棱C C1和棱B1C1的中点,求图中三棱锥E—ABD的侧视图的面积.解析 通过三视图可知直三棱柱A 1B 1C 1—ABC 的前侧面是边长为2的正方形,左侧面与前侧面互相垂直.将直三棱柱补形成正方体的方法,找到正方体右侧面作为几何体侧视图的投影面,可知三棱锥E —ABD 的侧视图为正方体右侧阴影部分.故有:三棱锥E —ABD 的侧视图的面积.21=∆G BB S 点评 例4通过外部补形成长方体得到斜线的三个投影面,例5通过外部补形成正方体得到三棱锥E —ABD 的侧视图的面积,体现了空间几何问题中由局部到整体的全局观察.总之,空间几何体中几何体和三视图问题虚实相间,该问题较能体现学生空间想象能力和学生对空间几何体的认知水平.本文通过直观构造、内部构造、外部补形、由下而上的建造思想为解决此类几何体和三视图问题奠定了坚实的思想基础.返回。
备战高考2021-三视图的难点突破方法

(A)112
(B)80
(C)72
(D)64
【答案】 B
第 3 页共 4 页
7.(2020 北京卷)4.某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为 ( ).
A. 6 3 B. 6 2 3 C. 12 3 D. 12 2 3
【答案】D
第 4 页共 4 页
【例】(2011 北京理,7)某四面体的三视图如图所示,该四面体四个面的面积中最大
的是( ).
A.8
B. 6 2
C.10
D.8 2
【解】在三视图中,“主左一样高”,所以,根据主视 图和左视图先确定几何体的高所在俯视图中的位置,然后 把笔放在俯视图高所在位置,最后想象将笔端连结俯视图 中其他顶点就得到相应的几何体形状。
俯视图
在正方体中画出 AB,CD(如图一),对照三视图就得到三棱锥 A-BCD(如图二)。
D
D
A
A
C
B
C
图一
计算可知三棱锥 A-BCD 体积为V 1 1 2 2 2 4 ,选 D
32
3
【三视图练习】
1. 某四棱锥的三视图如图所示,该四棱锥的表面积是
(A) 32
(B)16 16 2
B
图二
(C) 48 【答案】 B
三视图的难点突破方法 由于引入空间向量,立体几何中原来的平行、垂直证明和角度的计算对学生的空间想象 能力的要求大大降低。三视图就成为考查学生空间想象能力的重要考点。所以,高考中涉及 三视图的试题每年都有。但是学生的空间想象能力差异是很大的,有些空间想象能力强的学 生,做三视图试题时,能够很快想出原几何体形状,而另外不少学生就是凭感觉做题,有时 一道题需要想很长时间.那么,怎么突破三视图的难点呢? 一、找高法
2018高考三视图解题策略

长方体的高为 3 + 1 =
4 ,所以V长方体
=
22
4
= 16
,所以V
=
1 2 V长方体
=
8
.
【答案】D
4.如图,网格纸上的小正方形边长为 1,粗线是一个棱锥的三视图,则此棱锥的体积为( )
A. 8 3
B. 4 3
C. 4 3
D.2 3
【解析】本题很难直接看出棱锥的底面积与高,但通过观察可看出此棱锥可能由正方体
ABCD − A1B1C1D1 (棱长为 2)通过切割而成,所以先画出正方体,再根据三视图中的实
线虚线判断如何切割,正视图中可看出正方体用前后面的对角线所在平面将下方完全切掉, 从左视图可看出正方体的右侧面(虚线)有切痕,俯视图体现出正方体的上底面有切痕.进
而可得所求棱锥为一个四棱锥,底面是矩形 A1B1CD ,宽 CD = 2 ,长 B1C = 2 2 ,因为
2(侧视图),高为
2(正视图)所以可得面积
S3
=
1 2
2
2
=
2
,所
以该几何体的表面积为 S
=
S1
+ S2
+ S3
= 1+ 2
5
π+2.
【答案】A
2.圆柱被过轴一个平面截去一部分后与半球(半径为 r )组成一个几何体,该几何体三视
图中的正视图与俯视图如图所示,若该几何体的表面积为16 + 20π ,则 r = ( )
高为
3
(正视图的左侧直角边),所以
S△PAB
=
1 2
2
3=
3 .△PAD、△PBC 的底为
2,高为
专题三 三视图问题解题策略

A
B
A
B
D A'
D'
D C
B'
A'
C'
D'
C A
B' D C'
A'
B C
B'
D'
C'
【例题4】
如右上图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三
视图,则该多面体的各条棱中,最长的棱的长度为( B )
A.6 2 B.6
C.4 2 D.4
A
B
A
B
D
C
D
C
A'
M B'
A'
B'
D'
C'
D'
C'
【例题5】 已知一个四棱锥的三视图及有关数据如图所示,则该几何体的体积为( C)
A.2 3
B. 3
C.4 3
D.2 3
3
3
A
B
A
B
D
D
C
C
A'
B'
A'
B'
D'
C'
D'
C'
V 1 22 3 4 3
3
3
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某
【例题6】 多面体的三视图,则该多面体外接球的表面积为(D )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某 多面体的三视图,则该多面体外接球的表面积为( )
A.8 3
B.25 2
C. 12
A
高考数学中的三视图及相关方法

高考数学中的三视图及相关方法在高考数学中,三视图是一个常见的概念。
三视图是一个物体分别从三个不同的方向所观测到的图形,通过三个视图可以确定一个物体的形状、尺寸及空间位置。
在学习三视图时,需要掌握一些相关的知识和方法。
一、投影法与投影面在学习三视图之前,需要先掌握投影法和投影面的相关概念。
投影法是指从物体上某一点出发,将光线对着投影面射出,所形成的投影。
投影面是指用来做投影的平面。
在三视图中,通常使用前、上、侧三个平面来进行投影,这三个平面分别称为主平面。
二、主视图主视图是指在三视图中,以物体的正面朝前、上面朝上、左面朝左的方向所形成的视图。
主视图常常是确定一个物体的形状和尺寸的主要依据。
三、侧视图侧视图是指在三视图中,以物体左侧面朝上、物体正面朝前、物体下侧面朝下的方向所形成的视图。
侧视图和主视图相结合,可以确定一个物体的整体形状和尺寸。
四、俯视图俯视图是指在三视图中,以物体的上部朝上、物体的前面朝下、物体的左侧面朝左的方向所形成的视图。
俯视图主要用来确定一个物体的上部结构,例如天棚、台面等。
五、三视图的绘制方法在学习三视图时,需要掌握三视图的绘制方法。
绘制三视图时,需要确定主平面,然后将物体在主平面上分别绘出主视图、侧视图、俯视图。
在绘制时,需要按比例绘制,保持各个视图之间的比例关系一致。
六、三视图的应用在实际生活中,三视图有很多应用。
例如在工程设计中,可以通过三视图来确定一个建筑物或机械设备的形状和尺寸,以便进行制造和施工。
在家具设计方面,通过三视图可以确定家具的形状和尺寸,以便进行制造和销售。
总之,三视图在数学中是一个非常重要的概念。
通过学习三视图,可以帮助我们更好地了解物体的形状、尺寸和空间位置,从而更好地进行设计、制造和施工。
通过掌握三视图的相关知识和方法,我们可以在高考数学中取得更好的成绩。
高中数学 三视图 知识点总结及解题技巧专题汇总

高中数学三视图知识点总结及解题技巧专题汇总高中数学三视图知识点总结及解题技巧专题汇总三视图是指物体向投影面投影所得到的图形。
将物体在三个相互垂直的平面内作垂直投影所得的三个图形,称为三视图,分别为主视图(正)、俯视图和侧(左)视图。
正投影是指投影线互相平行,并都垂直于投影面的投影。
识图技巧包括试图位置、侧面与试图的关系、看图要领和选取的几何体。
一般三视图的放置方式是按照标准位置,便于尺寸的对应。
当几何体的侧面与投影面不平行时,该侧面的视图形状不是真实的形状,只有当侧面与投影面平行时,视图才能真实地反映几何体侧面的形状。
在看图时,主、俯视图长对正;主、侧视图高平齐;俯、侧视图宽相等。
在三视图考题中,选取的几何体一般有三种,包括常见的几何体、被平面截取后得到的几何体和组合体。
解题要领包括先确定底面、找视图中有线线垂直的地方和注意三视图与几何体的摆放位置直接相关。
大多数试题中下、俯视图的图形都是几何体底面的真实形状。
关键线往往对应着几何体中线面垂直、面面垂直的地方。
几何体的高很多情况就是视图平面图形的高,求几何体的体积时这一点显得尤为重要。
同样一个几何体若摆放位置不同,那么三视图的形状也会有变化。
典型例题讲解:某几何体的三视图如下,确定它的形状。
通过分析俯视图,可以知道底面是直角三角形;通过主视图,可以确定SA在几何体中是一条与底面垂直的棱。
重新画出三视图,放到标准位置,方便长度关系的计算。
由对应关系,可以算得底面三角形的高应为2,故底面的面积为4.高为2,则体积为18/3=6.综上所述,了解三视图的概念和识图技巧,掌握解题要领和典型例题的解法,能够有效提高解决三视图问题的能力。
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是多少?分析:1)看俯视图,确定底面为一个正方形。
2)看正视图和俯视图,最右边应该垂直于底面,且与底面垂直的是一个三角形的面。
3)这样就可以确定了,这个几何体是一个四棱锥,底面是正方形,一个侧面是等腰三角形且与底面垂直。
三视图解题技巧篇

高中数学解题技巧篇—三视图专题晋江一中数学教研组(内部资料,妥善保管)
1)三视图的定义:
正视图:光线从几何体的前面向后面正投影得到的投影图;
侧视图:光线从几何体的左面向右面正投影得到的投影图;
俯视图:光线从几何体的上面向下面正投影得到的投影图。
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
2)结合球、圆柱、圆锥的模型,从正面(自前而后)、侧面(自左而右)、上面(自上而下)三个角度,分别观察,画出观察得出的各种结果.
即正视图、侧视图、俯视图:
3)解题技巧:
4)连线法:。
高考三视图解题对策
t 励 他们一朵小红花 、 一些小 文具 等等 , 这些 都能对学生起 到很
好的激励作用, 使他们以更加积极的态度完成整节课的学习。 分析 : 几何体 由下部为边长 3 , 高 为 2的正六棱柱和上部为半 i
{
径为 1 , 高为 3的圆柱组合而成 。其体积为 :
q-
总之 , 身为一 名小学体育教师 , 我们不应该局限于此 , 还要
2 0 1 3年 8月 2 8日
- _ _ 】
同 考 三视图解题对 策
C=,
文/ 陈海彦 摘 要: 近年来 , 三视 图是高考考察 的重点和热点。 它对学生的空间想 象能力 的要求较高 , 再加上三视 图形式的多样性 , 使部分 学
生望而生畏 , 不知 如 何 下手 。 关 键词 : 三视 图 ; 切割式 ; 挖 空武; 组合式 ; 补体 式; 分 隔 式
例4 . 如 图是某 几何 体 的三 视 图 , 其 中正视 图是 腰长 为 2的
等腰三 角形 , 侧视 图是半 径为 1的半 圆 , 则该 几何体 的表 面积是
( )
陈雁 飞. 点击课 堂Biblioteka 聚焦质量. 高等教 育出版社
( 作者单位 内蒙古白音诺 尔学校)
俯 视 图
分析 : 几何体是一个不规则图形 , 可分割成两个 图形一个三棱
j
分析 : 几何体为一个半 径为 2 , 高为 1的圆柱 的中心又挖去一 锥和一个 四棱锥 , 其体积为 『 _ _ 。
个 半 径 为 手 的 等 高 圆 柱 后 所 得 部 分 , 其 体 积 为 = 盯 [ 2 一 ( 手) ] ×
己想象成小刺猬 , 并进行一 些与之相关 的小游戏 , 如: “ 刺 猬逃 ;
三视图高考题解题技巧

三视图高考题解题技巧
三视图高考题解题技巧
1、主视图和左视图如果都是三角形的必然是椎体,要么是棱锥要么是圆锥。
还有两种特殊的情况:
1、是棱锥和半圆锥的组合体。
2、就是半圆锥。
到底如何如确定就是通过俯视图观察。
(1) 若俯视图是三角形时,就是三棱锥。
(2) 若俯视图是多边形时,就是多棱锥。
(3) 若俯视图是半圆和三角形时,就是是棱锥和半圆锥的组合体。
(4) 若俯视图是半圆时,就是半圆锥。
(5) 注意虚线和实线的意义,虚线代表的是看不到的线,实线代表的是能看的见得都是一种平行投影所创造出来的。
2、三视图求体积时候,先观察主视图和侧视图,注意主视图和侧视图的高一定都是一样的,并且肯定是立体图形的高,先通过观察判定图形到底是什么立体图形,看看到底是棱锥,棱柱,还是组合体,通常的组合体都是较为简单的.组合体,无需过多考虑。
(1) 如果是棱锥的话,就看俯视图是什么图形,判定后算出俯视图的面积即可,应用体积公式。
(2) 如果是棱柱的话,同样看俯视图的图形,求出面积,应用公式即可。
(3) 如果是组合体,要分辨出是哪两种规则图形的组合,分别算出体积相加即可。
高考三视图问题常考题型及处理策略

--参谋高考三视图问题常考题型及处理策略!华中师范大学第一附属中学程季康三视图问题是立体几何的人门内容,也是高考数学中的一个重要考点.翻阅近年来的高考试卷,三视图问题是高考的必考内容;在学习之余,结合近年的高考真题,我总结近年来高考对三视图的考查主要有以下几个 方面,现分类例析,供参考:一、判断几何体的三视图问题给出一个几何体的直观图,然后根据几何体的形 状判断其三视图的问题.由于其难度较小,因此这类 直接判断型问题高考基本没有涉及过.但在2013年和 2014年的高考中,曾以空间直角坐标系中点的坐标来表 示几何体,利用考生的想象能力来判断几何体的三视图 的问题.例1(2014年湖北卷)在如图1所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号为①②③④的四 个图,则该四面体的正视图和俯视图分别为().① ②③④图1(A)①和② (B)③和①(C)④和③ (D)④和②解析:如图2,将四面体放人正方体中,四面体)- 即坐标系中四个点所围成的四面体,显然可以看出 其正视图为④,俯视图为②,故选D.图2""""""""""""""""""""""""""""""""""于基础较为差的学生,笔者则通过“启发式”的教学方 法,引导学生完成“函数性质”的研究,在有必要的情况 下,可以花费2!5分钟的时间,帮助学生复习初中阶段学 过的“一次函数”和“二次函数”的相关性质,在此基础上 在引导学生研究函数性质,进而认识到研究函数性质的 一般方法.综上所述,教科书是课堂教学的主要载体,所以作 为一线的教育工作者,要深人研读教科书,挖掘、提炼蕴 含的化归思想,进而使学生的综合素养和数学技能得到 锻炼和提升.同时,在日常教学的课堂上,教师应在日常 教学过程中有意地反复向学生讲解化归思想方法,使学 生逐渐达到一定的认识高度,最终能自觉地运用.除此 之外,教师还应该注重反思,及时分析学生的反馈信息,不断地创新和完善教学方法,开展具有针对性、目的性的教学,真正地贯彻“以生为本”的教学理念,落实素质教育.参考文献:1. 戴海林.迁移性教学—“等比数列性质的探究”教学设计[J].中小学数学&高中版),2014(04).2. 孙西洋.中学数学化归思想方法的教学策略$J%.江 苏教育,2013(02).3. 任兴发.化归思想在高中函数教学中的应用研究[D].内蒙古师范大学,2013.4. 倪晨旭.例谈化归思想在高中数学解题中的应用[J].新课程(下),2017(06).高中版十炎,?77参谋例2 (2013年全国卷!)一个四面体的顶点在空间 直角坐标系中的坐标分别是(1,〇,1),(1,1,〇), (0,1,1),(0,0,0),画该四面体三视图中的正视图时,以 平面为投影面,则得到正视图可以为(P(A ) (B ) (C ) (D )解析:在空间直角坐标系中,根据点的坐标先画出 四面体的直观图,再以'0(平面为投影面,沿)轴 负半轴方向看去则得到正视图,如图3可以观察得到A 符 合要求,故选A .点评:上述两题给出的均是空间直角坐标系中点的 坐标,直接由点的坐标想象出空间几何体的形状,然 后再判断其三视图,理论上是可以,但实际操作难度 较大;此时将该几何体在空间直角坐标系中还原,则判 断其三视图的问题即可迎刃而解.二、利用几何体的三视图还原几何体并计算纵观近年来的高考试题,大多数试题是先给出几何 体的三视图,要求计算几何体的体积、表面积及其他量. 其中以计算几何体的体积的问题居多,其次是计算几何 体的表面积,有时也会要求计算棱长或其余与几何体有 关的量.1.利用几何体的三视图计算几何体的体积例3 (2017年北京卷)某三棱锥的三视图如图4所示,则该三棱锥的体积为().(A )60(B )30(C )20(D )103_正(主)视图侧(左)视图俯视图图4解析:根据几何体的三视图,还原其直观图,如图5, 可以看出该几何体底面三角形两条直角边长为3和5,高为4,其体积为+=丄丄x 丄x 3x 5x 4=10.故选D .3 3 2点评:对于空间几何体的三视图问题,一般首先要 观察几何体的三视图,找出其特征及数量关系,再还原 该几何体的直观图;在还原几何体的直观图时,对于规 则的几何图形,一般将其放到长方体中来观察特征,进 行还原,最后根据还原后的图形计算几何体中边角关 系.需要注意的是本题中俯视图中的图形不是几何体的 底面,它只是俯视时看到的图形而已.例4 (2017年全国卷!)如图6,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何 体由一平面将一圆柱截去一部分所得,则该几何体的体 积为().(A )90! (B )63!(C )42!(D )36!7\77S一图6解析:由网格纸上的小正方形边长为1可以看出 该几何体的正视图由一个边长为6的正方形和一个直 径为6的半圆组成,其侧视图由一个长为6,宽为4的长 方形和一个直角边长为6的等腰直角三角形组成,其 俯视图是一个直径为6的圆;因此该几何体的下半部 分是一个底面半径为3,高为4的圆柱;上面部分是一 个底面半径为3,高为6的圆柱切去一半所得的部分.所以其体积为:+,+i ++2,!x 32x 4+ x !x 32x 6=3=63!.故2选B .点评:本题将几何体的三视图放人网格纸上,其作 用就是暗示其相关的边长,即相等于告知几何体三视图 中的边长.本题的难点在于利用几何体的正视图和俯视图综合判断几何体的形状.由三视图看出该几何体是两 个圆柱体叠放在一起,其中上面的一个圆柱体被分成相 等的两部分后剩下的其中的一部分.例5 (2015年课标全国卷!)一个正方体被一个平面截去一部分后,剩余部分的三视图如图7所示,则截去78 十•?炎,?高中版--参谋部分体积与剩余部分体积的比值为(2(A31⑶+(C)士(D)士6 5解析:根据题意,该几何体是由一个正方体截去部 分后剩下的图形,由该几何体的三视图还原其直观图得 到正方截去了一个三棱锥(-(a a后的图形如图8所示.易知= ^VABCD-AtBtCtDt,所以66点评:在由三视图还原为空间几何体的实际形状 时,要从三个视图综合考虑,根据三视图的规则,空间几 何体的可见轮廓线在三视图中为实线,不可见轮廓线在 三视图中为虚线.在还原空间几何体实际形状时,一般 以正视图和俯视图为主,结合侧视图进行综合考虑.求 解以三视图为载体的空间几何体的体积的关键是由三 视图确定直观图的形状以及直观图中线面的位置关系 和数量关系,利用相应体积公式求解.2.利用几何体的三视图计算几何体的表面积例6 (2017年全国卷I )某多面体的三视图如图9所示,其中正视图和左视图都由正方形和等腰直角三角 形组成,正方形的边长为2,俯视图为等腰直角三角形. 该多面体的各个面中有若干个是梯形,这些梯形的面积 之和为().(A)10 (B)12 (C)14 (D)16图9 图10解析:根据该几何体的三视图可以看出该几何体是一个三棱锥叠放在一个三棱柱上面形成的,其直观图如 图10所示,从直观图可以看出该几何体有2个全等的梯 形,其上底为2,下底为4,高为2,所以其面积之和为S=2x (2+4)!2!丄=12.故选 B.2点评:对于根据几何体的三视图计算几何体的表面 积问题,一般先要根据几何体的三视图还原其直观图,再根据直观图观察该几何体各个面的形状,从而计算其 表面积.例7 (2016年全国卷")如图11,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该 多面体的表面积为().图 11(A)18+36V T(B)54+18V T(C)90 (D)81解析:根据三视图,可以看出该几何体是一个斜四 棱柱,其底面是一个边长为3的正方形,高为6;其正视 图看到的平行四边形即为该几何体的前面,显然其是 一个平行四边形,底为3,高为6,面积为S1=3x6=18;其 上下两个面是两个边长为3的正方形,每一个面的面积 为S2=3x3=9;其左右两个面是两个竖着放的长方形,底为3,高为正视图中平行四边形的一个边长度为V3W,3 V T,即每一个侧面的面积为.3,3x3 V T,9 V T.综上,该几何体的表面积为.=2(.1+.2+.3)=54+18 V5.故 选B.点评:本题将三视图放在网格中,其目的就是给出 计算所需要的边的长度.本题中几何体的前后两个面和 上下两个面很直观,与其正视图及俯视图类似,但左右 两个侧面是两个竖放的长方形,其高线的长需要引起注 意,防止出错.3.利用几何体的三视图计算几何体中棱长或球体的半径例8 (2017年北京卷)某四棱锥的三视图如图12所 示,则该四棱锥的最长棱的长度为().高中版十炎,?79参谋W—2—H1<—2—H 正(主)视图侧(左)视图俯视图图12A------/2L/图13(a)3!t (C)2V T (b)2!3 (D)2解析:根据该几何体的三视图,还原该几何体如图 13所示,可以看出该几何体是边长为2的正方体中所截 得到部分,其底面是边长为2的正方形,顶点垂直于底 面.显然其最长棱为图中棱&4,其长度为V&*2+*#2+#$2, V22+22+22=2V T.故选 B.点评:本题考查空间几何体三视图的识别及几何体 边角的计算,首先要根据其三视图还原其直观图,再从 其直观图中判断出其中最长的边,最后根据给出的数值 进行计算.例9 (2015年全国卷I )圆柱被一个平面截去一部分后与半球(半径为!)组成 一个几何体,该几何体三视图中的正视图 和俯视图如图14所示.若该几何体的表面 积为 16+2〇!,则 r#( ).(A)1 (B)2 (C)4 (D)8解析:由三视图可知,此组合体的前半 部分是一个底面半径为!,高为2!的半圆柱 (水平放置),后半部分是一个半径为!的半-2r-正视图2r俯视图 图14球,其中半圆柱的一个底面与半球的半个圆面重合,所以此几何体的表面积为2r.2r+ !r2" !r2+!r.2r+222!r2#4r2+5!r2=16+2〇!,解得 r#2.故选 B.点评:本题只给出了三视图中的两部分,解决的关 键仍然是从正视图及俯视图中确定几何体的形状.从正 视图是个圆可以确定该圆柱是横放,从俯视图中的长方 形和半圆型可以确定半球在圆柱的后面,从而利用圆柱 和球体的表面积公式计算出球的半径.4.利用几何体的三视图既计算体积又计算表面积例10 (2016年全国卷I )如图15,某几何体的三视 图是三个半径相等的圆及每个圆中两条互相垂直的半28!径.若该几何体的体积是-,则它的表面积是(图15(A)17! (B)18! (C)20! (D)28!解析:由三视图可以看出该几何体是i个球,设球8的半径为-,则F s l x^4!-3,^,解得-,2,所以它的8 3 3表面积是丄x4!x22+丄x!x22,17!,故选A.84点评:本题解题的突破口在由三视图观察出几何体 的形状,从而根据体积的值计算出球体半径的长度,最 终计算出球体的表面积.例11 (2016年浙江卷)某几何体的三视图如图16所示(单位:cm),则该几何体的表面积是_____cm2,体积是____cm3.W~W<~>1K~~W正视图侧视图俯视图图16图17解析:根据三视图,可以发现该几何体是两个相同 的长方体靠在一起而形成的,它们的底面是边长为2的正方形,高是4,其中一个“站立”,另一个“平躺”.其直观 图如图17所示.所以其表面积为1,2x(2x2x2+2x4x4)-2x 2x2,72(cm2),体积为 F,2x2x2x4,32(cm3).点评:本题考查三视图的识别与几何体的表面积与 体积的计算.先根据三视图还原几何体的直观图,再计 算其表面积与体积'从上面近年来的高考真题可以看出,三视图问题往 往与几何体的体积、表面积以及空间线面关系、角、距离 等问题相结合,解决此类问题的关键是由几何体的三视 图准确确定几何体的形状及其结构特征,然后再根据要 求进行计算.一般说来,其难点主要有两点:一是根据三 视图确定几何体的形状及相关数量关系;二是根据相关 数量关系准确进行计算.只要解决了这两个难点,三视 图问题一般都能迎刃而解.80十•?炎,?高中版。
高中数学 三视图 知识点总结及解题技巧专题汇总

A.
B.
C.
D.
【答案】A
( )
4..(2013 年普通高等学校招生统一考试浙江数学(理)试题(纯 WORD 版))若某几何体
的三视图(单位:cm)如图所示,则此几何体的体积等于________ cm2 .
4
3
3
2 正视图
侧视图
3
俯视图 (第 12 题图)
【答案】24
已有出现 (07 高考广东卷第 17 题)
已知某几何体的俯视图是如图 4 所示的矩形,正视图(或称主视图)是一个底边长为 8, 高为 4 的等腰三角形,侧视图(或称左视图)是一个底边长为 6,高为 4 的等腰三角形.
(1)求该几何体的体积V ; (2)求该几何体的侧面积 S .
解: 由题设可知,几何体是一个高为 4 的四棱锥,其底面是长、宽分别为 8 和 6 的矩
4
4
4
4
第 6 题图
7 如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是 8.已知一个正三棱锥 P-ABC 的主视图如图所示,则此正三棱锥的侧面积等于___________
P 3
6 4
A
C
B
3
3
3
(第 8 题)
1. 6 2. 29 3. 12 4. 1
3
5.
6. 80 7
7. 45
四棱锥的底面边长为 2 ,高为 3 ,所以体积为 1
2
2
32
3
3
3
所以该几何体的体积为 2 2
3
.
3
答案:C
类似题
1.(2009 浙江卷理)若某几何体的三视图(单位: cm )如图所示,则此几何体的体积是 cm3 .
专题34:几何体三视图的解题策略(解析版)

专题34:几何体三视图的解题策略(解析版)一.空间几何体的三视图正视图:光线从几何体的前面向后面正投影得到的投影图;反映了物体的高度和长度 侧视图:光线从几何体的左面向右面正投影得到的投影图;反映了物体的高度和宽度 俯视图:光线从几何体的上面向下面正投影得到的投影图。
反映了物体的长度和宽度 三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”二.空间几何体的直观图斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上) ②建立斜坐标系'''x O y ∠,使'''x O y ∠=450(或1350) ③画对应图形在已知图形平行于X 轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y 轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半; 直观图与原图形的面积关系:42S ⋅=原图形直观图S一,切割法例1.某几何体的三视图如图所示,则该几何体的体积是( )A.20B.24C.18D.16【答案】A【分析】由三视图还原出该几何体的直观图,如图所示,该几何体是一个直三棱柱去掉一个三棱锥得到的,然后计算体积即可【详解】解:由几何体的三视图还原出该几何体的直观图,如图所示.该几何体是一个直三棱柱去掉一个三棱锥得到的.由题中数据可得三棱柱的体积为1344=242⨯⨯⨯,截去的三棱锥的体积为4,故该几何体的体积是20.故选:A【点睛】此题考查由三视图求几何体的体积,需熟记锥体的体积公式,属于基础题.切割法规律总结:1、还原到常见几何体中2、实线当面切,虚线背后切3、切完后对照三视图进行检验二,三点交汇法例2某三棱锥的三视图如图所示,如果网格纸上小正方形的边长为1,则该三棱锥的体积为( )A.4B.8C.12D.24【答案】A【分析】由三视图还原几体何体,可知该几何体是从长为4,宽为4,高为3的长方体中截得(如图),直接由三棱锥的体积公式可得答案.【详解】由三视图还原几体何体如图,三棱锥D ABC-是从长为4,宽为4,高为3的长方体中截得,所以11423432D ABCV-=⨯⨯⨯⨯=故选:A【点睛】此题考查由三视图求多面体的体积,关键是由三视图还原几何体,属于中档题. 三点交汇法规律:三线交汇得顶点,各顶必在其中选多顶可能用不完,个中取舍是关键:三、拔高法例3:3某几何体的三视图如图所示,则该几何体的表面积是( )A .424+B .228+C .428+D .12【答案】B【分析】 由三视图可得此几何体为如图所示的四棱锥,然后求出各个面的面积即可【详解】解:由三视图可得此几何体为如图所示的四棱锥E ABCD -,由题可得,2AB BC CD AD CE =====,22DE BE ==,所以该几何体的表面积为112222222282222⨯+⨯⨯⨯+⨯⨯⨯=+, 故选:B拔高法规律总结:1.标出俯视图所有结点,画出俯视图对应的直观图2.由主、侧视图的左中右找出被拔高的点.四、去点法例4:某四棱锥的三视图如图所示,则该四棱锥的体积是()A.6B.12C.24D.36【答案】B【分析】由三视图可得原图,结合原图,利用四棱锥的体积公式即可得解.【详解】原图如图所示,可得1334=123V=⨯⨯⨯,故选:B.【点睛】本题考查了三视图,考查了利用三视图画直观图,同时考查了锥体的体积公式,属于基础题.去点法规律:画立方体删多余点连剩余点六字真言:先去除、再确定走进高考1.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727B.59C.1027D.13【答案】A 【详解】因为加工前的零件半径为3,高为6,所以体积154Vπ=,又因为加工后的零件,左半部为小圆柱,半径为2,高4,右半部为大圆柱,半径为3,高为2,所以体积2161834Vπππ=+=,所以削掉部分的体积与原体积之比为5434105427πππ-=,故选A.考点:本小题主要考查立体几何中的三视图,考查同学们的空间想象能力.2.2018年全国卷Ⅲ文数高考试题中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A.B.C.D.【答案】A【详解】详解:由题意知,题干中所给的是榫头,是凸出的几何体,求得是卯眼的俯视图,卯眼是凹进去的,即俯视图中应有一不可见的长方形,且俯视图应为对称图形故俯视图为故选A.点睛:本题主要考查空间几何体的三视图,考查学生的空间想象能力,属于基础题.3.2017年全国普通高等学校招生统一考试文科数学(新课标1卷)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是A.B.C.D.【答案】A【解析】对于B,易知AB∥MQ,则直线AB∥平面MNQ;对于C,易知AB∥MQ,则直线AB∥平面MNQ;对于D,易知AB∥NQ,则直线AB∥平面MNQ.故排除B,C,D,选A.点睛:本题主要考查线面平行的判定定理以及空间想象能力,属容易题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.4.2017年全国普通高等学校招生统一考试文科数学(新课标2卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A .90πB .63πC .42πD .36π【答案】B【解析】 由题意,该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱,故其体积为2213634632V πππ=⋅⋅⋅+⋅⋅=,故选B. 点睛:(1)解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.(2)三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.5.2014年全国普通高等学校招生统一考试理科数学如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A .63B .6C .62D .4【答案】B【详解】由正视图、侧视图、俯视图形状,可判断该几何体为四面体,且四面体的长、宽、高均为4个单位,故可考虑置于棱长为4个单位的正方体中研究,如图所示,该四面体为D ABC -,且4AB BC ==, 42AC =,25DB DC ==,2(42)46DA =+=,故最长的棱长为6,选B .6.2016年全国普通高等学校招生统一考试理科数学(全国2卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A .20πB .24πC .28πD .32π【答案】C【解析】 试题分析:由三视图分析可知,该几何体的表面积为圆锥的表面积与圆柱的侧面积之和.,,所以几何体的表面积为.考点:三视图与表面积.7.2016年全国普通高等学校招生统一考试文科数学(新课标3卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.B.C.90D.81【答案】B【解析】【详解】试题分析:解:由已知中的三视图可得:该几何体是一个以俯视图为底面的斜四棱柱,其底面面积为:3×6=18,前后侧面的面积为:3×6×2=36,左右侧面的面积为:,故棱柱的表面积为:.故选:B.点睛:本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键,由三视图判断空间几何体(包括多面体、旋转体和组合体)的结构特征是高考中的热点问题.8.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r = ( )A .1B .2C .4D .8【答案】B【解析】试题分析:由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+="16" + 20π,解得r=2,故选B. 考点:简单几何体的三视图;球的表面积公式;圆柱的测面积公式9.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A .18B .17C .16D .15【答案】D【详解】试题分析:如图所示,截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为,故选D.考点:本题主要考查三视图及几何体体积的计算.10.2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】试题分析:由三视图中的正视图可知,由一个面为直角三角形,左视图和俯视图可知其它的面为长方形.综合可判断为三棱柱.考点:由三视图还原几何体.11.2014年全国普通高等学校招生统一考试文科数学(全国Ⅱ卷)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削的部分的体积与原来毛坯体积的比值为( )A .2717B .95C .2710D .31【答案】C【解析】试题分析:由三视图还原几何体为一个小圆柱和大圆柱组成的简单组合体.其中小圆柱底面半径为2、高为4,大圆柱底面半径为3、高为2,则其体积和为22243234πππ⨯⨯+⨯⨯=,而圆柱形毛坯体积为23654ππ⨯⨯=,故切削部分体积为20π,从而切削的部分的体积与原来毛坯体积的比值为20105427ππ=. 考点:三视图. 12.2020年全国统一高考数学试卷(理科)(新课标Ⅱ)如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为( )A .EB .FC .GD .H【答案】A【分析】根据三视图,画出多面体立体图形,即可求得M 点在侧视图中对应的点.【详解】根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N, ∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选:A【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.13.2020年全国统一高考数学试卷(理科)(新课标Ⅲ)下图为某几何体的三视图,则该几何体的表面积是( )A .6+42B .4+42C .6+23D .4+23【答案】C【分析】 根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.【详解】根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△ 根据勾股定理可得:22AB AD DB ===∴ADB △是边长为22根据三角形面积公式可得:2113sin 60(22)23222ADB S AB AD =⋅⋅︒==△∴该几何体的表面积是:2362332=⨯++故选:C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题.14.2017年全国普通高等学校招生统一考试理科数学(新课标1卷)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A.10B.12C.14D.16【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为12(24)2122⨯+⨯⨯=,故选B.点睛:三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合,解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅱ)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为()A .B .C .D .【答案】D【解析】试题分析:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,∴正方体切掉部分的体积为111111326⨯⨯⨯⨯=,∴剩余部分体积为15166-=,∴截去部分体积与剩余部分体积的比值为15. 故选D .考点:由三视图求体积16.2016年全国普通高等学校招生统一考试理科数学(新课标1卷)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是A .17πB .18πC .20πD .28π【答案】A试题分析:由三视图知,该几何体的直观图如图所示:是一个球被切掉左上角的,即该几何体是个球,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和,即,故选A.【考点】三视图及球的表面积与体积【名师点睛】由于三视图能有效地考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般与几何体的表面积与体积相结合.由三视图还原出原几何体是解决此类问题的关键.17.2016年全国普通高等学校招生统一考试理科数学(新课标2卷)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.B.C.D.【答案】C试题分析:由三视图分析可知,该几何体的表面积为圆锥的表面积与圆柱的侧面积之和。
高考数学中三视图还原空间几何体的解题技巧

高考数学中三视图还原空间几何体的解题技巧考纲解读与命题趋势探究空间立体几何的三视图是高中数学新课程的新增内容之一,也是近几年全国各地高考的热点内容,考纲不仅要求学生掌握『画空间几何体的三视图』还要求掌握它的逆过程,前者比较容易掌握,后者对空间想象力较弱的同学来说往往无从下手,特别是复杂一点的问题更是怎么也想象不出来。
Mr.Yang总结了一个简单可行的方法,虽不能解决所有三视图还原的问题,但对高中阶段的大部分问题都可解决,这里呈现出来,以期抛砖引玉,也请同行斧正。
一、简单几何体的三视图还原规律复杂的几何体是由简单几何体组合而成的,简单几何的分类:柱体(圆柱和棱柱);椎体(圆锥和棱锥);台体(圆台和棱台);球体.要掌握复杂几何体的三视图还原,先要搞清楚简单几何体的三视图还原规律,一般情况下简单几何体的三视图还原有如下规律:1. 三视图中如果其中两个视图是矩形(不要管内部的细节,只要外轮廓线为矩形就称该视图为矩形)那么该空间几何体为柱体.当第三个试图为圆时,该空间几何体为圆柱,否则为棱柱.2. 三视图中如果其中两个视图是三角形(不要管内部的细节,只要外轮廓线为矩形就称该视图为三角形)那么该空间几何体为锥体,当第三个试图为圆时,该空间几何体为圆锥,否则为棱锥.3. 三视图中如果其中两个视图是梯形(不要管内部的细节,只要外轮廓线为矩形就称该视图为梯形)那么该空间几何体为台体.当第三个试图两个同心圆时,该空间几何体为圆台,否则为棱台.球体的三视图很简单,这里就不加论述.以上规律简单好记,按照以上规律解决简单的三视图还原都不在话下,下面举例说明.例1:(2013年全国高考陕西卷理科试题)若某空间几何体的三视图如下,求其体积 .例2:(2012年全国高考江西卷理科试题)若某空间几何体的三视图如下,求其体积()例3:(2014年全国高辽宁卷理科试题)若某空间几何体的三视图如下求其体积()二、叠加式组合体的三视图还原方法组合体的组合形式可分为三种:叠加式、切割式、综合式.切割式与综合式在高中阶段见到的不是很多,这里只对高中阶段出现较多的叠加式组合体的三视图还原方法进行论述.既然组合体是由简单几何体组合而成的,那么就可以“化整为零”,把组合体的三视图划分为一个个简单几何体的三视图,再分别根据这些简单几何体的三视图按照上面论述的简单几何体三视图的还原规律把它们还原成简单几何体,再“积零为整',把这些简单几何体组合在一起就得了组合体的三视图.这样就将复杂的三视图问题转化成最基本的简单几何体的三视图还原问题来解决了,大大降低了对空间想象能力的要求,这一方法的难点在于如何把组合体的三视图划分为一个个简单几何体的三试图,该方法的具体过程如下:1. 分线框.一般从主视图入手,将主视图划分成一个个线框(一般是封闭的线框,但有时也可不完全封闭),这些线框就是组成组合体的一个个简单几何体的主视图.2. 对投影.在俯视图和左视图上把主视图中每个线框对应的投影找出来,主要是根据“长对正,高平齐,宽相等”和'三视图所反映的组合体各部分的方位”来找.3. 识形体.根据每一部分的三视图,逐个想象出每一部分所对应的几何体4. 合起来,想整体. 每一部分的形状确定后,再根据各部分的相对位置关系组合成整个组合体的形状.下面看该方法在高考题中的运用.例4 :(2015年全国高考天津卷试题)一个几何体的三视图如图4所示,则该几何体的体积为 .解析:如图4所示,第一步:分线框. 将主视图分为上面一个直角梯形与下面一个矩形两个线框.第二步:对投影. 这里只须用长对正,高平齐就可找到相对应的投影,如图5和图6中的加粗部分相对应.第三步:识形体. 由简单几何体三视图的还原规律知图5中加粗的三个视图对应的几何体为底面为直角梯形的直四棱柱. 图6中加粗的三个视图对应的几何体为长方体.第四步:合起来,想整体.由主视图知该组合体是一个底面为直角梯形的直四棱柱叠放在一个长方体上面组合而成的,如图7所示,进一步易求几何体体积为30.如果不用此方法,此题对很多同学来说都是一道较难想象的题,但用了以上方法后就可以化整为零,化难为易,将复杂的三视图还原问题转化为基本的简单几何体的三视图还原问题,大大降低了难度.例5 :(2015年全国高考山东卷试题)一个几何体的三视图如下图所示,则该几何体的体积为 .解析:如图下所示,第一步:分线框. 将主视图分为上面一个等腰三角形,下面一个正方形两个线框.第二步:对投影. 利用高平齐知主视图中的三角形与左视图中的三角形相对应,主视图中的正方形与左视图中的正方形相对应,利用长对正知主视图中的三角形与俯视图中的圆和正方形都是对正的,那到底哪一个与它相对应呢?这还要结合三视图所反应的各部分的方位来判断. 主视图中三角形在上,正方形在下,这说明原几何体中三角形所对应的简单几何体在正方形所对应的简单几何体的上面.在俯视图中正方形在圆的里面而且是用实线画的,所以俯视图中正方形所对应的简单几何体在圆所对应的简单几何体的上面.因此主视图中的三角形与俯视图中的正方形相对应,主视图中的正方形与俯视图中的圆相对应,第三步:识形体.由简单几何体三视图的还原规律知两部分所对应的几何体分别为正四棱锥和圆柱. 第四步,合起来想整体,由主视图知该组合体是上面一个正四棱锥下面一个圆柱组合而成的.进一步易求答案为C.。
专题三 三视图问题解题策略

专题三三视图问题解题策略【高考地位】在空间几何体部分,主要是以空间几何体的三视图为主展开,考查空间几何体三视图的识别判断,考查通过三视图给出的空间几何体的表面积和体积的计算等问题. 在高考中主要的题型主要是选择题或者填空题,在难度上也进行了一定的控制,尽管各地有所不同,但基本上都是中等难度或者较易的试题. 因此,牢牢抓住各种空间几何体的结构特征,通过三视图和直观图判断空间几何体的结构,在此基础上掌握好空间几何体的表面积和体积的计算方法.【知识要点】一、三视图相关问题1、画物体的三视图时,要符合如下原则:长对正,高平齐,宽相等.2、要求:能看见的轮廓线和棱用实线,不能看见的轮廓线和棱用虚线表示。
3、位置:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方.一、三视图的还原【典例分析】类型一三视图的识别与还原问题【例1】正方体ABCD﹣A1B1C1D1中E为棱BB1的中点(如图),用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的左视图为( )A B C D【例2】“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如下左图,图中四边形是为体现其直观性所作的辅助线.其实际直观图中四边形不存在,当其正视图和侧视图完全相同时,它的正视图和俯视图分别可能是( )A.,a b B.,a c C.,c b D.,b d类型二以三视图为载体考查空间几何体的表面积、体积等问题【例3】设某几何体的三视图如左下图(尺寸的长度单位为m),则该几何体的体积为3m.【例4】如右上图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6 2 B.6 C.4 2 D.4【例5】已知一个四棱锥的三视图及有关数据如下左图所示,则该几何体的体积为()A.B C D【例6】如上中图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )A.π8B.π225C.π12D.π441【例7】设某几何体的三视图如上右图(尺寸的长度单位为m),则该几何体的体积为.【课后练习】一、选择题1.如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()323221A B C DEFG HA .①②⑥B .①②③C .④⑤⑥D .③④⑤ 2.若某几何体的三视图如图所示,则此几何体的直观图是( )3.已知一三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )4.如左下图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( )A .64288++B .62288++C .6222++D .462221++5.如右上图是一个棱锥的三视图,则此棱锥的体积为( )A .83B .43C .D .6.如左下图是某几何体的三视图,则该几何体的体积是( )A.34 B.38C.328D.3247.某几何体的三视图如图所示,则该几何体的表面积为( )33A.4B.321+C.1233+D.8.已知点E 、F 、G 分别是正方体ABCD -A 1B 1C 1D 1的棱AA 1、CC 1、DD 1的中点,点M 、N 、Q 、P 分别在线段DF 、AG 、BE 、C 1B 1上.以M 、N 、Q 、P 为顶点的三棱锥P -MNQ 的俯视图不可能是( )二、填空题9.一个几何体的正视图和侧视图都是边长为1的正方形,且体积为12,则这个几何体的俯视图可能是下列图形中的________.(填入所有可能的图形前的编号)①锐角三角形;②直角三角形;③四边形;④扇形;⑤圆.10.棱长为2的正方体被一个平面截成两个几何体,其中一个几何体的三视图如左下图所示,那么该几何体的体积是11.某几何体的三视图如右上图所示,则该几何体的体积为 . 12.某几何体的三视图如下图所示,则该几何体的体积为 .9、 . 10、. 11、. 12、.专题三 三视图问题解题策略参考答案【例1】【答案】C【解析】过点A 、E 、C 1的平面截去该正方体的上半部分后,剩余部分的直观图如图,则该几何体的左视图为C ,所以C 选项是正确的。
(经典)高考数学三视图还原方法归纳
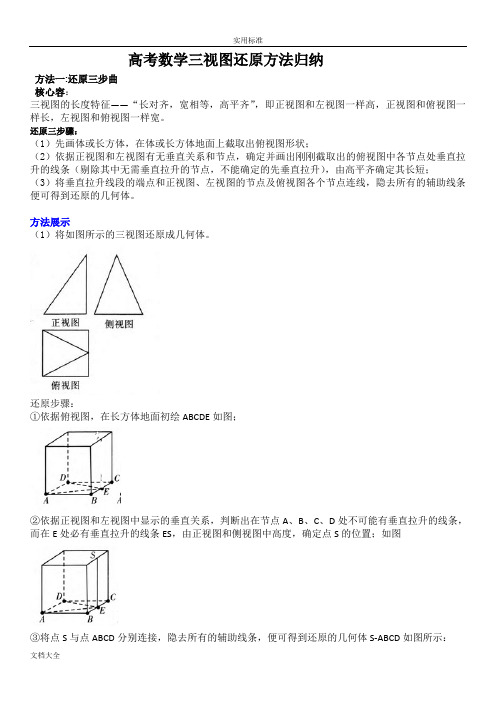
高考数学三视图还原方法归纳方法一:还原三步曲核心容:三视图的长度特征——“长对齐,宽相等,高平齐”,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。
还原三步骤:(1)先画体或长方体,在体或长方体地面上截取出俯视图形状;(2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短;(3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。
方法展示(1)将如图所示的三视图还原成几何体。
还原步骤:①依据俯视图,在长方体地面初绘ABCDE如图;②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D处不可能有垂直拉升的线条,而在E处必有垂直拉升的线条ES,由正视图和侧视图中高度,确定点S的位置;如图③将点S与点ABCD分别连接,隐去所有的辅助线条,便可得到还原的几何体S-ABCD如图所示:经典题型:例题1:若某几何体的三视图,如图所示,则此几何体的体积等于()cm³。
解答:(24)例题2:一个多面体的三视图如图所示,则该多面体的表面积为()答案:21+3计算过程:步骤如下:第一步:在体底面初绘制ABCDEFMN 如图;第二步:依据正视图和左视图中显示的垂直关系,判断出节点E 、F 、M 、N 处不可能有垂直拉升的线条,而在点A 、B 、C 、D 处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点''''',,,,,F E D B G G 地位置如图;第三步:由三视图中线条的虚实,将点G 与点E 、F 分别连接,将'G 与点'E 、'F 分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。
例题3:如图所示,网格纸上小形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )答案:(6)还原图形方法一:若由主视图引发,具体步骤如下:(1)依据主视图,在长方体后侧面初绘ABCM如图:(2)依据俯视图和左视图中显示的垂直关系,判断出在节点A、B、C出不可能有垂直向前拉升的线条,而在M出必有垂直向前拉升的线条MD,由俯视图和侧视图中长度,确定点D的位置如图:(3)将点D与A、B、C分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图所示:2,解:置于棱长为4个单位的体中研究,该几何体为四面体D—ABC,且AB=BC=4,AC=24,DB=DC=5可得DA=6.故最长的棱长为6.方法2若由左视图引发,具体步骤如下:(1)依据左视图,在长方体右侧面初绘BCD如图:(2)依据正视图和俯视图中显示的垂直关系,判断出在节点C、D处不可能有垂直向前拉升的线条,而在B处,必有垂直向左拉升的线条BA,由俯视图和左视图的长度,确定点A的位置,如图:(3)将点A与点B、C、D分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图:方法3:由三视图可知,原几何体的长、宽、高均为4,所以我们可以用一个体做载体还原:(1)根据正视图,在体中画出正视图上的四个顶点的原象所在的线段,用红线表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考有方法——三视图解题超级策略
一、三视图问题的常见类型及解题策略
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意
看到的部分用实线表示,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、
推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确
三视图的形成原理,结合空间想象将三视图还原为实物图.
二、还原三视图的常用方法
1、方体升点法;
2、方体去点法(方体切割法);
3、三线交汇得顶点法
方法一方体升点法
例 1:(2015·北京 ) 某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为 ( ) A.1
D .2
答案 C
解析根据三视图,可知该几何体的直观图为如图所示的四棱锥V- ABCD,其中 VB⊥平面 ABCD,且底面 ABCD是边长为1的正方形, VB=1.所以四棱锥中最长棱为VD.
2 2
连接 BD,易知 BD=2,在 Rt△VBD中,VD=VB+ BD= 3.
跟踪训练 1. 如图所示为三棱锥的三视图,求三棱锥的表面积或体积.
跟踪训练 2. 如图所示为三棱锥的三视图,求三棱锥的表面积或体积.
跟踪训练 3. 如图所示为三棱锥的三视图,求三棱锥的表面积或体积.
方法二方体去点法
例 2:如图所示为三棱锥的三视图,主视图、俯视图是直角边长为2 的等腰直角三
角形,求三棱锥的表面积或体积.
跟踪训练 4. 如图所示为三棱锥的三视图,主视图、侧视图是直
角边长为 4,宽为 3 的直角三角形,求三棱锥的表面积或体积 .
跟踪训练 5. 如图所示为三棱锥的三视图,三视图是直角边长为 4 等
腰直角三角形,虚线为中线,求三棱锥的表面积或体积 .
方法三三线交汇得顶点法
例 3:如图,网格纸上小正方形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是()
A.62B.6C.42D.4
正确答案是 B .
解:由三视图可知,原几何体的长、宽、高均为 4,所以我们可用一个正
方体作为载体对三视图进行还原.先画出一个正方体,如图( 1):
第一步,根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线
段,这里我们用红线表示.如图( 2),即正视图的四个顶点必定是由图
中红线上的点投影而成的.
第二步,侧视图有三个顶点,画出它们的原象所在的线段,用
蓝线表示,如图( 3).
第三步,俯视图有三个顶点,画出它们的原象所在的线段,用
绿线表示,如图( 4).
最后一步,三种颜色线的公共点(只有两种颜色线的交点不行)
即为原几何体的顶点,连接各顶点即为原几何体,如图( 5).至
此,易知哪条棱是最长棱,求出即可
跟踪训练 6.
首先在正方体框架中描出主视图,并将轮廓的边界点平
行延长,如图.
这样就可以找到三个方向的
类似地,将俯视图和侧视图也如法炮制.
交叉点.由这些交
叉点,不难得到直观图.
练习 1、
练习 2、
练
习 1 答 案 : 练习2答案:
跟踪训练 7. 如图所示为四棱锥的三视图, 主视 图是直角边长为 4 等腰
直角三角形,侧视
图是边长为 4 的正方形,求四棱锥的表面积或 体积 .
跟踪训练 8. 如图所示为四棱锥的三视图,主
视图是边长为 4 的正方
形,侧视图是直角边 长为 4 等腰直角三角形,求四棱锥的表面积或体积 . 跟踪训练 9. 如图所示为四棱锥的三视图,主视图是长为 4,高为 5 的长方形,侧视图的
长为 3
D 1 C 1
的长方形,俯视图为直角三角形,求四棱锥的表面积或体积.
三视图练习
A 1
B 1
D
1、若某几何体的三视图如图所示,则此几何体的表面积是
C
_____________. 40 4 2
4
_____________.
A
B
2、某几何体的三视图如图所示,则该几何体的体积为
A
B
2
3、如图,网格纸上小正方形的边长为
1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外
4
) D
C
接球的表面积为(
P
A 、 8
B
、
25
C 、12
D 、
41
2
D
4
4
2 的等腰直角三角形,正视图和俯视图中的虚 4、如图是一个四面体的三视图,这三个视图均是腰长为
线是三角形的中线,则四面体的体积为(
) A
A 、
2
B
、
4
C
、
8
D 、 2
3
3
3
5、一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分
体积与剩余部分体积的比值为 (
)D
(A )
1
(B )
1
(C )
1
(D )
8
7 6
1 5
6、如图,网格纸上正方形小格的边长为 1(表示 1cm ) , 图中粗线画出的是某零件 的三视图,该零件由一个底面半径为
3cm ,高为 6cm 的圆柱体毛坯切削得到,则切
削掉部分的体积与原来毛坯体积的比值为(
) C
A.
17B.
27
5
C.
10D. 1 9
27
3
7、一个四面体的顶点在空间直角坐标系
O xyz 中的坐标分别是 (1,0,1),(1,1,0),(0,1,1),(0,0,0),
z
(0,1,1)
画该四面体三视图中的正视图时, 以 zOx 平面为投影面,则得到正视图可以为 (
)
(1,0,1)
O (0,0,0)
y
x
(1,1,0)
A (A)
(B)
(C)
(D)
8、如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则此几
何体的体积为( B
)
9、在一个几何体的三视图中,正视图和俯视图如左图所示,则相应的侧视图可以
为(
) D
10 、某几何体的三视图如图所示,则该几何体的体积为
_____________.
11、已知某几何体的三视图如图所示,则其体积为或 16
12、若某几何体的三视图如图所示,则这个几何体中最长的棱长等于 33
_____________.
13、某几何体的三视图如图所示,则该几何体的体积为
8
.
2
32
3
14、2某几何体的2
三视图如图所示,则该几何体的体积为
_____________.
3
2
r )组成一个几何体,该几何体
15、圆柱被一个平面截去一部分后与半球(半径为
2
的三视图中的正视图和俯视图如图所示,若该几何体的表面积为
16 20 ,则
r
( B )
(A )1
(B ) 2
(C ) 4
(D )8
16、如图,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三视图,则
该多面体的各条棱中,最长的棱的长度为
( C )
A .6 2
B .4 2
C .6
D .4
A
P
17. 某几何体的三视图如图所示,则该几何体的体积为( A )
A .16 8
B .88
C .16
16
D .816
C
B。
