中考复习平行四边形的证明题专题训练
人教中考数学综合题专题复习【平行四边形】专题解析及答案
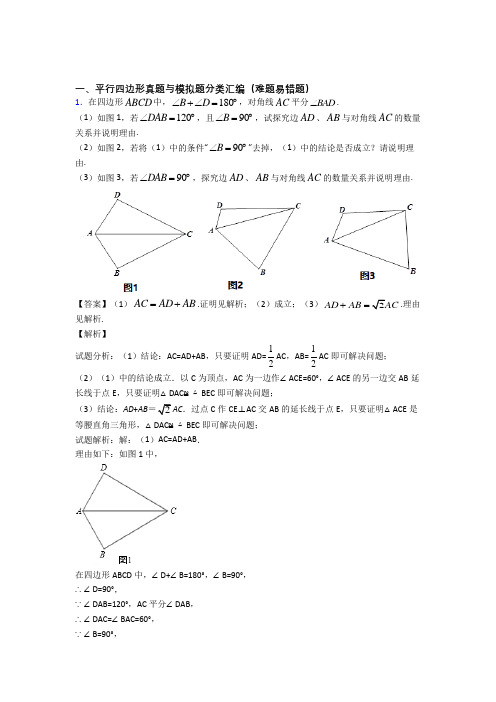
一、平行四边形真题与模拟题分类汇编(难题易错题)1.在四边形ABCD 中,180B D ∠+∠=︒,对角线AC 平分BAD ∠.(1)如图1,若120DAB ∠=︒,且90B ∠=︒,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图2,若将(1)中的条件“90B ∠=︒”去掉,(1)中的结论是否成立?请说明理由.(3)如图3,若90DAB ∠=︒,探究边AD 、AB 与对角线AC 的数量关系并说明理由.【答案】(1)AC AD AB =+.证明见解析;(2)成立;(3)2AD AB AC +=.理由见解析.【解析】试题分析:(1)结论:AC=AD+AB ,只要证明AD=12AC ,AB=12AC 即可解决问题; (2)(1)中的结论成立.以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 延长线于点E ,只要证明△DAC ≌△BEC 即可解决问题;(3)结论:AD +AB =2AC .过点C 作CE ⊥AC 交AB 的延长线于点E ,只要证明△ACE 是等腰直角三角形,△DAC ≌△BEC 即可解决问题;试题解析:解:(1)AC=AD+AB .理由如下:如图1中,在四边形ABCD 中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC 平分∠DAB ,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=12AC,同理AD=12AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠ABC=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CE,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.(3)结论:AD+AB=2AC.理由如下:过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°.∴AC=CE.又∵∠D+∠ABC=180°,∠D=∠CBE,∴△CDA ≌△CBE ,∴AD=BE ,∴AD+AB=AE .在Rt △ACE 中,∠CAB=45°,∴AE =245AC AC cos ︒= ∴2AD AB AC +=.2.在图1中,正方形ABCD 的边长为a ,等腰直角三角形FAE 的斜边AE =2b ,且边AD 和AE 在同一直线上.操作示例当2b <a 时,如图1,在BA 上选取点G ,使BG =b ,连结FG 和CG ,裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH .思考发现小明在操作后发现:该剪拼方法就是先将△FAG 绕点F 逆时针旋转90°到△FEH 的位置,易知EH 与AD 在同一直线上.连结CH ,由剪拼方法可得DH=BG ,故△CHD ≌△CGB ,从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置.这样,对于剪拼得到的四边形FGCH (如图1),过点F 作FM ⊥AE 于点M (图略),利用SAS 公理可判断△HFM ≌△CHD ,易得FH=HC=GC=FG ,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH 是正方形.实践探究(1)正方形FGCH 的面积是 ;(用含a , b 的式子表示)(2)类比图1的剪拼方法,请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图.联想拓展小明通过探究后发现:当b≤a 时,此类图形都能剪拼成正方形,且所选取的点G 的位置在BA 方向上随着b 的增大不断上移.当b >a 时(如图5),能否剪拼成一个正方形?若能,请你在图5中画出剪拼成的正方形的示意图;若不能,简要说明理由.【答案】(1)a2+b2;(2)见解析;联想拓展:能剪拼成正方形.见解析.【解析】分析:实践探究:根据正方形FGCH的面积=BG2+BC2进而得出答案;应采用类比的方法,注意无论等腰直角三角形的大小如何变化,BG永远等于等腰直角三角形斜边的一半.注意当b=a时,也可直接沿正方形的对角线分割.详解:实践探究:正方形的面积是:BG2+BC2=a2+b2;剪拼方法如图2-图4;联想拓展:能,剪拼方法如图5(图中BG=DH=b)..点睛:本题考查了几何变换综合,培养学生的推理论证能力和动手操作能力;运用类比方法作图时,应根据范例抓住作图的关键:作的线段的长度与某条线段的比值永远相等,旋转的三角形,连接的点都应是相同的.3.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.4.如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD 的延长线于点F,连接CF.(1)求证:四边形BCFD是菱形;(2)若AD=1,BC=2,求BF的长.【答案】(1)证明见解析(2)23【解析】(1)∵AF∥BC,∴∠DCB=∠CDF,∠FBC=∠BFD,∵点E为CD的中点,∴DE=EC,在△BCE与△FDE中,FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCE≌△FDE,∴DF=BC,又∵DF∥BC,∴四边形BCDF为平行四边形,∵BD=BC,∴四边形BCFD是菱形;(2)∵四边形BCFD是菱形,∴BD=DF=BC=2,在Rt△BAD中,AB=223BD AD-=,∵AF=AD+DF=1+2=3,在Rt△BAF中,BF=22AB AF+=23.5.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】(1)见解析;(2)能,t=10;(3)t=152或12.【解析】【分析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,∴AB=12AC=12×60=30cm,∵CD=4t,AE=2t,又∵在Rt△CDF中,∠C=30°,∴DF=12CD=2t,∴DF=AE;(2)能,∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;(3)若△DEF为直角三角形,有两种情况:①如图1,∠EDF=90°,DE∥BC,则AD=2AE,即60﹣4t=2×2t,解得:t=152,②如图2,∠DEF=90°,DE⊥AC,则AE=2AD,即2t2(604t)=-,解得:t=12,综上所述,当t=152或12时,△DEF为直角三角形.6.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=1MC,∴EG=CG.2(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.7.(问题发现)(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为;(拓展探究)(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;(解决问题)(3)如图(3)在正方形ABCD中,AB=2,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.【答案】(1)AC垂直平分BD;(2)四边形FMAN是矩形,理由见解析;(3)16+8或16﹣8【解析】【分析】(1)依据点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,即可得出AC 垂直平分BD;(2)根据Rt△ABC中,点F为斜边BC的中点,可得AF=CF=BF,再根据等腰三角形ABD 和等腰三角形ACE,即可得到AD=DB,AE=CE,进而得出∠AMF=∠MAN=∠ANF=90°,即可判定四边形AMFN是矩形;(3)分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,②以点A为旋转中心将正方形ABCD顺时针旋转60°,分别依据旋转的性质以及勾股定理,即可得到结论.【详解】(1)∵AB=AD,CB=CD,∴点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,∴AC垂直平分BD,故答案为:AC垂直平分BD;(2)四边形FMAN是矩形.理由:如图2,连接AF,∵Rt△ABC中,点F为斜边BC的中点,∴AF=CF=BF,又∵等腰三角形ABD和等腰三角形ACE,∴AD=DB,AE=CE,∴由(1)可得,DF⊥AB,EF⊥AC,又∵∠BAC=90°,∴∠AMF=∠MAN=∠ANF=90°,∴四边形AMFN是矩形;(3)BD′的平方为16+8或16﹣8.分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,如图所示:过D'作D'E⊥AB,交BA的延长线于E,由旋转可得,∠DAD'=60°,∴∠EAD'=30°,∵AB=2=AD',∴D'E=AD'=,AE=,∴BE=2+,∴Rt△BD'E中,BD'2=D'E2+BE2=()2+(2+)2=16+8②以点A为旋转中心将正方形ABCD顺时针旋转60°,如图所示:过B作BF⊥AD'于F,旋转可得,∠DAD'=60°,∴∠BAD'=30°,∵AB=2=AD',∴BF=AB=,AF=,∴D'F=2﹣,∴Rt△BD'F 中,BD'2=BF2+D'F2=()2+(2-)2=16﹣8综上所述,BD′平方的长度为16+8或16﹣8.【点睛】本题属于四边形综合题,主要考查了正方形的性质,矩形的判定,旋转的性质,线段垂直平分线的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理进行计算求解.解题时注意:有三个角是直角的四边形是矩形.8.如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC(1)求证:AC是⊙O的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.9.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F 的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP 的最小值.【答案】(1)AE=DF,AE⊥DF;(2)是;(3)成立,理由见解析;(4)CP=QC﹣QP=.【解析】试题分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD 的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.试题解析:(1)AE=DF,AE⊥DF.理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.在△ADE和△DCF中,,∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;(3)成立.理由:由(1)同理可证AE=DF,∠DAE=∠CDF延长FD交AE于点G,则∠CDF+∠ADG=90°,∴∠ADG+∠DAE=90°.∴AE⊥DF;(4)如图:由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,在Rt△QDC中,QC=,∴CP=QC﹣QP=.考点:四边形的综合知识.10.正方形ABCD的边长为1,对角线AC与BD相交于点O,点E是AB边上的一个动点(点E不与点A、B重合),CE与BD相交于点F,设线段BE的长度为x.(1)如图1,当AD=2OF时,求出x的值;(2)如图2,把线段CE绕点E顺时针旋转90°,使点C落在点P处,连接AP,设△APE 的面积为S,试求S与x的函数关系式并求出S的最大值.【答案】(1)x=﹣1;(2)S=﹣(x﹣)2+(0<x<1),当x=时,S的值最大,最大值为,.【解析】试题分析:(1)过O作OM∥AB交CE于点M,如图1,由平行线等分线段定理得到CM=ME,根据三角形的中位线定理得到AE=2OM=2OF,得到OM=OF,于是得到BF=BE=x,求得OF=OM=解方程,即可得到结果;(2)过P作PG⊥AB交AB的延长线于G,如图2,根据已知条件得到∠ECB=∠PEG,根据全等三角形的性质得到EB=PG=x,由三角形的面积公式得到S=(1﹣x)•x,根据二次函数的性质即可得到结论.试题解析:(1)过O作OM∥AB交CE于点M,如图1,∵OA=OC,∴CM=ME,∴AE=2OM=2OF,∴OM=OF,∴,∴BF=BE=x,∴OF=OM=,∵AB=1,∴OB=,∴,∴x=﹣1;(2)过P作PG⊥AB交AB的延长线于G,如图2,∵∠CEP=∠EBC=90°,∴∠ECB=∠PEG,∵PE=EC,∠EGP=∠CBE=90°,在△EPG与△CEB中,,∴△EPG≌△CEB,∴EB=PG=x,∴AE=1﹣x,∴S=(1﹣x)•x=﹣x2+x=﹣(x﹣)2+,(0<x<1),∵﹣<0,∴当x=时,S的值最大,最大值为,.考点:四边形综合题。
备战中考数学—平行四边形的综合压轴题专题复习含答案

备战中考数学—平行四边形的综合压轴题专题复习含答案一、平行四边形1.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.【答案】(1)①证明见解析;②AG⊥BE.理由见解析;(2)证明见解析;(3)∠BHO=45°.【解析】试题分析:(1)①根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;②根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;(2)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立;(3)如答图2所示,与(1)同理,可以证明AG⊥BE;过点O作OM⊥BE于点M,ON⊥AG于点N,构造全等三角形△AON≌△BOM,从而证明OMHN为正方形,所以HO 平分∠BHG,即∠BHO=45°.试题解析:(1)①∵四边形ABCD为正方形,∴DA=DC,∠ADB=∠CDB=45°,在△ADG和△CDG中,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCG;②AG⊥BE.理由如下:∵四边形ABCD为正方形,∴AB=DC,∠BAD=∠CDA=90°,在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF,∵∠DAG=∠DCG,∴∠DAG=∠ABE,∵∠DAG+∠BAG=90°,∴∠ABE+∠BAG=90°,∴∠AHB=90°,∴AG⊥BE;(2)由(1)可知AG⊥BE.如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.∴∠MON=90°,又∵OA⊥OB,∴∠AON=∠BOM.∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,∴∠OAN=∠OBM.在△AON与△BOM中,∴△AON≌△BOM(AAS).∴OM=ON,∴矩形OMHN为正方形,∴HO平分∠BHG.(3)将图形补充完整,如答图2示,∠BHO=45°.与(1)同理,可以证明AG⊥BE.过点O作OM⊥BE于点M,ON⊥AG于点N,与(2)同理,可以证明△AON≌△BOM,可得OMHN为正方形,所以HO平分∠BHG,∴∠BHO=45°.考点:1、四边形综合题;2、全等三角形的判定与性质;3、正方形的性质2.如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M 沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.(1)P点的坐标为多少(用含x的代数式表示);(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.【答案】(1)P点坐标为(x,3﹣x).(2)S的最大值为,此时x=2.(3)x=,或x=,或x=.【解析】试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.(3)本题要分类讨论:①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN 的长,联立CN的表达式即可求出x的值.试题解析:(1)过点P作PQ⊥BC于点Q,有题意可得:PQ∥AB,∴△CQP∽△CBA,∴∴解得:QP=x,∴PM=3﹣x,由题意可知,C(0,3),M(x,0),N(4﹣x,3),P点坐标为(x,3﹣x).(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,NC边上的高为,其中,0≤x≤4.∴S=(4﹣x)×x=(﹣x2+4x)=﹣(x﹣2)2+.∴S的最大值为,此时x=2.(3)延长MP交CB于Q,则有PQ⊥BC.①若NP=CP,∵PQ⊥BC,∴NQ=CQ=x.∴3x=4,∴x=.②若CP=CN,则CN=4﹣x,PQ=x,CP=x,4﹣x=x,∴x=;③若CN=NP,则CN=4﹣x.∵PQ=x,NQ=4﹣2x,∵在Rt△PNQ中,PN2=NQ2+PQ2,∴(4﹣x)2=(4﹣2x)2+(x)2,∴x=.综上所述,x=,或x=,或x=.考点:二次函数综合题.3.操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)连接AE,求证:△AEF是等腰三角形;猜想与发现:(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.结论1:DM、MN的数量关系是;结论2:DM、MN的位置关系是;拓展与探究:(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【答案】(1)证明参见解析;(2)相等,垂直;(3)成立,理由参见解析.【解析】试题分析:(1)根据正方形的性质以及等腰直角三角形的知识证明出CE=CF,继而证明出△ABE≌△ADF,得到AE=AF,从而证明出△AEF是等腰三角形;(2)DM、MN的数量关系是相等,利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直,利用三角形外角性质和等腰三角形两个底角相等性质,及全等三角形对应角相等即可得出结论;(3)成立,连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=AE,利用三角形全等证出AE=AF,而DM=AF,从而得到DM,MN数量相等的结论,再利用三角形外角性质和三角形全等,等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°.从而得到DM、MN的位置关系是垂直.试题解析:(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,∴△AEF是等腰三角形;(2)DM、MN的数量关系是相等,DM、MN的位置关系是垂直;∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN 是△AEF的中位线,∴AE=2MN,∵AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°,∴DM⊥MN;(3)(2)中的两个结论还成立,连接AE,交MD于点G,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=AE,由已知得,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF,∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=AF,∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.所以(2)中的两个结论还成立.考点:1.正方形的性质;2.全等三角形的判定与性质;3.三角形中位线定理;4.旋转的性质.4.在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.(1)如图①,当点D落在BC边上时,求点D的坐标;(2)如图②,当点D落在线段BE上时,AD与BC交于点H.①求证△ADB≌△AOB;②求点H的坐标.(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).【答案】(1)D(1,3);(2)①详见解析;②H(175,3);(3)30334-≤S 30334+【解析】【分析】(1)如图①,在Rt△ACD中求出CD即可解决问题;(2)①根据HL证明即可;②,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,根据AH2=HC2+AC2,构建方程求出m即可解决问题;(3)如图③中,当点D在线段BK上时,△DEK的面积最小,当点D在BA的延长线上时,△D′E′K的面积最大,求出面积的最小值以及最大值即可解决问题;【详解】(1)如图①中,∵A(5,0),B(0,3),∴OA=5,OB=3,∵四边形AOBC是矩形,∴AC=OB=3,OA=BC=5,∠OBC=∠C=90°,∵矩形ADEF是由矩形AOBC旋转得到,∴AD=AO=5,在Rt△ADC中,CD=22=4,AD AC∴BD=BC-CD=1,∴D(1,3).(2)①如图②中,由四边形ADEF是矩形,得到∠ADE=90°,∵点D在线段BE上,∴∠ADB=90°,由(1)可知,AD=AO,又AB=AB,∠AOB=90°,∴Rt△ADB≌Rt△AOB(HL).②如图②中,由△ADB≌△AOB,得到∠BAD=∠BAO,又在矩形AOBC中,OA∥BC,∴∠CBA=∠OAB,∴∠BAD=∠CBA,∴BH=AH,设AH=BH=m,则HC=BC-BH=5-m,在Rt△AHC中,∵AH2=HC2+AC2,∴m2=32+(5-m)2,∴m=17,5∴BH=175,∴H(175,3).(3)如图③中,当点D在线段BK上时,△DEK的面积最小,最小值=12•DE•DK=12×3×(5-342)=303344-,当点D在BA的延长线上时,△D′E′K的面积最大,最大面积=12×D′E′×KD′=12×3×(5+342)=303344+.综上所述,303344-≤S≤303344+.【点睛】本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建方程解决问题.5.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【答案】(1)见解析;(2)18°.【解析】【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【详解】(1)证明:∵AO=CO,BO=DO∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.【点睛】本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.6.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.7.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E ,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。
九年级中考数学专题复习-平行四边形专题
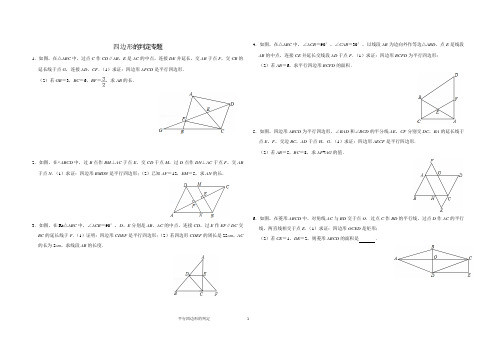
四边形的判定专题1.如图,在△ABC中,过点C作CD∥AB,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若GB=3,BC=6,BF =,求AB的长.2.如图,在▱ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB 于点N.(1)求证:四边形BMDN是平行四边形;(2)已知AF=12,EM=5,求AN的长.3.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25cm,AC 的长为5cm,求线段AB的长度.4.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.(1)求证:四边形BCFD为平行四边形;(2)若AB=6,求平行四边形BCFD的面积.5.如图,四边形ABCD为平行四边形,∠BAD和∠BCD的平分线AE,CF分别交DC,BA的延长线于点E,F,交边BC,AD于点H,G.(1)求证:四边形AECF是平行四边形.(2)若AB=5,BC=8,求AF+AG的值.6.如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,则菱形ABCD的面积是.7.如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD 的平分线于点E、F.(1)若CE=8,CF=6,求OC的长;(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.8.如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD =°时,四边形BECD 是矩形.9.如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.(1)求tan∠DBC的值;(2)求证:四边形OBEC是矩形.10.如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.12.如图,矩形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E、F.(1)求证:四边形BEDF是平行四边形;(2)只需添加一个条件,即,可使四边形BEDF为菱形.13.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.14.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD、AC、BC于点E、O、F,连接CE 和AF.(1)求证:四边形AECF为菱形;(2)若AB=4,BC=8,求菱形AECF的周长.15.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.16.如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C作CE∥AB交DO的延长线于点E,连接AE.(1)求证:四边形AECD是菱形;(2)若四边形AECD的面积为24,tan∠BAC =,求BC的长.17.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.(1)求证:四边形AECD是菱形;(2)若AB=6,BC=10,求EF的长.18.如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC =,tan∠DCB=3,求菱形AEBD 的面积.19.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.20.如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.21.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.22.如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.(1)求证:AF=CE;(2)若DE=2,BE=4,求sin∠DAF的值.23.如图,已知▱ABCD中,AB=AC,CO⊥AD,垂足为点O,延长CO、BA交于点E,联结DE.(1)求证:四边形ACDE是菱形;(2)联结OB,交AC于点F,如果OF=OC,求证:2AB2=BF•BO.24.如图,在▱ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,且AE=AF.(1)求证:▱ABCD是菱形;(2)若∠EAF=60°,CF=2,求菱形ABCD的面积.25.如图,菱形ABCD 的边长为,对角线AC、BD交于O,且DE∥AC,AE∥BD.(1)判断四边形AODE的形状并给予证明;(2)若四边形AODE的周长为14,求四边形AODE的面积.26.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,F是AD的中点,连接EC.(1)求证:四边形ADCE是平行四边形;27.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.(1)求证:四边形OBCE是平行四边形;(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.。
中考复习平行四边形的证明题专题训练

∵G,H分别为OA,OC的中点,∴OG= OA,OH= OC,∴OG=OH.
又∵AB∥CD,∴∠1=∠2.
在△OEB和△OFD中,
∠1=∠2,OB=OD,∠3=∠4,
∴△OEB≌△OFD,
∴OE=OF.∴四边形EHFG为平行四边形.
又由AB∥DC,得∠AED=∠EDC∴∠EDC=∠BFC,∴ME∥NF∴四边形MFNE为平行四边形.
7、解答:证明:连接AC交BD于点O,
∵四边形ABCD为平行四边形,∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.∴四边形AECF为平行四边形.
8、解答:证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
(2)若四边形APQB是平行四边形,则AP=BQ,∴t=30﹣2t∴t=10∴10秒后四边形APQB是平行四边形
11、解答:证明:∵D、E、F分别是△ABC各边的中点,根据中位线定理知:
DE∥AC,DE=AF,
EF∥AB,EF=AD,
∴四边形ADEF为平行四边形.故AE与DF互相平分.
12、解答:证明:∵▱ABCD中,对角线AC交BD于点O,∴OB=OD,
30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.
1、解答:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,∵AE⊥BD于E,CF⊥BD于F,
∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(A.A.S.),∴BE=DF;
∴OE=OF,OA=OC,AE∥CF,∴∠DFO=∠BEO,∠FDO=∠EBO,
中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)一、综合题1.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.(1)求证:DE=CF;(2)若AC=6cm,AB=10cm,求四边形DCFE的面积.2.已知△ABC内接于⊙O,AB是⊙O的直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;(2)若AD与⊙O相切,求∠B.3.已知:如图,点D在ΔABC的边AB上,CF//AB,DF交AC于E,EA=EC.(1)如图1,求证:CD=AF;(2)如图2,若AD=BD,请直接写出和ΔBDC面积相等的三角形.4.如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF//BE,过点C作CG⊥AB交AB的延长线于点G.(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=25,∠CBG=45°,BC=4√2,则▱ABCD的面积是.5.已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.(1)求证:△AFD≌△CEB;(2)四边形ABCD是平行四边形吗?请说明理由.6.如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)设ACBD=k,当k为何值时,四边形DEBF是矩形?请说明理由.7.如图,在ΔABC中,点D、E、F分别在AB、AC、BC上,DE // BC,EF // AB.(1)求证:ΔADE∽ΔEFC;(2)如果AB=6,AD=4,求SΔADESΔEFC的值.8.如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.BC,9.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=12连接CD和EF .(1)求证:DE=CF;(2)求EF的长.10.如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.(1)求证:四边形DEBC是平行四边形;(2)若BD=9,求DH的长.11.已知锐角△ABC内接于⊙O,AD⊥BC于点D,连接AO.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,CE⊥AB于点E,交AD于点F,过点O作OH⊥BC于点H,求证:AF=2OH;,BC=2√15,求AC的长.(3)如图3,在(2)的条件下,若AF=AO,tan∠BAO=1312.如图,抛物线y=x2+bx+c与x轴交于点A(−1,0),B(5,0),与y轴交于点C.(1)求抛物线的解析式和顶点D的坐标.(2)连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F(F在E的右侧),过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长.13.如图,CD是⊙O的直径,点A是⊙O外一点,AD与⊙O相切于点D,点B是⊙O上一点(点B不与点C,D重合),连接AO,AB,BC .(1)当BC与AO满足什么位置关系时,AB是⊙O的切线?请说明理由;(2)在(1)的条件下,当∠DAO=度时,四边形AOCB是平行四边形.(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足14.如图,已知函数y= kx为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点EOD,求a、b的值;(1)若AC= 32(2)若BC∥AE,求BC的长.15.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.16.如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起,使点A与点F重合,点C与点D重合(如图),其中∠ACB=∠DFE=90°,发现四边形ABDE是平行四边形.如图,小华继续将图中的纸片Rt△DEF沿AC方向平移,连结AE,BD,当点F与点C重合时停止平移.(1)请问:四边形ABDE是平行四边形吗?说明理由.cm时,请判断四边形ABDE的形(2)如图,若BC=EF=6cm,AC=DF=8cm,当AF=92状,并说明理由.参考答案与解析1.【答案】(1)证明:在△CDE 和△ECF 中,∵∠ACB=∠ECF=90°,点D 、E 是分别是AB 、BC 的中点.∴CD=BD=AD ,∴∠B=∠DCE ,∠CED=∠ECF=90°, 又∵∠FEC=∠B ..∠FEC=∠DCE ,又∵CE=EC .∴△CDE ≌△ECF (ASA ),∴DE=CF ;(2)解:在Rt △ABC 中,∵∠ACB=90°,∴BC=√AB 2−AC 2=√102−62=8cm , ∵点D 、E 分别是AB 、BC 的中点,∴DE ∥CF ,又DE=CF , ∴四边形DCFE 是平行四边形,∴DE=12AC=12×6=3cm ,CE=12BC=12×8=4cm , ∴S 四边形DCFE =DE ×CE=3×4=12cm . 2.【答案】(1)证明:∵OA =OC =AD , ∴∠OCA =∠OAC ,∠AOD =∠ADO , ∵OD ∥AC , ∴∠OAC =∠AOD ,∴180°﹣∠OCA ﹣∠OAC =180°﹣∠AOD ﹣∠ADO , 即∠AOC =∠OAD , ∴OC ∥AD , ∵OD ∥AC ,∴四边形OCAD 是平行四边形;(2)解:∵AD 与⊙O 相切,OA 是半径, ∴∠OAD =90°, ∵OA =OC =AD , ∴∠AOD =∠ADO =45°,∵OD∥AC,∴∠OAC=∠AOD=45°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠B=45°.3.【答案】(1)证明:∵CF//AB∴∠DFC=∠ADF,∠DAC=∠ACF又∵EA=EC∴ΔADE≌ΔCFE(AAS)∴CF=AD又∵CF//AD∴四边形ADCF为平行四边形∴DC=AF(有一组对边平行且相等的四边形为平行四边形)(2)解:ΔADC,ΔADF,ΔCFD,ΔCFA∵AD=BD,∴SΔADC=SΔBDC (等底等高面积相等)∵四边形ADCF是平行四边形,∴SΔADC=SΔCDF=SΔADF=SΔACFF (等底等高面积相等) .故与ΔBDC面积相等的三角形为:ΔADC,ΔADF,ΔCFD,ΔCFA.4.【答案】(1)证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE,∵DF//BE,∴∠DFA=∠BEC,∵DF=BE,∴ΔADF≅ΔCBE(SAS),∴AD=CB,∠DAF=∠BCE,∴AD//CB,四边形ABCD是平行四边形(2)245.【答案】(1)证明:∵DF∥BE,∴∠DFA=∠BEC,在△ADF和△CBE中{DF=BE∠DFA=∠BECAF=CE,∴△AFD≌△CEB(SAS).(2)解:四边形ABCD是平行四边形,理由如下:∵△AFD≌△CEB,∴AD=CB,∠DAF=∠BCE,∴AD∥BC,∴四边形ABCD是平行四边形.6.【答案】(1)证明:如图,连接DE,BF,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵E,F分别是OA,OC的中点,∴OE=12OA=12OC=OF,∴四边形DEBF是平行四边形,∴BE=DF .(2)解:由(1)已证:四边形DEBF是平行四边形,要使平行四边形DEBF是矩形,则BD=EF,∵OE=12OA=12OC=OF,∴EF=OE+OF=12OA+12OC=OA=12AC,即AC=2EF,∴k=ACBD =2EFEF=2,故当k=2时,四边形DEBF是矩形. 7.【答案】(1)证明:∵DE//BC,EF//AB,∴∠A=∠CEF,∠AED=∠C,∴△ADE∽△EFC.(2)解:∵AB=6,AD=4,∴DB=6-4=2,∵DE//BC,EF//AB,∴四边形DBFE是平行四边形,∴EF=DB=2,∵△ADE∽△EFC,SΔADE SΔEFC =(ADEF)2=(42)2=4.8.【答案】(1)证明∵四边形ABCD是平行四边形(已知),∴BC∥AD(平行四边形的对边相互平行)。
八年级平行四边形专题练习(含答案)

中考专题复习平行四边形知识考点:理解并掌握平行四边形的判定和性质 精典例题:【例1】已知如图:在四边形ABCD 中,AB =CD ,AD =BC ,点E 、F 分别在BC 和AD 边上,AF =CE ,EF 和对角线BD 相交于点O ,求证:点O 是BD 的中点。
分析:构造全等三角形或利用平行四边形的性质来证明BO =DO 略证:连结BF 、DE在四边形ABCD 中,AB =CD ,AD =BC ∴四边形ABCD 是平行四边形 ∴AD ∥BC ,AD =BC 又∵AF =CE∴FD ∥BE ,FD =BE ∴四边形BEDF 是平行四边形∴BO =DO ,即点O 是BD 的中点。
【例2】已知如图:在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形EFGH 是平行四边形。
分析:欲证四边形EFGH 是平行四边形,根据条件需从边上着手分析,由E 、F 、G 、H 分别是各边上的中点,可联想到三角形的中位线定理,连结AC 后,EF 和GH 的关系就明确了,此题也便得证。
(证明略)变式1:顺次连结矩形四边中点所得的四边形是菱形。
变式2:顺次连结菱形四边中点所得的四边形是矩形。
变式3:顺次连结正方形四边中点所得的四边形是正方形。
变式4:顺次连结等腰梯形四边中点所得的四边形是菱形。
变式5:若AC =BD ,AC ⊥BD ,则四边形EFGH 是正方形。
变式6:在四边形ABCD 中,若AB =CD ,E 、F 、G 、H 分别为AD 、BC 、BD 、AC 的中点,求证:EFGH 是菱形。
娈式6图娈式7图变式7:如图:在四边形ABCD 中,E 为边AB 上的一点,△ADE 和△BCE 都是等边三角形,P 、Q 、M 、N 分别是AB 、BC 、CD 、DA 边上的中点,求证:四边形PQMN 是菱形。
例1图 O F E D CB A 例2图探索与创新:【问题】已知如图,在△ABC 中,∠C =900,点M 在BC 上,且BM =AC ,点N 在AC 上,且AN =MC ,AM 和BN 相交于P ,求∠BPM 的度数。
平行四边形专题证明题33道-含答案

图1 平行四边形专题练习1.如果边长分别为4cm 和5cm 的矩形与一个正方形的面积相等,那么这个正方形的边长为______cm .2.(08贵阳市)如图1,正方形ABCD 的边长为4cm ,则图中阴影部分的面积为 cm 2.3.若四边形ABCD 是平行四边形,请补充条件 (写一个即可),使四边形ABCD 是菱形.4.在平行四边形ABCD 中,已知对角线AC 和BD 相交于点O ,△ABO 的周长为17,AB =6,那么对角线AC +BD =5.以正方形ABCD 的边BC 为边做等边△BCE ,则∠AED 的度数为 .6.已知菱形ABCD 的边长为6,∠A =60°,如果点P 是菱形内一点,且PB =PD =2那么AP 的长为 .7.在平面直角坐标系中,点A 、B 、C 的坐标分别是A(-2,5),B(-3,-1),C(1,-1),在第一象限内找一点D ,使四边形ABCD 是平行四边形,那么点D 的坐标是 .二、选择题(每题3分,共30分)8.如图2在平行四边形ABCD 中,∠B=110°,延长AD 至F ,延长CD 至E ,连结EF ,则∠E +∠F =( )A .110°B .30°C .50°D .70°图2 图3 图49.菱形具有而矩形不具有的性质是 ( )A .对角相等B .四边相等C .对角线互相平分D .四角相等10.如图3所示,平行四边形ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( )A .3 cmB .6 cmC .9 cmD .12 cm11.已知:如图4,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若AB =2,AD =4,则图中阴影部分的面积为 ( )A .8B .6C .4D .3E AF D C B H G12.将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形④等边三角形⑤等腰直角三角形( )A.①③⑤B.②③⑤C.①②③D.①③④⑤13.如图5所示,是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )A.88 mm B.96 mm C.80 mm D.84 mm图5 图614、(08甘肃省白银市)如图6所示,把矩形ABCD沿EF对折后使两部分重合,若150∠=,∠=()则AEFA.110° B.115°C.120° D.130°15、四边形ABCD,仅从下列条件中任取两个加以组合,使得ABCD是平行四边形,一共有多少种不同的组合?()AB∥CD BC∥AD AB=CD BC=ADA.2组B.3组C.4组D.6组16、下列说法错误的是()A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C. 对角线互相垂直的平行四边形是正方形.D.四个角都相等的四边形是矩形.三、解答题17、如图7,四边形ABCD是菱形,对角线AC=8 cm ,BD=6 cm, DH⊥AB于H,求:DH的长。
平行四边形证明典型题

平行四边形证明典型题1.如下图,已知平行四边形ABCD,E为AD上的点,且AE=AB,BE和CD的延长线交于F,且∠BFC=40°,求平行四边形ABCD各内角的度数.2.已知平行四边形一组邻角的比是2∶3,求它的四个内角的度数.3.如下图所示,ABCD是平行四边形,以AD、BC为边在形外作等边三角形ADE和CBF,连结BD、EF,且它们相交于O,求证:EO=FO,DO=BO.4.已知:平行四边形ABCD中,AD=2AB,延长AB到F,使BF=AB,延长BA到E使AE=AB,求证:CE⊥DF5.如图所示,已知平行四边形ABCD,直线FH与AB、CD相交,过A、B、C、D向FH作垂线,垂足为E、H、G、F,求证:AE-DF=CG-BH6.平行四边形ABCD中,E为DC中点,延长BE与AD的延长线交于F,求证:E为BF中点,D为AF的中点.7.如图所示,平行四边形ABCD中,以BC、CD为边向内作等边三角形BCE和CDF.求证:△AEF为等边三角形.8.如图所示,在△ABC中,BD平分∠B,DE∥BC交AB于E,EF∥AC交BC于F,求证:BE=FC9.如图所示,平行四边形ABCD中,E是AB的中点,F是CD中点,分别延长BA和DC到G、H,使AG=CH,连结GF、EH,求证:GF∥EH10.如图所示,平行四边形ABCD中,E、F分别在AD、BC上,且AE=CF,AF与BE相交于G,CE与DF相交于H.求证:EF与GH互相平分11.在四边形ABCD中,AB∥DC,对角线AC、BD交于O,EF过O交AB于E,交DC于F,且OE=OF,求证:四边形ABCD是平行四边形.12.如图所示,已知△ABC,分别以AB、BC、AC为边向BC同侧作等边三角形ABE、BCD、ACF.求证:DEAF为平行四边形.13.已知:如下图,在四边形ABCD中,AB=DC,AE⊥BD,CF⊥BD,垂足分别是E、F,AE=CF,求证:四边形ABCD是平行四边形.14.点O是平行四边形ABCD的对角线的交点,△AOB的面积为7cm2,求平行四边形ABCD 的面积.15.有两个村庄A和B位于一条河的两岸,假定河岸是两条平行的直线,现在要在河上架一座与河岸垂直的桥PQ,问桥应架在何处,才能使从A到B总的路程最短.【中考真题演练】1.(河南省中考题)已知:如图,平行四边形ABCD中,对角线AC的平行线MN分别交DA、DC延长线于点M、N,交AB、BC于点P、Q.求证:MQ=NP.2.(黄冈市中考题)如图所示,平行四边形ABCD中,G、H是对角线BD上两点,且DG=BH,DF=BE.求证:四边形EHFG是平行四边形.3.(江西省中考题)已知:如图,平行四边形ABCD中,AE⊥BC,CF⊥BD,垂足分别为E、F,G、H分别是AD、BC的中点,GH交BD于点O.求证:GH与EF互相平分.。
中考数学专题复习《以平行四边形为背景的计算与证明》经典题型讲解

中考数学专题复习《以平行四边形为背景的计算与证明》经典题型讲解类型之一 以平行四边形为背景的计算与证明【经典母题】已知:如图Z11-1,在▱ABCD 中,AC 是对角线,BE⊥AC ,DF ⊥AC ,垂足分别为E ,F .求证:BE =DF .证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠BAE =∠DCF .又∵BE ⊥AC ,DF ⊥AC ,∴∠AEB =∠CFD ,∵AB =CD ,∴Rt △AEB ≌Rt △CFD ,∴BE =DF .【思想方法】 (1)平行四边形是一种特殊的四边形,它具有对边平行且相等,对角线互相平分的性质,根据平行四边形的性质可以解决一些有关的计算或证明问题;(2)平行四边形的判定有四种方法:两组对边平行;两组对边分别相等;一组对边平行且相等;对角线互相平分.【中考变形】1.[2016·益阳]如图Z11-2,在▱ABCD 中,AE ⊥BD 于点E ,CF ⊥BD 于点F ,连结AF ,CE .求证:AF =CE .证明:∵四边形ABCD 是平行四边形,∴AD =BC ,∠ADB =∠CBD .又∵AE ⊥BD ,CF ⊥BD , 图Z11-1图Z11-2∴∠AED =∠CFB ,AE ∥CF .∴△AED ≌△CFB (AAS ).∴AE =CF .∴四边形AECF 是平行四边形.∴AF =CE .2.[2016·黄冈]如图Z11-3,在▱ABCD 中,E ,F 分别为边AD ,BC 的中点,对角线AC 分别交BE ,DF 于点G ,H .求证:AG =CH .证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠ADF =∠CFH ,∠EAG =∠FCH ,∵E ,F 分别为AD ,BC 边的中点,∴AE =DE =12AD ,CF =BF =12BC ,∵AD =BC ,∴AE =CF =DE =BF .∵DE ∥BF ,∴四边形BFDE 是平行四边形,∴BE ∥DF ,∴∠AEG =∠ADF ,∴∠AEG =∠CFH ,在△AEG 和△CFH 中,⎩⎪⎨⎪⎧∠EAG =∠FCH ,AE =CF ,∠AEG =∠CFH ,∴△AEG ≌△CFH (ASA ),∴AG =CH .【中考预测】[2016·义乌模拟]如图Z11-4,已知E ,F 分别是▱ABCD的边BC ,AD 上的点,且BE =DF .(1)求证:四边形AECF 是平行四边形;(2)若四边形AECF 是菱形,且BC =10,∠BAC =90°,图Z11-3图Z11-4求BE的长.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形;(2)如答图,∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠BAC=90°,中考预测答图∴∠3=90°-∠2,∠4=90°-∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE =12BC=5.类型之二以矩形、菱形或正方形为背景的计算与证明【经典母题】如图Z11-5,在菱形ABCD中,E,F分别是BC,CD的中点,且AE⊥BC,AF⊥CD.求菱形各个内角的度数.图Z11-5 经典母题答图解:如答图,连结AC.∵四边形ABCD是菱形,AE⊥BC,AF⊥CD且E,F分别为BC,CD的中点,∴AC=AB=AD=BC=CD,∴△ABC,△ACD均为等边三角形,∴菱形ABCD 的四个内角度数分别为∠B =∠D =60°,∠BAD =∠BCD =120°.【思想方法】 要掌握矩形、菱形、正方形的性质和判定方法,采用类比法,比较它们的区别和联系.对于矩形的性质,重点从“四对”入手,即从对边、对角、对角线及对称轴入手;判定菱形可以从一般四边形入手,也可以从平行四边形入手;正方形既具有矩形的性质又具有菱形的性质.【中考变形】1.[2017·日照]如图Z11-6,已知BA =AE =DC ,AD =EC ,CE ⊥AE ,垂足为E .(1)求证:△DCA ≌△EAC ;(2)只需添加一个条件,即__AD =BC __,可使四边形ABCD为矩形.请加以证明.解:(1)证明:在△DCA 和△EAC 中,⎩⎪⎨⎪⎧DC =EA ,AD =CE ,AC =CA ,∴△DCA ≌△EAC (SSS );(2)添加AD =BC ,可使四边形ABCD 为矩形.理由如下:∵AB =DC ,AD =BC ,∴四边形ABCD 是平行四边形,∵CE ⊥AE ,∴∠E =90°,由(1)得△DCA ≌△EAC ,∴∠D =∠E =90°,∴四边形ABCD 为矩形.故答案为AD =BC (答案不唯一).2.[2017·白银]如图Z11-7,矩形ABCD 中,AB =6,BC=4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F .(1)求证:四边形BEDF 是平行四边形; 图Z11-6图Z11-7(2)当四边形BEDF 是菱形时,求EF 的长.解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴AB ∥DC ,OB =OD ,∴∠OBE =∠ODF ,在△BOE 和△DOF 中,⎩⎪⎨⎪⎧∠OBE =∠ODF ,OB =OD ,∠BOE =∠DOF ,∴△BOE ≌△DOF (ASA ),∴EO =FO ,∴四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,BD ⊥EF ,设BE =x ,则 DE =x ,AE =6-x ,在Rt △ADE 中,DE 2=AD 2+AE 2,∴x 2=42+(6-x )2,解得x =133,∵BD =AD 2+AB 2=213,∴OB =12BD =13,∵BD ⊥EF ,∴OE =BE 2-OB 2=2133,∴EF =2EO =4133.3.[2017·盐城]如图Z11-8,矩形ABCD 中,∠ABD ,∠CDB 的平分线BE ,DF 分别交边AD ,BC 于点E ,F .(1)求证:四边形BEDF 是平行四边形;(2)当∠ABE 为多少度时,四边形BEDF 是菱形?请说明理由.解:(1)证明:∵四边形ABCD 是矩形,∴AB ∥DC ,AD ∥BC ,∴∠ABD =∠CDB ,∵BE 平分∠ABD ,DF 平分∠BDC ,∴∠EBD =12∠ABD ,∠FDB =12∠BDC ,图Z11-8∴∠EBD=∠FDB,∴BE∥DF,又∵AD∥BC,∴四边形BEDF是平行四边形;(2)当∠ABE=30°时,四边形BEDF是菱形,理由:∵BE平分∠ABD,∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,∵四边形ABCD是矩形,∴∠A=90°,∴∠EDB=90°-∠ABD=30°,∴∠EDB=∠EBD=30°,∴EB=ED,又∵四边形BEDF是平行四边形,∴四边形BEDF是菱形.4.[2016·株洲]如图Z11-9,在正方形ABCD中,BC=3,E,F分别是CB,CD延长线上的点,DF=BE,连结AE,AF,过点A作AH⊥ED于H点.(1)求证:△ADF≌△ABE;(2)若BE=1,求tan∠AED的值.解:(1)证明:正方形ABCD中,∵AD=AB,∠ADC=∠ABC=90°,∴∠ADF=∠ABE=90°,在△ADF与△ABE中,AD=AB,∠ADF=∠ABE,DF=BE,∴△ADF≌△ABE(SAS);(2)在Rt△ABE中,∵AB=BC=3,BE=1,∴AE=10,ED=CD2+CE2=5,∵S△AED=12ED·AH=12AD·BA=92,图Z11-9∴AH =95, 在Rt △AHD 中,DH =AD 2-AH 2=125,∴EH =ED -DH =135,∴tan ∠AED =AH EH =913.5.[2017·上海]已知:如图Z11-10,四边形ABCD 中,AD∥BC ,AD =CD ,E 是对角线BD 上一点,且EA =EC .(1)求证:四边形ABCD 是菱形;(2)如果BE =BC ,且∠CBE ∶∠BCE =2∶3,求证:四边形ABCD 是正方形.证明:(1)在△ADE 与△CDE 中,⎩⎪⎨⎪⎧AD =CD,DE =DE ,EA =EC ,∴△ADE ≌△CDE (SSS ),∴∠ADE =∠CDE ,∵AD ∥BC ,∴∠ADE =∠CBD ,∴∠CDE =∠CBD ,∴BC =CD ,∵AD =CD ,∴BC =AD ,∴四边形ABCD 为平行四边形,∵AD =CD ,∴四边形ABCD 是菱形;(2)∵BE =BC ,∴∠BCE =∠BEC ,∵∠CBE ∶∠BCE =2∶3,∴∠CBE =180×22+3+3=45°,∵四边形ABCD 是菱形,∴∠ABE =45°,∴∠ABC =90°,∴四边形ABCD 是正方形.图Z11-106.如图Z11-11,正方形ABCD的边长为8 cm,E,F,G,H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过某一定点,说明理由;(3)求四边形EFGH面积的最小值.图Z11-11中考变形6答图解:(1)证明:∵四边形ABCD是正方形,∴∠A=∠B=90°,AB=DA,∵AE=DH=BF,∴BE=AH,∴△AEH≌△BFE(SAS),∴EH=FE,∠AHE=∠BEF,同理,FE=GF=HG,∴EH=FE=GF=HG,∴四边形EFGH是菱形,∵∠A=90°,∴∠AHE+∠AEH=90°,∴∠BEF+∠AEH=90°,∴∠FEH=90°,∴四边形EFGH是正方形;(2)直线EG经过正方形ABCD的中心.理由:如答图,连结BD交EG于点O.∵四边形ABCD是正方形,∴AB∥DC,AB=DC,∴∠EBD=∠GDB,∵AE=CG,∴BE=DG,∵∠EOB=∠GOD,∴△EOB≌△GOD(AAS),∴BO=DO,即O为BD的中点,∴直线EG经过正方形ABCD的中心;(3)设AE=DH=x,则AH=8-x,在Rt△AEH中,EH2=AE2+AH2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,∵S四边形EFGH=EH·EF=EH2,∴四边形EFGH面积的最小值为32 cm2.【中考预测】如图Z11-12,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连结DF.图Z11-12(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定点E的位置,使∠EFD=∠BCD,并说明理由.解:(1)证明:∵AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC.∵AB=AD,∠BAF=∠DAF,AF=AF,∴△ABF≌△ADF(SAS),∴∠AFB=∠AFD.又∵∠CFE=∠AFB,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD.又∵∠BAC=∠DAC,∴∠DAC=∠ACD,∴AD=CD.∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当BE⊥CD时,∠EFD=∠BCD.理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF.又∵CF为公共边,∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF.∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠CBF+∠BCD=∠CDF+∠EFD,∴∠EFD=∠BCD.。
【精编版】数学中考专题训练——平行四边形的判定和性质

中考专题训练——平行四边形的判定和性质1.如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.(1)求证:△ABE≌△CDF.(2)求证:四边形AECF是平行四边形.2.如图,在▱ABCD中,E是AD的中点,F是BC延长线上一点,且CF=BC,连接CE、DF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DF的长.3.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:四边形DCFE是平行四边形;(2)求EF的长.4.如图,E、F是▱ABCD对角线AC上两点,且AE=CF.(1)求证:四边形BFDE是平行四边形.(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?(3)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?5.如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE ∥BD,EF⊥BC,CF=.(1)求证:四边形ABDE是平行四边形;(2)求AB的长.6.在△ABC中,AD为BC边上的中线,E为AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.(1)如图1,求证:四边形ADCF是平行四边形;(2)如图2,连接DF交AC于点G,连接EG,当∠BAC=90°,在不添加任何辅助线和字母的情况下,直接写出图中所有长度为2EG的线段.7.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.(1)求证:四边形AFHD为平行四边形;(2)若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.8.如图,过△ABC的顶点C作CD∥AB,E是AC的中点,连接DE并延长,交线段AB于点F,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若AB=4,∠BAC=60°,∠DCB=135°,求AC的长.9.如图,△ABC是等边三角形,AD是BC边上的高.点E在AB的延长线上,连接ED,∠AED=30°,过A作AF⊥AB与ED的延长线交于点F,连接BF,CF,CE.(1)求证:四边形BECF为平行四边形;(2)若AB=6,请直接写出四边形BECF的周长.10.如图,四边形ABCD中,点E在AD上,且EA=EB,∠ADB=∠CBD=90°,∠AEB+∠C=180°.(1)求证:四边形BCDE是平行四边形.(2)若AB=,DB=4.求四边形ABCD的面积.11.如图所示,在△ABC中,点D为边AB的中点,点E为AC边上一点,延长ED交AE 的平行线于点F,连接AF、BE.(1)猜想四边形AEBF的形状,并证明你的结论.(2)若BE⊥CE,CE=2AE=4,BC=9,求DE的长.12.已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.(1)如图1,求证:四边形ACEF是平行四边形;(2)如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的倍.13.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长到点F,使BF =BE,连接EC并延长到点H,使CH=CE,连接FH,点G在FH上,∠ADG=∠AFG,连接DG.(1)求证:四边形AFGD为平行四边形;(2)在不添加任何辅助线的情况下,直接写出图中长度为FH的一半的所有线段.14.已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.(1)求证:四边形ADCN是平行四边形.(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外).15.如图,在▱ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.(1)求证:四边形AFCE是平行四边形;(2)若去掉已知条件“∠DAB=∠60°”,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.16.如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)(1)当t为何值时,四边形ABQP是平行四边形?(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.17.如图1,在△ABC中,D是BC边上一点,且CD=BD,E是AD的中点,过点A作BC 的平行线交CE的延长线于F,连接BF.(1)求证:四边形AFBD是平行四边形;(2)如图2,若AB=AC=13,BD=5,求四边形AFBD的面积.18.如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,两个点同时出发,当有一个点到达终点时,另一点也随之停止运动.点G为BD上的一点,假设移动时间为t秒,BG的长度为y.(1)证明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和BG的长度y.19.在△ABC中,AB=AC,点P为△ABC为所在平面内一点,过点P分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点E.(1)当点P在BC边上(如图1)时,请探索线段PE,PF,AB之间的数量关系式为.(2)当点P在△ABC内(如图2)时,线段PD,PE,PF,AB之间有怎样的数量关系,请说明理由.(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB之间有怎样的数量关系,直接写出结论.20.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)在(1)的条件下,若BC的延长线交DF于点Q,连接QA与QE.试说明QA=QE.参考答案与试题解析1.如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.(1)求证:△ABE≌△CDF.(2)求证:四边形AECF是平行四边形.【分析】(1)根据平行四边形的性质得出AB=CD,∠B=∠D,根据SAS证出△ABE≌△CDF;(2)根据全等三角形的对应边相等即可证得.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,在△ABE和△CDF中,∴△ABE≌△CDF(SAS);(2)∵BE=DF,∴AF=CE,∵AF∥CE,∴四边形AECF是平行四边形.2.如图,在▱ABCD中,E是AD的中点,F是BC延长线上一点,且CF=BC,连接CE、DF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DF的长.【分析】(1)只要证明DE=CF,DE∥CF即可解决问题;(2)过D作DH⊥BE于H,想办法求出DH、HF即可解决问题;【解答】解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,又∵E是AD的中点,∴DE=AD,∵CF=BC∴DE=CF,又∵AD∥BC,∴四边形CEDF是平行四边形.(2)过D作DH⊥BE于H,在▱ABCD中,∵∠B=60°,AB∥CD,∴∠DCF=60°,∵AB=4,∴CD=4,∴CH=2,DH=2,∴FH=1,在Rt△DHF中,DF==.3.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF =BC,连接CD和EF.(1)求证:四边形DCFE是平行四边形;(2)求EF的长.(1)直接利用三角形中位线定理得出DE∥BC,DE=BC,进而得出DE=FC;【分析】(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长.【解答】(1)证明:∵D、E分别为AB、AC的中点,∴DE为△ABC的中位线,∴DE∥BC,DE=BC∵延长BC至点F,使CF=BC,∴DE=FC,∵DE∥FC,∴四边形DCFE是平行四边形.(2)解:∵DE∥FC,DE=FC∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF==.4.如图,E、F是▱ABCD对角线AC上两点,且AE=CF.(1)求证:四边形BFDE是平行四边形.(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?(3)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?【分析】(1)方法一:证明△BAE≌△DCF,推出BE=DF,BE∥DF即可.方法二:连接BD,交AC于点O.只要证明OE=OF,OB=OD即可;(2)是平行四边形.只要证明△BAE≌△DCF即可解决问题;(3)四边形BFDE不是平行四边形.因为把条件AE=CF改为BE=DF后,不能证明△BAE与△DCF全等;【解答】(1)证法一:∵ABCD是平行四边形∴AB=CD且AB∥CD(平行四边形的对边平行且相等)∴∠BAE=∠DCF又∵AE=CF∴△BAE≌△DCF(SAS)∴BE=DF,∠AEB=∠CFD∴∠BEF=180°﹣∠AEB∠DFE=180°﹣∠CFD即:∠BEF=∠DFE∴BE∥DF,而BE=DF∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)证法二:连接BD,交AC于点O.∵ABCD是平行四边形∴OA=OC OB=OD(平行四边形的对角线互相平分)又∵AE=CF∴OA﹣AE=OC﹣CF,即OE=OF∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)(2)四边形BFDE是平行四边形∵ABCD是平行四边形∴AB=CD且AB∥CD(平行四边形的对边平行且相等)∴∠BAE=∠DCF∵BE⊥AC,DF⊥AC∴∠BEA=∠DFC=90°,BE∥DF∴△BAE≌△DCF(AAS)∴BE=DF∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)(3)四边形BFDE不是平行四边形因为把条件AE=CF改为BE=DF后,不能证明△BAE与△DCF全等.5.如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE ∥BD,EF⊥BC,CF=.(1)求证:四边形ABDE是平行四边形;(2)求AB的长.【分析】(1)根据平行四边形的判定定理即可得到结论;(2)由(1)知,AB=DE=CD,即D是CE的中点,在直角△CEF中利用三角函数即可求得到CE的长,则求得CD,进而根据AB=CD求解.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,即AB∥DE,∵AE∥BD,∴四边形ABDE是平行四边形;(2)解:∵EF⊥BC,∴∠EFC=90°.∵AB∥EC,∴∠ECF=∠ABC=60°,∴∠CEF=30°∵CF=,∴CE=2CF=2,∵四边形ABCD和四边形ABDE都是平行四边形,∴AB=CD=DE,∴CE=2AB,∴AB=.6.在△ABC中,AD为BC边上的中线,E为AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.(1)如图1,求证:四边形ADCF是平行四边形;(2)如图2,连接DF交AC于点G,连接EG,当∠BAC=90°,在不添加任何辅助线和字母的情况下,直接写出图中所有长度为2EG的线段.【答案】(1)证明见解析;(2)CD,AF,BD,AD,CF.【分析】(1)由E是AD的中点,过点A作AF∥BC,易证得△AFE≌△DBE,然后证得AF=BD=CD,即可证得四边形ADCF是平行四边形;(2)根据平行四边形的性质和直角三角形的性质解答即可.【解答】(1)证明:∵E是AD的中点,∴AE=ED,∵AF∥BC,∴∠AFE=∠DBE,∠F AE=∠BDE,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS),∴AF=BD,∵AD是BC边中线,∴CD=BD,∴AF=CD,∴四边形CDAF是平行四边形;(2)解:∵四边形CDAF是平行四边形,∴AG=GC,AD=CF,∵E为AD的中点,∴EG是△ADC的中位线,∴2EG=DC,∵∠BAC=90°,AD为BC边上的中线,∴BD=DC=AD,由(1)可知,CD=AF=BD=2EG,即所有长度为2EG的线段是CD,AF,BD,AD,CF.7.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.(1)求证:四边形AFHD为平行四边形;(2)若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.(1)由平行四边形的性质得出AD=BC,AD∥BC;证明BC是△EFG的中位线,【分析】得出BC∥FG,BC=FG,证出AD∥FH,AD=FH,由平行四边形的判定方法即可得出结论;(2)由平行四边形的性质得出∠BCE=50°,再由等腰三角形的性质得出∠CBE=∠CEB,根据三角形内角和定理即可得出结果.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=FG,∵H为FG的中点,∴FH=FG,∴BC∥FH,BC=FH,∴AD∥FH,AD=FH,∴四边形AFHD是平行四边形;(2)解:∵∠BAE=70°,∴∠BCD=70°,∵∠DCE=20°,∴∠BCE=70°﹣20°=50°,∵CB=CE,∴∠CBE=∠CEB=(180°﹣50°)=65°.8.如图,过△ABC的顶点C作CD∥AB,E是AC的中点,连接DE并延长,交线段AB于点F,连接AD,CF.(1)求证:四边形AFCD是平行四边形.(2)若AB=4,∠BAC=60°,∠DCB=135°,求AC的长.【分析】(1)先证△AEF≌△CED(AAS),得AF=CD,再由CD∥AB,即AF∥CD,即可得出结论;(2)过C作CM⊥AB于M,先证△BCM是等腰直角三角形,得BM=CM,再由含30°角的直角三角形的性质得AC=2AM,BM=CM=AM,由AM+BM=AB求出AM=2﹣2,即可求解.【解答】(1)证明:∵E是AC的中点,∴AE=CE,∵CD∥AB,∴∠AFE=∠CDE,在△AEF和△CED中,,∴△AEF≌△CED(AAS),∴AF=CD,又∵CD∥AB,即AF∥CD,∴四边形AFCD是平行四边形;(2)解:过C作CM⊥AB于M,如图所示:则∠CMB=∠CMA=90°,∵CD∥AB,∴∠B+∠DCB=180°,∴∠B=180°﹣135°=45°,∴△BCM是等腰直角三角形,∴BM=CM,∵∠BAC=60°,∴∠ACM=30°,∴AC=2AM,BM=CM=AM,∵AM+BM=AB,∴AM+AM=4,解得:AM=2﹣2,∴AC=2AM=4﹣4.9.如图,△ABC是等边三角形,AD是BC边上的高.点E在AB的延长线上,连接ED,∠AED=30°,过A作AF⊥AB与ED的延长线交于点F,连接BF,CF,CE.(1)求证:四边形BECF为平行四边形;(2)若AB=6,请直接写出四边形BECF的周长.【分析】(1)根据等边三角形的性质可得BD=DC,∠BAD=∠CAD=30°,然后证明△ADF为等边三角形,可得ED=DF,进而可以证明四边形BECF为平行四边形;(2)根据AB=6和勾股定理可得BF的长,然后证明BE=BD,进而可得四边形BECF 的周长.【解答】(1)证明:∵AD是等边△ABC的BC边上的高,∴BD=DC,∠BAD=∠CAD=30°,∵∠AED=30°,∴ED=AD,∠ADF=∠AED+∠EAD=60°,∵AF⊥AB,∴∠DAF=90°﹣∠EAD=90°﹣30°=60°,∴△ADF为等边三角形,∴AD=DF,∵ED=AD,∴ED=DF,∵BD=DC,∴四边形BECF为平行四边形;(2)∵AB=6,∴BD=3,AD=3,∵△ADF为等边三角形,∴AF=AD=3,∴BF===3,∵∠ABC=60°,∠AED=30°,∴∠BDE=30°,∴BE=BD=3,∴四边形BECF的周长为:2(BF+BE)=2(3+3)=6+6.10.如图,四边形ABCD中,点E在AD上,且EA=EB,∠ADB=∠CBD=90°,∠AEB+∠C=180°.(1)求证:四边形BCDE是平行四边形.(2)若AB=,DB=4.求四边形ABCD的面积.【分析】(1)根据∠ADB=∠CBD=90°,可得DE∥CB,由∠AEB+∠C=180°.证明BE∥CD,进而可得四边形BEDC是平行四边形;(2)根据勾股定理先求出AD的长,再设DE=x,则EA=AD﹣DE=8﹣x,EB=EA=8﹣x.根据勾股定理列式计算得x的值,进而可以求出四边形ABCD的面积.【解答】解:(1)∵∠ADB=∠CBD=90°,∴DE∥CB,∵∠AEB+∠C=180°,∵∠AEB+∠BED=180°,∴∠C=∠BED,∴∠CDB=∠EBD,∴BE∥CD,∴四边形BEDC是平行四边形;(2)∵四边形BEDC是平行四边形.∴BC=DE,在Rt△ABD中,由勾股定理得,AD===8.设DE=x,则EA=AD﹣DE=8﹣x,∴EB=EA=8﹣x.在Rt△BDE中,由勾股定理得,DE2+DB2=EB2,∴x2+42=(8﹣x)2.解得x=3.∴BC=DE=3,∴S四边形ABCD=S△ABD+S△BDC=AD•DB+DB•BC=16+6=22.11.如图所示,在△ABC中,点D为边AB的中点,点E为AC边上一点,延长ED交AE 的平行线于点F,连接AF、BE.(1)猜想四边形AEBF的形状,并证明你的结论.(2)若BE⊥CE,CE=2AE=4,BC=9,求DE的长.【分析】(1)根据已知条件证明△AED≌△BFD,可得ED=FD,可得四边形AEBF是平行四边形;(2)根据BE⊥CE,可得四边形AEBF是矩形,根据CE=2AE=4,BC=9,再利用勾股定理即可求DE的长.【解答】解:(1)四边形AEBF是平行四边形,证明:∵点D为边AB的中点,∴AD=BD,∵AE∥BF,∴∠AED=∠BFD,在△AED和△BFD中,,∴△AED≌△BFD(AAS),∴ED=FD,∵AD=BD,∴四边形AEBF是平行四边形;(2)∵BE⊥CE,∴∠AEB=90°,∴平行四边形AEBF是矩形,∴EF=AB,DE=AB,在Rt△BEC中,CE=4,BC=9,根据勾股定理,得BE2=BC2﹣CE2=92﹣42=65,在Rt△ABE中,AE=2,BE2=65,根据勾股定理,得AB===,∴DE=AB=.12.已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.(1)如图1,求证:四边形ACEF是平行四边形;(2)如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的倍.【分析】(1)由三角形的中位线定理可证得DE∥AC,由直角三角形斜边中线定理得到CE=AB,根据平行线的性质定理和等腰三角形的性质证得∠F=∠CED,进而得到AF∥CE,根据平行四边形的判定即可证得四边形ACEF是平行四边形;(2)根据直角三角形的性质得到AC=AB,由(1)知CE=AB,求得AC=CE,推出四边形ACEF为菱形,得到AE⊥CF,根据直角三角形的性质即可得到结论.【解答】(1)证明:∵BD=CD,BE=AE,∴DE∥AC,∴∠AEF=∠EAC,∠CED=∠ECA,∵∠ACB=90°,BE=AE,∴CE=AE,∴∠EAC=∠ECA,∵AF=AE,∴∠F=∠AEF,∴∠F=∠CED,∴AF∥CE,∴四边形ACEF是平行四边形;(2)解:∵∠ACB=90°,∠B=30°,∴AC=AB,由(1)知CE=AB,∴AC=CE=BE,又∵四边形ACEF为平行四边形∴四边形ACEF为菱形,∴AE⊥CF,∵CE=BE,∴∠B=∠DCE=30°,∴∠BED=∠BAC=60°,∵DF∥AC,∠BDE=∠ACB=∠CDE=90°,∴BD=CD=DE,∵∠DEB=∠FEG=∠CEG=60°,∴∠CED=60°,∴∠FEG=∠CED,∵EF=CE,∠EGF=∠CDE=90°,∴△EFG≌△CED(AAS),∴EG=DE,FG=CD,∴FG=DE,∵CG=FG,∴CG=DE,∴等于线段DE的长度的倍的线段是FG,CG,CD,DB.13.如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长到点F,使BF =BE,连接EC并延长到点H,使CH=CE,连接FH,点G在FH上,∠ADG=∠AFG,连接DG.(1)求证:四边形AFGD为平行四边形;(2)在不添加任何辅助线的情况下,直接写出图中长度为FH的一半的所有线段.【分析】(1)只要证明AD∥FG,AF∥DG即可;(2)根据三角形的中位线的性质和平行四边形的性质即可得到结论.【解答】(1)证明:如图,∵EB=BF,EC=CH,∴BC∥FH,BC=FH,∵四边形ABCD是平行四边形,∴AD∥BC,∴AD∥FH,∴∠DAF+∠AFG=180°,∵∠ADG=∠AFG,∴∠DAF+∠ADG=180°,∴AF∥CD,∴四边形AFHD是平行四边形;(2)∵四边形ABCD为平行四边形,∴AD=BC,∵BF=BE,CH=CE,∴BC=FH,∴AD=FH,∵四边形AFHD是平行四边形,∴FG=AD=FH,∴HG=FH,∴长度为FH的一半的所有线段为:AD,BC,FG,HG.14.已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.(1)求证:四边形ADCN是平行四边形.(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外).【分析】(1)由CN∥AB,MA=MC,易证得△AMD≌△CMN,则可得MD=MN,即可证得:四边形ADCN是平行四边形.(2)由∠AMD=2∠MCD,可证得四边形ADCN是矩形,又由∠ACB=90°,AC=BC,可得四边形ADCN是正方形,继而求得答案.【解答】(1)证明:∵CN∥AB,∴∠DAM=∠NCM,在△ADM和△CNM中,,∴△AMD≌△CMN(ASA),∴MD=MN,∴四边形ADCN是平行四边形.(2)解:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC,∴MC=MD,∴AC=DN,∴▱ADCN是矩形,∵AC=BC,∴AD=BD,∵∠ACB=90°,∴CD=AD=BD=AB,∴▱ADCN是正方形,∴AN=AD=BD=CD=CN.15.如图,在▱ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.(1)求证:四边形AFCE是平行四边形;(2)若去掉已知条件“∠DAB=∠60°”,(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.【分析】(1)由已知条件可得△AED,△CFB是正三角形,可得∠AEC=∠BFC=60°,∠EAF=∠FCE=120°,所以四边形AFCE是平行四边形.(2)上述结论还成立,可以证明△ADE≌△CBF,可得∠AEC=∠BFC,∠EAF=∠FCE,所以四边形AFCE是平行四边形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,∠DCB=∠DAB=60°.∴∠ADE=∠CBF=60°.∵AE=AD,CF=CB,∴△AED,△CFB是正三角形.∴∠AEC=∠BFC=60°,∠EAF=∠FCE=120°.∴四边形AFCE是平行四边形.(2)解:上述结论还成立.证明:∵四边形ABCD是平行四边形,∴DC∥AB,∠CDA=∠CBA,∠DCB=∠DAB,AD=BC,DC=AB.∴∠ADE=∠CBF.∵AE=AD,CF=CB,∴∠AED=∠ADE,∠CFB=∠CBF.∴∠AED=∠CFB.又∵AD=BC,在△ADE和△CBF中.,∴△ADE≌△CBF(AAS).∴∠AED=∠BFC,∠EAD=∠FCB.又∵∠DAB=∠BCD,∴∠EAF=∠FCE.∴四边形EAFC是平行四边形.16.如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)(1)当t为何值时,四边形ABQP是平行四边形?(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.【分析】(1)求出AP=BQ和AP∥BQ,根据平行四边形的判定得出即可;(2)求出高AM和ON的长度,求出△DOC和△OQC的面积,再求出答案即可.【解答】解:(1)当t=2.5s时,四边形ABQP是平行四边形,理由是:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD=3cm,AD=BC=5cm,AO=CO,BO=OD,∴∠P AO=∠QCO,在△APO和△CQO中∴△APO≌△CQO(ASA),∴AP=CQ=2.5cm,∵BC=5cm,∴BQ=5cm﹣2.5cm=2.5cm=AP,即AP=BQ,AP∥BQ,∴四边形ABQP是平行四边形,即当t=2.5s时,四边形ABQP是平行四边形;(2)过A作AM⊥BC于M,过O作ON⊥BC于N,∵AB⊥AC,AB=3cm,BC=5cm,∴在Rt△ABC中,由勾股定理得:AC=4cm,∵由三角形的面积公式得:S△BAC==,∴3×4=5×AM,∴AM=2.4(cm),∵ON⊥BC,AM⊥BC,∴AM∥ON,∵AO=OC,∴MN=CN,∴ON=AM=1.2cm,∵在△BAC和△DCA中∴△BAC≌△DCA(SSS),∴S△DCA=S△BAC==6cm2,∵AO=OC,∴△DOC的面积=S△DCA=3cm2,当t=4s时,AP=CQ=4cm,∴△OQC的面积为 1.2cm×4cm=2.4cm2,∴y=3cm2+2.4cm2=5.4cm2.17.如图1,在△ABC中,D是BC边上一点,且CD=BD,E是AD的中点,过点A作BC 的平行线交CE的延长线于F,连接BF.(1)求证:四边形AFBD是平行四边形;(2)如图2,若AB=AC=13,BD=5,求四边形AFBD的面积.【分析】(1)根据全等三角形的性质和判定求出AF=CD,求出AF=BD,根据平行四边形的判定推出即可;(2)求出四边形AFBD的矩形,根据勾股定理求出AD,根据矩形的面积公式求出即可.【解答】(1)证明:∵AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AFE和△DCE中∴△AFE≌△DCE(AAS),∴AF=CD,∵BD=CD,∴BD=AF,∵AF∥BC,∴四边形AFBD是平行四边形;(2)解:∵AB=AC,CD=BD,∴AD⊥BC,∴∠ADB=90°,∵四边形AFBD是平行四边形,∴四边形AFBD是矩形,∵AB=AC=13,BD=5,∴由勾股定理得:AD==12,∴四边形AFBD的面积是12×5=60.18.如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,两个点同时出发,当有一个点到达终点时,另一点也随之停止运动.点G为BD上的一点,假设移动时间为t秒,BG的长度为y.(1)证明:AD∥BC;(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和BG的长度y.【分析】(1)利用平行四边形得判定和性质证明;(2)利用全等三角形的判定求解.【解答】解:(1)∵AD=BC,AB=CD,∴四边形ABCD是平行四边形,∴AD∥BC;(2)BG=y,DE=t,当0≤t≤时,CF=3t,则BF=8﹣3t,∵AD∥BC,∴∠DBC=∠ADB,若△DEG与△BFG全等,则BF=DE且BG=DG,或者BF=DG且BG=DE,即:或,解得:或(不合题意,舍去),当<t≤时,则BF=3t﹣8,若△DEG与△BFG全等,则BF=DE且BG=DG,或者BF=DG且BG=DE,即:或,解得:或,所以△DEG与△BFG全等的情况出现了三次,第一次是2秒时,y=6,第二次是4秒时,y=6,第三次是5秒时,y=5.19.在△ABC中,AB=AC,点P为△ABC为所在平面内一点,过点P分别作PF∥AC交AB于点F,PE∥AB交BC于点D,交AC于点E.(1)当点P在BC边上(如图1)时,请探索线段PE,PF,AB之间的数量关系式为PE+PF=AB.(2)当点P在△ABC内(如图2)时,线段PD,PE,PF,AB之间有怎样的数量关系,请说明理由.(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB之间有怎样的数量关系,直接写出结论.【分析】(1)先求出四边形PF AE是平行四边形,根据平行四边形对边相等可得PF=AE,再根据两直线平行,同位角相等可得∠BPE=∠C,然后求出∠B=∠BPE,利用等角对等边求出PE=BE,然后求解即可;(2)根据等边对等角可得∠B=∠C,再根据两直线平行,同位角相等可得∠B=∠CDE,然后求出∠C=∠CDE,再根据等角对等边可得CE=PD+PE,然后求出四边形PF AE是平行四边形,根据平行四边形对边相等可得PE=AF,然后求出PD+PE+PF=AC,等量代换即可得证;(3)证明思路同(2).【解答】解:(1)答:PE+PF=AB.证明如下:∵点P在BC上,∴PD=0,∵PE∥AC,PF∥AB,∴四边形PF AE是平行四边形,∴PF=AE,∵PE∥AC,∴∠BPE=∠C,∴∠B=∠BPE,∴PE=BE,∴PE+PF=BE+AE=AB,∵PD=0,∴PE+PF=AB;故答案为:PE+PF=AB(2)证明:∵AB=AC,∴∠B=∠C,∵PE∥AB,∴∠B=∠CDE,∴∠C=∠CDE,∴CE=PD+PE,∵PF∥AC,PE∥AB,∴四边形PF AE是平行四边形,∴PE=AF,∴PD+PE+PF=AC,∴PD+PE+PF=AB;(3)证明:同(2)可证DE=CE,PE=AF,∵AE+CE=AC,∴PF+PE﹣PD=AC,∴PE+PF﹣PD=AB.20.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)在(1)的条件下,若BC的延长线交DF于点Q,连接QA与QE.试说明QA=QE.【分析】(1)根据平行四边形的想知道的AD=AC,AD⊥AC,连接CE,根据全等三角形的判定和性质即可得到结论;(2)根据全等三角形的性质得到CF=AD,等量代换得到AC=CF,于是得到CP=AB =AE,根据平行四边形的判定定理即可得到四边形ACPE为平行四边形;(3)由(1)知AC=CF,根据三角形的中位线的性质得到DQ=FQ,根据直角三角形的性质即可得到结论.【解答】(1)证明:在▱ABCD中,∵AD=AC,AD⊥AC,∴AC=BC,AC⊥BC,连接CE,∵E是AB的中点,∴AE=EC,CE⊥AB,∴∠ACE=∠BCE=45°,∴∠ECF=∠EAD=135°,∵ED⊥EF,∴∠CEF=∠AED=90°﹣∠CED,在△CEF和△AED中,,∴△CEF≌△AED,∴ED=EF;(2)解:由(1)知△CEF≌△AED,CF=AD,∵AD=AC,∴AC=CF,∵DP∥AB,∴FP=PB,∴CP=AB=AE,∴四边形ACPE为平行四边形;(3)由(1)知AC=CF,∵CQ∥AD,∴DQ=FQ,∵在Rt△DAF与Rt△DEF中,∴AQ=EQ=DF.。
2022年中考复习《平行四边形》专项练习附答案

平行四边形1、〔德阳市2021年〕如图.在ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,假设BG=42,那么△CEF的面积是A、22B、2C、32D、42答案:A解析:∵在▱ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,∴∠BAF=∠DAF,∵AB∥DF,∠BAF=∠F,∴∠F=∠DAF,∴△ADF是等腰三角形,AD=DF=9;∵AB=CD=6,∴CF=3;∠BEA=∠DAF=∠BAF,所以,BA=BE,∴在△ABG中,BG⊥AE,AB=6,BG=42可得:AG=2,又∵BG⊥AE,∴AE=2AG=4,∴△ABE的面积等于82,又∵▱ABCD,∴△CEF∽△BEA,相似比为1:2,面积1:4,∴△CEF的面积为,22.2、〔2021杭州〕在▱ABCD中,以下结论一定正确的选项是〔〕A.AC⊥BD B.∠A+∠B=180°C.AB=AD D.∠A≠∠C考点:平行四边形的性质.分析:由四边形ABCD是平行四边形,可得AD∥BC,即可证得∠A+∠B=180°.解答:解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°.应选B.点评:此题考查了平行四边形的性质.此题比拟简单,注意掌握数形结合思想的应用.3、〔2021•内江〕如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,那么DE:EC=〔〕A.2:5 B.2:3 C.3:5 D.3:2考点:相似三角形的判定与性质;平行四边形的性质.分析:先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出 DE:EC的值,由AB=CD即可得出结论.解答:解:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠EAB=∠DEF,∠AFB=∠DFE,∴△DEF∽△BAF,∵S△DEF:S△ABF=4:25,∴DE:AB=2:5,∵AB=CD,∴DE:EC=2:3.应选B.点评:此题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.4、〔2021•自贡〕如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=,那么△EFC的周长为〔〕A.11 B.10 C.9D.8考点:相似三角形的判定与性质;勾股定理;平行四边形的性质.分析:判断出△ADF是等腰三角形,△ABE是等腰三角形,DF的长度,继而得到EC的长度,在Rt△BGE中求出GE,继而得到AE,求出△ABE的周长,根据相似三角形的周长之比等于相似比,可得出△EFC的周长.解答:解:∵在▱ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,∴∠BAF=∠DAF,∵AB∥DF,AD∥BC,∴∠BAF=∠F=∠DAF,∠BAE=∠AEB,∴AB=BE=6,AD=DF=9,∴△ADF是等腰三角形,△ABE是等腰三角形,∵AD∥BC,∴△EFC是等腰三角形,且FC=CE,∴EC=FC=9﹣6=3,在△ABG中,BG⊥AE,AB=6,BG=4,∴AG==2,∴AE=2AG=4,∴△ABE的周长等于16,又∵△CEF∽△BEA,相似比为1:2,∴△CEF的周长为8.应选D.点评:此题主要考查了勾股定理、相似三角形、等腰三角形的性质,注意掌握相似三角形的周长之比等于相似比,此题难度较大.5、〔2021•泸州〕四边形ABCD中,对角线AC、BD相交于点O,以下条件不能判定这个四边形是平行四边形的是〔〕A.A B∥DC,AD∥BC B.A B=DC,AD=BC C.A O=CO,BO=DO D.A B∥DC,AD=BC考点:平行四边形的判定.分析:根据平行四边形判定定理进行判断.解答:解:A、由“AB∥DC,AD∥BC〞可知,四边形ABCD的两组对边互相平行,那么该四边形是平行四边形.故本选项不符合题意;B、由“AB=DC,AD=BC〞可知,四边形ABCD的两组对边相等,那么该四边形是平行四边形.故本选项不符合题意;C、由“AO=CO,BO=DO〞可知,四边形ABCD的两条对角线互相平分,那么该四边形是平行四边形.故本选项不符合题意;D、由“AB∥DC,AD=BC〞可知,四边形ABCD的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意;应选D.点评:此题考查了平行四边形的判定.〔1〕两组对边分别平行的四边形是平行四边形.〔2〕两组对边分别相等的四边形是平行四边形.〔3〕一组对边平行且相等的四边形是平行四边形.〔4〕两组对角分别相等的四边形是平行四边形.〔5〕对角线互相平分的四边形是平行四边形.6、〔2021泰安〕如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,假设DG=1,那么AE的边长为〔〕A.2 B.4 C.4 D.8考点:平行四边形的性质;等腰三角形的判定与性质;含30度角的直角三角形;勾股定理.专题:计算题.分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC 中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF 的长,再由三角形ADF与三角形ECF全等,得出AF=EF,即可求出AE的长.解答:解:∵AE为∠ADB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,那么AF=2AG=2,在△ADF和△ECF中,,∴△ADF≌△ECF〔AAS〕,∴AF=EF,那么AE=2AF=4.应选B点评:此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解此题的关键.7、〔2021•益阳〕如图,在平行四边形ABCD中,以下结论中错误的选项是〔〕A.∠1=∠2B.∠BAD=∠BCD C.A B=CD D.A C⊥BD考点:平行四边形的性质.分析:根据平行四边形的性质,平行四边形对边平行以及对边相等和对角相等分别判断得出即可.解答:解:∵在平行四边形ABCD中,∴AB∥CD,∴∠1=∠2,故此选项正确,不合题意;∵四边形ABCD是平行四边形,∴∠BAD=∠BC D,AB=CD,故B,C选项正确,不合题意;无法得出AC⊥BD,故此选项错误,符合题意.应选D.点评:此题主要考查了平行四边形的性质,熟练掌握相关的性质是解题关键.8、〔2021•湘西州〕如图,在▱ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,那么△EDF与△BCF的周长之比是〔〕A.1:2 B.1:3 C.1:4 D.1:5考点:平行四边形的性质;全等三角形的判定与性质分析:根据平行四边形性质得出AD=BC,AD∥BC,推出△EDF∽△BCF,得出△EDF与△BCF 的周长之比为,根据BC=AD=2DE代入求出即可.解答:解:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴△EDF∽△BCF,∴△EDF与△BCF的周长之比为,∵E是AD边上的中点,∴AD=2DE,∵AD=BC,∴BC=2DE,∴△EDF与△BCF的周长之比1:2,应选A.点评:此题考查了平行四边形性质,相似三角形的性质和判定的应用,注意:平行四边形的对边平行且相等,相似三角形的周长之比等于相似比.9、〔2021•荆门〕四边形ABCD中,对角线AC、BD相交于点O,给出以下四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD从中任选两个条件,能使四边形ABCD为平行四边形的选法有〔〕A.3种B.4种C.5种D.6种考点:平行四边形的判定.分析:根据题目所给条件,利用平行四边形的判定方法分别进行分析即可.解答:解:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD 为平行四边形;③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;应选:B.点评:此题主要考查了平行四边形的判定,关键是熟练掌握平行四边形的判定定理.10、〔2021•恩施州〕如下图,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,那么DF:FC=〔〕A.1:4 B.1:3 C.2:3 D.1:2考点:相似三角形的判定与性质;平行四边形的性质.分析:首先证明△DFE∽△BAE,然后利用对应变成比例,E为OD的中点,求出DF:AB的值,又知AB=DC,即可得出DF:FC的值.解答:解:在平行四边形ABCD中,AB∥DC,那么△DFE∽△BAE,∴=,∵O为对角线的交点,∴DO=BO,又∵E为OD的中点,∴DE=DB,那么DE:EB=1:3,∴DF:AB=1:3,∵DC=AB,∴D F:DC=1:3,∴DF:FC=1:2.应选D.点评:此题考查了相似三角形的判定与性质以及平行四边形的性质,难度适中,解答此题的关键是根据平行证明△DFE∽△BAE,然后根据对应边成比例求值.11、〔2021•绥化〕如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,那么的值为〔〕A.1B.C.D.考点:三角形中位线定理;平行四边形的性质.分析:根据三角形的中位线平行于第三边并且等于第三边的一半求出H是AO的中点,再根据平行四边形的对角线互相平分可得AO=CO,然后求出CH=3AH,再求解即可.解答:解:∵点E,F分别是边AD,AB的中点,∴AH=HO,∵平行四边形ABCD的对角线AC、BD相交于点O,∴AO=CO,∴CH=3AH,∴=.应选C.点评:此题考查了平行四边形对角线互相平分的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记各性质是解题的关键.12、〔2021哈尔滨〕如图,在ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,那么AB的长为( ).(A)4 (B)3 (C) 52(D)2考点:平行四边形的性质及等腰三角形判定.分析:此题主要考查了平行四边形的性质:平边四边形的对边平行且相等;等腰三角形判定,两直线平行内错角相等;综合运用这三个性质是解题的关键解答:根据CECE平分∠BCD得∠BCE=∠ECD,AD∥BC得∠BCE=∠DEC从而△DCE为等腰三角形,ED=DC=AB,2AB=AD=AE+ED=3+AB,解得AB=3应选B13、〔2021•黔西南州〕▱ABCD中,∠A+∠C=200°,那么∠B的度数是〔〕A.100°B.160°C.80°D.60°考点:平行四边形的性质.分析:由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.解答:解:∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC,∵∠A+∠C=200°,∴∠A=100°,∴∠B=180°﹣∠A=80°.应选C.点评:此题考查了平行四边形的性质.此题比拟简单,注意掌握平行四边形的对角相等、邻角互补的知识.14、〔2021•钦州〕如图,图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图〔箭头表示行进的方向〕.其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为〔〕A.甲<乙<丙B.乙<丙<甲C.丙<乙<甲D.甲=乙=丙考点:平行四边形的判定与性质.专题:应用题.分析:延长ED和BF交于C,如图2,延长AG和BK交于C,根据平行四边形的性质和判定求出即可.解答:解:图1中,甲走的路线长是AC+BC的长度;延长ED和BF交于C,如图2,∵∠DEA=∠B=60°,∴DE∥CF,同理EF∥CD,∴四边形CDEF是平行四边形,∴EF=CD,DE=CF,即乙走的路线长是AD+DE+EF+FB=AD+CD+CF+BC=AC+BC的长;延长AG和BK交于C,如图3,与以上证明过程类似GH=CK,CG=HK,即丙走的路线长是AG+GH+HK+KB=AG+CG+CK+BK=AC+BC的长;即甲=乙=丙,应选D.点评:此题考查了平行线的判定,平行四边形的性质和判定的应用,注意:两组对边分别平行的四边形是平行四边形,平行四边形的对边相等.15、〔2021福省福州4分、8〕如图,△ABC,以点B为圆心,AC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在BC异侧,连结AD,量一量线段AD的长,约为〔〕A. B. C. D.考点:平行四边形的判定与性质;作图—复杂作图.分析:首先根据题意画出图形,知四边形ABCD是平行四边形,那么平行四边形ABCD的对角线相等,即AD=BC.再利用刻度尺进行测量即可.解答:解:如下图,连接BD、BC、AD.∵AC=BD,AB=CD,∴四边形ABCD是平行四边形,∴AD=BC.测量可得BC=AD=,应选:B.点评:此题主要考查了复杂作图,关键是正确理解题意,画出图形.16、〔2021台湾、31〕如图,甲、乙两人想在正五边形ABCDE内部找一点P,使得四边形ABPE 为平行四边形,其作法如下:〔甲〕连接BD、CE,两线段相交于P点,那么P即为所求〔乙〕先取CD的中点M,再以A为圆心,AB长为半径画弧,交AM于P点,那么P即为所求.对于甲、乙两人的作法,以下判断何者正确?〔〕A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确考点:平行四边形的判定.分析:求出五边形的每个角的度数,求出∠ABP、∠AEP、∠BPE的度数,根据平行四边形的判定判断即可.解答:解:甲正确,乙错误,理由是:如图,∵正五边形的每个内角的度数是=108°,AB=BC=CD=DE=AE,∴∠DEC=∠DCE=×〔180°﹣108°〕=36°,同理∠CBD=∠CDB=36°,∴∠ABP=∠AEP=108°﹣36°=72°,∴∠BPE=360°﹣108°﹣72°﹣72°=108°=∠A,∴四边形ABPE是平行四边形,即甲正确;∵∠BAE=108°,∴∠BAM=∠EAM=54°,∵AB=AE=AP,∴∠ABP=∠APB=×〔180°﹣54°〕=63°,∠AEP=∠APE=63°,∴∠BPE=360°﹣108°﹣63°﹣63°≠108°,即∠ABP=∠AEP,∠BAE≠∠BPE,∴四边形ABPE不是平行四边形,即乙错误;应选C.点评:此题考查了正五边形的内角和定理,等腰三角形的性质,三角形的内角和定理,平行四边形的判定的应用,注意:有两组对角分别相等的四边形是平行四边形.17、〔2021安顺〕在平行四边形ABCD中,E在DC上,假设DE:EC=1:2,那么BF:BE= .考点:相似三角形的判定与性质;平行四边形的性质.分析:由题可知△ABF∽△CEF,然后根据相似比求解.解答:解:∵DE:EC=1:2∴EC:CD=2:3即EC:AB=2:3∵AB∥CD,∴△ABF∽△CEF,∴BF:EF=AB:EC=3:2.∴BF:BE=3:5.点评:此题主要考查了平行四边形、相似三角形的性质.18、〔2021•滨州〕在▱ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,那么OE= 5 .考点:三角形中位线定理;平行四边形的性质.分析:先画出图形,根据平行线的性质,结合点E是边CD的中点,可判断OE是△DBC的中位线,继而可得出OE的长度.解答:解:∵四边形ABCD是平行四变形,∴点O是BD中点,∵点E是边CD的中点,∴OE是△DBC的中位线,∴OE=BC=5.故答案为:5.点评:此题考查了平行四边形的性质及中位线定理的知识,解答此题的关键是根据平行四边形的性质判断出点O是BD中点,得出OE是△DBC的中位线.19、〔13年安徽省4分、13〕如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,ΔPEF、ΔPDC、ΔPAB的面积分别为S、S1、S2。
中考考试重点-关于平行四边形的证明题

1、如图,四边形ABCD 的对角线AC 、BD 交于点O ,已知O 是AC 的中点,AE=CF ,DF ∥BE.(1)求证:△BOE ≌△DOF ;(2)若OD=21AC ,则四边形ABCD 是什么特殊四边形?请证明你的结论.2、已知:如图,在矩形ABCD 中,点E ,F 分别在AB ,CD 边上,BE=DF ,连接CE ,AF.求证:AF=CE.3、如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.(1)求证:四边形MNCD是平行四边形;(2)求证:BD=3MN. 4、如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.(1)求∠APB的度数;(2)如果AD=5 cm,AP=8 cm,求△APB的周长.5、如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF. 6、已知:如图,在平行四边形ABCD中,点E、F在AC 上,且AE=CF.求证:四边形BEDF是平行四边形.7、如图,四边形ABCD是平行四边形,AC是对角线,BE⊥AC,垂足为E,DF⊥AC,垂足为F.求证:BE=DF. 8、如图3-34所示,E,F分别为平行四边形ABCD中AD,BC的中点,G,H在BD上,且BG=DH,求证四边形EGFH是平行四边形.9、如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.⑴求证:△BAD≌△AEC;⑵若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE 的面积.11、如图,在平行四边形ABCD中,∠ABC的平分线BF 分别与AC、AD交于点E、F.(2)当AB=3,BC=5时,求的值.12、已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.13、如图所示,已知在平行四边形ABCD中,BE=DF,14、已知:如图,在△ABC中,,D是BC 求证:AE=CF.的中点,,CE∥AD.如果AC=2,CE=4.Array(1)求证:四边形ACED是平行四边形;(2)求四边形ACEB的周长;(3)直接写出CE和AD之间的距离.15、如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF ⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.16、如图9,平行四边形ABCD中,AE、CF分别平分∠DAC、∠BCA,则四边形AFCE是平行四边形吗?为什么?17、如图,在△ABC中,D是BC边上的一点,E是AD 的中点,过A点作BC的平行线交CE的延长线于F ,且AF=BD,连结BF(1)求证:D是BC的中点.(2)如果AB=AC ,试判断四边形AFBD的形状,并证明你的结论.18、如图,四边形ABCD是平行四边形,作AF∥CE,求证:△EBC≌△FDA.19、如图,在□ABCD中,为边上一点,且(1)求证:;(2)若平分,,求的度数.20、如图,已知平行四边形ABCD中,AE⊥BC于E,(2)若平行四边形的周长为36cm,AE=4cm,AF=5cm,求平行四边形ABCD的面积.21、如图,平行四边形ABCD中,AE⊥BD, CF⊥BD,求证:四边形AECF 是平行四边形.22、如图,在□ABCD 中,点E 、F 分别是AD 、BC 的中点,分别连接BE 、DF 、BD . (1)求证:△AEB ≌△CFD ;(2)若四边形EBFD 是菱形,求∠ABD 的度数.23、已知,如图,在▱ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 与BE 交于点G.求证:GF=GC.24、已知,如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.25、如图,在▱ABCD 中,点E 在边BC 上,点F 在BC 的延长线上,且BE=CF .求证:∠BAE=∠CDF .26、如图,四边形中,,点在的延长线上,联结,交于点,联结DB ,,且.(1) 求证:;(2)当平分时,求证:四边形是菱形.27、已知:如图,在□ABCD中,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.求证:(1)△ABE ≌△CDF;(2)BE∥DF.28、如图,在□ABCD中,AC、BD交于点O,EF过点O,分别交CB、AD的延长线于点E、F.。
中考数学模拟题汇总《平行四边形的证明》专项练习(附答案解析)

中考数学模拟题汇总《平行四边形的证明》专项练习(附答案解析)一、综合题1.如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.(1)求证:四边形ABEF是平行四边形;(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.2.如图,平形四边形ABCD中,E,F分别是边BC,AD的中点,∠BAC=90°(1)求证:四边形AECF是菱形;(2)若BC=4,∠B=60°,求四边形AECF的面积3.四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE.(1)如图1,求证:四边形AEFD是平行四边形;(2)如图2,若E是线段BC中点,连接AF、ED,在不添加任何辅助线和字母的情况下,请直接写出图2中面积是△ABE的面积2倍的三角形.4.如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;(2)若∠ACB=30°,菱形OCED的面积为8√3,求AC的长.5.如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.6.如图,将▱ABCD的边DC延长到点E,使得CE=DC,连接AE,交BC于点FBC;(1)求证:BF=12(2)若∠AFC=2∠D,连接AC,BE,求证:四边形ABEC是矩形7.已知:平行四边形ABCD,过点A、C分别作AD、BC的垂线,交BD于E、F 两点,连接AF、CE.(1)如图1,求证:四边形AECF是平行四边形;(2)如图2,当点F为DE中点时,请直接写出图2中与四边形AECF面积相等的所有三角形.8.如图,四边形ABCD中,对角线相交于点O,E,F,G,H分别是AD,BD,BC,AC的中点.(1)求证:四边形EFGH是平行四边形;(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论. 9.已知如图所示,与关于点成中心对称,连接,.(1)求证:四边形是平行四边形;(2)若的面积为15 ,求四边形的面积.10.如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且 BC.CF= 12(1)求证:DE=CF;(2)求证:BE=EF.x+3与x轴、y轴分别交于点B、A,动点C以每秒2 11.在平面直角坐标系中,直线y=12个单位长度的速度从点B向终点O运动,过点C作∠BCD=∠ABO,交直线AB于点D.设∠BDC=α°,将CD绕点C顺时针旋转α°得到线段CE,连接DE .设四边形BCED与ΔABO的重叠部分面积为S(平方单位),S>0,点C的运动时间为t秒.(1)求AB的长;(2)求证:四边形BCED是平行四边形;(3)求S与t的函数关系式,并直接写出自变量取值范围.12.如图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求sin ∠CAE的值.13.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN是平行四边形;(2)填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.14.如图是边长为1的小正三角形组成的网格.(1)在网格中画出一个以AB为边的▱ABCD,使BC的长为无理数且C,D均在格点(即每个小正三角形的顶点)上.(2)针对你所画的平行四边形(不添加任何条件),请你编制一个计算题,并直接写出答案.15.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ//DB,且CQ= DP,连接AP,BQ,PQ .(1)求证:AP=BQ;(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.16.如图,在梯形ABCD中,AD∥BC,AB=DC.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.(1)求证:四边形AEFG是平行四边形;(2)当∠FGC=2∠EFB时,求证:四边形AEFG是矩形.参考答案与解析1.【答案】(1)解:∵将△ABC 绕点C 顺时针旋转180°得到△EFC ,∴△ABC ≌△EFC ,∴CA=CE ,CB=CF ,∴四边形ABEF 是平行四边形;(2)解:当∠ABC=60°时,四边形ABEF 为矩形,理由是:∵∠ABC=60°,AB=AC ,∴△ABC 是等边三角形,∴AB=AC=BC . ∵CA=CE ,CB=CF ,∴AE=BF .∵四边形ABEF 是平行四边形,∴四边形ABEF 是矩形. 2.【答案】(1)证明:∵□ABCD , ∴BC =AD ,BC ∥AD. 又∵E ,F 分别是边BC ,AD 的中点, ∴EC = 12 BC ,AF = 12 AD , ∴ECAF ,∴四边形AECF 为平行四边形.在Rt △ABC 中,∠BAC =90°,E 是BC 边中点, ∴AE =EC ,∴四边形AECF 是菱形(2)解:如图,连接EF 交AC 于点O , 在Rt △ABC 中,∠BAC =90°,∠B =60°,BC =4, ∴AB =2,AC = 2√3 . ∵四边形AECF 是菱形, ∴AC ⊥EF ,OA =OC ,OE =OF , ∴OE 是△ABC 的中位线, ∴OE = 12 AB =1, ∴EF =2,∴S 菱形AECF = 12 AC •EF = 12 × 2√3 ×2= 2√3 3.【答案】(1)证明: ∵ 四边形 ABCD 是矩形,∴AB=DC,∠ABE=∠DCF=90°∵BE=CF∴△ABE≅△DCF(SAS)∴AE=DF,∠AEB=∠DFC∴AE//DF∴四边形AEFD是平行四边形;(2)解:有△AED,△AEF,△ADF,△EDF4.【答案】(1)证明:∵DE∥OC,CE∥OD,∴四边形OCED是平行四边形.∵四边形ABCD是矩形,∴AO=OC=BO=OD.∴四边形OCED是菱形;(2)解:∵∠ACB=30°,∴∠DCO=90°﹣30°=60°.又∵OD=OC,∴△OCD是等边三角形.过D作DF⊥OC于F,则CF=OC,设CF=x,则OC=2x,AC=4x.2,在Rt△DFC中,tan60°=AEEC∴DF=√3 x.∴OC•DF=8 √3.∴x=2.∴AC=4×2=8.5.【答案】(1)证明:∵D,E,F分别是边AB、BC、CA的中点,∴DE,EF是△ABC的中位线,∴DE∥AF,EF∥AD,∴四边形ADEF是平行四边形.(2)解:∵四边形ADEF是平行四边形,∴∠DEF=∠BAC,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠BAC,∴∠DEF=∠DHF=∠AHF+∠AHD=70°.6.【答案】(1)证明:因为四边形ABCD是平行四边形所以AB//CD,AB=CD∵CE=DC∴AB=EC所以四边形ABEC是平行四边形,∴BF=1BC .2(2)证明:由(1)知,四边形ABEC是平行四边形,∴FA=FE,FB=FC 因为四边形ABCD是平行四边形,∴∠ABC=∠D∵∠AFC=2∠ADC ∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB∴FA=FE=FB=FC,∴AE=BC所以四边形ABEC是矩形.7.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD//BC,∴∠ADE=∠CBD∵EA⊥AD,EC⊥BC,∴∠EAD=∠FCB=90°,∴△EAD≌△FCB,∴EA=FC,∠AED=∠CFB∴EA//FC.∴四边形AECF是平行四边形.(2)解:∵点F为DE中点时,∴EF=FD,由(1)得△EAD≌△FCB,∴ED=BF,∴BE=DF,∴BE=EF=FD,∴S△ABE=S△AEF=S△AFD,同理可证S△BEC=S△CEF=S△CFD,∵四边形AECF是平行四边形,∴S△AEF=S△CEF,∴S△ABE=S△AEF=S△AFD = S△BEC=S△CEF=S△CFD∴正确的三角形有△ABF,△ADE,△BCF,△DCE.8.【答案】(1)解:通过G、H分别为BC、AC中点,可以推出EF∥AB,进而求出EF∥GH.(2)解:∵E、F分别是AD,BD的中点,G、F分别是BC,AC的中点,∴EF=12AB,FG=12CD,∵AB=CD,∴EF=FG,∴平行四边形EFGH是菱形9.【答案】(1)证明:∵与关于点成中心对称,∴即四边形的对角线互相平分,∴四边形是平行四边形.(2)解:记底边上的高为h,那么平行四边形ABCD底边AB上的为2h,因为的面积为15,所以,所以2ABh=60,所以平行四边形ABCD的面积为60 .10.【答案】(1)证明:∵D,E分别为AB,AC的中点,∴DE为中位线,∴DE∥BC,且DE= 12BC,又∵CF= 12BC,∴DE=CF(2)证明:连接DC,由(1)可得DE∥CF,且DE=CF,∴四边形DCFE为平行四边形,∴EF=DC,∵AB=AC,且DE为中位线,∴四边形DBCE为等腰梯形,又∵DC,BE为等腰梯形DBCE的对角线,∴DC=BE,∴BE=EF.x+3与x轴、y轴分别交于点B、A 11.【答案】(1)解:∵直线y=12∴A(0,3),B(−6,0)∴OA=3,OB=6∴AB=3√5(2)解:∵∠DBC=∠DCB∴DB=DC由旋转知CD=CE,∠BDC=∠DCE∴BD∥CE,BD=CE∴四边形ABCD是平行四边形x+3与x轴、y轴分别交于点B、A(3)解:∵直线y=12∴A(0,3),B(−6,0)∴tan∠ABO=12过点D作DH⊥BC于点HBC=t∵BD=CD∴BH=12t∴DH=tan∠DBH⋅BH=12t=t2∴当0<t≤2时s=2t⋅12当2<t≤3时∵OM=12t∴AM=3−12t∵DE∥OB∴∠ADE=∠ABC∴tan∠ADE=tan∠ABC=12∴AMDM =3−12tDM=12∴DM=6−t∴EM=2t−(6−t)=3t−6∵平行四边形ABCD∴∠ABC=∠E∴tan∠E=tan∠ABC=12∴NM=tan∠E⋅ME=32t−3∴SΔMNE=12×12(3t−6)2=94t2−9t+9∴S=−54t2+9t−9∴S={t2(0<t≤2)−54t2+9t−9(2<t≤3)12.【答案】(1)证明:连接OD与BD.∵△BDC是Rt△,且E为BC中点,∴∠EDB=∠EBD.又∵OD=OB且∠EBD+∠DBO=90°,∴∠EDB+∠ODB=90°.∴DE是⊙O的切线.(2)解:∵∠EDO=∠B=90°,若要四边形AOED是平行四边形,则DE∥AB,D为AC中点,又∵BD⊥AC,∴△ABC为等腰直角三角形.∴∠CAB=45°.过E作EH⊥AC于H,设BC=2k,则EH= √22K,AE=√5K,∴sin∠CAE= EHAE =√1010.13.【答案】(1)证明:∵四边形ABCD是菱形,∴ND∥AM,∴∠NDE=∠MAE,∠DNE=∠AME,又∵点E是AD边的中点,∴DE=AE,∴△NDE≌△MAE,∴ND=MA,∴四边形AMDN是平行四边形(2)1;214.【答案】(1)解:画出其中一个即可.(2)解:问题:求CD的长;求∠ABC的度数或∠BAD的度数;求BC的长等.求平行四边形ABCD的面积或周长;求AB,CD之间的距离或AD,BC之间的距离;求某个锐角的三角函数值等.图1中,CD=1,∠ABC=30°,BC=√3,周长=2+2√3,AB,CD之间的距离为√32,面积=√32.图2中,CD=1,∠ABC=30°,BC=√3,周长=2+2√3,AB,CD之间的距离为√3,面积=√3 .图3与图4中,CD=1,BC=√7,周长=2+2√7,AB,CD之间的距离为3√32,面积=3√32.图3中,tan∠ABC=3√3,sin∠ABC=314√21,cos∠ABC=114√7 .15.【答案】(1)证明:∵CQ//DB,CQ=DP ∴四边形DCQP是平行四边形∴PQ//CD,PQ=CD∵四边形ABCD是平行四边形∴AB//CD,AB=CD∴AB//PQ,AB=PQ∴四边形ABQP是平行四边形∴AP=BQ(2)证明:∵CQ//DB∴∠DBQ+∠BQC=180°∵∠ABP+∠BQC=180°∴∠ABP=∠QBP由(1)知:四边形ABQP是平行四边形,AB//PQ∴∠ABP=∠QPB∴∠QBP=∠QPB∴BQ=PQ∴四边形ABQP为菱形16.【答案】(1)证明:∵在梯形ABCD中,AB=DC,∴∠B=∠C.∵GF=GC,∴∠C=∠GFC,∴∠B=∠GFC∴AB∥GF,即AE∥GF.∵AE=GF,∴四边形AEFG是平行四边形(2)证明:∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,∴2∠GFC+2∠EFB=180°,∴∠BFE+∠GFC=90°.∴∠EFG=90°.∵四边形AEFG是平行四边形,∴四边形AEFG是矩形.。
中考数学总复习——四边形证明(含答案)

专题. 四边形1、平行四边形1.如图,已知:▱ABCD中,∠ABC的平分线BG,交AD于G,∠BCD的平分线CE,交BG于F,交AD于E.(1)求证:BG⊥CE.(2)若AB=3,BC=4,求EG的长.2.如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.(1)求证:△ABF≌△DCE;(2)若∠BFA=40°,求∠BAF的度数.3.如图,在△ABC中,∠ACB=90°,AC=2,BC=3.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF ∥AB交直线DE于F.设CD=x.(1)当x=1时,求四边形EACF的面积;(2)当x为何值时,四边形EACF是菱形?请说明理由.4.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB.(1)求证:△ABE≌△ACD;(2)求证:四边形EFCD是平行四边形.2、菱形1.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG。
(1)求证:EB=GD;(2)若∠DAB=60°,AB=2,AG=,求GD的长.2.如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.(1)求证:△ACE≌△CBD;(2)求∠CGE的度数.3.菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60°(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离.4.如图1,菱形ABCD中,∠BAD=60°,点E、F分别是边AB、AD上两个动点,满足AE=DF,连接BF与DE相交于点G.(1)如图2,连接BD,求∠BGD的度数;(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.5.如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.6.如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求cos∠CDE的值.7.如图,已知ABCD是菱形,△EFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP.(1)证明:∠EPF+∠BAD=180°;(2)若∠BAD=120°,证明:AE+AF=AP;(3)若∠BAD=θ,AP=a,求AE+AF.8.如图.在菱形ABCD中,BC边的中垂线EF交AD边于F,G是CD中点.(1)求证:EG=FG;(2)若△DFG为等腰三角形,求∠D的度数.9.如图1,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE.(1)求证:∠F=∠EBC;(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠F的度数(如图2).10.在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点时,求证:BE=EF.(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论:.(填“成立”或“不成立”)(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.15.【感知】如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为.16.如图①,已知点O为菱形ABCD的对称中心,∠A=60°,将等边△OEF的顶点放在点O处,OE,OF分别交AB,BC于点M,N.(1)求证:OM=ON;(2)将图①中的△OEF绕O点顺时针旋转至图②所示的位置,请写出线段BM,BN与AB之间的数量关系,并进行证明.17.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)对角线AC的长是,菱形ABCD的面积是;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否会发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否会发生变化?若不变,请说明理由;若变化,请探究OE、OF之间的数量关系,并说明理由.3、矩形1.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若AB=2,求△OEC的面积.2.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;(2)若AB=2,∠BCD=120°,连接CE,求CE的长.3.如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.(1)求证:平行四边形ABCD是矩形;(2)求BF的长;(3)求折痕AF长.4.如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;(2)若EA=EG,求证:ED=EC.5.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?4、正方形6.已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N.(1)若连接BG、CE,求证:BG=CE.(2)试判断四边形PQMN为怎样的四边形,并证明你的结论.7.已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连接MN,作AH⊥MN,垂足为点H(1)如图1,猜想AH与AB有什么数量关系?并证明;(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?8.在图1到图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM垂直于直线AB于点E,PN垂直于直线BC于点F.(1)如图1,当点P与点O重合时,OE与OF的数量关系为;(2)如图2,当P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系?并对你的猜想结果给予证明;(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为;位置关系为.9.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.10.猜想与证明:如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.(1)试猜想写出DM与EM的数量关系,并证明你的结论.拓展与延伸:(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断.11.如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.(1)求证:AD=AF;(2)试判断四边形ABNE的形状,并说明理由.12.如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连接CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.(1)求证:△CDE≌△CBF;(2)当DE=时,求CG的长.13.如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.(1)求证:BF=DF;(2)连接CF,请直接写出的值为(不必写出计算过程).14.(1)如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O 作OE的垂线交AB于点F.求证:OE=OF.(2)若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF.▱)求证:∠OEF=∠BAC.▱)试探究线段AF,EF,CE之间数量上满足的关系,并说明理由.15.正方形ABCD中,对角线AC、BD交于点O,E为BD上一点,延长AE到点N,使AE=EN,连接CN、CE.(1)求证:△CAN为直角三角形.(2)若AN=4,正方形的边长为6,求BE的长.16.如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的数量关系是,位置关系是;(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断并给予证明.17.如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.(1)已知BD=,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.18.如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.(1)求证:△ABF≌△CBE;(2)填空:用等式表示线段FA、FE、FC之间的数量关系为.19.已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.20.如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.(1)若E是BC的中点,求证:DE=CF;(2)若∠CDE=30°,求的值.参考答案四边形1.【解答】(1)证明:∵▱ABCD,∴AB∥CD,∴∠ABC+∠BCD=180°,又∵BG、CE分别是∠ABC和∠BCD的角平分线,∴∠ABG=∠CBG,∠BCE=∠DCE,又∵∠ABG+∠CBG+∠BCE+∠DCE=180°,∴∠CBG+∠BCE=90°,在△BCF中,∠BFC=180°﹣∠CBF﹣∠BCF=90°;即BG⊥CE;(2)解:∵▱ABCD,∴AD∥BC,AB=CD=3,AD=BC=4,∴∠AGB=∠CBG,又∵BG是∠ABC的角平分线,∴∠ABG=∠CBG,∴∠AGB=∠ABG,∴AB=AG=3,∴GD=AD﹣AG=4﹣3=1,同理:AE=1,∴EG=AD﹣AE﹣GD=4﹣1﹣1=2.2.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC,∵BE=CF,∴BF=CE,在△ABF和△DCE中,,∴△ABF≌△DCE(SSS);(2)解:∵△ABF≌△DCE,∴∠B=∠C,∵AB∥DC,∴∠B+∠C=180°,∴∠B=90°,∴∠BAF=90°﹣∠BFA=90°﹣40°=50°.3.【解答】解:(1)∵DE⊥BC,∠ACB=90°;∴EF∥AC∵CF∥AB;∴▱EACF的面积=2×1=2(2)由(1)可知四边形EACF是平行四边形,则∠A=∠CFD,EF∥AC,故∠ACB=∠FDC,故△ABC∽△FCD,即AB:CF=BC:CD又∵AB==(勾股定理),BC=3所以当CF=AC=2时,四边形EACF是菱形.∴:2=3:CD所以x=CD=时,▱EACF是菱形.4.【解答】证明:(1)∵△ABC和△ADE都是等边三角形,∴AE=AD,AB=AC,∠EAD=∠BAC=60°,∴∠EAD﹣∠BAD=∠BAC﹣∠BAD,即:∠EAB=∠DAC,∴△ABE≌△ACD(SAS);(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,又∵BF=DC,∴BE=BF.∵△ABC是等边三角形,∴∠DCA=60°,∴△BEF为等边三角形.∴∠EFB=60°,EF=BF∵△ABC是等边三角形,∴∠ABC=60°,∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,∵EF=BF,BF=DC,∴EF=DC,∴四边形EFCD是平行四边形.菱形1.【解答】(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,∴∠EAG+∠GAB=∠BAD+∠GAB,∴∠EAB=∠GAD,∵AE=AG,AB=AD,∴△AEB≌△AGD,∴EB=GD;(2)解:连接BD交AC于点P,则BP⊥AC,∵∠DAB=60°,∴∠PAB=30°,∴BP=AB=1,AP==,AE=AG=,∴EP=2 ,∴EB===,∴GD=.2.【解答】解:(1)∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴BC=AC,∠ACB=∠ABC,∵BE=AD,∴BE+BC=AD+AB,即CE=BD,在△ACE和△CBD中,,∴△ACE≌△CBD(SAS);(2)如图,连接AC,易知△ABC是等边三角形,由(1)可知△ACE≌△CBD,∴∠E=∠D,∵∠BAE=∠DAG,∴∠E+∠BAE=∠D+∠DAG,∴∠CGE=∠ABC,∵∠ABC=60°,∴∠CGE=60°.3.【解答】(1)证明:连接AC,如图1中,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAE,在△BAE和△CAF中,,∴△BAE≌△CAF,∴BE=CF.(2)解:如图2中,过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,∵∠EAB=15°,∠ABC=60°,∴∠AEB=45°,在RT△AGB中,∵∠ABC=60°,AB=4,∴BG=AB=2,AG=BG=2 ,在RT△AEG中,∵∠AEG=∠EAG=45°,∴AG=GE=2 ,∴EB=EG﹣BG=2 ﹣2,∵△AEB≌△AFC,∴AE=AF,EB=CF=2 ﹣2,在RT△CHF中,∵∠HCF=180°﹣∠BCD=60°,CF=2 ﹣2,∴FH=CF•sin60°=(2 ﹣2)•=3﹣.∴点F到BC的距离为3﹣.4.【解答】(1)解:如图2中,∵四边形ABCD是菱形,∴AD=AB,∵∠A=60°,∴△ABD是等边三角形,∴AB=DB,∠A=∠FDB=60°,在△DAE和△BDF中,,∴△DAE≌△BDF,∴∠ADE=∠DBF,∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,∴∠BGD=180°﹣∠BGE=120°.(2)证明:如图3中,延长GE到M,使得GM=GB,连接BD、CG.∵∠MGB=60°,GM=GB,∴△GMB是等边三角形,∴∠MBG=∠DBC=60°,∴∠MBD=∠GBC,在△MBD和△GBC中,,∴△MBD≌△GBC,∴DM=GC,∠M=∠CGB=60°,∵CH⊥BG,∴∠GCH=30°,∴CG=2GH,∵CG=DM=DG+GM=DG+GB,∴2GH=DG+GB.5.【解答】(1)证明:∵四边形ABCD是菱形,∴CD=CB.在△CFD和△CEB中,,∴△CFD≌△CEB(SSS);(2)解:∵△CFD≌△CEB,∴∠CDB=∠CBE,∠DCF=∠BCE.∵四边形ABCD是菱形,∴∠CBD=∠ABD.∵CD=CB,∴∠CDB=∠CBD,∴∠ABD=∠CBD=∠CBE=60°.∴∠DCB=60°.∵∠FCE=60°,∵CF=CE,∴∠CFE=∠CEF=60°.6.【解答】(1)证明:∵四边形ABCD是菱形;∴AD∥BC,∠BOC=90°,∵DE⊥BD,∴∠BDE=90°,∴∠BDE=∠BOC,∴AC∥DE,∴四边形ACED是平行四边形.(2)解:∵四边形ACED是平行四边形,∴AD=CE,∵AD=BC,∴BC=CE,∵∠BDE=90°,∴DC=CE,∴∠CDE=∠E,∴cos∠CDE=cos∠E,∵BD=4,AC=3,∠BDE=90°,∴BE=5,∴cos∠E==,∴cos∠CDE=cos∠E=.7.【解答】解:(1)如图1中,作PM⊥AD于M,PN⊥AC于N.∵四边形ABCD是菱形,∴∠PAM=∠PAN,∴PM=PN,∵PE=PF,∴Rt△PMF≌Rt△PNE,∴∠MPF=∠NPE,∴∠EPF=∠MPF,∵∠BAD+∠MPN=360°﹣∠AMP﹣∠ANP=180°,∴∠EPF+∠BAD=180°.(2)如图2中,作PM⊥AD于M,PN⊥AC于N.由(1)可知Rt△PMF≌Rt△PNE,∴FM=NE,∵PA=PA,PM=PN,∴Rt△PAM≌Rt△PAN,∴AM=AN,∴AF+AE=(AM+FM)+(AN﹣EN)=2AM,∵∠BAD=120°,∴∠PAM=60°,易知PA=2AM,∴AE+AF=PA.(3)结论:AF+AE=PA•cos.理由:如图2中,作PM⊥AD于M,PN⊥AC于N.由(1)可知Rt△PMF≌Rt△PNE,∴FM=NE,∵PA=PA,PM=PN,∴Rt△PAM≌Rt△PAN,∴AM=AN,∴AF+AE=(AM+FM)+(AN﹣EN)=2AM,∵∠BAD=θ,∴∠PAM=,易知AM=PA•cos,∴AF+AE=PA•cos.8.【解答】(1)证明:如图1中,延长FH交BC的延长线于M/∵四边形ABCD是菱形,∴AD∥BM,∴∠DFH=∠M,在△FDH和△MCH中,‘,∴△FDH≌△MCH,∴FH=HM,∵FE⊥BC,∴∠FEM=90°,∴EH=FH=HM,∴EH=FH.(2)解:如图2中,①当FD=FH时,设∠M=∠DFH=x,∵BE=EC,CH=DH,BC=CD,∴EC=CH,∴∠CEH=∠CHE,∵HE=HM,∴∠CEH=∠CHE=∠M=x,∴∠HCM=∠ECH+∠EHC=2x=∠D=∠FHD,∵∠DFH+∠D+∠FHD=180°,∴x+2x+2x=180°,∴5x=180°,∴x=36°,∴∠D=72°.②当∠D=90°时,易知DF=DH,△DEF是等腰直角三角形,综上所述,当△DFH是等腰三角形时,∠D=72°或90°.9.【解答】(1)证明:∵四边形ABCD是菱形,∴CD=AB,∠ACD=∠ACB,在△DCE和△BCE中,,∴△DCE≌△BCE(SAS),∴∠CDE=∠CBE,∵CD∥AB,∴∠CDE=∠AFD,∴∠EBC=∠AFD,即∠F=∠EBC;(2)解:分两种情况:①如图1,当F在AB延长线上时,∵∠EBF为钝角,∴只能是BE=BF,设∠BEF=∠BFE=x°,解得:x=30,∴∠EFB=30°;②如图2,当F在线段AB上时,∵∠EFB为钝角,∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,可证得:∠AFD=∠FDC=∠CBE,得x+2x=90,解得:x=30,∴∠EFB=120°.综上:∠F=30°或120°.10.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠BCA=60°,∵E是线段AC的中点,∴∠CBE=∠ABE=30°,AE=CE,∵CF=AE,∴CE=CF,∴∠F=∠CEF=∠BCA=30°,∴∠CBE=∠F=30°,∴BE=EF;(2)解:结论成立;理由如下:过点E作EG∥BC交AB于点G,如图2所示:∵四边形ABCD为菱形,∴AB=BC,∠BCD=120°,AB∥CD,∴∠ACD=60°,∠DCF=∠ABC=60°,∴∠ECF=120°,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∠AGE=60°,∴BG=CE,∠BGE=120°=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF.(3)解:结论成立.证明如下:过点E作EG∥BC交AB延长线于点G,如图3所示:∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,∴∠ECF=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∠AGE=60°,∴BG=CE,∠AGE=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF.11.【解答】解:拓展:∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.∵∠A=∠F,∴∠BCD=∠ECG.∴∠BCD﹣∠ECD=∠ECG﹣∠ECD,即∠BCE=∠DCG.在△BCE和△DCG中,,∴△BCE≌△DCG(SAS),∴BE=DG.(6分)应用:∵四边形ABCD为菱形,∴AD∥BC,∵BE=DG,∴S△ABE+S△CDE=S△BEC=S△CDG=8,∵AE=2ED,∴S△CDE=×8=,∴S△ECG=S△CDE+S△CDG=,∴S菱形CEFG=2S△ECG=.故答案为:.(9分)12.【解答】(1)证明:取BC的中点G,连接OG∵四边形ABCD是菱形,∠A=60°∴∠A=∠C=∠ABD=60°,AB=BC=CD=DA,∵点O为菱形ABCD的对称中心,∴OD=OB∴OG∥CD ∴∠BGO=∠C=60°,OG=OB∵△OEF是等边三角形,∴∠EOF=60°,∴∠BOM=∠NOG又∵∠BGO=∠ABD=60°在△OBM和△OGN中,,∴△OBM≌△OGN(ASA),∴OM=ON;(2)证明:取BC中点G,同理可证:△OBM≌△OGN,∴BM=GN,∴BG=BN﹣NG,∴BN﹣BM=BG=AB.17.【解答】解:(1)如图,连接AC与BD相交于点G,在菱形ABCD中,AC⊥BD,BG=BD=×16=8,由勾股定理得,AG===6,∴AC=2AG=2×6=12,菱形ABCD的面积=AC•BD=×12×16=96;故答案为:12;96;(2)如图1,连接AO,则S△ABD=S△ABO+S△ADO,所以,BD•AG=AB•OE+AD•OF,即×16×6=×10•OE+×10•OF,解得OE+OF=9.6是定值,不变;(3)如图2,连接AO,则S△ABD=S△ABO﹣S△ADO,所以,BD•AG=AB•OE﹣AD•OF,即×16×6=×10•OE﹣×10•OF,解得OE﹣OF=9.6,是定值,不变,所以,OE+OF的值变化,OE、OF之间的数量关系为:OE﹣OF=9.6.3、矩形1.【解答】(1)证明:∵AD∥BC,∴∠ABC+∠BAD=180°,∵∠ABC=90°,∴∠BAD=90°,∴∠BAD=∠ABC=∠ADC=90°,∴四边形ABCD是矩形.(2)作OF⊥BC于F.∵四边形ABCD是矩形,∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,∴AO=BO=CO=DO,∴BF=FC,∴OF=CD=1,∵DE平分∠ADC,∠ADC=90°,∴∠EDC=45°,在Rt△EDC中,EC=CD=2,∴△OEC的面积=•EC•OF=1.2.【解答】(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOD=90°,又∵DE∥AC,AE∥BD,∴四边形AODE是平行四边形,∴四边形AODE是矩形.(2)解:∵∠BCD=120°,四边形ABCD是菱形,∴∠BAD=∠BCD=120°,∠CAB=∠CAD=60°,AB=BC,∴△ABC是等边三角形,∴AC=AB=2,OB=OD=AE=3,在Rt△AEC中,EC===.3.【解答】(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,∴AE=AB=10,AE2=102=100,又∵AD2+DE2=82+62=100,∴AD2+DE2=AE2,∴△ADE是直角三角形,且∠D=90°,又∵四边形ABCD为平行四边形,∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);(2)解:设BF=x,则EF=BF=x,EC=CD﹣DE=10﹣6=4cm,FC=BC﹣BF=8﹣x,在Rt△EFC中,EC2+FC2=EF2,即42+(8﹣x)2=x2,解得x=5,故BF=5cm;(3)解:在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,∵AB=10cm,BF=5cm,∴AF==5cm.4.【解答】证明:(1)∵AB∥CD,且FC=AB,∴四边形ABCF为平行四边形,∵∠B=90°,∴四边形ABCF是矩形;(2)∵EA=EG,∴∠EAG=∠EGA=∠FGC,∵四边形ABCF为矩形,∴∠AFC=∠AFD=90°,∴∠D+∠DAF=∠FGC+∠ECD=90°,∴∠D=∠ECD,∴ED=EC.5.【解答】(1)证明:∵AO=CO,BO=DO;∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴OC=OD,∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°.6.【解答】(1)证明:连接BG和CE交于O,∵四边形ABDE和四边形ACFG是正方形,∴AB=AE,AC=AG,∠EAB=∠GAC,∴∠EAB+∠EAG=∠GAC+∠EAG,∴∠GAB=∠EAC,在△BAG和△EAC中,,∴△BAG≌△EAC(SAS),∴BG=CE.(2)四边形PQMN为正方形,证明:∵EB、BC、CG、GE的中点分别是P、Q、M、N,∴PN∥BG,MN=CE,MN∥CE,PQ=CE,PQ∥CE,PN=BG,∵BG=CE,∴PN=MN,MN=PQ,MN∥PQ,∴四边形PQMN是菱形,∵△BAG≌△EAC,∴∠GBA=∠AEC,∵四边形ABDE是正方形,∴∠EAB=90°,∴∠ABG+∠BWA=90°,∵∠BWA=∠GWE,∴∠GWE+∠AEC=90°,∴∠EOW=180°﹣90°=90°,∵MN∥CE,PN∥BG,∴∠NZO=∠EOW=90°,∠NIO=90°,∴∠MNP=360°﹣90°﹣90°﹣90°=90°;∴菱形PQMN是正方形,即四边形PQMN为正方形.7.【解答】(1)答:AB=AH,证明:延长CB至E使BE=DN,连接AE,∵四边形ABCD是正方形,∴∠ABC=∠D=90°,∴∠ABE=180°﹣∠ABC=90°又∵AB=AD,∵在△ABE和△ADN中,,∴△ABE≌△ADN(SAS),∴∠1=∠2,AE=AN,∵∠BAD=90°,∠MAN=45°,∴∠2+∠3=90°﹣∠MAN=45°,∴∠1+∠3=45°,即∠EAM=45°,∵在△EAM和△NAM中,,∴△EAM≌△NAM(SAS),又∵EM和NM是对应边,∴AB=AH(全等三角形对应边上的高相等);(2)作△ABD关于直线AB的对称△ABE,作△ACD关于直线AC的对称△ACF,∵AD是△ABC的高,∴∠ADB=∠ADC=90°∴∠E=∠F=90°,又∵∠BAC=45°∴∠EAF=90°延长EB、FC交于点G,则四边形AEGF是矩形,又∵AE=AD=AF∴四边形AEGF是正方形,由(1)、(2)知:EB=DB=2,FC=DC=3,设AD=x,则EG=AE=AD=FG=x,∴BG=x﹣2;CG=x﹣3;BC=2+3=5,在Rt△BGC中,(x﹣2)2+(x﹣3)2=52;解得x1=6,x2=﹣1,故AD的长为6.8.【解答】(1)解:由题意得:∠BAC=∠BCA=45°,AO=PA,∠AEO=∠AFO,在△AEO和△CFO中,∴△AEO≌△CFO(AAS)∴OE=OF(相等);(1分)(2)解:OE=OF,OE⊥OF;(3分)证明:连接BO,∵在正方形ABCD中,O为AC中点,∴BO=CO,BO⊥AC,∠BCA=∠ABO=45°,(4分)∵PF⊥BC,∠BCO=45°,∴∠FPC=45°,PF=FC.∵正方形ABCD,∠ABC=90°,∵PF⊥BC,PE⊥AB,∴∠PEB=∠PFB=90°.∴四边形PEBF是矩形,∴BE=PF.(5分)∴BE=FC.∴△OBE≌△OCF,∴OE=OF,∠BOE=∠COF,(7分)∵∠COF+∠BOF=90°,∴∠BOE+∠BOF=90°,∴∠EOF=90°,∴OE⊥OF.(8分)(3)OE=OF(相等),OE⊥OF(垂直).(10分)9.【解答】(1)PB=PQ,证明:过P作PE⊥BC,PF⊥CD,∵P,C为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形,∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ;(2)PB=PQ,证明:过P作PE⊥BC,PF⊥CD,∵P,C为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形,∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ.10.【解答】解:(1)结论:DM=EM.理由:如图1,延长EM交AD于点H,∵四边形ABCD和ECGF是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,,∴△FME≌△AMH,∴HM=EM,在直角△HDE中,HM=EM,∴DM=HM=EM,∴DM=EM.(2)成立.(证明方法类似),11.【解答】(1)证明:∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∴∠ABF=135°,∵∠BCD=90°,∴∠ABF=∠ACD,∵CB=CD,CB=BF,∴BF=CD,在△ABF和△ACD中,,∴△ABF≌△ACD(SAS),∴AD=AF;(2)答:四边形ABNE是正方形;理由如下:证明:由(1)知,AF=AD,△ABF≌△ACD,∴∠FAB=∠DAC,∵∠BAC=90°,∴∠EAB=∠BAC=90°,∴∠EAF=∠BAD,在△AEF和△ABD中,,∴△AEF≌△ABD△AEF≌△ABD(SAS),∴BD=EF;∵CD=CB,∠BCD=90°,∴∠CBD=45°,∵∠EAB=90°,△AEF≌△ABD,∴∠AEF=∠ABD=90°,∴四边形ABNE是矩形,又∵AE=AB,∴四边形ABNE是正方形.12.【解答】证明:(1)如图,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,∴∠CBF=180°﹣∠ABC=90°,∠1+∠2=∠DCB=90°,∵CF⊥CE,∴∠ECF=90°,∴∠3+∠2=∠ECF=90°,∴∠1=∠3,在△CDE和△CBF中,,∴△CDE≌△CBF,(2)在正方形ABCD中,AD∥BC,∴△GBF∽△EAF,∴,由(1)知,△CDE≌△CBF,∴BF=DE=,∵正方形的边长为1,∴AF=AB+BF=,AE=AD﹣DE=,∴,∴BG=,∴CG=BC﹣BG=13.【解答】(1)证明:∵四边形ABCD和AEFG都是正方形,∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,∴BE=AB﹣AE,DG=AD﹣AG,∴BE=DG,在△BEF和△DGF中,,∴△BEF≌△DGF(SAS),∴BF=DF;(2)解:∵BF=DF;∴点F在对角线AC上,∵AD∥EF∥BC,∴CF:BE=AF:AE=AE:AE=,∴CF:BE=.14.【解答】证明:(1)连接OB,∵在正方形ABCD中,O是AC的中点,∴OB=OA,∠OAB=∠OBA=∠OBC=45°,∴∠AOB=90°,又∵OE⊥OF,∴∠AOF=∠BOE,在△AOF和△BOE中,,∴△AOF≌△BOE,∴OE=OF;(2)①∵∠EOF=∠FBE=90°,∴O,E,F,B四点共圆,∴∠OBA=∠OEF,∵在矩形ABCD中,O是AC的中点,∴OA=OB,∠OAB=∠OBA,∴∠OEF=∠BAC;②如图,连接BD,延长EO交AD于G,∵BD与AC交于O,则△OGD≌△DEB,∴OG=OE,∴AG=CE,∵OF⊥GE,∴FG=EF,在Rt△AGF中,GF2=AG2+AF2,即EF2=CE2+AF2.15.【解答】解:(1)证明:∵四边形ABCD是正方形,∴∠ABD=∠CBD=45°,AB=CB,在△ABE和∠CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE;∵AE=CE,AE=EN,∴∠EAC=∠ECA,CE=EN,∴∠ECN=∠N,∵∠EAC+∠ECA+∠ECN+∠N=180°,∴∠ACE+∠ECN=90°,即∠ACN=90°,∴△CAN为直角三角形;(2)∵正方形的边长为6,∴AC=BD=6,∵∠ACN=90°,AN=4,∴CN==2,∵OA=OC,AE=EN,∴OE=CN=,∵OB=BD=3,∴BE=OB+OE=4.16.【解答】解:(1)结论:FG=CE,FG∥CE.理由:如图1中,设DE与CF交于点M.∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠DCE=90°,在△CBF和△DCE中,,∴△CBF≌△DCE,∴∠BCF=∠CDE,CF=DE,∵∠BCF+∠DCM=90°,∴∠CDE+∠DCM=90°,∴∠CMD=90°,∴CF⊥DE,∵GE⊥DE,∴EG∥CF,∵EG=DE,CF=DE,∴EG=CF,∴四边形EGFC是平行四边形.∴GF=EC,∴GF=EC,GF∥EC.故答案为:FG=CE,FG∥CE;(2)结论仍然成立.理由:如图2中,设DE与CF交于点M.∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠DCE=90°,在△CBF和△DCE中,,∴△CBF≌△DCE,∴∠BCF=∠CDE,CF=DE,∵∠BCF+∠DCM=90°,∴∠CDE+∠DCM=90°,∴∠CMD=90°,∴CF⊥DE,∵GE⊥DE,∴EG∥CF,∵EG=DE,CF=DE,∴EG=CF,∴四边形EGFC是平行四边形.∴GF=EC,∴GF=EC,GF∥EC.17.【解答】解:(1)∵四边形ABCD是正方形,∴△ABD是等腰直角三角形,∴2AB2=BD2,∵BD=,∴AB=1,∴正方形ABCD的边长为1;(2)EM=CN.理由如下:连接FN,∵CF=CA,CE是∠ACF的平分线,∴CE⊥AF,∴∠AEN=∠CBN=90°,∵∠ANE=∠CNB,∴∠BAF=∠BCN,在△ABF和△CBN中,,∴△ABF≌△CBN(AAS),∴BF=BN,∴∠CBN=∠FNB=45°,∵四边形ABCD是正方形,∴∠DBC=45°,∵EO∥BC,∴∠EOM=∠DBC=45°,∠OEM=∠FCN,∴∠CFN=∠EOM,∴△CFN∽△EOM,∴,即.∴EM=CN.18.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,∴∠ABF=∠CBE.在△ABF和△CBE中,,∴△ABF≌△CBE(SAS).(2)解:结论:FE2=FA2+FC2.理由如下:∵△EBF是等腰直角三角形,∴∠BFE=∠FEB=45°,∴∠AFB=180°﹣∠BFE=135°,又∵△ABF≌△CBE,∴∠CEB=∠AFB=135°,∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,∴△CEF是直角三角形,∵FE2=FC2+EC2,∵△ABF≌△CBE,∴AF=EC,∴FE2=FA2+FC2.故答案为FE2=FA2+FC2.20.【解答】解:(1)BM=DF,BM⊥DF.理由:∵四边形ABCD、AMEF是正方形,∴AF=AM,AD=AB,∠FAM=∠DAB=90°,∴∠FAM﹣∠DAM=∠DAB﹣∠DAM,即∠FAD=∠MAB,∵在△FAD和△MAB中,,∴△FAD≌△MAB,∴BM=DF,∠FDA=∠ABD=45°,∵∠ADB=45°,∴∠FDB=45°+45°=90°,∴BM⊥DF,即BM=DF,BM⊥DF.(2)BM=DF,BM⊥DF都成立,理由是:∵四边形ABCD和AMEF均为正方形,∴AB=AD,AM=AF,∠BAD=∠MAF=90°,∴∠FAM+∠DAM=∠DAB+∠DAM,即∠FAD=∠MAB,∵在△FAD和△MAB中,,∴△FAD≌△MAB,∴BM=DF,∠ABM=∠ADF,由正方形ABCD知,∠ABM=∠ADB=45°,∴∠BDF=∠ADB+∠ADF=90°,即BM⊥DF,∴(1)中的结论仍成立.21.【解答】(1)证明:∵E是BC的中点,∴BE=CE,在正方形ABCD和正方形BFGE中,BC=CD,BE=BF,∴BF=CE,在△BCF和△CDE中,,∴△BCF≌△CDE(SAS),∴DE=CF;(2)解:设CE=x,∵∠CDE=30°,∴tan∠CDE==,∴CD=x,∵正方形ABCD的边BC=CD,∴BE=BC﹣CE=x﹣x,∵正方形BFGE的边长BF=BE,∴tan∠BCF===,∵正方形BGFE对边BC∥GF,∴∠BCF=∠GFH,∵tan∠GFH=,∴=.。
2023年中考九年级数学高频考点 专题训练--平行四边形的判定

2023年中考九年级数学高频考点专题训练--平行四边形的判定一、综合题1.如图,在□ ABCD中,点E、F在对角线BD上,且BE=DF.(1)求证:AE=CF;(2)求证:四边形AECF是平行四边形.2.如图,E、F是平行四边形ABCD对角线AC上两点,且AE=CF.(1)求证:四边形BFDE是平行四边形.(2)如果把条件AE=CF改为BE⊥AC,DF⊥AC,试问四边形BFDE是平行四边形吗?为什么?(3)如果把条件A E=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?3.如图,平行四边形ABCD 中,AB=8 cm,BC=12 cm,⊥B=60°,G 是CD 的中点,E 是边AD 上的动点,EG 的延长线与BC 的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF 是平行四边形;(2)①AE=cm 时,四边形CEDF 是矩形,请写出判定矩形的依据(一条即可);②AE=cm 时,四边形CEDF 是菱形,请写出判定菱形的依据(一条即可).4.如图,四边形ABCD中,AD⊥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.(1)求证:四边形ABCD是平行四边形.(2)若⊥BAE=⊥BDC,AE=3,BD=9,AB=4,求四边形ABCD的周长.5.如图,直线y=−2x+10与x轴交于点A,点B是该直线上一点,满足OB=OA.(1)求点B的坐标;(2)若点C是直线上另外一点,满足AB=BC,且四边形OBCD是平行四边形,试画出符合要求的大致图形,并求出点D的坐标.6.如图,在⊥ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若⊥A=50°,则当⊥BOD= °时,四边形BECD是矩形.7.如图,在⊥AFC中,⊥FAC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD。
中考数学总复习《平行四边形的性质》练习题及答案

中考数学总复习《平行四边形的性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图,在▱ABCD中,E为BC的中点,DE、AC交于点F,则EFDF的值为()A.1B.13C.23D.122.在□ ABCD中,∠A=70∘,则∠B度数为()A.110∘B.100∘C.70∘D.20∘3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是()A.AC⊥BD B.AO=OD C.AC=BD D.OA=OC4.如图,▱ABCD中,CE平分∠BCD,交AB于点E,AE=3,BE=5,DE=4,则CE的长为()A.4√5B.5√5C.5√2D.6√25.如图,在平行四边形ABCD中,⊥A=130°,在AD上取DE=DC,则⊥ECB的度数是()A.65°B.50°C.60°D.75°6.已知▱ABCD中,∠A+∠C=70°,则∠B的度数为()A.125°B.135°C.145°D.155°7.在平行四边形ABCD中,若⊥A+⊥C=80°,则⊥B的度数是()A.140°B.100°C.40°D.120°8.如图,在▱ABCD中,点F是线段CD上一点,点A作▱BFGE,当点F从点C向点D运动过程中,四边形BFGE的面积的变化情况是()A.保持不变B.一直减小C.一直增大D.先增大后减小9.如图,在平行四边形ABCD中,⊥BAD的平分线交BC于点E,⊥ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为()A.13B.14C.15D.1610.如图,在⊥ABCD中,点E是DC边上一点,连接AE,BE,若AE,BE分别是⊥DAB,⊥CBA的角平分线,且AB=4,则⊥ABCD的周长为()A.10B.8 C.5 D.1211.如图,▱ABCD的对角线AC,BD交于点O,EF和GH过点O,且点E,H在边DC上,点G,F 在边AB上,若▱ABCD的面积为10,则阴影部分的面积为()A.6B.4C.3D.5212.如图,平行四边形ABFC的对角线x∈(1,e)相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则SΔEOG的面积为()A.4B.5C.2D.3二、填空题13.如图,E是⊥ABCD边BC上一点,且AB=BE,连结AE,并延长AE与DC的延长线交于点F,⊥F=70°,则⊥D=度.14.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点处.若∠1=∠2=50∘,则为.15.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若⊥BOC的周长比⊥AOB的周长大2cm,则CD=cm.16.在平行四边形ABCD中,⊥BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于.17.如图,已知⊥ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标18.如图,E、F分别是⊥ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S⊥APD=10cm2,S⊥BQC=20cm2,则阴影部分的面积为cm2.三、综合题19.如图,▱ABCD中,以A为圆心,DA的长为半径画弧,交BA于点F,作⊥DAB的角平分线,交CD于点E,连接EF.(1)求证:四边形AFED是菱形;(2)若AD=4,⊥DAB=60°,求四边形AFED的面积.20.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC 是等边三角形.(1)求证:四边形ABCD是菱形.(2)若AC=8,AB=5,求ED的长.21.如图,在▱ABCD中AE⊥BC于E,AF⊥CD于F,且CE=CF.(1)求证:AE=AF;(2)求证:四边形ABCD是菱形.22.如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.(1)求证:四边形ACED是矩形;(2)若⊥AOD=120°,AC=4,求对角线CD的长.23.图1,图2都是8×8的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点.(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);(2)图2中所画的平行四边形的面积为.24.如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是⊥BAD的平分线,交边DC的延长线于点F.(1)证明:CE=CF;(2)若⊥B=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.(如图2所示)参考答案1.【答案】D2.【答案】A3.【答案】D4.【答案】A5.【答案】A6.【答案】C7.【答案】A8.【答案】A9.【答案】D10.【答案】D11.【答案】D12.【答案】C13.【答案】4014.【答案】105°15.【答案】416.【答案】217.【答案】(3,2),(﹣5,2),(1,﹣2)18.【答案】3019.【答案】(1)证明:∵AE为⊥DAB的角平分线∴⊥DAE=⊥EAF∵AB//CD∴⊥DEA=⊥EAF∴⊥DAE=⊥DEA∴AD=DE∵AD=AF∴DE=AF∵DE//AF∴四边形AFED为平行四边形∵AD=DE∴四边形AFED是菱形.(2)解:连接DF交AE于点O,如图所示:∵⊥DAB=60°,DA=AF ∴⊥DAF为等边三角形∵AD=4∴DF=4,DO=2∴AO= 2√3,AE= 4√3∴S四边形AFED= 12×4×4√3= 8√3.20.【答案】(1)证明:∵四边形ABCD是平行四边形∴AO=CO∵⊥EAC是等边三角形∴EA=EC∴EO⊥AC∴四边形ABCD是菱形(2)解:∵四边形ABCD是菱形,AC=8∴AO=CO=4,DO=BO在Rt⊥ABO中,BO=√AB2−AO2=3∴DO=BO=3在Rt⊥EAO中,EO=√EA2−AO2=4√3∴ED=EO-DO=4√3-3.21.【答案】(1)证明:∵AE⊥BC于E,AF⊥CD于F.∴△ACE与△ACF为直角三角形∵CE=CF,AC=AC∴Rt△ACE≌Rt△ACF(HL)∴AE=AF;(2)证明:∵在▱ABCD中,AE⊥BC于E,AF⊥CD于F ∴∠B=∠D∵AE=AF(已证)∴△ABE≌△ADF(AAS)∴AB=AD∴▱ABCD为菱形.22.【答案】(1)证明:四边形ABCD是平行四边形AD⊥BC,AD=BC,AB=DCCE=BCAD=CE,AD⊥CE四边形ACED是平行四边形AB=DC,AE=ABAE=DC四边形ACED是矩形;(2)解:四边形ACED是矩形,OA= 12AE,OC=12CD,AE=CD,OA=OC⊥AOC=180°-⊥AOD=180°-120°=60°⊥AOC是等边三角形OC=AC=4CD=8.23.【答案】(1)解:如图1,如图2;(2)624.【答案】(1)证明:如图(1)∵AE 是⊥BAD 的平分线 ∴⊥BAF=⊥DAF∵在平行四边形ABCD 中 ∴AB⊥DF ,AD⊥BC ∴⊥BAF=⊥F ,⊥DAF=⊥CEF ∴⊥F=⊥DAF=⊥CEF ∴CE=FC(2)解:四边形ABFC 是矩形 理由:如图(2)∵⊥B=60°,AD⊥BC ∴⊥BAD=120° ∵⊥BAF=⊥DAF ∴⊥BAF=60°则⊥ABE 是等边三角形可得AB=BE=AE ,⊥BEA=⊥AFC=60° ∵BC=2AB ∴AE=BE=EC∴⊥ABC 是直角三角形,⊥BAC=90° 在⊥ABE 和⊥FCE 中 ∵{∠ABE =∠FCE BE =EC ∠BEA =∠CEF ∴⊥ABE⊥⊥FCE (ASA ) ∴AB=FC 又∵AB⊥FC∴四边形ABFC 是平行四边形 再由⊥BAC=90°故四边形ABFC 是矩形.。
中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图在四边形ABCD中AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是()A.CF=AE B.OE=OFC.△CDE为直角三角形D.四边形ABCD是平行四边形2.如图四边形ABCD中AB∥CD,∥B=∥D点E为BC延长线上一点,连接AE,AE交CD于点H,∥DCE的平分线交AE于点G.若AB=2AD=10,点H为CD的中点,HE=6,则AC的值为()A.9B.√97C.10D.3 √103.如图在Rt∥ABC中∥ACB=90°,分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE,连结DE,CA的延长线交DE于点F,则与线段AF相等的是()A.AC B.AB C.BC D.AB4.如图在菱形ΑΒCD中∠Α=60∘,AD=8,F是ΑΒ的中点.过点F作FΕ⊥ΑD,垂足为Ε.将ΔΑΕF沿点Α到点Β的方向平移,得到ΔΑ′Ε′F ′.设Ρ、Ρ′分别是ΕF、Ε′F ′的中点,当点Α′与点Β重合时,四边形ΡΡ′CD的面积为()A.28√3B.24√3C.32√3D.32√3−85.下列说法中错误的是()A.平行四边形的对角线互相平分B.对角线互相垂直的四边形是菱形C.菱形的对角线互相垂直D.对角线互相平分的四边形是平行四边形6.如图.若要使平行四边形ABCD成为菱形.则需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD7.如图点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∥ABC+∥ADC=120°,则∥A的度数是()A.100°B.110°C.120°D.125°8.如图在∥ABC中AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则∥BED与∥DFC的周长的和为()A.34B.32C.22D.209.如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4),当四边形ABCD 的周长最小时,则m 的值为().A.√2B.32C.2D.310.如图分别在四边形ABCD的各边上取中点E,F,G,H,连接EG,在EG上取一点M,连接HM,过F作FN∥HM,交EG于N,将四边形ABCD中的四边形①和②移动后按图中方式摆放,得到四边形AHM′G′和AF′N′E,延长M′G′,N′F′相交于点K,得到四边形MM′KN′.下列说法中错误的是()A.S四边形MM′KN′=S四边形ABCD B.HM=NFC.四边形MM′KN′是平行四边形D.∠K=∠AHM′11.如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为()A.2B.3C.4D.512.如图P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若S四边形AHPE=3,S四边形PFCG=5,则S∥PBD为()A.0.5B.1C.1.5D.2二、填空题13.如图在平行四边形ABCD中点E,F分别在BC,AD上,请添加一个条件,使四边形AECF是平行四边形(只填一个即可).14.如图在Rt△ABC中AC=2√3,BC=2,点P是斜边AB上任意一点,D是AC的中点,连接PD并延长,使DE=PD.以PE,PC为边构造平行四边形PCQE,则对角线PQ的最小值为.15.如图▱ABCD中∥BAD=120°,E、F分别在CD和BC的延长线上,AE∥BD,EF∥BC,EF=5√3,则AB的长是16.如图在∥ABC中∥ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= 13BD,连接DM、DN、MN.若AB=6,则DN=.17.若AC=10,BD=8,那么当AO=DO=时,四边形ABCD是平行四边形。
中考数学复习《平行四边形》专项练习题-附带有答案

中考数学复习《平行四边形》专项练习题-附带有答案一、单选题1.平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为()A.1<AB<2 B.2<AB<10 C.4<AB<10 D.4<AB<202.如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是()A.四边形AEDF是平行四边形B.如果∠BAC=90°,那么四边形AEDF是矩形C.如果AD平分∠BAC,那么四边形AEDF是矩形D.如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形3.平行四边形ABCD与等边△AEF如图放置,如果∠B=45°,则∠BAE的大小是()A.75°B.70°C.65°D.60°4.如图是由七巧板拼成的正方形,则小正方形和大正方形的面积之比是()A.1:4 B.1:6 C.1:8 D.1:95.如图,D,E,F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是()A.∠BAC=90°B.BC=2AE C.DE平分∠AEB D.AE⊥BC6.如图,在菱形ABCD中∠A=60°,AB=4 O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则下列说法错误的是()A.点O为菱形ABCD的对称中心B.OE=2C.ΔCDB为等边三角形D.BD=47.如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若DF=2,BG=4则AE的长为( )A.4√7B.3√10C.10 D.128.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD,连接AC,交BE于点P,如图所示,若正方形ABCD的面积为28,AE+EB=7,则S△CFP−S△AEP的值是()A.3 B.3.5 C.4 D.7二、填空题9.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为cm.10.如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=3,则菱形ABCD的边长是.11.如图,平行四边形ABCD中AE⊥BC,AF⊥CD垂足分别为E、F,∠EAF=60°,DF=3cm则AD= cm.12.如图,在矩形ABCD中,AD=2AB,E是AD上一点,且BE=BC,则∠ECD的度数是.13.如图,正方形ABCD的边长为2,将它绕着中心O顺时针旋转45°得到正方形A′B′C′D′,与原正方形AD、AB边交于点M′,N,则M′N的长度是.三、解答题14.已知:如图,在▱ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.15.如图,在四边形ABCD中E,F分别为CD,AB上的点,且DE=BF,连接AE,CF若四边形AECF是平行四边形.求证:四边形ABCD是平行四边形.16.如图,矩形ABCD中,点P是BC中点,线段AP的延长线与DC的延长线交于点E.(1)求证:△ABP≌△ECP;(2)连接AC,BE,求证:四边形ABEC是平行四边形.17.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.18.如图,在□ABCD 中,以点 A 为圆心,AB 长为半径画弧交 AD 于点 F,再分别以点 B、F 为圆心, BF 的相同长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点 E,连接 EF.大于12(1)根据以上尺规作图的过程,证明四边形 ABEF 是菱形;(2)若菱形 ABEF 的边长为 2,AE= 2 √3,求菱形 ABEF 的面积.答案1.B2.C3.A4.C5.D6.B7.B8.B9.410.611.612.15°13.2√2−214.证明:在▱ABCD中,AB=CD,AB∥CD∴∠C=∠FBE∵BE=AB∴BE=CD在△BEF和△CDF中∴△BEF≌△CDF(AAS)15.解:∵四边形AECF是平行四边形∴AF=CE,AF//CE∵E,F分别为CD,AB上的点∴AB//CD∵DE=BF∴AF+BF=CE+DE,即AB=CD∴四边形ABCD是平行四边形.16.(1)证明:∵四边形ABCD矩形∴∠ABP=∠ECP=90°,AB//DC∴∠BAP=∠CEP∵点P是BC中点∴BP =CP∴△ABP ≌△ECP(AAS)(2)解:由△ABP ≌△ECP 可得AP =EP ∵点P 是BC 中点∴BP =CP∴四边形ABEC 是平行四边形.17.(1)证明:在△ABC 和△ADC 中{AB =AD CB =CD AC =AC∴△ABC ≌△ADC(SSS)∴∠BAC=∠DAC在△ABF 和△ADF 中{AB =AD∠BAF =∠DAF AF =AF∴△ABF ≌△ADF(SAS)∴∠AFB=∠AFD∵∠CFE=∠AFB∴∠AFD=∠CFE∴∠BAC=∠DAC ,∠AFD=∠CFE ;(2)证明:∵AB ∥CD∴∠BAC=∠ACD∵∠BAC=∠DAC∴∠BAC=∠ACD∴∠DAC=∠ACD∴AD=CD∵AB=AD ,CB=CD∴AB=CB=CD=AD∴四边形ABCD 是菱形;(3)解:BE ⊥CD 时,∠BCD=∠EFD ;理由如下: ∵四边形ABCD 是菱形∴BC=CD ,∠BCF=∠DCF∵CF=CF∴△BCF≌△DCF∴∠CBF=∠CDF∵BE⊥CD∴∠BEC=∠DEF=90°∴∠BCD=∠EFD.18.(1)解:根据题意由作法可知,AP平分∠BAF∴∠EAB=∠EAF∵AD∥BC∴∠EAF=∠AEB=∠EAB∴BE=AB=AF.∵AF∥BE∴四边形ABEF是平行四边形∵AB=BE∴四边形ABEF是菱形;(2)解:如图,连结BF,交AE于G.∵菱形ABEF的边长为2,AE= 2√3AE= √3,AE⊥BF ∴AB=BE=EF=AF=2,AG= 12∴∠AGF=90°,GF= √22−(√3)2=1∴BF=2GF=2×2√3×2=2√3∴菱形的面积为:S=12。
中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)

中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)学校:___________班级:___________姓名:___________考号:___________1.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,ab ≠0),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.2.(1)如图1,点P 为矩形ABCD 对角线BD 上一点,过点P 作//EF BC ,分别交AB 、CD 于点E 、F .若2BE =,PF=6,AEP △的面积为1S ,CFP 的面积为2S ,则12S S +=________;(2)如图2,点P 为ABCD 内一点(点P 不在BD 上),点E 、F 、G 、H 分别为各边的中点.设四边形AEPH 的面积为1S ,四边形PFCG 的面积为2S (其中21S S >),求PBD △的面积(用含1S 、S的代数式表示);2(3)如图3,点P为ABCD内一点(点P不在BD上)过点P作//EF AD,HG//AB与各边分别相交于点E、F、G、H设四边形AEPH的面积为1S,四边形PGCF的面积为2S(其中21),S S求PBD△的面积(用含1S、2S的代数式表示);(4)如图4 点A B C D把O四等分.请你在圆内选一点P(点P不在AC BD 上)设PB PC BC围成的封闭图形的面积为1S PA PD AD围成的封闭图形的面积为2S PBD△的面积为3S PAC△的面积为4S.根据你选的点P的位置直接写出一个含有1S2S3S4S的等式(写出一种情况即可).3.已知直线y=x+4与x轴y轴分别交于A B两点∠ABC=60°BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A C重合)同时动点Q从C点出发沿CBA向点A运动(不与C A重合) 动点P的运动速度是每秒1个单位长度动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S P点的运动时间为t秒求S与t的函数关系式并写出自变量的取值范围.(3)在(2)的条件下当△APQ的面积最大时y轴上有一点M 平面内是否存在一点N 使以A Q M N为顶点的四边形为菱形?若存在请直接写出N点的坐标;若不存在请说明理由.4.如图在等腰梯形ABCD中AB∥DC AB=8cm CD=2cm AD=6cm.点P 从点A出发以2cm/s的速度沿AB向终点B运动;点Q从点C出发以1cm/s的速度沿CD DA向终点A运动(P Q两点中有一个点运动到终点时所有运动即终止).设P Q同时出发并运动了t秒.(1)当PQ将梯形ABCD分成两个直角梯形时求t的值;(2)试问是否存在这样的t 使四边形PBCQ的面积是梯形ABCD面积的一半?若存在求出这样的t的值若不存在请说明理由.5.如图在平面直角坐标系中以坐标原点O为圆心2为半径画⊙O P是⊙O上一动点且P在第一象限内过点P作⊙O的切线与轴相交于点A与轴相交于点B.(1)点P在运动时线段AB的长度也在发生变化请写出线段AB长度的最小值并说明理由;(2)在⊙O上是否存在一点Q使得以Q O A P为顶点的四边形时平行四边形?若存在请求出Q点的坐标;若不存在请说明理由.6.如图已知长方形ABCD中AD=6cm AB=4cm 点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动同时点Q在线段BC上由点B向点C运动.(1)若点Q的运动速度与点P的运动速度相等经过1秒后△AEP与△BPQ是否全等请说明理由并判断此时线段PE和线段PQ的位置关系;(2)若点Q的运动速度与点P的运动速度相等运动时间为t秒设△PEQ的面积为Scm2请用t的代数式表示S;(3)若点Q的运动速度与点P的运动速度不相等当点Q的运动速度为多少时能够使△AEP与△BPQ全等?7.如图长方形ABCD中5cm,8cm==现有一动点P从A出发以2cm/s的速度沿AB BC----返回到点A停止设点P运动的时间为t秒.长方形的边A B C D At=时BP=___________cm;(1)当2(2)当t为何值时连接,,△是等腰三角形;CP DP CDP(3)Q为AD边上的点且6DQ=P与Q不重合当t为何值时以长方形的两个顶点及点P为顶点的三角形与DCQ全等.8.如图平行四边形ABCD中6cmB∠︒G是CD的中点E是BC==60AB=8cm边AD上的动点EG的延长线与BC的延长线交于点F连接CE DF.(1)求证:四边形CEDF是平行四边形;(2)①AE=______时四边形CEDF是矩形;②AE=______时四边形CEDF是菱形.9.在平面直角坐标系中点A在第一象限AB⊥x轴于点B AC⊥y轴于点C已知点B(b0)C(0 c)其中b c满足|b﹣8|6+-=0.c(1)直接写出点A坐标.(2)如图2 点D从点O出发以每秒1个单位的速度沿y轴正方向运动同时点E从点A出发以每秒2个单位的速度沿射线BA运动过点E作GE⊥y轴于点G设运动时间为t 秒当S四边形AEGC<S△DEG时求t的取值范围.(3)如图3 将线段BC平移使点B的对应点M恰好落在y轴负半轴上点C的对应点为N连接BN交y轴于点P当OM=4OP时求点M的坐标.10.如图在平面直角坐标系中点A B的坐标分别是(﹣4 0)(0 8)动点P从点O出发沿x轴正方向以每秒1个单位的速度运动同时动点C从点B出发沿12.在四边形ABCD中//,90,10cm,8cm∠=︒===点P从点A出发沿折线AB CD BCD AB AD BCABCD方向以3cm/s的速度匀速运动;点Q从点D出发沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发当一个点到达终点时另一点也停止运动设运动时间为()s t.(1)求CD的长;(2)当四边形PBQD为平行四边形时求四边形PBQD的周长;(3)在点P Q的运动过程中是否存在某一时刻使得BPQ的面积为220cm若存在请求出所有满足条件的t的值;若不存在请说明理由.13.在平面直角坐标系中矩形OABC的边OA任x轴上OC在y轴上B(4 3)点M从点A开始以每秒1个单位长度的速度沿AB→BC→CO运动设△AOM的面积为S 点M运动的时间为t.(1)当0<t<3时AM=当7<t<10时OM=;(用t的代数式表示)(2)当△AOM为等腰三角形时t=;(3)当7<t<10时求S关于t的函数关系式;(4)当S=4时求t的值.14.如图1 在平面直角坐标系中正方形OABC的边长为6 点A C分别在x y 正半轴上点B在第一象限.点P是x正半轴上的一动点且OP=t连结PC将线段PC绕点P顺时针旋转90度至PQ连结CQ取CQ中点M.(1)当t=2时求Q与M的坐标;(2)如图2 连结AM以AM AP为邻边构造平行四边形APNM.记平行四边形APNM 的面积为S.①用含t的代数式表示S(0<t<6).②当N落在△CPQ的直角边上时求∠CPA的度数;(3)在(2)的条件下连结AQ记△AMQ的面积为S'若S=S'则t=(直接写出答案).15.如图平面直角坐标系中矩形OABC的顶点B的坐标为(7 5)顶点A C 分别在x轴y轴上点D的坐标为(0 1)过点D的直线与矩形OABC的边BC交于点G 且点G不与点C重合以DG为一边作菱形DEFG 点E在矩形OABC的边OA 上设直线DG的函数表达式为y=kx+b(1)当CG=OD时求直线DG的函数表达式;(2)当点E的坐标为(5 0)时求直线DG的函数表达式;(3)连接BF 设△FBG的面积为S CG的长为a 请直接写出S与a的函数表达式及自变量a 的取值范围.16.如图 在四边形ABCD 中 //AD BC 3AD = 5DC = 42AB = 45B ∠=︒ 动点M 从点B 出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从点C 出发沿线段CD 以每秒1个单位长度的速度向终点D 运动 设运动的时间为s t .(1)求BC 的长.(2)当//MN AB 时 求t 的值(3)试探究:t 为何值时 MNC ∆为等腰三角形?参考答案:1.(1)证明:∵四边形ABCD 是矩形∴AD ∥BC∴∠CAD =∠ACB ∠AEF =∠CFE∵EF 垂直平分AC 垂足为O∴OA =OC∴△AOE ≌△COF∴OE =OF∴四边形AFCE 为平行四边形又∵EF ⊥AC∴四边形AFCE 为菱形设菱形的边长AF =CF =x cm 则BF =(8﹣x )cm在Rt △ABF 中 AB =4cm由勾股定理得42+(8﹣x )2=x 2解得x =5iii )如图3 当P 点在AB 上 Q 点在CD 上时 AP =CQ 即12﹣a =b 得a +b =12. 综上所述 a 与b 满足的数量关系式是a +b =12(ab ≠0).2.(1)过P 点作AB∥MN∵S 矩形AEPM +S 矩形DFPM =S 矩形CFPN +S 矩形DFPM =S 矩形ABCD -S 矩形BEPN又∵11,,22AEP CFP AEPM CFPN SS S S ==矩形矩形 ∴1==26=62AEP CFP S S ⨯⨯, ∴1212.S S +=(2)如图 连接PA PC在APB △中 因为点E 是AB 中点可设APE BPE S S a ==同理 ,,BPF CPF CPG DFG DPH APH S S b S S c S S d ======所以APE APH CPF AEPH PFCG CPG S S SS a b d S S c =+++=++++四边形四边形 BPE BPF DPH DPH EDFP HPGD S S S S S S a b c d +=+++=+++四边形四边形.所以12EBFP HPGD AEPH PFCG S S S S S S +++=+四边形四边形四边形四边形所以1212ABD ABCD SS S S ==+ 所以1DPH APH S S S a ==-. ()()()1121121PBD ABD BPE PDH S S S S S S S S a S a S S =-++=+-++-=-.(3)易证四边形EBGP 四边形HPFD 是平行四边形.EBP SHPD S .()()121211122222ABD ABCD EBF HPD EBP HPD SS S S S S S S S S ==+++=+++ ()()12112FBD ABD EBP HPD S S S S S S S =-++=-. (4)试题解析:(1)由已知得A 点坐标(﹣4﹐0) B 点坐标(0﹐43﹚ ∵OB=3OA ∴∠BAO=60° ∵∠ABC=60° ∴△ABC 是等边三角形 ∵O C=OA=4 ∴C 点坐标﹙4 0﹚ 设直线BC 解析式为y kx b =+∴ ∴直线BC 的解析式为343y x =-+; ﹙2﹚当P 点在AO 之间运动时 作QH⊥x 轴 ∵QH CQ OB CB= ∴2843QH t = ∴QH=3t ∴S △APQ =AP•QH=132t t ⋅=232t ﹙0<t≤4﹚ 同理可得S △APQ =t·﹙833t -﹚=23432t t -+﹙4≤t<8﹚∴223(04)2{343?(48)2t t S t t t <≤=-+≤<; (3)存在 如图当Q 与B 重合时 四边形AMNQ 为菱形 此时N 坐标为(4 0) 其它类似还有(﹣4 8)或(﹣4 ﹣8)或(﹣4 ).4.(1)53(2)存在 使四边形PBCQ 的面积是梯形ABCD 面积的一半.(1)过D 作DE⊥AB 于E 过C 作CF⊥AB 于F 通过Rt ADE Rt BCF ∆≅∆ 得AE BF = 若四边形APQD 是直角梯形 则四边形DEPQ 为矩形 通过AP AE EP =+ 代入t 值 即可求解(2)假设当时 通过点Q 在CD 上或在AD 上 两种情况进行讨论求解5.(1)线段AB 长度的最小值为4理由如下:连接OP如图② 设四边形APQO 为平行四边形因为OQ PA ∥ 90APO ︒∠=所以90POQ ︒∠= 又因为OP OQ =所以45PQO ︒∠= 因为PQ OA ∥所以PQ y ⊥轴.设PQ y ⊥轴于点H在Rt △OHQ 中 根据2,45OQ HQO ︒=∠= 得Q 点坐标为(2,2-)所以符合条件的点Q 的坐标为(2,2-)或(2,2-).6.(1)∵长方形ABCD∴∠A =∠B =90°∵点E 为AD 的中点 AD =6cm∴AE =3cm又∵P 和Q 的速度相等可得出AP =BQ =1cm BP =3 ∴AE =BP在△AEP 和△BQP 中∴y=xy 3=4-y⎧⎨⎩ 解得:x=1y=1⎧⎨⎩ (舍去). 综上所述,点Q 的运动速度为32cm /s 时能使两三角形全等.7.(1)1(2)54t =或4或232 (3) 3.5t = 5.5或10(1)解:动点P 的速度是2cm/s∴当2t =时 224AP =⨯=∵5cm AB =∴BP =1cm ;(2)解:①当点P 在AB 上时 CDP △是等腰三角形∴PD CP =在长方形ABCD 中 ,90AD BC A B =∠=∠=︒∴()HL DAP CBP ≌∴AP BP =∴1522AP AB ==∵动点P 的速度是2cm/s∵90D5DP CD == 2AB CB CD t ++=∴要使一个三角形与DCQ 全等①当点P运动到1P时16△≌△DCQ CDPCP DQ==此时1∴点P的路程为:1527AB BP+=+=∴72 3.5t=÷=;②当点P运动到2P时26△≌△CDQ ABPBP DQ==此时2∴点P的路程为:25611+=+=AB BP∴112 5.5t=÷=③当点P运动到3P时35△≌△CDQ BAP==此时3AP DQ∴点P的路程为:3585220AB BC CD DP+++=+++=∴20210t=÷=④当点P运动到4P时即P与Q重合时46△≌△CDQ CDPDP DQ==此时4∴点P的路程为:4585624+++=+++=AB BC CD DPt=÷=此结果舍去不符合题意∴24212综上所述t的值可以是: 3.5t= 5.5或10.8.(1)四边形ABCD是平行四边形∥∴BC AD∴∠=∠FCG EDGG是CD的中点∴=CG DG△中在CFG△和DEGCFG∴≅(ASA)DEGFG EG∴=又CG DG=∴四边形CEDF是平行四边形.2)①当5AE=如图过60B∠=12BM∴=5AE=DE AD∴=在MBA△BM DEB=⎧⎪∠=∠⎨⎪(SAS)MBA EDC∴≅CED AMB∴∠=∠四边形CEDF是平行四边形∴平行四边形CEDF②当2AE cm =时 四边形CEDF 是菱形 理由如下:四边形ABCD 是平行四边形8AD ∴= 6CD AB == 60CDE B ∠=∠=︒2AE =6DE AD AE ∴=-=DE CD ∴=CDE ∴∆是等边三角形CE DE ∴=四边形CEDF 是平行四边形∴平行四边形CEDF 是菱形故答案为:2;9.(1)解:∵|b ﹣8|6c +-=0∴b -8=0 c -6=0∴b =8 c =6∵B (b 0) C (0 c )∴B (8 0) C (0 6)又∵AB ⊥x 轴 AC ⊥y 轴∴A (8 6);(2)∵AB ⊥x 轴 AC ⊥y 轴 GE ⊥y 轴∴四边形AEGC 是矩形设运动时间为t 秒∴OD =t AE =2t DG =6+2t-t =6+t∴S 四边形AEGC =8×2t =16t S △DEG =12×(6+t )×8=4t +242∵OM=4OP∴-m=-4×62m解得m=-12综上所述m的值为-4或-12.10.(1)∵点A B的坐标分别是(﹣4 0)(0 8)∴OA=4 OB=8∵点C运动到线段OB的中点∴OC=BC=12OB=4∵动点C从点B出发沿射线BO方向以每秒2个单位的速度运动∴2t=4解之:t=2;∵PE=OA=4 动点P从点O出发沿x轴正方向以每秒1个单位的速度运动∴OE=OP+PE=t+4=2+4=6∴点E(6 0)(2)证明:∵四边形PCOD是平行四边形∴OC=PD OC∥PD当点C在y轴的负半轴上时③如果点M在DE上时24163(3)22t tt--=++解得423t=+④当N在CE上时28(3)8214tt tt-⋅++-=-+解得12t=综上分析可得满足条件的t的值为:t1=28﹣16 3t2=2 t3=4+2 3t4=12.11.(1) ()30D,,()1,3E;(2)933022933222572222t tS t tt t⎧⎛⎫-+≤≤⎪⎪⎝⎭⎪⎪⎛⎫=-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-≤⎪ ⎪⎝⎭⎩<(3)198s解:(1)3922y x=-+当y=0时39=022x-+则x=3 即点()30D,当y=3时39=322x-+则x=1 故点()1,3E故:()30D,,()1,3E;(2)如图1 ①当点P在OD段时此时0≤t<32119()2223233S PD OC t t=⨯⨯=⨯-⨯=-+;②当点P在点D时此时t=32此时三角形不存在0S=;''6ADP BEP S S -=-30232t t ⎛⎫≤≤ ⎪⎝⎭⎫<≤⎪;即当点P 在边AB 上运动 且PD PE +的值最小时 运动时间t 为198s . 12.(1)16cm ;(2)(8813)cm +;(3)53t =秒或395秒 解:(1)如图1过A 作AM DC ⊥于M在四边形ABCD 中 //AB CD 90BCD ∠=︒//AM BC ∴∴四边形AMCB 是矩形10AB AD cm == 8BC cm =8AM BC cm ∴== 10CM AB cm ==在Rt AMD ∆中 由勾股定理得:6DM cm =10616CD DM CM cm cm cm =+=+=;(2)如图2当四边形PBQD 是平行四边形时 PB DQ =即1032t t -=解得2t =此时4DQ = 12CQ = 22413BQ BC CQ =+=所以()28813PBQD C BQ DQ =+=+;1003t 14(102BPQ BP BC ==解得53t =;P 在BC 上时 63t1(32BP CQ t =此方程没有实数解;CD 上时:在点Q 的右侧54(34PQ BC =6< 不合题意若P 在Q 的左侧 如图6 即3485t <14(534)202BPQ S PQ BC t ∆==-= 解得395t =; 综上所述 当53t =秒或395秒时 BPQ ∆的面积为220cm . 13.(1)t 10-t ;(2)5;(3)S =20-2t ;(4)2或8. 解:(1)当0<t <3时 点M 在线段AB 上 即AM =t 当7<t <10时 点M 在线段OC 上 OM =10-t故填:t 10-t ;(2)∵四边形ABCO 是矩形 B (4 3)∴OA =BC =4 AB =OC =3∵△AOM 为等腰三角形∴只有当MA =MO 此时点M 在线段BC 上 CM =BM =2 ∴t =3+2=5故填:5;(3)∵当7<t <10时 点M 在线段OC 上∴114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-;(4)①当点M 在线段AB 上时 4=12×4t 解得t =2;②当点M 在线段BC 上时 S =6 不符合题意;当点M 在线段OC 上时 4=20-2t 解得t =8.∴OD =OP +PD =8∴Q (8 2)∵M 是CQ 的中点 C (0 6)∴M (4 4);(2)①∵△COP ≌△PDQ∴OP =OQ =t OC =PD =6∴OD =t +6∴Q (t +6 t )∵C (0 6)∴M (62t + 62t +) 当0<t <6时 S =AP ×y M =(6﹣t )×62t +=2362t -; ②分两种情况:a 当N 在PC 上时 连接OB PM 如图2﹣1所示:∵点M 的横 纵坐标相等∴点M 在对角线BD 上∵四边形OABC 是正方形∴OC =OA ∠COM =∠AOM∴∠MPA =12(180°﹣45°)=67.5° ∴∠CPA =67.5﹣45=22.5°;综上所述 当点N 在△CPQ 的直角边上时 ∠CPA 的度数为112.5°或22.5°;(3)过点M 作MH ⊥x 轴于点H 过点Q 作QG ⊥x 轴于点G∵AMQ AHM AGQ MHGQ S S S S =--△△△梯形∴S '=12(62t ++t )•62t +﹣12(6﹣62t +)•62t +﹣12t •t =3t ①当0<t <6时 即点AP 在点A 左侧时 如图3所示:∵S =S '∴2362t -=3t 解得:t =﹣3+35 或t =﹣3﹣35(舍去);②当t >6时 即点P 在点A 右侧时 如图4所示:S =AP ×y M =(t ﹣6)×62t +=2362t - ∵S =S '将D (0 1)G (10 5)代入y=kx+b 得:1105b k b =⎧⎪⎨+=⎪⎩解得:21051k b ⎧=⎪⎨⎪=⎩∴当CG=OD 时 直线DG 的函数表达式为y=2105x+1.(3)设DG 交x 轴于点P 过点F 作FM⊥x 轴于点M 延长MF 交BC 于点N 如图所示.∵DG∥EF∴∠FEM=∠GPO.∵BC∥OA∴∠DGC=∠GPO=∠FEM.在△DCG 和△FME 中90DCG FME DGC FEMDG FE⎧∠=∠=⎪∠=∠⎨⎪=⎩ ∴△DCG≌△FME(AAS )∴FM=DC=4.∵MN⊥x 轴∴四边形OMNC 为矩形在Rt△CDH 中 由勾股定理可得: HC=22543-=∴BC=BK+KH+HC=4+3+3=10;(2)如图② 过D 作DG∥AB 交BC 于G 点 则四边形ADGB 为平行四边形 ∴BG=AD=3∴GC=BC−BC=10−3=7由题意得 当M N 运动t 秒后 CN=t CM=10−2t∵AB∥DG MN∥AB∴DG∥MN∴∠NMC=∠DGC又∵∠C=∠C∴△MNC ~△GDC∴CN CM CD CG=, ∴10257tt -=解得t=5017; (3)第一种情况:当NC=MC 时 如图③22∵∠C=∠C∠MFC=∠DHC=90°∴△MFC~△DHC∴FC MCHC DC=即:1 102253tt-=解得:t=6017;综上所述当t=103t=258或t=6017时△MNC为等腰三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵∠DCF=∠BCD﹣∠BCF,∠BAE=∠DAB﹣∠DAE,
∴∠DCF=∠BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.
9、解答:证明:∵E是AC的中点,∴EC= AC,
又由AB∥DC,得∠AED=∠EDC∴∠EDC=∠BFC,∴ME∥NF∴四边形MFNE为平行四边形.
7、解答:证明:连接AC交BD于点O,
∵四边形ABCD为平行四边形,∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.∴四边形AECF为平行四边形.
8、解答:证明:∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
平行四边形的证明题
一.解答题(共30小题)
1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1)求证:BE=DF;
(2)若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状.
2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.
求证:四边形ABCD是平行四边形.
3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.
又∵四边形AODE是平行四边形,∴AE∥OD且AE=OD,∴AE∥OB且AE=OB,
∴四边形ABOE是平行四边形,同理可证,四边形DCOE也是平行四边形.
13、解答:证明:连接EG、GF、FH、HE,点E、F、G、H分别是AB、CD、AC、BD的中点.
在△ABC中,EG= BC;在△DBC中,HF= BC,
又∵D是EC的中点,∴DF=CD=DE=2,
在平行四边形ABCD中,AB∥CD,
∵∠ABC=60°,∴∠ECF=∠ABC=60°,∴△CDF是等边三角形,∴FC=DF=2.
故答案为:2.
19、解答:证明:(1)∵△ABC是等边三角形,∴∠ABC=60°,
∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥DC(内错角相等,两直线平行),
∴EG=HF.
同理EH=GF.
∴四边形EGFH为平行四边形.∴EF与GH互相平分.
14、解答:证明:∵四边形ABCD是平行四边形,∴AM∥QC,AP∥NC.
又∵MN∥AC,∴四边形AMQC为平行四边形,四边形APNC为平行四边形.
∴AC=MQ AC=NP.∴MQ=NP.
15、解答:证明:如答图所示,
(1)求证:AF=CE;
(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.
18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2
(1)求证:D是EC中点;
(2)求FC的长.
18题图 (19题图)
此时,BP=DQ=4,CQ=12∴
∴四边形PBQD的周长=2(BP+BQ)= ;
(3)①当点P在线段AB上时,即 时,如图
∴ .
②当点P在线段BC上时,即 时,如图
BP=3t﹣10,CQ=16﹣2t∴
化简得:3t2﹣34t+100=0,△=﹣44<,所以方程无实数解.
③当点P在线段CD上时,
求证:四边形AECF是平行四边形.
8.在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.
9.如图所示,DB∥AC,且DB= AC,E是AC的中点,求证:BC=DE.
10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
(2)四边形MENF是平行四边形.
证明:有(1)可知:BE=DF,∵四边形ABCD为平行四边行,
∴AD∥BC,∴∠MDB=MBD,
∵DM=BN,∴△DNF≌△BNE,∴NE=MF,∠MFD=∠NEB,∴∠MFE=∠NEF,
∴MF∥NE,∴四边形MENF是平行四边形.
2、解答:证明:∵四边形AECF是平行四边形
5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.
求证:四边形MFNE是平行四边形.
7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.
1、解答:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,∵AE⊥BD于E,CF⊥BD于F,
∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(A.A.S.),∴BE=DF;
19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.
证明:∵CE∥AB,∴∠DAO=∠ECO,
∵OA=OC,∴△ADO≌△ECO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD AE.
6、解答:证明:由平行四边形可知,AD=CB,∠DAE=∠FCB,
又∵AE=CF,∴△DAE≌△BCF,∴DE=BF,∠AED=∠CFB
又∵M、N分别是DE、BF的中点,∴ME=NF
又∵BA=DA,∴DA=EF
故四边形AFED为平行四边形(两组对边分别相等的四边形是平行四边形).
26、解答:解:(1)过点A作AM⊥CD于M,
根据勾股定理,AD=10,AM=BC=8,∴DM= =6,∴CD=16;
(2)当四边形PBQD为平行四边形时,
点P在AB上,点Q在DC上,如图,
由题知:BP=10﹣3t,DQ=2t∴10﹣3t=2t,解得t=2
12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.
13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD的中点,并且点E、F、G、H有在同一条直线上.
求证:EF和GH互相平分.
15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.
∵点O为平行四边形ABCD对角线AC,BD的交点,∴OA=OC,OB=OD.
∵G,H分别为OA,OC的中点,∴OG= OA,OH= OC,∴OG=OH.
又∵AB∥CD,∴∠1=∠2.
在△OEB和△OFD中,
∠1=∠2,OB=OD,∠3=∠4,
∴△OEB≌△OFD,
∴OE=OF.∴四边形EHFG为平行四边形.
(2)∵△ABE≌△CDF,∴∠ABE=∠CDF,∴AB∥CD,
∵AB=CD,∴四边形ABCD是平行四边形,∴AO=CO.
4、解答:证明:∵DE,DF是△ABC的中位线,∴DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,∴平行四边形AEDF是矩形,∴EF=AD.
5、解答:解:猜想线段CD与线段AE的大小关系和位置关系是:平行且相等.
16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
(1)求证:四边形GEHF是平行四边形;
(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
(17题图)
17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
证明如下:
在△BED与△BCA中,BE=BC,BD=BA(均为同一等边三角形的边)
∠DBE=∠ABC=60°﹣∠EBA
∴△BED≌△BCA(SAS)∴DE=AC
又∵AC=AF∴DE=AF
在△CBA与△CEF中,CB=CE,CA=CF
∠ACB=∠FCE=60°+∠ACE
∴△CBA≌△CEF(SAS)∴BA=EF
16、解答:(1)证明:∵四边形ABCD是平行四边形,
17、∴AB=CD,AB∥CD,∴∠GBE=∠HDF.
又∵AG=CH,∴BG=DH.
又∵BE=DF,∴△GBE≌△HDF.∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE,
∴GE∥HF,∴四边形GEHF是平行四边形.
(2)解:仍成立.(证法同上)
而∠ACB=135°,∴∠FCA=135°﹣90°=45°,∴∠FAC=45°,∴FC=FA,
∴矩形AFCE是正方形.
