常用傅里叶变换对
常见的傅里叶变换对

常见的傅里叶变换对
1.正弦函数:正弦函数是一种周期性的函数,其傅里叶变换是两个单独的脉冲,分别位于正负频率轴上。
2. 方形波:方形波是一种周期函数,其傅里叶变换包含了无限个频率成分,每个成分都是一个单独的脉冲,频率随着成分的增加而增加。
3. 三角波:三角波是一种周期函数,其傅里叶变换包含了无限个频率成分,每个成分都是一个单独的脉冲,频率随着成分的增加而增加,但比方形波少一半。
4. 高斯波包:高斯波包是一种非周期函数,其傅里叶变换也是一个高斯波包,但是频率上限是无限的。
5. 指数衰减波:指数衰减波是一种非周期函数,其傅里叶变换是一个复数,其幅度随着频率的增加而减小。
6. delta函数:delta函数是一种非常特殊的函数,其傅里叶变换是常数1,因此它是傅里叶变换中最简单的一种。
- 1 -。
常用傅里叶变换表

常用傅里叶变换表傅里叶变换(Fourier Transform)是一种重要的信号处理方法,可以将一个信号表示为频域上的复合波。
在实际应用中,我们常常需要用到一些常用的傅里叶变换表来简化计算过程。
下面是常用的傅里叶变换表。
1. 频域采样点数与时间域采样点数的对应关系:当时间域采样点数为 N 时,对应的频域采样点数为 N/2+1。
采样点数越多,则频域分辨率越高,对于高频信号的分析会更准确。
2. 傅里叶变换对称性:傅里叶变换具有一定的对称性,包括对称性、共轭对称性和反对称性。
利用这些对称性,我们可以简化计算过程。
- 偶函数的频谱是实数,在频域中左右对称;- 奇函数的频谱是虚数,具有共轭对称;- 复合偶函数和复合奇函数的频谱会具有反对称性。
3. 常用信号的傅里叶变换表:以下是一些常见的信号的傅里叶变换表:- 矩形脉冲信号(Rectangular Pulse)的傅里叶变换:矩形脉冲信号在时域上是一个宽度有限且幅度为常数的信号。
其傅里叶变换在频域上是一个 sinc 函数,表达式为:F(w) = wwww(ww/2) / (ww/2)其中,w是信号的宽度,w是频率。
- 高斯函数(Gaussian Function)的傅里叶变换:高斯函数在时域上是一个钟形曲线,其傅里叶变换仍然是一个高斯函数。
傅里叶变换的表达式如下:F(w) = ww^(−w^2w^2/4w^2)其中,w是高斯函数的标准差,w是时间尺度。
- 正弦函数(Sine Function)的傅里叶变换:正弦函数在时域上是一个连续的周期函数。
其傅里叶变换也是一个周期函数,表达式为:F(w) = 0.5j (w(w−w)−w(w+w))其中,w是正弦函数的频率。
4. 傅里叶变换的性质:傅里叶变换具有很多重要的性质,包括线性性质、平移性质、尺度性质、卷积定理等。
这些性质在信号处理中起到了重要的作用,可以简化傅里叶变换的计算过程。
- 线性性质:傅里叶变换具有线性性质,即线性组合的函数的傅里叶变换等于各个函数的傅里叶变换之和。
常用信号的傅里叶变换

ω1 Sa (ω 1t ) 2 cos ω c t f 5 ( t ) = f ( t ) 2 cos ω c t = π
东南大学 信息科学与工程学院
若再有 6 (ω ) = (ω ωc )t1
f 6 (t ) = f 5 (t t1 )
则
若又有 7
=
2ω1
π
Sa [ω1 (t t1 )] cos[ ω c (t t1 )]
东南大学 信息科学与工程学院
8. 周期信号
An jnΩt 2π fT (t ) = ∑ e , Ω = T n=∞ 2
+∞
+∞ +∞
An FT ( jω) = ∑ 2πδ(ω nΩ) = π ∑ An δ(ω nΩ) 则 n=∞ 2 n=∞
东南大学 信息科学与工程学院
9. 周期性冲激序列
f (t ) = =
π 4ω = {δ(ω+ ωc ) + δ(ω ωc )}+ 2 2 2 j(ω ωc )
东南大学 信息科学与工程学院
东南大学 信息科学与工程学院
4. 尺度变换(比例)性质:
1 ω f ( at ) F( j ) |a | a , a ≠ 0
< Bτ = 常数 >
例:
f ( at t 0 ) ?
j
ω
a
t0
=
dF ( j ω ) j ω dF ( j ω ) j e = e dω dω
j (ω +
π
2
)
东南大学 信息科学与工程学院
8. 卷积定理 (1) 时域卷积定理: f1 (t ) * f 2 (t ) F1 ( jω) F2 ( jω)
常用傅里叶变换

时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释1 线性2 时域平移3 频域平移,变换2的频域对应4 如果值较大,则会收缩到原点附近,而会扩散并变得扁平.当|?a?|?趋向无穷时,成为狄拉克δ函数。
5 傅里叶变换的二元性性质。
通过交换时域变量和频域变量得到.6 傅里叶变换的微分性质7 变换6的频域对应8 表示和的卷积—这就是卷积定理9 变换8的频域对应。
[编辑]平方可积函数傅里叶变换傅里叶变换10 矩形脉冲和归一化的sinc函数11 变换10的频域对应。
矩形函数是理想的低通滤波器,sinc函数是这类滤波器对反因果冲击的响应。
12 tri?是三角形函数13 变换12的频域对应14 高斯函数exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。
15 光学领域应用较多161718 a>019 变换本身就是一个公式20 J0(t)?是0阶第一类贝塞尔函数。
21 上一个变换的推广形式;?T n(t)?是第一类切比雪夫多项式。
22 U n?(t)是第二类切比雪夫多项式。
[编辑]分布时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释23 δ(ω)代表狄拉克δ函数分布.这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换24 变换23的频域对应25 由变换3和24得到.26 由变换1和25得到,应用了欧拉公式:?cos(at) = (e iat?+?e???iat) / 2.27 由变换1和25得到28 这里,?n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。
这个变换是根据变换7和24得到的。
将此变换与1结合使用,我们可以变换所有多项式。
29 此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的.30 变换29的推广.31 变换29的频域对应.32 此处u(t)是单位阶跃函数;此变换根据变换1和31得到.33 u(t)是单位阶跃函数,且a?> 0.34 狄拉克梳状函数——有助于解释或理解从连续到离散时间的转变.[编辑]二元函数三元函数。
常用信号的傅里叶变换

常用信号的傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学工具。
它是以法国数学家傅里叶的名字命名的,用于分析信号的频谱成分。
在信号处理和通信领域,傅里叶变换被广泛应用于信号的频谱分析、滤波、解调和压缩等方面。
1. 正弦信号的傅里叶变换正弦信号是最简单的周期信号之一,它可以表示为一个频率和幅度确定的正弦函数。
对于一个正弦信号,它的傅里叶变换是一个由两个峰值组成的频谱图。
其中一个峰值位于正弦信号的频率上,另一个峰值位于负频率上,其幅度与正弦信号的幅度相等。
2. 方波信号的傅里叶变换方波信号是一种以方波函数为基础的周期信号。
方波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个由多个峰值组成的频谱图。
频谱图上的峰值对应于方波信号中各个频率的成分。
3. 矩形脉冲信号的傅里叶变换矩形脉冲信号是一种在有限时间内突然变化的信号。
它在时域上表现为一个宽度有限的矩形脉冲,其傅里叶变换是一个以脉冲宽度为主要参数的频谱图。
频谱图上的峰值表示了矩形脉冲信号中各个频率的成分。
4. 高斯信号的傅里叶变换高斯信号是一种以高斯函数为基础的连续非周期信号。
高斯信号在时域上呈钟形分布,其傅里叶变换是一个以高斯函数为形状的频谱图。
频谱图上的峰值表示了高斯信号中各个频率的成分。
5. 三角波信号的傅里叶变换三角波信号是一种以三角函数为基础的周期信号。
三角波信号可以表示为一系列正弦信号的叠加,其傅里叶变换是一个以基频为主要参数的频谱图。
频谱图上的峰值对应于三角波信号中各个频率的成分。
6. 音频信号的傅里叶变换音频信号是一种连续时间的信号,它可以通过傅里叶变换转换为频域信号进行分析。
音频信号的傅里叶变换可以得到音频信号的频谱图,从而可以对音频信号进行频谱分析、滤波和合成等操作。
7. 语音信号的傅里叶变换语音信号是一种声音信号,它可以通过傅里叶变换转换为频域信号进行分析。
语音信号的傅里叶变换可以得到语音信号的频谱图,从而可以对语音信号进行声音分析、语音识别和语音合成等操作。
常用傅里叶变换公式大全

常用傅里叶变换公式大全傅里叶变换是一种重要的数学工具,它可以将时域信号转换为频域信号,从而更好地理解信号的特性。
下面就是常用的傅里叶变换公式大全:1、傅里叶变换:$$F(u)=\int_{-\infty}^{\infty}f(x)e^{-2\pi iux}dx$$2、傅里叶反变换:$$f(x)=\int_{-\infty}^{\infty}F(u)e^{2\pi iux}du$$3、离散傅里叶变换:$$F(u)=\sum_{n=-\infty}^{\infty}f(n)e^{-2\pi iun}$$4、离散傅里叶反变换:$$f(n)=\frac{1}{N}\sum_{u=-\infty}^{\infty}F(u)e^{2\pi iun}$$5、快速傅里叶变换:$$F(u)=\sum_{n=0}^{N-1}f(n)W_N^{nu}$$6、快速傅里叶反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)W_N^{-nu}$$7、离散余弦变换:$$F(u)=\sum_{n=0}^{N-1}f(n)\cos\frac{(2n+1)u\pi}{2N}$$8、离散余弦反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\cos\frac{(2n+1)u\pi}{2N}$$9、离散正弦变换:$$F(u)=\sum_{n=0}^{N-1}f(n)\sin\frac{(2n+1)u\pi}{2N}$$10、离散正弦反变换:$$f(n)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)\sin\frac{(2n+1)u\pi}{2N}$$以上就是常用的傅里叶变换公式大全,它们可以帮助我们更好地理解信号的特性,并且可以用来解决许多实际问题。
因此,傅里叶变换在科学研究和工程应用中都有着重要的作用。
五种傅里叶变换

五种傅里叶变换傅里叶变换是一种将信号从时域转换到频域的数学工具,它在信号处理、图像处理、通信等领域都有广泛的应用。
傅里叶变换可以分为五种:离散傅里叶变换(DFT)、快速傅里叶变换(FFT)、连续时间傅里叶变换(CTFT)、离散时间傅里叶变换(DTFT)和希尔伯特-黄变换(HHT)。
一、离散傅里叶变换(DFT)离散傅里叶变换是指将一个有限长的离散序列,通过一定的算法转化成一个同样长度的复数序列。
它是一种计算量较大的方法,但在某些情况下精度更高。
DFT 的公式如下:$$F(k)=\sum_{n=0}^{N-1}f(n)e^{-i2\pi kn/N}$$其中 $f(n)$ 是原始信号,$F(k)$ 是频域表示。
二、快速傅里叶变换(FFT)快速傅里叶变换是一种计算 DFT 的高效算法,它可以减少计算量从而加快计算速度。
FFT 的实现方法有多种,其中最常用的是蝴蝶运算法。
FFT 的公式与 DFT 相同,但计算方法不同。
三、连续时间傅里叶变换(CTFT)连续时间傅里叶变换是指将一个连续的时间信号,通过一定的算法转化成一个连续的频域函数。
CTFT 的公式如下:$$F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt$$其中 $f(t)$ 是原始信号,$F(\omega)$ 是频域表示。
四、离散时间傅里叶变换(DTFT)离散时间傅里叶变换是指将一个无限长的离散序列,通过一定的算法转化成一个同样长度的周期性复数序列。
DTFT 的公式如下:$$F(e^{j\omega})=\sum_{n=-\infty}^{\infty}f(n)e^{-j\omegan}$$其中 $f(n)$ 是原始信号,$F(e^{j\omega})$ 是频域表示。
五、希尔伯特-黄变换(HHT)希尔伯特-黄变换是一种基于经验模态分解(EMD)和 Hilbert 变换的非线性时频分析方法。
它可以对非平稳信号进行时频分析,并提取出信号中的本征模态函数(IMF)。
信号与系统傅里叶变换对总结

| z | 1
| z | 1
[r cos 0 n]u[n]
n
| z | r
[r sin 0 n]u[ n]
n
| z | r
te at u(t ), Re{a} 0
t n 1 e at u (t ), Re{a} 0 (n 1)!
减幅余弦
e at cos(0t )u (t )
减幅正弦
e at sin(0t )u (t )
0 (a j ) 2 +0 2
1 a t2
2
a
e
a
j
)
[n]
u[n]
单位阶跃序列
单边指数序列
nu[n], | | 1
1 1 e j
复指数序列
e
j0 n
l
2 (
0
2 l )
2 l ) ( 0 2 l )
余弦序列
cos 0 n
sin 0 n
l
sin(0t )
1
2 ( )
jk0t
周期波
k
ce
k
2
k
c ( k )
k 0
周期矩形脉冲
t T1 / 2 A, 0, T1 / 2 t T1 / 2
2 A sin(k0T1 / T0 ) ( k0 ) k k
1
单位冲激 延迟冲激
(t )
(t t0 )
sgn(t )
e jt0
2 j
正负号函数
单位阶跃
u(t )
1 ( ) j
j ( ) 1
常用的傅立叶变换对

常用的傅立叶变换对
以下是常用的傅立叶变换对:
1. 时间域和频率域:傅立叶变换可以将信号从时间域转换到频率域,从而揭示出信号的频率特性。
2. 时域序列和频域序列:傅立叶变换可以将一个时域序列转换为一个频域序列,其中包含了该信号的频率分量的幅度和相位信息。
3. 连续时间信号和离散时间信号:傅立叶变换可以用来分析连续时间信号和离散时间信号的频谱。
4. 实数信号和复数信号:傅立叶变换可以用来分析实数信号和复数信号的频谱内容。
5. 周期信号和非周期信号:傅立叶变换可以用来分析周期信号和非周期信号在频域上的特性。
这些是常见的傅立叶变换对,它们在信号处理和频谱分析中都有广泛的应用。
三角函数傅里叶变换常用公式大全

一、三角函数基本公式1. 正弦函数(sin)的定义:在单位圆上,角θ的终边与x轴的交点横坐标为sinθ。
1)反正弦函数(arcsin):y = arcsin(x) ⇔ sin(y) = x,定义域为[-1, 1],值域为[-π/2, π/2]。
2)余弦函数(cos)的定义:在单位圆上,角θ的终边与x轴的交点纵坐标为cosθ。
1)反余弦函数(arccos):y = arccos(x) ⇔ cos(y) = x,定义域为[-1, 1],值域为[0, π]。
3)正切函数(tan)的定义:在单位圆上,角θ的终边与x轴的交点横坐标与纵坐标的比值为tanθ。
1)反正切函数(arctan):y = arctan(x) ⇔ tan(y) = x,定义域为(-∞, +∞),值域为(-π/2, π/2)。
二、傅里叶级数与傅里叶变换1. 傅里叶级数公式:任意周期为2π的函数f(x)可展开为正弦和余弦函数的和。
f(x) = a0 + Σ(an*cos(nx) + bn*sin(nx)),式中,a0为直流分量,an 和bn为交流分量。
1)a0 = (1/2π) * ∫[0, 2π] f(x) dx,an = (1/π) * ∫[0, 2π] f(x) *cos(nx) dx,bn = (1/π) * ∫[0, 2π] f(x) * sin(nx) dx。
2. 傅里叶变换公式:非周期信号f(t)经过连续傅里叶变换得到频谱F(ω)。
F(ω) = ∫[-∞, +∞] f(t) * e^(-iωt) dt。
1)逆傅里叶变换:F(ω)经过逆变换得到原信号f(t)。
f(t) = (1/2π) * ∫[-∞, +∞] F(ω) * e^(iωt) dω。
三、常用傅里叶变换公式1. 矩形脉冲信号:f(t) = rect(t/T)。
1)F(ω) = T * sin(ωT) / (ωT),其中,sinc(u) = sin(u) / u。
2. 三角形脉冲信号:f(t) = tri(t/T)。
常用信号的傅里叶变换

不满足绝对 可积条件
1
sgn(t )
e
t
et , f (t ) t e ,
sgn( t ) lim f (t )
0
t0 t 0
0
e
t
O 1
t
f (t ) F (j )
1
j
1
j
j 2
2
2
j 2 2 sgn(t ) lim F (j ) lim 0 0 2 2 j
0
1
(t ) ( ) j
1
▲
■
第 7页
三、 直流信号的傅里叶变换F [1]
构造 f (t)=e-t ,> 0←→
F ( j ) 2
2
2
f (t ) 1 lim f (t )
0
所以 又
0
F ( j ) lim F ( j ) lim
F (j )
2. 常用信号 F 变换对: δ(t)
dt
1
2πδ(ω)
( )
1 j
f (t ) e
j t
1 ε(t)
1 j
t 域
1
j t
ω 域
e -t ε(t)
Gτ(t) sgn (t)
Sa 2 2
j
dt
F j
f t
1
et f (t ) e t
F (j ) e
0
O
t
t j t
e
傅里叶变换的性质及常用函数的傅里叶变换

连续傅里叶变换对
相对偶的连续傅里叶变换对
重要
连续时间函数
傅里叶变换
连续时间函数
傅里叶变换
重要
√
1
1
√
√
√
√
√
√
√
√
√
√
√
√
√
√
连续傅里叶变换性质及其对偶关系
连续傅里叶变换对
相对偶的连续傅里叶变换对
重要
名称
连续时间函数
傅里叶变换
名称
连续时间函数
傅里叶变换
重要
√
线性
√
尺度比例变换
对偶性
√
√
时移
频移
√
时域微分性质
频域微分性质
√
时域积分性质
频域积分性质
√
时域卷积性质
频域卷积性质
√
√
对
√
时域抽样
频域抽样
√
帕什瓦尔公式
取反----------取反
共轭----共轭取反
共轭取反---
常见函数的傅里叶变换

常见函数的傅里叶变换傅里叶变换是一种将一个函数映射到频域的数学工具。
通过它,我们可以将一个信号或者一个函数进行频域分析,对其进行处理、滤波、特征提取等。
在信号处理、图像处理、通信等领域中,傅里叶变换非常重要。
本文将介绍几种常见的函数的傅里叶变换及其应用。
一、常数函数常数函数f(x)=c,其中c为常数,其傅里叶变换为:F(k)=c\int_{-\infty}^\infty e^{-2\piikx}dx=c\delta(k)其中\delta(k)是狄拉克δ 函数,表示在k=0时存在一个单位脉冲。
显然,常数函数的傅里叶变换是一个单位脉冲。
在实际应用中,常数函数的傅里叶变换用于求解不同函数的卷积。
二、正弦函数正弦函数f(x)=sin(2πwx),其傅里叶变换为:F(k)=\int_{-\infty}^\infty sin(2\pi wx)e^{-2\pi ikx}dx=-\frac{iw}{2} (\delta(k-w)+\delta(k+w))正弦函数的傅里叶变换具有许多实用性质,例如:1. 它反映了信号在频域中的分布,即将正弦函数分解成不同频率的正弦函数的和。
2. 它可以用来提取频率信息。
3. 它还可以用来滤波。
三、余弦函数余弦函数f(x)=cos(2πwx),其傅里叶变换为:F(k)=\int_{-\infty}^\infty cos(2\pi wx)e^{-2\pi ikx}dx=\frac{w}{2} (\delta(k-w)+\delta(k+w))与正弦函数相似,余弦函数也可以用来分解信号,并且可以用来提取频率信息和滤波。
四、矩形脉冲函数矩形脉冲函数f(x)=rect(x)(即在[-0.5, 0.5]内为1,在其他地方为0),其傅里叶变换为:F(k)=\int_{-\infty}^\infty rect(x)e^{-2\piikx}dx=\int_{-0.5}^{0.5}e^{-2\piikx}dx=\frac{sin(\pi kw)}{\pi kw}矩形脉冲函数的傅里叶变换也称为sinc函数。
常见傅里叶变换对照表

常见傅里叶变换对照表一、傅里叶变换简介1.1 什么是傅里叶变换傅里叶变换是一种将函数从时域(时间域)转换到频域(频率域)的数学技术。
它可以将一个信号表示成若干不同频率的正弦波的叠加,从而揭示信号的频谱特征。
傅里叶变换在信号处理、图像处理、通信等领域广泛应用。
1.2 傅里叶级数与傅里叶变换的区别傅里叶级数只适用于周期信号,它将周期信号分解为一系列正弦和余弦函数的叠加。
而傅里叶变换则适用于非周期信号,它将非周期信号分解为连续的频谱成分。
1.3 傅里叶变换的基本公式傅里叶变换的基本公式如下:∞(t)⋅e−jωt dtF(ω)=∫f−∞其中,F(ω)表示信号f(t)在频率ω处的复幅,j为虚数单位。
二、时域与频域的对应关系2.1 时域和频域的意义时域表示信号随时间变化的情况,主要包括信号的幅度、相位等信息;频域则表示信号在不同频率上的成分及其对应的幅度、相位等信息。
2.2 原始信号与频域成分的对应关系原始信号在频域中可表示为若干个频率分量的叠加,傅里叶变换将原始信号转换为频域成分,每个频域成分对应一个复数值,表示该频率上的幅度和相位。
2.3 时域与频域之间的转换时域信号可以通过傅里叶变换转换为频域信号,频域信号可以通过傅里叶逆变换还原回时域信号,二者之间存在一一对应的关系。
三、常见傅里叶变换对照表3.1 常见信号及其频域表示下表列举了一些常见信号的时域表示和频域表示。
信号名称时域表示频域表示单频正弦信号Asin(ω0t+ϕ)Aδ(ω−ω0)+Aδ(ω+ω0)周期方波信号B0,B1,...,B n B0δ(ω)+B1δ(ω−ω0)+...+B nδ(ω−nω0)高斯脉冲信号f(t)=1√2πσ−t22σ2F(w)=e−σ2w22矩形脉冲信号f(t)={1,当−T2<t<T20,其他情况F(w)=T⋅sinc(T2w)3.2 常见运算及其在频域中的对应关系下表列举了一些常见运算及其在频域中的对应关系。
傅里叶变换 - 维基百科,自由的百科全书

代表狄拉克δ函数分布.这 个变换展示了狄拉克δ函数的重 要性:该函数是常函数的傅立叶 变换
变换23的频域对应
由变换3和24得到.
由变换1和25得到,应用了欧拉 公式:
由变换1和25得到
这里, 是一个自然数. 是狄拉克δ函数分布的
阶微分。这个变换是根据变换7 和24得到的。将此变换与1结合 使用,我们可以变换所有多项 式。
7/8
三元函数
时域信号
角频率表示 的
傅里叶变换
参见
正交变换 傅里叶级数 连续傅里叶变换 离散时间傅里叶变换 离散傅里叶变换 傅里叶分析 拉普拉斯变换 小波变换
参考资料
弧频率表示的 傅里叶变换
注释
此球有单位半径;fr是频率矢量的量值 {fx,fy,fz}.
1. ^ 林家翘、西格尔著《自然科学中确定性问题的应用数学》,科学出版社,北京。原版书名为C. C. Lin & L. A. Segel, Mathematics Applied to Deterministic Problems in the Natural Sciences, Macmillan Inc., New York, 1974
时频分析变换
小波变换,chirplet转换和分数傅里叶变换试图得到时间信号的频率信息。同时解析频率和时间的能力在数学上受不确 定性原理的限制。
傅里叶变换家族
下表列出了傅里叶变换家族的成员。容易发现,函数在时(频)域的离散对应于其像函数在频(时)域的周期性.反之连 续则意味着在对应域的信号的非周期性.
来自“/w/index.php?title=傅里叶变换&oldid=24462958”
其中an和bn是实频率分量的振幅。
傅里叶分析最初是研究周期性现象,即傅里叶级数的,后来通过傅里叶变换将其推广到了非周期性现象。理解这种推广 过程的一种方式是将非周期性现象视为周期性现象的一个特例,即其周期为无限长。
傅里叶变换常用公式推导

傅里叶变换常用公式推导傅里叶变换是一种将信号从时域(时序)转换到频域(频率)的数学技术。
它将任意周期函数或有限时间信号分解成一组不同频率的正弦和余弦函数的和。
傅里叶变换的常用公式包括(但不限于)傅里叶级数、傅里叶变换、傅里叶逆变换等。
傅里叶级数是将周期函数分解成一组正弦和余弦函数的和。
设周期为T的连续信号x(t),其傅里叶级数公式为:x(t) = Σ[aₙcos(nω₀t) + bₙsin(nω₀t)]= a₀/2 + Σ[aₙcos(nω₀t) + bₙsin(nω₀t)]其中,a₀、aₙ、bₙ为系数,通过以下推导可得出它们的表达式:1.对于周期为T的函数x(t),其傅里叶级数展开为:x(t) = A₀ + Σ[Aₙcos(nω₀t + φₙ)]其中,A₀、Aₙ、φₙ是系数。
2.将x(t)在一个周期内积分得到:∫[0,T]x(t)dt = A₀T + Σ[Aₙ/Tsin(φₙ)]3.由于x(t)在一个周期内的平方和等于其乘以自身的积分值,即:∫[0,T],x(t),²dt = ,A₀,²T + Σ[(Aₙ/T)²]4. 根据Dirichlet条件,对于x(t)在一个周期内可积,即:∫[0,T],x(t),²dt < ∞5.根据以上两个公式,可得:(A₀T)²+Σ[(Aₙ/T)²]<∞由于正弦函数和余弦函数的平方和有界,所以以上公式成立。
6.将傅里叶级数展开的表达式带入公式(5),可得:(A₀T)²+Σ[(Aₙ/T)²]<∞7.假设T=2π/ω₀,则ω₀T=2π,进一步有:(A₀(2π/ω₀))²+Σ[(Aₙ/(2π/ω₀))²]<∞8.将公式(7)整理,可得:(1/2π)Σ[A₀²+(2π/ω₀)²(Aₙ²+Bₙ²)]<∞根据以上推导,我们可以求解出傅里叶级数中的系数a₀、aₙ、bₙ。
常用傅里叶变换对

取反----------取反共轭-共轭取反共轭取反----共轭
常用傅里叶变换对
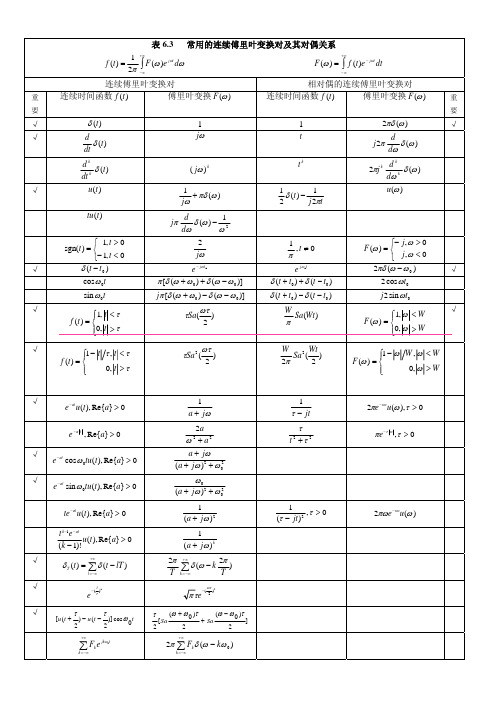
频域微 分性质 频域积 分性质 频域卷 积性质 奇偶虚 实性质
− jtf (t)
f (t) + πf (0)δ (t) − jt
f (t) p(t)
f (t) 是实函数
fo (t) = Od{f (t)} fe (t) = Ev{f (t)}
d F (ω )
√
dω
∫ω F (σ )dσ −∞
1 2π
tu (t )
1 s2 , Re{s} > 0
(n +1)u[n]
1 (1− z−1 )2 , z > 1
√
t k−1 u(t)
(k −1)! −u (−t )
1 , Re{s} > 0 sk 1 s , Re{s} < 0
(n + k − 1)! u[n]
n!(k − 1)!
−u[−n −1]
1 (1− z−1 )k , z > 1 1 (1− z−1 ) , z < 1
1
+∞
F (ω )e jωt dω
2π −∞
+∞
∫ F (ω ) = f (t)e − jωt dt −∞
∫ f (0) = 1 +∞ F (ω)dω
2π −∞
+∞
∫ F (0) = −∞
f (t)dt
离散傅里叶级数对
相对偶的离散傅里叶级数对
重
~
要
周期 N 的序列 f [n]
~
傅里叶级数系数 Fk
~
(n + k −1)! anu[n] n!(k −1)!
1 (1 − az−1 )k , z > a
−e− at u (−t )
